
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Cardiovasc. Med. , 05 July 2024
Sec. Precision Cardiology
Volume 11 - 2024 | https://doi.org/10.3389/fcvm.2024.1398290
This article is part of the Research Topic Insights in Coronary Artery Disease: 2023 View all 9 articles
Coronary artery disease is caused by the buildup of atherosclerotic plaque in the coronary arteries, affecting the blood supply to the heart, one of the leading causes of death around the world. X-ray coronary angiography is the most common procedure for diagnosing coronary artery disease, which uses contrast material and x-rays to observe vascular lesions. With this type of procedure, blood flow in coronary arteries is viewed in real-time, making it possible to detect stenoses precisely and control percutaneous coronary interventions and stent insertions. Angiograms of coronary arteries are used to plan the necessary revascularisation procedures based on the calculation of occlusions and the affected segments. However, their interpretation in cardiac catheterisation laboratories presently relies on sequentially evaluating multiple 2D image projections, which limits measuring lesion severity, identifying the true shape of vessels, and analysing quantitative data. In silico modelling, which involves computational simulations of patient-specific data, can revolutionise interventional cardiology by providing valuable insights and optimising treatment methods. This paper explores the challenges and future directions associated with applying patient-specific in silico models in catheterisation laboratories. We discuss the implications of the lack of patient-specific in silico models and how their absence hinders the ability to accurately predict and assess the behaviour of individual patients during interventional procedures. Then, we introduce the different components of a typical patient-specific in silico model and explore the potential future directions to bridge this gap and promote the development and utilisation of patient-specific in silico models in the catheterisation laboratories.
Coronary artery disease (CAD) is a pathological process characterised by atherosclerotic plaque accumulation in the epicardial coronary arteries. There are several clinical manifestations of this disease, including chronic stable angina and acute coronary syndromes. According to the World Health Organisation’s global health estimates and global burden of disease data (estimates for 2019), CAD is the most commonly diagnosed heart disease worldwide. It is estimated around 200 million people are living with CAD, and it kills an estimated 9 million people each year (1).
Investigation of CAD includes functional evaluations, such as stress echocardiography, perfusion stress magnetic resonance imaging, and nuclear scintigraphy in myocardial perfusion imaging. In addition, computed tomography coronary angiography and invasive x-ray angiography can be used to evaluate the coronary arteries directly. Invasive x-ray coronary angiography is particularly valuable in patients with more severe disease, informing treatment decisions including the possibility of revascularisation through percutaneous coronary intervention (PCI) or bypass surgery. Coronary angiography provides high-resolution images of the coronary arteries that are widely used for stent implantation. It is often augmented with additional techniques, such as pressure wire evaluation of fractional flow reserve (FFR), intravascular ultrasound (IVUS), and intravascular optical coherence tomography (IOCT).
Although x-ray angiography is one of the most invaluable tools, it does have some drawbacks. First of all, it is an invasive procedure with potential vascular injury, haemorrhage, and embolisation. Furthermore, this procedure involves the use of x-ray contrast media that can cause or exacerbate renal dysfunction and cause adverse allergic reactions. For example, the US National Cardiovascular Data Registry reported that 7.1% of patients undergoing elective and urgent coronary intervention experienced contrast-induced acute kidney injury (2). In addition, there are issues of ionising radiation exposure for both the patient and the operator (3). Finally, the interpretation of the angiographic images is partially subjective and is prone to misinterpretation or variable interpretation (4). It is estimated that 70% of treatment decisions still depend on the visual assessment of angiographic stenosis within clinical settings, which has limited accuracy (about 60%–65%) in predicting FFR < 0.80, as reported by Hae et al. (5).
To overcome such vagaries, additional physiological studies including FFR or intravascular imaging are often utilised. For example, Jones et al. (6)’s large observational study confirms that IVUS and IOCT-guided PCI reduces in-hospital major adverse cardiac event rates and improves long-term survival when compared with standard x-ray angiography-guided PCI. However, they are expensive and time-consuming (7).
Patient-specific in silico models have shown their capability to enhance qualitative assessment by introducing quantitative elements into the diagnostic, interventional, and prognostic processes in different cardiovascular diseases (8–10). With in silico techniques, coronary arteriography could be more accurately assessed in real-time, with fewer views, less radiation, less contrast, and easier administration, all of which would benefit clinical practice. Using artificial intelligence (AI)-assisted in silico models, cardiologists only need two series of x-ray angiography sequence to generate the 3D structure of a coronary arterial tree, as shown by (11), thus reducing the time of x-ray exposure and dye injection while providing an accurate quantitative assessment. Additionally, it offers the computation of haemodynamic metrics such as FFR non-invasively, through blood flow simulation over the 3D structure, using mechanistic (12, 13) or data-driven (14) approaches.
In this paper, we review the key components needed to create a patient-specific in silico coronary model, as shown in Figure 1. After acquiring comprehensive and high-quality x-ray angiography sequences of a patient, the coronary arteries can be segmented using automated approaches discussed in Section 2. Detailed anatomical 3D digital twins of the patient’s coronary tree can then be generated using the techniques discussed in Section 3. In the next steps, the digital twins of coronary arteries can be used for blood flow simulations, detailed in Section 4, which can be applied for computions of quantitative haemodynamic metrics to detect coronary stenoses and assess their severity (Section 5). Finally, Section 6 comprehensively discusses how patient-specific in silico models can be utilised to optimise the patientcare pathway in the catheterisation laboratory (cath. lab.). The paper concludes in Section 7.
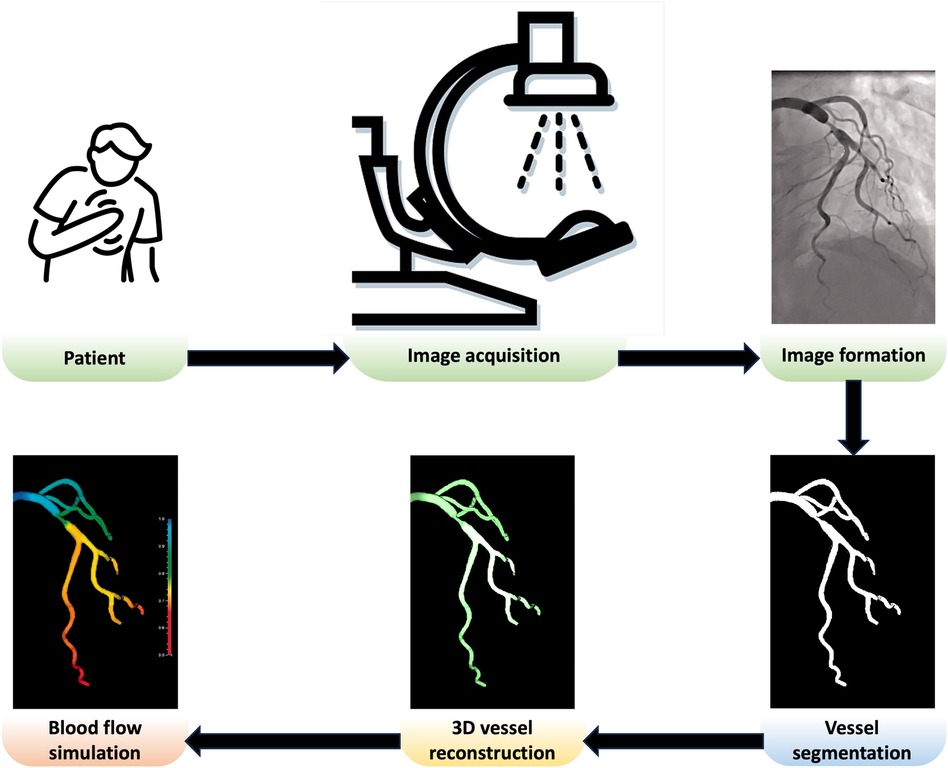
Figure 1 Overview of a patient-specific in silico model in the cath. lab. Adapted with permission from (15), © The Foundation Acta Radiologica 2021, https://doi.org/10.1177/0284185120983977.
3D reconstruction of the coronary arteries, discussed in detail in Section 3, often relies on the back-projection model-based methods, which require accurate skeletal representation and radius of coronary arteries as the inputs. The skeleton and radius of the vessels are typically obtained by segmenting the blood vessels. This section provides a comprehensive overview of different coronary vessel segmentation methods used for this purpose.
• Image thresholding is a simple image segmentation method in which grayscale images are turned into binary images by categorising each pixel according to its intensity level concerning a threshold value. To improve the result of image thresholding in x-ray angiography, the coronary vessels are usually enhanced by utilising different imaging filters (16–19).
• Vessel tracking is another form of segmentation that involves extracting a path along a vessel from a designated starting point (20). Some techniques focus on isolating individual paths with defined start and endpoints, while others can identify the entire vessel tree and adeptly manage vessel branching (21–25).
• Edge detection identifies and extracts a set of points representing changes in brightness on an image, commonly referred to as an edge contour, arising from variations in grayscale between vessels and the background (26–29).
• In region growing method, seed pixels are used to create regions, and neighbouring pixels meeting specific criteria are added to those regions (30). To improve the results of region growing for vessel segmentation, different approaches have been proposed such as incorporating directional information (31–33), integrating with different methods such as random forest (34), and variable searching method of the pixels (35).
• Graph-cut uses a graph model to represent the image, where nodes represent pixels and edges represent the relationships between pixels in a graph. It divides the image into segments based on certain criteria, such as colour or intensity, to find the optimal cut in the graph (36). Hernandez-Vela et al. (37), Sun et al. (38), Mabrouk et al. (39) developed automated multi-scale vessel extraction algorithms using the graph-cut method.
• Fuzzy inference uses the human-like reasoning style and offers potent and adaptable universal approximations, allowing interpretable IF-THEN rules (40). Sun et al. (41) used fuzzy mathematical morphology operations to extract coronary arteries, while Shoujun et al. (42) proposed a tracking approach that relied on both probabilistic vessel tracking and fuzzy structure pattern inference.
• In deformable models, a segmentation objective function (or energy function) is optimised through the calculus of variation. Image data constructs an energy function; minimising it yields segmentation results. These models use the original image for initial and boundary value problems. The contour, initially set as the desired region’s boundary, evolves based on geometric image regions (43). Different variations of deformable models have been used for coronary vessels segmentation, such as parametric active contours (44, 45), geometric active contours (32, 46, 47), gradient vector flow active contour (48), region-based active contour (49), etc.
• Methods based on machine learning models leverage intricate algorithms and training on diverse datasets to enhance the ability to discern intricate coronary vessels structures from a complex background of x-ray angiography. The machine learning methods used for coronary vessels segmentation include marginal space learning paradigm and probabilistic boosting trees (50), random forest (51), robust principal component analysis (PCA) (52, 53), etc.
Neural networks, modelled after the human brain, consist of interconnected neurons organised into layers. During training, they adjust connection strengths between neurons to minimise prediction errors using a method called backpropagation. Once trained, neural networks make predictions by passing new data through the network based on learned patterns. Success depends on training data quality, network architecture, and parameter selection. Neural networks generally segment images by classifying pixels into specific categories, such as objects or boundaries. This process involves leveraging patterns and features within the image data to accurately delineate different regions. One of the oldest applications of neural networks for identifying coronary vessels in x-ray angiograms was done by Sun (54), pioneering the use of neural networks in medical imaging for precise vessel localisation and analysis.
• Convolutional neural networks (CNNs), a type of deep learning model, have been employed for tasks of coronary vessels segmentation in multiple studies (55–58). CNNs, as shown in Figure 2A, utilise layers to learn hierarchical features through convolutional operations, pooling, and fully connected layers, enabling automatic and adaptive spatial feature learning from the input images.
• Encoder-decoder, illustrated in Figure 2B, is another type of deep learning neural network used for coronary vessel segmentation (59, 60). Encoding involves passing an image through a series of convolutional and pooling layers, e.g., Figure 2A. In these layers, spatial dimensions are downsampled while capturing the important features, thus extracting hierarchical features while condensing the input image. In the decoder, the spatial dimensions are gradually reconstructed using upsampling operations based on the feature map from the encoder.
• U-Net architecture, as shown in Figure 2C, is an example of encoder-decoder architecture designed to segment images. It was introduced by Ronneberger et al. (61) and has since become a popular and effective neural network used for coronary vessels segmentation (62–65). It is named after its distinct U-shaped structure and differs from other encoder-decoder networks because it uses skip connections to connect the corresponding layers of encoding and decoding, thus preserving fine-grained details during segmentation.
• Adversarial learning is another type of neural network applied for coronary vessels segmentation (66). This network involves training a model against adversarial examples generated to deceive the model. The model learns to be more robust by experiencing and adapting to these adversarial inputs. A popular branch of adversarial learning is generative adversarial networks (GANs), which have been used for vessel segmentation in x-ray angiography (67, 68). A GAN consists of two structures, a generator and a discriminator, as presented in Figure 2D. The generator generates data instances, while a discriminator evaluates them. Both are trained simultaneously, with the generator aiming to produce realistic data and the discriminator aiming to distinguish between the real and the generated data.
• Attention mechanism enables models to make predictions while focusing on specific details of coronary vessels in images (69). This mechanism is usually incorporated into various deep neural networks such as encoder-decoder (70), U-net (71), and adversarial network (66).
• Ensemble deep learning is intended to enhance the model’s generalisation, robustness, and accuracy by leveraging the diversity of multiple models. To improve the overall performance of vessel segmentation, ensemble deep learning models combine vessel predictions from multiple individual neural network models such as combining style transfer with dense extreme inception network and convolution block attention (72), EfficientNet with U-Net (73), gradient-boosting decision trees with deep forest classifiers (74), ensemble encoder-decoder networks (75), U-Net with DenseNet-121 (76), and bi-directional ConvLSTM algorithm with U-Net and DenseNet models (77).
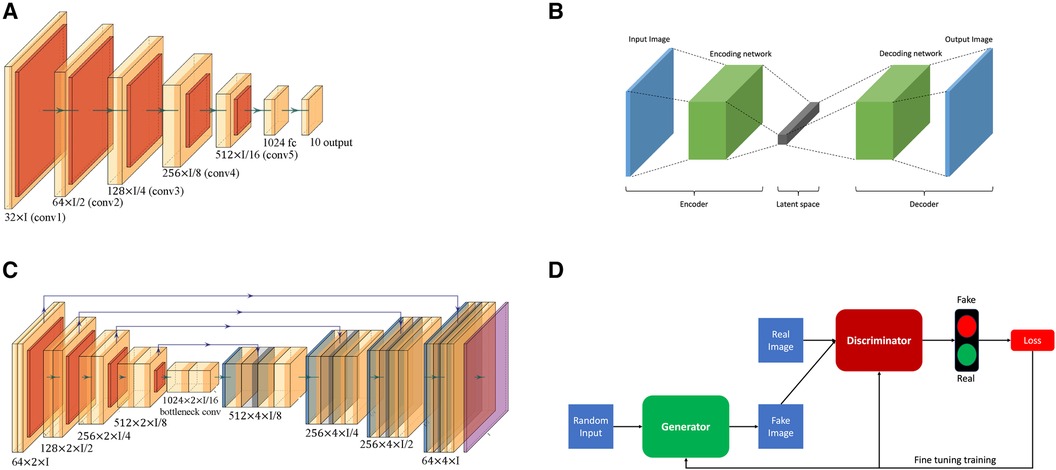
Figure 2 Overview of the basic neural network architectures used for coronary vessels segmentation: (A) Convolutional neural network (CNN); (B) Encoder-decoder; (C) U-Net; and (D) Generative adversarial network (GAN).
More recently, advanced deep learning architectures namely Nested U-Nets or UNet++ (78), graph neural network (79), etc. have been utilised for acheiving state-of-the-art performance for coronary vessels segmentation in x-ray angiography.
All the methods discussed in the previous subsection used a single frame to segment the coronary vessels. Some studies in the literature also utilised multiple invasive coronary angiography (ICA) frames to capture temporal information for vessels segmentation. These studies aimed at mitigating noise and motion, enhancing overall contrast, and were robust to variations in image quality, illumination, and other artifacts. Temporal methods have been applied to improve segmentation quality over a variety of techniques, including vessel tracking (80), region growing (81), graph cut (82, 83), machine learning (84), as well as neural network approaches of CNN (85, 86), encoder-decoder (87), U-Net (88, 89), ensemble learning (90), etc.
A patient-specific model relies heavily on 3D geometry of the coronary vessels or the whole coronary arterial (CA) tree. This helps cardiologists and medical professionals better understand the anatomy, structure, and any potential abnormalities in the arteries during the intervention, and guide catheters and devices to the target area with greater accuracy. Additionally, the reconstructed 3D CA tree model allows for personalised treatment plans tailored to the specific anatomy of the patient through simulating different treatment scenarios, leading to optimised outcomes and reducing the risk of complications. However, creating an accurate 3D model of coronary arteries is a sensitive task and crucial to a successful intervention as well as a personalised treatment plan. For example, Solanki et al. (91) using arterial phantom models showed that minor reconstruction errors led to clinically significant inaccuracies in “virtual” fractional flow reserve (vFFR) computation.
Çimen et al. (92) reviewed the leading methods for reconstructing the 3D surface of coronary arteries using high-contrast x-ray angiography. In this section, we explain briefly the categories introduced by Çimen et al. (92) along with a brief review of the most recent 3D CA tree reconstruction approaches.
Though several different approaches have been proposed for coronary artery reconstruction in the literature, back-projection based methods remain the most common. Back-projection methods fall into the model-based reconstruction categories, which aim to create a 3D/4D binary model of coronary arteries, typically comprising a centerline and sometimes the vessel surface. In back-projection modelling, the CA tree is constructed by projecting two-dimensional (2D) information derived from ECG-gated projection images. There are two types of methods: methods that rely on 2D feature matching and methods that use back-projection of vesselness responses (92).
Methods based on 2D feature matching, depicted in Figure 3A, begin by segmenting artery centerlines and identifying key structures such as bifurcations within projection images. Using epipolar geometry, correspondences between centerlines are established between different views, and computer vision algorithms are used to reconstruct 3D points representing the CA tree. The accuracy of these methods relies heavily on segmentation accuracy during centerlines extraction. Recently, Çimen et al. (92) represented 3D coronary artery centerlines as a mixture of Student’s t-distributions and performed a maximum-likelihood estimation of model parameters using 2D x-ray image segmentation. Unberath et al. (93) enhanced reconstruction quality by effectively removing erroneously reconstructed points on the centerline. Vukicevic et al. (94) used a robust genetic algorithm optimiser to identify calibration parameters for x-ray angiography views. A partial-matching approach was applied to establish correspondences between frames in x-ray acquisitions, and the same matching method was applied to reconstruct vessel centerlines efficiently. Galassi et al. (95) reconstructed the 3D centerlines by intersecting surfaces from matching branches from 2D views. Then, the 3D luminal contours were created by interpolating computed 3D boundary points with non-uniform rational basis splines. In another work, Banerjee et al. (11) first reduced angiographic motion artifacts for rigid and non-rigid motion (96, 97), and then used an innovative point-cloud based approach to 3D vessel centerline reconstruction by iteratively minimising reconstruction error. These methods are beneficial to non-calibrated systems since they can easily incorporate the estimation of geometry parameters that relate to the projection images used for reconstruction. The vascular start/end and bifurcation points, which are extracted during segmentation, are often used for this purpose. Although some works tried to match these corresponding points (98–103), most of the 3D reconstruction methods need clinicians to manually find these corresponding points in the projected images.
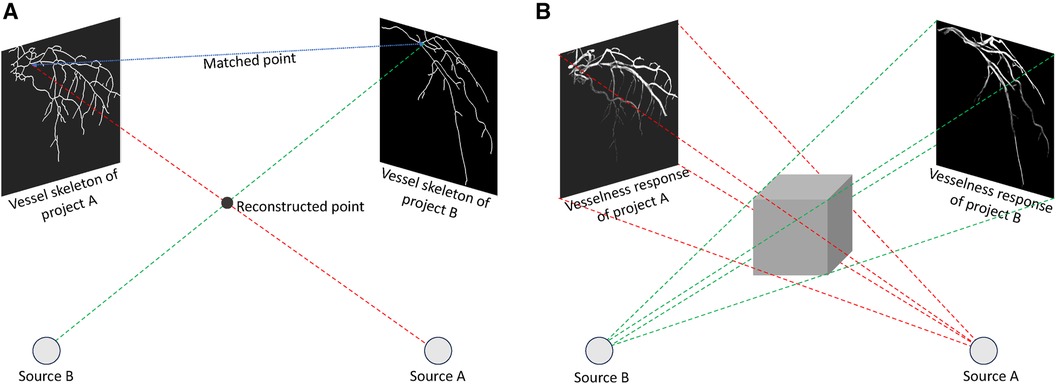
Figure 3 Back-projection methods to reconstruct 3D coronary arteries: (A) Techniques relying on 2D feature matching establish correspondences between centrelines in distinct 2D views and perform reconstruction through triangulation, (B) Approaches centered on the back-projection of vesselness response generate a 3D volumetric vesselness response from 2D vesselness responses for subsequent processing.
In contrast, in methods based on back-projection of vesselness responses, shown in Figure 3B, 2D projection images are used to calculate vesselness responses, such as binary segmentation (104), tubularity response (105), and distance map to centreline (106). These responses are then back-projected based on imaging geometry to generate 3D volumetric vesselness responses. Following this, coronary artery reconstruction is conducted using segmentation methods. One of the drawbacks of these methods is that they may require more rotational x-ray angiogrms in order to generate an accurate 3D reconstruction.
Another type of model-based reconstruction methods is forward-projection that employs 3D models that adapt to vessel structures in 2D x-ray projections. The forward-projection reconstruction often relies on 3D parametric active contour methods, where external and internal energy, computed from images, are used to adjust 3D active contours (107–109). In CA tree reconstruction, every artery branch has its active contour model, which presents a challenge in designing energy components. Cong et al. (107) compared common deformable model based methods, namely potential energy (110), gradient vector flow (111), and generalised gradient vector flow (112), on a series of experiments on phantom and clinical data.
Tomographic reconstruction creates coronary artery volumes directly from x-ray coronary angiography images. As opposed to binary model based reconstruction, it provides information on x-ray absorption coefficients, as well. Due to the minimal knowledge they require about the CA trees, these methods accommodate atypical anatomies (e.g., collaterals, tortuous branches). As a result, they provide more detailed vessel surface information without any preprocessing or manual inputs (113–115).
The drawbacks of these methods are they assume pre-acquisition calibration of the x-ray imaging system and typically require more x-ray images with wider angular coverage than modelling based reconstructions. For coronary artery branches to be visible, these methods require precise isocentering and consistent injection of contrast. Moreover, they ignore the propagation of contrast agents over time, assuming constant contrast distribution over time. Finally, these approaches typically require more computational resources than model based reconstructions. Also, it is often necessary to hold breath during coronary angiography to minimise respiratory motion to reconstruct tomographic images (92).
Model based methods can be extended to 4D coronary artery reconstructions. The basic 4D strategy involves independent 3D reconstructions for each cardiac phase, which requires vessels segmentation for each phase. To avoid this, temporal constraints which penalise differences between adjacent phases have been utilised, and temporal correspondences have been established through branch or tree-matching algorithms (116–118).
The final component for completing the patient-specific model in cath. lab. is to simulate hemodynamics in coronary arteries. The patient-specific model of blood flow in the coronary arteries using computed tomography has been well established due to fewer challenges in the creation of a 3D model of coronary arteries (12, 119). Some of the technological developments for blood flow simulation using computed tomography can be used directly over 3D vascular models from x-ray angiography, as these methods are often independent of imaging techniques. The following subsections describe the developments for coronary blood flow simulation.
The Navier-Stokes equations are a set of partial differential equations that represent the physics of a fluid dynamic. However, they are complex partial differential equations, which are difficult to solve analytically and computationally expensive to simulate accurately. There are two distinct approaches of mechanistic modelling and data-driven modelling (Figure 4) to simulate blood flow based on the Navier-Stokes equations, each with its own set of characteristics and advantages.
This approach involves formulating mathematical equations that represent these processes. This approach is commonly used in fields where a deep understanding of the system is available, and where the goal is to gain insights into the underlying processes, optimise system performance, or test hypotheses. The mechanistic models to solve Navier–Stokes equations can be divided into four groups (12, 13).
(a) 3D models use numerical methods such as finite elements to solve Navier–Stokes equations. Using this approach, circulation geometry can be accurately represented, 3D pulsatile flow (including turbulence) can be captured, and complex blood and vessel material models can be incorporated (120).
(b) 1D models are created by averaging the Navier-Stokes equations over a vessel’s cross-section. These models ignore non-axial velocity components, assume an axial velocity profile across locations of vessels, and maintain constant pressure across the vessel cross-section. However, these models are invalid near side branches, bifurcations, or diseased segments, especially for serial lesions or lesions at branches and bifurcations (120–123).
(c) The 0D model or lumped parameter circulation model, developed by Sagawa et al. (124), consolidates spatially varying properties into discrete components. Considering the flow steady, axisymmetric, unidirectional, and vessel segments as circular cylinders, this model simplifies fluid resistance in vessels to a single resistive element. It often results in a high level of inaccuracy in blood flow in diseased coronary arteries, where no steady or unidirectional flow occurs or no axisymmetry or circular shape to vessel segments exist (122, 124–126).
(d) The hybrid models aim to reduce computational time while providing more accurate simulation results. It includes a combination of the different mechanistic approaches such as 0D and 1D models (123, 125) and 1D and 3D models (13, 127–129).
Data-driven approaches extract patterns, relationships, or trends from observed data without explicitly considering underlying physical or mechanistic principles. The technique is often used for modelling complex, unknown, time-consuming, or difficult-to-model physical processes. There is, however, a lack of sufficient training data for data-driven methods (130). To address the lack of experimental data, two solutions exist: enhancing deep learning through physics-based losses, known as physics-informed neural networks (PINN) (131–134), or conducting high-fidelity in silico simulations to implicitly make the model sensitive to the underlying physics (135–139).
In the application of coronary blood flow using a large high-fidelity dataset, Itu et al. (140) introduced a machine learning model to predict fractional flow reserve (FFR), trained on a large database of synthetically generated coronary anatomies with flow parameters like velocity computed using the mechanistic approaches. Carson et al. (141) compared the performance of three AI models – feed-forward neural network (FFNN), long short-term memory, and multivariate polynomial regression, to measure FFR. Based on a 1D physics-based model, algorithms were trained and compared on a single vessel, multi-vessel network, as well as a virtual patient database, demonstrating the outperformance of a FFNN over two other methods in all cases. Gao et al. (142) proposed TreeVes-Net, a recurrent neural network (RNN) that captures geometric details for blood-related representation using a tree-structured representation encoder. This tree-structured RNN creates long-distance spatial dependencies, enhancing coronary flow modelling. Xie et al. (143) suggested a physics-informed graph neural network for FFR assessment, incorporating morphology and boundary conditions as inputs to learn conditioned features. In another work, Zhang et al. (144) proposed a PINN including a morphology feature encoder and an attention network to simulate the pressure and velocity along the centerline of the vessels based on the morphology features of coronary arteries.
Mechanistic model developed by Morris et al. (145), termed virtual FFR (vFFR), was one of the first to accurately predict coronary artery disease based on patients’ FFR using only x-ray angiography images. The initial vFFR model necessitated over 24 hours of computation, employing a fully transient, 3D-0D coupled model. Faster methods were introduced in 2017 (146) and 2023 (147), yielding results in just 3 min and less than 30 s, respectively, while maintaining the accuracy of a full 3D model (148). Recently, more studies have been developed to provide angiography-derived FFR based on mechanistic modelling (149–156).
With Data-driven models, Zhao et al. (157), Xie et al. (143) proposed deep neural networks based on CNN and graph neural network to compute the FFR and coronary flow reserve (CFR), respectively.
Functional metrics for coronary lesion severity assessment can be established through the development of patient-specific in silico models. Incorporating computational simulations with clinical data allows to gain a more detailed understanding of the complex dynamics inside coronary arteries, enabling better assessment metrics. According to several studies (158–161), quantitative measurements of arterial stenosis severity reduce unnecessary surgeries and cardiac events in patients with coronary artery disease. This section discusses the most important metrics used for this purpose.
(i) Fractional flow reserve (FFR) traditionally has been used for assessing the hemodynamics of coronary arteries. As part of the cardiac catheterisation procedure, a special wire is threaded through the coronary arteries, equipped with a pressure sensor. FFR is then calculated by comparing blood pressure before and after the stenosis as shown in Figure 5. Using this ratio, clinicians can determine how much blood flow to the heart has been impeded by the narrowing. FFR can provide valuable insights into whether coronary stenosis requires intervention, such as angioplasty or stent placement, or can be treated medically (162).
(ii) Coronary flow reserve (CFR) is another diagnostic metric in the decision-making process for coronary interventions. It is calculated by comparing coronary blood flow during maximal vasodilation and at rest. Three factors influence it: vascular resistance in the small and large coronary arteries, myocardial resistance, and factors that affect blood composition. CFR provides valuable information for evaluating coronary artery dilation ability and determining whether coronary interventions are necessary (163). By comparing the CFR of a stenotic coronary artery to a reference segment, such as a non-stenotic segment or one with minimal disease, relative CFR (rCFR) can be calculated. It is particularly useful when evaluating the functional implications of a coronary artery by comparing the blood flow through a particular stenosis to that of another less affected artery (158, 164, 165).
(iii) Index of microcirculatory resistance (IMR) was introduced in 2003, where a pressure wire uses its sensor as a thermistor and measures temperature. The tool functions as a thermometer and measures the mean transit time of room-temperature saline injected into a coronary artery using a thermodilution curve. As part of the test, pressure and temperature are measured in the heart’s small vessels, both at rest and at maximum blood flow. It allows the clinician to determine how well blood flows in the heart’s small vessels (166–168).
(iv) Instantaneous wave-free ratio (iFR) is a test using a special catheter to check the pressure in the heart’s blood vessels. It looks at pressure during both the wave-free period and the entire cardiac cycle. This helps doctors see how a blockage affects blood flow. One of the advantages of iFR is that it doesn’t need adenosine, a medicine used in other tests to stress the heart and check blood flow (169–171).
(v) Resting full-cycle ratio (RFR) is a new index that is used to evaluate the significance of coronary vessel lesions. In the cardiac cycle, it is defined as the lowest ratio of distal pressure to aortic pressure, measured at rest without the introduction of hyperemia (172–174).
Table 1 summarises the quantitative hemodynamic metrics for coronary artery assessment, along with the mathematical formula.
The development of patient-specific models in the cath. lab. can enhance patient care and improve outcomes in various ways. A patient-specific model can provide detailed insight into the anatomy and pathology of a patient’s vascular system. Clinicians can use this information to plan and customise cardiac interventions like angioplasty, stent placement, or other procedures. Furthermore, physicians can anticipate challenges by simulating procedures on patient-specific models before they are performed. In addition, patient-specific models help with the selection and size of medical devices, such as stents and catheters, based on accurate vessel dimensions and measurements. Additionally, patient-specific models enhance research by exploring new treatment strategies, testing innovative devices, and understanding underlying physiology.
As illustrated in Figure 1, a variety of medical image analysis methods should be employed to develop patient-specific models, including segmenting coronary arteries, reconstructing 3D geometry, and simulating blood flow to compute physiological biomarkers to detect and assess stenosis severity. There are potential sources of uncertainty in each stage of the modelling process, which can potentially propagate to the subsequent stages, resulting in an unreliable simulation result. For instance, Solanki et al. (91) demonstrated that the errors arising from the epipolar line projection method used to reconstruct 3D coronary anatomy from x-ray angiography images are small but result in clinically relevant errors in vFFR simulation, amounting to approximately 40% of the total error associated with vFFR. In the following paragraphs, we discuss the potential sources of uncertainty at each stage of the analysis.
Segmentation: According to Table 2, deep learning methods have significantly improved coronary vessels segmentation accuracy. However, there exist three potential challenges that limit the generalisation performance and result in discontinuity in segmented vessels. The first challenge is the imaging artifacts such as weak contrast between coronary arteries and the background, unknown vessel tree shape, and shadows of overlapping body structures. Secondly, due to the acquisition of a complex 3D structure in 2D projection planes, the coronary vessels overlap on x-ray angiography images, making segmentation and vessel delineation difficult, especially in regions where vessels are close together. Last but not least, the x-ray angiography captures contrast agents flowing through vessels during dynamic imaging. Hence, segmentation methods often face challenges with temporal changes and vessel appearance variations throughout the cardiac cycle. The recent advances in AI and deep learning have shown promising results in addressing some of these shortcomings, though they are often limited by the training datasets.
3D reconstruction: In recent years, 3D reconstruction methods for coronary arteries based on x-ray angiography have gone through significant advances, though they still face some challenges. First, the 3D surface reconstruction can be irregular due to non-orthogonal contours to the vessel centerline and difficulties defining its cross-sectional shape. The information available from 2D x-ray angiography projections is often limited, as they can only provide limited information at a finite number of projection planes and may not provide a complete representation of the vessel geometry. Secondly, movements in coronary arteries mainly due to cardiac and respiratory motions create difficulties in establishing correspondences between 2D segmented vessels and, as a result, affect the vessel centerlines reconstruction. Since correspondence is commonly based on epipolar constraints, significant vessels overlap and foreshortening may impact their performance.
The 3D vascular geometry can also be reconstructed using IVUS and IOCT, which are both intravascular imaging technologies to capture cross-sections of coronary arteries. In contrast to x-ray angiography, IVUS and IOCT images reveal external elastic membrane and plaque materials in addition to the coronary lumen. These approaches, however, are used to image a single branch of non-bifurcated vessels, and they considerably increase patient-care costs (175, 176). X-ray angiography, on the other hand, provides a very accurate image of the entire coronary arterial tree with minimal invasion, which makes it safer and more useful for automated 3D reconstruction of coronary vessels.
Blood flow simulation: The development of sophisticated computational fluid dynamics techniques has allowed researchers to model blood flow in complex coronary arteries with greater accuracy. There still exist some challenges and limitations. Limitations in segmenting small or terminal vessels limit coronary blood flow simulation in larger epicardial vessels. The boundary conditions at the outlet of the terminal vessel approximate downstream arterial circulation behaviour, and the lack of segmenting terminal vessels leads to a wrong boundary conditions assignment which invalidates assessment of the disease’s impact on myocardial blood flow (177, 178). Gamage et al. (179) showed that side branches downstream of stenosis result in a lower FFR, while those upstream have minimal impact. Moreover, to estimate FFR accurately, side branches with a diameter greater than one-third of the main vessel diameter should be taken into account. In addition, it is crucial to consider patient-specific boundary conditions and the associated uncertainties. If the associated parameters of the 3D inflow velocity profile cannot be specified, the domain flow field can be significantly impacted (180). Further research should try to calculate patient-specific boundary conditions by estimating the blood velocity in coronary arteries using cine x-ray angiographic sequence (181).
While coronary angiography remains a vital diagnostic tool in the assessment of coronary artery disease, the limitations inherent in the current interpretation methods call for a paradigm shift. Patient-specific in silico models, with their ability to simulate and analyse individualised data, present a promising avenue for advancing interventional cardiology. By addressing the challenges highlighted in this paper and accordingly embracing these models in catheterisation laboratories, we can unlock the full potential of in silico modelling. The integration of patient-specific in silico models into routine practice has the potential to revolutionise treatment optimisation, providing clinicians with valuable insights and enhancing the precision of interventions. Future research and development efforts should focus on bridging the existing gap and promoting the widespread adoption of these models in the cath. lab. settings.
ML: Conceptualization, Investigation, Visualization, Writing – original draft, Writing – review & editing. RPC: Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing. AB: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Supervision, Visualization, Writing – original draft, Writing – review & editing.
The authors declare financial support was received for the research, authorship, and/or publication of this article.
AB is a Royal Society University Research Fellow and is supported by the Royal Society Grant No. URF\R1\221314. The work of ML, RPC, and AB was supported by the British Heart Foundation (BHF) Project under Grant PG/20/21/35082. The work of RPC was supported in part by the BHF Centre of Research Excellence, Oxford and NIHR Oxford Biomedical Research Centre.
The authors acknowledge the use of the facilities and services of the Institute of Biomedical Engineering (IBME), Department of Engineering Science, University of Oxford.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Knuuti J, Wijns W, Saraste A, Capodanno D, Barbato E, Funck-Brentano C, et al. 2019 ESC guidelines for the diagnosis and management of chronic coronary syndromes: the task force for the diagnosis and management of chronic coronary syndromes of the European Society of Cardiology (ESC). Eur Heart J. (2020) 41:407–77. doi: 10.1093/eurheartj/ehz425
3. Sdogkos E, Xanthopoulos A, Giamouzis G, Skoularigis J, Triposkiadis F, Vogiatzis I. Data from: Diagnosis of coronary artery disease: potential complications of imaging techniques. (2022).
4. Giacoppo D, Laudani C, Occhipinti G, Spagnolo M, Greco A, Rochira C, et al. Coronary angiography, intravascular ultrasound, and optical coherence tomography for guiding of percutaneous coronary intervention: a systematic review and network meta-analysis. Circulation. (2024) 149:1065–86. doi: 10.1161/CIRCULATIONAHA.123.067583
5. Hae H, Kang S-J, Kim W-J, Choi S-Y, Lee J-G, Bae Y, et al. Machine learning assessment of myocardial ischemia using angiography: development and retrospective validation. PLoS Med. (2018) 15:e1002693. doi: 10.1371/journal.pmed.1002693
6. Jones DA, Rathod KS, Koganti S, Hamshere S, Astroulakis Z, Lim P, et al. Angiography alone versus angiography plus optical coherence tomography to guide percutaneous coronary intervention: outcomes from the pan-london pci cohort. JACC: Cardiovasc Interv. (2018) 11:1313–21. doi: 10.1016/j.jcin.2018.01.274
7. Gaede L, Möllmann H, Rudolph T, Rieber J, Boenner F, Tröbs M. Coronary angiography with pressure wire and fractional flow reserve. Dtsch Arztebl Int. (2019) 116:205–11. doi: 10.3238/arztebl.2019.0205
8. Corral-Acero J, Margara F, Marciniak M, Rodero C, Loncaric F, Feng Y, et al. The “digital twin” to enable the vision of precision cardiology. Eur Heart J. (2020) 41:4556–64. doi: 10.1093/eurheartj/ehaa159
9. Gray RA, Pathmanathan P. Patient-specific cardiovascular computational modeling: diversity of personalization and challenges. J Cardiovasc Transl Res. (2018) 11:80–8. doi: 10.1007/s12265-018-9792-2
10. Hokken TW, Ribeiro JM, De Jaegere PP, Van Mieghem NM. Precision medicine in interventional cardiology. Interv Cardiol Rev. (2020) 15. doi: 10.15420/icr.2019.23
11. Banerjee A, Galassi F, Zacur E, De Maria GL, Choudhury RP, Grau V. Point-cloud method for automated 3D coronary tree reconstruction from multiple non-simultaneous angiographic projections. IEEE Trans Med Imaging. (2019) 39:1278–90. doi: 10.1109/TMI.2019.2944092
12. Taylor CA, Petersen K, Xiao N, Sinclair M, Bai Y, Lynch SR, et al. Patient-specific modeling of blood flow in the coronary arteries. Comput Methods Appl Mech Eng. (2023) 14:116414. doi: 10.1016/j.cma.2023.116414
13. Yan Q, Xiao D, Jia Y, Ai D, Fan J, Song H, et al. A multi-dimensional CFD framework for fast patient-specific fractional flow reserve prediction. Comput Biol Med. (2024) 168:107718. doi: 10.1016/j.compbiomed.2023.107718
14. Schwarz EL, Pegolotti L, Pfaller MR, Marsden AL. Beyond CFD: emerging methodologies for predictive simulation in cardiovascular health and disease. Biophys Rev. (2023) 4:4. doi: 10.1063/5.0109400
15. Li Y, Qiu H, Hou Z, Zheng J, Li J, Yin Y, et al. Additional value of deep learning computed tomographic angiography-based fractional flow reserve in detecting coronary stenosis and predicting outcomes. Acta Radiol. (2022) 63:133–40. doi: 10.1177/0284185120983977
16. Cruz-Aceves I, Oloumi F, Rangayyan RM, Aviña-Cervantes JG, Hernandez-Aguirre A. Automatic segmentation of coronary arteries using Gabor filters and thresholding based on multiobjective optimization. Biomed Signal Process Control. (2016) 25:76–85. doi: 10.1016/j.bspc.2015.11.001
17. Felfelian B, Fazlali HR, Karimi N, Soroushmehr SMR, Samavi S, Nallamothu B, et al. Vessel segmentation in low contrast x-ray angiogram images. In: 2016 IEEE International Conference on Image Processing (ICIP). IEEE (2016). p. 375–9.
18. Kottke DP, Sun Y. Segmentation of coronary arteriograms by iterative ternary classification. IEEE Trans Biomed Eng. (1990) 37:778–85. doi: 10.1109/10.102793
19. Poli R, Valli G. An algorithm for real-time vessel enhancement and detection. Comput Methods Programs Biomed. (1997) 52:1–22. doi: 10.1016/S0169-2607(96)01773-7
20. Preim B, Botha CP. Visual Computing for Medicine: Theory, Algorithms, and Applications. Newnes (2013).
21. Ko C-C, Mao C-W, Sun Y-N, Chang S-H. A fully automated identification of coronary borders from the tree structure of coronary angiograms. Int J Biomed Comput. (1995) 39:193–208. doi: 10.1016/0020-7101(94)01067-B
22. Liu I, Sun Y. Recursive tracking of vascular networks in angiograms based on the detection-deletion scheme. IEEE Trans Med Imaging. (1993) 12:334–41. doi: 10.1109/42.232264
23. Sun Y. Automated identification of vessel contours in coronary arteriograms by an adaptive tracking algorithm. IEEE Trans Med Imaging. (1989) 8:78–88. doi: 10.1109/42.20365
24. Tsai Y-C, Lee H-J, Chen MY-C. Automatic segmentation of vessels from angiogram sequences using adaptive feature transformation. Comput Biol Med. (2015) 62:239–53. doi: 10.1016/j.compbiomed.2015.04.029
25. Yang G, Lv T, Shen Y, Li S, Yang J, Chen Y, et al. Vessel structure extraction using constrained minimal path propagation. Artif Intell Med. (2020) 105:101846. doi: 10.1016/j.artmed.2020.101846
26. Al-Fahoum A. Adaptive edge localisation approach for quantitative coronary analysis. Med Biol Eng Comput. (2003) 41:425–31. doi: 10.1007/BF02348085
27. Carballal A, Novoa FJ, Fernandez-Lozano C, García-Guimaraes M, Aldama-López G, Calviño-Santos R, et al. Automatic multiscale vascular image segmentation algorithm for coronary angiography. Biomed Signal Process Control. (2018) 46:1–9. doi: 10.1016/j.bspc.2018.06.007
28. Chen Z, Molloi S. Vascular tree object segmentation by deskeletonization of valley courses. Comput Med Imaging Graph. (2002) 26:419–28. doi: 10.1016/S0895-6111(02)00037-X
29. Li Z, Zhang Y, Gong H, Li W, Tang X. Automatic coronary artery segmentation based on multi-domains remapping and quantile regression in angiographies. Comput Med Imaging Graph. (2016) 54:55–66. doi: 10.1016/j.compmedimag.2016.08.006
30. Ikonomatakis N, Plataniotis K, Zervakis M, Venetsanopoulos A. Region growing and region merging image segmentation. In: Proceedings of 13th International Conference on Digital Signal Processing. IEEE (1997). Vol. 1. p. 299–302.
31. Kerkeni A, Benabdallah A, Manzanera A, Bedoui MH. A coronary artery segmentation method based on multiscale analysis and region growing. Comput Med Imaging Graph. (2016) 48:49–61. doi: 10.1016/j.compmedimag.2015.12.004
32. Wan T, Shang X, Yang W, Chen J, Li D, Qin Z. Automated coronary artery tree segmentation in x-ray angiography using improved Hessian based enhancement and statistical region merging. Comput Methods Programs Biomed. (2018) 157:179–90. doi: 10.1016/j.cmpb.2018.01.002
33. Wang S, Li B, Zhou S. A segmentation method of coronary angiograms based on multi-scale filtering and region-growing. In: 2012 International Conference on Biomedical Engineering and Biotechnology. IEEE (2012). p. 678–81.
34. Rodrigues E, Rodrigues L, Lima J, Casanova D, Favarim F, Dosciatti E, et al. X-ray cardiac angiographic vessel segmentation based on pixel classification using machine learning and region growing. Biomed Phys Eng Express. (2021) 7:055026. doi: 10.1088/2057-1976/ac13ba
35. Ma G, Yang J, Zhao H. A coronary artery segmentation method based on region growing with variable sector search area. Technol Health Care. (2020) 28:463–72. doi: 10.3233/THC-209047
36. Peng B, Zhang L, Zhang D. A survey of graph theoretical approaches to image segmentation. Pattern Recognit. (2013) 46:1020–38. doi: 10.1016/j.patcog.2012.09.015
37. Hernandez-Vela A, Gatta C, Escalera S, Igual L, Martin-Yuste V, Sabate M, et al. Accurate coronary centerline extraction, caliber estimation, and catheter detection in angiographies. IEEE Trans Inf Technol Biomed. (2012) 16:1332–40. doi: 10.1109/TITB.2012.2220781
38. Sun S-Y, Wang P, Sun S, Chen T. Model-guided extraction of coronary vessel structures in 2D x-ray angiograms. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014: 17th International Conference, Boston, MA, USA, September 14-18, 2014, Proceedings, Part II 17. Springer (2014). p. 594–602.
39. Mabrouk S, Oueslati C, Ghorbel F. Multiscale graph cuts based method for coronary artery segmentation in angiograms. IRBM. (2017) 38:167–75. doi: 10.1016/j.irbm.2017.04.004
40. Kar S, Das S, Ghosh PK. Applications of neuro fuzzy systems: a brief review and future outline. Appl Soft Comput. (2014) 15:243–59. doi: 10.1016/j.asoc.2013.10.014
41. Sun K, Chen Z, Jiang S, Wang Y. Morphological multiscale enhancement, fuzzy filter and watershed for vascular tree extraction in angiogram. J Med Syst. (2011) 35:811–24. doi: 10.1007/s10916-010-9466-3
42. Shoujun Z, Jian Y, Yongtian W, Wufan C. Automatic segmentation of coronary angiograms based on fuzzy inferring and probabilistic tracking. Biomed Eng Online. (2010) 9:1–21. doi: 10.1186/1475-925X-9-40
43. Kumar A, Jain SK. Deformable models for image segmentation: a critical review of achievements and future challenges. Comput Math Appl. (2022) 119:288–311. doi: 10.1016/j.camwa.2022.05.034
44. Klein AK, Lee F, Amini AA. Quantitative coronary angiography with deformable spline models. IEEE Trans Med Imaging. (1997) 16:468–82. doi: 10.1109/42.640737
45. Taghizadeh Dehkordi M, Doost Hoseini AM, Sadri S, Soltanianzadeh H. Local feature fitting active contour for segmenting vessels in angiograms. IET Computer Vision. (2014) 8:161–70. doi: 10.1049/iet-cvi.2013.0083
46. Lv T, Yang G, Zhang Y, Yang J, Chen Y, Shu H, et al. Vessel segmentation using centerline constrained level set method. Multimed Tools Appl. (2019) 78:17051–75. doi: 10.1007/s11042-018-7087-x
47. Sun K, Chen Z, Jiang S. Local morphology fitting active contour for automatic vascular segmentation. IEEE Trans Biomed Eng. (2011) 59:464–73. doi: 10.1109/TBME.2011.2174362
48. Nirmala Devi S, Kumaravel N. Comparison of active contour models for image segmentation in x-ray coronary angiogram images. J Med Eng Technol. (2008) 32:408–18. doi: 10.1080/09687630801889440
49. Liu Y, Wan W, Zhang X, Liu S, Liu Y, Liu H, et al. Segmentation and automatic identification of vasculature in coronary angiograms. Comput Math Methods Med. (2021) 2021:2747274. doi: 10.1155/2021/2747274
50. Socher R, Barbu A, Comaniciu D. A learning based hierarchical model for vessel segmentation. In: 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE (2008). p. 1055–8.
51. Gupta V, Kale A, Sundar H. A robust and accurate approach to automatic blood vessel detection and segmentation from angiography x-ray images using multistage random forests. In: Haynor DR, Ourselin S, editors. Medical Imaging 2012: Computer-Aided Diagnosis. SPIE (2012). Vol. 8315. p. 704–9
52. Jin M, Li R, Jiang J, Qin B. Extracting contrast-filled vessels in x-ray angiography by graduated RPCA with motion coherency constraint. Pattern Recognit. (2017) 63:653–66. doi: 10.1016/j.patcog.2016.09.042
53. Qin B, Jin M, Hao D, Lv Y, Liu Q, Zhu Y, et al. Accurate vessel extraction via tensor completion of background layer in x-ray coronary angiograms. Pattern Recognit. (2019) 87:38–54. doi: 10.1016/j.patcog.2018.09.015
54. Sun Y. Back-propagation network and its configuration for blood vessel detection in angiograms. IEEE Trans Neural Netw. (1995) 6:64–72. doi: 10.1109/72.363449
55. Nasr-Esfahani E, Karimi N, Jafari MH, Soroushmehr SMR, Samavi S, Nallamothu B, et al. Segmentation of vessels in angiograms using convolutional neural networks. Biomed Signal Process Control. (2018) 40:240–51. doi: 10.1016/j.bspc.2017.09.012
56. Zhang H, Gao Z, Zhang D, Hau WK, Zhang H. Progressive perception learning for main coronary segmentation in x-ray angiography. IEEE Trans Med Imaging. (2022) 42:864–79. doi: 10.1109/TMI.2022.3219126
57. Zhang J, Wang G, Xie H, Zhang S, Huang N, Zhang S, et al. Weakly supervised vessel segmentation in x-ray angiograms by self-paced learning from noisy labels with suggestive annotation. Neurocomputing. (2020) 417:114–27. doi: 10.1016/j.neucom.2020.06.122
58. Zhu X, Cheng Z, Wang S, Chen X, Lu G. Coronary angiography image segmentation based on PSPNet. Comput Methods Programs Biomed. (2021) 200:105897. doi: 10.1016/j.cmpb.2020.105897
59. Iyer K, Najarian CP, Fattah AA, Arthurs CJ, Soroushmehr SR, Subban V, et al. Angionet: a convolutional neural network for vessel segmentation in x-ray angiography. Sci Rep. (2021) 11:18066. doi: 10.1038/s41598-021-97355-8
60. Jun TJ, Kweon J, Kim Y-H, Kim D. T-net: nested encoder–decoder architecture for the main vessel segmentation in coronary angiography. Neural Netw. (2020) 128:216–33. doi: 10.1016/j.neunet.2020.05.002
61. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer (2015). p. 234–41.
62. Kaba Ş., Haci H, Isin A, Ilhan A, Conkbayir C. The application of deep learning for the segmentation and classification of coronary arteries. Diagnostics. (2023) 13:2274. doi: 10.3390/diagnostics13132274
63. Yang S, Kweon J, Kim Y-H. Major vessel segmentation on x-ray coronary angiography using deep networks with a novel penalty loss function. (2019). Available online at: https://api.semanticscholar.org/CorpusID:119097475 (Accessed May 05, 2023).
64. Yang S, Kweon J, Roh J-H, Lee J-H, Kang H, Park L-J, et al. Deep learning segmentation of major vessels in x-ray coronary angiography. Sci Rep. (2019) 9:16897. doi: 10.1038/s41598-019-53254-7
65. Zhao C, Tang H, McGonigle D, He Z, Zhang C, Wang Y-P, et al. Development of an approach to extracting coronary arteries and detecting stenosis in invasive coronary angiograms. J Med Imaging. (2022) 9:044002. doi: 10.1117/1.JMI.9.4.044002
66. Ma Y, Hua Y, Deng H, Song T, Wang H, Xue Z, et al. Self-supervised vessel segmentation via adversarial learning. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (2021). p. 7536–45.
67. Hamdi R, Kerkeni A, Bedoui MH, Ben Abdallah A. Res-GAN: residual generative adversarial network for coronary artery segmentation. In: International Conference on Intelligent Data Engineering and Automated Learning. Springer (2022). p. 391–8.
68. Huang J, Wu X, Qi H. Self-supervised segmentation using synthetic datasets via L-system. Control Theory Technol. (2023) 21:1–9. doi: 10.1007/s11768-023-00151-0
69. Zhang H, Zhang D, Gao Z, Zhang H. Joint segmentation and quantification of main coronary vessels using dual-branch multi-scale attention network. In: Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part I 24. Springer (2021). p. 369–78.
70. Tao X, Dang H, Zhou X, Xu X, Xiong D. A lightweight network for accurate coronary artery segmentation using x-ray angiograms. Front Public Health. (2022) 10:892418. doi: 10.3389/fpubh.2022.892418
71. Gao Y, Zhang L, Zhao J, Jiang Z. Improved U-Net with channel and spatial attention for coronary angiography segmentation. In: 2022 16th ICME International Conference on Complex Medical Engineering (CME). IEEE (2022). p. 123–6.
72. Mulay S, Ram K, Murugesan B, Sivaprakasam M. Style transfer based coronary artery segmentation in x-ray angiogram. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. (2021). p. 3393–401
73. Park T, Khang S, Jeong H, Koo K, Lee J, Shin J, et al. Deep learning segmentation in 2D x-ray images and non-rigid registration in multi-modality images of coronary arteries. Diagnostics. (2022) 12:778. doi: 10.3390/diagnostics12040778
74. Gao Z, Wang L, Soroushmehr R, Wood A, Gryak J, Nallamothu B, et al. Vessel segmentation for x-ray coronary angiography using ensemble methods with deep learning and filter-based features. BMC Med Imaging. (2022) 22:10. doi: 10.1186/s12880-022-00734-4
75. Han T, Ai D, Wang Y, Bian Y, An R, Fan J, et al. Recursive centerline-and direction-aware joint learning network with ensemble strategy for vessel segmentation in x-ray angiography images. Comput Methods Programs Biomed. (2022) 220:106787. doi: 10.1016/j.cmpb.2022.106787
76. Park J, Kweon J, Kim YI, Back I, Chae J, Roh J-H, et al. Selective ensemble methods for deep learning segmentation of major vessels in invasive coronary angiography. Med Phys. (2023) 50:7822–39. doi: 10.1002/mp.16554
77. Shen Y, Chen Z, Tong J, Jiang N, Ning Y. DBCU-Net: deep learning approach for segmentation of coronary angiography images. Int J Cardiovasc Imaging. (2023) 39:1–9. doi: 10.1007/s10554-023-02849-3
78. He H, Banerjee A, Beetz M, Choudhury RP, Grau V. Semi-supervised coronary vessels segmentation from invasive coronary angiography with connectivity-preserving loss function. In: 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI). IEEE (2022). p. 1–5.
79. He H, Banerjee A, Choudhury RP, Grau V. Automated coronary vessels segmentation in x-ray angiography using graph attention network. In: Statistical Atlases and Computational Models of the Heart. Regular and CMRxRecon Challenge Papers. Cham, Switzerland: Springer Nature (2024). p. 209–19.
80. Shin SY, Lee S, Noh KJ, Yun ID, Lee KM. Extraction of coronary vessels in fluoroscopic x-ray sequences using vessel correspondence optimization. In: Medical Image Computing and Computer-Assisted Intervention-MICCAI 2016: 19th International Conference, Athens, Greece, October 17–21, 2016, Proceedings, Part III 19. Springer (2016). p. 308–16.
81. O’Brien JF, Ezquerra NF. Automated segmentation of coronary vessels in angiographic image sequences utilizing temporal, spatial, and structural constraints. In: Robb RA, editor. Visualization in Biomedical Computing 1994. SPIE (1994). Vol. 2359. p. 25–37.
82. M’hiri F, Duong L, Desrosiers C, Leye M, Miró J, Cheriet M. A graph-based approach for spatio-temporal segmentation of coronary arteries in x-ray angiographic sequences. Comput Biol Med. (2016) 79:45–58. doi: 10.1016/j.compbiomed.2016.10.001
83. Sonka M, Winniford MD, Collins SM. Robust simultaneous detection of coronary borders in complex images. IEEE Trans Med Imaging. (1995) 14:151–61. doi: 10.1109/42.370412
84. Xia S, Zhu H, Liu X, Gong M, Huang X, Xu L, et al. Vessel segmentation of x-ray coronary angiographic image sequence. IEEE Trans Biomed Eng. (2019) 67:1338–48. doi: 10.1109/TBME.2019.2936460
85. Wan T, Chen J, Zhang Z, Li D, Qin Z. Automatic vessel segmentation in x-ray angiogram using spatio-temporal fully-convolutional neural network. Biomed Signal Process Control. (2021) 68:102646. doi: 10.1016/j.bspc.2021.102646
86. Wang L, Liang D, Yin X, Qiu J, Yang Z, Xing J, et al. Coronary artery segmentation in angiographic videos utilizing spatial-temporal information. BMC Med Imaging. (2020) 20:1–10. doi: 10.1186/s12880-020-00509-9
87. Zhang D, Zhang H, Zhang H, Xu L, Zhang J, Gao Z. Distance transform learning for structural and functional analysis of coronary artery from dual-view angiography. Future Gen Comput Syst. (2023) 145:136–49. doi: 10.1016/j.future.2023.03.007
88. Liang D, Wang L, Han D, Qiu J, Yin X, Yang Z, et al. Semi 3D-TENet: semi 3D network based on temporal information extraction for coronary artery segmentation from angiography video. Biomed Signal Process Control. (2021) 69:102894. doi: 10.1016/j.bspc.2021.102894
89. Qin B, Mao H, Liu Y, Zhao J, Lv Y, Zhu Y, et al. Robust PCA unrolling network for super-resolution vessel extraction in x-ray coronary angiography. IEEE Trans Med Imaging. (2022) 41:3087–98. doi: 10.1109/TMI.2022.3177626
90. Qin B, Jin M, Ding S. Extracting heterogeneous vessels in x-ray coronary angiography via machine learning. In: El-Baz AS, editor. Cardiovascular and Coronary Artery Imaging. Elsevier (2022). p. 89–127.
91. Solanki R, Gosling R, Rammohan V, Pederzani G, Garg P, Heppenstall J, et al. The importance of three dimensional coronary artery reconstruction accuracy when computing virtual fractional flow reserve from invasive angiography. Sci Rep. (2021) 11:19694. doi: 10.1038/s41598-021-99065-7
92. Çimen S, Gooya A, Grass M, Frangi AF. Reconstruction of coronary arteries from x-ray angiography: a review. Med Image Anal. (2016) 32:46–68. doi: 10.1016/j.media.2016.02.007
93. Unberath M, Taubmann O, Hell M, Achenbach S, Maier A. Symmetry, outliers, and geodesics in coronary artery centerline reconstruction from rotational angiography. Med Phys. (2017) 44:5672–85. doi: 10.1002/mp.12512
94. Vukicevic AM, Çimen S, Jagic N, Jovicic G, Frangi AF, Filipovic N. Three-dimensional reconstruction and NURBS-based structured meshing of coronary arteries from the conventional x-ray angiography projection images. Sci Rep. (2018) 8:1711. doi: 10.1038/s41598-018-19440-9
95. Galassi F, Alkhalil M, Lee R, Martindale P, Kharbanda RK, Channon KM, et al. 3D reconstruction of coronary arteries from 2D angiographic projections using non-uniform rational basis splines (NURBS) for accurate modelling of coronary stenoses. PLoS One. (2018) 13:e0190650. doi: 10.1371/journal.pone.0190650
96. Banerjee A, Choudhury RP, Grau V. Optimized rigid motion correction from multiple non-simultaneous x-ray angiographic projections. In: Deka B, Maji P, Mitra S, Bhattacharyya DK, Bora PK, Pal SK, editors. Pattern Recognition and Machine Intelligence. Cham: Springer International Publishing (2019). p. 61–9.
97. Banerjee A, Kharbanda RK, Choudhury RP, Grau V. Automated motion correction and 3D vessel centerlines reconstruction from non-simultaneous angiographic projections. In: Statistical Atlases and Computational Models of the Heart. Atrial Segmentation and LV Quantification Challenges Cham: Springer International Publishing (2019). p. 12–20.
98. Fang H, Zhu J, Ai D, Huang Y, Jiang Y, Song H, et al. Greedy soft matching for vascular tracking of coronary angiographic image sequences. IEEE Trans Circuits Syst Video Technol. (2019) 30:1466–80. doi: 10.1109/TCSVT.2019.2903883
99. Hwang M, Hwang S-B, Yu H, Kim J, Kim D, Hong W, et al. A simple method for automatic 3D reconstruction of coronary arteries from x-ray angiography. Front Physiol. (2021) 12:724216. doi: 10.3389/fphys.2021.724216
100. Tong J, Wang F, Li M, Xia S, Lin W. The optimization of parameters and matching point pairs in the 3D reconstruction of coronary artery. Biomed Signal Process Control. (2021) 67:102534. doi: 10.1016/j.bspc.2021.102534
101. Tong J, Xu S, Wang F, Qi P. 3D reconstruction with coronary artery based on curve descriptor and projection geometry-constrained vasculature matching. Information. (2022) 13:38. doi: 10.3390/info13010038
102. Xiao R, Yang J, Fan J, Ai D, Wang G, Wang Y. Shape context and projection geometry constrained vasculature matching for 3D reconstruction of coronary artery. Neurocomputing. (2016) 195:65–73. doi: 10.1016/j.neucom.2015.08.110
103. Zhu J, Li H, Ai D, Yang Q, Fan J, Huang Y, et al. Iterative closest graph matching for non-rigid 3D/2D coronary arteries registration. Comput Methods Programs Biomed. (2021) 199:105901. doi: 10.1016/j.cmpb.2020.105901
104. Law AK, Zhu H, Chan FH. 3D reconstruction of coronary artery using biplane angiography. In: Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE Cat. No. 03CH37439). IEEE (2003). Vol. 1. p. 533–6.
105. Jandt U, Schäfer D, Grass M, Rasche V. Automatic generation of 3d coronary artery centerlines using rotational x-ray angiography. Med Image Anal. (2009) 13:846–58. doi: 10.1016/j.media.2009.07.010
106. Li J, Cohen LD. Reconstruction of 3D tubular structures from cone-beam projections. In: 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE (2011). p. 1162–6.
107. Cong W, Yang J, Ai D, Chen Y, Liu Y, Wang Y. Quantitative analysis of deformable model-based 3D reconstruction of coronary artery from multiple angiograms. IEEE Trans Biomed Eng. (2015) 62:2079–90. doi: 10.1109/TBME.2015.2408633
108. Cong W, Yang J, Liu Y, Wang Y. Energy back-projective composition for 3D coronary artery reconstruction. In: 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE (2013). p. 5151–4.
109. Yang J, Cong W, Chen Y, Fan J, Liu Y, Wang Y. External force back-projective composition and globally deformable optimization for 3D coronary artery reconstruction. Phys Med Biol. (2014) 59:975. doi: 10.1088/0031-9155/59/4/975
110. Cohen LD, Cohen I. Finite-element methods for active contour models and balloons for 2D and 3D images. IEEE Trans Pattern Anal Mach Intell. (1993) 15:1131–47. doi: 10.1109/34.244675
111. Xu C, Prince JL. Snakes, shapes, and gradient vector flow. IEEE Trans Image Process. (1998) 7:359–69. doi: 10.1109/83.661186
112. Xu C, Prince JL. Generalized gradient vector flow external forces for active contours. Signal Process. (1998) 71:131–9. doi: 10.1016/S0165-1684(98)00140-6
113. Liu X, Li S, Wang B, Xu L, Gao Z, Yang G. Motion estimation based on projective information disentanglement for 3D reconstruction of rotational coronary angiography. Comput Biol Med. (2023) 157:106743. doi: 10.1016/j.compbiomed.2023.106743
114. Taubmann O, Unberath M, Lauritsch G, Achenbach S, Maier A. Spatio-temporally regularized 4D cardiovascular C-arm CT reconstruction using a proximal algorithm. In: 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017). IEEE (2017). p. 52–5.
115. Unberath M, Taubmann O, Aichert A, Achenbach S, Maier A. Prior-free respiratory motion estimation in rotational angiography. IEEE Trans Med Imaging. (2018) 37:1999–2009. doi: 10.1109/TMI.2018.2806310
116. Liu X, Hou F, Hao A, Qin H. A parallelized 4D reconstruction algorithm for vascular structures and motions based on energy optimization. Vis Comput. (2015) 31:1431–46. doi: 10.1007/s00371-014-1024-4
117. Royer-Rivard R, Girard F, Dahdah N, Cheriet F. End-to-end deep learning model for cardiac cycle synchronization from multi-view angiographic sequences. In: 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC). IEEE (2020). p. 1190–3.
118. Song S, Du C, Liu X, Huang Y, Song H, Jiang Y, et al. Deep motion tracking from multiview angiographic image sequences for synchronization of cardiac phases. Phys Med Biol. (2019) 64:025018. doi: 10.1088/1361-6560/aafa06
119. Farhad A, Reza R, Azamossadat H, Ali G, Arash R, Mehrad A, et al. Artificial intelligence in estimating fractional flow reserve: a systematic literature review of techniques. BMC Cardiovasc Disord. (2023) 23:407. doi: 10.1186/s12872-023-03447-w
120. Hoque K, Ferdows M, Sawall S, Tzirtzilakis E, Xenos M. Hemodynamic characteristics expose the atherosclerotic severity in coronary main arteries: one-dimensional and three-dimensional approaches. Phys Fluids. (2021) 33:121907. doi: 10.1063/5.0069106
121. Hu X, Liu X, Wang H, Xu L, Wu P, Zhang W, et al. A novel physics-based model for fast computation of blood flow in coronary arteries. Biomed Eng Online. (2023) 22:56. doi: 10.1186/s12938-023-01121-y
122. Pfaller MR, Pham J, Verma A, Pegolotti L, Wilson NM, Parker DW, et al. Automated generation of 0D and 1D reduced-order models of patient-specific blood flow. Int J Numer Method Biomed Eng. (2022) 38:e3639. doi: 10.1002/cnm.3639
123. Yin M, Yazdani A, Karniadakis GE. One-dimensional modeling of fractional flow reserve in coronary artery disease: uncertainty quantification and Bayesian optimization. Comput Methods Appl Mech Eng. (2019) 353:66–85. doi: 10.1016/j.cma.2019.05.005
124. Sagawa K, Lie RK, Schaefer J. Translation of Otto frank’s paper “die grundform des arteriellen pulses” Zeitschrift für Biologie 37: 483–526 (1899). J Mol Cell Cardiol. (1990) 22:253–4. doi: 10.1016/0022-2828(90)91459-K
125. Feng Y, Fu R, Li B, Li N, Yang H, Liu J, et al. Prediction of fractional flow reserve based on reduced-order cardiovascular model. Comput Methods Appl Mech Eng. (2022) 400:115473. doi: 10.1016/j.cma.2022.115473
126. Kim J, Jin D, Choi H, Kweon J, Yang DH, Kim Y-H. A zero-dimensional predictive model for the pressure drop in the stenotic coronary artery based on its geometric characteristics. J Biomech. (2020) 113:110076. doi: 10.1016/j.jbiomech.2020.110076
127. Blanco PJ, Bulant CA, Müller LO, Talou GM, Bezerra CG, Lemos PA, et al. Comparison of 1D and 3D models for the estimation of fractional flow reserve. Sci Rep. (2018) 8:17275. doi: 10.1038/s41598-018-35344-0
128. Grande Gutiérrez N, Sinno T, Diamond SL. A 1D –3D hybrid model of patient-specific coronary hemodynamics. Cardiovasc Eng Technol. (2022) 13:1–12. doi: 10.1007/s13239-021-00580-5
129. Pfaller MR, Pham J, Wilson NM, Parker DW, Marsden AL. On the periodicity of cardiovascular fluid dynamics simulations. Ann Biomed Eng. (2021) 49:3574–92. doi: 10.1007/s10439-021-02796-x
130. Deshpande S, Sosa RI, Bordas S, Lengiewicz J. Convolution, aggregation and attention based deep neural networks for accelerating simulations in mechanics. Front Mater. (2023) 10:1128954. doi: 10.3389/fmats.2023.1128954
131. Cai S, Mao Z, Wang Z, Yin M, Karniadakis GE. Physics-informed neural networks (PINNs) for fluid mechanics: a review. Acta Mech Sin. (2021) 37:1727–38. doi: 10.1007/s10409-021-01148-1
132. Mahmoudabadbozchelou M, Karniadakis GE, Jamali S. nn-PINNs: non-Newtonian physics-informed neural networks for complex fluid modeling. Soft Matter. (2022) 18:172–85. doi: 10.1039/D1SM01298C
133. Mao Z, Jagtap AD, Karniadakis GE. Physics-informed neural networks for high-speed flows. Comput Methods Appl Mech Eng. (2020) 360:112789. doi: 10.1016/j.cma.2019.112789
134. Rao C, Sun H, Liu Y. Physics-informed deep learning for incompressible laminar flows. Theor Appl Mech Lett. (2020) 10:207–12. doi: 10.1016/j.taml.2020.01.039
135. Deshpande S, Bordas S, Lengiewicz J. MAgNET: a graph U-Net architecture for mesh-based simulations. arXiv [Preprint]. arXiv:2211.00713 (2022).
136. Deshpande S, Lengiewicz J, Bordas SP. Probabilistic deep learning for real-time large deformation simulations. Comput Methods Appl Mech Eng. (2022) 398:115307. doi: 10.1016/j.cma.2022.115307
137. Fossan FE, Müller LO, Sturdy J, Bråten AT, Jørgensen A, Wiseth R, et al. Machine learning augmented reduced-order models for FFR-prediction. Comput Methods Appl Mech Eng. (2021) 384:113892. doi: 10.1016/j.cma.2021.113892
138. Jaegle A, Borgeaud S, Alayrac J-B, Doersch C, Ionescu C, Ding D, et al. Perceiver IO: a general architecture for structured inputs & outputs. arXiv [Preprint]. arXiv:2107.14795 (2021).
139. Montes de Oca Zapiain D, Stewart JA, Dingreville R. Accelerating phase-field-based microstructure evolution predictions via surrogate models trained by machine learning methods. NPJ Comput Mater. (2021) 7:3. doi: 10.1038/s41524-020-00471-8
140. Itu L, Rapaka S, Passerini T, Georgescu B, Schwemmer C, Schoebinger M, et al. A machine-learning approach for computation of fractional flow reserve from coronary computed tomography. J Appl Physiol. (2016) 121:42–52. doi: 10.1152/japplphysiol.00752.2015
141. Carson JM, Chakshu NK, Sazonov I, Nithiarasu P. Artificial intelligence approaches to predict coronary stenosis severity using non-invasive fractional flow reserve. Proc Inst Mech Eng H. (2020) 234:1337–50. doi: 10.1177/0954411920946526
142. Gao Z, Wang X, Sun S, Wu D, Bai J, Yin Y, et al. Learning physical properties in complex visual scenes: an intelligent machine for perceiving blood flow dynamics from static CT angiography imaging. Neural Netw. (2020) 123:82–93. doi: 10.1016/j.neunet.2019.11.017
143. Xie B, Liu X, Zhang H, Xu C, Zeng T, Yuan Y, et al. Conditional physics-informed graph neural network for fractional flow reserve assessment. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer (2023). p. 110–20.
144. Zhang D, Liu X, Xia J, Gao Z, Zhang H, de Albuquerque VHC. A physics-guided deep learning approach for functional assessment of cardiovascular disease in IoT-based smart health. IEEE Internet Things J. (2023) 10:18505–16. doi: 10.1109/JIOT.2023.3240536
145. Morris PD, Ryan D, Morton AC, Lycett R, Lawford PV, Hose DR, et al. Virtual fractional flow reserve from coronary angiography: modeling the significance of coronary lesions: results from the VIRTU-1 (VIRTUal fractional flow reserve from coronary angiography) study. JACC Cardiovasc Interv. (2013) 6:149–57. doi: 10.1016/j.jcin.2012.08.024
146. Morris PD, Silva Soto DA, Feher JF, Rafiroiu D, Lungu A, Varma S, et al. Fast virtual fractional flow reserve based upon steady-state computational fluid dynamics analysis: results from the VIRTU-Fast study. Basic Transl Sci. (2017) 2:434–46. doi: 10.1016/j.jacbts.2017.04.003
147. Newman T, Borker R, Aubiniere-Robb L, Hendrickson J, Choudhury D, Halliday I, et al. Rapid virtual fractional flow reserve using 3D computational fluid dynamics. Eur Heart J Digit Health. (2023) 4:ztad028. doi: 10.1093/ehjdh/ztad028
148. Pederzani G, Czechowicz K, Ghorab N, Morris PD, Gunn JP, Narracott AJ, et al. The use of digital coronary phantoms for the validation of arterial geometry reconstruction and computation of virtual FFR. Fluids. (2022) 7:201. doi: 10.3390/fluids7060201
149. Masdjedi K, van Zandvoort LJ, Balbi MM, Nuis R-J, Wilschut J, Diletti R, et al. Validation of novel 3-dimensional quantitative coronary angiography based software to calculate fractional flow reserve post stenting. Catheter Cardiovasc Interv. (2021) 98:671–7. doi: 10.1002/ccd.29311
150. Papafaklis MI, Muramatsu T, Ishibashi Y, Lakkas LS, Nakatani S, Bourantas CV, et al. Fast virtual functional assessment of intermediate coronary lesions using routine angiographic data and blood flow simulation in humans: comparison with pressure wire-fractional flow reserve. EuroIntervention. (2014) 10:574–83. doi: 10.4244/EIJY14M07-01
151. Pellicano M, Lavi I, De Bruyne B, Vaknin-Assa H, Assali A, Valtzer O, et al. Validation study of image-based fractional flow reserve during coronary angiography. Circ Cardiovasc Interv. (2017) 10:e005259. doi: 10.1161/CIRCINTERVENTIONS.116.005259
152. Saveljic I, Djukic T, Nikolic D, Djorovic S, Filipovic N. Numerical simulation of fractional flow reserve in atherosclerotic coronary arteries. In: 2021 IEEE 21st International Conference on Bioinformatics and Bioengineering (BIBE). IEEE (2021). p. 1–4.
153. Tar B, Jenei C, Dezsi CA, Bakk S, Beres Z, Santa J, et al. Less invasive fractional flow reserve measurement from 3-dimensional quantitative coronary angiography and classic fluid dynamic equations. EuroIntervention. (2018) 14:942–50. doi: 10.4244/EIJ-D-17-00859
154. Tu S, Barbato E, Köszegi Z, Yang J, Sun Z, Holm NR, et al. Fractional flow reserve calculation from 3-dimensional quantitative coronary angiography and TIMI frame count: a fast computer model to quantify the functional significance of moderately obstructed coronary arteries. JACC Cardiovasc Interv. (2014) 7:768–77. doi: 10.1016/j.jcin.2014.03.004
155. Tu S, Westra J, Yang J, von Birgelen C, Ferrara A, Pellicano M, et al. Diagnostic accuracy of fast computational approaches to derive fractional flow reserve from diagnostic coronary angiography: the international multicenter FAVOR pilot study. Cardiovasc Interv. (2016) 9:2024–35. doi: 10.1016/j.jcin.2016.07.013
156. Tufaro V, Torii R, Erdogan E, Kitslaar P, Koo B-K, Rakhit R, et al. An automated software for real-time quantification of wall shear stress distribution in quantitative coronary angiography data. Int J Cardiol. (2022) 357:14–9. doi: 10.1016/j.ijcard.2022.03.022
157. Zhao Q, Li C, Chu M, Gutiérrez-Chico JL, Tu S. Angiography-based coronary flow reserve: the feasibility of automatic computation by artificial intelligence. Cardiol J. (2023) 30(3):369–78. doi: 10.5603/CJ.a2021.0087
158. Kern MJ. Coronary physiology revisited: practical insights from the cardiac catheterization laboratory. Circulation. (2000) 101:1344–51. doi: 10.1161/01.CIR.101.11.1344
159. May AN, Kull A, Gunalingam B, Francis JL, Lau GT. The uptake of coronary fractional flow reserve in Australia in the past decade. Med J Aust. (2016) 205:127. doi: 10.5694/mja15.01225
160. Murphy J, Hansen P, Bhindi R, Figtree G, Nelson G, Ward M. Cost benefit for assessment of intermediate coronary stenosis with fractional flow reserve in public and private sectors in Australia. Heart Lung Circ. (2014) 23:807–10. doi: 10.1016/j.hlc.2014.03.027
161. Pijls NH, Sels J-WE. Functional measurement of coronary stenosis. J Am Coll Cardiol. (2012) 59:1045–57. doi: 10.1016/j.jacc.2011.09.077
163. Baumgart D, Haude M, Liu F, Ge J, Goerge G, Erbel R. Current concepts of coronary flow reserve for clinical decision making during cardiac catheterization. Am Heart J. (1998) 136:136–49. doi: 10.1016/S0002-8703(98)70194-2
164. Baumgart D, Haude M, Goerge G, Ge J, Vetter S, Dagres N, et al. Improved assessment of coronary stenosis severity using the relative flow velocity reserve. Circulation. (1998) 98:40–6. doi: 10.1161/01.CIR.98.1.40
165. Gould KL, Kirkeeide RL, Buchi M. Coronary flow reserve as a physiologic measure of stenosis severity. J Am Coll Cardiol. (1990) 15:459–74. doi: 10.1016/S0735-1097(10)80078-6
166. Fearon WF, Kobayashi Y. Invasive assessment of the coronary microvasculature: the index of microcirculatory resistance. Circ Cardiovasc Interv. (2017) 10:e005361. doi: 10.1161/CIRCINTERVENTIONS.117.005361
167. Martínez GJ, Yong AS, Fearon WF, Ng MK. The index of microcirculatory resistance in the physiologic assessment of the coronary microcirculation. Coron Artery Dis. (2015) 26:e15–e26. doi: 10.1097/MCA.0000000000000213
168. Ng MK, Yong AS, Ho M, Shah MG, Chawantanpipat C, O’Connell R, et al. The index of microcirculatory resistance predicts myocardial infarction related to percutaneous coronary intervention. Circ Cardiovasc Interv. (2012) 5:515–22. doi: 10.1161/CIRCINTERVENTIONS.112.969048
169. Götberg M, Christiansen EH, Gudmundsdottir IJ, Sandhall L, Danielewicz M, Jakobsen L, et al. Instantaneous wave-free ratio vs. fractional flow reserve to guide PCI. New Engl J Med. (2017) 376:1813–23. doi: 10.1056/NEJMoa1616540
170. Petraco R, Al-Lamee R, Gotberg M, Sharp A, Hellig F, Nijjer SS, et al. Real-time use of instantaneous wave–free ratio: results of the advise in-practice: an international, multicenter evaluation of instantaneous wave–free ratio in clinical practice. Am Heart J. (2014) 168:739–48. doi: 10.1016/j.ahj.2014.06.022
171. Pisters R, Ilhan M, Veenstra L, Gho B, Stein M, Hoorntje J, et al. Instantaneous wave-free ratio and fractional flow reserve in clinical practice. Neth Heart J. (2018) 26:385–92. doi: 10.1007/s12471-018-1125-1
172. Kumar G, Desai R, Gore A, Rahim H, Maehara A, Matsumura M, et al. Real world validation of the nonhyperemic index of coronary artery stenosis severity—resting full-cycle ratio—re-validate. Catheter Cardiovasc Interv. (2020) 96:E53–8. doi: 10.1002/ccd.28523
173. Malmberg S, Lauermann J, Karlström P, Gulin D, Barmano N. Resting full-cycle ratio versus fractional flow reserve: a swedeheart-registry-based comparison of two physiological indexes for assessing coronary stenosis severity. J Interv Cardiol. (2023) 2023:6461691. doi: 10.1155/2023/6461691
174. Muroya T, Kawano H, Hata S, Shinboku H, Sonoda K, Kusumoto S, et al. Relationship between resting full-cycle ratio and fractional flow reserve in assessments of coronary stenosis severity. Catheter Cardiovasc Interv. (2020) 96:E432–8. doi: 10.1002/ccd.28835
175. Ono M, Kawashima H, Hara H, Gao C, Wang R, Kogame N, et al. Advances in IVUS/OCT and future clinical perspective of novel hybrid catheter system in coronary imaging. Front Cardiovasc Med. (2020) 7:119. doi: 10.3389/fcvm.2020.00119
176. Wu W, Oguz UM, Banga A, Zhao S, Thota AK, Gadamidi VK, et al. 3D reconstruction of coronary artery bifurcations from intravascular ultrasound and angiography. Sci Rep. (2023) 13:13031. doi: 10.1038/s41598-023-40257-8
177. Liang H, Zhang Q, Gao Y, Chen G, Bai Y, Zhang Y, et al. Diagnostic performance of angiography-derived fractional flow reserve analysis based on bifurcation fractal law for assessing hemodynamic significance of coronary stenosis. Eur Radiol. (2023) 33:1–10. doi: 10.1007/s00330-023-09682-1
178. Papamanolis L, Kim HJ, Jaquet C, Sinclair M, Schaap M, Danad I, et al. Myocardial perfusion simulation for coronary artery disease: a coupled patient-specific multiscale model. Ann Biomed Eng. (2021) 49:1432–47. doi: 10.1007/s10439-020-02681-z
179. Gamage PT, Dong P, Lee J, Gharaibeh Y, Zimin VN, Bezerra HG, et al. Fractional flow reserve (FFR) estimation from OCT-based CFD simulations: role of side branches. Appl Sci. (2022) 12:5573. doi: 10.3390/app12115573
180. Zhuk S, Smith O, Thondapu V, Halupka K, Moore S. Using contrast motion to generate patient-specific blood flow simulations during invasive coronary angiography. J Biomech Eng. (2020) 142:021001. doi: 10.1115/1.4044095
Keywords: x-ray coronary angiography, coronary artery disease, catheterisation laboratory, patient-specific model, in silico medicine, segmentation, 3D reconstruction, blood flow simulation
Citation: Lashgari M, Choudhury RP and Banerjee A (2024) Patient-specific in silico 3D coronary model in cardiac catheterisation laboratories. Front. Cardiovasc. Med. 11:1398290. doi: 10.3389/fcvm.2024.1398290
Received: 9 March 2024; Accepted: 6 June 2024;
Published: 5 July 2024.
Edited by:
Tommaso Gori, Johannes Gutenberg University Mainz, GermanyReviewed by:
João Silva Marques, Centro Hospitalar Universitário Lisboa Norte (CHULN), Portugal© 2024 Lashgari, Choudhury and Banerjee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abhirup Banerjee, YWJoaXJ1cC5iYW5lcmplZUBlbmcub3guYWMudWs=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.