Fuzzy logic use case within the built environment for optimizing sustainability versus cost in the material selection process

This study aims to investigate the application of fuzzy logic in decision-making within the Built Environment. The research focuses on achieving a balance between reducing carbon emissions and increasing costs in the selection of materials and equipment. This balance is measured by Life Cycle Carbon Emissions (LCCE) and is evaluated using a Life Cycle Assessment (LCA) methodology. By modeling fuzzy logic against classical binary logic within MATLAB, the study demonstrates how fuzzy logic’s “degrees of truth” may be utilized to construct customized stakeholder buy-in profiles and also achieve increased mathematical precision. These decision-maker stakeholder profiles reflect different interpretations of linguistic expressions of value in terms of cost against carbon reduction trade-offs. The research develops a three-dimensional control surface by using the Fuzzy Logic Toolbox in MATLAB. This surface serves as a visual tool for purchasing professionals to optimize these trade-offs on a scale, which provides a practical strategy for large-scale construction projects.

Introduction

The material production phase has been quantified to represent 40% of the carbon footprint of urban buildings (Huang et al., 2017). As such, professionals within the built environment have a practical interest in comparing the life cycle carbon emissions (LCCE) calculation that reveals the entrained carbon as a result of the manufacturing process required to create a given material or piece of equipment, at the point of sale. By introducing competition at a carbon emissions level, an aggregate and net emissions reduction may be realized within capital projects and the greater built environment sector. Moreover, suppose the market indicates a growing demand for products on the basis of low entrained carbon emissions. In that case, this will send a powerful signal to the manufacturers of building materials and equipment to actively seek to reduce the carbon footprint of their products, creating further downward pressure on carbon emissions in the built environment (Marzouk and Eslam 2020).

The building sector has been shown to be one of the main contributors to environmental emissions, and those emissions are projected to increase with the rapid growth of urbanization. It has been well-established that there are numerous and often conflicting demands made upon construction projects, such as cost and enhancing environmental outcomes via sustainability initiatives (Seo et al., 2004).

To address this trade-off and compute linguistic imprecision, we look to fuzzy logic. Fuzzy logic is a mathematical means by which practitioners may move beyond a binary yes/no logic system of classical logic or classical set theory to one the spans a spectrum or gradient ranging from yes to no, describing “degrees of truth” otherwise known as a membership function. It is particularly helpful in adapting linguistic descriptors into machine interpretable numeric values which presents an opportunity for ease of use and intuitive application. “...Fuzzy sets allow us to handle linguistic uncertainties, as typified by the adage ‘words can mean different things to different people’” (Karnik et al., 1999). As such, the conditions by which Fuzzy Logic may be applied is expansive due to its ability to absorb variability. This is particularly useful in private industry in which capital project stakeholders introduce varying perspectives, even when using the same adjectives to describe capital project elements from project-to-project or entity-to-entity. For these reasons, fuzzy logic is particularly well suited to addressing trade-offs in construction and, as it relates to the hypothetical examined in this research paper, trade-offs between cost and the carbon-emissions inherent in material and equipment purchasing decisions within construction projects.

It is possible that a control surface may be generated as an output of a fuzzy inference system such that the control surface serves as a look-up reference guided by input variables to determine the output according to the fuzzy logic model. Such a reference may be simpler to adopt for construction managers or superintendents than having them interact with a fuzzy model directly or sophisticated software systems.

Within the Built Environment, capital project stakeholders may express an interest in sustainability but be unsure how to act upon that desire in a quantifiable or specific way. While numerous sustainability rating systems exist, such as LEED rating systems and many others, there may be instances in which the stakeholders with funding decision approval authority elect not to pursue a known or given rating system but would like to evidence their awareness of and commitment to sustainability concepts. Moreover, there exists numerous entities that track net life cycle carbon emissions of materials and equipment, however, many of these entities are either structured as non-profits and so have an intrinsic bias in ignoring private sector cost biases to further their organizational vision or, alternatively, monetize their indices and sell LCCE estimations as either a consulting service or a self-service tool at additional cost to a given Owner.

There is precedence for using Fuzzy Logic for comparison purposes within construction, such as with comparing construction labor productivity models (Sarihi et al., 2023), optimizing Health and Safety Plans (Jafari, 2022), cost control (Zeng and Gao, 2024), construction time/risk (Plebankiewicz et al., 2021), supplier selection (Jadidi et al., 2008), and construction risk (Zeng et al., 2007). There is, however, an absence of a targeted and practical use case for fuzzy logic at the point of material selection or purchase. This decision-point could feasibly be construed as speaking to the development of construction specifications, which could incorporate a decision-making logic for navigating cost and sustainability pressures that are in tension with each other. It could also apply to the actual point of purchase when construction professionals issue Purchase Orders (POs) for project materials or equipment and are forced to navigate between available options that satisfy the technical specifications but show variances according to Life Cycle Carbon Emissions (LCCE) and cost. Fuzzy logic is a mature field of mathematics and is commonly employed within numerous subject matter domains, to include medical research, e.g., (Hussain Hassan, 2020; Tan et al., 2022). It has been shown to aid group decision-making, and the academic literature cites crisp values as, “...inadequate to model real-life situations” (Chen, 2000). Beyond the boundaries of capital projects, the built environment uses fuzzy logic to assist with prioritizing maintenance work (Shahrivar et al., 2022). Interestingly, fuzz logic is assisting with accounting for conflicting objectives within construction management contexts (Chen and Pan, 2021). Common built environment tools, such as Building Information Modeling (BIM), are now being combined with fuzzy logic to impact design and construction outcomes (Tan et al., 2021).

This research paper will explore the viability of fuzzy logic and a fuzzy inference system upon optimizing material selection decisions when project stakeholders want to analyze the decision by Life Cycle Assessment (LCA) carbon emission related to a given material versus cost. The Fuzzy Inference System will be compared and contrasted to a classic logic exercise in which a collection of logic statements, such as if/then logic statements in an effort to identify if the Fuzzy Logic approach offers benefits. While research has been conducted on material selection within construction applications using fuzzy logic (Obradović and Pamucar, 2020), this research seeks a user-friendly methodology that might feasibly be deployed within a construction organization using software tool that is pervasive and intuitive and a method that is comparatively simple.

The Life Cycle Assessment is fundamental to supporting decision-making related to reducing carbon emissions in the built environment. This method recognizes the carbon emissions generated within the full lifecycle of the manufacturing process of a given piece of material or equipment, not simply the carbon emissions realized within time boundaries of a given construction endeavor. Existing material and equipment stocks may be viewed as already possessing a sunk cost of carbon emissions prior to the point of selection and use in design and construction. In a sense, the manufacture and warehousing of construction goods and equipment may be viewed as a form of pre-work for any given construction project, as such works could not be built without them.

Nomenclature

Research has been conducted to establish a timeline for the rise of fuzzy logic, succinctly summarized by a table titled, “Historical Development and Application of Fuzzy Theories from 1965 to 1994” which was then extended to show Fuzzy Logics incorporation into Construction Management Research, summarized by the table, “Applications of Fuzzy Set/Fuzzy Logic in Construction Management Research” (Chan Albert, Chan Daniel and Yeung John, 2009) based on a literature review of “top quality” journals until 2005.

Fuzzy Set Theory (FST) and, by extension, Fuzzy Logic were first described in the 1960s by the groundbreaking paper Fuzzy Sets that described the mathematics beyond the binary or true/false nature of classical set theory (Zadeh, 1965). It has been argued that Fuzzy Logic traces its origin to Greek philosophy, citing a debate in which the Law of the Excluded Middle and Law of Extended Contradiction which set out a binary true/false reasoning approach evoked thinking on a third “possible” value that could be assigned a numeric value between true and false (McBratney and Odeh, 1997).

• Fuzzy Logic – “Fuzzy logic is intended to model logical reasoning with vague or imprecise statements...where the truth-values are interpreted as degrees of truth. The truth-value of a logically compound proposition...is determined by the truth-value of its components. In other words, like in classical logic, one imposes truth-functionality. Fuzzy logic emerged in the context of the theory of fuzzy sets, introduced by Zadeh (1965). A fuzzy set assigns a degree of membership, typically a real number from the interval [0,1] [0,1], to elements of a universe. Fuzzy logic arises by assigning degrees of truth to propositions. The standard set of truth-values (degrees) is the real unit interval [0,1] [0,1], where 00 represents “totally false,” 11 represents “totally true,” and the other values refer to partial truth, i.e., intermediate degrees of truth” (Cintula et al., 2023).

• Fuzzy Inference System – “Fuzzy inference system is a system with the ability to handle fuzzy information based on fuzzy set theory and fuzzy inference methods. Fuzzy inference system mainly consists of four parts: input, fuzzy rule base, fuzzy inference method and output. Fuzzy inference system is also called multi-rule fuzzy inference system when there are multiple rules in the fuzzy rule base” (Deng et al., 2023).

•Fuzzy Sets – “Fuzzy sets were first introduced to represent the values of real-world parameters when the boundaries between different states of a parameter are not sharp (i.e., not crisp), due to the subjectivity or vagueness of the measure (e.g., warm weather), incomplete information, or ambiguity in specifying an exact value (i.e., nonspecificity or resolutional uncertainty)” (Pal and Bezdek, 1994). “A fuzzy set is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership (characteristic) function which assigns to each object a grade of membership ranging between zero and one. The notions of inclusion, union, intersection, complement, relation, convexity, etc., are extended to such sets, and various properties of these notions in the context of fuzzy sets are established” (Zadeh, 1965).

• Classical Set Theory – “Classical (i.e., crisp) set theory imposes a sharp boundary on uncertain concepts: an element either fully belongs or does not belong to a set. Fuzzy set theory provides a way to overcome these classification challenges by allowing an element to partially belong to a set through its membership degree” (Fayek, 2020).

• Membership Function – “Membership functions make it possible to capture the gradual transition and overlap between concepts” (Fayek, 2020).

•Fuzzy Inference System Mamdani–is intended to model logical reasoning “Fuzzy inference system Mamdani, known also as Min-Max method, was formulated by Ebrahim Mamdani in 1975. On Mamdani fuzzy systems both antecedent and consequent are linguistic terms and the output corresponds to the superposition of individual outputs given by each rule” (Putri and Saputro, 2021).

•Lifecycle Assessment (LCA) – “LCA, which was the earliest proposed method, has been applied to the construction industry and other related industries. In a building system, an LCA is performed to evaluate all resource loads, including land, energy, water, and materials, as well as environmental loads, including global warming, ozone depletion, acidification, eutrophication, and photochemical smog” (Huang et al., 2024).

•Life Cycle Carbon Emissions (LCCE) – “LCCE include both the production of building materials and their consumption in the construction sector. The production and transportation of building materials are determined by the demand of the construction sector. Therefore, measures to reduce building LCCE should account for the direct and indirect emissions generated by building operations, as well as the emissions generated by the production and transportation of building materials” (Huang et al., 2024).

•International Standards Organization (ISO) 21930 – “...issued by the International Organization for Standardization (ISO) in 2017 as a formal international rule for building LCA [7]; it specifies the principles, codes, and requirements for formulating an environmental product declaration for construction activities, establishes product category rules for construction products and services, and proposes calculation rules for life-cycle inventory analysis and life-cycle impact assessment in environmental product declaration reports. ISO 21930 categorizes the entire building life cycle into five modules or stages and 17 sub-stages: building material production (A1–A3), construction (A4–A5), use (B1–B7), end-of-life (C1–C4), and supplementary information beyond the system boundary (D). This provides a basis for the classification of life-cycle stages and the definition of system boundaries for calculating buildings’ LCCE (Figure 2)” (Huang et al., 2024).

This study explores whether the material selection process in construction projects presents a viable application for fuzzy logic. Specifically, it examines whether a fuzzy inference system can be effectively designed to guide material choices in a way that aligns with the varied trade-off preferences of project leaders and key stakeholders. Additionally, it assesses the suitability of using cost and Life Cycle Carbon Emissions (LCCE) as input metrics within such a system.

Methodology

Figure 1 is the workflow used to create the fuzzy logic components of this simulation using MATLAB’s Fuzzy Logic Designer application as it relates to the selected scenario under analysis: a situation in which cost and carbon emissions reduction values may be in tension when making a purchasing decision for construction materials or equipment, assuming all other specification elements have been equivalently satisfied. A “cetaris paribus” (other things being equal) approach was selected and employed with intentionality in this research paper such that the tension in built environment vocations between cost and sustainability could be directly explored. This is a common research approach and perspective, often employed within the field of economics.

Figure 1

Figure 1. MATLAB workflow to analyze cost versus carbon-emissions reduction trade-offs.

Within fuzzy logic, it is important to train or code a given model with expert knowledge. The experts in a given scenario may be the primary project stakeholders or they may be subject matter experts related to sustainability and project financial management. A key advantage of a fuzzy inference system is that the input values may be altered or improved to account for the possibility of change, without redefining the logic statements of the Fuzzy Inference System. Given this research is hypothetical in nature, experts were not used to create input nor output values and so the values presented should be interpreted as illustrative in nature.

This simulation will model the transitions from the crisp input points using smooth curves as opposed to assumed linear relationships or other alternatives. The research method will leverage the MATLAB software application with a specific emphasis on the Fuzzy Toolbox. The advantage of using MATLAB and its Fuzzy Logic Toolbox is the intuitive user-interface allows practitioners to step-through recognizing the required inputs and logic rules required for a fuzzy logic application, to easily infill them, and to run rapid simulations that create corresponding visualizations of both the inputs and resulting control structure and/or specific value outputs. The software serves as a both a calculator and a visualizer, quickly computing a vast number of calculations faster than would be capable by a human and generating visualizations to engage in multi-modal communication and an enhanced user interface experience. There may exist other solutions which may be equally appropriate; this research does not involve a critical evaluation of competing fuzzy logic software applications.

Two inputs consisting of three Gaussian shaped categories of data will be input into the model. The dispersion of the Gaussian shapes will be modeled to represent differing perspectives as to what constitutes a sustainable gain via a specific carbon emissions reduction and the differing perspectives of what constitutes a value proposition relative to price for carbon emission reduction. In this fashion, overlapping perspectives which represent the healthy tension and routine disagreement within the business will be mathematically modelled and visually depicted on graphs. It should be noted that the Mamdani method was selected for use within MATLAB and applied to this use case. There are typically three methods used within fuzzy inference systems and Mamdani is often used, as noted in similar built environment research.

An output function that is reliant upon and translates the input data will also be modelled within the Fuzzy Toolbox. The output will result in human understandable logic rules based on all the possible combinations of input data across their three respective categories. Upon completion, the MATLAB model will be able to generate a 3-dimensional control surface that is representative of every output point relative to the inputs, within the described range.

While the core function of this method may be demonstrated with hypothetical data, industry data related to material cost and net material LCA carbon emissions was source from XYZ source to enhance the realism of the exercise by presenting industry professionals with realistic data that they might expect to see during a capital project relative to the time span and geographic location assumptions made within this research exercise.

Classical Set Theory is introduced for comparative purposes via Figure 4 – Visual Comparison of Fuzzy Set Theory to Classical Set Theory that compares a crisp input versus a fuzzy input. The graph visually reveals “discontinuous jumps” that are inherent and problematic within classical set theory contexts and compare those to the spectrum of data employed by Fuzzy Logic.

Figure 2 represents three input ranges that represent the linguistic concepts of low, medium, and high as they relate to cost judgements. The x-axis represents cost expressed in the units of dollars. The exponential notation on the x-axis indicates that the units may be interpreted in terms of increments of 10,000 (e.g. $10,000, $20,000, et cetera). The y-axis is the degree of membership for a given value. That is, the percentage to which the linguistic concept can be said to be true and belong to a fuzzy set, relative to the value of the x-axis. A degree membership value of 0 = 0%, 0.5 = 50%, and 1 = 100%, and all permutations between the values of 0 and 100%s. A Gaussian curve was assumed for each input value, indicating a bell-shaped curve was modeled to approximate how the concepts of low, medium, and high would relate to incremental cost increase by the project stakeholders within this hypothetical scenario. It should be noted that the area beneath the curve of each bell-shaped curve sometimes overlaps with the other linguistic concepts; this indicates that the description belongs to both linguistic sets, to some partial degree, creating a contradiction of inputs that simulates differing opinions and perspectives in real world linguistic use.

Figure 2

Figure 2. Fuzzy logic Gaussian input value range for cost.

It is important to note that these input values could and likely would change if the composition of the capital project stakeholders were to change, resulting in differing interpretations of the concepts of low, medium, and high as it relates to this scenario. This is significant in the sense that the Fuzzy Logic model is being customized to the linguistic nuance of a particular, applicable set of people—those with a vested interest in the successful outcome of a given endeavor such as this exercise in optimizing costs relative to attaining quantifiable carbon emissions reduction values.

Figure 3 represents three input ranges that represent the linguistic concepts of red, yellow, and green as they relate to carbon emissions reduction judgements. The x-axis represents carbon emissions reduction expressed in the units of tons. The exponential notation on the x-axis indicates that the units may be interpreted in terms of increments of 10,000 (e.g. 10,000 tons, 20,000 tons, et cetera). The y-axis is the degree of membership for a given value related to the percentage to which the linguistic concept can be said to be true and belonging to a fuzzy set, relative to the value of the x-axis value. As with cost, a Gaussian curve was assumed for each input value, indicating a bell-shaped curve was modeled to approximate how the concepts of red, yellow, and green would relate to Life Cycle Carbon Emissions (LCCE) reduction by the project stakeholders within this hypothetical scenario. Red, yellow, and green were selected due to their common association with the concepts of low, medium, and high or bad, neutral, and good. As was true of the cost inputs, the area beneath the curve of each carbon emissions reduction bell-shaped curve sometimes overlaps with the other linguistic concepts; this indicates that the description belongs to both linguistic sets, to some partial degree, creating a contradiction of inputs that simulates differing opinions and perspectives in real world linguistic use.

Figure 3

Figure 3. Fuzzy logic Gaussian input value range for net LCA carbon emissions reduction.

In addition to re-emphasizing that each concept may relate to differing percentages of truth, the intersection of the curves can be understood as implying equivalent truth. For example, in Figure 2, the input value curves for red and yellow intersect at approximately 24,000 tons of reduced LCCE and approximately 20% membership agreement with both concepts. This is akin to saying that for this amount of carbon emission reduction, stakeholders perceive it to be equally true that the this could be classified as both red and yellow, two distinctive fuzzy sets.

Figure 4 represents output ranges that relate to the fuzzy input values noted in Figures 1, 2 for cost and LCCE reduction. The intent of the output values is to mathematically and visually model the buy value relative to the perception of the hypothetical stakeholders as to what constitutes value loss, value neutrality, and value gain given specific interactions of cost and LCCE reduction. The x-access represents the numeric score derived from the inputs. This scale was structured from 0 to 100. This scale represents an arbitrary range which could feasibly be changed to any range insofar as the membership function plots are readily decipherable. The y-axis remains the degree of membership, ranging in value from 0 to 1, or 0%–100% inclusion within a given fuzzy set.

Figure 4

Figure 4. Fuzzy logic Gaussian output value ranges representing buy value logic.

Fuzzy Logic Rules

Within the MATLAB Fuzzy Logic Designer, the fuzzy logic rules must be encoded. The following logic rules were developed for this simulation:

• If Cost is Low and Carbon Emissions Reduction is Red, then Buy Value is Value Loss

• If Cost is Medium and Carbon Emissions Reduction is Red, then Buy Value is Value Loss

• If Cost is High and Carbon Emissions Reduction is Red, then Buy Value is Value Loss

• If Cost is Low and Carbon Emissions Reduction is Yellow, then Buy Value is Value Neutral

• If Cost is Medium and Carbon Emissions Reduction is Yellow, then Buy Value is Value Neutral

• If Cost is High and Carbon Emissions Reduction is Yellow, then Buy Value is Value Loss

• If Cost is Low and Carbon Emissions Reduction is Green, then Buy Value is Value Gain

• If Cost is Medium and Carbon Emissions Reduction is Green, then Buy Value is Value Gain

• If Cost is High and Carbon Emissions Reduction is Green, then Buy Value is Value Neutral

These rules can be said to be “fuzzy” given all the encoded inputs employ Gaussian, bell-shaped curves that show a range of values relating to a degree of membership instead of the binary membership model of classical set theory (CST).

Adapted from the text Discrete Mathematics, Chapter 5.7 Fuzzy Sets, we see the illustrative comparison of Fuzzy Sets versus Classical “Crisp” Sets which may be applied to this use case (Grami, 2023).

Figure 5 is a visual representation of how carbon emission reduction quantities might be classified using classical set theory and fuzzy set theory, noting that in the case of classical set theory, binary logic does not allow for contradictory membership—it must either be a part of the set or not a part of it. As such, fuzzy logic differs from binary logic in the decision-making process within the underlying mathematical treatment of linguistic interpretation in which fuzzy logic acknowledges a waning spectrum of membership function inclusion, akin to a definitional smear, whereas binary logic creates abrupt definitional borders to appear graphically as logic cliffs within the Figure 5 visualization. Thus, we have sharp division between groups, and the degree of membership function is always expressed as 1 or 0 (i.e. 0% or 100%), with no in-between states recognized, even as the values approach a classification threshold. In this framework, there exists a “jump” in classification from zero membership to full membership from one classification to another up arriving at the respective threshold value. In this instance, “red” is associated with a low carbon emissions reduction value, “yellow” a medium carbon emissions reduction value, and “green” a high carbon emissions reduction value. These values are hypothetical only and created to convey the problematic nature of classical set theory and crisp inputs when dealing with linguistic terminology. Similarly, this visualization could be adapted for cost and buy value classifications, interpreting those fuzzy inputs/outputs in a classical fashion. Note, in this visualization, Grami opted to represent the fuzzy set using a straight line, creating a triangle, whereas in the proposed fuzzy inference system, the authors of this paper have opted to use a Gaussian, curved shape.

Figure 5

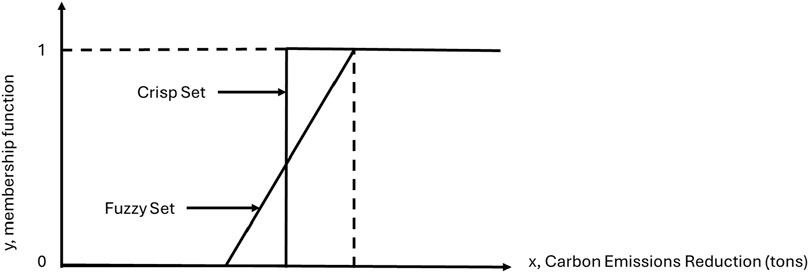
Figure 5. Visual comparison of fuzzy set theory to classical set theory (Source: Reprinted with permission of Elsevier from Discrete Mathematics (Grami, 2023), License Number 5991570523049).

Figure 6 shows an overview of the Mamdani Type 1 Fuzzy Logic method employed within MATLAB with relationships shown between Membership Functions (MFs) modelled as per Figures 1–3. Specifically, a two input Mamdani is shown. A Type 1 Fuzzy Inference System refers principally to the defuzzification process in that uses the centroid method to create a given output value. A Type 2 Fuzzy Inference System models uncertainty within the degree of membership in each fuzzy set (Mathworks, 2024b). While Type 2 could have been employed in this instance, this hypothetical focused on a Type 1 scenario. MATLAB’s Fuzzy Logic designer is capable of both Mamdani and Sugeno Fuzzy Logic. Mamdani was selected because it creates an output that is comprised of fuzzy sets, as Buy Value is more likely to be subjective and specific to the project stakeholders. Sugeno inferences yield outputs that are either a constant or linear mathematical expression which did not match the proposed use case as well (Mathworks, 2024a).

Figure 6

Figure 6. Overview of MATLAB fuzzy logic designer Mamdani Type 1.

Hypothesis testing

Hypothesis testing will be completed by simulating within MATLAB with Fuzzy Logic using the concepts of entrained carbon and cost as the inputs to determine when a given material ought to be selected by an Engineer, Procure, Construct (EPC) company. This simulation will be compared to if/then logic statements modeled in Excel which will represent “classic logic” to determine if the Fuzzy Logic Multi-Criteria Decision Analysis lends itself to a practical Built Environment use case of material selection involving trade-offs of cost and carbon emissions reduction within an environment of unknowns and vagueness.

For the method of ascertaining entrained carbon, this simulation could feasibly leverage industry software such as ProCore or look to indices or manufacturer disclosures revealing LCCE levels to compare the carbon emissions potentials of a basket of materials.

Results

A 3-dimensional control surface was successfully generated via MATLAB’s Fuzzy Toolbox.

Figure 7 is a graphic presentation of buy value output points represented in relation to their controlling input values of cost and net LCA carbon emissions reduction. This is the result of running numerous iterations of a Mamdani Type 1 calculation in which a centroid value is calculated from the shape resulting from the overlapping sections of partial or conflicting “truth”. While there are numerous ways to “defuzzify” values, the popular centroid method is to draw a line parallel to the x-axis to the chosen point of intersection where this are differing fuzzy sets represented as having some membership function value greater than 0. The area above the line is removed and the area below is retained. The resulting shapes are merged into a singular shape, and the centroid of that resulting shape is calculated. This is depicted in Figure 8. The three-dimensional control surface was generated by MATLAB by plotting the resulting values of numerous cost and carbon emissions reduction value combinations. The visualization may be understood to represent the results of a set of numerous, discrete calculations bounded by the constraints identified by the input values and interaction rules. The MATLAB Fuzzy Logic Toolbox then connected all of those resulting points with lines to convey the manner in which the results might conform to three-dimensional space. The control structure involves a 15 × 15 point grid that is adjusted according to the 3^rd dimension of “Buy Value” as defined by the logic rules infilled in the simulation, as noted in the section titled “Fuzzy Logic Rules.”

Figure 7

Figure 7. Fuzzy logic control surface of input values for cost and net LCA carbon emissions reduction quantity yielding a buy value decision output metric.

Figure 8

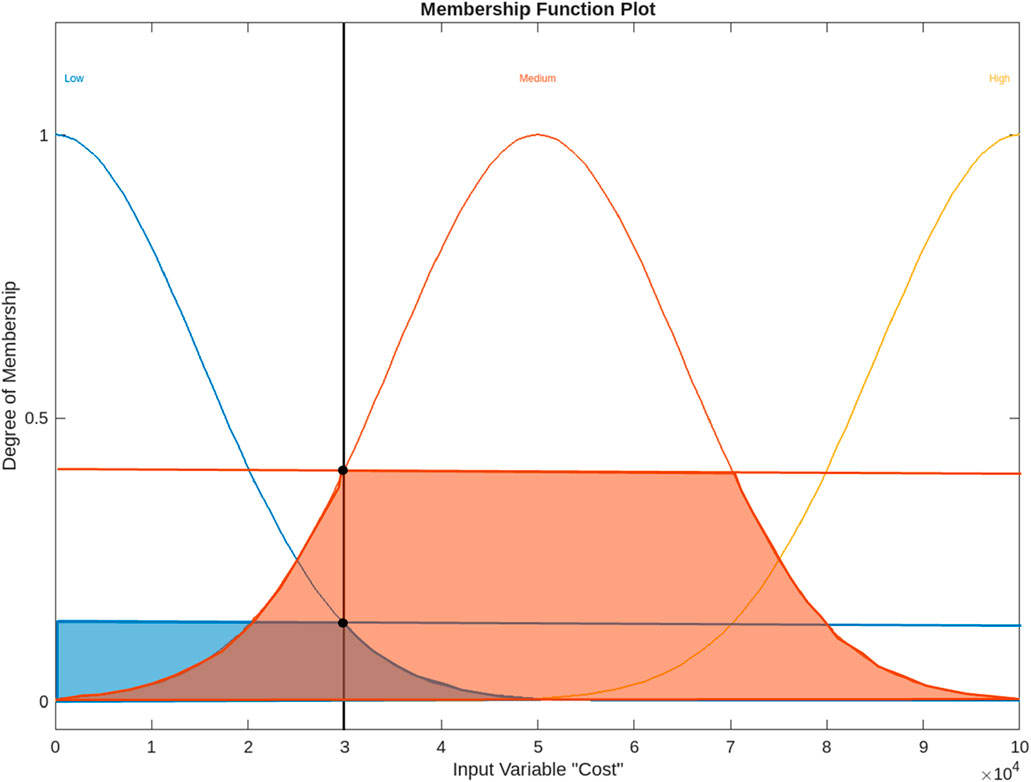
Figure 8. Defuzzification of a Chosen Cost Value by Creating a Single Shape Using the Area Beneath the y-axis point of Intersection for Each Fuzzy Set with a Value Greater than 0.

Recognizing that the control surface is the output of a large set of fuzzy logic projects, a user could quickly infer the buy value of a given purchasing decision by tracing the lines of a given cost and carbon emissions reduction input combination to its corresponding point of intersection on the chart. In instances where there is not perfect alignment along the lines, reasonable interpolation steps may be reasonably and quickly taken. In this fashion, a quick reference guide may be generated to facilitate purchasing decisions without requiring the purchasing professional to re-run the analysis repeatedly, insofar as the input values and logic rules remain unchanged based on stakeholder inputs.

Figure 8 shows the resulting overlap of the area remaining under the curve for the concepts of “low” and “medium” cost at the selected LCCE reduction value of 30,000 tons. The resulting centroid of this shape is the crisp output value for this selected input value. To simplify the geometry, one might choose a triangular input value instead of a curved shape to create trapezoid shapes, allowing end-users to more easily calculate the centroid by hand to facilitate understanding.

225-point outcomes are shown in 3-dimensional space and are linked via connecting lines into a plane that has been contorted to conform to the points of optimization balance between the competing cost and LCCE reduction forces. This visualization may serve as a de facto Decision Support System (DSS) insofar as the input values of the capital project primary stakeholders remain fixed.

Such control surfaces might serve as a clarifying visualization within a procurement procedure, for instance, and serve as reference at the point of purchase. It could feasibly be encoded into purchasing workflows that rely on manual interventions, or it could also be embedded mathematically within automated solutions that seek to simultaneously conform to material and equipment specifications but also enhance Owner value by layering additional trade-optimization logic atop of minimum or mandatory specification requirements. In this fashion, it yields benefits which, depending on the values of a specific entity or project, may take the form of cost savings or carbon emissions reduction or a negotiation of both competing market pressures. Other decision elements might be infilled, such as resistance to a particular corrosive environmental condition versus cost, or warranty duration versus cost, et cetera. Though more complex, the underlying MATLAB methodology represents increased accuracy relative to classical set theory, as graphically represented by Figure 9.

Figure 9

Figure 9. Diagram revealing the Area of the Region Ignored by Non-Binary Linguistic Meaning.

Figure 9 graphically depicts the region of contradictory, partial truth when the cost judgements of low overlap with medium, and the cost judgements of medium overlap with high if the classical sets depicted by the boxed with dashed-line boundaries were employed instead of the fuzzy inputs denoted by the Gaussian curves. By ignoring this in-between state or disagreement within a sample of people, classical set theory may erode the mathematical precision of Decision Support Systems (DSS). Secondarily, the region above the curve but within the boundaries of the crisp sets represents the amount by which the classical set theory is making a discontinuous logic jump, abruptly changing from the low to medium crisp set or from the medium to high crisp set. This figure serves as a representative example of the condition that would also be true for the LCCE reduction input values and the buy value logic output values.

Discussion

Research suggests a growing trend toward hybrid approaches that combine Fuzzy Logic with other mathematical or Multi-Criteria Decision Analysis (MCDA) methods to address its limitations. While hybrid models may improve precision, they also introduce added complexity, which could discourage practical application within the industry due to increased implementation challenges.

Although literature frequently highlights the suitability of Fuzzy Logic for the construction industry—due to its ability to handle vagueness and imprecision—there is often a lack of focus on the diversity of stakeholder priorities. Discussions generally emphasize technical aspects over the cost-reduction and profit-oriented needs of private-sector companies, which vary significantly. Fuzzy logic, however, offers potential as a stakeholder alignment tool, facilitating compromise among project participants and enhancing client satisfaction through consensus-driven decision-making. Stakeholder buy-in is driven by demonstrating to all stakeholders that their input has been mathematically included in the model and so is exerting influence within fuzzy logic application. It should be noted that equal weighting was given to all stakeholders; some entities might prefer custom weighting considerations that relate to the hierarchical position, influence, or technical knowledge of a given stakeholder on a particular decision. By demonstrating stakeholder inclusion, reassurance is given that their input is not being ignored but instead actioned via inclusion in plotting linguistic meaning within fuzzy logic inputs via a percentage of membership inclusion.

As generative AI technologies advance, there is potential for AI models to make faster, more precise decisions, potentially outpacing traditional human review of specifications and LCCE data. This research, while not a comparative study, underscores the current applicability of fuzzy logic as a decision tool for material selection in construction, acknowledging the evolving role of AI but focusing on the present value of fuzzy logic within today’s industry landscape.

It should be noted that the hypothetical fuzzy inputs and output values indicate instances in which the linguistic value associations do not add-up to 100%, indicating portion of the stakeholder population that did not or could associate the given value with one of the given classifications. In practice, this would be unlikely, though not impossible. In practice, the input value ranges may well be different from the assumed Gaussian inputs, leading to different interactions of concepts to varying degrees. The hypothetical illustrates an instance in which two fuzzy sets overlap with each other, but it is possible that additional overlaps might occur.

It may be beneficial to provide a brief explanation of fuzzy logic and its benefits within policies, procedures, and governance. Professionals are used to classical set theory, and this is especially true of built environment professionals who routinely use crisp sets within capital project management such as when applying risk matrices within risk registers. Using simple high, medium, low descriptors for cost, schedule, and probability associations is ubiquitous within industry. The challenge is, absent a learning curve related to fuzzy logic, a fuzzy logic inference system may be perceived as a “black box” in which the inner workers of the math are unknown to end-users. Two-input Mamdani methods are known to be intuitive and reasonably intuitive to understand.

Modeling additional material and equipment purchasing characteristics

There exist numerous material and equipment characteristics which may be of interest to a given capital project team. Durability, Maintenance Requirements and Cost, Installation Complexity represent possible considerations. All of these, conceptually, may be modelled using Fuzzy Logic by going beyond the binary classical set theory approach of affirming that a given material does or does not satisfy the defined specifications but instead model what represents “buy value” to the primary stakeholders across these dimensions, beyond their baseline acceptance threshold value of each one. This, however, would introduce a corresponding increase in the complexity of the creating the rules as the number of rules is an exponential expression of the number of inputs relative to the quantity of linguistic values for each input.

Additional dimensions for purchasing consideration, such as embodied energy and depletion attributable to a given material, are particularly interesting, as these attempt to go beyond a carbon-emissions perspective and address sustainability more comprehensively. The academic literature reveals a number of proposed methods to quantify embodied energy via the Life Cycle Energy Assessment (LCEA) and Life Cycle Impact Assessment (LCIA) that attempts to assess resource depletion (Klinglmair et al., 2014; Chau et al., 2015). While the proposed fuzzy logic method might be employed by encompassing one of the proposed LCEA and LCIA methods, respectively, as additional fuzzy inputs and correspondingly increase the number of fuzzy logic rules. This would require a significant investment of stakeholder and project team analysis to identify the desired method of measure and would further be complicated by the difficulty in accessing the required information on environmental disclosure labels or vendor specification sheets. That is, while it is conceptually possible, it may be practically difficult given the existing availability of product information and lack of unity of governing quantification methods.

Accessibility to non-expert users

Enhancing the accessibility of fuzzy logic framework such that non-experts might engage in its practical application is of great importance if industry adoption aspirations are to be realistically achieved. At core, recognizing which circumstances are best suited to the application of a given MCDA method, to include Fuzzy Logic, represents a great deal of complexity and expert knowledge that may seem insurmountable to a non-expert user. As such, a tool that recognizes the quality of existing data, the ability to develop additional data, and an analysis of the constraints and the underlying intent of a decision to propose best match would greatly enhance accuracy, utility, and user friendliness. Once Fuzzy Logic has been identified as the best match for a given scenario, improvements within the Human Machine Interface (HMI), such as speech recognition and interactivity could greatly enhance the tool. Additionally, instant and web-based linkage to expert assistance via the tool akin to that offered via tax software applications offering the on-demand assistance of Certified Publica Accounts (CPAs). Finally, integrating the MATLAB Fuzzy Logic Toolbox and Fuzzy Logic Designer with a digital polling solution to allow for direct importation of stakeholder linguistic interpretation would also ease the use of the approach for non-expert systems given the current solution requires aggregating and interpreting this data and its plotted shape to occur beyond the bounds of the MATLAB system, enhancing the risk of user input error. User Experience and User Interface (UX/UI) improvements represent a rich field for future research to address these concerns.

System integration with existing procurement software commonly used in construction management, for instance Enterprise Resource Planning (ERP) systems such as SAP, would additionally enhance end user ease of use for the proposed Fuzzy Logic method, as would integration of Environmental Disclosure Data relevant to the modeling exercise.

Limitations of research

This research does not explore alternatives to smooth curves within the Fuzzy Inference System, such as linear or other non-smooth relationships, which could impact the control surface output. Additionally, the simulation focuses solely on two input criteria—cost and entrained carbon reduction. In practice, material selection decisions often involve multiple factors, such as material longevity and lead time, which would increase complexity. Adding more criteria could make the control surface challenging to visualize, as it would require moving beyond a three-dimensional representation, limiting intuitive understanding for construction procurement specialists.

Furthermore, debates in academic literature on the precision of different fuzzy methodologies—such as standard versus extended fuzzy arithmetic or Mamdani versus alternative inference methods—are not addressed in this study. The research utilizes methods available within MATLAB’s Fuzzy Logic Designer, recognizing that more precise computational approaches may exist within academic literature, differing software solutions, or other bodies of knowledge. The emphasis on MATLAB is based on its prevalence within industry. Recognizing this, this research sought to put forth an applied science use case using common tools that may be familiar to built environment professionals.

This paper does not address Classic-Like Fuzzy Logic (Bedregal and Cruz, 2008), Fuzzy Sorting Methods (Yatsalo et al., 2024), or comparable explorations of Fuzzy Set Theory within the subject matter domain of mathematics, computer science, or like instances. This research is intended to present applied science that does not propose original math or science but instead seeks original use cases and applications for existing math and science.

Fuzzy logic limitations within the built environment

While the uses of fuzzy logic are vast, constrained primarily by the limitations placed on practitioners operating within a business environment of free market competition. It is possible to envision a future in which fuzzy logic is a commonly used branch of logic used by complex software in the guise of a Digital Assistant—a broad term the authors of this research will use to mean an artificial intelligence that evaluates multiple decision-making logic paths and proposes a technique that best optimizes the outcome given known information, constraints, and user preferences that will be paired to a team of humans. At the time of this research, great leaps are being made in such technological developments, however, it remains important to understand the underlying means and methods used by such methods on an individual and use case basis and the age of such wide-spread digital interactivity is not yet upon us. As such, we analyze the limitations of fuzzy logic in practical terms, through the eyes of built environment professionals.

The primary limitation of fuzzy logic in the built environment relates to the administrative burden it entails. The number of decisions that must be made in a given design, engineering, and construction endeavor are tremendous. The speed at which they must be made increases with market competition and the desire for continuous improvement. As such, time and cost limitations in gathering the required information to create this model present the greatest barrier.

Though fuzzy logic could certainly be employed without the aid of purpose-built software, its application would be greatly slowed in conflict with the previously noted time pressures that are ubiquitous within capital projects. Software, therefore, becomes a limitation to the application of fuzzy logic within the built environment. This limitation is two-fold: 1) the cost of such software 2) identifying a workforce with a blend of the requisite built environment knowledge and computing literacy required to successfully deploy such methods. Over-reliance of such means of analysis could create process-bottlenecks in which so many decisions are flowing through this method of analysis while the constraints of cost and capable personnel are unable to process such requests. Thus, identifying an appropriate threshold of value for a given decision may allow teams to triage fuzzy logic modeling requests to focus resources where they may yield the most value.

Future research and case study

This research was conceptual and has not yet been validated via the case study method. Future research must be conducted to verify if: 1) Existing specifications and material and equipment procurement methods fail to optimize trade-offs between the discussed decision dimensions 2) The proposed Fuzzy Logic method using MATLAB’s Fuzzy Logic Toolbox according to the described process flow yields an improvement to existing methods employed in industry 3) Quantify “buy value” improvement, cost savings, or carbon emissions reductions that might have been achieved 4) Determine if the use of Fuzzy Logic enhanced Stakeholder Management 5) If the control surface visualization has utility for procurement professionals 6) Assessing the administrative burden of implementing this method relative to any realized improvement measures. 7) Determine the sufficiency and uniformity of available material and equipment environmental disclosure labels to inform such an exercise at scale.

A case study could feasibly be undergone by identifying a willing Owner and contracted EPC entity to undergo a retrospective study of the material procurement that occurred on a given project, and to replicate the procurement exercise using the proposed Fuzzy Logic methodology. Such a study might focus on purchase decisions in which the alternatives remain known, such as if records of comparisons were maintained or if an Owner restricted purchases to a select few manufacturers, per specification. A review of the EPC procurement procedures may be conducted to determine how trade-off decisions are undertaken in the current state.

Conclusion

Fuzzy logic is particularly useful in guiding material and equipment selection decisions in the Built Environment, providing customizable inputs that correspond with stakeholders’ distinct interpretations and preferences. This method facilitates customized, “fit-for-purpose” solutions, circumventing the constraints of a standardized specification model. Updates to ISO standards, such as ISO 21930, should ideally include methods for addressing trade-offs in carbon emissions reporting. These modifications may facilitate a more effective equilibrium between sustainability objectives and competitive market forces, hence improving stakeholder involvement in sustainable decision-making. Numerous opportunities exist for the integration of Fuzzy Logic into work instructions, regulations, and processes. At scale, both in terms of large-scale construction projects but also at a portfolio or even sector level, such optimization improvements could yield tremendous reductions in carbon emissions while still satisfying cost considerations and adhering to project specifications.

Recognized occurrences of classical set theory in capital project management, typically categorized by high, medium, and low input assessments, can be enhanced through fuzzy logic. This implies that an audit should be conducted to identify instances of classical set theory, followed by an estimation to evaluate the impact of a series of prior decisions concerning fuzzy logic results, thereby quantifying the magnitude of the issue on a larger scale.

This study emphasizes how fuzzy logic helps avert sudden classification shifts characteristic of Classical Set Theory, which may lead to erroneous results in decision-making. Enhancing the granularity of classifications may render binary logic more feasible for procurement experts employing traditional methodologies. Subsequent study ought to investigate the practical carbon reduction effects of this strategy and evaluate whether hybrid fuzzy methodologies or novel generative AI models could potentially augment or surpass this method. Indeed, research of hybrid methods using fuzzy logic in concert with other tools exist within academic literature, to include medical use cases (Lefteh et al., 2022).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Visualization, Writing–original draft, Writing–review and editing. RM: Supervision, Validation, Writing–review and editing. CF: Conceptualization, Project administration, Supervision, Writing–review and editing. IN: Supervision, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bedregal, B. C., and Cruz, A. P. (2008). A characterization of classic-like fuzzy semantics. Log. J. IGPL 16 (4), 357–370. doi:10.1093/jigpal/jzn012

CrossRef Full Text | Google Scholar

Chan Albert, P. C., Chan Daniel, W. M., and Yeung John, F. Y. (2009). Overview of the application of “fuzzy techniques” in construction management research. J. Constr. Eng. Manag. 135 (11), 1241–1252. doi:10.1061/(ASCE)CO.1943-7862.0000099

CrossRef Full Text | Google Scholar

Chau, C. K., Leung, T. M., and Ng, W. Y. (2015). A review on life cycle assessment, life cycle energy assessment and life cycle carbon emissions assessment on buildings. Appl. Energy 143, 395–413. doi:10.1016/j.apenergy.2015.01.023

CrossRef Full Text | Google Scholar

Chen, L., and Pan, W. (2021). Review fuzzy multi-criteria decision-making in construction management using a network approach. Appl. Soft Comput. 102, 107103. doi:10.1016/j.asoc.2021.107103

CrossRef Full Text | Google Scholar

Chen, C.-T. (2000). Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 114 (1), 1–9. doi:10.1016/S0165-0114(97)00377-1

CrossRef Full Text | Google Scholar

Cintula, P., Christian, F. G., and Noguera, C. (2023). Fuzzy logic. The Stanford University, Department of Philosophy Summer, 2023.

Google Scholar

Deng, G., Zhang, M., Meng, X., and Yuan, J. (2023). Research on the problem of aggregation of multiple rules in fuzzy inference systems. J. Intelligent & Fuzzy Syst. 45 (2), 2393–2408. doi:10.3233/JIFS-230866

CrossRef Full Text | Google Scholar

Fayek, A. R. (2020). Fuzzy logic and fuzzy hybrid techniques for construction engineering and management. J. Constr. Eng. Manag. 146 (7), 04020064. doi:10.1061/(ASCE)CO.1943-7862.0001854

CrossRef Full Text | Google Scholar

Grami, A. (2023). “Chapter 5 - sets,” in Discrete mathematics. Editor A. Grami (Academic Press), 67–91.

Google Scholar

Huang, W., Li, F., Cui, S.-h., Li, F., Huang, L., and Lin, J.-y. (2017). Carbon footprint and carbon emission reduction of urban buildings: a case in Xiamen city, China. Procedia Eng. 198, 1007–1017. doi:10.1016/j.proeng.2017.07.146

CrossRef Full Text | Google Scholar

Huang, Z., Zhou, H., Miao, Z., Tang, H., Lin, B., and Zhuang, W. (2024). Life-cycle carbon emissions (LCCE) of buildings: implications, calculations, and reductions. Engineering 35, 115–139. doi:10.1016/j.eng.2023.08.019

CrossRef Full Text | Google Scholar

Hussain Hassan, N. M. (2020). Highly-efficient technique for automatic segmentation of X-ray bone images based on fuzzy logic and an edge detection technique. Multidimensional Syst. Signal Process. Int. J. 31 (2), 591–617. doi:10.1007/s11045-019-00677-0

CrossRef Full Text | Google Scholar

Jadidi, O., Hong, T., Firouzi, F., Yusuff, R. M., and Zulkifli, N. (2008). TOPSIS and fuzzy multi-objective model integration for supplier selection problem. J. Achiev. Mater. Manuf. Eng. 31 (2), 762–769.

Google Scholar

Jafari, H. E. M. (2022). Approach to implementing Health and environmental safety system in construction projects using fuzzy logic. Int. J. Innovation Eng. 2, 27–40. doi:10.59615/ijie.2.4.27

CrossRef Full Text | Google Scholar

Karnik, N. N., Mendel, J. M., and Qilian, L. (1999). Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 7 (6), 643–658. doi:10.1109/91.811231

CrossRef Full Text | Google Scholar

Klinglmair, M., Sala, S., and Brandão, M. (2014). Assessing resource depletion in LCA: a review of methods and methodological issues. Int. J. Life Cycle Assess. 19 (3), 580–592. doi:10.1007/s11367-013-0650-9

CrossRef Full Text | Google Scholar

Lefteh, A., Houshmand, M., Khorrampanah, M., and Smaisim, G. F. (2022). “Optimization of modified adaptive neuro-fuzzy inference system (MANFIS) with artificial Bee Colony (ABC) Algorithm for classification of bone Cancer,” in Paper presented at the 2022 Second international Conference on Distributed computing and high performance computing (DCHPC), Qom, Iran, Islamic Republic of, March 02–03, 2022

Google Scholar

Marzouk, M. A., and Eslam, M. (2020). A hybrid fuzzy-optimization method for modeling construction emissions. Grow. Sci. - Decis. Sci. Lett. 9 (1) 202. doi:10.5267/j.dsl.2019.9.002

CrossRef Full Text | Google Scholar

Mathworks. (2024a). Mamdani and Sugeno fuzzy inference systems.

Google Scholar

Mathworks. (2024b). Type-2 fuzzy inference systems.

Google Scholar

McBratney, A. B., and Odeh, I. O. A. (1997). Application of fuzzy sets in soil science: fuzzy logic, fuzzy measurements and fuzzy decisions. Geoderma 77 (2), 85–113. doi:10.1016/S0016-7061(97)00017-7

CrossRef Full Text | Google Scholar

Obradović, R., and Pamucar, D. (2020). Multi-criteria model for the selection of construction materials: an approach based on fuzzy logic. Teh. Vjesn. 27, 1531–1543.

Google Scholar

Pal, N. R., and Bezdek, J. C. (1994). Measuring fuzzy uncertainty. IEEE Trans. Fuzzy Syst. 2 (2), 107–118. doi:10.1109/91.277960

CrossRef Full Text | Google Scholar

Plebankiewicz, E., Zima, K., and Wieczorek, D. (2021). Modeling of time, cost, and risk of construction using fuzzy logic. J. Civ. Eng. & Manag. 27 (6), 412–426. doi:10.3846/jcem.2021.15255

CrossRef Full Text | Google Scholar

Putri, S., and Saputro, D. (2021). Construction fuzzy logic with curve shoulder in inference system mamdani. J. Phys. Conf. Ser. 1776, 012060. doi:10.1088/1742-6596/1776/1/012060

CrossRef Full Text | Google Scholar

Sarihi, M., Shahhosseini, V., and Banki, M. T. (2023). Development and comparative analysis of the fuzzy inference system-based construction labor productivity models. Int. J. Constr. Manag. 23 (3), 423–433. doi:10.1080/15623599.2021.1885117

CrossRef Full Text | Google Scholar

Seo, S., Aramaki, T., Hwang, Y., and Hanaki, K. (2004). Fuzzy decision-making tool for environmental sustainable buildings. J. Constr. Eng. Manag. 130 (3), 415–423. doi:10.1061/(ASCE)0733-9364(2004)130:3(415)

CrossRef Full Text | Google Scholar

Shahrivar, F., Mahmoodian, M., and Li, C. Q. (2022). Comparative analysis of fuzzy multi-criteria decision-making methods in maintenance prioritisation of infrastructure assets. Int. J. Crit. Infrastructures 18 (2), 172–195. doi:10.1504/IJCIS.2022.123422

CrossRef Full Text | Google Scholar

Tan, T., Mills, G., Papadonikolaki, E., and Liu, Z. N. (2021). Combining multi-criteria decision making (MCDM) methods with building information modelling (BIM): a review. Automation Constr. 121, 103451. doi:10.1016/j.autcon.2020.103451

CrossRef Full Text | Google Scholar

Tan, X., Obaid, R., Smaisim, G., Esfahani, M. H., Alsaikhan, F., Baghaei, S., et al. (2022). Investigation of addition of calcium phosphate ceramic to multilayer scaffold for bone applications with improved mechanical properties: fuzzy logic analysis. Ceram. Int. 49, 8339–8349. doi:10.1016/j.ceramint.2022.10.366

CrossRef Full Text | Google Scholar

Yatsalo, B., Radaev, A., Haktanir, E., Skulimowski, A. M. J., and Kahraman, C. (2024). A family of fuzzy multi-criteria sorting models FTOPSIS-Sort: features, case study analysis, and the statistics of distinctions. Expert Syst. Appl. 237, 121486. doi:10.1016/j.eswa.2023.121486

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8 (3), 338–353. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

Zeng, Z., and Gao, Y. (2024). Cost control management of construction projects based on fuzzy logic and auction theory. IEEE Access 12, 130292–130304. doi:10.1109/ACCESS.2024.3438291

CrossRef Full Text | Google Scholar

Zeng, J., An, M., and Smith, N. J. (2007). Application of a fuzzy based decision making methodology to construction project risk assessment. Int. J. Proj. Manag. 25 (6), 589–600. doi:10.1016/j.ijproman.2007.02.006

CrossRef Full Text | Google Scholar