Device topology optimization for an inerter-based structural dynamic vibration absorber

A tuned viscous mass damper (TVMD) and a tuned inerter damper (TID) have been proposed as devices that can achieve weight reduction by replacing the mass element of a structural dynamic vibration absorber (DVA) with an inerter. In the TID, the damping element is arranged in parallel with the spring, making its device topology the same as conventional dynamic vibration absorbers. In contrast, in the TVMD the damping element is arranged in parallel with the inerter. This parallel mechanism of inerter and damping element can be realized in a single device, and the member of the building that supports the device can be used as the spring element, making the TVMD highly practical. In fact, TVMDs with a mass effect equivalent to thousands of tons have been commercialized and applied to high-rise buildings in Japan. This paper aims to clarify the effects of the choice of objective functions and damping element arrangement on the seismic response control effectiveness of inerter-based structural DVAs, providing guidelines for structural engineers in selecting suitable devices to achieve desired control effects. The method of investigation considers a model that encompasses both TVMD and TID configurations and formulates a multi-objective optimization problem to simultaneously minimize the displacement amplification factor and floor response acceleration amplification factor. The results of the multi-objective optimization reveal that the TVMD is optimal when the focus is on controlling displacement response, while the TID is optimal when prioritizing the control of floor response acceleration. It was found that the floor response acceleration amplification factor of a structure containing TVMD could be significantly improved by slightly compromising the displacement response amplification factor, leading to the recommendation of adopting the TVMD configuration as an inerter-based structural DVA.

1 Introduction

Owing to simplicity and independence from external power supplies, passive control technologies are widely applied in practice to suppress undesirable vibrations, including viscous and viscoelastic dampers (Housner et al., 1997; De Domenico et al., 2019; Licari et al., 2015; Kim et al., 2006; Mazza and Labernarda, 2020). However, these conventional dampers generate insufficient control forces when subjected to long-period ground motions, and thus their seismic performance is compromised (Keivan et al., 2017; Luo et al., 2019; Luo and Ikago, 2021). Inerter-based vibration control systems (IVCSs) that can enhance energy dissipation at certain frequencies have been proven to be more effective in addressing this challenge (Ikago et al., 2012a; Lazar et al., 2014; Zhang et al., 2020; Ji et al., 2020; Wang et al., 2024).

An inerter produces force proportional to the relative acceleration between its two terminals, serving as a crucial element in mechanical networks (Smith, 2002; Makris and Moghimi, 2022). The physical realization methods of an inerter include the use of hydraulics (Nakamura et al., 1988; Domenico et al., 2019; Wang et al., 2011), ball-screw mechanisms (Arakaki et al., 1999; Hwang et al., 2007; Papageorgiou et al., 2009; Watanabe et al., 2012; Kida et al., 2012; Nakamura et al., 2014), rack-and-pinion systems (Smith, 2002; Papageorgiou et al., 2009; Saitoh, 2012; Makris and Kampas, 2016), and living hinges (John and Wagg, 2019). Owing to the attractive characteristics of mass amplification effects and frequency-dependent negative stiffness yielded by inerters, various types of inerter-based vibration control systems (IVCSs) have been proposed (Ma et al., 2021). Ikago et al. (2012a) developed a tuned viscous mass damper (TVMD) consisting of a supporting spring connected in series with a parallel arrangement of an inerter and dashpot, and they verified its control effectiveness through numerical analysis and shaking table tests. Watanabe et al. (2012) and Kida et al. (2012) introduced a force-restriction mechanism to the TVMD to limit excessive control forces caused by the large mass amplification effects and extreme excitations. TVMD devices have been put to practical use in high-rise buildings in Japan (Sugimura et al., 2012; Ogino and Sumiyama, 2014; Ishii et al., 2014). Figure 1 is a photograph of a rotary inerter-damper having 6,400 tons of inertance incorporated into a telecommunications building in Sendai, Japan.

Figure 1

Figure 1. TVMD device installed in a telecommunications building.

Zhao et al. (2016) proposed a viscoelastically supported viscous mass damper (VeVMD) by connecting a viscoelastic element to a parallel inerter-damper device in series and investigated its application to base-isolated structures. Unlike TVMD and VeVMD, the configuration of the tuned inerter damper (TID) proposed by Lazar et al. (2014) is similar to that of a traditional tuned mass damper (TMD). Another way of using an inerter to improve the performance of a TMD is the tuned mass damper inerter (TMDI) proposed by Marian and Giaralis (2014). Further different configurations of IVCSs have been investigated by Hu and Chen (2015) and Pan and Zhang (2018).

Analytical solutions for the $H_{\infty }$ and $H_2$ control designs for a single-degree-of-freedom (SDOF) structure containing an IVCS have been presented (Ikago et al., 2012a; Marian and Giaralis, 2014; Hu et al., 2015). It is difficult to directly extend the design formulas for a SDOF structure to a multi-degree-of-freedom (MDOF) structure because a MDOF system containing IVCSs is generally non-classically damped, and thus modal interactions and the device distribution pattern significantly influence their performance (Qiao et al., 2023). Ikago et al. (2012b) found that the fixed-point method can be expanded to a MDOF shear building structure containing TVMDs when their inertance distribution is proportional to the primary stiffnesses. Kang and Ikago (2023) derived an approximated closed-form design formula for a concentratedly arranged TVMD in a MDOF structure by using the Sherman–Morrison formula. In the tuning of a MDOF structure containing a TID, Lazar et al. (2014) assumed that only the first vibration mode was significant ingnoring the modal interaction the modal interaction. Numerical algorithms were also adopted in the optimization of IVCSs for MDOF structures (Ji et al., 2021; Cao and Li, 2022; Caicedo et al., 2021).

Although single-objective optimum design using relative displacement or floor response acceleration as an objective function is simple and thus convenient for the design of IVCS systems, more than two response values that are in a trade-off relationship are considered simultaneously in structural design practice. Pan et al. (2018) examined a multi-objective optimum design problem (MODP) to minimize response and cost for a TVMD-variant damper by using an $\epsilon$-constraint approach. Taflanidis et al. (2019) developed a design method that considered suppressing seismic responses and control forces simultaneously and sought Pareto optimal designs for three types of IVCS: TVMD, TID, and TMDI. However, the selection of proper devices for diverse seismic control demands remains unclear for structural engineers, particularly when dealing with long-period ground motions.

This study intends to identify the benefits and drawbacks of the IVCSs in controlling displacement and absolute acceleration through illustrative multi-objective designs of the VeVMD with a device topology that encompasses those of the two major inerter-based structural DVAs studied in the literature—the TVMD and TID. The peak displacement and peak absolute acceleration amplification factors employed as objective functions are highly associated with damage to structural and nonstructural components, which are highlighted as major issues for the seismic resilience of high-rise buildings (Ji et al., 2020). The rest of this paper is organized as follows. In Section 2, an analytical model of a SDOF structure containing a VeVMD is presented, and two transfer functions are introduced as objective functions for a multi-objective optimum design problem. Section 3 shows how the multi-objective optimum design of VeVMD converges to TVMD and TID device topologies when the focus is on displacement and absolute acceleration control, respectively. In Section 4, an analytical example using a ten-story shear building equipped with TVMD and TID subjected to strong ground motions, demonstrating that the $H_{\infty }$ control designs effectively mitigate seismic displacement responses and floor response accelerations, respectively. Section 5 concludes this study.

2 Amplification factors

2.1 Single-degree-of-freedom structural model and equations of motion

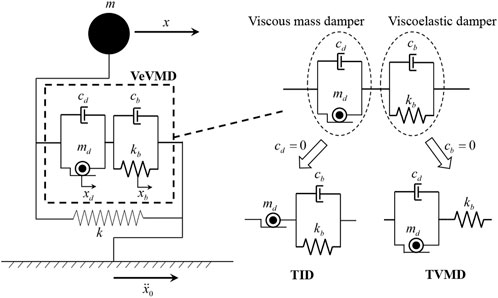
The analytical model of a SDOF structure equipped with a VeVMD is presented in Figure 2. The mass and stiffness of the primary SDOF structure are $m$ and $k$, respectively. The SDOF structure is assumed to be undamped for simplicity’s sake. As shown in Figure 2, the VeVMD comprises an inerter-damper and viscoelastic element in series. The inertance and stiffness of the VeVMD are $m_d$ and $k_b$, respectively. The damping coefficients of the dampers arranged in parallel with the inerter and spring are $c_d$ and $c_b$, respectively. The device topology of a VeVMD encompasses those of TVMD and TID. When the dashpot arranged in parallel with the inerter is removed—$c_d=0$—the VeVMD reduces to a TID. Similarly, the VeVMD reduces to a TVMD when the dashpot arranged in parallel with the spring is removed—$c_b=0$.

Figure 2

Figure 2. Analytical model of a SDOF structure containing a VeVMD.

$x$ is the displacement of the primary mass relative to the ground. $x_b$ and $x_d$ are the deformations of the spring and inerter, respectively. Accordingly, the equations of motion of the SDOF structure equipped with a VeVMD are

$\left\{\begin{array}{c}m\ddot{x}+kx+m_d{\ddot{x}}_d+c_d{\dot{x}}_d=-m{\ddot{x}}_0\hfill \\ m_d{\ddot{x}}_d+c_d{\dot{x}}_d=k_b{x}_b+c_b{\dot{x}}_b\hfill \\ x=x_b+x_d\hfill \end{array}\right..(1)$

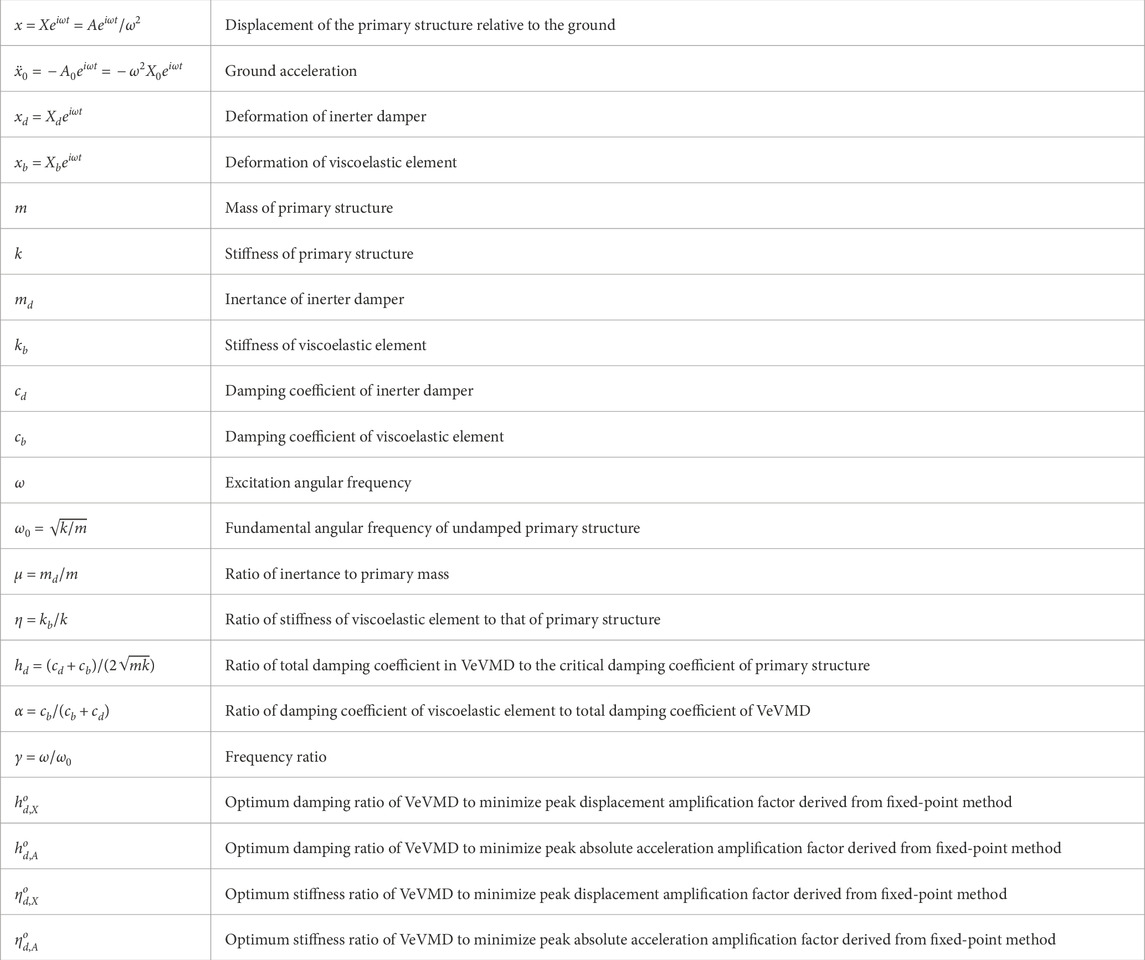
Table 1 summarizes the notations used in this paper.

Table 1

Table 1. Nomenclature.

2.2 Transfer functions

Here we consider a harmonic ground excitation ${\ddot{x}}_0=-{\omega }^2{X}_0{e}^{i\omega t}=-A_0{e}^{i\omega t}$, where $i=\sqrt{-1}$, $\omega$, and $t$ are the imaginary unit, excitation angular frequency, and time, respectively. The responses of the primary structure and VeVMD are expressed in Equation 2.

$x=X{e}^{i\omega t},\ddot{x}=-{\omega }^{2}X{e}^{i\omega t}=-A{e}^{i\omega t},x_d=X_d{e}^{i\omega t},x_b=X_b{e}^{i\omega t}.(2)$

Accordingly, Equation 1 can be rewritten as

$-m{\omega }^{2}X+\left(k+K\left(i\omega \right)\right)X=m{A}_0=m{\omega }^2{X}_0,(3)$

$K\left(i\omega \right)=\frac{\left(c_{b}i\omega +k_b\right)\left(c_{d}i\omega -m_d{\omega }^2\right)}{k_b-m_d{\omega }^2+\left(c_b+c_d\right)i\omega },(4)$

where $K(i\omega )$ represents the dynamic stiffness of the VeVMD.

In this study, we examined two transfer functions, $H_X(i\omega )$ and $H_A(i\omega )$, which are defined as a transfer function from the ground acceleration $(A_0)$ to the displacement of the primary structure relative to the ground $(X)$ and a transfer function from the ground acceleration $(A_0)$ to the absolute response acceleration of the primary structure $(A+A_0)$, respectively.

$\begin{array}{cc}\hfill H_X\left(i\omega \right)& \hfill =\frac{X\left(i\omega \right)}{A_0}\hfill \\ \hfill H_A\left(i\omega \right)& \hfill =\frac{A\left(i\omega \right)+A_0}{A_0}.\hfill \end{array}(5)$

Substituting Equations 3 and 4 into Equation 5 obtains

$\begin{array}{l}{\omega }_0^2{H}_X\left(i\omega \right)\\ =\frac{k\left\{k_b-m_d{\omega }^2+\left(c_b+c_d\right)i\omega \right\}}{\left(-m{\omega }^2+k\right)\left\{k_b-m_d{\omega }^2+\left(c_b+c_d\right)i\omega \right\}+\left(c_{b}i\omega +k_b\right)\left(c_{d}i\omega -m_d{\omega }^2\right)},\end{array}(6)$

$\begin{array}{l}{H}_A\left(i\omega \right)\\ =\frac{k\left\{k_b-m_d{\omega }^2+\left(c_b+c_d\right)i\omega \right\}+\left(c_{b}i\omega +k_b\right)\left(c_{d}i\omega -m_d{\omega }^2\right)}{\left(-m{\omega }^2+k\right)\left\{k_b-m_d{\omega }^2+\left(c_b+c_d\right)i\omega \right\}+\left(c_{b}i\omega +k_b\right)\left(c_{d}i\omega -m_d{\omega }^2\right)}.\end{array}(7)$

Introducing the nondimensional parameters are expressed in Equation 8.

${\omega }_0=\sqrt{\frac{k}{m}},\mu =\frac{m_d}{m},\eta =\frac{k_b}{k},h_d=\frac{c_b+c_d}{2\sqrt{mk}},\alpha =\frac{c_b}{c_b+c_d},\gamma =\frac{\omega }{{\omega }_0}.(8)$

Equations 6 and 7 can be rewritten as

$\begin{array}{l}{\omega }_0^2{H}_X\left(i\omega \right)\\ =\frac{\eta -\mu {\gamma }^2+2h_d\gamma i}{\left(1-{\gamma }^2\right)\left(\eta -\mu {\gamma }^2\right)-\mu \eta {\gamma }^2-4h_d^2\alpha \left(1-\alpha \right){\gamma }^2+2\left\{1-{\gamma }^2+\eta \left(1-\alpha \right)-\left.\alpha \mu {\gamma }^2\right)\right\}{h}_d\gamma i},\end{array}(9)$

$\begin{array}{l}{H}_A\left(i\omega \right)\\ =\frac{\eta -\mu {\gamma }^2-\mu \eta {\gamma }^2-4h_d^2\alpha \left(1-\alpha \right){\gamma }^2+2\left\{1+\eta \left(1-\alpha \right)\left.-\alpha \mu {\gamma }^2\right)\right\}{h}_d\gamma i}{\left(1-{\gamma }^2\right)\left(\eta -\mu {\gamma }^2\right)-\mu \eta {\gamma }^2-4h_d^2\alpha \left(1-\alpha \right){\gamma }^2+2\left\{1-{\gamma }^2+\eta \left(1-\alpha \right)\left.-\alpha \mu {\gamma }^2\right)\right\}{h}_d\gamma i}.\end{array}(10)$

Note that ${\omega }_0^2$ is multiplied to both sides of Equation 9 such that they are dimensionless.

3 Single- and multi-objective $H_{\infty }$ optimization

3.1 Fixed-point method for single-objective $H_{\infty }$ optimization

The dimensionless displacement transfer function shown in Equation 9 can be rewritten as Equation 11.

$|{\omega }_0^2{H}_X|=\sqrt{\frac{B^2+D^2\cdot 4h_d^2}{E^2+G^2\cdot 4h_d^2}},(11)$

where $B$ and $E$ are the real parts of the numerator and denominator of Equation 9, respectively; $D$ and $G$ are the imaginary parts of the numerator and denominator of Equation 9 divided by $2h_d$, respectively. There exist fixed points at which the curves of the transfer function pass though regardless of the damping ratio $h_d^2$ when $B^2/E^2=D^2/G^2$ (Hartog, 1985). The condition can be rewritten as

$\frac{{\left(\eta -\mu {\gamma }^2\right)}^2}{{\left\{\left(1-{\gamma }^2\right)\left(\eta -\mu {\gamma }^2\right)-\mu \eta {\gamma }^2-4h_d^2\alpha \left(1-\alpha \right){\gamma }^2\right\}}^2}=\frac{1}{{\left\{1-{\gamma }^2+\eta \left(1-\alpha \right)-\alpha \mu {\gamma }^2\right\}}^2}.(12)$

The denominator of the right-hand side of Equation 12 indicates that $E$ is independent of $h_d^2$ when $\alpha =0$ and 1. Thus, $\alpha$ should be 0 (TVMD) or 1 (TID) for fixed-points to exist. Indeed, the fixed-point method can be used to derive $H_{\infty }$ optimum designs of a SDOF structure equipped with TVMD $(\alpha =0)$ and TID $(\alpha =1)$ (Ikago et al., 2012a; Lazar et al., 2014; Hu and Chen, 2015; Lobato and Steffen Jr, 2017). This method utilizes the feature that transfer function curves pass through fixed points regardless of damping, and decreasing the ordinate of one of the fixed points increases that of another in TVMD and TID. Provided that the values of transfer function never fall below those of fixed points, the $H_{\infty }$ norm can be minimized by equalizing the ordinates of the fixed points and rendering the transfer function to take peak values at the fixed points. It is similar with the acceleration transfer function (Equation 10). Table 2 summarizes the closed-form expressions of the optimum designs obtained by the fixed-point method for TVMD $(\alpha =0)$ and TID $(\alpha =1)$ (Ikago et al., 2012a; Saito et al., 2008; Lazar et al., 2014; Hu et al., 2015), where superscript ^o denotes optimum designs. Subscripts $X$ and $A$ denote optimum designs of displacement and absolute acceleration control, respectively.

Table 2

Table 2. $H_{\infty }$ control design for inerter-based structural DVAs derived from the fixed-point method (Ikago et al., 2012a; Lazar et al., 2014; Saito et al., 2008; Hu et al., 2015).

3.2 Definition of non-inferiority

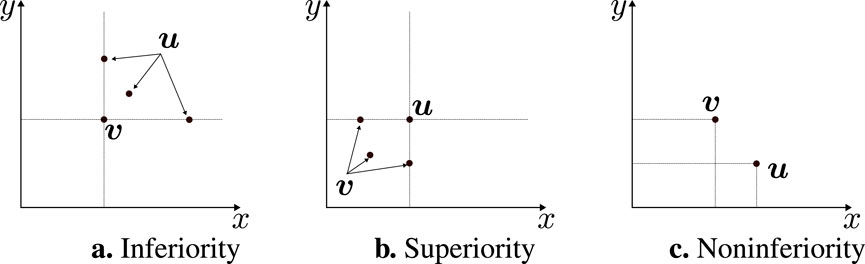
Since we consider a multi-objective minimization problem in this study, the following definitions apply (Fonseca and Fleming, 1993) (Figure 3).

Figure 3

Figure 3. Non-inferiority. (A) Inferiority, (B) superiority, and (C) non-inferiority.

3.2.1 Inferiority

A vector $\mathit{u}=(u_1,u_2,\dots ,u_n)$ is said to be inferior to $\mathit{v}=(v_1,v_2,\dots ,v_n)$ if and only if $v$ is partially less than $u$ which is expressed by Equation 13.

$\forall j=\mathrm{1,2},\dots ,n:v_j\le u_j\wedge \exists j=\mathrm{1,2},\dots ,n:v_j<u_j.(13)$

3.2.2 Superiority

A vector $\mathit{u}=(u_1,u_2,\dots ,u_n)$ is said to be superior to $\mathit{v}=(v_1,v_2,\dots ,v_n)$ if and only if $v$ is inferior to $u$.

3.2.3 Non-inferiority

Vectors $\mathit{u}=(u_1,u_2,\dots ,u_n)$ and $\mathit{v}=(v_1,v_2,\dots ,v_n)$ are said to be non-inferior to one another if $v$ is neither inferior nor superior to $u$.

3.3 Multi-objective optimum design problems

Here, Equation 14 defines the infinity norms of the transfer functions as follows:

$\begin{array}{cc}\hfill {\rho }_X& \hfill ={\omega }_0^2\underset{\omega }{\max }\left\{H_X\left(i\omega \right)\right\},\hfill \\ \hfill {\rho }_A& \hfill =\underset{\omega }{\max }\left\{H_A\left(i\omega \right)\right\}.\hfill \end{array}(14)$

The multi-objective optimum design problem is formulated as shown in Equation 15. [MODP]

$\begin{array}{cc}\text{Find}\hfill & \mathit{\nu }=\left\{\mu ,\eta ,\alpha \right\}\hfill \\ \text{to\hspace{0.17em}minimize}\hfill & \left\{{\rho }_X,{\rho }_A\right\}\hfill \\ \text{subject\hspace{0.17em}to}\hfill & \left\{\begin{array}{c}0\le \mu \le 1.0\hfill \\ 0\le \eta \le 1.0\hfill \\ 0\le \alpha \le 1.0.\hfill \end{array}\right.\hfill \end{array}(15)$

The solution of this problem is not a single design but a set of non-inferior designs, referred to as the “Pareto-optimal set”.

Here, the total damping coefficient in the VeVMD is preset such that $h_d=0.1$ $(c_b+c_d=0.1\times 2\sqrt{mk})$, and the ratio $\alpha$ determines the distribution of damping coefficient assigned to $c_b$ and $c_d$. The MODP can be converted to a series of single objective optimum design problems with varying weight $\xi =[\mathrm{0,1}]$ as follows (Marler and Arora, 2010; Steuer, 1986; Japan Society of Seismic Isolation, 2013):

[Scalarized optimum design problem]

$\begin{array}{cc}\text{Find}\hfill & \mathit{\nu }\hfill \\ \text{to\hspace{0.17em}minimize}\hfill & \sigma \left(\xi \right)=\left(1-\xi \right){\rho }_X+\xi {\rho }_A\hfill \\ \text{subject\hspace{0.17em}to}\hfill & \left\{\begin{array}{c}0\le \mu \le 1.0\hfill \\ 0\le \eta \le 1.0\hfill \\ 0\le \alpha \le 1.0,\hfill \end{array}\right.\hfill \end{array}(16)$

where $\sigma (\xi )$ is a scalarized objective function.

3.4 Pareto-optimal set

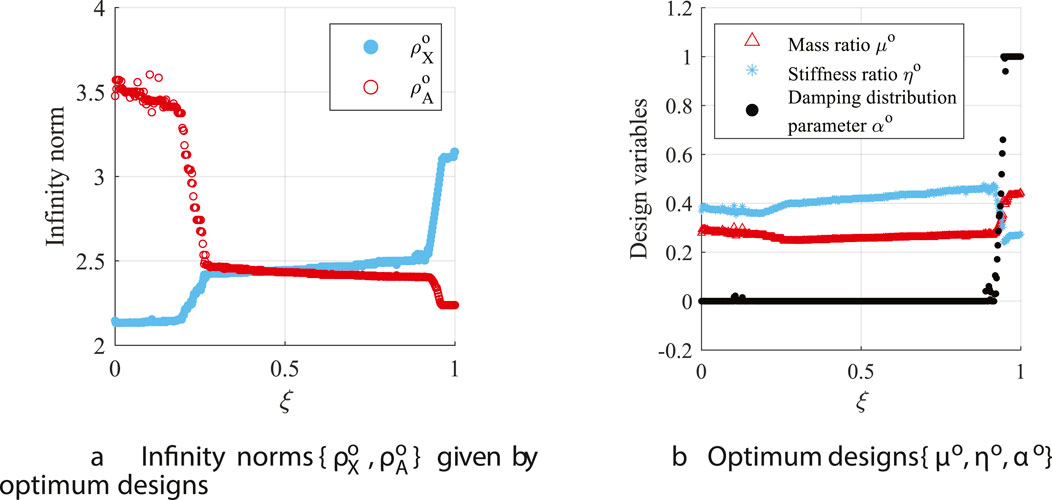
The Pareto-optimal set obtained by solving Equation 16 are functions of $\xi$ and are represented by ${\mathit{\nu }}^o(\xi )=\{{\mu }^o(\xi ),{\eta }^o(\xi ),{\alpha }^o(\xi )\}$. The objective functions given by ${\nu }^o(\xi )$ are represented by ${\rho }_X^o(\xi )$ and ${\rho }_A^o(\xi )$. Similarly, the value of scalarized objective function yielded by an optimum design for $\xi$ is represented by ${\sigma }^o(\xi )=(1-\xi ){\rho }_X^o(\xi )+\xi {\rho }_A^o(\xi )$. Figures 4A and B show the optimum designs and the values of the objective functions yielded by them with respect to $\xi$ varying from 0 to 1 with an interval of $\mathrm{\Delta }\xi =0.002$. ${\rho }_A^o(\xi )$ naturally decreases at the expense of ${\rho }_X^o(\xi )$ as the weight $\xi$ increases. While $\xi$ is in between 0 and 0.9, a slight change is observed in the optimum design variables. However, when $\xi$ increases beyond 0.9, ${\alpha }^o(\xi )$ suddenly jumps from a value around 0 to that around 1. This indicates that an optimal design of the VeVMD gives a design that is close to the TVMD device topology $(\alpha =0)$ while $\xi$ is between 0 and 0.9; once $\xi$ exceeds 0.9, it shifts to the TID device topology $(\alpha =1)$.

Figure 4

Figure 4. Optimum designs $(h_d=0.10)$: (A) infinity norms $\{{\rho }_X^o,{\rho }_A^o\}$ given by optimum designs, (B) optimum designs $\{{\mu }^o,{\eta }^o,{\alpha }^o\}$.

Thus, as shown in Figure 5A, the optimum designs are classified into TVMD, VeVMD, and TID configurations when ${\alpha }^o<0.05$, $0.05\le {\alpha }^o<0.95$, and $0.95\le {\alpha }^o$ and identified by red, black, and blue colors, respectively. Figure 5 plots $\{{\rho }_X^o,{\rho }_A^o\}$ for a series of $\xi$ varying from 0 to 1 with an interval of $\mathrm{\Delta }\xi =0.002$, which is referred to as the Pareto front. In Figure 5B, the colors of the solid circle notations represent $\xi$ value as indicated by the color bar. The minima of the peak displacement amplification factor ${\rho }_X^o(\xi )$ and peak absolute acceleration amplification factor ${\rho }_A^o(\xi )$ are attained at $\xi =0$ and $\xi =1$, respectively. The TVMD and TID configurations thus perform effectively in mitigating displacement and absolute acceleration, respectively. This is because, while the excitation frequency is relatively low, the dynamic stiffness of the inerter is relatively low compared to the spring element in the VeVMD (Figure 2), resulting in larger motion and thereby efficient energy dissipation in the damper arranged parallel to the inerter $(c_d)$. As the excitation frequency increases, the dynamic stiffness of the inerter increases to hinder the motion of the damper arranged parallel to it, which lead to the dominated energy dissipation in the damper arranged parallel to the spring $(c_b)$.

Figure 5

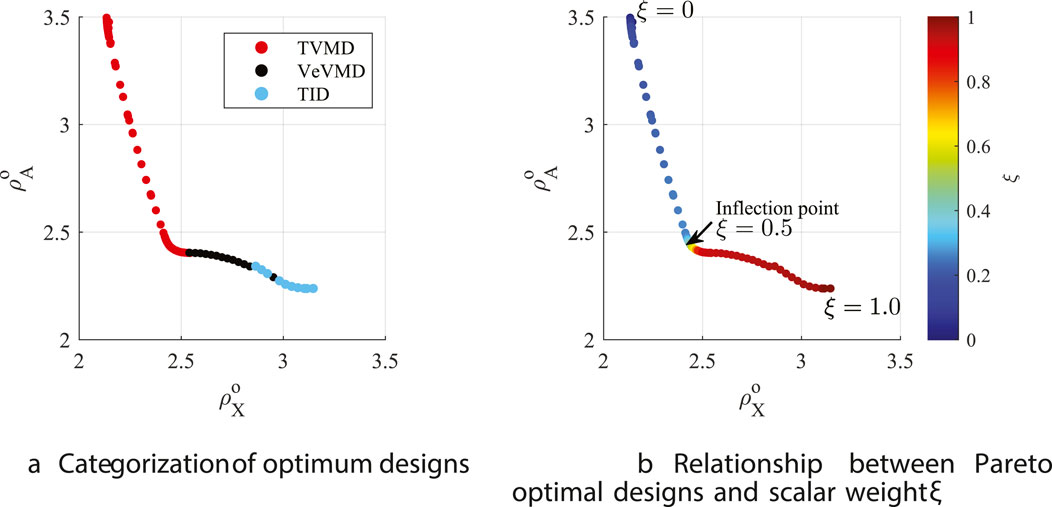
Figure 5. Pareto front $(h_d=0.10)$: (A) categorization of optimum designs; (B) relationship between Pareto optimal designs and scalar weight $\xi$.

As shown in Figure 5B, the inclination of the Pareto front curve significantly changes at the inflection point of the curve at $\xi =0.5$. The improvement of ${\rho }_X^o(\xi )$ demands significant expense of ${\rho }_A^o(\xi )$ when $\xi <0.5$, whereas the sensitivity of ${\rho }_A^o(\xi )$ with respect to $\xi$ significantly decreases beyond $\xi =0.5$. Thus, the solution at the inflection point, which is hereafter referred as the inflection point design, is one of the best options for structural engineers to pick from the Pareto-optimal set. Another benefit of choosing the inflection point design is that its device topology is TVMD that has been put to practical use in real-life buildings. The rest of this paper exclusively focuses on the inflection point design for the multi-objective optimum design problem.

3.5 Comparison between single- and multi-objective optimum designs

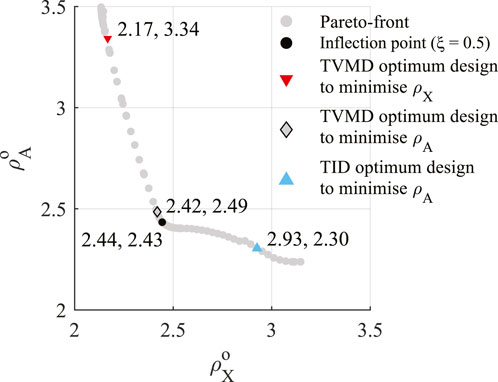
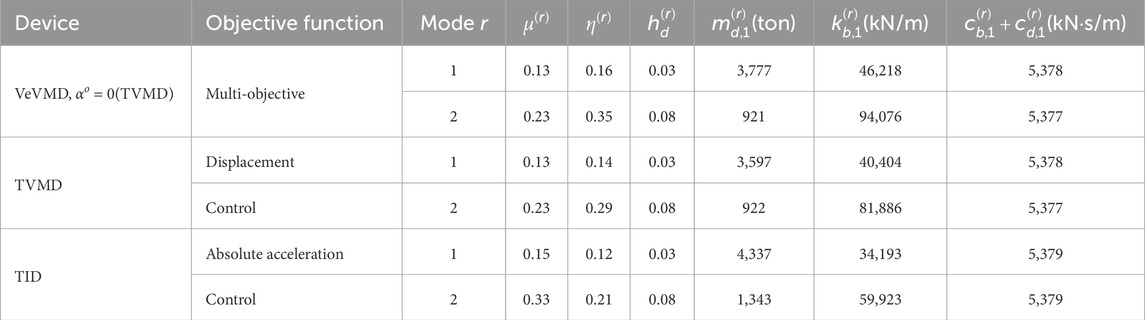
Here, we compare the single objective optimum designs and inflection point design derived from the multi-objective optimum design problem. Table 2 summarizes the closed form expressions for single objective optimum designs (Ikago et al., 2012a; Lazar et al., 2014; Saito et al., 2008; Hu et al., 2015). The superscript of the design variables, TVMD and TID, represents the device topologies. The subscript $X$ and $A$ represent displacement and absolute acceleration control designs, respectively. For example, ${\eta }_X^{\text{TVMD}},h_{d,X}^{\text{TVMD}}$ represent the $H_{\infty }$ control design of TVMD to minimize the peak displacement amplification factor.

To compare the performance of the inflection point design of the multi-objective optimum design problem and the solution obtained from fixed point methods, the values of design variables are determined under the constraint that all systems maintain an identical damping ratio $h_d=0.10$.

For the $H_{\infty }$ control of displacement amplification factor of TVMD system as shown in Equation 17;

$h_{d,X}^{\text{TVMD}}=\frac{\mu }{2}\sqrt{\frac{3\mu }{\left(1-\mu \right)\left(2-\mu \right)}}=0.10(17)$

was solved with respect to $\mu$ and accordingly ${\eta }_X^{\text{TVMD}}$ was obtained. ${\mu }_A^{\text{TVMD}},{\eta }_A^{\text{TVMD}},{\mu }_A^{\text{TID}}$, and ${\eta }_A^{\text{TID}}$ were calculated in a similar manner. Table 3 summarizes the optimum designs of IVCSs when $h_d=0.10$.

Table 3

Table 3. Optimum designs of IVCSs incorporated into the SDOF structure.

Figure 6 plots the $H_{\infty }$ norms of the IVCSs. Any point on the curve of the Pareto-optimal set in Figure 6 is noninferior to another according to the definition of noninferiority presented in Section 3.2., demonstrating the validity of the scalarization method in deriving multi-objective optimal design. The multi-objective design problem at $\xi =0$ yields TVMD configuration minimizing the peak displacement amplification factor, which is equivalent to the single-objective design problem to minimize the peak displacement amplification factor of the TVMD system. However, the $H_{\infty }$ norm obtained from the fixed-point method represented by red downward triangle notation is dislocated from the upper-left endpoint of the Pareto front. Similarly, the $H_{\infty }$ norm of the fixed-point solution minimizing the peak absolute acceleration amplification factor represented by blue triangle notation is dislocated from the bottom-right endpoint of the Pareto front. This is because the closed form solutions are approximations.

Figure 6

Figure 6. $H_{\infty }$ norms of IVCSs.

The inflection point design (solid black circle in Figure 6) improves ${\rho }_A^o$ by 27% at the 12% expense of ${\rho }_X^o$ compared to the fixed-point TVMD displacement control design (solid red downward-pointed triangle), while it improves ${\rho }_X^o$ by 17% at the 6% expense of ${\rho }_A^o$ compared to the fixed-point TID acceleration control design (sold blue triangle).

Figure 7A depicts the displacement amplification factors when $h_d=0.10$. The $H_{\infty }$ optimum design to minimize ${\rho }_X$ shown in a red dashed line exhibits two aligned peaks attaining the minimum peak displacement amplification factor among the four optimum designs, and other optimum designs exhibit uneven peaks because they are detuned in terms of displacement control objective. Conversely, the red dashed line exhibits slightly uneven peaks, whereas the other three optimum designs with the acceleration control objective exhibit aligned peaks (Figure 7B).

Figure 7

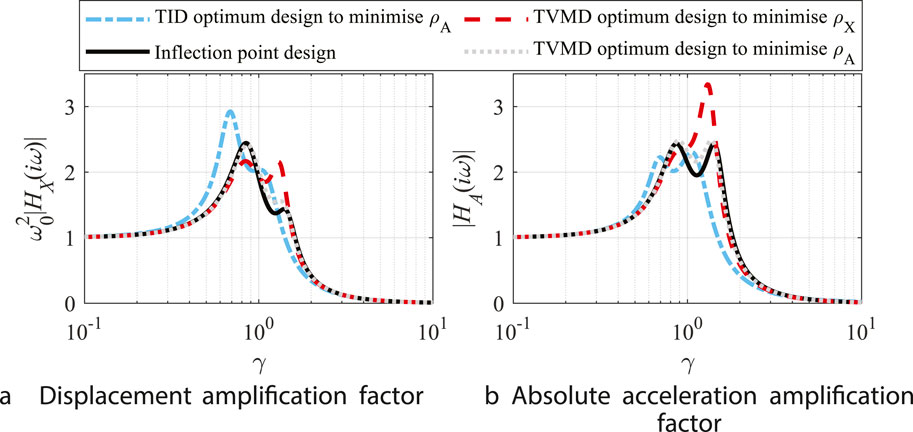
Figure 7. Amplification factors: (A) displacement amplification factor and (B) absolute acceleration amplification factor.

From Table 2, the single objective $H_{\infty }$ control design of TVMD to minimize peak acceleration amplification factor $({\mu }_A^{\text{TVMD}}=0.24,{\eta }_A^{\text{TVMD}}=0.39)$, is similar to that of the inflection point design derived from the multi-objective optimum design problem $({\mu }^o=0.25,{\eta }^o=0.42)$, which results in similar amplification factor curves shown by black solid and gray dashed lines in Figures 7A and B. This means that the closed form expression of TVMD acceleration control design $({\mu }_A^{\text{TVMD}},{\eta }_A^{\text{TVMD}},h_{d,A}^{\text{TVMD}})$ serves as an excellent initial guess in seeking a numerical solution for the inflection point design. The fixed-point TVMD acceleration control design can be an acceptable alternative to the inflection point design when a high precision in manufacturing the device is not required.

Figure 8 demonstrates that the fixed-point TVMD acceleration control designs give good approximations of the inflection point designs in general cases, including those other than $h_d=0.10$.

Figure 8

Figure 8. Comparison of Pareto fronts with a different additional damping ratio $h_d$.

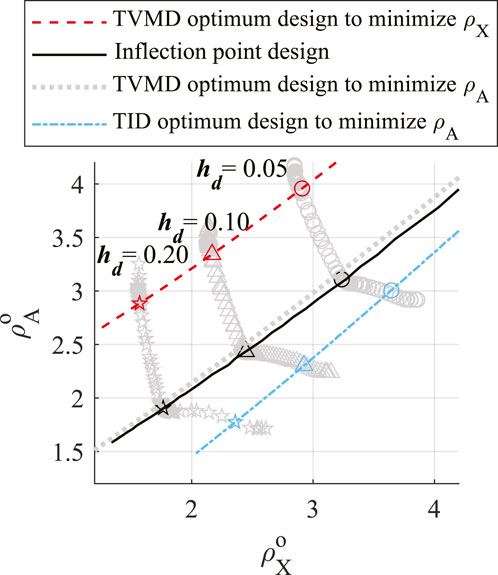
3.6 Robustness of TVMD with respect to the variation in design variables

To examine the robustness of a TVMD with respect to the variation of design variables, Equation 18 defines two indices.

${\zeta }_X\left(\mu ,\eta \right)=\frac{{\rho }_X\left(\mu ,\eta ,\alpha =0\right)}{{\rho }_X^o},{\zeta }_A\left(\mu ,\eta \right)=\frac{{\rho }_A\left(\mu ,\eta ,\alpha =0\right)}{{\rho }_A^o}.(18)$

Since we examine TVMD exclusively, $\alpha =0$.

Figures 9A and B show the contour of ${\zeta }_X(\mu ,\eta )$ and ${\zeta }_A(\mu ,\eta )$ when $h_d=0.10$. The solid-colored circles represent the Pareto optimal designs of the VeVMD. The colors represent $\xi$ value as indicated by the color bar. The fixed-point TVMD acceleration control design $({\mu }_A^{\text{TVMD}},{\eta }_A^{\text{TVMD}})$, represented by solid gray diamond notation and inflection point design $({\mu }^o(\xi =0.5),{\eta }^o(\xi =0.5))$ represented by a solid black circle are located in an area where contour lines are sparse (less sensitive). On the other hand, the fixed-point TVMD displacement control design $({\mu }_X^{\text{TVMD}},{\eta }_X^{\text{TVMD}})$, represented by a solid red downward-pointing triangle, is located in an area where contour lines are dense (sensitive), indicating that the fixed-point TVMD acceleration control design $({\mu }_A^{\text{TVMD}},{\eta }_A^{\text{TVMD}})$, and inflection point design $({\mu }^o(\xi =0.5),{\eta }^o(\xi =0.5))$ are more robust to variations in design variables than fixed-point TVMD displacement control design $({\mu }_X^{\text{TVMD}},{\eta }_X^{\text{TVMD}})$.

Figure 9

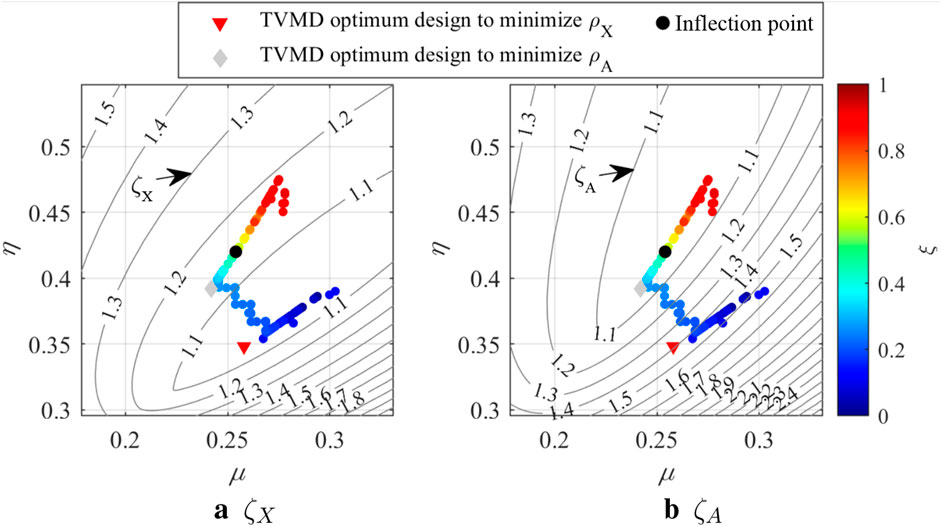
Figure 9. Performance indices: (A) displacement amplification factor and (B) absolute acceleration amplification factor.

4 Analytical example

4.1 Ten-story shear building

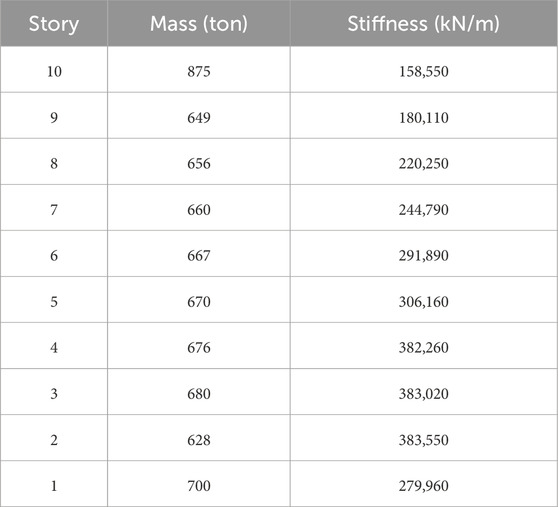
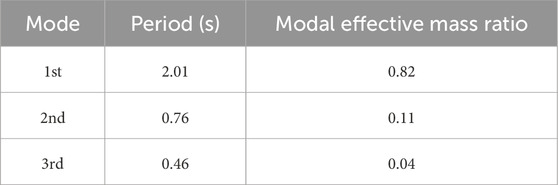
To examine the performance of inflection point design and fixed point designs in a multi-story structure, we use a ten-story benchmark shear building model presented by the Japan Society of Seismic Isolation (2013). Figure 10 shows the analytical model of the benchmark structure. $m_j,k_j,c_j$, and $x_j$ are the mass, stiffness, damping coefficient, and the displacement relative to the ground, respectively. ${\ddot{x}}_0$ is the ground acceleration. Table 4 lists the mass and stiffness distribution of the structural model. The inherent damping is assumed to be 2% of the critical damping. Thus, $c_j=\frac{2\times 0.02}{{\omega }^{(1)}}{k}_j$, where ${\omega }^{(1)}=3.12$ is the fundamental natural angular frequency of the structure. As for conventional viscous damper design, the additional damping is set to 6% of the critical damping and the damping coefficients $c_{a,j}=\frac{2\times 0.06}{{\omega }^{(1)}}{k}_j$. The structure is assumed to remain elastic when subjected to strong ground motions. Table 5 lists the fundamental natural periods and modal effective mass ratio of the first three modes.

Figure 10

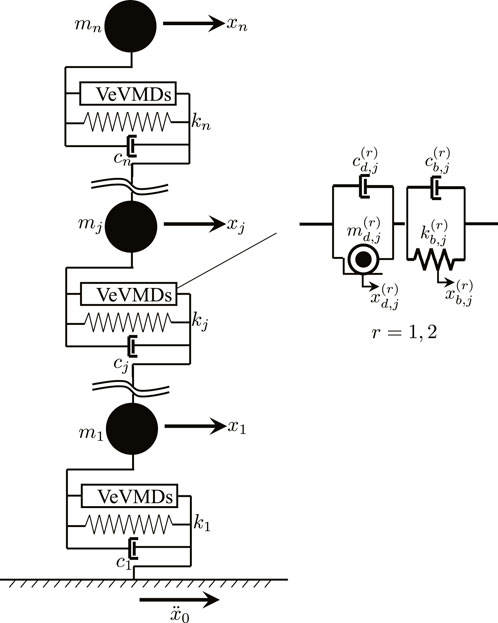
Figure 10. Ten-story benchmark shear building (Japan Society of Seismic Isolation, 2013).

Table 4

Table 4. Mass and stiffness distribution of the ten-story shear building.

Table 5

Table 5. Fundamental natural periods and modal effective mass ratio.

4.2 VeVMD parameters

The structure is equipped with VeVMDs tuned to the first and second modes. The inertance, stiffness, damping coefficient of the damper parallel to the inerter, and that parallel to the spring in a VeVMD are $m_{d,j}^{(r)},k_{b,j}^{(r)},c_{d,j}^{(r)}$, and $c_{b,j}^{(r)}$ where $r$ and $j$ are the target mode and the story where the device is installed, respectively. If the distribution of inertance of the VeVMDs is stiffness proportional and the ratio of the modal effective inertance and modal effective mass of the primary structure for the $r$^th mode is ${\mu }^{(r)}$, the inertance of VeVMD tuned to the $r$^th mode (Ikago et al., 2012b) can be expressed by Equation 19.

$m_{d,j}^{\left(r\right)}=\frac{{\mu }^{\left(r\right)}}{{\left\{{\omega }^{\left(r\right)}\right\}}^2}{k}_j\left(r=\mathrm{1,2}\right).(19)$

Similarly, letting the stiffness ratio and damping ratio for the VeVMD tuned to the $r$^th mode be ${\eta }^{(r)}$ and $h_d^{(r)}$, respectively, obtains Equations 20, 21.

$k_{b,j}^{\left(r\right)}={\eta }^{\left(r\right)}{k}_j,(20)$

$c_{b,j}^{\left(r\right)}+c_{d,j}^{\left(r\right)}=\frac{2h_d^{\left(r\right)}}{{\mu }^{\left(r\right)}{\omega }^{\left(r\right)}}{k}_j.(21)$

4.3 Damping ratio

Before designing VeVMDs, the total damping coefficient assigned to the devices is determined as shown in Equation 22.

${\displaystyle \sum _{r=1}^2}{\displaystyle \sum _{j=1}^{10}}\left(c_{b,j}^{\left(r\right)}+c_{d,j}^{\left(r\right)}\right)=\left({\displaystyle \sum _{r=1}^2}\frac{2h_d^{\left(r\right)}}{{\mu }^{\left(r\right){\omega }^{\left(r\right)}}}\right){\displaystyle \sum _{j=1}^{10}}{k}_j=\frac{2h_e}{{\omega }^{\left(1\right)}}{\displaystyle \sum _{j=1}^{10}}{k}_j,h_e=0.06.(22)$

Thus, Equation 23 holds.

${\displaystyle \sum _{r=1}^2}\frac{2h_d^{\left(r\right)}}{{\mu }^{\left(r\right){\omega }^{\left(r\right)}}}=\frac{2h_e}{{\omega }^{\left(1\right)}}.(23)$

The damping distribution factor $\lambda$ determines the damping allocated to the second mode:

$\frac{2h_d^{\left(1\right)}}{{\mu }^{\left(1\right){\omega }^{\left(1\right)}}}=\left(1-\lambda \right)\frac{2h_e}{{\omega }^{\left(1\right)}},(24)$

$\frac{2h_d^{\left(2\right)}}{{\mu }^{\left(2\right){\omega }^{\left(2\right)}}}=\lambda \frac{2h_e}{{\omega }^{\left(1\right)}}.(25)$

For a fixed-point design, substituting $h_d^{(r)}$ obtained from Equations 24 and 25 into $h_d$ (Table 2) and solving them with respect to ${\mu }^{(r)}$ obtains the inertance ratio of VeVMD tuned to the $r$^th mode. Then, ${\eta }^{(r)}$ can be obtained. For a flection point design, ${\mu }^{(r)}$, ${\eta }^{(r)}$, and ${\alpha }^{(r)}$ are numerically derived for a given $h_d^{(r)}$ following the procedure discussed in Section 3.3. Table 6 summarizes the parameters obtained through the above procedures.

Table 6

Table 6. IVCS parameters.

4.4 Input ground motions

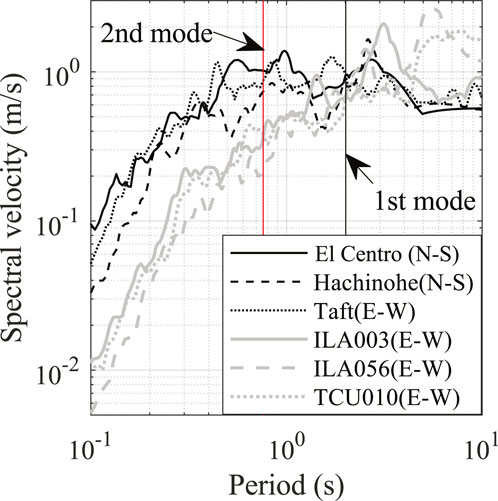
As for design ground motions, three historic ground motion records, three synthetic ground motions, and three long-period ground motion records (listed respectively in Tables 7–9) are used. The first six ground motions were selected in accordance with the practice in Japan, and three long-period ground motions (Xu et al., 2008) were added to examine the effect of long-period ground motion on the displacement control performance of TVMD. Figure 11 depicts the response velocity spectra of recorded ground motions (No. 1–3, 7–9).

Table 7

Table 7. Design ground motions (recorded ground motions, scaled to PGV = 0.5 m/s).

Table 8

Table 8. Synthetic design ground motions whose spectra are compatible with design spectrum.

Table 9

Table 9. Design ground motions (long-period ground motions, scaled to PGV = 0.5 m/s).

Figure 11

Figure 11. Response velocity spectra of recorded ground motions (Nos 1–3 and 7–9).

When conducting seismic response analyses using normalized ground motion records, the variability in maximum response tends to be smaller when the records are normalized by PGV rather than by PGA, particularly for structures with natural periods of 2 s or longer (Editorial Committee of Structural Design Practice of High-rise Buildings, 2019). For this reason, it is standard practice in Japan to normalize ground motion records by PGV when designing high-rise buildings. Adopting this approach, the recorded ground motions (No. 1–3 and 7–9) are scaled such that their peak ground velocities (PGVs) are 0.5 m/s.

In Japanese structural design practice, artificial ground motions whose response spectra are compatible with the design response spectrum are used to avoid underestimating responses when the natural period of a building coincides with that of a notch in the spectra of recorded ground motions.

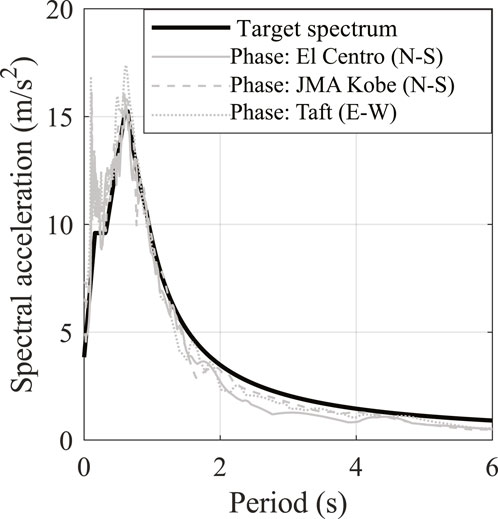
The synthetic ground motions are generated such that their response acceleration spectra are compatible with the design response acceleration spectra of Japan’s building code (Figure 12). They adopt the phase properties of recorded ground motions (Table 8).

Figure 12

Figure 12. Response acceleration spectra of synthetic ground motions (Nos 4–6).

The detailed parameters to derive the design spectrum can be found in Supplementary Figures S1 and S2 and Supplementary Table S1. Soil type 2 as the most common soil type in Japan is adopted for the surface subsoil type. The target spectrum shown in black solid line in Figure 12 is obtained by multiplying the response acceleration spectrum at the bed rock shown in Supplementary Figure S1 by the type 2 soil amplification factor shown in Supplementary Figure S2. As the amplitudes of the synthetic ground motions are determined by the target spectrum, their PGVs are not exactly 0.5 m/s (Table 8).

4.5 Analytical results and discussion

$d_j^q$ and $a_j^q$ represent the maximum inter-story drift of the $i$^th story and maximum floor response acceleration of the $i$^th floor yielded by the No. $q$ ground motion.

We first compare the seismic response analysis results with the damping coefficient allocated to the second mode $\lambda =0.5$. Figures 13A and B compare the maximum inter-story drift $(\{d_j^q;i=\mathrm{1,2},\dots ,10;q=\mathrm{1,8}\})$ and maximum floor response acceleration $(\{a_j^q;i=\mathrm{1,2},\dots ,10;q=\mathrm{1,8}\})$ yielded by El Centro 1940 N–S (No. 1) and ILA056 1999 E–W records (No. 8). Figures 14A and B compare the maximum response in the entire building through all the ground motions: ${\max }_{j,q}\{d_j^q\}$ and ${\max }_{j,q}\{a_j^q\}$. ‘*’ represents the performance of the conventional viscous damper design. These figures suggest that fixed-point TID acceleration control design performs the best in mitigating floor response acceleration response, whereas the fixed-point TVMD displacement control design performs better in mitigating inter-story drift. Inflection point design slightly improves both the inter-story drift and floor response acceleration yielded by the fixed-point TVMD displacement control design except for long-period ground motions.

Figure 13

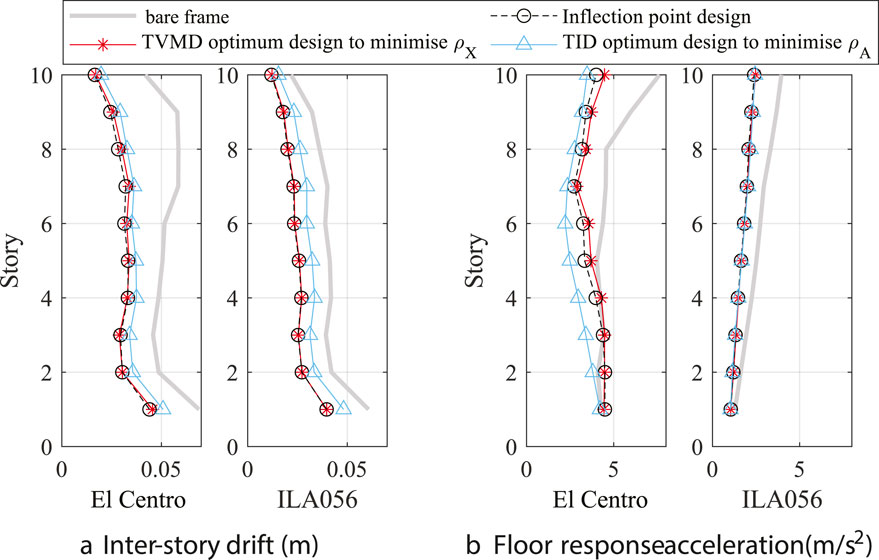
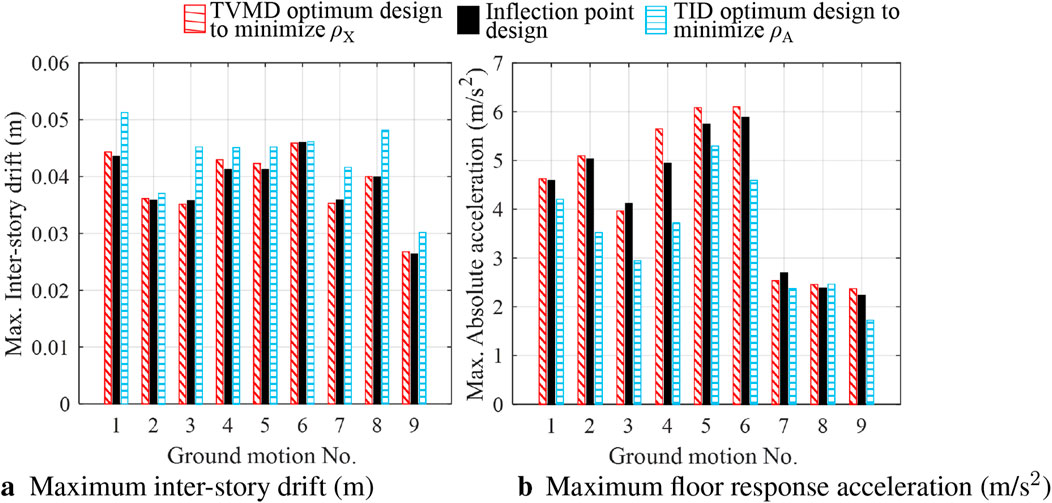
Figure 13. Maximum seismic responses ($\lambda =0.5$, El Centro 1940 N-S and ILA056 1999 N-S): (A) inter-story drift; (B) floor response acceleration.

Figure 14

Figure 14. Maximum seismic responses $(\lambda =0.5)$: (A) inter-story drift; (B) floor response acceleration.

Figures 15A and B plot $({\max }_{j,q=\mathrm{1,2},\dots ,6}\{d_j^q\},{\max }_{j,q=\mathrm{1,2},\dots ,6}\{a_j^q\})$ and $({\max }_{j,q=\mathrm{7,8,9}}\{d_j^q\},{\max }_{j,q=\mathrm{7,8,9}}\{a_j^q\})$ with respect to varying $\lambda$. The color bars indicate the $\lambda$ value. As shown in the figure, acceleration responses yielded by inflection point design and fixed-point TVMD displacement control design significantly decrease when $\lambda$ increases, whereas displacement responses yielded by the fixed-point TID acceleration control design increase significantly. The displacement responses yielded by inflection point design and fixed-point TVMD displacement control design are barely affected by the variation of $\lambda$. Similarly, the acceleration responses yielded by the fixed-point TID acceleration control design are barely affected by the variation of $\lambda$. Allocating 80$\sim$90% of damping coefficient to the second mode control yielded excellent performance for TVMD configuration designs, whereas allocating 0$\sim$10% of damping coefficient to the second mode control yielded excellent performance for TID configuration design. The TVMD topology designs with $\lambda =0.8$ and TID topology designs with $\lambda =0$ are not inferior to each other for the design ground motions (Figure 15A). Nonetheless, the fixed-point TVMD displacement control design with $\lambda =0.8$ represented by a downward-pointing triangle notation is superior to any inflection point designs represented by solid circles for long-period ground motions (Figure 15B). When subjected to design ground motions (No. 1–6), both the TVMD and TID configuration designs outperform the conventional damper design in inter-story drifts with slightly increased absolute accelerations. Nonetheless, for the long-period ground motion cases, the TVMD configuration designs simultaneously suppress inter-story drifts and absolute accelerations whereas the TID configuration designs have no significant advantage.

Figure 15

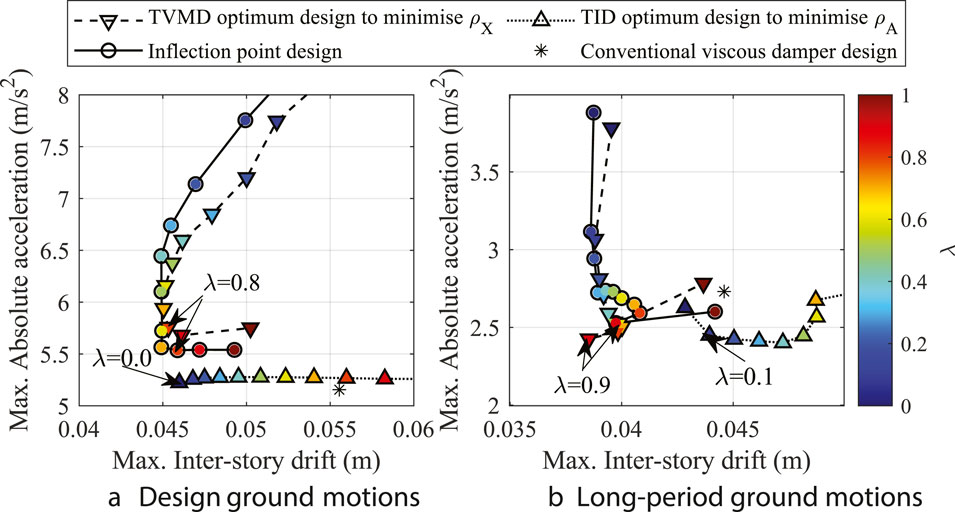
Figure 15. Performance curves: (A) design ground motions (Nos 1–6); (B) long-period ground motions (Nos 7–9).

5 Conclusion

This paper has examined the effect of damper arrangement in inerter-based structural DVAs. Therefore, a comprehensive multi-objective optimization was performed on a VeVMD with a device topology to encompass those of two major inerter-based structural DVAs—the TVMD and TID. Removing a damper arranged parallel to the spring in a VeVMD yields a TVMD device topology, while removing a damper arranged in parallel to the inerter yields a TID device topology. Multi-objective optimization to simultaneously minimize peak displacement and peak absolute acceleration amplification factors of a SDOF structure containing VeVMD subject to the constraint on the total supplemental damping coefficient revealed that the designs that has advantage in controlling displacement and absolute accelerations converge to TVMD and TID device topologies, respectively. There is an inflection point on the Pareto frontier curve where the inclination of its tangential line drastically changes. The Pareto optimum design on the inflection point is found to be robust against the variation of design variables, offering one of the best options for effective simultaneous control of displacement and floor response acceleration. The device topology yielded by the inflection point design is that of TVMD, and its solution can be approximated by the closed-form formula derived by the fixed-point method for a TVMD to minimize the peak absolute acceleration amplification factor.

An analytical example using a ten-story shear building model demonstrated that the multi-objective optimum designs to minimize peak amplification factors are effective in mitigating seismic responses. The inflection point design and fixed-point TVMD displacement control design performed effectively in mitigating displacement response, while fixed-point TID acceleration control design effectively mitigated floor response acceleration. This means that the performances of TVMD and TID with the same total damping coefficient are not inferior to one another. The inflection point design slightly outperformed fixed-point TVMD displacement control design for design ground motions, whereas there are cases in which fixed-point TVMD displacement control design outperformed the inflection point design for long-period ground motions. For such motions, the TVMD configuration designs generally outperform the conventional damper design in both inter-story drifts and absolute accelerations.

In this study, the device topology optimization was conducted on a SDOF structure and exclusively focused on the TVMD and TID. As for a MDOF structure, the effectiveness of IVCSs is also affected by the installation positions along the height, which should be further studied. Furthermore, topological configurations of IVCSs other than TVMD and TID should be considered in future studies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RX: investigation, methodology, visualization, writing–original draft, and writing–review and editing. KI: conceptualization, supervision, writing–original draft, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. The first author is supported by the scholarship provided by the Ministry of Education, Culture, Sports, Science, and Technology, Japan (scholarship number 211503).

Acknowledgments

The authors would like to thank Editage (www.editage.jp) for English language editing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2024.1508190/full#supplementary-material

References

Arakaki, T., Kuroda, H., Arima, F., Inoue, Y., and Baba, K. (1999). Development of seismic devices applied to ball screw: Part 1 basic performance test of rd-series. AIJ J. Technol. Des. 5, 239–244. doi:10.3130/aijt.5.239_1

CrossRef Full Text | Google Scholar

Caicedo, D., Lara-Valencia, L., Blandon, J., and Graciano, C. (2021). Seismic response of high-rise buildings through metaheuristic-based optimization using tuned mass dampers and tuned mass dampers inerter. J. Build. Eng. 34, 101927. doi:10.1016/j.jobe.2020.101927

CrossRef Full Text | Google Scholar

Cao, L., and Li, C. (2022). A high performance hybrid passive base-isolated system. Struct. Control Health Monit. 29, e2887. doi:10.1002/stc.2887

CrossRef Full Text | Google Scholar

De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design strategies of viscous dampers for seismic protection of building structures: a review. Soil Dyn. Earthq. Eng. 118, 144–165. doi:10.1016/j.soildyn.2018.12.024

CrossRef Full Text | Google Scholar

Domenico, D. D., Deastra, P., Ricciardi, G., Sims, N., and Wagg, D. (2019). Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Frankl. Inst. 356, 7626–7649. doi:10.1016/j.jfranklin.2018.11.012

CrossRef Full Text | Google Scholar

Editorial Committee of Structural Design Practice of High-rise Buildings (2019). Structural design practice of high-rise buildings (in Japanese) (Building Center of Japan).

Google Scholar

Fonseca, C. M., and Fleming, P. J. (1993). Genetic algorithms for multiobjective optimization: formulation, discussion, and generalization. Icga 93, 416–423.

Google Scholar

Hartog, J. D. (1985). Mechanical vibrations. Dover Publications.

Google Scholar

Housner, G., Bergman, L., Caughey, T., Chassiakos, A., Claus, R., Masri, S., et al. (1997). Structural control: past, present, and future. J. Eng. Mech. 123, 897–971. doi:10.1061/(asce)0733-9399(1997)123:9(897)

CrossRef Full Text | Google Scholar

Hu, Y., and Chen, M. (2015). Performance evaluation for inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 99, 297–307. doi:10.1016/j.ijmecsci.2015.06.003

CrossRef Full Text | Google Scholar

Hu, Y., Chen, M., Shu, Z., and Huang, L. (2015). Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution. J. Sound Vib. 346, 17–36. doi:10.1016/j.jsv.2015.02.041

CrossRef Full Text | Google Scholar

Hwang, J., Kim, J., and Kim, Y. (2007). Rotational inertia dampers with toggle bracing for vibration control of a building structure. Eng. Struct. 29, 1201–1208. doi:10.1016/j.engstruct.2006.08.005

CrossRef Full Text | Google Scholar

Ikago, K., Saito, K., and Inoue, N. (2012a). Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 41, 453–474. doi:10.1002/eqe.1138

CrossRef Full Text | Google Scholar

Ikago, K., Sugimura, Y., Saito, K., and Inoue, N. (2012b). Modal response characteristics of a multiple-degree-of-freedom structure incorporated with tuned viscous mass dampers. J. Asian Archit. Build. Eng. 11, 375–382. doi:10.3130/jaabe.11.375

CrossRef Full Text | Google Scholar

Ishii, M., Kazama, H., Miyazaki, K., and Murakami, K. (2014). “Application of tuned viscous mass damper to super-high-rise buildings,” in Proceedings of the 6th world Conference of structural Control and health monitoring, (Barcelona, Sapin: International Center for Numerical Methods in Engineering CIMNE), 2825–2833.

Google Scholar

Japan Society of Seismic Isolation (2013). Manual for design and fabrication for passive vibration control of structures. 3rd ed. (in Japanese).

Google Scholar

Ji, X., Cheng, Y., and Hutt, C. (2020). Seismic response of a tuned viscous mass damper (TVMD) coupled wall system. Eng. Struct. 225, 111252. doi:10.1016/j.engstruct.2020.111252

CrossRef Full Text | Google Scholar

Ji, X., Zhang, J., Ikago, K., Chakraborty, S., and Kanno, H. (2021). Tuned viscous mass damper (TVMD) coupled wall system for enhancing seismic performance of high-rise buildings. Eng. Struct. 240, 112307. doi:10.1016/j.engstruct.2021.112307

CrossRef Full Text | Google Scholar

John, E., and Wagg, D. (2019). Design and testing of a frictionless mechanical inerter device using living-hinges. J. Frankl. Inst. 356, 7650–7668. doi:10.1016/j.jfranklin.2019.01.036

CrossRef Full Text | Google Scholar

Kang, J., and Ikago, K. (2023). Seismic control of multidegree-of-freedom structures using a concentratedly arranged tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 52, 4708–4732. doi:10.1002/eqe.3977

CrossRef Full Text | Google Scholar

Keivan, A., Phillips, B. M., Ikenaga, M., and Ikago, K. (2017). Causal realization of rate-independent linear damping for the protection of low-frequency structures. J. Eng. Mech. 143, 04017058. doi:10.1061/(asce)em.1943-7889.0001259

CrossRef Full Text | Google Scholar

Kida, H., Ikago, K., and Inoue, N. (2012). “Applicability of force-restricted tuned viscous mass dampers to high-rise buildings subjected to long-period ground motions,” in Proceedings of the 15th world conference on earthquake engineering (Lisbon, Portugal: LISBOA).

Google Scholar

Kim, J., Ryu, J., and Chung, L. (2006). Seismic performance of structures connected by viscoelastic dampers. Eng. Struct. 28, 183–195. doi:10.1016/j.engstruct.2005.05.014

CrossRef Full Text | Google Scholar

Lazar, I., Neild, S., and Wagg, D. (2014). Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 43, 1129–1147. doi:10.1002/eqe.2390

CrossRef Full Text | Google Scholar

Licari, M., Sorace, S., and Terenzi, G. (2015). Nonlinear modeling and mitigation of seismic pounding between r/c frame buildings. J. Earthq. Eng. 19, 431–460. doi:10.1080/13632469.2014.984370

CrossRef Full Text | Google Scholar

Lobato, F., and Steffen, Jr V. (2017). Multi-objective optimization problems: concepts and self-adaptive parameters with mathematical and engineering applications. Springer.

Google Scholar

Luo, H., and Ikago, K. (2021). Unifying causal model of rate-independent linear damping for effectively reducing seismic response in low-frequency structures. Earthq. Eng. Struct. Dyn. 50, 2355–2378. doi:10.1002/eqe.3450

CrossRef Full Text | Google Scholar

Luo, H., Ikago, K., Chong, C., Keivan, A., and Phillips, B. (2019). Performance of low-frequency structures incorporated with rate-independent linear damping. Eng. Struct. 181, 324–335. doi:10.1016/j.engstruct.2018.12.022

CrossRef Full Text | Google Scholar

Ma, R., Bi, K., and Hao, H. (2021). Inerter-based structural vibration control: a state-of-the-art review. Eng. Struct. 243, 112655. doi:10.1016/j.engstruct.2021.112655

CrossRef Full Text | Google Scholar

Makris, N., and Kampas, G. (2016). Seismic protection of structures with supplemental rotational inertia. J. Eng. Mech. 142, 04016089. doi:10.1061/(asce)em.1943-7889.0001152

CrossRef Full Text | Google Scholar

Makris, N., and Moghimi, G. (2022). Response of seismic isolated structures with supplemental rotational inertia. Earthq. Eng. Struct. Dyn. 51, 2956–2974. doi:10.1002/eqe.3709

CrossRef Full Text | Google Scholar

Marian, L., and Giaralis, A. (2014). Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 38, 156–164. doi:10.1016/j.probengmech.2014.03.007

CrossRef Full Text | Google Scholar

Marler, R., and Arora, J. (2010). The weighted sum method for multi-objective optimization: new insights. Struct. Multidiscip. Optim. 41, 853–862. doi:10.1007/s00158-009-0460-7

CrossRef Full Text | Google Scholar

Mazza, F., and Labernarda, R. (2020). Magnetic damped links to reduce internal seismic pounding in base-isolated buildings. Bull. Earthq. Eng. 18, 6795–6824. doi:10.1007/s10518-020-00961-6

CrossRef Full Text | Google Scholar

Nakamura, Y., Fukukita, A., Tamura, K., Yamazaki, I., Matsuoka, T., Hiramoto, K., et al. (2014). Seismic response control using electromagnetic inertial mass dampers. Earthq. Eng. Struct. Dyn. 43, 507–527. doi:10.1002/eqe.2355

CrossRef Full Text | Google Scholar

Nakamura, Y., Watanabe, H., and Kawamata, S. (1988). “Seismic response control of structures by accelerated liquid mass damper,” in Proceedings of the 9th world conference on earthquake engineering, 785–790.

Google Scholar

Ogino, M., and Sumiyama, T. (2014). “Structural design of a high-rise building using tuned viscous mass dampers installed across three consecutive sotreys,” in Proceedings of the 12th international Conference on computational structures Technology (Naples, Italy), 225. doi:10.4203/ccp.106.225

CrossRef Full Text | Google Scholar

Pan, C., and Zhang, R. (2018). Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 25, e2169. doi:10.1002/stc.2169

CrossRef Full Text | Google Scholar

Pan, C., Zhang, R., Luo, H., Li, C., and Shen, H. (2018). Demand-based optimal design of oscillator with parallel-layout viscous inerter damper. Struct. Control Health Monit. 25, e2051. doi:10.1002/stc.2051

CrossRef Full Text | Google Scholar

Papageorgiou, C., Houghton, N., and Smith, M. (2009). Experimental testing and analysis of inerter devices. J. Dyn. Syst. Meas. Control 131, 011001. doi:10.1115/1.3023120

CrossRef Full Text | Google Scholar

Qiao, H., Huang, P., Domenico, D. D., and Wang, Q. (2023). Targeted modal response control of structures with inerter-based vibration absorbers considering modal interaction effects. J. Build. Eng. 64, 105692. doi:10.1016/j.jobe.2022.105692

CrossRef Full Text | Google Scholar

Saito, K., Sugimura, Y., Nakaminami, S., Kida, H., and Inoue, N. (2008). “Vibration tests of 1-story response control system using inertial mass and optimized softy spring and viscous element,” in Proceedings of the 15th world conference on earthquake engineering (Beijing, China: WCEE).

Google Scholar

Saitoh, M. (2012). On the performance of gyro-mass devices for displacement mitigation in base isolation systems. Struct. Control Health Monit. 19, 246–259. doi:10.1002/stc.419

CrossRef Full Text | Google Scholar

Smith, M. (2002). Synthesis of mechanical networks: the inerter. IEEE Trans. automatic control 47, 1648–1662. doi:10.1109/tac.2002.803532

CrossRef Full Text | Google Scholar

Steuer, R. (1986). “Multiple criteria optimization: theory, computation, and applications,” in Wiley series in probability and mathematical statistics.

Google Scholar

Sugimura, Y., Goto, W., Tanizawa, H., Saito, K., and Ninomiya, T. (2012). “Response control effect of steel building structure using tuend viscous mass damper,” in Proceedings of the 15th international Conference on earthquake engineering (Lisbon, Portugal: LISBOA).

Google Scholar

Taflanidis, A., Giaralis, A., and Patsialis, D. (2019). Multi-objective optimal design of inerter-based vibration absorbers for earthquake protection of multi-storey building structures. J. Frankl. Inst. 356, 7754–7784. doi:10.1016/j.jfranklin.2019.02.022

CrossRef Full Text | Google Scholar

Wang, B., Ikago, K., and Kezuka, S. (2024). Causal rate-independent damping device using a rotary inerter damper. Front. Built Environ. 10, 1411170. doi:10.3389/fbuil.2024.1411170

CrossRef Full Text | Google Scholar

Wang, F., Hong, M., and Lin, T. (2011). Designing and testing a hydraulic inerter. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 225, 66–72. doi:10.1243/09544062jmes2199

CrossRef Full Text | Google Scholar

Watanabe, Y., Ikago, K., Inoue, N., Kida, H., Nakaminami, S., Tanaka, H., et al. (2012). “Full-scale dynamic tests and analytical verification of a force-restricted tuned viscous mass damper,” in 15th World Conference On Earthquake Engineering (Lisbon, Portugal: LISBOA).

Google Scholar

Xu, L., Hu, J., and Xie, L. (2008). On characteristics of ground motion parameters for special long-period ground motions (in Chinese). J. Earthq. Eng. Eng. Vib. 28, 20–27.

Google Scholar

Zhang, R., Zhao, Z., Pan, C., Ikago, K., and Xue, S. (2020). Damping enhancement principle of inerter system. Struct. Control Health Monit. 27, e2523. doi:10.1002/stc.2523

CrossRef Full Text | Google Scholar

Zhao, C., Kikuchi, J., Ikenaga, M., Ikago, K., and Inoue, N. (2016). Viscoelastically supported viscous mass damper incorporated into a seismic isolation system. J. Earthq. Tsunami 10, 1640009. doi:10.1142/s1793431116400091

CrossRef Full Text | Google Scholar