Seismic responses of isolated bridges subjected to near-fault ground motions: simple pulses vs. whole records

Velocity pulse with strong energy input is the significant feature of near-fault ground motions. Bridges close to or passing across seismic faults may suffer from higher failure risk, which is inseparable from the influence of velocity pulse. This study aims to evaluate the nonlinear response characteristics of bridge structures under various near-fault ground motion conditions. A typical isolated continuous girder bridge is adopted, and two corresponding finite element models, i.e., considering and ignoring the heating effect of lead core bearings (LRBs), are established based on the OpenSees platform. Then, a total of 40 near-fault ground motion records are selected, and the pulses are extracted. Both the energy-based and deformation-based seismic responses are captured and compared to reveal the differences for the isolated bridge subjected to the original waves and the extracted pulses. The results highlight that the accuracy of the seismic evaluation based on the extracted pulses strongly depends on the precondition that the pulse period is close to the fundamental period of the isolated bridge. Hence, inputting the extracted pulses for predicting the in-elastic seismic response of isolated bridges locating at near-fault region is not an adequate replacement for those original waves of near-fault ground motions. In addition, the heating effect of LRBs will be magnified for the seismic response of isolated bridges subjected to the extracted pulses, and it will mainly affect the seismic responses of bearings and piers, i.e., the former increases and the latter decreases.

1 Introduction

Bridges are not only the hubs of traffic lines, but also an important part of the lifeline project. Usually, bridges close to or passing across seismic faults are suffering from higher failure risk, which has been widely realized in accordance with the previous investigations on post-earthquake damages (Hall et al., 1995; Kawashima, 2002; Han et al., 2018; Cheng et al., 2019; Hui et al., 2023; Jiang et al., 2024), such as the Northridge Earthquake in 1994, Kobe Earthquake in 1995, ChiChi Earthquake in 1999, Kocaeli Earthquake in 1999, and Wenchuan Earthquake in 2008. The most key factor is that near-fault ground motions containing strong velocity pulses with high energy input will increase the seismic demands of bridges, and consequently, resulting in severer damages compared with those attacked by far-fault ground motions (Cheng et al., 2016; Pang et al., 2022; Zhong et al., 2023a; Zhong et al., 2023b; Yang et al., 2023). Up to now, near-fault ground motions with velocity pulses and their influences on engineering structures have been vital topics to both researchers and engineers.

In fact, evaluating the seismic behaviors of engineering structures is closely related to the ground motion characteristics and the numerical modeling (Castaldo and Miceli, 2023; Wu et al., 2024). Different from those normal structures, the seismic isolated structures should be more prone to large displacement (Wu et al., 2019). As for the near-fault ground motion records, utilizing simple pulses to evaluate the structural responses has been focused on for a long time due to the impulsive nature (Biggs, 1964), and different mathematical models of simple pulses were presented to describe the significant characteristic of near-fault ground motions (Hall et al., 1995; Makris, 1997; Makris and Chang, 2000; Mavroeidis and Papageorgiou, 2003; He and Agrawal, 2008). These above simple pulse models were found to be able to adequately evaluate the peak response of long-period single degree of freedom (SDOF) systems under near-fault ground motions, and some researchers concluded that the structural seismic responses could be assessed by utilizing those proposed simple pulse models (Mavroeidis and Papageorgiou, 2003; Alavi and Krawinkler, 2004; Mavroeidis et al., 2004). Meanwhile, any numerical model is always affected by epistemic uncertainties (Bertagnoli et al., 2024). Furthermore, simple pulses were deemed that they could adequately estimate the response of a multiple degree of freedom (MDOF) system if they could capture the response of the first mode of the system (Alavi and Krawinkler, 2004). Though this assumption may be valid for short-period structures primarily responding in the form of the first vibration mode, it is questionable for those structures (i.e., bridges and tall buildings) responding with multiple vibration modes coupled, because the response of higher vibration modes cannot be captured by the simple pulse models without high frequencies (Rupakhety and Sigbjörnsson, 2011). Similarly, it is vital to figure out whether the seismic response of isolated bridges subjected to near-fault ground motions can be adequately evaluated by the impulse waves extracted from whole records.

As noted above, near-fault ground motions usually contain strong velocity pulses with high energy input. Estimating the seismic response of isolated bridges in terms of energy offers a new view to reveal the seismic damage process to structures. More and more attentions have been paid to since the energy-based seismic design was first proposed by Housner (1956). The energy-based seismic responses of isolated bridges includes the total input energy, the hysteretic energy dissipations of bearings and piers, kinetic energy, and the damping energy. Kawashima (1998) studied the hysteretic energy dissipations of isolation bearings and piers affected by the ratio of their yield strengths. They found that the energy-based seismic response of piers decreased when the ratio of yield strengths of isolation beatings and piers decreased, and the opposite conclusion was obtained for the isolation bearings. Based on the energy equilibrium theory, Li et al. (2011) established the energy equations of bridges of passenger dedicated line, and studied the seismic energy response and its distribution rules at the nonlinear state via finite element analysis based on the software of ANSYS. It turned out that the seismic input energy was mainly consumed by the structural hysteretic energy dissipation and damping energy dissipation, and the soil-structure interaction effects and peak ground acceleration significantly affected the seismic input energy, structural hysteretic energy dissipation, and damping energy dissipation. Jiang et al. (Jiang and Zhu, 2006; Jiang et al., 2009; Jiang et al., 2011) presented an energy-based seismic design method for bridges subjected near-fault ground motions, and discussed the influencing factors (i.e., the structural damping, ductility coefficient, and self-vibration period of the structure) for hysteretic energy distribution ratio. However, their research work mainly focused on the SDOF system or the short-period structures primarily responding in the first vibration mode, further studies on long-period structures need to be performed.

This paper tries to reveal the seismic response of isolated bridges subjected to near-fault ground motions by inputting the whole records and the extracted pulses. Meanwhile, the transformation of seismic energy is traced. In the following sections, the calculation method for seismic energy of MDOF system is introduced firstly, including the input energy, the hysteretic energy dissipations of bearings and piers, kinetic energy, and the damping energy. Then, a total of 40 near-fault ground motion records containing velocity pulses are selected, and decomposed as the extracted pulse and the residual ground motion. After that, an illustrative example of isolated bridges is adopted, and two finite element models, which are established to investigate the effect of lead core heating of the LRBs on the seismic response of isolated bridges, are established based on the OpenSees platform. Further, nonlinear dynamic time history analyses are carried out by inputting the original waves and the extracted pulses of near-fault ground motions, and the energy-based and deformation-based seismic responses are both estimated and compared to investigate their differences under different inputs.

2 Seismic energy in structures

The kinetic equation of MDOF system excited by ground motions can be expressed as

$\left[M\right]\left\{\ddot{u}\left(t\right)\right\}+\left[C\right]\left\{\dot{u}\left(t\right)\right\}+\left[K\right]\left\{u\left(t\right)\right\}=-\left[M\right]\left\{r\right\}{\ddot{u}}_g\left(t\right)(1)$

where $\left\{u\left(t\right)\right\}$, $\left\{\dot{u}\left(t\right)\right\}$ and $\left\{\ddot{u}\left(t\right)\right\}$ are the displacement, velocity and acceleration vectors of the masses; $\left[M\right]$, $\left[C\right]$ and $\left[K\right]$ are the mass, damping and stiffness matrixes of the MDOF system; ${\ddot{u}}_g\left(t\right)$ is the ground acceleration; and $\left\{r\right\}={\left\{0,\cdots ,\stackrel{r}{1},\cdots ,0\right\}}^{\mathrm{T}}$ is a vector with some elements equal to unity which subjected to effective earthquake forces, and the others equal to zero.

The attack of earthquakes to a structure is a process of energy transfer, transform and consumption. The use of energy method helps to reveal the seismic failure mechanism of structures (Housner, 1956; Shi et al., 2020), and the equation of energy balance should always be applicable for a structure under seismic loadings as Eq. 2 (Uang and Bertero, 1990; Decanini and Mollaioli, 2001)

$E_{\mathrm{i}}\left(t\right)=E_{\mathrm{k}}\left(t\right)+E_{\mathrm{\xi }}\left(t\right)+E_{\mathrm{a}}\left(t\right)(2)$

where $E_{\mathrm{i}}\left(t\right)$ is the input energy; $E_{\mathrm{k}}\left(t\right)$ is the kinetic energy; $E_{\mathrm{\xi }}\left(t\right)$ is the damping energy; and $E_{\mathrm{a}}\left(t\right)$ is the absorbed energy that consists of the recoverable elastic strain energy $E_{\mathrm{s}}\left(t\right)$ and the irrecoverable hysteretic energy directly related to the damage $E_{\mathrm{h}}\left(t\right)$. In accordance with Eq. 1, the above items of various energies can be written as

$E_{\mathrm{i}}\left(t\right)=-{\int }_0^t{\left\{\dot{u}\left(t\right)\right\}}^{\mathrm{T}}\left[M\right]\left\{r\right\}{\ddot{u}}_g\left(t\right)\mathrm{d}t(3)$

$E_{\mathrm{k}}\left(t\right)={\int }_0^t{\left\{\dot{u}\left(t\right)\right\}}^{\mathrm{T}}\left[M\right]\left\{\ddot{u}\left(t\right)\right\}\mathrm{d}t(4)$

$E_{\mathrm{\xi }}\left(t\right)={\int }_0^t{\left\{\dot{u}\left(t\right)\right\}}^{\mathrm{T}}\left[C\right]\left\{\dot{u}\left(t\right)\right\}\mathrm{d}t(5)$

$E_{\mathrm{a}}\left(t\right)={\int }_0^t{\left\{\dot{u}\left(t\right)\right\}}^{\mathrm{T}}\left[K\right]\left\{u\left(t\right)\right\}\mathrm{d}t(6)$

Note that Eqs 3–6 should be “relative” energy equations, which are derived by integrating Eq. 1 with respect to $u$ (Uang and Bertero, 1990). Uang (Uang and Bertero, 1990) compared the uses of “relative” and “absolute” energy equations and concluded that no significant differences observed for a constant displacement ductility in the period range of practical interest, i.e., 0.3–5.0 s. Therefore, the “relative” energy equations are adopted in this study in consideration of calculation efficiency and practicality.

3 Near-fault ground motions and their decompositions

3.1 Selected near-fault ground motions

Using the Next-Generation Attenuation (NGA) Project ground motion library, Baker (2007) proposed an algorithm to select ground motions for the Transportation Research Program of the Pacific Earthquake Engineering Research Center (PEER). Besides, some sets of ground motions were also provided, which can be widely adopted to satisfy numerous needs since they were not developed as structure-specific or site-specific (Cheng et al., 2021a).

The set of pulse-like ground motions, which contain strong velocity pulses in the strike-normal components, is adopted in this study. The details of the selected near-fault ground motions are summarized in Table 1. Where M_s is the moment magnitude of ground motions; R is the closest distance from the recording site to the fault rupture; T_p is the period of the velocity pulse in strike-normal direction; and V_s30 is the average shear wave velocity in the top 30 m.

Table 1

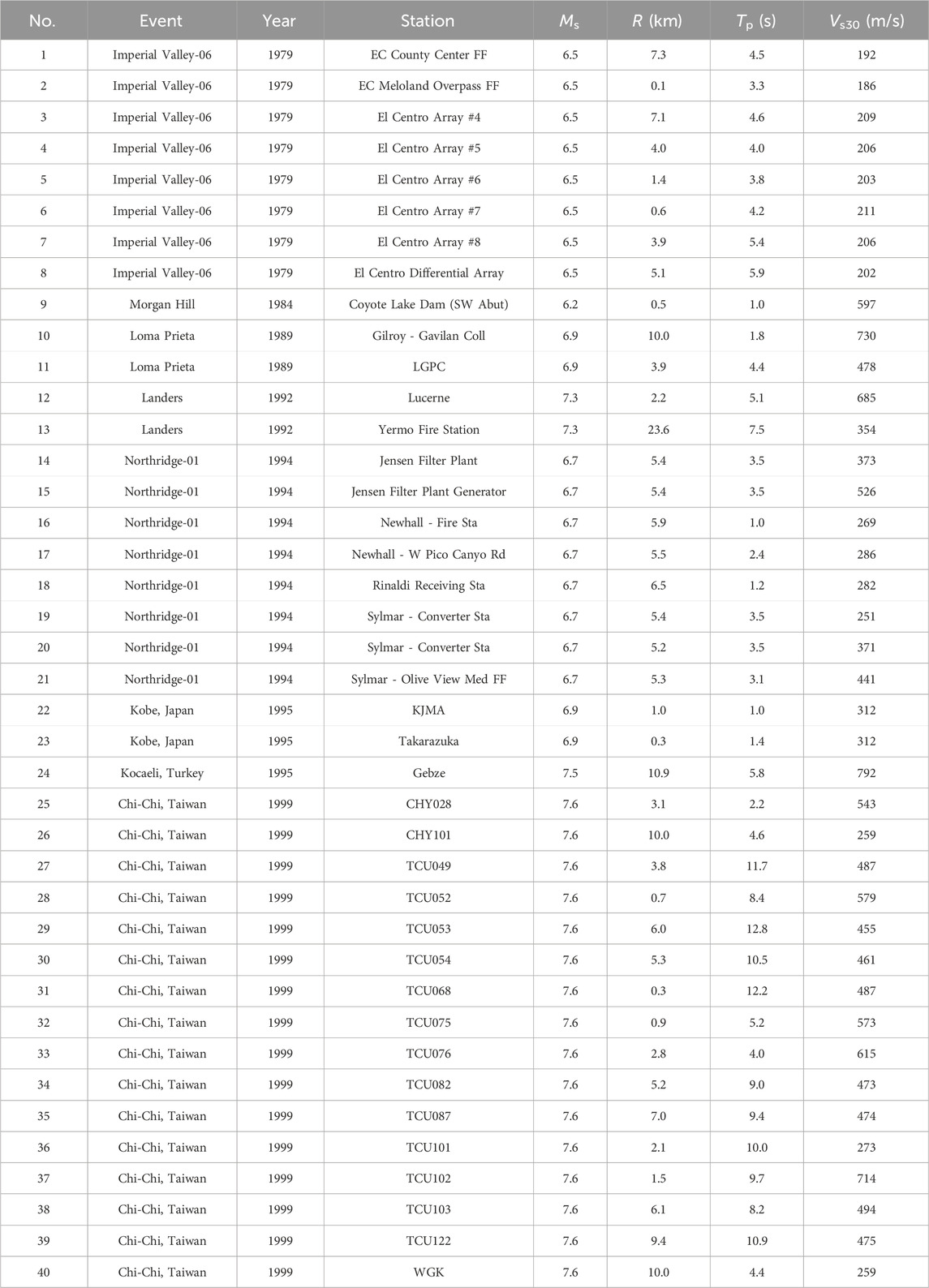
Table 1. Information of the selected 40 near-fault ground motions (Baker, 2007).

3.2 Decomposition of ground motions

One of the most significant characteristics of near-fault ground motions is the strong velocity pulses. Based on wavelet analysis, Baker (2007) presented an approach to quantitatively identify near-fault ground motions, and meanwhile, the pulse could be effectively extracted from the original ground motion. According to their method, a near-fault ground motion, which is recorded by TCU075 Station in the 1999 Chi-Chi earthquake, is taken as an example to show the decomposition result in Figure 1. Where the peak ground velocities (PGVs) are 88.58, 72.8, and 49.65 cm/s, respectively, corresponding to the original wave, the extracted pulse, and the residual ground motion.

Figure 1

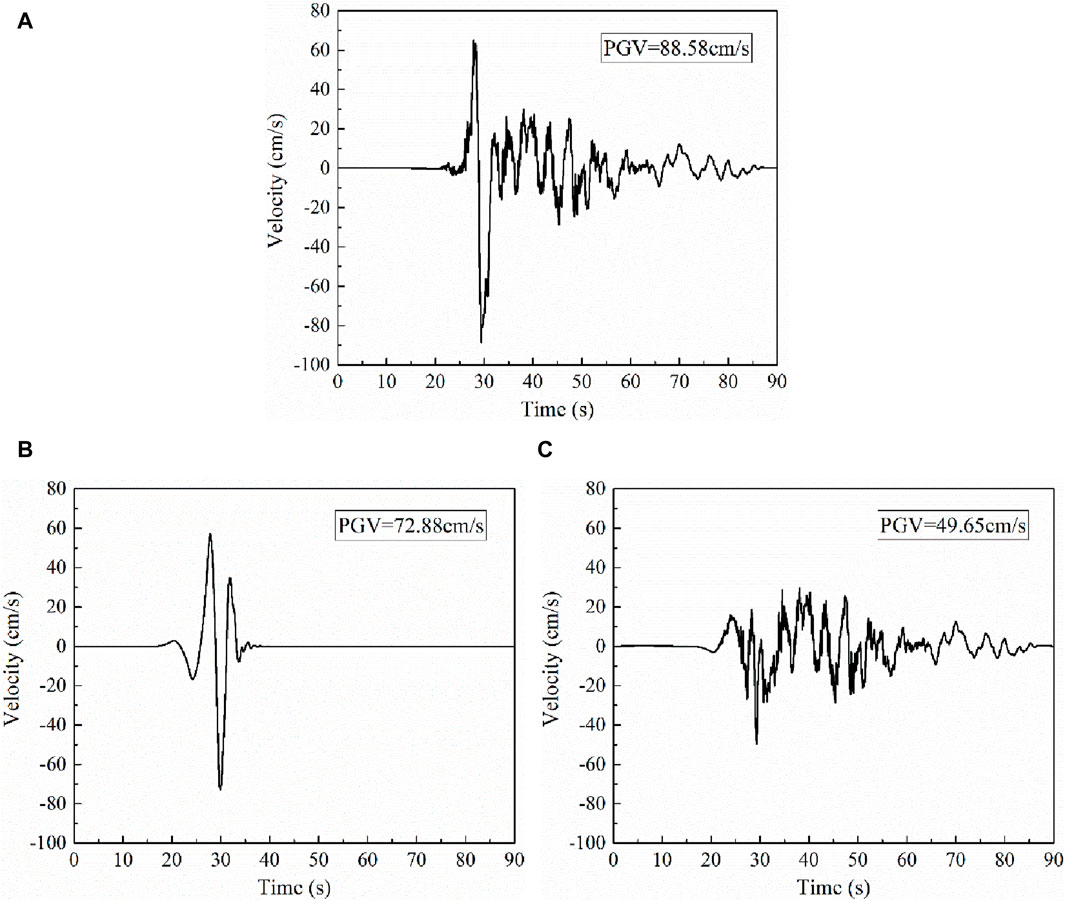
Figure 1. Velocity time history recorded by TCU075 Station in the 1999 Chi-Chi Earthquake. (A) Original wave, (B) Extracted pulse, (C) Residual ground motion.

As the critical parameters related to the typical characteristics of near-fault ground motions, i.e., the pulse period T_p and the PGV/PGA ratio (where PGA stands for the peak ground acceleration), their relationships are explored and compared for the original and extracted ground motions in Figures 2, 3. Note that the PGV_O and PGA_O are the peak ground velocity and acceleration of original ground motions, and the PGV_P and PGA_P are the peak ground velocity and acceleration of extracted ground motions. Figure 2 displays a trend that the peak ground motions, both PGA and PGV, decrease when the pulse period increases, but the discreteness is relatively large for both the original and extracted ground motions. As revealed in Figure 3, though the PGV/PGA ratio of extracted ground motions shows a strong positive correlation with the pulse period T_p, the discreteness is still significant for the original ground motions. However, linear fit can be effectively performed between the pulse period T_p and the PGV/PGA ratio for the extracted ground motions, and the goodness of fit (R²) equals to 0.9629. Hence, it should be both feasible to describe the effect of pulse like on the structural dynamic response with the pulse period T_p and the PGV/PGA ratio.

Figure 2

Figure 2. Relationship between the peak ground motion and T_p. (A) PGA vs. T_p, (B) PGV vs. T_p.

Figure 3

Figure 3. Relationship between the PGV/PGA ratio and T_p.

4 Illustrative example of isolated bridges

The original and extracted ground motions of the selected near-fault ground motions are adopted to investigate the seismic behavior of isolated bridges. Meanwhile, the temperature-dependent performance of LRBs, which is caused by the lead core heating under seismic loadings, is taken into account.

4.1 Basic information of adopted example

A six-span continuous girder bridge, which is the approach part of an isolated bridge, is adopted in this study, and the schematic diagram is displayed in Figure 4. The total length of the adopted continuous girder bridge is 510 m, with each span of 85 m. The steel-concrete composite section, which utilizes Grade C50 concrete and Q345 steel, is applied to the girder. The height of the seven reinforced concrete bridge piers is 19 m, and the Grades of concrete and reinforcing steel are C50 and HRB335, respectively. The longitudinal reinforcement ratio is calculated to be 1.195%, and the concrete cover is 70 mm. More details about the reinforcement configuration of the pier cross-section can be seen in Figure 4C and Table 2 (Fu et al., 2022).

Figure 4

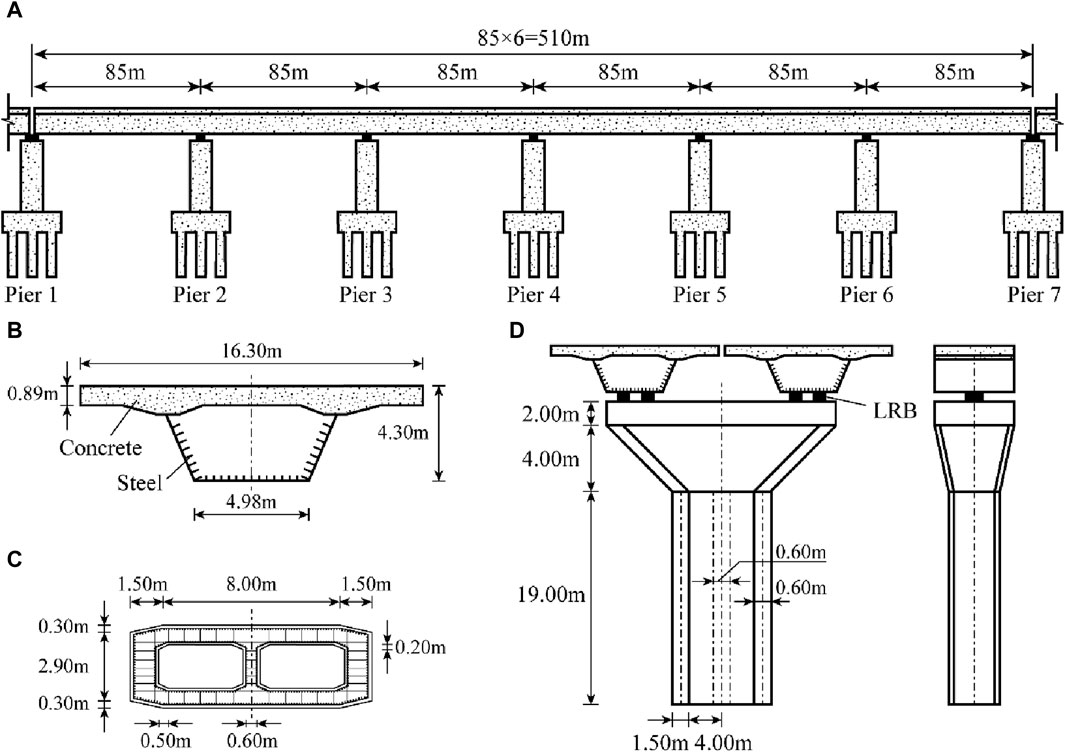
Figure 4. Details of the adopted isolated bridge. (A) Overview of the isolated bridge, (B) Cross-section of the grider, (C) Cross-section of the pier, (D) Elevation of the pier.

Table 2

Table 2. Reinforcement configuration of the pier cross-section.

A total of four LRBs are set along the transverse direction of bridge for each pier, and the parameters of LRBs are summarized in Table 3. Where F_y is the yield strength; K_e is the elastic stiffness; and α is the post-yield stiffness ratio. Note that the adopted LRBs of the side piers (Piers 1 and 7) are different from that of the middle ones (Piers 2–6), which can be seen in Figure 5.

Table 3

Table 3. Parameters of the LRBs.

Figure 5

Figure 5. Schematic diagram of the LRBs.

4.2 Finite element model

Two finite element models (FEMs) of the isolated bridge are built with the OpenSees to investigate the seismic performance of isolated bridge affected by the lead core heating, as shown in Figure 6. Note that the soil-structure interaction effect is not taken into account here. The main differences between the two FEMs are the adopted elements of bearings, i.e., the elastomeric bearing (plasticity) element (corresponding to FEM 1 of the adopted bridge) and the LeadRubberX bearing element (corresponding to FEM 2 of the adopted bridge), which are utilized for the conditions that ignoring and considering the lead core heating of the LRBs, respectively.

Figure 6

Figure 6. FEMs of the isolated bridge.

The girders and bent caps are modelled via the elastic beam column elements, while the piers, which may be inelastic during seismic loadings, are simulated by the nonlinear beam-column element. A total of five elements are adopted for each pier, and the number of Gauss-Lobatto integration points along each element is five. With respect to the cross section of each pier, meshes with 7 cm × 7 cm are utilized. The constitutive laws of concrete and reinforcing steels are simulated with the Concrete 01 and Steel 02 material models, respectively. Analysis of natural vibration characteristics is performed based on the established FEM, and the first five natural periods of vibration are 1.09, 0.87, 0.85, 0.84, and 0.79 s, respectively.

4.3 Nonlinear dynamic time history analyzes

The Rayleigh damping model is adopted, and the damping ratio is 0.05. Nonlinear dynamic time history analyzes are carried out to quantitatively investigate the seismic response of the isolated bridge affected by the lead core heating of the LRBs. Both the original waves and extracted pulses of the selected 40 near-fault ground motions (as shown in Table 1) are adopted, and the energy-based seismic responses of the whole bridge structure and the individual components are calculated and compared.

4.3.1 Energy-based seismic responses

4.3.1.1 Input energies to the whole isolated bridge

The input energies to the whole isolated bridge subjected to different ground motions, including the original waves and extracted pulses, are shown in Figures 7, 8. As can be seen from Figure 7, the input energies of extracted pulses to the whole isolated bridge E_iP are significantly less than that of original waves E_iO, and this trend is almost not affected by the lead core heating of LRBs. The results shown in Figure 7B exhibits that the E_iP/E_iO ratios generally increase first and then, decrease when the pulse period increases, and finally approaches to zero when the pulse period is larger than 6.0 s. Besides, the E_iP/E_iO ratio reaches the maximum (83.81%) when the pulse period is about 2.5 s.

Figure 7

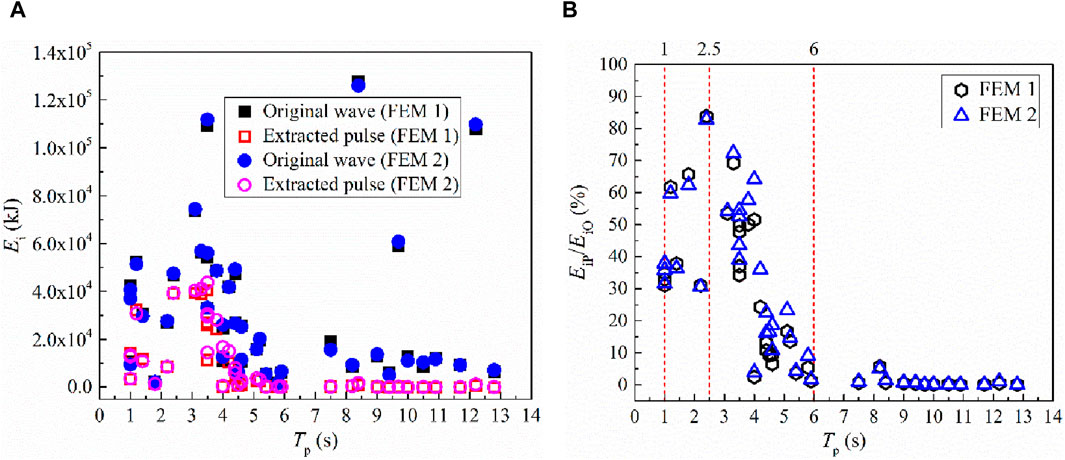
Figure 7. Input energies to the whole isolated bridge versus T_p. (A) The input energies of original waves and extracted pulses, (B) The proportion of input energies of extracted pulses.

Figure 8

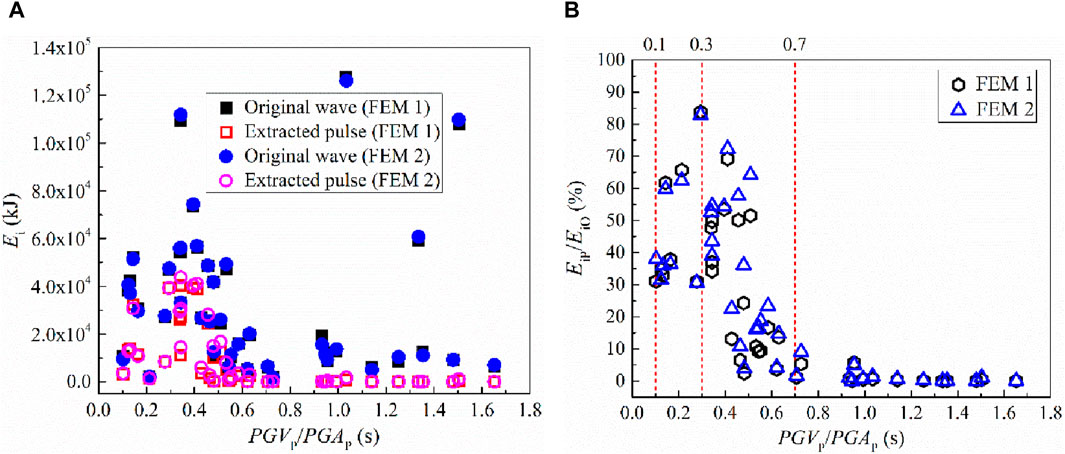
Figure 8. Input energies to the whole isolated bridge versus PGV_P/PGA_P ratio. (A) The input energies of original waves and extracted pulses, (B) The proportion of input energies of extracted pulses.

Note that, as displayed in Figure 8, the changing trend of the E_iP/E_iO ratio influenced by the PGV_P/PGA_P ratio is consistent with that shown in Figure 7, and the critical values of the PGV_P/PGA_P ratios are 0.3 and 0.7 (the corresponding T_p values are 2.5 and 6.0 s in Figure 7), respectively, which match well with the linear fitted relationship between the PGV_P/PGA_P ratio and T_p in Figure 3. Hence, it should be equivalent to reveal the effect of velocity pulse on the seismic response of the adopted bridge via the pulse period and the PGV_P/PGA_P ratio. For simplify, only the pulse period is mainly focused on in the following study.

In addition, as displayed in Figures 7A, 8A, by comparing the input energies of original waves to the whole isolated bridge, slight differences can be observed when the lead core heating of the LRBs is ignored and considered. However, the E_iP/E_iO ratio is significantly lager with the pulse period varying in the range of 2.5–6.0 s after considering the heating effect of lead core, which can be visually observed from Figures 7B, 8B. Furthermore, the relative energy variations (REVs) calculated by Eq. 7 are illustrated in Figure 9.

$REV=\frac{E_{\text{FEM}2}-E_{\text{FEM}1}}{E_{\text{FEM}1}}\times 100\%(7)$

where E_FEM1 and E_FEM2 are the corresponding energies determined by Eqs 3–6 in accordance with the numerical results based on FEMs 1 and 2.

Figure 9

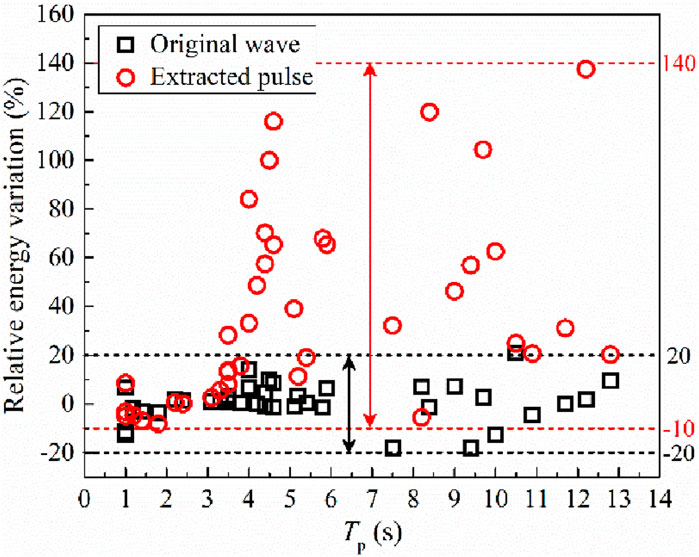
Figure 9. Relative variation of input energies to the whole isolated bridge considering the heating effect of lead core.

Note that the relative variation range shown in Figure 9 covers −20%– to 20% for the input energies of original waves, while for the input energies of extracted pulses, the variation range is −10% to 140%. However, the wide variation range corresponding to extracted pluses should be attributed to the low calculated input energies. For instance, the input energies to the whole bridge are 127,595 kJ and 126,050 kJ under the attack of the original wave of TCU052 (T_p = 8.4 s), respectively, and the relative variation according to Eq. 7 is −1.2%. While the corresponding values are 800 kJ and 1759 kJ when subjected to the extracted pulse of TCU052, and the relative variation according to Eq. 7 is 119.9%.

4.3.1.2 Absorbed energies of bearings

The ratio of absorbed energies of all the bearings under the attack of extracted pulses and original waves, i.e., the E_aBP/E_aBO ratio, affected by the pulse period is displayed in Figure 10. When the heating effect of lead core is considered during nonlinear dynamic time history analyses, both the absorbed energies of all the bearings under the original waves and extracted pulses increase, and the increased amplitude is much larger under extracted pulses.

Figure 10

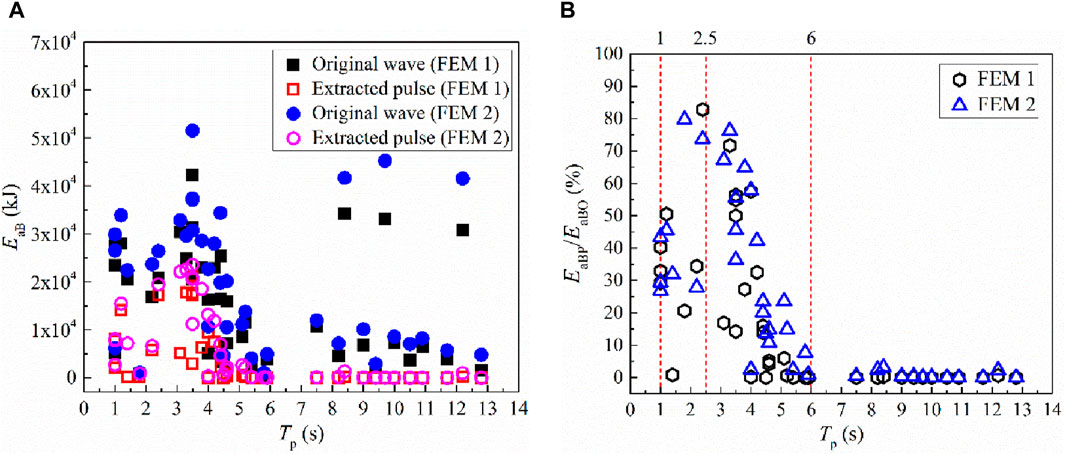
Figure 10. Absorbed energies of all the bearings. (A) Original waves vs. extracted pulses, (B) The E_aBP/E_aBO ratio.

Table 4 summarizes the subdivided relative energy variation for counting the concentrated range. The energy variations less than 50% account for 85.0% for the adopted bridge attacked by the original waves. However, the proportion that the variation ranges of absorbed energies of all the bearings exceeding 100% reach 67.5% for the adopted bridge subjected to extracted pulses.

Table 4

Table 4. Change of absorbed energies of all the bearings after considering the lead core heating.

4.3.1.3 Absorbed energies of piers

Figure 11 displays the absorbed energies of all the piers (E_aP), which trend to decrease when the heating effect of lead core is considered for the isolated bridge, whether excited by the original waves or the extracted pulses. Meanwhile, the extracted pulses are easy to cause a wider relative variation of E_aP, and the variation ranges are about −60%–20%, as displayed in Figure 11C.

Figure 11

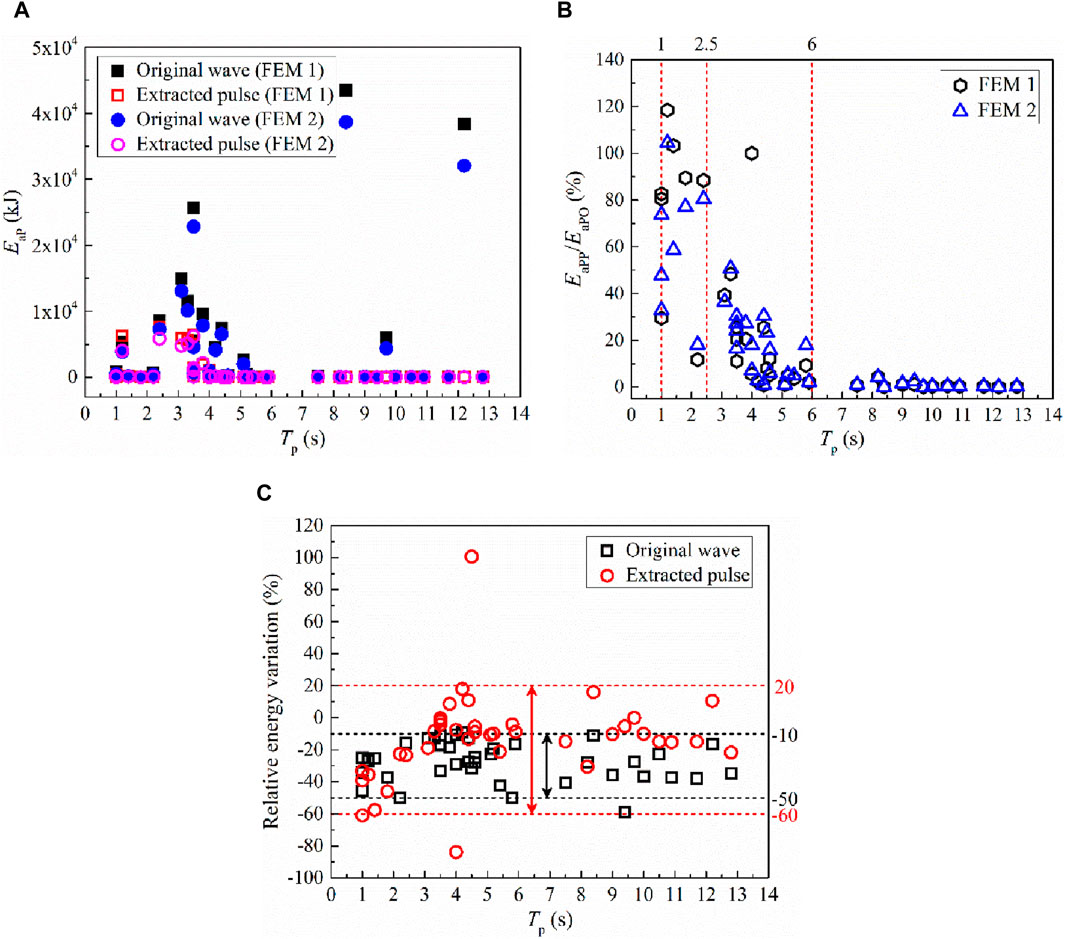
Figure 11. Absorbed energies of all the piers. (A) Original waves vs. extracted pulses, (B) The E_aPP/E_aPO ratio, (C) Relative energy variation.

In addition, no matter the heating effect of lead core is considered or not, the absorbed energies of all the piers obtained based on the excitations of extracted pulses (E_aPP) are larger than that of original waves (E_aPO) when the pulse period approximately equals to 1.0 s, which may be caused by the resonance since the first-order period of the isolated bridge is 1.09 s. Subsequently, the E_aPP/E_aPO ratio varies from 15% to 90% when the pulse period changes in the range of 1.0–2.5 s, and gradually decreases as the pulse period increases to 6.0 s. Also, the absorbed energies of all the piers under the excitations of extracted pulses are very close to zero since the pulse period exceeds 6.0 s.

4.3.1.4 Damping energies

The calculated damping energies are shown in Figure 12 for the adopted isolated bridge subjected to different kinds of seismic loadings. Generally, the ratio of damping energies excited by the extracted pulses (E_ξP) and original waves (E_ξO) increases first and then decreases until zero, and the critical values of pulse period are 1.0, 2.5, and 6.0 s. Besides, the damping energies excited by the extracted pulses are even larger than that obtained by the original waves when the heating effect of lead core is ignored. Moreover, based on the results shown in Figures 12A, C, the damping energies tend to decrease when the heating effect of lead core is considered, and the variation range is wider for the isolated bridge subjected to extracted pulses.

Figure 12

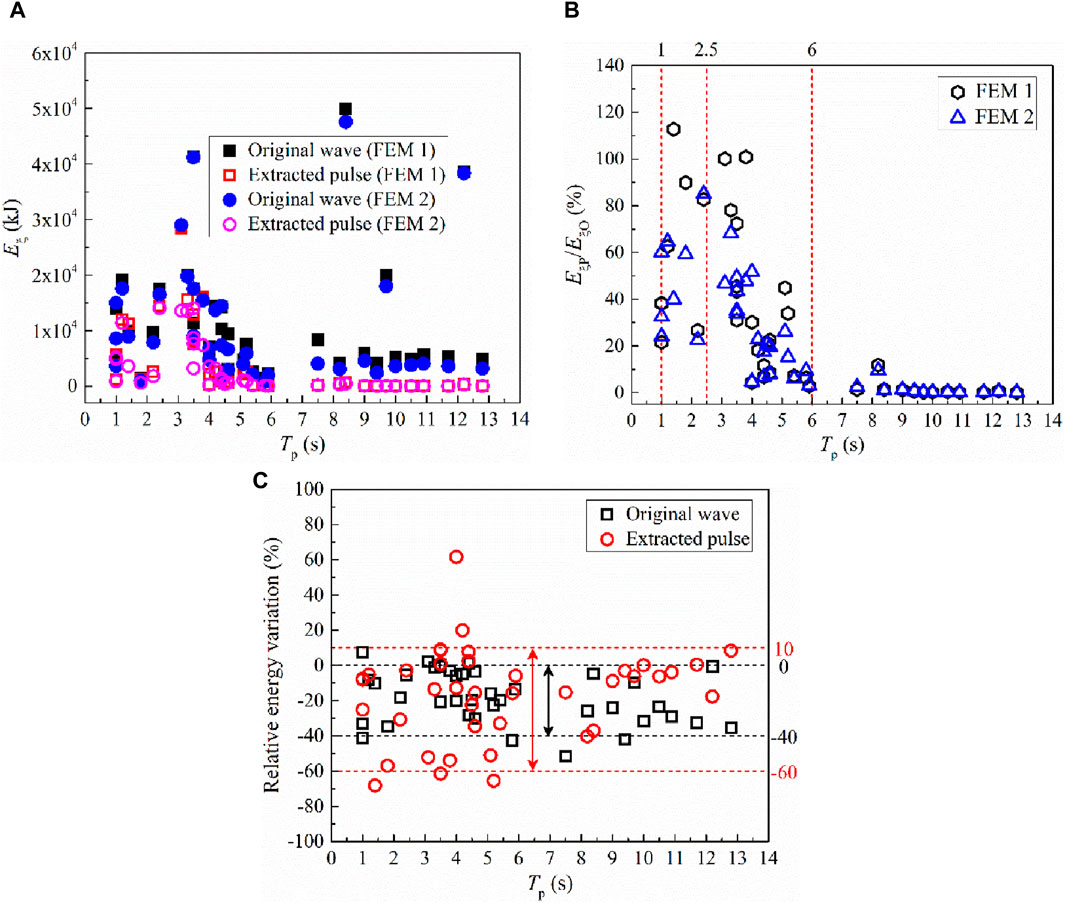
Figure 12. Damping energy. (A) Original waves vs. extracted pulses, (B) The E_ξP/E_ξO ratio, (C) Relative energy variation.

4.3.2 Deformation-based seismic responses

4.3.2.1 The maximum displacement of girders

The maximum displacement of girders is slightly magnified when considering the lead core heating of LRBs, as can be observed in Figures 13A, C. When the adopted isolated bridge is excited by the extracted pulses and the original waves, the ratio of the corresponding maximum displacements of girders (Δ_GirderP/Δ_GirderO) generally presents a trend of first increasing and then decreasing with the increase of pulse period, whether the lead core heating of LRBs is taken into account. As shown in Figure 13B, most of the ratios exceeds 100% when the pulse period is close to 1.09 s, i.e., the first-order period of the isolated bridge. Meanwhile, the ratios obtained based on FEM 1 are generally larger than that obtained based on FEM 2 in the condition that the pulse period is shorter than 1.5 s, while the opposite phenomenon can be observed after that.

Figure 13

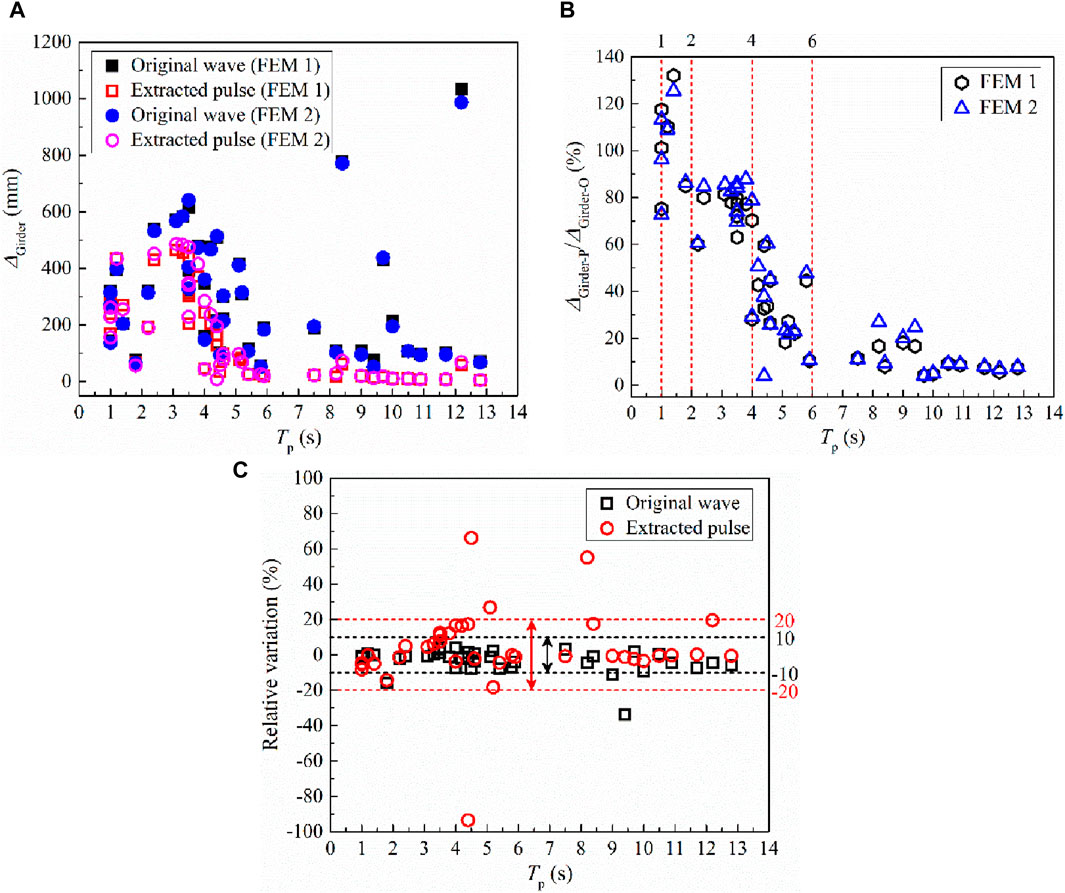
Figure 13. The maximum displacement of girders. (A) Original waves vs. extracted pulses, (B) The Δ_Girder-P/Δ_Girder-O ratio, (C) Relative variation.

4.3.2.2 The maximum shearing strain of bearings

As the ratio of the horizontal shearing deformation and the total thickness of rubber layer, the shearing strain is an effective indicator to describe the seismic response of bearings, as displayed in Figure 14. It is obvious that the maximum shearing strain of bearings will be magnified when the lead core heating of LRBs is considered, and this trend can be both observed from the conditions that the isolated bridge under the excitations of original waves and extracted pulses. Note that the relative variations are larger when subjected to the extracted pulses, as shown in Figure 14C. In addition, this above magnification is unrelated to the pulse period. As can be seen from Figures 14A, B, the maximum shearing strains of bearings obtained based on the input of extracted pulses are less than that of original waves, especially when the pulse period is larger than 6.0 s. The inverse pattern can be found when the pulse period changes in the range of 1.0–1.5 s.

Figure 14

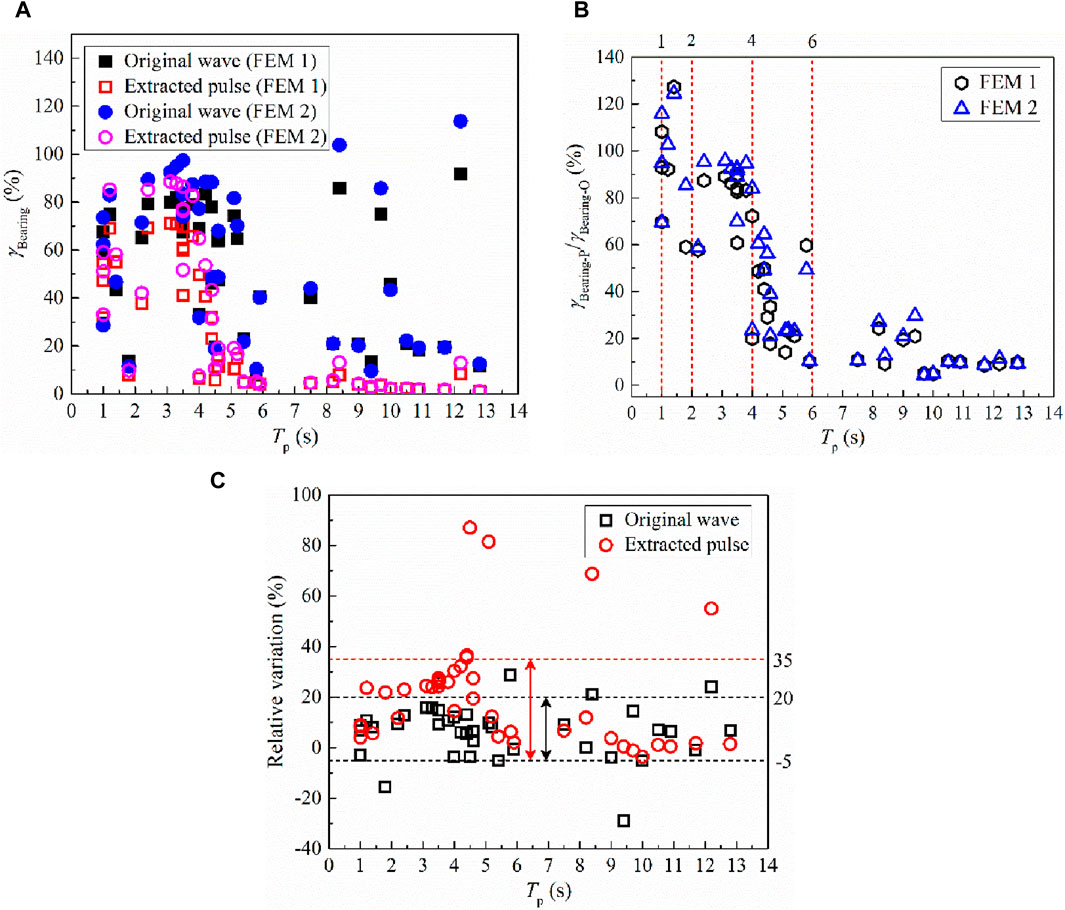
Figure 14. The maximum shearing strain of bearings. (A) Original waves vs. extracted pulses, (B) The γ_Bearing-P/γ_Bearing-O ratio, (C) Relative variation.

4.3.2.3 The maximum drift ratio of piers

The drift ratio of pier, which can be calculated by dividing the tip lateral displacement by the pier height, is adopted and compared. Figure 15 illustrates the effects of lead core heating of LRBs on the maximum drift ratios of bridge piers when subjected to the original waves and extracted pulses. As can be seen from Figures 15A, C, the maximum drift ratio of piers decrease slightly when considering the effect of lead core heating of LRBs. Besides, no matter the heating effect of lead core is considered, the maximum drift ratio obtained by extracted pulses will be larger than that by original waves when the pulse period is close to 1.09 s (i.e., the first-order period of the isolated bridge). Then, the opposite trend can be observed, and the ratio of the maximum drifts obtained by extracted pulses and original waves decreases sharply with the increase of the pulse period. When the pulse period is larger than 6.0 s, the ratio is less than 20%, as can be seen in Figure 15B.

Figure 15

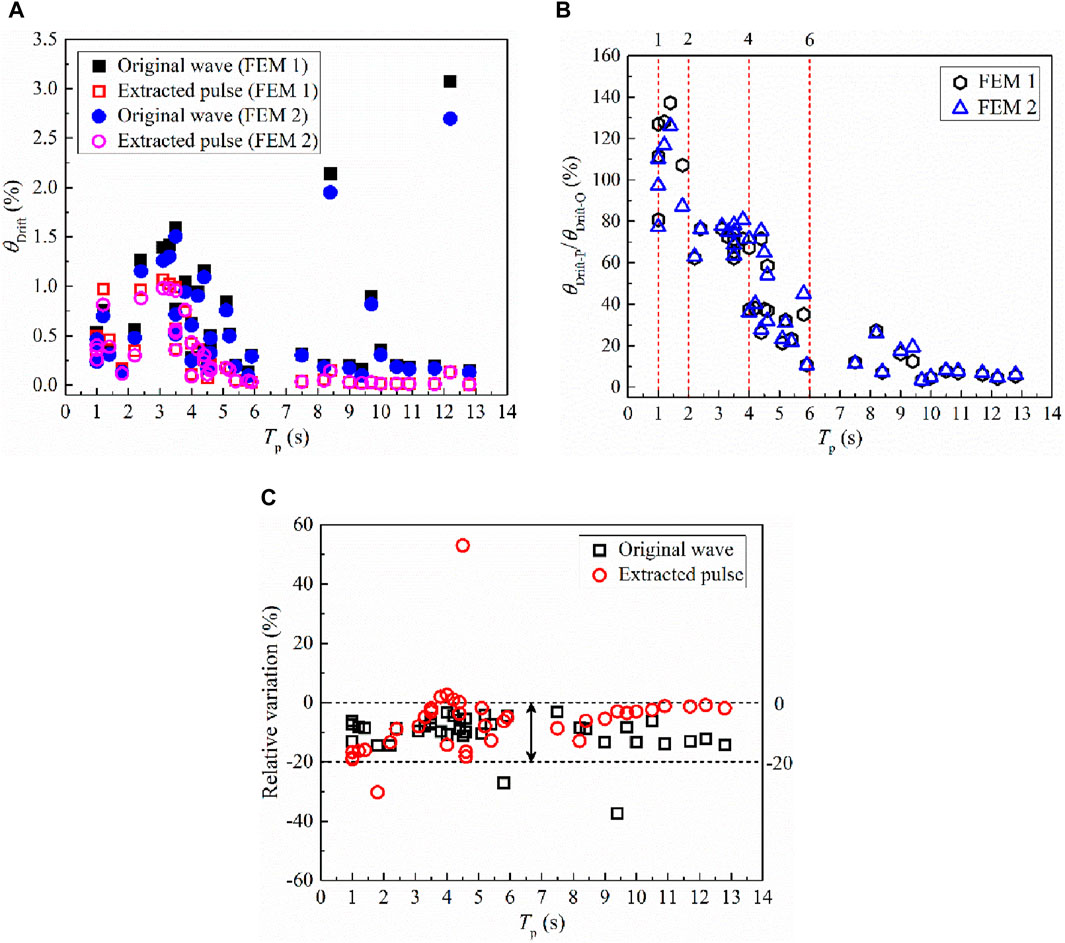
Figure 15. The maximum drift ratio of piers. (A) Original waves vs. extracted pulses, (B) The θ_Drift-P/θ_Drift-O ratio, (C) Relative variation.

Moreover, previous studies (Li et al., 2018; Cheng et al., 2021b) usually divide the damage states of bridge piers into several different levels, i.e., no damage, slight damage, moderate damage, severe damage, and collapse, and the corresponding threshold values of drift ratio are 0.7%, 1.5%, 2.5%, and 5.0%, respectively (Dutta, 1999). As can be seen from Figure 15A, it can be inferred that the seismic damage of bridge piers may be markedly underestimated by utilizing the extracted pulses.

5 Conclusion

This study presents a systematic numerical investigation on the seismic responses of isolated bridges under original records of near-fault ground motions and the corresponding extracted pulses. A typical isolated continuous girder bridge was adopted, and two sets of finite element models considering and ignoring the effect of lead core heating of LRBs were established based on the OpenSees platform. The seismic behaviors of the isolated bridge were evaluated by inputting the original waves and the extracted pulses. Based on the nonlinear dynamic time history analyses, both the energy-based and deformation-based seismic responses were captured and compared in detail. The main conclusions are summarized as below:

(1) The lead core heating of the LRBs mainly affects the seismic responses of bearings and piers, including the absorbed energies and the maximum shearing stain of bearings, the absorbed energies and maximum drift ratio of piers. Considering the heating effect of lead core will enhance the seismic responses of bearings and decrease the seismic responses of piers, as well as the damping energies, which are consistent for the isolated bridge subjected to the original waves and the corresponding extracted pulses. Besides, the lead core heating of the LRBs will be magnified for the seismic response of isolated bridges subjected to the extracted pulses.

(2) The ratios of the seismic responses (i.e., the absorbed energy of bearings E_aB, the absorbed energy of piers E_aP, the damping energy E_ξ, the maximum displacement of girders Δ_Girder, the maximum shearing strain of bearings γ_Bearing, and the maximum drift ratio of piers θ_Drift) obtained by extracted pulses and original waves generally increase first and then, decrease when the pulse period increases, and finally approach to zero when the pulse period is larger than 6.0 s. Besides, these ratios reach the maximum when the pulse period is about 1.0–2.5 s.

(3) Compared with the input of whole records of near-fault ground motions, the accuracy of the seismic evaluation based on the extracted pulses strongly depends on the precondition that the pulse period is close to the fundamental period of the isolated bridge. In addition, isolated bridges respond with multiple vibration modes coupled when subjected to seismic excitations. Hence, inputting the extracted pulses for predicting the in-elastic seismic response of isolated bridges locating at near-fault region is not an adequate replacement for those original waves of near-fault ground motions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Y-XH: Conceptualization, Funding acquisition, Methodology, Supervision, Writing–review and editing. JW: Formal Analysis, Investigation, Software, Visualization, Writing–original draft. J-LL: Formal Analysis, Investigation, Methodology, Validation, Writing–review and editing. T-TX: Writing–review and editing, Supervision, Validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by the National Natural Science Foundation of China (Grant No. 52268077) and the Key Research and Development Project in Ningxia Hui Autonomous Region (Grant No. 2022BEG03062).

Acknowledgments

The authors greatly appreciate the financial supports.

Conflict of interest

Authors Y-XH, J-LL were employed by Ningxia Communications Construction Co., Ltd. Author JW was employed by Ningxia Haiping Expressway Management Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alavi, B., and Krawinkler, H. (2004). Behavior of moment-resisting frame structures subjected to near-fault ground motions. Earthq. Eng. Struct. Dyn. 33 (6), 687–706. doi:10.1002/eqe.369

CrossRef Full Text | Google Scholar

Baker, J. W. (2007). Quantitative classification of Near-Fault Ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 97 (5), 1486–1501. doi:10.1785/0120060255

CrossRef Full Text | Google Scholar

Bertagnoli, G., Ferrara, M., Miceli, E., Castaldo, P., and Giordano, L. (2024). Safety assessment of an existing bridge deck subject to different damage scenarios through the global safety format ECOV. Eng. Struct. 306, 117859. doi:10.1016/j.engstruct.2024.117859

CrossRef Full Text | Google Scholar

Biggs, J. M. (1964). Introduction to structural dynamics. New York: McGraw-Hill.

Google Scholar

Castaldo, P., and Miceli, E. (2023). Optimal single concave sliding device properties for isolated multi-span continuous deck bridges depending on the ground motion characteristics. Soil Dyn. Earthq. Eng. 173, 108128. doi:10.1016/j.soildyn.2023.108128

CrossRef Full Text | Google Scholar

Cheng, H., Li, H. N., Biondini, F., Wang, D. S., and Zou, Y. (2021a). Strain penetration effect on cyclic response of corroded RC columns. Eng. Struct. 243, 112653. doi:10.1016/j.engstruct.2021.112653

CrossRef Full Text | Google Scholar

Cheng, H., Li, H. N., Wang, D. S., Sun, Z. G., Li, G. Q., and Jin, J. N. (2016). Research on the influencing factors for residual displacements of RC bridge columns subjected to earthquake loading. Bull. Earthq. Eng. 14 (8), 2229–2257. doi:10.1007/s10518-016-9902-y

CrossRef Full Text | Google Scholar

Cheng, H., Li, H. N., Yang, Y. B., and Wang, D. S. (2019). Seismic fragility analysis of deteriorating RC bridge columns with time-variant capacity index. Bull. Earthq. Eng. 17 (7), 4247–4267. doi:10.1007/s10518-019-00628-x

CrossRef Full Text | Google Scholar

Cheng, H., Wang, D. S., Li, H. N., Zou, Y., and Zhu, K. N. (2021b). Investigation on ultimate lateral displacements of coastal bridge piers with different corrosion levels along height. J. Bridge Eng. 26 (4), 04021015. doi:10.1061/(asce)be.1943-5592.0001696

CrossRef Full Text | Google Scholar

Decanini, L. D., and Mollaioli, F. (2001). An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 21 (2), 113–137. doi:10.1016/s0267-7261(00)00102-0

CrossRef Full Text | Google Scholar

Dutta, A. (1999). On energy based seismic analysis and design of highway bridges. Buffalo (NY): State University of New York.

Google Scholar

Fu, J. Y., Cheng, H., Wang, D. S., Zhang, R., and Xu, T. T. (2022). Temperature-dependent performance of LRBs and its effect on seismic responses of isolated bridges under near-fault earthquake excitations. Strucs. 41, 619–628. doi:10.1016/j.istruc.2022.05.046

CrossRef Full Text | Google Scholar

Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthq. Spectra. 11 (4), 569–605. doi:10.1193/1.1585828

CrossRef Full Text | Google Scholar

Han, Q., Wen, J. N., Zhong, Z. L., and Du, X. L. (2018). Numerical simulation of frictional heating effects of sliding friction bearings for isolated bridges. Int. J. Struct. Stab. Dyn. 18 (8), 1840008. doi:10.1142/s0219455418400084

CrossRef Full Text | Google Scholar

He, W. L., and Agrawal, A. K. (2008). Analytical model of ground motion pulses for the design and assessment of seismic protective systems. J. Struct. Eng. 134 (7), 1177–1188. doi:10.1061/(asce)0733-9445(2008)134:7(1177)

CrossRef Full Text | Google Scholar

Housner, G. W. (1956) “Limit design of structures to resist earthquake,” in Proceedings of 1st world conference on earthquake engineering. Berkeley: California.

Google Scholar

Hui, Y. X., Li, L. S., Cheng, H., Zhang, Y. J., and Wang, D. S. (2023). Seismic mitigation of continuous girder bridges equipped with U-shaped stainless steel dampers under near-fault earthquake excitations. Strucs. 58, 105597. doi:10.1016/j.istruc.2023.105597

CrossRef Full Text | Google Scholar

Jiang, H., and Zhu, X. (2006). Energy input design spectra for near-fault regions and application in energy-based seismic design. Earthq. Eng. Eng. Vib. 26 (5), 102–108. (in Chinese).

Google Scholar

Jiang, H., Zhu, X., and Ni, Y. J. (2009). Simplified computational models of input energy based on spectrum velocity for near-fault earthquakes. World Earthq. Eng. 25 (3), 86–90. (in Chinese).

Google Scholar

Jiang, H., Zhu, X., and Ni, Y. J. (2011). Research on seismic hysteretic energy dissipation ratio spectra for bridge structure based on multi-factor analysis. China J. Highw. Transp. 24 (1), 50–58. (in Chinese).

Google Scholar

Jiang, X. Y., Li, J. Z., and Xiang, N. L. (2024). Effect of bearing friction on seismic performance of bridges with massive piers isolated by friction pendulum bearings. Int. J. Struct. Stab. Dyn. doi:10.1142/s0219455425500567

CrossRef Full Text | Google Scholar

Kawashima, K. (1998). Interaction of hysteretic behavior between isolator/damper and pier in an isolated bridge. J. Struct. Eng. JSCE 44, 733–741.

Google Scholar

Kawashima, K. (2002). Damage of bridges resulting from fault rupture in the 1999 Kocaeli and Duzce, Turkey earthquakes and the 1999 Chi-Chi, Taiwan earthquake. Struct. Eng./Earthq. Eng. 19 (2), 171–190.

CrossRef Full Text | Google Scholar

Li, H. N., Cheng, H., and Wang, D. S. (2018). Time-variant seismic performance of offshore RC bridge columns with uncertainty. Int. J. Struct. Stab. Dyn. 18 (12), 1850149. doi:10.1142/s0219455418501493

CrossRef Full Text | Google Scholar

Li, Y., Zhao, G. H., and Bai, H. (2011). Analysis on seismic energy response for bridges of passenger dedicated line. China Saf. Sci. J. 21 (10), 143–149. (in Chinese).

Google Scholar

Makris, N. (1997). Rigidity-plasticity-viscosity: can electrorheological dampers protect base-isolated structures from near-source ground motions? Earthq. Eng. Struct. Dyn. 26 (5), 571–591. doi:10.1002/(sici)1096-9845(199705)26:5<571::aid-eqe658>3.0.co;2-6

CrossRef Full Text | Google Scholar

Makris, N., and Chang, S. P. (2000). Effect of viscous, viscoplastic and friction damping on the response of seismic isolated structures. Earthq. Eng. Struct. Dyn. 29 (1), 85–107. doi:10.1002/(sici)1096-9845(200001)29:1<85::aid-eqe902>3.0.co;2-n

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., Dong, G., and Papageorgiou, A. S. (2004). Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems. Earthq. Eng. Struct. Dyn. 33 (9), 1023–1049. doi:10.1002/eqe.391

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., and Papageorgiou, A. S. (2003). A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 93 (3), 1099–1131. doi:10.1785/0120020100

CrossRef Full Text | Google Scholar

Pang, Y. T., Meng, R., Li, C. D., and Li, C. (2022). A probabilistic approach for performance-based assessment of highway bridges under post-earthquake induced landslides. Soil Dyn. Earthq. Eng. 155, 107207. doi:10.1016/j.soildyn.2022.107207

CrossRef Full Text | Google Scholar

Rupakhety, R., and Sigbjörnsson, R. (2011). Can simple pulses adequately represent near-fault ground motions? J. Earthq. Eng. 15 (8), 1260–1272. doi:10.1080/13632469.2011.565863

CrossRef Full Text | Google Scholar

Shi, Y., Zhong, Z. W., Qin, H. G., Han, J. P., and Sun, Z. G. (2020). Toggle buckling-restrained brace systems and a corresponding design method for the seismic retrofit of bridge bents. Eng. Struct. 221, 110996. doi:10.1016/j.engstruct.2020.110996

CrossRef Full Text | Google Scholar

Uang, C. M., and Bertero, V. V. (1990). Evaluation of seismic energy in structures. Earthq. Eng. Struct. Dyn. 19, 77–90. doi:10.1002/eqe.4290190108

CrossRef Full Text | Google Scholar

Wu, Y. F., Wang, Z. J., Li, A. Q., Zhang, G. D., Fu, J. D., and Wang, H. (2024). The normalized inelastic displacement spectra for seismic response estimation of a SDOF system with a generalized flag-shaped hysteretic model. Bull. Earthq. Eng. 22, 3011–3029. doi:10.1007/s10518-024-01886-0

CrossRef Full Text | Google Scholar

Wu, Y. F., Wang H, H., Li, J., Ben, S., and Li, A. Q. (2019). Inelastic displacement spectra and its utilization of DDB design for seismic isolated bridges subjected to near-fault pulse-like ground motions. Earthq. Spectra. 35 (3), 1109–1140. doi:10.1193/033017eqs056m

CrossRef Full Text | Google Scholar

Yang, T., Yuan, X. Z., Zhong, J., and Yuan, W. C. (2023). Near-fault pulse seismic ductility spectra for bridge columns based on machine learning. Soil Dyn. Earthq. Eng. 164, 107582. doi:10.1016/j.soildyn.2022.107582

CrossRef Full Text | Google Scholar

Zhong, J., Zhu, Y. T., and Han, Q. (2023b). Impact of vertical ground motion on the statistical analysis of seismic demand for frictional isolated bridge in near-fault regions. Eng. Struct. 278, 115512. doi:10.1016/j.engstruct.2022.115512

CrossRef Full Text | Google Scholar

Zhong, J., Zhu, Y. T., Zheng, X. L., and Han, Q. (2023a). Multivariable probabilistic seismic demand models for parametric fragility prediction of isolated bridges portfolios under pulse-like GMs. Eng. Struct. 292, 116517. doi:10.1016/j.engstruct.2023.116517

CrossRef Full Text | Google Scholar