Domenico Camassa
Nicolò Vaiana
Anna Castellano- 1Department of Civil Engineering Sciences and Architecture, Polytechnic University of Bari, Bari, Italy
- 2Department of Structures for Engineering and Architecture, University of Naples Federico II, Napoli, Italy
- 3Department of Mechanics, Mathematics, and Management, Polytechnic University of Bari, Bari, Italy
Modal testing is one of the most effective experimental techniques for the structural health monitoring of masonry constructions, as it provides useful information for the calibration of structural models and for the assessment of structural damage. However, the application of modal testing to masonry constructions is sometimes hindered by the complexity of the conventional experimental set-up, which is generally based on contact sensors. In order to overcome this issue, several researchers are exploring the application of the ground-based radar interferometry, which is an increasingly popular measurement technique for remotely monitoring displacement and vibration of structures. Given the recently increasing number of articles on this subject, here we propose a mini review on the most significant works dealing with the application of ground-based radar interferometry for modal testing of masonry constructions. In particular, we show the current state of the art and highlight the main research gaps with the purpose of assessing the effectiveness of ground-based radar interferometry for the structural health monitoring of these constructions. Our mini review is primarily aimed at engineers and scientists who already know about modal testing and radar interferometry technique and are interested in the specific application to masonry constructions.
1 Introduction
Historical masonry constructions represent the most widespread architectural and cultural heritage of our territory. Due to the high vulnerability to damage, masonry constructions must be preserved and safeguarded over time. Appropriate conservation and restoration interventions require suitable investigation procedures (Binda et al., 2000), which mainly involves non-destructive techniques (Carpinteri et al., 2007; Ramos et al., 2010a; Castellano et al., 2015; Castellano et al., 2016; Camassa et al., 2019; Camassa et al., 2020; Pallarés et al., 2021). Among them, modal testing has the very appealing feature of monitoring the global response of a structure. This experimental technique provides the modal properties of a structure (natural frequencies, mode shapes, modal damping ratios) by measuring and analyzing structural vibration due to the external load (Salawu and Williams, 1995; Peeters and Ventura, 2003; Ivorra and Pallarés, 2006; Ramos et al., 2010b; Bartoli et al., 2013).
Structural vibration is generally measured through contact sensors (e.g., accelerometers). Despite the high measurement accuracy of these sensors, their installation on the structure is time consuming and require the full access to the structure. These issues often hinder the application of modal testing on masonry constructions and encourage the development of contactless sensing techniques. A promising and increasingly popular technique is the ground-based radar interferometry, or more briefly radar interferometry.
Radar interferometry exploits phase information of back-reflected microwave signals for detecting small displacement and vibration of structures at great distance. Its working principles have been thoroughly described in several works (Gocał et al., 2013; Pieraccini, 2013; Pieraccini and Miccinesi, 2019). Radar interferometry stems from space technology, which encouraged the development of portable sensors for remotely monitoring civil structures. After pioneering works (Tarchi et al., 1997; 1999; Farrar et al., 1999; Pieraccini et al., 2000; 2003), commercial systems have been properly designed for static and dynamic testing of structures (Gentile and Bernardini, 2010; Diaferio et al., 2017). The main applications concern bridges, towers, wind turbines, dams, and buildings. Compared with accelerometers, the interferometric radar is quick and easy to install and requires no access to the structure. However, it still shows some drawbacks mainly related to atmospheric influence, presence of clutters, phase jumps, broadband noise, and projection of displacement along the line-of-sight directions (Michel and Keller, 2021).
Some researchers have explored the possibility of using interferometric radar systems for monitoring the dynamic behavior of masonry constructions. The main applications concern modal testing of masonry towers and bridges. Furthermore, a recent promising application concerns the dynamic identification of tensile force in tie rods (Gioffré et al., 2017; Camassa et al., 2021).
Here we discuss some meaningful works studying the employment of the radar interferometry technique for modal testing of masonry constructions. In particular, we explore the capability of estimating natural frequencies and mode shapes highlighting the promising effectiveness for Structural Health Monitoring (SHM) of masonry constructions and the main experimental and theoretical issues, also outlining possible research directions to enhance this application.
2 Identification of natural frequencies
In SHM of masonry constructions, the estimation of natural frequencies is of great importance both for the calibration of structural models and for the damage assessment. Natural frequencies are global properties of a structure that, in principle, do not depend on the measured point (except for nodal points), but only on the measurement accuracy. The interferometric radar is a device that could provide a good accuracy of displacement determination without the distinct location of the observed point (Gocał et al., 2013); consequently, it is particularly suitable for identifying natural frequencies of structures.
Several researchers have explored the capability of identifying natural frequencies of masonry towers (i.e., bell towers and civic towers) and masonry bridges by radar interferometry. In (Fratini et al., 2011) the natural frequencies of the dome of the Baptistery of San Giovanni (Firenze, Italy) were characterized. As for towers, the estimation of natural frequencies has proved to be as accurate as conventional accelerometers; nevertheless, a slight frequency shift has been observed (Castagnetti et al., 2019). As shown in Table 1, the frequencies associated with the first two bending modes (along orthogonal directions) are generally detected. Five frequencies were only estimated in (Calcina et al., 2016). As for bridges, in (Pieraccini et al., 2019) five natural frequencies of a very slender bridge were determined. To our knowledge, there are no articles in the literature on the topic that demonstrate the possibility of estimating higher frequencies.
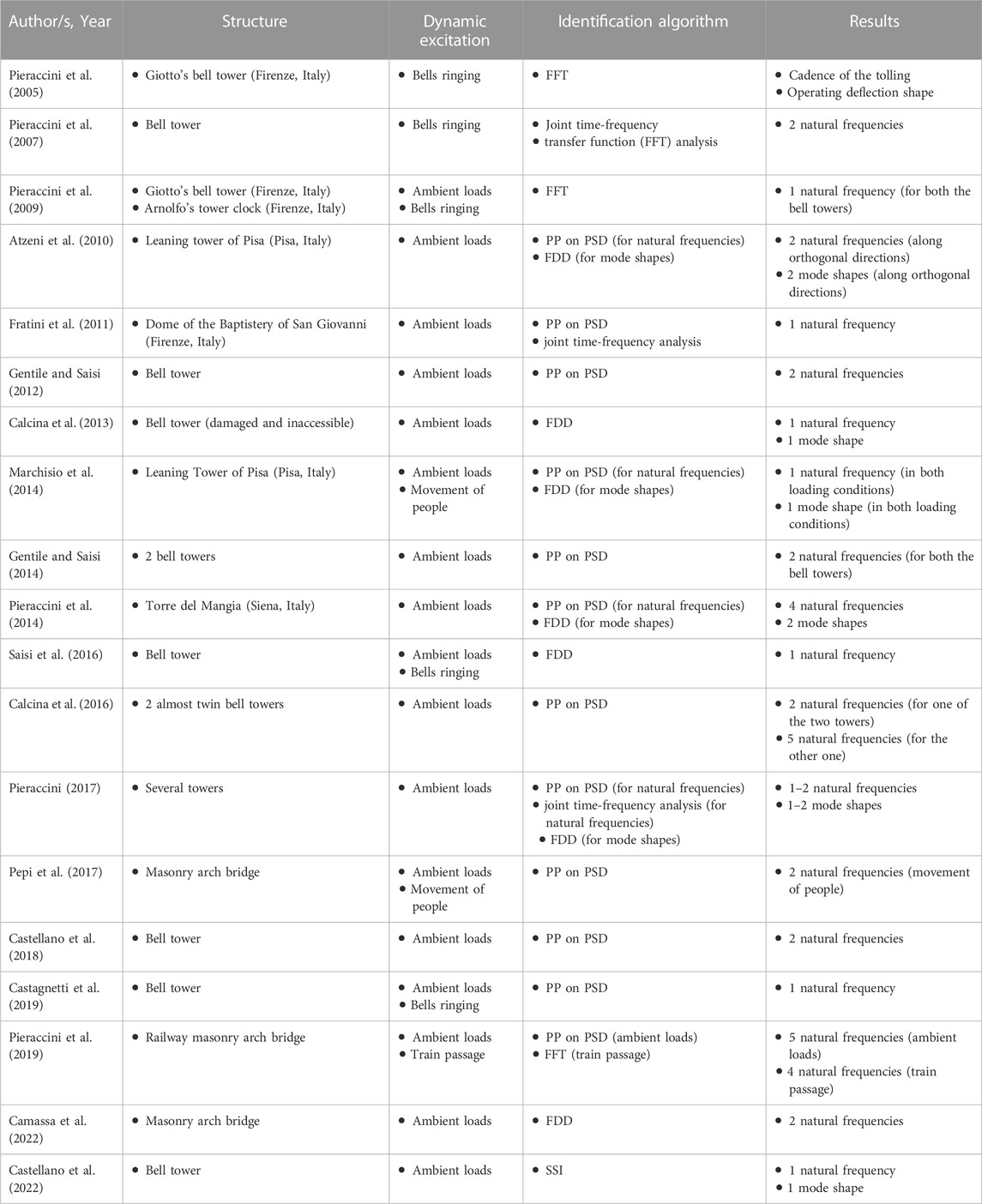
TABLE 1. Summary of the reviewed papers related to modal testing of masonry constructions by radar interferometry.
The reliability of frequency identification primarily depends on the Signal-to-Noise Ratio (SNR) of the acquired displacement signals, which is related to both the measurement accuracy of the interferometric radar and the magnitude of the radar line-of-sight component of displacements of the observed point. Furthermore, the identification algorithm may play a fundamental role in the estimation of natural frequencies. Here, we discuss some fundamental key concepts on these aspects focusing on the dynamic excitation and the identification algorithm.
The accuracy of the interferometric radar mainly depends on the SNR of the echoes received by the surveyed targets (Thermal SNR). The higher is the Thermal SNR, the better is the measurement accuracy. Masonry constructions, however, poorly reflect electromagnetic waves due to the low reflectivity and the limited presence of “corner zones” (Gentile and Saisi, 2012; 2014). To improve the Thermal SNR, short-range measurements should be preferred (Pieraccini et al., 2009). Another possible strategy concerns the installation of corner reflectors on the structure (Pepi et al., 2017). However, this solution requires the access to the structure and reduces the very appealing feature of contactless monitoring of radar interferometry.
The magnitude of the displacement of an observed point could be increased either by properly setting the geometry of acquisition or enhancing the dynamic excitation. The relation between the geometry of acquisition and the magnitude of the line-of-sight displacement can be found by simple projection operations (Michel and Keller, 2021). The discussion about dynamic excitation requires deeper considerations.
2.1 Dynamic excitation
Regarding to the dynamic excitation of masonry constructions, which generally have a considerable historical and artistic value, Operational Modal Analysis (OMA), which only involves ambient loads (wind, vehicular and pedestrian traffic), is considered the most suitable modal testing technique since it does not cause any risk of damage. Several works exploit ambient loads for modal testing by radar interferometry on towers (Atzeni et al., 2010) and bridges (Camassa et al., 2022). Anyway, depending on the mass and stiffness of the structure, natural excitations may induce very low structural vibration, which results in radar signals with low SNR. Here artificial loads could be used. The main applications in the literature concern “random” impulsive and steady-state loads generated by the movement of people or the operation of the monitored structure (bells ringing for bell towers, train passage for railway bridges). Invasive artificial devices (vibrodynes, shakers, etc.) for generating structural vibrations are generally not used on masonry constructions because they may cause damage, especially on already damaged constructions.
Forced vibration induced by coordinate movement of people has been shown to effectively improve the SNR of radar signals. In (Marchisio et al., 2014), a good correspondence between the natural frequencies of the Leaning Tower of Pisa (Italy) estimated in ambient and forced loading conditions was found; furthermore, radar signals measured under artificial loads turned out to be more regular and smoother, and the maximum amplitude of vibration was up to thirty times greater than in ambient conditions. Movement of people was used as source of excitation also on a historic single-span arch bridge (Pepi et al., 2017). Ambient vibration test did not provide any significant result due to the very low level of vibration; quite the opposite, two natural frequencies of the bridge were estimated from forced vibration.
The bells ringing in masonry towers has proved to be effective to enhance the SNR of the measured signals. Some authors show that the dynamic response associated to the swinging of bells was four times larger than under ambient loads (Saisi et al., 2016). As for railway masonry bridges, an effective artificial dynamic load concerns the passage of a train (Pieraccini et al., 2019).
The above-mentioned artificial loads are able to induce larger vibration than ambient loads and, consequently, to increase the SNR of displacement signals acquired by the interferometric radar. Hence, the use of these solicitations is generally encouraged. However, in our opinion, some critical issues, often ignored, should be considered.
Coordinate movement of people may violate the assumptions of OMA methods. Movement should be nearly random and non-stationary; otherwise, the cadence of movement may arise in the spectra of the measured displacements and may be mixed up with structural frequencies. The bells ringing is a periodic excitation, with a spectrum quite different to broadband white noise (assumed in OMA methods). Consequently, some natural frequencies could not be excited enough to be detected in the spectra of the measured displacements; furthermore, the frequency of the bells oscillation can appear in the spectra, as in (Pieraccini et al., 2005; 2009), and may be misinterpreted as a natural frequency of the tower. To avoid the latter problem, further studies could investigate strategies to distinguish the frequency of the bells oscillation from the structural ones. Possible solutions may include the application of harmonic detection algorithms. Alternatively, only the free decay of the structural vibration induced by the bells may be monitored. Regarding the passage of trains on railway masonry bridges, it should be considered that the train has a considerable mass with the respect to the mass of the structure. Accordingly, as shown in (Pieraccini et al., 2019), a frequency drop should be expected.
Finally, when artificial loads are used to obtain a reliable estimation of natural frequencies, the non-linear behavior of masonry constructions should be also considered. Masonry constructions generally exhibit, even in the range of small strains, amplitude dependency effects, which cause frequency drops when the amplitude of vibration increases (Michel et al., 2011; Gentile and Saisi, 2013; Martakis et al., 2021; 2022). Information about frequency drops is of utmost importance for the structural monitoring and the early warning of damage (Gentile and Saisi, 2013). However, to our knowledge, a frequency drop has been detected by interferometric radar surveys only in (Saisi et al., 2016).
2.2 Identification methods
Although artificial loads make it possible to increase the SNR of the acquired signals, in many cases pure ambient loads are only available. For instance, structures that are not accessible and have no internal sources of vibration (bells, moving loads, etc.) can be only excited by wind and vehicular and pedestrian traffic in the surrounding area. In such situations, the application of appropriate signal processing and identification techniques may play a major role.
The identification procedures applied in the literature mainly concern methods in the frequency domain. In the first applications (Pieraccini et al., 2009), natural frequencies of masonry towers have been estimated from the Discrete Fourier Transform (DFT) of acquired signals calculated by using the Fast Fourier Transform (FFT) algorithm. Ambient vibrations, however, are generally considered as random processes. As done in subsequent works, e.g., in (Atzeni et al., 2010), more advanced analysis of ambient vibration should be based on the application of suitable OMA methods, which generally require either the calculation of Power Spectral Density (PSD) functions in the frequency domain or Correlation Functions (CF) in the time domain.
Several authors have applied the Peak Picking (PP) method and the Frequency Domain Decomposition (FDD) method (Table 1), which are both based on the PSD functions. Due to the low SNR of radar signals acquired in low ambient vibration, the estimation of PSD should be based on methods capable of reducing noise in signals, such as the Welch’s method. Furthermore, identification methods capable of rejecting noise (e.g., the FDD method) should be preferred. Very few studies have explored the application of methods in the time domain (Castellano et al., 2022) or in the joint time-frequency domain (Pieraccini et al., 2007; Fratini et al., 2011; Pieraccini, 2017).
It should be pointed out that, in the literature reviewed, well-established identification methods are just applied to radar signals. To improve the estimation of natural frequencies, further research should deeply address the application of more advanced methods (in any domain) by taking into account both the main features of radar signals and the mechanical behavior of masonry structures (e.g., the amplitude dependency effects). In particular, the application of robust methods capable of handling signals with low SNR measured from non-linear structures, such as the CoS-SSI (Liu et al., 2019) method, should be explored. Furthermore, comparative studies should be conducted by applying different dynamic identification methods on the same case study.
3 Reconstruction of mode shapes
Contrary to natural frequencies, a full reconstruction of mode shapes of masonry constructions requires information about both the position of the measured points and the measurement of the whole three-dimensional displacement vector of the observed points. The interferometric radar does not provide the exact position of the observed points nor the component of displacement orthogonal to the line-of-sight direction. Therefore, radar interferometry has inherent limitations in determining three-dimensional displacement vectors and full three-dimensional mode shapes of masonry structures. Nevertheless, information about mode shapes is of utmost importance both for the calibration of structural models and the identification of damage.
A first study for assessing the operating deflection shape of a masonry tower under the oscillation of its own bells is shown in (Pieraccini et al., 2005). The application of a more standard approach for identifying the mode shapes of the Leaning Tower of Pisa was explored in (Atzeni et al., 2010). The authors were able to identify two closely spaced bending modes in the orthogonal planes of the tower by applying the FDD method.
Since the interferometric radar only provide the line-of-sight displacement of a target, these studies are based on kinematic assumptions about the possible displacements of the monitored structure. Without such assumptions, only the projection of mode shapes along the line-of-sight directions can be achieved. However, kinematic assumptions can only be applied to few types of constructions because, in general, the effective motion of a structure is unknown.
Some authors have proposed a number of solutions for reconstructing the whole displacement vector of a target. Except for a method able to detect both vertical and torsional movements of the sections of a bridge using an interferometric radar (Dei et al., 2009), other solutions are all based on the use of multiple interferometric radar sensors or bistatic radar systems (Michelini and Coppi, 2017; Monti-Guarnieri et al., 2018; Miccinesi et al., 2021; Michel and Keller, 2021; Olaszek et al., 2021).
The capability of estimating the displacement vector, however, does not directly imply the ability to reconstruct full three-dimensional mode shapes of large and complex masonry structures. In fact, it would be necessary to measure the vibration of the structure with multiple interferometric radar sensors from different points of view and, consequently, in different acquisitions (Figure 1). By applying OMA methods, it is possible to obtain partial three-dimensional mode shapes from each acquisition (i.e., mode shapes related to the degrees of freedom of the structure that are monitored in that acquisition), as shown in (Castellano et al., 2022). However, since OMA methods provide unscaled mode shapes (Rainieri and Fabbrocino, 2014), partial mode shapes estimated in different acquisition cannot be assembled in full mode shapes of the structure. This is a major limit of the use of radar interferometry for dynamic testing of masonry constructions. Further research to develop ad hoc methods for reconstructing mode shapes of masonry structures could lead to a great improvement in this application.
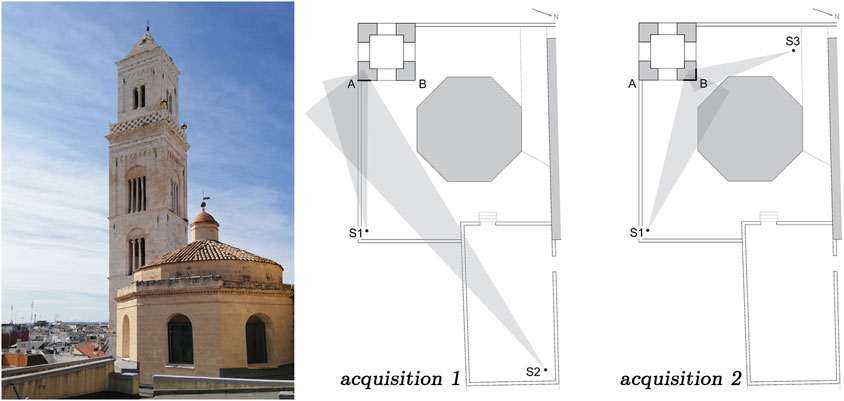
FIGURE 1. Different acquisitions that should be carried out with multiple interferometric radar systems to reconstruct full three-dimensional mode shapes of masonry constructions (S1, S2, and S3 represent the radar positions; the gray triangles represent the cone of view of the interferometric radar systems) (Castellano et al., 2022).
4 Discussion and future perspectives
Starting from the previous literature review, here we evaluate the advantages that radar interferometry can bring to the SHM of masonry constructions. We discuss the possibility of using modal properties estimated from interferometric radar measurements for the calibration of structural models (model updating) and the structural assessment.
Regarding the estimation of modal properties, the interferometric radar measurements make it possible to estimate the natural frequencies of the first bending modes and the projection of mode shapes along the line-of-sight directions. In general, neither higher natural frequencies nor full three-dimensional mode shapes can be obtained. The estimation of modal damping ratios is not explored in the literature, albeit information about the energy dissipation could be useful for damage detection (Ivorra et al., 2020).
In model updating, uncertain mechanical parameters are generally identified by minimizing the difference between theoretical and experimental modal behavior. A good updating may be obtained by just considering lower natural frequencies (Calcina et al., 2016; Castellano et al., 2018). More accurate results could be achieved by also considering mode shapes (Gentile and Saisi, 2007), which however cannot be completely estimated by radar interferometry.
As for structural assessment, it should be firstly noticed that, in general, structural damage is a local phenomenon. Therefore, the most useful modal properties for damage characterization are higher frequencies and mode shapes since they contain local information (Doebling et al., 1998; Fan and Qiao, 2011). Quite the opposite, lower frequencies are not very sensitive to localized damage because they are global properties of structures. Nevertheless, information about the fundamental frequency can still be used to detect damage that affects the whole structure, such as damage caused by seismic events (Calcina et al., 2013) or by foundation settlements (Castellano et al., 2021).
Finally, these considerations suggest that the interferometric radar can be effectively used to perform prompt dynamic tests on masonry constructions, especially in emergency conditions such as controls after seismic events (Saisi et al., 2016; Saisi and Gentile, 2020). In this vein, expeditious and no-contact approaches, as proposed in (Pieraccini et al., 2014), can provide pre-diagnostic information that may suggest deeper investigation with conventional contact sensors. Nevertheless, it emerged that, to date, the interferometric radar does not provide enough information to perform comprehensive structural monitoring of masonry constructions.
To enhance this application, in our opinion, future studies should be oriented toward two possible directions. One research line should be aimed at overcoming the limitations that emerged from this mini review, with a special focus on the identification of higher frequencies and the reconstruction of full mode shapes. Another research direction could involve the integration of radar interferometry with both Internet of Things (IoT) devices and satellite InSAR data (Selvakumaran et al., 2020; Scuro et al., 2021).
Author contributions
All authors contributed to the conception and intellectual framing of the review, and prepared the literature review and the first draft of the manuscript. All authors read and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Atzeni, C., Bicci, A., Dei, D., Fratini, M., and Pieraccini, M. (2010). Remote survey of the leaning tower of Pisa by interferometric sensing. IEEE Geoscience Remote Sens. Lett. 7, 185–189. doi:10.1109/LGRS.2009.2030903
Bartoli, G., Betti, M., and Giordano, S. (2013). In situ static and dynamic investigations on the “ Torre Grossa” masonry tower. Eng. Struct. 52, 718–733. doi:10.1016/j.engstruct.2013.01.030
Binda, L., Saisi, A., and Tiraboschi, C. (2000). Investigation procedures for the diagnosis of historic masonries. Constr. Build. Mater 14, 199–233. doi:10.1016/S0950-0618(00)00018-0
Calcina, S. V., Piroddi, L., and Ranieri, G. (2013). Fast dynamic control of damaged historical buildings: A new useful approach for structural health monitoring after an earthquake. ISRN Civ. Eng. 2013, 1–6. doi:10.1155/2013/527604
Calcina, S. v., Piroddi, L., and Ranieri, G. (2016). Vibration analysis of historic bell towers by means of contact and remote sensing measurements. Nondestruct. Test. Eval. 31, 331–359. doi:10.1080/10589759.2015.1121264
Camassa, D., Castellano, A., Fraddosio, A., Miglionico, G., and Piccioni, M. D. (2021). Dynamic identification of tensile force in tie-rods by interferometric radar measurements. Appl. Sci. Switz. 11, 3687. doi:10.3390/app11083687
Camassa, D., Castellano, A., Fraddosio, A., and Piccioni, M. D. (2020). A new ultrasonic amplitude tomography approach, with validation on masonry tuff blocks. J. Nondestr Eval. 39, 49. doi:10.1007/s10921-020-00693-2
Camassa, D., Castellano, A., Fraddosio, A., and Piccioni, M. D. (2019). Improvements of the ultrasonic tomography for applications to historical masonry constructions (Cham: Springer). doi:10.1007/978-3-319-99441-3_48
Camassa, D., Castellano, A., Fraddosio, A., Silla, M., and Piccioni, M. D. (2022). “Ambient vibration tests of a historical masonry bridge by means of radar interferometry,” in 2022 IEEE International Workshop on Metrology for Living Environment, MetroLivEn 2022 - Proceedings, Cosenza, Italy, 25-27 May 2022, 159–163. doi:10.1109/MetroLivEnv54405.2022.9826977
Carpinteri, A., Lacidogna, G., and Pugno, N. (2007). Structural damage diagnosis and life-time assessment by acoustic emission monitoring. Eng. Fract. Mech. 74, 273–289. doi:10.1016/j.engfracmech.2006.01.036
Castagnetti, C., Bassoli, E., Vincenzi, L., and Mancini, F. (2019). Dynamic assessment of masonry towers based on terrestrial radar interferometer and accelerometers. Sensors Switz. 19, 1319. doi:10.3390/s19061319
Castellano, A., Camassa, D., Fraddosio, A., and Piccioni, M. D. (2022). Radar interferometric experimental reconstruction of three-dimensional displacement vectors and mode shapes for masonry constructions. J. Phys. Conf. Ser. 2204, 012055. doi:10.1088/1742-6596/2204/1/012055
Castellano, A., Camassa, D., Fraddosio, A., Scacco, J., Piccioni, M. D., and Milani, G. (2021). Dynamic damage identification for a full-scale parabolic tuff barrel vault under differential settlements of the supports. Constr. Build. Mater 291, 123271. doi:10.1016/j.conbuildmat.2021.123271
Castellano, A., Foti, P., Fraddosio, A., Galietti, U., Marzano, S., and Piccioni, M. D. (2015). Characterization of material damage by ultrasonic immersion test. Procedia Eng. 109, 395–402. doi:10.1016/j.proeng.2015.06.248
Castellano, A., Foti, P., Fraddosio, A., Marzano, S., Paparella, F., and Piccioni, M. D. (2016). “Monitoring applied and residual stress in materials and structures by non-destructive acoustoelastic techniques,” in EESMS 2016 - 2016 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, Proceedings, Bari, Italy, 13-14 June 2016. doi:10.1109/EESMS.2016.7504830
Castellano, A., Fraddosio, A., Martorano, F., Mininno, G., Paparella, F., and Piccioni, M. D. (2018). “Structural health monitoring of a historic masonry bell tower by radar interferometric measurements,” in EESMS 2018 - Environmental, Energy, and Structural Monitoring Systems, Proceedings, Salerno, Italy, 21-22 June 2018. doi:10.1109/EESMS.2018.8405824
Dei, D., Pieraccini, M., Fratini, M., Atzeni, C., and Bartoli, G. (2009). Detection of vertical bending and torsional movements of a bridge using a coherent radar. NDT E Int. 42, 741–747. doi:10.1016/j.ndteint.2009.07.001
Diaferio, M., Fraddosio, A., Piccioni, M. D., Castellano, A., Mangialardi, L., and Soria, L. (2017). “Some issues in the structural health monitoring of a railway viaduct by ground based radar interferometry,” in 2017 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, EESMS 2017 - Proceedings, Milan, Italy, 24-25 July 2017. doi:10.1109/EESMS.2017.8052699
Doebling, S. W., Farrar, C. R., and Prime, M. B. (1998). A summary review of vibration-based damage identification methods. Shock Vib. Dig. 30, 91–105. doi:10.1177/058310249803000201
Fan, W., and Qiao, P. (2011). Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 10, 83–111. doi:10.1177/1475921710365419
Farrar, C. R., Darling, T. W., Migliori, A., and Baker, W. E. (1999). Microwave interferometers for non-contact vibration measurements on large structures. Mech. Syst. Signal Process 13, 241–253. doi:10.1006/mssp.1998.1216
Fratini, M., Pieraccini, M., Atzeni, C., Betti, M., and Bartoli, G. (2011). Assessment of vibration reduction on the Baptistery of San Giovanni in Florence (Italy) after vehicular traffic block. J. Cult. Herit. 12, 323–328. doi:10.1016/j.culher.2011.01.003
Gentile, C., and Bernardini, G. (2010). An interferometric radar for non-contact measurement of deflections on civil engineering structures: Laboratory and full-scale tests. Struct. Infrastructure Eng. 6, 521–534. doi:10.1080/15732470903068557
Gentile, C., and Saisi, A. (2007). Ambient vibration testing of historic masonry towers for structural identification and damage assessment. Constr. Build. Mater 21, 1311–1321. doi:10.1016/j.conbuildmat.2006.01.007
Gentile, C., and Saisi, A. (2014). Dynamic testing of masonry towers using the microwave interferometry. Key Eng. Mater. 628, 198–203. doi:10.4028/www.scientific.net/KEM.628.198
Gentile, C., and Saisi, A. (2013). Operational modal testing of historic structures at different levels of excitation. Constr. Build. Mater 48, 1273–1285. doi:10.1016/j.conbuildmat.2013.01.013
Gentile, C., and Saisi, A. (2012). “Radar-based vibration measurement on historic masonry towers,” in Emerging Technologies in Non-Destructive Testing V - Proceedings of the 5th Conference on Emerging Technologies in NDT. doi:10.1201/b11837-11
Gioffré, M., Cavalagli, N., Pepi, C., and Trequattrini, M. (2017). Laser Doppler and radar interferometer for contactless measurements on unaccessible tie-rods on monumental buildings: Santa Maria della Consolazione Temple in Todi. J. Phys. Conf. Ser. 778, 012008. doi:10.1088/1742-6596/778/1/012008
Gocał, J., Ortyl, Ł., Owerko, T., Kuras, P., Kocierz, R., Ćwiąkała, P., et al. (2013). Determination of displacements and vibrations of engineering structures using ground-based radar interferometry. Kraków: AGH University of Science and Technology Press.
Ivorra, S., Camassa, D., Bru, D., Gisbert, I., Castellano, A., Fraddosio, A., et al. (2020). “Assessment of the trm reinforcement of windowed masonry walls through oma identification,” in Proceedings of the international conference on structural dynamic (Athens, Greece: EURODYN).
Ivorra, S., and Pallarés, F. J. (2006). Dynamic investigations on a masonry bell tower. Eng. Struct. 28, 660–667. doi:10.1016/j.engstruct.2005.09.019
Liu, F., Wu, J., Gu, F., and Ball, A. D. (2019). An introduction of a robust OMA method: CoS-SSI and its performance evaluation through the simulation and a case study. Shock Vib. 2019, 6581516. doi:10.1155/2019/6581516
Marchisio, M., Piroddi, L., Ranieri, G., Calcina, S. v., and Farina, P. (2014). Comparison of natural and artificial forcing to study the dynamic behaviour of bell towers in low wind context by means of ground-based radar interferometry: The case of the Leaning Tower in Pisa. J. Geophys. Eng. 11, 055004. doi:10.1088/1742-2132/11/5/055004
Martakis, P., Reuland, Y., and Chatzi, E. (2022). “Amplitude dependency effects in the structural identification of historic masonry buildings,” in Lecture notes in civil engineering (Cham: Springer). doi:10.1007/978-3-030-91877-4_17
Martakis, P., Reuland, Y., and Chatzi, E. (2021). Amplitude-dependent model updating of masonry buildings undergoing demolition. Smart Struct. Syst. 27, 157. doi:10.12989/sss.2021.27.2.157
Miccinesi, L., Beni, A., and Pieraccini, M. (2021). Multi-monostatic interferometric radar for bridge monitoring. Electron. Switz. 10, 247. doi:10.3390/electronics10030247
Michel, C., and Keller, S. (2021). Advancing ground-based radar processing for bridge infrastructure monitoring. Sensors 21, 2172. doi:10.3390/s21062172
Michel, C., Zapico, B., Lestuzzi, P., Molina, F. J., and Weber, F. (2011). Quantification of fundamental frequency drop for unreinforced masonry buildings from dynamic tests. Earthq. Eng. Struct. Dyn. 40, 1283–1296. doi:10.1002/eqe.1088
Michelini, A., and Coppi, F. (2017). “Deformation vector measurement by means of ground based interferometric radar system,” in Proceedings Volume 10426, Active and Passive Microwave Remote Sensing for Environmental Monitoring, Warsaw, Poland, 3 October 2017. doi:10.1117/12.2279147
Monti-Guarnieri, A., Falcone, P., d’Aria, D., and Giunta, G. (2018). 3D vibration estimation from ground-based radar. Remote Sens. (Basel) 10, 1670. doi:10.3390/rs10111670
Olaszek, P., Świercz, A., and Boscagli, F. (2021). The integration of two interferometric radars for measuring dynamic displacement of bridges. Remote Sens. (Basel) 13, 3668. doi:10.3390/rs13183668
Pallarés, F. J., Betti, M., Bartoli, G., and Pallarés, L. (2021). Structural health monitoring (SHM) and nondestructive testing (ndt) of slender masonry structures: A practical review. Constr. Build. Mater 297, 123768. doi:10.1016/j.conbuildmat.2021.123768
Peeters, B., and Ventura, C. E. (2003). Comparative study of modal analysis techniques for bridge dynamic characteristics. Mech. Syst. Signal Process 17, 965–988. doi:10.1006/mssp.2002.1568
Pepi, C., Gioffrè, M., Comanducci, G., Cavalagli, N., Bonaca, A., and Ubertini, F. (2017). Dynamic characterization of a severely damaged historic masonry bridge. Procedia Eng. 199, 3398–3403. doi:10.1016/j.proeng.2017.09.579
Pieraccini, M., Dei, D., Betti, M., Bartoli, G., Tucci, G., and Guardini, N. (2014). Dynamic identification of historic masonry towers through an expeditious and no-contact approach: Application to the “Torre del Mangia” in Siena (Italy). J. Cult. Herit. 15, 275–282. doi:10.1016/j.culher.2013.07.006
Pieraccini, M. (2017). Extensive measurement campaign using interferometric radar. J. Perform. Constr. Facil. 31. doi:10.1061/(asce)cf.1943-5509.0000987
Pieraccini, M., Fratini, M., Dei, D., and Atzeni, C. (2009). Structural testing of historical heritage site towers by microwave remote sensing. J. Cult. Herit. 10, 174–182. doi:10.1016/j.culher.2008.09.006
Pieraccini, M., Fratini, M., Parrini, F., Pinelli, G., and Atzeni, C. (2005). Dynamic survey of architectural heritage by high-speed microwave interferometry. IEEE Geoscience Remote Sens. Lett. 2, 28–30. doi:10.1109/LGRS.2004.840616
Pieraccini, M., Luzi, G., Mecatti, D., Noferini, L., and Atzeni, C. (2003). A microwave radar technique for dynamic testing of large structures. IEEE Trans. Microw. Theory Tech. 51, 1603–1609. doi:10.1109/TMTT.2003.810145
Pieraccini, M., and Miccinesi, L. (2019). Ground-based radar interferometry: A bibliographic review. Remote Sens. (Basel) 11, 1029. doi:10.3390/rs11091029
Pieraccini, M., Miccinesi, L., Nejad, A. A., and Fard, A. N. N. (2019). “Monitoring of veresk rail bridge using a radar interferometer,” in Proceedings - CAMA 2019: IEEE International Conference on Antenna Measurements and Applications, Kuta, Bali, Indonesia, 23-25 October 2019, 8–11. doi:10.1109/CAMA47423.2019.8959608
Pieraccini, M. (2013). Monitoring of civil infrastructures by interferometric radar: A review. Sci. World J. 2013, 1–8. doi:10.1155/2013/786961
Pieraccini, M., Parrini, F., Dei, D., Fratini, M., Atzeni, C., and Spinelli, P. (2007). Dynamic characterization of a bell tower by interferometric sensor. NDT E Int. 40, 390–396. doi:10.1016/j.ndteint.2006.12.010
Pieraccini, M., Tarchi, D., Rudolf, H., Leva, D., Luzi, G., Bartoli, G., et al. (2000). Structural static testing by interferometric synthetic radar. NDT E Int. 33, 565–570. doi:10.1016/S0963-8695(00)00027-X
Rainieri, C., and Fabbrocino, G. (2014). Operational modal analysis of civil engineering structures. New York, NY.: Springer. doi:10.1007/978-1-4939-0767-0
Ramos, L. F., de Roeck, G., Lourenço, P. B., and Campos-Costa, A. (2010a). Damage identification on arched masonry structures using ambient and random impact vibrations. Eng. Struct. 32, 146–162. doi:10.1016/j.engstruct.2009.09.002
Ramos, L. F., Marques, L., Lourenço, P. B., de Roeck, G., Campos-Costa, A., and Roque, J. (2010b). Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process 24, 1291–1305. doi:10.1016/j.ymssp.2010.01.011
Saisi, A., and Gentile, C. (2020). Investigation strategy for structural assessment of historic towers. Infrastructures (Basel) 5, 106. doi:10.3390/infrastructures5120106
Saisi, A., Gentile, C., and Ruccolo, A. (2016). Pre-diagnostic prompt investigation and static monitoring of a historic bell-tower. Constr. Build. Mater 122, 833–844. doi:10.1016/j.conbuildmat.2016.04.016
Salawu, O. S., and Williams, C. (1995). Review of full-scale dynamic testing of bridge structures. Eng. Struct. 17, 113–121. doi:10.1016/0141-0296(95)92642-L
Scuro, C., Lamonaca, F., Porzio, S., Milani, G., and Olivito, R. S. (2021). Internet of Things (IoT) for masonry structural health monitoring (SHM): Overview and examples of innovative systems. Constr. Build. Mater 290, 123092. doi:10.1016/j.conbuildmat.2021.123092
Selvakumaran, S., Rossi, C., Marinoni, A., Webb, G., Bennetts, J., Barton, E., et al. (2020). Combined InSAR and terrestrial structural monitoring of bridges. IEEE Trans. Geoscience Remote Sens. 58, 7141–7153. doi:10.1109/TGRS.2020.2979961
Tarchi, D., Ohlmer, E., and Sieber, A. (1997). Monitoring of structural changes by radar interferometry. Res. Nondestruct. Eval. 9, 213–225. doi:10.1080/09349849709414475
Tarchi, D., Rudolf, H., Luzi, G., Chiarantini, L., Coppo, P., and Sieber, A. J. (1999). “SAR interferometry for structural changes detection: A demonstration test on a dam,” in International Geoscience and Remote Sensing Symposium (IGARSS), Hamburg, Germany, 28 June 1999. doi:10.1109/igarss.1999.772006
Keywords: radar interferometry, modal testing, masonry constructions, remote sensing, structural health monitoring, cultural heritage
Citation: Camassa D, Vaiana N and Castellano A (2023) Modal testing of masonry constructions by ground-based radar interferometry for structural health monitoring: A mini review. Front. Built Environ. 8:1065912. doi: 10.3389/fbuil.2022.1065912
Received: 10 October 2022; Accepted: 22 December 2022;
Published: 09 January 2023.
Edited by:
Michele Betti, University of Florence, ItalyReviewed by:
Giacomo Zini, University of Florence, ItalyMarco Valente, Politecnico di Milano, Italy
Carmelo Scuro, University of Calabria, Italy
Copyright © 2023 Camassa, Vaiana and Castellano. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Domenico Camassa, domenico.camassa@poliba.it