Cyclic peptide membrane permeability prediction using deep learning model based on molecular attention transformer

Membrane permeability is a critical bottleneck in the development of cyclic peptide drugs. Experimental membrane permeability testing is costly, and precise in silico prediction tools are scarce. In this study, we developed CPMP (https://github.com/panda1103/CPMP), a cyclic peptide membrane permeability prediction model based on the Molecular Attention Transformer (MAT) frame. The model demonstrated robust predictive performance, achieving determination coefficients (R²) of 0.67 for PAMPA permeability prediction, and R² values of 0.75, 0.62, and 0.73 for Caco-2, RRCK, and MDCK cell permeability predictions, respectively. Its performance outperforms traditional machine learning methods and graph-based neural network models. In ablation experiments, we validated the effectiveness of each component in the MAT architecture. Additionally, we analyzed the impact of data pre-training and cyclic peptide conformation optimization on model performance.

1 Introduction

Cyclic peptides have emerged as promising therapeutic candidates owing to their favorable pharmacological properties, including low metabolic toxicity, enhanced stability, high binding affinities, and remarkable efficacy in disrupting protein-protein interactions (Zhang and Chen, 2022; Muttenthaler et al., 2021). Recent advancements in artificial intelligence have significantly enhanced computer-aided design of cyclic peptide drugs, enabling high-throughput screening of cyclic peptides (Kosugi and Ohue, 2023; Rettie et al., 2023). Among the critical factors in cyclic peptide drug development, membrane permeability plays a pivotal role as it directly influences oral bioavailability and intracellular target accessibility (Bockus et al., 2015; Bhardwaj et al., 2022; Hewitt et al., 2015). Traditional experimental approaches for assessing membrane permeability, such as the parallel artificial membrane permeability assay (PAMPA) (Ottaviani et al., 2006), colon epithelial cancer cell (Caco-2) assay (van Breemen and Li, 2005), Ralph Russ canine kidney cell (RRCK) assay (Di et al., 2011), and Madin-Darby canine kidney cell (MDCK) assay (Irvine et al., 1999), are often limited by their time-consuming nature and substantial costs. In response to these challenges, several computational methods have been developed, including MultiCycGT (Cao et al., 2024), PharmPapp (Tan et al., 2024) and CycPeptMP (Li et al., 2024). However, these approaches present notable limitations. MultiCycGT simplifies the prediction of continuous permeability values into a binary classification task, providing only a rough determination of whether cyclic peptides are permeable. The PharmPapp analysis pipeline is specifically designed for the KNIME platform and lacks the flexibility to be extended to mainstream analysis environments. Moreover, its performance is unsatisfactory, with R² values ranging from 0.484 to 0.708 for the Caco-2 and RRCK permeability predictions. CycPeptMP, a multi-level molecular feature fusion model, requires specific molecular features as input, which can only be generated using the commercial software MOE.

In this study, we propose the Cyclic Peptide Membrane Permeability prediction model (CPMP), an accessible and open-source solution designed for seamless integration into high-throughput cyclic peptide screening pipelines. Built upon the Molecular Attention Transformer (MAT) neural network (Maziarka et al., 2020), a specialized variant of the Transformer architecture (Vaswani et al., 2017), CPMP leverages interatomic distances and molecular graph structures to enhance its attention mechanism. The MAT framework has previously demonstrated exceptional performance in predicting diverse molecular properties (Maziarka et al., 2020). To predict cyclic peptide permeability, the CPMP model was trained from scratch or fine-tuned using four distinct datasets: PAMPA, Caco-2, RRCK and MDCK. Our results demonstrate that CPMP achieves robust predictive performance, significantly surpassing traditional machine learning methods and other deep learning models across key metrics, including Mean Squared Error (MSE), Mean Absolute Error (MAE), and R². This work introduces a powerful computational tool for cyclic peptide membrane permeability prediction, offering substantial potential to accelerate the development of cyclic peptide-based therapeutics.

2 Methods

2.1 Dataset

The cyclic peptide structures and membrane permeability data were obtained from CycPeptMPDB (Li et al., 2023). Peptide structures were recorded using SMILES notation, and permeability was represented as the log-scaled value, LogP_exp. Samples with LogP_exp < −10.0 were excluded. The permeability data were categorized into four types based on experimental methods: PAMPA, Caco-2, RRCK, and MDCK, with sample counts of 6,701, 1,310, 185, and 64, respectively. For the PAMPA and Caco-2 datasets, we split the data into training, validation, and test sets in a ratio of 8:1:1 (Supplementary Figures S1A, B). For the RRCK and MDCK datasets, the data were divided into training and test sets in a ratio of 7:3 (Supplementary Figures S1C, D). We also analyzed the distribution of six molecular properties, including molecular weight, TPSA (Topological Polar Surface Area), LogP (lipophilicity), ratio of modified amino acids, monomer length in the main chain, and ring count (Supplementary Figures S2–S7).

2.2 Architecture

The architecture of the CPMP model is shown in Figure 1A. The core of the CPMP model is MAT (Molecule Attention Transformer) (Maziarka et al., 2020). MAT is a deep learning framework designed for predicting molecular properties. It is based on the Transformer architecture and augmented with molecular graph structure and inter-atomic distances. The framework consists of an embedding layer, multiple Molecule Multi-Head Self-Attention layers, position-wise feed-forward layers, a global pooling layer, and a fully-connected layer for prediction. The attention mechanism in MAT is enhanced by incorporating distance and graph structure information, making it more effective in capturing the complex relationships within molecules. In MAT, the attention scores are computed using three weighted components: the atomic self-attention, distance (D), and adjacency (A) matrices, with weights λ_a, λ_d, and λ_g summing to 1 (Equation 1).

$A=\left({\lambda }_a\rho \left(\frac{{\mathbf{Q}}_i{\mathbf{K}}_i^T}{\sqrt{d_k}}\right)+{\lambda }_{d}g\left(\mathbf{D}\right)+{\lambda }_g\mathbf{A}\right){\mathbf{V}}_i,(1)$

g is the softmax normalization. The optimal λ values are determined via grid search. We use MSE (Equation 2) to calculate the loss between the actual (y) and predicted (ŷ) permeability:

$Loss=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2,(2)$

Figure 1

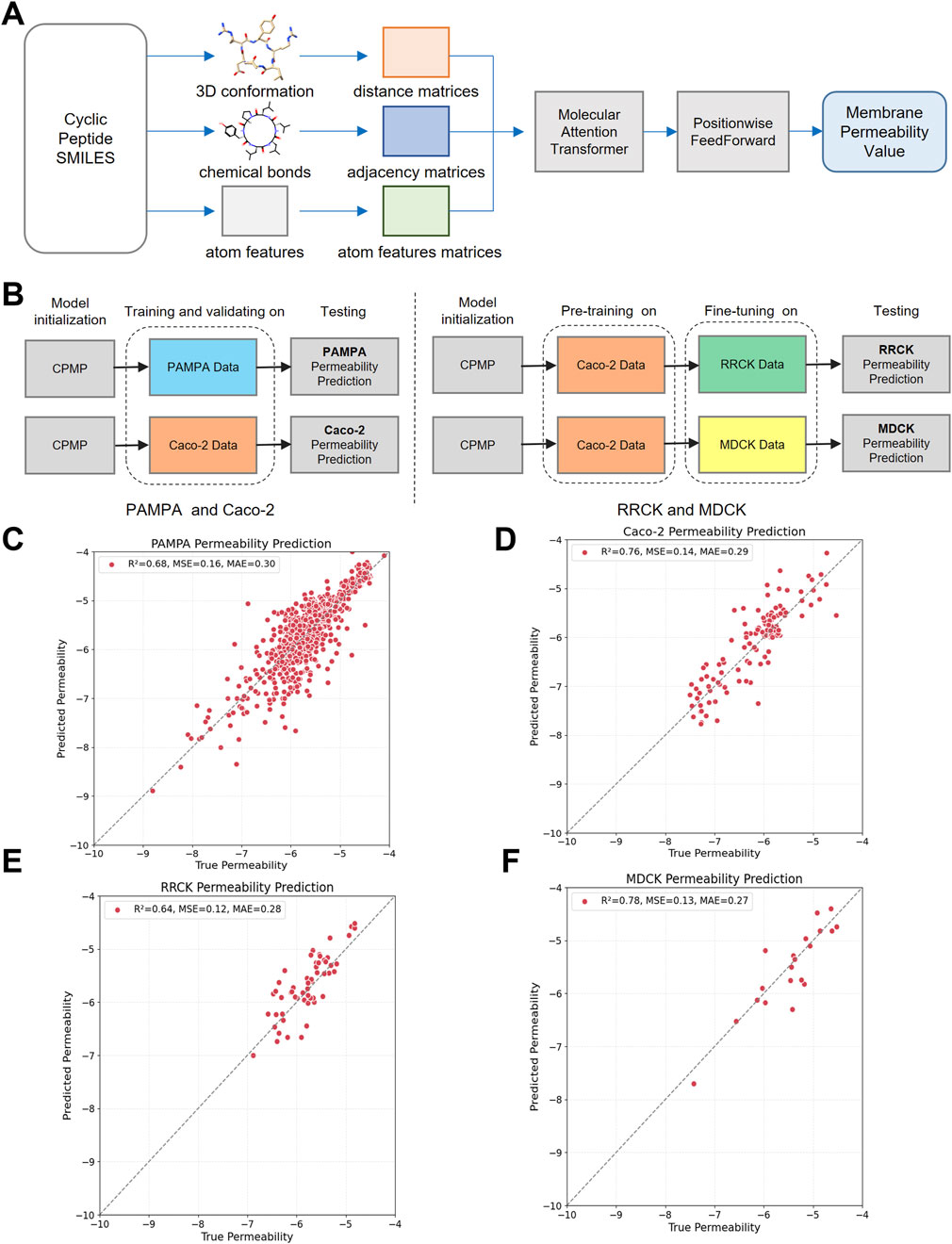
Figure 1. The architecture, training process and testing results of the CPMP model. (A) CPMP architecture for predicting cyclic peptide membrane permeability. The CPMP model predicts cyclic peptide membrane permeability from SMILES strings. It processes 3D molecular conformations, bond information, and atom features to construct distance, adjacency, and atom feature matrices. By integrating a molecular attention transformer with position wise feed forward networks, the model generates a permeability value as its output. (B) The CPMP model was trained on four different datasets: PAMPA, Caco-2, RRCK, and MDCK. (C–F) The testing results of the PAMPA, Caco-2, RRCK, and MDCK membrane permeability prediction model. The number of samples in the testing set are 671, 131, 56, and 20, respectively.

2.3 Training and testing

The training process is illustrated in Figure 1B. The PAMPA and Caco-2 permeability prediction models are initially trained on the training set, followed by parameter optimization using the validation set, and evaluated on the test set. For the RRCK and MDCK permeability prediction models, the pre-trained Caco-2 model is fine-tuned on the training set, and performance is then evaluated using the test set.

2.4 Baseline methods

We validated the performance of CPMP by comparing it with the RFR, SVR and MGNN models. The Random Forest Regressor (RFR) and Support Vector Regression (SVR) models were implemented using scikit-learn (Pedregosa et al., 2011) and utilized 1024-bit Morgan fingerprints generated by RDKit (Landrum et al., 2024) as input features. For the RFR model, the number of trees was set to 100. A series of tree depths, including [5, 10, 15, 20, 25, 30, 35, 40], were tested, and ultimately, 20 was selected as the optimal depth. For the SVR model, we used a Radial Basis Function (RBF) kernel and determined the optimal regularization parameter (C) and tolerance (epsilon) via grid search. Specifically, the search range for C was [0.1, 1, 10, 100], and for epsilon, it was [0.01, 0.1, 0.5, 1]. The model was trained and evaluated using cross-validation for each combination of C and epsilon. The combination that yielded the best performance on the validation set was selected as the optimal set. For the MGNN model, we select its regression task mode. Similarly, the hyperparameters for this model were also determined through grid search, including the dimension of hidden layers in the GNN network, the number of linear layers for fingerprint feature processing, batch size, and learning rate.

2.5 Y-randomization test

To assess the risk of chance correlations, we conducted a y-scrambling validation by randomly permuting the cyclic peptides’ permeability labels (Y-values) across the dataset. Following the identical training protocol as our primary models, we retrained 20 scrambled models with distinct label permutations. Performance metrics from these randomized models were then systematically compared with those of the original models to assess whether the observed correlations arose from chance associations.

3 Results

3.1 Performance of CPMP for PAMPA and Caco-2 permeability prediction

The PAMPA and Caco-2 cell assays are widely used to measure cyclic peptide membrane permeability, providing sufficient data for model training and evaluation (Supplementary Figures S1A, B) (Li et al., 2023). Therefore, we first evaluated the performance of CPMP using PAMPA and Caco-2 data. We compared CPMP with two machine learning models: RFR and SVR (Pedregosa et al., 2011), as well as a deep learning model based on Molecular Graph Neural Networks (MGNN) (Tsubaki et al., 2019).

As shown in Table 1; Figures 1C, D, CPMP outperforms the baseline methods across all evaluation metrics. Specifically, CPMP achieves the lowest MSE of 0.169, significantly better than RFR (0.590), SVR (0.582), and MGNN (0.542). Similarly, the MAE of CPMP (0.308) is lower than those of RFR (0.485), SVR (0.436), and MGNN (0.466), demonstrating its higher accuracy in predicting membrane permeability. Furthermore, CPMP achieves the highest R² value of 0.671, indicating stronger explanatory power than RFR (0.388), SVR (0.396), and MGNN (0.546). For Caco-2 permeability prediction, CPMP also shows superior performance. It achieves the lowest MSE of 0.151, better than RFR (0.218), SVR (0.182), and MGNN (0.178). The MAE of CPMP (0.286) is also the lowest among the compared methods, with RFR at 0.349, SVR at 0.322, and MGNN at 0.305. Additionally, CPMP obtains the highest R² value of 0.746, indicating a stronger predictive capability compared to RFR (0.643), SVR (0.694), and MGNN (0.702).

Table 1

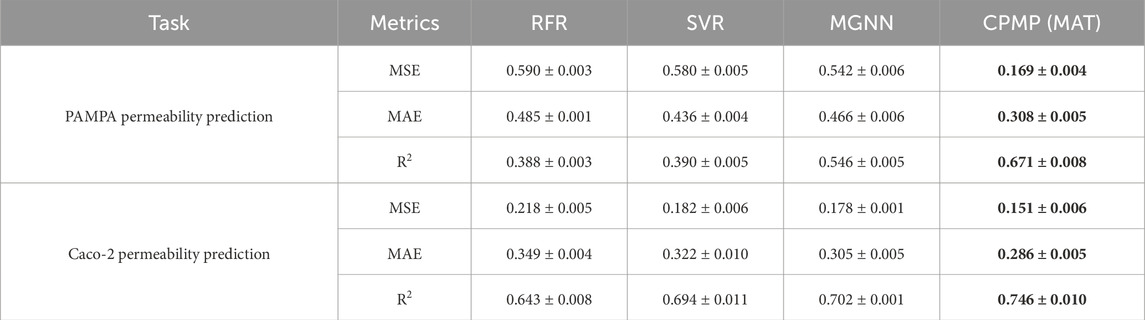
Table 1. Performance comparison between three baseline methods and CPMP for PAMPA and Caco-2 permeability prediction. The metrics are the average values of three repeated runs; the best result for each metric is indicated in bold.

To assess the model’s generalizability, we analyzed its performance across a diverse range of molecular properties, including molecular weight, TPSA, LogP, ratio of modified amino acids, monomer length in the main chain, and ring count. For the PAMPA model (Figure 2), CPMP exhibits robust performance for mid-range molecular weights (800–900 Da: MSE = 0.114, MAE = 0.258, R² = 0.71) and achieves the highest R² (0.76) for larger molecules (>1,100 Da). However, MSE increases slightly for very large (>1,100 Da: MSE = 0.22) or small (≤700 Da: MSE = 0.174) molecules, suggesting room for refinement in extreme size categories. Notably, the model excels for cyclic peptides with moderate TPSA (100–150 Ų: R² = 0.775) and high LogP (>4.0: R² = 0.798), while showing reduced accuracy for highly polar molecules (TPSA 350–400 Ų: R² = 0.148). For the Caco-2 model (Supplementary Figure S8), CPMP demonstrates strong predictive capability across broad molecular weight ranges (>1,400 Da: MSE = 0.0508, R² = 0.821) and maintains high R² values for peptides with low-to-moderate TPSA (≤300 Ų: R² ≥ 0.703). Performance improves significantly for modified amino acid ratios >0.6 (R² = 0.772–0.890), indicating particular strength in modeling heavily modified peptides. While monomer lengths ≥10 show excellent R² (0.784), shorter chains (7–9 units: R² = 0.602) exhibit slightly reduced performance, potentially reflecting imbalanced distribution of training data.

Figure 2

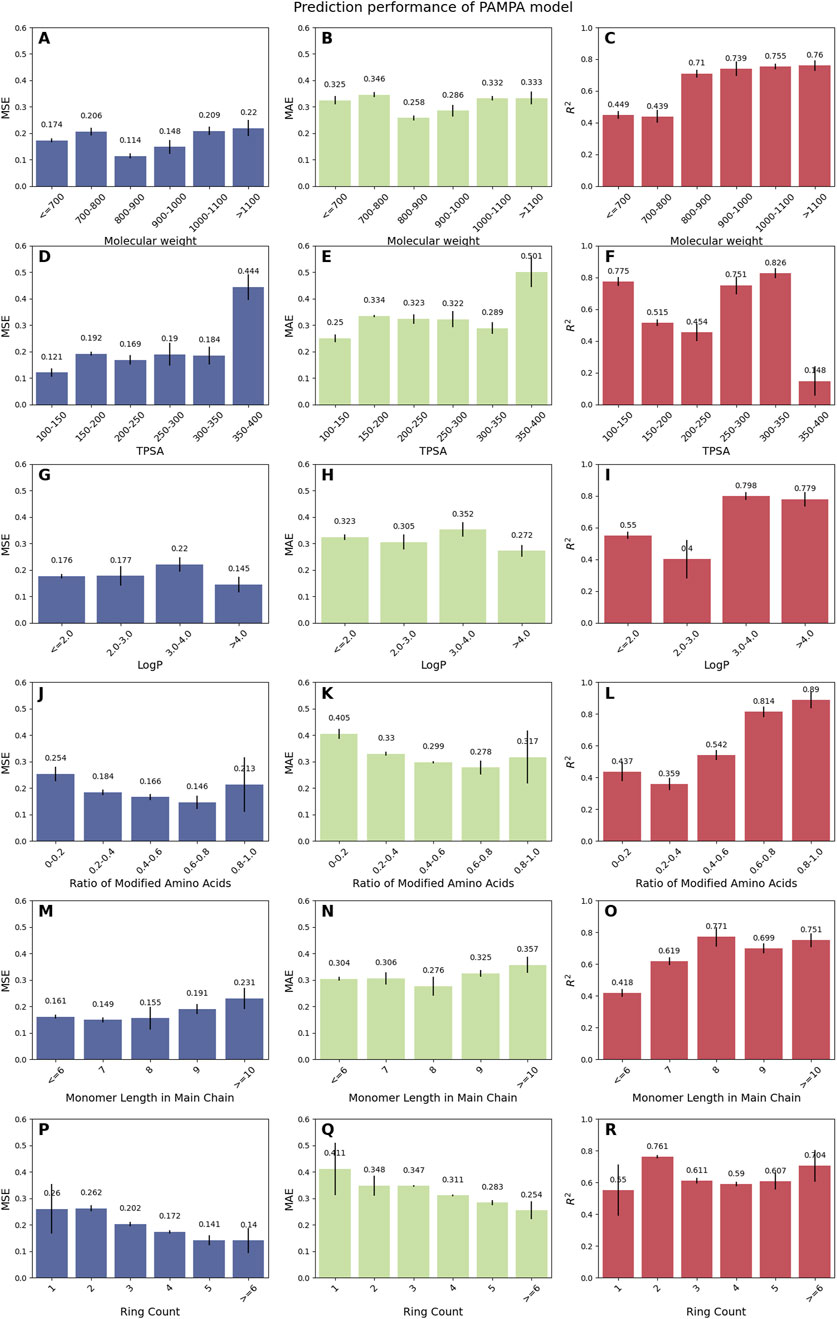
Figure 2. Prediction performance of the PAMPA model across diverse cyclic peptide properties. Peptides were categorized based on molecular weight (A–C), TPSA (D–F), LogP (G–I), the ratio of modified amino acids (J–L), monomer length in main chain (M–O), and ring count (P–R), with each category comprising over 20 samples to ensure robust statistical analysis.

These findings demonstrate that the CPMP model, based on the MAT neural network, performs exceptionally well in delivering accurate and reliable predictions for both PAMPA and Caco-2 permeability. However, there are areas where further improvement is needed, particularly for very large or very small molecules, as well as highly polar molecules. Despite these limitations, the overall performance of CPMP remains superior compared to existing models, highlighting its potential in advancing cyclic peptide drug discovery.

3.2 Pre-training enhances performance for RRCK and MDCK permeability prediction

The RRCK and MDCK cell assays are used to study cyclic peptide transmembrane transport in the kidneys. However, the data for RRCK and MDCK are relatively limited (Supplementary Figures S1C, D), which may lead to underfitting during model training. Considering that cyclic peptides from RRCK and MDCK show no significant differences in chemical space compared to those from the Caco-2 dataset (Supplementary Figure S9), we first pre-train the model using Caco-2 data and then fine-tune it with RRCK and MDCK data to enhance its predictive accuracy.

As shown in Table 2; Figures 1E, F, pre-training significantly enhances the predictive capabilities of the CPMP model for RRCK and MDCK permeability predictions. Specifically, for RRCK, the MSE decreases from 0.181 to 0.129, the MAE decreases from 0.328 to 0.288, and the R² value increases from 0.470 to 0.623. For MDCK, the MSE decreases from 0.354 to 0.165, the MAE decreases from 0.477 to 0.305, and the R² value increases from 0.412 to 0.727.

Table 2

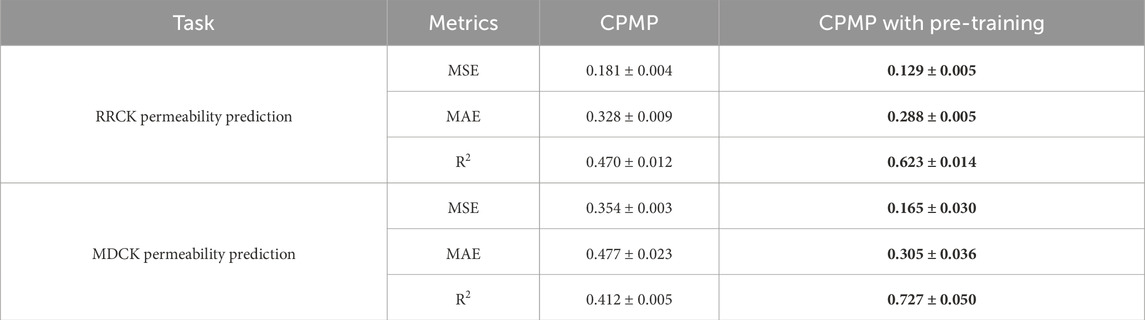
Table 2. Comparison of performance between the CPMP model without pre-training and with pre-training for RRCK and MDCK permeability prediction. The metrics are the average values of three repeated runs; the best result for each metric is indicated in bold.

3.3 Ablation study and Y-randomization test

In the CPMA model, three key components—the distance matrix, adjacency matrix, and dummy node—are used to characterize molecular features. To assess the impact of each component, we conducted a series of ablation experiments. As shown in Supplementary Table S1, all three components have a significant impact on the model’s performance. In the baseline model, the R² values for PAMPA and Caco-2 permeability predictions are 0.671 and 0.746, respectively. Removing the distance matrix results in the largest performance drop, with R² decreasing to 0.554 (PAMPA) and 0.556 (Caco-2). MSE and MAE also increase noticeably. Removing the adjacency matrix decreases R² to 0.642 (PAMPA) and 0.700 (Caco-2), while MSE and MAE increase slightly. Removing the dummy node decreases R² values to 0.628 (PAMPA) and 0.629 (Caco-2), with smaller increases in MSE and MAE. Overall, the distance matrix has the greatest impact, followed by the dummy node, with the adjacency matrix being the least influential but still important.

The Y-randomization test results show that both the PAMPA and Caco-2 models perform significantly better on real data than on scrambled data (Supplementary Figure S10), indicating that the models are reliable and effective. The PAMPA model has an average R² value of about 0.67 for real data and 0.10 for scrambled data, while the Caco-2 model has an average R² value of about 0.75 for real data and 0.09 for scrambled data.

3.4 Comparative analysis of force fields used for conformational optimization

During the passive membrane permeation process, the conformation of cyclic peptides changes from “open” to “close” and then back to “open” (Linker et al., 2023; Noonan et al., 2022). Molecular dynamics simulations indicate that the “close” conformation is the main permeable species (Dougherty et al., 2019). In MAT, distance matrices, which are important input features, are derived from molecular conformations that were optimized using force fields (Maziarka et al., 2020). Ideally, we should find an appropriate molecular force field to optimize and generate the “close” conformation of cyclic peptides. However, the force fields required for molecular dynamics simulations demand high computational resources, making it impractical to simulate nearly ten thousand cyclic peptide molecules. In order to quickly generate the conformation, we tested the two built-in force fields in RDKit (Landrum et al., 2024), the Universal Force Field (UFF) and the Merck Molecular Force Field (MMFF), both with options to consider or ignore non-bonded interactions within the molecule.

As shown in Supplementary Table S1, for PAMPA permeability prediction, UFF-NB achieves the best performance with the highest R² value of 0.673. The difference in MSE between the best and worst is approximately 0.006 (UFF-NB vs. UFF + NB), and the difference in MAE is approximately 0.009 (UFF-NB vs. UFF + NB). In contrast, for Caco-2 permeability prediction, MMFF-NB shows the best performance with the highest R² value of 0.751. The difference in MSE between the best and worst is approximately 0.004 (MMFF-NB vs. UFF + NB), and the difference in MAE is approximately 0.007 (MMFF-NB vs. UFF-NB). These differences are small relative to the inherent variability in the model’s repeated runs, indicating that the choice of force field parameters has a relatively minor impact on model performance.

4 Conclusion

The CPMP model, based on the MAT, shows strong performance in predicting the membrane permeability of cyclic peptides. It achieves high R² values of 0.67 for PAMPA, 0.75 for Caco-2, 0.62 for RRCK, and 0.73 for MDCK, outperforming traditional machine learning and other deep learning models. The pre-training on the Caco-2 dataset and fine-tuning on RRCK and MDCK datasets partially alleviates the issue of limited data, improving performance across these datasets and demonstrating the model’s adaptability to different cell lines. Overall, the CPMP model is a promising tool for membrane permeability prediction, aiding in cyclic peptide drug development.

However, the model also has some limitations. Firstly, the PAMPA and Caco-2 models show reduced prediction accuracy for certain molecular properties (Figure 2; Supplementary Figure S9). Both models struggle with larger molecules, as evidenced by higher MSE and MAE values for molecular weights >1,100 in PAMPA and >1,400 in Caco-2. Additionally, the models perform poorly for molecules with high TPSA (>350 for PAMPA and >320 for Caco-2) and extreme LogP values (≤2.0 or >4.0). The PAMPA model also exhibits decreased accuracy for molecules with a high ratio of modified amino acids (>0.8) and longer monomer chains in the main chain (≥10). Secondly, the limited size and imbalance of the RRCK and MDCK datasets may lead to model underfitting, which could undermine its generalizability. Future efforts should focus on data augmentation to enhance model’s generalizability (Chandrasekar et al., 2022; Mone et al., 2023; Dhage et al., 2021). In addition to the challenges mentioned above, the computational resources required for training and predicting with Transformer models also pose a problem. How to utilize parallel computation to address this issue in the future may be an important research direction. Given the increasing demand for efficient and scalable models in various applications, exploring the potential of parallel computation to optimize the training and prediction processes of Transformers could significantly enhance their practicality and broaden their applicability (Zhai et al., 2020; Esfahani et al., 2020; Zhai et al., 2019).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DJ: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. ZC: Conceptualization, Visualization, Writing–review and editing. HD: Conceptualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Program of China (2024YFF1206603, 2018YFC0910201), and the Key R&D Program of Guangdong Province (2019B020226001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbinf.2025.1566174/full#supplementary-material

References

Bhardwaj, G., O’Connor, J., Rettie, S., Huang, Y., Ramelot, T. A., Mulligan, V. K., et al. (2022). Accurate de novo design of membrane-traversing macrocycles. Cell 185, 3520–3532.e26. doi:10.1016/j.cell.2022.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Bockus, A. T., Lexa, K. W., Pye, C. R., Kalgutkar, A. S., Gardner, J. W., Hund, K. C. R., et al. (2015). Probing the physicochemical boundaries of cell permeability and oral bioavailability in lipophilic macrocycles inspired by natural products. J. Med. Chem. 58, 4581–4589. doi:10.1021/acs.jmedchem.5b00128

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, L., Xu, Z., Shang, T., Zhang, C., Wu, X., Wu, Y., et al. (2024). Multi_CycGT: a deep learning-based multimodal model for predicting the membrane permeability of cyclic peptides. J. Med. Chem. 67, 1888–1899. doi:10.1021/acs.jmedchem.3c01611

PubMed Abstract | CrossRef Full Text | Google Scholar

Chandrasekar, V., Singh, A. V., Maharjan, R. S., Dakua, S. P., Balakrishnan, S., Dash, S., et al. (2022). Perspectives on the technological aspects and biomedical applications of virus-like particles/nanoparticles in reproductive biology: insights on the medicinal and toxicological outlook. Adv. Nanobiomed Res. 2, 2200010. doi:10.1002/anbr.202200010

CrossRef Full Text | Google Scholar

Dhage, P. A., Sharbidre, A. A., Dakua, S. P., and Balakrishnan, S. (2021). Leveraging hallmark Alzheimer's molecular targets using phytoconstituents: current perspective and emerging trends. Biomed. Pharmacother. 139, 111634. doi:10.1016/j.biopha.2021.111634

PubMed Abstract | CrossRef Full Text | Google Scholar

Di, L., Whitney-Pickett, C., Umland, J. P., Zhang, H., Zhang, X., Gebhard, D. F., et al. (2011). Development of a new permeability assay using low-efflux MDCKII cells. J. Pharm. Sci. 100, 4974–4985. doi:10.1002/jps.22674

PubMed Abstract | CrossRef Full Text | Google Scholar

Dougherty, P. G., Sahni, A., and Pei, D. (2019). Understanding cell penetration of cyclic peptides. Chem. Rev. 119, 10241–10287. doi:10.1021/acs.chemrev.9b00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Esfahani, S. S., Zhai, X., Chen, M., Amira, A., Bensaali, F., AbiNahed, J., et al. (2020). Lattice-Boltzmann interactive blood flow simulation pipeline. Int. J. Comput. Assist. Radiol. Surg. 15, 629–639. doi:10.1007/s11548-020-02120-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hewitt, W. M., Leung, S. S. F., Pye, C. R., Ponkey, A. R., Bednarek, M., Jacobson, M. P., et al. (2015). Cell-permeable cyclic peptides from synthetic libraries inspired by natural products. J. Am. Chem. Soc. 137, 715–721. doi:10.1021/ja508766b

PubMed Abstract | CrossRef Full Text | Google Scholar

Irvine, J. D., Takahashi, L., Lockhart, K., Cheong, J., Tolan, J. W., Selick, H. E., et al. (1999). MDCK (Madin-Darby canine kidney) cells: a tool for membrane permeability screening. J. Pharm. Sci. 88, 28–33. doi:10.1021/js9803205

PubMed Abstract | CrossRef Full Text | Google Scholar

Kosugi, T., and Ohue, M. (2023). Design of cyclic peptides targeting protein-protein interactions using alphaFold. Int. J. Mol. Sci. 24, 13257. doi:10.3390/ijms241713257

PubMed Abstract | CrossRef Full Text | Google Scholar

Landrum, G., Tosco, P., Kelley, B., and Cosgrove, D. (2024). RDKit: open-source cheminformatics. Available online at: https://www.rdkit.org.

Google Scholar

Li, J., Yanagisawa, K., and Akiyama, Y. (2024). CycPeptMP: enhancing membrane permeability prediction of cyclic peptides with multi-level molecular features and data augmentation. Brief. Bioinform 25, bbae417. doi:10.1093/bib/bbae417

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Yanagisawa, K., Sugita, M., Fujie, T., Ohue, M., and Akiyama, Y. (2023). CycPeptMPDB: a comprehensive database of membrane permeability of cyclic peptides. J. Chem. Inf. Model 63, 2240–2250. doi:10.1021/acs.jcim.2c01573

PubMed Abstract | CrossRef Full Text | Google Scholar

Linker, S. M., Schellhaas, C., Kamenik, A. S., Veldhuizen, M. M., Waibl, F., Roth, H., et al. (2023). Lessons for oral bioavailability: how conformationally flexible cyclic peptides enter and cross lipid membranes. J. Med. Chem. 66, 2773–2788. doi:10.1021/acs.jmedchem.2c01837

PubMed Abstract | CrossRef Full Text | Google Scholar

Maziarka, A., Danel, T., Mucha, S., Rataj, K., Tabor, J., and Jastrzębski, S. (2020). Molecule attention transformer. Graph Represent. Learn. Workshop Mach. Learn. Phys. Sci. Workshop A. T. NeurIPS. doi:10.48550/arXiv.2002.08264

CrossRef Full Text | Google Scholar

Mone, N. S., Syed, S., Ravichandiran, P., Kamble, E. E., Pardesi, K. R., Salunke-Gawali, S., et al. (2023). Synergistic and additive effects of menadione in combination with antibiotics on multidrug-resistant Staphylococcus aureus: insights from structure-function analysis of naphthoquinones. ChemMedChem 18, e202300328. doi:10.1002/cmdc.202300328

PubMed Abstract | CrossRef Full Text | Google Scholar

Muttenthaler, M., King, G. F., Adams, D. J., and Alewood, P. F. (2021). Trends in peptide drug discovery. Nat. Rev. Drug Discov. 20, 309–325. doi:10.1038/s41573-020-00135-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Noonan, B. J. W., Speer, M. N., Le, T. C., Sadek, M. M., Thompson, P. E., Norton, R. S., et al. (2022). Membrane permeating macrocycles: design guidelines from machine learning. J. Chem. Inf. Model 62, 4605–4619. doi:10.1021/acs.jcim.2c00809

CrossRef Full Text | Google Scholar

Ottaviani, G., Martel, S., and Carrupt, P. (2006). Parallel artificial membrane permeability assay: a new membrane for the fast prediction of passive human skin permeability. J. Med. Chem. 49, 3948–3954. doi:10.1021/jm060230+

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in python. J. Mach. Learn Res. 12, 2825–2830. doi:10.5555/1953048.2078195

CrossRef Full Text | Google Scholar

Rettie, S. A., Campbell, K. V., Bera, A. K., Kang, A., Kozlov, S., De La Cruz, J., et al. (2023). Cyclic peptide structure prediction and design using AlphaFold. bioRxiv. doi:10.1101/2023.02.25.529956

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, X., Liu, Q., Fang, Y., Zhu, Y., Chen, F., Zeng, W., et al. (2024). Predicting peptide permeability across diverse barriers: a systematic investigation. Mol. Pharm. 21, 4116–4127. doi:10.1021/acs.molpharmaceut.4c00478

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsubaki, M., Tomii, K., and Sese, J. (2019). Compound-protein interaction prediction with end-to-end learning of neural networks for graphs and sequences. Bioinformatics 35, 309–318. doi:10.1093/bioinformatics/bty535

PubMed Abstract | CrossRef Full Text | Google Scholar

van Breemen, R. B., and Li, Y. (2005). Caco-2 cell permeability assays to measure drug absorption. Expert Opin. Drug Metab. Toxicol. 1, 175–185. doi:10.1517/17425255.1.2.175

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. NIPS'17 Proc. 31st Int. Conf. Neural Inf. Process. Syst., 6000–6010. doi:10.5555/3295222.3295349

CrossRef Full Text | Google Scholar

Zhai, X., Amira, A., Bensaali, F., Al-Shibani, A., Al-Nassr, A., El-Sayed, A., et al. (2019). Zynq SoC based acceleration of the lattice Boltzmann method. Concurrency Comput. Pract. Exp. 31, 10. doi:10.1002/cpe.5184

CrossRef Full Text | Google Scholar

Zhai, X., Chen, M., Fsfahani, S. S., Amira, A., Bensaali, F., Abinahed, J., et al. (2020). Heterogeneous system-on-chip-based Lattice-Boltzmann visual simulation system. IEEE Syst. J. 14, 1592–1601. doi:10.1109/JSYST.2019.2952459

CrossRef Full Text | Google Scholar

Zhang, H., and Chen, S. (2022). Cyclic peptide drugs approved in the last two decades (2001-2021). RSC Chem. Biol. 3, 18–31. doi:10.1039/d1cb00154j

CrossRef Full Text | Google Scholar