- Doctorado en Technologías de Información, Universidad de Guadalajara, Centro Universitario de Ciencias Económicas Administrativas, Zapopan, Jalisco, Mexico
The application of quantum principles in computing has garnered interest since the 1980s. Today, this concept is not only theoretical, but we have the means to design and execute techniques that leverage the quantum principles to perform calculations. The emergence of the quantum walk search technique exemplifies the practical application of quantum concepts and their potential to revolutionize information technologies. It promises to be versatile and may be applied to various problems. For example, the coined quantum walk search allows for identifying a marked item in a combinatorial search space, such as the quantum hypercube. The quantum hypercube organizes the qubits such that the qubit states represent the vertices and the edges represent the transitions to the states differing by one qubit state. It offers a novel framework to represent k-mer graphs in the quantum realm. Thus, the quantum hypercube facilitates the exploitation of parallelism, which is made possible through superposition and entanglement to search for a marked k-mer. However, as found in the analysis of the results, the search is only sometimes successful in hitting the target. Thus, through a meticulous examination of the quantum walk search circuit outcomes, evaluating what input-target combinations are useful, and a visionary exploration of DNA k-mer search, this paper opens the door to innovative possibilities, laying down the groundwork for further research to bridge the gap between theoretical conjecture in quantum computing and a tangible impact in bioinformatics.
1 Introduction
This paper embarks on a journey through quantum computing basics, providing readers with a foundational understanding of quantum mechanics, qubits, and quantum algorithms. It then delves into quantum software stacks, elucidating the essential tools, programming languages, and development environments that drive quantum computing’s practical applications. Moving forward, it explores the coined quantum walk search, unraveling the intricate algorithm’s potential applications in fields such as combinatorial problems. Shifting gears, the paper investigates DNA 2-bit Encoding, a cutting-edge approach to data storage, and discusses the practical implications and prospects of this novel technology. Lastly, it presents a technique to input DNA patterns into a quantum register to execute a coined quantum walk search for DNA pattern matching. It highlights the unique research objectives, methodologies, and results at this paper’s heart, promising to contribute to the ongoing dialogue in these exciting fields.
1.1 DNA 2bit encoding
The DNA genetic code is based on the monomer nucleotides
1.2 K-mer sequencing
In dealing with comparisons and searching, a technique used in genomics to analyze DNA data breaks down DNA sequences in fragments of k-lenght of monomers (Langmead, 2016). These fragments are named according to the number of monomers in the fragment. If the number of monomers k is 1, the k-mer is called a 1-mer. If the number of monomers k is 2, the k-mer is called a 2-mer, and so forth. Examples of 2-mer DNA fragments are CA and GC.
1.3 Quantum computing basics
While the concepts in quantum mechanics have been around for about a century (Born, 1926), it was in the 1980s that those concepts were theorized as options in the computer science disciplines (Benioff, 1982). Applying these quantum mechanics principles to computing is now known as quantum computing (Steane, 1998). Over the years, quantum computing has evolved from a theoretical hypothesis into a tangible reality. In the contemporary landscape of technological advancement, the theoretical underpinnings of quantum computing have transformed into practical methodologies that allow us to execute techniques reliant on quantum principles for complex computations.
The basic unit of information in quantum computing is the qubit (Schumacher, 1995). While a binary bit can only be in a state of 0 or 1, the qubit has the property that it can be in a combined state of
One fundamental difference between a binary computer and a quantum computer is that measuring the binary bit state does not alter its state, whereas in quantum computing, measuring a qubit collapses it into a pure state
Qubits perform calculations using quantum gates or operators to manipulate the qubit states. One such gate is the Pauli-X gate, represented by the
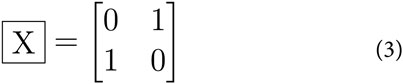
The
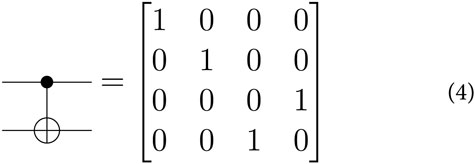
With both superposition and entanglement, qubit interference may be leveraged to perform computation. Since the qubit status is based on the quantum wave function, when two different qubits are entangled and subject to operators, their amplitudes will interact constructively or destructively. This phenomenon allows for computations beyond the capability of binary computing.
1.4 Quantum software stacks
Since the conception of the quantum computing concept, human ingenuity has been at work to explore the potential of this new computing paradigm. Quantum computing may increase cybersecurity (Bova et al., 2021), or break widely used cybersecurity technologies such as public key cryptography (Mavroeidis et al., 2018). It also may be used to speed up searching for a marked item in unstructured data through a quantum search. Since quantum computing has a promising outlook, companies worldwide are interested in facilitating quantum computing for research and commercial use through Quantum Software Stacks (QSS) (Wang et al., 2021). Google provides Cirq, Rigetti PyQuil, and IBM provides the Qiskit. The current work was researched, developed, and executed using IBM’s Qiskit QSS.
1.5 IBM quantum platform
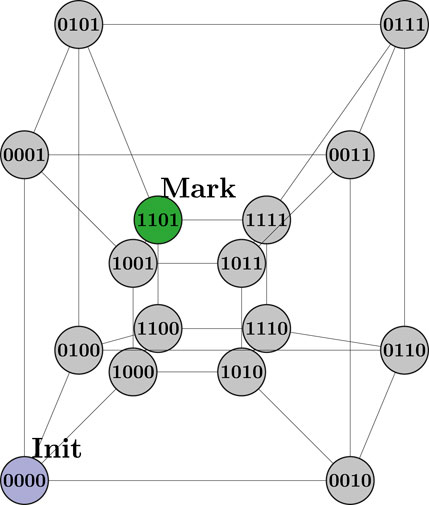
The IBM Quantum Platform, formerly known as the IBM Quantum Experience (Cross, 2018), is an open platform intended to ease the work of designing, developing, and running quantum circuits. Anyone interested may create these circuits through the Quantum Composer (Lehka et al., 2022), a cloud-based visual development environment. They also may be written in OpenQASM (Cross et al., 2017), an assembly-like computer language. Another familiar option is to write the quantum circuits using Python programming with the Qiskit (Qiskit contributors, 2023), modules installed. Qiskit allows for different quantum system backends to be used, both simulators and actual quantum processors with limited access. In addition, educational materials, such as the Qiskit Textbook (various authors, 2023), demonstrate tools available to create quantum algorithms. In this book, the coined quantum walk search algorithm (Wanzambi and Andersson, 2021), is implemented to search for a marked node in a tesseract, a hypercube with four dimensions as shown in Figure 1. This tesseract is built within the QuantumCircuit instance pointed by the circuit variable with the following Python code:
circuit.x(4)
circuit.x(5)
circuit.ccx(4,5,i)
This qubit arrangement allows us to represent the
1.6 The coined quantum walk search
The coined quantum walk search is a search algorithm targeted at unstructured databases. This search algorithm employs a quantum version of classical random walks executed on Markov chains (Shenvi et al., 2003; Boettcher et al., 2015). In the quantum version of the random walk, the walker evaluates several paths on the graph simultaneously through the superposition of states of the coin operator. The shift operator then takes the step influenced by the coin state. The phase estimation serves as the state evaluation tool to determine if a state is the search target. The coin is a set of qubits used to evaluate the walker’s next step. The coined quantum walk search demonstrated in the Qiskit textbook in chapter 3.10 uses 11 qubits. Four are used as the theta qubits for phase estimation, four for the tesseract nodes, two for the Grover’s coin, and one as an auxiliary (ancilla) qubit.
The coined quantum walk search stands out as a particularly promising paradigm. It holds the potential to transcend its theoretical origins and address an extensive array of problems, spanning an impressive spectrum of applications. Among these applications are solutions to combinatorial (Bova et al., 2021), problems where the search space is all the combinations of a finite set of symbols. DNA pattern matching belongs to this type of problem. In bioinformatics, DNA pattern matching and prediction plays such an important role that brilliant minds have designed practical algorithms to leverage traditional computing (Rahate and Chandak, 2018; Neamatollahi et al., 2020); and even advanced deep learning model techniques such as the Convolution Autoencoder (Guo et al., 2024). Poising our attention towards quantum computing, the quantum hypercube, with its exponential information density, also enables the prospect to execute the coined quantum walk search for a marked state.
1.7 The quantum hypercube as a K-mer graph
The current work researches a technique to encode DNA information to input it to a quantum computer and provide a target k-mer in the quantum hypercube search space for a coined quantum walk search algorithm to find. The coined quantum walk search is executed with each of the 16 possible combinations as a starting node. In addition, the 11-qubit quantum register is tested with all the possible initialization states. Each initialization state is executed with each of the 16 possible target nodes. The results generated are analyzed to provide insights into the effects of initializing the 11-qubit quantum register on the execution of the coined quantum walk search. The information is useful for peeking into the possibilities of leveraging the quantum hypercube as a k-mer graph to perform DNA pattern matching.
2 Materials and methods
2.1 Development platform
The IBM Quantum Software Platform facilitates the use of a quantum computer through the use of Python modules. These modules implement potent methods to build up and execute quantum circuits. The two packages used for the experiments in this research are the
2.2 Loading DNA binary data into a quantum circuit
When using the Qiskit QSS, a QuantumCircuit instance is initialized to a
The corresponding Python code with the modules installed and imported into the program is:
...
...
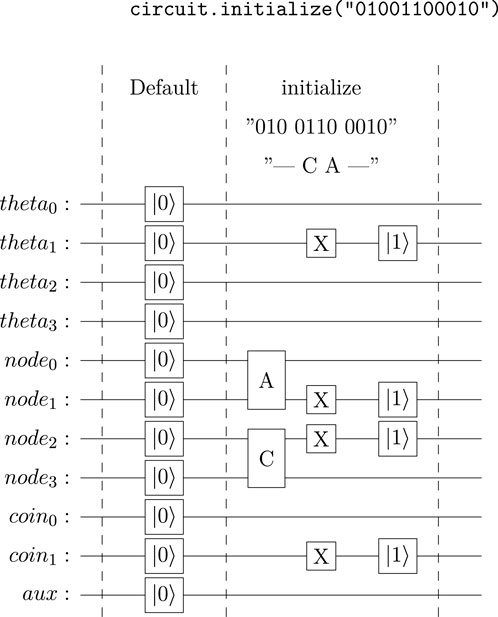
circuit.initialize(
...
After calling the circuit. initialize method, the circuit is modified to set the quantum register into the specified state before executing the circuit. Thus, applying “01001100010” as the circuit initialization string to the coined quantum walk modifies the beginning of the circuit as illustrated in Figure 2.
The
2.3 The DNA hypercube space
After the initialization method is called, the coined quantum walk implementation presented in the Qiskit Textbook is used to find the marked node in a hypercube with 4-bit vertices. These 4 bits represent two-letter DNA patterns, also called 2-mer substrings. This way, the hypercube in Figure 1 becomes the hypercube in Figure 3.
2.4 The coined quantum walk search circuit
The coined quantum walk implementation has three parts: A set of Hadamard gates applied to the node and coin qubits to set them into a superposition state; the phase oracle, where the target state is marked; and the phase estimation. The phase oracle and the phase estimation sections may be repeated as many times as desired. The last step is measuring the states of the tesseract nodes, which collapses the quantum circuit into a binary state. Figure 4 illustrates the complete quantum walk search algorithm. The entire circuit was implemented and executed using the Python programming language.
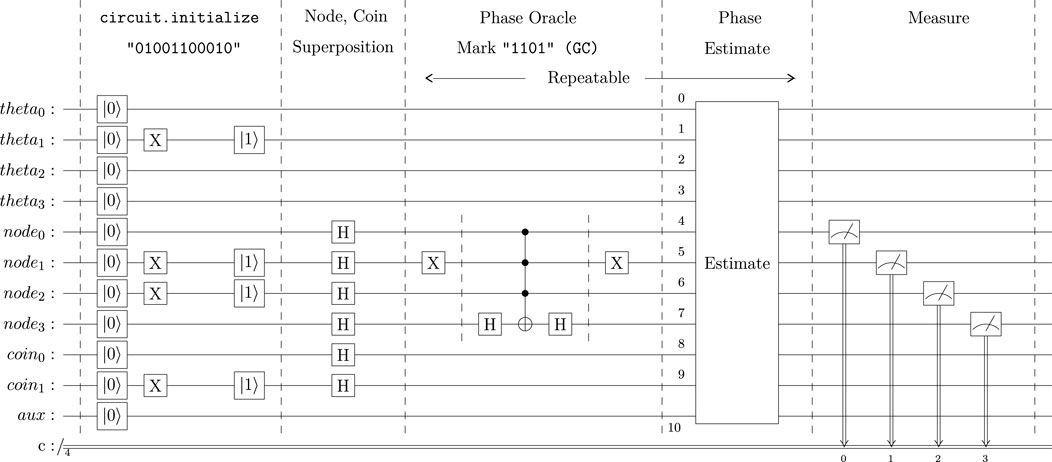
Figure 4. Complete Coined Quantum Walk Circuit with the CA DNA pattern provided as the initialization node and the node GC as a marked pattern.
The mark section in the QuantumCircuit object, circuit, is implemented with the Python snippet:
circuit.x(
circuit.h(3)
circuit.mct(
circuit.h(3)
circuit.x (
To cover all the 32768 possible input-mark, the circuit illustrated in Figure 4 was executed through a Python program. This Python program ran each execution with 1024 shots. The reader can find this Python program in the Supplementary Materials section.
2.5 Supplementary Materials
The data used in this study and its original program are available in GitHub at: https://github.com/dti-data/quantum-k-mer-graph.
3 Experiments and results
Each combination of input-mark outputs a line of data. Since the 15 bits (11 for the quantum hypercube, four for the mark) have

Table 1. Sample output data line with the initialization string set to “00000000000” and the mark set to “0000”.
For ease of reading, this initialization string is separated into the values used for the different quantum registers: Auxiliary (1), Coin (2), Node (4), and Theta (4). The “mark” column contains the binary values provided to the oracle as marks. The remaining 16 columns contain the frequency for each state measured at the Node register when the quantum circuit collapses.
The expected result is for the quantum walk search to hit the marked state regardless of the initialization state. Table 2 presents the number of hits for each node state when the QauntumCircuit four is initialized to the string “00000000000” and executed with 1024 shots.
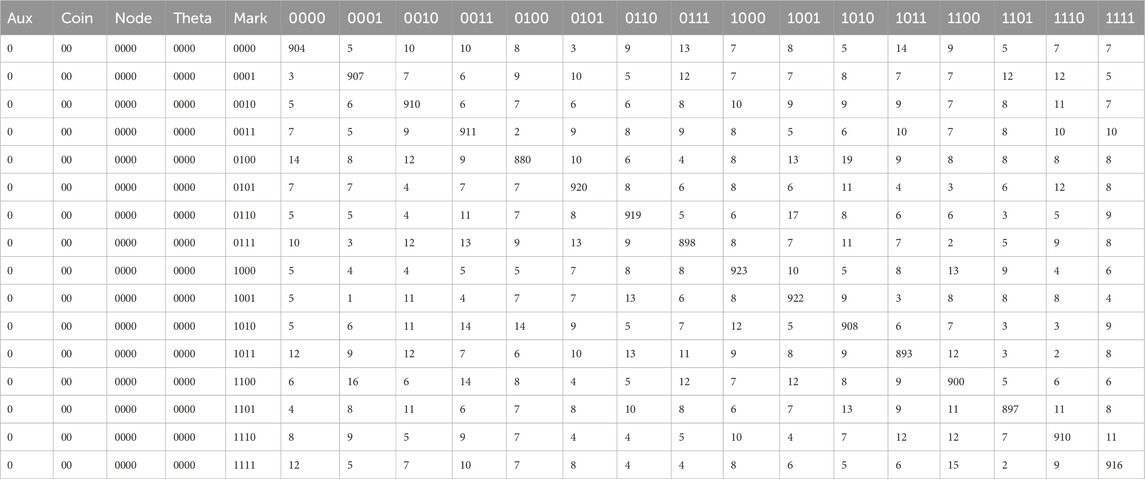
Table 2. Number of hits for each vertex out of 1024 shots taken for the initialization string “00000000000”.
Notably, the number of hits for each marked state is not 1024. Indeed, the quantum walk search circuit sometimes collapses to a state other than the marked state. This effect is intrinsic to quantum computing (Brassard et al., 1998). The gates applied to the qubits introduce the probability that the system will collapse into the wrong answer. Although theoretically possible, as the quantum circuits grow larger and involve more qubits, calculating the probability that a quantum circuit will collapse to a particular state becomes prohibitively complex. However, we can still shed light on the effects of an initialization state on a quantum circuit. Since the number of shots is known, Shots = 1024, and the Accuracy is directly proportional to the number of Hits for the mark when the quantum circuit is executed, the Accuracy comes to be
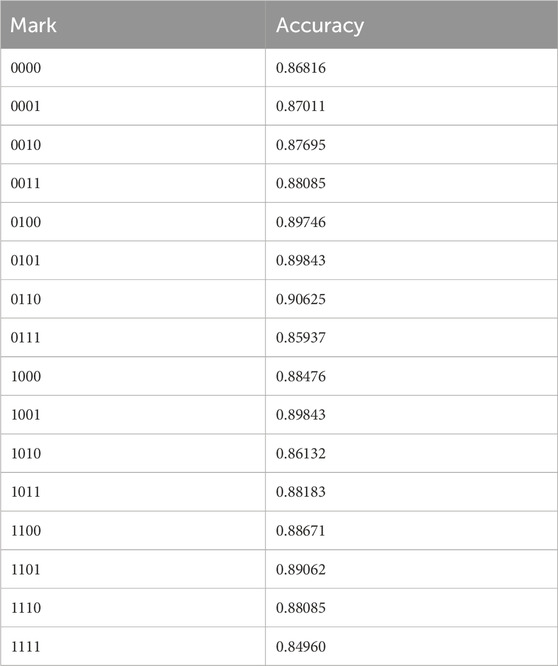
Table 3. Accuracy when executing the coined quantum walk wearch circuit with initialization string “00000000000” applied.
In addition, since in quantum computing, the results are based on the probability that a circuit will collapse into a binary state for the measured qubits, the result may vary between circuit executions. One way to measure the expected variation for executions of the same circuit using a particular backend platform is to calculate the difference in hits for each state from different executions for the exact initialization string. This is the technique used in this research to determine if setting the auxiliary qubit to a
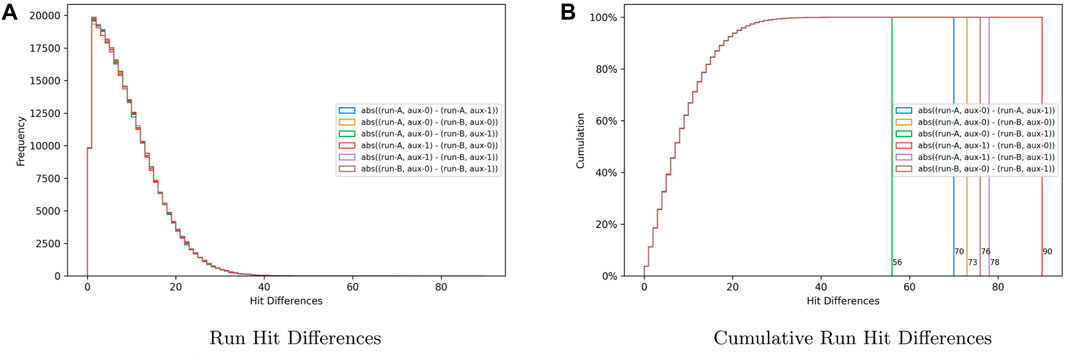
Figure 5. Hit differences used to determine the effect of setting the auxiliary bit to
The differences and similarities in the hit difference distribution are readily apparent. The six distributions follow a similar skewed right distribution with slight variations, which are accounted for by the random nature of quantum computing. Figure 5B shows the cumulative distributions. This set of graphs presents the maximum difference for each distribution. Given that all the graphs display similar skewed right distributions and the mode is calculated to be 1.5 for every one of them, the conclusion is that the samples are equivalent, and, therefore, initializing the auxiliary qubit to 0 or one does not have an effect on the results when executing the quantum coined search circuit.
Since the tesseract used for the coined quantum walk contains 16 nodes, each of which may be used as a target, each unique initialization string is used 16 times in this experiment. In addition, each execution of the quantum circuit using a particular initialization string is a 1024-size sample since the circuit execution is set to attempt 1024 shots. Also, each shot is an independent event. Therefore, calculating the standard deviation, denoted as
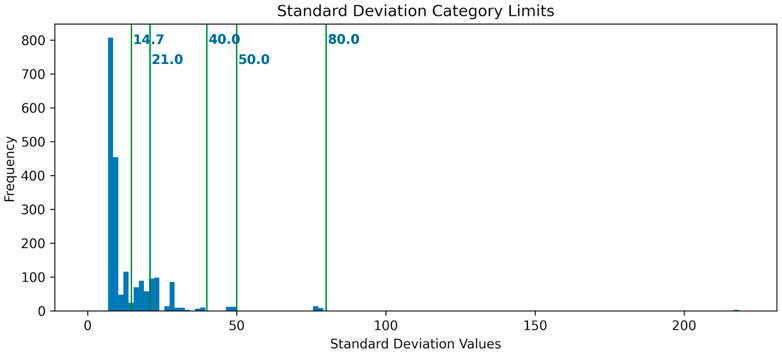
Figure 6. Standard deviation distributions plotted as a histogram along with arbitrary limits to organize the results for initialization string according to how randomized the results are.
The standard deviation measures how close the number of hits for a state is to the expected value of 64 hits (1024 shots/16 possible states). The smaller the value of
Classifying the initialization strings based on the standard deviation values aids in visualizing the patterns for the hit distributions. To leverage this analysis technique, let us define six arbitrary categories such that
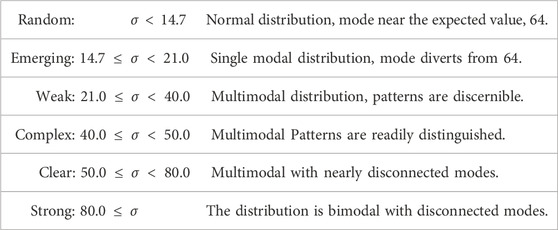
Table 4. Hit distribution categories based on the standard deviation calculated for the hit distribution for each initialization string.
The set of Figure 7 displays the six resulting hit distributions with the limits for
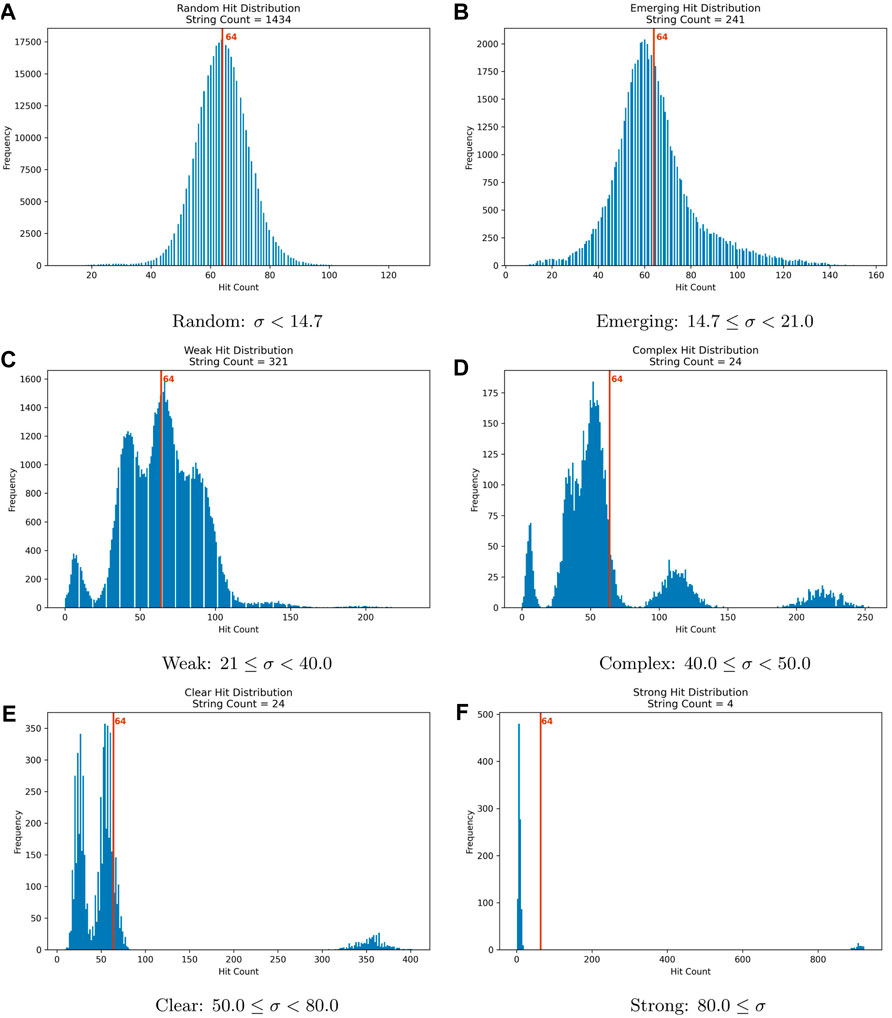
Figure 7. Hit distributions for the categories in Table 4 based on the standard deviation of each execution with 1024 shots. (A) Random: σ < 14.7; (B) Emerging 14.7 ≤ σ < 21.0; (C) Weak: 21 ≤ σ < 40.0; (D) Complex: 40.0 ≤ σ < 50.0; (E) Clear: 50.0 ≤ σ < 80.0; (F) Strong: 80.0 ≤ σ.
The standard deviation,
The results for “00000110010” have a standard deviation of 49.26 which belongs to the Complex category.
4 Discussion
Quantum computing is a relatively new but rapidly evolving field. Currently, the manipulation of quantum circuits is done at the gate level. This activity requires detailed knowledge of quantum computing. While efforts are underway to ease the expertise requirements through software stacks, executing quantum circuits may not produce the expected results. Take, for instance, the experiments performed in this research. Although the inputs and marks were applied to the circuit using the same techniques, the results are inconsistent. This finding prompts us to dissect the quantum circuit and analyze what happens deeper into the different execution levels to leverage those phenomena and the information density from the quantum hypercube to implement faster k-mer searching techniques. The effort to organize and summarize the data in the categories presented in Table 4, is to reference the outcomes and focus further research, beyond the scope of the current work, on the different behaviors prompted by the inputs.
One of the surprising outcomes of the experiments was that only four initialization strings produced a “Strong” output pattern using the coined quantum walk as is. This outcome is the expected behavior. The marked k-mer in the hypercube is hit the most times. Those four initialization strings are: “00000000000”, “00011110001”, “10000000000”, “10011110001”. The bit in position 10 is loaded into the auxiliary qubit which has no effect. Therefore, the set is reduced to “0000000000”, and “0011110001”.
Another finding is that While the quantum circuits, when implemented with superposition, may leverage the parallel processing of a quantum device, changing even the initial state of a qubit may change the quantum circuit behavior so dramatically that when measured, it collapses to a random state. This is the output of 1434 initialization strings with a hit distribution with a standard deviation less than 14.2; therefore, the results are “Random”, Figure 7A. This count is already more than half of the possible initialization strings.
The “Emerging” category is close to having a normal distribution but with some distortions. Some states get hits that diverge significantly from the expected value but more is needed to establish a pattern.
The “Weak” patterns already show an accumulation of hits around values other than 64. One feature in this category is that the quantum search establishes a pattern on the marked state by hitting it with the least frequency, as is the case with the initialization string “00000000001” as shown in Table 5. This effect may be useful in finding the marked state through avoidance since “finding” is an interpretation exercise.
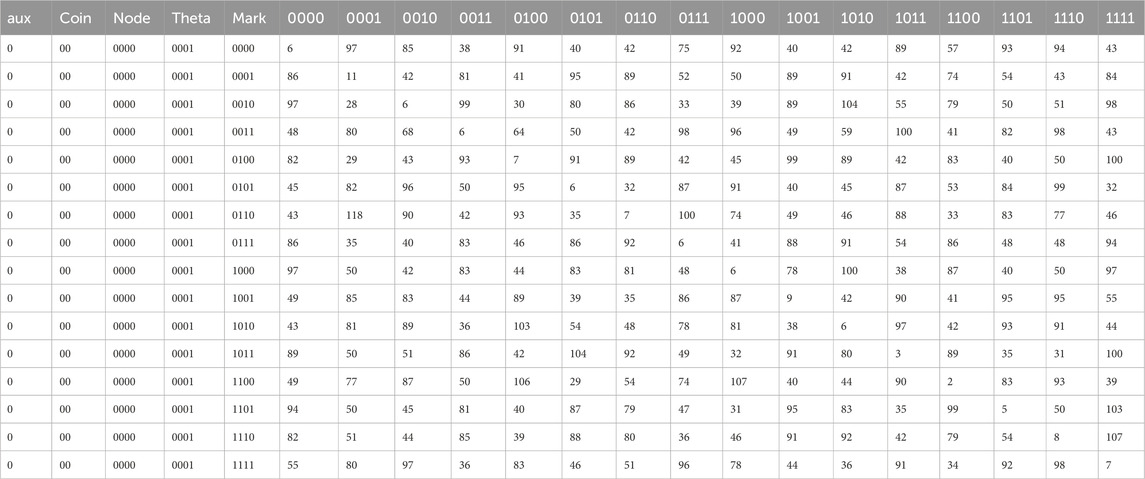
Table 5. Results for executing the coined quantum walk search on a 2-mer hypercube with initialization string “00000000001”.
The “Clear” category displays hits consolidating on the marked state, just as in the Strong category, but the hit count is far from being 100%.
The category “Complex” is named as such based on the patterns displayed on the hit distribution. The hits are accumulated around the marked state, but the node with the binary inverse of the marked state is also avoided. Even more, the circuit hits other states, forming a complex pattern. As shown in Table 6.‘’ The input-mark combinations in this category output are intriguing and may be the subject of deeper studies.
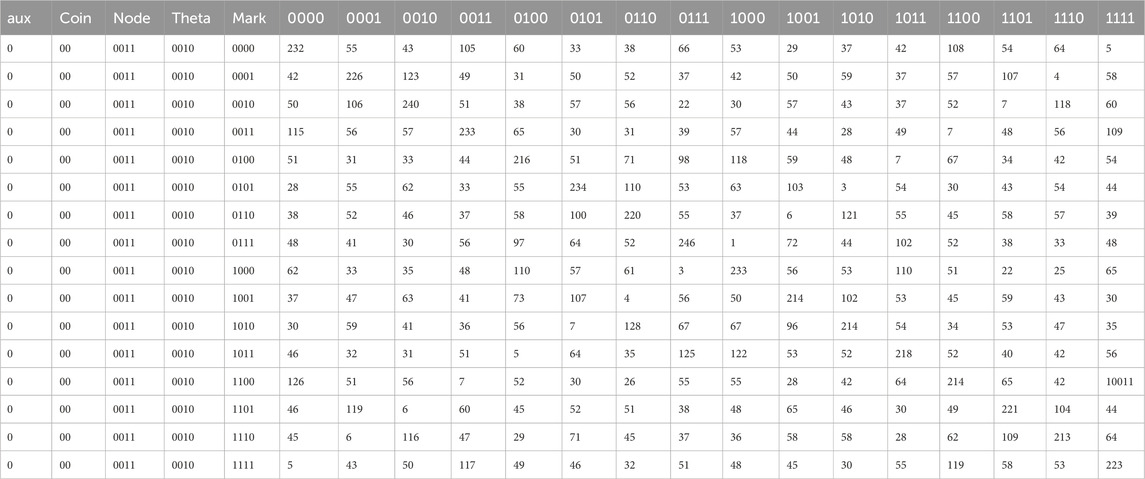
Table 6. Results for executing the coined quantum walk search on a 2-mer hypercube with initialization string “00000110010”.
The presented categories show that there is much to be researched and developed for the coined quantum walk search on a 2-mer quantum hypercube to be practical. In theory, the quantum hypercube has an exponential information density. The fact that a quantum N-dimensional hypercube can represent
5 Conclusion
Encoding binary data into a quantum computer is possible through the initialization string and marking the desired quantum states. Thus, it is possible to encode DNA sequences into such a device. Once the hypercube is built with marked DNA k-mer fragments, the coined quantum walk search is able to return useful results on some instances. However, only some initialization strings output useful repeatable patterns from which information may be extracted.
One limitation of the coined quantum walk search on a 2-mer hypercube is that it is not a universal search technique. The search design has to be adapted to the specific input string. The wide difference in results supports this assertion. Therefore, while a quantum computer can represent an N-dimensional hypercube with N qubits and exploit parallelism in searching, a substantial limitation is that the circuit does not behave consistently for all input-mark combinations.
Another limitation is that the k-mers in the hypercube are of fixed length, in this research, 2-mer, as the hypercube was created. If a different size of k-mer is required, a new hypercube needs to be constructed.
Since quantum computing is still a young field, much research is being done to explore and demonstrate its usefulness. One possible improvement beneficial for adopting this powerful paradigm is developing high-level methods or functions that behave consistently in the face of different inputs.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
GB-G: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. LB-S: Methodology, Supervision, Writing–review and editing, Conceptualization.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Benioff, P. (1982). Quantum mechanical Hamiltonian models of turing machines. J. Stat. Phys. 29, 515–546. doi:10.1007/bf01342185
Boettcher, S., Falkner, S., and Portugal, R. (2015). Relation between random walks and quantum walks. Phys. Rev. A 91, 052330. doi:10.1103/physreva.91.052330
Bova, F., Goldfarb, A., and Melko, R. G. (2021). Commercial applications of quantum computing. EPJ quantum Technol. 8, 2. doi:10.1140/epjqt/s40507-021-00091-1
Brassard, G., Chuang, I., Lloyd, S., and Monroe, C. (1998). Quantum computing. Proc. Natl. Acad. Sci. 95, 11032–11033. doi:10.1073/pnas.95.19.11032
Cross, A. (2018). The IBM Q experience and QISKit open-source quantum computing software. Bull. Am. Phys. Soc.
Cross, A. W., Bishop, L. S., Smolin, J. A., and Gambetta, J. M. (2017). Open quantum assembly language. arXiv preprint arXiv:1707.03429.
Dirac, P. A. M. (1939). A new notation for quantum mechanics. Math. Proc. Camb. Phil. Soc. 35, 416–418. doi:10.1017/s0305004100021162
Guo, L.-X., Wang, L., You, Z.-H., Yu, C.-Q., Hu, M.-L., Zhao, B.-W., et al. (2024). Likelihood-based feature representation learning combined with neighborhood information for predicting circrna–mirna associations. Briefings Bioinforma. 25, bbae020. doi:10.1093/bib/bbae020
Hughes, C., Isaacson, J., Perry, A., Sun, R. F., and Turner, J. (2021). Quantum computing for the quantum curious. Springer Nature.
Lehka, L. V., Shokaliuk, S. V., and Osadchyi, V. V. (2022). Hardware and software tools for teaching the basics of quantum informatics to students of specialized (high) schools. CTE Workshop Proc. 9, 228–244. doi:10.55056/cte.117
Mavroeidis, V., Vishi, K., Zych, M. D., and Jøsang, A. (2018). The impact of quantum computing on present cryptography. arXiv preprint arXiv:1804.00200.
Neamatollahi, P., Hadi, M., and Naghibzadeh, M. (2020). Simple and efficient pattern matching algorithms for biological sequences. IEEE Access 8, 23838–23846. doi:10.1109/access.2020.2969038
Nemzer, L. R. (2017). A binary representation of the genetic code. Biosystems 155, 10–19. doi:10.1016/j.biosystems.2017.03.001
Nielsen, M. A., and Chuang, I. L. (2000). Quantum computation and quantum information. 10th Anniversary Edition. USA: Cambridge University Press.
Qiskit contributors (2023). Qiskit: an open-source framework for quantum computing. doi:10.5281/zenodo.2573505
Rahate, P. M., and Chandak, M. (2018). Comparative study of string matching algorithms for dna dataset. Int. J. Comput. Sci. Eng. 6, 1067–1074. doi:10.26438/ijcse/v6i5.10671074
Shenvi, N., Kempe, J., and Whaley, K. B. (2003). Quantum random-walk search algorithm. Phys. Rev. A 67, 052307. doi:10.1103/physreva.67.052307
Wang, J., Zhang, Q., Xu, G. H., and Kim, M. (2021). “Qdiff: differential testing of quantum software stacks,” in 2021 36th IEEE/ACM international conference on automated software engineering (ASE) (IEEE), 692–704.
Keywords: k-mer graph, coined quantum walk, quantum search, quantum computing with python, qiskit, quantum register initialization
Citation: Becerra-Gavino G and Barbosa-Santillan LI (2024) The quantum hypercube as a k-mer graph. Front. Bioinform. 4:1401223. doi: 10.3389/fbinf.2024.1401223
Received: 14 March 2024; Accepted: 19 June 2024;
Published: 12 September 2024.
Edited by:
Lei Wang, Guangxi Academy of Sciences, ChinaReviewed by:
Meineng Wang, Yichun University, ChinaHasan Zulfiqar, University of Electronic Science and Technology of China, China
Copyright © 2024 Becerra-Gavino and Barbosa-Santillan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gustavo Becerra-Gavino, Z3VzdGF2by5iZWNlcnJhNTY2NkBhbHVtbm9zLnVkZy5teA==
 Gustavo Becerra-Gavino
Gustavo Becerra-Gavino Liliana Ibeth Barbosa-Santillan
Liliana Ibeth Barbosa-Santillan