The effects of plasma source on adiabatic electron acceleration at dipolarization fronts

Particle acceleration is a commonly observed phenomenon at dipolarization fronts. Many studies have attempted to determine the acceleration mechanism, with betatron acceleration being a major candidate. In previous work, we attempted to match the observed change in electron energy to the change predicted by betatron acceleration, but found that although this worked in some cases, overall betatron acceleration alone could not describe the observed energy spectrum changes. In this work, we attempted to study whether ion acceleration showed similar behavior and whether a quasi-adiabatic correction would be more accurate. On average the betatron acceleration equation overestimated the observed acceleration and the quasi-adiabatic correction did not account for the difference, although there are limitations to this study due to data fidelity. We then turned to study whether our assumptions about the source population having the same phase space density as the cold pre-existing background population in the plasma sheet are valid. We indirectly studied this by comparing the relative abundances of ${\mathrm{O}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ as proxies for ionospheric and solar wind populations respectively. We found the betatron acceleration equation method performs slightly better when there is a stronger ionospheric component. This suggests that when more plasma containing ${\mathrm{O}}^{+}$ is present in the dipolarization front, it indicates that the source population is more local and therefore this method of using betatron acceleration is more valid.

1 Introduction

Dipolarization fronts (DFs) are a commonly observed phenomenon in the tail of Earth’s magnetosphere. They are observed as a sudden increase in the z-component of the magnetic field (e.g., Russell and McPherron, 1973; Angelopoulos et al., 1992; Nakamura et al., 2002). This increased z-component is a result of the fact that DFs carry a more dipolar field than the stretched tail field around it. Accompanying reconnection in the tail, there is often a high-speed earthward flow such as a bursty bulk flow (BBF) (e.g., Angelopoulos et al., 1992). Dipolarizing flux bundles (DFBs) are smaller flux tubes embedded in BBFs that carry a more dipolar field than the surrounding plasma (e.g., Liu et al., 2014). DFs are the kinetic-scale boundaries between DFBs and are often considered a tangential discontinuity between the dipolar field and the stretched tail field (e.g., Sergeev et al., 2009; Fu et al., 2012), although not always (Balikhin et al., 2014). This process is associated with substorms (e.g., Baumjohann et al., 1999; Fu et al., 2020, and references therein) with evidence that they are more common with higher geomagnetic activity (e.g., Liu et al., 2014), a link furthered by the occurrence rate of DFs being about five events per day (Liu et al., 2013; Xiao et al., 2017), which is comparable to substorms.

An increase in the flux of energetic (a few 10 s of keV) ions has been found in many cases at DFs (e.g., Runov et al., 2011; Pan et al., 2014; Birn et al., 2015; Malykhin et al., 2018), most prominently at DFs with the strongest increase in $B_z$ (Malykhin et al., 2018). At lower energies, below around 20 keV, the proton flux can decrease due to those ions coming from less dense sources (Birn et al., 2015). The energetic ions at $\sim$20 keV-$\sim$80 keV are found earthward of the DF, while they are found closer to the DF above that energy (Birn et al., 2015). This is because the ions are often accelerated when reflected by the DF, so they end up in front of it (Zhou et al., 2010; Zhou et al., 2019). These ions are typically anisotropic, sometimes with pancake-like (i.e., trapped) pitch-angle distributions, likely as a result of betatron-type acceleration (Birn et al., 2017; Zhou et al., 2018). Zhou et al. (2018) tested the anisotropy against an adiabaticity parameter and found that the anisotropy was stronger when the plasma was more adiabatic. Although these energetic ions are primarily ${\mathrm{H}}^{+}$, ${\mathrm{O}}^{+}$ can be efficiently accelerated at DFs as well, and are accelerated even further when the DFs are followed by turbulence (Panasyuk et al., 2021).

The acceleration of ions at DFs is much more complicated than electrons at the same location because in general the thickness of the front is smaller than the ion gyroradius, so fully adiabatic acceleration is not possible (e.g., Malykhin et al., 2018), producing orbits that are “partially adiabatic and weakly chaotic” (Büchner and Zelenyi, 1989). For example, a typical DF thickness is $\sim$1,000 km (e.g., Runov et al., 2011) while the gyroradius of a 50 keV proton in a 10 nT field can be up to $>\mathrm{3,000}$ km but a 50 keV electron in the same field has a gyroradius of $<75$ km, so nonadiabatic effects that are not relevant for electrons are for protons and heavier ions. An example of the type of particle motion occurring in this situation is a Speiser orbit (Speiser, 1965) with half orbits around $B_z$ in the equatorial plane followed by quasi-adiabatic motion out of the plane (Birn et al., 2015). Ions can also be reflected at DFs multiple times (e.g., Zhou et al., 2010; Zhou et al., 2012; Birn et al., 2015; Lu et al., 2016; Zhou et al., 2018). Another way in which the ions can be not fully adiabatic is when they originate near the reconnection site and initially gain energy nonadiabatically before adiabatic or quasi-adiabatic acceleration once they reach the DFs (Pan et al., 2014). There are other fully non-adiabatic ways in which ions can be accelerated as well however. They can be trapped if the DF has a negative $B_z$ dip or quasi-trapped if $B_z$ never drops below 0. Quasi-trapping can accelerate particle over 40 keV depending on the number of encounters with the front before getting magnetized and trapping can accelerate particles up to 100 keV depending on how much time the particle is in phase with the front. Additionally wave-particle interactions can accelerate ions. Some of these include waves in turbulent magnetic structures (Grigorenko et al., 2015) and lower hybrid drift (LHD) waves, especially in slower DFs (Greco et al., 2017).

These ions present in the plasma sheet are a mix of ions from the ionosphere like ${\mathrm{H}}^{+}$, ${\mathrm{O}}^{+}$, ${\mathrm{H}\mathrm{e}}^{+}$, and ${\mathrm{N}}^{+}$ and ions from the solar wind like ${\mathrm{H}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ (e.g., Young et al., 1982; Daglis, 2006; Kistler, 2020). ${\mathrm{H}}^{+}$ is present at both sources, so it is not useful for distinguishing between the two populations. The solar wind is highly ionized, with the most common species after ${\mathrm{H}}^{+}$ being ${\mathrm{H}\mathrm{e}}^{++}$ at $\sim$1%–4% of the plasma depending on the solar cycle and whether it is in the fast or slow solar wind. Meanwhile, the ionosphere is mostly singly ionized, with ${\mathrm{O}}^{+}$ as the most common species after ${\mathrm{H}}^{+}$, followed by ${\mathrm{H}\mathrm{e}}^{+}$, and ${\mathrm{N}}^{+}$ (e.g., Kistler, 2020). ${\mathrm{O}}^{+}$ can enter the plasma sheet from either the nightside auroral region or dayside cusp, especially during storms (e.g., Kistler et al., 2010; Kistler et al., 2016; Kistler et al., 2019). During storms, ${\mathrm{O}}^{+}$ in the plasma sheet is enhanced (Kistler et al., 2005) and the source evolves from being primarily solar wind dominated to primarily ionosphere dominated (Kistler et al., 2023). ${\mathrm{O}}^{+}$ is also enhanced in the plasma sheet during substorms (Pandya et al., 2018) and more specifically the levels of ${\mathrm{O}}^{+}$ increase with higher Kp index (Young et al., 1982; Mouikis et al., 2010; Pandya et al., 2018). These cold ionospheric ions can be found behind a DF (Wang et al., 2017; Xu et al., 2019) and can even affect the DF itself, such as by making the DF slower (Liang et al., 2016). ${\mathrm{O}}^{+}$ density is enhanced at DFs like ${\mathrm{H}}^{+}$ density is, but it occurs more gradually (Zhao et al., 2018).

${\mathrm{O}}^{+}$ can reach the plasma sheet from two origins: either the cusp on the dayside or the auroral region on the nightside (e.g., Yau et al., 1985). Of these two, both can be relevant but generally the auroral zone is a larger contributor (e.g., Yau et al., 1985; Winglee, 2003). The tail is generally more disturbed when more ${\mathrm{O}}^{+}$ is from the cusp than the auroral zone (Yu and Ridley, 2013). These ions are most commonly deposited into the plasma sheet at a distance of $\sim$ 20–40 $R_E$ downtail (Li et al., 2013; Artemyev et al., 2020), which is often tailward of a DF (Liang et al., 2017). In fact, increased levels of ${\mathrm{O}}^{+}$ can cause the nightside reconnection site to move earthward, so ${\mathrm{O}}^{+}$ is often deposited near the reconnection site or sometimes even downtail of it (Wiltberger et al., 2010). Polar wind plasma, which is primarily ${\mathrm{H}}^{+}$, reaches the plasma sheet first, followed by the hot cusp plasma and auroral outflow that have more ${\mathrm{O}}^{+}$ (Kistler et al., 2023). The distance downtail ions are transported into the plasma sheet depends on the particle velocity, not energy, so for the same energy ${\mathrm{O}}^{+}$ will enter closer to Earth than ${\mathrm{H}}^{+}$ will (Kistler, 2020). There is also a dawn-dusk asymmetry in where ions are transported, with more on the dusk side despite there not being a corresponding asymmetry in the source region (Li et al., 2013), with this asymmetry also present for energetic ${\mathrm{O}}^{+}$ in addition to cold ions (Kronberg et al., 2015). Once the ions are in the plasma sheet, their flow is primarily earthward, but there is a very small dawnward component on the dawnside and a more significant duskward component on the duskside (Hori et al., 2000).

This work builds off of the study we previously undertook in Chepuri et al. (2023). In that study we studied how well adiabatic acceleration equations explained energetic electron observations at DFs. We found that betatron acceleration overestimated the observed electron acceleration while a combined betatron and Fermi acceleration equation underestimated it while having a high error. Two potential explanations are that there are non-adiabatic processes occurring or that the implicit assumption in this method that the quiet plasma sheet before the DF is similar to the source population is not generally valid. In this work, first we attempt to study ion acceleration to see if they exhibit similar behavior to electrons. Then, we study the composition of the plasma as a proxy for what the source population is to try to answer the open questions from the previous study.

2 Instruments

The Magnetospheric Multiscale (MMS) mission consists of four spacecraft in tight formation launched in 2015 (Burch et al., 2016). Starting in 2017, the orbit had an apogee of $\sim 25R_E$ to spend the most amount of time possible in the nightside reconnection region (Fuselier et al., 2016). The orbit is such that MMS has a tail season when apogee is on the nightside in the Northern hemisphere summer, meaning we can focus our search for events in that time range.

The primary instruments used to measure energetic particles for this study came from the Energetic Particle Detector (EPD) investigation (Mauk et al., 2016). These were the Fly’s Eye Energetic Particle Spectrometer (FEEPS) for electrons (Blake et al., 2016) and the Energetic Ion Spectrometer (EIS) for ions (Mauk et al., 2016). FEEPS measures electrons in the energy range of 25–650 keV while EIS can measure ${\mathrm{H}}^{+}$ in an energy range of 20–500 keV and ${\mathrm{O}}^{+}$ above $\sim$130 keV. FEEPS has 16 energy channels and observes nearly a full sky with 2.5 s time resolution in survey mode. EIS uses time-of-flight measurements to determine energies as well as basic differentiation between Hydrogen, Helium, and Oxygen. In addition to EPD data, we also used the Fast Plasma Investigation (FPI) to measure lower energies up to 30 keV (Pollock et al., 2016). Each spacecraft has four dual 180-degree that spectrometers for electrons, which allow for a $4\pi$-sr field of view. To study the composition of the thermal plasma, we used the Hot Plasma Composition Analyzer (HPCA) (Young et al., 2016). It measures ions from 1 eV to 40 keV and can differentiate between ${\mathrm{H}}^{+}$, ${\mathrm{H}\mathrm{e}}^{+}$, ${\mathrm{H}\mathrm{e}}^{++}$, and ${\mathrm{O}}^{+}$. It does this all with a time resolution of around 10 s.

Data from the FIELDS instrument suite (Torbert et al., 2016), especially the fluxgate magnetometer (FGM) (Russell et al., 2016) was also necessary to measure magnetic fields and provide other context. Finally, we studied waves with the search coil magnetometer (Le Contel et al., 2016) and the electric field double probes (Lindqvist et al., 2016; Ergun et al., 2016).

3 Ion acceleration

3.1 Quasi-adiabatic correction to betatron acceleration

The first complicating factor in using adiabatic acceleration to describe ion acceleration at dipolarization fronts is the fact the ions have larger gyroradii than electrons. Because of this, it is not always accurate to assume the acceleration is adiabatic, and is often described as “quasi-adabatic” (e.g., Birn et al., 2015; Runov et al., 2017), as described in Section 1. One way to account for this mathematically is with an equation describing the variation in the magnetic moment as adiabaticity is violated. Delcourt and Moore (1992) derived Equation 1:

$\frac{{\mu }_f}{{\mu }_0}={\left(1\pm \frac{q{C}_{\mathrm{\Delta }A}|\sin \left(\pi \chi \right)|}{m{v}_0\pi \chi |\left({\chi }^2-1\right)|}\right)}^2,(1)$

where ${\mu }_f$ and ${\mu }_0$ are the magnetic moment before and after the dipolarization and $q$, $m$, and $v_0$ are the charge, mass, and initial velocity of the particle. $\chi$ is defined in Equation 2:

$\chi =\frac{\tau }{{\tau }_c},(2)$

where $\tau$ is the dipolarization time and ${\tau }_c$ is the cyclotron period. Finally, $C_{\mathrm{\Delta }A}$ is defined in Equation 3:

$C_{\mathrm{\Delta }A}=\tau E_p,(3)$

where $E_p$ is half of the peak electric field. Expanding this equation yields the change in velocity from the change in magnetic field from $B_0$ to $B_f$ in Equation 4:

$v_f^2=\frac{B_f}{B_0}{\left(v_0\pm \frac{q{C}_{\mathrm{\Delta }A}|\sin \left(\pi \chi \right)|}{m\pi \chi |\left({\chi }^2-1\right)|}\right)}^2,(4)$

(Delcourt and Sauvaud, 1994). When $\chi$ is large, the final term goes as ${\chi }^{-3}$ and the correction goes to 0, so this is the adiabatic limit. In this regime, ion behavior resembles previously studied electron behavior. When $\chi$ is small however, the final term goes as $\frac{\sin (\pi \chi )}{\pi \chi }$ and the correction is significant. Turning this change in velocity to a change in energy, the quasi-adiabatic betatron acceleration change in energy is given by Equation 5:

$W_2=\left(\frac{B_{z2}-B_{z1}}{|B_1|}+1\right){\left(\sqrt{W_1}\pm A\right)}^2,(5)$

where $A=\frac{q{C}_{\mathrm{\Delta }A}|\sin (\pi \chi )|}{\sqrt{2m}\pi \chi |{\chi }^2-1|}$. For the purposes of this study, change in flux is more useful than change in energy, so similar to Chepuri et al. (2023), we assumed a piecewise power law with a power law index $n$ to give Equation 6 for change in flux:

$j_2=j_1{\left[\frac{1}{W_1}\left(\frac{B_{z2}-B_{z1}}{B_{t1}}+1\right){\left(\sqrt{W_1}+A\right)}^2\right]}^n.(6)$

3.2 Event selection

We used the same sample of DFs as in Chepuri et al. (2023), based on criteria from Schmid et al. (2011) and Wu et al. (2013), which were:

- $\mathrm{\Delta }{B}_z>4$ nT

- Maximum elevation angle, $\theta >45°$, where $\theta ={\tan }^{-1}\left(\frac{B_z}{B_{xy}}\right)$

- Increase in elevation angle, $\mathrm{\Delta }\theta >10°$

- Maximum earthward flow $v_x>150$ km/s

- Maximum plasma $\beta >0.5$ to ensure the spacecraft is in the plasma sheet

- Maximum $B_z$ occurs after the minimum $B_z$ so the dipolarization is propagating towards the spacecraft and located at a distance of beyond $10R_E$ and in an MLT range between 19–5.

Then, to select for events with ion acceleration, we found events with at least a 5x increase in proton flux at either the 54 keV or 80 keV channel in EIS, which are the energies in the range where we expect to see acceleration at DFs. We simply used EIS protons rather than looking at all ion species because ${\mathrm{H}}^{+}$ is the dominant ion species, so using these protons alone can describe the larger energetic ion population. In addition, to ensure that the observed acceleration was not a fluke of small number statistics, we imposed a limit of 30% error in counts from Poisson statistics. With this definition, we identified 70 events with ion acceleration to use in this study.

3.3 Results: ion acceleration

To study how well this equation described ion acceleration, we used energetic proton data from the EIS instrument on MMS. However, the survey level EIS data showed a data artifact with a periodicity similar to the spacecraft spin period. For example, this could be the instrument measuring an ion beam which is only visible as the spacecraft spins to face it. Looking into the data more for some examples provided more evidence that it was in fact a beam. The periodic signal was visible in both EIS protons and FEEPS ions, but the flux peak was offset in a way that is consistent with the offset look direction of the two instruments. Additionally, inspection of EIS angle-angle plots show evidence of a beam in protons. These type of artifacts were very common, potentially because they are a result of gyroradius effects of the approaching DF. As a result, we were limited to spin-averaged data to avoid misleading measurements facing different directions. This produces one data point every $\sim$19.5 s, so it is difficult to match up changes in proton flux at this low time-resolution with changes in the magnetic field that can occur within seconds or even less than a second. Figure 1 shows MMS data for one example event on 26 June 2017 and illustrates this data issue. Panel (a) shows the magnetic field vector in GSM coordinates, panel (b) shows the magnetic elevation angle, panel (c) shows the energetic proton flux from EIS with the periodic data artifact clearly visible and the approximate peaks for some of the periods marked by arrows, panel (d) shows the spin-averaged EIS energetic proton flux, and panel (e) shows the thermal ion flux from FPI. The vertical lines show the minimum $B_z$ value before the DF and the peak $B_z$. This level of data cannot be used to precisely test the validity of the equations, but it can at least give a lower bound since the data point we use will include some of the pre-accelerated ion flux in addition to the accelerated ion flux. This means we would expect the modeled flux given by the equation to be lower than the observed flux. We can test it by comparing the observed and modeled energy spectra similar to what we did for the electron spectra in Chepuri et al. (2023). Figure 2 shows these spectra for the same example event shown in Figure 1. The green squares show the observed ion spectrum before the dipolarization, the black circles show the observed ion spectrum at the peak of the dipolarization, and the purple diamonds show the modeled betatron acceleration with a quasi-adiabatic correction as calculated by Equation 6. The error bars are derived from Poisson statistics assuming a $\sqrt{N}$ error associated with an observation of $N$ counts. For the energies with overlap between FPI and EIS measurements, the observed fluxes from the two instruments are consistent, validating our choice to assume that measuring energetic protons with EIS is sufficient to explain the overall energetic ion behavior. Similar to the results for betatron acceleration of electrons, we found that on average this method actually overestimated the flux, despite our expectations. Because of the lack of detail in the data, we were not able to examine this more precisely. However, there were two potential factors in this method not being accurate: either there are non-adiabatic processes occurring or this method does not identify the source population being accelerated correctly. Because adding a correction to account for breaking adiabaticity does not improve the method’s performance, this suggests that the source population is a bigger problem. To address the question of source population, we will return to the electron events identified in Chepuri et al. (2023) and add to it the analysis of plasma composition for these events.

Figure 1

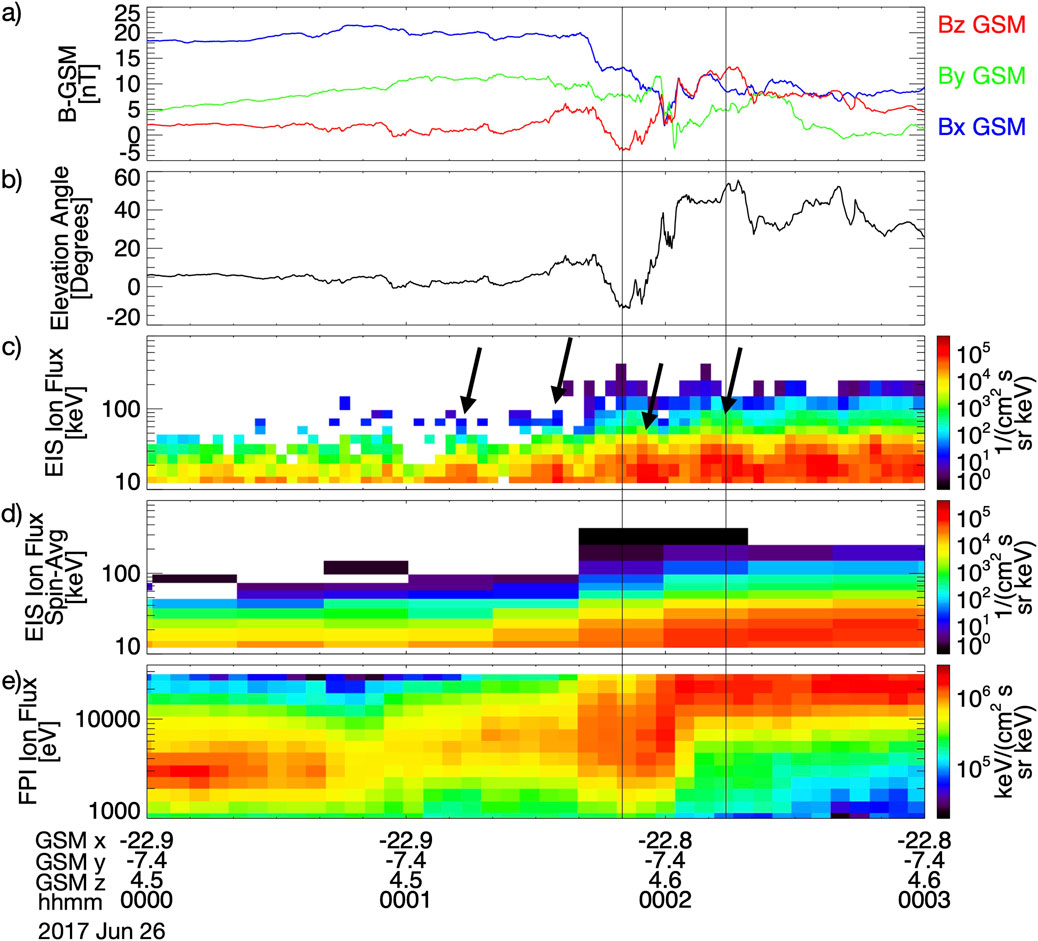
Figure 1. MMS data from an example DF with energetic ion acceleration. (A) Magnetic field vector in GSM coordinates, (B) Magnetic elevation angle, (C) EIS energetic proton flux, (D) Spin-averaged EIS energetic proton flux, (E) FPI thermal ion flux. The vertical lines show the minimum $B_z$ value before the DF and the peak $B_z$ and the arrows point to the approximate peaks of some of the periodic data artifacts.

Figure 2

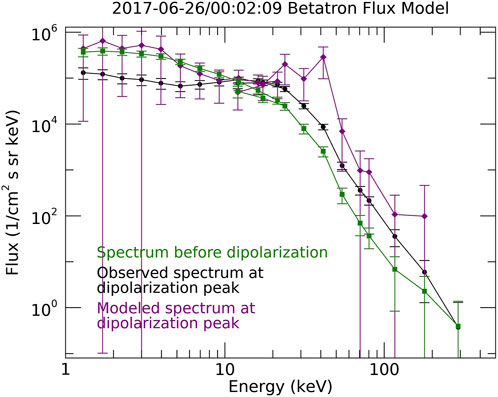
Figure 2. Energy spectrum of observed ions before the dipolarization (green squares), observed ions at peak of dipolarization (black circles), and betatron model with quasi-adiabatic correction of ions at peak (purple diamonds).

4 Plasma population at electron acceleration events

4.1 Ion composition data

With in situ spacecraft data, we are unable to measure both the source population and the particles that have been accelerated by the DF without extremely fortuitous geometry, so we are unable to definitively test how well betatron acceleration explains acceleration using these equations. However, one way we can gain some information about where the plasma originates is by studying the plasma composition. As discussed in Section 1, we can use the relative levels of different ions to determine how much of the plasma is from different sources, and specifically ${\mathrm{O}}^{+}$ as a marker of plasma from the ionosphere and ${\mathrm{H}\mathrm{e}}^{++}$ as a marker of plasma from the solar wind. We will test the plasma composition of the DFs with electron acceleration that were used in Chepuri et al. (2023).

We used the HPCA instrument on MMS to measure the prevalence of these species. However, the compression scheme used on HPCA data gave anomalously low values for minor ion fluxes, including both ${\mathrm{H}\mathrm{e}}^{++}$ and ${\mathrm{O}}^{+}$, so data from times when this compression scheme was active must be discarded. This leaves us with the periods that this scheme was turned off, which were 27 May 2018 - 25 September 2018, 16 April 2019 - 17 August 2019, and after 24 May 2021 (Kistler, private communication). Luckily for our purposes, the dates when the data is usable from 2018 to 2019 were during the tail season, so most of our data from those years in addition to 2021 and later are reliable. This left us with 70 out of the original 168 events with non-compressed HPCA data.

HPCA can differentiate between four different species: ${\mathrm{H}}^{+}$, ${\mathrm{H}\mathrm{e}}^{+}$, ${\mathrm{H}\mathrm{e}}^{++}$, and ${\mathrm{O}}^{+}$. We can compare the relative amounts of the two sources by comparing the ratio of the ${\mathrm{O}}^{+}$ density to the ${\mathrm{H}\mathrm{e}}^{++}$ density, and we can also look at the absolute amount of each by using the ratio of ${\mathrm{O}}^{+}$ density to ${\mathrm{H}}^{+}$ density for ionosphere and ${\mathrm{H}\mathrm{e}}^{++}$ density to ${\mathrm{H}}^{+}$ density. Figure 3 shows data for an example DF with electron acceleration. Panel (a) shows the basic field and particle data for the DF: magnetic field vector in GSM coordinates in panel (a-i), magnetic elevation angle in panel (a-ii), FFEPS energetic electron flux in panel (a-iii), and FPI thermal electron flux in panel (a-iv). Panel (b) shows the HPCA data with the plasma composition. Panel (b-i) shows the ${\mathrm{H}}^{+}$ density, panel (b-ii) shows the ${\mathrm{H}\mathrm{e}}^{+}$ density, panel (b-iii) shows the ${\mathrm{H}\mathrm{e}}^{++}$ density, panel (b-iv) shows the ${\mathrm{O}}^{+}$ density, and panel (b-v) shows the ratio of ${\mathrm{O}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ density. Finally, panel (c) shows the energy spectra of observed electrons before the dipolarization (green squares), observed electrons at peak of dipolarization (black circles), and the expected spectrum of electrons based on the betatron acceleration equation (purple diamonds) for this event. For each of our events, we compared the normalized error of the model to the levels of these ion species.

Figure 3

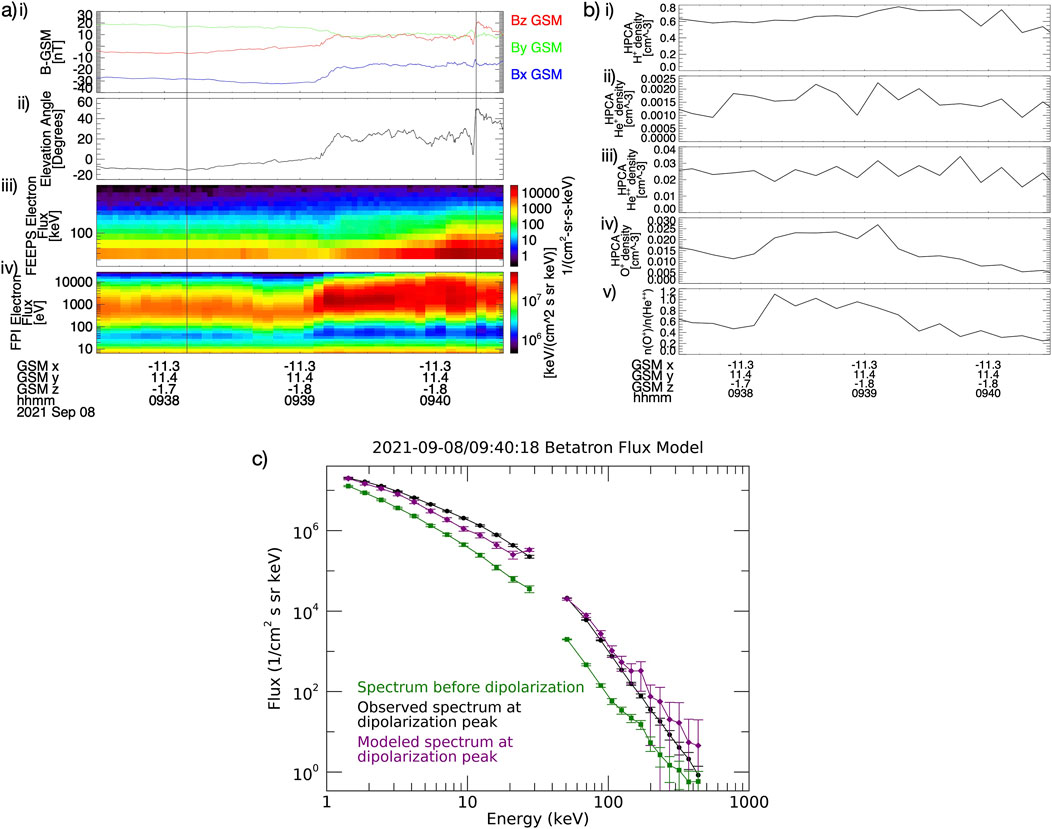
Figure 3. MMS data including plasma composition from an example DF with energetic electron acceleration. (A–I) Magnetic field vector in GSM coordinates, (A–II) Magnetic elevation angle, (A–III) FEEPS energetic electron flux, (A–IV) FPI thermal electron flux, (B–I) ${\mathrm{H}}^{+}$ density, (B–II) ${\mathrm{H}\mathrm{e}}^{+}$ density (B–III) ${\mathrm{H}\mathrm{e}}^{++}$ density, (B–IV) ${\mathrm{O}}^{+}$ density, (B–V) Ratio of ${\mathrm{O}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ density, (C) Energy spectrum of observed electrons before the dipolarization (green squares), observed electrons at peak of dipolarization (black circles), and betatron model of electrons at peak (purple diamonds).

4.2 Results: source population

To quantify the accuracy of the model, we used the root mean square error of each energy channel for each event normalized to the standard deviation. This was chosen because when this normalized error is greater than 1, we cannot say with any confidence that the equation accurately describes the data. In Figure 4, we show the normalized error for each event as a function of the ${\mathrm{O}}^{+}$ level (panel (a)), ${\mathrm{H}\mathrm{e}}^{++}$ level (panel (b)), and the ratio between the two species (panel (c)). The events are marked if the initial magnetic field is greater than 10 nT (blue), or less (orange), following our results from the previous study that high error events tend to have an initial magnetic field $<$10 nT. From these figures, focusing on the blue data points for high magnetic field, we can see that in panel (c) there appears to be lower error for events with a higher level of ${\mathrm{O}}^{+}$ in relation to ${\mathrm{H}\mathrm{e}}^{++}$. Looking at the two individual species, there does not appear to be any correlation with ${\mathrm{H}\mathrm{e}}^{++}$, but it does seem that error is reduced with higher ${\mathrm{O}}^{+}$ levels, although there are not enough data points for this relationship to be conclusive. This suggests that higher levels of ${\mathrm{O}}^{+}$ are more important for the improved accuracy of the betatron acceleration equation than lower levels of ${\mathrm{H}\mathrm{e}}^{++}$.

Figure 4

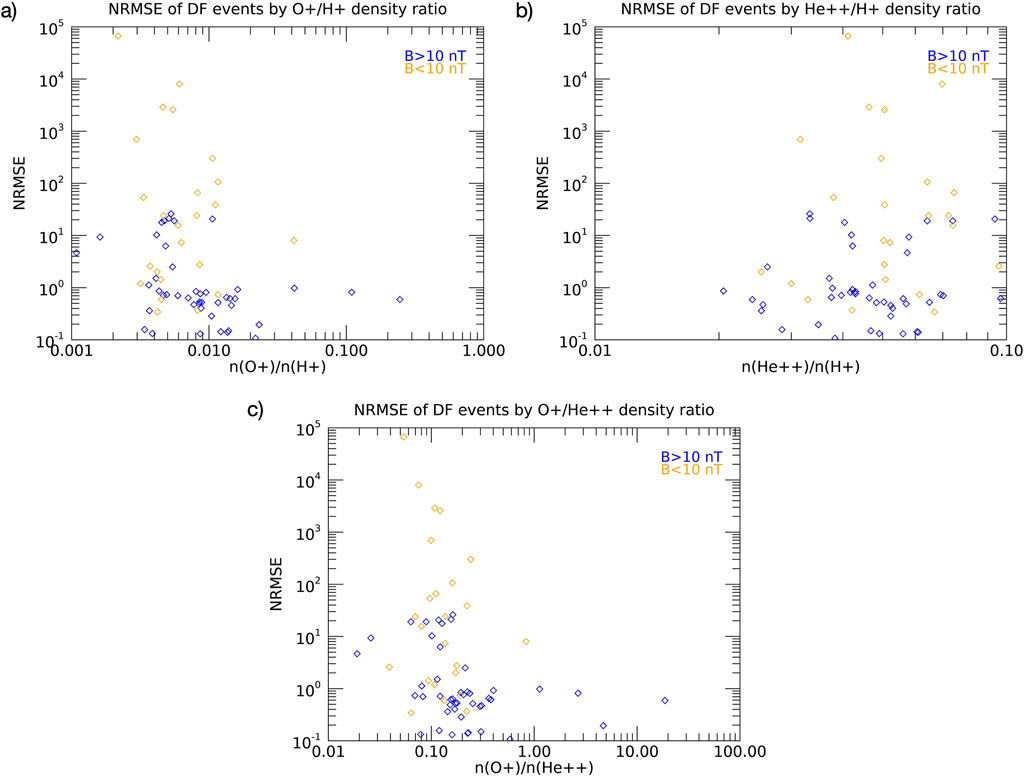
Figure 4. The normalized root mean square error of the betatron acceleration model for each energetic electron event with respect to the plasma composition. (A) ${\mathrm{O}}^{+}$ density, (B) ${\mathrm{H}\mathrm{e}}^{++}$ density, (C) Ratio of ${\mathrm{O}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ density.

We also looked at a few characteristics of plasma composition in our events to ensure that there were not other factors that we were overlooking in our analysis. Some of these are shown in Figure 5. First we confirmed that there was no correlation between ${\mathrm{O}}^{+}$ and ${\mathrm{H}\mathrm{e}}^{++}$ (panel (a)), so our analysis in the previous paragraph treating the two species as separate is reasonable. We also compared the radial distance from Earth to the densities of the two species. We found that in the regions where we were sampling, there was also no correlation with either ${\mathrm{O}}^{+}$ density (panel (b)) or the ratio between ${\mathrm{O}}^{+}$ density and ${\mathrm{H}\mathrm{e}}^{++}$ density (panel (d)), so we are also not measuring a process related to distance. In Section 5, we will discuss why these patterns may be occurring.

Figure 5

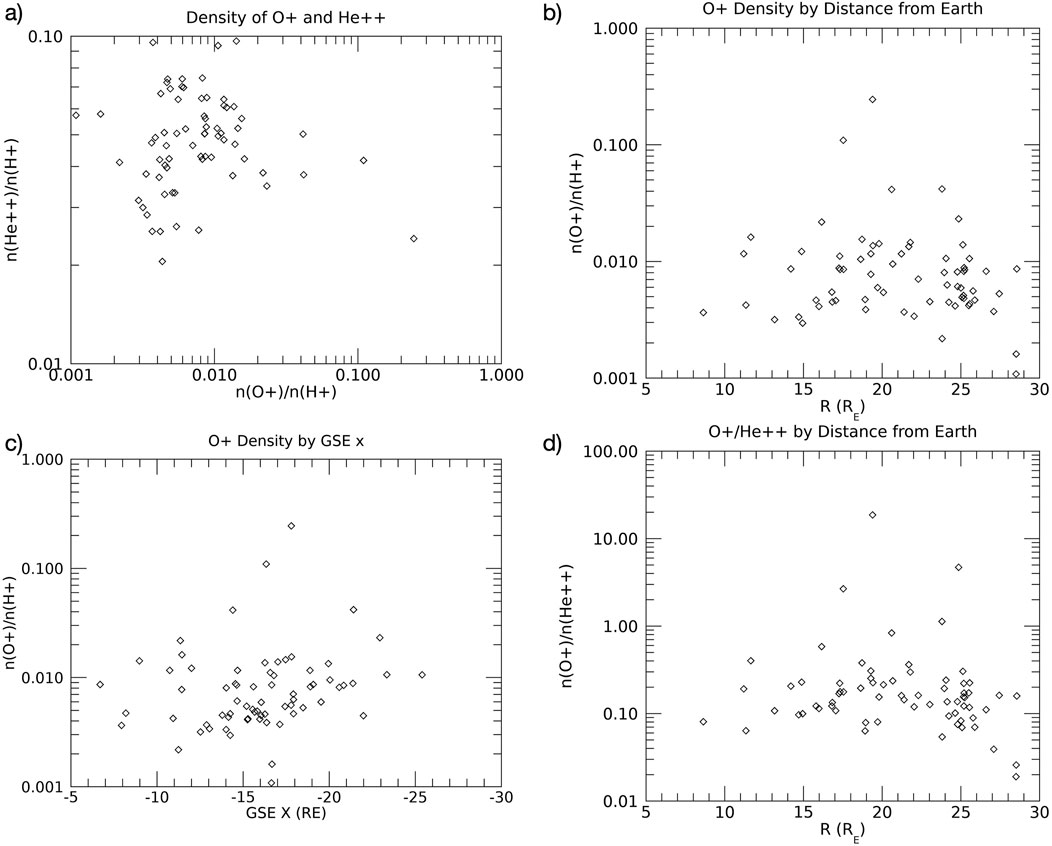
Figure 5. (A) ${\mathrm{O}}^{+}$ density vs. ${\mathrm{H}\mathrm{e}}^{++}$ density, (B) ${\mathrm{O}}^{+}$ density by distance from Earth, (C) ${\mathrm{O}}^{+}$ density by GSE x, (D) Ratio of ${\mathrm{O}}^{+}$ density and ${\mathrm{H}\mathrm{e}}^{++}$ density by distance from Earth.

5 Discussion and conclusion

We were not able to conclusively test this method of ion betatron acceleration at DFs, but we still were able to test some aspects of it. Adding a quasi-adiabatic correction did not improve the method’s results, which points to focusing on the source population as the main driver of error. However, the imprecise data introduces even more uncertainty. Each measurement of energetic protons covers nearly 20 s, while the changes in the magnetic field occur on the order of a few seconds. This could potentially lead to an underestimate of the acceleration since the measurement of energetic ions after the dipolarization includes some time from before the dipolarization as well. It could lead to other less predictable errors as well though, so this data is not generally reliable, meaning most of the conclusions we can draw from this work are related to the composition of the plasma.

Using HPCA data to study the plasma source provided some more useful results. We are using this data to determine the source of the plasma because that is potentially one of the biggest reasons why the implemented does not work. This method relies on the source population being similar to the quiet plasma sheet. Birn et al. (2014) showed that is not necessarily accurate. They found in simulations that the distance the source population traveled to the DF was dependent on energy and pitch angle. Parallel electrons above $\sim$100 keV are from the inner tail with x$>-22.5$, but below $\sim$10 keV they are from the plasma sheet boundary layer or lobes, with the intermediate energies being from the distant tail. For perpendicular electrons, the lower energy boundary is similar, but it goes up to a few 100 s of keV before the electrons are primarily from the near tail.

We were able to see that using betatron acceleration is more accurate when there are higher levels of ${\mathrm{O}}^{+}$. ${\mathrm{O}}^{+}$ outflowing from the ionosphere tends to be deposited relatively closer to Earth, with those ions being transported to the plasma sheet around 85% of the time, typically Earthward of 40–55 $R_E$ during disturbed times, as many of our events are (Li et al., 2013). More precisely, ${\mathrm{O}}^{+}$ typically reaches the plasma sheet at around 20–40 $R_E$ (Artemyev et al., 2020). This would put the bulk of ${\mathrm{O}}^{+}$ ions near the tail reconnection site. As is shown in Figure 5 (panel (c)), this is around or not far downtail of our observations. There may be a slight trend towards having higher levels of ${\mathrm{O}}^{+}$ at higher x distances, which could be a result of being closer to the location in the plasma sheet where ${\mathrm{O}}^{+}$ is deposited. Therefore, if the plasma during an event has high levels of ${\mathrm{O}}^{+}$, it is likely from a more local location in the tail and therefore more likely to be similar to the plasma sheet prior to the dipolarization. The same, however, is not true of ${\mathrm{H}\mathrm{e}}^{++}$ entering the tail from the solar wind (e.g., Winglee, 2003) so we do not have a comparable relationship between ${\mathrm{H}\mathrm{e}}^{++}$ levels and accuracy of this method.

We have statistically studied dipolarization fronts in the tail with observations of energetic particles by MMS, following the work in (Chepuri et al., 2023). First, we attempted to test the accuracy of an equation for betatron acceleration of ions, including a quasi-adiabatic correction. However, because of the quality of the data, we could not determine a precise relationship beyond setting a bound for the acceleration level. This led us to test the composition of the plasma at these DFs to learn more about the source population. For the DFs with energetic electron acceleration, we found that this method of testing betatron acceleration was more accurate when more ${\mathrm{O}}^{+}$ was present. We hypothesize that this is because ${\mathrm{O}}^{+}$ that flows out of the ionosphere reaches the tail closer to our observations, so higher levels of ${\mathrm{O}}^{+}$ are indicative of a source closer to the observed DF, which makes this method more accurate.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://lasp.colorado.edu/mms/sdc.

Author contributions

SC: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. AJ: Funding acquisition, Supervision, Writing–review and editing. JJ: Writing–review and editing. DT: Writing–review and editing. CG: Writing–review and editing. IC: Writing–review and editing. DB: Writing–review and editing. BM: Writing–review and editing. TL: Writing–review and editing. JF: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by funding from the MMS mission, under NASA contract NNG04EB99C.

Acknowledgments

The authors would like to acknowledge L. M. Kistler for her help with interpreting HPCA data.

Conflict of interest

Authors CG and JF were employed by The Aerospace Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angelopoulos, V., Baumjohann, W., Kennel, C., Coroniti, F. V., Kivelson, M., Pellat, R., et al. (1992). Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. Space Phys. 97, 4027–4039. doi:10.1029/91ja02701

CrossRef Full Text | Google Scholar

Artemyev, A., Angelopoulos, V., Runov, A., and Zhang, X.-J. (2020). Ionospheric outflow during the substorm growth phase: themis observations of oxygen ions at the plasma sheet boundary. J. Geophys. Res. Space Phys. 125, e2019JA027612. doi:10.1029/2019ja027612

CrossRef Full Text | Google Scholar

Balikhin, M., Runov, A., Walker, S., Gedalin, M., Dandouras, I., Hobara, Y., et al. (2014). On the fine structure of dipolarization fronts. J. Geophys. Res. Space Phys. 119, 6367–6385. doi:10.1002/2014ja019908

CrossRef Full Text | Google Scholar

Baumjohann, W., Hesse, M., Kokubun, S., Mukai, T., Nagai, T., and Petrukovich, A. (1999). Substorm dipolarization and recovery. J. Geophys. Res. Space Phys. 104, 24995–25000. doi:10.1029/1999ja900282

CrossRef Full Text | Google Scholar

Birn, J., Runov, A., and Hesse, M. (2014). Energetic electrons in dipolarization events: spatial properties and anisotropy. J. Geophys. Res. Space Phys. 119, 3604–3616. doi:10.1002/2013ja019738

CrossRef Full Text | Google Scholar

Birn, J., Runov, A., and Hesse, M. (2015). Energetic ions in dipolarization events. J. Geophys. Res. Space Phys. 120, 7698–7717. doi:10.1002/2015ja021372

CrossRef Full Text | Google Scholar

Birn, J., Runov, A., and Zhou, X.-Z. (2017). Ion velocity distributions in dipolarization events: distributions in the central plasma sheet. J. Geophys. Res. Space Phys. 122, 8014–8025. doi:10.1002/2017ja024230

CrossRef Full Text | Google Scholar

Blake, J., Mauk, B., Baker, D., Carranza, P., Clemmons, J., Craft, J., et al. (2016). The fly’s eye energetic particle spectrometer (feeps) sensors for the magnetospheric multiscale (mms) mission. Space Sci. Rev. 199, 309–329. doi:10.1007/s11214-015-0163-x

CrossRef Full Text | Google Scholar

Büchner, J., and Zelenyi, L. M. (1989). Regular and chaotic charged particle motion in magnetotaillike field reversals: 1. basic theory of trapped motion. J. Geophys. Res. Space Phys. 94, 11821–11842. doi:10.1029/ja094ia09p11821

CrossRef Full Text | Google Scholar

Burch, J., Moore, T., Torbert, R., and Giles, B. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Chepuri, S., Jaynes, A., Turner, D., Gabrielse, C., Cohen, I., Baker, D., et al. (2023). Testing adiabatic models of energetic electron acceleration at dipolarization fronts. Front. Astronomy Space Sci. 10, 1266412. doi:10.3389/fspas.2023.1266412

CrossRef Full Text | Google Scholar

Daglis, I. A. (2006). Ring current dynamics. Space Sci. Rev. 124, 183–202. doi:10.1007/978-0-387-69532-7_13

CrossRef Full Text | Google Scholar

Delcourt, D., and Moore, T. (1992). Precipitation of ions induced by magnetotail collapse. J. Geophys. Res. Space Phys. 97, 6405–6415. doi:10.1029/91ja03142

CrossRef Full Text | Google Scholar

Delcourt, D., and Sauvaud, J. (1994). Plasma sheet ion energization during dipolarization events. J. Geophys. Res. Space Phys. 99, 97–108. doi:10.1029/93ja01895

CrossRef Full Text | Google Scholar

Ergun, R., Tucker, S., Westfall, J., Goodrich, K., Malaspina, D., Summers, D., et al. (2016). The axial double probe and fields signal processing for the mms mission. Space Sci. Rev. 199, 167–188. doi:10.1007/978-94-024-0861-4_7

CrossRef Full Text | Google Scholar

Fu, H., Grigorenko, E. E., Gabrielse, C., Liu, C., Lu, S., Hwang, K., et al. (2020). Magnetotail dipolarization fronts and particle acceleration: a review. Sci. China Earth Sci. 63, 235–256. doi:10.1007/s11430-019-9551-y

CrossRef Full Text | Google Scholar

Fu, H. S., Khotyaintsev, Y. V., Vaivads, A., André, M., and Huang, S. (2012). Electric structure of dipolarization front at sub-proton scale. Geophys. Res. Lett. 39. doi:10.1029/2012gl051274

PubMed Abstract | CrossRef Full Text | Google Scholar

Fuselier, S., Lewis, W., Schiff, C., Ergun, R., Burch, J., Petrinec, S., et al. (2016). Magnetospheric multiscale science mission profile and operations. Space Sci. Rev. 199, 77–103. doi:10.1007/s11214-014-0087-x

CrossRef Full Text | Google Scholar

Greco, A., Artemyev, A., Zimbardo, G., Angelopoulos, V., and Runov, A. (2017). Role of lower hybrid waves in ion heating at dipolarization fronts. J. Geophys. Res. Space Phys. 122, 5092–5104. doi:10.1002/2017ja023926

CrossRef Full Text | Google Scholar

Grigorenko, E., Malykhin, A. Y., Kronberg, E., Malova, K. V., and Daly, P. (2015). Acceleration of ions to suprathermal energies by turbulence in the plasmoid-like magnetic structures. J. Geophys. Res. Space Phys. 120, 6541–6558. doi:10.1002/2015ja021314

CrossRef Full Text | Google Scholar

Hori, T., Maezawa, K., Saito, Y., and Mukai, T. (2000). Average profile of ion flow and convection electric field in the near-earth plasma sheet. Geophys. Res. Lett. 27, 1623–1626. doi:10.1029/1999gl003737

CrossRef Full Text | Google Scholar

Kistler, L., Asamura, K., Kasahara, S., Miyoshi, Y., Mouikis, C., Keika, K., et al. (2023). The variable source of the plasma sheet during a geomagnetic storm. Nat. Commun. 14, 6143. doi:10.1038/s41467-023-41735-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kistler, L., Mouikis, C., Asamura, K., Yokota, S., Kasahara, S., Miyoshi, Y., et al. (2019). Cusp and nightside auroral sources of o+ in the plasma sheet. J. Geophys. Res. Space Phys. 124, 10036–10047. doi:10.1029/2019ja027061

CrossRef Full Text | Google Scholar

Kistler, L., Mouikis, C., Klecker, B., and Dandouras, I. (2010). Cusp as a source for oxygen in the plasma sheet during geomagnetic storms. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009ja014838

CrossRef Full Text | Google Scholar

Kistler, L., Mouikis, C., Möbius, E., Klecker, B., Sauvaud, J., Reme, H., et al. (2005). Contribution of nonadiabatic ions to the cross-tail current in an o+ dominated thin current sheet. J. Geophys. Res. Space Phys. 110. doi:10.1029/2004ja010653

CrossRef Full Text | Google Scholar

Kistler, L., Mouikis, C., Spence, H., Menz, A., Skoug, R. M., Funsten, H. O., et al. (2016). The source of o+ in the storm time ring current. J. Geophys. Res. Space Phys. 121, 5333–5349. doi:10.1002/2015ja022204

CrossRef Full Text | Google Scholar

Kistler, L. M. (2020). Ionospheric and solar wind contributions to the storm-time near-earth plasma sheet. Geophys. Res. Lett. 47, e2020GL090235. doi:10.1029/2020gl090235

CrossRef Full Text | Google Scholar

Kronberg, E. A., Grigorenko, E., Haaland, S., Daly, P. W., Delcourt, D. C., Luo, H., et al. (2015). Distribution of energetic oxygen and hydrogen in the near-earth plasma sheet. J. Geophys. Res. Space Phys. 120, 3415–3431. doi:10.1002/2014ja020882

CrossRef Full Text | Google Scholar

Le Contel, O., Leroy, P., Roux, A., Coillot, C., Alison, D., Bouabdellah, A., et al. (2016). The search-coil magnetometer for mms. Space Sci. Rev. 199, 257–282. doi:10.1007/s11214-014-0096-9

CrossRef Full Text | Google Scholar

Li, K., Haaland, S., Eriksson, A., André, M., Engwall, E., Wei, Y., et al. (2013). Transport of cold ions from the polar ionosphere to the plasma sheet. J. Geophys. Res. Space Phys. 118, 5467–5477. doi:10.1002/jgra.50518

CrossRef Full Text | Google Scholar

Liang, H., Ashour-Abdalla, M., Lapenta, G., and Walker, R. J. (2016). Oxygen impacts on dipolarization fronts and reconnection rate. J. Geophys. Res. Space Phys. 121, 1148–1166. doi:10.1002/2015ja021747

CrossRef Full Text | Google Scholar

Liang, H., Lapenta, G., Walker, R. J., Schriver, D., El-Alaoui, M., and Berchem, J. (2017). Oxygen acceleration in magnetotail reconnection. J. Geophys. Res. Space Phys. 122, 618–639. doi:10.1002/2016ja023060

CrossRef Full Text | Google Scholar

Lindqvist, P.-A., Olsson, G., Torbert, R., King, B., Granoff, M., Rau, D., et al. (2016). The spin-plane double probe electric field instrument for mms. Space Sci. Rev. 199, 137–165. doi:10.1007/978-94-024-0861-4_6

CrossRef Full Text | Google Scholar

Liu, J., Angelopoulos, V., Runov, A., and Zhou, X.-Z. (2013). On the current sheets surrounding dipolarizing flux bundles in the magnetotail: the case for wedgelets. J. Geophys. Res. Space Phys. 118, 2000–2020. doi:10.1002/jgra.50092

CrossRef Full Text | Google Scholar

Liu, J., Angelopoulos, V., Zhou, X.-Z., and Runov, A. (2014). Magnetic flux transport by dipolarizing flux bundles. J. Geophys. Res. Space Phys. 119, 909–926. doi:10.1002/2013ja019395

CrossRef Full Text | Google Scholar

Lu, S., Angelopoulos, V., and Fu, H. (2016). Suprathermal particle energization in dipolarization fronts: particle-in-cell simulations. J. Geophys. Res. Space Phys. 121, 9483–9500. doi:10.1002/2016ja022815

CrossRef Full Text | Google Scholar

Malykhin, A. Y., Grigorenko, E. E., Kronberg, E. A., Koleva, R., Ganushkina, N. Y., Kozak, L., et al. (2018). Contrasting dynamics of electrons and protons in the near-earth plasma sheet during dipolarization. Ann. Geophys. 36, 741–760. doi:10.5194/angeo-36-741-2018

CrossRef Full Text | Google Scholar

Mauk, B., Blake, J., Baker, D., Clemmons, J., Reeves, G., Spence, H. E., et al. (2016). The energetic particle detector (epd) investigation and the energetic ion spectrometer (eis) for the magnetospheric multiscale (mms) mission. Space Sci. Rev. 199, 471–514. doi:10.1007/s11214-014-0055-5

CrossRef Full Text | Google Scholar

Mouikis, C., Kistler, L., Liu, Y., Klecker, B., Korth, A., and Dandouras, I. (2010). H+ and o+ content of the plasma sheet at 15–19 re as a function of geomagnetic and solar activity. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010ja015978

CrossRef Full Text | Google Scholar

Nakamura, R., Baumjohann, W., Klecker, B., Bogdanova, Y., Balogh, A., Rème, H., et al. (2002). Motion of the dipolarization front during a flow burst event observed by cluster. Geophys. Res. Lett. 29, 3–1. doi:10.1029/2002gl015763

CrossRef Full Text | Google Scholar

Pan, Q., Ashour-Abdalla, M., Walker, R. J., and El-Alaoui, M. (2014). Ion energization and transport associated with magnetic dipolarizations. Geophys. Res. Lett. 41, 5717–5726. doi:10.1002/2014gl061209

CrossRef Full Text | Google Scholar

Panasyuk, M. I., Zhukova, E. I., Kalegaev, V. V., Malova, H. V., Popov, V. Y., Vlasova, N. A., et al. (2021). Earth’s magnetotail as the reservoir of accelerated single-and multicharged oxygen ions replenishing radiation belts. J. Geophys. Res. Space Phys. 126, e2020JA028217. doi:10.1029/2020ja028217

CrossRef Full Text | Google Scholar

Pandya, M., Veenadhari, B., Nosé, M., Kumar, S., Reeves, G. D., and Lui, A. (2018). Characteristics of storm time ion composition in the near-earth plasma sheet using geotail and rbsp measurements. Earth, Planets Space 70, 203–216. doi:10.1186/s40623-018-0977-3

CrossRef Full Text | Google Scholar

Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 199, 331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

Runov, A., Angelopoulos, V., Artemyev, A., Birn, J., Pritchett, P., and Zhou, X.-Z. (2017). Characteristics of ion distribution functions in dipolarizing flux bundles: event studies. J. Geophys. Res. Space Phys. 122, 5965–5978. doi:10.1002/2017ja024010

CrossRef Full Text | Google Scholar

Runov, A., Angelopoulos, V., Zhou, X.-Z., Zhang, X.-J., Li, S., Plaschke, F., et al. (2011). A themis multicase study of dipolarization fronts in the magnetotail plasma sheet. J. Geophys. Res. Space Phys. 116. doi:10.1029/2010ja016316

CrossRef Full Text | Google Scholar

Russell, C., Anderson, B., Baumjohann, W., Bromund, K., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/978-94-024-0861-4_8

CrossRef Full Text | Google Scholar

Russell, C., and McPherron, R. (1973). The magnetotail and substorms. Space Sci. Rev. 15, 205–266. doi:10.1007/bf00169321

CrossRef Full Text | Google Scholar

Schmid, D., Volwerk, M., Nakamura, R., Baumjohann, W., and Heyn, M. (2011). A statistical and event study of magnetotail dipolarization fronts. Ann. Geophys. 29, 1537–1547. doi:10.5194/angeo-29-1537-2011

CrossRef Full Text | Google Scholar

Sergeev, V., Angelopoulos, V., Apatenkov, S., Bonnell, J., Ergun, R., Nakamura, R., et al. (2009). Kinetic structure of the sharp injection/dipolarization front in the flow-braking region. Geophys. Res. Lett. 36. doi:10.1029/2009gl040658

CrossRef Full Text | Google Scholar

Speiser, T. (1965). Particle trajectories in model current sheets: 1. analytical solutions. J. Geophys. Res. 70, 4219–4226. doi:10.1029/jz070i017p04219

CrossRef Full Text | Google Scholar

Torbert, R., Russell, C., Magnes, W., Ergun, R., Lindqvist, P.-A., LeContel, O., et al. (2016). The fields instrument suite on mms: scientific objectives, measurements, and data products. Space Sci. Rev. 199, 105–135. doi:10.1007/s11214-014-0109-8

CrossRef Full Text | Google Scholar

Wang, J., Cao, J., Fu, H., Liu, W., and Lu, S. (2017). Enhancement of oxygen in the magnetic island associated with dipolarization fronts. J. Geophys. Res. Space Phys. 122, 185–193. doi:10.1002/2016ja023019

CrossRef Full Text | Google Scholar

Wiltberger, M., Lotko, W., Lyon, J., Damiano, P., and Merkin, V. (2010). Influence of cusp o+ outflow on magnetotail dynamics in a multifluid mhd model of the magnetosphere. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010ja015579

CrossRef Full Text | Google Scholar

Winglee, R. (2003). Circulation of ionospheric and solar wind particle populations during extended southward interplanetary magnetic field. J. Geophys. Res. Space Phys. 108. doi:10.1029/2002ja009819

CrossRef Full Text | Google Scholar

Wu, M., Lu, Q., Volwerk, M., Voeroes, Z., Zhang, T., Shan, L., et al. (2013). A statistical study of electron acceleration behind the dipolarization fronts in the magnetotail. J. Geophys. Res. Space Phys. 118, 4804–4810. doi:10.1002/jgra.50456

CrossRef Full Text | Google Scholar

Xiao, S., Zhang, T., Wang, G., Volwerk, M., Ge, Y., Schmid, D., et al. (2017). Occurrence rate of dipolarization fronts in the plasma sheet: cluster observations. Ann. Geophys. 35, 1015–1022. doi:10.5194/angeo-35-1015-2017

CrossRef Full Text | Google Scholar

Xu, Y., Fu, H., Norgren, C., Toledo-Redondo, S., Liu, C., and Dong, X. (2019). Ionospheric cold ions detected by mms behind dipolarization fronts. Geophys. Res. Lett. 46, 7883–7892. doi:10.1029/2019gl083885

CrossRef Full Text | Google Scholar

Yau, A., Shelley, E., Peterson, W., and Lenchyshyn, L. (1985). Energetic auroral and polar ion outflow at de 1 altitudes: Magnitude, composition, magnetic activity dependence, and long-term variations. J. Geophys. Res. Space Phys. 90, 8417–8432. doi:10.1029/ja090ia09p08417

CrossRef Full Text | Google Scholar

Young, D., Balsiger, H., and Geiss, J. (1982). Correlations of magnetospheric ion composition with geomagnetic and solar activity. J. Geophys. Res. Space Phys. 87, 9077–9096. doi:10.1029/ja087ia11p09077

CrossRef Full Text | Google Scholar

Young, D., Burch, J., Gomez, R., De Los Santos, A., Miller, G., Wilson, P., et al. (2016). Hot plasma composition analyzer for the magnetospheric multiscale mission. Space Sci. Rev. 199, 407–470. doi:10.1007/s11214-014-0119-6

CrossRef Full Text | Google Scholar

Yu, Y., and Ridley, A. J. (2013). Exploring the influence of ionospheric o+ outflow on magnetospheric dynamics: dependence on the source location. J. Geophys. Res. Space Phys. 118, 1711–1722. doi:10.1029/2012ja018411

CrossRef Full Text | Google Scholar

Zhao, S., Fu, S., Sun, W., Parks, G., Zhou, X., Pu, Z., et al. (2018). Oxygen ion reflection at earthward propagating dipolarization fronts in the magnetotail. J. Geophys. Res. Space Phys. 123, 6277–6288. doi:10.1029/2018ja025689

CrossRef Full Text | Google Scholar

Zhou, X.-Z., Angelopoulos, V., Runov, A., Liu, J., and Ge, Y. (2012). Emergence of the active magnetotail plasma sheet boundary from transient, localized ion acceleration. J. Geophys. Res. Space Phys. 117. doi:10.1029/2012ja018171

CrossRef Full Text | Google Scholar

Zhou, X.-Z., Angelopoulos, V., Sergeev, V., and Runov, A. (2010). Accelerated ions ahead of earthward propagating dipolarization fronts. J. Geophys. Res. Space Phys. 115. doi:10.1029/2010ja015481

CrossRef Full Text | Google Scholar

Zhou, X.-Z., Runov, A., Angelopoulos, V., Artemyev, A. V., and Birn, J. (2018). On the acceleration and anisotropy of ions within magnetotail dipolarizing flux bundles. J. Geophys. Res. Space Phys. 123, 429–442. doi:10.1002/2017ja024901

CrossRef Full Text | Google Scholar

Zhou, X.-Z., Xu, Y., Runov, A., Liu, J., Artemyev, A. V., Angelopoulos, V., et al. (2019). On the origin of perpendicular ion anisotropy inside dipolarizing flux bundles. J. Geophys. Res. Space Phys. 124, 4009–4021. doi:10.1029/2019ja026519

CrossRef Full Text | Google Scholar