The toroidal curvatures of interplanetary coronal mass ejection flux ropes from multi-point observations

Interplanetary coronal mass ejections (ICMEs), characterized by their magnetic flux ropes, could potentially trigger geomagnetic disturbances. They have been attracting extensive investigations for decades. Despite numerous ICME models proposed in the past, few account for the curvature of the flux rope axis. In this study, we use conjunction observations from ACE, STEREO A and B, Juno and Solar Orbiter to analyze the evolution of the rope orientation of ICME flux ropes. Our findings indicate that the orientation of these ropes changes independently of the scale of the ropes or the distance they travel between spacecrafts. Furthermore, we estimate and compare the major radii of these flux ropes, uncovering a diverse range of distributions that do not seem to depend on the flux rope’s width. These results provide fresh insights and constraints for global ICME models, thereby contributing to the advancement of space weather research.

1 Introduction

A coronal mass ejection (CME) is a substantial expulsion of magnetized solar plasma, often carrying twisted magnetic fields in a flux-rope structure. When travelling through interplanetary space, it becomes an interplanetary coronal mass ejection (ICME). The configuration and evolution of flux ropes significantly influence their propagation and interaction with various obstacles, including Earth (Eastwood 2008).

Figure 2 by Zurbuchen and Richardson (2006) presents an illustrative depiction of an ICME, shaped in a torus. This torus is characterized by two key radii: The minor radius $\mathrm{r}$ corresponds to the rope’s cross-section, and the major radius ${\mathrm{R}}_{\mathrm{C}}$ corresponds to the radius of curvature of the torus axis. Typically, such observations are characterized by structures with their coherent magnetic field rotation, coupled with an increase in field strength in the middle (e.g., Klein and Burlaga, 1982; Gosling 1990). When the speed of an ICME is sufficiently high, an upstream interplanetary shock will be formed. These interplanetary shocks are crucial in the generation and evolution of solar wind turbulence (e.g., Zank et al., 2002; Hu et al., 2013; Adhikari et al., 2016).

Assuming a static, force-free and cylindrically symmetric flux rope, Goldstein (1983) and Lepping et al. (1990) developed the minimum variance analysis (MVA) technique to reconstruct ICMEs. This method involves determining the orientations of minimum, intermediate, and maximum variance in the magnetic field, with the axis orientation assumed to align with the direction of intermediate variance. This method is particularly valuable for single-spacecraft analyses, especially when magnetic field data is the only available information. When plasma thermal pressure measurements are available, Hu and Sonnerup (2002) introduced a novel method for determining the axis orientation of a cylindrical flux rope by balancing the transverse pressure. This technique, later referred as HS2002, shows that the axis orientations derived from MVA and HS2002 are generally similar, especially when the spacecraft’s impact parameters are small. Even when a spacecraft passes near the edge of the flux rope, the deviation in the MVA result remains relatively small, with a maximum deviation of up to 20° from the “true” direction.

Once the axis of a flux rope is determined, its geometry can be modeled. Early models envisioned flux ropes as force-free circular cylinders with infinitely long axes (e.g., Lundquist 1951; Burlaga et al., 1981; Lepping et al., 1990). Subsequently, magnetohydrostatic force balance models were introduced (e.g., Hu and Sonnerup, 2002; Hidalgo et al., 2002; Hu 2017). More recent models, such as those produced by Nieves-Chinchilla et al. (2016) and Nieves-Chinchilla et al. (2018) have incorporated polynomial representation for current density and employed cylinders with elliptical cross sections.

In addition to two-dimensional cross-section models assuming zero gradient along the rope axis, there are models accounting for the curvature ${\mathrm{R}}_{\mathrm{C}}^{-1}$ of the flux rope axis. For instance, Hidalgo et al. (2000) and Hidalgo (2013), considered a toroidal flux rope with a major diameter corresponding to the Sun-spacecraft distance. Nieves-Chinchilla et al. (2023) also adopted a toroidal geometry but chose the minor radius to estimate the major radius: ${\mathrm{R}}_{\mathrm{C}}=1.5\sim 2.5\mathrm{r}$. However, the major radius remains not constrained in single spacecraft observations.

In reality, the coherence of ICMEs is maintained within approximately 0.3AU (Owens et al., 2017). As these ICMEs travel towards 1AU, their shape and orientation of ICMEs can undergo substantial changes due to interactions with other ICMEs (Rollett et al., 2014) or ambient solar wind (e.g., Cargill et al., 1995, Cargill et al., 1996, Cargill et al., 2000, Cargill and Schmidt, 2002; Farrugia et al., 2005; Owens et al., 2006; Savani et al., 2010; Wang et al., 2014; Chi et al., 2021). Consequently, in situ observations play a crucial role in accurately reconstructing the three-dimension structure of the ICMEs.

Now, with numerous spacecraft observing the inner heliosphere, more information regarding the three-dimensional configuration of ICMEs can be obtained, albeit with some challenges posed by their time evolution (Foullon et al., 2007, Good et al., 2018). Notably, studies by Farrugia et al. (2011) and Möstl et al. (2012) leveraged multiple spacecraft observations to calculate the rope orientations at different points and noticed variations that may be associated with the curvature of the rope axis. In this study, we meticulously select ICMEs observed by multiple spacecraft with small longitudinal separations around the Earth to elucidate the spatial variation of the flux rope axis and subsequently infer the major radius.

2 Data

This study utilizes data from ACE, STEREO A and B, Juno and Solar Orbiter (SO). Specifically, magnetometer data at 1 Hz from ACE spanning from 2007 to 2021 (Smith et al., 1998), at 8 Hz from STEREO A/B from 2007 to 2008 (Acuũa et al., 2008) and at 1-min resolution from SO from 2020 to 2021 (Horbury et al., 2020) are accessible on the Coordinate Data Analysis Web (CDAWeb). Meanwhile, the 1 Hz magnetic field data from Juno during its cruise phase from 2011 to 2012 (Connerney et al., 2017) can be downloaded from the Planetary Data System (PDS). The observation period is selected based on when the spacecraft are in close proximity to ACE. During the specified timeframe, 64-s plasma data from ACE (McComas et al., 1998), and 1-min plasma data STEREO A/B (Galvin et al., 2008) are also available on CDAWeb.

In our investigation, four coordinate systems are used: the spacecraft-centered Radial Tangential Normal (RTN) coordinate system where ACE, STEREO A and B, and SO data are based on, the Spacecraft-Solar equator coordinate system (SE) where Juno data are based on, the Heliocentric Ecliptic (HE) coordinate system to reconstruct the ICME torus, and the spacecraft-centered MVA coordinate system where flux rope structure can be best illustrated.

We selected the MVA technique to analyze the magnetic field data, not only because Juno and SO had only magnetic field data available during the study period, but also because this method allows for better comparison of magnetic field profiles from different spacecraft. To ensure the robustness of the MVA technique, we also applied the HS2002 method to events detected by ACE and STEREO A/B, which have both magnetic and plasma data. We retained events where the deviation between the MVA and HS2002 axis orientations was less than 10°. For events detected by Juno and SO, which had only magnetic field data, we relied solely on the MVA technique. In this technique, a high ratio of intermediate to minimum variance eigenvalues indicates a small impact parameter, meaning the spacecraft’s path was close to the center of the structure. For the most reliable results, we concentrated on events with high-ratio eigenvalues in this study.

In addition to the aforementioned stringent selection criteria, we also require: 1) the longitudinal separation of the spacecraft is less than 15°; 2) the difference in the velocities between the leading and trailing boundaries of the flux rope is less than $50\text{km}/\mathrm{s}$; 3) similar magnetic field profiles in MVA coordinates; and (4) the ratio of the intermediate variance eigenvalue to the minimum variance eigen value is greater than 5. These criteria ensure minimal expansion of the flux ropes and consistent impact parameters between the conjunction spacecraft, thereby warranting accurate estimations of the rope’s orientations. In total, nine conjunction events were identified by cross-referencing the ACE observation with the STEREO event list (https://stereo-dev.epss.ucla.edu/media/ICMEs.pdf), the SO event list (https://figshare.com/articles/dataset/HELCATS_Interplanetary_Coronal_Mass_Ejection_Catalog_v2_0/6356420?file=40241752), and the Juno ICME list (Davies et al., 2021), as summarized in Table 1.

Table 1

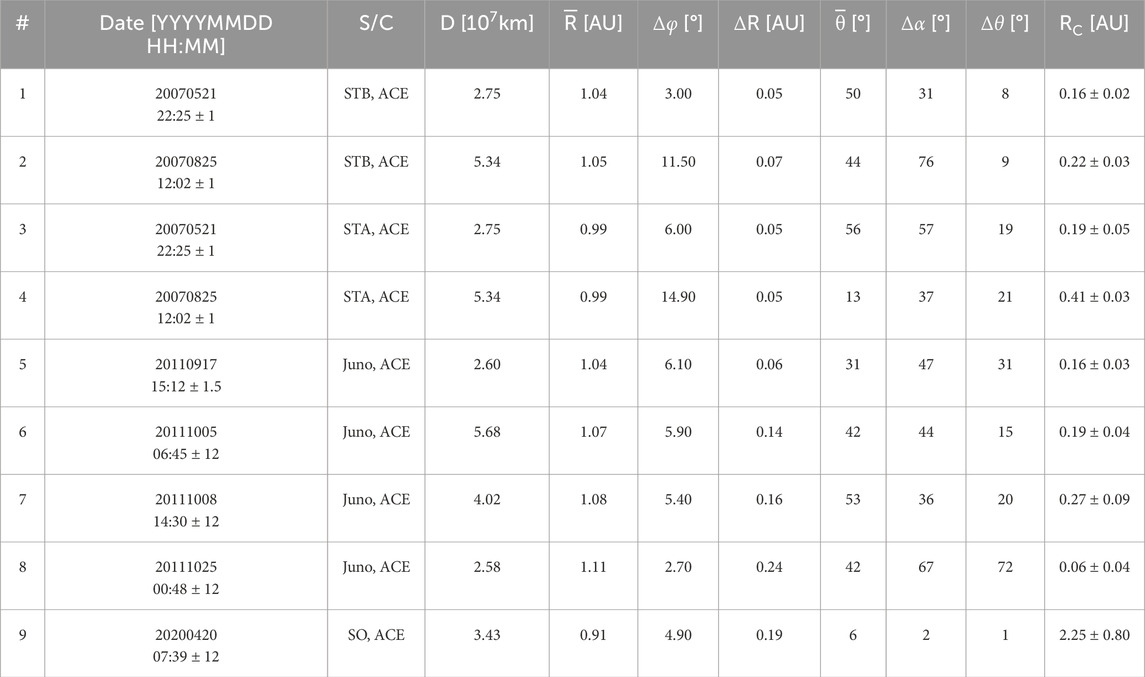
Table 1. Event list of the ICMEs investigated in this study. The flux rope date and time (arrival time at ACE), detected spacecraft, the diameter ($\mathrm{D}$), average heliocentric distance ($\overline{\mathrm{R}}$), longitudinal separation ($\Delta \phi$), heliocentric distance difference ($\Delta \mathrm{R}$) between the two spacecraft, the average inclination of the flux rope ($\overline{\mathrm{\theta }}$), the difference between rope orientation calculated from two spacecraft observations ($\Delta \alpha$ and $\Delta \theta$) and major radius (${\mathrm{R}}_{\mathrm{C}}$) are listed. The uncertainties associated with ${\mathrm{R}}_{\mathrm{C}}$ are estimated based on error propagation technique.

To determine the boundaries of the flux rope embedded within each ICME, we identify an increase in magnetic field strength compared to the background, accompanied by a smooth rotation in the field components (Zurbuchen and Richardson 2006) (e.g., the case in Figure 2B). When plasma data is available, we utilize the criteria summarized by Wang et al. (2014): 1) a decrease in bulk flow velocity; 2) the presence of bidirectional streaming of suprathermal electrons; 3) a decrease in proton temperature; and 4) low proton beta.

During the period of interest, we analyze the 64-s ACE/SWE and 1-min STEREO/PLASTIC plasma data to determine the boundaries of the flux rope (not shown). This introduces approximately 1min uncertainties in the start/end time. In cases where there is a data gap in the 64-s ACE/SWE data, we refer to the 12-min ACE/SWI data and introduce a 12-min uncertainty. For event #5, no plasma data from ACE is available, so we consult the 94-s Wind plasma data (Ogilvie et al., 1995), which introduces approximately 1.5 min uncertainty. To assess whether these uncertainties significantly influence our results, we test all cases and find that a 10-min change in the start/end points, when applied to a flux rope lasting tens of hours, does not significantly impact the statistical results. Additionally, we use the calculated diameter in HS2002 to estimate the “minor” diameter of the flux rope (D).

Parameters for the nine events are provided in Table 1. For event #1, 2, 3, and 4, D is the averaged HS2002 result from ACE, STEREO A/B results. For the rest events, D is the HS2002 result from ACE. In the HE coordinate system, the longitudinal separations ($\Delta \phi$) between the conjunction spacecraft range from 2.70° to 14.90° in longitude, and the radial distance ($\Delta \mathrm{R}$) varies between 0.05AU and 0.24AU. These values are comparable to the radial scale of the ICMEs at 1AU (Hidalgo et al., 2000), making them suitable for this study.

Event #9 is shown in Figure 1A: Both ACE and SO simultaneously detected an ICME when two spacecraft were radially separated by 0.19AU ($\Delta \mathrm{R}$) and longitudinally apart by 4.90° ($\Delta \phi$). The SO data have been time-shifted by 21.23 h to maximize the correlation coefficient in field strength. This ICME drives an interplanetary shock in front of it and the turbulence and wave transmission at that shock has been extensively studied by Zhao et al. (2021). As Figure 1A shows, ACE spent a longer time in the sheath region, but both spacecraft spent comparable time in the flux rope. In addition, we utilize the time delay between observations to estimate the velocity at the leading and trailing boundaries of the flux rope and find that the difference in the velocities between the two boundaries is approximately 25 km/s. This result indicates a negligible change in the diameter of the flux rope. As Figure 1A shows, even in the original RTN coordinate system, the structures in ACE and SO data are highly comparable. Therefore, we suggest that both spacecraft observed similar regions with similar impact parameters. During this ICME, the Br component varies the least, the Bt component is enhanced, and the Bn component smoothly rotates from negative to positive. This suggests that the flux rope’s axis is mainly in the tangential direction in the original RTN coordinate and consequently azimuthal in the HE coordinates.

Figure 1

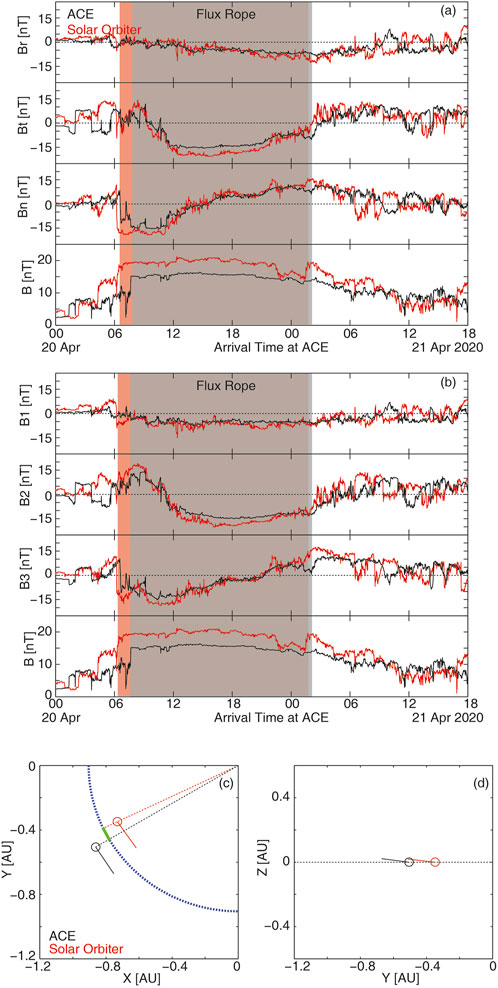
Figure 1. Magnetic field data of an ICME detected by ACE and SO. The SO data are shifted by 21.23 h. (A) Magnetic field profiles in the RTN coordinate system; (B) in the MVA coordinate system (B1, B2 and B3 represent the minimum, intermediate and maximum components, respectively) and (C, D) flux tube orientations in HE coordinates. In (A) and (B), the different shadings mark the flux rope detected by different spacecraft. In (C), the blue dashed line and green solid line represent circular arcs with a radius of $\overline{\mathrm{R}}$ and ${\mathrm{R}}_{\mathrm{C}}$, respectively.

For ACE and SO observations, the ratio of intermediate to minimum variance eigenvalues is 39.8 and 18.4, respectively. This substantial ratio indicates small impact parameters for both spacecraft (Imber et al., 2014), with the MVA technique providing a rope orientation estimated closely aligned with the “true” value (Hu & Sonnerup, 2002). Figure 1B displays the magnetic field in the MVA coordinate system from both spacecraft. Since the MVA technique has a 180-degree degeneracy, we choose the direction in which the observations from the two spacecraft are most similar. Figures 1C, D show the projected rope directions (intermediate variance direction “2”) from both sites in X-Y and Y-Z planes (HE coordinates). As anticipated, the axis primarily aligns with the azimuthal direction. The inclination angle in HE coordinates, averaged between the two spacecraft, is $\overline{\mathrm{\theta }}=6°$. The difference between the rope orientations calculated from the two spacecraft observations is minimal: $\Delta \alpha =2°$ in the ecliptic plane and $\Delta \theta =1°$ in the $z_{HE}$ direction.

From the distinctions in measurements between the two spacecraft, we can calculate the major radius of the torus, ${\mathrm{R}}_{\mathrm{C}}$, assuming a toroidal shape in this region while ignoring the three-dimensional warping of the torus ring. Consequently, the azimuthal separation $\Delta \phi$ is proportional to the arc length of the torus (Figure 1C): $\frac{\Delta \alpha }{180}\mathrm{\pi }{\mathrm{R}}_{\mathrm{C}}=\frac{\Delta \phi }{180}\frac{\pi \overline{\mathrm{R}}}{\cos \overline{\theta }}$. Therefore, the radius of the torus is calculated as ${\mathrm{R}}_{\mathrm{C}}=\frac{\Delta \phi }{\Delta \alpha }\frac{\overline{\mathrm{R}}}{\cos \overline{\theta }}$. As anticipated, the calculated ${\mathrm{R}}_{\mathrm{C}}$ for event #9 is relatively large due to the similarity in tube orientations. The green line in Figure 1C depicts the axial geometry of the flux rope, derived from the ${\mathrm{R}}_{\mathrm{C}}$ values. The uncertainties arising from the boundary determination and rounding errors are propagated to the final results, as listed in Table 1.

Two more examples from Table 1 are illustrated in Figure 2. Figure 2A shows an ACE-Juno conjunction event (event # 5) in the MVA coordinate system. Here a time delay has been introduced to shift the Juno data to better illustrate the similarity between the flux rope from two spacecraft. Figure 2B features an ICME detected by three spacecraft (events # 1 and 3) simultaneously, which we designate as ACE-STEREO A and ACE-STEREO B conjunction events, respectively. Another three-spacecraft conjunction event observed on 25 August 2011, is registered in the same manner (identified as #2 and #4 in Table 1). Notably, the event in Figure 2B has been the subject of extensive research (e.g., Liu et al., 2008; Möstl et al., 2009; Kilpua et al., 2009; Mulligan et al., 2013; Hu 2021). Both Kilpua et al. (2009) and Mulligan et al. (2013) suggested that STEREO A had a grazing encounter with the ICME. After removing two discontinuities embedded in the flux rope observed by STEREO A on 22 May (from 0113 to 0147UT and from 0504 to 0527UT), introducing appropriate time adjustments, and the application of the MVA technique, magnetic field profiles vary in the same trend. MVA calculations for the STEREO A data also satisfied our eigenvalue criterion, justifying the inclusion of this event in our analysis.

Figure 2

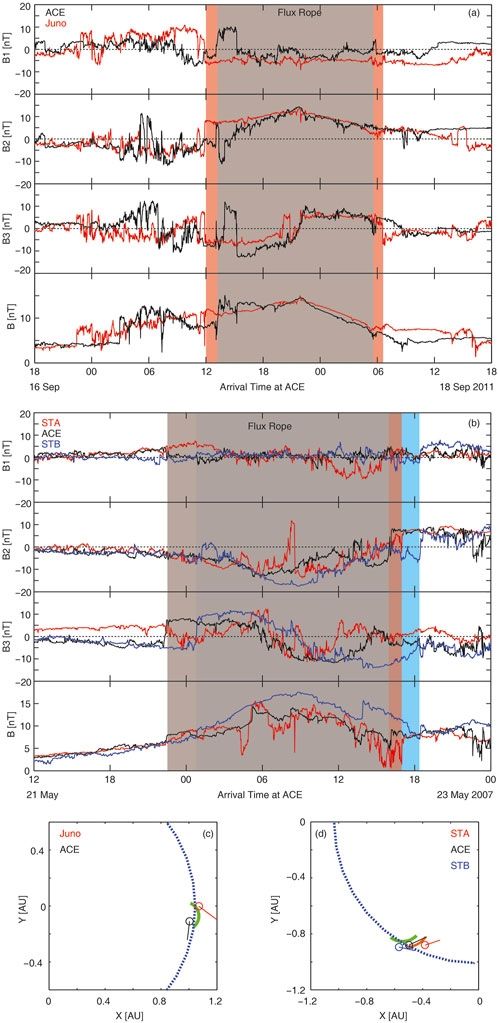
Figure 2. Magnetic field profiles of three ICME conjunction events in the MVA coordinate system. Panel (A) depicts event #5, while panel (B) displays events #1 and #3. The shadings mark the flux ropes. Panels (C) and (D) are in the same format as in Figure 1C. Green and orange solid lines in (D) indicate circular arcs with a radius of the ${\mathrm{R}}_{\mathrm{C}}$ calculated from STB-ACE and STA-ACE conjunctions, respectively.

For each event, we calculated the relevant parameters and listed them in Table 1. We find that the median value of $\Delta \alpha$ and $\Delta \theta$ is 44° and 20°, respectively. Additionally, the last column of Table 1 indicates that the toroidal radius (${\mathrm{R}}_{\mathrm{C}}$) for most conjunction events is less than 0.5AU (Hidalgo et al., 2000).

3 Global properties

In a prior study by Kilpua et al. (2009), our event #1, which corresponds to the STEREO event in their analysis, along with a subsequent ICME (not included in this study due to the limited impact parameter), were examined. The authors found that even with small separation angles between spacecraft, flux ropes can exhibit significant differences. They proposed that these differences may be attributed to the high inclination angle of the flux rope axis. With nine reliable conjunction events at our disposal, we embark on a systematic exploration of rope orientations from multi-site observations.

Figure 3 presents a comparison of variance in rope orientations, encompassing azimuthal ($\Delta \alpha$) and inclination ($\Delta \theta$) angles calculated from ACE and another paired spacecraft observations. These angles are plotted against several parameters: the minor diameter of the flux rope $\mathrm{D}$, the radial separation between spacecraft $\Delta \mathrm{R}$, the azimuthal separation $\Delta \phi$, and the inclination of the flux rope axis $\overline{\mathrm{\theta }}$. The minor diameter of the rope ($\mathrm{D}$), exhibits the highest level of uncertainty, stemming from the selection of the start/end times. However, introducing a 10-min change in the start/end points does not alter the results significantly. Therefore, we include this comparison in our statistical analysis.

Figure 3

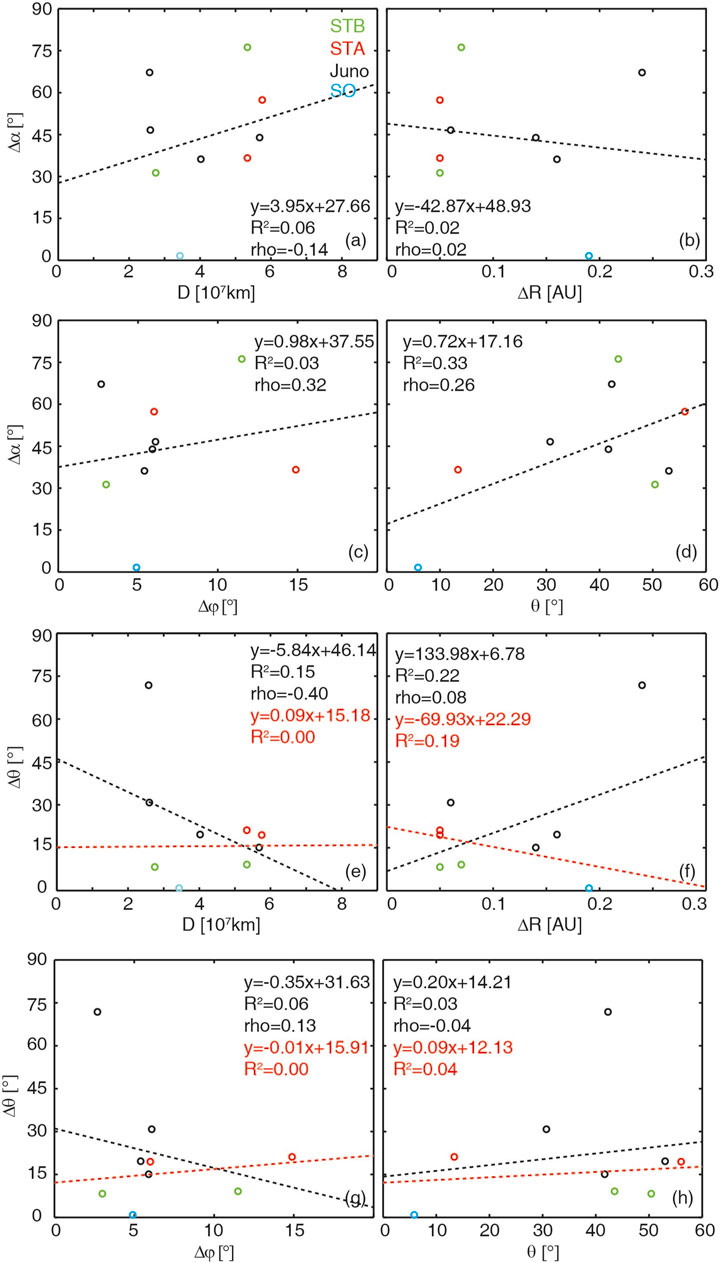
Figure 3. Azimuthal axis difference $\Delta \alpha$ from different spacecraft (color-coded circles) as functions of (A) minor diameter of the flux rope, (B) spacecraft separation in the radial distance, (C) in azimuthal direction and (D) inclination of the flux ropes. Panels (E–H) show the vertical axis difference $\Delta \theta$ as functions of the above parameters. The black dotted lines represent linear fits of all the data with the formula and the coefficient of determination (${\mathrm{R}}^2$) displayed. The Spearman correlation coefficient (rho) are also listed. The red dotted lines indicate linear fits excluding event #8 (the highest point).

As depicted in Figures 3A–D, the data points exhibit a considerable dispersion, and both the coefficients of determination (${\mathrm{R}}^2$) from a linear fit based on the least-squares method and the Spearman correlation coefficient (rho), in general, are notably low. The most significant correlation, with a coefficient of 0.33 (Figure 3D), suggests that as the inclination increases, the rope orientation tends to differ among different observation sites. This observation aligns with the findings of Kilpua et al. (2009), reinforcing the notion that in highly inclined flux ropes, azimuthally aligned spacecraft may observe similar regions but find different rope orientations.

Another notable event, event #8, stands out as having experienced a vertical change in rope orientation exceeding 45° between two sites. Whether we consider this case or not, $\Delta \theta$ does not exhibit a significant correlation with the flux rope minor diameter $\mathrm{D}$, spacecraft separation, and flux rope inclination, as shown in Figure 3.

Excluding event #8 from our analysis due to its unique rope orientation change from the ecliptic plane, the remaining eight toroidal radius values (${\mathrm{R}}_{\mathrm{C}}$) are presented as a function of the minor diameter of the flux rope $\mathrm{D}$ in Figure 4. Event #9 exhibits an unusually high toroidal radius due to its small $\Delta \alpha$. When this data point is omitted, the coefficient of determination of the linear fit remains low, and even lower ($0.01$, not shown here) when event #9 is included. This suggests that the toroidal radius is not influenced by the scale of the flux rope.

Figure 4

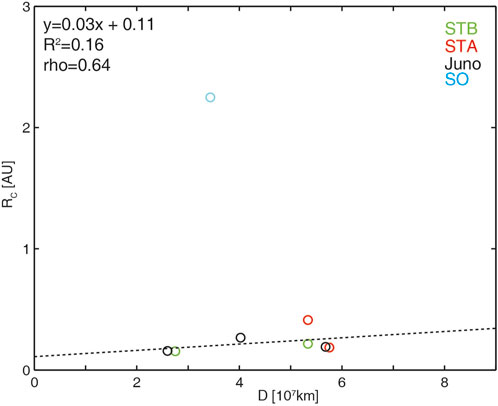
Figure 4. The toroidal radius of the ICME-related flux ropes as a function of the minor diameter of the flux rope. The black line is a linear fit without event #9 data. The formula, coefficient of determination and Spearman correlation coefficient are also shown in the figure.

4 Discussion and conclusion

According to our estimates, the median toroidal radius of ICME-related flux ropes is approximately 0.19AU (excluding event #8). This value is notably smaller than the assumption (0.5AU) made by Hidalgo et al. (2000). On the other hand, the ratio of the major radii (${\mathrm{R}}_{\mathrm{C}}$) to their flux rope cross-section radius varies from 0.7 to 19.6, with a median value of 1.84. This range encompasses the value of 1.5–2.5 used by Nieves-Chinchilla et al. (2023).

Events #8 and #9 are exceptional cases in our study. These events exhibit moderate minor diameter of the flux rope, substantial radial separation, and minimal azimuthal separation between observation sites. Despite excluding the influence of flux rope scale and spacecraft separation, event #9, which was detected upstream of the Earth by both spacecraft, experiences the least rope orientation change from site to site, whereas event #8, with Juno downstream of the Earth, exhibits the most significant change. Although the likelihood of Earth’s influence on ICMEs is theoretically low due to the significant size difference, further investigation is warranted. In the following paragraph, we particularly examine the 3-spacecraft conjunction events that happened to be situated across the Earth.

Since the flux rope evolves as it moves from one point to another, the calculated ${\mathrm{R}}_{\mathrm{C}}$ represents an average value between the two points. Comparing event #1 to #3 and #2 to #4, we observe that the toroidal radius ${\mathrm{R}}_{\mathrm{C}}$ is 0.03AU and 0.19AU larger in the ACE-STEREO A conjunction (both upstream of the Earth) than in the ACE-STEREO B conjunction. For all three events (20070521, 20070825, and 20111025) with one spacecraft downstream of the Earth, ${\mathrm{R}}_{\mathrm{C}}$ is found smaller than in the remaining events. These differences imply that downstream of the Earth, the flux rope’s axis may experience more pronounced curvature. While it is generally accepted that, compared to ICME-related flux ropes, which measure approximately ${10}^7$ km across, the terrestrial magnetosphere, at roughly ${10}^5$ km, is too small to significantly influence the ICMEs. Although the analysis of only three events does not provide substantial significant statistical evidence, the consistency observed across all three events suggests that the axes of these flux ropes may undergo some distortion after passing the Earth. This distortion could potentially be attributed to magnetic reconnection between the flux ropes and the Earth’s magnetosphere (Eastwood 2008). To further explore these speculations, more comprehensive studies involving additional observations and numerical simulations are necessary.

This study examines ICME-related flux ropes from conjunction observations and calculates their major radii. The results reveal that the orientation of the rope remains independent of the ICME’s scale and the separation between observation sites. By assuming a toroidal-shape for the flux rope, we estimate their toroidal radii, which provides additional constraints on existing flux rope models.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: Data from ACE, STEREO and SO are available on the NASA Space Physics Data Facility CDAWeb (https://cdaweb.gsfc.nasa.gov/index.html). Data from Juno are available on the Planetary Data System (https://pds-ppi.igpp.ucla.edu/search/?t=Solar%20Wind&sc=Juno&facet=SPACECRAFT_NAME&depth=1).

Author contributions

HL: Writing–original draft. Y-DJ: Writing–review and editing. LJ: Writing–review and editing. CR: Writing–review and editing. XB-C: Writing–review and editing. JL: Writing–review and editing. CZ: Writing–review and editing. JC: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Supported by the National Natural Science Foundation of China (Grant No. 42074209) and Pinghu Laboratory Open Fund.

Acknowledgments

The authors thank the ACE, STEREO, SO, and Juno teams for making their data available. The authors also express their gratitude to C. Möstl and C. J. Farrugia for providing the open-source code for the HS2002 method.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor CS declared a past co-authorship with the authors.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acuña, M. H., Curtis, D., Scheifele, J. L., Russell, C. T., Schroeder, P., Szabo, A., et al. (2008). The STEREO/IMPACT magnetic field experiment. Space Sci. Rev. 136, 203–226. doi:10.1007/s11214-007-9259-2

CrossRef Full Text | Google Scholar

Adhikari, L., Zank, G. P., Hunana, P., and Hu, Q. (2016). The interaction of turbulence with parallel and perpendicular shocks: theory and observations at 1 AU. Astrophy. J. 833 (2), 218. doi:10.3847/1538-4357/833/2/218

CrossRef Full Text | Google Scholar

Burlaga, L. F., Sittler, E., Mariani, F., and Schwenn, R. (1981). Magnetic loop behind an interplanetary shock: voyager, Helios and IMP-8 observations. J. Geophys. Res. 86, 6673–6684. doi:10.1029/ja086ia08p06673

CrossRef Full Text | Google Scholar

Cargill, P. J., Chen, J., Spicer, D. S., and Zalesak, S. T. (1995). Geometry of interplanetary magnetic clouds. Geophys. Res. Lett. 22, 647–650. doi:10.1029/95gl00013

CrossRef Full Text | Google Scholar

Cargill, P. J., Chen, J., Spicer, D. S., and Zalesak, S. T. (1996). Magnetohydrodynamic simulations of the motion of magnetic flux tubes through a magnetized plasma. J. Geophys. Res. 101, 4855–4870. doi:10.1029/95JA03769

CrossRef Full Text | Google Scholar

Cargill, P. J., Schmidt, J., Spicer, D. S., and Zalesak, S. T. (2000). The magnetic structure of over-expanding CMEs. J. Geophys. Res. 105, 7509. doi:10.1029/1999JA900479

CrossRef Full Text | Google Scholar

Cargill, P. J., and Schmidt, J. M. (2002). Modelling interplanetary CMEs using magnetohydrodynamic simulations. Ann. Geophys. 20 (7), 879–890. doi:10.5194/angeo-20-879-2002

CrossRef Full Text | Google Scholar

Chi, Y., Scott, C., Shen, C., Barnard, L., Owens, M., Xu, M., et al. (2021). Modeling the observed distortion of multiple (ghost) CME fronts in STEREO heliospheric imagers. Astrophys. J. Lett. 917, L16. doi:10.3847/2041-8213/ac1203

CrossRef Full Text | Google Scholar

Connerney, J. E. P., Benn, M., Bjarno, J. B., Denver, T., Espley, J., Jorgensen, J. L., et al. (2017). The Juno magnetic field investigation. Space Sci. Rev. 213 (1-4), 39–138. doi:10.1007/s11214-017-0334-z

CrossRef Full Text | Google Scholar

Davies, E. E., Forsyth, R. J., Winslow, R. M., Möstl, C., and Lugaz, N. A. (2021). A Catalog of Interplanetary Coronal Mass Ejections Observed by Juno between 1 and 5.4 au. Astrophys. J. 923, 136. doi:10.3847/1538-4357/ac2ccb

CrossRef Full Text | Google Scholar

Eastwood, J. P. (2008). The science of space weather. Philosophical Trans. R. Soc. A 366, 4489–4500. doi:10.1098/rsta.2008.0161

PubMed Abstract | CrossRef Full Text | Google Scholar

Farrugia, C. J., Berdichevsky, D. B., Möstl, C., Galvin, A. B., Leitner, M., Popecki, M. A., et al. (2011). Multiple, distant (40°) in situ observations of a magnetic cloud and a corotating interaction region complex. J. Atmos. Solar-Terrestrial Phys. 73 (10), 1254–1269. doi:10.1016/j.jastp.2010.09.011

CrossRef Full Text | Google Scholar

Farrugia, C. J., Matsui, H., Kucharek, H., Torbert, R. B., Smith, C. W., Jordanova, V. K., et al. (2005). Interplanetary coronal mass ejection and ambient interplanetary magnetic field correlations during the Sun-Earth connection events of October–November 2003. J. Geophys. Res. 110, A09S13. doi:10.1029/2004JA010968

CrossRef Full Text | Google Scholar

Foullon, C., Owen, C. J., Dasso, S., Green, L. M., Dandouras, I., Elliott, H. A., et al. (2007). Advancing in situ modeling of ICMEs: New techniques for new observations. Sol. Phys. 244, 139–165. doi:10.1007/s11207-007-0355-y

CrossRef Full Text | Google Scholar

Galvin, A. B., Kistler, L. M., Popecki, M. A., Farrugia, C. J., Simunac, K. D. C., Ellis, L., et al. (2008). The plasma and suprathermal ion composition (PLASTIC) investigation on the STEREO observatories. Space Sci. Rev. 136, 437–486. doi:10.1007/s11214-007-9296-x

CrossRef Full Text | Google Scholar

Goldstein, H. (1983). On the field configuration in magnetic clouds. Sol. Wind Five 2280, 731.

Google Scholar

Good, S. W., Forsyth, R. J., Eastwood, J. P., and Möstl, C. (2018). Correlation of ICME magnetic fields at radially aligned spacecraft. Sol. Phys. 293 (3), 52. doi:10.1007/s11207-018-1264-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Gosling, J. T. (1990). “Coronal mass ejections and magnetic flux ropes in interplanetary space,” in Physics of magnetic flux ropes. Editors C. T. Russell, L. C. Lee, and E. R. Priest, 343–364.

CrossRef Full Text | Google Scholar

Hidalgo, M. A. (2013). A global magnetic topology model for magnetic clouds. II. Astrophysical J. 766 (2), 125. doi:10.1088/0004-637x/766/2/125

CrossRef Full Text | Google Scholar

Hidalgo, M. A., Cid, C., Medina, J., and Viñas, A. F. (2000). A new model for the topology of magnetic clouds in the solar wind. Sol. Phys. 194, 165–174. doi:10.1023/a:1005206107017

CrossRef Full Text | Google Scholar

Hidalgo, M. A., Cid, C., Viñas, A. F., and Sequeiros, J. (2002). A non force-free approach to the topology of magnetic clouds in the solar wind. J. Geophys. Res. 107 (A1), 1002. doi:10.1029/2001JA900100

CrossRef Full Text | Google Scholar

Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., Bendyk, M., Brown, P., Hudson, R., et al. (2020). The solar orbiter magnetometer. Astronomy Astrophysics 642 (December), A9–A11. doi:10.1051/0004-6361/201937257

CrossRef Full Text | Google Scholar

Hu, Q. (2017). The Grad-Shafranov reconstruction in twenty years: 1996–2016. Sci. China Earth Sci. 60, 1466–1494. doi:10.1007/s11430-017-9067-2

CrossRef Full Text | Google Scholar

Hu, Q. (2021). Optimal fitting of the freidberg solution to in situ spacecraft measurements of magnetic clouds. Sol. Phys. 296, 101. doi:10.1007/s11207-021-01843-z

CrossRef Full Text | Google Scholar

Hu, Q., and Sonnerup, B. U. (2002). Reconstruction of magnetic clouds in the solar wind: orientations and configurations. J. Geophys. Res. 107 (A7), 1142. doi:10.1029/2001JA000293

CrossRef Full Text | Google Scholar

Hu, Q., Zank, G. P., Li, G., and Ao, X. (2013). A power spectral analysis of turbulence associated with interplanetary shock waves. AIP Conf. Proc. 1539, 175–178. doi:10.1063/1.4811016

CrossRef Full Text | Google Scholar

Imber, S. M., Slavin, J. A., Boardsen, S. A., Anderson, B. J., Korth, H., McNutt, Jr. R. L., et al. (2014). MESSENGER observations of large dayside flux transfer events: do they drive Mercury's substorm cycle? J. Geophys. Res. Space Phys. 119, 5613–5623. doi:10.1002/2014JA019884

CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Liewer, P. C., Farrugia, C., Luhmann, J. G., Möstl, C., Li, Y., et al. (2009). Multispacecraft observations of magnetic clouds and their solar origins between 19 and 23 May 2007. Sol. Phys. 254 (2), 325–344. doi:10.1007/s11207-008-9300-y

CrossRef Full Text | Google Scholar

Klein, L. W., and Burlaga, L. F. (1982). Interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 87, 613–624. doi:10.1029/ja087ia02p00613

CrossRef Full Text | Google Scholar

Lepping, R. P., Jones, J. A., and Burlaga, L. F. (1990). Magnetic field structure of interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 95 (A8), 11957–11965. doi:10.1029/JA095iA08p11957

CrossRef Full Text | Google Scholar

Liu, Y., Luhmann, J. G., Huttunen, K. E. J., Lin, R. P., Bale, S. D., Russell, C. T., et al. (2008). Reconstruction of the 2007 May 22 magnetic cloud: how much can we trust the flux-rope geometry of CMEs? Astrophysical J. 677 (2), L133–L136. doi:10.1086/587839

CrossRef Full Text | Google Scholar

Lundquist, S. (1951). On the stability of magneto-hydrostatic fields. Phys. Rev. 83, 307–311. doi:10.1103/physrev.83.307

CrossRef Full Text | Google Scholar

McComas, D. J., Bame, S. J., Barker, P., Feldman, W. C., Phillips, J. L., Riley, P., et al. (1998). Solar wind electron proton alpha monitor (SWEPAM) for the advanced composition explorer. Space Sci. Rev. 86 (1/4), 563–612. doi:10.1023/A:1005040232597

CrossRef Full Text | Google Scholar

Möstl, C., Farrugia, C. J., Kilpua, E. K. J., Jian, L. K., Liu, Y., Eastwood, J. P., et al. (2012). Multi-point shock and flux rope analysis of multiple interplanetary coronal mass ejections around 2010 August 1 in the inner heliosphere. Astrophysical J. 758, 10. doi:10.1088/0004-637X/758/1/10

CrossRef Full Text | Google Scholar

Möstl, C., Farrugia, C. J., Temmer, M., Miklenic, C., Veronig, A. M., Galvin, A. B., et al. (2009). Linking remote imagery of a coronal mass ejection to its in situ signatures at 1 AU. Astrophys. J. Lett. 705, L180–L185. doi:10.1088/0004-637X/705/2/L180

CrossRef Full Text | Google Scholar

Mulligan, T., Reinard, A. A., and Lynch, B. J. (2013). Advancing in situ modeling of ICMEs: New techniques for new observations. J. Geophys. Res. Space Phys. 118 (4), 1410–1427. doi:10.1002/jgra.50101

CrossRef Full Text | Google Scholar

Nieves-Chinchilla, T., Linton, M. G., Hidalgo, M. A., and Vourlidas, A. (2018). Elliptic-cylindrical analytical flux rope model for magnetic clouds. Astrophys. J. 861, 139. doi:10.3847/1538-4357/aac951

CrossRef Full Text | Google Scholar

Nieves-Chinchilla, T., Linton, M. G., Hidalgo, M. A., Vourlidas, A., Savani, N. P., Szabo, A., et al. (2016). A circular-cylindrical flux-rope analytical model for magnetic clouds. Astrophys. J. 823, 27. doi:10.3847/0004-637x/823/1/27

CrossRef Full Text | Google Scholar

Nieves-Chinchilla, T., Hidalgo, M. A., and Cremades, H. (2023). Distorted-toroidal flux rope model. Astrophys. J 947, 79. doi:10.3847/1538-4357/acb3c1

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, A comprehensive plasma instrument for the Wind spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326

CrossRef Full Text | Google Scholar

Owens, M. J., Lockwood, M., and Barnard, L. A. (2017). Coronal mass ejections are not coherent magnetohydrodynamic structures. Sci. Rep. 7, 4152. doi:10.1038/s41598-017-04546-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Owens, M. J., Merkin, V. G., and Riley, P. (2006). A kinematically distorted flux rope model for magnetic clouds. J. Geophys. Res. 111, A03104. doi:10.1029/2005JA011460

CrossRef Full Text | Google Scholar

Rollett, T., Mostl, C., Temmer, M., Frahm, R. A., Davies, J. A., Veronig, A. M., et al. (2014). Combined multipoint remote and in situ observations of the asymmetric evolution of A fast solar coronal mass ejection. Astrophys. J. Lett. 790 (7), L6. doi:10.1088/2041-8205/790/1/L6

CrossRef Full Text | Google Scholar

Savani, N. P., Owens, M. J., Rouillard, A. P., Forsyth, R. J., and Davies, J. A. (2010). Observational evidence of a coronal mass ejection distortion directly attributable to a structured solar wind. Astrophys. J. Lett. 714, L128–L132. doi:10.1088/2041-8205/714/1/L128

CrossRef Full Text | Google Scholar

Smith, C. W., L’Heureux, J., Ness, N. F., Acuña, M. H., Burlaga, L. F., and Scheifele, J. (1998). The ACE magnetic fields experiment. Space Sci. Rev. 86, 613–632. doi:10.1007/978-94-011-4762-0_21

CrossRef Full Text | Google Scholar

Wang, Y., Wang, B., Shen, C., Shen, F., and Lugaz, N. (2014). Deflected propagation of a coronal mass ejection from the corona to interplanetary space. J. Geophys. Res. Space Phys. 119, 5117–5132. doi:10.1002/2013JA019537

CrossRef Full Text | Google Scholar

Zank, G. P., Zhou, Y., Matthaeus, W. H., and Rice, W. K. M. (2002). The interaction of turbulence with shock waves: a basic model. Phys. Fluids 14 (11), 3766–3774. doi:10.1063/1.1507772

CrossRef Full Text | Google Scholar

Zhao, L.-L., Zank, G. P., He, J. S., Telloni, D., Hu, Q., Li, G., et al. (2021). Turbulence and wave transmission at an ICME-driven shock observed by the Solar Orbiter and Wind. Astronomy and Astrophys 656, A3. doi:10.1051/0004-6361/202140450

CrossRef Full Text | Google Scholar

Zurbuchen, T. H., and Richardson, I. G. (2006). In-situ solar wind and magnetic field signatures of interplanetary coronal mass ejections. Space Sci. Rev. 123 (1), 31–43. doi:10.1007/s11214-006-9010-4

CrossRef Full Text | Google Scholar