Deriving improved plasma fluid equations from collisional kinetic theory

Introduction: Developing a quantitative understanding of wave plasma processes in the lower ionosphere requires a reasonably accurate theoretical description of the underlying physical processes. For such a highly collisional plasma environment as the E-region ionosphere, kinetic theory represents the most accurate theoretical description of wave processes. For the analytical treatment, however, collisional kinetic theory is extremely complicated and succeeds only in a limited number of physical problems. To date, most research has applied oversimplified fluid models that lack a number of critical kinetic aspects, so the coefficients in the corresponding fluid equations are often accurate only to an order of magnitude.

Methods: This paper presents a derivation for the highly collisional, partially magnetized case relevant to E-region conditions, using methods of the collisional kinetic theory with a new set of analytic approximations.

Results: This derivation provides a more accurate reduction of the ion and, especially, electron kinetic equations to the corresponding 5-moment fluid equations. It results in a more accurate fluid model set of equations appropriate for most E-region problems.

Discussion: The results of this paper could be used for a routine practical analysis when working with actual data. The improved equations can also serve as a basis for more accurate plasma fluid computer simulations.

1 Introduction

At altitudes of the equatorial and high-latitude E-region ionospheres, the ionosphere is highly collisional in such a way that ions are almost demagnetized by their frequent collisions with the surrounding neutral molecules while electrons remain strongly magnetized. Strong DC electric fields perpendicular to the geomagnetic field cause electrojets and give rise to plasma instabilities whose nonlinear development produces plasma density irregularities that can be observed by radars and rockets.

Developing a quantitative understanding of wave plasma processes in the lower ionosphere requires an accurate theoretical description of the underlying physical processes. For such a dissipative environment, collisional plasma kinetic theory represents the most accurate theoretical description of wave processes. Particle-in-cell (PIC) simulations apply the kinetic approach as a comprehensive numeric experiment, but such massive computer simulations (Oppenheim and Dimant, 2004; Oppenheim et al., 2008; Oppenheim and Dimant, 2013; Oppenheim et al., 2020) are usually quite costly. In many cases, simple estimates and parameter dependencies provided by an analytic approach will suffice. For the analytical treatment, however, the collisional kinetic theory is extremely complicated and succeeds only in a limited number of physical problems. To date, most research has applied an oversimplified fluid model that lacks many critical kinetic aspects. These models mostly apply to weakly collisional conditions. The coefficients in the simple fluid equations are often accurate only to an order of magnitude because they were not obtained using the full kinetic theory of electron-neutral collisions. This paper presents the derivation of improved fluid equations for the highly collisional, partially magnetized case relevant to E-region conditions, starting from a more consistent kinetic approach. It provides more accurate values for the fluid model coefficients.

There are different approaches to analytically describing low-frequency plasma processes in the E-region ionosphere, including both the kinetic theory and fluid models. Traditionally, the kinetic theory of the Farley–Buneman (FB) instability applied an oversimplified Bhatnagar–Gross–Krook (BGK) collision operator (Bhatnagar et al., 1954). This operator does not follow from an accurate Boltzmann collision operator [except assuming special conditions (St-Maurice and Schunk, 1977)] but represents an artificial construct. It dramatically simplifies the analytical treatment and satisfies the particle number conservation and the momentum and energy balances (albeit under certain conditions; see below). This simplified approach is reasonably applicable to the description of the heavy ions, but it is totally unacceptable to the description of the light electrons (Dimant and Sudan, 1995a).

More accurate approaches to the kinetic description of electrons under conditions of the E-region wave processes, such as the FB instability, have been developed by a few research groups. Stubbe (1990) modified the BGK terms to allow for different rates of electron energy and momentum losses. This simple modification, however, does not follow from the Boltzmann operator, and its applicability for given physical conditions should be verified. Later, two independent research groups developed more sophisticated and accurate approaches. Kissack and collaborators (Kissack et al., 1995; 1997; 2008a; b) applied Grad’s method (Grad, 1949; Rodbard et al., 1995), while Dimant and Sudan (1995a) used an expansion in Legendre polynomials with respect to the angles in the velocity space (Gurevich, 1978; Allis, 1982). The latter kinetic approach has allowed the authors to predict a new electron thermal-driven instability in the lower-E/upper-D regions (Dimant and Sudan, 1995b; c), which has been later explained in terms of a much simpler fluid model (Dimant and Sudan, 1997). This effect has been verified by others (Robinson, 1998; St. -Maurice and Kissack, 2000). Later, a similar thermal-instability process has been suggested for ions (Kagan and Kelley, 2000; Dimant and Oppenheim, 2004; Dimant et al., 2023).

This paper presents a consistent reduction of the ion and electron kinetic equations to the 5-moment fluid equations by using a new set of analytic approximations. This derivation results in a more accurate fluid model appropriate for most E-region plasma problems. The main contribution of this work comes from relaxing the assumption of constant electron-neutral collision frequency and allowing significant deviations of the electron velocity distribution from the Maxwellian distribution (although the pitch-angle anisotropy of the electron distribution function always remains weak, as described in the text).

The results of this work could be used for a routine practical analysis when working with actual data. The improved equations can also serve as a basis for more accurate plasma fluid computer simulations. Concerning the latter, we note the following. These improved fluid equations include no Landau damping, so they cannot properly model the FB instability in the short-wavelength range of turbulence (of the order of the ion-neutral collisional mean free path and shorter), where this kinetic effect plays an important role. However, these improved fluid equations can successfully model plasma waves generated by the larger-scale gradient drift and thermal instabilities; see Dimant et al. (2023) and references therein. Even more so, as PIC simulations demonstrate (Oppenheim and Dimant, 2013), after the brief evolution of the FB instability to its dynamic nonlinear saturation, the energetically dominant part of the developed turbulence spectrum usually moves to longer wavelengths. In this later stage, the kinetic effects of Landau damping become less important, so the improved set of fluid equations could also be successfully employed for reasonably accurate modeling of the FB instability. A recent work has demonstrated the satisfactory applicability of fluid modeling to FB instability, both in the E-region ionosphere (Rojas et al., 2023) and in the solar chromosphere (Evans et al., 2023). Furthermore, the improved fluid equations can also model the dynamics of such plasma objects as quickly ionized chemically released gas clouds, sporadic E-layers, long-lived meteor plasma, etc.

The paper is organized as follows. Section 2 introduces the collisional kinetic equation and reviews the generic procedure for obtaining the moment equations. The collisional parts are not specified and remain in the general integral form. Section 3 describes the ion momentum equation obtained using the BGK collision model. The most important part is Section 4. It derives low-frequency electron fluid equations using a kinetic theory based on the efficient isotropization of the electron distribution function in the velocity space (Gurevich, 1978; Dimant and Sudan, 1995a). This requires a more detailed and sophisticated treatment. Section 4.1 derives the moment equations where the heat conductivity and frictional heating are given in terms of a still unspecified small directional part of the velocity distribution function. To illustrate major ideas of closing the derivation, Section 4.2 describes the simplest case of the constant (i.e., velocity-independent) kinetic collision parameters. Section 4.3 presents the general results obtained in detail in the Supplementary Appendix. Compared to the simplest electron fluid equations from Section 4.2, the general momentum and thermal-balance equations include more coefficients, as well as additional heat conductivity terms. The latter may appear collisionless, but they have arisen exclusively due to the velocity dependence of the kinetic electron-neutral collision frequency.

2 General kinetic framework

This section discusses a general approach to deriving the fluid model from the kinetic theory for any plasma particles. To avoid confusion, we will use the following nomenclature throughout this article. We denote various kinds of particles (charged or neutral) by Latin subscripts: $p$, $q$, etc., that stand for electrons $(e)$, ions of various kinds $(i)$, and neutrals $(n)$, while denoting vector components by Greek subscripts: $\alpha$, $\beta$, etc.

The non-relativistic kinetics of charged particles of the kind $p$ with the velocity ${\vec{v}}_p$ at a given location $\vec{r}$ and time $t$ are described by the Boltzmann kinetic equation,

${\partial }_t{f}_p+\nabla \cdot \left({\vec{v}}_p{f}_p\right)+{\partial }_{{\vec{v}}_p}\cdot \left[\frac{q_p}{m_p}\left(\vec{E}+{\vec{v}}_p\times \vec{B}\right)f_p\right]={\left(\frac{d{f}_p}{dt}\right)}_{col},(1)$

where $f_p({\vec{v}}_p,\vec{r},t)$ is the single-particle velocity distribution function. The left-hand side (LHS) of Equation (1) describes the collisionless (Vlasov) dynamics of the $p$-species charged particles in smoothed-over-many-particles electric $(\vec{E})$ and magnetic $(\vec{B})$ fields (for simplicity, we ignore here a gravity force). $q_p$ and $m_p$ are the $p$-particle charge and mass, respectively. The LHS of Equation (1) is intentionally written in a conservative (divergence) form that is more convenient for deriving the moment equations.

The right-hand side (RHS) of Equation (1), term ${(d{f}_p/dt)}_{col}={\sum }_q{S}_{pq}$, is the collisional operator describing binary collisions of the $p$-particles with all available kinds of charged and neutral particles denoted by $q$ (including the $p$-particles themselves). In the general case, the partial components $S_{pq}$ represent integral operators that involve products of $f_p({\vec{v}}_p,\vec{r},t)$ by $f_q({\vec{v}}_q,\vec{r},t)$. The partial operator $S_{qq}$ is quadratically nonlinear, while $S_{pq}$ with $p\ne q$ are linear with respect to $f_p$. The linear integral operators describe electron-neutral (e-n) and ion-neutral (i-n) collisions, while the quadratically nonlinear operators describe electron–electron (e-e) and ion–ion (i-i) collisions. The latter redistribute the energy and momentum within the same-species population. In the E-region ionosphere, where the Coulomb collisions are usually relatively weak, the e-e and i-i collisions can often be neglected. In a sufficiently dense day-time ionosphere, the e-e collisions can sometimes play a role, resulting mostly in the evolution of $f_e({\vec{v}}_q,\vec{r},t)$ to a “more Maxwellian” distribution. This only helps improve the applicability of the fluid model compared to the more complicated kinetic theory (Dimant and Sudan, 1995a).

The binary collisions can be either elastic or inelastic. Elastic collisions conserve the total kinetic energy, momentum, and angular momentum of the colliding pair. The corresponding partial collisional operator, $S_{pq}$, can be described by the well-known Boltzmann collision integral (Shkarofsky et al., 1966; Gurevich, 1978; Lifshitz and Pitaevskii, 1981; Schunk and Nagy, 2009; Khazanov, 2011). During an inelastic collision of a charged particle with a neutral particle, a fraction of the total kinetic energy goes to the excitation (de-excitation) of the neutral particle (or ion) or to the release of electrons via ionization. Inelastic processes in the lower ionosphere often involve molecular dissociation, recombination with ions, and electron attachment, accompanied by photon radiation or absorption. The complete kinetic description of all these processes is complicated. In many cases, however, inelastic collisions are close to elastic, and one can continue using Boltzmann’s integral with minor modifications (Gurevich, 1978; Shkarofsky et al., 1966). Kinetic Equation (1) with Boltzmann’s collision integral per se represents a significant simplification over the full multi-particle kinetics, but it still remains quite difficult for a mathematical treatment and requires further simplifications.

Being interested in the fluid-model equations that follow from kinetic Equation (1), we review the conventional approach to deriving equations for the lowest-order moments of the distribution function below. The material in this section will serve as a guide for more specific derivations of the following sections.

The three lowest-order velocity moments include the $p$-species particle density,

$n_p\left(\vec{r},t\right)\equiv \int f_p{d}^3{v}_p,(2)$

the mean fluid velocity,

${\vec{V}}_p\left(\vec{r},t\right)\equiv ⟨{\vec{v}}_p⟩=\frac{1}{n_p}\int {\vec{v}}_p{f}_p{d}^3{v}_p,(3)$

and the effective temperature,

$T_p\left(\vec{r},t\right)=\frac{m_p}{3}⟨{\left({\vec{v}}_p-{\vec{V}}_p\right)}^2⟩=\frac{m_p}{3n_p}\int {\left({\vec{v}}_p-{\vec{V}}_p\right)}^2{f}_p{d}^3{v}_p.(4)$

Note that in all equations, here and below, the temperatures are given in the energy units; that is, we imply that the temperatures in Kelvin (K) units are multiplied by the Boltzmann constant, although the K units will also be used in the text. The derivations below will also involve other velocity-averaged quantities defined by

$⟨\cdots ⟩\equiv \frac{1}{n_p}\int \left(\cdots \right)f_p{d}^3{v}_p.(5)$

Integrations in Equations 2–5 are performed over the entire 3-D velocity space.

First, we consider the particle number balance. Integrating Equation 1 over the particle velocities with $f_p\to 0$ as $v_p\equiv |{\vec{v}}_p|\to \infty$, we easily obtain the continuity equation for the $p$-particle fluid,

${\partial }_t{n}_p+\nabla \cdot \left(n_p{\vec{V}}_p\right)=\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p.(6)$

The RHS of Equation 6 includes various particle sources and losses, like ionization, recombination, and electron attachment. The collisions between the charged particles of the same species usually conserve the average particle number and, hence, do not contribute to the RHS of Equation 6.

Second, we obtain the momentum balance equation that involves the mean fluid drift velocity, ${\vec{V}}_p$. Integrating Equation 1 with the weighting function $m_p{\vec{v}}_p$, for a given vector-component $\alpha$ of the momentum density, we obtain

$\begin{array}{ll}\hfill & m_p{\partial }_t\left(n_p{V}_{p_{\alpha }}\right)+{\displaystyle \sum _{\beta =1}^3}{\partial }_{x_{\beta }}{\mathbf{P}}_{p_{\alpha \beta }}+m_p{\displaystyle \sum _{\beta =1}^3}{\partial }_{x_{\beta }}\left(n_p{V}_{p_{\alpha }}{V}_{p_{\beta }}\right)\hfill \\ \hfill & =q_p\left[E_{\alpha }+\frac{1}{c}{\left({\vec{V}}_p\times \vec{B}\right)}_{\alpha }\right]n_p+m_p\int v_{p_{\alpha }}{\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,\hfill \end{array}(7)$

where ${\mathbf{P}}_p$ is the total pressure tensor with vector components defined as

${\mathbf{P}}_{p_{\alpha \beta }}\equiv m_p\int \left(v_{p_{\alpha }}-V_{p_{\alpha }}\right)\left(v_{p_{\beta }}-V_{p_{\beta }}\right)f_p{d}^3{v}_p.(8)$

It combines the isotropic pressure, $P_p{\delta }_{mn}$ (${\delta }_{mn}=1$ if $m=n$; otherwise${\delta }_{mn}=0$), $P_p=n_p{T}_p$, with the viscosity tensor, ${\mathbf{\Pi }}_{p_{\alpha \beta }}\equiv {\mathbf{P}}_{p_{\alpha \beta }}-P_p{\delta }_{\alpha \beta }$. Equation 7 includes momentum changes due to various average forces and those caused by particle density variations. To exclude the latter and separate the net effect of the total force, we multiply Equation 6 by $m_p{\vec{V}}_p$ and subtract the resultant equation from Equation 7. This yields the conventional momentum balance equation,

$m_p{n}_p\frac{D_p{\vec{V}}_p}{Dt}=q_p{n}_p\left[\vec{E}+\frac{1}{c}\left({\vec{V}}_p\times \vec{B}\right)\right]-\nabla \cdot {\mathbf{P}}_p+{\vec{R}}_p,(9)$

where $D_p/Dt\equiv {\partial }_t+{\vec{V}}_p\cdot \nabla$ is the convective (also called substantial or material) derivative for the average $p$-particle flow and

${\vec{R}}_p\equiv m_p\int \left({\vec{v}}_p-{\vec{V}}_p\right){\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{\mathit{v}}_p.(10)$

Here and below, the “dot”-products of a vector, $\vec{a}$, with a two-component tensor, $\mathbf{A}$, depending on the multiplier order, denote vectors with the components ${\left(\vec{a}\cdot \mathbf{A}\right)}_{\alpha }\equiv {\sum }_{\beta =1}^3{a}_{\beta }{\mathbf{A}}_{\beta \alpha }$ or ${\left(\mathbf{A}\cdot \vec{a}\right)}_{\alpha }\equiv {\sum }_{\beta =1}^3{\mathbf{A}}_{\alpha \beta }{a}_{\beta }$. The tensor divergence, $\nabla \cdot {\mathbf{P}}_p=\nabla P_p+\nabla \cdot {\mathbf{\Pi }}_p$, represents a vector which uses the obvious symmetry ${\mathbf{P}}_{p_{\alpha \beta }}={\mathbf{P}}_{p_{\beta \alpha }}$ following from Equation 8. The RHS of Equation 9 includes all smooth forces acting on the average particle flow of the charged particles, such as the total Lorentz force, pressure gradient, and total friction, ${\vec{R}}_p$. The latter is associated with collisions of the given $p$-particles with all other charged or neutral particles. It includes no momentum exchange between the same-species particles because their mutual collisions automatically conserve the total momentum, $\int {\vec{v}}_p{S}_{pp}{d}^3{v}_p=0$.

Third, to obtain the total energy balance equation, we integrate Equation 1 with the weighting function $m_p{v}_p^2/2$ and obtain

${\partial }_t{\mathcal{E}}_p+\nabla \cdot \int \frac{m_p{v}_p^2}{2}{\vec{v}}_p{f}_p{d}^3{v}_p={\vec{j}}_p\cdot \vec{E}+\frac{m_p}{2}\int v_p^2{\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,(11)$

where ${\mathcal{E}}_p$ is the $p$-species average kinetic energy density and ${\vec{j}}_p$ is their electric current density,

${\mathcal{E}}_p\equiv \int \frac{m_p{v}_p^2}{2}{f}_p{d}^3{v}_p,{\vec{j}}_p\equiv q_p{n}_p{\vec{V}}_p.(12)$

Note that the particle gyromotion does not contribute to the kinetic energy balance. Before proceeding, we separate the mean drift velocity ${\vec{V}}_p$ from the kinetic particle velocity ${\vec{v}}_p$ so that (11) becomes

$\begin{array}{ll}\hfill & {\partial }_t\left[n_p\left(\frac{m_p{V}_p^2}{2}+\frac{3T_p}{2}\right)\right]\hfill \\ \hfill & +\nabla \cdot \left[n_p\left(\frac{m_p{V}_p^2}{2}+\frac{5T_p}{2}\right){\vec{V}}_p+{\mathbf{\Pi }}_p\cdot {\vec{V}}_p+\frac{n_p{m}_p}{2}⟨{\left({\vec{v}}_p-{\vec{V}}_p\right)}^3⟩\right]\hfill \\ \hfill & ={\vec{j}}_p\cdot \vec{E}+{\vec{V}}_p\cdot {\vec{R}}_p+\frac{m_p}{2}\int {\left({\vec{v}}_p-{\vec{V}}_p\right)}^2{\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p\hfill \\ \hfill & +\frac{m_p{V}_p^2}{2}\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,\hfill \end{array}(13)$

where ${\left({\vec{v}}_p-{\vec{V}}_p\right)}^3={\left|{\vec{v}}_p-{\vec{V}}_p\right|}^2\left({\vec{v}}_p-{\vec{V}}_p\right)$. Equation 13 describes dynamic variations of the total energy density. It includes a part associated with the average fluid motion, $n_p{m}_p{V}_p^2/2$, and the internal thermal energy, $n_p{T}_p$. To extract the equation exclusively for the particle temperature, $T_p$, we multiply Equation 6 by $\left(m_p{V}_p^2/2+3T_p/2\right)$, take the scalar product of Equation 9 with ${\vec{V}}_p$, and subtract the resultant two equations from Equation 13. This yields

$\begin{array}{ll}\hfill & \frac{3n_p}{2}\frac{D_p{T}_p}{Dt}+n_p{T}_p\nabla \cdot {\vec{V}}_p+{\mathbf{\Pi }}_p\cdot \nabla \cdot {\vec{V}}_p+\nabla \cdot \left[\frac{n_p{m}_p}{2}⟨{\left({\vec{v}}_p-{\vec{V}}_p\right)}^3⟩\right]\hfill \\ \hfill & =\frac{m_p}{2}\int {\left({\vec{v}}_p-{\vec{V}}_p\right)}^2{\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p+\left(\frac{m_p{V}_p^2}{2}-\frac{3T_p}{2}\right)\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,\hfill \end{array}(14)$

where ${\mathbf{\Pi }}_p\cdot \nabla \cdot {\vec{V}}_p\equiv {\sum }_{\alpha ,\beta =1}^3{\mathbf{\Pi }}_{p_{\alpha \beta }}{\nabla }_{\alpha }{\vec{V}}_{p_{\beta }}$. Note that after this step, the electric field has been eliminated from the energy-balance equation. This is a crucial step in deriving the proper form of the frictional heating, as described below.

Typically, equations like Equation 14 represent the final form of the thermal-balance equation. These equations are most convenient for calculations. In order to clarify the physical meaning of some terms, however, it is helpful to recast Equation 14 in a slightly different form. Rewriting the continuity Equation 6 as

$\frac{D_p{n}_p}{Dt}+n_p\nabla \cdot {\vec{V}}_p=\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,$

we recast the two first terms in the LHS of Equation 14 as

$\begin{array}{ll}\hfill \frac{3n_p}{2}\frac{D_p{T}_p}{Dt}+n_p{T}_p\nabla \cdot {\vec{V}}_p& =\frac{3n_p}{2}\frac{D_p{T}_p}{Dt}-T_p\frac{D_p{n}_p}{Dt}\hfill \\ \hfill & +T_p\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p\hfill \\ \hfill & =n_p{T}_p\frac{D_p{s}_p}{Dt}+T_p\int {\left(\frac{d{f}_p}{dt}\right)}_{col}{d}^3{v}_p,\hfill \end{array}(15)$

where $s_p\equiv \ln (T_p^{3/2}/n_p)=\ln (P_p^{3/2}/n_p^{5/2})$ represents the specific entropy of the $p$-species fluid (Braginskii, 1965) (for a single-atomic gas, this is the adiabatic coefficient $\gamma =5/3$). This recast allows interpreting $n_p{T}_p\nabla \cdot {\vec{V}}_p$ as the adiabatic heating (cooling) term. The two remaining terms in the LHS of Equation 14 describe the work performed by viscous forces and the fluid heat conductance. All these processes are collisionless.

All collisional processes in the thermal balance Equation 14 are described by its RHS. After rearranging the last term in Equation 15 to the RHS of Equation 14, the last term there becomes $\left(m_p{V}_p^2/2-5T_p/2\right)\int {\left(d{f}_p/dt\right)}_{col}{d}^3{v}_p$. All integral terms involving ${\left(d{f}_p/dt\right)}_{col}$ describe the frictional heating and thermal inflows (outflows) associated with possible emergence (disappearance) of $p$-particles as a result of ionization, recombination, etc. For the general form of ${\left(d{f}_p/dt\right)}_{col}$, calculating the frictional heating is not an easy task. Below, we use two different kinds of further approximation: one is more appropriate for heavy single-charged ions (Section 3), while the other is suitable for light electrons (Section 4).

Before proceeding further, we emphasize that, in general, no truncated chain of moment equations is closed because, starting from the momentum equation, every further moment equation involves higher-order moments. To allow the moment equation chain to be rigorously truncated, the most appropriate is the near-equilibrium case when the particle distribution function, along with its small perturbations, remains reasonably close to Maxwellian (Dimant and Sudan, 1995a; Kissack et al., 1995). This case allows describing the particle kinetics using a restricted number of spatially and temporarily varying parameters, such as the particle density, temperature, and average drift velocity (5-moment equations). In real situations, however, this is not always the case. That is why inconsistencies in the fluid description often happen (e.g., García-Colín et al., 2004; Velasco et al., 2002). Higher-order sets of equations allow more serious deviations from Maxwellian but still have a restricted number of additional fluid parameters. Fluid models that include restricted numbers of equations using approximate closures, such as the 5-, 8-, or 13-moment models (Schunk and Nagy, 2009), can be successfully employed in situations when there are no sharp gradients, extreme fields, abundant superthermal particles, or extremely large temperature differences between different species of the colliding particles. These conditions are usually met at the equatorial electrojet. If they cannot be met, then the adequate description of plasma dynamics may require a direct solution of the corresponding collisional kinetic equation.

3 BGK collision kinetics and the fluid model for ions

For ionospheric ions, an accurate fluid theory has been developed by several authors who derived the fluid-model equations using a rigorous collisional kinetic approach; see, for example, Schunk and Walker (1971), Schunk and Walker (1972), and St-Maurice and Schunk (1977); for references, see Shkarofsky et al. (1966), Gurevich (1978), and Schunk and Nagy (2009). This theory results, for example, in a comprehensive set of 13-moment fluid equations that contain many transport terms (Schunk and Nagy, 2009). For typical plasma processes in the E-region ionosphere, however, such comprehensive equations are often excessive, and a much simpler set of 5-moment ion equations would usually suffice.

The goal of this section is to demonstrate that the derivation of the 5-moment ion fluid equations that have been successfully used, for example, for the treatment of the E-region instabilities (Dimant and Oppenheim, 2004; Kovalev et al., 2008; Makarevich, 2020), does not require a full and rigorous kinetic theory. This set of equations can be derived from the ion kinetic equation, where the complicated Boltzmann collision integral is replaced by a much simpler and more practical model discussed below. Under certain conditions, usually fulfilled automatically in the E-region ionosphere, the resultant 5-moment ion equations provide quantitatively accurate frictional heating and cooling terms.

In the lower-E/upper-D regions of the ionosphere (or similar media), one can usually neglect Coulomb collisions between the charged particles, compared to their much more frequent collisions with the dominant neutrals. For the ion-neutral collision integral, one can use the simple BGK model (Bhatnagar et al., 1954). Disregarding ionization-recombination processes and assuming in the general case a neutral wind with the local velocity ${\vec{V}}_n$, for the laboratory frame of reference, we write the simplest BGK collision operator as

${\left(\frac{d{f}_i}{dt}\right)}_{col}^{\text{BGK}}={\nu }_i\left(f_{\text{eff}}-f_i\right),(16)$

where $f_i$ is the real ion distribution function (IDF), while $f_{\text{eff}}$ is a fictitious Maxwellian function, normalized to the locally varying ion density, $n_i(\vec{r},t)$, with the constant neutral temperature $T_n$:

$f_{\text{eff}}\left({\vec{v}}_i,\vec{r},t\right)\equiv n_i\left(\vec{r},t\right){\left(\frac{m_i}{2\pi T_n}\right)}^{3/2}\exp \left(-\frac{m_i{\left({\vec{v}}_i-{\vec{V}}_n\right)}^2}{2T_n}\right).(17)$

This simple linear algebraic form of the model collision operator has also been called the “relaxation collision model” (St-Maurice and Schunk, 1973; St-Maurice and Schunk, 1974; St-Maurice and Schunk, 1977), the “Krook collision model” (Schunk and Nagy, 2009), the “model integral of elastic collisions” (Aleksandrov et al., 1984), and by some other terms. Note that the BGK collision model noticeably exaggerates the IDF distortion effect (Schunk and Nagy, 2009; Koontaweepunya et al., 2024). This happens for several reasons (Schunk and Nagy, 2009); in particular, because the BGK operator does not include any collisional angular scattering and hence does not include particle redistribution in the velocity space between the preferred direction of the imposed electric field and the two perpendicular directions.

For the BGK model, it is essential that the ion-neutral collision frequency, ${\nu }_i$, is assumed constant. The standard justification for this is that at sufficiently low energies, the ion-neutral collisions are dominated by the long-range polarization interaction (Dalgarno et al., 1958; Schunk and Walker, 1971; Schunk and Walker, 1972), which results in the approximate constancy of ${\nu }_i$ (“Maxwell molecule collisions”) (Schunk and Nagy, 2009). The model collision term in the form of Equation 16 conserves the local number of particles. Applied to both ions and neutrals, the BGK model also conserves the total momentum of the two colliding particles and, after some adjustment to the temperature in $f_{\text{eff}}$ for unequal masses of the colliding species, conserves the total energy of the colliding particles as well (Aleksandrov et al., 1984).

Generally, the BGK model does not follow from Boltzmann’s collision integral under any rigorous approximations, although this becomes possible under certain conditions (St-Maurice and Schunk, 1977). This model is a reasonable and simple fit for single-charged ions that collide, predominantly elastically, with the surrounding neutrals of the same (or close) mass. Recent 2-D hybrid computer simulations of the Farley–Buneman instability that used this kinetic equation for ions (Kovalev et al., 2008) have demonstrated a good agreement with similar results of the more accurate fully kinetic PIC or hybrid simulations (Janhunen, 1995; Oppenheim et al., 2008; Oppenheim et al., 1996; Oppenheim et al., 1995; Oppenheim and Dimant, 2004; Koontaweepunya et al., 2024). There are two major reasons why this oversimplified model works well for the ion-neutral collisions typical for the lower ionosphere. First, within a 1000 K temperature range, the ion-neutral collision frequency is almost velocity-independent (Schunk and Nagy, 2009). Second, collisions of ions with neutral particles of the same or close mass have roughly equal rates of the average momentum and energy transfer, described by the single parameter ${\nu }_i$. Both these factors distinguish dramatically the ion-neutral collisions from the electron-neutral ones, as we discuss in the following section.

For the distribution function of single-charged positive ions, $f_i({\vec{v}}_i,\vec{r},t)$, the BGK kinetic equation in the conservative (divergence) form is given by

${\partial }_t{f}_i+\nabla \cdot \left({\vec{v}}_i{f}_i\right)+{\partial }_{{\vec{v}}_i}\cdot \left[\left(\frac{e\vec{E}}{m_i}+{\mathrm{\Omega }}_i{\vec{v}}_i\times \widehat{b}\right)f_i\right]={\nu }_i\left(f_{\text{eff}}-f_i\right).(18)$

In this section, we derive the 5-moment ion fluid model equations for $n_i=\int f_i{d}^3{v}_i$, ${\vec{V}}_i=⟨{\vec{v}}_i⟩=\int {\vec{v}}_i{f}_i{d}^3{v}_i$, and $T_i=m_i⟨\delta {\vec{v}}_i^2⟩/3=(m_i/3n_i)\int \delta {\vec{v}}_i^2{f}_i{d}^3{v}_i$, where $\delta {\vec{v}}_i\equiv {\vec{v}}_i-{\vec{V}}_i$.

Following the steps described in the preceding section and assuming the laboratory frame of reference, we obtain from Equation 18 the ion continuity, momentum, and energy-balance equation,

${\partial }_t{n}_i+\nabla \cdot \left(n_i{\vec{V}}_i\right)=\frac{D_i{n}_i}{Dt}+n_i\nabla \cdot {\vec{V}}_i=0,(19)$

$m_i{n}_i\frac{D_i{\vec{V}}_i}{Dt}=m_i{n}_i\left(\frac{e\vec{E}}{m_i}+{\mathrm{\Omega }}_i{\vec{V}}_i\times \widehat{b}\right)-\nabla \cdot {\mathbf{P}}_i-{\nu }_i{n}_i{m}_i\left({\vec{V}}_i-{\vec{V}}_n\right),(20)$

$\begin{array}{ll}\hfill & \frac{3n_i}{2}\frac{D_i{T}_i}{Dt}-T_i\frac{D_i{n}_i}{Dt}+\nabla \cdot \int m_i\delta {\vec{v}}_i\frac{\delta v_i^2}{2}{f}_i{d}^3{v}_i+{\mathbf{\Pi }}_{i_{\alpha \beta }}{\nabla }_{\alpha }{V}_{i\beta }\hfill \\ \hfill & =\frac{{\nu }_i{m}_i{n}_i{\left(V_i-{\vec{V}}_n\right)}^2}{2}+\frac{3}{2}{\nu }_i{n}_i\left(T_n-T_i\right).\hfill \end{array}(21)$

The two last terms in the LHS of Equation 21 describe heat conduction. Generally, the thermal flux is given by the integral term, and ${\mathbf{\Pi }}_{i_{\alpha \beta }}$ should be determined from higher-order moment equations. In the strongly collisional lower ionosphere, assuming sufficiently long-wavelength processes (so that the fluid theory is applicable), these two terms can usually be neglected. This makes Equations 19–21 a closed set of the 5-moment equations for the ion density, $n_i$, temperature, $T_i$, and the three components of the ion drift velocity, ${\vec{V}}_i$. We should bear in mind, however, that the IDF may deviate from an isotropic Maxwellian function so that $T_i$ is an effective temperature determined in the general case by Equation 4 (substituting $p=i$). For example, if the ion velocity distribution is approximated by a bi-Maxwellian function $\propto \exp [-(m_i/2)(V_{\perp }^2/T_{\perp }+V_{\Vert }^2/T_{\Vert })]$, then $T_i=(2T_{\perp }+T_{\Vert })/3$.

The first term in the RHS of Equation 21 describes the total rate of ion frictional heating. This term equals the rate that follows from a more detailed kinetic theory (Schunk and Nagy, 2009), ${\nu }_i{m}_i{m}_n{n}_i{(V_i-V_n)}^2/(m_i+m_n)$, provided $m_i=m_n$. Coincidentally, in the E region, the masses of the major ions (${\mathrm{N}\mathrm{O}}^{+}$ and ${\mathrm{O}}_2^{+}$) and neutrals (${\mathrm{N}}_2$ and ${\mathrm{O}}_2$) are indeed close to each other, $m_i\simeq m_n\simeq$ 30 amu. Thus, in the E-region ionosphere, the BGK model of ion-neutral collisions should correctly describe the ion frictional heating so that one can successfully use it for ions Equations 19–21. The applicability of the fluid equations is better under moderate conditions when the IDF is reasonably close to Maxwellian so that their closing is better justified. Such moderate conditions mostly occur at the equatorial E region rather than at the high-latitude ionosphere, especially during the events of the strongly disturbed magnetosphere–ionosphere–thermosphere system.

To conclude this section, note that closed Equations 19–21 are mostly applicable to moderately disturbed conditions when the IDF is reasonably close to Maxwellian; otherwise, more equations for the higher-order moments are required. For strongly perturbed conditions, however, even higher-order closed sets of fluid equations are not fully applicable because, unlike the original kinetic Equation 18, any closed fluid equations do not include the important kinetic effect of Landau damping and hence they have limited applicability, for example, to describe the Farley–Buneman instability in the short-wavelength range of the turbulence spectrum where the wavelengths become comparable to, or shorter than, the ion mean free path.

4 Collisional kinetics and the fluid model for electrons

This section is the central piece of this paper. It derives the electron-fluid equations from an approximate but rigorous kinetic theory based on characteristics of the actual physical conditions and wave processes in the E-region ionosphere. For electrons, the oversimplified BGK collision model (employed above for ions) can apply only to plasma processes whose characteristic wave frequencies substantially exceed the electron collision frequencies. However, for low-frequency processes in the highly collisional E/D-region ionosphere, where the opposite condition usually holds (see Dimant and Sudan, 1995a, and references therein), the electron BGK collision model is totally unsuitable. The main reason is that the rate of electron-neutral collisional exchange of momentum, ${\nu }_e$, is a few orders of magnitude larger than the corresponding rate of the energy exchange, ${\delta }_{en}{\nu }_e$ (Gurevich, 1978). This means that during collisions with heavy neutrals, the light electrons scatter over angles in the velocity space much more frequently than they change their kinetic energy. In low-frequency processes of the lower ionosphere, this leads to an efficient isotropization of the electron distribution function (EDF). The BGK model, however, completely ignores this feature. In addition, the BGK model does not cover the clearly pronounced velocity dependence of the kinetic electron-neutral collision frequency ${\nu }_e(v_e)$ (Gurevich, 1978; Schunk and Nagy, 2009). This velocity dependence plays an important role in some E-region instabilities (see, e.g., Dimant and Sudan, 1997, and references therein), and it modifies the instability and wave characteristics.

4.1 General kinetic approach and momentum equations

In a weakly ionized plasma of the lower ionosphere, collisions of an electron with other charged particles, including other electrons, ${\nu }_{ee},{\nu }_{ei}$, are usually negligible compared to electron-neutral collisions, ${\nu }_e\approx {\nu }_e$. At altitudes above 75 km, strongly magnetized electrons, involved in low-frequency processes with $\omega \ll {\nu }_e\ll {\mathrm{\Omega }}_e$, have an almost isotropic velocity distribution whose speed dependence can deviate significantly from Maxwellian. For such processes, an adequate kinetic description is by expanding the velocity distribution function $f_e(\vec{r},t,{\vec{v}}_e)$ in Legendre polynomials with respect to angles in the velocity space (Shkarofsky et al., 1966; Gurevich, 1978; Khazanov, 2011). To the first-order accuracy with respect to a small anisotropy of $f_e(\vec{r},t,{\vec{v}}_e)$, one can represent the total EDF as a combination of the major isotropic part, $F_0(\vec{r},t,v_e)$, where $v_e\equiv |{\vec{v}}_e|$, and a relatively small directional part determined by a single vector-function ${\vec{f}}_1(\vec{r},t,v_e)$ (Gurevich, 1978; Dimant and Sudan, 1995a),

$f_e\left(\vec{r},t,{\vec{v}}_e\right)\approx F_0\left(\vec{r},t,v_e\right)+\frac{{\vec{f}}_1\left(\vec{r},t,v_e\right)\cdot {\vec{v}}_e}{v_e}=F_0+|{\vec{f}}_1|\cos \vartheta ,(22)$

where $\vartheta$ is the angle between ${\vec{f}}_1$ and ${\vec{v}}_e$. Here, we assume that $|{\vec{f}}_1|\ll F_0$, along with similar inequalities for the speed derivatives (see below). The major isotropic part, $F_0$, determines scalar velocity-averaged characteristics of the electron fluid, such as the electron density and temperature, while the small directional part, $|{\vec{f}}_1|\cos \vartheta$, determines vector characteristics, such as the average drift velocity and various fluxes. The other (neglected) terms of the expansion in Legendre polynomials are smaller than the two highest order terms by positive powers of the small parameter ${\delta }_{en}$, which is discussed in the following paragraph. In this approximation, any higher-order anisotropies of the EDF are neglected. For electrons in the highly collisional E-region ionosphere, the higher-order anisotropies usually play no role (see below).

The assumption of $|{\vec{f}}_1|\ll F_0$ is well justified for electrons within the kinetic energy range ${\mathcal{E}}_e<2$ eV ($v_e<1000$ km/s). This range usually includes both the thermal bulk of electrons (${\mathcal{E}}_e\lesssim 0.03$ eV for the cold E-region ionosphere) and a significant fraction of superthermal electrons. In this energy rate, the ratio of the mean, mostly inelastic, collisional energy loss to that of the predominantly elastic momentum loss, ${\delta }_{en}(v_e){\nu }_e(v_e)/{\nu }_e(v_e)={\delta }_{en}(v_e)$, is usually quite small: ${\delta }_{en}(v_e)\sim \left(2--4\right)\times 10^{-3}$ (Gurevich, 1978) (although it is two orders of magnitude larger than the corresponding purely elastic rate, ${\delta }_{en}^{\text{elas}}\approx 2m_e/m_n$). The ratio of $|{\vec{f}}_1|$ to $F_0$ is typically $\sim \sqrt{{\delta }_{en}}$ so that the directional part of the EDF in Equation 22 turns out to be automatically small compared to the major isotropic part, $|{\vec{f}}_1|\ll F_0$. However, this raises the following question. If there were an imposed DC electric field, $\vec{E}\perp \vec{B}$, so strong that the corresponding $\vec{E}\times \vec{B}$-drift velocity, ${\vec{V}}_{\text{dr}}=\vec{E}\times \vec{B}/B^2$, would be comparable to the mean electron thermal speed, $v_{Th}^e={(T_e/m_e)}^{1/2}$, then the condition of $|{\vec{f}}_1|\ll F_0$ would become invalid. As a matter of fact, however, such a strong field would heat electrons so much that the heated thermal velocity $v_{Th}^e$ would automatically exceed ${\vec{V}}_{\text{dr}}$. If the new electron temperature is $\lesssim \mathrm{23,000}$K (corresponding to 2 eV), then the approximation given by Equation 22 still holds. This is a significant difference of electrons from heavy ions with ${\delta }_{in}\simeq 1$.

If there was an imposed electric field, $\vec{E}$, and no magnetic field, then the electron distribution function $f({\vec{v}}_e)$ would depend only on the electron speed $v_e$ and the angle between the electron velocity ${\vec{v}}_e$ and the only preferred direction, that is, the direction $\vec{E}$. If one expands the EDF in the orthogonal polynomials with respect to $\cos \vartheta$ [see, for example, Equation (2.63) in Gurevich (1978)] and applies this expansion to the electron kinetic equation with the Boltzmann collision operator, then this will form an infinite chain of coupled equations for the corresponding terms of expansion, $f_n$.

Based on the smallness of the parameter ${\delta }_{en}(v_e)$, one can restrict the entire expansion to the first two Legendre polynomials, 1 and $\cos \vartheta$, that is, to the approximation given by Equation 22. The kinetic equation with the general electron-neutral collision operator, ${(d{f}_e/dt)}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}}$, leads to the two coupled equations for $F_0(v_e,\vec{r},t)$ and ${\vec{f}}_1(v_e,\vec{r},t)$ (Gurevich, 1978; Dimant and Sudan, 1995a).

${\partial }_t{F}_0+\frac{v_e}{3}\nabla \cdot {\vec{f}}_1-\frac{e}{3m_e{v}_e^2}\frac{\partial }{\partial v_e}\left(v_e^2\vec{E}\cdot {\vec{f}}_1\right)=S_0,(\mathrm{23a})$

${\partial }_t{\vec{f}}_1-{\mathrm{\Omega }}_e\widehat{b}\times {\vec{f}}_1+v_e\nabla F_0-\frac{e\vec{E}}{m_e}\frac{\partial F_0}{\partial v_e}={\vec{S}}_1,(\mathrm{23b})$

where

$S_0\equiv \frac{1}{2}{\int }_{-1}^1{\left(\frac{d{f}_e}{dt}\right)}_{col}d\left(\cos \vartheta \right),{\vec{S}}_1\equiv \frac{3}{2}{\int }_{-1}^1{\left(\frac{d{f}_e}{dt}\right)}_{col}\frac{{\vec{f}}_1}{|{\vec{f}}_1|}\cos \vartheta d\left(\cos \vartheta \right)(24)$

(note that the expressions for $S_{\mathrm{0,1}}$ in Dimant and Sudan (1995a) missed the correct normalization factors). Bearing in mind moderately fast wave processes, ${\tau }_{\text{rec}}^{-1}\ll \omega \ll {\nu }_e$, where ${\tau }_{\text{rec}}$ is an effective recombination lifetime at a given altitude, we will ignore ionization-recombination processes, as we did above for the ions. The kinetic description of electrons based on Equation 23a differs dramatically from any kinetic description based on the BGK collision model.

The theoretical approach leading to Equation 23a, b is explained in Gurevich (1978), Sect. 2.2.1. Here, we only outline it, starting from the simplest case of a totally unmagnetized plasma, $\vec{B}=0$, where, in addition to that, all spatial gradients are directed parallel to $\vec{E}$. In this case, the only preferred direction is parallel to $\vec{E}$ so that the EDF $f_e$ at a given location, $\vec{r}$, at a given time, $t$ depends only on the electron speed $v_e$ and the polar angle $\vartheta$ between ${\vec{v}}_e$ and the preferred direction. Expanding the angular part of $f_e(v_e,\vartheta ,\vec{r},t)$ in the Legendre polynomials $P_k(x)$ as $f_e(v_e,\vartheta ,\vec{r},t)={\sum }_{k=0}^{\infty }{P}_k(\cos \vartheta )f_k(v_e,\vec{r},t)$ [see Equation (2.63) in Gurevich (1978)], substituting this expansion into the electron kinetic equation with the Boltzmann collision operator where only the electron-neutral collision component matters, and using the orthogonality of the Legendre polynomials $P_k(x)$, one obtains an infinite chain of coupled equations for $f_k(v_e)$. Using the conditions discussed above [and analyzed in more detail in Gurevich (1978)], one can cut the expansion in $P_k(\cos \vartheta )$ and the resultant infinite chain of equations to only the two first terms, $f_{\mathrm{0,1}}$, corresponding to $F_0$ and $|{\vec{f}}_1|\cos \vartheta$ in our Equation 22.

When the magnetic field $\vec{B}$ is present and spatial gradients are arbitrarily directed, the situation is more complicated because there is no single preferred direction. However, because electrons are highly gyrotropic due to the fast Larmor rotation (in the perpendicular to $\vec{B}$ plane) and are prone to fast collisional scattering (in all directions), their velocity distribution remains mostly isotropic with only a small directional part. It is natural to assume that there is always a direction, ${\vec{f}}_1/|{\vec{f}}_1|$, around which the small angular-dependent part of the distribution function is almost axially symmetric and is proportional to ${\vec{f}}_1\cdot {\vec{v}}_e$. Unlike the unmagnetized case discussed above, this direction is not necessarily fixed but may be $v_e$-dependent and vary with $\vec{r}$, $t$. Restriction of the entire EDF to the ansatz given by Equation 22 reduces the electron kinetic equation with the Boltzmann collision operator to Equation (2.74) in Gurevich (1978), that is, to our Equations 23a, b. The unknown vector ${\vec{f}}_1$ is determined by solving the vectorial differential equation given by Equation 23b. Needless to say, the directional part of the electron velocity distribution $\propto {\vec{f}}_1$, that is, the second term in the RHS of Equation 22, always remains scalar.

Fluid equations based on Equations 23a, b, usually implying a nearly Maxwellian velocity distribution, have been successfully explored by a number of researchers [see, e.g., Gurevich (1978), Dimant and Sudan (1995a), and references therein]. However, the form of major fluid equations presented in Gurevich (1978), Chapter 5, does not clearly show the basic structure of generic Equations 9 and 14 or similar ions Equations 20 and 21. By this, we mean that Gurevich’s equations show neither explicit adiabatic heating and cooling nor frictional heating $\propto V_{e,i}^2$. Adiabatic terms proportional to $({\gamma }_{e,i}-1)$ in Gurevich (1978) Equations (5.3) and (5.4) and the corresponding terms in the following equations appear to have been introduced “by hand” and are actually extraneous. One can verify that these adiabatic terms have already been implicitly distributed among other terms of the temperature balance equations within the corresponding fluxes given by Equations (5.8)–(5.11) in Gurevich (1978) so that they are accounted for in Gurevich (1978) Equations (5.3)–(5.4) twice.

The explicit adiabatic terms show up naturally in the kinetic approaches based on small perturbations of the distribution function shifted by the average particle drift velocity. These approaches differ from those based on perturbations of the non-shifted velocity distribution, as in Equation 22, resulting in Equations 23a, b. For relatively small drift velocities, however, the two different approaches should yield the same results. Below, we demonstrate that the kinetic approach based on Equation 22 and Equations 23a, b reproduces the electron-fluid equations in a rigorous and natural way with the correct adiabatic heating and cooling, frictional heating, etc. We will also calculate kinetic corrections associated with the general velocity dependence of the electron-neutral collision frequency and non-Maxwellian velocity distribution. The Supplementary Appendix contains details of these calculations.

In accord with the low-frequency condition of $\omega \ll {\nu }_e\ll {\mathrm{\Omega }}_e$, we neglect in Equation (23b) the electron inertia term ${\partial }_t{\vec{f}}_1$ and use a standard approximation ${\vec{S}}_1\approx -{\nu }_e(v_e){\vec{f}}_1$ (Gurevich, 1978; Dimant and Sudan, 1995a). The latter follows from the Legendre polynomial expansion of the Boltzmann operator if we completely neglect the electron collisional energy losses and take into account only the angular scattering. This procedure is explained, for example, in Gurevich (1978), Section 2.2.2. This approximation allows us to close this set of equations in a simple way. As a result, we obtain

$-\frac{e\vec{E}}{m_e}\frac{\partial F_0}{\partial v_e}-{\mathrm{\Omega }}_e\widehat{b}\times {\vec{f}}_1+v_e\nabla F_0=-{\nu }_e\left(v_e\right){\vec{f}}_1.(25)$

Resolving this vector equation with respect to ${\vec{f}}_1$, we obtain

${\vec{f}}_1\left(v_e\right)=-\mathbf{N}\left(v_e\right)\cdot \vec{K}{F}_0,(26)$

where the kinetic electron mobility tensor $\mathbf{N}(v)$ and the differential vector operator $\vec{K}$ are given by

$\mathbf{N}\left(v_e\right)\approx \left[\begin{array}{ccc}\hfill \frac{{\nu }_e\left(v_e\right)}{{\mathrm{\Omega }}_e^2}\hfill & \hfill \frac{1}{{\mathrm{\Omega }}_e}\hfill & \hfill 0\hfill \\ \hfill -\frac{1}{{\mathrm{\Omega }}_e}\hfill & \hfill \frac{{\nu }_e\left(v_e\right)}{{\mathrm{\Omega }}_e^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{{\nu }_e\left(v_e\right)}\hfill \end{array}\right],(27)$

$\vec{K}\equiv v_e\nabla -\frac{e\vec{E}}{m_e}\frac{\partial }{\partial v_e}.(28)$

Here and elsewhere, we neglect second-order small terms $\sim {\nu }_e^2$ compared to ${\mathrm{\Omega }}_e^2$ and represent all tensors in the matrix form for the Cartesian system $\widehat{x},\widehat{y},\widehat{z}$ with the $\widehat{z}$-axis along $\vec{B}$. We can write Equations 26 and 27 explicitly in terms of the parallel $(\Vert )$ and perpendicular $(\perp )$ to $\vec{B}$ components as

$f_{1\Vert }=-\frac{1}{{\nu }_e\left(v_e\right)}{K}_{\Vert }{F}_0,{\vec{f}}_{1\perp }=-\left(\frac{{\nu }_e\left(v\right){\vec{K}}_{\perp }}{{\mathrm{\Omega }}_e^2}+\frac{\widehat{b}}{{\mathrm{\Omega }}_e}\times {\vec{K}}_{\perp }\right)F_0,(29)$

where $\widehat{b}=\widehat{z}$ is the unit vector along $\vec{B}$. The spatial derivatives in Equation 26 or 29 express the drift-diffusion approximation in the collisional kinetic theory, while the velocity derivatives describe electron energy variations caused by the electric field $\vec{E}$.

Now, we turn to the term $S_0$ in the RHS of Equation 23a. When using the approximate form for the term ${\vec{S}}_1$, we implied above that the collisional losses of the electron energy had been totally neglected. Calculation of the $k$-th degree term of the collision operator $S_k$ involves an integration over the angle $\vartheta$ with the integrand proportional to $[1-P_k(\vartheta )]$ (Shkarofsky et al., 1966; Gurevich, 1978). This integration works nicely for all $k\ge 1$, but for $S_0$ $(P_0(\vartheta )=1)$, it yields 0. This means that in order to calculate the term $S_0$, one needs better accuracy by taking into account the small collisional energy losses. Using proper Taylor expansions, such calculation yields a Fokker–Planck-like expression (Shkarofsky et al., 1966; Gurevich, 1978)

$S_0=\frac{1}{2v_e^2}\frac{\partial }{\partial v_e}\left[v_e^2{\delta }_{en}{\nu }_e\left(v_e{F}_0+\frac{T_n}{m_e}\frac{\partial F_0}{\partial v_e}\right)\right],(30)$

where the parameter ${\delta }_{en}(v)$ describes the average fraction of energy lost by an electron with speed $v$ during one electron-neutral collision. As a result, we obtain (Dimant and Sudan, 1995a)

${\partial }_t{F}_0+\frac{1}{3v_e^2}\vec{K}\cdot \left(v_e^2{\vec{f}}_1\right)=\frac{1}{2v_e^2}\frac{\partial }{\partial v_e}\left[v_e^2{\delta }_{en}{\nu }_e\left(v_e{F}_0+\frac{T_n}{m_e}\frac{\partial F_0}{\partial v_e}\right)\right].(31)$

Expressing here ${\vec{f}}_1$ in terms of $F_0$ via Equation (26) or (29), we obtain a closed kinetic equation for the major isotropic distribution function, $F_0(\vec{r},t,v)$. Its solution, with the use of Equation (26) or (29), provides both parts of the distribution function so that its scalar and vector moments can be calculated by a straightforward speed integration. Using the standard expressions for lowest-order moments of the distribution function, such as the particle density, mean drift velocity, and temperature (see Equations 2–4) for the approximate electron velocity distribution given in the neutral frame of reference by Equation 22, after the integrations over the phase space angles, $d^3{v}_e=2\pi v_e^{2}d{v}_{e}d(\cos \vartheta )$, we obtain

$n_e\approx 4\pi {\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e,{\vec{V}}_e\approx \frac{4\pi }{3n_e}{\int }_0^{\infty }{\vec{f}}_1{v}_e^{3}d{v}_e,T_e\approx \frac{4\pi m_e}{3n_e}{\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e.(32)$

A direct solution of the kinetic Equation 31 would be the most accurate and general way of describing the electron behavior (Dimant and Sudan, 1995a). However, the goal of this paper is to obtain a set of the lowest-order fluid equations in order to properly describe E-region plasma processes, even if this set of equations is not fully closed due to possible deviations of the EDF from Maxwellian.

As mentioned above, we start from particle conservation. Using the definitions of Equation 32 and integrating Equation 31 over $v_e$ with the weighting function $4\pi v_e^2$, we obtain the standard electron continuity equation,

${\partial }_t{n}_e+\nabla \cdot \left(n_e{\vec{V}}_e\right)=0.(33)$

The conventional way of obtaining the momentum equation is by integrating the kinetic equation with the weighting function $m_p{\vec{v}}_p$, as in obtaining Equation 7. For the light electrons, however, we have already reduced the original kinetic equation to the two coupled equations, where the second one, Equation 25, has a vectorial form. Integrating it with the weighting function $4\pi v_e^3/(3n_e)$ and applying the integration by parts, we obtain

$\frac{e\vec{E}}{m_e}-{\mathrm{\Omega }}_e\widehat{b}\times {\vec{V}}_e+\frac{\nabla \left(n_e{T}_e\right)}{m_e{n}_e}+\frac{4\pi }{3n_e}{\int }_0^{\infty }{\vec{f}}_1{\nu }_e{v}_e^{3}d{v}_e=0,(34)$

This equation describes the momentum balance of the inertialess electron fluid. Equation 34 includes the Lorentz force, pressure gradient, and collisional friction. As we show in the Supplementary Appendix, in the general case of a velocity-dependent collision frequency, ${\nu }_e(v)$, the last term in the LHS of Equation 34, in addition to the collisional friction, may also include an anisotropic addition to the total pressure gradient.

Taking a scalar product of Equation 34 with $m_e{n}_e{\vec{V}}_e$, we obtain the expression

${\vec{V}}_e\cdot \left[n_{e}e\vec{E}+\nabla \left(n_e{T}_e\right)\right]+\frac{4\pi m_e}{3}{\vec{V}}_e\cdot {\int }_0^{\infty }{\vec{f}}_1{\nu }_e{v}_e^{3}d{v}_e=0.(35)$

This expression represents the total work done by the electric field and other forces on the average electron flow. We will use this expression below.

Now, we derive an equation describing the total energy balance. Integrating Equation 31 with the weighting function $2\pi m_e{v}_e^4$, we obtain

$\begin{array}{ll}\hfill & {\partial }_t\left(\frac{3n_e{T}_e}{2}\right)+\frac{2\pi m_e}{3}\nabla \cdot {\int }_0^{\infty }{\vec{f}}_1{v}_e^{5}d{v}_e+n_{e}e\vec{E}\cdot {\vec{V}}_e\hfill \\ \hfill & =-2\pi m_e{\int }_0^{\infty }\left(v_e{F}_0+\frac{T_n}{m_e}\frac{d{F}_0}{d{v}_e}\right){\delta }_{en}{\nu }_e{v}_e^{3}d{v}_e.\hfill \end{array}(36)$

Using Equation 35, we eliminate from Equation 36 the work done by the electric field on the average flow, $n_{e}e\vec{E}\cdot {\vec{V}}_e$, and obtain

$\begin{array}{ll}\hfill & {\partial }_t\left(\frac{3n_e{T}_e}{2}\right)-{\vec{V}}_e\cdot \nabla \left(n_e{T}_e\right)+\frac{2\pi m_e}{3}\nabla \cdot {\int }_0^{\infty }{\vec{f}}_1{v}_e^{5}d{v}_e\hfill \\ \hfill & =\frac{4\pi m_e}{3}{\vec{V}}_e\cdot {\int }_0^{\infty }{\vec{f}}_1{\nu }_e{v}_e^{3}d{v}_e-2\pi m_e{\int }_0^{\infty }\left(v_e{F}_0+\frac{T_n}{m_e}\frac{d{F}_0}{d{v}_e}\right){\delta }_{en}{\nu }_e{v}_e^{3}d{v}_e.\hfill \end{array}(37)$

Here, we have rearranged the terms between the two sides of the equation in such a way that all terms proportional to the collision frequency remain in the RHS while all other terms are put in the LHS. After so doing, it may be tempting to interpret the first term in the RHS of Equation 37 as the electron frictional heating. In the general case of velocity-dependent ${\nu }_e(v)$, however, this interpretation would not be perfectly accurate, as we show in the Supplementary Appendix and Section 4.3 below.

Equation 37 is not yet the final form of the thermal-balance equation. It needs to be further transformed into a form similar to Equation (14) or (21). In Supplementary Appendix, we develop this recast for the general case of velocity-dependent ${\nu }_e(v)$. However, we proceed with the simplest model of constant ${\nu }_e$ and ${\delta }_{en}$ below. This model is inaccurate for electron-neutral collisions of the lower ionosphere (Gurevich, 1978; Schunk and Nagy, 2009), but it will allow us to clarify basic ideas of closing Equation 37.

4.2 Constant collisional parameters

For constant ${\nu }_e$ and ${\delta }_{en}$, using the definitions of Equation 32 and integrating the last term of Equation 37 by parts, we obtain

$\begin{array}{ll}\hfill & {\partial }_t\left(\frac{3n_e{T}_e}{2}\right)-{\vec{V}}_e\cdot \nabla \left(n_e{T}_e\right)+\frac{2\pi m_e}{3}\nabla \cdot {\int }_0^{\infty }{\vec{f}}_1{v}_e^{5}d{v}_e\hfill \\ \hfill & =m_e{\nu }_e{n}_e{V}_e^2+\frac{3}{2}{\delta }_{en}{\nu }_e{n}_e\left(T_n-T_e\right),\hfill \end{array}(38)$

Using Equation 26, we rewrite the third term in the LHS as

$\frac{2\pi m_e}{3}\nabla \cdot {\int }_0^{\infty }{\vec{f}}_1{v}_e^{5}d{v}_e=-\frac{5}{2m_e}\nabla \cdot \mathbf{N}\cdot \left[\nabla \left(\lambda n_e{T}_e^2\right)+n_e{T}_{e}e\vec{E}\right].(39)$

Here, the double-dot product involving a tensor means $\nabla \cdot \mathbf{N}\cdot \nabla \dots ={\sum }_{\alpha ,\beta =1}^3{\partial }_{x_{\alpha }}({\mathbf{N}}_{\alpha \beta }{\partial }_{x_{\beta }}\dots )$ (and similarly for $\nabla \cdot \mathbf{N}\cdot \vec{E}$), and we have also introduced a dimensionless parameter of order unity, $\lambda$,

$\lambda \equiv \frac{4\pi m_e^2}{15n_e{T}_e^2}{\int }_0^{\infty }{v}_e^6{F}_{0}d{v}_e=\frac{m_e{\int }_0^{\infty }{v}_e^6{F}_{0}d{v}_e}{5T_e{\int }_0^{\infty }{v}_e^4{F}_{0}d{v}_e}=\frac{3\left({\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e\right){\int }_0^{\infty }{F}_0{v}_e^{6}d{v}_e}{5{\left({\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e\right)}^2}.(40)$

Note that for the Maxwellian isotropic part of the EDF,

$F_0=n_e{\left(\frac{m_e}{2\pi T_e}\right)}^{3/2}\exp \left(-\frac{m_e{v}_e^2}{2T_e}\right),(41)$

we have $\lambda =1$.

Using Equations 32 and 28, we obtain

${\vec{V}}_e=-\frac{4\pi }{3n_e}\mathbf{N}\cdot {\int }_0^{\infty }{v}_e^3\vec{K}{F}_{0}d{v}_e=-\mathbf{N}\cdot \left[\frac{e\vec{E}}{m_e}+\frac{\nabla \left(n_e{T}_e\right)}{m_e{n}_e}\right].(42)$

Multiplying Equation 42 by $m_e{n}_e{T}_e$, we can rewrite it as

$-\mathbf{N}\cdot \left(n_e{T}_{e}e\vec{E}\right)=m_e{n}_e{T}_e{\vec{V}}_e+\mathbf{N}\cdot T_e\nabla \left(n_e{T}_e\right).$

This relation allows us to eliminate the electric field from Equation 39 so that the latter becomes

$\begin{array}{ll}\hfill & \frac{2\pi m_e}{3}\nabla \cdot {\int }_0^{\infty }{\vec{f}}_1{v}_e^{5}d{v}_e\hfill \\ \hfill & =\frac{5}{2m_e}\nabla \cdot \left\{\mathbf{N}\cdot \left[\left(1-\lambda \right)T_e^2\nabla n_e-\left(2\lambda -1\right)n_e{T}_e\nabla T_e\right]+m_e{n}_e{T}_e{\vec{V}}_e\right\}.\hfill \end{array}(43)$

Using Equations 33 and 43, after a simple algebra,

$\begin{array}{ll}\hfill & {\partial }_t\left(\frac{3n_e{T}_e}{2}\right)-{\vec{V}}_e\cdot \nabla \left(n_e{T}_e\right)+\frac{5}{2}\nabla \cdot \left(n_e{T}_e{\vec{V}}_e\right)\hfill \\ \hfill & ={\partial }_t\left(\frac{3n_e{T}_e}{2}\right)-{\vec{V}}_e\cdot \nabla \left(n_e{T}_e\right)+\frac{5}{2}\nabla \cdot \left(n_e{T}_e{\vec{V}}_e\right)\hfill \\ \hfill & -\frac{5T_e}{2}\left[{\partial }_t{n}_e+\nabla \cdot \left(n_e{\vec{V}}_e\right)\right]=\frac{3n_e}{2}\frac{D_e{T}_e}{Dt}-T_e\frac{D_e{n}_e}{Dt},\hfill \end{array}(44)$

we obtain the sought-for temperature balance equation in a more standard form,

$\frac{3n_e}{2}\frac{D_e{T}_e}{Dt}-T_e\frac{D_e{n}_e}{Dt}-\nabla \cdot {\vec{q}}_e=m_e{\nu }_e{n}_e{V}_e^2+\frac{3}{2}{\delta }_{en}{\nu }_e{n}_e\left(T_n-T_e\right).(45)$

Here, the electron thermal flux density, ${\vec{q}}_e$, is given by

${\vec{q}}_e=\frac{5T_e}{2m_e}\mathbf{N}\cdot \left[\left(2\lambda -1\right)n_e\nabla T_e+\left(\lambda -1\right)T_e\nabla n_e\right]={\vec{q}}_{e\Vert }+{\vec{q}}_{e\mathrm{P}}+{\vec{q}}_{e\mathrm{H}},(46)$

where its explicit parallel, Pedersen, and Hall components are given by

$\begin{array}{ll}\hfill {\vec{q}}_{e\Vert }& =\frac{5T_e\left[\left(2\lambda -1\right)n_e{\nabla }_{\Vert }{T}_e+\left(\lambda -1\right)T_e{\nabla }_{\Vert }{n}_e\right]}{2m_e{\nu }_e},\hfill \\ \hfill {\vec{q}}_{e\mathrm{P}}& =\frac{5T_e{\nu }_e\left[\left(2\lambda -1\right)n_e{\nabla }_{\perp }{T}_e+\left(\lambda -1\right)T_e{\nabla }_{\perp }{n}_e\right]}{2m_e{\mathrm{\Omega }}_e^2},\hfill \\ \hfill {\vec{q}}_{e\mathrm{H}}& =\frac{{\mathrm{\Omega }}_e}{{\nu }_e}\left(\widehat{b}\times {\vec{q}}_{e\mathrm{P}}\right)=\frac{5T_e\widehat{b}\times \left[\left(2\lambda -1\right)n_e{\nabla }_{\perp }{T}_e+\left(\lambda -1\right)T_e{\nabla }_{\perp }{n}_e\right]}{2m_e{\mathrm{\Omega }}_e}.\hfill \end{array}(47)$

The two first terms in the LHS of Equation 45, as well as the similar ones in Equation 14 or (21), describe adiabatic heating or cooling of the electron fluid, while $\nabla \cdot {\vec{q}}_e$ describes the heat conductivity. Note that the Hall component of ${\vec{q}}_e$ can contribute to electron heat conductance only as a quadratically nonlinear effect because $\nabla \cdot {\vec{q}}_{e\mathrm{H}}\propto ({\nabla }_{\perp }{n}_e\times {\nabla }_{\perp }{T}_e)$ only if the gradients of $n_e$ and $T_e$ are not parallel.

As mentioned above, for Maxwellian $F_0(v_e)$, we have $\lambda =1$ so that the term in ${\vec{q}}_e$ proportional to $\nabla n_e$ disappears. This fact can be understood as follows. If the major part of the EDF remains Maxwellian, then it is determined only by two space-dependent parameters: the density, $n_e$, and the temperature, $T_e$. If there is a density gradient but no temperature gradient, then electrons of all energies will diffuse from denser regions to less dense ones with no redistribution of the temperature and, hence, with no heat conductivity.

If the electron velocity distribution deviates from Maxwellian [this happens, for example, when a low-ionized plasma heated by strong electric fields is embedded in an abundant cold neutral atmosphere with a significantly different temperature (Milikh and Dimant, 2003)], then the situation is more complicated.

The effective electron temperature $T_e$, which is proportional to the mean electron chaotic energy, can be uniformly distributed, but the details of the electron energy distribution may differ significantly in different regions of space. The energy transport is stronger for electrons with higher energies than it is for lower-energy electrons. Hence, if there are spatial gradients of high-energy distribution tails, then more energetic particles provide stronger energy redistribution. This may make, for example, some less dense regions to be, on average, more energetic than the denser regions, even if they initially had equal effective temperatures. Moreover, it is even possible to imagine a situation when electron heat is transferred from cooler regions to hotter ones, leading to a further electron temperature elevation in the latter. This counter-intuitive but theoretically possible effect should not surprise because a strongly non-Maxwellian, that is, a strongly non-equilibrium plasma, cannot be adequately described by conventional equilibrium thermodynamics.

4.3 Velocity-dependent parameters

In the actual lower ionosphere, the electron-neutral kinetic collision frequency, ${\nu }_e$, and the energy loss fraction, ${\delta }_{en}$, have clearly pronounced velocity dependencies (Gurevich, 1978; Schunk and Nagy, 2009). This does not allow ${\nu }_e(v_e)$ and ${\delta }_{en}(v_e)$ to be factored out from the integrals in Equations 34–37, making the derivation of the general momentum and temperature balance equations more complicated than that described in Section 4.2. Such a derivation is developed in detail in the Supplementary Appendix, while we only present the results here. One of the major important outcomes of these calculations will be simple integral relations for the electron transport coefficients (see Equations 56–61), assuming not only the general velocity dependencies of ${\nu }_e$ but also general non-Maxwellian isotropic velocity distributions $F_0(v_e)$.

We note that the velocity dependence of the collisional frequency, ${\nu }_e(v_e)$, may automatically lead to the non-Maxwellian shape of the EDF. Indeed, if there is a sufficiently strong electric field parallel to $\vec{B}$, then the EDF becomes a Druyvesteyn kind (Shkarofsky et al., 1966; Gurevich, 1978). This parallel field should not necessarily be a DC field, but it can also be, for example, a turbulent AC field. In particular, such instability-driven turbulent fields lead to the well-known effect of anomalous electron heating (AEH) [see, for example, St-Maurice and Goodwin (2021), Zhang and Varney (2024), and references therein]. When strong AEH occurs, the EDF inevitably becomes non-Maxwellian, as can be seen from Figure 1 in Milikh and Dimant (2003). This fact could also be deduced from comparing the kinetic terms responsible for the electron differential collisional heating and cooling [see Equations 18 and 19 in Dimant and Sudan (1995a)]. Electric fields perpendicular to $\vec{B}$ are typically much stronger, but they often lead to smaller heating and are expected to cause lesser non-Maxwellian distortions of the EDF. The latter is because the kinetic heating and cooling terms are both linearly proportional to ${\nu }_e$ in the perpendicular direction. If ${\delta }_{en}$ has a weak velocity dependence, then this proportionality partially neutralizes the effect of ${\nu }_e(v_e)$.

Figure 1

Figure 1. Fluid model coefficients for the power-law dependent e-n collision frequency, ${\nu }_e(v_e)\propto v_e^{2\alpha }$.

When the dominant heating occurs mostly in the direction parallel to $\vec{B}$, it spreads over all angles in the velocity space due to electron-neutral collisions with strong momentum changes. These momentum changes are determined by the rate ${\nu }_e$, while the speed changes are determined by the much smaller rate ${\delta }_{en}{\nu }_e$. As a result, the EDF becomes close to isotropic, but its Druyvesteyn-like $v_e$-dependence may deviate significantly from Maxwellian. Other factors may also cause significant deviations from a Maxwellian EDF in the E region. These factors include, for example, some chemical/ionization reactions, photoelectrons, and electron precipitation. Regarding the latter, we note that even superthermal particles at a high-energy tail of the EDF can affect the mean transport coefficients of the entire electron population (Dimant et al., 2021). Note also that the non-Maxwellian shape of the EDF has serious implications for the accurate interpretation of radar measurements, as discussed in Section 2.2 of Milikh and Dimant (2003).

Now, we proceed with presenting the results. In the general case of velocity-dependent ${\nu }_e$ and ${\delta }_{en}$, electron continuity Equation (33) stays the same. The other two moment equations have the same basic structure as Equations (42) and (45), but they contain additional terms and include many dimensionless factors of order unity listed in Equations 56–61 below.

The general inertialess expression for the average electron drift velocity ${\vec{V}}_e$ is given by

${\vec{V}}_e=-\frac{1}{m_e}\mathbf{M}\cdot \left[e\vec{E}+\frac{{\nabla }_{\perp }\left(n_e{T}_e\right)}{n_e}+\frac{{\beta }_{\Vert }}{{\alpha }_{\Vert }}\frac{{\nabla }_{\Vert }\left(n_e{T}_e\right)}{n_e}\right],(48)$

where

$\mathbf{M}\equiv \frac{4\pi }{3n_e}{\int }_0^{\infty }\frac{d\left(v^3\mathbf{N}\left(v\right)\right)}{dv}{F}_{0}dv=\left[\begin{array}{ccc}\hfill \frac{{\alpha }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill \frac{1}{{\mathrm{\Omega }}_e}\hfill & \hfill 0\hfill \\ \hfill -\frac{1}{{\mathrm{\Omega }}_e}\hfill & \hfill \frac{{\alpha }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{\Vert }⟨\frac{1}{{\nu }_e}⟩\hfill \end{array}\right],(49)$

The tensor $\mathbf{N}$ is given by Equation 27, and ${⟨\cdots ⟩}_e$ denotes the velocity average over the major (isotropic) part of the EDF,

${⟨\cdots ⟩}_e=\frac{4\pi {\int }_0^{\infty }\left(\cdots \right)F_0\left(v_e\right)v_e^{2}d{v}_e}{n_e}=\frac{{\int }_0^{\infty }\left(\cdots \right)F_0\left(v_e\right)v_e^{2}d{v}_e}{{\int }_0^{\infty }{F}_0\left(v_e\right)v_e^{2}d{v}_e}.(50)$

The electron current density is given by ${\vec{j}}_e=e{n}_e{\vec{V}}_e$ so that the electric conductivity tensor is given by ${\mathit{\sigma }}_e=(n_e{e}^2/m_e)\mathbf{M}$. The corresponding diagonal terms represent the Pedersen $(\propto {\alpha }_P)$ and parallel $(\propto {\alpha }_{\Vert })$, while the antisymmetric off-diagonal terms $(\propto 1/{\mathrm{\Omega }}_e)$ represent the Hall conductivity.

The general thermal-balance equation is given by

$\begin{array}{ll}\hfill & \frac{3n_e}{2}\frac{D_e{T}_e}{Dt}-T_e\frac{D_e{n}_e}{Dt}\hfill \\ \hfill & +\frac{5}{2}\left(\frac{{\rho }_{\Vert }-{\beta }_{\Vert }}{{\alpha }_{\Vert }}\right)n_e{T}_e{\nabla }_{\Vert }\cdot {\vec{V}}_{e\Vert }+\left(\frac{5{\rho }_{\Vert }-3{\alpha }_{\Vert }-2{\beta }_{\Vert }}{2{\alpha }_{\Vert }}\right){\vec{V}}_{e\Vert }\cdot {\nabla }_{\Vert }\left(n_e{T}_e\right)-\nabla \cdot {\vec{q}}_e\hfill \\ \hfill & ={\alpha }_P{⟨{\nu }_e⟩}_e{m}_e{n}_e\left(V_{e\perp }^2+\frac{V_{\Vert }^2}{{\alpha }_{\Vert }\xi }\right)-2\pi m_e{\int }_0^{\infty }{v}_e^3{\delta }_{en}{\nu }_e\left(v_e{F}_0+\frac{T_n}{m_e}\frac{d{F}_0}{d{v}_e}\right)d{v}_e,\hfill \end{array}(51)$

where

${\vec{q}}_e\equiv {\vec{q}}_{eP}+{\vec{q}}_{eH}+{\vec{q}}_{e\Vert }=\mathbf{X}\cdot \frac{\nabla T_e}{T_e}+\left(\mathbf{X}-\mathbf{\Lambda }\right)\cdot \frac{\nabla n_e}{n_e},(52)$

is the thermal-flux density with

$\mathbf{X}=\frac{5n_e{T}_e}{2m_e}\left[\begin{array}{ccc}\hfill \frac{{\chi }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill \frac{{\chi }_H}{{\mathrm{\Omega }}_e}\hfill & \hfill 0\hfill \\ \hfill -\frac{{\chi }_H}{{\mathrm{\Omega }}_e}\hfill & \hfill \frac{{\chi }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\chi }_{\Vert }}{⟨{\nu }_e⟩}\hfill \end{array}\right],(\mathrm{53a})$

$\mathbf{\Lambda }=\frac{5n_e{T}_e}{2m_e}\left[\begin{array}{ccc}\hfill \frac{{\mu }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill \frac{\lambda }{{\mathrm{\Omega }}_e}\hfill & \hfill 0\hfill \\ \hfill -\frac{\lambda }{{\mathrm{\Omega }}_e}\hfill & \hfill \frac{{\mu }_P⟨{\nu }_e⟩}{{\mathrm{\Omega }}_e^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\mu }_{\Vert }}{⟨{\nu }_e⟩}\hfill \end{array}\right].(\mathrm{53b})$

The explicit Pedersen, Hall, and parallel components of ${\vec{q}}_e$ are given by

$\begin{array}{ll}\hfill {\vec{q}}_{eP}& \equiv \frac{5T_e⟨{\nu }_e⟩\left[{\chi }_P{n}_e{\nabla }_{\perp }{T}_e+\left({\chi }_P-{\mu }_P\right)T_e{\nabla }_{\perp }{n}_e\right]}{m_e{\mathrm{\Omega }}_e^2},\hfill \\ \hfill {\vec{q}}_{eH}& \equiv \frac{5T_e\widehat{b}\times \left[{\chi }_H{n}_e{\nabla }_{\perp }{T}_e+\left({\chi }_H-\lambda \right)T_e{\nabla }_{\perp }{n}_e\right]}{m_e{\mathrm{\Omega }}_e},\hfill \\ \hfill {\vec{q}}_{e\Vert }& \equiv \frac{5T_e\left[{\chi }_{\Vert }{n}_e{\nabla }_{\Vert }{T}_e+\left({\chi }_{\Vert }-{\mu }_{\Vert }\right)T_e{\nabla }_{\Vert }{n}_e\right]}{m_e{⟨{\nu }_e⟩}_e},\hfill \end{array}(54)$

${\chi }_P\equiv 2{\mu }_P+{\alpha }_P-{\beta }_P-{\rho }_P,{\chi }_H\equiv 2\lambda -1,{\chi }_{\Vert }\equiv 2{\mu }_{\Vert }-{\beta }_{\Vert },(55)$

In addition to $\lambda$ defined by (40), Equations 48–55 include

${\alpha }_P\equiv \frac{{\int }_0^{\infty }\frac{d\left(v^3{\nu }_e\left(v_e\right)\right)}{d{v}_e}{F}_{0}d{v}_e}{3{\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0{v}_e^{2}d{v}_e},{\alpha }_{\Vert }\equiv \frac{{\int }_0^{\infty }\frac{d\left(v_e^3/{\nu }_e\left(v_e\right)\right)}{dv}{F}_{0}d{v}_e}{3{\int }_0^{\infty }\frac{1}{{\nu }_e\left(v_e\right)}{F}_0{v}^{2}d{v}_e},(56)$

${\rho }_{\Vert }\equiv \frac{\left({\int }_0^{\infty }\frac{d}{d{v}_e}\left(\frac{v_e^5}{{\nu }_e\left(v_e\right)}\right)F_{0}d{v}_e\right)\left({\int }_0^{\infty }{v}_e^2{F}_{0}d{v}_e\right)}{5\left({\int }_0^{\infty }{v}_e^4{F}_{0}d{v}_e\right)\left({\int }_0^{\infty }\frac{v_e^2}{{\nu }_e\left(v_e\right)}{F}_{0}d{v}_e\right)},(\mathrm{57a})$

${\rho }_P\equiv \frac{\left({\int }_0^{\infty }\frac{d}{d{v}_e}\left({\nu }_e\left(v_e\right)v_e^5\right)F_{0}dv\right)\left({\int }_0^{\infty }{v}_e^2{F}_{0}d{v}_e\right)}{5\left({\int }_0^{\infty }{v}_e^4{F}_{0}d{v}_e\right)\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)v_e^2{F}_{0}d{v}_e\right)},(\mathrm{57b})$

${\beta }_P\equiv \frac{\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0{v}_e^{4}d{v}_e\right){\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e}{\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0{v}_e^{2}d{v}_e\right){\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e},(\mathrm{58a})$

${\beta }_{\Vert }\equiv \frac{\left({\int }_0^{\infty }\frac{F_0{v}_e^4}{{\nu }_e\left(v_e\right)}d{v}_e\right){\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e}{\left({\int }_0^{\infty }\frac{F_0{v}^2}{{\nu }_e\left(v_e\right)}d{v}_e\right){\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e},(\mathrm{58b})$

${\delta }_P\equiv \frac{\left({\int }_0^{\infty }{\nu }_e^2{F}_0{v}_e^{4}d{v}_e\right){\left({\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e\right)}^2}{{\left({\int }_0^{\infty }{\nu }_e{F}_0{v}_e^{2}d{v}_e\right)}^2\left({\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e\right)},(59)$

${\mu }_P\equiv \frac{3\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0{v}_e^{6}d{v}_e\right){\left({\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e\right)}^2}{5\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0{v}_e^{2}d{v}_e\right){\left({\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e\right)}^2},(\mathrm{60a})$

${\mu }_{\Vert }\equiv \frac{3\left({\int }_0^{\infty }\frac{F_0{v}^6}{{\nu }_e\left(v_e\right)}d{v}_e\right){\left({\int }_0^{\infty }{F}_0{v}_e^{2}d{v}_e\right)}^2}{5\left({\int }_0^{\infty }\frac{F_0{v}^2}{{\nu }_e\left(v_e\right)}d{v}_e\right){\left({\int }_0^{\infty }{F}_0{v}_e^{4}d{v}_e\right)}^2},(\mathrm{60b})$

$\xi \equiv {⟨\frac{1}{{\nu }_e}⟩}_e{⟨{\nu }_e⟩}_e=\frac{\left({\int }_0^{\infty }{\nu }_e\left(v_e\right)F_0\left(v_e\right)v_e^{2}d{v}_e\right)\left({\int }_0^{\infty }{\nu }_e^{-1}\left(v_e\right)F_0\left(v_e\right)v_e^{2}d{v}_e\right)}{{\left({\int }_0^{\infty }{F}_0\left(v_e\right)v_e^{2}d{v}_e\right)}^2}.(61)$

For constant ${\nu }_e$ and arbitrary $F_0(v)$, we have ${\alpha }_{P,\Vert }={\rho }_{P,\Vert }={\beta }_{P,\Vert }=\mu ={\delta }_P=\xi =1$, ${\mu }_{P,\Vert }=\lambda$, ${\chi }_{P,H,\Vert }=2\lambda -1$, and $\mathbf{M}=\mathbf{N}$ so that Equations 51–54 reduce to Equations 45–47. If, additionally, $F_0(v)$ is Maxwellian, then we have even simpler parameters: ${\mu }_{P,\Vert }={\chi }_{P,H,\Vert }=\lambda =1$.

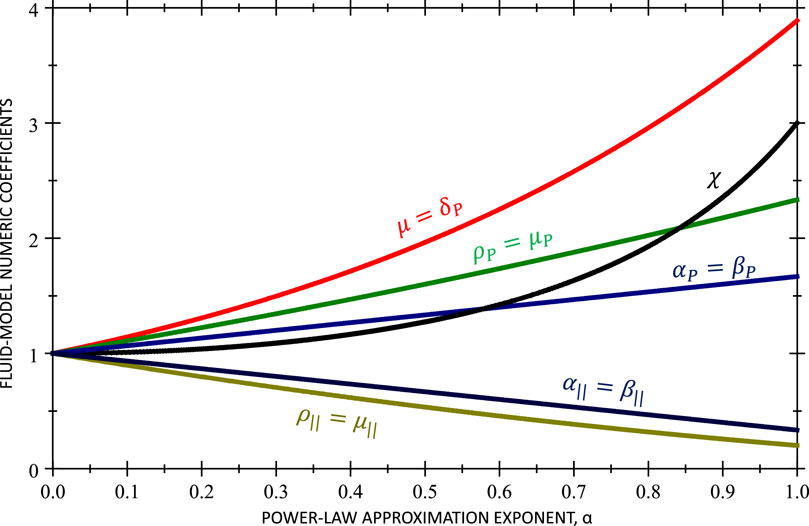
In a broad range of electron energies, ${\mathcal{E}}_e\lesssim 0.3$ eV, which usually includes the entire electron thermal bulk, the velocity dependence of ${\nu }_e$ in the lower ionosphere can be approximated by a simple power-law dependence, ${\nu }_e\propto v_e^{2\alpha }$, with $\alpha \approx 5/6$ [(Gurevich, 1978), Sect. 2.3.1, see Fig. 7 there] or, practically to the same or even better accuracy, with $\alpha =1$ (Dimant and Sudan, 1995a). For the general power-law dependent ${\nu }_e\propto v_e^{2\alpha }$ with $\alpha$ in the range between 0 and 1 and Maxwellian $F_0(v_e)$, Equations 56–61 simplify dramatically,

${\alpha }_P={\beta }_P=1+\frac{2\alpha }{3},{\alpha }_{\Vert }={\beta }_{\Vert }=1-\frac{2\alpha }{3},$

${\rho }_{\Vert }={\mu }_{\Vert }=\frac{\left(3-2\alpha \right)\left(5-2\alpha \right)}{15},{\rho }_P={\mu }_P=\frac{\left(3+2\alpha \right)\left(5+2\alpha \right)}{15},(62)$

$\mu ={\delta }_P=\frac{\sqrt{\pi }\mathrm{\Gamma }\left(5/2+2\alpha \right)}{3{\mathrm{\Gamma }}^2\left(3/2+\alpha \right)},\xi =\frac{1-4{\alpha }^2}{\sin \frac{\pi \left(2\alpha +1\right)}{2}}=\frac{4{\alpha }^2-1}{\sin \frac{\pi \left(2\alpha -1\right)}{2}}.$

The case of $\alpha =1/2$ corresponds to hard-sphere collisions. In this case, the indeterminate expression for $\xi$ yields $4/\pi \approx 1.273$. For $\alpha =5/6$ (Gurevich, 1978), we have ${\alpha }_P={\beta }_P\approx 1.556$, ${\alpha }_{\Vert }={\beta }_{\Vert }\approx 0.444$, ${\rho }_{\Vert }={\mu }_{\Vert }\approx 0.296$, ${\rho }_P={\mu }_P\approx 2.074$, $\mu ={\delta }_P\approx 3.095$, and $\xi \approx 2.053$. For $\alpha =1$ (Dimant and Sudan, 1995a), all these factors deviate from unity even further; for example, ${\alpha }_{\Vert }={\beta }_{\Vert }\approx 0.333$, $\mu ={\delta }_P\approx 3.889$, and $\xi =3$. Thus, the quantitative effect of the velocity dependence of ${\nu }_e(v)$ is significant and should not be ignored. Figure 1 shows the coefficients given by Equation 62 for general values of the power-law exponent $\alpha$ within the physically realistic range $0\le \alpha \le 1$.

Comparison of the general energy balance Equation 51 with Equation 45 shows that the velocity dependence of the collision parameters results not only in the more complicated heat conductivity, frictional heating, and cooling but also in additional terms associated with the plasma motion and gradients in the parallel to $\vec{B}$ direction (see the two terms in the LHS of Equation 51 that precede $-\nabla \cdot {\vec{q}}_e$). It is important that these seemingly collisionless terms originate entirely from electron-neutral collisions due to the velocity distribution of ${\nu }_e(v)$. Formally, these terms appear because the collision frequencies ${\nu }_e(v)$ mutually cancel each other in some fractions while their velocity dependencies still play a role. Similar effects in the Hall and Pedersen directions are absent because there is no such canceling. However, the Hall and Pedersen components hidden within the heat conductivity flux ${\vec{q}}_e$ may play an important role, provided there are sharp gradients in those directions.

Now, we discuss the last (cooling) term in the RHS of Equation 51. For general velocity-dependent ${\delta }_{en}(v)$, but a Maxwellian distribution function $F_0\propto \exp [-m_e{v}^2/(2T_e)]$, we use Equation (32) to reduce this term to

$-2\pi m_e{\int }_0^{\infty }{v}_e^3{\delta }_{en}{\nu }_e\left(v_e{F}_0+\frac{T_n}{m_e}\frac{d{F}_0}{d{v}_e}\right)d{v}_e=\frac{3}{2}\frac{{⟨{\delta }_{en}{v}_e^2{\nu }_e⟩}_e{n}_e}{{⟨v_e^2⟩}_e}\left(T_n-T_e\right).(63)$

For general $F_0$, but constant ${\delta }_{en}$, we can rewrite the cooling term in Equation 51 as

$-2\pi m_e{\int }_0^{\infty }{v}_e^3{\delta }_{en}{\nu }_e\left(v_e{F}_0+\frac{T_n}{m_e}\frac{d{F}_0}{d{v}_e}\right)d{v}_e=\frac{3}{2}{\delta }_{en}{⟨{\nu }_e⟩}_e{n}_e\left({\alpha }_P{T}_n-{\beta }_P{T}_e\right),(64)$

where we integrated by parts and used Equations 56 and 58a. Equation 64 shows that for general non-Maxwellian $F_0$, the cooling term is not necessarily proportional to the temperature difference $(T_n-T_e)$. However, for the power-law dependent ${\nu }_e\propto v_e^{2\alpha }$ and Maxwellian $F_0$, according to Equation 62, we have ${\beta }_P={\alpha }_P=1+2\alpha /3$. In this case, the structure of the cooling term proportional to ${\alpha }_P⟨{\nu }_e⟩n_e$ matches that of the frictional heating term for a purely perpendicular field, ${\alpha }_P⟨{\nu }_e⟩m_e{n}_e{V}_{e\perp }^2$, as seen from the first term in the RHS of Equation 51.

5 Discussion

When applying a fluid model for analytic calculations or simulations, it is important to have the corresponding equations with accurate parameters applicable to the relevant physical conditions. These equations and parameters are usually derived from the kinetic theory, so their accuracy is determined by the accuracy of the underlying kinetic approach.

Based on two different kinetic approaches, this article derives the fluid model equations that describe low-frequency plasma processes in the highly dissipative E-region ionosphere. The treatment is restricted to collisions of the plasma particles, ions, or electrons with the neutral molecules only; no Coulomb collisions are considered. The neglect of Coulomb collisions at the E-region ionosphere is usually well justified, although sometimes electron–electron collisions may play a role, resulting in a more efficient “Maxwellization” of the electron distribution function (Dimant and Sudan, 1995a). Such Maxwellization makes the fluid model (as opposed to the pure kinetic theory) more applicable. For the plasma particle collisions with neutrals (elastic or inelastic), here, we assume the known cross sections relevant for various elastic and inelastic collisional processes as functions of the colliding particle velocities. Assuming these known cross sections, we can always calculate velocity dependencies of the kinetic collision frequencies, ${\nu }_p({\vec{v}}_p)$ $(p=i,e,n)$. These velocity dependencies of the collisional cross-sections can be taken from the literature [e.g., for the dominant electron-nitrogen collisions, see Itikawa (2006), Song et al. (2023), and references therein]. The resultant fluid model parameters are expressed in general integral forms through these known velocity dependencies. For the most important plasma processes, such as the small-to medium-scale cross-field plasma instabilities (the thermal Farley–Buneman and gradient drift instabilities), closed 5-moment multi-fluid models are usually sufficient for the accurate fluid description. Given the plasma species $p$, the 5-moment set of unknowns includes the particle densities $(n_p)$, temperatures $(T_p)$, and the three components of the mean drift velocity, ${\vec{V}}_p$.

For the ionospheric ions $(p=i)$, we have employed the well-known and fairly simple BGK collisional model. For the heavy ions, the applicability of the BGK collision operator can be justified by the fact that within the thermal bulk and around, the kinetic ion-neutral collision frequency ${\nu }_{in}$ is approximately constant, that is, velocity-independent; this approximation corresponds to Maxwell molecule collisions (Schunk and Nagy, 2009). Additionally, the ion masses in the E-region ionosphere are fairly close to the neutral-molecule masses, $m_i\simeq m_n$. As we demonstrate in Section 3, in the case of $m_i=m_n$, the oversimplified BGK model results even in quantitatively accurate frictional heating and cooling terms; see the RHS of Equation 21. We should bear in mind, however, that for sufficiently strong electric field, $E\gtrsim m_i{\nu }_i{v}_{Ti}/e$, that is, when the mean ion drift speed, $eE/(m_i{\nu }_i)$, becomes on the order or larger than the ion thermal speed $v_{Ti}$, the ion distribution function can be significantly distorted with an appreciable deviation from Maxwellian (Koontaweepunya et al., 2024). Although the major ion fluid terms remain valid in this case, the entire 5-moment model cannot be easily closed, and hence its validity may be questionable. The factor of strong electric field is usually of importance for the high-latitude E region under conditions of severe magnetospheric perturbations (geomagnetic storms or substorms), while at the equatorial E region, the electric fields are typically much weaker so that the closed 5-moment ion-fluid model is usually much more applicable.

The central part of this paper is the derivation of the 5-moment fluid equations for electrons. For the light electrons, unlike the ions, the simple BGK model cannot serve even as a crude approximation. As we explained in Section 4, the reasons for the total BGK model inapplicability are the two major facts: (1) the mean rate of the collisional loss of the electron energy is much less than the corresponding loss of the electron momentum so that the electron behavior cannot be described by a single collisional parameter; (2) the kinetic collisional frequency ${\nu }_e$ has a pronounced electron velocity dependence. The first fact leads to a strong isotropization of the electron velocity distribution, while the speed dependence of the electron velocity distribution is effectively decoupled from the angular dependence in the velocity space. The second fact leads to noticeable modifications of the electron-fluid coefficients and even to the occurrence of additional thermo-diffusion terms. As a result, in the general case, the fluid model coefficients acquire numerical multipliers whose values are determined by some integral relations over the entire electron distribution function, see Equations 52–61. For the Maxwellian function, and especially for the power-law dependencies of the ${\nu }_e$-speed dependence, these general integral relations reduce to simple algebraic ones, ${\nu }_e(v_e)\propto v_e^{2\alpha }$; see Equation 62 and Figure 1. From that figure, we see that some numerical multipliers can deviate significantly from unity although remaining in the same order of magnitude. A better knowledge of these fluid coefficients is important for accurate calculations and predictions of the physical characteristics of various wave processes. As our future knowledge of the speed dependence of the kinetic collision rates becomes more precise, using the more general integral relationships obtained here, one can obtain the improved values of the corresponding fluid model coefficients.

The kinetic approach employed in this paper is based on the expansion of the electron velocity distribution in Legendre polynomials (in the velocity space) and keeping the two first terms of such expansion, see Equation 22: the dominant isotropic part, $F_0(\vec{r},t,v_e)$, and a small directional part, $|{\vec{f}}_1(\vec{r},t,v_e)|\cos \vartheta$, where $\vartheta$ is the angle between ${\vec{f}}_1$ and ${\vec{v}}_e$, and $v_e=|{\vec{v}}_e|$ is the electron speed. This approach is analogous to that employed by Gurevich (1978) [see also Dimant and Sudan (1995a)], although, as we explained in Section 4.1, Gurevich’s fluid equations for electrons, Gurevich (1978), Chapter 5, derived through this kinetic approach, differ from ours. Gurevich’s equations are written in a form that does not include explicit adiabatic and frictional heating terms. Purely mathematically, however, these equations might be equivalent to ours, except for the “adiabatic” terms proportional to $({\gamma }_{e,i}-1)$ in Gurevich (1978) Equations (5.3) and (5.4). These terms are extraneous, and their correct equivalent has already been implicitly distributed within the other terms in Gurevich (1978) Equation (5.8)–(5.11) and hence included twice (Gurevich, 1978).

An alternative kinetic approach to electron-fluid description is based on Grad’s method (Kissack et al., 1995; Kissack et al., 1997; Kissack et al., 2008a; Kissack et al., 2008b). The latter assumes that only a finite number of parameters characterize the velocity distribution and also implies that the electron velocity distribution is reasonably close to Maxwellian. Our approach is much more general in terms of the $v_e$-dependence, but it restricts the angular distribution of the EDF to the simplest linear deviation from the isotropy. This approximation allows calculating vector fluxes like $n_e{\vec{V}}_e$ or energy fluxes (see below), but higher-order tensor characteristics like an anisotropic pressure, etc., may require an accuracy beyond its field of applicability. Note, however, that high-order tensor characteristics for electrons are not expected to be significant due to the relatively high rate of EDF isotropization associated with a small value of ${\delta }_{en}\sim \left(2--4\right)\times 10^{-3}$ within the low-energy electron energy range, ${\mathcal{E}}_e\equiv m_e{v}_e^2/2<2$eV (Gurevich, 1978). Note also that under physical conditions when the two methods are applicable, both techniques provide reasonably close quantitative results. At the same time, our kinetic approach provides much simpler, and hence much more practical, algebraic expressions applicable to various small- and medium-scale E-region processes.

6 Conclusion

Based on relevant physical conditions, we have derived improved fluid equations for the E-region ionosphere. In this derivation, we have used two different approximate kinetic approaches for the E-region ions and electrons.

For the ions, we have employed the simple BGK collision operator (Section 3). This resulted in a full 5-moment set of the continuity, momentum, and energy-balance equations, see Equations 19–21. Although these equations look conventional, our derivation has demonstrated that for the E-region ions with almost equal masses of the ions and neutrals, the BGK collision operator leads to quantitatively accurate frictional and cooling rates.

The central part of this paper is the derivation of the electron-fluid equations. For the electrons, the BGK collisional operator is inapplicable, and we have employed the kinetic approach based on the expansion of the electron distribution function, $f_e({\vec{v}}_e)$, in Legendre polynomials over the angles in the velocity space. Physical conditions resulting in efficient isotropization of $f_e({\vec{v}}_e)$ allowed us to restrict the treatment to the two highest terms of the Legendre expansion: the dominant isotropic part, $F_0(v_e)$ and a small directional part $\overrightarrow{f_1}\cdot {\vec{v}}_e/v_e$. The former is responsible for calculating the scalar fluid quantities, such as the electron density and temperature, while the directional part allows the calculation of the electron flux (or electric current) density. An important factor in our derivations is the fact that the electron-neutral collisional frequencies are strongly velocity-dependent. Assuming these velocity dependencies to be known, we have derived the full set of the 5-moment equations: the continuity equation, the momentum equation, and the thermal balance equation. Because the E-region electrons in all relevant low-frequency processes are essentially inertialess, the momentum equation reduces to an explicit expression for the electron mean drift velocity given by Equation 48. The most non-trivial result is the thermal balance equation given in the general case by Equation 51, where the parameters are given by Equations 40, 56–55. For the Maxwellian distribution function and the power-law speed dependence of the electron-neutral collision frequency, ${\nu }_e(v_e)\propto v_e^{2\alpha }$, the integral relationships for the fluid model parameters reduce to simple algebraic expressions given by Equation 62; see also Figure 1.

Comparison of the general energy balance Equation 51with the corresponding equation for the velocity-independent electron collision frequency (see Equation 45) shows that the velocity dependence of the collision parameters results in more complicated heat conductivity, frictional heating, and cooling, as well as in additional terms associated with the plasma motion and gradients in the parallel to $\vec{B}$ direction. These terms look collisionless, but they originate exclusively from the velocity distribution of ${\nu }_e(v)$. Similar effects in the Hall and Pedersen directions are inconsequential and have been neglected. However, one should not neglect the Hall and Pedersen components in the heat conductivity because the plasma temperature and density gradients in those directions can be much sharper than those in the parallel direction.

In this paper, we discuss only the simple 5-moment sets of fluid equations, although more sophisticated sets of equations, like the 13-moment transport equations, could be used (Schunk and Nagy, 2009). In the highly collisional E-region ionosphere, however, the need for such complicated fluid equations is questionable because the difficulties of implementing them may become comparable to, or even exceed, the difficulties of implementing the more accurate and comprehensive full kinetic theory.

The results of this paper could be used for a routine practical analysis when working with actual data. The improved equations can also serve as a basis for more accurate plasma fluid computer simulations. In the general case, the applicability of the closed 5-moment equations is restricted by reasonably moderate conditions of the equatorial E region. For the high-latitude E-region ionosphere, an accurate description may require using a fully kinetic treatment.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YD: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by NSF Grants 1755350, 1007789, and 0442075 and NASA Grants 80NSSC21K1322 and 80NSSC19K0080.

Acknowledgments

The author is deeply grateful to Prof. Oppenheim for his long-term support, extensive help, and multiple discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1466909/full#supplementary-material

References

Aleksandrov, A. F., Bogdankevich, L. S., and Rukhadze, A. A. (1984). Principles of plasma electrodynamics, 9. New York: Springer Verlag.

Google Scholar

Allis, W. P. (1982). Semidivergence of the Legendre expansion of the Boltzmann equation. Phys. Rev. A 26, 1704–1712. doi:10.1103/PhysRevA.26.1704

CrossRef Full Text | Google Scholar

Bhatnagar, P. L., Gross, E. P., and Krook, M. (1954). A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525. doi:10.1103/PhysRev.94.511

CrossRef Full Text | Google Scholar

Braginskii, S. I. (1965). Transport processes in a plasma. Rev. Plasma Phys. 1, 205.

Google Scholar

Dalgarno, A., McDowell, M. R. C., and Williams, A. (1958). The mobilities of ions in unlike gases. Philosophical Trans. R. Soc. Lond. Ser. A 250, 411–425. doi:10.1098/rsta.1958.0002

CrossRef Full Text | Google Scholar

Dimant, Y. S., Khazanov, G. V., and Oppenheim, M. M. (2021). Effects of electron precipitation on E-region instabilities: theoretical analysis. J. Geophys. Res. 126, e29884. doi:10.1029/2021JA029884

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Oppenheim, M. M. (2004). Ion thermal effects on E-region instabilities: linear theory. J. Atmos. Solar-Terr. Phys. 66, 1639–1654. doi:10.1016/j.jastp.2004.07.006

CrossRef Full Text | Google Scholar

Dimant, Y. S., Oppenheim, M. M., Evans, S., and Martinez-Sykora, J. (2023). Unified fluid theory of the collisional thermal Farley-Buneman instability including magnetized multi-species ions. Phys. Plasmas 30, 102101. doi:10.1063/5.0155500

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1995a). Kinetic theory of low-frequency cross-field instability in a weakly ionized plasma. I. Phys. Plasmas 2, 1157–1168. doi:10.1063/1.871394

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1995b). Kinetic theory of low-frequency cross-field instability in a weakly ionized plasma. II. Phys. Plasmas 2, 1169–1181. doi:10.1063/1.871395

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1995c). Kinetic theory of the Farley-Buneman instability in the E region of the ionosphere. J. Geophys. Res. 100, 14605–14623. doi:10.1029/95JA00794

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1997). Physical nature of a new cross-field current-driven instability in the lower ionosphere. J. Geophys. Res. 102, 2551–2564. doi:10.1029/96JA03274

CrossRef Full Text | Google Scholar

Evans, S., Oppenheim, M., Martínez-Sykora, J., Dimant, Y., and Xiao, R. (2023). Multifluid simulation of solar chromospheric turbulence and heating due to thermal farley-buneman instability. Astrophys. J. 949, 59. doi:10.3847/1538-4357/acc5e5

CrossRef Full Text | Google Scholar

García-Colín, L. S., Velasco, R. M., and Uribe, F. J. (2004). Inconsistency in the Moment’s method for solving the Boltzmann equation. J. Non Equilib. Thermodyn. 29, 257–277. doi:10.1515/JNETDY.2004.054

CrossRef Full Text | Google Scholar

Grad, H. (1949). On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2, 331–407. doi:10.1002/cpa.3160020403

CrossRef Full Text | Google Scholar

Gurevich, A. V. (1978). Nonlinear phenomena in the ionosphere, 10. New York: Springer Verlag. doi:10.1007/978-3-642-87649-3

CrossRef Full Text | Google Scholar

Itikawa, Y. (2006). Cross sections for electron collisions with nitrogen molecules. J. Phys. Chem. Reference Data 35, 31–53. doi:10.1063/1.1937426

CrossRef Full Text | Google Scholar

Janhunen, P. (1995). On recent developments in E-region irregularity simulations and a summary of related theory. Ann. Geophys. 13, 791–806. doi:10.1007/s00585-995-0791-7

CrossRef Full Text | Google Scholar

Kagan, L. M., and Kelley, M. C. (2000). A thermal mechanism for generation of small-scale irregularities in the ionospheric E region. J. Geophys. Res. 105, 5291–5303. doi:10.1029/1999JA900415

CrossRef Full Text | Google Scholar

Khazanov, G. V. (2011). Kinetic theory of the inner magnetospheric plasma. New York: Springer.

Google Scholar

Kissack, R. S., Kagan, L. M., and St. -Maurice, J. P. (2008a). Thermal effects on Farley-Buneman waves at nonzero aspect and flow angles. I. Dispersion relation. Phys. Plasmas 15, 022901. doi:10.1063/1.2834275

CrossRef Full Text | Google Scholar

Kissack, R. S., Kagan, L. M., and St. -Maurice, J. P. (2008b). Thermal effects on Farley-Buneman waves at nonzero aspect and flow angles. II. Behavior near threshold. Phys. Plasmas 15, 022902. doi:10.1063/1.2834276

CrossRef Full Text | Google Scholar

Kissack, R. S., St-Maurice, J. P., and Moorcroft, D. R. (1995). Electron thermal effects on the Farley-Buneman fluid dispersion relation. Phys. Plasmas 2, 1032–1055. doi:10.1063/1.871383

CrossRef Full Text | Google Scholar

Kissack, R. S., St. -Maurice, J. P., and Moorcroft, D. R. (1997). The effect of electron-neutral energy exchange on the fluid Farley-Buneman instability threshold. J. Geophys. Res. 102, 24091–24116. doi:10.1029/97JA02036

CrossRef Full Text | Google Scholar

Koontaweepunya, R., Dimant, Y. S., and Oppenheim, M. M. (2024). Non-maxwellian ion distribution in the equatorial and auroral electrojets. arXiv e-prints , arXiv2408. doi:10.48550/arXiv.2408.06339

CrossRef Full Text | Google Scholar

Kovalev, D. V., Smirnov, A. P., and Dimant, Y. S. (2008). Modeling of the Farley-Buneman instability in the E-region ionosphere: a new hybrid approach. Ann. Geophys. 26, 2853–2870. doi:10.5194/angeo-26-2853-2008

CrossRef Full Text | Google Scholar

Lifshitz, E. M., and Pitaevskii, L. P. (1981). Physical kinetics. Elsevier.

Google Scholar

Makarevich, R. A. (2020). Toward an integrated view of ionospheric plasma instabilities: 5. Ion-thermal instability for arbitrary ion magnetization, density gradient, and wave propagation. J. Geophys. Res. 125, e28349. doi:10.1029/2020JA028349

CrossRef Full Text | Google Scholar

Milikh, G. M., and Dimant, Y. S. (2003). Model of anomalous electron heating in the E region: 2. Detailed numerical modeling. J. Geophys. Res. 108, 1351. doi:10.1029/2002JA009527

CrossRef Full Text | Google Scholar

Oppenheim, M., Dimant, Y., Longley, W., and Fletcher, A. C. (2020). Newly discovered source of turbulence and heating in the solar chromosphere. Astrophys. J. 891, L9. doi:10.3847/2041-8213/ab75bc

CrossRef Full Text | Google Scholar

Oppenheim, M., Otani, N., and Ronchi, C. (1995). Hybrid simulations of the saturated Farley-Buneman instability in the ionosphere. Geophys. Res. Lett. 22, 353–356. doi:10.1029/94GL03277

CrossRef Full Text | Google Scholar

Oppenheim, M., Otani, N., and Ronchi, C. (1996). Saturation of the Farley-Buneman instability via nonlinear electron E×B drifts. J. Geophys. Res. 101, 17273–17286. doi:10.1029/96JA01403

CrossRef Full Text | Google Scholar

Oppenheim, M. M., Dimant, Y., and Dyrud, L. P. (2008). Large-scale simulations of 2-D fully kinetic Farley-Buneman turbulence. Ann. Geophys. 26, 543–553. doi:10.5194/angeo-26-543-2008

CrossRef Full Text | Google Scholar

Oppenheim, M. M., and Dimant, Y. S. (2004). Ion thermal effects on E-region instabilities: 2D kinetic simulations. J. Atmos. Solar-Terr. Phys. 66, 1655–1668. doi:10.1016/j.jastp.2004.07.007

CrossRef Full Text | Google Scholar

Oppenheim, M. M., and Dimant, Y. S. (2013). Kinetic simulations of 3-D Farley-Buneman turbulence and anomalous electron heating. J. Geophys. Res. 118, 1306–1318. doi:10.1002/jgra.50196

CrossRef Full Text | Google Scholar

Robinson, T. R. (1998). The effects of small scale field aligned irregularities on E-region conductivities: implications for electron thermal processes. Adv. Space Res. 22, 1357–1360. doi:10.1016/S0273-1177(98)80034-3

CrossRef Full Text | Google Scholar

Rodbard, M. G., Bezerra, J. A. G., and Kremer, G. M. (1995). A combined Chapman-Enskog and Grad method. II. Ionized gases. Phys. Plasmas 2, 642–648. doi:10.1063/1.871416

CrossRef Full Text | Google Scholar

Rojas, E. L., Burns, K. J., and Hysell, D. L. (2023). Fluid models capturing Farley-Buneman instabilities. Ann. Geophys. 41, 281–287. doi:10.5194/angeo-41-281-2023

CrossRef Full Text | Google Scholar

Schunk, R., and Nagy, A. (2009). Ionospheres: Physics, plasma Physics, and chemistry. Cambridge: University Press. doi:10.1017/CBO9780511635342

CrossRef Full Text | Google Scholar

Schunk, R. W., and Walker, J. C. G. (1971). Transport processes in the E region of the ionosphere. J. Geophys. Res. 76, 6159–6171. doi:10.1029/JA076i025p06159

CrossRef Full Text | Google Scholar

Schunk, R. W., and Walker, J. C. G. (1972). Ion velocity distributions in the auroral ionosphere. Planet. Space Sci. 20, 2175–2191. doi:10.1016/0032-0633(72)90071-2

CrossRef Full Text | Google Scholar

Shkarofsky, J. P., Johnston, T. W., and Bachynski, M. P. (1966). The particle kinetics of plasmas. Reading: Addison-Wesley.

Google Scholar

Song, M.-Y., Cho, H., Karwasz, G. P., Kokoouline, V., and Tennyson, J. (2023). Cross sections for electron collisions with N2, N2*, and N2+. J. Phys. Chem. Reference Data 52, 023104. doi:10.1063/5.0150618

CrossRef Full Text | Google Scholar

St-Maurice, J. P., and Goodwin, L. (2021). Revisiting the behavior of the E region electron temperature during strong electric field events at high latitudes. J. Geophys. Res. 126, e8288. doi:10.1029/2020JA028288

CrossRef Full Text | Google Scholar

St. -Maurice, J. P., and Kissack, R. S. (2000). The role played by thermal feedback in heated Farley-Buneman waves at high latitudes. Ann. Geophys. 18, 532–546. doi:10.1007/s00585-000-0532-x

CrossRef Full Text | Google Scholar

St-Maurice, J. P., and Schunk, R. W. (1973). Auroral ion velocity distributions using a relaxation model. Planet. Space Sci. 21, 1115–1130. doi:10.1016/0032-0633(73)90200-6

CrossRef Full Text | Google Scholar

St-Maurice, J. P., and Schunk, R. W. (1974). Behaviour of ion velocity distributions for a simple collision model. Planet. Space Sci. 22, 1–18. doi:10.1016/0032-0633(74)90119-6

CrossRef Full Text | Google Scholar

St-Maurice, J. P., and Schunk, R. W. (1977). Auroral ion velocity distributions for a polarization collision model. Planet. Space Sci. 25, 243–260. doi:10.1016/0032-0633(77)90135-0

CrossRef Full Text | Google Scholar

Stubbe, P. (1990). The concept of a kinetic transport theory. Phys. Fluids B 2, 22–33. doi:10.1063/1.859535

CrossRef Full Text | Google Scholar

Velasco, R. M., Uribe, F. J., and García-Colín, L. S. (2002). Inconsistencies in moment methods. Phys. Rev. E 66, 032103. doi:10.1103/PhysRevE.66.032103

CrossRef Full Text | Google Scholar

Zhang, Y., and Varney, R. H. (2024). A statistical survey of e-region anomalous electron heating using poker flat incoherent scatter radar observations. J. Geophys. Res. 129, e2023JA032360. doi:10.1029/2023JA032360

CrossRef Full Text | Google Scholar