Study of the isomeric yield ratio in the photoneutron reaction of natural holmium induced by laser-accelerated electron beams

Introduction: An accurate knowledge of the isomeric yield ratio (IR) induced by the photonuclear reaction is crucial to study the nuclear structure and reaction mechanisms. ¹⁶⁵Ho is a good candidate for the investigation of the IR since the Ho target has a natural abundance of 100% and the residual nuclide has a good decay property.

Methods: In this study, the photoneutron production of ^{164m, g}Ho induced by laser-accelerated electron beams is investigated experimentally. The γ-ray spectra of activated Ho foils are off-line detected. Since the direct transitions from the ^164mHo are not successfully observed, we propose to extract the IRs of the ^{164m, g}Ho using only the photopeak counts from the ground-state decay.

Results: The production yields of ^{164m, g}Ho are extracted to be (0.45 ± 0.10) × 10⁶ and (1.48 ± 0.14) × 10⁶ per laser shot, respectively. The resulting IR is obtained to be 0.30 ± 0.08 at the effective γ-ray energy of 12.65 MeV.

Discussion: The present data, available experimental data, and TALYS calculations are then compared to examine the role of the excitation energy. It is found that besides the giant dipole resonance, the excitation energy effect also plays a key role in the determination of the IRs.

1 Introduction

Nuclear isomers have been widely studied due to their fascinating applications, including medical imaging (Habs et al., 2011; Pan et al., 2021), nuclear clocks (Peik et al., 2021), and nuclear batteries (Prelas et al., 2014). They still play a crucial role in various aspects of astrophysical nuclear reactions (Hayakawa et al., 2008; Zilges et al., 2022). In many nuclear reactions, the residual nuclei have isomeric states with narrow energy levels and relatively long half-lives. The isomeric cross-section or yield ratio (IR) of high-spin to low-spin states of the residual nucleus provides valuable information about nuclear structure and reaction mechanisms, such as the transfer of angular momentum, the spin dependence of nuclear level density, the amelioration in γ-ray transition theory, and tests of different models (Naik et al., 2016; Rahman et al., 2020). In addition, the IR plays a key role in calculating the total production cross-section of the residual products when the production cross-section of one isomer is known in advance.

The excitation energy and angular momentum of incident particles can significantly affect the IR values of the residual products. The IRs have been studied in nuclear reactions induced by different incident particles, such as photon (Rahman et al., 2016), proton (Hilgers et al., 2007), neutron (Luo et al., 2014), and alpha (Kim et al., 2015). Compared to other particles, photons carry a smaller angular momentum of 1ℏ or 2ℏ. Furthermore, intense bremsstrahlung photons can be readily produced using radio-frequency (RF) electron accelerators. As a result, the photonuclear reactions seem to be a good tool to investigate the effect of the excitation energy on the IR. Kolev et al. (1995) deduced the experimental IRs of (γ, 3n)^{110m, g}In, (γ, n)^{164m, g}Ho, and (γ, 3n) ^{162m, g}Ho by a bremsstrahlung source with an end-point energy of 43 MeV. Thiep et al. (2011) determined the IRs of ¹⁶⁵Ho(γ, n)^{164m, g}Ho and ¹⁷⁵Lu (γ, n)^{174m, g}Lu reactions in the bremsstrahlung energy region from 14 to 25 MeV. Do et al. (2013) measured the IRs of ^{164m, g}Ho and ^{162m, g}Ho via ¹⁶⁵Ho(γ, n) and ¹⁶⁵Ho(γ, 3n) reactions in the bremsstrahlung energy region from 45 to 65 MeV. It is noticeable that the available IRs for the ¹⁶⁵Ho(γ, n)^{164m, g}Ho reactions are still scarce. It particularly lacks experimental data in the energy region below 11 MeV. With the rapid development of high-intensity laser technology (Danson et al., 2019), laser–plasma interactions are used to study various nuclear phenomena (Schlenvoigt et al., 2008; Günther et al., 2022; Cao et al., 2023). Recently, the efficient production of nuclear isomers, including ^{113m, 115m}In and ^93mMo, has been studied experimentally using the laser-accelerated electron beam (e⁻ beam) (Feng et al., 2022; Fan et al., 2023 under review).

In this study, we experimentally investigate the production of ^{164m, g}Ho by laser-induced photoneutron reactions. The γ-ray spectra of the activated Ho foils are detected by an offline γ-ray spectrometry technique. Since the direct transitions from ^164mHo were not successfully observed, we propose to extract the ground and isomeric yields of ¹⁶⁴Ho using only the photopeak counts from the ground-state decay. We should note that this approach differs from determining the counts of two photopeaks that directly characterize the isomeric and ground states. The IR value of ¹⁶⁵Ho(γ, n)^{164m, g}Ho is obtained for a given excitation energy. The present and similar literature data on IRs are compared to examine the role of excitation energy. Furthermore, the cross-section and IR curves of the ¹⁶⁵Ho(γ, n)^{164m, g}Ho reaction are calculated by the TALYS software to examine the compatibility of the theoretical model with the experimental data.

2 Experimental setup

The ^{164m, g}Ho production experiment was performed on the XingGuang-III laser facility at the Laser Fusion Research Center in Mianyang. The experimental setup is schematically shown in Figure 1A. An intense laser pulse with a duration of ∼0.8 ps and energy of ∼100 J was focused by an f/2.6 off-axis parabola (OAP) mirror (Robbie et al., 2018) onto a supersonic gas jet with a well-defined uniform density distribution (Feng et al., 2022). In the first stage of the experiment, high-charge multi-MeV e⁻ beams were produced during the laser–gas interactions. An image plate (IP) stack with a central hole was used to measure the spatial distribution of the laser-accelerated e⁻ beam. It should be noted that the IP stack is composed of seven IPs, with each IP being stuck on a tantalum foil with a thickness of 0.5 mm. Meanwhile, an electron magnetic spectrometer (EMS) was placed downstream of the IP stack to accurately diagnose the energy of the e⁻ beam passing through the central hole of the IP stack. In the second stage of the experiment, a metal stack composed of Ta foil and stacked Ho foils was installed, and both the IP stack and EMS were uninstalled. The Ta foil is 2 mm thick, in which energetic bremsstrahlung photons are generated. The stacked Ho foils used for activation have 10 layers in total, with each layer having a thickness of 1 mm and a natural abundance of 99.99% (Inagaki et al., 2020). During the activation, the bremsstrahlung radiations irradiate the Ho foils, successfully triggering photoneutron reactions and then producing a large number of ^{164m, g}Ho, as shown in Figure 1B. After the activation, the Ho foils are taken out from the target chamber of the XingGuang-III laser facility. The activation spectra are recorded using a high-purity germanium (HPGe) detector. The response of the HPGe detector has been well calibrated by standard γ-ray sources, including ⁶⁰Co, ¹⁵²Eu, ¹³³Ba, ²²⁶Ra, ¹³⁷Cs, and ²⁴¹Am. In order to reduce the self-absorption effect induced by the stacked Ho foils, the 10 layers are spread out at the surface of the Al window of the HPGe detector.

FIGURE 1

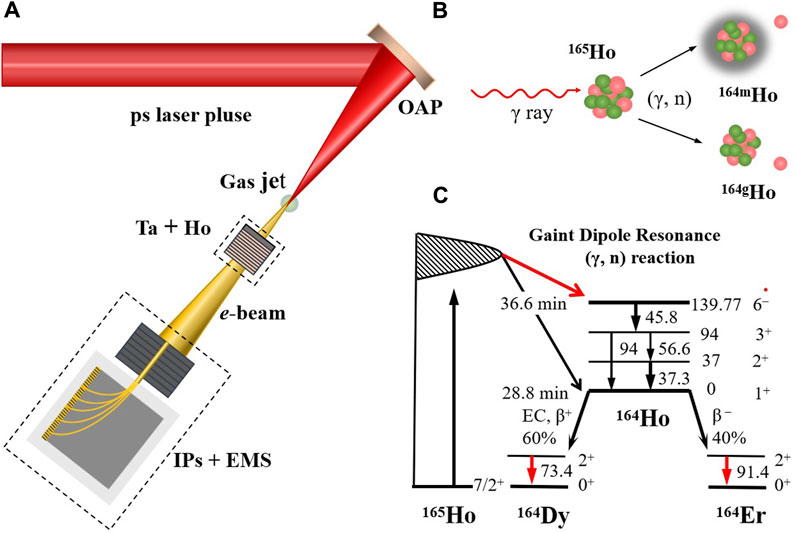
FIGURE 1. Experimental setup for the production of ^{164m, g}Ho at the XingGuang-III laser facility (not to scale) (A). Schematic view of the photoneutron production of ^{164m, g}Ho (B) and the partial-level scheme of ^{164m, g}Ho and the decay property of ^164gHo (not to scale) (C). As the laser-accelerated e⁻ beam fires to the metal stack (Ta + Ho), a large number of bremsstrahlung photons are generated, and subsequently, the Ho stacks are activated via photoneutron reactions, producing ¹⁶⁴Ho in both the ground state (J^π = 1⁺) and isomeric state (J^π = 6⁻) (Singh et al., 2018). The 6⁻ isomer in ¹⁶⁴Ho decays, via only internal decay, to the ground state. The decay from the 6⁻ isomer to the 3⁺ excited state is an E3 transition. This 3⁺ excited state subsequently de-excites to the ground state. The resulting transition energies are 94.0, 56.6, and 37.3 keV. Finally, the ground-state decays to the daughter nucleus ¹⁶⁴Dy or ¹⁶⁴Er, emitting two characteristic γ-rays at 73.4 and 91.4 keV.

3 Isomeric yield ratio determination

The temporal evolution of the numbers of nuclei that are formed in the isomeric and ground states is described by the following kinetic equations (Thiep et al., 2011):

$\left\{\begin{array}{l}\frac{d{N}_m}{dt}=p_m-{\lambda }_m{N}_m,\\ \frac{d{N}_g}{dt}=p_g+\eta {\lambda }_m{N}_m-{\lambda }_g{N}_g,\end{array}\right.(1)$

where the subscripts $m$ and $g$ designate the isomeric and ground states of ¹⁶⁴Ho, respectively; $p_m$ and $p_g$ are the production rates leading to ¹⁶⁴Ho in the isomeric and ground states; $N_m$ and $N_g$ are the numbers of nuclei in the corresponding states; ${\lambda }_m$ and ${\lambda }_g$ are the constants of nuclear decay; and $\eta$ is the transition coefficient from the isomeric state to the ground state. These equations describe the processes involved in the direct production of the desired isotopes during the target irradiation and the reduction of the number of nuclei as a result of their radioactive decay. The production rate $p_x$ with $x$ being the subscript $m$ or $g$ (similarly hereinafter) can be written as (Kolev et al., 1995)

$p_x=N_0{\int }_{E_{th}}^{E_{\mathit{max}}}\phi \left(E_{\gamma }\right){\sigma }_x\left(E_{\gamma }\right)d{E}_{\gamma }=N_0\mathrm{\Phi }〈{\sigma }_x〉,(2)$

where $N_0$ is the number of target nuclei, $\phi \left(E_{\gamma }\right)$ represents the bremsstrahlung photon flux; ${\sigma }_x\left(E_{\gamma }\right)$ is the reaction cross-section leading to the formation of ¹⁶⁴Ho in both the isomeric and ground states; $E_{th}$ and $E_{\mathit{max}}$ are the reaction threshold and bremsstrahlung end-point energy, respectively; $\mathit{\Phi }={\int }_{{\mathit{E}}_{\mathit{th}}}^{{\mathit{E}}_{\mathit{max}}}\mathit{\phi }\left({\mathit{E}}_{\mathit{\gamma }}\right)\mathit{d}{\mathit{E}}_{\mathit{\gamma }}$ is the integrated photon flux; and $〈{\mathit{\sigma }}_{\mathit{x}}〉={\int }_{{\mathit{E}}_{\mathit{th}}}^{{\mathit{E}}_{\mathit{max}}}\mathit{\phi }\left({\mathit{E}}_{\mathit{\gamma }}\right){\mathit{\sigma }}_{\mathit{x}}\left({\mathit{E}}_{\mathit{\gamma }}\right)\mathit{d}{\mathit{E}}_{\mathit{\gamma }}/{\int }_{{\mathit{E}}_{\mathit{th}}}^{{\mathit{E}}_{\mathit{max}}}\mathit{\phi }\left({\mathit{E}}_{\mathit{\gamma }}\right)\mathit{d}{\mathit{E}}_{\mathit{\gamma }}$ is the flux-weighted average cross-section leading to the isomeric or ground state.

Since the gamma spectroscopy method is used in the experiment, the photopeak counts ($C_x$) of the characteristic γ-ray of interest can be readily obtained over the detection time $t_d$. When taking into account the irradiation time $t_{irr}$ and the cooling time $t_c$, the solution of Eq. 1 in three time intervals ($t_{irr}$, $t_c$, and $t_d$) and the consequent integration of the relevant activity over the $t_d$ lead to

$C_m=I_m{\epsilon }_m{Ap}_m,(\mathrm{3a})$

$C_g=I_g{\epsilon }_g\left(B{p}_g+D{p}_m\right),(\mathrm{3b})$

where $I_x$ and ${\epsilon }_x$ are the branching intensity and source-peak detection efficiency of the characteristic γ-rays to be detected, respectively. The other variables are listed as follows: $A=\frac{1}{{\lambda }_m}\left(1-e^{-{\lambda }_m{t}_{irr}}\right)e^{-{\lambda }_m{t}_c}\left(1-e^{-{\lambda }_m{t}_d}\right)$, $B=\frac{1}{{\lambda }_g}\left(1-e^{-{\lambda }_g{t}_{irr}}\right)e^{-{\lambda }_g{t}_c}\left(1-e^{-{\lambda }_g{t}_d}\right)$, and $D=\frac{\eta }{{\lambda }_g-{\lambda }_m}\left[\frac{{\lambda }_g}{{\lambda }_m}\left(1-e^{-{\lambda }_m{t}_{irr}}\right)\right.$$\left.e^{-{\lambda }_m{t}_c}\left(1-e^{-{\lambda }_m{t}_d}\right)-\frac{{\lambda }_m}{{\lambda }_g}\left(1-e^{-{\lambda }_g{t}_{irr}}\right)e^{-{\lambda }_g{t}_c}\left(1-e^{-{\lambda }_g{t}_d}\right)\right]$.

In the case of the bremsstrahlung photon, the expression of the IR reads (Jonsson et al., 1977) as follows:

$IR=\frac{〈{\sigma }_m〉}{〈{\sigma }_g〉}=\frac{p_m}{p_g}.(4)$

Usually, the IR in a nuclear reaction is determined by measuring the counts of photopeaks that characterize the isomeric and ground states, respectively. When one or more photopeaks induced by the isomeric state are directly detected, the $p_x$ and the resulting $\text{IR}$ values can be readily obtained by solving Eq. 3 and Eq. 4, respectively (Rahman et al., 2020). In the case of the Ho sample, the photopeak at 37.3 keV is popularly used to characterize the isomeric state, while that at 73.4 and 91.4 keV is used to characterize the ground state, as shown in Figure 1C. In our experiment, the 37.3 keV photopeak was not successfully observed. This is because only single-shot irradiation is performed, and both the ${\sigma }_m$ and ${\epsilon }_m$ values are relatively small. As a result, the abovementioned approach used to extract the IR value becomes invalid. It is shown in Eq. 3b that both the isomeric and ground states contribute to the $C_g$ value, which varies with the $t_d$. It suggests that the $p_x$ values can also be obtained by solving only Eq. 3b at two different time instants. More specifically, the $p_x$ values can be deduced by solving the simultaneous equations of Eq. 3b at $t_d^i$ and $t_d^j$, with i and j denoting two arbitrary time instants.

$\left\{\begin{array}{c}{p}_g=\frac{D_j{Y}_i-D_i{Y}_j}{B_i{D}_j-B_j{D}_i},\\ p_m=\frac{B_i{Y}_j-B_j{Y}_i}{B_i{D}_j-B_j{D}_i},\end{array}\right.(5)$

where $Y_i=C_g^i/I_g{\epsilon }_g$. This indicates that using only the photopeak counts from the ground-state decay, the $IR$ value can be obtained. Furthermore, a group of data on $IR$ can be obtained by reasonably changing the time increments. According to the error propagation, the uncertainties of the $p_x$ values can be determined by the following formula:

$\left\{\begin{array}{c}\sigma \left(p_g\right)=\sqrt{\frac{{D_j}^2{\sigma \left(Y_i\right)}^2+{D_i}^2{\sigma \left(Y_j\right)}^2}{{\left(B_i{D}_j-B_j{D}_i\right)}^2}},\\ \sigma \left(p_m\right)=\sqrt{\frac{{B_i}^2{\sigma \left(Y_j\right)}^2+{B_j}^2{\sigma \left(Y_i\right)}^2}{{\left(B_i{D}_j-B_j{D}_i\right)}^2}}.\end{array}\right.(6)$

As a result, the uncertainty of the $IR$ value can be written as

$\sigma \left(IR\right)=IR\sqrt{\frac{{\sigma \left(p_g\right)}^2}{{p_g}^2}+\frac{{\sigma \left(p_m\right)}^2}{{p_m}^2}}.(7)$

4 Results and discussion

4.1 Electron spectra

In our experiment, high-energy electrons are mainly produced by the parametrically enhanced direct laser acceleration (Cao et al., 2023). As the electron yield and charge are sensitive to the plasma density, the e^–beam generation can be optimized by adjusting the backing pressure of the gas jet. Figure 2A shows the energy distributions of truncated e^–beams recorded by the EMS at two backing pressures of 2.0 and 2.6 MPa. The spectral pattern of the e^–beam can be described by a Boltzmann distribution $\frac{dN}{dE}\propto e^{-\frac{E}{T_e}}$, where the $T_e$ is the slope temperature (Qi et al., 2019). The fitting results show that the $T_e$ values are 7.8 MeV and 4.8 MeV for backing pressures of 2.0 MPa and 2.6 MPa, respectively. In addition, the charge of the laser-accelerated electrons higher than 1 MeV is Q_e ∼ 42 nC at 2.0 MPa, which is 2.5 times higher than that at 2.6 MPa. The spatial distribution of the e^–beam is shown in Figure 2B. It is visibly seen that a bright spot is located beneath the central hole. According to the experimental arrangement and the spot size of the e⁻ beam, the laser-accelerated e^–beam has an angular divergence of approximately 200 mrad (FWHM).

FIGURE 2

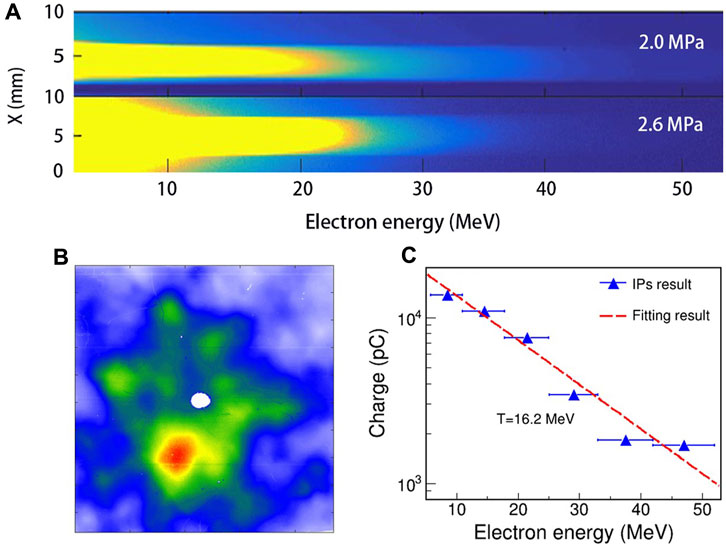
FIGURE 2. Spectral distributions of the laser-accelerated e⁻ beam diagnosed by the EMS (A), spatial distribution of the laser-accelerated e⁻ beam recorded at the backing pressure of 2.0 MPa (B), and the electron charge in dependence on the electron energy (C).

Generally, only high-energy electrons can be used to induce isomer production. However, the bright electron spot is located beneath the central hole, as shown in Figure 2B. This suggests that most of the electrons with high energy did not pass through the central hole of the IP stack and were not recorded by the EMS in our experiment. To understand more about the spectral pattern of the laser-accelerated e⁻ beam, we utilized the Geant4 toolkit (Agostinelli et al., 2003) to simulate the attenuation of monoenergetic electrons inside the IP stack. For a given energy, when the number of incident electrons reduces by a factor of 0.9, such energy is regarded as the minimum energy recorded by each IP. Then, the spectral distribution of the e⁻ beam can be figured out but with a relatively large uncertainty. Similar studies have been conducted by Bonnet et al. (2013) and Nishiuchi et al. (2020). Figure 2C shows the simulated electron spectral distribution, which matches well with the Boltzmann distribution. Note that the uncertainty represents the detectable energy range for each IP. The slope temperature is fitted to be 16.2 MeV, which is two times higher than the one recorded by the EMS. This is because the bright e⁻ beam was not centered with the hole on the IP stack so that the EMS only detected the low-energy part of the e^– beam, as presented earlier. Since the slope temperature is sufficiently high, such an e^– beam interacting with a Ta foil can generate a high flux of bremsstrahlung radiation.

4.2 Characteristic γ-ray spectrum

The characteristic γ-rays emitted from the Ho sample were measured with the HPGe detector, as mentioned earlier. In our case, the cooling time $t_c$ is 30 min. Figure 3A shows the measured characteristic γ-ray spectra for $t_d$ = 240 min, from which two photopeaks at 73.4 keV ($I_g$ = 1.88%) and 91.4 keV ($I_g$ = 2.30%) are clearly observed, whereas the 37.3 keV γ-ray for ^164mHo does not appear. This is because the amount of ^164mHo produced during a single-shot irradiation was not enough to be detectable after the cooling time of 30 min. However, the signal and background counts around the γ-ray energy at 37.3 keV can be used to safely determine an upper limit for the yield of ^164mHo. By integrating over the energy region of the characteristic γ-ray at 37.3 keV, the signal and background counts are 242, which gives an upper limit of 0.85 × 10⁶ for the ^164mHo yield according to Eq. 3a.

FIGURE 3

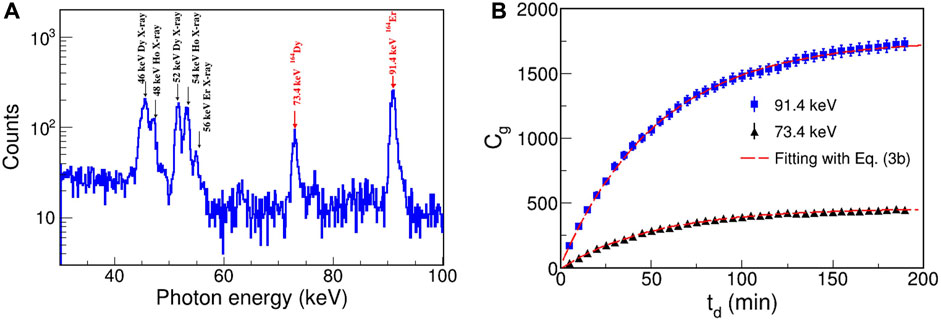
FIGURE 3. Typical γ-ray spectrum from the activated Ho foils ($t_c$ = 30 min and $t_d$ = 240 min) (A) and accumulated photopeak counts as a function of detection time (B).

As mentioned previously, reasonably partitioning the $C_g$ is vital to obtain the $p_x$ and the resulting IR. The $C_g$ values for 73.4 and 91.4 keV lines as functions of $t_d$ are shown in Figure 3B. The temporal variation of $C_g$ can be fitted well with Eq. 3b. The fitting curve can be re-written as

$C_g=P_0{e}^{-{\lambda }_g{t}_d}+P_1{e}^{-{\lambda }_m{t}_d}+P_2,(8)$

where $P_0$, $P_1$, and $P_2$ are the coefficients dependent on the $p_x$. More specifically, the coefficients $P_0$ and $P_2$ are associated with both the $p_m$ and $p_g$. $P_1$ is the function of $p_m$. From Eq. 8, one can see that the $C_g$ value is not only contributed by the ground state of ¹⁶⁴Ho but also induced by its isomeric state. In our case, the $P_1$ is fitted to be −1865 ± 229, and the $p_m$ value is then obtained to be (0.44 ± 0.05) × 10⁶. The resulting confidence level is approximately 9.0 σ.

4.3 Isomeric ratio calculation

The calculation of the IR relies on the determination of $p_m$ and $p_g$. Since the characteristic γ-ray line at 37.3 keV is not observed in our case, we employ the approach shown in Eq. 5 to extract the $p_x$ values of ^{164m, g}Ho. Figure 4A presents 10 groups of $p_x$ values obtained with the photopeak counts at 91.4 keV. The average $\overline{p_m}$ and $\overline{p_g}$ are calculated to be 0.45 × 10⁶ and 1.48 × 10⁶ per laser shot, respectively. The uncertainty of $p_x$ is determined by $\sigma \left(p_x\right)=\sqrt{{\displaystyle {\sum }_{i=1}^{i=n}}{\sigma }_i^2\left(p_x\right)/n}$, where the ${\sigma }_i\left(p_x\right)$ is the uncertainty of $p_x^i$ calculated by Eq. 6. Finally, the $p_m$ and $p_g$ of Ho produced in the experiment are obtained to be (0.45 ± 0.10) × 10⁶ and (1.48 ± 0.14) × 10⁶ per laser shot, respectively. Accordingly, the confidence level of $p_m$ is 4.5 σ. It should be noted that the $p_m$ value is in good agreement with the one obtained by fitting the $C_g$ curve, as discussed earlier. However, its confidence level is smaller than the confidence level of $P_1$. This is reasonable since the former reasonably considers the error propagation. In addition, the $p_m$ value is almost two times lower than the upper limit of 0.85 × 10⁶ mentioned earlier, which in turn validates the feasibility of extracting the ^164mHo yield using only the peak counts from the ground-state decay. Similarly, the $IR$ value and its uncertainty $\sigma \left(IR\right)$ are calculated with Eq. 4 and 7, respectively. Figure 4B shows 10 groups of $IRs$ and their average value. The $IR$ value of ^{164m, g}Ho is 0.30 ± 0.08, which is less than unity. This is because the spin (J = 6) of the isomeric state is visibly higher than the ground state with J = 1.

FIGURE 4

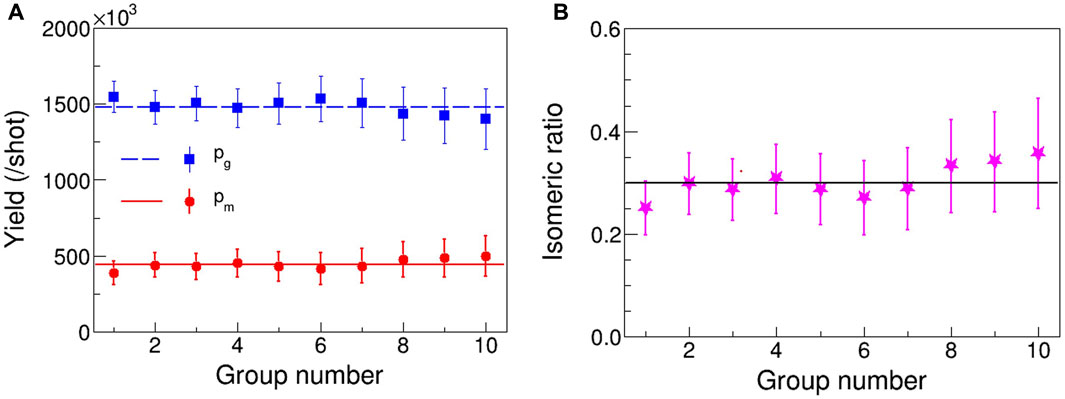
FIGURE 4. Ten groups of $p_m$, $p_g$ (A), and $IRs$ (B) for the 91.4 keV photopeak. Group No. i ($i=1,2,\dots \dots ,10$) indicates the data calculated with the photopeak counts at $t_d^i$ $=5i+40$ min and $t_d^j=5i+120$ min. In (A), the blue and red lines stand for the average $\overline{p_m}$ and $\overline{p_g}$, respectively. In (B), the black line represents the average value of $IR$ s.

Photoneutron reaction cross-section of ¹⁶⁵Ho calculated with TALYS 1.9 (Koning et al., 2019) and the data from the Experimental Nuclear Reaction Database (EXFOR) are compared and shown in Figure 5A. One can see that the ¹⁶⁵Ho(γ, n)^164gHo reaction plays a dominant role in the giant dipole resonance (GDR) region. The ¹⁶⁵Ho(γ, n)^164mHo reaction has a similar distribution with the ¹⁶⁵Ho(γ, n)^164gHo. However, its maximum cross-section, ∼60 mb, is visibly lower than that of the latter. As the photon energy continues to increase, the multiple emission reactions take over. The maximum cross-section decreases as the number of emitted particles increases. The TALYS calculations are in overall good agreement with the EXFOR data obtained from previous measurements using photon sources caused by positron annihilation in flight (Bergère et al., 1968; Berman et al., 1969). This indicates the reliability of the TALYS inputs and calculations. In addition, it is noticeable that the available experimental data in terms of isomer production are very rare, which can potentially be measured using state-of-the-art laser-Compton scattering facilities generating high-intensity and quasi-monoenergetic γ-ray beams (An et al., 2018; Wang et al., 2022).

FIGURE 5

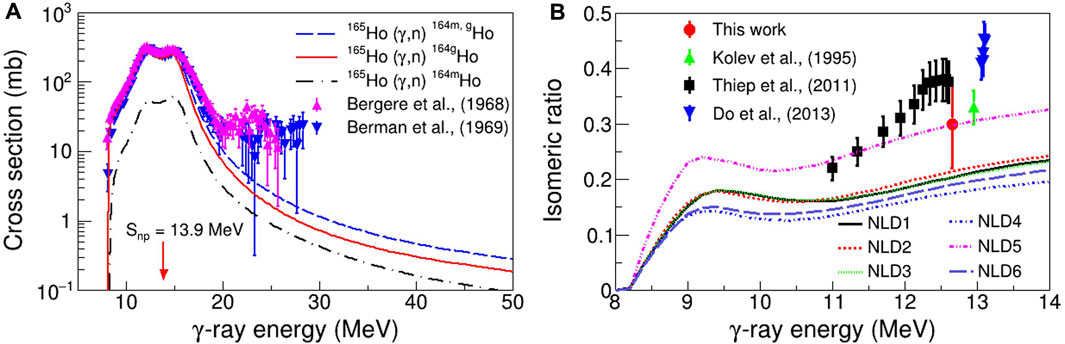
FIGURE 5. Calculated (γ, n) cross-sections for ¹⁶⁵Ho and the available EXFOR data for comparison (A) and the flux-averaged IR of ^{164m, g}Ho in the ¹⁶⁵Ho(γ, n) reaction as a function of excitation energy (B). In (A), the experimental data are total cross-sections of the ¹⁶⁵Ho(γ, n) and ¹⁶⁵Ho(γ, np) reactions, and $S_{np}$ denotes the threshold energy for the ¹⁶⁵Ho(γ, np) reaction. In (B), the previous experimental data (Kolev et al., 1995; Thiep et al., 2011; Do et al., 2013) are obtained by bremsstrahlung photons from RF electron accelerators, and TALYS calculations considering different nuclear level density (NLD) models are also presented for comparison.

The $IR$s of ^{164m, g}Ho can be examined by using different bremsstrahlung radiations from both the laser-plasma accelerator and the RF accelerator. For this purpose, the effective γ-ray energy $〈E_{\gamma }〉$ from the threshold to the end-point energy can be obtained by using the following relation (Jacobs et al., 1979):

$〈E_{\gamma }〉=\frac{{\int }_{E_{th}}^{E_{\mathit{max}}}\phi \left(E_{\gamma }\right){\sigma }_R\left(E_{\gamma }\right)E_{\gamma }d{E}_{\gamma }}{{\int }_{E_{th}}^{E_{\mathit{max}}}\phi \left(E_{\gamma }\right){\sigma }_R\left(E_{\gamma }\right)d{E}_{\gamma }},(9)$

where the $\phi \left(E_{\gamma }\right)$ is calculated with the Geant4 toolkit considering their realistic target arrangements, and ${\sigma }_R\left(E_{\gamma }\right)$ is the cross-section for the ¹⁶⁵Ho(γ, n)^{164m, g}Ho reaction, which is calculated by using the default option in the TALYS software. In order to understand the effect of excitation energy, the measured $IR$ value of ^{164m, g}Ho from the present work, literature values, and TALYS calculations are plotted in Figure 5B as a function of $〈E_{\gamma }〉$. From the EXFOR data, one can see that when $〈E_{\gamma }〉$ > 11 MeV, the $IR$ of ^{164m, g}Ho increases with the $〈E_{\gamma }〉$ and then gets saturated. This is because the input angular momentum brought in by photons is very low. Since the experimental data are not available within the energy range $〈E_{\gamma }〉$ < 11 MeV, the $IR$s are further calculated with the TALYS software considering different NLD models. It is found that the $IR$ clearly depends on the $〈E_{\gamma }〉$. The increasing and decreasing trends of the IR values appear within the energy range of 8.5 < $〈E_{\gamma }〉$ <11.0 MeV. Such trends are not only due to the excitation energy effect but also due to the GDR effect. In our experiment, the $IR$ value of ^{164m, g}Ho is 0.30 ± 0.08 at $〈E_{\gamma }〉$ = 12.65 MeV, which is in agreement with both TALYS calculations and the data of Kolev et al. (1995) within the statistical uncertainty. However, the experimental $IR$s provided by Thiep et al. (2011) and Do et al. (2013) are higher than the TALYS calculations at $〈E_{\gamma }〉$ > 12 MeV.

5 Conclusion

We carried out the experiment to produce ^{164m, g}Ho via photoneutron reaction induced by a laser-accelerated electron beam, in which the IR value of ^{164m, g}Ho is determined by using the activation and offline γ-ray spectrometry technique. However, since the characteristic γ-rays from the isomeric decay of ^164mHo were not successfully observed, we propose to extract the production yields of ^{164m, g}Ho by partitioning counts of photopeak characterizing the ground-state decay. This is different from the approach by extracting the counts of two photopeaks characterizing directly the isomeric and ground states. The production yields of ^{164m, g}Ho were successfully extracted to be (0.45 ± 0.10) × 10⁶ and (1.48 ± 0.14) × 10⁶ per laser shot. Accordingly, the IR value is calculated to be 0.30 ± 0.08 at $〈E_{\gamma }〉$ = 12.65 MeV. The IR as a function of $〈E_{\gamma }〉$ is further calculated with the TALYS software considering different NLD models. It is found that our result is in agreement with both TALYS calculations and the available experimental data within the statistical uncertainty. In addition, the increasing and decreasing trends of the IR values are observed within the energy range of 8.5 < $〈E_{\gamma }〉$ <11.0 MeV, suggesting that excitation energy is crucial to determine the IR value of ^{164m, g}Ho.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

JZ: Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–original draft. WQ: Data curation, Investigation, Resources, Writing–review and editing. WF: Data curation, Visualization, Writing–review and editing. ZC: Data curation, Software, Writing–review and editing. KL: Data curation, Visualization, Writing–review and editing. CT: Software, Writing–review and editing. XZ: Resources, Writing–review and editing. ZD: Resources, Writing–review and editing. ZZ: Resources, Writing–review and editing. XL: Writing–review and editing. YY: Writing–review and editing. WL: Funding acquisition, Supervision, Writing–review and editing. WZ: Funding acquisition, Supervision, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key R&D Program of China (Grant No. 2022YFA1603300), the National Natural Science Foundation of China (Grant No. U2230133), the Independent Research Project of the Key Laboratory of Plasma Physics, CAEP (Grant No. JCKYS2021212009), the Open Fund of the Key Laboratory of Nuclear Data, CIAE (Grant No. JCKY2022201C152), the Research Foundation of Education Bureau of Hunan Province, China (No. 22B0453), the Hunan Provincial Natural Science Foundation of China (No. 2023JJ40525), and the Hengyang Municipal Science and Technology Project (No. 202150054076).

Acknowledgments

The authors thank the XingGuang-III operation team for operating the laser system and providing the laser-accelerated electron beam.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agostinelli, S., Allison, J., Amako, K., Apostolakis, J., Araujoa, H., Arce, P., et al. (2003). GEANT4-a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 506 (3), 250–303. doi:10.1016/S0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

An, G., Chi, Y., Dang, Y., Fu, G., Guo, B., Huang, Y., et al. (2018). High energy and high brightness laser Compton backscattering gamma-ray source at IHEP. Matter Radiat. Extrem 3 (4), 219–226. doi:10.1016/j.mre.2018.01.005

CrossRef Full Text | Google Scholar

Bergère, R., Beil, H., and Veyssière, A. (1968). Photoneutron cross sections of La, Tb, Ho and Ta. Nucl. Phys. 121 (2), 463–480. doi:10.1016/0375-9474(68)90433-8

CrossRef Full Text | Google Scholar

Berman, B. L., Kelly, M. A., Bramblett, R. L., Caldwell, J. T., and Fultz, S. C. (1969). Giant resonance in deformed nuclei: photoneutron cross sections for Eu¹⁵³, Dd¹⁶⁰, Ho¹⁶⁵, and W¹⁸⁶. Phys. Rev. 185 (4), 1576–1590. doi:10.1103/PhysRev.185.1576

CrossRef Full Text | Google Scholar

Bonnet, T., Comet, M., Denis-Petit, D., Gobet, F., Hannachi, M., Tarisien, M., et al. (2013). Response functions of fuji imaging plates to monoenergetic protons in the energy range 0.6–3.2 MeV. Rev. Sci. Instrum. 84 (1), 013508. doi:10.1063/1.4775719

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Z., Qi, W., Lan, H., Cui, B., Zhang, X., Deng, Z., et al. (2023). Experimental study of medical isotopes ^62,64Cu and ⁶⁸Ga production using intense picosecond laser pulse. Plasma Phys. control. Fusion 65, 055007. doi:10.1088/1361-6587/acc090

CrossRef Full Text | Google Scholar

Danson, C., Haefner, C., Bromage, J., Butcher, T., Chanteloup, J., Chowdhury, E., et al. (2019). Petawatt and exawatt class lasers worldwide. High. Power Laser Sci. 7, E54. doi:10.1017/hpl.2019.36

CrossRef Full Text | Google Scholar

Do, N. V., Khue, P. D., Thanh, K. T., Hien, N. T., Kim, G., Lee, M., et al. (2013). Measurement of isomeric yield ratios for the ^natHo(γ, xn)^{164m, g; 162m, g}Ho reactions in the bremsstrahlung energy region from 45 to 65 MeV. J. Radioanal. Nucl. 298, 1447–1452. doi:10.1007/s10967-013-2608-6

CrossRef Full Text | Google Scholar

Fan, W., Qi, W., Zhang, J., Cao, Z., Lan, H., Li, X., et al. (2023). Efficient production of nuclear isomer ^93mMo with laser-accelerated proton beam and an astrophysical implication on ⁹²Mo production. Available at: https://arxiv.org/ftp/arxiv/papers/2308/2308.02994.pdf.

Google Scholar

Feng, J., Li, Y., Tan, J., Wang, W., Li, Y., Zhang, X., et al. (2022). Laser plasma accelerated ultra-intense electron beam for efficiently exciting nuclear isomers. doi:10.48550/arXiv.2203.06454

CrossRef Full Text | Google Scholar

Günther, M. M., Rosmej, O. N., Tavana, P., Gyrdymov, M., Skobliakov, A., Kantsyrev, A., et al. (2022). Forward-looking insights in laser-generated ultra-intense γ-ray and neutron sources for nuclear application and science. Nat. Commun. 13, 170. doi:10.1038/s41467-021-27694-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Habs, D., and Köster, U. (2011). Production of medical radioisotopes with high specific activity in photonuclear reactions with γ-beams of high intensity and large brilliance. Appl. Phys. B 103, 501–519. doi:10.1007/s00340-010-4278-1

CrossRef Full Text | Google Scholar

Hayakawa, T., Miyamoto, S., Hayashi, Y., Kawase, K., Horikawa, K., Chiba, S., et al. (2008). Half-life of the 164Ho by the (γ,n) reaction from laser Compton scattering γ rays at the electron storage ring NewSUBARU. Phys. Rev. C 74, 065802. doi:10.1103/physrevc.74.065802

CrossRef Full Text | Google Scholar

Hilgers, K., Qaim, S. M., and Sudar, S. (2007). Formation of the isomeric pairs ¹³Nd^m,g and ¹¹Nd^m,g in proton and ³He-particle-induced nuclear reactions. Phys. Rev. C 76, 064601. doi:10.1103/PHYSREVC.76.064601

CrossRef Full Text | Google Scholar

Inagaki, M., Sekimoto, S., Tadokoro, T., Ueno, Y., Kani, Y., Ohtsuki, T., et al. (2020). Production of ⁹⁹Mo/^99mTc by photonuclear reaction using a ^natMoO₃ target. J. Radioanal. Nucl. Chem. 324, 681–686. doi:10.1007/s10967-020-07086-9

CrossRef Full Text | Google Scholar

Jacobs, E., Thierens, H., Frenne, D. D., Clercq, A. D., D'hondt, P., Gelder, P. D., et al. (1979). Product yields for the photofission of ²³⁸U with 12-15-20-30-and 70-MeV bremsstrahlung. Phys. Rev. C 19 (2), 422–432. doi:10.1103/PhysRevC.19.422

CrossRef Full Text | Google Scholar

Jonsson, G., and Eriksson, M. (1977). Isomeric ratios in photon-induced spallation reactions at intermediate energies. Z. Phys. A 281, 53–56. doi:10.1007/BF01408612

CrossRef Full Text | Google Scholar

Kim, K., Kim, G., Naik, H., Zaman, M., Yang, S., Song, T., et al. (2015). Excitation function and isomeric ratio of Tc-isotopes from the ⁹³Nb(α, xn) reaction. Nucl. Phys. 935, 65–78. doi:10.1016/j.nuclphysa.2014.12.006

CrossRef Full Text | Google Scholar

Kolev, D., Dobreva, E., Nenov, N., and Todorov, V. (1995). A convenient method for experimental determination of yields and isomeric ratios in photonuclear reactions measured by the activation technique. Nucl. Instrum. Methods Phys. Res. Sect. A 356 (2-3), 390–396. doi:10.1016/0168-9002(94)01319-5

CrossRef Full Text | Google Scholar

Koning, A. J., Rochman, D., Sublet, J., Dzysiuk, N., Fleming, M., and Marck, S. V. D. (2019). TENDL: complete nuclear data library for innovative nuclear science and technology. Nucl. Data Sheets 155, 1–55. doi:10.1016/j.nds.2019.01.002

CrossRef Full Text | Google Scholar

Luo, J., and Jiang, L. (2014). Ground-state and isomeric-state cross sections for ¹⁶⁵Ho(n, 2n)¹⁶⁴Ho reaction from the reaction threshold to 20 MeV. Phys. Rev. C 89, 014604. doi:10.1103/PhysRevC.89.014604

CrossRef Full Text | Google Scholar

Naik, H., Kim, G. N., Schwengner, R., Kim, K., Zaman, M., Yang, S. C., et al. (2016). Measurement of isomeric ratios for ^89g,mZr, ^91g,mMo, and ^97g,mNb in the bremsstrahlung end-point energies of 16 and 45-70 MeV. Eur. Phys. J. 52, 47. doi:10.1140/epja/i2016-16047-8

CrossRef Full Text | Google Scholar

Nishiuchi, M., Sakaki, H., Dover, N. P., Miyahara, T., Shiokawa, K., Manabe, S., et al. (2020). Ion species discrimination method by linear energy transfer measurement in Fujifilm BAS-SR imaging plate. Rev. Sci. Instrum. 91, 093305. doi:10.1063/5.0016515

PubMed Abstract | CrossRef Full Text | Google Scholar

Peik, E., Schumm, T., Safronova, M. S., Pálffy, A., Weitenberg, J., and Thirolf, P. G. (2021). Nuclear clocks for testing fundamental physics. Quantum Sci. Technol. 6, 034002. doi:10.1088/2058-9565/abe9c2

CrossRef Full Text | Google Scholar

Prelas, M. A., Weaver, C. L., Watermann, M. L., Lukosi, E. D., Schott, R. J., and Wisniewskiet, A. (2014). A review of nuclear batteries. Prog. Nucl. Energ 75, 117–148. doi:10.1016/j.pnucene.2014.04.007

CrossRef Full Text | Google Scholar

Qi, W., Zhang, X., Zhang, B., He, S., Zhang, F., Cui, B., et al. (2019). Enhanced photoneutron production by intense picoseconds laser interacting with gas-solid hybrid targets. Phys. Plasmas. 26, 043103. doi:10.1063/1.5079773

CrossRef Full Text | Google Scholar

Rahman, M. S., Kim, K., Kim, G., Naik, H., Nadeem, M., Hien, N. T., et al. (2016). Measurement of flux-weighted average cross-sections and isomeric yield ratios for ¹⁰³Rh(γ, xn) reactions in the bremsstrahlung end-point energies of 55 and 60 MeV. Eur. Phys. J. A 52, 194. doi:10.1140/epja/i2016-16194-x

CrossRef Full Text | Google Scholar

Rahman, M. S., Kim, K., Nguyen, T. H., Kim, G., Naik, H., Yang, S., et al. (2020). Measurement of flux-weighted average cross sections of ^natIn(γ, xn) reactions and isomeric yield ratios of ^{112mg, 111m,g, 110m,g} in with bremsstrahlung. Eur. Phys. J. A 56, 235. doi:10.1140/epja/s10050-020-00245-2

CrossRef Full Text | Google Scholar

Robbie, W., Martin, K., Ross, G., David, C., Rachel, D., Nicholas, B., et al. (2018). Development of focusing plasma mirrors for ultraintense laser-driven particle and radiation sources. Quantum Beam Sci. 2 (1), 1. doi:10.3390/qubs2010001

CrossRef Full Text | Google Scholar

Schlenvoigt, H. P., Haupt, K., Debus, A., Budde, F., Jäckel, O., Pfotenhauer, S., et al. (2008). A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nat. Phys. 4, 130–133. doi:10.1038/nphys811

CrossRef Full Text | Google Scholar

Pan, W., Song, T., Lan, H., Ma, Z., Zhang, J., Zhu, Z., and Luo, W. (2021). Photo-excitation production of medically interesting isomers using intense γ-ray source. Appl Radiat Isotopes 168, 109534. doi:10.1016/j.apradiso.2020.109534

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, B., and Chen, J. (2018). Nuclear data sheets for A=164. Nucl. Data Sheets 147, 1–381. doi:10.1016/j.nds.2018.01.001

CrossRef Full Text | Google Scholar

Thiep, T. D., An, T. T., Cuong, P. V., Vinh, N. T., and Belov, A. G. (2011). Study of the isomeric ratios in photonuclear reactions of natural holmium and lutetium induced by bremsstrahlungs with endpoint energies in the giant dipole resonance region. J. Radioanal. Nucl. Chem. 290, 515–524. doi:10.1007/s10967-011-1257-x

CrossRef Full Text | Google Scholar

Wang, H., Fan, G., Liu, L., Xu, H., Shen, W., Ma, Y., et al. (2022). Commissioning of laser electron gamma beamline SLEGS at SSRF. Nucl. Sci. Tech. 33, 87. doi:10.1007/s41365-022-01076-0

CrossRef Full Text | Google Scholar

Zilges, A., Balabanski, D., Isaak, J., and Pietralla, N. (2022). Photonuclear reactions-From basic research to applications. Prog. Part. Nucl. Phys. 122, 103903. doi:10.1016/j.ppnp.2021.103903

CrossRef Full Text | Google Scholar

Appendix

The photopeak counts $C_x$ ($x=m,g$) is the integration of the Activity $A_x$ for x-state considering $I_x$ and ${\epsilon }_x$ over a detection time $t_d$ as follows:

$C_x={\int }_0^{t_d}{I}_x{\epsilon }_x{A}_{x}dt.(\mathrm{A1})$

As shown above, the activity $A_x$ is the key factor in the $C_x$ solution. According to Eq. 1 in the proof (on line 204), in irradiation interval, both the productions and the decay properties contribute to the activities of the isomeric and ground states. And in the cooling and the detection interval, only the decay properties of two states contribute to the activities. So, we deduce the activities of the isomeric and ground states for two intervals, i.e., the irradiation interval and the natural decay interval (including cooling interval and detection interval).

Firstly, the number of x-state $N_x$ at the irradiation time $t_{irr}$ can be solved out. In irradiation interval, the $N_x$ changes as a function of $t_{irr}$ and the formula is like to Eq. 1 in the proof. By solving the Eq. 1 in the proof, the $N_x$ at the irradiation time $t_{irr}$ can be obtained as:

$N_m=\frac{1}{{\lambda }_m}{p}_m\left(1-e^{-{\lambda }_m{t}_{irr}}\right),(\mathrm{A2})$

$\begin{array}{ll}\hfill N_g& =\eta p_m\frac{1}{{\lambda }_g\left({\lambda }_g-{\lambda }_m\right)}\left({\lambda }_g\left(1-e^{-{\lambda }_m{t}_{irr}}\right)-{\lambda }_m\left(1-e^{-{\lambda }_g{t}_{irr}}\right)\right)\hfill \\ \hfill & +\frac{1}{{\lambda }_g}{p}_g\left(1-e^{-{\lambda }_g{t}_{irr}}\right).\hfill \end{array}(\mathrm{A3})$

And then, in the cooling and the detection intervals, the production doesn’t do any contribution to the activities of the isomeric and ground states. Therefore, the Eq. 1 in the proof for the cooling and detection intervals can be written as:

$\left\{\begin{array}{c}\hfill \frac{d{N}_m}{dt}=-{\lambda }_m{N}_m,\hfill \\ \hfill \frac{d{N}_g}{dt}=\eta {\lambda }_m{N}_m-{\lambda }_g{N}_g.\hfill \end{array}\right.(\mathrm{A4})$

By solving it, the $N_x$ changes as a function of the cooling $t_c$ and the detection $t_d$ times can be obtained as:

$N_m=\frac{1}{{\lambda }_m}{p}_m\left(1-e^{-{\lambda }_m{t}_{irr}}\right)e^{-{\lambda }_m{t}_d}{e}^{-{\lambda }_m{t}_m},(\mathrm{A5})$

$\begin{array}{ll}\hfill N_g& =\frac{{{\eta }_{m}p}_m}{{\lambda }_g\left({\lambda }_g-{\lambda }_m\right)}\left({\lambda }_g\left(1-e^{-{\lambda }_m{t}_{irr}}\right)e^{-{\lambda }_m{t}_c}{e}^{-{\lambda }_m{t}_d}-{\lambda }_m\left(1-e^{-{\lambda }_g{t}_{irr}}\right)\right.\hfill \\ \hfill & \times \left.e^{-{\lambda }_g{t}_c}{e}^{-{\lambda }_g{t}_d}\right)+\frac{1}{{\lambda }_g}{p}_g\left(1-e^{-{\lambda }_g{t}_{irr}}\right)e^{-{\lambda }_g{t}_c}{e}^{-{\lambda }_g{t}_d}.\hfill \end{array}(\mathrm{A6})$

Due to $A_x={\lambda }_x{N}_x$, the $A_x$ can be obtained as the following:

$A_m=p_m\left(1-e^{-{\lambda }_m{t}_{irr}}\right)e^{-{\lambda }_m{t}_d}{e}^{-{\lambda }_m{t}_m},(\mathrm{A7})$

$\begin{array}{ll}\hfill A_g& =\frac{{{\eta }_{m}p}_m}{\left({\lambda }_g-{\lambda }_m\right)}\left({\lambda }_g\left(1-e^{-{\lambda }_m{t}_{irr}}\right)e^{-{\lambda }_m{t}_c}{e}^{-{\lambda }_m{t}_d}-{\lambda }_m\left(1-e^{-{\lambda }_g{t}_{irr}}\right)\right.\hfill \\ \hfill & \times \left.e^{-{\lambda }_g{t}_c}{e}^{-{\lambda }_g{t}_d}\right)+p_g\left(1-e^{-{\lambda }_g{t}_{irr}}\right)e^{-{\lambda }_g{t}_c}{e}^{-{\lambda }_g{t}_d}.\hfill \end{array}(\mathrm{A8})$

Substituting Eq. 7 into Eq. 1 and solving it, the $C_m$ can be gotten as:

$C_m=I_m{\epsilon }_m{p}_m\frac{\left(1-e^{-{\lambda }_m{t}_{irr}}\right)}{{\lambda }_m}{e}^{-{\lambda }_m{t}_c}\left(1-e^{-{\lambda }_m{t}_d}\right),(\mathrm{A9})$

where the Eq. 3a in the proof is deduced out.

And do the same performance to Eq. 8 like Eq. 7. The $C_g$ can be obtained as:

$\begin{array}{ll}\hfill C_g& =I_g{\epsilon }_g\left\{p_g\frac{1-e^{-{\lambda }_g{t}_{irr}}}{{\lambda }_g}{e}^{-{\lambda }_g{t}_c}\left(1-e^{-{\lambda }_g{t}_d}\right)+p_m\frac{\eta }{{\lambda }_g-{\lambda }_m}\left[\frac{{\lambda }_g}{{\lambda }_m}\left(1-e^{-{\lambda }_m{t}_{irr}}\right)\right.\right.\hfill \\ \hfill & \times \left.\left.e^{-{\lambda }_m{t}_c}\left(1-e^{-{\lambda }_m{t}_d}\right)-\frac{{\lambda }_m}{{\lambda }_g}\left(1-e^{-{\lambda }_g{t}_{irr}}\right)e^{-{\lambda }_g{t}_c}\left(1-e^{-{\lambda }_g{t}_d}\right)\right]\right\},\hfill \end{array}(\mathrm{A10})$

where the Eq. 3b in the proof is deduced out.