Solitary wave characteristics on the fine structure of the mesospheric sporadic sodium layer

The so-called sporadic sodium layers (SSLs or Na_S) are proposed to be strongly related to wave fluctuations. The solitary wave is a particular solution of the partial differential equation whose energy travels as a localized wave packet. A soliton, on the other hand, is a special type of solitary wave that exhibits a particle-like behavior with a strong stable form. For the first time, the solitary wave theory has been used in this research to study the fine structure of SSL/Na_S. We performed soliton fitting processes on the observed data from the Andes Lidar Observatory and found out that 24/27 Na_S events had exhibited similar features/characteristics to a soliton. Time series of the net anomaly of the Na_S revealed the same variation process to the solution of a generalized five-order KdV equation. Our results, therefore, suggested that the Na_S phenomenon would be a pertinent tracer for non-linear wave studies in the atmosphere.

Highlights

• The solitary wave theory is proposed to be a candidate to explain the fine structure of some particular Na_S events.

• A solitary wave fit was made to the observations from the Andes Lidar Observatory, and 24/27 Na_S events exhibited similar features to a soliton.

• Time series of the net anomaly of the Na_S revealed a similar dynamical process to the solution of a generalized five-order KdV equation.

1 Introduction

The sodium layer is located around an altitude of 80–110 km. Normally, the ablationof meteors produces a Gaussian distribution of mesospheric metals including sodium and iron atoms (Kane and Gardner, 1993; Kopp, 1997). The most interesting phenomenon of the sodium layer is the so-called sporadic sodium layer (SSL or Na_S) (Cox et al., 1993; Gardner et al., 1993; Mathews et al., 1993). For the Na_S event, the sodium density increases rapidly and could be more than double the background value (e.g., with an intensity factor >2) within several minutes in a narrow altitude range (Hansen and von Zahn, 1990). Na_S lasts from tens of minutes to several hours (Nagasawa and Abo, 1995; Prasanth et al., 2007), and their full width at half maximum (FWHM) is usually less than 5 km or sometimes only 1–2 km (Hansen and von Zahn, 1990; Nagasawa and Abo, 1995; Prasanth et al., 2007). Since first reported in 1978 (Clemesha et al., 1978), a lot of viable mechanisms have been proposed (Cox et al., 1993; von Zahn et al., 1987; Zhou et al., 1993). The current evidence suggests that the ion–molecule theory is a possible mechanism for Na_S, based on local observations (Dou et al., 2009; Dou et al., 2010; Hansen and von Zahn, 1990; Heinrich et al., 2008; Heinselman et al., 1998; Kirkwood and Nilsson, 2000; Nesse et al., 2008; Qiu et al., 2016; von Zahn and Hansen, 1988; Williams et al., 2006) and model simulations (Cox et al., 1993; Cox and Plane, 1998; Collins et al., 2002; Plane, 2003; Plane et al., 2015). The sodium ions from E_S could potentially offer a sufficient neutral sodium atom source through recombination with free electrons (Cox et al., 1993; Cox and Plane, 1998; Collins et al., 2002; Plane, 2003; Plane et al., 2015; Qiu et al., 2020). On the other hand, it has also been shown that some regions of the sodium layer can be used as tracers for dynamic disturbances under normal conditions. This means that dynamic influence cannot be ruled out in SSL-related investigations (Gardner and Shelton, 1985; Gardner and Voelz, 1987; Hickey and Plane, 1995; Xu and Smith, 2003).

Mesospheric sodium layer observations by lidars provide a tracer for identifying the atmospheric wave signals (Gardner and Voelz, 1987; Xu and Smith, 2004; Li et al., 2007a; Li et al., 2007b; Gong et al., 2015; Gardner et al., 2019). The existing mechanisms indicate that Na_S is closely related to wave fluctuations (Kane et al., 1991; Zhou et al., 1993; Zhou and Mathews, 1995; Clemesha et al., 1997; Qian et al., 1998). Many observational results reveal that Na_S is frequently accompanied and associated with gravity waves (Qian et al., 1998; Li et al., 2007a; Li et al., 2007b; Ban et al., 2015). Meanwhile, the fine structures of Na_S manifest distinct characters related to waves on short timescales (Liu and Yi, 2009; Chen and Yi, 2011; Liu et al., 2013). The bursts of the sodium atoms show a pulse period of 30 s (Liu and Yi, 2009), indicating a wave fluctuation effect on the evolution of Na_S.

In the last decade and earlier, a peculiar kind of the non-linear wave, which is called the solitary wave, has been widely studied (Belashov and Vladimirov, 2005; Wazwaz, 2009; Benci and Fortunato, 2014). It was first reported by John Scott Russell (1808–1882), when he was observing the motion of a boat rapidly drawn along a narrow channel (Russell, 1884). Ever since then, many researchers have conducted in-depth studies on the theoretical derivation and exploration on this non-linear problem. In general, a solitary wave is a wave which propagates without any temporal evolution in shape or size when viewed in the reference frame moving with the group velocity of the wave and a soliton is a self-reinforcing single wave packet that maintains its shape while it propagates at a constant velocity. It is a stable solution within a non-linear wave equation (Benci and Fortunato, 2014). Soliton is a fascinating topic of interest in modern physics and mathematics (Belashov and Vladimirov, 2005; Wazwaz, 2009; Benci and Fortunato, 2014). It is a physical description and representation for the non-linear wave processes, which plays an important role in the wide spectrum of areas of research related to the wave physics, e.g., in hydrodynamics, plasma physics, condensed matter, and optics (Belashov and Vladimirov, 2005). Nowadays, solitary waves are commonly utilized in Earth Sciences, especially involving oceanic and atmospheric applications, such as surface wave, ion-acoustic wave, magneto-sonic wave, internal gravity wave, and Raleigh wave transmission from the seismic source (Belashov and Vladimirov, 2005).

The non-linear solitary wave theory was first asserted by Diederik Korteweg and Gustav de Vries as the simplified model equation for surface waves on shallow water,

$\frac{\partial \mathit{u}}{\partial \mathit{t}}+\mathit{\alpha }\mathit{u}\frac{\partial \mathit{u}}{\partial \mathit{x}}+\mathit{\beta }\frac{{\partial }^{\mathbf{3}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{3}}}=\mathbf{0},(1)$

with solutions of stable solitary waves (Korteweg and de Vries, 1895). The term soliton was first introduced in 1965 by Zabusky and Kruskal who demonstrated that the Korteweg–de Vries equation (KdV equation) reveals hidden linear properties, allowing a solution in the form of a non-linear solitary wave propagating without changing its profile (Zabusky and Kruskal, 1965). These authors also pointed out that the soliton has two important properties: 1) extremely stable wave packet like a particle and 2) invariant even under particle collisions (Zabusky and Kruskal, 1965).

In this research, the solitary wave theory has been utilized to interpret and explain lidar observations. We performed particular data processing on the observed results from a narrow band lidar at the Andes Lidar Observatory (Liu et al., 2016). We discovered that the fine structure of Na_S evolutions exhibit similar characters to a soliton, indicating a common existence of solitary waves in the mesopause region. The evolution of the net anomaly of the Na_S peak profiles exhibit the same characters to the solution of five-order KdV equation. Our results, therefore, suggest the Na_S phenomenon would be a possible tracer for non-linear wave studies of the mesosphere.

2 Solitary wave theory and data processing

2.1 Non-linear and dispersion effects

Considering a one-dimensional wave at time moment $t$, the particle number density at $x$ in the medium is given by $n\left(x,t\right)$. Under the conservation of particle number, there is

$\frac{\mathit{d}\mathit{n}}{\mathit{d}\mathit{t}}=\mathbf{0},(2)$

where $\mathrm{n}$ could possibly be regarded as the input of sodium sources from Na⁺ through chemical molecule reactions (Cox and Plane, 1998), dynamic processes (Xu and Smith, 2003), or meteor injection (Richter and Sechrist, 1979). Without the non-linear effect, the input of the neutral sodium atoms (which could not be concentrated by electric field or wind shear like the ions) would diffuse away quickly. Fick’s law for the newly created particle flux into the background gas leads to the classical diffusion equation as follows (Schunk and Nagy, 2009):

$n\left(x,t\right)=\frac{N}{2{\left(\pi Dt\right)}^{1/2}}{e}^{-x^2/4Dt},(3)$

where N is the newly generated particle number per unit area (e.g., column density); $D=1.3\frac{kT}{m\nu }$ is the diffusion coefficient; $k=1.381\times {10}^{-23}J/K$ is the Boltzmann constant; $\mathrm{T}=180\mathrm{K}$ is the approximate kinetic temperature deduced from lidar observations; $\mathrm{\nu }=\sqrt{2}n\overline{v}\sigma =\sqrt{2}n\sqrt{\frac{8kT}{\pi m}}\pi {\left(d\right)}^2$ is the averaged collision frequency between the sodium atoms and atmospheric particles; $n={10}^{13}{m}^{-3}$ is the number density of the atmosphere according to results from SABER; $m_p=1.66\times {10}^{-27}km$ and $m_{{Na}_S}=23amu$; and $\mathrm{d}=2\times 186\times {10}^{-12}m$ is the diameter of the sodium atom.

We assign the parameters with appropriate values as $N=3\times {10}^{13}{m}^{-2}$ (assuming at the initial time t₀ the input sodium density $\mathrm{n}=6000{cm}^{-3}$ and the width of Na_S equal to 5 km). Then, after one second, the input of $6000{cm}^{-3}$ would be attenuated to be $\mathrm{n}\left(\mathrm{0,1}\right)=1455{cm}^{-3}$. Within 3.5 min, the input will reduce to nearly zero (e.g., less than 100cm^-3, which is a minor amount compared with the normal sodium layer density).

After the input, $n\left(x,t\right)$ would possibly undergo the evolution in two ways: a convergence or divergence. The full derivative form for $n\left(x,t\right)$ can be expanded as follows:

$\frac{\partial \mathit{n}}{\partial \mathit{t}}+\mathit{v}\frac{\partial \mathit{n}}{\partial \mathit{x}}=\mathbf{0},(4)$

where $\frac{dx}{\partial t}=v$ is the velocity of the particle movement. This equation has a generalized solution:

$\mathit{n}\left(\mathit{x},\mathit{t}\right)=\mathit{f}\left(\mathit{x}-\mathit{v}\left(\mathit{n}\right)\mathit{t}\right).(5)$

This solution indicates each part of the wave has a different speed of $v\left(n\right)$. When $\frac{dv}{dn}>0$, $v\left(n\right)$ increases with an increase in density n and the wave packet front becomes steeper and steeper as the wave propagates, leading to a non-linear effect of convergence (Figure 1A).

FIGURE 1

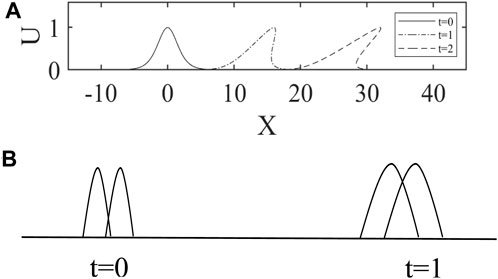
FIGURE 1. Convergence (A) and dispersion (B) effects of a wave. (A) Wave packet front becomes steeper and steeper as the wave propagates, leading to a non-linear effect of convergence. (B) Dispersion effect for the wave packet.

On the other hand, a wave propagating in the $x$ direction can be expressed as follows:

$\mathit{u}\left(\mathit{x},\mathit{t}\right)=\mathit{A}\mathit{e}\mathit{x}\mathit{p}\left[\mathit{i}\left(\mathit{k}\mathit{x}-\mathit{\omega }\mathit{t}\right)\right],(6)$

where $u$ is the wave function, $A$ is the amplitude, $k$ is the wave number, and $\omega$ is the angular frequency. The phase velocity $v_p$ and group velocity $v_g$ are given by

${\mathit{v}}_{\mathit{p}}=\frac{\mathit{\omega }}{\mathit{k}}(7)$

and

${\mathit{v}}_{\mathit{g}}=\frac{\partial \mathit{\omega }}{\partial \mathit{k}},(8)$

respectively. If $\frac{\omega }{k}\ne \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$, each wavelet will have a distinct velocity due to its individual wave vector. Hence, the term $\omega =\omega \left(k\right)$ indicates a dispersion effect of the wave packet (Figure 1B).

Start with Euler’s equations for ideal fluid:

$\begin{array}{c}\frac{\partial \mathit{u}}{\partial \mathit{t}}=-\frac{\mathbf{1}}{\mathit{\rho }}\frac{\partial {\mathit{p}}^{\prime }}{\partial \mathit{x}},\\ \frac{\partial \mathit{w}}{\partial \mathit{t}}=-\frac{\mathbf{1}}{\mathit{\rho }}\frac{\partial {\mathit{p}}^{\prime }}{\partial \mathit{z}},\\ \frac{\partial \mathit{u}}{\partial \mathit{x}}+\frac{\partial \mathit{w}}{\partial \mathit{z}}=\mathbf{0}.\end{array}(9)$

The boundary conditions are

$\left({\left.w\right|}_{z=0}=0,{\left.\left(\frac{\partial {\mathit{p}}^{\prime }}{\partial \mathit{t}}-\rho gw\right)\right|}_{z=h}=0,\right.(10)$

where $u$ represents the horizontal velocity, $w$ represents the vertical velocity, and $p^{\prime }$ is pressure.

Let $\mathcal{L}\equiv \frac{\partial }{\partial \mathit{t}}\left(\frac{{\partial }^{\mathbf{2}}}{\partial {\mathit{x}}^{\mathbf{2}}}+\frac{{\partial }^{\mathbf{2}}}{\partial {\mathit{z}}^{\mathbf{2}}}\right)$, then the formula for Eq. 9 can be compactly written as follows:

$\mathcal{L}\mathit{w}=\mathbf{0}.(11)$

Let

$\mathit{w}=\mathit{W}\left(\mathit{z}\right){\mathit{e}}^{\mathit{i}\left(\mathit{k}\mathit{x}-\mathit{\omega }\mathit{t}\right)},(12)$

and we substitute Eq. 12 into Eq. 11:

$\frac{{\mathit{d}}^{\mathbf{2}}\mathit{W}}{\mathit{d}{\mathit{z}}^{\mathbf{2}}}-{\mathit{k}}^{\mathbf{2}}\mathit{W}=\mathbf{0}.(13)$

Consequently,

$\mathit{W}\left(\mathit{z}\right)=\mathit{A}{\mathit{e}}^{\mathit{k}\mathit{z}}+\mathit{B}{\mathit{e}}^{-\mathit{k}\mathit{z}},(14)$

where $A$ and $B$ are constants.

Substituting Eq. 14 into Eq. 11, we can get

$\mathit{w}=\left(\mathit{A}{\mathit{e}}^{\mathit{k}\mathit{z}}+\mathit{B}{\mathit{e}}^{-\mathit{k}\mathit{z}}\right){\mathit{e}}^{\mathit{i}\left(\mathit{k}\mathit{x}-\mathit{\omega }\mathit{t}\right)}.(15)$

Then, substituting Eq. 15 into Eq. 9,

${\mathit{p}}^{\prime }=\frac{\mathit{i}\mathit{\omega }\mathit{\rho }}{\mathit{k}}\left(\mathit{A}{\mathit{e}}^{\mathit{k}\mathit{z}}-\mathit{B}{\mathit{e}}^{-\mathit{k}\mathit{z}}\right){\mathit{e}}^{\mathit{i}\left(\mathit{k}\mathit{x}-\mathit{\omega }\mathit{t}\right)}.(16)$

According to the lower boundary conditions,

$\mathit{B}=-\mathit{A},(17)$

and according to the upper boundary conditions,

$\left[\left(\frac{{\mathit{\omega }}^{\mathbf{2}}}{\mathit{k}}-\mathit{g}\right){\mathit{e}}^{\mathit{k}\mathit{h}}-\left(\frac{{\mathit{\omega }}^{\mathbf{2}}}{\mathit{k}}+\mathit{g}\right){\mathit{e}}^{-\mathit{k}\mathit{h}}\right]\mathit{A}=\mathbf{0}.(18)$

Thus, we can obtain

$\mathit{\omega }=\sqrt{\mathit{g}\mathit{k}\mathit{t}\mathit{a}\mathit{n}\mathit{h}\left(\mathit{k}\mathit{h}\right).}(19)$

Especially, in shallow water conditions,

$\begin{array}{ll}\mathit{\omega }& =\sqrt{\mathit{g}\mathit{k}\left[\mathit{k}\mathit{h}-\frac{\mathbf{1}}{\mathbf{3}}{\left(\mathit{k}\mathit{h}\right)}^{\mathbf{3}}\right]}\approx \sqrt{{\mathit{k}}^{\mathbf{2}}{\mathit{c}}_{\mathbf{0}}^{\mathbf{2}}\left(\mathbf{1}-\frac{\mathbf{1}}{\mathbf{3}}{\mathit{k}}^{\mathbf{2}}{\mathit{H}}^{\mathbf{2}}\right),}\\ & =\mathit{k}{\mathit{c}}_{\mathbf{0}}\left(\mathbf{1}-\frac{\mathbf{1}}{\mathbf{6}}{\mathit{k}}^{\mathbf{2}}{\mathit{H}}^{\mathbf{2}}\right)=\mathit{k}{\mathit{c}}_{\mathbf{0}}-\frac{\mathbf{1}}{\mathbf{6}}{\mathit{k}}^{\mathbf{3}}{\mathit{c}}_{\mathbf{0}}{\mathit{H}}^{\mathbf{2}},\end{array}(20)$

where $\omega$ is a real number. Then, phase velocity $v_p$ and group velocity $v_g$ can be obtained, respectively, as follows:

${\mathit{v}}_{\mathit{p}}=\frac{\mathit{\omega }}{\mathit{k}}={\mathit{c}}_{\mathbf{0}}-\mathit{\beta }{\mathit{k}}^{\mathbf{2}},{\mathit{v}}_{\mathit{g}}=\frac{\partial \mathit{\omega }}{\partial \mathit{k}}={\mathit{c}}_{\mathbf{0}}-\mathbf{3}\mathit{\beta }{\mathit{k}}^{\mathbf{2}},(21)$

whereas

$\mathit{\beta }={\mathit{c}}_{\mathbf{0}}{\mathit{H}}^{\mathbf{2}}/\mathbf{6}.(22)$

Therefore, when $\beta \ne 0$, $v_p\ne v_g$, which fully indicates that the $\beta \frac{{\partial }^{3}u}{\partial x^3}$ term of the KdV equation characterizes the dispersion effect.

In addition,

$\frac{\mathit{d}{\mathit{v}}_{\mathit{g}}}{\mathit{d}\mathit{k}}=-\mathbf{6}\mathit{\beta }\mathit{k}.(23)$

Therefore, the effect of $\beta \frac{{\partial }^{3}u}{\partial x^3}$ causes wave dispersion. With the increase of $\beta$, the wavelength becomes shorter and the wave dispersion becomes stronger; such waves are known as dispersion waves. Of course, for waves with long wavelength (when $k$ is small), it is a weakly dispersive wave, characterized by $\omega$ containing only the odd degree term of $k$.

On the other hand, since the layer density response is highly dependent on the density gradients occurring in the layer, the steady-state layer density profile becomes important (Gardner and Shelton, 1985). Large density gradients encourage non-linearities in the layer response (Gardner and Shelton, 1985). Therefore, when the non-linear effect affected by the gradient of the Na density profile is balanced with the dispersion effect mentioned previously, the wave shows neither dispersion nor non-linear characteristics, but propagates in the form of solitary waves.

So, the dispersion term of a surface wave in incompressible shallow fluid is given by

$\mathit{\omega }\left(\mathit{k}\right)=\sqrt{\mathit{g}\mathit{h}}\mathit{k}-\frac{\mathbf{1}}{\mathbf{6}}\sqrt{\mathit{g}\mathit{h}}{\mathit{h}}^{\mathbf{2}}{\mathit{k}}^{\mathbf{3}},(24)$

where $h$ is the fluid depth and $g$ is the gravitational acceleration (Belashov and Vladimirov, 2005).

In the complex space, we have $\frac{\partial }{\partial t}\leftrightarrow -i\omega$ and $\frac{\partial }{\partial x}\leftrightarrow ik$. Substituting into Eq. 24, we obtain

$\frac{\partial \mathit{u}}{\partial \mathit{t}}+\left(\sqrt{\mathit{g}\mathit{h}}+\mathit{u}\right)\frac{\partial \mathit{u}}{\partial \mathit{x}}+\frac{\mathbf{1}}{\mathbf{6}}\sqrt{\mathit{g}\mathit{h}}{\mathit{h}}^{\mathbf{2}}\frac{{\partial }^{\mathbf{3}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{3}}}=\mathbf{0}.(25)$

We set $u^{\prime }=u+\sqrt{gh}$ and $\beta =\frac{1}{6}\sqrt{gh}{h}^2$; then, the equation is given by

$\frac{\partial {\mathit{u}}^{\prime }}{\partial \mathit{t}}+{\mathit{u}}^{\prime }\frac{\partial {\mathit{u}}^{\prime }}{\partial \mathit{x}}+\mathit{\beta }\frac{{\partial }^{\mathbf{3}}{\mathit{u}}^{\prime }}{\partial {\mathit{x}}^{\mathbf{3}}}=\mathbf{0}.(26)$

This equation (similar to Eq. 1) is one of the simplest forms of the KdV equation, balanced by both the non-linear term $u\frac{\partial u}{\partial x}$ and dispersion term $\frac{{\partial }^{3}u}{\partial x^3}$. Hereby, the solution satisfying this equation will undergo no convergence or dispersion effect, and the wave shape could be maintained for a long time.

2.2 Solution of the KdV equation and numerical simulation

The travelling wave could be represented by the form $u\left(x,t\right)=f\left(x-ct\right)$, where $u\left(x,t\right)$ represents a disturbance moving in the negative or positive x-direction if $c<0$ or $c>0$, respectively (Wazwaz, 2009). If the solution $u\left(x,t\right)$ depends only on the difference between the two coordinates of the partial differential equations, then the solution keeps its exact shape and, therefore, is called a solitary wave. So, a solitary wave is a travelling wave whose transition from the asymptotic state at $\xi =-\infty$ to the other asymptotic state at $\xi =\infty$ is localized in ξ, where ξ = x-ct, and c is the wave speed (Wazwaz, 2009).

Eq. 26 or Eq. 1 has a special solution given by

$\mathit{u}\left(\mathit{x},\mathit{t}\right)={\mathit{u}}_{\mathbf{2}}+\left({\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}\right)\mathit{sec}{\mathit{h}}^{\mathbf{2}}\sqrt{\frac{{\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}}{\mathbf{12}\mathit{\beta }}}\left(\mathit{x}-\mathit{c}\mathit{t}\right),(27)$

where $u_1$ and $u_2$ are exhibited by Figure 2A, and sech is referred to the hyperbolic secant function (Zabusky and Kruskal, 1965). This is just the bow wave observed by Russell in those early years, e.g., a solitary wave (Zabusky and Kruskal, 1965). Then, $u_2$ represents the limiting wave amplitude of Eq. 27 at infinity, and $u_1$ characterizes the peak of the wave. We set $a=u_1-u_2$ and $d=\sqrt{12\beta /a}$, where $a$ is the amplitude and $d$ is the width of the wave (shown by the vertical distance between the two red dashes of Figure 2A). Figure 2A could possibly corroborate some descriptions of solitary wave properties as follows: 1) this wave propagates along the $x$-direction, e.g., with the form of $u\left(x-ct\right)$; 2) this wave is distributed in a limited space, e.g., $\underset{x\to \pm \infty }{\mathit{lim}}u\to 0$; and 3) the shape of the wave does not change with time. This specific kind of non-linear wave is, therefore, called a soliton.

FIGURE 2

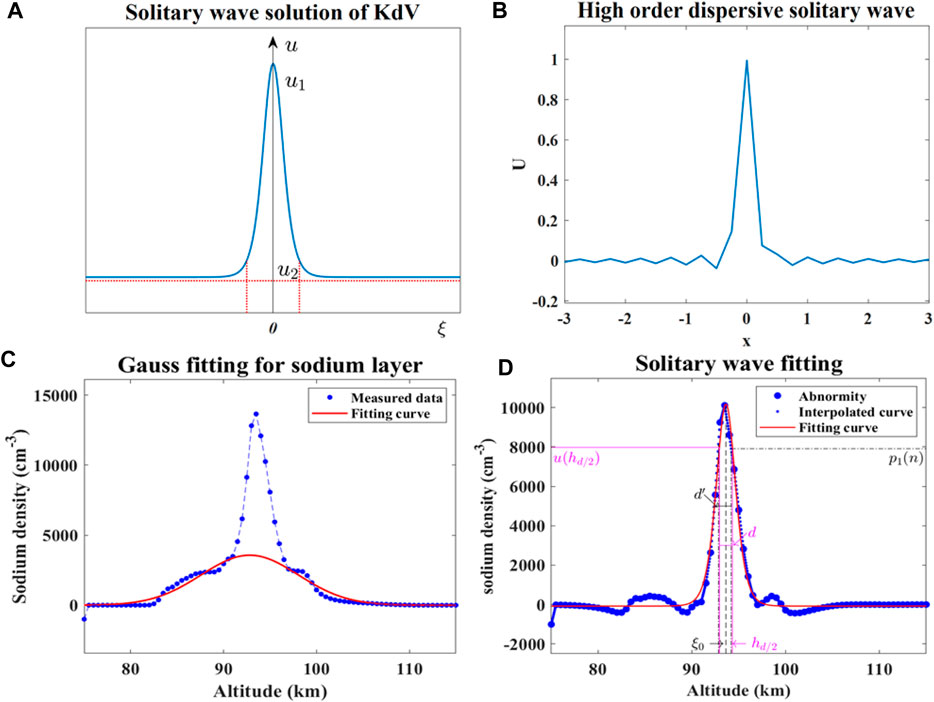
FIGURE 2. Comparison of the theoretical solitary wave profiles and observed peak density profiles of Na_S. (A) Solitary wave profile according to Eq. 11, with u2 representing the limiting wave amplitude at infinity and u1 characterizing the peak of the wave. The width $\mathrm{d}=\sqrt{12\mathrm{\beta }/\mathrm{a}}$ is determined by the vertical distance between the two red dashes. (B) Simulated solution of the five-order solitary wave. (C) Peak density profile of the Na_S. The blue dash–dot line represents the peak sodium density observed on 03 November 2016. The red curve indicates fitted background Gaussian distribution throughout the whole night. (D) Fitting image of the peak profile. The blue dotted line shows the distribution of the observed data after subtracting the background Gaussian distribution from 2c, while the red curve is simulated according to Eq. 11 with appropriate parameters. The blue dotted line is very close to the red curve, except some wing features similar to 2b. The fitting parameters of $h_{d/2}$, $d$, $d^{\prime }$, $u\left(h_{d/2}\right)$, and $p_1\left(n\right)$ are also given.

Eq. 27 is the soliton solution of Eq. 26 (similar to Eq. 1), and its evolution image is shown in Figure 3A when taking $\beta$ as 1 and the parameter conditions are chosen as $u_2=-1$ and $u_1=2$. The soliton’s shape is unaltered, and it advances uniformly in the positive $x$-direction. In the observed time series, the Na_S waveform of Figure 3B has a stable and prolonged propagation time, which is consistent with the temporal evolution of solitary waves. Additionally, the sodium density was only distributed over a narrow range of heights during the evolution of the Na_S event; i.e., at long distance from the peak height, the sodium density value is zero, indicating that this sort of Na_S event has properties similar to solitary waves. Some other patterns of isolated waves are affected by the non-linear and dispersion terms. In Section 3, the significance of non-linearity and dispersion in the evolution of Na_S will be discussed in relation to the Na_S occurrences recorded at the Andes lidar station.

FIGURE 3

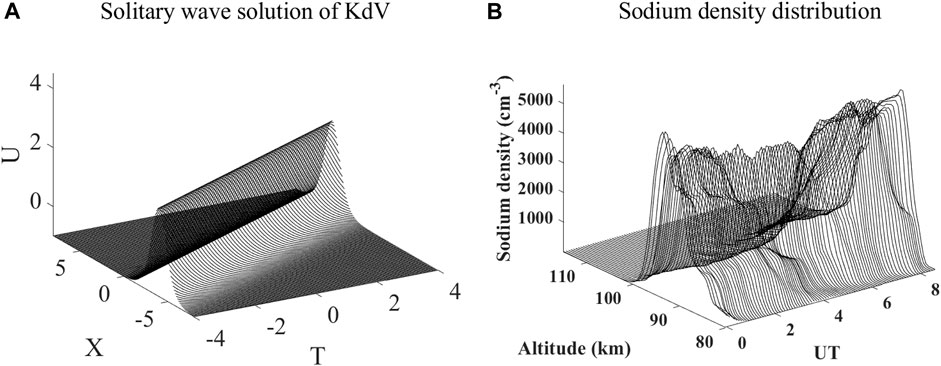
FIGURE 3. (A) By solving the KdV equation with specific condition and assumption (see text), a solitary wave solution was obtained. (B) Na_S event detected by the Andes lidar station.

3 Observational results and discussion

The observational data from the Andes lidar from 20 August 2014 to 7 July 2019 are processed in detail as follows: 1) The typical Na_S event with intensity factor $>3$ is selected, and the Gaussian distribution function of the background sodium density profile on that day is determined. 2) The Gaussian distribution is subtracted from the original peak density profile of the Na_S. The net anomaly peak is obtained and next fitted by the soliton solution from the standard KdV equation. The net anomaly distribution function is found out, and the quality of the fitting is evaluated. 3) Evolutions of the net anomaly are compared with the solution of a generalized five-order KdV equation. A video is made to illustrate their variation processes, and single frames are intercepted for this comparison.

3.1 Gaussian distribution of the sodium density profile

It is shown that the sodium density variation with height can be approximated by the Gaussian distribution.

${\mathit{n}}_{\mathit{s}}\left(\mathit{z}\right)=\frac{{\mathit{C}}_{\mathit{s}}}{\sqrt{\mathbf{2}\mathit{\pi }}{\mathit{\sigma }}_{\mathit{s}}}\mathit{exp}\left[-\frac{{\left(\mathit{z}-{\mathit{z}}_{\mathit{s}}\right)}^{\mathbf{2}}}{\mathbf{2}{\mathit{\sigma }}_{\mathit{s}}^{\mathbf{2}}}\right],(28)$

where $n_s\left(z\right)$ is the sodium number density at $z$, $C_s$ is the total column density of the sodium layer, ${\mathrm{z}}_{\mathrm{s}}$ is the centroid height, and ${\mathrm{\sigma }}_{\mathrm{s}}^2$ is the RMS width (Xue, 2007).

When the Na_S occurs, the sodium density suddenly increases in a narrow and confined altitude range and the density profile obviously deviates from the Gaussian distribution. To quantitatively explore this anomaly, the Gaussian distribution function of the background sodium density should be determined first.

The sodium density data observed at one night by the lidar compose of a two-dimensional matrix: the elements on the column vectors of the matrix represent the sodium densities at different heights at a given moment, and the elements on the row vectors represent the results at different moments at a given height. Now, we choose the column vector of the matrix for data processing.

The origin observation data matrix of the day is set to be $M$, and then, $M$ is represented by the column vector as follows:

$M=\left[{\overrightarrow{m}}_1,{\overrightarrow{m}}_2,\cdots ,{\overrightarrow{m}}_{n-1},{\overrightarrow{m}}_n\right],(29)$

where n is the number of observational points on the day. The maximum element in $M$ is marked as $d_{\mathit{max}}$. If we select an Na_S event with intensity factor>3, the critical value d_c for determining the anomalies is defined as follows:

${\mathit{d}}_{\mathit{c}}=\frac{{\mathit{d}}_{\mathit{max}}}{\mathbf{3}}.(30)$

When the value of an element in the column vector is greater than d_c, it reflects the anomaly of Na density. Otherwise, it is considered that the column vector conforms to the Gaussian distribution of Na density on that day. The column vector reflecting the Na density anomaly is arranged into a matrix in the order of the observed time as follows:

$A=\left[{\overrightarrow{a}}_1,{\overrightarrow{a}}_2,\cdots ,{\overrightarrow{a}}_{k-1},{\overrightarrow{a}}_k\right].(31)$

Then, we set the matrix of column vectors matching the Gaussian distribution in the order of observational moments to be

$G=\left[{\overrightarrow{g}}_1,{\overrightarrow{g}}_2,\cdots ,{\overrightarrow{g}}_{n-k-1},{\overrightarrow{g}}_{n-k}\right].(32)$

To obtain the Gaussian distribution of Na density on that day, we average all column vectors in $G$ with a mark of ${\stackrel{\rightharpoonup }{g}}_{ave}$:

${\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{a}\mathit{v}\mathit{e}}=\frac{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}-\mathit{k}}}{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{i}}}{\mathit{n}-\mathit{k}},(33)$

where ${\stackrel{\rightharpoonup }{g}}_{ave}$ reflects the distribution of Na density at the confined altitude. As mentioned previously, it is considered that ${\stackrel{\rightharpoonup }{g}}_{ave}$ is consistent with the Gaussian distribution, i.e., the result of a Gaussian fit with ${\stackrel{\rightharpoonup }{g}}_{ave}$ to the altitude h should satisfy Eq. 28. Taking the Na_S observed on 3 November 2016, for example, the Gaussian fitting is made with the column vector ${\stackrel{\rightharpoonup }{g}}_{ave}$ and $\stackrel{\rightharpoonup }{h}$ according to Eq. 28. The fitting results are as follows:

${\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}}=\mathbf{4330}\mathit{exp}\left[-\frac{{\left(\stackrel{\rightharpoonup }{\mathit{h}}-\mathbf{92.86}\right)}^{\mathbf{2}}}{\mathbf{7.798}}\right],(34)$

where ${\stackrel{\rightharpoonup }{g}}_h$ represents the modeled value that corresponds to the Gaussian distribution. The fitting result is shown as the red curve in Figure 2C.

3.2 Net anomaly of sodium density and solitary wave fitting

Based on the observational data at Andes station from 20 August 2014 to 7 July 2019, 27 Na_S events are distinguished among 147 observation days. We continue to take the case on 3 November 2016 as an example. The column vector of $d_{\mathit{max}}$ is denoted as ${\stackrel{\rightharpoonup }{a}}_d\left(1\le d\le k\right)$. The profile of ${\stackrel{\rightharpoonup }{a}}_d$ with $\stackrel{\rightharpoonup }{h}$ is shown as the blue dash–dot line in Figure 2C. The observed Na density can be regarded as the sum of Gaussian distribution and the anomaly. Thus, vector $\stackrel{\rightharpoonup }{p}$ reflecting the net anomaly of Na density is given by the following equation:

$\stackrel{\rightharpoonup }{\mathit{p}}={\stackrel{\rightharpoonup }{\mathit{a}}}_{\mathit{d}}-{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}},(35)$

and the distribution of $\stackrel{\rightharpoonup }{p}$ with $\stackrel{\rightharpoonup }{h}$ is shown as the blue dotted line in Figure 2D. Then, the peak density of $\left|\stackrel{\rightharpoonup }{p}\right|$ equals to 10180.95 $\mathrm{c}{\mathrm{m}}^{-3}$, with $\left|\stackrel{\rightharpoonup }{p}\right|$ settled to about zero at infinity.

Then, the solitary wave fitting is performed on the vector $\stackrel{\rightharpoonup }{p}$. Since $\stackrel{\rightharpoonup }{p}$ reflects the net anomaly at a determined time (the moment of the peak density profile), the parameter t in the fitted formula is a constant. At this time, the traveling wave $\xi =x-ct$ represents a specific phase. In order to better represent the altitude corresponding to the peak Na density, Eq. 27 could be written as follows:

$\mathit{u}\left(\mathit{\xi }\right)={\mathit{u}}_{\mathbf{2}}+\left({\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}\right)\mathit{sec}{\mathit{h}}^{\mathbf{2}}\sqrt{\frac{{\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}}{\mathbf{12}\mathit{\beta }}}\left(\mathit{\xi }-{\mathit{\xi }}_{\mathbf{0}}\right),(36)$

where ${\mathrm{\xi }}_0$ is the altitude corresponding to the maximum amplitude of the solitary wave. The fitting expression is finally deduced as follows:

$\mathit{u}\left(\mathit{\xi }\right)=-\mathbf{82.17}+\mathbf{10263.12}*\mathit{sec}{\mathit{h}}^{\mathbf{2}}\sqrt{\frac{\mathbf{10263.12}}{\mathbf{19494.36}}}\left(\mathit{\xi }-\mathbf{93.63}\right),(37)$

which means $u_2=-82.17$, $u_1-u_2=10263.12$ (or $u_1=10180.95$), $12\beta =19494.36$, and

${\xi }_0$ = $93.63$.

The fitting results are shown as the red curve in Figure 2D. Now, we know $u_1$ represents the peak density of the modeled curve, and $u_2$ corresponds to the density at infinity, i.e.,

$\underset{\mathit{\xi }\le \mathbf{80}}{\mathit{u}\left(\mathit{\xi }\right)}\approx \underset{\mathit{\xi }\ge \mathbf{110}}{\mathit{u}\left(\mathit{\xi }\right)}\approx \underset{\mathit{\xi }\to \mathit{\infty }}{\mathit{lim}}\mathit{u}\left(\mathit{\xi }\right)\to \mathbf{0}.(38)$

Let

${\mathit{\xi }}_{\mathbf{1}}=\pm \frac{\mathit{d}}{\mathbf{2}}=\pm \sqrt{\frac{\mathbf{3}\mathit{\beta }}{\mathit{a}}}=\pm \sqrt{\frac{\mathbf{3}\mathit{\beta }}{\left({\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}\right)}.}(39)$

Substituting it into Eq. 37, we have

$\mathit{u}\left({\mathit{\xi }}_{\mathbf{1}}\right)={\mathit{u}}_{\mathbf{2}}+\frac{\mathbf{4}\mathit{e}}{{\left(\mathit{e}+\mathbf{1}\right)}^{\mathbf{2}}}\left({\mathit{u}}_{\mathbf{1}}-{\mathit{u}}_{\mathbf{2}}\right)=\mathit{u}\left(\pm \mathbf{0.6891}\right)=\mathbf{8071.41},(40)$

which means the density at 0.6891 km from the peak is predicted to be 8071.41 $\left(c{m}^{-3}\right)$. From Figure 2D, we can find all these simulated values; $u_1,u_2$ and $u\left({\xi }_1\right)$ are close to the observed results.

Furthermore, the height value at the theoretical full width at half maximum (FWHM) of a soliton is given as follows:

${\mathbf{h}}_{\mathbf{d}/\mathbf{2}}={\mathrm{\xi }}_{\mathbf{0}}+\frac{\mathbf{d}}{\mathbf{2}}={\mathrm{\xi }}_{\mathbf{0}}+\frac{\sqrt{\frac{\mathbf{12}\mathrm{\beta }}{{\mathbf{u}}_{\mathbf{1}}-{\mathbf{u}}_{\mathbf{2}}}}}{\mathbf{2}}\left(\mathbf{k}\mathbf{m}\right).(41)$

To test the fitting results, the observed altitude of the selected case needs to be close to the calculated $h_{0.5}$. Since the vertical resolution of the lidar is limited to 0.5 km, we can perform linear interpolation for the observed altitude series. The interpolated vector $\stackrel{\rightharpoonup }{p}$ is denoted as $\stackrel{\rightharpoonup }{p_1}$, and the altitude series of $\stackrel{\rightharpoonup }{p_1}$ is marked as $\stackrel{\rightharpoonup }{h_1}$. The Na density at half-width is $u\left(h_{d/2}\right)$; then, it is always possible to find a value closest to $u\left(h_{d/2}\right)$ on both sides of the peak of $\stackrel{\rightharpoonup }{p_1}$ (denoted as $p_1\left(m\right)$ and $p_1\left(n\right)$). The corresponding altitudes for $p_1\left(m\right)$ and $p_1\left(n\right)$ are noted as $h_1\left(m\right)$ and $h_1\left(n\right)$, respectively. Then, the observed width of the soliton could be given as follows:

${\mathit{d}}^{\prime }={\mathit{h}}_{\mathbf{1}}\left(\mathit{n}\right)-{\mathit{h}}_{\mathbf{1}}\left(\mathit{m}\right).(42)$

According to the definition of the soliton, $d^{\prime }$ is also written as follows:

${\mathit{d}}^{\prime }=\sqrt{\frac{\mathbf{12}{\mathit{\beta }}^{\prime }}{\mathbf{max}\left(\stackrel{\rightharpoonup }{{\mathit{p}}_{\mathbf{1}}}\right)-\mathbf{0}}},(43)$

where $\mathit{max}\left(\stackrel{\rightharpoonup }{p_1}\right)$ is the peak of $\stackrel{\rightharpoonup }{p_1}$; 0 is the density at infinity; and ${\beta }^{\prime }$ is the $\beta$ value deduced from the observations. It is shown that

${\mathit{\beta }}^{\prime }=\frac{{{\mathit{d}}^{\prime }}^{\mathbf{2}}\mathit{max}\left(\stackrel{\rightharpoonup }{{\mathit{p}}_{\mathbf{1}}}\right)}{\mathbf{12}}.(44)$

The deduced values of $h_{d/2}$, $d$, $d^{\prime }$, $u\left(h_{d/2}\right)$, $p_1$, $\beta$, and ${\beta }^{\prime }$, for each Na_S event, are listed in Table 1. The fitting parameters on 3 November 2016 are also exhibited in Figure 2D. Indeed, the results show the fitting parameters are close to the observed values.

TABLE 1

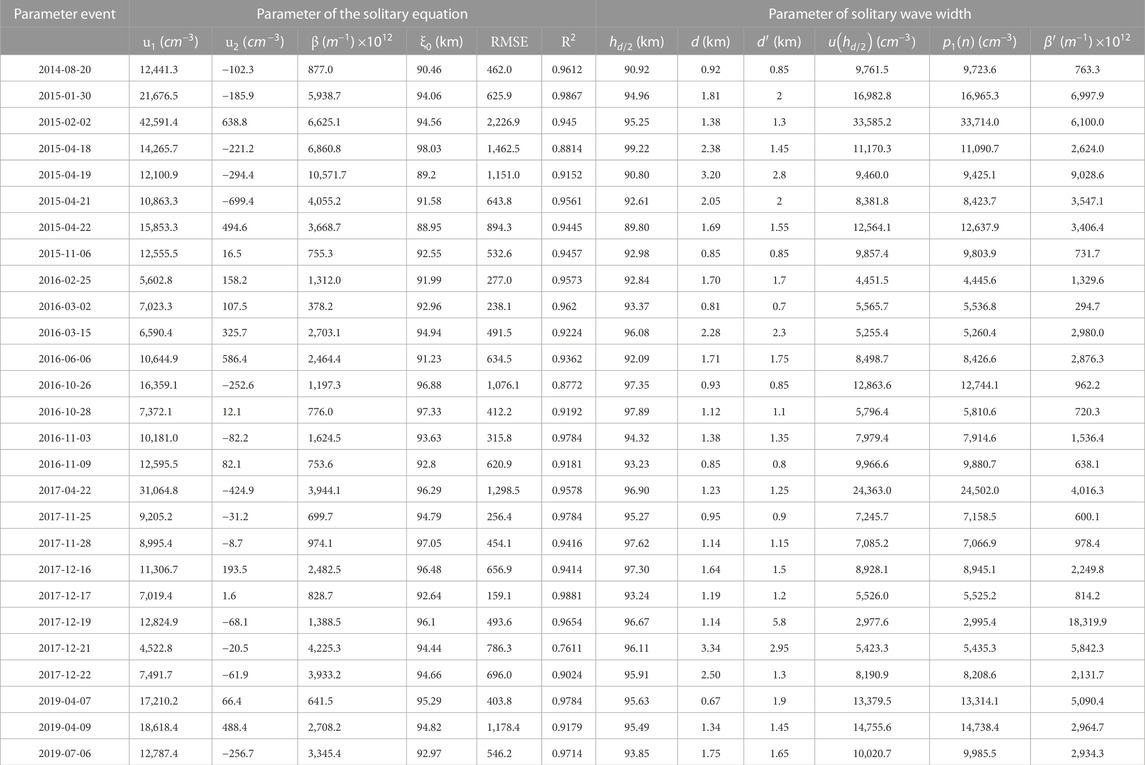
TABLE 1. Statistics of fitting parameters and fitting quality evaluation for the observations at the Andes station from 20 August 2014 to 7 July 2019.

Alternatively, the column vector obtained by Eq. 37 is denoted as $\stackrel{\rightharpoonup }{q}$; then, $\stackrel{\rightharpoonup }{q}$ is the predicted value at altitude h. The coefficient of determination ($\left|R^2\right|<1$) and the root mean square error (RMSE) are then utilized to evaluate the fitting quality. They are calculated, respectively, as

${\mathit{R}}^{\mathbf{2}}=\mathbf{1}-\frac{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{L}}}{\left({\mathit{q}}_{\mathit{i}}-{\mathit{p}}_{\mathit{i}}\right)}^{\mathbf{2}}}{{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{L}}}{\left({\mathit{p}}_{\mathit{i}}-{\overline{\mathit{p}}}_{\mathit{i}}\right)}^{\mathbf{2}}}(45)$

and

$\mathit{R}\mathit{M}\mathit{S}\mathit{E}=\sqrt{\frac{\mathbf{1}}{\mathit{L}}{\displaystyle {\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{L}}}{\left({\mathit{q}}_{\mathit{i}}-{\mathit{p}}_{\mathit{i}}\right)}^{\mathbf{2}}},(46)$

where $L$ is the length of vector $\stackrel{\rightharpoonup }{p}$ or $\stackrel{\rightharpoonup }{q}$ , i.e., the number of observed altitude points.

The denominator of Eq. 45 denotes the residuals obtained by predicting the net anomaly vector $\stackrel{\rightharpoonup }{p}$, and the numerator represents the residuals predicted using the modeled vector $\stackrel{\rightharpoonup }{q}$.

The values of the parameters $R^2$ and RMSE obtained by fitting $\stackrel{\rightharpoonup }{p}$ and $\stackrel{\rightharpoonup }{q}$ for this Na_S event are calculated, respectively, as $R^2=0.9784$ and $RMSE=315.8402$, showing a good fit with $R^2$ close to 1. Through the evaluation of fitting quality, it is confirmed that Eq. 37 can fit the net anomaly vector $\stackrel{\rightharpoonup }{p}$ within an allowable error (i.e., with $R^2>0.9$). The fitting results and quality evaluation parameters are obtained, with 24/27 events having $R^2>0.9$ as shown in Table 1. Therefore, the fitting results indicate u(ξ) are consistent with the net anomaly $\left|\stackrel{\rightharpoonup }{p}\right|$.

Figure 4 shows a simple data mining operation in Table 1. The net anomalous sodium density data $\stackrel{\rightharpoonup }{p}$ were used for the fit, and the calculation of the fit results (as described in Eqs 35–44 produced two additional parameters β, d, which describe the soliton characteristics. In contrast, ${\beta }^{\prime }{,d}^{\prime }$ are the corresponding parameters derived directly from the observed data. Assuming that the error bars’ lengths represent 10% of the parameter values, the ratios of ${\beta }^{\prime }{,d}^{\prime }$ within the errors are 17/27 and 20/27, respectively, showing that we have had some success fitting the data.

FIGURE 4

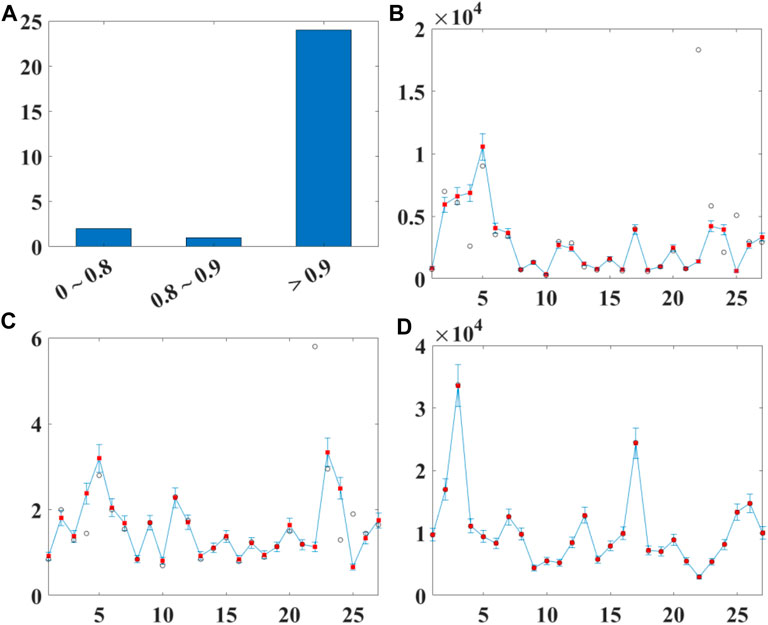
FIGURE 4. (A) A statistical histogram of the parameter $R^2$, with two cases in the range of 0–0.8, one case in the range of 0.8–0.9, and 24 cases more than 0.9; (B–D) Error bar graphs for fitted parameters $\beta ,d,\&u\left(h_{d/2}\right)$, in that order (horizontal coordinates in the graph correspond to the numbers in Table 1 in that order, vertical coordinates are parameter values, and the length of the error bar is taken to be one tenth of the parameter value). Red dots represent the corresponding parameter values ($\beta ,d,\&u\left(h_{d/2}\right)$). Parameters computed from the observed data (${\beta }^{\prime }{,d}^{\prime },p_1\left(n\right)$) are indicated by black circles.

3.3 Further explanation of Na_S by the higher-order solitary wave equation

In Figure 2D, it is shown that some small wavelets appear on both wings of the blue dotted line drawn from the net anomaly vector $\stackrel{\rightharpoonup }{p}$, which could not be explained by the standard solitary equation with the red fitting curve. These wavelets, however, have similar characteristics to the higher-order solitary wave with a waveform shown in Figure 2B.

Kawahara and Takuji proposed to add a higher-order dispersion term to the KdV equation, which considers dissipation, instability, and higher-order dispersion effects in the fluid medium (Kawahara and Takuji, 2007). This generalized KdV equation is written as follows:

$\frac{\partial \mathit{u}}{\partial \mathit{t}}+\mathit{u}\frac{\partial \mathit{u}}{\partial \mathit{x}}+\mathit{\beta }\frac{{\partial }^{\mathbf{3}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{3}}}+\mathit{\gamma }\frac{{\partial }^{\mathbf{5}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{5}}}=\mathbf{0},(47)$

which is also called the Kawahara equation (Kawahara and Takuji, 2007).

The numerical simulation results show that the Kawahara equation has two types of solutions: in the case of $\gamma >0$ and $\beta \le 0$, a soliton is formed with monotonic asymptotics similar to the soliton shown in Figure 2A; in the case of $\gamma >0$ and $\beta >0$, the two wings of the soliton will have oscillation characteristics (Mamun and Shukla, 2009; Mamun and Shukla, 2009). Taking $\beta =1$ and $\gamma ={10}^{-4}$, the expression of Eq. 47 will be

$\frac{\partial \mathit{u}}{\partial \mathit{t}}+\mathit{u}\frac{\partial \mathit{u}}{\partial \mathit{x}}+\frac{{\partial }^{\mathbf{3}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{3}}}+{\mathbf{10}}^{-\mathbf{4}}\frac{{\partial }^{\mathbf{5}}\mathit{u}}{\partial {\mathit{x}}^{\mathbf{5}}}=\mathbf{0},(48)$

whose solution at $t=0.0016$ is shown in Figure 2B.

Furthermore, we can study the evolution of the waveform over time using the Fourier transform method. Let the initial conditions be $\beta =0.0023$, $\gamma ={10}^{-4}$, and $u\left(x,0\right)=e^{-36x^2}$. Since the Kawahara equation contains two variables, x and t, the simulation results are denoted as a two-dimensional matrix $W$. Then, we arrange $W$ by column vectors as follows:

$\mathit{W}=\left[{\stackrel{\rightharpoonup }{\mathit{w}}}_{\mathbf{1}}\mathbf{,}{\stackrel{\rightharpoonup }{\mathit{w}}}_{\mathbf{2}}\mathbf{,}\mathbf{\cdots }\mathbf{,}{\stackrel{\rightharpoonup }{\mathit{w}}}_{\mathit{n}\mathbf{-}\mathit{1}}\mathbf{,}{\stackrel{\rightharpoonup }{\mathit{w}}}_{\mathit{n}}\right].(49)$

Since the vertical scale of Na_S observed by the lidar is generally less than 10 km, while the horizontal scale is often reported to be more than 300 km or even over 1,000 km (Fan et al., 2007; Ma et al., 2019), this scenario is inconsistent with the shallow water model. The solitary waves could particularly appear at the interface between upper and lower stratifications in the fluid medium (Bogucki and Garrett, 1993). They are frequently found in the stratified or sheared places in the ocean and atmosphere (Huthnance, 1989; Doviak et al., 1991; Gan and Ingram, 1992). In fact, in the lower atmosphere, in rotating, magnetized dusty plasma and in the dayside tropical mesosphere, many solitary wave events have also been observed (Christie et al., 1977; Christie et al., 1981; Mushtaq, 2006). This might suggest that solitary waves propagate beyond the mesospheric Na layer (the Na lidar range) with a larger vertical scale. Therefore, it is more effective to look for observational results related to stable stratifications or shears. The Na_S event on 9 April 2019 is selected as an example of this scenario (Figure 5A). This Na_S appears before the beginning of the observation at about 95 km altitude, with a downward propagation. The deduced vertical wind confirms the Na_S occurs in downward vertical wind (shown as the negative value region in Figure 5B). The vertical wind velocity field in this example has a low-velocity band with a width of around 3 km, and this low-velocity band (as shown in Figure 5B) decreases by roughly 9 km (95–86 km) in 10 hours (8 April 2019, 23:00–9 April 2019, 09:00), and the downward speed is roughly 0.9 km/h. Furthermore, the spatial and temporal distribution of Na_S on that day corresponds well with the distribution of this vertical wind low-velocity zone. The results of numerical simulations demonstrate that the non-linear term factor affects the propagation of the solitons along the spatial axis. Moreover, the downward vertical phase of the Na_S is consistent with the aforementioned properties of solitons. This implies that vertical wind speed has a non-linear function in this Na_S event, influencing the sodium density transfer. As stated in previous studies (Chen et al., 2021a; Chen et al., 2021b), Na_S is also modulated by the horizontal wind field. Figures 5C–E show the zonal wind, meridional wind, and the temperature profiles, respectively. These three profiles indicate the Na_S has been located near the stratification with strong shear. Furthermore, the stability of the stratification is determined by the Richardson number $\left(Ri\right)$ (Nappo, 2002; Liu and Liu, 2011). Under stable stratification, both convection and turbulence are less likely to develop.

FIGURE 5

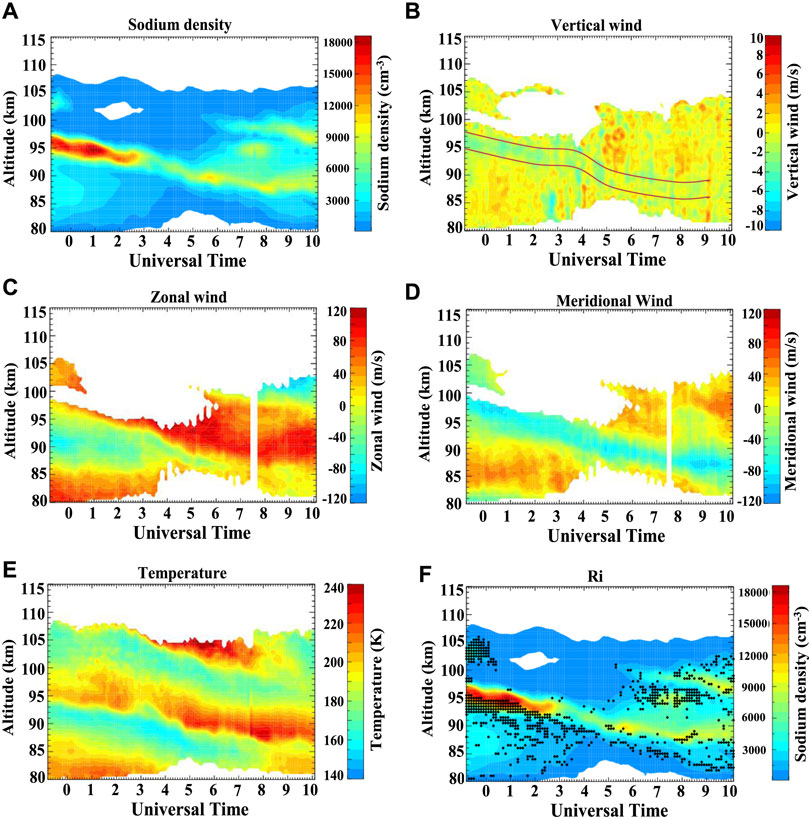
FIGURE 5. Observations and results from the Andes lidar on 9 April 2019. The empty areas indicate a low signal-to-noise ratio and large error of the observed data. (A) Sodium density profile. The Na_S appears before the beginning of the observation, at about 95 km altitude. (B) Vertical wind observations. (C) Zonal wind profile. (D) Meridional wind profile. (E) Temperature variations. (F) Calculated Ri distributions. The black scatter dots represent Ri with a value >1.5.

In unit time, due to vertical displacement, for a unit mass of air, the convective flow energy to resist the net Archimedes buoyancy is as follows:

${\mathit{W}}_{\mathbf{1}}=-\overline{\frac{\mathit{d}}{\mathit{d}\mathit{t}}\left(\frac{\mathbf{1}}{\mathbf{2}}{\mathit{w}}^{\mathbf{2}}\right)}={\mathit{K}}_{\mathit{H}}{\mathit{N}}^{\mathbf{2}},(50)$

where w = dz/dt is the vertical speed; $K_H=\overline{wz}>0$ is the convective conductivity coefficient; $N^2=\frac{g}{T}\left(\frac{\partial T}{\partial z}+\frac{g}{C_p}\right)$ is the buoyancy frequency; $g=9.5m{s}^{-2}$ is the gravitational acceleration in the mesopause; $C_p=1004J{K}^{-1}{kg}^{-1}$ is the specific heat at constant pressure; and T is the atmospheric thermodynamic temperature.

On the other hand, for unit mass of air, the horizontal kinetic energy consumed per unit time in the presence of vertical wind shear, i.e., the kinetic energy provided to convective motion, is as follows:

${\mathit{W}}_{\mathbf{2}}=-\overline{\frac{\mathit{d}}{\mathit{d}\mathit{t}}\left(\frac{\mathbf{1}}{\mathbf{2}}{\stackrel{\rightharpoonup }{\mathit{V}}}_{\mathit{h}}^{\mathbf{2}}\right)}={\mathit{K}}_{\mathit{M}}\left[{\left(\frac{\partial \mathit{u}}{\partial \mathit{z}}\right)}^{\mathbf{2}}+{\left(\frac{\partial \mathit{v}}{\partial \mathit{z}}\right)}^{\mathbf{2}}\right],(51)$

where u and v are the zonal and meridional wind velocities, respectively. $K_M>0$ is the momentum transport coefficient and is usually approximately equal to $K_H$.

Thus, the stability of the layer depends on the value of $W_1/W_2$. When $W_2$ is less than $W_1$, it means that the disturbance kinetic energy converted by the basic airflow is less than the disturbance kinetic energy consumed by stable stratification. In this situation, even if convection or turbulence occurs, it will be suppressed or weakened so that the atmosphere is in a stable state. The dimensionless ratio, $W_1/W_2$, is defined as follows:

$\mathit{R}\mathit{i}=\frac{{\mathit{W}}_{\mathbf{1}}}{{\mathit{W}}_{\mathbf{2}}}=\frac{\frac{\mathit{g}}{\mathit{T}}\left(\frac{\partial \mathit{T}}{\partial \mathit{z}}+\frac{\mathit{g}}{{\mathit{C}}_{\mathit{p}}}\right)}{\left[{\left(\frac{\partial \mathit{u}}{\partial \mathit{z}}\right)}^{\mathbf{2}}+{\left(\frac{\partial \mathit{v}}{\partial \mathit{z}}\right)}^{\mathbf{2}}\right]},(52)$

which could be deduced from the wind and temperature results observed by the lidar (Figures 5C–E). The calculated Ri with a value $>1.5$ are shown as black scatters in Figure 5F. The Na_S locates around the area where scatters are concentrated, i.e., a special stable area near 95 km. It is obvious that the Na_S and stable region evolved synchronously, and finally, both become blurred. Therefore, the lidar observations and the deduced results are all consistent with the appearance of a solitary wave. A stable stratification with $Ri>1.5$ exists nearly about 95 km, accompanied by the zonal wind, meridional wind, and temperature being also stratified around 95 km. Once a fluctuation is excited in the vicinity of the stratification and just satisfies the balance of non-linear and dispersion effects, the waveform will maintain through the propagation; i.e., a solitary wave appears.

Furthermore, the evolution of the observed net anomaly for the Na_s throughout whole night is also needed for comparison. In Section 3.1, the initial observation of sodium density is denoted as $M=\left[{\overrightarrow{m}}_1,{\overrightarrow{m}}_2,\cdots {\overrightarrow{m}}_{n-1},{\overrightarrow{m}}_n\right]$.

The Gaussian distribution model of the current day is noted as a two-dimensional matrix ${\stackrel{⃡}{G}}_0$, and we define ${\stackrel{⃡}{G}}_0$ as isomorphic to $\stackrel{⃡}{M}$. Then, ${\stackrel{⃡}{G}}_0$ could be written in the form of a column vector as follows:

$G_{\mathbf{0}}=\left[{\overrightarrow{g}}_h,{\overrightarrow{g}}_h,\cdots {,\overrightarrow{g}}_h,{\overrightarrow{g}}_h\right].(53)$

Obviously, the net anomaly evolution of the Na_S is obtained by observation data matrix $\stackrel{⃡}{M}$ subtracting the Gaussian distribution model ${\stackrel{⃡}{G}}_0$, which could be denoted as $\stackrel{⃡}{S}$. There are

$\begin{array}{c}\mathit{S}=\mathit{M}-{\mathit{G}}_{\mathbf{0}}=\left[{\stackrel{\rightharpoonup }{\mathit{m}}}_{\mathbf{1}}-{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}},{\stackrel{\rightharpoonup }{\mathit{m}}}_{\mathbf{2}}-{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}},\dots {,\stackrel{\rightharpoonup }{\mathit{m}}}_{\mathit{n}-\mathbf{1}}-{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}},{\stackrel{\rightharpoonup }{\mathit{m}}}_{\mathit{n}}-{\stackrel{\rightharpoonup }{\mathit{g}}}_{\mathit{h}}\right]\\ =\left[{\stackrel{\rightharpoonup }{\mathit{s}}}_{\mathbf{1}},{\stackrel{\rightharpoonup }{\mathit{s}}}_{\mathbf{2}},\dots {,\stackrel{\rightharpoonup }{\mathit{s}}}_{\mathit{n}-\mathbf{1}},{\stackrel{\rightharpoonup }{\mathit{s}}}_{\mathit{n}}\right],\end{array}(54)$

where ${\stackrel{\rightharpoonup }{s}}_i(i=1,2,\dots ,n-1,n$) is the column vector of $\stackrel{⃡}{S}$.

In order to compare the numerical simulation results $\stackrel{⃡}{W}$ with the Na_S evolution model $\stackrel{⃡}{S}$ more intuitively, the Fourier transform method is used uniformly to disperse a certain period of time on time variable t into n moments in numerical simulation. Thus, both $\stackrel{⃡}{W}$ and $\stackrel{⃡}{S}$ are two-dimensional matrices with the same column number n. To better show them, a dynamic video of the variation of their column vectors with time is uploaded as Supplementary Movie S1. The five images on the left in Figure 6 (i.e., Figures 6A, C, E, G, I) are single-frame captures from $\stackrel{⃡}{W}$ of the video, showing the evolutions of the five-order solitary wave over time. The five images on the right (i.e., Figures 6B, D, F, H, J) are intercepted from $\stackrel{⃡}{S}$, indicating variations of the net anomaly of the Na_S. Figures 6A, B show at this moment, the simulated wave shapes are similar to the observed peak density profile. Figures 6C, D show the huge peaks attenuate gradually. Figures 6E, Fshow the peaks decay to about zero value. Figures 6G, H show the peaks change phase and resume. Figures 6I, J show the peaks recover to a sharp form similar to the initial condition, except with different phases. By comparison, it is verified that the numerical simulation results $\stackrel{⃡}{W}$ are in good agreement with the evolution process $S$ of the Na_S. So, the five-order solitary wave theory is a potential candidate in explaining this Na_S event.

FIGURE 6

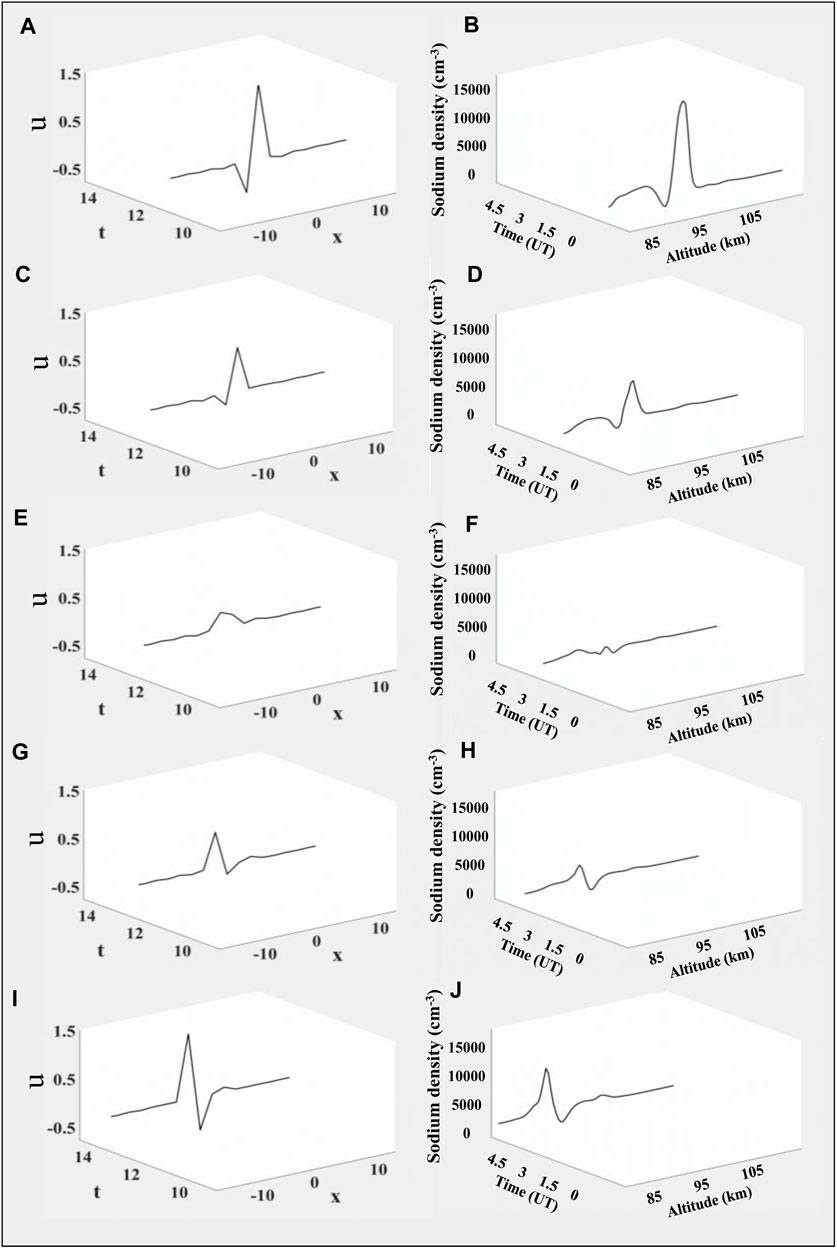
FIGURE 6. Comparison of five-order solitary wave evolution images over time and Na density net anomalies observed at the Andes station on 9 April 2019. (A,B) At this moment, the simulated wave shape is similar to the observed peak density profile. (C,D) Huge peaks attenuate synchronously. (E,F) Peaks decay to about zero value. (G,H) Peaks change phase and resume. (I,J) Peaks recover to a sharp form similar to the initial condition, except with different phase. A dynamic video of the variation of their column vectors with time is uploaded as Supplementary Movie S1.

However, it is worth noting that the numerical simulation of the higher-order KdV equation is probably only suitable for explaining the events similar to the selected case. These events are typically characterized by occurrence heights below 95 km, longer durations, and descending patterns similar to tidal fluctuations. In contrast, the other events with shorter durations and cloud-like shapes are less consistent with the higher-order simulation results. This discrepancy also implies that Na_S with different characteristics may have different fine structures.

The fluctuations can affect various physical parameters in the upper mesosphere. During the Na_S event on 9 April 2019, the temperature in the mesosphere displayed a distinct wave signature similar to the solitary wave observed in sodium density.

Similar to the approach used to analyze sodium density data, in the current study, the background temperature distribution (illustrated in Figure 7A) was obtained by averaging the temperature data of April 2019, excluding the temperature data recorded during the Na_S event. The temperature anomaly distribution (illustrated in Figure 7B) was obtained by differencing the temperature observations on 9 April 2019 when the Nas event occurred with the background temperature.

FIGURE 7

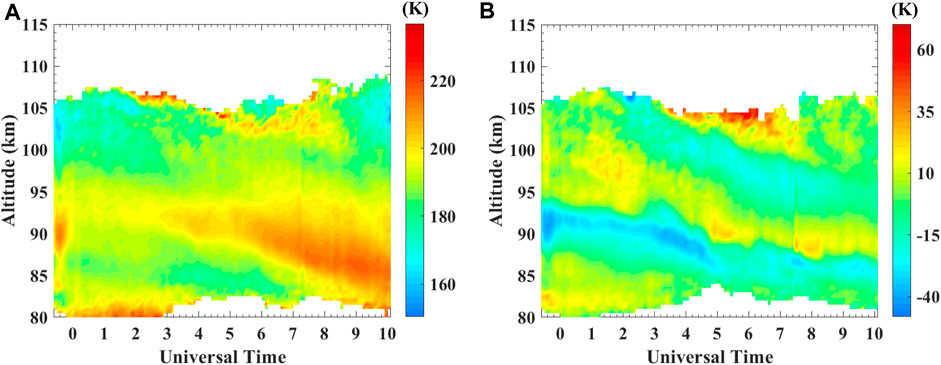
FIGURE 7. (A) Temperature distribution in the mesopause region (80–115 km) near the Andes station in April 2019, obtained by averaging temperature observations at the same UT time and altitude in April 2019 when no Na_S event was observed at the Andes station. When analyzing the Nas event on 9 April 2019, this background temperature was used. (B) Distribution of temperature anomalies from 93 to 97 km above the Andes lidar station on 9 April 2019. The temperature anomaly distribution was obtained by differencing the temperature observations on 9 April 2019 with the background temperature.

Figure 7A displays the background temperature distribution in the 93–97 km region consistently maintaining 190–200 K from −0.8 UT to 2.8 UT (where 9 April 2019 00:00 UT is marked as 0 UT), with no significant anomaly. The distribution of temperature anomalies from 93 to 97 km above the Andes lidar station on 9 April 2019 is shown in Figure 7B. Compared with the background temperature profile, there is a stripe or band of warming region with an amplitude of approximately 15 K within 93–97 km from −0.8 UT to 2.8 UT, overlapping the region of Na_S. Figure 8 presents the temperature plots (black lines) vs. the background temperature profiles (red lines) for 93–97 km, with (a) to (f) corresponding to the time sequence from −0.1 UT, 0.1 UT, 0.3 UT, 0.5 UT, and 0.7 UT, to 0.9 UT. Figures 8A–F show that the temperature anomalies in this region persist at approximately 10–15 K throughout the Na_S event (−0.8 UT∼2.8 UT), indicating a stable propagation pattern/signal similar to that expected for solitary wave.

FIGURE 8

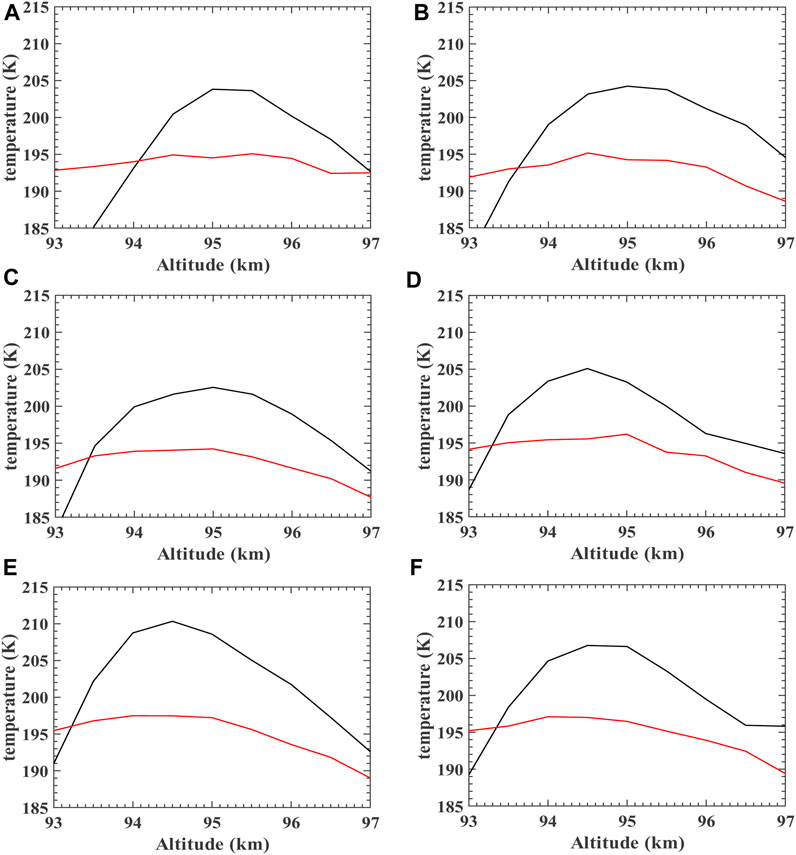
FIGURE 8. Temperature profiles (black lines) vs. background temperature profiles (red lines) for 93–97 km above the Andes lidar station on 9 April 2019, with (A–F) corresponding to the time sequences of −0.1 UT, 0.1 UT, 0.3 UT, 0.5 UT, 0.7 UT, and 0.9 UT.

Moreover, in contrast to Figure 2C, the temperature profile does not undergo any significant changes as the sodium density varies during the occurrence of the Na_S event. This discrepancy could potentially be explained by the following factors: 1) The occurrence of Na_S involves an input source (the sodium ions from E_S could potentially offer a sufficient neutral sodium atom source through recombination with free electrons). This implies that passive temperature variations may not be as sensitive to fluctuations as Na_S. 2) The temperature in the mesopause is also affected by atmospheric dynamical processes such as solar radiation, photochemical reactions, gravity waves, and tidal waves. Therefore, accurately determining the background temperature becomes challenging, which can result in less-pronounced fluctuation features in the temperature profile.

4 Conclusion

In this research, the solitary wave theory is applied to study the Na_S phenomenon of the mesosphere. Among the observations of Andes lidar from 20 August 2014 to 7 July 2019, 27 Na_S cases with intensity factor >3 have been selected for processing through the Gaussian and soliton fitting steps. The original observed peak density profile of the Na_S is subtracted by the Gaussian distribution, and then, the net anomaly peak is obtained. The net peak is fitted by the soliton solution from the standard KdV equation, and the quality of the fitting is then evaluated. The statistical results reveal that in 24/27 cases, the net peak of Na_S exhibits similar features to a soliton. Time series of the net anomaly on 9 April 2019 reveals a similar dynamical process to the solution of a five-order KdV equation. Although still uncertain, this solitary wave theory could possibly explain some characteristics of Na_S.

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found at: http://lidar.erau.edu/data/nalidar/.

Author contributions

SQ conceived this study and wrote this manuscript. MS performed data analysis and prepared Figures 1–4 and Supplementary Movie S1. WS was in charge of the organization and English polishing of the whole manuscript. MJ prepared Figure 5 and gave some useful comments on the content. PJ contributed to the discussion of KdV equations. XD designed this study. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 41974178 and 42130203) and CNSA Pre-research Project on Civil Aerospace Technologies (No. D020105).

Acknowledgments

The authors acknowledge the use of data from the Andes Lidar Observatory database. They express sincere gratitude to Prof. Alan Liu from the Center for Space and Atmospheric Research and Department of Physical Sciences, Embry-Riddle Aeronautical University, United States, for providing the valuable data.

Conflict of interest

Author MJ was employed by Shandong Guoyao Quantum Lidar Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1241663/full#supplementary-material

References

Ban, C., Li, T., Fang, X., Dou, X. K., and Xiong, J. G. (2015). Sodium lidar-observed gravity wave breaking followed by an upward propagation of sporadic sodium layer over Hefei, China. J. Geophys. Res. Space Phys. 120, 7958–7969. doi:10.1002/2015JA021339

CrossRef Full Text | Google Scholar

Belashov, V. Y., and Vladimirov, S. V. (2005). Solitary waves in dispersive complex media. Berlin, Heidelberg, XIV: Springer Series in Solid-State Sciences, Springer, 294.

Google Scholar

Benci, V., and Fortunato, D. (2014). Variational methods in non-linear field equations. Cham, Switzerland, XIX: Springer Monographs in Mathematics, Springer, 253.

Google Scholar

Bogucki, D., and Garrett, C. (1993). A simple model for the shear-induced decay of an internal solitary wave. J. Phys. Oceanogr. 23, 1767–1776. doi:10.1175/1520-0485(1993)023<1767:asmfts>2.0.co;2

CrossRef Full Text | Google Scholar

Chen, L., and Yi, F. (2011). Average properties and small-scale variations of the mesospheric Na and Fe layers as observed simultaneously by two closely colocated lidars at 30° N. Ann. Geophys. 29, 1037–1048. doi:10.5194/angeo-29-1037-2011

CrossRef Full Text | Google Scholar

Chen, X. C., Huang, W. T., Ban, C., Kosch, M. J., Murphy, D. J., Hu, Z. J., et al. (2021a). Dynamic properties of a sporadic sodium layer revealed by observations over zhongshan, Antarctica: A case study. J. Geophys. Res. Space Phys. 127. doi:10.1029/2021JA029787

CrossRef Full Text | Google Scholar

Chen, X. C., Liu, J. J., Kosch, M. J., Hu, Z. J., Wang, Z. W., Zhang, B. C., et al. (2021b). Simultaneous observations of a sporadic E layer by digisonde and SuperDARN HF radars at zhongshan, Antarctica. J. Geophys. Res. Space Phys. 127. doi:10.1029/2021JA029921

CrossRef Full Text | Google Scholar

Christie, D. R., Muirhead, K. J., and Hales, A. L. (1977). On solitary waves in the atmosphere. J. Atmos. Sci. 35, 805–825. doi:10.1175/1520-0469(1978)035<0805:oswita>2.0.co;2

CrossRef Full Text | Google Scholar

Christie, D. R., Muirhead, K. J., and Clarke, R. H. (1981). Solitary waves in the lower atmosphere. Nature 293, 46–49. doi:10.1038/293046a0

CrossRef Full Text | Google Scholar

Clemesha, B. R., Batista, P. P., and Simonich, D. M. (1997). Wave–associated sporadic neutral layers in the upper atmosphere. Rev. Bras. Geof. 15, 237–250. doi:10.1590/S0102–261X1997000300003

CrossRef Full Text | Google Scholar

Clemesha, B. R., Kirchhoff, V. W. J. H., Simonich, D. M., and Takahashi, H. (1978). Evidence of an extra-terrestrial source for the mesospheric sodium layer. Geophys. Res. Lett. 5, 873–876. doi:10.1029/gl005i010p00873

CrossRef Full Text | Google Scholar

Collins, S. C., Plane, J. M. C., Kelleya, M. C., Wright, T. G., Soldán, P., Kanee, T. J., et al. (2002). A study of the role of ion–molecule chemistry in the formation of sporadic sodium layers. J. Atmos. Sol. Terr. Phys. 64, 845–860. doi:10.1016/s1364-6826(02)00129-3

CrossRef Full Text | Google Scholar

Cox, R. M., and Plane, J. M. C. (1998). An ion-molecule mechanism for the formation of neutral sporadic Na layers. J. Geophys. Res. Atmos. 103, 6349–6359. doi:10.1029/97jd03376

CrossRef Full Text | Google Scholar

Cox, R. M., Plane, J. M. C., and Green, J. S. A. (1993). A modelling investigation of sudden sodium layers. Geophys. Res. Lett. 20, 2841–2844. doi:10.1029/93gl03002

CrossRef Full Text | Google Scholar

Dou, X. K., Xue, X. H., Chen, T. D., Wan, W. X., Li, T., Chen, C., et al. (2009). A statistical study of sporadic sodium layer observed by Sodium lidar at Hefei (31.8° N, 117.3° E). Ann. Geophys. 27, 2247–2257. doi:10.5194/angeo-27-2247-2009

CrossRef Full Text | Google Scholar

Dou, X. K., Xue, X. H., Li, T., Chen, T. D., Chen, C., and Qiu, S. C. (2010). Possible relations between meteors, enhanced electron density layers, and sporadic sodium layers. J. Geophys. Res. Space Phys. 115, A06311. doi:10.1029/2009ja014575

CrossRef Full Text | Google Scholar

Doviak, R. J., Chen, S. S., and Christie, D. R. (1991). A thunderstorm–generated solitary wave observation compared with theory for non-linear waves in a sheared atmosphere. J. Atmos. Sci. 48, 87–111. doi:10.1175/1520-0469(1991)048<0087:atgswo>2.0.co;2

CrossRef Full Text | Google Scholar

Fan, Z. Y., Plane, J. M. C., and Gumbel, J. (2007). On the global distribution of sporadic sodium layers. Geophys. Res. Lett. 34, 87–101. doi:10.1029/2007gl030542

CrossRef Full Text | Google Scholar

Gan, J., and Ingram, R. G. (1992). Internal hydraulics, solitons and associated mixing in a stratified sound. J. Geophys. Res. 97, 9669–9688. doi:10.1029/92JC00491

CrossRef Full Text | Google Scholar

Gardner, C. S., Guo, Y., and Liu, A. Z. (2019). Parameterizing wave-driven vertical constituent transport in the upper atmosphere. Earth Space Sci. 6, 904–913. doi:10.1029/2019ea000625

CrossRef Full Text | Google Scholar

Gardner, C. S., Kane, T. J., Senft, D. C., Qian, J., and Papen, G. C. (1993). Simultaneous observations of sporadic E, Na, Fe, and Ca⁺ layers at urbana, Illinois: three case studies. J. Geophys. Res. Atmos. 98, 16865–16873. doi:10.1029/93jd01477

CrossRef Full Text | Google Scholar

Gardner, C. S., and Shelton, J. D. (1985). Density response of neutral atmospheric layers to gravity wave perturbations. J. Geophys. Res. 90, 1745. doi:10.1029/JA090iA02p01745

CrossRef Full Text | Google Scholar

Gardner, C. S., and Voelz, D. G. (1987). Lidar studies of the nighttime sodium layer over urbana, Illinois: 2. Gravity waves. J. Geophys. Res. Space Phys. 92, 4673–4694. doi:10.1029/ja092ia05p04673

CrossRef Full Text | Google Scholar

Gong, S. H., Yang, G. T., Cheng, X. W., Gong, S. S., Xu, J. Y., Li, F. Q., et al. (2015). Lidar observation campaigns on diurnal variations of the sodium layer in Beijing and Wuhan, China. Sci. China Earth Sci. 58 (8), 1377–1386. doi:10.1007/s11430-015-5099-1

CrossRef Full Text | Google Scholar

Hansen, G., and von Zahn, U. (1990). Sudden sodium layers in polar latitudes. J. Atmos. Sol. Terr. Phys. 52, 585–608. doi:10.1016/0021-9169(90)90055-r

CrossRef Full Text | Google Scholar

Heinrich, D., Nesse, H., Blum, U., Acott, P., Williams, B., and Hoppe, U. P. (2008). Summer sudden Na number density enhancements measured with the ALOMAR Weber Na Lidar. Ann. Geophys. 26, 1057–1069. doi:10.5194/angeo-26-1057-2008

CrossRef Full Text | Google Scholar

Heinselman, C. J., Thayer, J. P., and Watkins, B. J. (1998). A high–latitude observation of sporadic sodium and sporadic E-layer formation. Geophys. Res. Lett. 25, 3059–3062. doi:10.1029/98gl02215

CrossRef Full Text | Google Scholar

Hickey, M. P., and Plane, J. M. C. (1995). A chemical-dynamical model of wave-driven sodium fluctuations. Geophys. Res. Lett. 22, 2861–2864. doi:10.1029/95gl02784

CrossRef Full Text | Google Scholar

Huthnance, J. M. (1989). Internal tides and waves near the continental shelf edge. Geophys. Astrophys. Fluid Dyn. 48, 81–106. doi:10.1080/03091928908219527

CrossRef Full Text | Google Scholar

Kane, T. J., and Gardner, C. S. (1993). Lidar observations of the meteoric deposition of mesospheric metals. Science 259, 1297–1300. doi:10.1126/science.259.5099.1297

PubMed Abstract | CrossRef Full Text | Google Scholar

Kane, T. J., Hostetler, C. A., and Gardner, C. S. (1991). Horizontal and vertical structure of the major sporadic sodium layer events observed during ALOHA–90. Geophys. Res. Lett. 18, 1365–1368. doi:10.1029/91gl01154

CrossRef Full Text | Google Scholar

Kawahara, T. (2007). Oscillatory solitary waves in dispersive media. J. Phys. Soc. Jpn. 33, 260–264. doi:10.1143/JPSJ.33.260

CrossRef Full Text | Google Scholar

Kirkwood, S., and Nilsson, H. (2000). High–latitude sporadic–E and other thin layers – The role of magnetospheric electric fields. Space Sci. Rev. 91, 579–613. doi:10.1023/a:1005241931650

CrossRef Full Text | Google Scholar

Kopp, E. (1997). On the abundance of metal ions in the lower ionosphere. J. Geophys. Res. Space Phys. 102, 9667–9674. doi:10.1029/97ja00384

CrossRef Full Text | Google Scholar

Korteweg, D. J., and de Vries, G. (1895). XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39 (240), 422–443. doi:10.1080/14786449508620739

CrossRef Full Text | Google Scholar

Li, T., She, C. Y., Liu, H. L., and Montgomery, M. T. (2007b). Evidence of a gravity wave breaking event and the estimation of the wave characteristics from sodium lidar observation over Fort Collins, CO (41°N, 105°W). Geophys. Res. Lett. 34, L05815. doi:10.1029/2006gl028988

CrossRef Full Text | Google Scholar

Li, T., She, C. Y., Liu, H. L., Leblanc, T., and Mcdermid, I. S. (2007a). Sodium lidar–observed strong inertia-gravity wave activities in the mesopause region over Fort Collins, Colorado (41°N, 105°W). J. Geophys. Res. Atmos. 112, D22104. doi:10.1029/2007jd008681

CrossRef Full Text | Google Scholar

Liu, A. Z., Guo, Y., Vargas, F., and Swenson, G. R. (2016). First measurement of horizontal wind and temperature in the lower thermosphere (105–140 km) with a Na Lidar at Andes Lidar Observatory. Geophys. Res. Lett. 43, 2374–2380. doi:10.1002/2016GL068461

CrossRef Full Text | Google Scholar

Liu, S. D., and Liu, S. K. (2011). Dynamics of the atmosphere. Beijing: The Publishing House of Beijing University.

Google Scholar

Liu, Y. J., Clemesha, B. R., H Wang, J., and Cheng, X. W. (2013). Comparison of sporadic sodium layer characteristics observed at different time resolutions. Ann. Geophys. 31, 1899–1912. doi:10.5194/angeo-31-1899-2013

CrossRef Full Text | Google Scholar

Liu, Y., and Yi, F. (2009). Behavior of sporadic Na layers on small time scale. J. Atmos. Solar–Terrestrial Phys. 71, 1374–1382. doi:10.1016/j.jastp.2009.06.013

CrossRef Full Text | Google Scholar

Ma, J., Xue, X. H., Dou, X. K., Chen, T. D., Tang, Y. H., Jia, M. J., et al. (2019). Large–scale horizontally enhanced sodium layers coobserved in the midlatitude region of China. J. Geophys. Res. Space Phys. 124, 7614–7628. doi:10.1029/2018JA026448

CrossRef Full Text | Google Scholar

Mamun, A. A., and Shukla, P. K. (2009). Effects of nonthermal distribution of electrons and polarity of net dust–charge number density on nonplanar dust–ion–acoustic solitary waves. Phys. Rev. E 80, 037401. doi:10.1103/PhysRevE.80.037401

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathews, J. D., Zhou, Q. H., Philbrick, C. R., Morton, Y. T., and Gardner, C. S. (1993). Observations of ion and sodium layer coupled processes during AIDA. J. Atmos. Terr. Phys. 55, 487–498. doi:10.1016/0021-9169(93)90083-b

CrossRef Full Text | Google Scholar

Mushtaq, A., Shah, H. A., Rubab, N., and Murtaza, G. (2006). Study of obliquely propagating dust acoustic solitary waves in magnetized tropical mesospheric plasmas with effect of dust charge variations and rotation of the plasma. Phys. Plasmas 13. doi:10.1063/1.2206547

CrossRef Full Text | Google Scholar

Nagasawa, C., and Abo, M. (1995). Lidar observations of a lot of sporadic sodium layers in mid–latitude. Geophys. Res. Lett. 22, 263–266. doi:10.1029/94gl03008

CrossRef Full Text | Google Scholar

Nappo, C. J. (2002). Fundamentals. Int. Geophys. 85, 1–28. doi:10.1016/b978–0–12–385223–6.00001–x

CrossRef Full Text | Google Scholar

Nesse, H., Heinrich, D., Williams, B., Hoppe, U. P., Stadsnes, J., Rietveld, M., et al. (2008). A case study of a sporadic sodium layer observed by the ALOMAR Weber Na lidar. Ann. Geophys. 26, 1071–1081. doi:10.5194/angeo-26-1071-2008

CrossRef Full Text | Google Scholar

Plane, J., Feng, W., and Dawkins, E. (2015). The mesosphere and metals: chemistry and changes. Chem. Rev. 115, 4497–4541. doi:10.1021/cr500501m

PubMed Abstract | CrossRef Full Text | Google Scholar

Plane, J. M. C. (2003). Atmospheric chemistry of meteoric metals. Chem. Rev. 103, 4963–4984. doi:10.1021/cr0205309

PubMed Abstract | CrossRef Full Text | Google Scholar

Prasanth, P. V., Kumar, Y. B., Rao, D. N., and Narayana Rao, D. (2007). Lidar observations of sporadic Na layers over Gadanki (13.5° N, 79.2° E). Ann. Geophys. 25, 1759–1766. doi:10.5194/angeo–25–1759–2007

CrossRef Full Text | Google Scholar

Qian, J., Gu, Y., and Gardner, C. S. (1998). Characteristics of the sporadic Na layers observed during the airborne lidar and observations of Hawaiian airglow/airborne noctilucent cloud (ALOHA/ANLC–93) campaigns. J. Geophys. Res. Atmos. 103, 6333–6347. doi:10.1029/97jd03374

CrossRef Full Text | Google Scholar

Qiu, S. C., Tang, Y. H., Jia, M. J., Xue, X. H., Dou, X. K., Li, T., et al. (2016). A review of latitudinal characteristics of sporadic sodium layers, including new results from the Chinese Meridian Project. Earth–Science Rev. 162, 83–106. doi:10.1016/j.earscirev.2016.07.004

CrossRef Full Text | Google Scholar

Qiu, S. C., Wang, N., Soon, W., Lu, G. P., and Dou, X. K. (2020). Sporadic sodium layer: A possible tracer for the conjunction between the upper and lower atmospheres. Atmos. Chem. Phys. 21, 11927–11940. doi:10.5194/acp–2020–1079

CrossRef Full Text | Google Scholar

Richter, E. S., and Sechrist, C. F. (1979). A meteor ablation-cluster ion atmospheric sodium theory. Geophys. Res. Lett. 6, 183–186. doi:10.1029/gl006i003p00183

CrossRef Full Text | Google Scholar

Russell, J. M. (1884). Report of the fourteenth meeting of the. London: British Association for the Advancement of Science, 311–390.

Google Scholar

Schunk, R., and Nagy, A. (2009). Ionospheres: Physics, plasma physics, and chemistry. Cambridge: Cambridge University Press, 206–230. doi:10.1017/CBO9780511635342

CrossRef Full Text | Google Scholar

von Zahn, U., and Hansen, T. L. (1988). Sudden neutral sodium layers: A strong link to sporadic E layers. J. Atmos. Terr. Phys. 50, 93–104. doi:10.1016/0021-9169(88)90047-5

CrossRef Full Text | Google Scholar

von Zahn, U., von der Gathen, P., and Hansen, G. (1987). Forced release of sodium from upper atmospheric dust particles. Geophys. Res. Lett. 14, 76–79. doi:10.1029/gl014i001p00076

CrossRef Full Text | Google Scholar

Wazwaz, A. M. (2009). Partial differential equations and solitary waves theory, non-linear physical science. Berlin, Heidelberg: Springer.

Google Scholar

Williams, B. P., Croskey, C. L., She, C. Y., Mitchell, J. D., and Goldberg, R. A. (2006). Sporadic sodium and E layers observed during the summer 2002 MaCWAVE/MIDAS rocket campaign. Ann. Geophys. 24, 1257–1266. doi:10.5194/angeo-24-1257-2006

CrossRef Full Text | Google Scholar

Xu, J. Y., and Smith, A. K. (2003). Perturbations of the sodium layer: controlled by chemistry or dynamics? Geophys. Res. Lett. 30. doi:10.1029/2003gl018040

CrossRef Full Text | Google Scholar

Xu, J. Y., and Smith, A. K. (2004). Studies of gravity wave-induced fluctuations of the sodium layer using linear and non-linear models. J. Geophys. Res. Atmos. 109, D02306. doi:10.1029/2003jd004038

CrossRef Full Text | Google Scholar

Xue, X. H. (2007). Studies on geoeffectiveness of coronal mass ejections and near–earth space environment. Hefei, China: Ph.D, University of Science and Technology of China.

Google Scholar

Zabusky, N. J., and Kruskal, M. (1965). Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243. doi:10.1103/PhysRevLett.15.240

CrossRef Full Text | Google Scholar

Zhou, Q. H., and Mathews, J. D. (1995). Generation of sporadic sodium layers via turbulent heating of the atmosphere? J. Atmos. Terr. Phys. 57, 1309–1319. doi:10.1016/0021-9169(95)97298-i

CrossRef Full Text | Google Scholar

Zhou, Q. H., Mathews, J. D., and Tepley, C. A. (1993). A proposed temperature dependent mechanism for the formation of sporadic sodium layers. J. Atmos. Terr. Phys. 55, 513–521. doi:10.1016/0021-9169(93)90085-d

CrossRef Full Text | Google Scholar