Influence of magnetic reconnection on the eruptive catastrophes of coronal magnetic flux ropes

Introduction: Large-scale solar eruptive activities have a close relationship with coronal magnetic flux ropes. Previous numerical studies have found that the equilibrium of a coronal flux rope system could be disrupted if the axial magnetic flux of the rope exceeds a critical value, so that the catastrophe occurs, initiating the flux rope to erupt. Further studies discovered that the catastrophe does not necessarily exist: The flux rope system with certain photospheric flux distributions could be non-catastrophic. It is noteworthy that most previous numerical studies are under the ideal magnetohydrodynamic (MHD) condition, so that it is still elusive whether there is the catastrophe associated with the critical axial flux if magnetic reconnection is included in the flux rope system.Methods: In this paper, we carried out numerical simulations to investigate the evolutions of coronal magnetic rope systems under the ideal MHD and the resistive condition.Results and discussions: Under the ideal MHD condition, our simulation results demonstrate that the flux rope systems with either too compact or too weak photospheric magnetic source regions are non-catastrophic versus varying axial flux of the rope, and thus no eruption could be initiated; if there is magnetic reconnection in the rope system, however, those flux rope systems could change to be capable of erupting via the catastrophe associated with increasing axial flux. Therefore, magnetic reconnection could significantly influence the catastrophic behaviors of flux rope system. It should be both the magnetic topology and the local physical parameters related to magnetic reconnection that determine whether the increasing axial flux is able to cause flux rope eruptions.

1 Introduction

Large-scale solar eruptive activities are the principal cause of extreme space weather in Earth and planetary space environments (Švestka, 2001; Cheng et al., 2014; Lugaz et al., 2017; Gopalswamy et al., 2018). Different kinds of large-scale solar eruptions, including prominence/filament eruptions (Li et al., 2016; Jenkins et al., 2018; Fan, 2020; Devi et al., 2021), flares (Chen et al., 2015; Li et al., 2016; Cheung et al., 2019), and coronal mass ejections (CMEs, Shen et al., 2014; Lamy et al., 2019; Bemporad et al., 2022), are generally considered to be different manifestations of the eruptions of coronal magnetic flux rope (Zhang et al., 2001; Vršnak et al., 2005; Jiang et al., 2016; Chen et al., 2020; Liu, 2020). Therefore, investigating the initiation and evolution of flux rope eruptions is crucial not only for understanding solar eruptions, but also for space weather forecasting. Many theoretical models have been proposed to shed light on the physical scenario of coronal flux rope eruptions. These models are based on different kinds of physical mechanisms, such as ideal magnetohydrodynamic (MHD) instabilities (Török and Kliem, 2003; Aulanier et al., 2010; Guo et al., 2010; Savcheva et al., 2012; Keppens et al., 2019), magnetic reconnection (Antiochos et al., 1999; Chen and Shibata, 2000; Moore et al., 2001; Sterling and Moore, 2004; Archontis and Hood, 2008; Inoue et al., 2015), and the catastrophes of coronal flux ropes (Van Tend and Kuperus, 1978; Forbes and Priest, 1995; Lin and van Ballegooijen, 2002; Kliem et al., 2014; Zhang et al., 2021).

Many theoretical studies suggested that flux rope catastrophes are intriguing candidates for the source of solar eruptions (e.g., Isenberg et al., 1993; Lin and Forbes, 2000). In the flux rope catastrophe theory, the onset of the eruption is approached as the loss of equilibrium of the coronal flux rope system. Before the onset, the flux rope should be static or quasi-static (Török et al., 2013; Liu, 2020), indicating that the flux rope system is in equilibrium. If the equilibrium is not disrupted, the net force on the flux rope will always be zero, so that its state of motion will remains unchanged, i.e., no eruption of the flux rope could occur. Therefore, loss of equilibrium must occur during the onset of the eruption, and the resultant net force initiates the flux rope to erupt. This is the fundamental scenario of the catastrophe of coronal flux ropes. The investigation about when and how the catastrophe occurs is based on the equilibrium manifold (Forbes and Priest, 1995; Isenberg and Forbes, 2007; Kliem et al., 2014), which consists of all the equilibrium states of the flux rope system. For example, by analytically deriving the equilibrium manifold as a function of current within the flux rope, Van Tend and Kuperus. (1978) for the first time discovered that there is a critical value of the current, beyond which there are no neighbouring equilibrium states so that the catastrophe occurs, which results in a discontinuous equilibrium manifold; this critical value is referred to as the catastrophic point. Many more analytical studies have verified that the catastrophe could occur in various types of coronal flux rope systems, resulting in the eruption of the flux rope (Priest and Forbes, 1990; Forbes and Priest, 1995; Lin and Forbes, 2000; Démoulin and Aulanier, 2010; Kliem et al., 2014; Longcope and Forbes, 2014). In addition, numerical simulations have also been carried out in many previous studies to investigate the catastrophes of coronal flux ropes (Forbes, 1990; Chen et al., 2007; Zhang et al., 2017a; Zhang et al., 2021). In numerical studies, the equilibrium manifold as a function of a certain physical parameter is obtained by simulating the equilibrium solutions of the flux rope system with different values of this parameter. For example, Su et al. (2011) discovered that the equilibrium manifold versus the axial magnetic flux of the flux rope is discontinuous at a critical value, beyond which a catastrophe occurs. Similar results are obtained in many other numerical studies (Bobra et al., 2008; Su et al., 2009; Su et al., 2011; Zhang et al., 2017a; Zhang et al., 2017b), indicating that the axial flux of the rope should play an important role in initiating solar eruptions.

The catastrophe associated with the critical axial flux does not necessarily exist in coronal flux rope system. Previous numerical studies have demonstrated that the photospheric flux distributions of the background field greatly influence the catastrophic behaviors of coronal flux rope systems (Sun et al., 2007; Zhang et al., 2017a; Zhang et al., 2017b). Previous studies found that there are two types of non-catastrophic flux rope systems: if the photospheric flux is too concentrated toward the polarity inversion line (hereafter “compact” cases), or the total magnetic flux originating from the photospheric magnetic source regions is too weak (hereafter “weak” cases), the equilibrium manifold as a function of the rope’s axial flux will be continuous so that no catastrophe could occur. It is still an open question why there is no catastrophe in these two types of flux rope system; Zhang et al. (2017b) inferred that the constraint from the background field on the flux rope might probably plays an considerable role. It is noteworthy that magnetic reconnection is completely prohibited in those studies, so that their conclusion about the two types of non-catastrophic flux rope systems is under the ideal MHD condition. Since the actual solar corona is resistive, there should be reconnection in actual coronal flux rope systems (Jiang et al., 2021; Bian et al., 2022; Yan et al., 2022). In fact, magnetic reconnection could not only change the magnetic topology, resulting in the redistribution of the Ampère’s force (also known as Lorentz force in many papers), but the reconnection outflow could also push the flux rope upward (Chen et al., 2004; Wang et al., 2007; Xue et al., 2016; Cheng et al., 2020). This indicates that magnetic reconnection could contribute to the force balance of a coronal flux rope system, implying that the catastrophic behaviors of the rope system might differ under the ideal MHD and the resistive condition. Therefore, it is critical to assess the influence of magnetic reconnection on the catastrophic behaviors of coronal flux rope systems, so as to shed more light on the catastrophe theory for solar eruptions. To achieve this, we use a 2.5-dimensional MHD numerical model to simulate the catastrophic behaviors of the coronal flux rope systems with either compact or weak photospheric source regions. Both the equilibrium manifolds versus the axial magnetic flux under the ideal MHD and the resistive condition are simulated, based on which the influence of magnetic reconnection is investigated. The rest of this paper is arranged as follows: the numerical model and simulating procedures are introduced in Section 2, the simulation results are presented in Section 3, and the conclusion and discussion are given in Sect. 4.

2 Numerical model

2.1 Basic equations

The numerical model in our simulation is similar as those used in Zhang et al., 2017a; Zhang et al., 2017b. For 2.5-dimensional cases, by assuming all the quantities satisfy ∂/∂z = 0, the magnetic field can be written in form of magnetic flux function ψ:

$\mathbf{B}=▿\psi \times \widehat{\mathit{z}}+B_z\widehat{\mathit{z}}.(1)$

Here z is the unit vector in z−direction. Obviously, the divergence-free condition (▿⋅B = 0) is always satisfied. With the form given in Eq. 1, the MHD equations in our simulations could be rewritten in the following form:

$\frac{\partial \rho }{\partial t}+▿\cdot \left(\rho \mathit{v}\right)=0,(2)$

$\begin{array}{ll}\hfill & \frac{\partial \mathit{v}}{\partial t}+\frac{2}{\rho {\beta }_0}\left(▵\psi ▿\psi +B_z▿B_z+▿\psi \times ▿B_z\right)+\mathit{v}\cdot ▿\mathit{v}\hfill \\ \hfill & +▿T+\frac{T}{\rho }▿\rho +g\widehat{\mathit{y}}=0,\hfill \end{array}(3)$

$\begin{array}{ll}\hfill & \frac{\partial \psi }{\partial t}+\mathit{v}\cdot ▿\psi -\eta ▵\psi =0,\hfill \end{array}(4)$

$\begin{array}{ll}\hfill & \frac{\partial B_z}{\partial t}+▿\cdot \left(B_z\mathit{v}\right)+\left(▿\psi \times ▿v_z\right)\cdot \widehat{\mathit{z}}-\eta ▵B_z=0,\hfill \end{array}(5)$

$\begin{array}{ll}\hfill & \frac{\partial T}{\partial t}-\frac{\eta \left(\gamma -1\right)}{\rho R}\left[{\left(▵\psi \right)}^2+|▿\times \left(B_z\widehat{\mathit{z}}\right){|}^2\right]\hfill \\ \hfill & +\mathit{v}\cdot ▿T+\left(\gamma -1\right)T▿\cdot \mathit{v}=0,\hfill \end{array}(6)$

where

$▵\psi =\frac{{\partial }^2\psi }{\partial x^2}+\frac{{\partial }^2\psi }{\partial y^2},▵B_z=\frac{{\partial }^2{B}_z}{\partial x^2}+\frac{{\partial }^2{B}_z}{\partial y^2}.(7)$

Here ρ is the density, v the velocity, T the temperature, γ = 5/3 the polytropic index, g the gravity, η the resistivity, and β₀ = .1 the characteristic ratio of the gas pressure to the magnetic pressure, which is comparable to the value in quiescent regions (Anzer and Heinzel, 2007; Hillier et al., 2012; Xia et al., 2012). The x, y, and z−component of the quantities are denoted by the subscript x, y, z. The radiation and the heat conduction in the energy equation are neglected. The numerical domain in our simulation is 0 < x < 200 Mm, 0 < y < 500 Mm; it is discretized into 200 × 250 uniform meshes.

2.2 Initial state

Table 1 The initial states in our simulations are constructed by numerical procedures. Here we first use the complex variable method (e.g., Hu and Liu, 2000; Zhang et al., 2017a) to construct the background field originating from photospheric magnetic source regions. The background field is a partially open bipolar field, with a negative surface magnetic charge located at the lower boundary within −b < x < − a, and a positive one within a < x < b; the distance between the two source regions is D = 2a, and the width of the source region W = b−a. The background field in x−y plane could then be expressed in the complex variable form as:

$f\left(\omega \right)\equiv B_x-i{B}_y=\lambda \frac{{\left(\omega +i{y}_N\right)}^{1/2}{\left(\omega -i{y}_N\right)}^{1/2}}{F\left(a,b,y_N\right)}\text{ln}\left(\frac{{\omega }^2-a^2}{{\omega }^2-b^2}\right),(8)$

where ω = x + iy,

$\begin{array}{ll}\hfill F\left(a,b,y_N\right)& =\frac{1}{b-a}{\int }_a^b{\left(x^2+y_N^2\right)}^{1/2}dx=\frac{1}{2\left(b-a\right)}\hfill \\ \hfill & \times \left[b{\left(b^2+y_N^2\right)}^{1/2}-a{\left(a^2+y_N^2\right)}^{1/2}\right.\hfill \\ \hfill & +\left.y_N^2\text{ln}\left(\frac{b+{\left(b^2+y_N^2\right)}^{1/2}}{a+{\left(a^2+y_N^2\right)}^{1/2}}\right)\right],\hfill \end{array}(9)$

and the neutral point of the background field is at (y = y_N, x = 0). As indicated by Eq. 8, the magnetic field strength of the background field is proportional to the dimensionless parameter λ. The magnetic flux function within the domain could then be calculated by:

$\psi \left(x,y\right)=\mathrm{I}\mathrm{m}\left\{\int f\left(\omega \right)d\omega \right\},(10)$

With calculated the flux function ψ, and by letting B_z = 0 in the background field, the magnetic configuration of the background field is obtained (Eq. 1). In particular, the flux function of the background field at the lower base, ψ_i, could be calculated as:

$\begin{array}{ll}\hfill {\psi }_i& =\psi \left(x,0\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}\lambda \widehat{{\psi }_0}\pi \left(b-a\right),\hfill & |x|<a\hfill \\ \lambda \widehat{{\psi }_0}\pi \left(b-a\right)F\left(|x|,b,y_N\right)/F\left(a,b,y_N\right),\hfill & a⩽|x|⩽b\hfill \\ 0,\hfill & |x|>b\hfill \end{array}\right.\hfill \end{array}(11)$

and the flux function at the neutral point of the background field is

${\psi }_N=\psi \left(0,y_N\right)=\frac{\lambda \widehat{{\psi }_0}\pi \left(b^2-a^2\right)}{2F\left(a,b,y_N\right)}(12)$

here ${\psi }_c=\lambda \pi (b-a)\widehat{{\psi }_0}$ $(\widehat{{\psi }_0}=37.25\mathrm{M}\mathrm{x}\mathrm{c}{\mathrm{m}}^{-\mathrm{2}})$ is the total magnetic flux emanating upward from the positive photospheric source region per unit length along z−direction, i.e. ψ_c represents the intensity of background magnetic field originating from the photospheric source regions. The ratio of the background field’s open magnetic flux to its total magnetic flux could then be calculated by:

$\kappa =\frac{{\psi }_N}{{\psi }_c}.(13)$

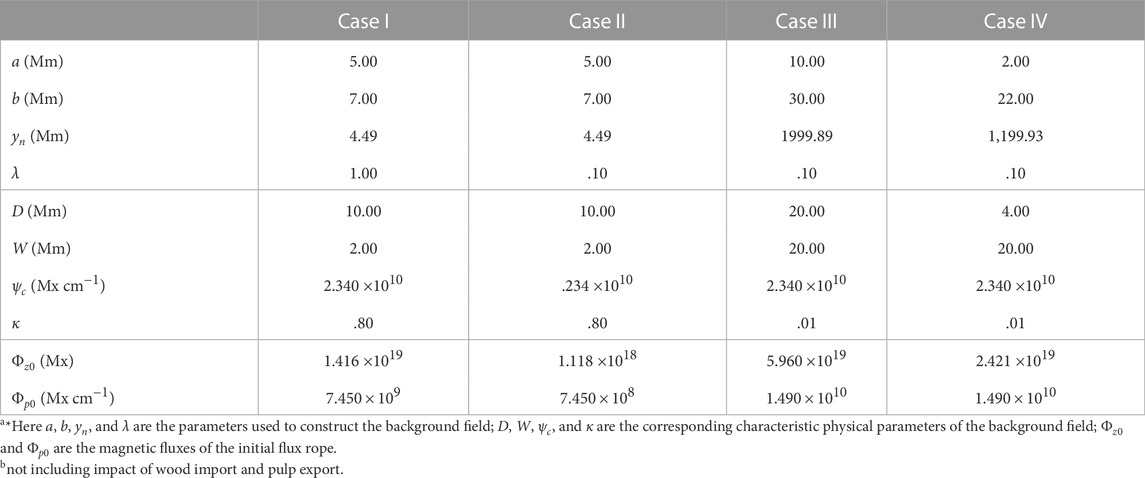
For a given background magnetic field, its characteristic physical parameters include D, W, ψ_c and κ, which could be calculated with a group of given a, b, y_N, and λ. For example, by letting a = 5.00 Mm, b = 7.00 Mm, y_N = 4.49 Mm, λ = 1.0, the calculated background configuration is plotted in Figure 1A, and the characteristic parameters of this background field are: D = 10 Mm, W = 2 Mm, ψ_c = 2.34 × 10¹⁰ Mx cm⁻¹, and κ = .80, as tabulated in the second column (Case I) in Table 1. The initial corona in our simulations is static and isothermal:

$T_c\equiv T\left(0,x,y\right)=1\times 10^6\mathrm{K},{\rho }_c\equiv \rho \left(0,x,y\right)={\rho }_0{\mathrm{e}}^{-gy},(14)$

where ρ₀ = 3.34 × 10^–13 kg m⁻³.

TABLE 1

TABLE 1. The parameters of the background fields and the initial states for Case I–IV.

FIGURE 1

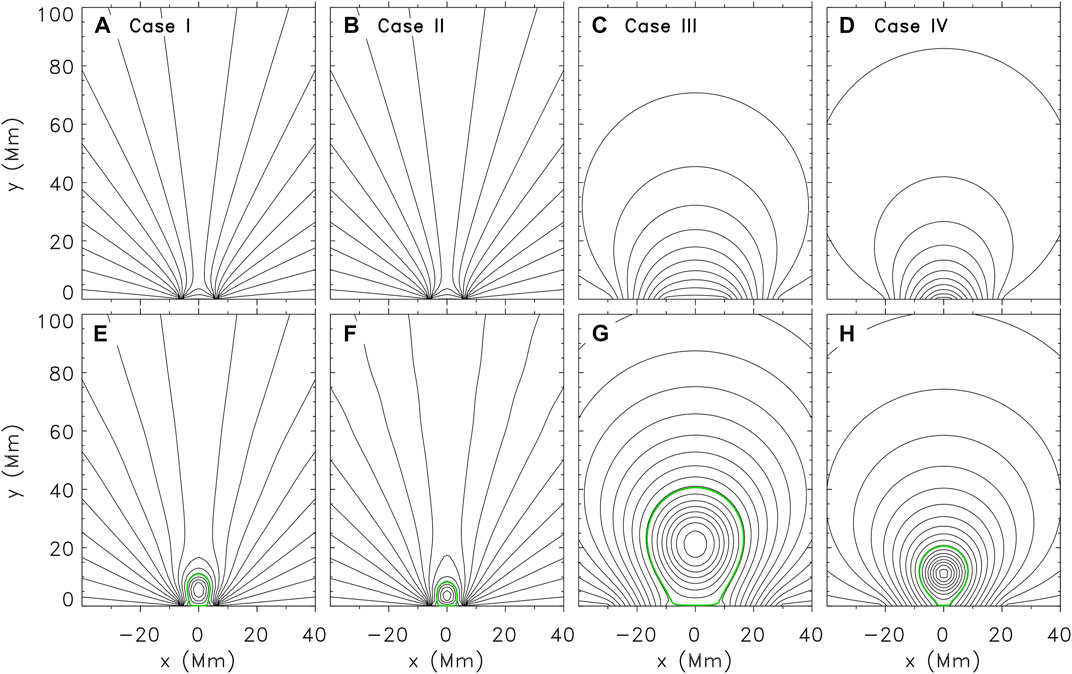
FIGURE 1. The magnetic configurations of the background fields and initial states in the simulation. Panel (A) is the background field for Case I, and panel (E) is the corresponding initial state; panels (B) and (F), (C) and (G), (D) and (H) are those for Case II, III, IV, respectively. The black curves are the magnetic field lines, and the green curves mark the boundary of the flux rope. The physical parameters for the background fields and initial states are tabulated.

With the background field obtained above, we let a flux rope emerge from the lower base of the domain with similar simulating procedures as those introduced in, e.g., Zhang et al. (2017a) and Zhang et al. (2020), and then relax the flux rope system to equilibrium. The resultant equilibrium state consisting of a flux rope embedded in the background field is the constructed initial state. For the background field plotted in Figure 1A, the constructed initial state is illustrated in Figure 1E. The magnetic properties of a flux rope could be characterized by its magnetic fluxes, including the total axial flux passing through the rope’s cross section, Φ_z = ∬ B_zdS, and the annular flux per unit length along z-direction of the rope, Φ_p; in 2.5 dimensional cases, the poloidal flux is calculated as:

${\mathrm{\Phi }}_p={\psi }_{rc}-{\psi }_{rb},(15)$

where ψ_rc and ψ_rb are the flux function ψ at the center and the boundary of the flux rope, respectively. For the initial state illustrated in Figure 1E, Φ_z0 = 1.416 × 10¹⁹ Mx and Φ_p0 = 7.450 × 10⁹ Mx cm⁻¹. With this initial state, we could further simulate the catastrophic behaviors of the coronal flux rope system with the given photospheric magnetic conditions (detailed simulating procedures are introduced in Section 2.3). It is noteworthy that the radius of the flux rope in our simulation is finite, so that the thin-rope approximation is not satisfied. Under this circumstance, the initial state could only be obtained by numerical procedures.

In our simulations, apart from those plotted in Figure 1A and Figure 1E, we also construct another three groups of background field and initial state with similar procedures introduced above, and their parameters are tabulated in Table 1; all these 4 cases are marked as Case I ∼IV, respectively. The background field and the initial state in Case II are illustrated in Figure 1B and Figure 1F, respectively. As shown by the second and the third column in Table 1, D, W, and κ in Case I and Case II are the same; the only difference in the characteristic parameters of the background field between these two cases is that ψ_c in Case II is much smaller than that in Case I (achieved by adjusting λ to .1 in Case II), i.e. the intensity of the background magnetic field originating from the photospheric source regions in Case II is much weaker than those in Case I. For Case III and Case IV, the corresponding background fields and initial states are illustrated in Figures 1C–D and Figures 1G–H), respectively. As shown in the last two columns in Table 1, the characteristic parameters of the background field in these two cases are the same, except that the distance between the source regions, D, is much smaller in Case IV than that in Case III.

2.3 Simulating procedures

Starting from each of the four initial states obtained above, we simulate the equilibrium states of the corresponding flux rope system with different axial magnetic fluxes of the rope: from 0 ∼ 20τ_A (τ_A = 17.4 s is the typical Alfvén transit time), the axial flux Φ_z and the poloidal flux Φ_p are adjusted from the initial values to a certain group of target values (${\mathrm{\Phi }}_z^1$, ${\mathrm{\Phi }}_p^t$), and from 20 ∼ 300τ_A, the magnetic system is relaxed to equilibrium, with the magnetic fluxes fixed at the target values (${\mathrm{\Phi }}_z^1$, ${\mathrm{\Phi }}_p^t$). We note that the conservation of the poloidal flux is achieved by fixing the flux function at the rope center, ψ_rc, during the relaxation (Eq. 15). The final state at t = 300τ_A is regarded as the equilibrium state of the flux rope system for ${\mathrm{\Phi }}_z^1$. During the relaxation, magnetic reconnection is either included or completely prohibited during the relaxation, corresponding to the resistive condition and ideal MHD condition, respectively. For the simulations under the resistive condition, anomalous resistivity is used:

$\eta =\left\{\begin{array}{cc}0,\hfill & j\le j_c\hfill \\ {\eta }_m{\mu }_0{v}_0{L}_0{\left(\frac{j}{j_c}-1\right)}^2.\hfill & j>j_c\hfill \end{array}\right.(16)$

here η_m = .10, L₀ = 10⁷ m, v₀ = 128.57 km s⁻¹, j_c = 2.96 × 10^–5 A m⁻², and μ₀ is the vacuum magnetic permeability. On the other hand, for the simulations under the ideal MHD conditions, we use similar simulating procedures as those in Zhang et al. (2017a,b) during the relaxation to prohibit the reconnection: first set the resistivity η to be 0, and then reassign the flux function ψ along the current sheet with the initial values at each time step, so as to keep ψ invariant along the current sheet. Since any reconnection will reduce the value of ψ at the current sheet, both physical and numerical reconnections are prohibited with the simulating procedures introduced above. For the given target values ${\mathrm{\Phi }}_z^1$, we are able to simulate two equilibrium states with the simulating procedures above: if reconnection is prohibited during the relaxation, the resultant equilibrium state is under ideal MHD condition, whereas the resultant equilibrium state is under resistive condition if reconnection is included during the relaxation.

Similar simulations are repeated for different target values ((${\mathrm{\Phi }}_z^2$, ${\mathrm{\Phi }}_p^t$), (${\mathrm{\Phi }}_z^3$, ${\mathrm{\Phi }}_p^t$), …) so as to obtain equilibrium states with different Φ_z. Eventually, all the calculated equilibrium states without reconnection constitute a equilibrium manifold under the ideal MHD condition, and all those with reconnection constitute the equilibrium manifold under the resistive condition.

In our simulations, the quantities at the lower boundary of the domain are fixed, so that the lower boundary corresponds to the photosphere. Symmetric boundary condition is used at the left side of the domain (x = 0). At the other boundaries, increment equivalent extrapolation (Zhang et al., 2017a; b) is used to prescribe the boundary quantities:

$U_b^{n+1}=U_{b-1}^{n+1}+U_b^n-U_{b-1}^n,(17)$

where U represents the quantities. The superscript n denote the quantities at the current time step, and n+1 the next time step; the subscript b indicates the quantities at the boundary, and b−1 those at the grids next to the boundary.

3 Simulation results

3.1 Weak cases

The equilibrium manifold as a function of the axial flux Φ_z under the ideal MHD condition for Case I is plotted in Figure 2A. All the equilibrium states have the same Φ_p = 7.45 × 10⁹ Mx cm⁻¹. Obviously, this equilibrium manifold is discontinuous: the flux rope keeps sticking to the photosphere (Figures 2B–C)) before reaching a critical axial flux at about 1.527 × 10¹⁸ Mx, which is marked by the black vertical dotted line in Figure 2A; otherwise, the flux rope jumps upward (Figure 2D), indicating that a catastrophe occurs. Therefore, the flux rope system in Case I is catastrophic under the ideal MHD condition.

FIGURE 2

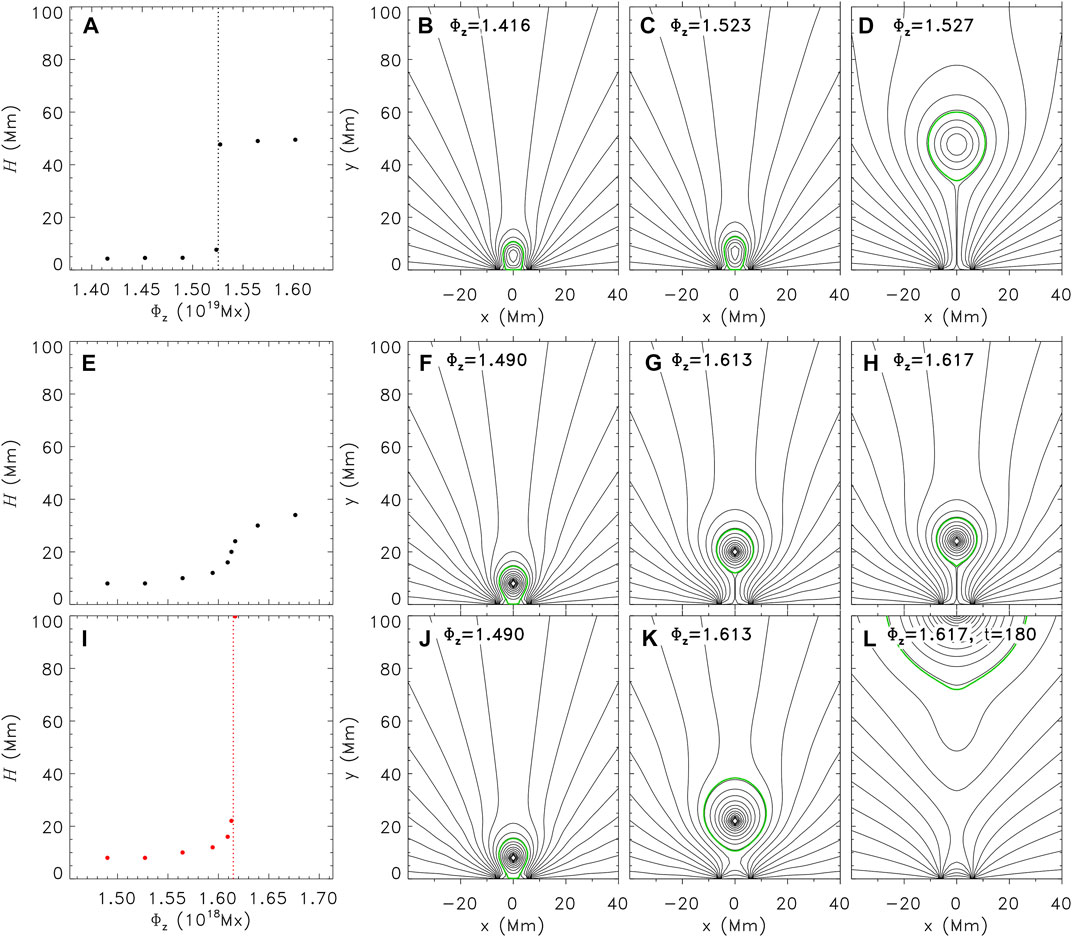
FIGURE 2. The simulation results for Case I and Case II. Panel (A) is the equilibrium manifold for Case I under the ideal MHD condition; panels (B–D) are the magnetic configuration of the simulated equilibrium states for Case I, and the corresponding Φ_z is marked at the top of each panel. Panels (E–H) and panels (I–(L) are the simulation results for Case II under the ideal MHD and the resistive condition, respectively; the red vertical dotted line in panel (I) denote the catastrophic point ${\mathrm{\Phi }}_{zc}^w$. The green curves mark the boundary of the flux rope.

The equilibrium manifold under the ideal MHD condition for Case II is plotted in Figure 2E, and all the equilibrium states have the same Φ_p = 2.980 × 10⁹ Mx cm⁻¹. Different from that in Figure 2A, the equilibrium manifold under the ideal MHD condition for Case II is continuous: the height of the rope axis, H, gradually rises as Φ_z increases, and the magnetic configurations of some equilibrium states are illustrated in Figure 2F-2h). The evolution of the flux rope system during the relaxation to simulate the equilibrium state in Figure 2G is shown in Figures 3A1-A4. After Φ_z is increased to 1.613 × 10¹⁸ Mx at t = 20τ_A (Figure 3A1), the flux rope gradually rises and then is suspended in the corona (Figures 3A2–A3), until it reaches equilibrium (Figure 3A4), the same as Figure 2G). Although a current sheet is formed by the magnetic field of opposite directions below the rope, the magnetic reconnection is prohibited by the simulating procedures introduced in Section 2.3. These simulation results demonstrate that the flux rope system in Case II is non-catastrophic so that no eruption could be initiated under the ideal MHD condition. As introduced in Section 2.2, the only difference in the characteristic parameters of the background field in Case I and Case II is ψ_c: the intensity of the background magnetic field originating from the photospheric source regions in Case II is much weaker than those in Case I, i.e. Case II is a “weak” case. This result is consistent with the conclusions in Zhang et al., 2017a; Zhang et al.,2017b.

FIGURE 3

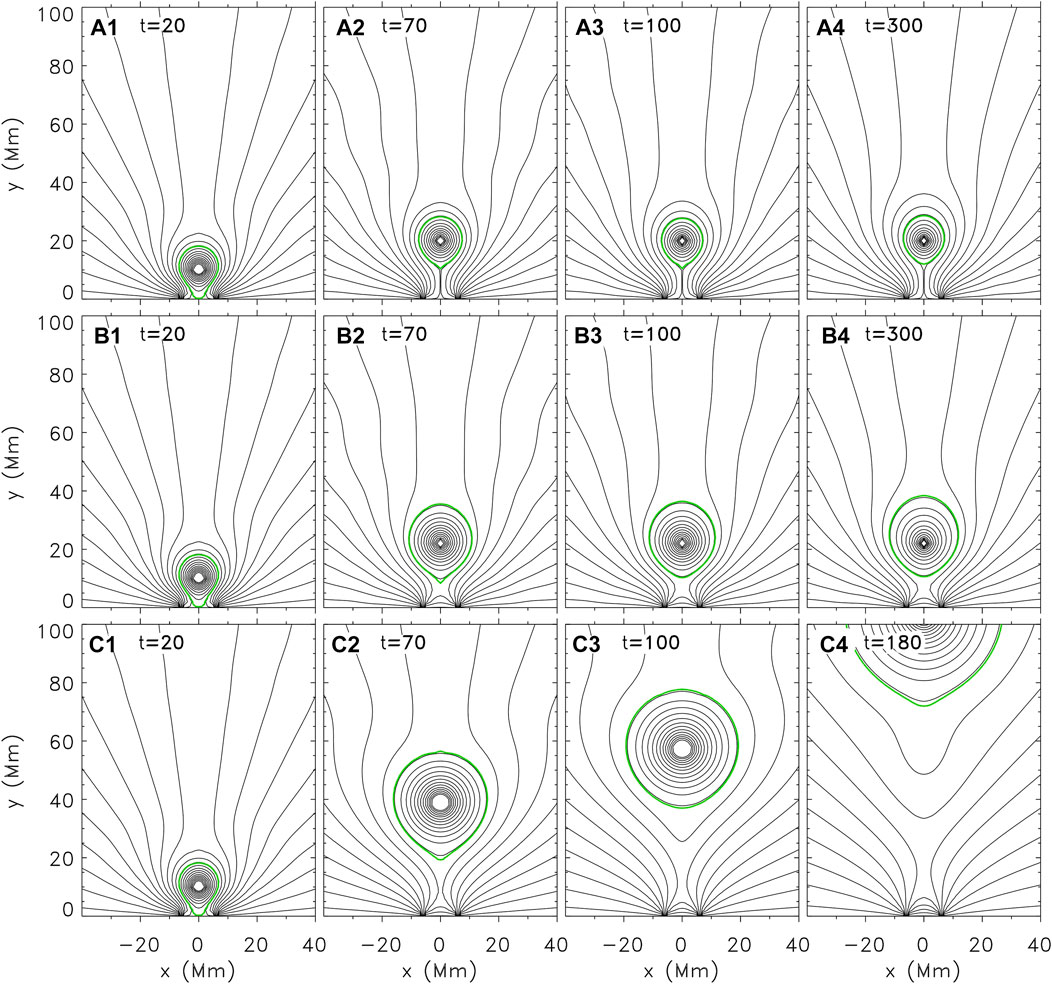
FIGURE 3. The temporal evolutions of the flux rope for Case II. Panels (A1–A4) illustrate the evolution of the flux rope during the relaxation to simulate the equilibrium state in Figure 2G. Panels (B1–B4) illustrate the evolution of the flux rope during the relaxation to simulate the equilibrium state in Figure 2K, which is the equilibrium state right before ${\mathrm{\Phi }}_z={\mathrm{\Phi }}_{zc}^w$ is reached under the resistive condition; Panels (B1–B4) illustrate the evolution right after ${\mathrm{\Phi }}_z={\mathrm{\Phi }}_{zc}^w$ is reached under the resistive condition.

To investigate the influence of magnetic reconnection on the catastrophic behaviors of flux rope systems with weak photospheric source regions, we also simulate the equilibrium manifold under the resistive condition for Case II, as plotted in Figure 2I. Obviously, if there is magnetic reconnection in the flux rope system, the equilibrium manifold is discontinuous: there is a critical axial magnetic flux ${\mathrm{\Phi }}_{zc}^w\approx 1.617\times 10^{18}$ Mx, which is marked by the red vertical dotted line in Figure 2I. As shown in Figure 2I, H gradually rises as Φ_z increases before reaching ${\mathrm{\Phi }}_{zc}^w$. Figure 2K illustrate the magnetic configuration of the equilibrium state with Φ_z = 1.613 × 10¹⁸ Mx, i.e., the equilibrium state right before ${\mathrm{\Phi }}_{zc}^w$ is reached, and the evolution of the flux rope system to reach this equilibrium state is shown in Figures 3B1–B4). Comparing with the simulation results without reconnection in Figures 3A1–A4, it is demonstrated that magnetic reconnection occurs in the current sheet below the flux rope (Figures 3B1–B4), resulting in closed arcades below the rope. The flux rope does not further rises but remains suspended, and eventually evolves to equilibrium (Figure 3B4), the same as Figure 2G). As introduced in Section 2.2, B_z = 0 in the background field, so that the reconnection has no effect on the total axial magnetic flux of the rope. If Φ_z increases to reach ${\mathrm{\Phi }}_{zc}^w$, the flux rope is initiated to erupt, as shown by the evolution of the flux rope system illustrated in Figures 3C1–C4: the flux rope does not remains suspended in the corona, but keeps rising after Φ_z is increased to ${\mathrm{\Phi }}_{zc}^w$, resulting in the eruption of the flux rope. Obviously, the evolutions of the flux rope system before and after Φ_z reaches ${\mathrm{\Phi }}_{zc}^w$ are quite different if magnetic reconnection is included, indicating that there is a catastrophe in the flux rope system, and ${\mathrm{\Phi }}_{zc}^w$ is the catastrophic point. We note that there is no equilibrium state if the catastrophe occurs under the ressitive condition, so that we illustrate the state at t = 180τ_A in Figure 2l) (the same as Figure 3C4) as the characteristic state for ${\mathrm{\Phi }}_z={\mathrm{\Phi }}_{zc}^w$, and the corresponding red point in Figure 2I is plotted at the top boundary. Our simulation results suggest that the magnetic flux rope system with weak photospheric source regions could also be catastrophic if magnetic reconnection is included in the system.

3.2 Compact cases

The simulation results under the ideal MHD condition for Case III and Case IV are illustrated in Figures 4A–D and Figures 4E–H), respectively, in which all the simulated equilibrium states have the same Φ_p = 1.490 × 10¹⁰ Mx cm⁻¹. As introduced in Section 2.2 and Table 1, the distance between the photospheric source regions is much smaller in Case IV than that in Case III. As shown in Figure 4A, the flux rope system in Case III is catastrophic: the catastrophe occurs if Φ_z reaches 6.072 × 10¹⁹ Mx, as marked by the black vertical dotted line in Figure 4A. The flux rope system in Case IV, however, is non-catastrophic; its equilibrium manifold is continuous. This indicates Case IV is a “compact” case, which is also consistent with Zhang et al. (2017a,b). The evolution of the flux rope system to reach the equilibrium state in Figure 4G is shown in Figures 5A1–A4.

FIGURE 4

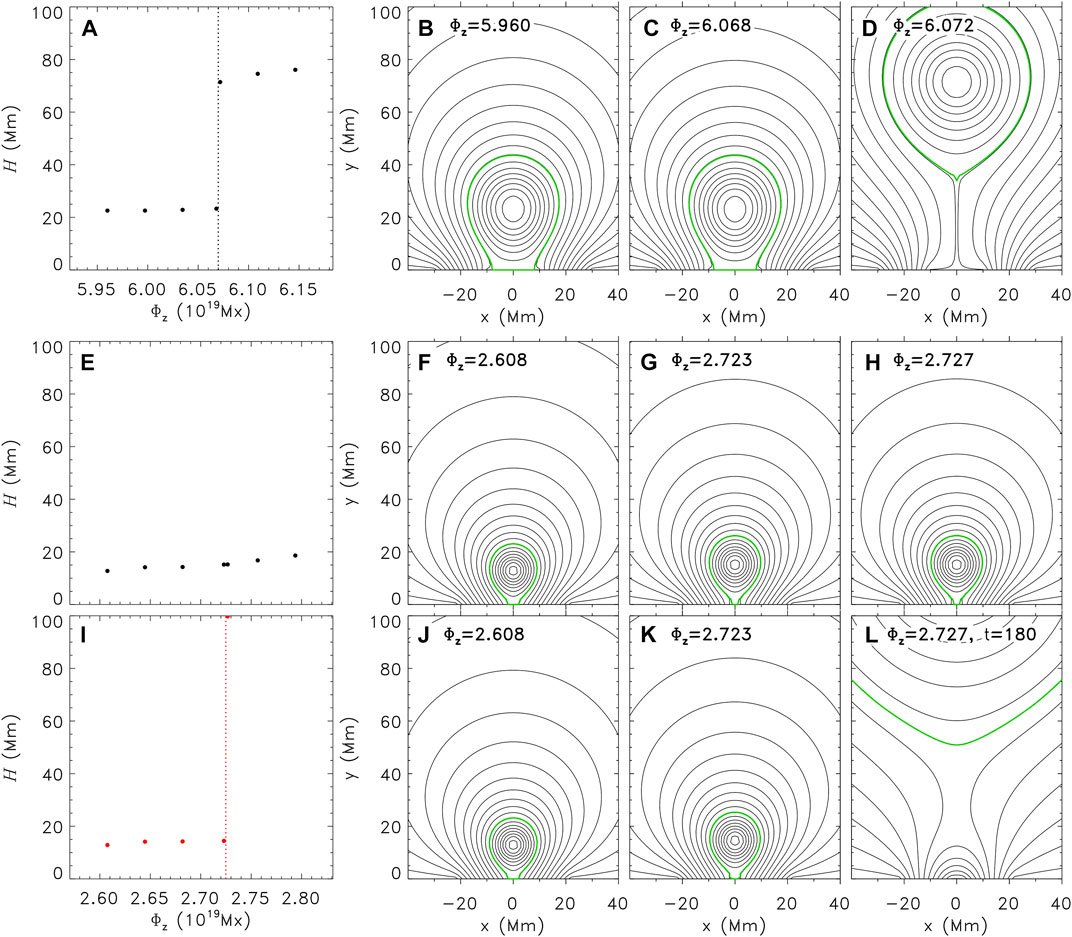
FIGURE 4. The simulation results for Case III and Case IV. Panel (A–D) are the simulation results for Case III under the ideal MHD condition. Panels (E–H) and panels (I–L) are the simulation results for Case IV under the ideal MHD condition and the resistive condition, respectively; the red vertical dotted line in panel (I) denote the catastrophic point ${\mathrm{\Phi }}_{zc}^c$. The green curves mark the boundary of the flux rope.

FIGURE 5

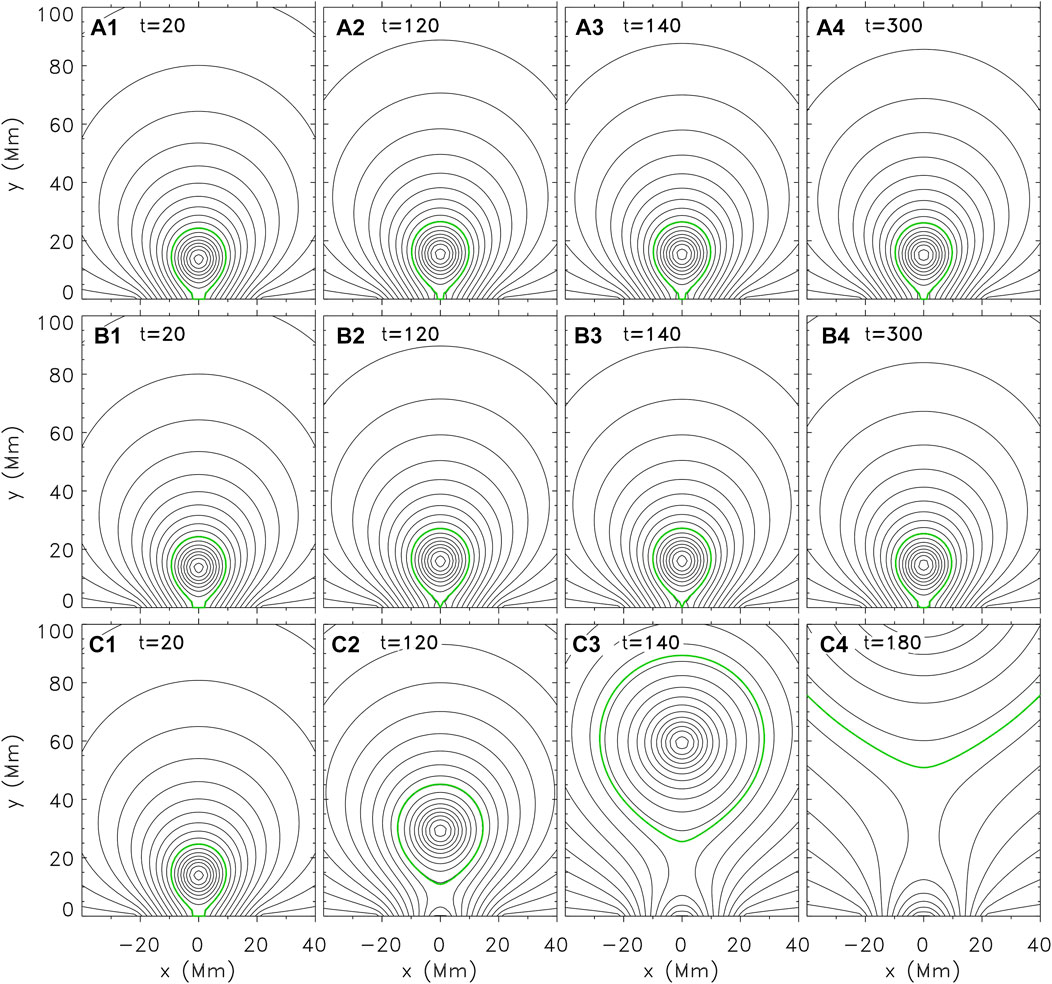
FIGURE 5. The temporal evolution of the flux rope for Case IV. Panels (A1–A4) illustrate the evolution of the flux rope during the relaxation to simulate the equilibrium state in Figure 4G. Panels (B1–B4) illustrate the evolution of the flux rope during the relaxation to simulate the equilibrium state in Figure 4K, which is the equilibrium state right before ${\mathrm{\Phi }}_z={\mathrm{\Phi }}_{zc}^c$ is reached under the resistive condition; Panels (B1–B4) illustrate the evolution right after ${\mathrm{\Phi }}_z={\mathrm{\Phi }}_{zc}^c$ is reached under the resistive condition.

Similar as those in Section 3.1, we also simulate the equilibrium manifold under the ressitive condition for Case IV, so as to investigate the influence of magnetic reconnection on the catastrophic behaviors of flux rope systems with compact photospheric source regions. As plotted in Figure 4I, there is a critical axial magnetic flux ${\mathrm{\Phi }}_{zc}^c\approx 2.727\times 10^{19}$ Mx if magnetic reconnection is included in the simulation, as marked by the red vertical dotted lines in Figure 4I. The evolutions of the flux rope system before and after Φ_z reaches ${\mathrm{\Phi }}_{zc}^c$ are quite different: if Φ_z is smaller than ${\mathrm{\Phi }}_{zc}^c$, the flux rope does not erupt but evolves to equilibrium (Figures 5B1–B4); if ${\mathrm{\Phi }}_{zc}^c$ is reached, the flux rope erupts (Figures 5C1–C4). This indicates that a catastrophe associated with the increasing axial magnetic flux of the rope could occur under the ressitive condition. For comparison, the topologies of the equilibrium states before and after Φ_z reaches ${\mathrm{\Phi }}_{zc}^c$ are quite similar if there is no reconnection (Figure 4G; Figure 4H). This further confirms that it is the magnetic reconnection that changes the catastrophic behaviors of the flux rope system versus varying axial flux. Therefore, the flux rope system with compact photospheric source regions could also be catastrophic if there is magnetic reconnection in the rope system.

4 Discussion and conclusion

In this paper, we investigate the influence of magnetic reconnection on the catastrophic behaviors of coronal flux rope systems associated with increasing axial magnetic flux of the rope. Under the ideal MHD condition, our simulation results demonstrate that coronal flux rope systems with either too compact or too weak photospheric source regions are non-catastrophic versus varying axial magnetic flux. Under the resistive condition, however, both the flux rope system with too compact and too weak photospheric source regions could change to be catastrophic: the catastrophe occurs when the axial flux of the rope increases to reach the critical value, so that the eruption of the flux rope is initiated.

Our simulation results demonstrate that the equilibrium manifolds of a coronal flux rope system could be quite different under the ideal MHD and the resistive condition (e.g., Figure 2E; Figure 2I). This indicates that magnetic reconnection should play a considerable role in determining the force balance and the corresponding the loss of equilibrium associated with increasing axial magnetic flux in coronal flux rope systems. We note that the continuous equilibrium manifold (Figure 2E) is different from the discontinuous equilibrium manifold (Figure 2I) in essence. It is widely accepted that solar eruptions should be caused by photospheric and coronal disturbances (Lin et al., 2003), the spatial range of which, however, is much smaller than that of solar eruptions (Priest, 2014). If the equilibrium manifold of a flux rope system is continuous, the variations of Φ_z caused by photospheric or coronal disturbances could only cause flux rope movements on a spatial scale comparable to the disturbance itself. In contrast, if the equilibrium manifold is discontinuous, there is a critical axial flux of Φ_z, so that even an infinitesimal increment of Φ_z to reach this critical value could cause the catastrophe of the flux rope, resulting in much larger scale of movement of the flux rope than that of the disturbances. Therefore, solar eruptions could only be initiated in the coronal flux rope system whose equilibrium manifold is discontinuous.

In previous studies, the forecasting of solar eruptions is generally based on the photospheric magnetic flux distributions within solar active regions (e.g., Leka and Barnes, 2007; Bobra and Couvidat, 2015; Toriumi and Wang, 2019; Korsós et al., 2020). However, as revealed by our simulation results, not only do different photospheric flux distributions result in different evolutions of the flux rope system, but the catastrophic behaviors of a particular flux rope system with given photospheric flux distribution could also differ under the ideal MHD condition and the resistive condition. This implies that two active regions with similar photospheric flux distribution might be quite different in their ability to initiate solar eruptions, provided that the local resistivity and characteristic spatial scale differs in the two active regions. Therefore, it should not be sufficient to predict whether a solar active region will be a potential source region for solar eruptions based solely on its photospheric magnetic flux distributions. Our simulation results suggest that both the magnetic topology and the local physical parameters related to magnetic reconnection determine whether increasing axial flux is able to cause flux rope eruptions.

There are also catastrophes associated with other physical parameters of flux rope systems, such as increasing shear of the background field (Chen et al., 2006) and decreasing mass of the rope (Jenkins et al., 2019; Zhang et al., 2021). It could be inferred that the catastrophic behaviors associated with those parameters might probably also be determined by both the magnetic topology and whether the magnetic system is resistive. In our future work, we will carry out more simulations to further investigate the influence of magnetic reconnection on different kinds catastrophes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

QZ carried out the numerical simulation, analyzed the simulation results, and prepared the manuscript. XC contributed to the initial inspiration of this study, and the improvement of the numerical model. RL contributed to the analysis of the simulation results. AS, XL, and YW joined in the discussions about the simulation results.

Funding

This research is supported by the National Natural Science Foundation of China (NSFC 42174213, 42188101, 42130204, 41804161, 41774178, 41774150), the Strategic Priority Program of CAS (XDB41000000 and XDA15017300), the Informatization Plan of Chinese Academy of Sciences, Grant No.CAS-WX2021PY-0101, and the Key Research Program of the Chinese Academy of Sciences, Grant NO. ZDBS-SSW-TLC00103. This research is also supported by USTC Research Funds of the Double First-Class Initiative.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antiochos, S. K., DeVore, C. R., and Klimchuk, J. A. (1999). A model for solar coronal mass ejections. Astrophysical J. 510, 485–493. doi:10.1086/306563

CrossRef Full Text | Google Scholar

Anzer, U., and Heinzel, P. (2007). Is the magnetic field in quiescent prominences force-free? Astronomy Astrophysics 467, 1285–1288. doi:10.1051/0004-6361:20066817

CrossRef Full Text | Google Scholar

Archontis, V., and Hood, A. W. (2008). A flux emergence model for solar eruptions. Astrophysical J. Lett. 674, L113–L116. doi:10.1086/529377

CrossRef Full Text | Google Scholar

Aulanier, G., Török, T., Démoulin, P., and DeLuca, E. E. (2010). Formation of torus-unstable flux ropes and electric currents in erupting sigmoids. Astrophysical J. 708, 314–333. doi:10.1088/0004-637X/708/1/314

CrossRef Full Text | Google Scholar

Bemporad, A., Andretta, V., Susino, R., Mancuso, S., Spadaro, D., Mierla, M., et al. (2022). Coronal mass ejection followed by a prominence eruption and a plasma blob as observed by solar orbiter. Astronomy Astrophysics 665, A7. doi:10.1051/0004-6361/202243162

CrossRef Full Text | Google Scholar

Bian, X., Jiang, C., and Feng, X. (2022). The role of photospheric converging motion in initiation of solar eruptions. Front. Astronomy Space Sci. 9, 982108. doi:10.3389/fspas.2022.982108

CrossRef Full Text | Google Scholar

Bobra, M. G., and Couvidat, S. (2015). Solar flare prediction using sdo/hmi vector magnetic field data with a machine-learning algorithm. Astrophysical J. 798, 135. doi:10.1088/0004-637X/798/2/135

CrossRef Full Text | Google Scholar

Bobra, M. G., van Ballegooijen, A. A., and DeLuca, E. E. (2008). Modeling nonpotential magnetic fields in solar active regions. Astrophysical J. 672, 1209–1220. doi:10.1086/523927

CrossRef Full Text | Google Scholar

Chen, B., Yu, S., Reeves, K. K., and Gary, D. E. (2020). Microwave spectral imaging of an erupting magnetic flux rope: Implications for the standard solar flare model in three dimensions. Astrophysical J. Lett. 895, L50. doi:10.3847/2041-8213/ab901a

CrossRef Full Text | Google Scholar

Chen, H., Zhang, J., Ma, S., Yang, S., Li, L., Huang, X., et al. (2015). Confined flares in solar active region 12192 from 2014 october 18 to 29. Astrophysical J. Lett. 808, L24. doi:10.1088/2041-8205/808/1/L24

CrossRef Full Text | Google Scholar

Chen, P. F., and Shibata, K. (2000). An emerging flux trigger mechanism for coronal mass ejections. Astrophysical J. 545, 524–531. doi:10.1086/317803

CrossRef Full Text | Google Scholar

Chen, P. F., Shibata, K., Brooks, D. H., and Isobe, H. (2004). A reexamination of the evidence for reconnection inflow. Astrophysical J. Lett. 602, L61–L64. doi:10.1086/382479

CrossRef Full Text | Google Scholar

Chen, Y., Chen, X. H., and Hu, Y. Q. (2006). Catastrophe of coronal flux rope in unsheared and sheared bipolar magnetic fields. Astrophysical J. 644, 587–591. doi:10.1086/503540

CrossRef Full Text | Google Scholar

Chen, Y., Hu, Y. Q., and Sun, S. J. (2007). Catastrophic eruption of magnetic flux rope in the corona and solar wind with and without magnetic reconnection. Astrophysical J. 665, 1421–1427. doi:10.1086/519551

CrossRef Full Text | Google Scholar

Cheng, X., Ding, M. D., Zhang, J., Sun, X. D., Guo, Y., Wang, Y. M., et al. (2014). Formation of a double-decker magnetic flux rope in the sigmoidal solar active region 11520. Astrophysical J. 789, 93. doi:10.1088/0004-637X/789/2/93

CrossRef Full Text | Google Scholar

Cheng, X., Zhang, J., Kliem, B., Török, T., Xing, C., Zhou, Z. J., et al. (2020). Initiation and early kinematic evolution of solar eruptions. Astrophysical J. 894, 85. doi:10.3847/1538-4357/ab886a

CrossRef Full Text | Google Scholar

Cheung, M. C. M., Rempel, M., Chintzoglou, G., Chen, F., Testa, P., Martínez-Sykora, J., et al. (2019). A comprehensive three-dimensional radiative magnetohydrodynamic simulation of a solar flare. Nat. Astron. 3, 160–166. doi:10.1038/s41550-018-0629-3

CrossRef Full Text | Google Scholar

Démoulin, P., and Aulanier, G. (2010). Criteria for flux rope eruption: Non-equilibrium versus torus instability. Astrophysical J. 718, 1388–1399. doi:10.1088/0004-637X/718/2/1388

CrossRef Full Text | Google Scholar

Devi, P., Démoulin, P., Chandra, R., Joshi, R., Schmieder, B., and Joshi, B. (2021). Observations of a prominence eruption and loop contraction. Astronomy Astrophysics 647, A85. doi:10.1051/0004-6361/202040042

CrossRef Full Text | Google Scholar

Fan, Y. (2020). Simulations of prominence eruption preceded by large-amplitude longitudinal oscillations and draining. Astrophysical J. 898, 34. doi:10.3847/1538-4357/ab9d7f

CrossRef Full Text | Google Scholar

Forbes, T. G. (1990). Numerical simulation of a catastrophe model for coronal mass ejections. J. Geophys. Res. 95, 11919–11931. doi:10.1029/JA095iA08p11919

CrossRef Full Text | Google Scholar

Forbes, T. G., and Priest, E. R. (1995). Photospheric magnetic field evolution and eruptive flares. Astrophysical J. 446, 377. doi:10.1086/175797

CrossRef Full Text | Google Scholar

Gopalswamy, N., Akiyama, S., Yashiro, S., and Xie, H. (2018). Coronal flux ropes and their interplanetary counterparts. J. Atmos. Solar-Terrestrial Phys. 180, 35–45. doi:10.1016/j.jastp.2017.06.004

CrossRef Full Text | Google Scholar

Guo, Y., Ding, M. D., Schmieder, B., Li, H., Török, T., and Wiegelmann, T. (2010). Driving mechanism and onset condition of a confined eruption. Astrophysical J. Lett. 725, L38–L42. doi:10.1088/2041-8205/725/1/L38

CrossRef Full Text | Google Scholar

Hillier, A., Hillier, R., and Tripathi, D. (2012). Determination of prominence plasma β from the dynamics of rising plumes. Astrophysical J. 761, 106. doi:10.1088/0004-637X/761/2/106

CrossRef Full Text | Google Scholar

Hu, Y. Q., and Liu, W. (2000). A 2.5-dimensional ideal magnetohydrodynamic model for coronal magnetic flux ropes. Astrophysical J. 540, 1119–1125. doi:10.1086/309381

CrossRef Full Text | Google Scholar

Inoue, S., Hayashi, K., Magara, T., Choe, G. S., and Park, Y. D. (2015). Magnetohydrodynamic simulation of the X2.2 solar flare on 2011 february 15. II. Dynamics connecting the solar flare and the coronal mass ejection. Astrophysical J. 803, 73. doi:10.1088/0004-637X/803/2/73

CrossRef Full Text | Google Scholar

Isenberg, P. A., and Forbes, T. G. (2007). A three-dimensional line-tied magnetic field model for solar eruptions. Astrophysical J. 670, 1453–1466. doi:10.1086/522025

CrossRef Full Text | Google Scholar

Isenberg, P. A., Forbes, T. G., and Demoulin, P. (1993). Catastrophic evolution of a force-free flux rope: A model for eruptive flares. Astrophysical J. 417, 368. doi:10.1086/173319

CrossRef Full Text | Google Scholar

Jenkins, J. M., Hopwood, M., Démoulin, P., Valori, G., Aulanier, G., Long, D. M., et al. (2019). Modeling the effect of mass-draining on prominence eruptions. Astrophysical J. 873, 49. doi:10.3847/1538-4357/ab037a

CrossRef Full Text | Google Scholar

Jenkins, J. M., Long, D. M., van Driel-Gesztelyi, L., and Carlyle, J. (2018). Understanding the role of mass-unloading in a filament eruption. Sol. Phys. 293, 7. doi:10.1007/s11207-017-1224-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, C., Feng, X., Liu, R., Yan, X., Hu, Q., Moore, R. L., et al. (2021). A fundamental mechanism of solar eruption initiation. Nat. Astron. 5, 1126–1138. doi:10.1038/s41550-021-01414-z

CrossRef Full Text | Google Scholar

Jiang, C., Wu, S. T., Yurchyshyn, V., Wang, H., Feng, X., and Hu, Q. (2016). How did a major confined flare occur in super solar active region 12192? Astrophysical J. 828, 62. doi:10.3847/0004-637X/828/1/62

CrossRef Full Text | Google Scholar

Keppens, R., Guo, Y., Makwana, K., Mei, Z., Ripperda, B., Xia, C., et al. (2019). Ideal mhd instabilities for coronal mass ejections: Interacting current channels and particle acceleration. Rev. Mod. Plasma Phys. 3, 14. doi:10.1007/s41614-019-0035-z

CrossRef Full Text | Google Scholar

Kliem, B., Lin, J., Forbes, T. G., Priest, E. R., and Török, T. (2014). Catastrophe versus instability for the eruption of a toroidal solar magnetic flux rope. Astrophysical J. 789, 46. doi:10.1088/0004-637X/789/1/46

CrossRef Full Text | Google Scholar

Korsós, M. B., Georgoulis, M. K., Gyenge, N., Bisoi, S. K., Yu, S., Poedts, S., et al. (2020). Solar flare prediction using magnetic field diagnostics above the photosphere. Astrophysical J. 896, 119. doi:10.3847/1538-4357/ab8fa2

CrossRef Full Text | Google Scholar

Lamy, P. L., Floyd, O., Boclet, B., Wojak, J., Gilardy, H., and Barlyaeva, T. (2019). Coronal mass ejections over solar cycles 23 and 24. Space Sci. Rev. 215, 39. doi:10.1007/s11214-019-0605-y

CrossRef Full Text | Google Scholar

Leka, K. D., and Barnes, G. (2007). Photospheric magnetic field properties of flaring versus flare-quiet active regions. iv. a statistically significant sample. Astrophysical J. 656, 1173–1186. doi:10.1086/510282

CrossRef Full Text | Google Scholar

Li, H., Liu, Y., Elmhamdi, A., and Kordi, A. S. (2016a). Relationship between distribution of magnetic decay index and filament eruptions. Astrophysical J. 830, 132. doi:10.3847/0004-637X/830/2/132

CrossRef Full Text | Google Scholar

Li, T., Yang, K., Hou, Y., and Zhang, J. (2016b). Slipping magnetic reconnection of flux-rope structures as a precursor to an eruptive X-class solar flare. Astrophysical J. 830, 152. doi:10.3847/0004-637X/830/2/152

CrossRef Full Text | Google Scholar

Lin, J., and Forbes, T. G. (2000). Effects of reconnection on the coronal mass ejection process. J. Geophys. Res. 105, 2375–2392. doi:10.1029/1999JA900477

CrossRef Full Text | Google Scholar

Lin, J., Soon, W., and Baliunas, S. L. (2003). Theories of solar eruptions: A review. New Astron. Rev. 47, 53–84. doi:10.1016/S1387-6473(02)00271-3

CrossRef Full Text | Google Scholar

Lin, J., and van Ballegooijen, A. A. (2002). Catastrophic and noncatastrophic mechanisms for coronal mass ejections. Astrophysical J. 576, 485–492. doi:10.1086/341737

CrossRef Full Text | Google Scholar

Liu, R. (2020). Magnetic flux ropes in the solar corona: Structure and evolution toward eruption. Res. Astronomy Astrophysics 20, 165. doi:10.1088/1674-4527/20/10/165

CrossRef Full Text | Google Scholar

Longcope, D. W., and Forbes, T. G. (2014). Breakout and tether-cutting eruption models are both catastrophic (sometimes). Sol. Phys. 289, 2091–2122. doi:10.1007/s11207-013-0464-8

CrossRef Full Text | Google Scholar

Lugaz, N., Farrugia, C. J., Winslow, R. M., Small, C. R., Manion, T., and Savani, N. P. (2017). Importance of cme radial expansion on the ability of slow cmes to drive shocks. Astrophysical J. 848, 75. doi:10.3847/1538-4357/aa8ef9

CrossRef Full Text | Google Scholar

Moore, R. L., Sterling, A. C., Hudson, H. S., and Lemen, J. R. (2001). Onset of the magnetic explosion in solar flares and coronal mass ejections. Astrophysical J. 552, 833–848. doi:10.1086/320559

CrossRef Full Text | Google Scholar

Priest, E. (2014). Magnetohydrodynamics of the Sun. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Priest, E. R., and Forbes, T. G. (1990). Magnetic field evolution during prominence eruptions and two-ribbon flares. Sol. Phys. 126, 319–350. doi:10.1007/BF00153054

CrossRef Full Text | Google Scholar

Savcheva, A. S., van Ballegooijen, A. A., and DeLuca, E. E. (2012). Field topology analysis of a long-lasting coronal sigmoid. Astrophysical J. 744, 78. doi:10.1088/0004-637X/744/1/78

CrossRef Full Text | Google Scholar

Shen, F., Shen, C., Zhang, J., Hess, P., Wang, Y., Feng, X., et al. (2014). Evolution of the 12 july 2012 CME from the Sun to the Earth: Data-constrained three-dimensional MHD simulations. J. Geophys. Res. (Space Phys. 119, 7128–7141. doi:10.1002/2014JA020365

CrossRef Full Text | Google Scholar

Sterling, A. C., and Moore, R. L. (2004). Evidence for gradual external reconnection before explosive eruption of a solar filament. Astrophysical J. 602, 1024–1036. doi:10.1086/379763

CrossRef Full Text | Google Scholar

Su, Y., Surges, V., van Ballegooijen, A., DeLuca, E., and Golub, L. (2011). Observations and magnetic field modeling of the flare/coronal mass ejection event on 2010 april 8. Astrophysical J. 734, 53. doi:10.1088/0004-637X/734/1/53

CrossRef Full Text | Google Scholar

Su, Y., van Ballegooijen, A., Lites, B. W., Deluca, E. E., Golub, L., Grigis, P. C., et al. (2009). Observations and nonlinear force-free field modeling of active region 10953. Astrophysical J. 691, 105–114. doi:10.1088/0004-637X/691/1/105

CrossRef Full Text | Google Scholar

Sun, S. J., Hu, Y. Q., and Chen, Y. (2007). Influence of photospheric magnetic flux distribution on coronal flux rope catastrophe. Astrophysical J. Lett. 654, L167–L170. doi:10.1086/511304

CrossRef Full Text | Google Scholar

Švestka, Z. (2001). Varieties of coronal mass ejections and their relation to flares. Space Sci. Rev. 95, 135–146. doi:10.1023/A:1005225208925

CrossRef Full Text | Google Scholar

Toriumi, S., and Wang, H. (2019). Flare-productive active regions. Living Rev. Sol. Phys. 16, 3. doi:10.1007/s41116-019-0019-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Török, T., and Kliem, B. (2003). The evolution of twisting coronal magnetic flux tubes. Astronomy Astrophysics 406, 1043–1059. doi:10.1051/0004-6361:20030692

CrossRef Full Text | Google Scholar

Török, T., Temmer, M., Valori, G., Veronig, A. M., van Driel-Gesztelyi, L., and Vršnak, B. (2013). Initiation of coronal mass ejections by sunspot rotation. Sol. Phys. 286, 453–477. doi:10.1007/s11207-013-0269-9

CrossRef Full Text | Google Scholar

Van Tend, W., and Kuperus, M. (1978). The development of coronal electric current systems in active regions and their relation to filaments and flares. Sol. Phys. 59, 115–127. doi:10.1007/BF00154935

CrossRef Full Text | Google Scholar

Vršnak, B., Sudar, D., and Ruždjak, D. (2005). The cme-flare relationship: Are there really two types of cmes? Astronomy Astrophysics 435, 1149–1157. doi:10.1051/0004-6361:20042166

CrossRef Full Text | Google Scholar

Wang, T., Sui, L., and Qiu, J. (2007). Direct observation of high-speed plasma outflows produced by magnetic reconnection in solar impulsive events. Astrophysical J. Lett. 661, L207–L210. doi:10.1086/519004

CrossRef Full Text | Google Scholar

Xia, C., Chen, P. F., and Keppens, R. (2012). Simulations of prominence formation in the magnetized solar corona by chromospheric heating. Astrophysical J. Lett. 748, L26. doi:10.1088/2041-8205/748/2/L26

CrossRef Full Text | Google Scholar

Xue, Z., Yan, X., Cheng, X., Yang, L., Su, Y., Kliem, B., et al. (2016). Observing the release of twist by magnetic reconnection in a solar filament eruption. Nat. Commun. 7, 11837. doi:10.1038/ncomms11837

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, X., Xue, Z., Jiang, C., Priest, E. R., Kliem, B., Yang, L., et al. (2022). Fast plasmoid-mediated reconnection in a solar flare. Nat. Commun. 13, 640. doi:10.1038/s41467-022-28269-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Dere, K. P., Howard, R. A., Kundu, M. R., and White, S. M. (2001). On the temporal relationship between coronal mass ejections and flares. Astrophysical J. 559, 452–462. doi:10.1086/322405

CrossRef Full Text | Google Scholar

Zhang, Q., Liu, R., Wang, Y., Li, X., and Lyu, S. (2021). Confined and eruptive catastrophes of solar magnetic flux ropes caused by mass loading and unloading. Astrophysical J. 921, 172. doi:10.3847/1538-4357/ac1fef

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, Y., Hu, Y., Liu, R., and Liu, J. (2017a). Influence of photospheric magnetic conditions on the catastrophic behaviors of flux ropes in solar active regions. Astrophysical J. 835, 211. doi:10.3847/1538-4357/835/2/211

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, Y., Hu, Y., Liu, R., Liu, K., and Liu, J. (2017b). Upward and downward catastrophes of coronal magnetic flux ropes in quadrupolar magnetic fields. Astrophysical J. 851, 96. doi:10.3847/1538-4357/aa9ce6

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, Y., Liu, R., Zhang, J., Hu, Y., Wang, W., et al. (2020). Eruption of solar magnetic flux ropes caused by flux feeding. Astrophysical J. Lett. 898, L12. doi:10.3847/2041-8213/aba1f3

CrossRef Full Text | Google Scholar