Coupling Between Alfvén Wave and Kelvin–Helmholtz Waves in the Low Latitude Boundary Layer

The Kelvin–Helmholtz (KH) instability of magnetohydrodynamic surface waves at the low latitude boundary layer is examined using both an eigenfrequency analysis and a time-dependent wave simulation. The analysis includes the effects of sheared flow and Alfvén velocity gradient. When the magnetosheath flows are perpendicular to the ambient magnetic field direction, unstable KH waves that propagate obliquely to the sheared flow direction occur at the sheared flow surface when the Alfvén Mach number is higher than an instability threshold. Including a shear transition layer between the magnetosphere and magnetosheath leads to secondary KH waves (driven by the sheared flow) that are coupled to the resonant surface Alfvén wave. There are remarkable differences between the primary and the secondary KH waves, including wave frequency, the growth rate, and the ratio between the transverse and compressional components. The secondary KH wave energy is concentrated near the shear Alfvén wave frequency at the magnetosheath with a lower frequency than the primary KH waves. Although the growth rate of the secondary KH waves is lower than the primary KH waves, the threshold condition is lower, so it is expected that these types of waves will dominate at a lower Mach number. Because the transverse component of the secondary KH waves is stronger than that of the primary KH waves, more efficient wave energy transfer from the boundary layer to the inner magnetosphere is also predicted.

1 Introduction

The Kelvin–Helmholtz (KH) instability has been widely investigated in the Earth’s magnetosphere (Johnson et al., 2014). Unstable KH waves generally occur at the interface between two fluids having different velocities and are fundamentally important for understanding dynamics within the boundary layer that develops between the flows. These waves can affect the exchange of mass, momentum, and energy across those boundaries (e.g., Miura, 1984; Thomas and Winske, 1993; Otto and Fairfield, 2000; Nykyri and Otto, 2001; Matsumoto and Hoshino, 2006; Cowee et al., 2010; Hwang et al., 2011; Nakamura et al., 2011; Moore et al., 2016; Nykyri et al., 2017; Johnson et al., 2021). Mass transport due to KH instability can result from diffusion through thin boundaries created by the instability (e.g., Nakamura et al., 2017) and/or as the result of secondary reconnection (e.g., Otto and Nykyri, 2003; Ma et al., 2017) which results in more effective transport (Ma et al., 2019). Cross-scale energy transport associated with the KH instability may result from the generation of plasma waves leading to both ion and electron heating (Johnson and Cheng, 2001; Chaston et al., 2007; Moore et al., 2017; Nykyri et al., 2021a; Nykyri et al., 2021b; Delamere et al., 2021). The KH waves are also critical to the interaction between the solar wind and other planetary magnetospheres (McComas and Bagenal, 2008; Delamere and Bagenal, 2010; Delamere et al., 2021).

KH waves are surface waves because they are localized near the interface and exponentially decay away from the interface (e.g., Southwood, 1968; Pu and Kivelson, 1983). However, because the wave number is relatively small, the wave energy can still penetrate into the plasma sheet and/or the inner magnetosphere (e.g., Pu and Kivelson, 1983) and play a role in the generation of geomagnetic pulsations and mode conversion to the shear Alfvén waves (e.g., Chen and Hasegawa, 1974; Engebretson et al., 1998).

The magnetopause boundary is often assumed for simplicity to have zero thickness (Pu and Kivelson, 1983; Mills and Wright, 1999; Turkakin et al., 2013), and this assumption is valid for waves with wavelengths longer than the thickness of the boundary layer. When the shear velocity and the Alfvén speed jump at the zero-thickness interface, the linear dispersion relation of KH waves in a slab geometry for an incompressible plasma can be derived as follows (Chandrasekhar, 1961):

$\begin{array}{ccc}\hfill \omega & =\hfill & \frac{\mathbf{k}\cdot \left({\rho }_{msh}{\mathbf{V}}_{msh}+{\rho }_{msp}{\mathbf{V}}_{msp}\right)}{{\rho }_{msp}+{\rho }_{msh}}\hfill \\ \hfill & \pm \hfill & i\sqrt{\frac{{\rho }^{*}}{{\rho }_{msh}+{\rho }_{msp}}\left({\left[\mathbf{k}\cdot \left({\mathbf{V}}_{msh}-{\mathbf{V}}_{msp}\right)\right]}^2-\frac{{\left(\mathbf{k}\cdot {\mathbf{B}}_{msh}\right)}^2+{\left(\mathbf{k}\cdot {\mathbf{B}}_{msp}\right)}^2}{{\mu }_0{\rho }^{*}}\right)},\hfill \end{array}(1)$

where ω and k are a wave frequency and vector, respectively, V and B are shear flow velocity and magnetic field, ρ and ${\rho }^{*}$ = ρ_mshρ_msp/(ρ_msh + ρ_msp) are a mass density and a mean mass density, respectively, μ₀ is the magnetic permeability of free space, and msp(msh) denotes the magnetosphere (magnetosheath). When B_msp = B_msh and ρ_msp = ρ_msh, the KH wave frequency in Equation 1 is reduced to $\omega ={\omega }_{KH0}=\frac{1}{2}\mathbf{k}\cdot {\mathbf{V}}_{msh}$. In Equation 1, the KH waves become unstable when

${\left[\mathbf{k}\cdot \left({\mathbf{V}}_{msh}-{\mathbf{V}}_{msp}\right)\right]}^2>\left[{\left(\mathbf{k}\cdot {\mathbf{B}}_{msh}\right)}^2+{\left(\mathbf{k}\cdot {\mathbf{B}}_{msp}\right)}^2\right]/{\mu }_0{\rho }^{*}(2)$

is satisfied; and the stability threshold condition (2) may be used to determine a critical Alfvén Mach number (M_As) above which the KH wave is unstable.

In addition to the velocity transition at the magnetopause boundary, there is also a large gradient in the Alfvén velocity, which is typically wider in extent than the velocity shear layer (Paschmann et al., 1993). When an Alfvén velocity (V_A) transition layer is included between the magnetosheath and magnetosphere, it can modify the KH wave properties. Strong coupling between the Alfvén surface wave and KH surface wave can result when the frequencies are comparable. This interaction between the two surface waves can lead to instability at a slower flow velocity. This new instability has been referred to as the resonant flow instability (RFI) as it results when Doppler-shifted compressional waves originating at the velocity interface have approximately the same frequency as the Alfvén resonance frequency (Taroyan and Erdélyi, 2003). The RFI includes a negative absorption of the magnetosonic waves, and it has been investigated for the solar corona (Tirry et al., 1998; Andries et al., 2000; Andries and Goossens, 2001; Taroyan and Ruderman, 2011; Antolin and Van Doorsselaere, 2019), magnetopause (Ruderman and Wright, 1998; Taroyan and Erdélyi, 2002, 2003), and magnetotail (Turkakin et al., 2014), respectively. While these works focused on shear in the velocity along the magnetic field direction, a similar instability can also result in velocity shear across the magnetic field or for discontinuous changes in the magnetic field direction at velocity interfaces. These modes can generally be referred to as secondary KH instabilities and are characterized by instability at a slower flow speed than the primary KH instability with growth occurring in a narrow range of propagation angle or Mach number (e.g., González and Gratton, 1994; Taroyan and Erdélyi, 2002; Turkakin et al., 2013). Turkakin et al. (2013) examined the primary and the secondary KH waves in the magnetopause and magnetotail when the magnetic fields in the magnetosheath and magnetosphere are perpendicular to each other. This mode may be particularly important during periods of low solar wind Alfvén Mach number (Lavraud and Borovsky, 2008; Lavraud et al., 2013; Génot and Lavraud, 2021) as it may be unstable even when the primary KH mode is stabilized. Although the (primary) KH wave is considered to be one source of the field-line resonances, the secondary KH instability is strongly coupled to the Alfvén waves. While it has been shown that the secondary KH instability is important in the solar corona, in this article, we show that the secondary KH waves also appear when the shear transition layer exists between the magnetosheath and magnetosphere. Using both eigenmode analysis and a newly developed time-dependent MHD wave model, detailed characteristics of the secondary waves are examined.

This article is structured as follows: in Section 2, the MHD wave equations are presented. Section 3 describes the dispersion relation of the KH waves when the zero-thickness interfaces are assumed. The eigenmode frequency, growth rate, and the KH wave amplitude ratio are also shown. In Section 4, we introduce a new time-dependent MHD wave simulation code. The simulation results are compared with the eigenfrequency analysis from Section 3. We also discuss the wave coupling between KH and Alfvén waves. The last section contains a brief discussion and conclusions.

2 MHD WAVE EQUATIONS IN COLD PLASMA

In a cold plasma, basic equations of an ideal MHD plasma are

$\begin{array}{ccc}\hfill \rho \left[\frac{\partial }{\partial t}+\mathbf{V}\cdot \nabla \right]\mathbf{V}-\nu \mathbf{V}& =\hfill & \frac{1}{{\mu }_0}\left(\nabla \times \mathbf{B}\right)\times \mathbf{B},\hfill \end{array}(3)$

$\begin{array}{ccc}\hfill \frac{\partial \mathbf{B}}{\partial t}& =\hfill & \nabla \times \left(\mathbf{V}\times \mathbf{B}\right),\hfill \end{array}(4)$

where ν is a collisional frequency that is introduced to damp waves propagating outside the region of interest, which effectively imposes outgoing boundary conditions. It should be noted that collisional effects play no role in the stability of the primary or secondary KH instabilities that we analyze in the rest of this article.

We assume that a field variable consists of background equilibrium (0) and small perturbation (1) components (B = B₀ + B₁, ρ = ρ₀ + ρ₁, and V = V₀ + V₁), and a shear flow $({\mathbf{V}}_0(x)=V_0(x)\widehat{y})$ and a uniform background magnetic field $({\mathbf{B}}_0=B_0\widehat{z})$ lie in the y- and z-directions, respectively. Then, the perturbed quantities can be Fourier analyzed in the y- and z-directions (∂/∂y → ik_y and ∂/∂z → ik_∥, where k_y and k_∥ are wavenumbers in the y and field-aligned (z) directions). Thus, the linearized MHD wave equations are

$\begin{array}{ccc}\hfill {\rho }_0\left(\frac{\partial }{\partial t}+i{k}_y{V}_0\right)V_{1x}+\nu V_{1x}& =\hfill & \frac{B_0}{{\mu }_0}\left(i{k}_{\parallel }{B}_{1x}-\frac{\partial B_{1z}}{\partial x}\right),\hfill \end{array}(5)$

$\begin{array}{ccc}\hfill {\rho }_0\left(\frac{\partial }{\partial t}+i{k}_y{V}_0\right)V_{1y}+\nu V_{1y}& =\hfill & \frac{B_0}{{\mu }_0}\left(i{k}_{\parallel }{B}_{1y}-i{k}_y{B}_{1z}\right)-{\rho }_0{V}_{1x}\frac{\partial V_0}{\partial x},\hfill \end{array}(6)$

$\begin{array}{ccc}\hfill \left(\frac{\partial }{\partial t}+i{k}_y{V}_0\right)B_{1x}& =\hfill & i{k}_{\parallel }{B}_0{V}_{1x},\hfill \end{array}(7)$

$\begin{array}{ccc}\hfill \left(\frac{\partial }{\partial t}+i{k}_y{V}_0\right)B_{1y}& =\hfill & i{k}_{\parallel }{B}_0{V}_{1y}+B_{1x}\frac{\partial V_0}{\partial x},\hfill \end{array}(8)$

$\begin{array}{ccc}\hfill \left(\frac{\partial }{\partial t}+i{k}_y{V}_0\right)B_{1z}& =\hfill & -i{k}_y{B}_0{V}_{1y}-B_0\frac{\partial V_{1x}}{\partial x}.\hfill \end{array}(9)$

In Section 3, we solve the spectrum of eigenmodes of these equations in slab geometry, while in Section 4, we solve these equations using a finite-difference time-domain method.

To proceed with the spectral analysis, we define an auxiliary set of variables including the fluid displacement (ξ)

${\mathbf{V}}_1\equiv \left(\frac{\partial }{\partial t}+{\mathbf{V}}_0\cdot \nabla \right)\xi ,(10)$

the total pressure perturbation (p), and compressibility (ψ),

$\begin{array}{ccc}\hfill p& \equiv \hfill & B_0{B}_{1z},\hfill \end{array}(11)$

$\begin{array}{ccc}\hfill \psi & \equiv \hfill & \nabla \cdot V_1.\hfill \end{array}(12)$

Taking the Fourier transform in time $(\frac{\partial }{\partial t}\to -i\omega )$ and ignoring the collision term (ν → 0), Equations 5–9 become

$\begin{array}{ccc}\hfill {\mu }_0{\rho }_0{\tilde{\omega }}^2{\xi }_x& =\hfill & -i{B}_0{k}_{\parallel }{B}_{1x}+\frac{\partial p}{\partial x},\hfill \end{array}(13)$

$\begin{array}{ccc}\hfill {\mu }_0{\rho }_0{\tilde{\omega }}^2{\xi }_y& =\hfill & -i\tilde{\omega }{\mu }_0{\rho }_0{\xi }_x\frac{\partial V_0}{\partial x}-i{B}_0{k}_{\parallel }{B}_{1y}+i{k}_{y}p,\hfill \end{array}(14)$

$\begin{array}{ccc}\hfill \tilde{\omega }{B}_{1x}& =\hfill & i\tilde{\omega }{B}_0{k}_{\parallel }{\xi }_x,\hfill \end{array}(15)$

$\begin{array}{ccc}\hfill \tilde{\omega }{B}_{1y}& =\hfill & i\tilde{\omega }{B}_0{k}_{\parallel }{\xi }_y+i{B}_{1x}\frac{\partial V_0}{\partial x},\hfill \end{array}(16)$

$\begin{array}{ccc}\hfill \tilde{\omega }{B}_{1z}& =\hfill & -i{B}_0\psi ,\hfill \end{array}(17)$

where $\tilde{\omega }=\omega -k_y{V}_0$.

Then, Equations 11–17 can be reduced to two coupled first-order differential equations,

$\begin{array}{ccc}\hfill \frac{dp}{dx}& =\hfill & {\mu }_0{\rho }_0\left({\tilde{\omega }}^2-k_{\Vert }^2{V}_A^2\right){\xi }_x,\hfill \end{array}(18)$

$\begin{array}{ccc}\hfill {\mu }_0{\rho }_0\frac{d{\xi }_x}{dx}& =\hfill & -\left(\frac{{\tilde{\omega }}^2-k_y^2{V}_A^2+k_{\Vert }^2{V}_A^2}{{\tilde{\omega }}^2-k_{\Vert }^2{V}_A^2}\right)\frac{p}{B_0^2}.\hfill \end{array}(19)$

We solve Equations 18 and 19 to analyze the eigenmode frequency in Section 3.

3 Wave Dispersion Relation at the Plasma Interfaces

Eigenfrequency analysis is performed when the shear transition layer exists between magnetosheath and magnetosphere. For calculations, V₀ and V_A are assumed to vary only in the direction of the x-axis, as shown in Figure 1A,

$\begin{array}{ccc}\hfill V_0\left(x\right)& =\hfill & V_{0I}\mathrm{\Theta }\left(x\right),\hfill \end{array}(20)$

$\begin{array}{ccc}\hfill V_A\left(x\right)& =\hfill & V_{AI}+\left(V_{AIII}-V_{AI}\right)\mathrm{\Theta }\left(x-d\right),\hfill \end{array}(21)$

where Θ(x) = 0(x < 0) or 1(x ≥ 0) is a Heaviside step function. Figure 1A illustrates the transition from magnetosheath (I) to magnetosphere (III). The flow is sheared between regions I and II, while the Alfvén velocity increases between regions II and III. Region II is the shear layer, which divides the plasma into two semi-infinite homogeneous regions (I and III) separated with a width d. It is generally expected that velocity shear between layers I and II can drive a KH instability that is localized at this interface, while the jump in Alfvén velocity between regions II and III supports surface Alfvén waves satisfying the Alfvén resonance condition. In the following analysis, we show how these modes couple when the transitions occur in close proximity.

FIGURE 1

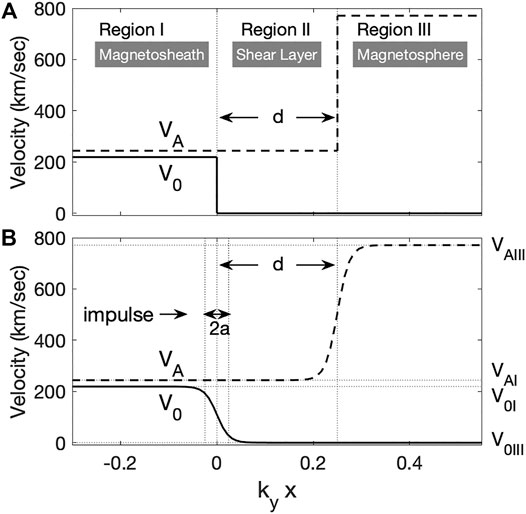
FIGURE 1. Illustration of the adopted background plasma profile. We assume (A) zero and (B) finite boundary width for eigenfrequency analysis and the numerical simulation, respectively. Regions I and III correspond to the magnetosheath and magnetosphere, respectively, and region II is the shear transition layer.

The eigenmodes of these equations are localized, so they must satisfy exponentially decaying boundary conditions in regions I and III. Moreover, it is also expected that in region II that the solution decays away from either boundary. As such, the analytical forms of the solutions in each region J are as follows:

$\begin{array}{ccc}\hfill p_J\left(x\right)& =\hfill & p_J^{-}\exp \left(-{\kappa }_{J}x\right)+p_J^{+}\exp \left({\kappa }_{J}x\right),\hfill \end{array}(22)$

$\begin{array}{ccc}\hfill {\xi }_{xJ}\left(x\right)& =\hfill & {\xi }_{xJ}^{-}\exp \left(-{\kappa }_{J}x\right)+{\xi }_{xJ}^{+}\exp \left({\kappa }_{J}x\right),\hfill \end{array}(23)$

where ± signs represent waves toward positive or negative directions in x.

For a surface wave, it is required that $p_I^{-}=p_{III}^{+}={\xi }_{xI}^{-}={\xi }_{xIII}^{+}=0$, and ξ_x and p must be continuous at each interface; thus, at x = 0

$\begin{array}{ccc}\hfill p_I^{+}& =\hfill & p_{II}^{-}+p_{II}^{+},\hfill \end{array}(24)$

$\begin{array}{ccc}\hfill {\xi }_{xI}^{+}& =\hfill & {\xi }_{xII}^{-}+{\xi }_{xII}^{+},\hfill \end{array}(25)$

and at x = d,

$\begin{array}{ccc}\hfill p_{III}^{-}\exp \left(-{\kappa }_{III}x\right)& =\hfill & p_{II}^{-}\exp \left(-{\kappa }_{II}x\right)+p_{II}^{+}\exp \left({\kappa }_{II}x\right),\hfill \end{array}(26)$

$\begin{array}{ccc}\hfill {\xi }_{xIII}^{-}\exp \left(-{\kappa }_{III}x\right)& =\hfill & {\xi }_{xII}^{-}\exp \left(-{\kappa }_{II}x\right)+{\xi }_{xII}^{+}\exp \left({\kappa }_{II}x\right).\hfill \end{array}(27)$

The wave dispersion relation is obtained by inserting the solutions into Equations 18 and 19 and noting that for solutions of the form exp(±κx) that

$\begin{array}{ccc}\hfill \kappa p& =\hfill & \mp {\mu }_0{\rho }_0\left({\tilde{\omega }}^2-k_{\parallel }^2{V}_A^2\right){\xi }_x,\hfill \end{array}(28)$

$\begin{array}{ccc}\hfill \kappa {\mu }_0{\rho }_0{\xi }_x& =\hfill & \pm \left(\frac{{\tilde{\omega }}^2-k_y^2{V}_A^2+k_{\parallel }^2{V}_A^2}{{\tilde{\omega }}^2-k_{\parallel }^2{V}_A^2}\right)\frac{p}{B_0^2},\hfill \end{array}(29)$

and the relationship between p and ξ_x in each region J = I, II, and III in Figure 1A becomes

$H_J{\xi }_{xJ}=p_J,(30)$

where $H_J={\mu }_0{\rho }_{0J}({\tilde{\omega }}^2-k_{\Vert }^2{V}_{AJ}^2)/{\kappa }_J$.

From Equations 24–27 and 30, the wave dispersion can be derived as

$D\left(\omega ,k_y,k_{\Vert },V_0,V_A\right)=\left(H_I+H_{II}\right)\left(H_{II}+H_{III}\right)-\left(H_I-H_{II}\right)\left(H_{II}{H}_{II}\right)\exp \left(-2{\kappa }_{II}d\right)=0.(31)$

The amplitude ratio (A_p) of the magnetic compressional component (p) between the two interfaces (x = 0 and d) can also be determined:

$\begin{array}{ccc}\hfill A_p\equiv \frac{p_{x=d}}{p_{x=0}}& =\hfill & \frac{p_{II}^{+}\exp \left({\kappa }_{II}d\right)+p_{II}^{-}\exp \left(-{\kappa }_{II}d\right)}{p_{II}^{+}+p_{II}^{-}}\hfill \\ \hfill & =\hfill & \frac{H_{III}}{H_I}\frac{H_I^2-H_{II}^2}{H_{III}^2-H_{II}^2}.\hfill \end{array}(32)$

3.1 Primary and Secondary Kelvin–Helmholtz Waves

Using Equations 31 and 32, we calculate the eigenfrequency (ω), growth rate (γ), and amplitude ratio between magnetic compressional component (A_p) for various widths of the shear transition layer, k_yd = 0, 0.25, 0.75, and 2.0, as shown in Figure 2. For these plots, the plasma densities in region I and region III are assumed to be N_0I = 5 × 10⁶/m³ and N_0III = 5 × 10⁵/m³, and the background magnetic field strength is B₀ = 25nT. We also specify an angle of propagation (ϕ) with respect to the ambient magnetic field, ϕ = tan⁻¹(k_y/k_‖) = 80° and $\sqrt{k_y^2+k_{\Vert }^2}=\pi /(2R_E)$. For complete stability analysis, this angle would be varied to determine the maximum growth rate for a given Mach number. The upper panels of Figure 2 are the calculated real (black and red) and imaginary (blue, growth rate γ) frequencies as functions of the Alfvén Mach number (M_A ≡ V_0I/V_AI), and the lower panels plot the amplitude ratio A_p of unstable wave modes.

FIGURE 2

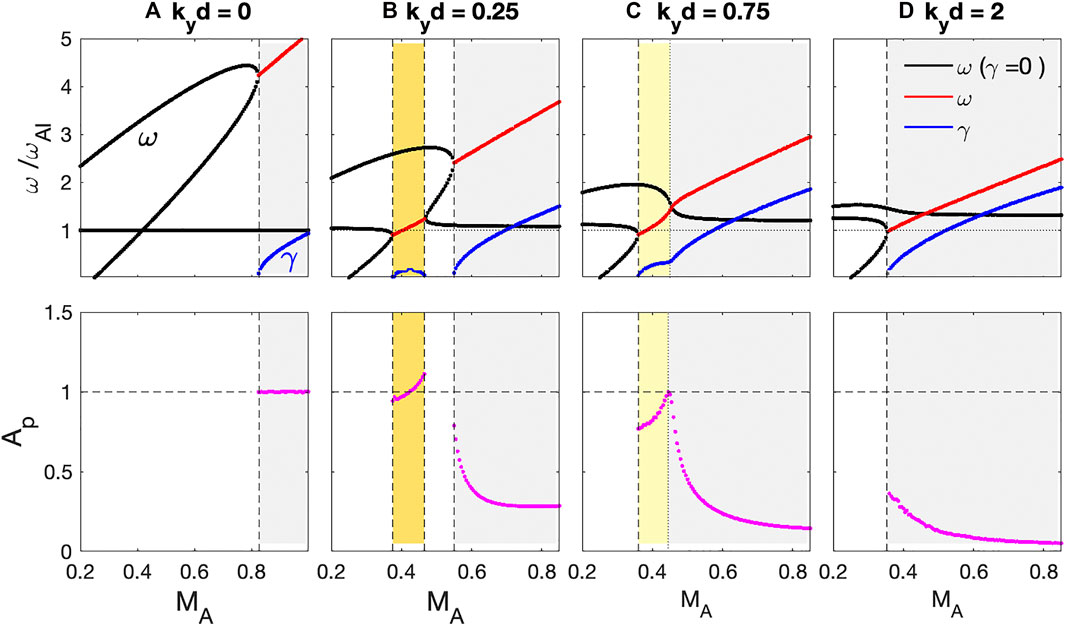
FIGURE 2. (Upper) Normalized eigenfrequencies (ω) and wave growth rate (γ) to Alfvén wave frequency at the magnetosheath (ω_AI). (Lower) The amplitude ratio of the magnetic compressional component (A_p) at the two interfaces for k_yd = 0, 0.25, 0.75, and 2.0, respectively.

In the absence of the shear transition layer (k_yd = 0) as shown in Figure 2A, forward and backward propagating fast waves, which have positive and negative frequencies at M_A = 0, occur when M_A is small (Taroyan and Erdélyi, 2002). These waves are stable until M_A reaches the threshold of the KH instability, $M_{As}={\tan }^{-1}(\varphi )\sqrt{2(1+V_{AI}/V_{AIII})}$. For M_A > M_As marked as a gray-shaded region in Figure 2A, the waves develop a complex frequency and become unstable. For the given range of M_A, ω and γ increase linearly with M_A. Because the characteristics of this wave mode are the same as the typical KH waves (e.g., Johnson et al., 2014), this wave corresponds to primary KH waves (hereafter PKHW). In this figure, we also found a shear Alfvén wave mode at ω = ω_AI = k_‖V_AI. The fast and shear Alfvén waves cross each other near M_A ∼ 0.45, but the coupling of the two wave modes does not occur.

Introducing a finite width of the shear transition layer significantly changes the wave dispersion relations. In Figure 2, the PKHWs also occur for the cases of k_yd ≠ 0. The M_A threshold decreases from 0.83 for k_yd = 0 to 0.35 for k_yd = 2.0. Overall, the wave frequency ω decreases, while the growth rate γ increases as k_yd increases. For example, for M_A = 0.85, ω/ω_AI = (4.35, 3.68, 2.95, 2.48) and γ/ω_AI = (0.35, 1.5, 1.85, 1.89) when k_yd = (0.0, 0.25, 0.75, 2.0). Thus, when a shear transition layer is included, lower frequency PKHWs are excited with a stronger growth rate and lower M_A threshold.

For k_yd = 0.25 in Figure 2B, coupling between the backward propagating fast and shear Alfvén waves occurs near ω/ω_AI ∼ 1, and unstable waves also appear for 0.355 ≤ M_A ≤ 0.47 (shaded yellow in Figure 2B). These waves correspond to the secondary KH waves (hereafter SKHW) (Turkakin et al., 2013). In this case, the SKHWs are clearly separated from the PKHWs and have lower ω, lower γ, and lower M_A threshold than the PKHWs. The compressional amplitude ratio (A_p) in the lower panel shows significant differences between PKHWs and SKHWs; A_p ≪ 1 for the PKHWs and A_p ∼ 1 for the SKHWs. Therefore, for SKHWs, the amplitude of the instability is similar at both the V₀ and V_A interfaces, indicating a spreading of wave power over a more extended region, while the PKHWs are localized about the V₀ interface. When the Mach number is low, it is expected that only the SKHWs would be excited.

When the V_A interface is further away from the V₀ interface (k_yd = 0.75), as shown in Figure 2C, the PKHW and SKHW modes merge near M_A ∼ 0.47. Although ω and γ monotonically increase as a function of M_A, the KH waves have similar behavior to the SKHW (A_p ∼ 1 and ω ∼ ω_AI) at smaller M_A and the PKHWs (A_p < 1 and ω ≫ ω_AI) at larger M_A. Thus, the waves may still be divided into the semi-SKHW marked as a light yellow-shaded region and PKHW marked as a gray-shaded region in Figure 2C.

For k_yd = 2, as shown in Figure 2D, only a single unstable wave mode corresponding to the PKHWs occurs localized at the V₀ interface. The V_A profile can be treated as a constant at the V₀ interface and the M_A threshold becomes M_As ∼ 2 tan⁻¹(ϕ) = 0.359. The threshold occurs near ω/ω_AI ∼ 1; thus, the wave frequencies are always higher than ω_AI.

It is also useful to examine how ω and A_p depend on M_A and k_yd. Figure 3A,B shows contour plots of ω normalized to 1) ω_KH0 and 2) ω_AI, respectively. In this figure, two wave modes are clearly organized by ranges of M_A; the PKHW for M_A > 0.47 and the SKHW for 0.355 ≤ M_A ≤ 0.47. Red and magenta lines in Figure 3A represent the M_A threshold for the PKHW and SKHW, respectively. The M_A threshold of the PKHWs decreases and the upper M_A limit of the SKHWs increases as k_yd increases. The thresholds merge near k_yd ∼ 0.534 and M_A ∼ 0.47. Thus, for M_A > 0.47, a single wave mode appears (see Figure 2C); however, wave characteristics at lower and higher M_A are significantly different.

FIGURE 3

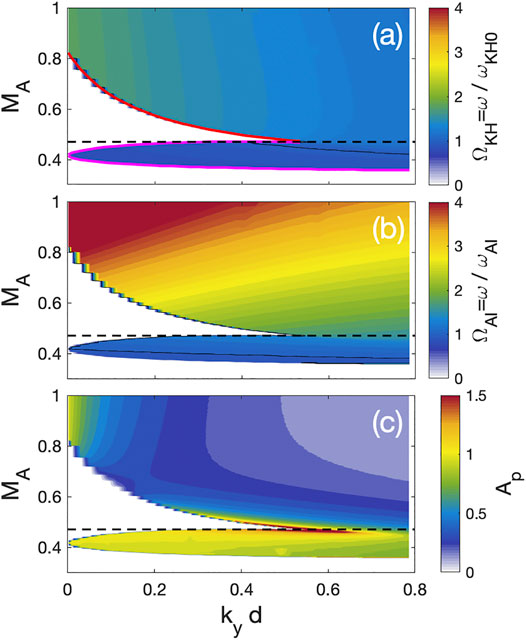
FIGURE 3. (A,B) Normalized eigenfrequencies to ${\omega }_{KH0}=\frac{1}{2}{k}_y{V}_0$ and ω_AI = k_‖V_AI. (C) The amplitude ratio of the compressional magnetic field component A_p. Here, the horizontal and vertical axes are normalized shear layer width (k_yd) and Alfvén Mach number (M_A).

The PKHWs show that all parameters (ω/ω_KH0, ω/ω_AI, and A_p) have a strong dependence on k_yd, and they decrease as k_yd increases. For most M_A, ω/ω_KH0 ∼ 1 and 1 < ω/ω_KH0 < 2. Because both ω and ω_KH0 increase proportionally to M_A, ω/ω_KH0 has less dependence on M_A. However, because ω_AI does not depend on k_y and ω increases as M_A increases, ω/ω_AI depends on both M_A and k_yd. For the given conditions, ω/ω_AI is maximized when k_yd is small and M_A is large. Figure 3C shows A_p < 1 for M_A ≥ 0.47, except k_yd → 0. Thus, it shows that the PKHWs are almost always dominant at the V₀ interface. For k_yd → 0, a strong amplitude of the pressure term occurs at the secondary interface. However, this increase in A_p is not an indicator of a separate instability, but rather it simply indicates that the decay of the wave power from the V₀ interface to the V_A interface reduced as the shear layer vanishes.

On the other hand, the eigenmode frequency of the SKHWs is comparable to ω_KH0 and ω_AI (0.9 ≤ ω/ω_KH0(AI) ≤ 1.2) in the entire range of k_yd and M_A because this wave mode appears due to the coupling between shear Alfvén mode and the fast compressional waves (thus, ω_KH0(AI) ∼ ω_AI). For the entire range of k_yd, A_p is always close to or even higher than 1. These results suggest that the KH instability occurs at both the V₀ and V_A interfaces with almost the same amplitude even though the interfaces are well separated.

The eigenmode calculations can be summarized as follows: the PKHWs are localized at the V₀ interface having a higher frequency than ω_A in the magnetosheath for faster shear flow velocity, while the SKHWs can be detected at both the V₀ and V_A interfaces with similar wave frequency to ω_AI in the magnetosheath for slower shear flow velocity.

4 MHD Wave Simulations

In order to examine the PKHWs and SKHWs, we also developed an MHD wave simulation model. Similar to the previous fluid wave simulation codes (Kim and Lee, 2003; Kim et al., 2007), the finite-difference method is used in both time and space to solve the MHD Equations 5–9 as an initial-valued problem. We adopt a box model in which B₀ is assumed to lie along the z-direction and inhomogeneity is introduced in the x-direction, while the boundary layer plasma flows in the y-direction with variation in the x-direction. Perfect reflecting boundaries are assumed and strong collisions are applied near the boundaries to describe semi-infinite space. Therefore, the total energy of traveling waves decreases once the initial waves reach the boundary. Seed perturbations in the simulation domain result in linear growth of unstable modes, and the growth rate can be calculated once the unstable waves exceed the amplitudes of the initial perturbation.

4.1 KH Waves in Uniform V_A Plasma

We first examine the KH waves in a plasma where V_A does not vary in space. In this simulation, a hyperbolic tangent V₀ profile along with constant V_A was adopted in the wave code:

$V_0\left(x\right)=\frac{V_{0I}}{2}\left[1-\tanh \left(\frac{x}{a}\right)\right],(33)$

where V_0I is the flow velocity in region I, and this profile characterizes the V₀ discontinuity in a scale length a, as shown in Figure 1B. One of the primary differences between the background profile used in the time-dependent analysis, and the previously discussed eigenmode analysis (a → 0) is the fact that the discontinuous profile has been smoothed.

We assume that the length of the simulation box is L_x ∼ 45/k_y. Since the KH surface wave is expected to not fully decay by the time it reaches the edge of the simulation domain in the x-direction, we add an absorption layer near the boundary (∼30/k_y) in the simulation box to prevent reflection. An initial perturbation is launched as a compressional component of V_1x at the source location (k_yx_source ∼ − 7.5) in region I (i.e., magnetosheath). This source is assumed to have a narrow spatial width (k_yδ_source = 0.093) and to include broadband frequencies, $V_{1x}(x,t)=\exp \left(-1.5\frac{t^2}{t_{KH}^2}\right)\exp \left(-\frac{{(x-x_{source})}^2}{{\delta }_{source}^2}\right)$, where k_KH = 2π/ω_KH0. The simulation is run from t = 0 to t = 5.6t_KH, and all components of B₁ and V₁ at each time step are stored during the simulation run time. The background densities in the magnetosheath (region I) and the magnetosphere (region III), the background magnetic field strength, k_y, and k_z are the same as in the eigenmode analysis of Section 3.

Figure 4 shows the time evolution of the magnetic compressional component (B_1z) in the x-direction for M_A = 1 and k_ya = 0.025. Two vertical lines represent the source location (k_ya = − 7.5) and the V₀ interface (k_yx = 0), and thick dashed lines represent Alfvén speed (V_A). Since the initial wave packet includes broadband frequencies, the wave packet disperses in time and space. Leftward propagating waves reach a strong collisional layer near the boundary (k_yx < − 10.5) and are totally absorbed. Rightward propagating waves reach the V₀ interface at k_yx = 0 around t/t_KH = 0.7, and they partially reflect from the interface due to a steepened density gradient. The rest of the waves penetrates the V₀ interface and reach the collisional layer (k_yx > 3.0). Once the magnetic field and velocities are perturbed near the interface, an unstable wave mode begins to grow at around t/t_KH ∼ 1.2. Unlike the initial perturbation, these waves decay in the x-direction rather than propagate. The wave amplitude in Figure 4 saturates at ± 100.

FIGURE 4

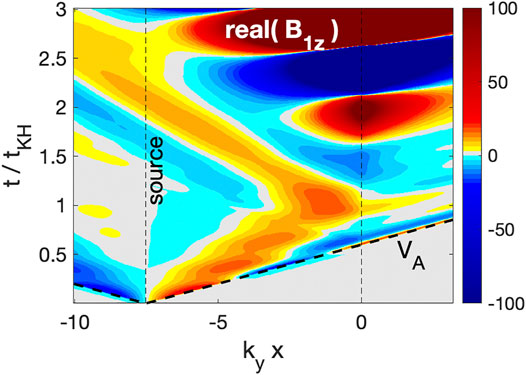
FIGURE 4. The time evolution of the magnetic compressional component (B_1z) in the x-direction. The time and space are normalized to t_KH = 2π/ω_KH0 and k_y, respectively. The interface is assumed to be located at k_yx = 0. It is noted that the wave power is saturated at a 100 in this figure.

We focus on the surface waves at k_yx = 0 and determine the growth rate, wave frequency, and polarization. Time histories of B_1z and B_1y at x = 0 in Figure 5A rapidly grow in time; thus, the sinusoidal wave form is not clearly seen. However, the wave growth term can be removed from the time histories using the magnetic (U_B), kinetic energy (U_V), or total energy (U = U_B + U_V). We plot U_tot(t) = ∑_xU(x, t) in the simulation box in Figure 6A. Early in the simulation period (t/t_KH < 1.2) U_tot is quasi-stable; however, once an unstable waves generated, it increases linearly. The wave magnetic field with a constant growth rate γ can be written as

$B_1\left(x,t\right)\sim b_1\left(x,t\right)\exp \left[\gamma \left(x,t\right)t\right],(34)$

and because of the magnetic energy U_B ∝ |B|², the wave growth rate γ in each grid point can be estimated from

$\gamma \left(x,t\right)\sim \frac{\partial }{\partial t}\ln \left(\sqrt{U_B\left(x,t\right)}\right).(35)$

FIGURE 5

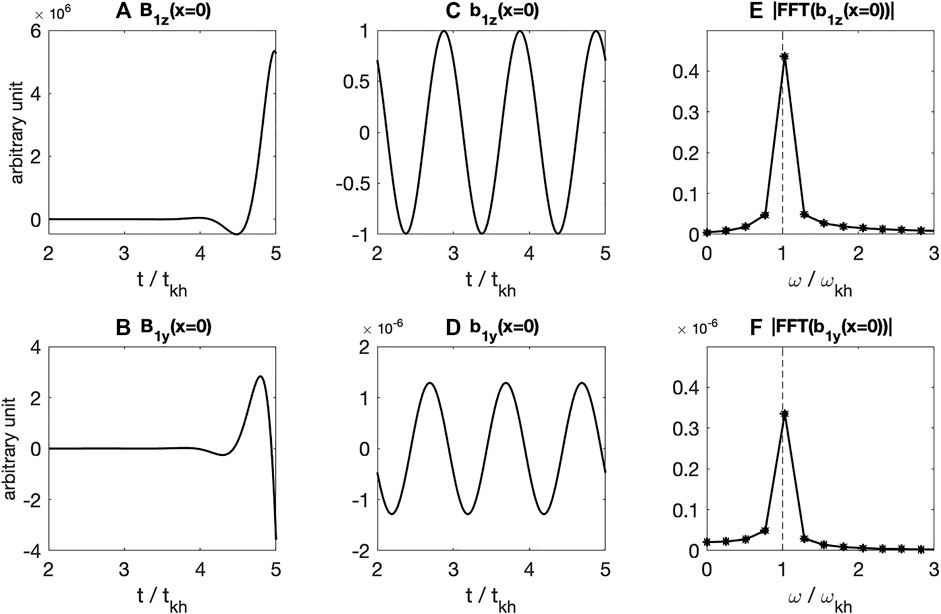
FIGURE 5. (A,B) Time histories of magnetic compressional (B_1z) and transverse (B_1y) components, (C,D) time histories removing the growth rate of b_1z and b_1y, and (E,F) fast Fourier transform in time of b_1z and b_1y at the interface (k_yx = 0).

FIGURE 6

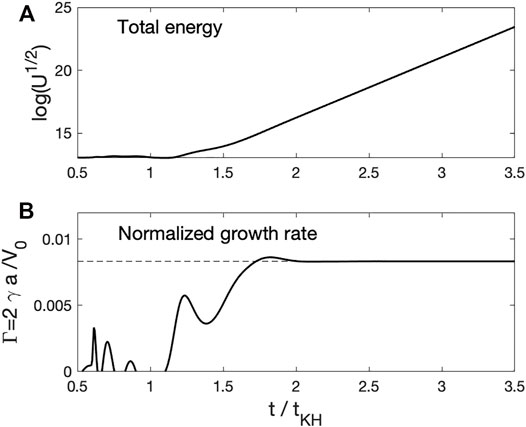
FIGURE 6. (A) Time evolution of wave energy (U) and (B) normalized growth rate (Γ = 2γa/V_0I) in time.

We also confirmed that γ calculated using either the magnetic (U_B) or kinetic energies (U_V) are identical; thus, $\gamma (x,t)=\frac{\partial }{\partial t}\ln (\sqrt{U(x,t)})=\frac{\partial }{\partial t}\ln (\sqrt{U_B(x,t)})=\frac{\partial }{\partial t}\ln (\sqrt{U_V(x,t)})$. Furthermore, once the initial wave vanishes near the boundary, only the localized surface waves (such as KH waves) remain in the simulation domain; thus, γ also can be calculated using U_tot:

$\gamma \left(t\right)=\frac{\partial }{\partial t}\ln \left(\sqrt{U_{tot}\left(t\right)}\right).(36)$

When a boundary has a finite thickness, the normalized growth rate (Γ ≡ 2aγ/V_0I) becomes a function of normalized boundary width (2k_ya) (Miura and Pritchett, 1982). To illustrate, the time evolution of Γ(t) is plotted in Figure 6B for k_yd = 0.025 and M_A = 1, and it converges to $\sim 0.0083$. Therefore, for these parameters, the normalized growth rate can be estimated as Γ = 0.0083.

Once the growth rate is determined, the wave components (and polarization) can be obtained from

$b_1\left(t\right)\sim {\left.B_1\left(t\right)/\exp \left(\gamma \left(t-t_0\right)\right)\right|}_{t>t_0},(37)$

where t₀ is the time at which the wave growth begins. Figures 5C,D show that b_1z and b_1y have clear sinusoidal structures with a single frequency. The wave spectra of b_1z and b_1y in Figures 5E,F confirm that the single peak corresponds the KH wave frequency, ${\omega }_{KH0}=\frac{1}{2}{k}_y{V}_0$. In this manner, we can determine both the real and imaginary components of the frequency, which can be compared with the eigenmode analysis.

For code validation, we also compared the simulation results with prior analytical results in Miura and Pritchett (1982). Figure 7 shows the growth rate, Γ, as a function of (a) 2k_ya for M_A = 1 and (b) as a function of M_A for 2k_ya = 1. In this figure, the prior analytic results (gray lines) and our simulations (red stars) show excellent agreement with each other. For M_A = 1 in Figure 7A, wave growth only occurs for a limited value of the normalized boundary width 0 < 2k_ya < 1.8 and maximizes near 2k_ya = 0.8. For 2k_ya = 1, the maximum Γ occurs for M_A → 0 and has a value of 0.144, as predicted from Miura and Pritchett (1982). The growth rate decreases as M_A increases and no KH wave arises for M_A > 1.6. Therefore, the new MHD wave code successfully demonstrates KH waves and benchmarking comparisons of the simulations with previous analytical results validate the code accuracy.

FIGURE 7

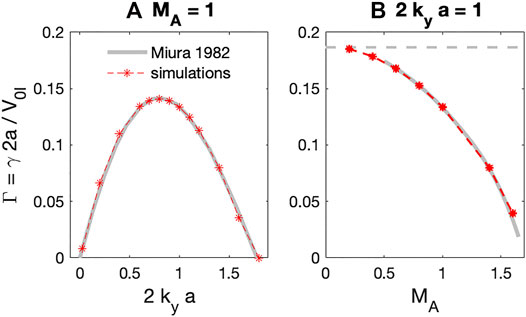
FIGURE 7. Normalized growth rates (Γ = 2γa/V_0I) of KH surface waves (A) as a function of normalized tangential wavenumber 2k_ya for M_A = 1 and (B) as a function of M_A for 2k_ya = 1. Here, gray and red star dashed lines are from Miura and Pritchett (1982) and simulation results.

4.2 Coupling Between KH and Alfvén Resonant Waves

In this section, the simulation results include the shear transition layer between the magnetosphere and the magnetosheath, as shown in Figure 1B. In contrast to the results of Section 3, we consider a finite width of the boundary layer. Similar to the V₀ profile in Equation 33, V_A is assumed to have a hyperbolic tangent profile:

$V_A\left(x\right)=V_{AI}+\frac{V_{AI}+V_{AIII}}{2}\left[\tanh \left(\frac{x-d}{a}\right)\right].(38)$

The two interfaces are separated with width d, although each interface has its own width, a. From the eigenfrequency calculations in Figure 2, we showed that the inclusion of a shear transition layer effectively generates the SKHWs when the shear flow velocity is slow; thus, we ran the simulations for k_yd = 0.25 and 0.75 and M_A < 0.85 to compare with the eigenmode calculation.

We used the time histories of b₁, which does not include the exponential growth, in order to analyze the real frequency and relative strength of the field components. Figure 8 presents wave spectra of perturbed magnetic field and the Poynting flux for k_yd = 0.25. For M_A = 0.45 in Figure 8A, only the waves at ω/ω_AI ∼ 1.2 have strong amplitude. This frequency is close to the eigenmode frequency of ω/ω_AI = 1.17 in Figure 2. The estimated growth rate near the V₀ and V_A interfaces are identical with γ/ω_AI = 0.128. This growth rate is also in good agreement with the analytical results of γ/ω_AI = 0.142 in Section 3.

FIGURE 8

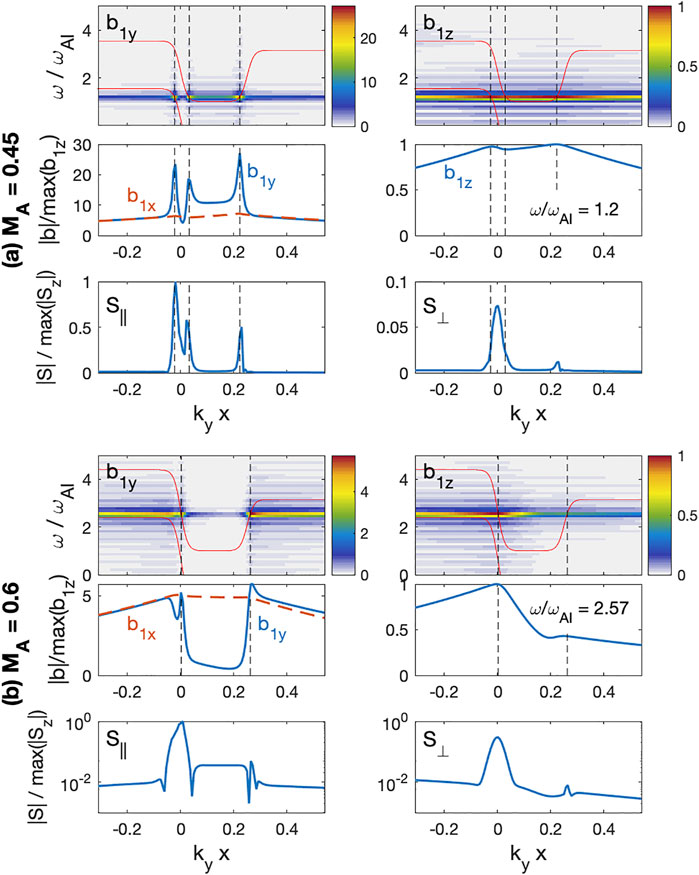
FIGURE 8. Wave spatial distribution for k_yd = 0.25 (A) M_A = 0.45 and (B) M_A = 0.6. Upper panels are perturbed magnetic field compressional (b_1z) and transverse (b_1y) components, middle panels are the spatial structure of the peak frequency, and lower panels are the Poynting flux parallel (S_‖) and perpendicular (S_⊥) to B₀.

In order to examine the detailed wave properties, we plot spatial structures of the fluctuating magnetic field (b_1x, b_1y, and b_1z) at ω/ω_AI = 1.2 in the middle row of Figure 8A. In this case, the compressional components (b_1x and b_1z) maximize at the V_A and V₀ interfaces and decay in the x-direction away from the interfaces. The b_1z and b_1x amplitudes at the two interfaces are comparable; thus, b_1z(x = d)/b_1z(x = 0) = 1.025. This ratio is almost identical to the amplitude ratio of the pressure A_p = 1.06 from Figure 2B.

On the other hand, the transverse component b_1y is enhanced at three different locations near $V_0\left(k_{y}x=-0.022\right.$ and 0.033) and V_A interfaces (k_y = 0.22), where the wave frequency matches the Alfvén resonance condition (ω_AR):

$\omega ={\omega }_{AR}^{\pm }\equiv k_y{V}_0\pm k_{\Vert }{V}_A.$

Due to the finite width of the V₀ interface near x = 0, ${\omega }_{AR}^{-}$ can be positive at the V₀ interface; thus, two separate regions of enhanced wave power can occur corresponding to Doppler-shifted resonance with both Alfvén resonances. In this case, b_1y is significantly stronger than b_1z or b_1x, and b_1y/max(b_1z) ∼ 28 at the V_A interface. Furthermore, strong field-aligned Poynting flux occurs at the interfaces, as shown in the lower panels of Figure 8A. The Poynting flux parallel (S_‖) and perpendicular (S_⊥) to B₀ show that the wave energy predominantly flows along the magnetic field line at both interfaces. Since we launch compressional waves (with V_1x) in the magnetosheath, and the growing KH waves are compressional waves, the amplitude enhancement of the magnetic transverse component and intense field-aligned Poynting flux at the interfaces are clear evidences of the mode conversion from the surface KH waves to the surface Alfvén waves.

For the higher M_A case in Figure 8B, the amplitude is maximized at ω = 2.57ω_AI, which is similar to the analytical value of ω = 2.6ω_AI in Section 3. The b_1z component maximizes near x = 0 and the secondary peak near k_yx = 0.25 becomes weaker. The b_1z amplitude ratio between the two interfaces is 0.64, which is in good agreement with the analytical value of A_p = 0.4. The b_1y component shows strong amplitude near k_yx = 0 and k_yx = 0.26. In this case, because the eigenmode frequency is higher than ${\omega }_{AR}^{-}$, b_1y enhanced only at $\omega ={\omega }_{AR}^{+}$. The amplitude ratio between b_1y and b_1z is much lower than that for the case with M_A = 0.45 in Figure 8A, having b_1y/max(b_1z) ∼ 6 at x ∼ d. Strong field-aligned flux S_‖ appears at the V₀ interface in the bottom panels, but S_⊥ becomes stronger than the case of M_A = 0.45. The analytic eigenmode calculations predict that the PKHWs occur under (k_yd, M_A) = (0.25, 0.75). The simulation results show that the mode conversion from the PKHWs to the surface Alfvén wave still occurs at each interface, but this process is less effective than that from the SKHWs.

For k_yd = 0.75, the waves have a strong amplitude peak near ω/ω_AI = 1.4 and 2.03 for M_A = 0.45 and 0.6, respectively, and the spatial structures of these waves are presented in Figure 9. In this case, the PKHWs and SKHWs are not separated anymore (See Figure 2) and we define the KH waves in the lower M_A as semi-SKHWs in Section 3. For M_A = 0.45 in Figure 9A, b_1z maximizes near x = 0 and a weak secondary peak appears near x = d. On the other hand, three amplitude peaks near k_yx = − 0.025 4, 0.018, and 0.754 appear in b_1y. The power ratio |b_1y/max(b_1z)| at the V₀ interface is reduced to |b_1y/max(b_1z)| ∼ 7 from 23 for (k_yd, M_A) = (0.25, 0.45) in Figure 8A. The enhancement of S_‖ is also seen at both interfaces and relatively strong S_⊥ also appears. Near x = 0 at the V₀ interface, |S_⊥/S_∥|_x=0 is about 0.39, which is almost twice as large as |S_⊥/S_∥|_x=0 = 0.195 for (k_yd, M_A) = (0.25, 0.45). Therefore, even though the compressional wave behavior of the semi-SKHWs is similar to the SKHWs, the mode conversion from semi-SKHWs becomes much weaker than that from the SKHWs.

For M_A = 0.6 in Figure 9B, b_1z decays along the x-direction from the V₀ interface and no amplitude bump occurs at the V_A interface. The b_1y component shows a discontinuity at the V_A interface following the compressional Alfvén wave dispersion relation. Therefore, S_⊥ becomes comparable to S_‖ for k_yx > 0.75. In this case, the mode conversion at the V_A interface does not occur, but energy still flows along the magnetic field line at the V₀ interface.

FIGURE 9

FIGURE 9. Wave spatial distribution for k_yd = 0.75 (A) M_A = 0.45 and (B) M_A = 0.6.

We also analyzed the cases for M_A for k_yd = 0, 0.25, and 0.75 at various M_A. Figure 10 shows the extracted eigenmode frequency and growth rate from the simulations. In this figure, the red and blue circled lines represent simulations, and the gray lines are taken from the eigenfrequency analysis from Figure 2 in Section 3. Although the boundary thicknesses used in Section 2 (slab) and Section 3 (width a) are different because the inhomogeneity scale length for the numerical simulation is much shorter than the wavelength, the eigenmode analytical and simulation results in ω and γ show excellent agreement.

FIGURE 10

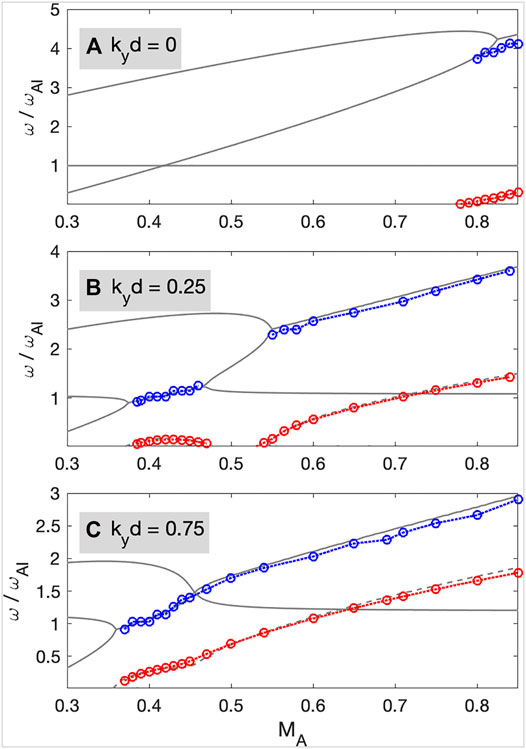
FIGURE 10. Calculated wave frequency (blue circles) and growth rate (red circles) from time-dependent simulations and eigenmode analysis (gray lines) for k_yd = 0.25 and 0.75.

We also calculate the amplitude ratios between the compressional component at the two interfaces (A_p) and between transverse (b_1y) and compressional $(\sqrt{b_{1x}^2+b_{1z}^2})$ components at each interface. Due to the finite thickness of the boundary, two wave amplitude peaks can occur within the V₀ interface as shown in Figures 8, 9, so we average the amplitude near x = 0, if $\omega ={\omega }_{AR}^{\pm }=k_y{V}_0\pm k_z{V}_A$. The simulated A_p and eigenfrequency calculations show good agreement with each other in Figure 11A,B. In particular, A_p of the SKHWs in Figure 11A are almost identical to the analytic calculations. Thus, these results confirm that the SKHWs occur with nearly the same amplitude at both interfaces, while the PKHWs only happen at the V₀ interface. The amplitude ratio between the transverse and compressional components in Figure 11C,D suggests that the transverse magnetic component of the SKHWs is dominant. In other words, the mode conversion to the shear Alfvén wave from the SKHWs effectively occurs at the interfaces. The PKHWs in Figure 11C and semi-SKHWs and PKHWs in Figure 11D show that the transverse mode amplitudes are comparable to the compressional mode amplitude; therefore, weaker or no mode conversion occurs under given conditions at the V_A interface.

FIGURE 11

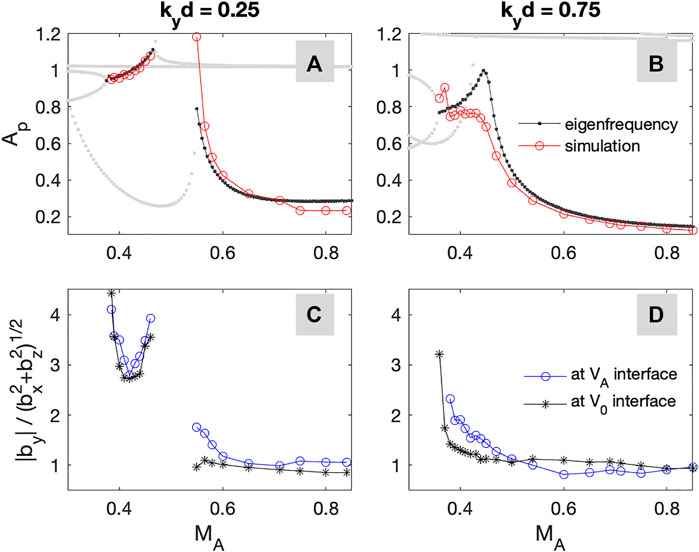
FIGURE 11. (A,B) A_p from the simulations (red circles) eigenfrequency calculations (black dots) for k_yd = 0.25 and 0.75. (C,D) The amplitude ratio between the transverse and compressional components at the V₀ interface (black stars) and the V_A interface (blue circles), respectively.

5 Conclusion and Discussion

This article investigates the coupling between KH and Alfvén waves when a shear transition layer exists between the magnetosheath and magnetosphere. Using the eigenfrequency analysis and time-dependent wave simulations, we showed that the SKHWs are generated when the shear velocity is slower than the typical threshold value for the onset of the KH instability.

The SKHWs occur with a frequency comparable to both KH wave frequency $({\omega }_{KH0}=\frac{1}{2}{k}_y{V}_0)$ and the Alfvén frequency at the magnetosheath (ω_AI = k_‖V_AI), while the PKHWs have a much higher frequency than ω_AI. These results suggest that PKHWs and SKHWs can be identified using the frequency ratio to ω_KH0 and ω_AI from in situ observations. The SKHWs appear at both the V₀ and V_A interfaces with nearly the same amplitude, while the PKHWs appear only at the V₀ interface. Since V₀ is uniform at the V_A interface, no KH waves can be generated at the V_A interface without coupling between the KH and Alfvén waves. For the given conditions of 0 < k_yd ≤ 0.5, where the SKHWs are well separated from the PKHWs in Figure 3 and the shear transition layer width is 0 < d ≤ 0.3R_E; thus, if the thickness of each boundary (a) is much shorter than the width of the transition layer (d), the SKHWs can be detected at the V_A interface.

The simulation results in Figures 8, 9 show that the magnetic transverse component is dominant at the interface and a strong field-aligned Poynting flux appears. Therefore, the energy transfer from the boundary layer to the Earth via mode-converted shear Alfvén waves occurs, which is similar to observations (Chaston et al., 2007). The wave simulations predict that a stronger mode conversion occurs from the SKHWs than from the PKHWs. However, the wave growth rate should be considered as well. Even though the mode conversion efficiency from the PKHWs is weaker than the SKHWs, the PKHWs amplitude can be strong enough due to the higher growth rate. Thus, a strong transverse component also can be detected from the PKHWs, but the compressional components are still comparable to the transverse components.

Although we clearly show the characteristics of PKHWs and SKHWs, this article only considers that the magnetic field is perpendicular to the flow velocity, and the magnetic field is assumed to be a constant. Indeed, the magnetic field in the magnetosheath and magnetosphere can be perpendicular in the magnetopause, and also the magnetic field and the flow velocity can be parallel in space, such as the solar corona and magnetotail. The secondary KH instability or resonant flow instability can occur under such conditions (Taroyan and Erdélyi, 2002, 2003; Turkakin et al., 2013). Furthermore, compressional waves bounded in the inner magnetosphere can contribute to the generation of the secondary KH instability (Turkakin et al., 2013) and also mode conversion to the shear Alfvén wave (Taroyan and Erdélyi, 2002). The total length of our numerical simulation model, including the collisional layer in Section 4, is somewhat comparable to $\sim 10R_E$; thus, the bounded plasma effect should be considered in the future.

We also used a cold plasma approximation in the magnetosheath. The inclusion of thermal effects leads to an additional KH wave branch (Taroyan and Erdélyi, 2003). In warm plasmas, the Alfvén waves propagate as kinetic Alfvén waves (KAW). The KAW can have a larger wavenumber across the magnetic field line and field-aligned electric field and velocity components (Lin et al., 2010, 2012). Similar to Alfvén waves, KAW also transfers the energy away from the mode conversion location along the magnetic field line; thus, it is expected that a strong transverse component at each interface would also be detected with thermal effect.

In addition, a high level of turbulent fluctuations in the magnetosheath is observed in multiple satellites (e.g., Rakhmanova et al., 2021); however, nonlinear effects are not included in our analysis. It is possible that if these modes grow to sufficient amplitude, vortices will form and nonlinear interactions may become important, leading to plasma heating and transport. These nonlinear effects are left for future studies.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. Digital data can be found in the DataSpace of Princeton University http://arks.princeton.edu/ark:/88435/dsp013r074z09k

Author Contributions

E-HK developed the real-time simulation code and ran both eigenfrequency calculation and simulation code, JRJ solved the dispersion relation of the KH waves and built the eigenfrequency calculation code, and KN discussed the observational background.

Funding

This material is based upon work supported by the United States Department of Energy, Office of Science, Office of Fusion Energy Sciences under contract DE-AC02-09CH11466. Work at Princeton University is under National Science Foundation (NSF) grant AGS1602855 and National Aeronautics and Space Administration (NASA) grants 80HQTR18T0066, 80HQTR19T0076, and NNX17AI50G. Work at Andrews University is supported by NASA grants NNX16AQ87G, 80NSSC19K0270, 80NSSC19K0843, 80NSSC18K0835, 80NSSC20K0355, NNX17AI50G, NNX17AI47G, 80HQTR18T0066, 80NSSC20K0704, and 80NSSC18K1578 and NSF grants AGS1832207 and AGS1602855. Work at Embry-Riddle Aeronautical University is under NASA grant NNX17AI50G.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andries, J., and Goossens, M. (2001). Kelvin-Helmholtz Instabilities and Resonant Flow Instabilities for a Coronal Plume Model with Plasma Pressure. A&A 368, 1083–1094. doi:10.1051/0004-6361:20010050

CrossRef Full Text | Google Scholar

Andries, J., Tirry, W. J., and Goossens, M. (2000). Modified Kelvin‐Helmholtz Instabilities and Resonant Flow Instabilities in a One‐dimensional Coronal Plume Model: Results for Plasma \documentclass{aastex} \usepackage{amsbsy} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{bm} \usepackage{mathrsfs} \usepackage{pifont} \usepackage{stmaryrd} \usepackage{textcomp} \usepackage{portland,xspace} \usepackage{amsmath,amsxtra} \usepackage[OT2,OT1]{fontenc} \newcommand\cyr{ \renewcommand\rmdefault{wncyr} \renewcommand\sfdefault{wncyss} \renewcommand\encodingdefault{OT2} \normalfont \selectfont} \DeclareTextFontCommand{\textcyr}{\cyr} \pagestyle{empty} \DeclareMathSizes{10}{9}{7}{6} \begin{document} \landscape $\beta =0$ \end{document}. ApJ 531, 561–570. doi:10.1086/308430

CrossRef Full Text | Google Scholar

Antolin, P., and Van Doorsselaere, T. (2019). Influence of Resonant Absorption on the Generation of the Kelvin-Helmholtz Instability. Front. Phys. 7, 85. doi:10.3389/fphy.2019.00085

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1961). Hydrodynamic and Hydromagnetic Stability. Oxford, U.K.: Oxford University Press.

Google Scholar

Chaston, C. C., Wilber, M., Mozer, F. S., Fujimoto, M., Goldstein, M. L., Acuna, M., et al. (2007). Mode Conversion and Anomalous Transport in Kelvin-Helmholtz Vortices and Kinetic Alfvén Waves at the Earth's Magnetopause. Phys. Rev. Lett. 99, 175004. doi:10.1103/PhysRevLett.99.175004

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., and Hasegawa, A. (1974). Plasma Heating by Spatial Resonance of Alfvén Wave. Phys. Fluids 17, 1399–1403. doi:10.1063/1.1694904

CrossRef Full Text | Google Scholar

Cowee, M. M., Winske, D., and Gary, S. P. (2010). Hybrid Simulations of Plasma Transport by Kelvin-Helmholtz Instability at the Magnetopause: Density Variations and Magnetic Shear. J. Geophys. Res. 115, A06214. doi:10.1029/2009JA015011

CrossRef Full Text | Google Scholar

Delamere, P. A., and Bagenal, F. (2010). Solar Wind Interaction with Jupiter's Magnetosphere. J. Geophys. Res. 115, A10201. doi:10.1029/2010JA015347

CrossRef Full Text | Google Scholar

Delamere, P. A., Ng, C. S., Damiano, P. A., Neupane, B. R., Johnson, J. R., Burkholder, B., et al. (2021). Kelvin-Helmholtz‐Related Turbulent Heating at Saturn's Magnetopause Boundary. J. Geophys. Res. Space Phys. 126, e2020JA028479. doi:10.1029/2020JA028479

CrossRef Full Text | Google Scholar

Engebretson, M., Glassmeier, K.-H., Stellmacher, M., Hughes, W. J., and Lühr, H. (1998). The Dependence of High-Latitude Pcs Wave Power on Solar Wind Velocity and on the Phase of High-Speed Solar Wind Streams. J. Geophys. Res. 103, 26271–26283. doi:10.1029/97JA03143

CrossRef Full Text | Google Scholar

Génot, V., and Lavraud, B. (2021). Solar Wind Plasma Properties during Ortho-parker Imf Conditions and Associated Magnetosheath Mirror Instability Response. Front. Astron. Space Sci. 8, 153. doi:10.3389/fspas.2021.710851

CrossRef Full Text | Google Scholar

González, A. G., and Gratton, J. (1994). The Role of a Density Jump in the Kelvin-Helmholtz Instability of Compressible Plasma. J. Plasma Phys. 52, 223–244. doi:10.1017/S0022377800017888

CrossRef Full Text | Google Scholar

Hwang, K.-J., Kuznetsova, M. M., Sahraoui, F., Goldstein, M. L., Lee, E., and Parks, G. K. (2011). Kelvin-Helmholtz Waves under Southward Interplanetary Magnetic Field. J. Geophys. Res. 116, A08210. doi:10.1029/2011JA016596

CrossRef Full Text | Google Scholar

Johnson, J. R., and Cheng, C. Z. (2001). Stochastic Ion Heating at the Magnetopause Due to Kinetic Alfvén Waves. Geophys. Res. Lett. 28, 4421–4424. doi:10.1029/2001gl013509

CrossRef Full Text | Google Scholar

Johnson, J. R., Wing, S., and Delamere, P. A. (2014). Kelvin Helmholtz Instability in Planetary Magnetospheres. Space Sci. Rev. 184, 1–31. doi:10.1007/s11214-014-0085-z

CrossRef Full Text | Google Scholar

Johnson, J. R., Wing, S., Delamere, P., Petrinec, S., and Kavosi, S. (2021). Field‐Aligned Currents in Auroral Vortices. J. Geophys. Res. Space Phys. 126, e28583. doi:10.1029/2020JA028583

CrossRef Full Text | Google Scholar

Kim, E.-H., Cairns, I. H., and Robinson, P. A. (2007). Extraordinary-Mode Radiation Produced by Linear-Mode Conversion of Langmuir Waves. Phys. Rev. Lett. 99, 015003. doi:10.1103/physrevlett.99.015003

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, E.-H., and Lee, D.-H. (2003). Resonant Absorption of Ulf Waves Near the Ion Cyclotron Frequency: A Simulation Study. Geophys. Res. Lett. 30, 2240. doi:10.1029/2003gl017918

CrossRef Full Text | Google Scholar

Lavraud, B., and Borovsky, J. E. (2008). Altered Solar Wind-Magnetosphere Interaction at Low Mach Numbers: Coronal Mass Ejections. J. Geophys. Res. 113, A00B08. doi:10.1029/2008JA013192

CrossRef Full Text | Google Scholar

Lavraud, B., Larroque, E., Budnik, E., Génot, V., Borovsky, J. E., Dunlop, M. W., et al. (2013). Asymmetry of Magnetosheath Flows and Magnetopause Shape during Low Alfvén Mach Number Solar Wind. J. Geophys. Res. Space Phys. 118, 1089–1100. doi:10.1002/jgra.50145

CrossRef Full Text | Google Scholar

Lin, Y., Johnson, J. R., and Wang, X. (2012). Three-Dimensional Mode Conversion Associated with Kinetic Alfvén Waves. Phys. Rev. Lett. 109, 125003. doi:10.1103/PhysRevLett.109.125003

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Y., Johnson, J. R., and Wang, X. Y. (2010). Hybrid Simulation of Mode Conversion at the Magnetopause. J. Geophys. Res. 115, A04208. doi:10.1029/2009JA014524

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P. A., Nykyri, K., Burkholder, B., Neupane, B., and Rice, R. C. (2019). Comparison between Fluid Simulation with Test Particles and Hybrid Simulation for the Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 124, 6654–6668. doi:10.1029/2019JA026890

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P., Otto, A., and Burkholder, B. (2017). Plasma Transport Driven by the Three‐Dimensional Kelvin‐Helmholtz Instability. J. Geophys. Res. Atmos. 122, 10,382–10,395. doi:10.1002/2017JA024394

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Hoshino, M. (2006). Turbulent Mixing and Transport of Collisionless Plasmas across a Stratified Velocity Shear Layer. J. Geophys. Res. 111, A05213. doi:10.1029/2004JA010988

CrossRef Full Text | Google Scholar

McComas, D. J., and Bagenal, F. (2008). Reply to comment by s. w. h. cowley et al. on “jupiter: A fundamentally different magnetospheric interaction with the solar wind”. Geophys. Res. Lett. 35, L10103. doi:10.1029/2008GL034351

CrossRef Full Text | Google Scholar

Mills, K. J., and Wright, A. N. (1999). Azimuthal Phase Speeds of Field Line Resonances Driven by Kelvin-Helmholtz Unstable Waveguide Modes. J. Geophys. Res. 104, 22667–22677. doi:10.1029/1999JA900280

CrossRef Full Text | Google Scholar

Miura, A. (1984). Anomalous Transport by Magnetohydrodynamic Kelvin-Helmholtz Instabilities in the Solar Wind-Magnetosphere Interaction. J. Geophys. Res. 89, 801–818. doi:10.1029/JA089iA02p00801

CrossRef Full Text | Google Scholar

Miura, A., and Pritchett, P. L. (1982). Nonlocal Stability Analysis of the MHD Kelvin-Helmholtz Instability in a Compressible Plasma. J. Geophys. Res. 87, 7431–7444. doi:10.1029/JA087iA09p07431

CrossRef Full Text | Google Scholar

Moore, T. W., Nykyri, K., and Dimmock, A. P. (2016). Cross-scale Energy Transport in Space Plasmas. Nat. Phys 12, 1164–1169. doi:10.1038/NPHYS3869

CrossRef Full Text | Google Scholar

Moore, T. W., Nykyri, K., and Dimmock, A. P. (2017). Ion‐Scale Wave Properties and Enhanced Ion Heating across the Low‐Latitude Boundary Layer during Kelvin‐Helmholtz Instability. J. Geophys. Res. Space Phys. 122, 11128–11153. doi:10.1002/2017JA024591

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Hasegawa, H., Daughton, W., Eriksson, S., Li, W. Y., and Nakamura, R. (2017). Turbulent Mass Transfer Caused by Vortex Induced Reconnection in Collisionless Magnetospheric Plasmas. Nat. Commun. 8, 1582. doi:10.1038/s41467-017-01579-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Hasegawa, H., Shinohara, I., and Fujimoto, M. (2011). Evolution of an MHD-Scale Kelvin-Helmholtz Vortex Accompanied by Magnetic Reconnection: Two-Dimensional Particle Simulations. J. Geophys. Res. 116, A03227. doi:10.1029/2010JA016046

CrossRef Full Text | Google Scholar

Nykyri, K., Ma, X., Burkholder, B., Rice, R., Johnson, J. R., Kim, E.-K., et al. (2021a). Mms Observations of the Multiscale Wave Structures and Parallel Electron Heating in the Vicinity of the Southern Exterior Cusp. J. Geophys. Res. Space Phys. 126, e2019JA027698. doi:10.1029/2019JA027698

CrossRef Full Text | Google Scholar

Nykyri, K., Ma, X., Dimmock, A., Foullon, C., Otto, A., and Osmane, A. (2017). Influence of Velocity Fluctuations on the Kelvin-Helmholtz Instability and its Associated Mass Transport. J. Geophys. Res. Space Phys. 122, 9489–9512. doi:10.1002/2017JA024374

CrossRef Full Text | Google Scholar

Nykyri, K., Ma, X., and Johnson, J. (2021b). Cross-Scale Energy Transport in Space Plasmas. Washington, D.C., United States: American Geophysical Union, 109–121. chap. 7. doi:10.1002/9781119815624.ch7

CrossRef Full Text | Google Scholar

Nykyri, K., and Otto, A. (2001). Plasma Transport at the Magnetospheric Boundary Due to Reconnection in Kelvin-Helmholtz Vortices. Geophys. Res. Lett. 28, 3565–3568. doi:10.1029/2001GL013239

CrossRef Full Text | Google Scholar

Otto, A., and Fairfield, D. H. (2000). Kelvin-Helmholtz Instability at the Magnetotail Boundary: MHD Simulation and Comparison with Geotail Observations. J. Geophys. Res. 105, 21175–21190. doi:10.1029/1999JA000312

CrossRef Full Text | Google Scholar

Otto, A., and Nykyri, K. (2003). “Kelvin-Helmholtz Instability and Magnetic Reconnection: Mass Transport at the LLBL,” in Geophysical Monograph Series. Editors P. T. Newell, and T. Onsager (Washington DC: American Geophysical Union), 133, 53–62. doi:10.1029/133GM05

CrossRef Full Text | Google Scholar

Paschmann, G., Baumjohann, W., Sckopke, N., Phan, T.-D., and Lühr, H. (1993). Structure of the Dayside Magnetopause for Low Magnetic Shear. J. Geophys. Res. 98, 13409–13422. doi:10.1029/93JA00646

CrossRef Full Text | Google Scholar

Pu, Z.-Y., and Kivelson, M. G. (1983). Kelvin:Helmholtz Instability at the Magnetopause: Solution for Compressible Plasmas. J. Geophys. Res. 88, 841–852. doi:10.1029/JA088iA02p00841

CrossRef Full Text | Google Scholar

Rakhmanova, L., Riazantseva, M., and Zastenker, G. (2021). Plasma and Magnetic Field Turbulence in the Earth's Magnetosheath at Ion Scales. Front. Astron. Space Sci. 7, 115. doi:10.3389/fspas.2020.616635

CrossRef Full Text | Google Scholar

Ruderman, M. S., and Wright, A. N. (1998). Excitation of Resonant Alfvén Waves in the Magnetosphere by Negative Energy Surface Waves on the Magnetopause. J. Geophys. Res. 103, 26573–26584. doi:10.1029/98JA02296

CrossRef Full Text | Google Scholar

Southwood, D. J. (1968). The Hydromagnetic Stability of the Magnetospheric Boundary. Planet. Space Sci. 16, 587–605. doi:10.1016/0032-0633(68)90100-1

CrossRef Full Text | Google Scholar

Taroyan, Y., and Erdélyi, R. (2002). Resonant and Kelvin-Helmholtz Instabilities on the Magnetopause. Phys. Plasmas 9, 3121–3129. doi:10.1063/1.1481746

CrossRef Full Text | Google Scholar

Taroyan, Y., and Erdélyi, R. (2003). Resonant Surface Waves and Instabilities in Finite β Plasmas. Phys. Plasmas 10, 266–276. doi:10.1063/1.1532741

CrossRef Full Text | Google Scholar

Taroyan, Y., and Ruderman, M. S. (2011). MHD Waves and Instabilities in Space Plasma Flows. Space Sci. Rev. 158, 505–523. doi:10.1007/s11214-010-9737-9

CrossRef Full Text | Google Scholar

Thomas, V. A., and Winske, D. (1993). Kinetic Simulations of the Kelvin-Helmholtz Instability at the Magnetopause. J. Geophys. Res. 98, 11425–11438. doi:10.1029/93JA00604

CrossRef Full Text | Google Scholar

Tirry, W. J., Cadez, V. M., Erdelyi, R., and Goossens, M. (1998). Resonant Flow Instability of MHD Surface Waves. Astron. Astrophysics 332, 786–794.

Google Scholar

Turkakin, H., Mann, I. R., and Rankin, R. (2014). Kelvin-Helmholtz Unstable Magnetotail Flow Channels: Deceleration and Radiation of MHD Waves. Geophys. Res. Lett. 41, 3691–3697. doi:10.1002/2014GL060450

CrossRef Full Text | Google Scholar

Turkakin, H., Rankin, R., and Mann, I. R. (2013). Primary and Secondary Compressible Kelvin-Helmholtz Surface Wave Instabilities on the Earth's Magnetopause. J. Geophys. Res. Space Phys. 118, 4161–4175. doi:10.1002/jgra.50394

CrossRef Full Text | Google Scholar