- 1Mathematics, Statistics, and Computer Science Department, Macalester College, Saint Paul, MN, United States
- 2Department of Mathematics, Purdue University, West Lafayette, IN, United States
- 3Mathematical Institute, University of Oxford, Oxford, United Kingdom
- 4Department of Mathematical Sciences, University of Delaware, Newark, DE, United States
Cycle representatives of persistent homology classes can be used to provide descriptions of topological features in data. However, the non-uniqueness of these representatives creates ambiguity and can lead to many different interpretations of the same set of classes. One approach to solving this problem is to optimize the choice of representative against some measure that is meaningful in the context of the data. In this work, we provide a study of the effectiveness and computational cost of several
1 Introduction
Topological data analysis (TDA) uncovers mesoscale structure in data by quantifying its shape using methods from algebraic topology. Topological features have proven effective when characterizing complex data, as they are qualitative, independent of choice of coordinates, and robust to some choices of metrics and moderate quantities of noise (Carlsson, 2009; Ghrist, 2014). As such, topological features extracted from data have recently drawn attention from researchers in various fields including, for example, neuroscience (Bendich et al., 2016; Giusti et al., 2016; Sizemore et al., 2019), computer graphics (Singh et al., 2007; Brüel-Gabrielsson et al., 2020), robotics (Vasudevan et al., 2011; Bhattacharya et al., 2015), and computational biology (Bhaskar et al., 2019; Ulmer et al., 2019; McGuirl et al., 2020) [including the study of protein structure (Xia and Wei, 2014; Kovacev-Nikolic et al., 2016; Xia et al., 2018)].
The primary tool in TDA is persistent homology (PH) (Ghrist, 2008), which describes how topological features of data, colloquially referred to as “holes,” evolve as one varies a real-valued parameter. Each hole comes with a geometric notion of dimension which describes the shape that encloses the hole: connected components in dimension zero, loops in dimension one, shells in dimension two, and so on. From a parameterized topological space
A basic problem in the practical application of PH is interpretability: given an interval
An important challenge, however, is that cycle representatives are not uniquely defined. For example, in the left-hand image in Figure 1 adapted from Carlsson (2009), two curves enclose the same topological feature and thus, represent the same persistent homology class. We often want to find a cycle that captures not only the existence but also information about the location and shape of the hole that the homology class has detected. This often means optimizing an application-dependent property using the underlying data, e.g. finding a minimal length or bounding area/volume using an appropriate metric. The algorithmic problem of selecting such optimal representatives is currently an active area of research (Chen and Freedman, 2010a; Dey et al., 2011; Wu et al., 2017; Obayashi, 2018; Dey et al., 2019).
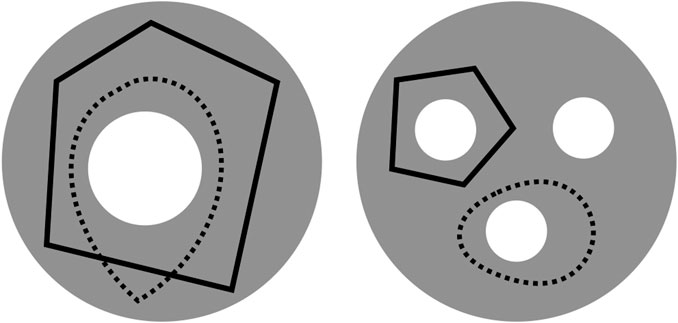
FIGURE 1. Two disks (gray) — which we regard as 2-dimensional simplicial complexes, though the explicit decomposition into simplices is not shown—with different numbers of holes (white) and cycle representatives (black solid or dotted) adapted from (Carlsson, 2009). The disk on the left has a single 2-dimensional “hole”
There are diverse notions of optimality we may wish to consider in a given context, and which may have significant impact on the effectiveness or suitability of optimization, including.
• weight assignment to chains (uniform vs. length or area weighted),
• choice of loss function
• formulation of the optimization problem (cycle size vs. bounded area or volume), and
• restrictions on allowable coefficients (rational, integral, or
Each has a unique set of advantages and disadvantages. For example, optimization using the
Q1 How do the computational costs of the various optimization techniques compare? How much do these costs depend on the choice of a particular linear solver?
Q2 What are the statistical properties of optimal cycle representatives? For example, how often does the support of a representative form a single loop in the underlying graph? And, how much do optimized cycles coming out of an optimization pipeline differ from the representative that went in?
Q3 To what extent does choice of technique matter? For example, how often does the length of a length-weighted optimal cycle match the length of a uniform-weighted optimal cycle? And, how often are
Given the conceptual and computational complexity of these problems [see Chen and Freedman (2010b)], the authors expect that formal answers are unlikely to be available in the near future. However, even where theoretical results are available, strong empirical trends may suggest different or even contrary principles to the practitioner. For example, while the persistence calculation is known to have matrix multiplication time complexity (Milosavljević et al., 2011), in practice the computation runs almost always in linear time. Therefore, the authors believe that a careful empirical exploration of questions one to three will be of substantial value.
In this paper, we undertake such an exploration in the context of one-dimensional persistent homology over the field of rationals,
The paper is organized as follows. Section 2 provides an overview of some key concepts in TDA to inform a reader new to algebraic topology and establish notation. Then, we provide a survey of previous work on finding optimal persistent cycle representatives in Section 3, and formulate the methods used in this paper to find different notions of minimal cycle representatives via LP and MIP in Section 4. Section 5 describes our experiments, including overviews of the data and the hardware and software we use for our analysis. In Section 6, we discuss the results of our experiments. We conclude and describe possible future work in Section 7.
2 Background: Topological Data Analysis and Persistent Homology
In this section, we introduce key terms in algebraic and computational topology to provide minimal background and establish notation. For a more thorough introduction see, for example, Hatcher et al. (2002), Ghrist (2008), Edelsbrunner and Harer (2008), Carlsson (2009), Edelsbrunner and Harer (2010), and Topaz et al. (2015).
Given a discrete set of sample data, we approximate the topological space underlying the data by constructing a simplicial complex. This construction expresses the structure as a union of vertices, edges, triangles, tetrahedrons, and higher dimensional analogues (Carlsson, 2009).
2.1 Simplicial Complexes
A simplicial complex is a collection K of non-empty subsets of a finite set V. The elements of V are called vertices of K, and the elements of K are called simplices. A simplicial complex has the following properties: 1)
Additionally, we say that a simplex has dimension n or is an n-simplex if it has cardinality n + 1. We use
While there are a variety of approaches to create a simplicial complex from data, our examples use a standard construction for approximation of point clouds. Given a metric space X with metric d and real number
That is, given a set of discrete points X and a metric d, we build a VR complex at scale ε by forming an n-simplex if and only if
2.2 Chains and Chain Complexes
Given a simplicial complex K and an abelian group G, the group of n-chains in K with coefficients in G is defined as
Formally, we regard
Remark 2.1. We will focus on the cases where G is
An element
The
Remark 2.2 (Indexing conventions for chains and simplices). As chains play a central role in our discussion, it will be useful to establish some special conventions to describe them. These conventions depend on the availability of certain linear orders, either on the set of vertices or the set of simplices.
Case 1: Vertex set V has a linear order
for the n-chain that places a coefficient of 1 on
Case 2: Simplex set
such that
where
Remark 2.3 (Indexing conventions for boundary matrices). In general, boundary matrix
2.3 Cycles, Boundaries
The boundary of an n-chain
It can be shown that
2.4 Homology, Cycle Representatives
The nth homology group of K is defined as the quotient.
Concretely, elements of
Example: Consider the example in Figure 2A, which illustrates two homologous 1-cycles and the example in Figure 2B, which illustrates two non-homologous cycles.
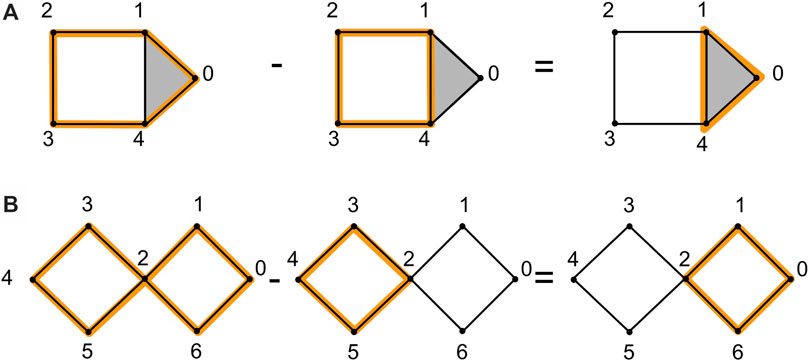
FIGURE 2. We show an example of homologous cycles in (A), adapted from (Topaz et al., 2015). The 1-cycle
Remark 2.4. The term homological generator has been used differently by various authors: to refer to an arbitrary nontrivial homology class, an element in a (finite) representation of
2.5 Betti Numbers, Cycle Bases
A (dimension-n) homological cycle basis for
Homological cycle bases have several useful interpretations. It is common, for example, to think of a 1-cycle as a type of “loop,” generalizing the intuitive notion of a loop as a simple closed curve to include more intricate structures, and to regard the operation of adding boundaries as a generalized form of “loop-deformation.” Framed in this light, a homological cycle basis
Another interpretation construes each nontrivial homology class
therefore quantifies the “number of gray independent holes” in K. We call
Example: Consider the gray disks in Figure 1 [similar to Carlsson (2009)] with different numbers of holes and cycle representatives.
2.6 Filtrations of Simplicial Complexes
A filtration on a simplicial complex K is a nested sequence of simplicial complexes
where
Example Let X be a metric space with metric d, and let
The data of a filtered complex is naturally captured by the birth function on simplices, defined
We regard the pair
Definition 2.5. A filtration
2.7 Filtrations of Chain Complexes
If we regard
Given a simplex-wise refinement
Similar observations hold when one replaces
2.8 Persistent Homology, Birth, Death
The notion of birth for simplices has a natural extension to chains, as well as a variant called death. Formally, the birth and death parameters of
In the special case where
is the range of parameters over which
A (dimension-n) persistent homology cycle basis is a subset
1. Each
2. For each
is a homological cycle basis for
Every filtration of simplicial complexes
is invariant over all possible choices of persistent homological cycle bases
Example: Consider the sequence of simplicial complexes (
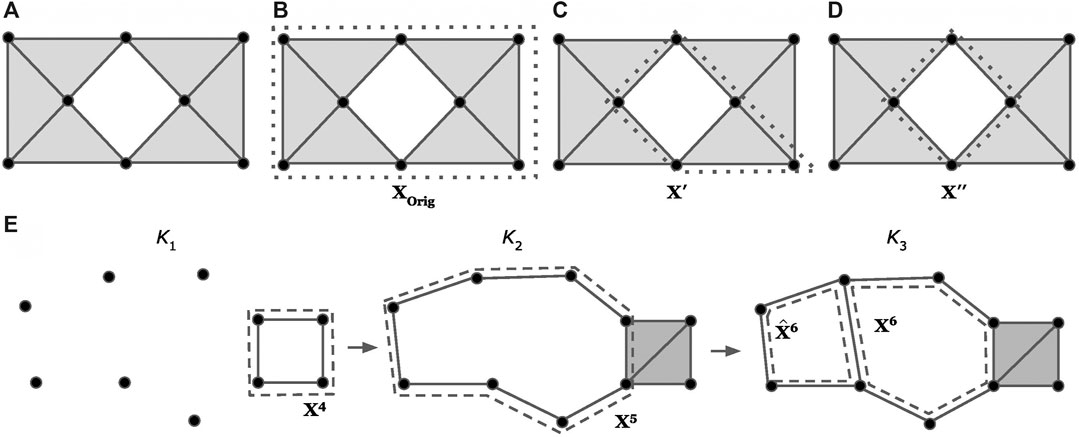
FIGURE 3. Examples of optimizing a cycle representative (using the notion of minimizing edges) within the same homology class (A-D) and using a basis of cycle representatives (E), modified examples adapted from (Escolar and Hiraoka, 2016; Obayashi, 2018). The dotted lines represent a cycle representative for the enclosed “hole.” Intuitively, we consider
Barcodes are among the foremost tools in topological data analysis (Ghrist, 2008; Edelsbrunner and Harer, 2008), and they contain a great deal of information about a filtration. For example, it follows immediately from the definition of persistent homological cycle bases that
2.9 Computing PH Cycle Representatives
Barcodes and persistent homology bases may be computed via the so-called
3 Related Work on Minimizing Cycle Representatives
One important problem in TDA is interpreting homological features. In general, a lifetime interval
Minimal cycle representatives have proven useful in many applications. Hiraoka et al. (2016) use TDA to geometrically analyze amorphous solids. Their analysis using minimal cycle representatives explicitly captures hierarchical structures of the shapes of cavities and rings. Wu et al. (2017) discuss an application of optimal cycles in Cardiac Trabeculae Restoration, which aims to reconstruct trabeculae, very complex muscle structures that are hard to detect by traditional image segmentation methods. They propose to use topological priors and cycle representatives to help segment the trabeculae. However, the original cycle representative can be complicated and noisy, causing the reconstructed surface to be messy. Optimizing the cycle representatives makes the cycle more smooth and thus, leads to more accurate segmentation results. Emmett et al. (2015) use PH to analyze chromatin interaction data to study chromatin conformation. They use loops to represent different types of chromatin interactions. To annotate particular loops as interactions, they need to first localize a cycle. Thus, they propose an algorithm to locate a minimal cycle representative for a given PH class using a breadth-first search, which finds the shortest path that contains the edge that enters the filtration at the birth time of the cycle and is homologically independent from the minimal cycles of all PH classes born before the current cycle.
There are several approaches used to define an optimal cycle representative. Dey et al. (2011) propose an algorithm to find an optimal homologous 1-cycle for a given homology class via linear programming. That is, they consider a single homology class
In addition to linear programming, many researchers have contributed to the problem of computing optimal cycles: Wu et al. (2017) propose an algorithm for finding shortest persistent 1-cycles. They first construct a graph based on the given simplicial complex and then compute annotation for the given complex. The annotation assigns all edges different vectors and can be used to verify if a cycle belongs to the desired group of cycles. They then find the shortest path between two vertices of the edge born at the birth time of the original cycle representative using a new
In the next subsection, we briefly introduce some basic notions of linear programming, and then in the subsequent three subsections, we survey the optimization problems on which the present work is based.
3.1 Background: Linear Programming
Linear programming seeks to find a set of decision variables
where A is the
The optimal solution
Standard LPs search for real-valued optimal solutions, but in some instances, a restriction of the decision variables, such as requiring integral solutions, may be necessitated. The mixed integer programming (MIP) problem is written
for matrices
In this paper, we determine optimal cycle representatives with both LP and MIP formulations.
3.2 Minimal Cycle Representatives of a Homology Class
Given a homology class
This formulation considers all cycle representatives homologous to
In practice, a cycle representative
Several variants of the program in Eq. 3 have been studied, especially where
An interesting variant of the minimal cycle representative problem is the minimal persistent cycle representative problem. This problem was described in Chen et al. (2008) and may be formulated as follows: given an interval
for
3.3 Minimal Homological Cycle Bases
The program in Eq. 3 has a natural extension when G is a field. This extension focuses not on the smallest representative of a single homology class, but the smallest homological cycle basis. It may be formally expressed as follows:
where
It is natural to wonder whether a solution to the program in Eq. 5 could be obtained by first calculating an arbitrary (possibly non-minimal) homological cycle basis
As with the minimal cycle representative problem, the minimal homological cycle basis problem has been well-studied in the special case where
A natural variant of the minimal homological cycle basis program in Eq. 5 is the minimal persistent homological cycle basis problem
where
The program in Eq. 6 is much more recent than the program in Eq. 5, and consequently appears less in the literature. In the special case where every bar in the multiset
3.4 Minimal Filtered Cycle Space Bases
A close cousin of the minimal homological cycle basis the program in Eq. 5 is the minimal filtered cycle basis problem, which may be formulated as follows
where
Escolar and Hiraoka (2016) provide a polynomial time solution via linear programming when.
1.
2.
3.
Their key observation is that
1. the set
2. for each
The authors formulate this problem as
where
The algorithm developed in Escolar and Hiraoka (2016) is cleverly constructed to extract
Remark 3.1. It is important to distinguish between
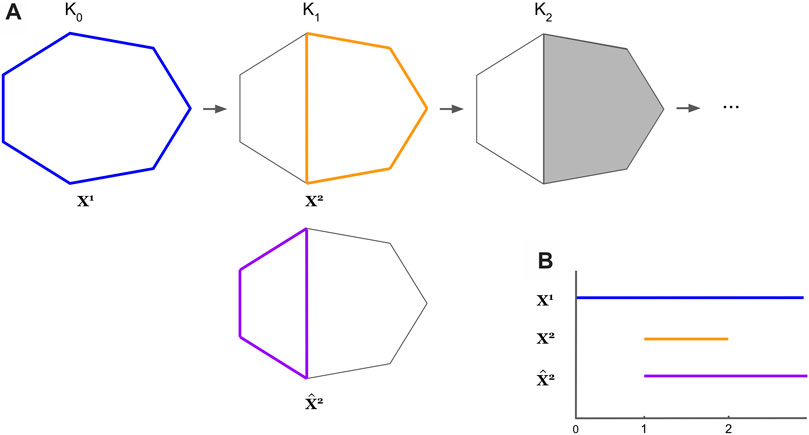
FIGURE 4. An example where the optimal cycles obtained from Eq. 8 do not form a persistent homological cycle basis. The thickened colored cycles in Subfigure (A) represent a cycle representative for the hole it encloses, and the bar with the corresponding color in Subfigure (B) records the lifespan of the cycle. In Subfigure (A), we see
Though Remark 3.1 is a bit disappointing for those interested in persistent homology, the machinery developed to study the program in Eq. 7 is nevertheless interesting, and we will discuss an adaptation.
3.5 Volume-Optimal Cycles: Minimizing Over Bounding Chains
Schweinhart (2015) and Obayashi (2018) consider a different notion of minimization: volume5 optimality. This approach focuses on the “size” of a bounding chain; it is specifically designed for cycle representatives in a persistent homological cycle basis.
Obayashi (2018) formalizes the approach as follows. First, assume a simplex-wise filtration
A persistent volume
where
We interpret these equations as follows: Given a persistence interval
Theorem 3.2. (Obayashi, 2018). Suppose that
1. Interval
2. If
3. Suppose that
By Theorem 3.2, for any barcode composed of finite intervals, one can construct a persistent homological cycle basis from nothing but (boundaries of) persistent volumes! Were we to build such a basis, it would be natural to ask for volumes that are optimal with respect to some loss function; that is, we might like to solve
for each barcode interval

FIGURE 5. A situation in which a volume-optimal cycle is different from the uniform minimal cycle. Consider the filtered simplicial complex pictured. For the persistence interval
3.6
As mentioned above, it is common to choose
The
Requiring the solution to be integral also allows us to understand the optimal solution more intuitively than having fractional coefficients. Such an optimization problem is called a mixed integer program (MIP), which is known to be slower than linear programming and is NP-hard (Obayashi, 2018). Many variants of integer programming special to optimal homologous cycles, in particular, have been shown to be hard as well (Borradaile et al., 2020). In Section 4, we discuss the optimization problems we implement, where each is solved both as an LP with an
Dey et al. (2011) gives the totally unimodularity sufficient condition which guarantees that an LP and MIP give the same optimal solution. A matrix is totally unimodular if the determinant of each square submatrix is
3.7 Software Implementations
Edge-minimal cycles: Software implementing the edge-loss method introduced in Escolar and Hiraoka (2016) can be found at Escolar and Hiraoka (2021). This is a C++ library specialized for 3-dimensional point clouds.
Triangle-loss optimal cycles: The volume optimization technique introduced in Obayashi (2018) is available through the software platform HomCloud, available at Obayashi et al. (2021). The code can be accessed by unarchiving the HomCloud package (for example, https://homcloud.dev/download/homcloud-3.1.0.tar.gz) and picking the file homcloud-x.y.z/homcloud/optvol.py.
4 Programs and Solution Methods
The present work focuses on linear programming (LP) and mixed integer programming (MIP) optimization of 1-dimensional persistent homology cycle representatives with
Concerning implementation, we find that triangle-loss methods [namely, Obayashi (2018)] can be applied essentially as discussed in that paper. The greatest challenge to implementing this approach is the assumption of an underlying simplex-wise filtration. This necessitates parameter choices and preprocessing steps not included in the optimization itself; we discuss how to execute these steps below.
Implementation of edge-loss methods is slightly more complex. For binary coefficients
Neither of the approaches presented here is guaranteed to solve the minimal persistent homology cycle basis problem, the program in Eq. 6. In the case of triangle-loss methods, this is due to the (arbitrary) choice of a total order on simplices. In the case of edge-loss methods, it is due to the choice of an initial persistent homology cycle basis.
In the remainder of this section, we present the eight programs studied, including any modifications from existing work.
4.1 Structural Parameters
Each program addressed in our empirical study may be expressed in the following form
where
1. Chain dimension of x. If
2. Integrality. The program is integral if each
3. Weighting. For each loss type (edge vs. triangle) we consider two possible values for W: identity and non-identity. In the identity case, all edges (or triangles) are weighted equally; we call this a uniform-weighted problem. In the non-identity case we weigh each entry according to some measurement of “size” of the underlying simplex (length, in the case of edges, and area, in the case of triangles).9 There is precedent for such weighting schemes in existing literature (Chen et al., 2008; Dey et al., 2011).
Edge-loss and triangle-loss programs will be denoted
4.2 Edge-Loss Methods
Our approach to edge-loss minimization, based on work by Escolar and Hiraoka (2016), is summarized in Algorithm 1. As in Escolar and Hiraoka (2016), we obtain
Our pipeline differs from Escolar and Hiraoka (2016) in three respects. First, we perform all optimizations after the persistence calculation has run. On the one hand, this means that our persistence calculations fail to benefit from the memory advantages offered by optimized cycles; on the other hand, separating the calculations allows one to “mix and match” one’s favorite persistence solver with one’s favorite linear solver, and we anticipate that this will be increasingly important as new, more efficient solvers of each kind are developed. Second, we introduce additional constraints which guarantee that
The program in Eq. 14 optimizes the jth element of an ordered sequence of cycle representatives
That is, ℙ indexes the set of cycles
With these definitions in place, we now formalize the general edge-loss problem as the program in Eq. 14, where
Recall from Section 4.1 that this program varies along two parameters (integrality and weighting). In integral programs
The program in Eq. 14 may have many more variables than needed, because
A simple means to reduce the size of the program in Eq. 14, therefore, is to replace
4.3 Triangle-Loss Methods
Our approach to triangle-loss optimization is essentially that of Obayashi (2018), plus a preprocessing step that converts more general problem data into the simplex-wise filtration format assumed in Obayashi (2018). There are several noteworthy methods for time and memory performance enhancement developed in Obayashi (2018), which we do not implement (e.g., using restricted neighborhoods
The original method makes the critical assumption that
However, in many applied settings the filtration
To accommodate this more general form of problem data, we employ Algorithm 2. This procedure works by (implicitly) defining a simplex-wise refinement
A key component of Algorithm 2 is the program in Eq. 15, which we refer to as the triangle-loss program.
This terminology is motivated by the special case
Remark 4.1.Algorithm 2 offers an effective means to apply the methods of Obayashi (2018) to some of the most common data sets in TDA. However, this is done at the cost of parameter-dependence; in particular, outputs depend on the choice of linear orders
4.4 Acceleration Techniques
We consider acceleration techniques to reduce the computational costs of the programs in Eqs 14, 15.
4.4.1 Edge-Loss Methods
The technique used for edge-loss problems aims to reduce the number of decision variables in the program in Eq. 14. It does so by replacing a (large) set of decision variables indexed by
4.4.2 Triangle-Loss Methods
When
The difference between these two techniques can be seen as a speed/memory tradeoff. As we will see in Section 6.2, the first approach is generally faster to optimize the entire basis of homology cycle representatives, but when the data set is large, the full boundary matrix
5 Experiments
In order to address the questions raised in Section 1, we conduct an empirical study of minimal homological cycle representatives in dimension one—as defined by the optimization problems detailed in Section 4 — on a collection of point clouds, which includes both real world data sets and point samples drawn from four common probability distributions of varying dimension.
5.1 Real-World Data Sets
We consider 11 real world data sets from Otter et al. (2017), a widely used reference for benchmark statistics concerning persistent homology computations. There are 13 data sets considered by Otter et al. (2017), however, one of them (gray-scale image) is not available, and one of them is a randomly generated data set similar to our own synthetic data. We summarize information about the dimension, number of points, persistence computation time of each point cloud in Table 1. Below we provide brief descriptions of each data set, but we refer the interested reader to Otter et al. (2017) for further details.12
1. Vicsek biological aggregation model. The Vicsek model is a dynamical system describing the motion of particles. It was first introduced in Vicsek et al. (1995) and was analyzed using PH in Topaz et al. (2015). We consider a snapshot in time of a single realization of the model with each point specified by its
2. Fractal networks. These networks are self-similar and are used to explore the connection patterns of the cerebral cortex (Sporns, 2006). The distances between nodes in this data set are defined uniformly at random by Otter et al. (2017). In another data set, the authors of Otter et al. (2017) define distances between nodes by using linear weight-degree correlations. We consider both data sets and found the results to be similar. Therefore, we opt to use the one with distances defined uniformly at random. We denote this data set by Fract R.
3. C.elegans neuronal network. This is an undirected network in which each node is a neuron, and edges represent synapses. It was studied using PH in Petri et al. (2013). Each nonzero edge weight is converted to a distance equal to its inverse by Otter et al. (2017). We denote this data by C.elegans.
4. Genomic sequences of the HIV virus. This data set is constructed by taking
5. Genomic sequences of H3N2. This data set contains
6. Human genome. This is a network representing a sample of the human genome studied using PH in Petri et al. (2013), which was created using data retrieved from Davis and Hu (2011). Distances are measured using Euclidean distance. We denote this data set by Genome.
7. U.S. Congress roll-call voting networks. In the two networks below, each node represents a legislator, and the edge weight is a number in
1. House. This is a weighted network of the House of Representatives from the 104th United States Congress.
2. Senate. This is a weighted network of the Senate from the 104th United States Congress.
8. Network of network scientists. This data set represents the largest connected component of a collaboration network of network scientists (Newman, 2006). The edge weights indicate the number of joint papers between two authors. Distances are defined as the inverse of edge weight. We denote this data set by Network.
9. Klein. The Klein bottle is a non-orientable surface with one side. This data set was created in Otter et al. (2017a) by linearly sampling 400 points from the Klein bottle using its “figure 8” immersion in
10. Stanford Dragon graphic. This data set contains 1,000 points sampled uniformly at random by Otter et al. (2017) from 3-dimensional scans of the dragon (Stanford University Computer Graphics Laboratory, 1999). Distances are measured using the Euclidean distance. We denote this data set Drag.
5.2 Randomly Generated Point Clouds
We also generate a large corpus of synthetic point clouds, each containing 100 points in
5.3 Erdős-Rényi Random Complexes
To investigate which properties of homological cycle representatives could arise as the result of the underlying geometry of the point clouds, we also consider a common non-geometric model for random complexes: Erdős-Rényi random clique complexes. Here, we construct 100 symmetric dissimilarity matrices of size
5.4 Computations
For each of the data sets, we perform Algorithms 1, 2 (using Vietoris-Rips complexes with
5.5 Hardware and Software
We test our programs on an iMac (Retina 5K, 27-inch, 2019) with a 3.6 GHz Intel Core i9 processor and 40 GB 2667 MHz DDR4 memory.
Software for our experiments is implemented in the programming language Julia; source code is available at Li and Thompson (2021). This code specifically implements Algorithms 1, 2 and the program in Eq. 8.13
Since our interest lies not only with the outputs of these algorithms but with the structure of the linear programs themselves Li and Thompson (2021), implements a standalone workflow that exposes the objects built internally within each pipeline. This library is simple by design, and does not implement the performance-enhancing techniques developed in Escolar and Hiraoka (2016) and Obayashi (2018). Users wishing to work with optimal cycle representatives for applications may consider these approaches discussed in Section 3.7.
To implement Algorithms 1, 2 in homological dimension one, the test library (Li and Thompson, 2021) provides three key functions: A novel solver for persistence with
Formatting of Inputs to Linear Programs. Having computed barcodes and persistent homology cycle representatives, library (Li and Thompson, 2021) provides built-in functionality to format the linear the program in Eqs 14, 15 for input to a linear solver. This “connecting” step is executed in pure Julia.
Wrappers for Linear Solvers. We use the Gurobi linear solver (Gurobi Optimization, 2020) and the GLPK solver (GNU Project, 2012). Both solvers can optimize both LPs and MIPs. Experiments indicate that Gurobi executes much faster than GLPK on this class of problems, and thus, we use it in the bulk of our computations. Both solvers are free for academic users.
6 Results and Discussion
In this section, we investigate each of the questions raised in Section 1 with the following analyses.
6.1 Computation Time Comparisons
We summarize results for Programs EdgeNIUnif, EdgeIUnif, EdgeNILen, EdgeILen, TriNIUnif, and TriIUnif in Table 1 for data described in Section 5.1 and Table 2 for data described in Section 5.2 and Section 5.3. Further, we summarize results for Programs TriNIArea and TriIArea in Table 2 for data described in Section 5.2.14 We use
The two numbers in parenthesis in the third row of Table 1 indicate the actual number of representatives we were able to optimize using the triangle-loss methods (all edge-loss representatives were optimized). For the Genome and H3N2 data sets, we are not able to compute all triangle-loss cycle representatives due to the large number of 2-simplices born between the birth and death interval of some cycles. For instance, for a particular cycle representative in the Genome data set, there were 10,522,991 2-simplices born in this cycle’s lifespan. Also, given the large number of 2-simplices in the simplicial complex, we are not able to build the full
Below we describe some insights on computation time drawn from the two tables.
6.1.1 Persistence and Optimization
We observe that
This somewhat surprising result highlights the computational complexity of the algorithms used both to compute persistence and to optimize generators. A common feature of both the persistence computation and linear optimization is that empirical performance typically outstrips asymptotic complexity by a wide margin; the persistence computation, for example, has cubic complexity in the size of the complex, but usually runs in linear time. Thus, worst-case complexity paints an incomplete picture. Moreover, naive “back of the envelope” calculations are often hindered by lack of information. For example, the persistence computation (which essentially reduces to Gaussian elimination) typically processes each of the m columns of a boundary matrix
6.1.2 Integral and Nonintegral Programs
In Tables 1 and 2, we observe that
Let
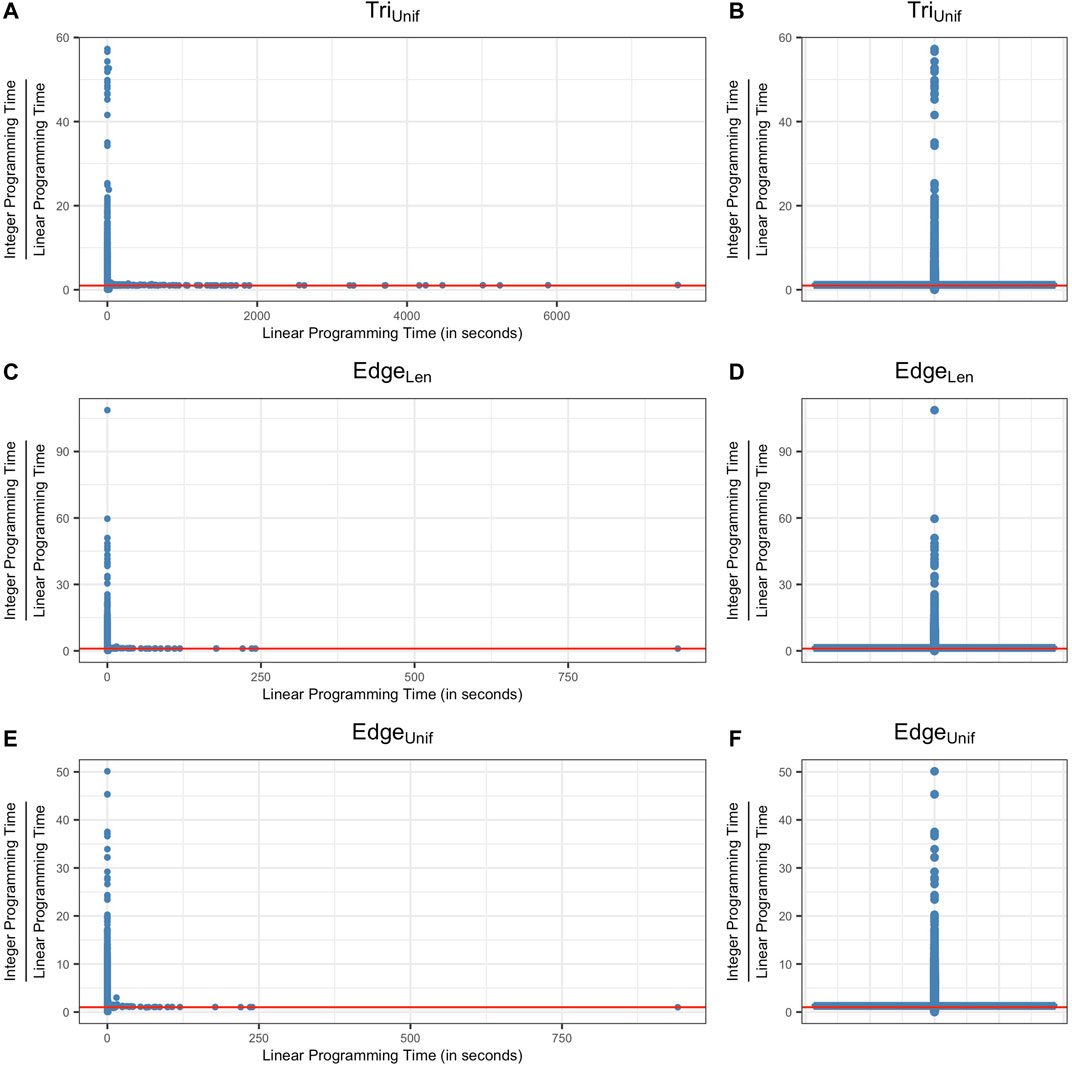
FIGURE 6. Ratio between the computation time of solving an integer programming problem (Programs TriIUnif, EdgeILen, EdgeNIUnif) and the computation time of solving a linear programming problem (Programs TriNIUnif, EdgeNILen, EdgeNIUnif) for all of the cycle representatives from data sets described in Sections 5.1, 5.2 and 5.3. Subfigures (A) (C) (E) plot the data using scatter plots and subfigures (B) (D) (F) show the same data using box plots. The vertical axis represents the ratio between the integer programming time and linear programming time of optimizing a cycle representative and the horizontal axis represents the computation time to solve the linear program. The red line in each subfigure represents the horizontal line y = 1, where the time for each optimization is equivalent. As we can see from the box plots, the ratio between the computation time of integer programming and linear programming for most of the cycle representatives (>50%) center around 1.
6.1.3 Triangle-Loss Vs. Edge-Loss Programs
We observe that the edge-loss optimal cycles are more efficient to compute than the triangle-loss cycles for more than
6.1.4 Different Linear Solvers
The choice of linear solver can significantly impact the computational cost of the optimization problems. We perform experiments on length/uniform-minimal cycle representatives using the GLPK (GNU Project, 2012; Gurobi Optimization, 2020) linear solvers on 90 data sets drawn from the normal distribution with dimensions from 2 to 10 with a total of
6.2 Performance of Acceleration Techniques
6.2.1 Edge-Loss Optimal Cycles
As discussed in Section 4.4, we accelerate edge-loss problems by replacing
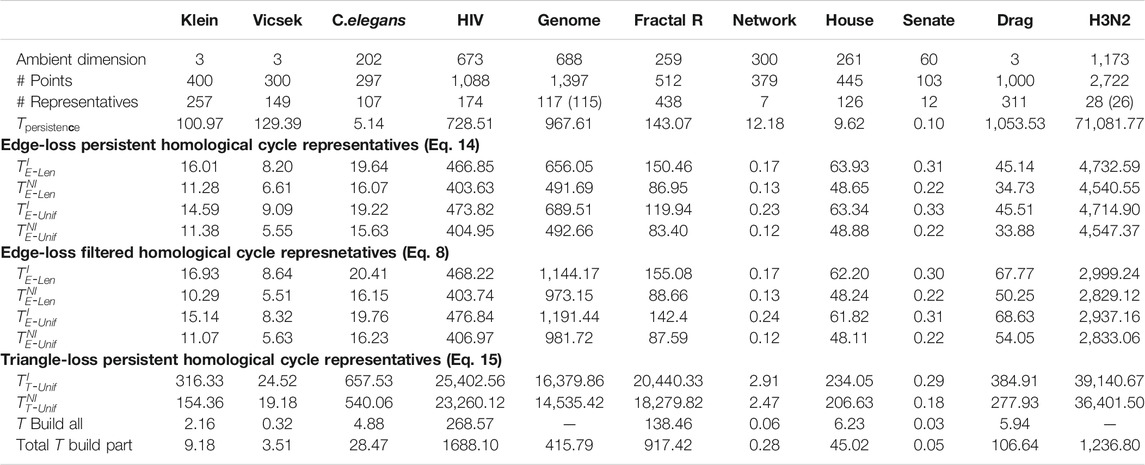
TABLE 1. Summary of the experimental results of the data sets from Otter et al. (2017) as described in Section 5.1. The rows include the ambient dimension, number of points, the number of cycle representatives in
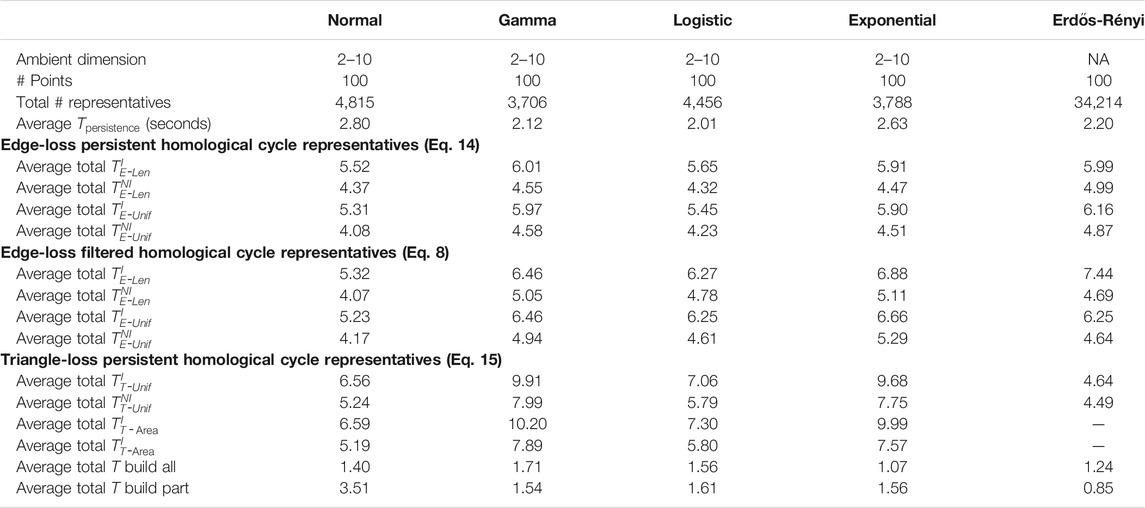
TABLE 2. Summary of the experimental results for the synthetic, randomly generated data sets described in Section 5.2 and Section 5.3. For each distribution, we sample 10 data sets each containing 100 points in ambient dimensions from 2–10. The computation time in this table averages the 10 random samples for each dimension and distribution combination. The number of cycle representatives is totaled over the 90 samples for each distribution. The rows of this table are analogous to those of Table 1, excluding the penultimate row of that table, as the time comparison is only done for the large real-world data sets.
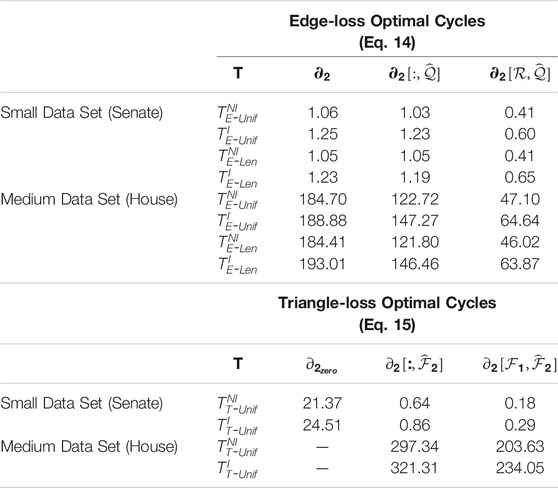
TABLE 3. Computation time of three differently sized input boundary matrices to edge-loss and triangle-loss methods. The superscripts denote whether the program requires an integral solution or not, and the subscripts indicate the type of optimal cycle. All time is measured in seconds. We perform experiments on a small-sized data set (Senate) that consists of 103 points in dimension 60 and a medium-sized data set (House) that contains 445 points in dimension 261. For edge-loss methods, we consider three implementations to solve these optimization problems: using the full boundary matrix
6.2.2 Triangle-Loss Optimal Cycles
As discussed in Section 4.4, there are also multiple approaches to creating the input to the triangle-loss problems. To recap, we restrict the boundary matrix
In Table 3, we summarize the computation time of solving Programs
We also ran experiments on the real-world data sets to compare the timing of building
6.3 Coefficients of Optimal Cycle Representatives in Data Sets From Section 5.1 and Section 5.2
As discussed in Section 3.6, the problem of solving an
We find that
We then systematically check each solution of the eight programs
All optimal solutions to the program in Eq. 8 (edge-loss minimization of filtered cycle bases) and all but one of the solutions returned by Algorithm 1 (edge-loss minimization of persistent cycle bases) had coefficients in
On the one hand, this exceptional behavior could bear some connection to Algorithm 1. Recall that Algorithm 1 operates by removing a sequence of cycles from a cycle basis, replacing each cycle with a new, optimized cycle on each iteration (that is, we swap the
When solving the integral triangle-loss problem by Algorithm 2, we obtain two solutions whose boundaries x = ∂2v have coefficients in {-1,0,1,2} for two different cycle representatives from the logistic distribution data set. However, the corresponding solutions v of these cycle representatives do have coefficients in {-1,0,1}.
The surprising predominance of solutions in
6.4 Comparing Optimal Cycle Representatives Against Different Loss Functions
We compare the optimal cycle representatives against different loss functions to study the extent to which the solutions produced by each technique vary. We consider two loss functions on an
where
the number of 1-simplices (edges) in a representative.
We also consider two loss functions on 2-chains
where
Remark 6.1. These weighted
where, by convention,
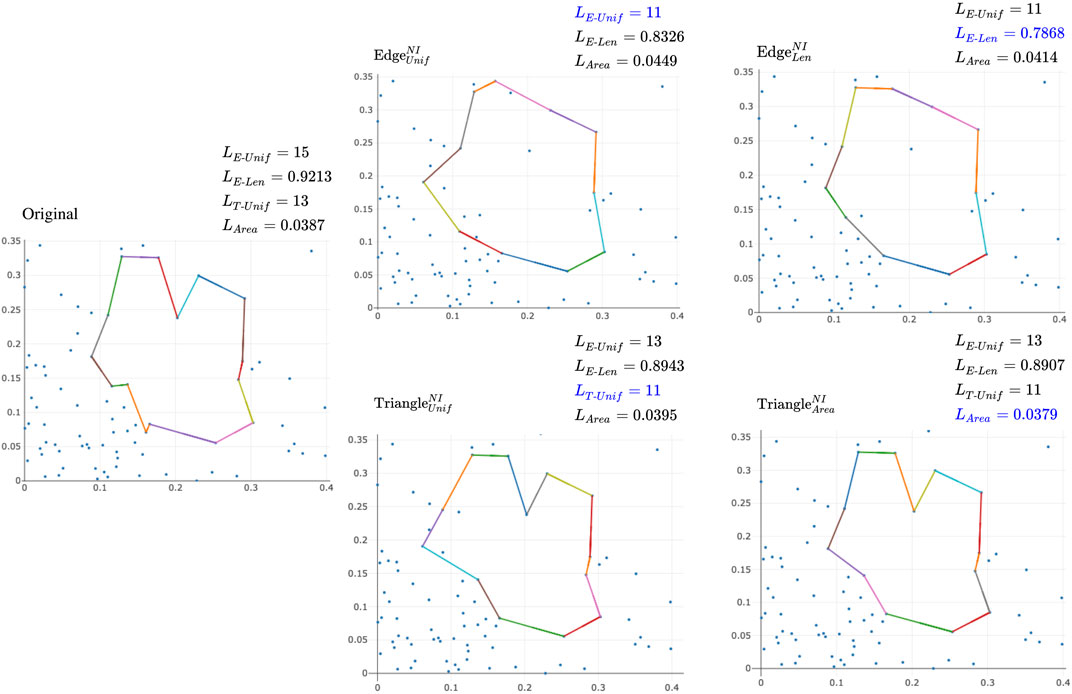
FIGURE 7. Examples of different optimal cycles and cost against different loss functions using a point cloud of 100 points with ambient dimension two randomly drawn from a normal distribution. The upper left corner of each subfigure labels the optimization algorithm used to optimize the original cycle representative. The upper right corner of each subfigure records the different measures of the size of the optimal representative. Blue text represents the measure an algorithm sets out to optimize.
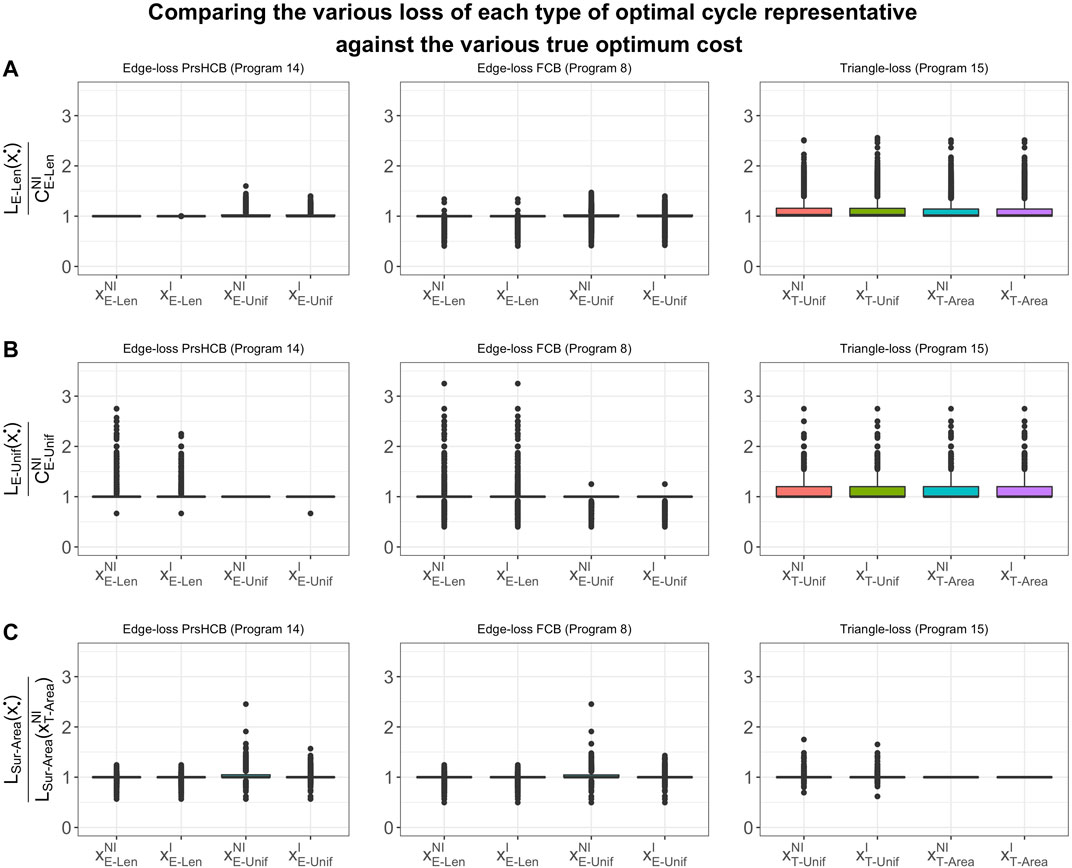
FIGURE 8. Box plots of the ratios between (A)
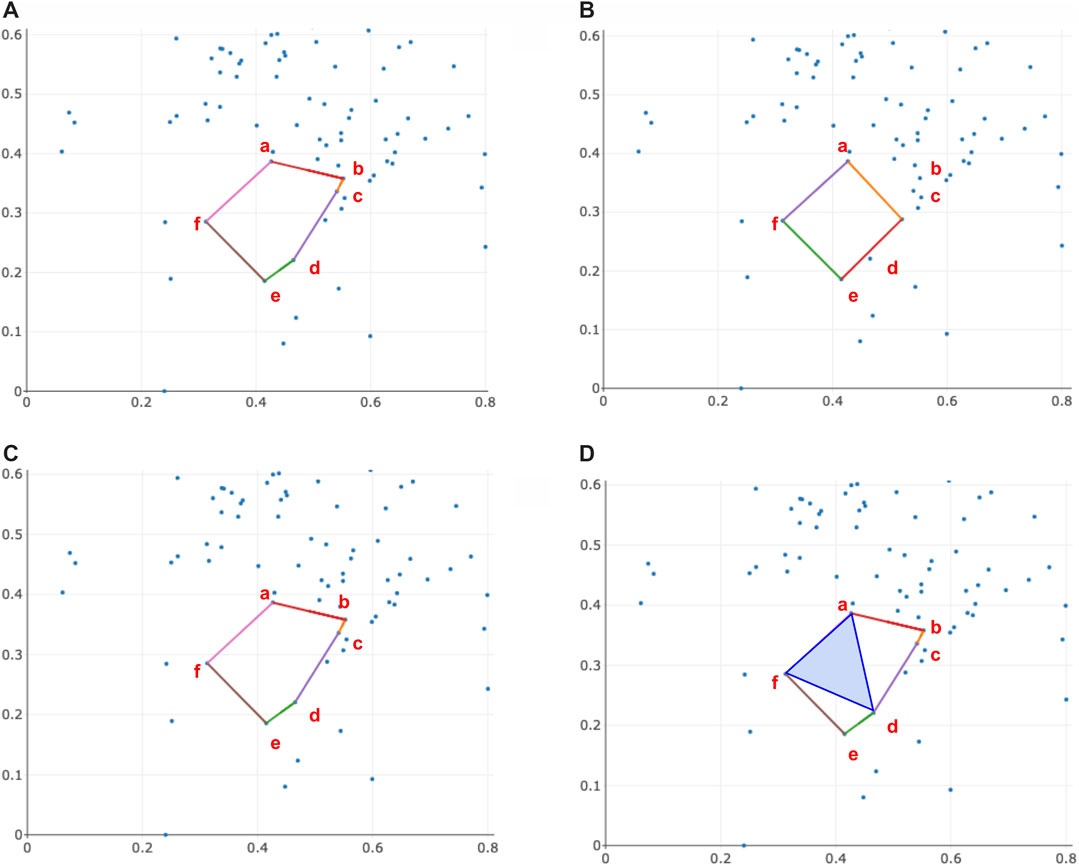
FIGURE 9. An example illustrating when the area enclosed by the triangle-loss area-weighted optimal cycle, solution to Program
6.5 Comparative Performance and Precision of LP Solvers
Our experiments demonstrate that the choice of linear solver may impact speed, frequency of obtaining integer solutions, and frequency of obtaining
As discussed in Section 6.1, the GLPK solver performs much slower than the Gurobi solver in an initial set of experiments. The GLPK solver also finds non-integral solutions when solving a linear programming problem in Programs
6.6 Statistical Properties of Optimal Cycle Representatives With Regard to Various Other Quantities of Interest
6.6.1 Support of a Representative Forming a Single Loop in the Underlying Graph
The support of the original cycle,
We are interested in exploring how often the support of an original cycle representative forms a single loop in the underlying graph. We analyze each of the 360 synthetic data sets of various dimensions and distributions discussed in Section 5.2 as well as the 100 Erdős-Rényi random complexes discussed in Section 5.3 and display the results in Figure 10. We find that the majority of the original cycle representatives have one loop. After optimizing these cycle representatives with the edge-loss methods, we verify that all
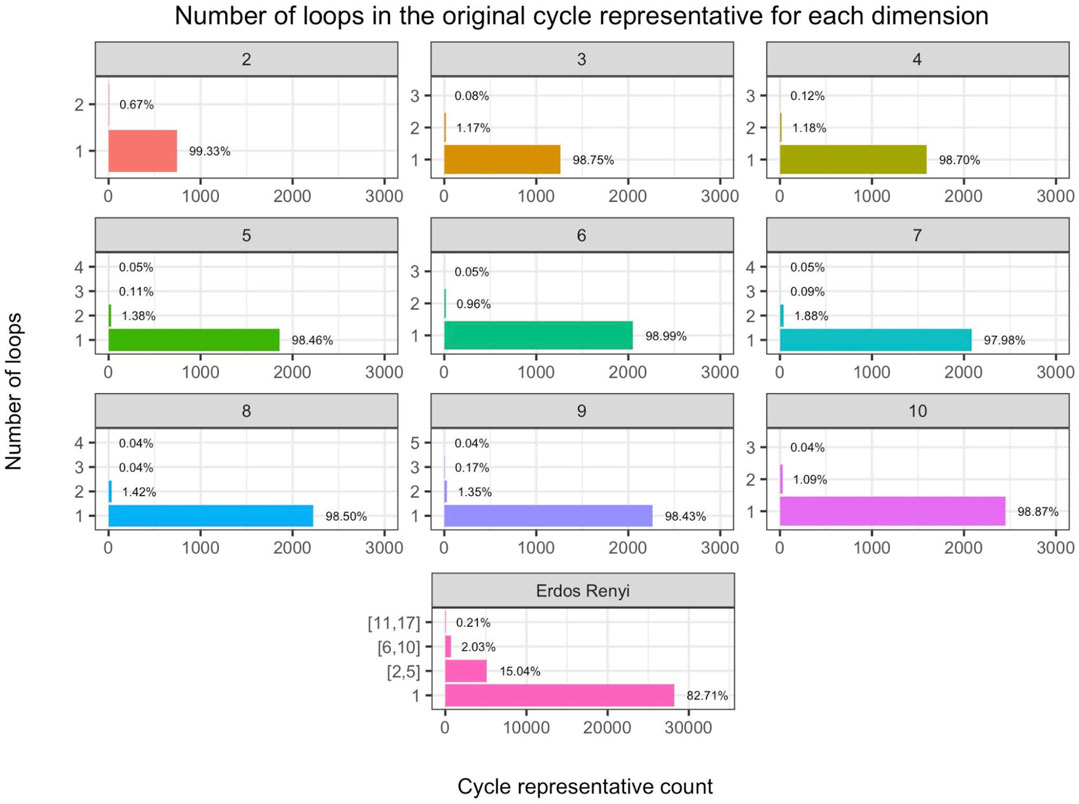
FIGURE 10. (Rows 1–3) Number of loops in the original cycle representative aggregated by dimension (labeled by subfigure title) in the 360 randomly generated distribution data sets discussed in Section 5.2 and (Row 4) same for the Erdős-Rényi random complexes discussed in Section 5.3, where we bin cycle representatives that have two to five loops, 6–10, loops, or more than 10 loops. The horizontal axis is the number of cycle representatives and the vertical axis is the number of loops in the original representative. We observe that for the distribution data, an original cycle representative can have up to 5 loops in higher dimensions, and in general, it is uncommon to find an original representative with multiple loops. However, we observe that
As shown in Figure 11 the reduction in size of the original cycle, formalized as
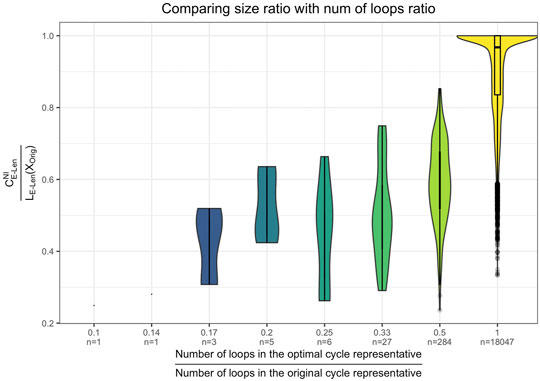
FIGURE 11. Violin plot of the effectiveness of the optimization as a function of the number of loops in the original cycle representative. Results are aggregated over the data sets from Section 5.1 and Section 5.2. The x-axis shows the size reduction in terms of number of loops, and the y-axis shows the size reduction in terms of the length of the cycle. We see that in general, the reduction in size of the original cycle mostly comes from the reduction in the number of loops by the optimization.
6.6.2 Overall Effectiveness of Optimization
We compare the optimal representatives against the original cycle representatives21 with respect to edge-loss functions
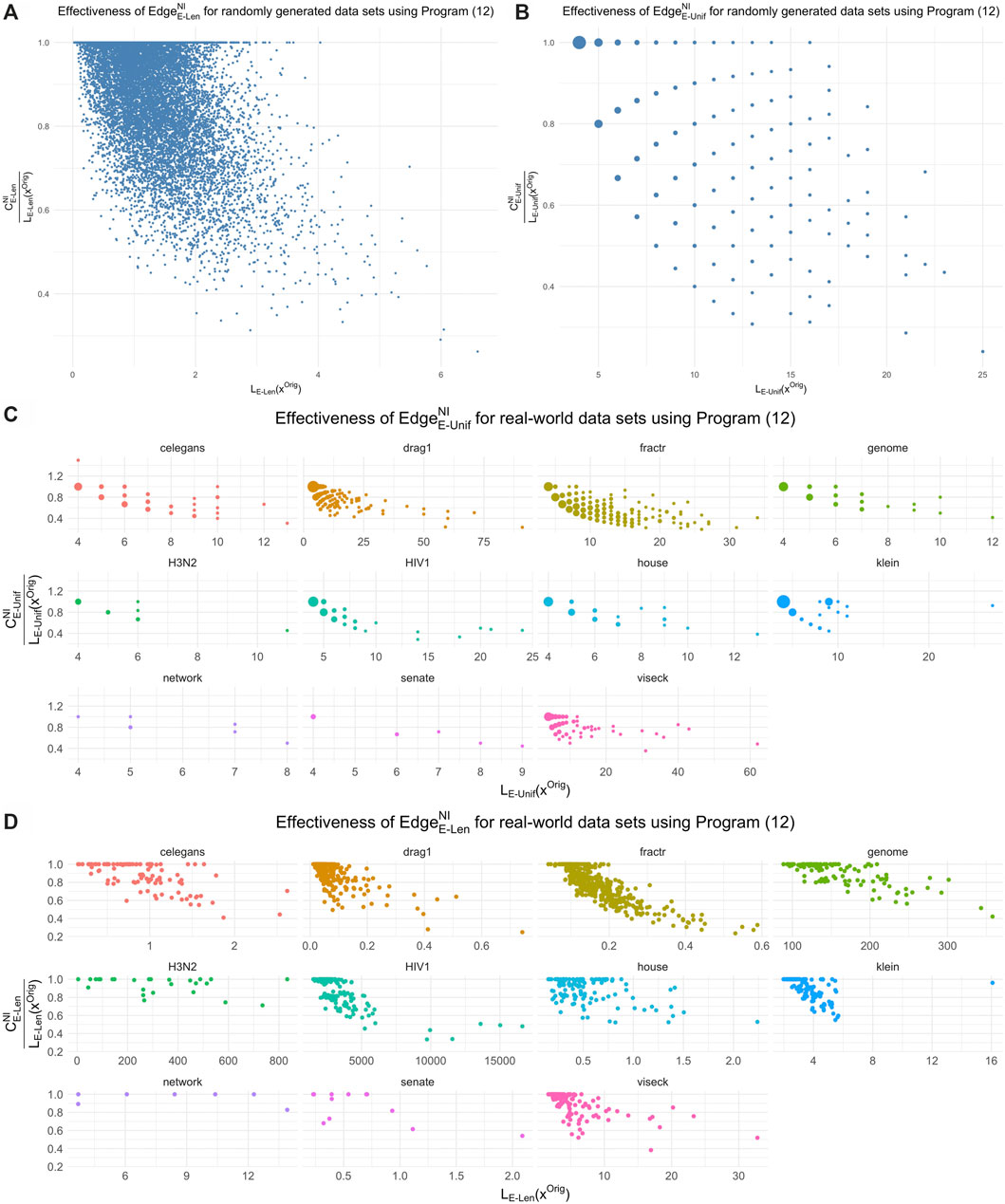
FIGURE 12. The effectiveness of length-weighted and uniform-weighted optimization for the data sets in Sections 5.1 and 5.2 in reducing the size of the original cycle representative found by the persistence algorithm. In each subfigure, the horizontal axis is the size of the original representative and the vertical axis is the ratio between the size of the optimal representative and the size of the original representative. The uniform-weighted graphs appear more sparse because reductions in the cost
The average ratio
6.6.3 Comparing Solutions to Integral Programs and Non-Integral Programs
Among all cycle representatives found by solving the program in Eq. 14,
6.6.4 Cycle Representative Size for Different Distributions and Dimensions
Figure 13 provides a summary of the size and number of cycle representatives found for each distribution data set described in Section 5.2. We observe that there tend to be more and larger (with respect to
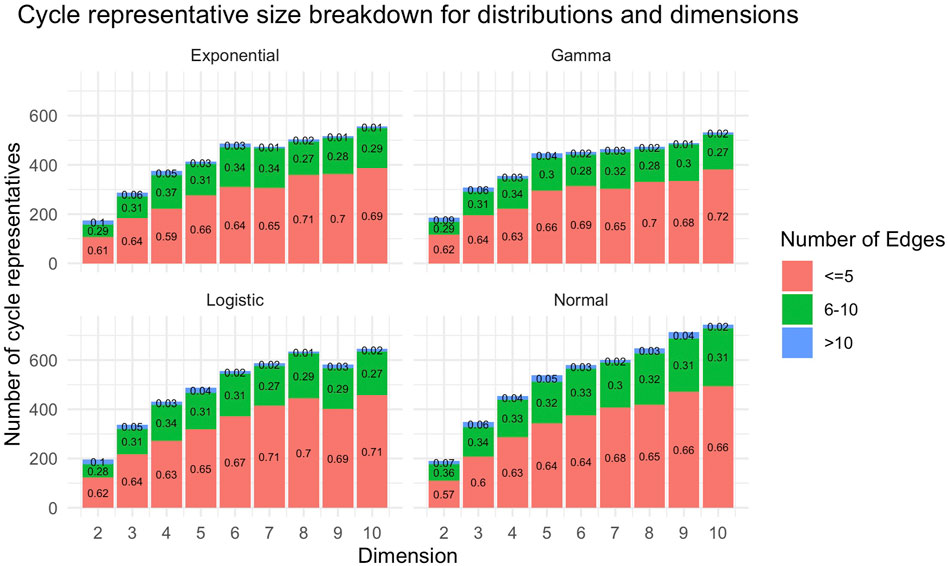
FIGURE 13. The number of original cycle representatives and the number of edges within each original representative for data described in Section 5.2. These plots aggregate all cycle representatives for each dimension of a particular distribution. The horizontal axis for each subplot is the dimension of the data set, and the vertical axis is the number of cycle representatives found in each dimension. In general, we see there are more cycle representatives in higher dimensional data sets. Each bar is partitioned by the number of edges of the representative. We observe that as dimension increases, there tend to be more cycle representatives with more edges.
6.6.5 Duplicate Intervals in the Barcode
Of all data sets analyzed, only Klein and C.elegans have barcodes in which two or more intervals had equal birth and death times (that is, bars with multiplicity
Among the 257 total intervals of the Klein data set, there are 179 unique intervals, 1 interval that is repeated twice, and two intervals that are repeated 38 times. For the Klein data set, if we replace the distance matrix provided by Otter et al. (2017) with the Euclidean distance matrix calculated using Julia (the maximum difference between the two matrices is on the scale of
6.6.6 Edge-Loss Cycle Representatives
We find that for
6.7 Optimal Cycle Representatives for Erdős-Rényi Random Clique Complexes
We observe qualitatively different behavior in cycle representatives from the Erdős-Rényi random clique complexes. Among the
We find
Because of the non-integrality of some original cycle representatives found by the persistence algorithm, we fail to find an integral solution for
A partial explanation for this behavior can be found in the work of (Costa et al., 2015). Here, the authors show that a connected two-dimensional simplicial complex for which every subcomplex has fewer than three times as many edges as vertices must have the homotopy type of a wedge of circles, 2-spheres, and real projective planes. With high probability, certain ranges of thresholds for the i.i.d. dissimilarity matrices on which the Erdős-Rényi random complexes are built produces random complexes with approximately such density patterns at each vertex. Thus, some of the persistent cycles are highly likely to correspond to projective planes. Because of their non-orientability, the corresponding minimal generators could be expected to have entries outside of the range
7 Conclusion
In this work, we provide a theoretical, computational, and empirical user’s guide to optimizing cycle representatives against four criteria of optimality: total length, number of edges, internal volume, and area-weighted internal volume. Utilizing this framework, we undertook a study on statistical properties of minimal cycle representatives for
1. We developed a publicly available code library (Li and Thompson, 2021) to compute persistent homology with rational coefficients, building on the software package Eirene (Henselman and Ghrist, 2016) and implemented and extended algorithms from (Escolar and Hiraoka, 2016; Obayashi, 2018) for computing minimal cycle representatives. The library employs standard linear solvers (GLPK and Gurobi) and implements various acceleration techniques described in Section 4.4 to make the computations more efficient.
2. We formulated specific recommendations concerning procedural factors that lie beyond the scope of the optimization problems per se (for example, the process used to generate inputs to a solver) but which bear directly on the overall cost of computation, and of which practitioners should be aware.
3. We used this library to compute optimal cycle representatives for a variety of real-world data sets and randomly generated point clouds. Somewhat surprisingly, these experiments demonstrate that computationally advantageous properties are typical for persistent cycle representatives in data. Indeed, we find that we are able to compute uniform/length-weighted optimal cycles for all data sets we considered, and that we are able to compute triangle-loss optimal cycles for all but six cycle representatives, which fail due to the large number of triangles (more than 20 million) used in the optimization problem. Computation time information is summarized in Table 1 and Table 2.
Consequently, heuristic techniques may provide efficient means to extract solutions to cycle representative optimization problems across a broad range of contexts. For example, we find that edge-loss optimal cycles are faster to compute than triangle-loss optimal cycles for cycle representatives with a longer persistence interval, whereas for cycles with shorter persistence intervals, the triangle-loss cycle can be less computationally expensive to compute.
4. We provided statistics on various minimal cycle representatives found in these data, such as their effectiveness in reducing the size of the original cycle representative found by the persistence algorithm and their effectiveness evaluated against different loss functions. In doing so, we identified consistent trends across samples that address the questions raised in Section 1.
a. Optimal cycle representatives are often significant improvements in terms of a given loss function over the initial cycle representatives provided by persistent homology computations (typically, by a factor of 0.3–1.0). Interestingly, we find that area-weighted triangle-loss optimal cycle representatives can enclose a greater area than length- or uniform-weighted optimal cycle representatives.
b. We find that length-weighted edge-loss optimal cycles are also optimal with respect to a uniform-weighted edge-loss function upwards of
c. Strikingly, all but one
Several questions lie beyond the scope of this text and merit future investigation. For example, while the methods discussed in Section 4 apply equally to homology in any dimension, we have focused our empirical investigation exclusively in dimension one; it would be useful and interesting to compare these results with homology in higher dimensions. It would likewise be interesting to compare with different weighting strategies on simplices, and loss functions other than
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/TDAMinimalGeneratorResearch/minimal-generator.
Author Contributions
GH-P wrote the Eirene code. LL and CT wrote the rest of the code and performed all experiments. LL created all figures and tables. GH-P and LZ designed, directed, and supervised the project. GH-P developed the theory in the Supplementary Material. All authors contributed to the analysis of the results and to the writing of the manuscript.
Funding
This material is based upon work supported by the National Science Foundation under grants no. DMS-1854683, DMS-1854703, and DMS-1854748. GH-P is a member of the Centre for Topological Data Analysis, supported by the EPSRC grant New Approaches to Data Science: Application Driven Topological Data Analysis EP/R018472/1.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to David Turner for helpful advice on selection of linear solvers. They also thank and acknowledge the initial work done by Robert Angarone and Sophia Wiedemann on this study.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frai.2021.681117/full#supplementary-material
Footnotes
1The
2See Remark 2.1 These choices of groups have a natural notion of absolute value.
3More generally, we denote the groups of cycles and boundaries with coefficients in G as
4Because of the assumption that
5This notion of volume differs from that of Chen and Freedman (2010b). The latter refers to volume as the
6If we regard
7Technically, this notion is not well-defined; to be formal, we should fix a persistent homology cycle basis
8Other choices of loss function, e.g., the
9These notions make sense due to our use of coefficient field
10Recall volume is undefined for infinite intervals.
11We compute the area of a 2-simplex using Heron’s Formula. We calculate area only for VR complexes whose vertices are points in Euclidean space, though more general metrics could also be considered.
12We use the distance matrices found on the associated github page (Otter et al., 2017b), except in two cases. For the Vicsek data, we use a distance to account for the intended periodic boundary conditions of the model, and for the genome data, we use Euclidean distance as the distance matrix in Otter et al. (2017b) resulted in an integer overflow error.
13The program in Eq. 8 is implemented analogously.
14We compute the area of a 2-simplex using Heron’s Formula for data whose distances are measured using the Euclidean distance. For data with non-Euclidean distances, we find that there are triangles that do not obey the triangle inequality, thus, we only compute area-weighted triangle-loss cycles for data described in Section 5.2. As such, TriNIArea, TriNIArea do not appear in Table 1 and the Erős‐Rényi column of Table 2.
15Including the time of constructing the input to the optimization programs.
16Obayashi (2018) proposes a few techniques for accelerating the triangle-loss methods which we did not implement.
17We discuss the coefficients of the Erdős-Rényi complexes of Section 5.3 in Section 6.7.
18Recall that, in the current discussion,
19We formulated an Obayashi-style linear program similar to Program in Eq. 15 to compute the volume of edge-loss optimal cycles but in many cases it had no feasible solution.
20Recall, we only compute
21The remainder of this subsection excludes the Erdős-Rényi cycles.
References
Bendich, P., Marron, J. S., Miller, E., Pieloch, A., and Skwerer, S. (2016). Persistent Homology Analysis of Brain Artery Trees. Ann. Appl. Stat. 10, 198–218. doi:10.1214/15-AOAS886
Bertsimas, D., and Tsitsiklis, J. (1997). Introduction to Linear Optimization. (Belmont, MA: Athena Scientific).
Bhaskar, D., Manhart, A., Milzman, J., Nardini, J. T., Storey, K. M., Topaz, C. M., et al. (2019). Analyzing Collective Motion with Machine Learning and Topology. Chaos: Interdiscip. J. Nonlinear Sci. 29, 123125. doi:10.1063/1.5125493
Bhattacharya, S., Ghrist, R., and Kumar, V. (2015). Persistent Homology for Path Planning in Uncertain Environments. IEEE Trans. Robotics 31, 578–590. doi:10.1109/TRO.2015.2412051
Borradaile, G., Maxwell, W., and Nayyeri, A. (2020). “Minimum Bounded Chains and Minimum Homologous Chains in Embedded Simplicial Complexes,” in 36th International Symposium on Computational Geometry (SoCG 2020). Leibniz Int. Proc. Informatics 21, 21:1–21:15.
Boyd, S., and Vandenberghe, L. (2004). Convex Optimization. Belmont, MA: Cambridge University Press.
Braden, B. (1986). The Surveyor’s Area Formula. Coll. Math. J. 17, 326–337. doi:10.1080/07468342.1986.11972974
Brüel-Gabrielsson, R., Ganapathi-Subramanian, V., Skraba, P., and Guibas, L. J. (2020). Topology-aware Surface Reconstruction for point Clouds. Comput. Graphics Forum 39, 197–207. doi:10.1111/cgf.14079
Chan, J. M., Carlsson, G., and Rabadan, R. (2013). Topology of Viral Evolution. Proc. Natl. Acad. Sci. 110, 18566–18571. doi:10.1073/pnas.1313480110
Chen, C., and Freedman, D. (2010a). Measuring and Computing Natural Generators for Homology Groups. Comput. Geometry 43, 169–181. doi:10.1016/j.comgeo.2009.06.004
Chen, C., and Freedman, D. (2010b). “Hardness Results for Homology Localization,” in SODA ’10: Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms. USA: Society for Industrial and Applied Mathematics).
Chen, C., and Freedman, D. (2008). “Quantifying Homology Classes. Albers S,” in 25th International Symposium On Theoretical Aspects Of Computer Science. (Dagstuhl, Germany: Schloss Dagstuhl–Leibniz-Zentrum Fuer Informatik). Editor P. Weil, 1, 169–180. doi:10.4230/LIPIcs.STACS.2008.1343
Cohen-Steiner, D., Edelsbrunner, H., and Morozov, D. (2006). “Vines and Vineyards by Updating Persistence in Linear Time,” in Proceedings of the Twenty-Second Annual Symposium on Computational Geometry, 119–126.
Costa, A., Farber, M., and Horak, D. (2015). Fundamental Groups of Clique Complexes of Random Graphs. Trans. Lond. Math. Soc. 2, 1–32. doi:10.1112/tlms/tlv001
Davis, T. A., and Hu, Y. (2011). The university of florida Sparse Matrix Collection. ACM Trans. Math. Softw. 38, 1–25. doi:10.1145/2049662.2049663
Dey, T. K., Sun, J., and Wang, Y. (2010). “Approximating Loops in a Shortest Homology Basis from point Data,” in SoCG ’10: Proceedings of the Twenty-Sixth Annual Symposium on Computational Geometry. (New York, NY, USA: Association for Computing Machinery), 166–175. doi:10.1145/1810959.1810989
Dey, T. K., Hirani, A. N., and Krishnamoorthy, B. (2011). Optimal Homologous Cycles, Total Unimodularity, and Linear Programming. SIAM J. Comput. 40, 1026–1044. doi:10.1137/100800245
Dey, T. K., Li, T., and Wang, Y. (2018). ”Efficient Algorithms for Computing a Minimal Homology Basis,” in Latin American Symposium on Theoretical Informatics. Springer, 376–398.
Dey, T. K., Hou, T., and Mandal, S. (2019). “Persistent 1-cycles: Definition, Computation, and its Application,” in International Workshop on Computational Topology in Image Context. Málaga, Spain: Springer, 123–136.
Edelsbrunner, H., and Harer, J. (2008). Persistent Homology–A Survey. Discrete Comput. Geometry - DCG 453, 257–282. doi:10.1090/conm/453/08802
Edelsbrunner, H., and Harer, J. (2010). Computational Topology: An Introduction. Providence, RI: Applied Mathematics (American Mathematical Society).
Emmett, K., Schweinhart, B., and Rabadan, R. (2015). Multiscale Topology of Chromatin Folding. arXiv preprint arXiv:1511.01426.
Erickson, J., and Whittlesey, K. (2009). “Greedy optimal homotopy and homology generators. SODA 5, 1038–1046.
Escolar, E. G., and Hiraoka, Y. (2016). “Optimal Cycles for Persistent Homology via Linear Programming,” in Optimization in the Real World. Tokyo: Springer, 79–96.
Escolar, E., and Hiraoka, Y. (2021). OptiPersLP - optimal cycles in persistence via linear programming. Available at: https://bitbucket.org/remere/optiperslp/src/master/.
Ghrist, R. (2008). Barcodes: the Persistent Topology of Data. Bull. Am. Math. Soc. 45, 61–75. doi:10.1090/s0273-0979-07-01191-3
Ghrist, R. (2014). Elementary Applied Topology. (Seattle: CreateSpace Independent Publishing Platform).
Giusti, C., Ghrist, R., and Bassett, D. S. (2016). Two’s Company, Three (Or More) Is a Simplex. J. Comput. Neurosci. 41, 1–14.
Hatcher, A., and Press, C. U. of Mathematics CUD (2002). Algebraic Topology. Algebraic Topology. Cambridge, UK: Cambridge University Press.
Henselman, G., and Dłotko, P. (2014). “Combinatorial Invariants of Multidimensional Topological Network Data,” In IEEE Global Conference on Signal and Information Processing (GlobalSIP). IEEE, 828–832.
Henselman, G., and Ghrist, R. (2016). Matroid Filtrations and Computational Persistent Homology. Available at: http://adsabs.harvard.edu/abs/2016arXiv160600199H (Accessed May, 2021).
Henselman-Petrusek, G. (2016). Eirene (Julia Library for Computational Persistent Homology). Available at: https://github.com/Eetion/Eirene.jl (Accessed May, 2021). Commit 4f57d6a0e4c030202a07a60bc1bb1ed1544bf679.
Hiraoka, Y., Nakamura, T., Hirata, A., Escolar, E. G., Matsue, K., and Nishiura, Y. (2016). Hierarchical Structures of Amorphous Solids Characterized by Persistent Homology. Proc. Natl. Acad. Sci. 113, 7035–7040. doi:10.1073/pnas.1520877113
Kovacev-Nikolic, V., Bubenik, P., Nikolić, D., and Heo, G. (2016). Using Persistent Homology and Dynamical Distances to Analyze Protein Binding. Stat. App. Genet. Mol Biol. 15, 19–38. doi:10.1515/sagmb-2015-0057
Li, L., and Thompson, C. (2021). Source Code, Minimal Cycle Representatives In Persistent Homology Using Linear Programming: An Empirical Study With User’s Guide. Available at: https://github.com/TDAMinimalGeneratorResearch/minimal-generator (Accessed May, 2021).
Los Alamos National Laboratory (2021). HIV Database. Available at: http://www.hiv.lanl.gov/content/index.
McGuirl, M. R., Volkening, A., and Sandstede, B. (2020). Topological Data Analysis of Zebrafish Patterns. Proc. Natl. Acad. Sci. 117, 5113–5124. doi:10.1073/pnas.1917763117
Milosavljević, N., Morozov, D., and Skraba, P. (2011). “Zigzag Persistent Homology in Matrix Multiplication Time,” in SoCG ’11: Proceedings of the Twenty-Seventh Annual Symposium on Computational Geometry. New York, NY, USA: Association for Computing Machinery), 216–225. doi:10.1145/1998196.1998229
Newman, M. E. (2006). Finding Community Structure in Networks Using the Eigenvectors of Matrices. Phys. Rev. E 74, 036104. doi:10.1103/physreve.74.036104
Obayashi, I., Wada, T., Tunhua, T., Miyanaga, J., and Hiraoka, Y. (2021). HomCloud: Data Analysis Software Based on Persistent Homology). Available at: https://homcloud.dev/.
Obayashi, I. (2018). Volume-optimal Cycle: Tightest Representative Cycle of a Generator in Persistent Homology. SIAM J. Appl. Algebra Geometry 2, 508–534.
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., and Harrington, H. A. (2017a). A Roadmap for the Computation of Persistent Homology. EPJ Data Sci. 6, 17. doi:10.1140/epjds/s13688-017-0109-5
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., and Harrington, H. A. (2017b). A Roadmap for the Computation of Persistent Homology. Available at: https://github.com/n-otter/PH-roadmap
Petri, G., Scolamiero, M., Donato, I., and Vaccarino, F. (2013). Topological Strata of Weighted Complex Networks. PloS one 8, e66506. doi:10.1371/journal.pone.0066506
Schweinhart, B. (2015). Statistical Topology of Embedded Graphs. Ph.D. thesis. Princeton, NJ: Princeton University.
Singh, G., Mémoli, F., and Carlsson, G. E. (2007). Topological Methods for the Analysis of High Dimensional Data Sets and 3d Object Recognition. SPBG 91, 100. doi:10.2312/SPBG/SPBG07/091-100
Sizemore, A. E., Phillips-Cremins, J. E., Ghrist, R., and Bassett, D. S. (2019). The Importance of the Whole: Topological Data Analysis for the Network Neuroscientist. Netw. Neurosci. 3, 656–673. doi:10.1162/netn_a_00073
Sporns, O. (2006). Small-world Connectivity, Motif Composition, and Complexity of Fractal Neuronal Connections. Bio. Syst. 85, 55–64. doi:10.1016/j.biosystems.2006.02.008
Stanford University Computer Graphics Laboratory (1999). The Stanford 3D Scanning Repository. (Accessed May, 2021).
Tahbaz-Salehi, A., and Jadbabaie, A. (20082008). Distributed Coverage Verification in Sensor Networks without Location Information. IEEE Conf. Decis. Control., 4170–4176. doi:10.1109/CDC.2008.4738751
Tahbaz-Salehi, A., and Jadbabaie, A. (2010). Distributed Coverage Verification in Sensor Networks without Location Information. IEEE Trans. Automatic Control. 55, 1837–1849. doi:10.1109/TAC.2010.2047541
Topaz, C. M., Ziegelmeier, L., and Halverson, T. (2015). Topological Data Analysis of Biological Aggregation Models. PloS one 10, e0126383. doi:10.1371/journal.pone.0126383
Ulmer, M., Ziegelmeier, L., and Topaz, C. M. (2019). A Topological Approach to Selecting Models of Biological Experiments. PLOS ONE 14, 1–18. doi:10.1371/journal.pone.0213679
Vanderbei, R. J. (2014). “Linear Programming Foundations and Extensions,” in International Series in Operations Research Management Science. 4th ed. edn.v.2014 New York: Springer.
Vasudevan, R., Ames, A. D., and Bajcsy, R. (2011). Human Based Cost from Persistent Homology for Bipedal Walking,” in 18th IFAC World Congress. IFAC Proc. Volumes 44, 3292–3297. doi:10.3182/20110828-6-IT-1002.03807
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., and Shochet, O. (1995). Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 75, 1226–1229. doi:10.1103/PhysRevLett.75.1226
Wu, P., Chen, C., Wang, Y., Zhang, S., Yuan, C., Qian, Z., et al. (2017). “Optimal Topological Cycles and Their Application in Cardiac Trabeculae Restoration,” in Proceedings of the Twenty- IJCAI-19, International Joint Conferences on 1136 Artificial Intelligence Organization, 80–92.
Xia, K., and Wei, G. W. (2014). Persistent Homology Analysis of Protein Structure, Flexibility, and Folding. Int. J. Numer. Methods Biomed. Eng. 30, 814–844. doi:10.1002/cnm.2655
Xia, K., Li, Z., and Mu, L. (2018). Multiscale Persistent Functions for Biomolecular Structure Characterization. Bull. Math. Biol. 80, 1–31. doi:10.1007/s11538-017-0362-6
Zhang, X., Wu, P., Yuan, C., Wang, Y., Metaxas, D., and Chen, C. (2019). Heuristic Search for Homology Localization Problem and its Application in Cardiac Trabeculae Reconstruction. Proceedings of the Twenty-Eighth1135International Joint Conference on Artificial Intelligence, IJCAI-19, 1312–1318. doi:10.24963/ijcai.2019/182
Keywords: topological data analysis, computational persistent homology, minimal cycle representatives, generators, linear programming, l1 and l0 minimization
Citation: Li L, Thompson C, Henselman-Petrusek G, Giusti C and Ziegelmeier L (2021) Minimal Cycle Representatives in Persistent Homology Using Linear Programming: An Empirical Study With User’s Guide. Front. Artif. Intell. 4:681117. doi: 10.3389/frai.2021.681117
Received: 15 March 2021; Accepted: 14 May 2021;
Published: 11 October 2021.
Edited by:
Kathryn Hess, École Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Gard Spreemann, Telenor Research, NorwayHenri Riihimäki, University of Aberdeen, United Kingdom
Copyright © 2021 Li, Thompson, Henselman-Petrusek, Giusti and Ziegelmeier. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lori Ziegelmeier, bHppZWdlbDFAbWFjYWxlc3Rlci5lZHU=
 Lu Li
Lu Li Connor Thompson2
Connor Thompson2 Gregory Henselman-Petrusek
Gregory Henselman-Petrusek Chad Giusti
Chad Giusti Lori Ziegelmeier
Lori Ziegelmeier
