- 1Department of Mathematics, Rajalakshmi Engineering College, Chennai, India
- 2Department of Mathematics, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Chennai, India
- 3Department of Control Systems and Instrumentation, Faculty of Mechanical Engineering, VSB-Technical University of Ostrava, Ostrava, Czechia
- 4Department of Mechanical Engineering, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Chennai, India
- 5Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, India
- 6Department of Mechanical Engineering, Faculty of Engineering, Gazi University, Ankara, Türkiye
Introduction: A two-warehouse deterministic inventory system for purchases of short-expiry items with low purchasing costs is modelled. The total cost of the replenishment cycle is arrived at by implementing multiple just-in-time (JIT) purchases for the slotted backlogged customers. It avoids the loss of impatient customers who are virtually waiting for a long time.
Methods: The inventory system consists of an own warehouse (OW) with finite capacity and an integral rental warehouse (RW) with unlimited capacity. Handlingand selling items with short expiry is a challenging task in revenue generation in commercial inventory management. Two categories of identical items are purchased: Category 1 consists of items whose expiry date falls within the replenishment cycle period, while Category 2 includes items with longer expiry dates. Unlike the traditional assumption in the literature, the items in Category 1 are purchased for a low price and stored in RW. Items in Category 2 are stored in OW. Due to short expiry of items, demands are first satisfied from the RW. The items in the RW are emptied before the expiry date of the items, due to expiry date-dependent deterioration and constant demand. At the same time, the items in the OW are decreasing due to exponential demand and constant deterioration. All customers are backlogged during the stock-out period and slotted into three intervals. The finite number of JIT purchases is employed to satisfy the backlogged slotted demands that occur before the last slot.
Results and Discussion: We optimize the total cost of the replenishment cycle, RW utility, and total items purchased. The model is illustrated with an appropriate numerical example, and extensive sensitivity analysis is conducted on the system’s performance.
1 Introduction
Just-in-time (JIT) purchasing is a strategic approach to establishing and managing the supply chain that effectively minimizes inventory, facilitates frequent purchases, ensures high quality, fosters strong supplier relationships, and improves production efficiency. This study is based on an unusual two-warehouse inventory model with a finite JIT purchase to satisfy the backlog slots. Supply chain management is the main portfolio of any industrial system. JIT production and JIT purchasing policies have revolutionized cost optimization in supply chain management for large-scale industries. The inventory model assists managers in controlling inventory levels by addressing the queries of how much, when, and what to buy to purchase in order to maintain sufficient quantities of inventory to meet customer demand. The supplier offers discounts on the purchase of items that either have a short expiration date or are purchased in bulk. Any commercial business faces business risks that lead to an inadequate amount of profit due to some uncertainties, including changes in environmental conditions, customer needs and preferences, item deterioration, and heavy and increasing competition in the market. Retailers often make risky decisions to maximize profits by purchasing items with short expiration dates, items on discount, and items at regular prices. It increases their income if all items are sold within the stipulated time limit. The literature study that contributed to initiating the current study is as follows:
The article (1) links supply chain management, just-in-time delivery, and quality management and analyzes how these elements contribute to improved company performance. The results exhibit the organization’s point of view on the links at both strategic and operational levels. In Ismail Salaheldin (2), it is identified that JIT performance is strongly related to human resource modification initiatives. The findings indicate that, with careful consideration of each unique enterprise, the JIT concept can be effectively applied to Egyptian manufacturing enterprises. JIT is a strategic theory that encourages uniqueness and worth. It has practical consequences. In the work of Duclos et al. (3), Toyota Motor Company was commended for creating and executing a strategy that boosted its competitiveness in the automobile industry. JIT is defined by the American Production and Inventory Control Society as a production excellence mindset focused on organized waste removal and continued output growth. It covers all phases of the production process, from raw material conversion to the level of distribution. The JIT purchasing method was investigated in Christensen (4) as an aspect of the Freight Transport Association’s response to the transportation argument and was found to reduce container movements due to improvements in technology and vehicle utilization. It also allows the company to show advancements, environmental advantages, and customer relations and suggests additional savings.
The supplier–manufacturer ties in the JIT setting and their influence on the effectiveness of JIT execution is discussed in Wafa et al. (5). Additionally, it investigates the functions of data, collaboration, vendor relationships, and supplier closeness in JIT performance. A metric for assessing JIT effectiveness is proposed, incorporating both monetary and non-monetary factors. The existence of complementarity among the internal and external bundles is tested in Furlan et al. (6). It is shown that the upstream and downstream of JIT are complemented by analyzing the international research project data set in optimizing operational performances. In Hwang and Hahn (7), it examines the best strategy for purchasing items with the assumption that the demand rate is a function of the present stock level and that each unit has an expiry date. The susceptibility of decision factors while changing the parameter values is investigated using a mathematical model and solution technique. An inventory model with price, freshness, and stock-dependent demand is proposed in Feng et al. (8). They determine unit price, total cycle time, and ending-inventory level, which maximize the total profit. The study (9) examines a more realistic scenario in which a product’s deterioration rate steadily rises as the expiration date approaches. The factors of choice that minimize the overall cost are the optimum cycle duration and the cycle fraction of no shortages. The model is validated by a numerical example.
The retailers’ and suppliers’ purchasing policies are established in Hsu et al. (10) with the constraints of product deterioration, expiry date, lead time, capital limits, and seasonal demand. Total order quantity, stock-out period, optimum replenishment cycle, and source handling cost for the supplier are estimated. In Wu et al. (11), an EOQ model for retailers is suggested to determine the optimum credit period and cycle time for the supplier-retailer–buyer supply chain. It explains how to increase sales and income while increasing trade credit. This article (12) shows that the optimum restocking cycle time for a store is not just something that happens; it is also unique, making it easier to identify a solution. The DCF analysis is used to calculate all pertinent costs. Both numerical examples and risk analysis are used to explain the different issues and gain management insights. The optimum lot-sizing strategies for retailers who sell deteriorating goods to trade payables while providing partial trade credit to reduce risk are suggested in Wu et al. (13). The pseudo-convex fractional functions are used to attain the best answer and to get better discrimination terms. A deterministic replenishment system involving multiple warehouses with restricted storage space and a time-dependent demand rate is discussed in Zhou (14). The products from the rented warehouse are moved to the owned warehouse in a continuous release pattern.
A two-storage inventory system was developed for deteriorating goods with advanced payment, a constant partial backlog, and selling price-dependent demand (15). Product promotion is an essential component of inventory research, as both price and availability play a vital role in attracting customers. The study (16) considered these aspects along with deteriorating items of price- and stock-dependent demand in partially backlogged storage. A two-storage inventory approach with an advance payment option has been developed in Khan et al. (17) for three different scenarios based on varying beginning times for degradation in both warehouses. Three optimal issues have been identified, and their optimality is mathematically demonstrated. An algorithm is suggested to solve the model. This article (18) includes an EOQ inventory model based on the price and stock-dependent demand with the shortfalls in backlog. The inventory issue is transformed into a non-linear constraint optimum issue, and the cycle duration and overall cost are calculated using the Taylor series.
The study by Mashud et al. (19) explores product deterioration in a production-inventory newsboy model using just-in-time deliveries. The classical optimization techniques of the distribution-free approach are employed with the consideration of a return and post-sale warranty policy to improve business and attract customers. Validity is demonstrated through theoretical development and numerical examples. The article by Mashud et al. (20) presents a two-warehouse sustainable inventory model by considering the factors of price-dependent demand, non-instantaneous deterioration rate, discount facility, partial backlog, and various payment options for both retailers and suppliers. The classical optimization technique is employed to maximize the total profit of the system. In Mashud et al. (21), the study on the inventory model explores optimal pricing and inventory strategies for deteriorating products with price-dependent demand and advanced payment systems, incorporating time-dependent holding costs. It highlights how advanced payment periods, installment numbers, product lifecycle, purchasing cost, and demand function significantly impact total profit. A solution to the problem involves placing two orders one period apart, with the second order designed to fulfill any demand unmet by the first order (22). It facilitates the reduction of shortages and minimizes the total costs.
The study (23) facilitates anyone to know the impact of monetary inflation on a two-warehouse inventory system by emphasizing stock-dependent demand and flexible payment options in attaining optimum total cost. The article (24) projects a two-warehouse inventory model with ramp-type demand and constant deterioration, utilizing a rental warehouse for surplus goods and prepayment in equal installments. Stock-outs are addressed through emergency purchases, and the model’s effectiveness is demonstrated through numerical examples. The article (25) investigates two-warehouse inventory systems integrated with a production unit, aiming to optimize the total production cycle and cost. It employs an analytical optimization approach using the discriminant method, focusing on unit utility, fluctuating deterioration rates, and varying demand and production parameters. The sensitivity of unit utility, fluctuating deterioration rates, variable demand, and production parameters are revealed by numerical values. The article (26) analyses a single product inventory with two warehouses, varying storage costs to maintain quality and prevent deterioration, and unpredictable demand patterns. It proposes an instantaneous replenishment policy and assumes payment delays, demonstrating the optimal overall cost.
In today’s unpredictable market conditions and due to rapidly changing customer demands, any business faces a stock-out state in the course of the entire replenishment cycle. Customers’ behaviors are presently more unpredictable and less dependable, which results in a small percentage of customers only willing to wait for the product until it gets replenished in the inventory during the stock-out period. The complementary percentage of the customer is treated as lost customers. It is a great challenge to retailers, and they are forced to go for a finite number of JIT purchases by slotting the stock-out time interval. Since the JIT purchase policy is not always profitable in scenarios of inventory management, the cost price of the product also increases continuously. Moreover, retailers are offered a variety of discount offers upon bulk ordering.
The article flow is depicted in Figure 1.
2 Notations and assumptions
2.1 Notations
This model is developed with the following notations:
2.2 Assumptions
The optimization study of the model proceeded with the following assumptions:
• The rate of replenishment is infinite, and replenishment happens instantly.
• The lead time is negligible.
• The planning horizon is limited.
• All items are subject to deterioration, and items should never be sold just after their’ expiry date not even for a lower cost.
• A finite number of JIT ordering strategies is implemented.
• Items with unconstrained expiry date (That means the items whose expiry date falls after the time point ) are stored in .
• Items with constrained expiry date (That means, the items whose expiry date ends at which lies within the time point ) are stored in .
• The space of is limited, but is of infinite capacity.
• The deterioration cost of an item in is smaller than the deterioration cost of an item in .
• The first and second purchases satisfy the backlog customers of slot-1 and slot-2, respectively.
• The slot-3 backlog customers are satisfied by the purchase of constrained expiry date items at the start of the next replenishment cycle.
• Items in are of a non-instantaneous deteriorated nature.
3 Model formulation and solution
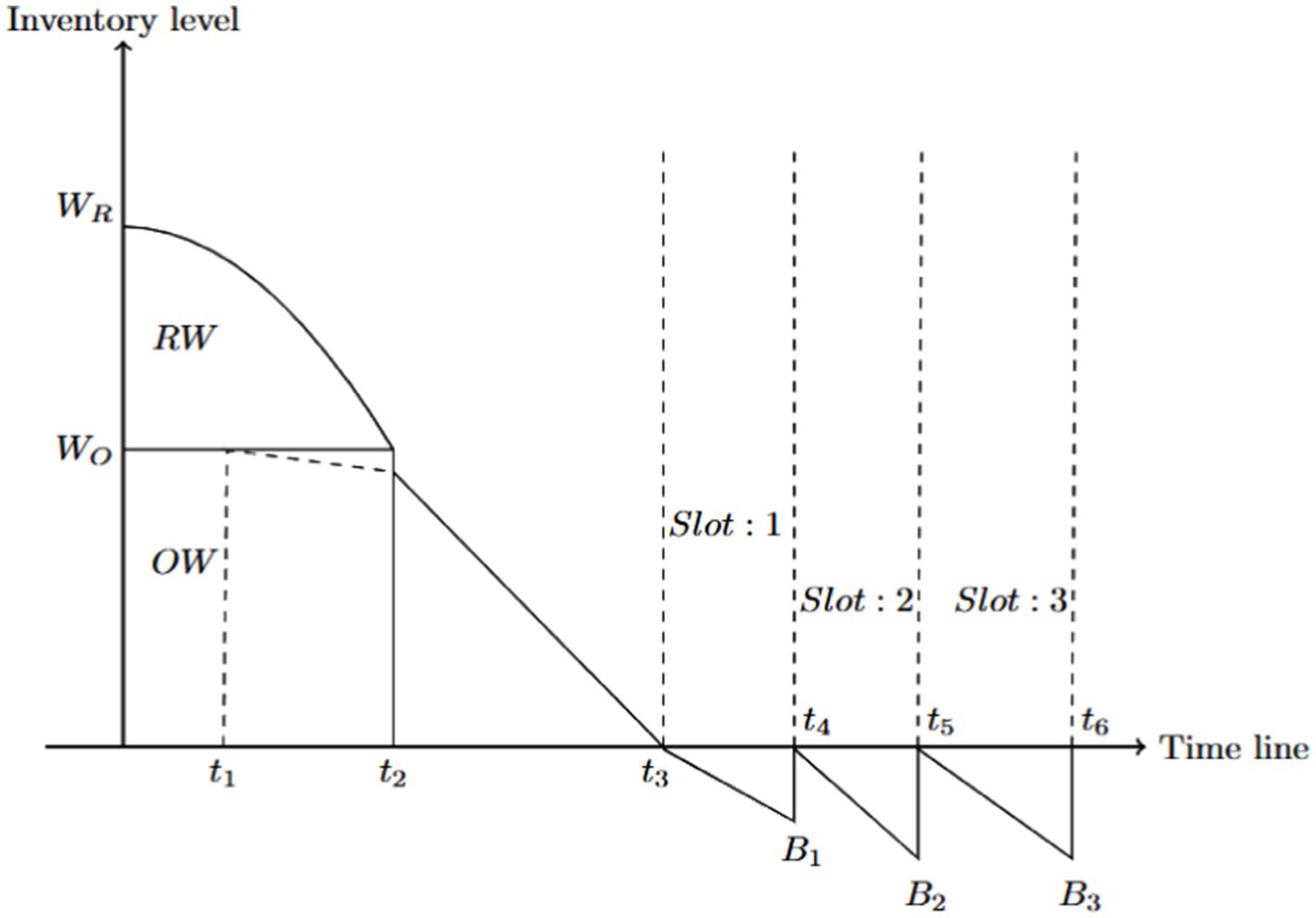
The retailer purchases (includes the fraction of constrained expiry date items) items at first. It is stored number of unconstrained expiry date items in as it is its maximum capacity. The remaining items are stored in after satisfying the backlogs of slot-3 of the previous cycle. The items in reach zero at due to the joint effect of demand and deterioration. Once is empty, further demands are satisfied by the items from . Items in are subject to non-instantaneous deteriorated nature, which prolongs time . After the time point , the items in start to decline because of the demand and deterioration; finally, it reaches zero at . The demands in the stock-out period are partitioned into three slots, say slot-i, . First purchase is made at the time point to satisfy the backlogged customers in slot-1, and second purchase is made at to satisfy the backlogged customers in slot 2. Such an implementation of purchase helps to avoid and reduce the backlog customers’ waiting time in the system. Backlogs in the interval are satisfied by the constrained expiry date items at the beginning of the next replenishment cycle (see Figure 2).
The occurrence of dynamic change of items in the is subject to the expiry date-dependent deterioration and constant demand. It is represented by the following differential equation, which depicts that the rate of change of the inventory level in the is equal to the decrease in the inventory level due to deterioration among the items and the occurrence of demand. The inventory level at any time point in is governed by the following equation:
Solving Equation 1, with the boundary condition , we get Equation 2
At the same time, there is no demand for the items in up to the time point . However, item deterioration starts after the time point as the effect of non-instantaneous deterioration. The following differential equation represents the inventory level at .
Solving Equation 3 with the boundary condition, , we get Equation 4
After , the demands are satisfied by the items stored in the because the becomes empty at . So, the inventory level at the decreases due to both exponential demand rate and constant deterioration, and the inventory level at is expressed by the following differential equations,
Solving Equation 5 by applying the boundary condition, , we get Equation 6.
After the time point , the demands are fully backlogged and considered as three slots, such as the backlogs in the intervals , and . The number of demands in the stock-out period is of exponential demand. The following differential equation represents the number of backlogs in the stock-out period, irrespective of the slots.
The Equation 7 may be solved by using the conditions , , and
, we get Equation 8
The total number of backlogged occurred in the three slots are represented in Equations 9–11.
The total number of items purchased from the regular supplier is derived as Equation 12.
The cost functions of the model are presented from Equations 13–18.
1) Ordering Cost: Ordering costs are the charges a business incurs when placing an order with a supplier for goods, services, or raw materials. They are sometimes referred to as procurement costs or start-up costs. Here, we are considering three orders, such as ordinary, JIT 1 and JIT 2.
2) Purchasing Cost: Purchasers must pay suppliers a certain sum called a purchasing cost when purchasing an inventory item. Here, we consider four purchasing costs, namely the purchase cost for a regular order, the purchase cost for expiry date constrained items, and the purchase cost for JIT 1 and JIT 2 items.
Purchasing cost is associated with the cost of
3) Holding Cost: Holding costs are the costs incurred to store inventory. Here, represents the holding cost per unit of time in . Moreover, represents the holding cost per unit of time in
4) Deterioration Cost: This cost is the amount of money lost due to inventory deterioration during storage.
5) Backlog Cost: The term “backlog cost” refers to the cost of running out of products. The loss of potential item sales profit, the damage to goodwill resulting from a permanent customer loss, and the resulting loss of future sales profit are all included in this cost. Therefore, the backlog cost is calculated as follows:
1. 6) Total cost of the system: The total cost of the system in a unit of time is the sum of all the associated costs.
The classical analytic optimization method for two variables is used to optimize the system’s total cost The following algorithm using MATLAB code is designed to achieve cost optimization:
Step 1: Initialize all the parameters.
Step 2: compute and . Apply the below necessary conditions to arrive at the critical points of the cost surface:
Step 3: Find all second-order partial derivatives , , .
Step 4: Generate the Hessian matrix as follows:
Check for the critical points for which all second derivatives are as follows:
If, , and
Select the critical point that yields the discriminative value as follows:
Then, the Hessian matrix will be positive definite for such a point. Hence, the surface of the total cost function is convex in nature.
Otherwise, go to step 3 and proceed with other critical points.
Step 5: Best optimum total cost is identified and denoted by .
Step 6: Stop the procedure.
The time point and , which minimizes the total cost function, say . It leads us to obtain the optimum total order quantity and backlog period.
4 Numerical example and sensitivity analysis
4.1 Numerical example
The model is validated in the particular environment with the following parameter values:
; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; in appropriate units.
We have arrived at the optimum outputs as follows:
; ; ; ; ; ;
; ; ; ;
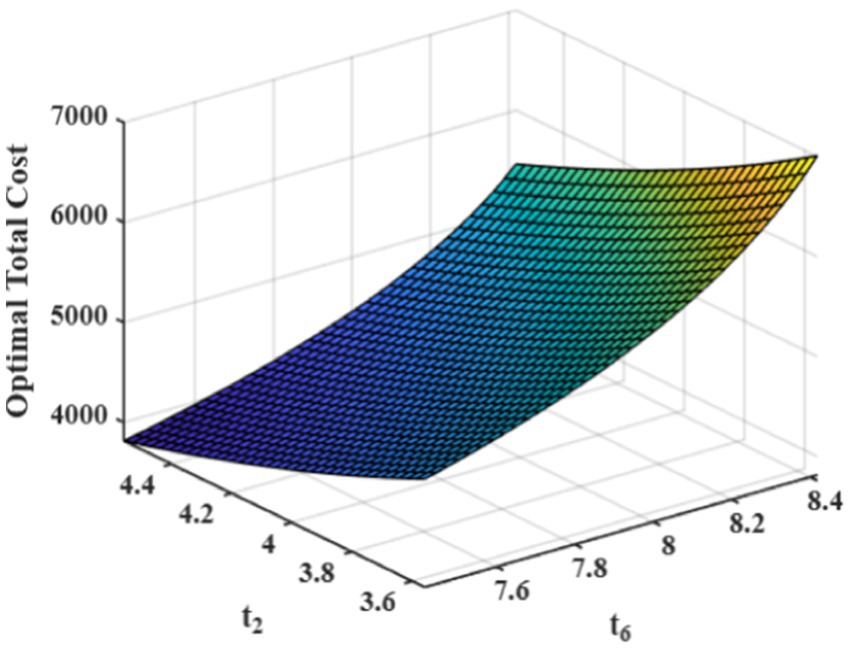
The total cost function for the above-said environment is presented in Figure 3.
4.2 Sensitivity analysis
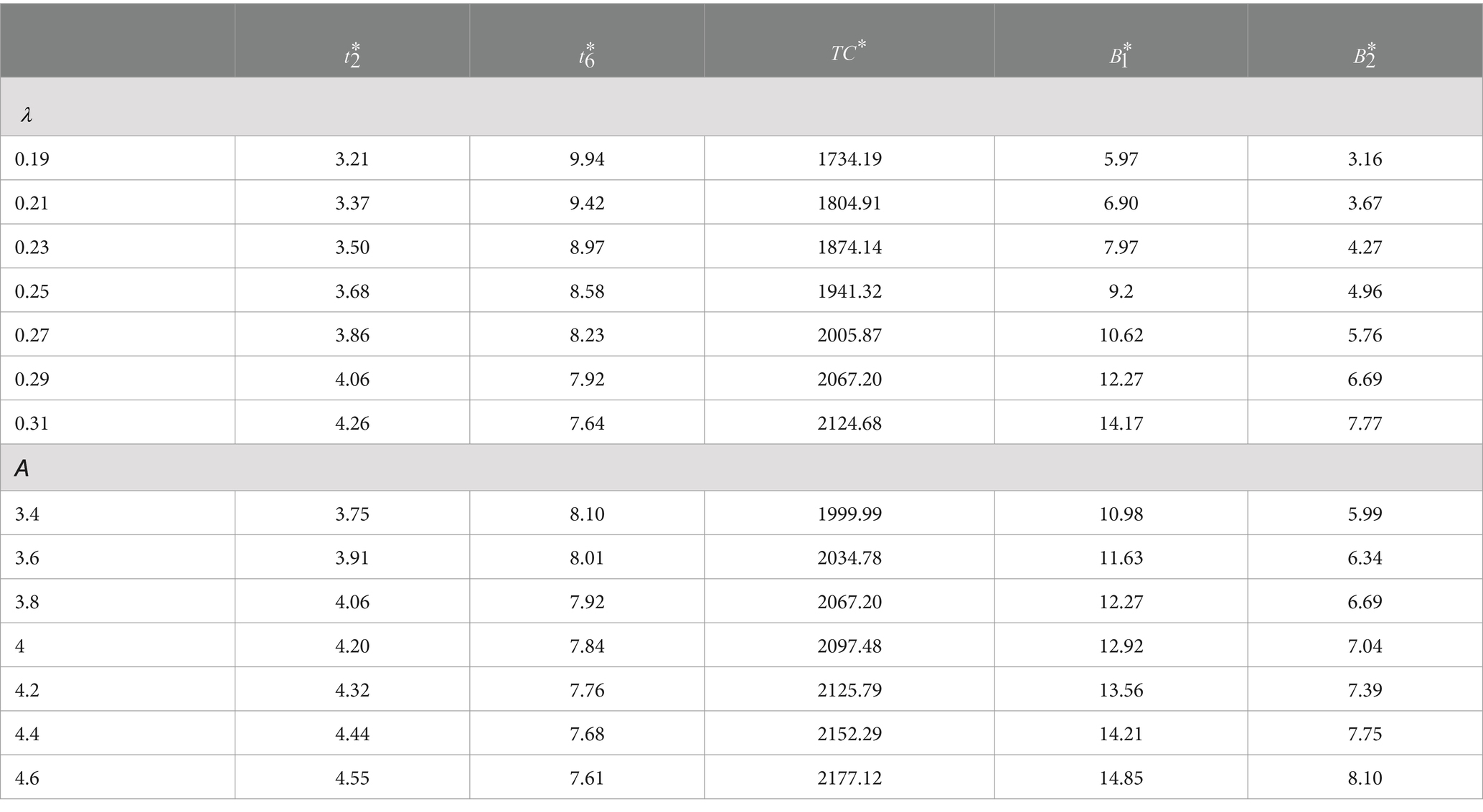
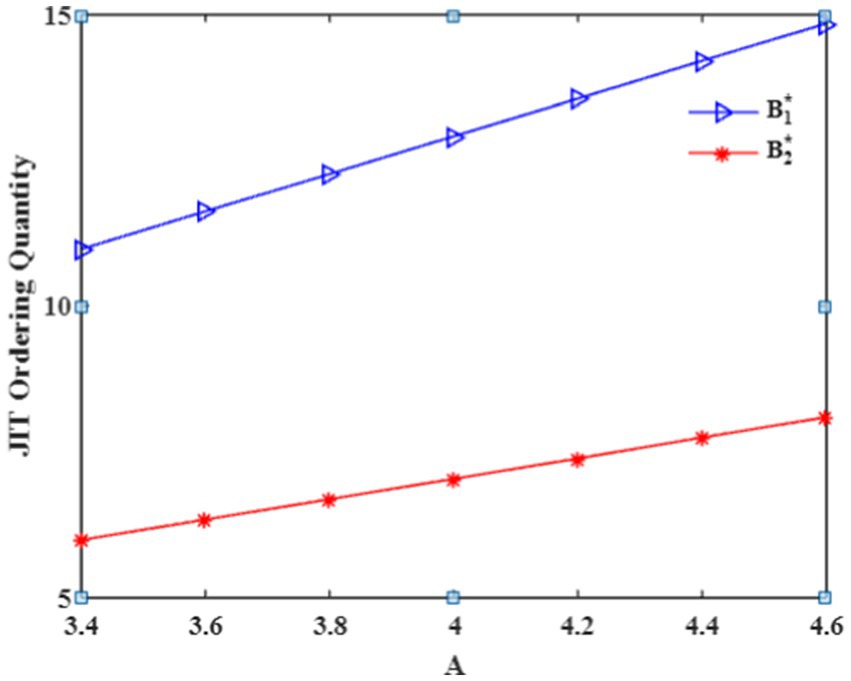
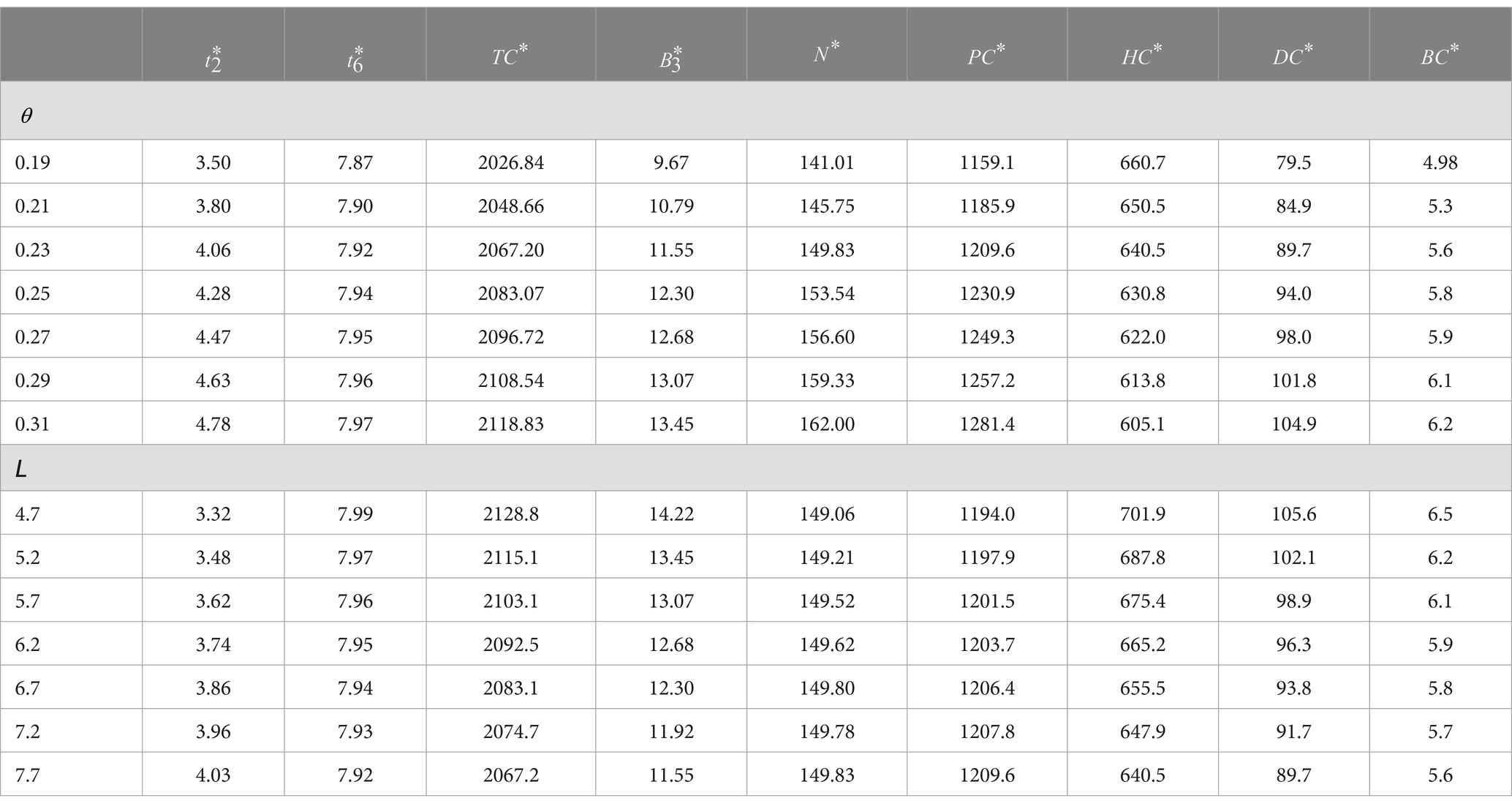
Any situation that involves decision-making may encounter a shift in parameter values due to uncertainty. The sensitivity analysis will play a significant role in decision-making when examining the effects of these adjustments. The sensitivity analysis of factors was performed using the same parameters considered in the same environment as in the numerical illustration. First, the demand parameter is varied from 0.19 to 0.31. Furthermore, the demand parameter is varied from 3.4 to 4.6. The corresponding optimum measures of the model are listed in Table 1.
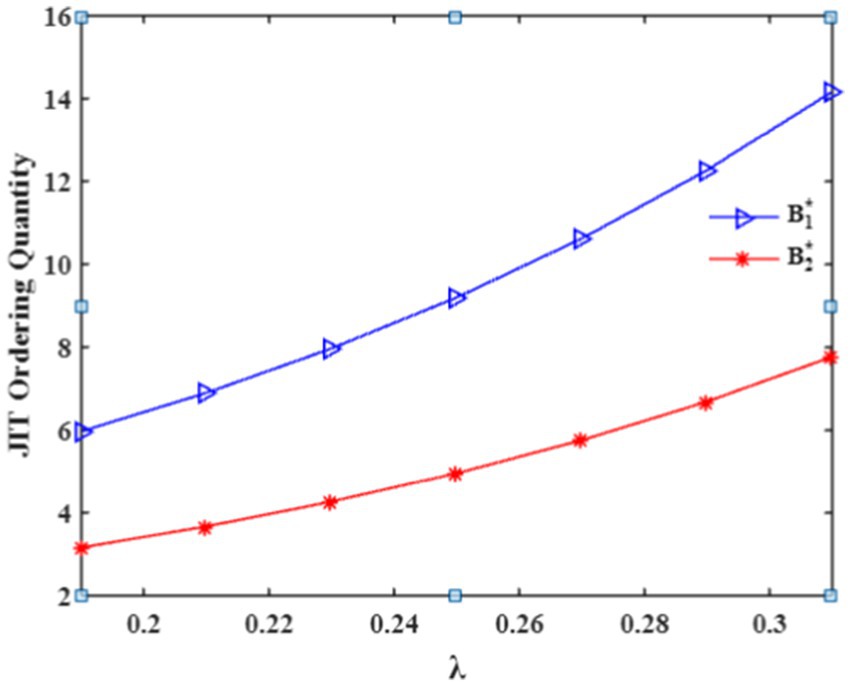
Based on the values in Table 1, we infer the following results: If the demand parameters and are increased, then the optimum ordering quantities and are also increased by the impact of the decrease in the optimum total length of the cycle. As a result, the total optimal cost per unit of time also increases in an exponential trend. Such effect is depicted in Figures 4, 5.
That is, the increase in both and values are negatively correlated with optimum total cycle length, which is true in nature, and positively correlated with optimum JIT purchasing quantities and optimum time interval in which the RW becomes empty. As a result, the optimum total cost is increased. Such an effect is depicted in Table 1.
Additionally, the effect of variation of deterioration parameter and expiry date on the optimum measures is shown in Table 2.
The following managerial insights are obtained based on the computational findings.
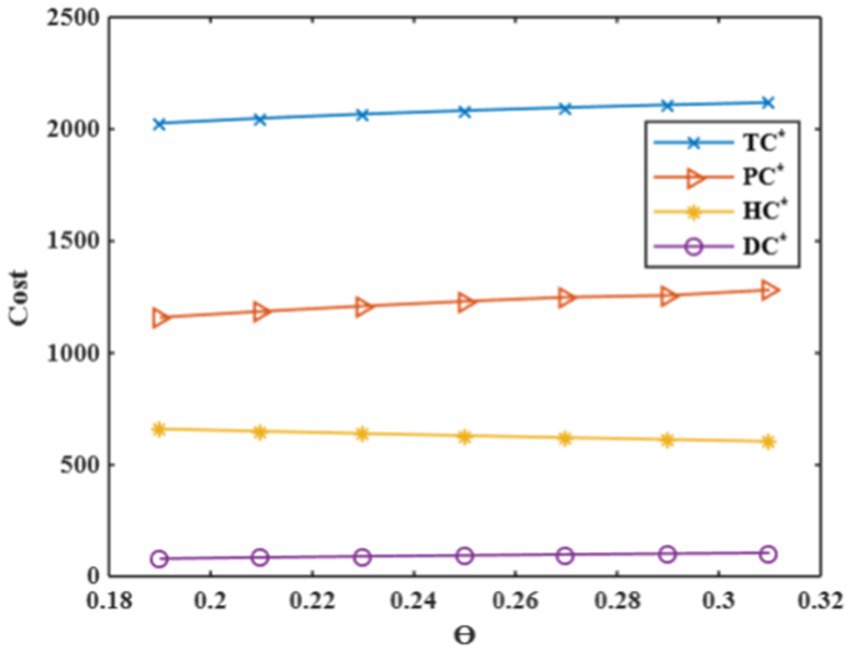
It emphasizes the impact of the deterioration parameter on purchase cost, holding cost, and deterioration cost. One may observe that the purchasing cost exhibits an increase, reflecting higher procurement expenses to compensate for the faster rate of deterioration. Holding cost demonstrates a decrease, indicating reduced storage costs due to decreased inventory levels caused by deterioration. Deterioration cost increases, corresponding to the amplified deterioration rate within the inventory system. It increases the optimum total cost of the system. It provides critical insights into the model’s performance, showcasing its robustness and effectiveness in capturing real-world dynamics. The observed trends are shown in Table 2 and Figure 6, reinforcing the soundness and practical applicability of the inventory model in managing costs under varying deterioration rates.
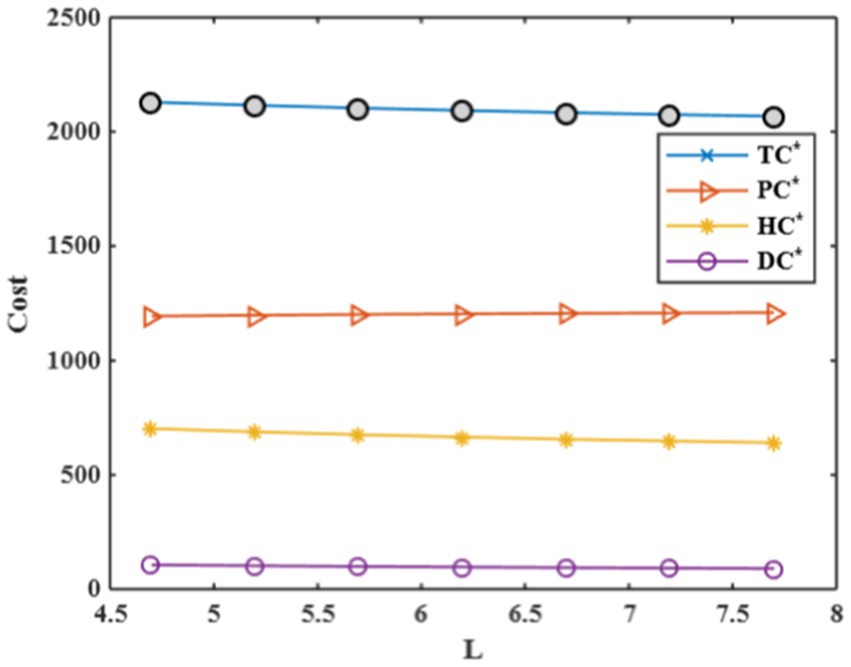
Now, it is discussed the influence of prolonging the items’ expiry date in inventory modeling for optimizing the total cost. As the expiry date extends, purchasing cost increases, indicating short-expiry items are purchased for less price. Holding costs demonstrate a decrease, reflecting reduced storage expenses as inventory can be managed more efficiently over time, and deterioration costs experience a decrease, too. This results in a decrease in the total system’s optimum cost. It confirms the model’s robustness in adapting to variations in expiry dates while achieving cost optimization. The findings are substantiated by Table 2 and Figure 7, illustrating the model’s capability to address practical scenarios effectively and affirming its sound performance in inventory management.
5 Conclusion and future work
We have developed a two-warehouse deterministic inventory model with multiple purchases. The unconstrained expiry date items are stored in the . In addition, we incorporate finite purchases for the partial backlog customers to avoid the lost sale. The model suggested the effect of reducing the lost sales by a finite number of purchases in the stock-out interval. The model is validated in a specific environment by numerical examples, and it suggests that the retailer should opt for appropriate managerial decisions to optimize his total cost.
• The effect of changes in exponential demand parameters, deterioration rate, and extension of the constrained expiry date of the items on optimizing the cost functions are listed in tables and depicted in the figures, which are the recommendations and suggestions to the retailers to fix their optimum strategies and finalize their decisions to succeed in the highly competitive business environment.
• If the demand parameters and are increased, then the optimum ordering quantities and are also increased by the impact on the decrease of the optimum total length of the cycle. As a result, the total optimal cost per unit of time also increases.
• The holding cost and deterioration cost are moderately increased for the increase in the deterioration parameter , whereas the purchase cost is highly decreased due to the increase of in the .
In the future, the present study may extend its scope to include factors such as price and advertisement-dependent demand, retailers’ late payment options with and without installment payments, screening of items, and system re-do facility. Incorporating these factors could yield fruitful suggestions and recommendations for many retailers in different business environments.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
RT: Conceptualization, Resources, Supervision, Writing – original draft, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing – review & editing. JV: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. MM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. JU: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. SS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This article was co-funded by the European Union under the REFRESH—Research Excellence For Region Sustainability and High-tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Programme Just Transition.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Kannan, V. Just in time, total quality management, and supply chain management: understanding their linkages and impact on business performance. Omega. (2005) 33:153–62. doi: 10.1016/j.omega.2004.03.012
2. Ismail Salaheldin, S. JIT implementation in Egyptian manufacturing firms: some empirical evidence. Int J Oper Prod Manag. (2005) 25:354–70. doi: 10.1108/01443570510585543
3. Duclos, LK, Sih, SM, and Lummus, RR. JIT in services: a review of current practices and future directions for research. Int J Serv Ind Manag. (1995) 6:36–52. doi: 10.1108/09564239510101518
4. Christensen, L. JIT sensitive distribution - cutting waste and serving the customer. Logist Inf Manag. (1996) 9:7–9. doi: 10.1108/09576059610113214
5. Wafa, MA, Yasin, MM, and Swinehart, K. The impact of supplier proximity on JIT success: an informational perspective. Int J Phys Distrib Logist Manag. (1996) 26:23–34. doi: 10.1108/09600039610116495
6. Furlan, A, Dal Pont, G, and Vinelli, A. On the complementarity between internal and external just-in-time bundles to build and sustain high performance manufacturing. Int J Prod Econ. (2011) 133:489–95. doi: 10.1016/j.ijpe.2010.07.043
7. Hwang, H, and Hahn, KH. An optimal procurement policy for items with an inventory level-dependent demand rate and fixed lifetime. Eur J Oper Res. (2000) 127:537–45. doi: 10.1016/s0377-2217(99)00337-9
8. Feng, L, Chan, Y-L, and Cárdenas-Barrón, LE. Pricing and lot-sizing polices for perishable goods when the demand depends on selling price, displayed stocks, and expiration date. Int J Prod Econ. (2017) 185:11–20. doi: 10.1016/j.ijpe.2016.12.017
9. Teng, J-T, Cárdenas-Barrón, LE, Chang, H-J, Wu, J, and Hu, Y. Inventory lot-size policies for deteriorating items with expiration dates and advance payments. Appl Math Model. (2016) 40:8605–16. doi: 10.1016/j.apm.2016.05.022
10. Hsu, P-H, Wee, HM, and Teng, H-M. Optimal ordering decision for deteriorating items with expiration date and uncertain lead time. Comput Ind Eng. (2007) 52:448–58. doi: 10.1016/j.cie.2007.02.002
11. Wu, J, Ouyang, L-Y, Cárdenas-Barrón, LE, and Goyal, SK. Optimal credit period and lot size for deteriorating items with expiration dates under two-level trade credit financing. Eur J Oper Res. (2014) 237:898–908. doi: 10.1016/j.ejor.2014.03.009
12. Wu, J, Al-khateeb, FB, Teng, J-T, and Cárdenas-Barrón, LE. Inventory models for deteriorating items with maximum lifetime under downstream partial trade credits to credit-risk customers by discounted cash-flow analysis. Int J Prod Econ. (2016) 171:105–15. doi: 10.1016/j.ijpe.2015.10.020
13. Wu, J, and Chan, Y-L. Lot-sizing policies for deteriorating items with expiration dates and partial trade credit to credit-risk customers. Int J Prod Econ. (2014) 155:292–301. doi: 10.1016/j.ijpe.2014.03.023
14. Zhou, Y-W. A multi-warehouse inventory model for items with time-varying demand and shortages. Comput Oper Res. (2003) 30:2115–34. doi: 10.1016/s0305-0548(02)00126-0
15. Al-Amin Khan, M, Shaikh, AA, Panda, GC, and Konstantaras, I. Two-warehouse inventory model for deteriorating items with partial backlogging and advance payment scheme. RAIRO Oper Res. (2019) 53:1691–708. doi: 10.1051/ro/2018093
16. Panda, GC, Khan, MAA, and Shaikh, AA. A credit policy approach in a two-warehouse inventory model for deteriorating items with price- and stock-dependent demand under partial backlogging. J Ind Eng Int. (2018) 15:147–70. doi: 10.1007/s40092-018-0269-3
17. Khan, MAA, Shaikh, AA, Panda, GC, Bhunia, AK, and Konstantaras, I. Non-instantaneous deterioration effect in ordering decisions for a two-warehouse inventory system under advance payment and backlogging. Ann Oper Res. (2020) 289:243–75. doi: 10.1007/s10479-020-03568-x
18. Mashud, AHM. An EOQ deteriorating inventory model with different types of demand and fully backlogged shortages. Int J Logist Syst Manage. (2020) 36:16. doi: 10.1504/ijlsm.2020.107220
19. Mashud, AHM, Wee, HM, Huang, CV, and Wu, JZ. Optimal replenishment policy for deteriorating products in a newsboy problem with multiple just-in-time deliveries. Mathematics. (2020) 8:1981. doi: 10.3390/math8111981
20. Mashud, AHM, Wee, HM, Sarkar, B, and Chiang Li, YH. A sustainable inventory system with the advanced payment policy and trade-credit strategy for a two-warehouse inventory system. Kybernetes. (2021) 50:1321–48. doi: 10.1108/K-01-2020-0052
21. Mashud, AHM, Roy, D, Daryanto, Y, and Wee, HM. Joint pricing deteriorating inventory model considering product life cycle and advance payment with a discount facility. RAIRO Oper Res. (2021) 55:S1069–88. doi: 10.1051/ro/2020106
22. Izevbizua, O, and Mukoro, ES. Fixed lifetime inventory system with double order under useful lifetime-based model. Afr J Math Comput Sci Res. (2020) 13:17–23. doi: 10.5897/AJMCSR2019.0796
23. Thilagavathi, R, Viswanath, J, Cepova, L, and Schindlerova, V. Effect of inflation and permitted three-slot payment on two-warehouse inventory system with stock-dependent demand and partial backlogging. Mathematics. (2022) 10:3943. doi: 10.3390/math10213943
24. Viswanath, J, Thilagavathi, R, Karthik, K, and Mahdal, M. A study of a two-storage single product inventory system with ramp type demand, n-phase prepayment and purchase for exigency. Mathematics. (2023) 11:1728. doi: 10.3390/math11071728
25. Jagadeesan, V, Rajamanickam, T, Schindlerova, V, Subbarayan, S, and Cep, R. A study on two-warehouse inventory systems with integrated multi-purpose production unit and partitioned rental warehouse. Mathematics. (2023) 11:3986. doi: 10.3390/math11183986
Keywords: warehouse, inventory, just-in-time purchases, backlog, expiry date
Citation: Thilagavathi R, Viswanath J, Mahdal M, Udaya Prakash J and Salunkhe S (2025) Two-warehouse deterministic inventory model of expiry date known deteriorating items with just-in-time purchases for slotted backlogs. Front. Appl. Math. Stat. 11:1410533. doi: 10.3389/fams.2025.1410533
Edited by:
Aceng Sambas, Sultan Zainal Abidin University, MalaysiaReviewed by:
Nataliya Protsakh, Lviv Polytechnic National University, UkraineHui-Ling Yang, Hungkuang University, Taiwan
Copyright © 2025 Thilagavathi, Viswanath, Mahdal, Udaya Prakash and Salunkhe. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sachin Salunkhe, c2FjaGluc2FsdW5raGVAZ2F6aS5lZHUudHI=; J. Viswanath, anZpc3dhbmF0aEB2ZWx0ZWNoLmVkdS5pbg==
 R. Thilagavathi
R. Thilagavathi J. Viswanath
J. Viswanath Miroslav Mahdal3
Miroslav Mahdal3 Jayavelu Udaya Prakash
Jayavelu Udaya Prakash Sachin Salunkhe
Sachin Salunkhe