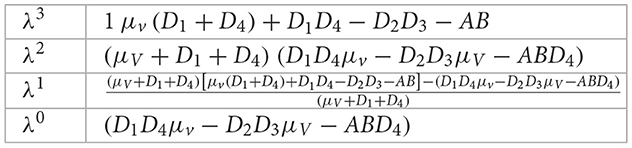Sensitivity analysis of a mathematical model for malaria transmission accounting for infected ignorant humans and relapse dynamics

This article presents and analyzes a deterministic model for malaria transmission that incorporates infected individuals who are unaware of their infectious status (ignorant infected humans) and accounts for relapse dynamics. We explore the invariant region and positivity of the model and calculate the effective reproduction number using the next-generation matrix method. We demonstrate the local and global stability of disease-free equilibrium points using the Routh-Hurwitz criterion and Lyapunov function, respectively. The proposed model shows that a disease-free equilibrium point is globally asymptotically stable when the basic reproduction number R_e < 1. We conducted a sensitivity analysis on the effective reproduction number to identify which basic parameter most significantly influences the increase or decrease of malaria cases. This study focuses on individuals who have been treated and cured but continue to carry dormant Plasmodium parasites in their blood, which can potentially cause relapse or reinfection. Additionally, we introduce a protected compartment to carefully evaluate how preventive measures influence the spread and persistence of malaria within the population.

1 Introduction

Malaria is a serious infectious disease with significant clinical and economic impacts, particularly in developing countries and regions where it greatly affects socioeconomic development. This disease is caused by single-celled protozoan parasites from the Plasmodium genus, which can infect a variety of hosts, including humans, birds, mammals, and reptiles [1]. Among the different Plasmodium species that cause malaria in humans, five are especially important, namely Plasmodium falciparum, Plasmodium malariae, Plasmodium ovale, Plasmodium vivax, and Plasmodium knowlesi. Plasmodium falciparum is widespread in Africa and is the primary cause of infections in that region and Southeast Asia. In Ethiopia, the predominant Plasmodium species causing malaria are Plasmodium vivax and Plasmodium falciparum [2].

Malaria is transmitted to humans by female Anopheles mosquitoes that carry the parasite. These mosquitoes spread the infection by biting and feeding on blood, which is necessary for them to lay their eggs. The parasite relies on both the female Anopheles mosquito and a human host to complete its life cycle. Transmission occurs when an infected mosquito bites a human [3]. Furthermore, if an Anopheles mosquito bites a person already infected with the malaria parasite, it becomes a carrier of the disease. Malaria can also be transmitted through blood transfusions and from mother to child during pregnancy [4]. The main vectors responsible for malaria transmission in tropical Africa include Anopheles funestus, Anopheles gambiae, and Anopheles arabiensis [5].

Mathematical modeling provides researchers and public health officials with tools to understand the spread of infectious diseases, predict future trends, evaluate the effectiveness of interventions, and devise strategies for disease control and prevention. By applying mathematical models, experts can better understand the dynamics of disease transmission, identify key factors influencing the spread of infections, and make informed decisions to mitigate the impact of outbreaks. Numerous studies have developed various mathematical models to illustrate disease control and its dynamics. The first mathematical model for malaria transmission was developed by Ronald Ross, who won the Nobel Prize in 1902 for his work on the malaria parasite's life cycle [6]. Ross's model was based on an SIS (Susceptible-Infected-Susceptible) framework, which categorized the population into susceptible, infected, and susceptible groups, assuming that the total population could be divided into specific compartments at any given time. He used this model to demonstrate that reducing the mosquito population below a certain threshold could eradicate malaria, with this threshold being influenced by biological factors such as the mosquito biting rate and vectorial capacity [7]. A new non-linear mathematical model for malaria has been developed, dividing infected individuals into two categories: those who are aware of their infection and those who are unaware. The model assumes that awareness campaigns help decrease the number of unaware infected individuals, while those who are aware take precautions to avoid mosquito contact. The solutions derived from the model were verified to be positive and bounded using differential equations. Stability analysis, based on the basic reproductive number R₀, showed that the system remains stable when R₀ is < 1. The model also identified conditions for the existence of a unique endemic equilibrium. Solutions were obtained using the Runge-Kutta method, and simulations were carried out for different populations of humans and Anopheles mosquitoes in each category. The results revealed an increase in susceptible humans and a decrease in infected mosquitoes [8].

The global fight against malaria faces significant challenges. While efforts to control malaria have successfully reduced the incidence of Plasmodium falciparum, the reduction in cases of Plasmodium ovale and Plasmodium vivax has been less pronounced [9, 10]. As a result, the proportion of malaria cases caused by P. ovale and P. vivax is rising. Research indicates that ongoing transmission of P. vivax is prevalent in many regions south of the Sahara Desert [11]. The difficulty in substantially reducing the prevalence of P. vivax and P. ovale is partly due to the relapsing nature of these parasites [12, 13]. Dormant forms of the parasites in the liver can cause the disease to recur, leading to symptoms weeks or even years after initial treatment. Any remaining Plasmodium in the bloodstream can trigger a relapse [14]. This study focuses on individuals who have been treated and cured but still harbor dormant Plasmodium parasites in their blood, which can lead to relapse and reinfection.

2 Methods

2.1 Model formulation

A mathematical modeling approach will be utilized to construct the model using deterministic ordinary differential equations.

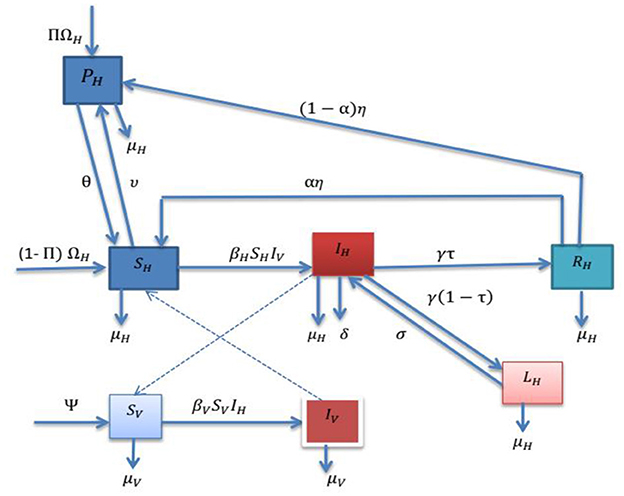
The model divides the total human population at time t, denoted as N_H(t), into several sub-populations: susceptible humans S_H(t) (healthy individuals not infected with malaria), protected humans P_H(t) (individuals employing mosquito prevention measures to avoid contact with vectors), infected humans I_H(t) (those infected with malaria who can transmit the disease), infected ignorant humans L_H(t) (individuals who still carry the Plasmodium parasites in their blood after a certain period of treatment), and recovered individuals with temporary immunity R_H(t) (those who have recovered from the disease and possess temporary immunity at time t).

Infected ignorant individuals may become infectious again if their immune system weakens. A compromised immune response can lead to the reactivation (relapse) of the Plasmodium parasites, causing re-infection without requiring a mosquito bite. The total human population is represented as follows:

$\begin{array}{l}{N}_H(t)=S_H(t)+P_H(t)+I_H(t)+L_H(t)+R_H(t).\end{array}$

The mosquito (vector) population is categorized into susceptible and infected populations at time t (see Figure 1). The model consists of seven ordinary differential equations.

Figure 1

Figure 1. A flowchart of the malaria model.

2.2 Model equations

$\begin{array}{ll}\{\begin{array}{c}\frac{d{S}_H}{dt}=\left(1-\Pi \right){\Omega }_H+\theta P_H+\alpha \eta R_H-{\beta }_h{S}_H{I}_V-({\mu }_H+\upsilon )S_H\\ \frac{d{P}_H}{dt}=\Pi {\Omega }_H+\left(1-\alpha \right)\eta R_H+\upsilon S_H-({\mu }_H+\theta )P_H\\ \begin{array}{c}\begin{array}{c}\frac{d{I}_H}{dt}={\beta }_H{S}_H{I}_V+\sigma L_H-\left(\gamma +{\mu }_H+\delta \right)I_H\\ \frac{d{L}_H}{dt}=\gamma \left(1-\tau \right)I_H-({\mu }_H+\sigma )L_H\\ \frac{d{R}_H}{dt}=\gamma \tau I_H-\left({\mu }_H+\eta \right)R_H\end{array}\\ \begin{array}{c}\frac{d{S}_V}{dt}=\Psi -{\beta }_V{S}_V{I}_H-{\mu }_V{S}_V\\ \begin{array}{c}\frac{d{I}_V}{dt}={\beta }_V{S}_V{I}_H-{\mu }_V{I}_V\end{array}\end{array}\end{array}\end{array}& (1)\end{array}$

With initial conditions:

$\begin{array}{c}{S}_H(0)=S_{H0},P_H(0)={P_{H0},I}_H(0)=I_{H0},L(0)=L_{H0},\\ R_H(0)=R_{H0},S_V(0)=S_{V0},I_V(0)=I_{V0}& (2)\end{array}$

The description of the state variables and parameters used in the model (Equation 1) is provided in the table below (Table 1). This table offers a comprehensive breakdown of each state variable and parameter outlining their definitions, roles within the model and the relationships they represent.

Table 1

Table 1. Description of the system's state variables and parameters.

2.3 Feasible region

The following outlines a biologically plausible region where model system (Equation 1) will be examined. Given that model system (Equation 1) split into two components, Δ = Δ_H× Δ_V.

Lemma 1. For model system (Equation 1), the feasible region Δ contains the solution set $\left\{S_H,{P_H,I}_H,L_H,R_H,S_V,I_V\right\}\in R_{+}^7$.

Proof: Assume that for any t>0, $\left\{S_H,{P_H,I}_H,L_H,R_H,S_V,I_V\right\}\in R_{+}^7$. To analyze the dynamics of model system (Equation 1), we demonstrate that the region Δ is positively invariant. This region is determined by considering the entire human population.

N_H(t) = S_H(t) + P_H + I_H(t) + L_H(t) + R_H(t) and differentiating both sides with respect to time. Adding the system's first four equations, we get the following:

$\begin{array}{l}\frac{d}{dt}(S_H+{P_H+I}_H+L_H+R_H)={\Omega }_H-{\mu }_H{N}_H-\delta I_H\\ \Rightarrow \frac{d}{dt}(S_H+{P_H+I}_H+L_H+R_H)\le {\Omega }_H-{\mu }_H{N}_H& (3)\end{array}$

$\begin{array}{ll}\frac{d{N}_H}{dt}\le {\Omega }_H-{\mu }_H{N}_H& (4)\end{array}$

Integrating and simplifying both sides of Equation 4, we get the following:

$\begin{array}{ll}{\Omega }_H-{\mu }_H{N}_H\ge A{e}^{-{\mu }_{H}t},& (5)\end{array}$

where A is a constant value. Using the initial conditions and rearranging Equation 5, we get the following equation:

$\begin{array}{ll}{N}_H\le \frac{{\Omega }_H}{{\mu }_H}-\frac{N_{H0}{e}^{-{\mu }_{H}t}}{{\mu }_H}& (6)\end{array}$

In Equation 6, as t → ∞ the total human population $N_H\to \frac{{\Omega }_H}{{\mu }_H}$, which indicates that $0\le N_H\le \frac{{\Omega }_H}{{\mu }_H}$. Thus, for the human population, the invariant region of system (Equation 1) is given by

$\begin{array}{ll}\begin{array}{r}\hfill {\Delta }_H=\{\left(S_H,P_H,I_H,L_H,R_H\right)ϵR_{+}^5:0\le S_H+P_H+I_H+L_H\\ \hfill +R_H\le \frac{{\Omega }_H}{{\mu }_H}\}\end{array}& (7)\end{array}$

is positively invariant.

Similarly, the total mosquito population of the system (Equation 1) is as follows:

$\begin{array}{ll}{N}_V(t)=S_V(t)+I_V(t).& (8)\end{array}$

Differentiating both sides of Equation 8 with respect to time, we get the following equation:

$\begin{array}{ll}\frac{d}{dt}(S_V+I_V)=\text{Ψ}-{\mu }_V{N}_V& (9)\end{array}$

$\begin{array}{ll}\frac{d{N}_V}{dt}=\text{Ψ}-{\mu }_V{N}_V& (10)\end{array}$

By solving Equation 10, we obtain $0\le N_V\le \frac{\text{Ψ}}{{\mu }_V}.$ Hence, the invariant region of system (Equation 1) for mosquito population is given by

$\begin{array}{ll}{\Delta }_V=\left\{(S_V,I_V)ϵR_{+}^2:0\le S_V+I_V\le \frac{\text{Ψ}}{{\mu }_V}\right\}& (11)\end{array}$

Therefore, the invariant region of the whole system for human and mosquito populations of system (Equation 1) is given by

$\begin{array}{ll}\begin{array}{r}\hfill \Delta ={\Delta }_H\times {\Delta }_V=\{\left(S_H,P_H,I_H,L_H,R_H,S_V,I_V\right)\\ \hfill ϵR_{+}^7:N_H\le \frac{{\Omega }_H}{{\mu }_H},N_V\le \frac{\Psi }{{\mu }_V}\}\end{array}& (12)\end{array}$

is positively invariant. Thus, all the solution set of system (Equation 1) is bounded in Δ.

2.4 Positivity of the solutions

It must be shown that for all t≥0, all solutions to system (Equation 1) with positive initial conditions will remain positive.

Theorem 2.4.1. The solution of model system (Equation 1) given by S_H(t),_{PH(t), IH}(t), L_H(t), R_H(t), S_V(t) and I_V(t) with non-negative initial conditions S_H(0),_{PH(0), IH}(0), L_H(0), R_H(0), S_V(0) and I_V(0) remains non-negative for all time t≥ 0.

Proof: We will demonstrate that all state variables in each equation of system (Equation 1) are positive.

Starting with the first equation of system (Equation 1), where we have

$\begin{array}{ll}\begin{array}{c}\frac{d{S}_H}{dt}=\left(1-\Pi \right){\Omega }_H+\theta P_H+\alpha \eta R_H-{\beta }_H{S}_H{I}_V-({\mu }_H+\upsilon )S_H\\ \frac{d{S}_H}{dt}\ge -({\beta }_H{I}_V+{\mu }_H+ \upsilon )S_H\end{array}& (13)\end{array}$

Integrating by applying the method of separation of variables along with initial conditions, we obtain

$\begin{array}{ll}{S}_H(t)\ge S_H(0)e^{-({\beta }_H{I}_V+{\mu }_H+\upsilon )t}\ge 0 & (14)\end{array}$

From the second equation in system (Equation 1), we obtain

$\begin{array}{r}\frac{d{P}_H}{dt}=\Pi {\Omega }_H+(1-\alpha )\eta R_H+\upsilon S_H-({\mu }_H+\theta )P_H\\ \frac{d{P}_H}{dt}\ge -({\mu }_H+\theta )P_H& (15)\end{array}$

Integrating by applying the method of separation of variables along with initial conditions, we obtain:

$\begin{array}{ll}{P}_H\left(t\right)\ge P_H\left(0\right)e^{-({\mu }_H+\theta )t}\ge 0& (16)\end{array}$

From the third equation of system (Equation 1), we obtain

$\begin{array}{r}\frac{d{I}_H}{dt}={\beta }_H{S}_H{I}_V+\sigma L_H-(\gamma +{\mu }_H+\delta )I_H\\ \frac{d{I}_H}{dt}\ge -({\mu }_H+\delta +\gamma )IH\ge 0& (17)\end{array}$

Integrating both sides by applying separation of variables, we obtain

$\begin{array}{ll}{I}_H(t)\ge I_H(0)e^{-(\gamma +{\mu }_H+\delta )t}\ge 0& (18)\end{array}$

From the fourth equation of system (Equation 1), we obtain

$\begin{array}{ll}\begin{array}{c}\frac{d{L}_H}{dt}=\gamma \left(1-\tau \right)I_H-({\mu }_H+\sigma )L_H\\ \frac{d{L}_H}{dt}\ge -({\mu }_H+\sigma )L_H\ge 0 \end{array}& (19)\end{array}$

Integrating by applying the method of separation of variables along with initial conditions, we obtain

$\begin{array}{ll}{L}_H\left(t\right)\ge L_H\left(0\right)e^{-({\mu }_H+\sigma )t}\ge 0& (20)\end{array}$

From the fifth equation of system (Equation 1), we have

$\begin{array}{c}\frac{d{R}_H}{dt}=\gamma \tau I_H-({\mu }_H+\eta )R_H\\ \frac{d{R}_H}{dt}\ge -({\mu }_H+\eta )R_H& (21)\end{array}$

Integrating by applying the method of separation of variables along with initial conditions, we obtain

$\begin{array}{ll}{R}_H\left(t\right)\ge R_H\left(0\right)e^{-({\mu }_H+\eta )t}\ge 0& (22)\end{array}$

From the sixth equation of system (Equation 1), we have

$\begin{array}{c}\frac{d{S}_V}{dt}=\text{Ψ}-{\beta }_V{S}_V{I}_H-{\mu }_V{S}_V\\ \frac{d{S}_V}{dt}\ge -({\beta }_V{I}_H+{\mu }_V)S_V& (23)\end{array}$

Integrating using separation of variables along with initial conditions, we obtain

$\begin{array}{ll}\Rightarrow S_V(t)\ge S_V(0)e^{-({\beta }_V{I}_H+{\mu }_V)t}& (24)\end{array}$

From the seventh equation of system (Equation 1), we have

$\begin{array}{c}\frac{d{I}_V}{dt}={\beta }_V{S}_V{I}_H-{\mu }_V{I}_V\\ \Rightarrow \frac{d{I}_V}{dt}\ge -{\mu }_V{I}_V& (25)\end{array}$

Integrating using separation of variables along with initial conditions, we obtain

$\begin{array}{ll}{I}_V(t)\ge I_V(0)e^{-{\mu }_{V}t}& (26)\end{array}$

3 Model analysis

3.1 Disease-free equilibrium point(s)

Disease-free equilibrium points (DFE) are steady-state solutions where the disease (malaria) is absent, meaning I_H = L_H = I_V = 0. The disease-free equilibrium in the model is determined by identifying

$\begin{array}{ll}\frac{d{S}_H}{dt}=\frac{d{P}_H}{dt}=\frac{d{I}_H}{dt}=\frac{d{L}_H}{dt}=\frac{d{R}_H}{dt}=\frac{d{S}_V}{dt}=\frac{d{I}_V}{dt}=0.& (27)\end{array}$

From the fifth equation of system (Equation 1), we have

$\begin{array}{r}\frac{d{R}_H}{dt}=\gamma \tau I_H-({\mu }_H+\eta )R_H=0\\ \Rightarrow \gamma \tau I_H-({\mu }_H+\eta )R_H=0\\ R_H^0=0& (28)\end{array}$

From the first equation of system (Equation 1), we obtain

$\begin{array}{r}\frac{d{S}_H}{dt}=(1-\Pi ){\Omega }_H+\theta P_H+\alpha \eta R_H-{\beta }_H{S}_H{I}_V\\ -({\mu }_H+\upsilon )S_H=0\\ (1-\Pi ){\Omega }_H+\theta P_H-({\mu }_H+\upsilon )S_H=0\\ \to S_H=\frac{(1-\Pi ){\Omega }_H+\theta P_H}{({\mu }_H+\upsilon )}& (29)\end{array}$

From the second equation of system (Equation 1), we have

$\begin{array}{l}\frac{d{P}_H}{dt}=\Pi {\Omega }_H+(1-\alpha )\eta R_H+\upsilon S_H-({\mu }_H+\theta )P_H=0\\ \Pi {\Omega }_H+\upsilon S_H-({\mu }_H+\theta )P_H=0\to P_H=\frac{\Pi {\Omega }_H+\upsilon S_H}{({\mu }_H+\theta )}& (30)\end{array}$

From Equations 29, 30, we obtain

$\begin{array}{ll}{S}_H^0=\frac{{\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}& (31)\end{array}$

$\begin{array}{r}{N}_H(0)=S_H^0+P_H^0=\frac{{\Omega }_H}{{\mu }_H}\to \frac{{\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ +P_H^0=\frac{{\Omega }_H}{{\mu }_H}\to P_H^0=\frac{{\Omega }_H(\upsilon +{\mu }_H\Pi )}{{\mu }_H({\mu }_H+\upsilon +\theta )}& (32)\end{array}$

From the sixth equation of the model system (Equation 1), we obtain

$\begin{array}{ll}\begin{array}{r}\hfill \frac{d{S}_V}{dt}=\Psi -{\beta }_V{S}_V{I}_H-{\mu }_V{S}_V=0\\ \hfill \Rightarrow \Psi -({\beta }_V(0)+{\mu }_V)S_V=0\Rightarrow \Psi -{\mu }_V{S}_V=0\\ \hfill \Rightarrow S_V^0=\frac{\Psi }{{\mu }_V}\end{array} & (33)\end{array}$

From the seventh equation of the model system (Equation 1), we obtain

$\begin{array}{ll}\frac{d{I}_V}{dt}={\beta }_V{S}_V{I}_H-{\mu }_V{I}_V=0\Rightarrow I_V^0=0& (34)\end{array}$

Therefore, the disease-free equilibrium point of system (Equation 1) is given by

$\begin{array}{r}{E}_0=(S_H^0,P_H^0,I_H^0,L_H^0,R_H^0,S_V^0,I_V^0)\\ =(\frac{{\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )},\frac{{\Omega }_H(\upsilon +{\mu }_H\Pi )}{{\mu }_H({\mu }_H+\upsilon +\theta )},0,0,0,\frac{\text{Ψ}}{{\mu }_V},0)& (35)\end{array}$

3.2 Effective reproduction number

Given that $F_i(x)$ represents the rate of appearance of new infections in compartment (i), $V_i^{+}(x)$ represents the rate of individual transfer into compartment (i), by all other ways, and $V_i^{-}(x)$ represents the rate of individual transfer out of compartment (i) [15]. Each function $({ℱ}_i,V_i^{+}$, and $V_i^{-})$ is considered to be continuously differentiable at least twice for each variable, and ${V_i=V}_i^{-}-V_i^{+}$. To take the infected compartments and use the next-generation technique to calculate the effective reproduction number. $\rho (F{V}^{-1})$ represents the dominant eigenvalue in magnitude, or spectral radius of the matrix $\left[\rho (F{V}^{-1})\right]$ where $F=\frac{\partial F_i(E_0)}{\partial x_j}$ and $V=\frac{\partial V_i(E_0)}{\partial x_j}$ where i≥1, denotes the number of compartments and 1 ≤ j ≤ n denotes the infected compartments only. Considering the model's infected compartments to be I_H, L_H and I_V, we now obtain

$ℱ=\left[\begin{array}{c}{\beta }_H{S}_H{I}_V\\ \begin{array}{c}0\\ {\beta }_V{S}_V{I}_H\end{array}\end{array}\right]andV=\left[\begin{array}{c}({\mu }_H+\delta +\gamma )I_H-\sigma L_H\\ \begin{array}{c}({\mu }_H+\sigma )L_H-\gamma \left(1-\tau \right)I_H\\ {\mu }_V{I}_V\end{array}\end{array}\right]$

Finding the Jacobian of Matrices $F$ and V with respect to I_H, L_H and I_V, we have

$\begin{array}{l}F=\left[\begin{array}{ccc}0& 0& {\beta }_H{S}_H\\ 0& 0& 0\\ {\beta }_V{S}_V& 0& 0\end{array}\right]andV=\left[\begin{array}{ccc}({\mu }_H+\delta +\gamma )& -\sigma & 0\\ -\gamma (1-\tau )& {\mu }_H+\sigma & 0\\ 0& 0& {\mu }_V\end{array}\right]\end{array}$

Jacobian of $F$ at disease-free equilibrium ($\epsilon \ast$) is given by

$\begin{array}{r}\hfill J(\epsilon \ast )=\left[\begin{array}{ccc}0& 0& \frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ 0& 0& 0\\ \frac{{\beta }_V\Psi }{{\mu }_V}& 0& 0\end{array}\right]and\\ \hfill V=\left[\begin{array}{ccc}({\mu }_H+\delta +\gamma )& -\sigma & 0\\ -\gamma \left(1-\tau \right)& {\mu }_H+\sigma & 0\\ 0& 0& {\mu }_V\end{array}\right]\end{array}$

where

$\begin{array}{l}\left|V\right|={\mu }_V\left[{\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau )\right]\end{array}$

We need to find the inverse of Matrix V to find the effective reproduction number (R_e).

Hence,

$\begin{array}{r}{V}^{-1}=\left[\begin{array}{ccc}\frac{{\mu }_V({\mu }_H+\sigma )}{\left|V\right|}& \frac{{\mu }_V\sigma }{\left|V\right|}& 0\\ \frac{{\mu }_V\gamma (1-\tau )}{\left|V\right|}& \frac{{\mu }_V({\mu }_H+\delta +\gamma )}{\left|V\right|}& 0\\ 0& 0& \frac{{\mu }_H({\mu }_H+\delta +\gamma +\sigma )+\sigma (\delta +\gamma \delta )}{\left|V\right|}\end{array}\right]\\ V^{-1}=\left[\begin{array}{ccc}\frac{({\mu }_H+\sigma )}{C}& \frac{\sigma }{C}& 0\\ \frac{\gamma (1-\tau )}{C}& \frac{({\mu }_H+\delta +\gamma )}{C}& 0\\ 0& 0& \frac{1}{{\mu }_V}\end{array}\right],\end{array}$

where $C={\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta + \gamma \tau )$

$\begin{array}{r}F{V}^{-1}=\left[\begin{array}{ccc}0& 0& \frac{{{\beta }_H\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ 0& 0& 0\\ \frac{{\beta }_V\text{Ψ}}{{\mu }_V}& 0& 0\end{array}\right]\left[\begin{array}{ccc}\frac{({\mu }_h+\sigma )}{C}& \frac{\sigma }{C}& 0\\ \frac{\gamma (1-\tau )}{C}& \frac{({\mu }_h+\delta +\gamma )}{C}& 0\\ 0& 0& \frac{1}{{\mu }_v}\end{array}\right]\end{array}$

$\begin{array}{r}F{V}^{-1}=\left[\begin{array}{ccc}0& 0& \frac{{{\beta }_H\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H{\mu }_V({\mu }_H+\upsilon +\theta )}\\ 0& 0& 0\\ \frac{{\beta }_V\text{Ψ}({\mu }_H+\sigma )}{{\mu }_V({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}& \frac{{\beta }_v\text{Ψ}\sigma }{{\mu }_V({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}& 0\end{array}\right]\end{array}$

Finding the eigenvalues of $F{V}^{-1}$ at the disease-free equilibrium point(s) is

$\begin{array}{c}\left|\begin{array}{ccc}-\lambda & 0& \frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H{\mu }_V({\mu }_H+\upsilon +\theta )}\\ 0& -\lambda & 0\\ \frac{{\beta }_V\Psi ({\mu }_H+\sigma )}{{\mu }_V({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}& \frac{{\beta }_V\psi \sigma }{{\mu }_V({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}& -\lambda \end{array}\right|\\ -\lambda \left({\lambda }^2\right)+\frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H{\mu }_V({\mu }_H+\upsilon +\theta )}\\ \left(\lambda \frac{{\beta }_V\Psi ({\mu }_H+\sigma )}{{\mu }_V({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}\right)=0\end{array}$

The characteristic equation is as follows:

$\begin{array}{ll}\begin{array}{c}-{\lambda }^3\\ +\left(\lambda \frac{{\beta }_H{\beta }_V\Psi ({\mu }_H+\sigma ){\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H{\mu }_V({\mu }_H+\upsilon +\theta ){\mu }_V({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}\right)=0\\ \lambda \left(\frac{{\beta }_H{\beta }_V\Psi ({\mu }_H+\sigma ){\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H{\mu }_V({\mu }_H+\upsilon +\theta ){\mu }_V({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}-{\lambda }^2\right)=0\end{array}& (36)\end{array}$

$\begin{array}{ll}J\text{(}\epsilon \ast \text{)}=\left[\begin{array}{ccccccc}-({\mu }_H+\upsilon )& \theta & 0& 0& \alpha \eta & 0& -\frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ \upsilon & -({\mu }_H+\theta )& 0& 0& \left(1-\alpha \right)\eta & 0& 0\\ 0& 0& -\left(\gamma +{\mu }_H+\delta \right)& \sigma & 0& 0& \frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ 0& 0& \gamma \left(1-\tau \right)& -\left({\mu }_H+\sigma \right)& 0& 0& 0\\ 0& 0& \gamma \tau & 0& -\left({\mu }_H+\eta \right)& 0& 0\\ 0& 0& -\frac{{\beta }_V\Psi }{{\mu }_v}& 0& 0& -{\mu }_V& 0\\ 0& 0& \frac{{\beta }_V\Psi }{{\mu }_V}& 0& 0& 0& -{\mu }_V\end{array}\right] & (37)\end{array}$

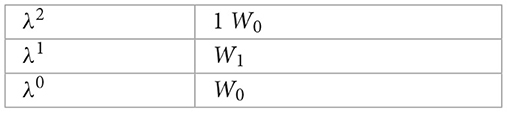
From Equation 36, the Eigen values of the characteristic equation can be obtained as follows:

$\begin{array}{ll}\begin{array}{c}\lambda =0,\frac{{\beta }_H{\beta }_V\Psi D_4{\Omega }_H({\mu }_h\left(1-\Pi \right)+\theta )}{{\mu }_H{\mu }_V^2({\mu }_H+\upsilon +\theta )({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}\\ -{\lambda }^2=0,\end{array}& (38)\end{array}$

where D₄ = (μ_H+ σ)

From Equation 37, we have

$\begin{array}{c}\frac{{{\beta }_H{\beta }_V\Psi \Omega }_H({\mu }_H(1-\Pi )+\theta )({\mu }_H+\sigma )}{{\mu }_H{\mu }_V^2({\mu }_H+\upsilon +\theta )({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}\\ -{\lambda }^2=0\\ \lambda =\pm \sqrt{\frac{{{\beta }_H{\beta }_V\Psi \Omega }_H({\mu }_H(1-\Pi )+\theta )({\mu }_H+\sigma )}{{\mu }_H{\mu }_V^2({\mu }_H+\upsilon +\theta )({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}}\end{array}$

Therefore, the effective reproduction number (R_e) is the maximum Eigen value or the spectral radius of $F{V}^{-1}$:

$\begin{array}{ll}{R}_e=\sqrt{\frac{{{\beta }_H{\beta }_V\Psi \Omega }_H({\mu }_H(1-\Pi )+\theta )({\mu }_H+\sigma )}{{\mu }_H{\mu }_V^2({\mu }_H+\upsilon +\theta )({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}}& (39)\end{array}$

Hence, the effective reproduction number is computed as $\rho (F{V}^{-1}),$ where ρ represents the spectral radius of $F{V}^{-1},$ which corresponds to its dominant eigenvalue.

3.3 Local stability of disease-free equilibrium

Theorem 3.3.1. If R_e < 1, the disease-free equilibrium point(s) of the system (Equation 1) is locally asymptotically stable in Δ.

Proof: To prove Theorem 3.3.1, we first calculate the Jacobian matrix of system (Equation 1):

where: (Equation 39)

$\begin{array}{r}{D}_1=({\mu }_H+\delta +\gamma ),D_2=\sigma ,D_3=\gamma (1-\tau ),\\ D_4=({\mu }_H+\sigma )\text{and let }{D}_5=({\mu }_H+\upsilon ),\\ D_6=({\mu }_H+\theta ),D_7=(1-\alpha )\eta ,D_8=({\mu }_H+\eta )& (40)\end{array}$

The eigenvalues of the Jacobian matrix are obtained by solving the characteristic equation: $\left|J(\epsilon \ast )-\lambda I\right|= 0$

$\begin{array}{ll}\left|\begin{array}{ccccccc}-D_5-\lambda & \theta & 0& 0& \alpha \eta & 0& -\frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ \upsilon & -D_6-\lambda & 0& 0& D_7& 0& 0\\ 0& 0& -D_1-\lambda & D_2& 0& 0& \frac{{\beta }_H{\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ 0& 0& D_3& -D_4-\lambda & 0& 0& 0\\ 0& 0& \gamma \tau & 0& -D_8-\lambda & 0& 0\\ 0& 0& -\frac{{\beta }_V\Psi }{{\mu }_V}& 0& 0& -{\mu }_V-\lambda & 0\\ 0& 0& \frac{{\beta }_V\Psi }{{\mu }_V}& 0& 0& 0& -{\mu }_V-\lambda \end{array}\right|=0& (41)\end{array}$

We focus on the first and second columns of the 7 × 7 matrix. When considering the fifth and the sixth columns, we the result is a zero matrix due to the presence of zero-column matrices in the reduction process. Thus, we have two eigenvalues: _{λ1 = −μV} < 0 and λ₂ = −D₈ = −(μ_H+η) < 0. The remaining eigenvalues can be derived from the rest of the matrix.

$\begin{array}{l}\left|\begin{array}{ccccc}-D_5-\lambda & \theta & 0& 0& -\frac{{{\beta }_H\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ \upsilon & -D_6-\lambda & 0& 0& 0\\ 0& 0& -D_1-\lambda & D_2& \frac{{{\beta }_H\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}\\ 0& 0& D_3& -D_4-\lambda & 0\\ 0& 0& \frac{{\beta }_V\text{Ψ}}{{\mu }_V}& 0& -{\mu }_V-\lambda \end{array}\right|=0\end{array}$

Let $B=\frac{{{\beta }_H\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )}$ and $A=\frac{{\beta }_V\text{Ψ}}{{\mu }_V}$

$\begin{array}{r}\left|\begin{array}{ccccc}-D_5-\lambda & \theta & 0& 0& -B\\ \upsilon & -D_6-\lambda & 0& 0& 0\\ 0& 0& -D_1-\lambda & D_2& B\\ 0& 0& D_3& -D_4-\lambda & 0\\ 0& 0& A& 0& -{\mu }_V-\lambda \end{array}\right|=0\\ (-D_5-\lambda )(-D_6-\lambda )\left|\begin{array}{ccc}-D_1-\lambda & D_2& B\\ D_3& -D_4-\lambda & 0\\ A& 0& -{\mu }_v-\lambda \end{array}\right|\\ -\theta \upsilon \left|\begin{array}{ccc}-D_1-\lambda & D_2& B\\ D_3& -D_4-\lambda & 0\\ A& 0& -{\mu }_V-\lambda \end{array}\right|=0\\ \left[(-D_5-\lambda )(-D_6-\lambda )-\theta \upsilon \right]\left|\begin{array}{ccc}-D_1-\lambda & D_2& B\\ D_3& -D_4-\lambda & 0\\ A& 0& -{\mu }_V-\lambda \end{array}\right|=0& (42)\end{array}$

The characteristic equation of the first sub-matrix (Equation 42) is

$\begin{array}{r}(-D_5-\lambda )(-D_6-\lambda )-\theta \upsilon =0\\ {\lambda }^2+W_1\lambda +W_0=0,& (43)\end{array}$

where

$\begin{array}{r}{W}_1=D_5+D_6=2{\mu }_H+\theta +\upsilon ,W_0=D_5{D}_6\\ {-\theta \upsilon =\mu }_H({\mu }_H+\theta +\upsilon )\end{array}$

$\begin{array}{ll}\begin{array}{c}\left({\mu }_V+D_1+D_4\right)>0,\frac{\left({\mu }_V+D_1+D_4\right)\left[{\mu }_v\left(D_1+D_4\right)+D_1{D}_4-D_2{D}_3-AB\right]-\left(D_1{D}_4{\mu }_v-D_2{D}_3{\mu }_V-AB{D}_4\right)}{\left({\mu }_V+D_1+D_4\right)}>0,\\ \left(D_1{D}_4{\mu }_v-D_2{D}_3{\mu }_V-AB{D}_4\right)>0\end{array}& (44)\end{array}$

We use the Routh Hurwitz matrix array to show that all eigenvalues of Equation 43 have negative real parts.

According to Routh-Hurwitz stability criteria, all eigenvalues of the characteristic Equation 43 have negative real parts if all terms of the first column of the Routh array are positive. Therefore, from the Routh array above, W₁ = (2μ_H+θ+υ)>0 and W₀ = μ_H(μ_H+θ+υ)>0. Therefore, using the Routh-Hurwitz stability criterion, the two eigenvalues λ₃ and λ₄ of the Jacobian matrix have negative real parts.

From the second sub-matrix of the matrix (Equation 42), we have

$\begin{array}{ll}\begin{array}{r}\hfill \left|\begin{array}{ccc}-D_1-\lambda & D_2& B\\ D_3& -D_4-\lambda & 0\\ A& 0& -{\mu }_V-\lambda \end{array}\right|=0\\ \hfill \left(-D_1-\lambda \right)\left|\begin{array}{cc}-D_4-\lambda & 0\\ 0& -{\mu }_V-\lambda \end{array}\right|\\ \hfill -D_2\left|\begin{array}{cc}{D}_3& 0\\ A& -{\mu }_V-\lambda \end{array}\right|+B\left|\begin{array}{cc}{D}_3& -D_4-\lambda \\ A& 0\end{array}\right|=0\end{array}& (45)\end{array}$

$\begin{array}{r}{-\lambda }^3-({\mu }_V+D_1+D_4){\lambda }^2-({\mu }_V(D_1+D_4)+D_1{D}_4)\lambda \\ -D_1{D}_4{\mu }_V+D_2{D}_3{\mu }_V+D_2{D}_3\lambda +AB{D}_4+AB\lambda =0& (46)\end{array}$

Rearranging the like terms in Equation 45 and multiplying both sides by −1 results in:

$\begin{array}{ll}\begin{array}{r}\hfill {\lambda }^3+\left({\mu }_V+D_1+D_4\right){\lambda }^2+({\mu }_V\left(D_1+D_4\right)+D_1{D}_4\\ \hfill -D_2{D}_3-AB)\lambda +\left(D_1{D}_4{\mu }_V-D_2{D}_3{\mu }_V-AB{D}_4\right)=0\end{array}& (47)\end{array}$

The characteristic polynomial is given by

$\begin{array}{ll}{\lambda }^3+N_2{\lambda }^2{+N}_1\lambda +N_0=0,& (48)\end{array}$

where

$\begin{array}{r}{N}_2=({\mu }_V+D_1+D_4),\\ N_1={{\mu }_v(D_1+D_4)+D}_1{D}_4-D_2{D}_3-AB\\ \text{and }{N}_0=(D_1{D}_4{\mu }_v-D_2{D}_3{\mu }_V-AB{D}_4)& (49)\end{array}$

Now, we use Routh-Hurwitz stability criteria to show that the condition of the characteristic Equation 47 all have eigenvalues with negative real parts:

From the above Routh Hurwitz all eigenvalues of the characteristic Equation 47 have negative real parts if the first column of the Routh array is non-negative, as shown below:

From Equation 49

$\begin{array}{c}\frac{({\mu }_V+D_1+D_4)\left[{{\mu }_v(D_1+D_4)+D}_1{D}_4-D_2{D}_3-AB\right]-(D_1{D}_4{\mu }_v-D_2{D}_3{\mu }_V-AB{D}_4)}{({\mu }_V+D_1+D_4)}\\ =\frac{({\mu }_V+D_1+D_4)\left[{{\mu }_v(D_1+D_4)+D}_1{D}_4\right]+D_2{D}_3{\mu }_V+AB{D}_4-\left[({\mu }_V+D_1+D_4)(D_2{D}_3+AB)\right]}{({\mu }_V+D_1+D_4)}\\ >0& (50)\end{array}$

is true if

$\begin{array}{c}\left[({\mu }_V+D_1+D_4)\left[{{\mu }_v(D_1+D_4)+D}_1{D}_4\right]+D_2{D}_3{\mu }_V+AB{D}_4\right]\\ >\left[({\mu }_V+D_1+D_4)(D_2{D}_3+AB)\right]& (51)\end{array}$

and

$\begin{array}{ll}(D_1{D}_4{\mu }_v-D_2{D}_3{\mu }_V-AB{D}_4)>0& (52)\end{array}$

divide Equation 52 both sides by D₁D₄μ_V−D₂D₃μ_V yields.

$\begin{array}{c}1-\frac{AB{D}_4}{{\mu }_V(D_1{D}_4-D_2{D}_3)}\to 1\\ -\frac{{{\beta }_H{\beta }_V\Psi \Omega }_H({\mu }_H(1-\Pi )+\theta )({\mu }_H+\sigma )}{{{\mu }_V}^2{\mu }_H({\mu }_H+\upsilon +\theta )({\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau ))}\\ \Rightarrow 1-R_e>0.Thisistrueif{R}_e<1.\end{array}$

Therefore, if all the above conditions are satisfied, including R_e < 1, all the first columns of the Routh Hurwitz array are positive. Consequently, the remaining eigenvalues λ₅, λ₆ and λ₇ of the Jacobian at the disease-free equilibrium have a negative real part. This indicates that the disease-free equilibrium point ₀ is locally asymptotically stable if R_e < 1 and unstable if R_e> 1.

3.4 Global stability of disease-free equilibrium point

Theorem 3.4.1 (Global stability of the disease-free equilibrium point): For system (Equation 1), the disease-free equilibrium is globally asymptotically stable in the feasible region if $R_e<1$.

Proof: To demonstrate the global asymptotic stability of the equilibrium point ₀, we employ the Lyapunov function method. We establish an appropriate Lyapunov function V(t) using the approach outlined in [16].

V = E₁I_H+E₂L_H+E₃I_V, where E₁, E₂, and E₃ are positive constants, and I_H, L_H and I_V are positive state variables.

$\begin{array}{ll}\frac{dV}{dt}=E_1\frac{d{I}_H}{dt}+E_2\frac{d{L}_H}{dt}+E_3\frac{d{I}_V}{dt}& (53)\end{array}$

By substituting expressions for $\frac{d{I}_H}{dt},\frac{d{L}_H}{dt},$and $\frac{d{I}_V}{dt}$ from the system (Equation 1) to Equation 53 and simplifying it by collecting like terms of the equation we obtain the following:

$\begin{array}{r}\hfill \frac{dV}{dt}=E_1{\beta }_H{S}_H{I}_V+E_1\sigma L_H-E_1\left(\gamma +{\mu }_H+\delta \right)I_H\\ \hfill +E_2\gamma \left(1-\tau \right)I_H-E_2\left({\mu }_H+\sigma \right)L_H+E_3{\beta }_V{S}_V{I}_H-E_3{\mu }_V{I}_V\\ \hfill \frac{dV}{dt}=(E_3{\beta }_V{S}_v+E_2\gamma \left(1-\tau \right)\\ \hfill -E_1\left(\gamma +{\mu }_H+\delta \right))I_H\\ \hfill +\left(E_1\sigma -E_2\left({\mu }_H+\sigma \right)\right)L_H+(E_1{\beta }_H{S}_H-E_3{\mu }_V)I_V\end{array}$

Taking the coefficients of I_H and L_H equal with zero, we obtain

$\begin{array}{ll}\frac{dV}{dt}=(E_1{\beta }_H{S}_H-E_3{\mu }_V)I_V& (54)\end{array}$

From the coefficient of L_H, we have $E_1\sigma -E_2({\mu }_H+\sigma )=0\Rightarrow E_1=\frac{({\mu }_H+\sigma )}{\sigma }{E}_2$

From the coefficient of I_H, we have

$\begin{array}{r}{E}_3{\beta }_V{S}_V+E_2\gamma (1-\tau )-E_1(\gamma +{\mu }_H+\delta )=0\\ \text{but }{E}_1=\frac{({\mu }_H+\sigma )}{\sigma }{E}_2\\ E_3{\beta }_V{S}_V=\frac{({\mu }_H+\sigma )(\gamma +{\mu }_H+\delta )}{\sigma }{E}_2{-E}_2\gamma (1-\tau )\\ E_3{\beta }_v{S}_V=\frac{\left[({\mu }_H+\sigma )(\gamma +{\mu }_H+\delta )-\sigma \gamma (1-\tau )\right]E_2}{\sigma }\\ \Rightarrow E_3=\frac{\left[({\mu }_H+\sigma )(\gamma +{\mu }_H+\delta )-\sigma \gamma (1-\tau )\right]E_2}{{\beta }_V{S}_V\sigma }& (55)\end{array}$

Substituting $E_1=\frac{({\mu }_H+\sigma )}{\sigma }{E}_2$ and Equation 55 in Equation 54, we obtain

$\begin{array}{r}\hfill \frac{dV}{dt}=(\frac{{\beta }_H{S}_H\left({\mu }_H+\sigma \right)}{\sigma }{E}_2\\ \hfill -\frac{{\mu }_V\left[\left({\mu }_H+\sigma \right)\left(\gamma +{\mu }_H+\delta \right)-\sigma \gamma \left(1-\tau \right)\right]E_2}{{\beta }_V{S}_V\sigma })I_V\end{array}$

Multiplying the right-side terms by $\frac{{\beta }_V{S}_V\sigma }{{\mu }_V\left[({\mu }_H+\sigma )(\gamma +{\mu }_H+\delta )-\sigma \gamma (1-\tau )\right]E_2}$, we obtain

$\begin{array}{r}\hfill \frac{dV}{dt}=(\frac{{\beta }_H{S}_H{\beta }_V{S}_V\left({\mu }_H+\sigma \right)}{{\mu }_V\left[\left({\mu }_H+\sigma \right)\left(\gamma +{\mu }_H+\delta \right)-\sigma \gamma \left(1-\tau \right)\right]}-1)I_v,\\ \hfill \text{where }{S}_V=\frac{\Psi }{{\mu }_V}\text{ and }{S}_H=\frac{{\Omega }_H\left({\mu }_H\left(1-\Pi \right)+\theta \right)}{{\mu }_H\left({\mu }_H+\upsilon +\theta \right)}\end{array}$

Hence,

$\begin{array}{c}\frac{dV}{dt}\\ =(\frac{{\beta }_H{\beta }_V{\Omega }_H\text{Ψ}({\mu }_H(1-\Pi )+\theta )({\mu }_H+\sigma )}{{\mu }_V^2{\mu }_H({\mu }_H+\upsilon +\theta )\left[{\mu }_H({\mu }_H+\sigma +\delta +\gamma )+\sigma (\delta +\gamma \tau )\right]}-1)I_v=\left[R_e^2-1\right]I_V.\end{array}$

Therefore, if $R_e\le 1,$then $\left[R_e^2-1\right]I_V\le 0$. Accordingly, we obtain $\frac{dV}{dt}\le 0$. Furthermore, $\frac{dV}{dt}=0$ if and only if I_V = 0. This shows that the disease-free equilibrium point $E_0=(\frac{{\Omega }_H({\mu }_H(1-\Pi )+\theta )}{{\mu }_H({\mu }_H+\upsilon +\theta )},\frac{{\Omega }_H(\upsilon +{\mu }_H\Pi )}{{\mu }_H({\mu }_H+\upsilon +\theta )},0,0,0,\frac{\text{Ψ}}{{\mu }_V},0)$ is globally asymptotically stable.

Remarks on stability analysis based on the effective reproduction number

i. If R_e < 1, the disease-free equilibrium is stable, and the endemic equilibrium does not exist.

ii. If R_e>1, the disease-free equilibrium is unstable, and an endemic equilibrium may exist and be stable.

4 Sensitivity analysis of model parameters

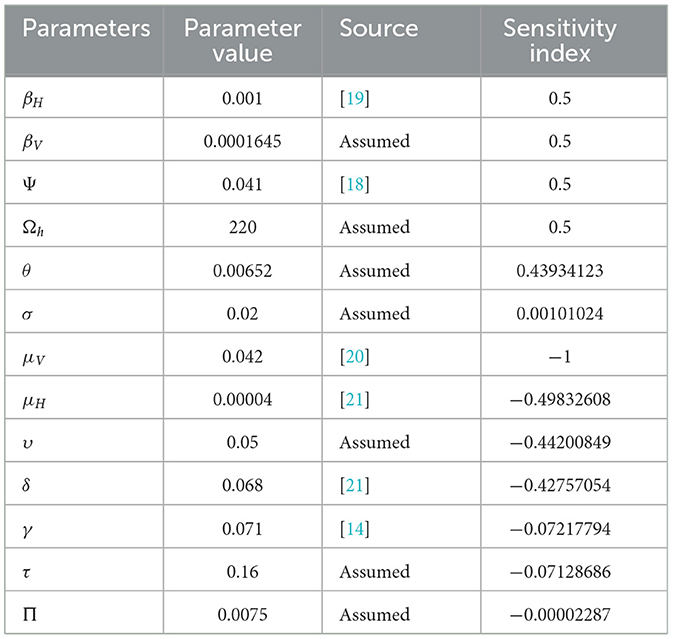
The parameters within the model system (Equation 1) have their own influence on the value of the effective reproduction number. Sensitivity analysis is used to determine which parameters have a significant impact on the effective reproduction number R_e, applying the method outlined in references [17, 18] to conduct the analysis.

Definition 4.1. The normalized forward sensitivity index of R_e, differentiable with respect to a given basic parameter k is defined as $\underset{\kappa }{R_e}=\frac{\partial R_e}{\partial \kappa }x\frac{\kappa }{R_e}$ [17, 18]:

We establish the sensitivity of every basic parameter in R_e as follows:

$\begin{array}{l}{R}_e=\sqrt{\frac{{\beta }_H{\beta }_V\psi {\Omega }_H({\mu }_H\left(1-\Pi \right)+\theta )\left({\mu }_H+\sigma \right)}{{\mu }_H{\mu }_V^2({\mu }_H+\upsilon +\theta )({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma (\delta +\gamma \tau ))}} \\ \{\begin{array}{c}{T}_{{\beta }_H}^{R_e}=\frac{\partial R_e}{\partial {\beta }_H}\times \frac{{\beta }_H}{R_e}=+\frac{1}{2}\\ T_{{\beta }_V}^{R_e}=\frac{\partial R_e}{\partial {\beta }_V}\times \frac{{\beta }_V}{R_e}=+\frac{1}{2}\\ T_{\Psi }^{R_e}=\frac{\partial R_e}{\partial \Psi }\times \frac{\Psi }{R_e}=+\frac{1}{2}\\ T_{{\Omega }_h}^{R_e}=\frac{\partial R_e}{\partial {\Omega }_h}\times \frac{{\Omega }_h}{R_e}=+\frac{1}{2}\\ T_{\theta }^{R_e}=\frac{\partial R_e}{\partial \theta }\times \frac{\theta }{R_e}=\frac{\theta [\left({\mu }_H+\upsilon +\theta \right)-\left({\mu }_H\left(1-\Pi \right)+\theta \right)]}{2[\left({\mu }_H\left(1-\Pi \right)+\theta \right)\left({\mu }_H+\upsilon +\theta \right)]}\\ T_{\sigma }^{R_e}=\frac{\partial R_e}{\partial \sigma }\times \frac{\sigma }{R_e}=\frac{\sigma [{\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma \left(\delta +\gamma \tau \right)-\left({\mu }_H+\sigma \right)\left({\mu }_H+\delta +\gamma \tau \right)]}{2[\left({\mu }_H\left({\mu }_H+\sigma +\delta +\gamma \right)+\sigma \left(\delta +\gamma \tau \right)\right)\left({\mu }_H+\sigma \right)]}\\ T_{{\mu }_V}^{R_e}=\frac{\partial R_e}{\partial {\mu }_V}\times \frac{{\mu }_V}{R_e}=-1\\ S_{{\mu }_H}^{R_e}=\frac{\partial R_e}{\partial {\mu }_H}\times \frac{{\mu }_H}{R_e}\\ T_{\delta }^{R_e}=\frac{\partial R_e}{\partial \delta }\times \frac{\delta }{R_e}=-\frac{1}{2}\frac{\left({\mu }_H+\sigma \right)\delta }{{\mu }_H\left({\mu }_H+\delta +\gamma +\sigma \right)+\sigma \left(\gamma \tau +\delta \right)}\\ T_{\gamma }^{R_e}=\frac{\partial R_e}{\partial \gamma }\times \frac{\gamma }{R_e}=-\frac{1}{2}\frac{\gamma \left(\tau \sigma +{\mu }_H\right)}{{\mu }_H\left({\mu }_H+\delta +\gamma +\sigma \right)+\sigma \left(\gamma \tau +\delta \right)}\\ T_{\tau }^{R_e}=\frac{\partial R_e}{\partial \tau }\times \frac{\tau }{R_e}=-\frac{1}{2}\frac{\gamma \sigma \tau }{{\mu }_H\left({\mu }_H+\delta +\gamma +\sigma \right)+\sigma \left(\gamma \tau +\delta \right)}\\ T_{\upsilon }^{R_e}=\frac{\partial R_e}{\partial \upsilon }\times \frac{\upsilon }{R_e}=-\frac{1}{2}\frac{\upsilon }{{\mu }_H+\upsilon +\theta }\\ T_{\Pi }^{R_e}=\frac{\partial R_e}{\partial \Pi }\times \frac{\Pi }{R_e}=-\frac{1}{2}\frac{{\mu }_H\Pi }{{\mu }_H(1-\Pi )+\theta }\end{array}\end{array}$

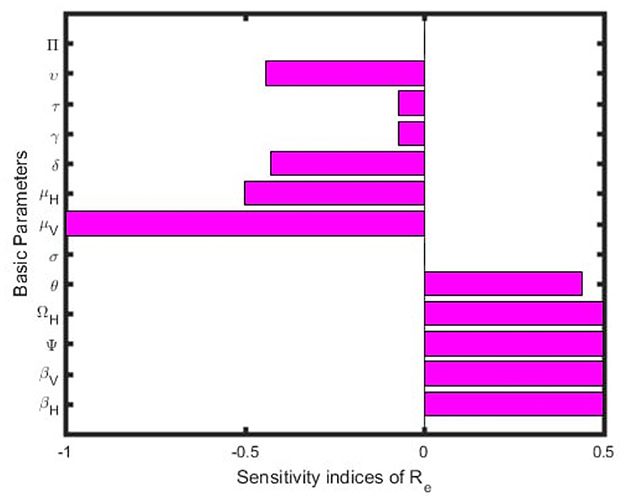
Figure 2 presents a sensitivity analysis of the effective reproductive number R_e with respect to 13 basic parameters, based on the values of the parameters provided in Table 2. From this analysis, we conclude that the parameters β_H, β_V, Ψ, Ω_h, and θ, which have positive sensitivity indices, contribute to an increase R_e as their values rise, provided other parameters remain constant. Conversely, the basic parameters μ_V, μ_H, δ, υ, γ, and τ have negative sensitivity indices, potentially mitigating malaria transmission while other parameters are held constant.

Figure 2

Figure 2. Graph of sensitivity indices of the effective reproduction number.

Table 2

Table 2. Parameters and their sensitivity indices for model (1) (units: day⁻¹).

5 Numerical simulations

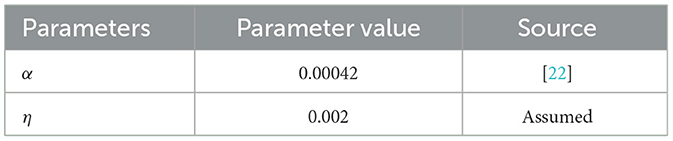
Presented here are the numerical simulations for the system described in Equation 1. The solutions obtained using MATLAB, within the time interval t ∈ [0, T] = [0, 100], along with the parameter values provided in Tables 2, 3. The initial conditions for each compartment are assumed as follows:

Table 3

Table 3. Parameters and their corresponding values for model (1) (units: day⁻¹).

S_H = 20, 000, P_H = 100, I_H = 50, L_H = 50, R_H = 100, S_V = 1, 000, and I_V = 100.

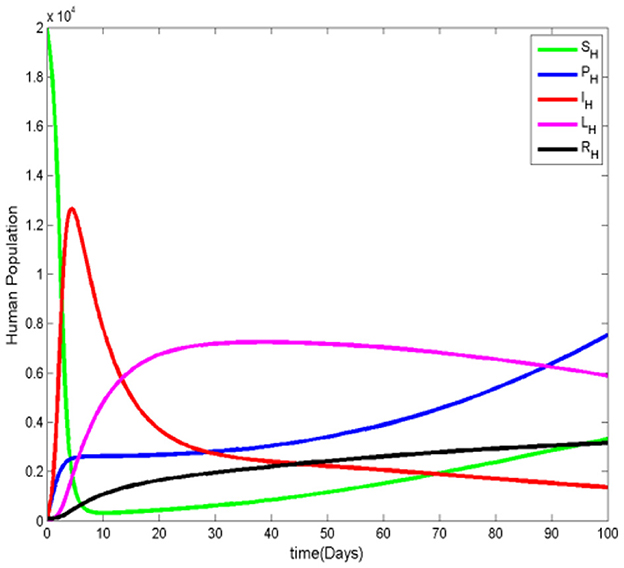
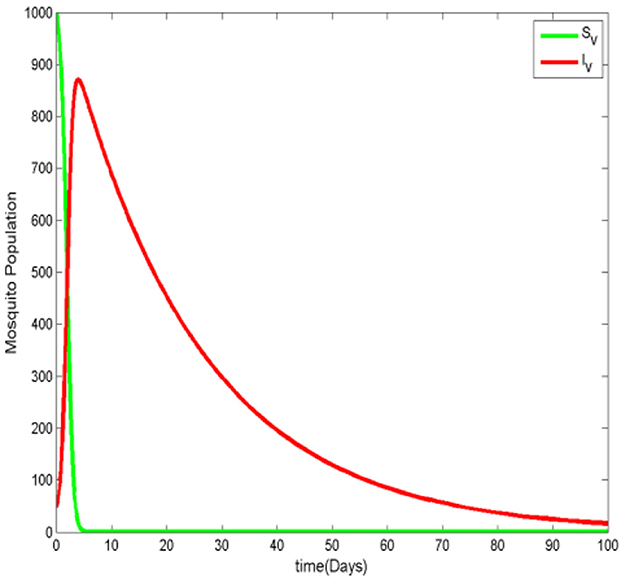
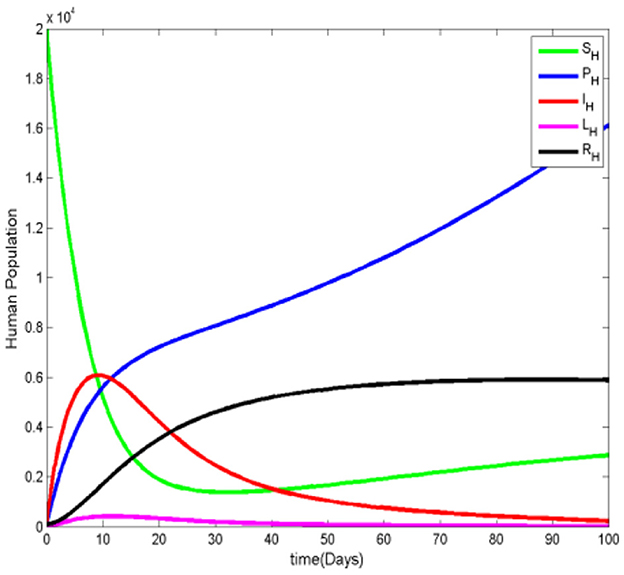
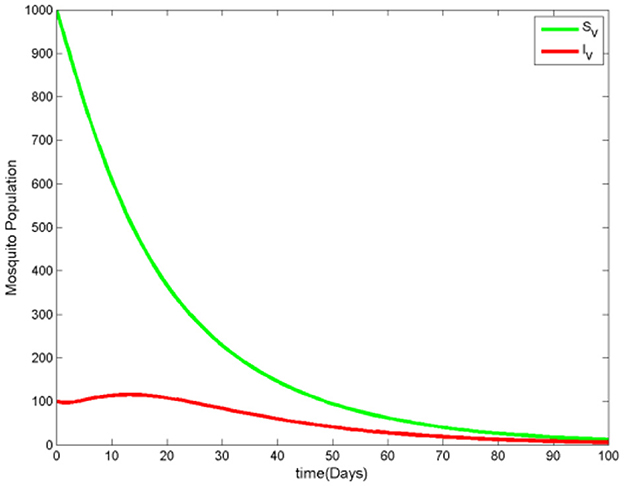
Figures 3, 4 illustrate the malaria transmission model when $R_e>1$. From Figure 3, we observe that although the number of infected humans decreases over time, the number of infected ignorant humans increases initially, indicating that malaria persists in the population. Additionally, the number of susceptible humans decreases as the protected human population grows. In Figure 4, we observe that the number of susceptible mosquitoes decreases, while the number of infected mosquitoes increases. However, after some time, the infected mosquito population also declines as humans become more aware and adopt mosquito-prevention measures, reducing mosquitos' access to essential resources for their survival.

Figure 3

Figure 3. The human population when $R_e=5.5381$.

Figure 4

Figure 4. The mosquito population when $R_e=5.5381$.

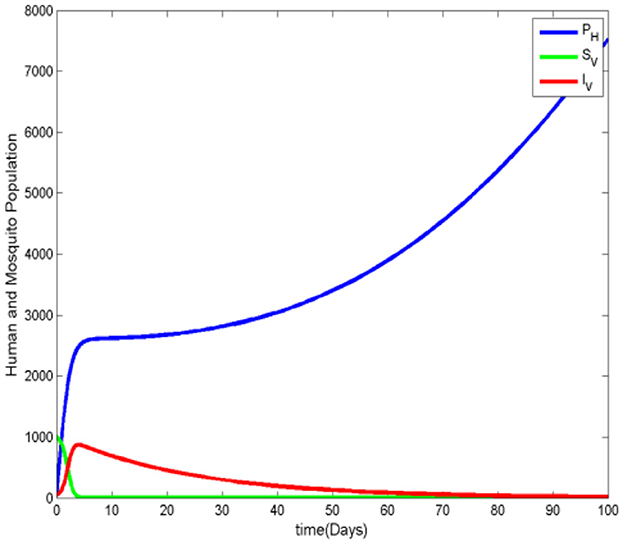
Figure 5 shows a steady increase in the number of protected humans. Initially, the susceptible human population drops sharply as the number of protected and infected humans increases. However, as the number of infected humans declines, the susceptible population begins to rise again and eventually stabilizes. The number of recovered humans also increases, while the infected ignorant individuals show no significant growth. This trend suggests that people adopt mosquito protective measures to avoid contact with the vector, reducing the spread of malaria. In Figure 6, we observe that the susceptible mosquito population decreases from the beginning, alongside a decline in the overall mosquito population, both susceptible and infected. This decrease occurs because mosquitoes struggle to find human hosts for blood meals, which are essential for their survival, as the human population increasingly adopts protective measures. Figure 7 reinforces the observation that as the protected human population grows, the number of both susceptible and infected mosquitoes decreases. This supports the overall pattern shown in the previous figures, highlighting the impact of human preventive behavior on reducing the mosquito population and, consequently, malaria transmission.

Figure 5

Figure 5. The human population when $R_e=0.0586$.

Figure 6

Figure 6. The mosquito population when $R_e=0.0586$.

Figure 7

Figure 7. Human and mosquito population.

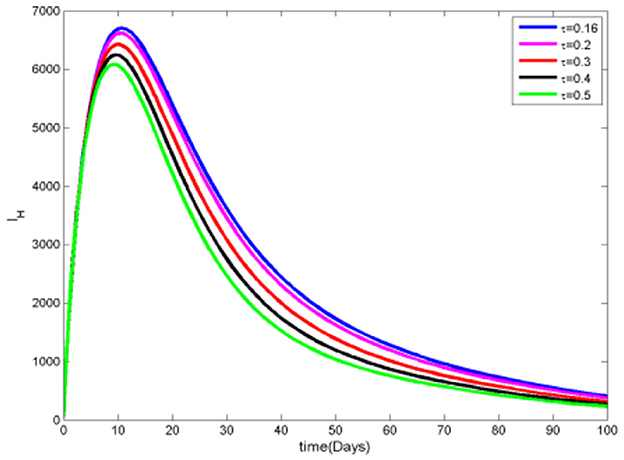
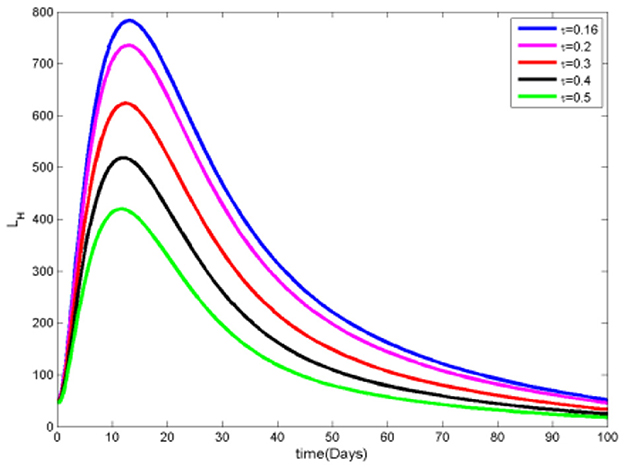
The data in Figures 8, 9 clearly show that as the proportion of infected individuals receiving treatment increases, the number of both infected and infected ignorant individuals decreases. This trend occurs because, as more infected individuals receive effective treatment, the probability of recovery from the disease rises, leading them to move into the recovered category. Consequently, increased access to treatment not only reduces the total number of infected individuals but also diminishes the pool of those who are infected and ignorant of their infection status.

Figure 8

Figure 8. Infected Humans at various τ values.

Figure 9

Figure 9. Infected ignorant humans at various τ values.

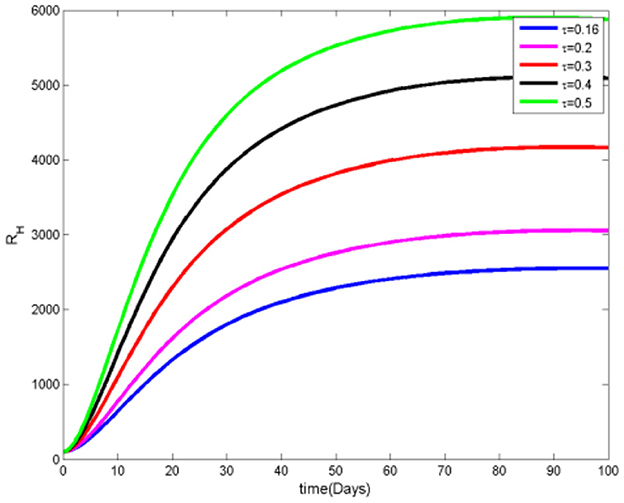
Figures 10, 11 indicate that, initially, the number of recovered individuals increases as both the proportion and rate of infectious humans receiving treatment rise. However, this upward trend gradually reverses, leading to a decline in the number of recovered individuals as more people adopt mosquito protective measures. This shift suggests that while treatment initially supports recovery rates, the increased use of preventive actions impacts the spread and recovery dynamics, ultimately reducing the number of new cases requiring recovery.

Figure 10

Figure 10. Recovered humans at various τ values.

Figure 11

Figure 11. Recovered humans at various γ values.

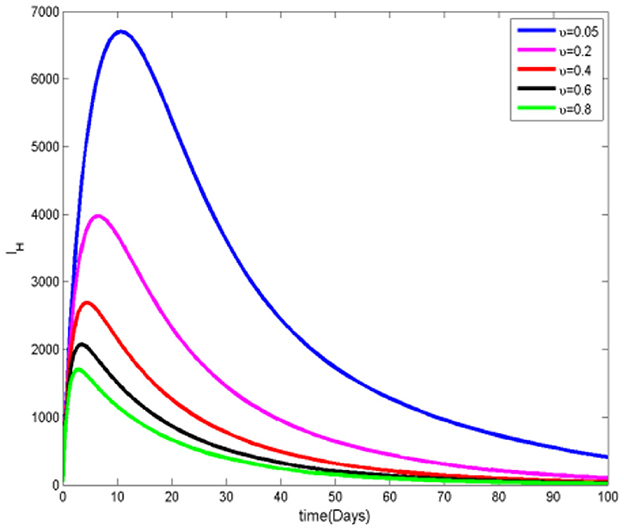
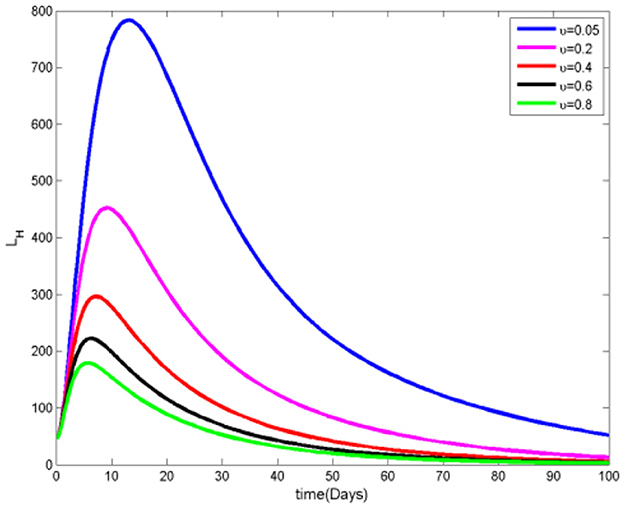
Figures 12, 13 reveal that as the rate of transition from the susceptible class to the protected class increases, there is a corresponding decrease in the number of both infected and infected ignorant individuals. This trend occurs because a larger portion of the population becomes aware of mosquito protection measures and actively uses them, thereby reducing interactions between humans and mosquitoes. As a result, the likelihood of transmission decreases, leading to a lowered infection risk across human populations. These findings underscore the effectiveness of protective behaviors in mitigating the spread of mosquito-borne diseases.

Figure 12

Figure 12. Infected humans at various υ values.

Figure 13

Figure 13. Infected ignorant humans at various υ values.

6 Conclusion

In this article, we developed a mathematical model of malaria transmission that incorporates infected individuals unaware of their infection (ignorant infected humans) and accounts for relapse. The positivity and well-posedness of the model equations were analyzed. Numerical simulations, based on the data from the literature and parameter assumptions, indicate that increasing the treatment proportion among infected individuals reduces the number of humans carrying the Plasmodium parasites without displaying symptoms for a period of time. Additionally, raising awareness of mosquito protection measures not only reduces the number of infected and infected ignorant humans but also decreases the susceptible human population.

The sensitivity analysis of the model reveals that the most positively sensitive factors are the human-to-mosquito transmission rate (β_H), the mosquito-to-human transmission rate (β_V), the mosquito recruitment rate (Ψ), and the rate of transfer from protected to susceptible humans (θ). Conversely, the parameters sensitive to negative values include the natural death rate of humans (μ_H), the natural death rate of mosquitoes (μ_V), the disease-induced death rate of humans (δ), the rate of transfer from susceptible to protected humans (υ), the recovered rate (γ), and the proportion of infected individuals who recover (τ). Therefore, these negatively sensitive parameters reduces the number of infected and ignorant infected individuals, thereby decreasing disease transmission.

The results of the model reveal that mosquito protection measures are more effective than treatment alone in reducing disease transmission. While providing treatment to infected individuals helps reduce the number of infected humans and prevent relapses, mosquito protection measures directly limit human–mosquito interactions, addressing the root cause of transmission. By reducing contact between mosquitoes and humans, these preventive measures effectively lower the overall spread of infection across the population. This finding highlights the importance of prioritizing preventive strategies, such as the use of insecticide-treated bed nets and repellents, alongside treatment efforts, to achieve comprehensive malaria control.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

GH: Conceptualization, Formal analysis, Methodology, Software, Writing – original draft, Writing – review & editing. PK: Conceptualization, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Methodology, Software. FM: Conceptualization, Formal analysis, Methodology, Software, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sato S. Plasmodium—a brief introduction to the parasites causing human malaria and their basic biology. J Physiol Anthropol. (2021) 40:1. doi: 10.1186/s40101-020-00251-9

PubMed Abstract | Crossref Full Text | Google Scholar

2. Assemie A. The occurrence and distribution of plasmodium species in Woyn Wuha health center, Ethiopia. Biomed Res Int. (2022) 2022:2881879. doi: 10.1155/2022/2881879

PubMed Abstract | Crossref Full Text | Google Scholar

3. Mandal S, Sarkar RR, Sinha S. Mathematical models of malaria-a review. Malar J. (2011) 10:1–19. doi: 10.1186/1475-2875-10-202

PubMed Abstract | Crossref Full Text | Google Scholar

4. Abiodun GJ. A Mathematical Model for Studying the Impact of Climate Variability on Malaria Epidemics in South Africa. University of the Western Cape (2017).

Google Scholar

5. Coetzee M. Distribution of the African malaria vectors of the anopheles Gambiae complex. Am J Tropic Med Hygiene. (2004) 70:103–4. doi: 10.4269/ajtmh.2004.70.103

Crossref Full Text | Google Scholar

6. Ross R. The Prevention of Malaria. London: John Murray. (1911).

Google Scholar

7. Gebremeskel AA, Krogstad HE. Mathematical modelling of endemic malaria transmission. Am J Appl Mathem. (2015) 3:36–46 doi: 10.11648/j.ajam.20150302.12

Crossref Full Text | Google Scholar

8. Ibrahim MM, Kamran MA, Naeem Mannan MM, Kim S, Jung IH. Impact of awareness to control malaria disease: a mathematical modeling approach. Complexity. (2020) 2020:1–13. doi: 10.1155/2020/8657410

Crossref Full Text | Google Scholar

9. Yman V, Wandell G, Mutemi DD, Miglar A, Asghar M, Hammar U, et al. Persistent transmission of Plasmodium malariae and Plasmodium ovale species in an area of declining Plasmodium falciparum transmission in eastern Tanzania. PLoS Negl Trop Dis. (2019) 13:e0007414. doi: 10.1371/journal.pntd.0007414

PubMed Abstract | Crossref Full Text | Google Scholar

10. Battle KE, Lucas TCD, Nguyen M, Howes RE, Nandi AK, Twohig KA, et al. Mapping the global endemicity and clinical burden of Plasmodium vivax, 2000–17: a spatial and temporal modelling study. Lancet. (2019) 394:332–43. doi: 10.1016/S0140-6736(19)31096-7

PubMed Abstract | Crossref Full Text | Google Scholar

11. Baird JK. African Plasmodium vivax malaria improbably rare or benign. Trends Parasitol. (2022) 38:683–96. doi: 10.1016/j.pt.2022.05.006

PubMed Abstract | Crossref Full Text | Google Scholar

12. Dayananda KK, Achur RN, Gowda DC. Epidemiology, drug resistance, and pathophysiology of Plasmodium vivax malaria. J Vector Borne Dis. (2018) 55:1–8. doi: 10.4103/0972-9062.234620

PubMed Abstract | Crossref Full Text | Google Scholar

13. Collins WE, Jeffery GM. Plasmodium ovale: parasite and disease. Clin Microbiol Rev. (2005) 18:570–81. doi: 10.1128/CMR.18.3.570-581.2005

PubMed Abstract | Crossref Full Text | Google Scholar

14. Mangongo YT, Bukweli JDK, Kampempe JDB, Mabela RM, Munganga JMW. Stability and global sensitivity analysis of the transmission dynamics of malaria with relapse and ignorant infected humans. Physica Scripta. (2022) 97:024002. doi: 10.1088/1402-4896/ac4862

Crossref Full Text | Google Scholar

15. Van den Driessche P, & Watmough J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathem Biosci. 180:29–48. doi: 10.1016/S0025-5564(02)00108-6

PubMed Abstract | Crossref Full Text | Google Scholar

16. Gebremichael S, Mekonnen T. Impact of climatic factors and intervention strategies on the dynamics of malaria in Ethiopia: a mathematical model analysis. Int J Sci.: Basic Appl Res. (2020) 54:120–50.

Google Scholar

17. Khan MA, Wahid A, Islam S, Khan I, Shafie S, Gul T. Stability analysis of an SEIR epidemic model with non-linear saturated incidence and temporary immunity. Int J Adv Appl Math Mech. (2015) 2:1−14.

Google Scholar

18. Chitnis N, Hyman JM, Cushing JM. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol. (2008) 70:1272–96. doi: 10.1007/s11538-008-9299-0

PubMed Abstract | Crossref Full Text | Google Scholar

19. Obabiyi O, Olaniyi S. Global Stability Analysis of Malaria Transmission Dynamics with Vigilant Compartment. Texas State University (2019).

Google Scholar

20. Klinck J. Transmission model details. Philippine Sci Lett. (2016) 5:1–3.

Google Scholar

21. Makinde OD, Okosun KO. Impact of chemo-therapy on optimal control of malaria disease with infected immigrants. BioSystems. (2011) 104:32–41. doi: 10.1016/j.biosystems.2010.12.010

PubMed Abstract | Crossref Full Text | Google Scholar

22. Menbiko DK, Deressa CT. Modeling and analysis of an age-structured malaria model in the sense of Atangana–Baleanu fractional operators. J Mathemat. (2024). doi: 10.1155/2024/6652037

Crossref Full Text | Google Scholar