Expand-contract plasticity on the real line

The study deals with plastic and non-plastic sub-spaces A of the real-line ℝ with the usual Euclidean metric d. It investigates non-expansive bijections, proves properties of such maps, and demonstrates their relevance by hands of examples. Finally, it is shown that the plasticity property of a sub-space A contains at least two complementary questions, a purely geometric and a topological one. Both contribute essential aspects to the plasticity property and get more critical in higher dimensions and more abstract metric spaces.

1 Introduction

Here, we investigate properties of plastic metric spaces. Shortly speaking, a metric space is plastic if every non-expansive bijection is an isometry, cf. Section 2.

We will observe that the plasticity property consists of a geometrical sub-problem and a topological sub-problem. That is the reason why plasticity of a metric space, which can be easily defined, evolves as a challenging mathematical problem. In particular, we observe that the plasticity of a metric space is not inherited from sup-spaces, i. e., from including spaces, and it does not inherit to sub-spaces, i. e., to included spaces.

In this study, we concentrate on metric spaces which are sub-spaces of the real axis, and in this apparently simple situation, the typical difficulties come to the light.

The probably first study devoted to the plasticity problem is the study mentioned in the reference [1]; however, the term "plasticity" appeared much later and the problem itself remained unnoticed for several decades. A short literature survey and the information about the current progress in solution of the problem are shown in Section 2.2.

The study is organized as follows. Section 2 introduces the basic concepts and illustrates the existence of non-expansive bijections in the case that the metric space is a union of closed intervals. This case demonstrates the geometrical aspects of the problem. Then, Section 3 discusses the plasticity of metric spaces by means of metric spaces which are unbounded sequences of points, investigates the relevance of accumulation points and continuous subsets, and attacks the more topological parts of the plasticity concept. Finally, Section 4 resumes the observations and gives a short outlook to further research.

2 Basic concepts

We denote a metric space by (A, d) where A is the set of points and d: A × A → ℝ₊ = {x ∈ ℝ: x ≥ 0} is the distance obeying the known axioms of positivity, symmetry, non-degeneracy, and the triangle inequality.

2.1 Non-expansive maps

A map φ: A→A from the metric space A into itself is called non-expansive if

$\begin{array}{ll}d(\phi (x),\phi (y))\le d(x,y)\text{ for all }x,y\in A& (1)\end{array}$

is fulfilled. If the equality holds for all pairs x, y ∈ A, φ is an isometry.

The condition in Equation (1) is equivalent to the Lipschitz-continuity of the map φ on A with Lipschitz constant 1. Thus, a non-expansive φ is also continuous on A.

We will investigate metric spaces A ⊆ A_ex which are embedded in a metric sup-space (A_ex, d_ex) because the space A_ex might be known and well understood, and thus, its points or rather a selection of them serve as elements of A. Now, it is obvious that the restriction of the metric space (A_ex, d_ex) to the set A leads to the metric space (A, d) by the restriction of the distance d = d_ex|_A×A to the set A. It is less obvious whether a metric space (A, d) can be extended to a sup-set A_ex by choosing an appropriate d_ex. However, it is always possible, to choose a function ${\widehat{d}}_{\text{ex}}:A_{\text{ex}}\times A_{\text{ex}}\to {ℝ}_{+}$, which fulfills the properties of symmetry, non-degeneracy, and positivity with ${\widehat{d}}_{\text{ex}}{|}_{A\times A}=d$, which of course is not a metric in general. Then, we can define the metric

${\tilde{d}}_{\text{ex}}(x,y)={\displaystyle \underset{n,\left\{z_0,\dots ,z_n\right\}}{inf}}\left[{\widehat{d}}_{\text{ex}}(x,z_0)+{\displaystyle \sum _{i=0}^{n-1}}{\widehat{d}}_{\text{ex}}(z_i,z_{i+1})+{\widehat{d}}_{\text{ex}}(z_n,y)\right]$

as the infimum over all possible paths of arbitrary length between x and y. However, such a metric ${\tilde{d}}_{\text{ex}}$ may not really be an extension. As in the real life, if one builds a new paths, which are shorter, the old ones may no longer be used. In our notation, this means that it may happen ${\tilde{d}}_{\text{ex}}(x,y)<d(x,y)$ for some x, y ∈ A.

Nevertheless, one may define a real extension d_ex of the metric d, which is more artificial and a bit similar to the French railways metric in the following way. Let us fix a point x₀ of the set A and define an arbitrary metric d_Aex on the set (A_ex\A) ∪ {x₀}, which might be the discrete metric or any other metric. Although less intuitive, the needed extension is

$d_{\text{ex}}=\{\begin{array}{ll}d(x,y),\hfill & \text{for }x,y\in A;\hfill \\ d_{A_{\text{ex}}}(x,y),\hfill & \text{for }x,y\in (A_{\text{ex}}\setminus A)\cup \left\{x_0\right\};\hfill \\ d(x,x_0)+d_{A_{\text{ex}}}(x_0,y)\hfill & \text{for }x\in A,y\in (A_{\text{ex}}\setminus A).\hfill \end{array}$

existing and easily available. Therefore, we will not distinguish between d_ex and d in the following but use the distance d in the extended metric space and sub-space.

Oppositely, it is not evident whether the existence of a non-expansive map φ_ex: A_ex → A_ex provides a non-expansive map φ: A → A because the simple restriction φ = φ_ex|A, although still Lipschitz continuous, is not necessarily a map into A. It might happen that the image imφ = φ(A) ⊆ A_ex is not a subset of A. The opposite question whether a non-expansive φ: A → A can be extended to a non-expansive map on the extended space A_ex is the question about the extension of Lipschitz maps, preserving the Lipschitz constant. In particular, it is always possible for real-valued functions according to McShane's extension theorem [2]. For functions from a subset of ℝⁿ to ℝⁿ, the extension to the whole Euclidean space is possible due to Kirszbraun's theorem [3]. We will observe that non-expansive maps pose a lot of interesting questions and some of them can be answered.

2.2 Plastic metric spaces

Let us define a plastic metric space.

Definition 2.1. A metric space A is called expand-contract plastic (EC-plastic)—or just plastic—if every bijective non-expansive map φ: A → A is an isometry.

Definition 2.1 defines a plastic metric space A via the non-existence of any non-expansive bijection of the metric space A to itself, which is not an isometry. Some simple examples are the non-plastic metric space A = ℝ with the non-isometric non-expansive bijective map φ: x ↦ x/2 and the plastic metric space A = [0, 1] ⊂ ℝ with exactly the two non-expansive bijections φ₁ = id. and φ₂: x ↦ 1−x, which are both isometries.

The only general result concerning plasticity of metric space states that every totally bounded metric space is plastic, see Naimpally et al. [4] for details. In fact, in the study mentioned in the reference [4], a more general result was obtained, i. e., so-called strong plasticity of totally bounded metric spaces was shown.

Definition 2.2. A metric space A is called strongly plastic if for every mapping φ: A → A the existence of points x, y ∈ A with d(φ(x), φ(y)) > d(x, y) implies the existence of two points $\tilde{x},ỹ\in A$ for which $d(\phi (\tilde{x}),\phi (ỹ))<d(\tilde{x},ỹ)$ holds true.

This property and its uniform version were researched in the study mentioned in the reference [5]. It says that any expansion of a distance between two points implies the existence of two other points which are contracted by the map φ. Observe it is extremely important not to interchange expansion and contraction.

In the study mentioned in the reference [6], the following intriguing question was posed.

Problem 2.3. Is it true, that the unit ball of an arbitrary Banach space is plastic?

Observe that in finite dimensions, this question is answered positively since in finite dimensions, the unit ball is compact and thus totally bounded. Moreover, the question is open only in the infinite dimensional case and the following more general problem.

Problem 2.4. For which pairs (X, Y) of Banach spaces, every bijective non-expansive map φ: B_X(0) → B_Y(0) between the unit balls is an isometry?

There are a number of relatively recent particular results, devoted to these problems, see Angosto et al. [7], Haller et al. [8], Kadets andd Zavarzina [9], Leo [10], and Zavarzina [11]. There exists also a circle of problems connected with plasticity property of the unit balls. In the study mentioned in the references [12] and [13], the so called linear expand-contract plasticity of ellipsoids in separable Hilbert spaces was studied, which means that only the linear non-expansive bijections were considered in the definition of plasticity.

Many natural questions concerning plasticity seem to have no answer or even have not yet been considered. In 2020, Behrends [14] draw attention to the fact that nobody studied the subsets of the real line with respect to the plasticity problem. He tried to attack this problem and received some results in this direction, however, decided not to publish them. Moreover, the following problem is still open.

Problem 2.5. What characterizes plastic sub-spaces of the real line ℝ with the usual metric d?

In spite of the seeming simplicity of the question, it is not so easy to deal with. Let us first list the previously known results. As we mentioned before, the set ℝ itself with the usual metric is not plastic. If one considers any bounded subset, it is already plastic due to its total boundedness.

On the other hand, it is easy to show that the set of integers ℤ with the same usual metric is plastic in spite of its unboundedness and the set ℝ\ℤ. The proof of the plasticity of both mentioned spaces may be found in the study mentioned in the reference [4]. In the proof of plasticity of the set ℝ\ℤ, one of the possible cases was missed; nevertheless, the statement is still correct.

Already, these examples show that there is no simple answer to the question whether a metric space is plastic or not. Rather we could give the interpretation that there are some critical points, e. g., the integers in these examples, which every non-expansive bijection φ definitely has to pass, what relates to the geometry of the metric space A, and that there are some parts of the metric space which cannot be glued to each other such as singular points or open intervals, what relates to the topological aspects of plasticity. We observe that sub-spaces of the real axis are already sufficiently multifaceted to study the plasticity problem of metric spaces. The question whether more general metric spaces are plastic, provoke analogous difficulties, and again contain geometrical and topological aspects.

Here, we will generalize the known results and say something more about plastic sub-spaces of the real line. The previously mentioned results explain why we consider only unbounded sets in what follows.

All over the text, we use the notion d for the usual Euclidean metric d(x, y) = |x − y| for x, y ∈ ℝ. Round brackets denote open intervals (x, y) = {z ∈ ℝ: x < z < y} and square brackets denote closed intervals [x, y] = {z ∈ ℝ: x ≤ z ≤ y}.

2.3 A subset of the real axis

We have observed that the real axis ℝ has sufficiently interesting metric sub-spaces for the investigation of plasticity. The Lipschitz condition in Equation (1) lets us easily decide whether a map φ:ℝ → ℝ is non-expansive or not—just by the graph of the map φ, see Figure 1. Due to our considerations in Section 2.1, which is applied here with A as union of intervals and A_ex = ℝ, the map φ can be extended—not necessarily in a unique manner—as non-expansive function φ_ex on the entire axis ℝ. Thus, φ_ex is continuous on ℝ.

Figure 1

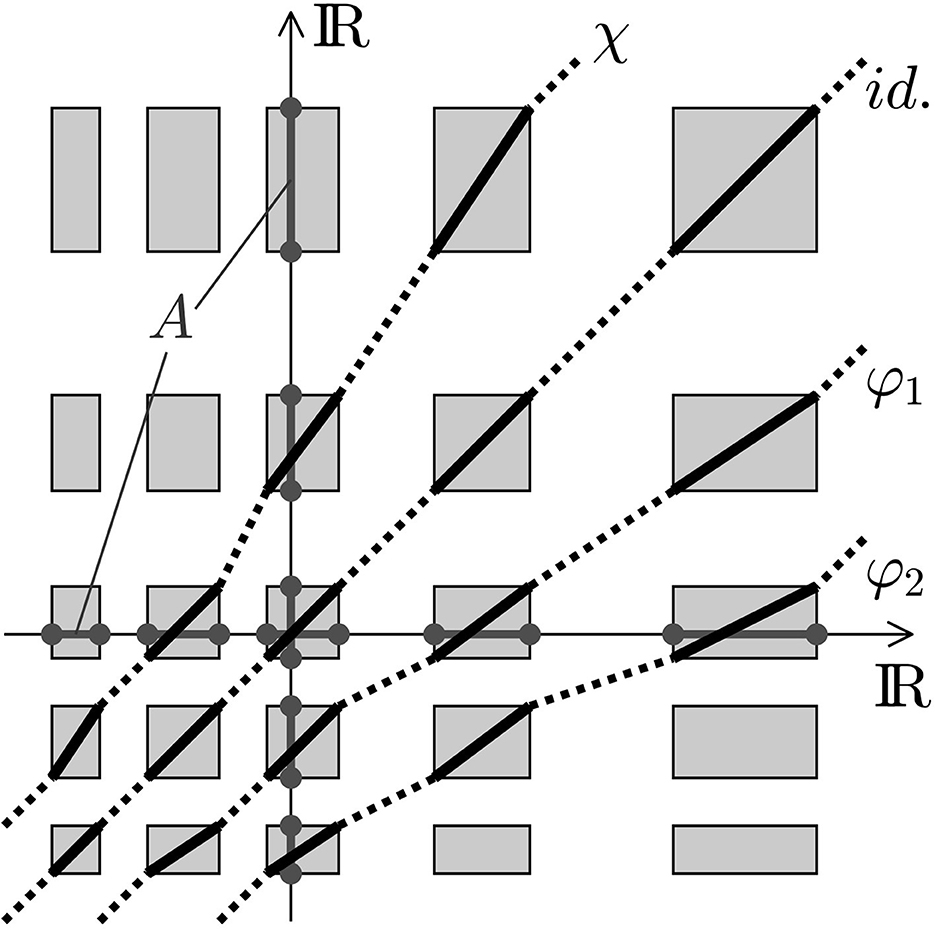
Figure 1. Non-expansive maps φ₁, φ₂, and id. and an expansive map χ for a union A ⊂ ℝ of closed intervals of increasing length. The Cartesian product A × A is given in gray, and the bijections are black.

Figure 1 shows examples of bijective maps from the union of intervals A = …∪[a₂, a₃]∪[a₄, a₅]∪… ⊂ ℝ onto itself. In this example, the closed interval and the interspaces have increasing lengths, in detail a_ℓ+1−a_ℓ ≥ a_ℓ−1−a_ℓ−2 for all ℓ ∈ ℤ. Due to its continuity, every bijection φ passes monotonically a rectangle in A × A. In this example, with increasing lengths of the respective intervals, we easily detect particular extensions φ_ex:ℝ → ℝ with φ_ex|_A = φ and a slope bounded by 1 because the endpoints of the interspace could be used in Equation (1). Hence, the functions id. and φ_i, i = 1, 2 below the diagonal are non-expansive, and the function χ above the diagonal is expansive.

3 Main results

Let us start with some interesting observations on simple situations of A, e. g., some sets of singular points.

Proposition 3.1. Let $A={\left\{a_i\right\}}_{i=-\infty }^{+\infty }\subset ℝ$ be an increasing sequence that obeys

$\begin{array}{ll}d(a_{i-1},a_i)\le d(a_i,a_{i+1})\text{ for all }i\in \mathbb{Z}& (2)\end{array}$

and

$\begin{array}{ll}d(a_{j-1},a_j)<d(a_j,a_{j+1})\text{ for at least one }i\in \mathbb{Z}.& (3)\end{array}$

Then (A, d) is not plastic.

Proof. The shift φ: a_i ↦ a_i−1 is an example of a non-expansive bijection which is not an isometry.

Remark 3.2. The relation sign in Equations (2), (3) might be commonly inverted so that the distances between two subsequent points of A decrease instead of increase, and the statement remains unchanged.

Furthermore, let us consider sets which are bounded from one side. Let us recall the definition of an accumulation point, which we will use in what follows.

Definition 3.3. An accumulation point (or limit point) of a set A in a metric space X is a point x, such that every neighborhood of x with respect to the metric on X contains a point of A which differs from the point x.

An accumulation point of a set A does not have to be an element of A. We will proceed with the following lemma.

Lemma 3.4. Let A ⊂ ℝ be a set without accumulation points which is bounded from one side. Let a be a minimal—or maximal—element of A and φ: A → A be a bijective non-expansive map. Then φ(a) = a.

Proof. Without loss of generality, we may consider the case when a is a minimal element. Assume φ(a) ≠ a. Then there is b ∈ A such that φ(b) = a.

Claim: Let be c ∈ A. Then c ≤ b implies φⁿ(c) ≤ b for every n ∈ ℕ.

Proof of the Claim: We will use the induction in n. Indeed, if φⁿ(c) ≤ b and φⁿ⁺¹(c) > b we have

$d({\phi }^n(c),b)\ge d({\phi }^{n+1}(c),a)>d(b,a).$

This contradiction completes the proof of the Claim.

Since

$d(a,b)\ge d(\phi (a),\phi (b))=d(\phi (a),a),$

we have φ(a) ≤ b. Thus, the Claim provides φⁿ(a) ≤ b for every n ∈ ℕ. Now, the segment [a, b] is a trap for those points, which were mapped there. Our aim is to find such a “trapped” point out of the interior of the segment [a, b] and show that this leads to a contradiction. There are only two possible cases.

Case 1: φ(a) = b. In this case, points a and b were swapped by φ. Then, such a “trapped” point is the closest from the right-hand side point to b. There is c > b such that d(b, c) < d(b, d) for any d > b. Such point c exists since A is unbounded from above and there is no accumulation points. The point c cannot be mapped outside the segment [a, b] since it gives the contradiction with non-expansiveness of φ.

Case 2: φ(a) < b. With such a condition, a “trapped” point is φ(a) itself.

In both cases, we have a point t which does not belong to the interior of the segment [a, b] such that φ(t) belongs to this interior. Consider an orbit of this point t, i. e., the set ${\left\{{\phi }^n(t)\right\}}_{n=1}^{\infty }$. Due to the bijectivity of φ, this orbit does not have repeating elements. Thus, we have obtained a bounded infinite subset in A which contradicts the fact that A does not have accumulation points.

Remark 3.5. The condition about the absence of accumulation points in Lemma 3.4 cannot be omitted.

This remark is confirmed by the following example.

Example 3.6. Let A = ℤ₊ ∪ Q, where $Q=\left\{\frac{1}{4}+\frac{1}{n},n\ge 4\right\}$. The bijective non-expansive map φ is

$\phi (a)=\{\begin{array}{ll}a-1,\hfill & \text{for }a\in \mathbb{N},\hfill \\ \frac{1}{2},\hfill & \text{for }a=0,\hfill \\ \frac{1}{4}+\frac{1}{n+1},\hfill & \text{for }a=\frac{1}{4}+\frac{1}{n}\in Q.\hfill \end{array}$

We observe that φ is bijective and it does not save the minimal element of A. We check that it is non-expansive.

1. For all a, b ∈ ℕ, the isometry d(φ(a), φ(b)) = d(a, b) is valid.

2. For a ∈ ℕ, b = 0, it holds $d(\phi (a),\phi (b))=|a-\frac{3}{2}|<a=d(a,b)$.

3. For a ∈ ℕ, $b=\frac{1}{4}+\frac{1}{n}\in Q$, we have $d(\phi (a),\phi (b))=|a-\frac{5}{4}-\frac{1}{n+1}|<|a-\frac{1}{4}-\frac{1}{n}|=d(a,b)$.

4. For a = 0, $b=\frac{1}{4}+\frac{1}{n}\in Q$, it holds $d(\phi (a),\phi (b))=|\frac{1}{4}-\frac{1}{n+1}|<|\frac{1}{4}+\frac{1}{n}|=d(a,b)$.

5. In the case $a=\frac{1}{4}+\frac{1}{n}\in Q$, $b=\frac{1}{4}+\frac{1}{m}\in Q$, without loss of generality we may assume n < m. Then

$d(\phi (a),\phi (b))=\frac{1}{n+1}-\frac{1}{m+1}<\frac{1}{n}-\frac{1}{m}=d(a,b).$

The described set is shown on the left of Figure 2.

Figure 2

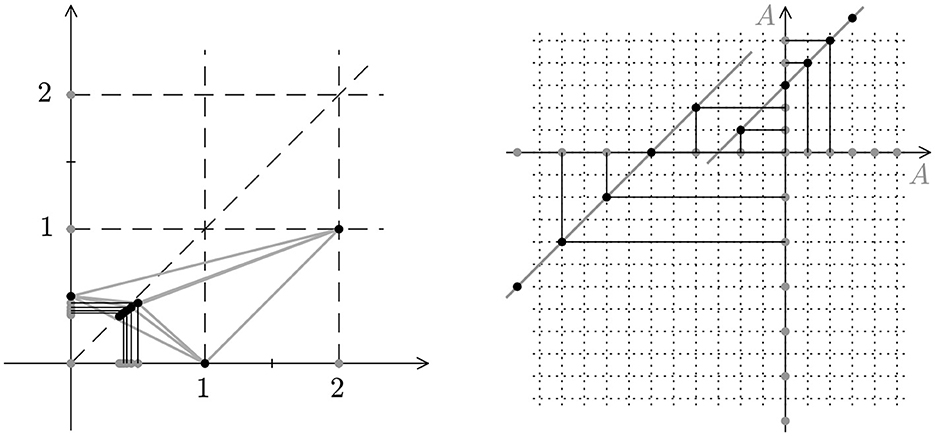
Figure 2. (Left) Illustration of Example 3.6. (Right) Illustration of Example 3.8. The gray dots on the axes indicate A. The black dots mark the respective bijection. Clearly, no connection of two points has a slope larger than 1.

Lemma 3.4 immediately implies the following corollary.

Corollary 3.7. Let A ⊂ ℝ be an unbounded set without accumulation points. Let A have a minimal or maximal element and let φ: A → A be a bijective non-expansive map. Then, φ is an isometry, moreover, the identity.

Proof. Without loss of generality, we may consider the case when a is a minimal element. Let us show that φ(x) = x for every x ∈ A. Indeed, for the minimal element a, Lemma 3.4 ensures that φ(a) = a. Now suppose for some fixed y ∈ A, the condition φ(x) = x holds for every x < y, x ∈ A. Consider

$A_1=A\backslash \left\{{\displaystyle \bigcup _{x\in A,x<y}}\left\{x\right\}\right\}.$

Then, φ|_A1: A₁ → A₁ is a bijective non-expansive map, and y is a minimal element. Then φ(y) = y due to Lemma 3.4.

Proposition 4.1 in Naimpally et al. [4] states that for convex (in the sense of the same study) metric spaces, hereditarily EC-plasticity implies boundedness. Moreover, for convex subsets in Euclidean ℝⁿ, hereditarily EC-plasticity and boundedness are equivalent. However, the authors note that convexity is a too strong condition.

In Naimpally et al. [4], Theorem 4.3 states that an unbounded metric space with at least one accumulation point contains a non-plastic subspace. Corollary 3.7 demonstrates that the presence of an accumulation point is essential in the mentioned theorem, since it allows to build examples of unbounded hereditarily plastic spaces.

Let us go back to Example 3.6 and remark another interesting property of non-expansive bijections on ℝ. Suppose we have a set A ⊂ ℝ and a function φ: A → A. We will say that φ preserves the relation “between” on the set A if for any x, y, z ∈ A with x < y < z we have φ(x) < φ(y) < φ(z). Example 3.6 shows that non-expansive bijections do not have to preserve the relation “between.” Surprisingly, there is an example demonstrating the same property with a set without any accumulation points.

Example 3.8. Let A = ℕ ∪ Q, where Q = {2k, k ∈ ℤ₋}. The bijective non-expansive map φ is defined by

$\phi (a)=\{\begin{array}{ll}a+6,\hfill & \text{if }a\le -4,\hfill \\ a+3,\hfill & \text{otherwise}.\hfill \end{array}$

The map φ does not preserve the relation “between” since −4 < −2 < 0 but φ(−2) < φ(−4) < φ(0). Let us check that φ is non-expansive.

1. If both a, b ≥ −2 or both a, b ≤ −4, the non-expansiveness of φ is obvious.

2. If a ≥ −2 and b ≤ −4, d(φ(a), φ(b)) = |a − b − 3| ≤ |a − b| = d(a, b). Only for a = −2 and b = −4, the inequality a − b < 3 is valid, but even in this case, the previous inequality is true.

The described set is shown on the right of Figure 2.

Furthermore, we are going to present a sufficient condition for a set in ℝ to be plastic. Let us introduce the set

$D_A=\left\{p\in ℝ:p=d(a,b)\text{ for some }a,b\in A\text{ with }\left[a,b\right]\cap A=\left\{a,b\right\}\right\}.$

Obviously, several pairs of points may be situated in the same distance. That is why for every p ∈ D_A, we call its multiplicity the number of pairs of points in A which are on the distance p. This multiplicity may be finite or infinite.

Theorem 3.9. Let A ⊂ ℝ has no accumulation points and let D_A has a maximal element of finite multiplicity or a minimal element of finite multiplicity. Then, (A, d) is a plastic metric space.

Proof. Without loss of generality, we may assume that D_A has a minimal element a ∈ ℝ of finite multiplicity k ∈ ℕ. Let us denote

$X_a=\left\{x_n\in A,n=1,\dots ,2k,d(x_i,x_{i+1})=a,i=1,3,\dots ,2k-1\right\}.$

Let us take x_i ≤ x_j for all i, j with 1 ≤ i < j ≤ 2k. Consider an arbitrary non-expansive bijection φ: A → A. Due to the non-expansiveness of φ, we may conclude that φ maps X_a bijectively onto itself. Thus, φ|_Xa is an isometry on X_a. In particular, we find d(x₁, x_2k) = d(φ(x₁), φ(x_2k)). Since this distance is the biggest one on X_a, either φ(x₁) = x₁ and φ(x_2k) = x_2k or φ(x₁) = x_2k and φ(x_2k) = x₁. We will refer them as cases 1 and 2, respectively. In the first case, obviously, for every x ∈ A with x₁ < x < x_2k, we get φ(x) = x, so, in this case, φ|_{[x1, x2k]∩A} is the identity. In the second case, if the structure of A allows it, φ|_{[x1, x2k]∩A} is the inversion, called total symmetry. Furthermore, following the similar procedure as in Lemma 3.4, we have that in the first case, φ is the identity, and in the second case φ is the total symmetry.

Remark 3.10. The conditions of Theorem 3.9 are sufficient but not necessary for the plasticity of a set without accumulation points.

To make sure that the previous Remark 3.10 is true, one may consider the space (ℤ, d). For D_ℤ, the minimal and the maximal elements are equal to 1 and have infinite multiplicity, but the space is plastic. However, we constructed the next example, which is less trivial, to show that plastic spaces which do not satisfy the condition of the previous theorem may have richer structure.

Example 3.11. Let $A={\left\{a_i\right\}}_{i=-\infty }^{i=\infty }\subset ℝ$, where ${\left\{a_i\right\}}_{i=-\infty }^{i=\infty }$ is an increasing sequence such that

$d(a_i,a_{i+1})=\{\begin{array}{ll}\left|k\right|+1,\hfill & \text{for }i=2k,k\in \mathbb{Z},\hfill \\ \frac{1}{k+1},\hfill & \text{for }i=2k-1,k\in \mathbb{N},\hfill \\ \frac{1}{\left|k\right|+2},\hfill & \text{for }i=2k-1,k\in {\mathbb{Z}}_{-}.\hfill \end{array}$

The corresponding D_A has no minimal or maximal element. However, (A, d) is plastic. In fact, let φ: A → A be a non-expansive bijection. Then,

$d(\phi (a_0),\phi (a_1))\le d(a_0,a_1)=1.$

Suppose $d(\phi (a_0),\phi (a_1))=\frac{1}{n}$, where n ≥ 2. Consider the open ball with the radius n − 1 centered in φ(a₀). Due to the structure of A, this ball contains only the point φ(a₁), except for the center. On the other hand, the open ball with the radius n − 1 centered in a₀, and for n ≥ 3, it contains more than two points, and for n = 2, it contains two points but does not contain a₁. In both cases, we have a contradiction to the non-expansiveness of the map φ. That is why the only possible option is as follows:

$d(\phi (a_0),\phi (a_1))=d(a_0,a_1)=1.$

Furthermore, just in the same way as in Theorem 3.9, we have that φ is either the identity or the inversion.

Now let us speak about the subsets which contain a continuous part. One may prove the following statement in the same way as the Proposition 3.1.

Proposition 3.12. Let be

$A={\displaystyle \bigcup _{i=-\infty }^{+\infty }}(a_i,b_i)\subset ℝ,$

where b_i < a_i+1 be such a sequence of intervals that

$\begin{array}{ll}d(a_i,b_i)\le d(a_{i+1},b_{i+1})& (4)\end{array}$

and

$\begin{array}{ll}d(b_{i-1},a_i)\le d(b_i,a_{i+1})& (5)\end{array}$

for all i ∈ ℤ. Furthermore, there exists j ∈ ℤ such that

$\begin{array}{ll}d(a_j,b_j)<d(a_{j+1},b_{j+1})\text{ or }d(b_{i-1},a_i)<d(b_i,a_{i+1}).& (6)\end{array}$

Then, (A, d) is not plastic.

Remark 3.13. In the same way as in Proposition 3.1, the relation signs in Equations (4-6) might be commonly inverted.

Here is one more observation.

Proposition 3.14. Let A ⊂ ℝ contain an interval (a, +∞) or (−∞, a). Then, (A, d) is not plastic.

Proof. Without loss of generality, we discuss the case with (a, +∞). Let us define the map φ with

$\phi (x)=\{\begin{array}{ll}\phi (x)=x,\hfill & \text{if }x\notin (a,+\infty ),\hfill \\ \phi (x)=\frac{x+a}{2},\hfill & \text{otherwise}.\hfill \end{array}$

This map is non-expansive, bijective, and, at the same time, not an isometry.

In Naimpally et al. [4], Theorem 3.9 shows the plasticity of the space ℝ\ℤ. Unfortunately, the proof misses the case that the non-expansive bijection is a symmetry. However, the statement itself is true. One may use the same reasoning to prove the next proposition.

Proposition 3.15. Let

$A={\displaystyle \bigcup _{i=-\infty }^{+\infty }}(a_i,b_i)\subset ℝ,$

where

$d(a_i,b_i)=d(a_{i+1},b_{i+1})\text{ and }d(b_i,a_{i+1})=d(b_{i-1},a_i).$

Then, (A, d) is plastic.

Remark 3.16. Propositions 3.12 and 3.15 hold true with the closed intervals.

Remark 3.17. On the other hand, if we consider in the statement of Proposition 3.15 half-intervals,

$A={\displaystyle \bigcup _{i=-\infty }^{+\infty }}[a_i,b_i)\subset ℝ\text{ or }A={\displaystyle \bigcup _{i=-\infty }^{+\infty }}(a_i,b_i]\subset ℝ$

(A, d) is already a non-plastic space.

Remark 3.18. If we consider in the same statement the set of the form,

$A={\displaystyle \bigcup _{i=-\infty }^n}\left[a_i,b_i\right]\cup {\displaystyle \bigcup _{i=n+1}^{+\infty }}(a_i,b_i]\subset ℝ,\text{ where }n\in \mathbb{N},$

(A, d) is also a non-plastic space.

Figure 3 illustrates the previous remark.

Figure 3

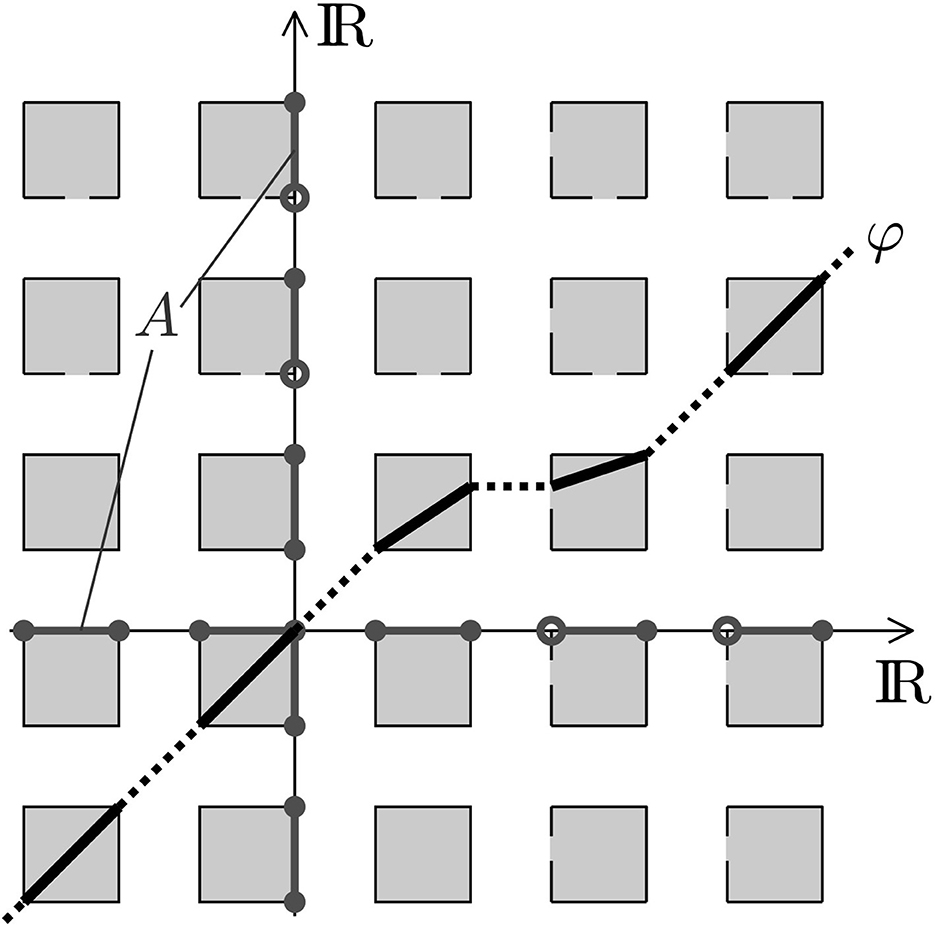
Figure 3. Oppositely to Figure 1, half-open intervals allow that φ does not pass entire rectangles in A × A. Rather, it might jump where the intervals can be glued to each other. Remark that this example contains a first half-open interval and all the following intervals are half-open, cf. bijectivity. The topological properties of the intervals in A enter the plasticity problem.

The reader easily provides more examples which consist of open or closed intervals together with half-intervals, all with the same lengths. Again, we remark that the end-points of the intervals are critical points for the plasticity property.

4 Conclusion

The analysis of plastic sub-spaces A of the real-line ℝ has shown that first, the Lipschitz continuity of the map φ: A → A with Lipschitz constant 1 leads to useful and instructive illustrations of the non-expansivity of the map φ, to which it is identical.

The plasticity property of a metric space turned out to contain two complementary aspects, a purely geometrical one and a topological one. Already on the real-line ℝ, the different nature of both aspects become visible. Whereas the geometrical aspect is an extension of the non-expansivity of φ on a simply connected interval, the topological aspect leads to the question whether two or more sub-intervals can be glued at critical points by piecewise translations. Therefore, the investigation of sub-spaces of the real-line ℝ gives an appropriate framework for the investigation of the plasticity of metric spaces.

We expect that the interplay between the two types of nature of the problem gets more severe in higher dimensions. Already unions of rectangles and cuboids as sub-spaces of the d-dimensional Euclidean space ℝ^d give a tremendous multiplicity of open, half-open, and closed edges and sides—complete or partial.

The named interplay between geometry and topology of the metric spaces gets more and more complicated and less intuitive the more abstract and the more elaborated the metric spaces are. We do not expect any clarification, for example, metric spaces of functions before sub-spaces of the Euclidean spaces are understood.

Future research will concentrate on the question, what else can be said about plastic and non-plastic sub-spaces of the space (ℝ, d). Furthermore, we will explore the extension of a metric space A to larger sets in A_ex which contain A. In particular, the metric hull, i. e., the set

$\begin{array}{r}{hull}_{A_{\text{ex}}}(A)=\left\{x\in A_{\text{ex}}:\exists y,z\in A:d(y,z)=d(y,x)+d(x,z)\right\}\\ \subseteq A_{\text{ex}},\end{array}$

gives interesting perspectives in the context of the plasticity problem for the specification A_ex = ℝ. We conjecture that the metric hull is the smallest proper extension of the metric space, which is simply connected to A_ex and where the plasticity is dominated by the geometry. Therefore, the topology might be sub-ordinated. In the medium term, we hope for an insight into the question how geometry and topology interact in the plasticity of a metric space.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

OZ: Writing – review & editing, Writing – original draft, Project administration, Formal analysis, Conceptualization. DL: Validation, Writing – review & editing, Writing – original draft, Visualization, Methodology.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was partially supported by the Volkswagen Foundation grant within the frameworks of the international project “From Modeling and Analysis to Approximation.” OZ was also partially supported by Akhiezer Foundation grant, 2023.

Acknowledgments

The authors are grateful to Vladimir Kadets for valuable remarks and pointing us the results about the extension of Lipschitz maps. The authors are also thankful to Ehrhard Behrends for drawing our attention to the problem considered in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Freudenthal H, Hurewicz W. Dehnungen, verkürzungen, isometrien. Fund Math. (1936) 26:120–2. doi: 10.4064/fm-26-1-120-122

Crossref Full Text | Google Scholar

2. McShane EJ. Extension of range of functions. Bull Amer Math Soc. (1934) 40:837–42. doi: 10.1090/S0002-9904-1934-05978-0

Crossref Full Text | Google Scholar

3. Kirszbraun MD. Über die zusammenziehende und lipschitzsche transformationen. Fund Math. (1934) 22:77–108. doi: 10.4064/fm-22-1-77-108

Crossref Full Text | Google Scholar

4. Naimpally SA, Piotrowski Z, Wingler EJ. Plasticity in metric spaces. J Math Anal Appl. (2006) 313:38–48. doi: 10.1016/j.jmaa.2005.04.070

Crossref Full Text | Google Scholar

5. Kadets V, Zavarzina O. Plastic pairs of metric spaces. J Math Anal Appl. (2023) 127435. doi: 10.1016/j.jmaa.2023.127435

Crossref Full Text | Google Scholar

6. Cascales B, Kadets V, Orihuela J, Wingler EJ. Plasticity of the unit ball of a strictly convex Banach space. Rev Real Acad Cienc Exactas Fís Nat A Mat. (2016) 110:723–7. doi: 10.1007/s13398-015-0261-3

Crossref Full Text | Google Scholar

7. Angosto C, Kadets V, Zavarzina O. Non-expansive bijections, uniformities and polyhedral faces. J Math Anal Appl. (2019) 471:38–52. doi: 10.1016/j.jmaa.2018.10.058

Crossref Full Text | Google Scholar

8. Haller R, Leo N, Zavarzina O. Two new examples of Banach spaces with a plastic unit ball. Acta Comment Univ Tartu Math. (2022) 26:89–101. doi: 10.12697/ACUTM.2022.26.07

Crossref Full Text | Google Scholar

9. Kadets V, Zavarzina O. Nonexpansive bijections to the unit ball of the ℓ_1-sum of strictly convex Banach spaces. Bull Aust Math Soc. (2018) 97:285–92. doi: 10.1017/S0004972717001150

Crossref Full Text | Google Scholar

10. Leo N. Plasticity of the unit ball of c and c_0. J Math Anal Appl. (2022) 507:125718. doi: 10.1016/j.jmaa.2021.125718

Crossref Full Text | Google Scholar

11. Zavarzina O. Nonexpansive bijections between unit balls of Banach spaces. Ann Funct Anal. (2018) 9:271–81. doi: 10.1215/20088752-2017-0050

Crossref Full Text | Google Scholar

12. Karpenko I, Zavarzina O. Linear expand-contract plasticity of ellipsoids revisited. Mat Stud. (2022) 57:192–201. doi: 10.30970/ms.57.2.192-201

Crossref Full Text | Google Scholar

13. Zavarzina O. Linear expand-contract plasticity of ellipsoids in separable Hilbert spaces. Mat Stud. (2019) 51:86–91. doi: 10.15330/ms.51.1.86-91

Crossref Full Text | Google Scholar

14. Behrends E. Free University of Berlin, Private Communication. (2020).

Google Scholar