- Department of Mathematics, University of British Columbia, Vancouver, BC, Canada
For a 2-D coupled PDE-ODE bulk-cell model, we investigate symmetry-breaking bifurcations that can emerge when two bulk diffusing species are coupled to two-component nonlinear intracellular reactions that are restricted to occur only within a disjoint collection of small circular compartments, or “cells,” of a common small radius that are confined in a bounded 2-D domain. Outside of the union of these cells, the two bulk species with comparable diffusivities and bulk degradation rates diffuse and globally couple the spatially segregated intracellular reactions through Robin boundary conditions across the cell boundaries, which depend on certain membrane reaction rates. In the singular limit of a small common cell radius, we construct steady-state solutions for the bulk-cell model and formulate a nonlinear matrix eigenvalue problem that determines the linear stability properties of the steady-states. For a certain spatial arrangement of cells for which the steady-state and linear stability analysis become highly tractable, we construct a symmetric steady-state solution where the steady-states of the intracellular species are the same for each cell. As regulated by the ratio of the membrane reaction rates on the cell boundaries, we show for various specific prototypical intracellular reactions, and for a specific two-cell arrangement, that our 2-D coupled PDE-ODE model admits symmetry-breaking bifurcations from this symmetric steady-state, leading to linearly stable asymmetric patterns, even when the bulk diffusing species have comparable or possibly equal diffusivities. Overall, our analysis shows that symmetry-breaking bifurcations can occur without the large diffusivity ratio requirement for the bulk diffusing species as is well-known from a Turing stability analysis applied to a spatially uniform steady-state for typical two-component activator-inhibitor systems. Instead, for our theoretical compartmental-reaction diffusion bulk-cell model, our analysis shows that the emergence of stable asymmetric steady-states can be controlled by the ratio of the membrane reaction rates for the two species. Bifurcation theoretic results for symmetric and asymmetric steady-state patterns obtained from our asymptotic theory are confirmed with full numerical PDE simulations.
1. Introduction
A central issue in many chemical and biological systems that involve the coupling of diffusive processes and nonlinear reactions is to determine conditions for which spatio-temporal patterns can form from either a patternless or a pre-patterned state. In a pioneering theoretical study, Turing [1] established that diffusing morphogens with different diffusivities can destablilize a spatially uniform and stable steady-state of the nonlinear reaction kinetics. As applied to two-component activator-inhibitor reaction-diffusion (RD) systems, this Turing stability analysis shows that a sufficiently large diffusivity ratio is typically needed to obtain spatial pattern formation from the destabilization of a spatially uniform state, unless the nonlinear reaction kinetics are finely tuned (cf. Pearson and Horsthemke [2], Baker et al. [3], and Diambra et al. [4]). For certain chemical systems, this large diffusivity ratio requirement needed for pattern formation may be feasible to achieve in situations where one of the chemical species can bind to a substrate, which has the consequence of reducing the effective diffusivity of this species (cf. Lengyel and Epstein [5] and Dulos et al. [6]). However, in many cellular processes related to developmental biology and morphogenesis, the theoretical large diffusivity ratio threshold needed for freely diffusing morphogens to create symmetry-breaking patterns is often unrealistic as different small molecules typically have very comparable diffusivities (cf. Müller et al. [7] and Rauch and Millonas [8]). In Müller et al. [7], various modifications of the simple “freely diffusing” morphogen paradigm such as facilitated diffusion, transient binding, immobilization and transcytosis, among others, have been postulated to play a central role in specific applications of diffusive transport at the cellular level. Qualitatively, the postulated overall effect of these mechanisms is to modify an effective diffusivity ratio of the morphogens, which can, therefore, lead to the emergence of spatial patterns and symmetry-breaking behavior in cellular processes related to developmental biology and early morphogenesis (cf. Sozen et al. [9]).
As a result, one key long-standing theoretical question in RD theory is how to modify the two-component RD paradigm so as to robustly generate stable spatial patterns from a spatially homogeneous state when the time scales for diffusion of the interacting species are comparable. By including an additional non-diffusible component, which roughly models either membrane-bound proteins or an immobile chemically active substrate, it has been shown (cf. Pearson [10], Klika et al. [11], and Korvasová et al. [12]) that this “2+1” extension of the two-component RD framework can yield stable spatial patterns even when the two diffusible species have a common diffusivity. In another direction, which is based on graph-theoretic properties associated with nonlinear reactions between multiple species that are either immobile or freely diffusing, it has been shown that with certain activating and inhibiting feedback relations in the chemical kinetics, spatial patterns can form without the large diffusivity ratio requirement (cf. Marcon et al. [13], Diego et al. [14], and Landge et al. [15]). More recently, the authors in Haas and Goldstein [16] have revealed that in random, multi-component, RD systems the required diffusivity threshold for pattern formation typically decreases as the number of interacting and diffusing species increases.
From a theoretical viewpoint, in specific applications where a large diffusivity ratio is a realistic assumption, it has been shown both analytically and from numerical simulations (cf. Vanag and Epstein [17], Ward [18], Halatek et al. [19], and Halatek and Frey [20]) that two-component RD systems admit a wide range of spatially localized patterns and instabilities that occur in the “far-from-equilibrium” regime, far from where a Turing linear stability analysis will provide any insight into pattern-forming properties.
The goal of this paper is to formulate and quantitatively analyze a new theoretical model in a 2-D setting that robustly leads to pattern formation even when the two diffusing species have a comparable or equal diffusivity. More specifically, we analyze symmetry-breaking pattern formation for a 2-D PDE-ODE bulk-cell RD model in which spatially segregated localized reaction compartments, referred to as “cells,” are coupled to a two-component linear bulk diffusion field with constant bulk degradation rates. In the cells, which are assumed to have a common radius that is small compared to the domain length-scale and the inter-cell distances, two-component intracellular activator-inhibitor reaction kinetics are specified. The intracelluar species undergo an exchange with the two bulk species across the cell boundaries, as mediated by membrane reaction rates in a Robin boundary condition that is specified on each cell boundary. The two extracellular diffusing bulk species, with comparable diffusivities and degradation rates, provide the mechanism that couples the nonlinear intracellular reactions that occur in the union of the spatially segregated cells. We refer to this modeling framework as a compartmental-reaction diffusion system.
The numerical implementation of our theoretical analysis for this model for various specific intracellular reaction kinetics reveals that it is the ratio of the reaction rate of the inhibitor component to that of the activator component on the compartment boundaries that plays a central role in the initiation of symmetry-breaking bifurcations of a symmetric steady-state. The magnitude of this ratio ultimately controls whether linearly stable asymmetric steady-states for the bulk-cell model can occur even when the bulk diffusivities are comparable or equal. The bifurcation threshold condition for this key membrane reaction rate ratio parameter is distinct from the usual large diffusivity ratio threshold that is required for pattern formation from a spatially uniform state for typical two-component activator-inhibitor RD systems (cf. Maini et al. [21] and Krause et al. [22]). We emphasize that our linear stability analysis predicting symmetry-breaking bifurcations for the bulk-cell model, as regulated by the membrane reaction rate ratio, is significantly more challenging than performing a simple Turing stability analysis [1] since it is based on the linearization of the bulk-cell model around a spatially non-uniform symmetric steady-state. In our previous 1-D study [23], where nonlinear reactions were restricted either to domain boundaries or at lattice site on a 1-D periodic chain, it has been shown for some specific nonlinear kinetics that symmetry-breaking bifurcations can occur from a symmetric steady-state when the ratio of membrane reaction rates exceeds a threshold.
We remark that our 2-D study, and related 1-D analysis in Pelz and Ward [23], is largely inspired by the agent-based numerical computations in Rauch and Millonas [8] where it was shown that nonlinear kinetic reactions restricted to lattice sites on a 2-D lattice can generate stable Turing-type spatial patterns when coupled through a spatially discretized two-component bulk diffusion field in which the two diffusible species have a comparable diffusivity.
In a broader context, the study of novel pattern-forming properties associated with compartmentalized reactions interacting through a passive bulk diffusion field originates from the 1-D analysis in Gomez-Marin et al. [24] for the FitzHugh-Nagumo model and the bulk-membrane analysis of Levine and Rappel [25] in disk-shaped domains. In a 1-D context, and with one bulk diffusing species, this compartmental-reaction diffusion system modeling paradigm has been shown to lead to triggered oscillatory instabilities for various reaction kinetics involving conditional oscillators (cf. Gou et al. [26] Gou and Ward [27], and Gou et al. [28]). Amplitude equations characterizing the local branching behavior for these triggered oscillations have been derived in Paquin-Lefebvre et al. [29] using a weakly nonlinear analysis. Applications of this framework have been used to model intracellular polarization and oscillations in fission yeast (cf. Xu and Bressloff [30] and Xu and Jilkine [31]). In a 2-D domain, similar bulk-cell models, but with only one diffusing bulk species, have been formulated and used to model quorum-sensing behavior (cf. Gou and Ward [32], Iyaniwura and Ward [33], Ridgway et al. [34], and Gomez et al. [35]). With regards to bulk-membrane RD models in a multi-spatial dimensional context, where nonlinear kinetics are restricted to the membrane, the associated pattern-forming properties have been studied both theoretically (cf. Rätz [36], Elliott et al. [37], Madzvamuse et al. [38], Madzvamuse and Chung [39], and Paquin-Lefebvre et al. [40]), and for some specific biological applications (cf. Cusseddu et al. [41], Rätz and Röger [42, 43], Stolerman et al. [44], and Paquin-Lefebvre et al. [45]).
The outline of this paper is as follows. In Section 2 we formulate our bulk-cell model and use a singular perturbation approach in the limit of a small common cell radius to derive a nonlinear algebraic system characterizing all steady-state solutions of the model. In Section 3 we show that the discrete eigenvalues of the linearization of the bulk-cell model around a steady-state solution are determined by a root-finding condition on a nonlinear matrix eigenvalue problem. For a certain type of spatial configuration of the cells, the bulk-cell model is shown to admit a symmetric steady-state solution in which the steady-states of the intracellular reactions are identical. The possibility of symmetry-breaking bifurcations along this symmetric steady-state solution branch, leading to the existence of linearly stable asymmetric patterns, are analyzed by applying solution path continuation software to our bifurcation-theoretic analytical results. For a certain two-cell configuration in the unit disk, and for either Rauch and Millonas [8], Gierer and Meinhardt [46], or FitzHugh and Nagumo [24] intracellular reactions, we show in Section 4 that it is the magnitude of the ratio of the reaction rates for the two bulk species on the cell membranes that controls whether linearly stable asymmetric patterns can bifurcate from the symmetric steady-state. Our theoretical predictions of symmetry-breaking behavior, leading to stable asymmetric steady-states even when the two bulk species have comparable or equal diffusivities, are confirmed from full PDE numerical simulations. For a closely-spaced arrangement of cells as is typical in biological tissues, and where our asymptotic theory no longer applies, the PDE numerical simulations shown in Section 4.4 illustrate that symmetry-breaking bifurcations can still be controlled by the reaction rate ratio on the cell boundaries. In particular, our numerical results suggest that such bifurcations occur with a smaller membrane reaction-rate ratio than for the situation where the cells are more spatially segregated. In Section 5 we discuss our theoretical results in a wider context, and suggest a few open directions.
2. Compartmental-reaction diffusion system in 2-D
2.1. Model formulation
We consider a bounded 2-D domain with length scale L, denoted by ΩL ⊂ ℝ2, that contains m disconnected circular compartments ΩLj, for j ∈ {1, …, m}, referred to as “cells”. We will assume that these cells have a common radius that is small in comparison with the length scale L of the domain. The bulk or extracellular medium is the region ΩL\⋃mj=1ΩLj.
In the bulk we assume that there are two extracellularly diffusing and degrading chemical species with concentrations U and V. These messenger molecules are synthesized on the “cell” membranes through the interaction with two corresponding intracellular species Mj and Hj. With the molecule counts 𝔘, 𝔙, 𝔐j and ℌj corresponding to respectively U, V, Mj and Hj, the chemical equations are
Here we made the assumption that the exponential forward reaction rates equal the backward reaction rates and that all compartments are identical in that they have common membrane reaction rates. The intra-compartmental species, in turn, are produced by certain reaction kinetics, denoted by f(M, H) and g(M, H), that are assumed to be identical in each compartment.
More precisely, in dimensional variables, our bulk-cell coupled model is
with j ∈ {1, …, m} and where nj,X is the outward unit normal vector to ΩLj while ˜nX is the outward unit normal vector to ΩL. The diffusivities (diffusion coefficients) for U and V are DU and DV, and U and V are degrading in the bulk with exponential rate constants κU and κV, respectively. The exponential reaction rates on the compartment boundaries are βU and βV with corresponding rates βU,1 and βV,1 per area times length and βU,2 and βV,2 per length and time units, and μc is a normalizing constant for the intracellular species. Lastly, κR is a dimensional reaction rate for the intracellular reactions.
In Appendix A we non-dimensionalize (Equation 2.2) to obtain the dimensionless PDE-ODE model
for j ∈ {1, …, m}. Here n and ˜n are the outward unit normal vectors to Ωj and Ω, respectively, and we have dropped the label “x" for Δ and the outward unit normal vectors. In Equation (2.3), the compartments are disks of a common radius ε ≪ 1 centered at xj ∈ Ω, i.e. Ωj ≡ {x||x − xj| ≤ ε}. We will refer to du1, dv1, du2, and dv2 as dimensionless membrane reaction rates. An illustration of the bulk-cell model is shown in Figure 1.
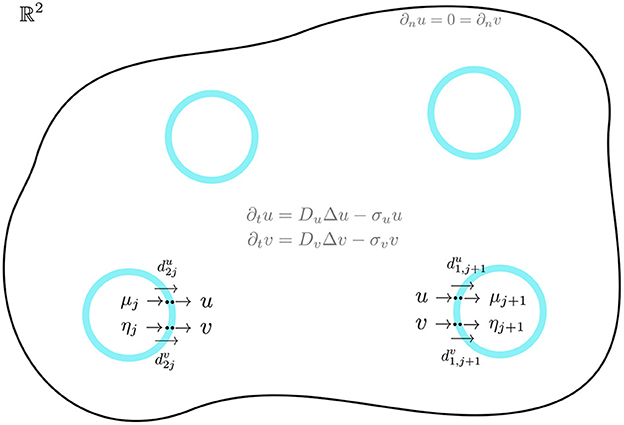
Figure 1. A 2-D bounded domain with four diffusion-coupled circular cells of a common radius. In the jth cell, activator-inhibitor reaction kinetics occur for the activator μj and inhibitor ηj. Across the cell membrane, there is an exchange between the intracellular and bulk species. In the bulk, u and v diffuse and undergo degradation. The cells are assumed to be small but are drawn larger here for illustration only.
We will use strong localized perturbation theory [18] to construct the steady-state solutions of Equation (2.3) and to analyze their linear stability properties in the asymptotic limit ε ≪ 1 and under the assumption that m circular cells are well-separated in the sense that the cell centers satisfy |xi-xj|=O(1), for i, j ∈ {1, …, m} and i ≠ j.
2.2. Asymptotic construction of the steady-states
Our main goal is to construct a symmetric steady-state solution for Equation (2.3) in which the concentration of each species is the same inside and in the local vicinity of each compartment. We will show below that even when the bulk diffusing species have comparable diffusivities this symmetric steady-state is unstable to symmetry-breaking perturbations that occur beyond a pitchfork bifurcation point associated with the membrane reaction rate ratio ρ≡dv1/du1=dv2/du2. This leads to the existence of linearly stable asymmetric steady-state solutions to Equation (2.3).
In the absence of diffusion, the ODE system for the intra-compartmental species is decoupled from the bulk medium and reduces to
Let (μe, ηe) be an equilibrium point for Equation (2.4) and label F(μ, η) ≡ (f(μ, η), g(μ, η)). For a specific parameter set, the linear stability property of the equilibrium state is characterized by whether the eigenvalues λ of the Jacobian matrix DF(μe, ηe) have positive (unstable, exponentially growing perturbations) or negative (stable, exponentially decaying perturbations) real parts Re(λ). However, when there is bulk diffusion and the compartments are coupled through the bulk, the steady-state solution in the compartments depends on the bulk diffusivities, the membrane reaction rates, and the spatial configuration of the cells.
We now use the method of matched asymptotic expansions to construct steady-state solutions for Equation (2.3). In the jth inner region, defined within an O(ε) neighborhood of the boundary of the jth cell, we introduce the local variables yj=ε-1(x-xj), uj(x) = u(εyj + xj), and vj(x) = v(εyj + xj), where pj ≡ |yj|. Upon writing the steady-state of Equation (2.3a) in terms of the inner variables, for ε → 0 the steady-state problem in the jth inner region is Δuj = 0 and Δvj = 0, for pj ≥ 1, subject to Du∂pjuj=du1uj-du2μj and Dv∂pjvj=dv1vj-dv2ηj on pj = 1. The radially symmetric solutions to these problems are
for j ∈ {1, …, m}, where and for j = 1, …, m are constants to be determined. Upon substituting (Equation 2.5) into the steady-state problem of Equation (2.3c), we obtain for the jth cell that
Next, we must determine and by matching the far-field behavior of the inner solutions (Equation 2.5) to the outer solutions defined in the bulk region.
In the limit ε → 0, in the bulk region the compartments formally shrink to points and from the far-field behavior of Equation (2.5), when written in outer variables, we obtain that the steady-state bulk species U satisfies
where ν ≡ −1/log ε ≪ 1 and . Similarly, with , for the bulk species V we have that
To represent solutions to (2.7) and (2.8), we introduce the reduced-wave Green's function Gω(x, xj) that satisfies
Here Rω(xj) is the regular, or non-singular, part of the singularity at x = xj. The solutions to (2.7) and (2.8) are represented as
The pre-specification of the regular part of each singularity condition in Equations (2.7), (2.8) yields a constraint. These constraints provide algebraic systems for and for j ∈ {1, …, m}. By expanding (Equation 2.10) as x → xj, we enforce that that the non-singular terms in the resulting expression agree with the conditions that are required in Equations (2.7b), (2.8b) for each j ∈ {1, …, m}. This leads to linear algebraic systems for and , given in matrix form by
where and . In Equation (2.11), with either ω = ωu or ω = ωv is the symmetric reduced-wave Greens' interaction matrix defined by
Here Gωji = Gωij ≡ Gω(xj; xi) for i ≠ j, and Rωj ≡ Rω(xj) for j ∈ {1, …, m}, are obtained from the solution to Equation (2.9).
To determine a nonlinear algebraic system that characterizes our steady-state solution, we solve (Equation 2.11) for and , and substitute the resulting expressions into Equation (2.6). In this way, we obtain a 2m dimensional nonlinear algebraic system for μj and ηj, for j = 1, …, m, given by
Where is the unit vector in the jth direction. In Equation (2.13a), Θu and Θv are defined by
We can simplify our steady-state analysis for the special case where g(μ, η) is linear and inhibiting in η, with the form
where g2 ≥ 0 is a constant. This specific form applies to Rauch and Millonas [8], FitzHugh and Nagumo [24], and Gierer and Meinhardt [46], reaction kinetics, and is relevant for the illustrations of the theory given in Section 4. In this case, we obtain from the second equation in Equation (2.13a) that
Then, from the first equation in Equation (2.13a) we obtain an m dimensional nonlinear algebraic system for given by
Next, we define a symmetric cell arrangement for which the steady-state analysis can be further simplified.
Definition 2.1. A symmetric cell arrangement is defined by the condition that the symmetric Green's matrix satisfies the following two properties:
• Property 1: e ≡ (1, …, 1)T is an eigenvector of for all ω > 0:
• Property 2: The eigenspace of orthogonal to e is independent of ω.
These two properties certainly hold when is a circulant matrix. In particular, is a circulant matrix when m small cells are equidistantly spaced on a ring that is concentric within a circular domain Ω. Such an arrangement of cells is called a ring pattern.
For a symmetric cell arrangement, and have a common eigenspace, and so we can seek a symmetric solution to Equation (2.13) of the form
where the scalars μc, ηc, , and are to be found. Upon substituting (Equation 2.17) into Equation (2.13), we obtain that μc and ηc satisfy the nonlinear algebraic system
where αu and αv, denoting the eigenvalues of Θu and Θv for the eigenvector e, respectively, are defined by
Here κu and κv are the eigenvalues of the Green's matrices for the eigenvector e, given by
Moreover, if g(μ, η) has the specific form in Equation (2.14), we obtain from Equation (2.16) that for a symmetric pattern of cells, there is a symmetric steady-state solution whenever there is a root μc to the scalar nonlinear algebraic equation
In summary, for a symmetric pattern of cells, the asymptotic construction of a symmetric steady-state solution for Equation (2.3) is reduced to the much simpler problem of determining a solution to the two-dimensional nonlinear algebraic problem (Equation 2.18) for general reaction kinetics, or to Equation (2.20) when g has the specific form in Equation (2.14). In these algebraic problems, the eigenvalues κu and κv, as needed in Equation (2.19a), are the constant row sums of the Green's matrices for the two bulk species. The bulk diffusivities, the membrane reaction rates, and the spatial configuration of the cells all influence αu and αv.
2.3. Symmetry-breaking bifurcations
To detect any symmetry-breaking pitchfork bifurcation points along the symmetric steady-state solution branch we can perform a linear stability analysis of Equation (2.3) around the steady-state solution and seek λ = 0 eigenvalue crossings. An equivalent, but simpler, approach to detect zero-eigenvalue crossings for the linearized problem is to determine bifurcation points associated with the linearization of the nonlinear algebraic system (Equation 2.13) around a symmetric steady-state.
To do so, we introduce the perturbations
into Equation (2.13) and linearize the resulting system. In this way, we obtain that a symmetry-breaking bifurcation occurs if and only if there is a non-trivial solution to the 2m × 2m homogeneous linear system
at some point along the symmetric solution branch given by Equation (2.18). In Equation (2.22) we have labeled by when evaluated at μ = μc and η = ηc, while I is the m × m identity matrix. For the special case where g has the specific form in Equation (2.14), we can solve (Equation 2.22) for and reduce (Equation 2.22) to the m-dimensional homogeneous linear system
Next, by Property 2 for a symmetric cell arrangement, it follows that and have a common orthogonal eigenspace , where for j ∈ {2, …, m} and for i ≠ j. The eigenvalues of and in this common eigenspace are labeled by
so that
with
By setting and in Equation (2.22), we conclude that a symmetry-breaking bifurcation occurs for the jth mode with j ∈ {2, …, m} whenever
has a nontrivial solution. This is equivalent to the condition that
is satisfied at some point along the symmetric solution branch defined by the solution to (2.18).
Finally, for the special case where g has the specific form in Equation (2.14), we obtain that there is a symmetry-breaking bifurcation for the jth mode, with j ∈ {2, …, m}, when there is a root to the scalar problem
whenever ηc = g1(μc)/(g2 + αv) where μc satisfies (Equation 2.20).
In the examples shown in Section 4 we will use as the bifurcation parameter to detect whether symmetry-breaking bifurcations can occur along the symmetric solution branch.
2.4. A symmetric cell arrangement with two cells
Consider a symmetric cell arrangement with two cells, i.e. m = 2, for the special case where g has the form in Equation (2.14). Then, to determine all steady-state solutions we need only solve the nonlinear algebraic system (Equation 2.16) for μ1 and μ2. The symmetric steady-state solution, for which μc ≡ μ1 = μ2, is obtained by solving the scalar problem (Equation 2.20). To detect whether symmetry-breaking bifurcations can occur, we note that spans the common eigenspace of and orthogonal to e, and that κu = Rωu1 − Gωu12 and κv = Rωv1 − Gωv12 are the associated eigenvalues for q2. This yields that the root-finding condition (Equation 2.29) becomes
where in terms of the entries of the Green's matrices we have
To detect any pitchfork bifurcation points on the symmetric steady-state branch parameterized by we numerically solve (Equation 2.20) together with Equation (2.30). In Section 4 we illustrate this approach for certain reaction kinetics when Ω is the unit disk. The advantage of considering a disk-shaped confining domain is that the reduced-wave Green's function is known analytically by using separation of variables (see Appendix B). We remark that it would also be readily feasible to illustrate our asymptotic theory for a rectangular-shaped confining domain, since the reduced-wave Green's function is also available analytically for such a domain.
3. The linear stability analysis
In this section, we formulate the linear stability problem for the steady-state solutions constructed in Section 2.2. We denote the bulk steady-state solutions of Section 2.2 by ue(x) and ve(x), and the steady-state vector of intracellular steady-states by and .
To formulate the linear stability problem, we first introduce the perturbations
into Equation (2.3) and linearize the resulting system. This yields the eigenvalue problem
Here the Jacobian matrix Jj of the intracellular kinetics, as well as Ωu and Ωv are defined by
We now use strong localized perturbation theory [18] to analyze (Equation 3.1) in the limit ε → 0. In this way we will derive a nonlinear matrix eigenvalue problem, referred to as the globally coupled eigenvalue problem (GCEP), for the discrete eigenvalues λ of the linearization. This GCEP will be used to investigate various instabilities of the steady-state solutions constructed in Section 2.2.
In the inner region near the jth cell we introduce the local variables , ϕj(x) ≡ ϕ(xj + εyj) and ψj(x) ≡ ψ(xj + εyj), with pj = |yj|. Upon writing (Equation 3.1a) in terms of the inner variables, for ε → 0 we obtain in the jth inner region that Δϕj = 0 and Δψj = 0, for pj ≥ 1, subject to and on pj = 1. The radially symmetric solutions to these problems are
for j ∈ {1, …, m}, where and for j ∈ {1, …, m} are constants to be determined. Upon substituting (Equation 3.3) into Equation (3.1c) we obtain, in terms of the Jacobian Jj of Equation (3.2), that
To determine and we must match the far-field behavior of the inner solutions (Equation 3.3) to the outer solutions defined in the bulk region. Similar to the analysis of the steady-state solution, we obtain that
where ν ≡ −1/log ε ≪ 1. Similarly, for the perturbation of the other bulk species we obtain
The solutions to Equations (3.5), (3.6) are represented as
where, to simplify the notation and emphasize the dependence on the eigenvalue parameter λ, we have defined
where Gω(x; xj) is defined by the solution to Equation (2.9). Upon letting x → xj in Equation (3.7) and ensuring that the singularity conditions in Equations (3.5b), (3.6b) are satisfied, we obtain a linear algebraic system for the vectors and , given in matrix form by
where and . In Equation (3), and denote the reduced-wave Green's matrix given in Equation (2.12) with either ω = Ωu or ω = Ωv, respectively. Here Ωu and Ωv are defined in terms of λ by Equation (3.2).
Assuming that λ is not an eigenvalue of Jj for any j ∈ {1, …, m}, we obtain upon inverting (Equation 3.4) and writing the system in matrix form that
where and . Here K11, K12, K21, and K22 are the diagonal matrices defined by
with diagonal entries given by
where and .
Then, upon substituting (Equation 3) into Equation (3.10), we obtain the 2m × 2m homogeneous algebraic system, which we write in block matrix form as
with
The nonlinear matrix eigenvalue problem (Equation 3.12) is referred to as the globally coupled eigenvalue problem (GCEP). The GCEP has a nontrivial solution (cu, cv)T ≠ (0, 0)T, if and only λ satisfies . The set , defined by
is the union of all such roots. Any element satisfying Re(λ) > 0 provides an approximation, valid as ε → 0, for an unstable discrete eigenvalue of the linearized problem (Equation 3.1). However, if for all we have Re(λ) < 0, then the steady-state solution is linearly stable.
When there is a large number of cells m, the determination of the discrete eigenvalues comprising is in general a very challenging numerical problem. A survey of nonlinear matrix eigenvalue problems and available solution strategies that apply to only certain classes of matrices is given in Güttel and Tisseur [47] and Betcke et al. [48]. Specific applications of nonlinear matrix problems in simpler contexts where is either a polynomial or a rational function of λ are discussed in Betcke et al. [49]. Since for our problem, is not symmetric and has a complicated dependence on the eigenvalue parameter through the Green's matrices and from the diagonal K matrices of Equation (3.11), these previously developed numerical strategies are not applicable for computing the set in Equation (3.13) for a steady-state solution with an arbitrary collection of cells.
For a symmetric steady-state solution corresponding to a symmetric cell arrangement, we now verify that the condition in Equation (3.12) is equivalent to the zero-eigenvalue crossing condition derived in Equation (2.22), which was based on a linearization of the nonlinear algebraic system around the symmetric steady-state. When λ = 0, we have
where Θu and Θv are defined in Equation (2.13b). Since K11, K12, K22, and K21 are all multiples of the identity for a symmetric steady-state, we obtain from Equation (3.12) together with Equation (3) that when λ = 0 we have in block matrix form
Here we have re-defined the scalars K11, K12, K21, and K22 by K11 = K11I, K12 = K12I, K21 = K21I, and K22 = K22I. When λ = 0, we calculate that
Finally, upon multiplying (Equation 3.14) by Jc, and using , we readily obtain that
which is precisely the same as in Equation (2.22).
3.1. Re-formulation of the linear stability problem
A simpler formulation of the linear stability problem that applies to both symmetric and asymmetric steady-state solutions can be done when g has the specific form in Equation (2.14). In this situation, we can write (Equation 3.4) in the form
Then, upon relating and to ζj and ξj by using Equation (3), we obtain in matrix form that
Where Θu,λ,Θv,λ, and the diagonal matrices Λ2, Λ3, and Λ4 are defined by
Upon eliminating ζ in Equation (3.16), we obtain the following nonlinear eigenvalue problem for the case where g has the form in Equation (2.14):
Observe that setting involves root-finding on the determinant of a matrix of size m × m rather than that for the larger 2m × 2m matrix, as needed for Equation (3.13).
The characterization (Equation 3.18) is particularly useful for determining the linear stability properties of a symmetric steady-state for a symmetric cell arrangement when g has the form in (2.14). For a symmetric steady-state with λ = 0, we obtain from Equation (3.17) that , , and . From Equation (3.18), this yields that
Since Θu,λ = Θu and Θv,λ = Θv when λ = 0, where Θu and Θv were defined in Equation (2.13b), we obtain that the condition is equivalent to the formulation (Equation 2.23) derived in Section 2.3, which was based on linearizing the nonlinear algebraic system around the symmetric steady-state solution.
For a symmetric steady-state solution of a symmetric cell arrangement, one key advantage of the re-formulation (Equation 3.18) is that the discrete eigenvalues of the linearization (Equation 3.1) can be determined by finding the union of the roots of m scalar problems. This is done by using , where σj(λ) for j = {1, …, m} are the eigenvalues of . More specifically, since and have the common eigenspace
the eigenvalue σ1(λ) corresponding to e and the eigenvalues σj(λ) corresponding to qj, for j ∈ {2, …, m} are readily calculated. A simple calculation yields that
where we have defined
With this re-formulation, for a symmetric steady-state of a symmetric cell arrangement, and with g of the form in Equation (2.14), the set of discrete eigenvalues of the linearization, , in Equation (3.13) can be written conveniently as
In summary, to determine the linear stability properties of this symmetric steady-state solution we need only solve m scalar root-finding problems and determine whether there are any roots in Re(λ) > 0. This is considerably more tractable numerically than performing a root-finding based on the determinant of the GCEP in Equation (3.18).
4. Illustrations of the theory: A ring pattern of cells
In this section we illustrate the steady-state and linear stability theory developed in Sections 2.2, 3 for a ring pattern of cells inside unit disk Ω, for which the Green's function is given analytically in Appendix B. We will show that symmetry-breaking bifurcations can occur for the Rauch and Millonas [8], Gomez-Marin et al. [24], and Gierer and Meinhardt [46] reaction kinetics. The theoretical prediction of stable asymmetric patterns will be confirmed through full time-dependent numerical simulations of Equation (2.3) computed using FlexPDE [50].
For a ring pattern of m cells in the unit disk with ring radius r, with 0 < r < 1, the cell centers are located at
For a ring pattern of cells, all Green matrices are symmetric and circulant and have the common eigenspace
which are a basis of ℂm. In Equation (B.2) of Appendix B we summarize how to obtain the matrix spectrum of a symmetric and circulant matrix that has a real-valued basis for the eigenspace.
In our illustrations of the theory below, we will assume for simplicity that the membrane reaction rates satisfy
and that g(μ, η) has the specific form in Equation (2.14). We will focus on a two-cell ring pattern in the unit disk, as shown schematically in Figure 2, for three specific reaction kinetics.
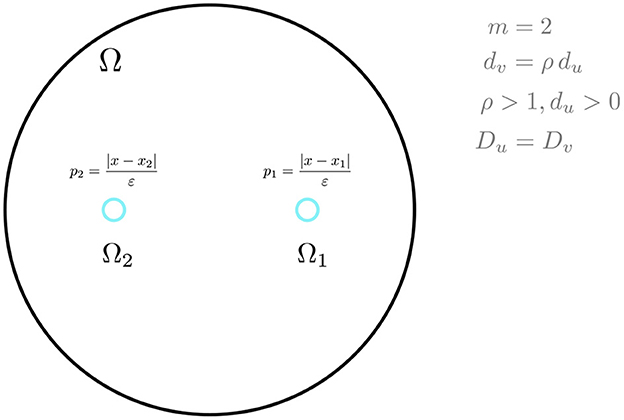
Figure 2. A schematic plot of a ring pattern in the unit disk with two cells. The bifurcation parameter for symmetry-breaking is ρ, while the diffusivities satisfy Du = Dv.
To numerically implement our asymptotic theory, the steady-state solution branches are computed from Equation (2.16) with m = 2 using the parameter continuation software MatCont [51], while the symmetric solution branch is obtained from Equation (2.20). Symmetry-breaking bifurcation points in ρ along the symmetric branch are identified by numerically solving (Equation 2.30) together with Equation (2.20). Finally, to determine the linear stability properties of the symmetric branch we need only determine if there exists a λ with Re(λ) > 0 in the set given in Equation (3.21). For m = 2, this is done by calculating all the roots of σ1(λ) = 0 and σ2(λ) = 0 by using Equation (3.20) and the explicit expressions for the eigenvalues of the Green's matrices as can be obtained from Appendix B.
4.1. Gierer-Meinhardt reaction kinetics
We consider a prototypical Gierer-Meinhardt model (GM), where the nonlinear reaction kinetics are confined within the compartments. The original GM model, introduced in Gierer and Meinhardt [46] and Gierer [52] to model pattern formation in biological morphogenesis, has the form
This model disregards that in biological tissues morphogen-producing reactions mostly occur intracellularly and on the membranes of cells. For simplicity, we illustrate our compartmental-reaction diffusion theory for the specific case where ϱ0 ≡ 0, cuϱu(x) ≡ 1, and cvϱv ≡ 1. When there is no bulk diffusion, the compartments are uncoupled from the bulk and we impose the intracellular reaction kinetics
The uncoupled equilibrium for Equation (4.3) given by μe = 0, and where ηe is an arbitrary constant, is non-hyberbolic in all directions.
To apply the bulk-cell steady-state analysis of Section 2 for a two-cell ring pattern, we first identify that g(μ, η) = g1(μ) − g2η, where and g2 = 0. For m = 2, we conclude from Equation (2.16) that all steady-states of the bulk-cell system are associated with the nonlinear algebraic problem
The symmetric equilibrium (μe, ηe), which satisfies (Equation 2.20), is readily calculated as
where αu and αv are defined in Equation (2.19). By combining (Equation 4.5) with Equation (2.30), we conclude that a symmetry-breaking bifurcation from the symmetric steady-state occurs whenever the condition
is satisfied at some point along the symmetric solution branch. Here and were defined in (2.31).
In Figure 3, Left we plot the bifurcation diagram of solutions to Equation (4.4) for a parameter set where Dv = Du and with the other parameter values as in the figure caption. We observe that a supercritical symmetry-breaking pitchfork bifurcation from the symmetric branch occurs at the critical value ρ = ρp ≈ 9.79168. In Figure 4 we show full PDE results for Equation (2.3) computed with FlexPDE [50] for values of ρ on either side of this theoretically predicted bifurcation value. In the left panels of this figure, we observe that when ρ = 5 < ρp, an initial perturbation of the symmetric steady-state converges back to the symmetric steady-state as time increases. In contrast, when ρ = 15 > ρp, we observe from the Figure 4, Right that, for an initial condition near the symmetric steady-state, the time-dependent PDE solution converges as time increases to the asymmetric steady-state predicted in Figure 3, Left.
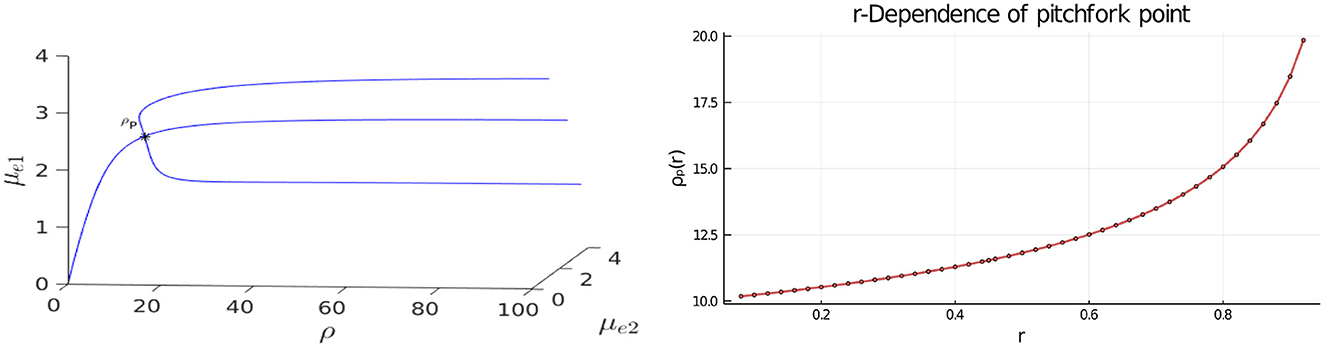
Figure 3. Left: 3-D Bifurcation diagram, computed from Equation (4.4), showing symmetric and asymmetric steady-states of a two-cell ring pattern with ring radius r = 0.5 and GM kinetics (Equation 4.3). Asymmetric steady-states emerge at the supercritical pitchfork bifurcation point ρ = ρp ≈ 9.79168 along the symmetric branch. Right: The pitchfork bifurcation value of ρ increases rapidly as the ring radius r, and consequently the distance between the cells, increases. The dots are the values computed from Equation (4.6), while the curve is the interpolation by the plotting function in Bezanson et al. [53]. Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.09, and ε = 0.03.
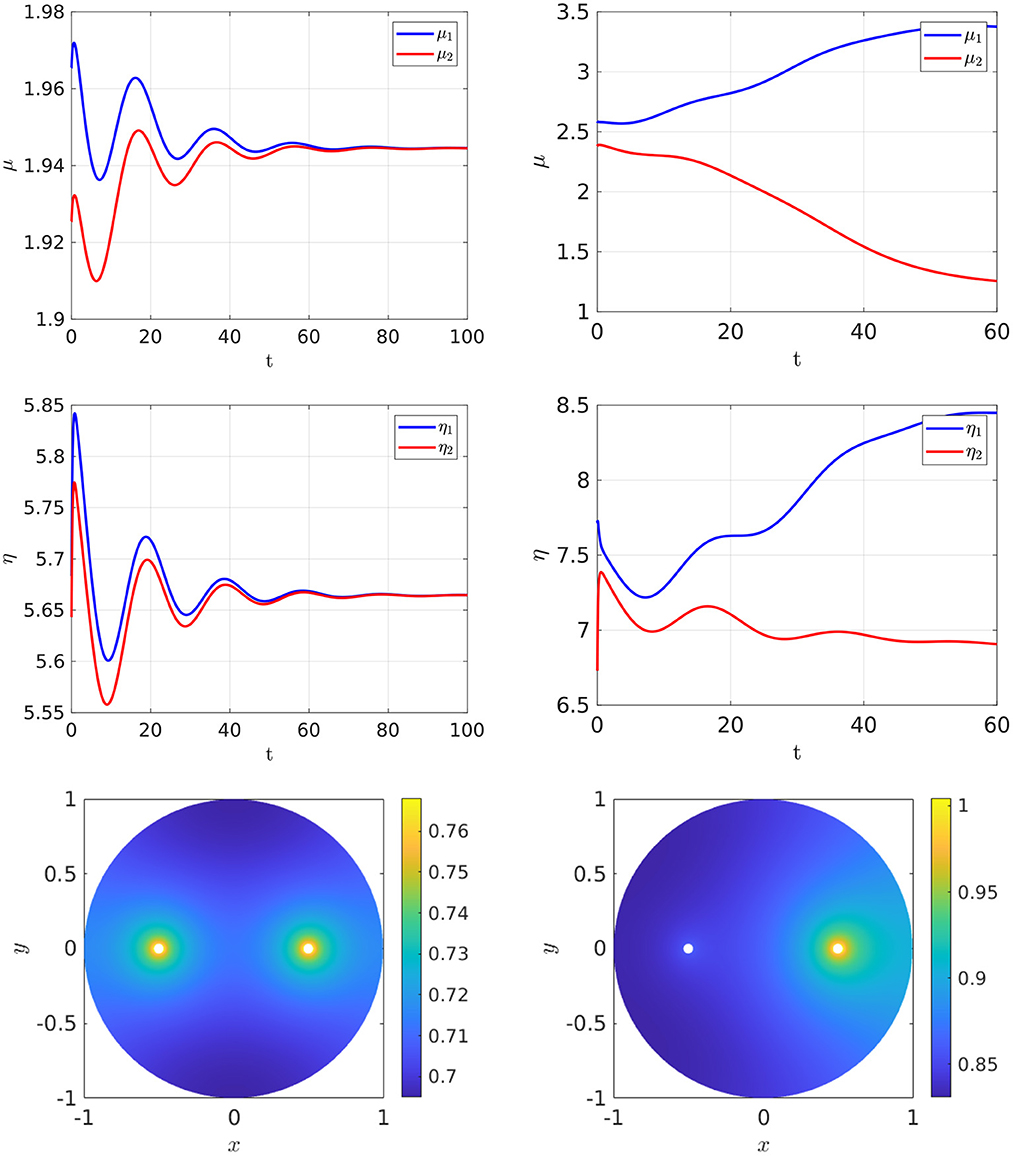
Figure 4. Full numerical PDE simulation results of Equation (2.3) with FlexPDE [50] for GM kinetics Equation (4.3). The bottom panels show the concentration of u. Left: convergence to the symmetric branch for ρ = 5 before the supercritical pitchfork point ρp = 9.79168, for an initial condition close to the symmetric branch. Right: convergence to the asymmetric branch selected by the eigenperturbation direction for ρ = 15 and starting near the symmetric branch. Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.09, ε = 0.03, and r = 0.5.
In the Figure 3, Right we show that the pitchfork bifurcation value for the emergence of asymmetric steady-states increases substantially when the ring radius for the two-cell pattern increases. As a result, we conclude that for cells that are farther apart, a larger value of ρ is needed to create a stable asymmetric pattern.
We now show that by varying the membrane reaction rate du, which necessarily varies the membrane reaction rate to the v-species according to dv = ρdu, the steady-state solution branches with GM kinetics (Equation 4.3) computed from Equation (4.4) can exhibit a hysteresis structure for low du. The numerical results of Figure 5 show such a hysteretic bifurcation structure between the asymmetric and symmetric solution branches for two values of du. We observe that as du decreases the extent of the hysteresis increases. The range where hysteresis occurs is given by the separation ρp − ρs between the pitchfork point ρp and the secondary fold bifurcation point ρs along each asymmetric branch. Numerical results for this range for a parameter set where hysteresis occurs when du < 0.09 is given in Table 1.
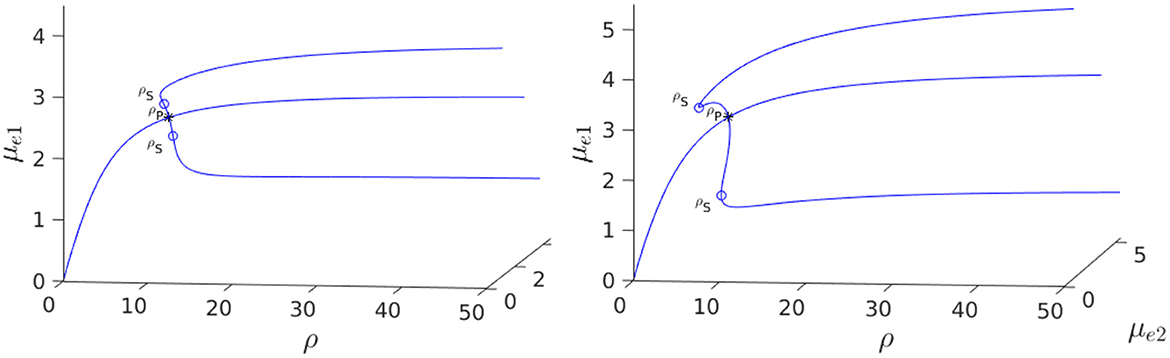
Figure 5. 3-D Bifurcation diagram, computed from Equation (4.4), for symmetric and asymmetric steady-states of a two-cell ring pattern with ring radius r = 0.5 and two different values of du with GM kinetics (4.3). Left: du = 0.08. Right: du = 0.05. For these values of du, the steady-states exhibit hysteresis, i.e., a subcritical pitchfork bifurcation occurs from the symmetric equilibrium branch, with the emerging unstable asymmetric equilibrium branches regaining stability at a secondary fold point. Observe that the extent of the hysteresis increases when du decreases. Parameters: Du = Dv = 5, σu = σv = 0.6, ε = 0.03, and r = 0.5.
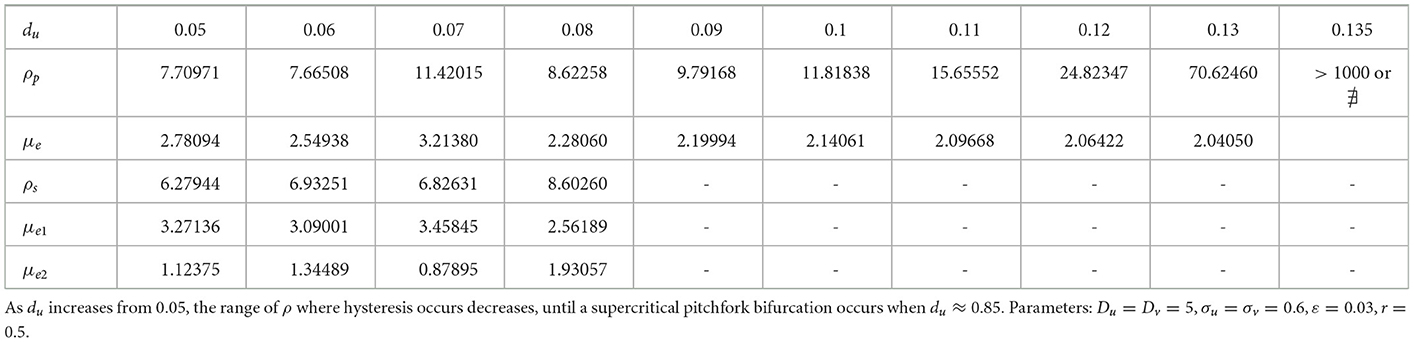
Table 1. Numerical values (rounded to 5th decimal place) of the subcritical (or supercritical) pitchfork bifurcation point ρp, the fold bifurcation point ρs, and the associated values for the symmetric μe and one of the asymmetric (μe1, μe2) solution branches.
For the parameter set with du = 0.05, which corresponds to the bifurcation diagram shown in the Figure 5, Right, the full time-dependent computations of Equation (2.3) with FlexPDE [50], as shown in Figure 6, illustrate that for an initial condition near the symmetric steady-state branch, and with ρ either satisfying ρ < ρs or ρs < ρ < ρp, the time-dependent solution converges to the stable symmetric steady-state solution. However, as shown in Figure 7, Left, for an initial condition near the asymmetric branch when ρ is in the hysteresis region ρs < ρ < ρp, the time-dependent solution converges to the asymmetric steady-state. Moreover, if ρ > ρp, the Figure 7, Right shows that for an initial condition near the unstable symmetric steady-state the time-dependent solution converges to the asymmetric steady-state solution.
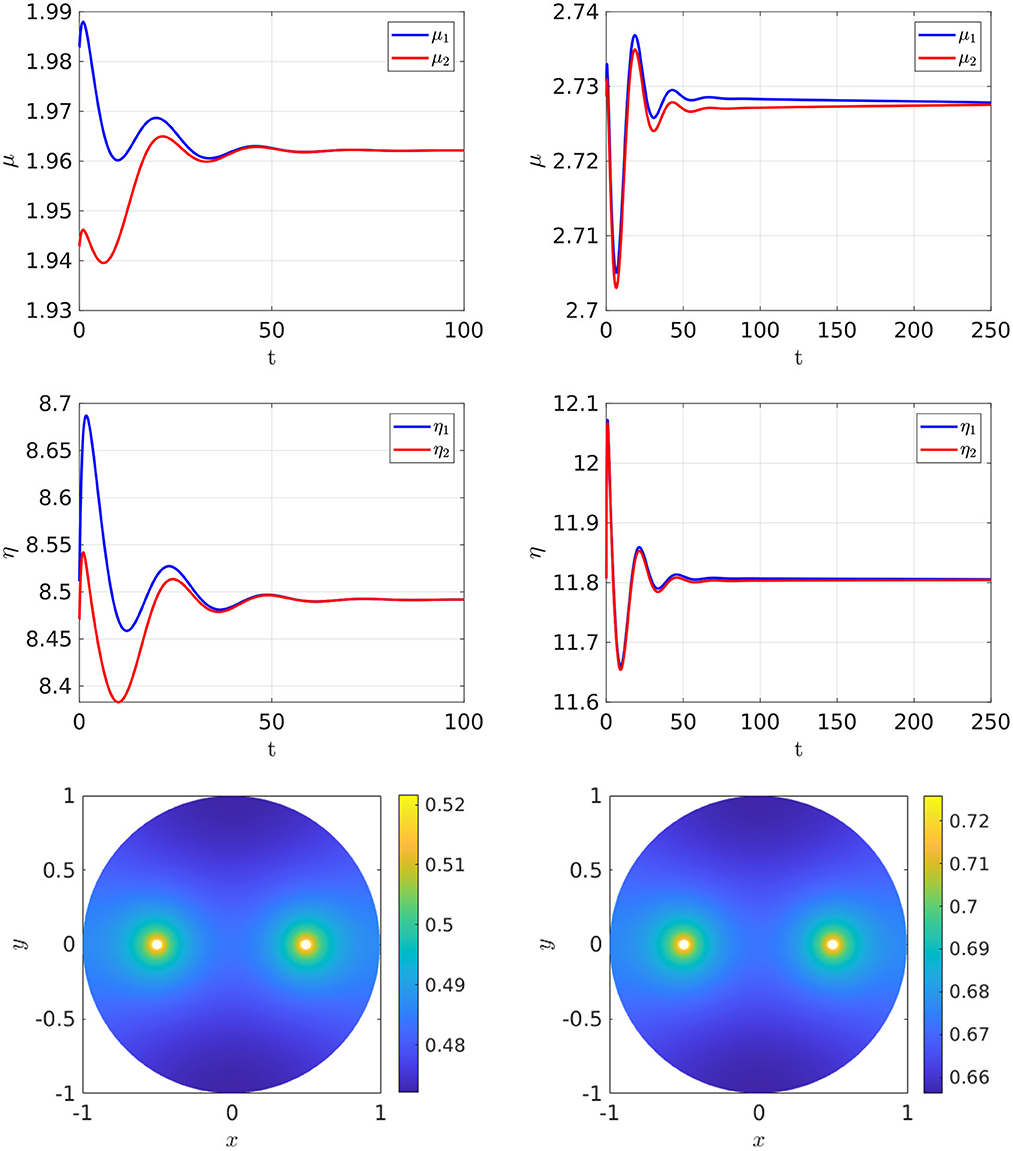
Figure 6. Full numerical simulation results of Equation (2.3) with FlexPDE [50] for GM kinetics (Equation 4.3). Left: for an initial condition near the symmetric branch we observe convergence to the symmetric branch when ρ = 4, which is before the hysteresis region bounded by the fold point ρs ≈ 6.27945 and the subcritical pitchfork point ρp ≈ 7.70971. Right: convergence to the symmetric branch for ρ = 7.2, which lies on the range ρs < ρ < ρp, when starting near the symmetric branch. The bottom panels show the concentration of u. Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.05, ε = 0.03, r = 0.5.
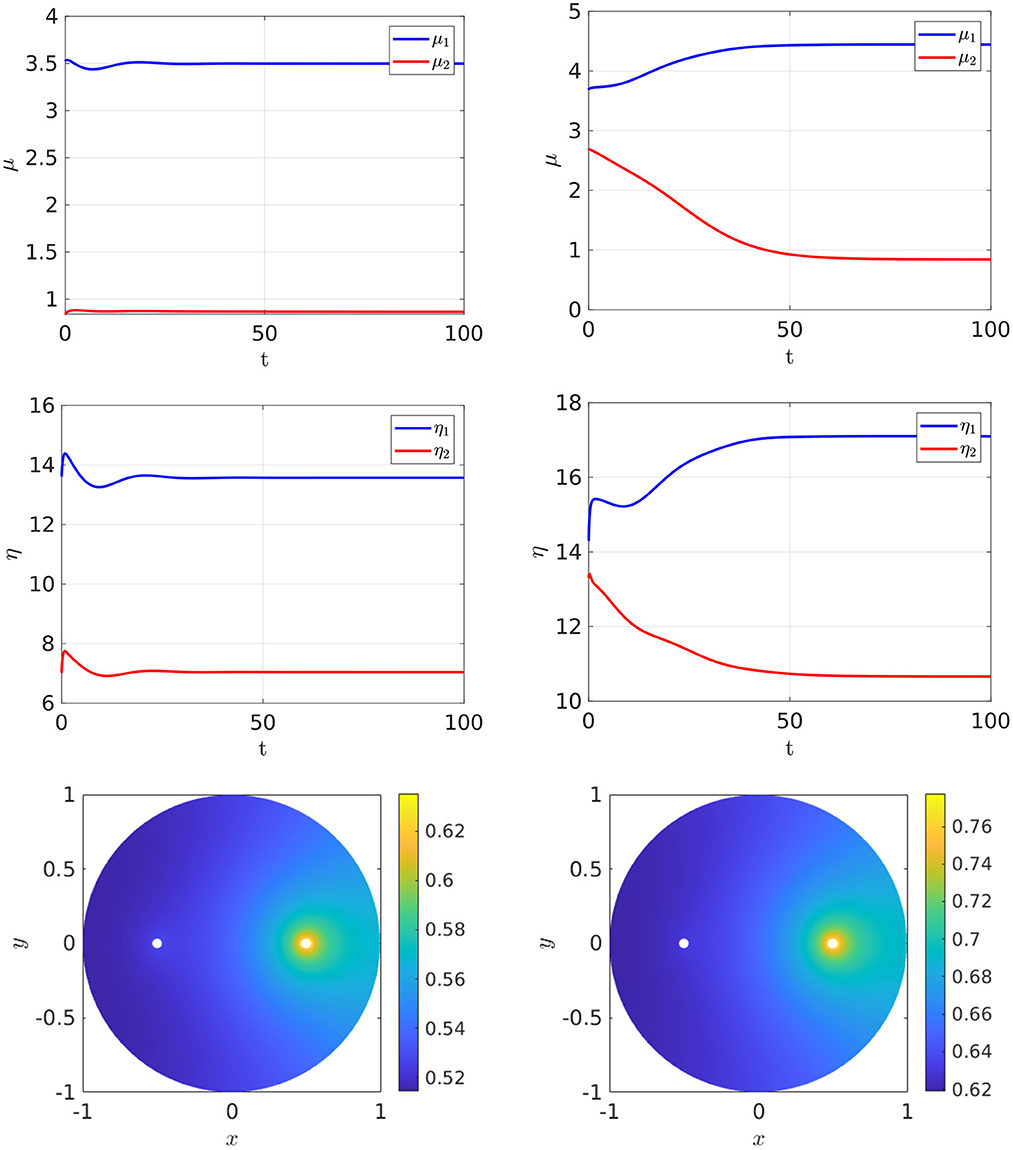
Figure 7. Full numerical simulation results of Equation (2.3) with FlexPDE [50] for GM kinetics (Equation 4.3). Left: convergence to the asymmetric branch for an initial condition near this branch when ρ = 7.2 lies in the hysteresis region between the fold point ρs ≈ 6.27945 and the subcritical pitchfork point ρp ≈ 7.70971. Right: convergence to an asymmetric steady-state as selected by a small initial perturbation of the symmetric solution in the direction q2 = (1, −1) when ρ = 15 > ρp. The bottom panels show the concentration of u. Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.05, ε = 0.03, and r = 0.5.
To determine the linear stability properties of the symmetric steady-state solution branch as ρ is varied in Figures 3, 5 we must determine the eigenvalues λ in the set (3.21). This is done by numerically computing the largest roots to σ1(λ) = 0 and to σ2(λ) = 0, as defined in Equation (3.20). In Figure 8 we plot these roots vs. ρ for two values of du. From this figure, we observe that in-phase perturbations of the symmetric steady-state solution branch, as determined by the roots of σ1(λ) = 0, are always linearly stable. In contrast, anti-phase perturbations of the symmetric steady-state, as characterized by the roots of σ2(λ) = 0, are linearly stable only for ρ < ρp, where ρp is the symmetry-breaking threshold. For ρ > ρp, the symmetric steady-state solution branch is unstable to an anti-phase eigenperturbation .
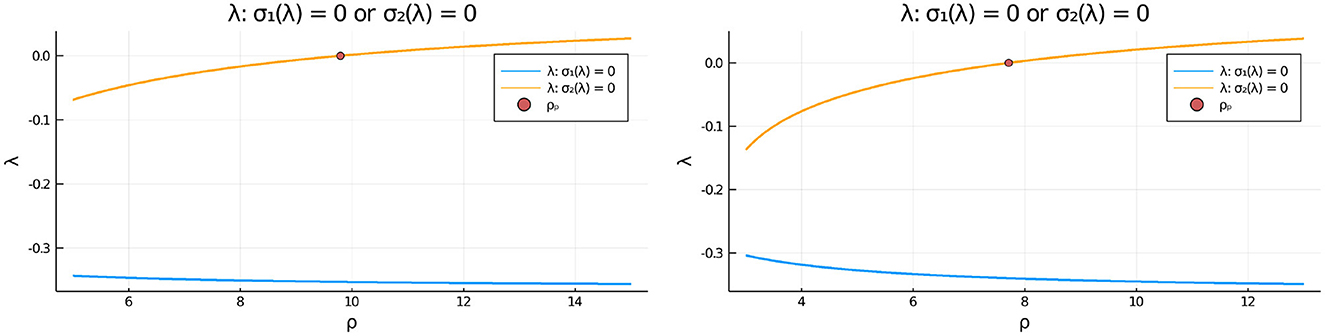
Figure 8. Plots of the numerically computed largest roots of σ1(λ) = 0 and σ2(λ) = 0 vs. ρ, as defined in Equation (3.20), that determine the linear stability properties to either in-phase e = (1, 1)T or anti-phase eigenperturbations of the symmetric steady-state solution, respectively. Left: for du = 0.09 we have ρp ≈ 9.79168. Right: for du = 0.05 we have ρp ≈ 7.70971. Observe that in-phase eigenperturbations are always linearly stable, whereas anti-phase eigenperturbations are linearly stable only on the range ρ < ρp before the pitchfork point ρp. Parameters: Du = Dv = 5, σu = σv = 0.6, ε = 0.03, r = 0.5.
Next, to study the linear stability properties of the asymmetric steady-state solution branches we must determine whether the root-finding condition in Equation (3.18) yields an eigenvalue with Reλ > 0. The numerical results shown in Figure 9 for du = 0.05 (corresponding to in Figure 5, Right), establishes that the asymmetric branch on the subcritical range ρs < ρ < ρp, which emanates from the symmetric steady-state branch, is unstable. However, as observed from Figure 9, the upper portion of the asymmetric branch for ρ > ρs is linearly stable.
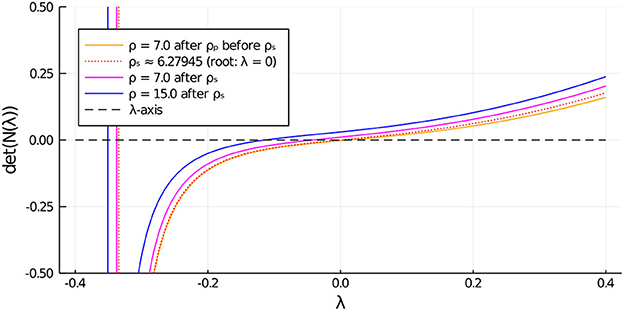
Figure 9. Zero-crossings of , as defined in Equation (3.18), determine the linear stability properties of an asymmetric steady-state solution with two cells. On the range ρp < ρ < ρs, before the secondary fold point along the asymmetric branch, we observe that λ > 0. This implies that the subcritical portion of the asymmetric steady-state branch between the pitchfork point and the fold point is unstable. Further along past the fold point the asymmetric branch regains stability.
Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.05, ε = 0.03, r = 0.5.
We now explore how the pitchfork bifurcation point depends on decreasing values of the diffusion coefficient ratio Dv/Du when du = 0.09. When this ratio is unity, there was no hysteresis between the symmetric and asymmetric steady-state solution branches (see Table 1). We remark that a similar numerical experiment was performed in Section 2.3 of Pelz and Ward [23] for a 1-D compartmental-reaction diffusion model with GM kinetics with dynamically reactive boundaries. In our 2-D setting, we observe from the numerical results in Table 2 that a symmetry-breaking bifurcation can occur on the range Dv/Du < 1, but only up until some minimum diffusion ratio threshold at which the pitchfork bifurcation point given by the root of Equation (4.6) no longer exists. In addition, we observe that reducing the diffusion ratio threshold Dv/Du below unity for fixed du = 0.09 does not introduce new hysteresis behavior, and the symmetry-breaking bifurcation remains supercritical.
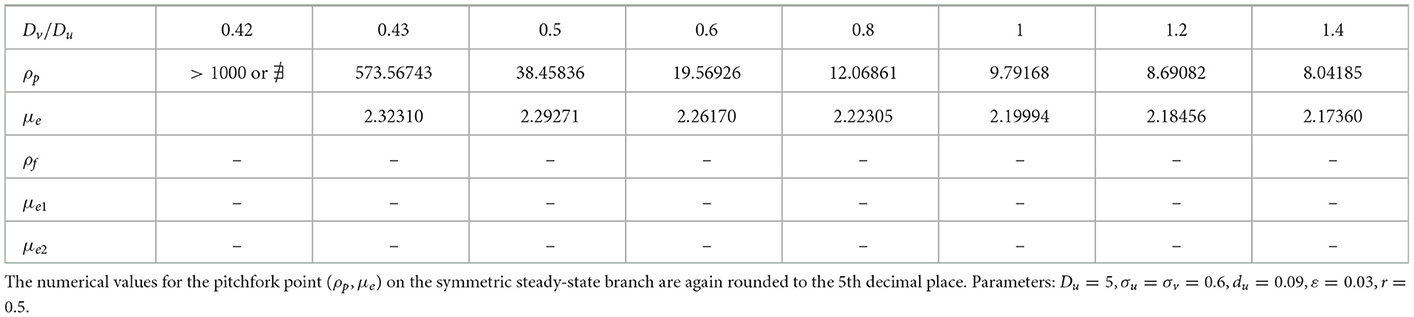
Table 2. Decreasing the ratio Dv/Du does not trigger hysteresis when du = 0.09, but rather there is a minimum threshold of the diffusivity ratio where the symmetry-breaking pitchfork bifurcation point exists.
Next, we set du = 0.08 where hysteresis occurs when Dv/Du = 1, and we vary this diffusion ratio to determine whether hysteresis can be eliminated. Our numerical results in Figure 10 and Table 3 indicates that varying Dv/Du does not eliminate the hysteresis between the symmetric and asymmetric steady-state branches. However, the extent of the hysteresis decreases as the ratio Dv/Du increases.
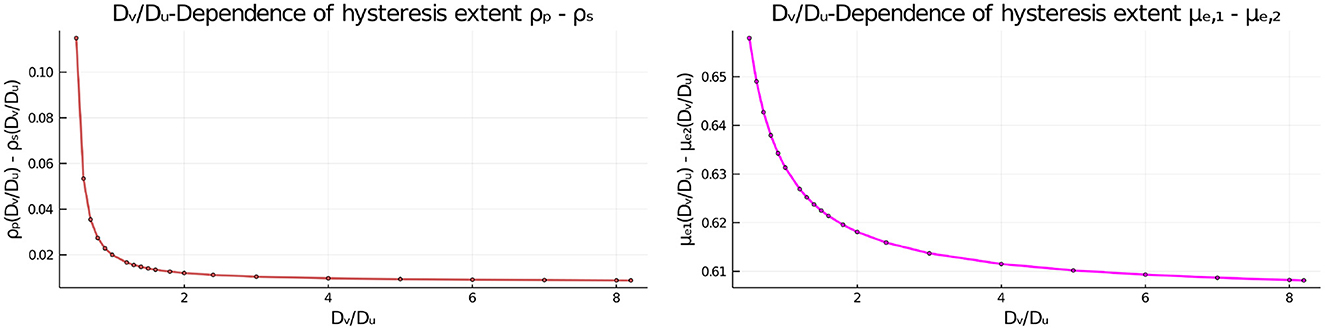
Figure 10. Effect of the diffusivity ratio Dv/Du of the two bulk species on the extent of the hysteresis when du = 0.08, as measured by the distance between the fold bifurcation points and the subcritical pitchfork bifurcation point (Left) and by the distance of the two asymmetric equilibria μe1 and μe2 from each other (Right). The diffusivity Du = 5 is fixed and the remaining parameters are as in Table 2. The dots are the numerically computed values using MatCont [51] that are interpolated by the plotting function in Julia [53].
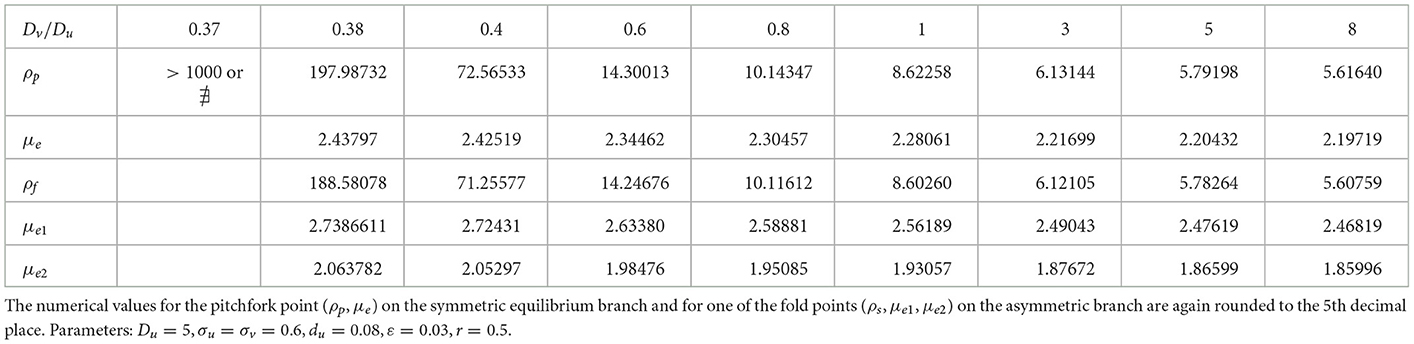
Table 3. Increasing the diffusivity ratio Dv/Du when du = 0.08 does not eliminate hysteresis, as the symmetry-breaking bifurcation point remains subcritical.
To obtain some analytical insight into the disappearance of the pitchfork point as shown in Tables 2, 3 when the diffusivity ratio Dv/Du decreases below a threshold, in Figure 11 we plot the function vs. ρ, representing the left-hand side of the pitchfork bifurcation condition (Equation 4.6), for several values of Dv/Du, and for either du = 0.08 (Figure 11, Left) or du = 0.09 (Figure 11, Right). From Equation (4.6) a root of Fα(ρ) = 0 corresponds to a symmetry-breaking bifurcation point along the symmetric solution branch. From Figure 11 we observe that the asymptote of Fα(ρ) as ρ → ∞ is positive when Dv/Du is below a threshold, which eliminates the possibility of a pitchfork bifurcation point.
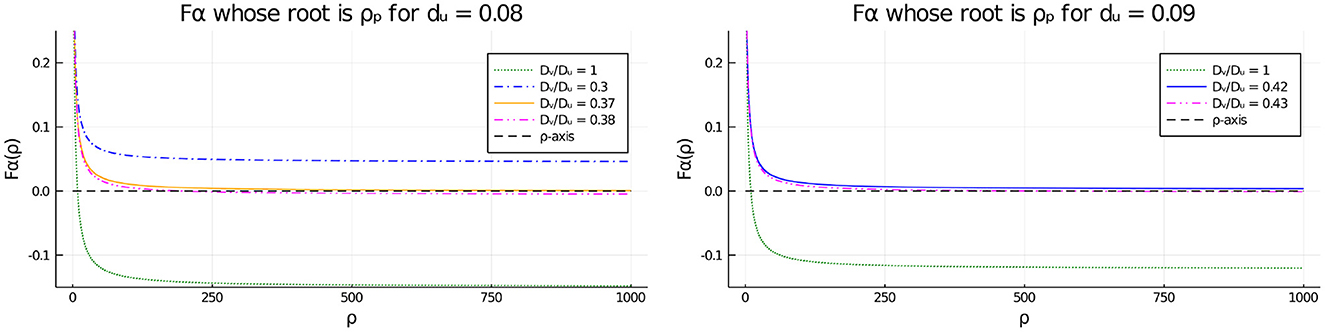
Figure 11. Effect of the diffusivity ratio Dv/Du on the existence of the pitchfork point when du = 0.08 (Left) and du = 0.09 (Right). The numerical results show that the asymptote of is positive for smaller values of Dv/Du, as suggested by Tables 2, 3. Therefore, when Dv/Du falls below a threshold, the pitchfork bifurcation condition Fα(ρ) = 0, which is equivalent to Equation (4.6), no longer holds for any ρ > 0.
4.2. Rauch-Millonas reaction kinetics
Next, we consider the activator-inhibitor system proposed in Rauch and Millonas [8] to universally model two-species signal transduction reaction kinetics between cells. This Rauch-Millonas (RM) intracellular kinetics of Rauch and Millonas [8] is given by
Since g has the form in Equation (2.14), we identify that g1(μ) = cv + wvμ and g2 = qv. We will choose a parameter set for which the reaction kinetics when uncoupled from the bulk has a unique linearly stable steady-state.
From Equation (2.16), all steady-states of the bulk-cell model for a two-cell ring pattern are associated with the nonlinear algebraic system
By using Equation (2.20), the symmetric steady-state solution branch is obtained from the solution μe to
where αu and αv are given in Equation (2.19). Symmetry-breaking bifurcation points are obtained by solving the zero-eigenvalue crossing condition (Equation 2.30) together with Equation (4.9). By solving for wv = wv(μe) in Equation (2.30), we calculate
where and are defined in Equation (2.31). By using Equation (4.10) to eliminate ωv in Equation (4.9) we obtain a nonlinear algebraic equation that determines any symmetry-breaking bifurcation value for μe along the symmetric solution branch. The corresponding bifurcation value for wv is obtained from Equation (4.10).
For the parameter set given in the figure caption, we show in Figure 12, Left that, for the fixed value ρ = 15, there is a degenerate wv-pitchfork bubble, which is characterized by the emergence of asymmetric steady-state solutions at two values of wv. From the Figure 12, Right we observe that in terms of ρ, and at a fixed wv, the symmetry-breaking bifurcation is supercritical in ρ. For the parameter set in Figure 12, Right, we observe from Figure 13 that the eigenvalue λ determined by the root-finding condition σ2(λ) = 0, with σ2 given in Equation (3.20), crosses through zero at the ρ-pitchfork bifurcation point along the symmetric steady-state branch. As a result, when , the symmetric steady-state solution is linearly stable for ρ < ρp = 15, and is unstable on the range ρ > ρp = 15 to eigenperturbations in the direction of .
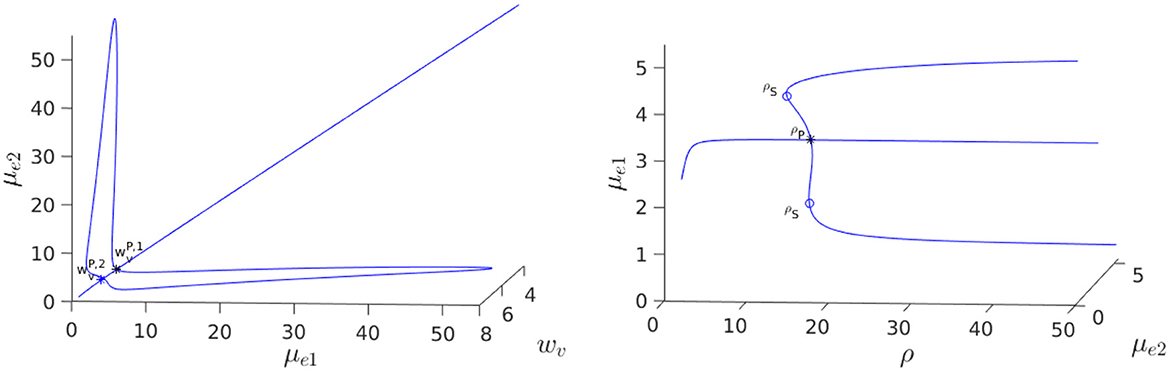
Figure 12. 3-D Bifurcation diagram, computed from Equation (4.8) using MatCont [51], for symmetric and asymmetric steady-states of a two-cell ring pattern with ring radius r = 0.5 and with RM kinetics Equation (4.7). Left: 3-D Plot of (μe1, μe2) vs. the kinetic parameter wv in Equation (4.7) at a fixed ρ = dv/du = 15, showing that asymmetric steady-states occur inside the degenerate pitchfork bubble delimited by and . Note that the bubble lobes are stretching into decreasing wv and that there exists hysteresis at . Right: In terms of ρ, a supercritical pitchfork bifurcation from the symmetric branch occurs when . The asymmetric branches are linearly stable past this bifurcation threshold in ρ. Parameters: , and du = 0.14.
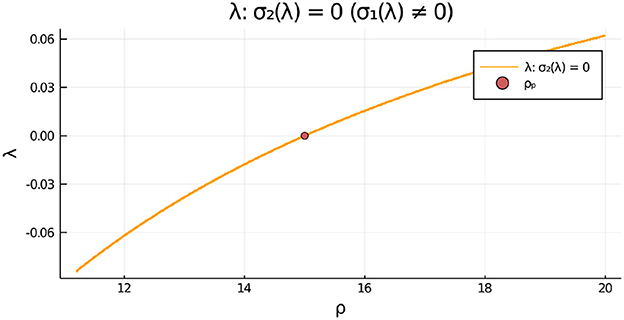
Figure 13. For the two-cell system with RM kinetics (Equation 4.7) and parameters as in the caption of Figure 12 with , we plot the eigenvalue λ, satisfying σ2(λ) = 0 in Equation (3.20), vs. ρ that determines the linear stability of the symmetric steady-state solution branch to eigenperturbations of the form . We observe that the symmetric steady-state branch is unstable only for ρ > ρp = 15. There is no root to σ1(λ) = 0 on this range.
4.3. FitzHugh-Nagumo reaction kinetics
Finally, we consider a ring pattern for the bulk-cell system (Equation 2.3) with two cells and with FitzHugh-Nagumo (FN) intracellular reaction kinetics [24]. The uncoupled intracellular kinetics are
with q > 0, δ > 0 and z > 0. Since g has the form in Equation (2.14), we identify that g1(μ) = δz and g2 = δ.
We will choose a parameter set for which there is a unique linearly stable steady-state of the intra-compartmental dynamics (Equation 4.11). From Equation (2.16), all steady-states of the bulk-cell model for a two-cell ring pattern are obtained from the nonlinear algebraic problem
The symmetric steady-state solution branch, as characterized by Equation (2.20), is obtained from the root μe of the cubic equation
where αu and αv are given in Equation (2.19). The symmetry-breaking bifurcation condition (Equation 2.30) along the symmetric steady-state solution branch yields that
where and are defined in Equation (2.31). We substitute z(μe) into Equation (4.13), and solve the resulting equation numerically for μe. For ρ = 150, and with the parameters as in the caption of Figure 13, we obtain that there are two supercritical pitchfork bifurcation points zP,1 and zP,2 on the symmetric steady-state branch. The linearly stable asymmetric steady-state branches that exist on the range zP,1 < z < zP,2 between the two pitchfork points are shown in the Figure 14, Left. When z = zP,2, we observe from the bifurcation diagram in the Figure 14, Right, together with the eigenvalue computations in Figure 15, that the symmetry-breaking bifurcation is supercritical in terms of ρ.
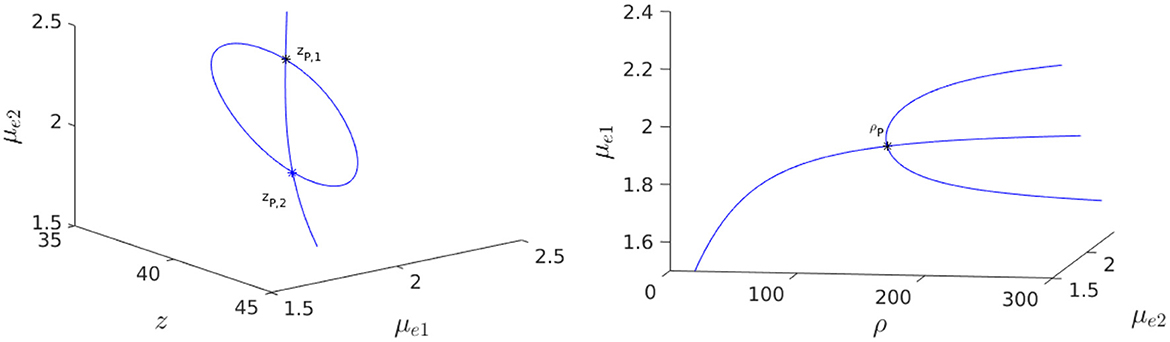
Figure 14. 3-D Bifurcation diagram, computed from Equation (4.12) using MatCont [51], for symmetric and asymmetric steady-states of a two-cell ring pattern with ring radius r = 0.5 and with FN kinetics (Equation 4.11). Left: 3-D Plot of (μe1, μe2) showing that asymmetric steady-states occur inside the supercritical pitchfork bubble delimited by zP,1 ≈ 36.75458 and zP,2 ≈ 41.26889 when ρ = dv/du = 150. Right: Supercritical pitchfork bifurcation from the symmetric branch occurs at ρp = 150 when z = zP,2. Linearly stable asymmetric branches exist past this threshold in ρ. Parameters: Du = 1, Dv = 4, σu = σv = 1, ε = 0.03, r = 0.5, q = 1, δ = 0.1, and du = 0.04.
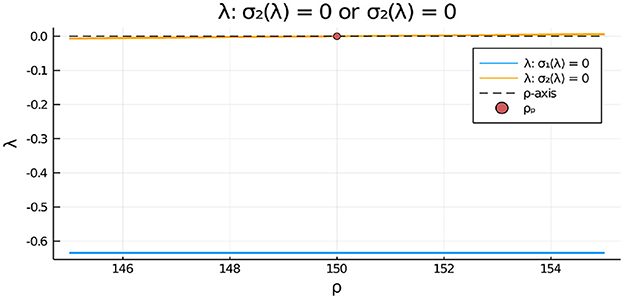
Figure 15. For the two-cell system with FN kinetics (Equation 4.11) and parameters as in the caption of Figure 14 with z = zP,2, we plot the numerically computed eigenvalue λ, satisfying σ2(λ) = 0 in Equation (3.20), vs. ρ. Since λ > 0 only on the range ρ > ρp = 150, we conclude that the symmetric steady-state solution is linearly stable to anti-phase eigenperturbations of the form only when ρ < ρp = 150. Moreover, since the root to σ1(λ) = 0 satisfies λ < 0, we conclude that the symmetric steady-state branch is always linearly stable to in-phase eigenperturbations of the symmetric steady-state.
Next, we illustrate that the bulk-cell model with FN kinetics can also exhibit oscillatory instabilities for in-phase perturbations of the symmetric steady-state. In Figure 16 we plot the bifurcation diagram of μe1 vs. z for the same parameter set as in the caption of Figure 14 except that the bulk degradation rates have been decreased slightly to σu = σv = 0.9. We observe that there are now two Hopf bifurcation values zH,1 and zH,2 of z along the symmetric steady-state branch for the in-phase mode that lie within the interval delimited by the two pitchfork bifurcation points. In the Figure 16, Right, we plot the real and imaginary parts of the complex-valued root of σ1(λ) = 0, as computed from Equation (3.20), which shows that Re(λ) > 0 and Im(λ) ≠ 0 when zH,1 < z < zH,2. This leads to the possibility of a synchronous oscillatory instability. As a result, on the range zH,1 < z < zH,2, the symmetric steady-state solution branch is unstable to both anti-phase and in-phase perturbations. However, as seen from the Figure 16, Right, where we also plot the growth rate λ for the anti-phase mode as obtained by setting σ2(λ) = 0 in Equation (3.20), the anti-phase instability has a larger growth rate than the in-phase instability.
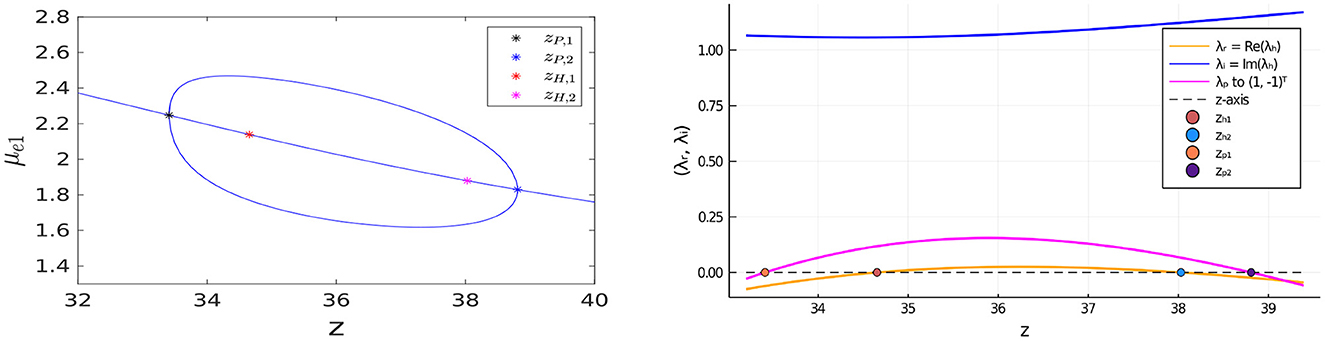
Figure 16. Left: Bifurcation diagram of μe1 vs. z, computed from Equation (4.12) using MatCont [51], for symmetric and asymmetric steady-states of a two-cell ring pattern with the same parameters as in the Figure 14, Left except that now the degradation rates are decreased slightly to σu = σv = 0.9. For this parameter set, there are Hopf bifurcation points associated with in-phase perturbations of the symmetric steady-state that emerge at z = zH,1 ≈ 34.65328 and z = zH,2 ≈ 38.02834 between the two symmetry-breaking pitchfork bifurcation points located at z = zP,1 ≈ 33.41022 and z = zP,2 ≈ 38.80742. Right: the root λ of σ2(λ) = 0 vs. z (pink curve), as computed from Equation (3.20), shows that the symmetric steady-state solution branch is unstable to anti-phase perturbations on the range zP,1 < z < zP,2. The plotted real and imaginary parts of the complex-valued root λh ≡ λr + iλi to σ1(λh) = 0, from Equation (3.20), shows that Re(λh) > 0 on the range zH,1 < z < zH,2. On this range of z, a synchronous oscillatory instability of the symmetric steady-state solution can also occur, but it has a smaller growth rate than that for the anti-phase mode.
4.4. Numerical experiments with closely-spaced cells: GM kinetics
We now briefly explore, from full PDE simulations of Equation (2.3), symmetry-breaking behavior leading to stable asymmetric patterns that can occur for closely spaced cells when the ratio ρ = dv/du is increased. For realistic modeling of pattern formation properties of biological tissues one needs to consider the situation where cells are closely spaced in the sense that the cell radii are either comparable to the distance between the cells, or that there are only narrow gaps between cells. Although the asymptotic theory of Sections 2, 3 is no longer valid for such closely spaced cell arrangements, the FlexPDE simulations of Equation (2.3) shown below reveal a similar qualitative solution behavior as we have analyzed for spatially segregated cells. More specifically, although we no longer have an analytical theory to predict a bifurcation diagram of all steady-state solutions, our full PDE numerical results suggest that stable symmetric steady-states occur only when ρ is below some threshold. When ρ exceeds some symmetry-breaking threshold, stable asymmetric steady-states will be the preferred state. Our numerical results suggest that the critical threshold of ρ that is needed to establish this symmetry-breaking behavior for closely spaced cells is smaller than that needed for spatially segregated cells, if in fact such a threshold exists.
To illustrate this, in Figure 17 we take two closely spaced cells centered near the origin that have a minimum separation of 0.002. The degradation rates, cell radius, and the value of du used for Figure 17 are the same as in Table 3, where bifurcation values were given for the two-cell arrangement at different ratios of Dv/Du with Du = 5 and for a ring radius r = 0.5. In the cell arrangement in Figure 17, the only difference is that the two cells are now much more closely spaced than in Table 3 and we fix Dv/Du = 0.3 and Du = 5. For these parameter values, we observe from Table 3 that no symmetry-breaking bifurcations are possible for this diffusivity ratio when the ring radius is r = 0.5. However, as suggested from the results shown in Figure 17, when the cells are closely spaced there is a symmetry-breaking pitchfork bifurcation point that occurs on the range 3 < ρ < 8. We remark that, rather surprisingly, if we use the symmetry-breaking bifurcation condition (Equation 4.6) from the asymptotic theory for this case of two-closely spaced cells it predicts that ρp ≈ 6.53, which lies within the range 3 < ρ < 8. However, we emphasize that the asymptotic theory is not valid for closely-spaced cells.
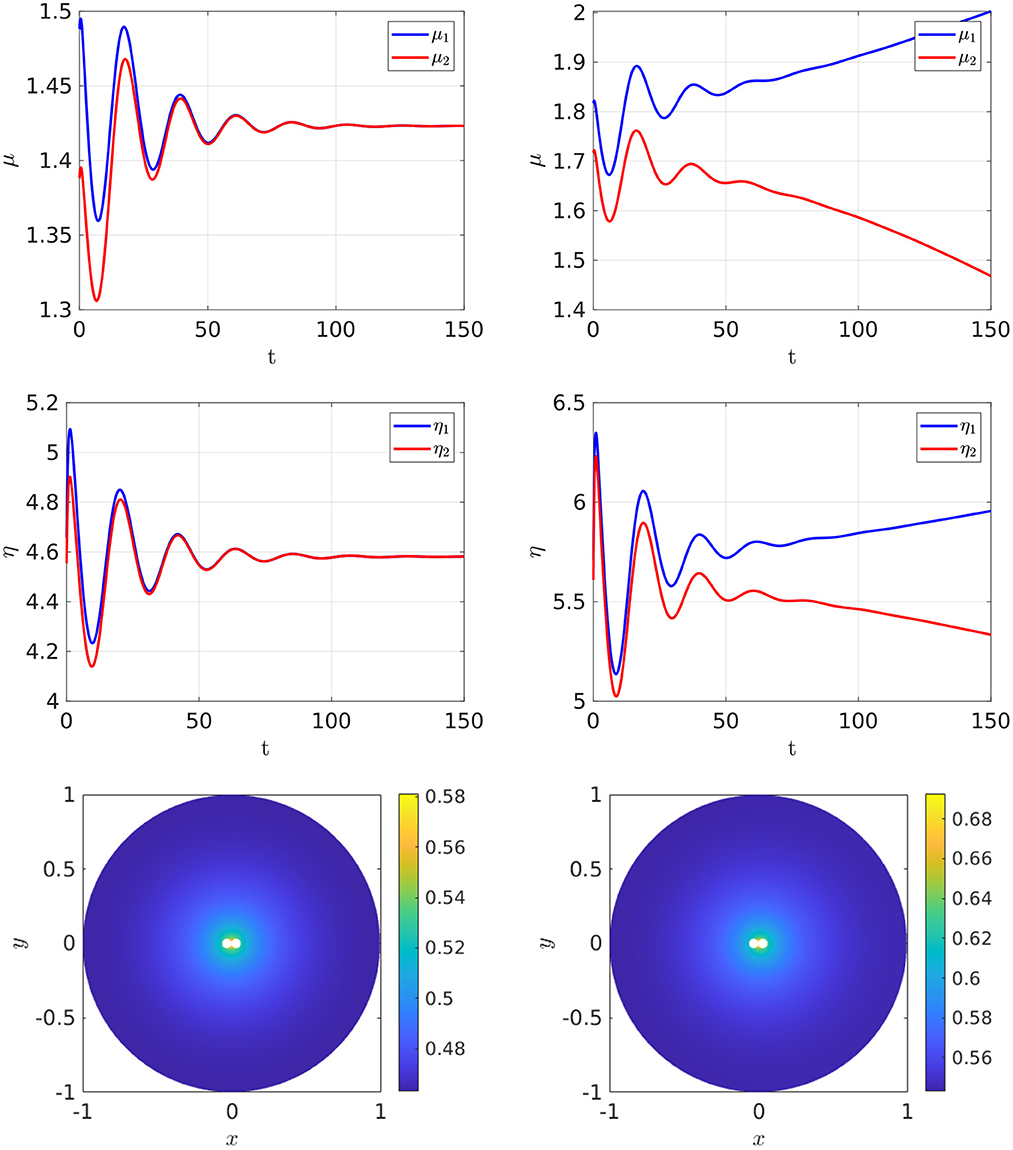
Figure 17. Full numerical simulation results of Equation (2.3) with FlexPDE [50] for GM kinetics (Equation 4.3) with two closely spaced cells centered on a ring of radius r = 0.031 and with minimum cell separation of 0.002. The other parameters are the same as in Table 3. The only difference here is that the cells are now much more closely spaced. The bottom two panels show the concentration of u. Left: convergence to a stable symmetric steady-state solution when ρ = 3. Right: convergence to a stable asymmetric steady-state soluton for ρ = 8 when starting with a symmetric initial condition. Parameters: Du = 5, Dv = 1.5, σu = σv = 0.6, du = 0.08, and ε = 0.03.
Finally, in Figure 18 we show that the stable asymmetric steady-state patterns can also occur for three closely-spaced cells when ρ exceeds some threshold.
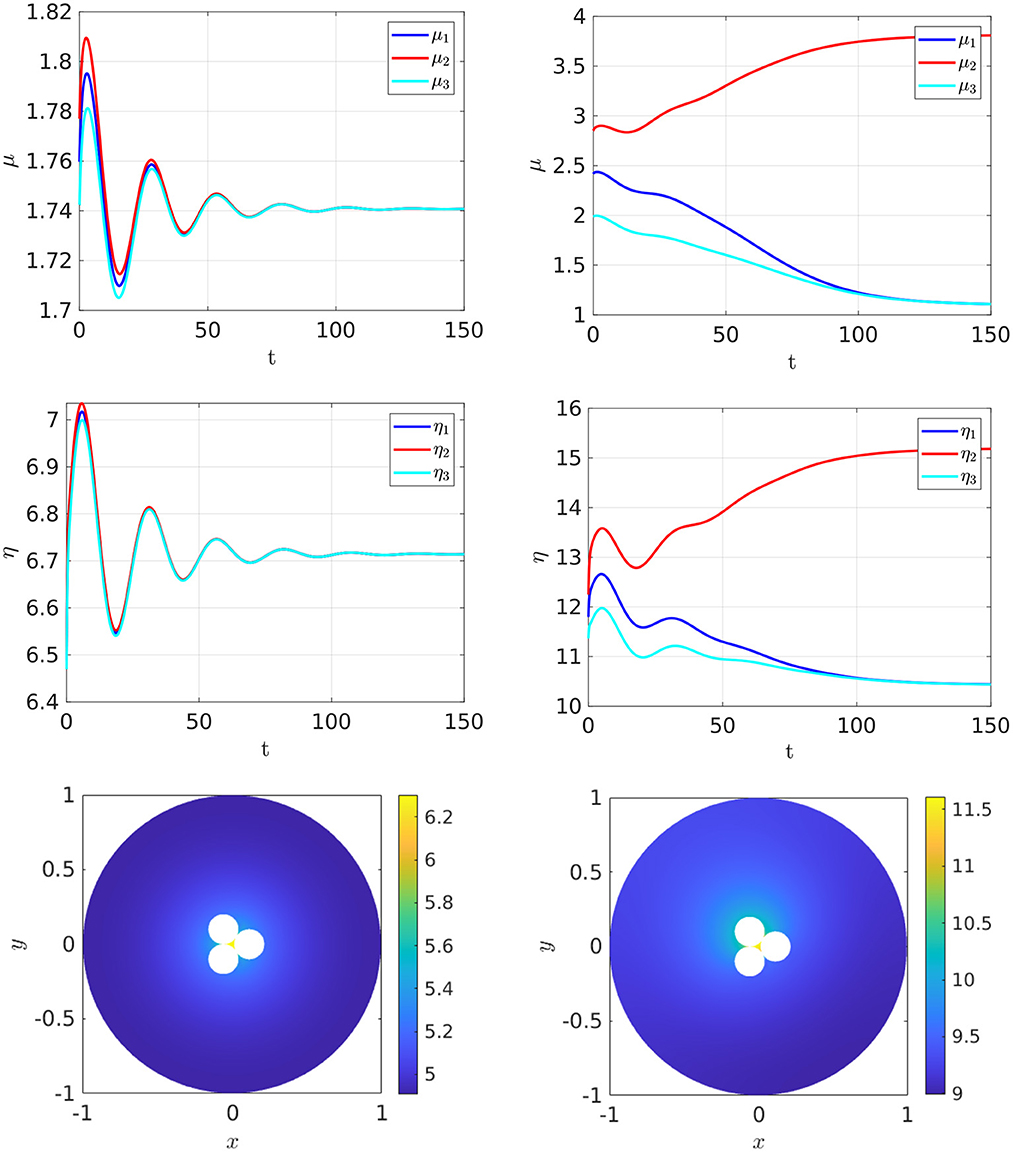
Figure 18. Full numerical simulation results of Equation (2.3) with FlexPDE [50] for GM kinetics (Equation 4.3) with three closely spaced cells with cell centers located on the vertices of an equilateral triangle centered at the origin. The ring radius is . Left: convergence to a symmetric steady-state when ρ = 5. Right: convergence to an asymmetric steady-state when ρ = 10. Parameters: Du = Dv = 5, σu = σv = 0.6, du = 0.05, ε = 0.099. The cells have a minimum separation of 0.002. The bottom two panels show the concentration of v. By plotting v rather than u, the bottom right panel clearly shows the asymmetry in the three cells.
5. Discussion
We have analyzed symmetry-breaking behavior associated with the PDE-ODE bulk-cell model (Equation 2.3) where identical two-component intra-compartmental reactions occur only within a disjoint collection of small circular compartments, or “cells,” of a common radius within a bounded 2-D domain. In the bulk, or extra-cellular, medium two bulk species with comparable diffusivities and bulk degradation rates diffuse and globally couple the spatially segregated intracellular reactions. The bulk species are coupled to the intracellular species through an exchange across the compartment boundaries, as modeled by a Robin boundary condition that depends on certain membrane reaction rates. In the limit of a small cell radius, we have used a singular perturbation methodology to derive a nonlinear algebraic system (Equation 2.13) characterizing all the steady-states for the bulk-cell model (Equation 2.3). Moreover, the linear stability properties of the steady-state solutions of the bulk-cell model were shown to be determined by the nonlinear matrix eigenvalue problem (Equation 3.12) of size 2m × 2m, where m is the number of compartments. A root-finding condition on the determinant of this matrix yields the discrete eigenvalues of the linearization (Equation 3.1) around an arbitrary steady-state solution, as defined by the set (Equation 3.13).
We have shown that the steady-state and linear stability theory simplifies considerably for a symmetric cell arrangement, as characterized by Definition (Equation 2.1), and when one of the intracellular species has a linear dependence of the form Equation (2.14). In this more restricted scenario, we have shown that a symmetric steady-state solution, in which the steady-states of the intracellular species are the same for each cell, will exist if the scalar nonlinear algebraic (Equation 2.20) has a solution. We emphasize that since our bulk-cell model does not admit spatially homogeneous steady-state solutions that can be analyzed by a simple Turing-type linear stability approach [1], this symmetric steady-state solution of the bulk-cell model (2.3) represents the base state in our construction. Instabilities and bifurcations associated with this base state are challenging to analyze owing to the fact that the base state is not spatially uniform. Asymmetric steady-state solutions, as determined from Equation (2.16), were shown to bifurcate from the symmetric steady-state solution branch whenever the algebraic criterion (Equation 2.29) is satisfied at some point on the symmetric branch. For a symmetric cell arrangement, the linear stability properties of the symmetric and asymmetric steady-state solution branches are characterized by Equation (3.21) and the roots of the nonlinear matrix eigenvalue problem (Equation 3.18), respectively.
We have implemented our steady-state and linear stability theory for a specific symmetric cell arrangement in which two cells are equally spaced on a ring concentric within a unit disk, and where we have specified either Gierer-Meinhardt, Rauch-Millonas, or FitzHugh-Nagumo intracellular reactions, which all have the simplified form in Equation (2.14). By using parameter continuation numerical software [51] to implement the asymptotic theory, we have shown that the symmetric steady-state solution branch can undergo symmetry-breaking pitchfork bifurcations, leading to linearly stable asymmetric patterns, even when the two bulk diffusing species have identical diffusivities and degradation rates. Overall, we have shown that it is the magnitude of the ratio of the reaction rates for the two bulk species to the cell membranes that determines whether stable asymmetric patterns can occur. This membrane reaction rate ratio threshold condition for the emergence of symmetry-breaking bifurcations is in marked contrast to the well-known large diffusivity ratio threshold condition for pattern formation from a spatially uniform state that is typically derived by a Turing stability analysis for two-component activator-inhibitor RD systems. For FitzHugh-Nagumo and Rauch-Millonas kinetics we have also shown that stable asymmetric patterns can also emerge from a symmetric steady-state pattern at a fixed, but large, membrane reaction rate ratio when a control parameter in the intracellular kinetics is varied. Our theoretical predictions of symmetry-breaking behavior leading to linearly stable asymmetric patterns for a symmetric two-cell arrangement were confirmed through full time-dependent PDE computations of Equation (2.3).
We now briefly relate our theoretical results to some qualitative behavior that has been suggested in chemical and biological applications. Firstly, compartmental-reaction diffusion models of the form Equation (2.3) could potentially be useful for theoretically modeling the collective behavior that occurs for a microemulsion consisting of Belousov-Zhabotinsky (BZ) chemical reactants that are confined within small aqueous droplets that is dispersed in oil [54] (see also Epstein and Xu [55] and Budroni et al. [56]). In this experimental set-up, polar BZ reactants and a catalyst are confined within small immobile droplets, while two non-polar intermediate species generated during the reaction can be transported across the droplet boundaries. These intermediate species diffuse across the domain, with comparable diffusivities, and provide the mechanism for inter-drop coupling [54]. The recent experimental study of Budroni et al. [56] has suggested that it is the relative magnitude of the membrane reaction rates of these intermediates on the droplet boundaries that plays a key role for determining pattern-forming properties for BZ microemulsions. Secondly, with regards to the transport of biological morphogens, it has been suggested in Müller et al. [7] that a differential reaction rate ratio on the cell boundaries for two morphogen species with comparable diffusivities can yield the large effective diffusivity ratio that is needed for pattern formation and symmetry-breaking in tissues. This membrane attachment mechanism, which reduces the effective diffusivity of one of the morphogens and is referred to in Müller et al. [7] as a binding-mediated hindrance diffusion process, may be relevant in many biological applications. Moreover, detailed intracellular mechanisms in biological cells, such as signaling pathways and gene expression rate constants, may also play a pivotal role in large-scale pattern-forming properties of biological tissues [7]. By way of qualitiative comparison, our theoretical analysis of the 2-D bulk-cell model (Equation 2.3) for a very simple 2-cell pattern has revealed that a large membrane reaction rate ratio, together possibly with changes in a parameter in the intracellular kinetics, can trigger the emergence of stable asymmetric steady-state patterns that bifurcate from a symmetry steady-state. However, owing to the complexity of the analysis needed for Equation (2.3), where certain Green's matrices were found to be central to the analysis, it appears rather intractable analytically to isolate via a simple scaling analysis an effective diffusivity for the bulk species that incorporates the membrane reaction rates.
Although we have only applied our theoretical framework to a simple two-cell arrangement, it is rather straightforward to numerically implement the steady-state and linear stability theory for a symmetric cell arrangement with a much larger number of cells. For this scenario, the symmetric steady-state solutions are again determined by the scalar nonlinear algebraic (Equation 2.20) and the linear stability properties of this steady-state are readily studied by computing the union of all the roots of the scalar problems σj(λ) = 0, for j ∈ {1, …, m}, in Equation (3.20) that comprise the set (Equation 3.21) that approximates the discrete eigenvalues of the linearization (Equation 3.1) of Equation (2.3) around the steady-state. However, for an arbitrary spatial arrangement of a large number of cells, one key impediment for implementing the linear stability theory for steady-state solutions is with regards to numerically computing the eigenvalues λ from a root-finding condition on the determinant of the full 2m × 2m GCEP matrix in Equation (3.12). This matrix is non-Hermitian, is not sparse, and has an intricate dependence on λ through the Green's matrices. In contrast to the availability of efficient numerical solution strategies for nonlinear matrix eigenvalue problems with special structure, as was discussed in Güttel and Tisseur [47], Betcke et al. [48], and Betcke et al. [49], it appears to a significant open challenge to develop efficient numerical methods to determine all such eigenvalues λ for which is a singular matrix when m is large. Recall that if there are any such eigenvalues in Re(λ) > 0, the steady-state for Equation (2.3) is unstable.
A few other open problems related to our analysis are as follows. Firstly, it would be interesting to analyze symmetry-breaking bifurcation for Equation (2.3) on ℝ2 where identical cells of small radii are centered at the lattice points of an arbitrary Bravais lattice. In this periodic setting, it should be possible to analyze symmetry-breaking bifurcations of a periodic steady-state solution by using Floquet-Bloch theory, combined with the explicit analytical formulae for the reduced-wave Bloch Green's function as derived in Iyaniwura et al. [57]. Secondly, it would be interesting to develop an extension of our asymptotic approach to treat closely-spaced cell configurations that are more relevant to modeling pattern-forming properties in biological tissues. Our numerical results shown in Section 4.4 have suggested that only a smaller membrane reaction rate ratio is needed to initiate symmetry-breaking behavior for closely-spaced cells than for arrangements with more spatially segregated cells. To theoretically analyze pattern-forming properties of the bulk-cell model with closely-spaced cells, an extension of the approach developed in Iyaniwura and Ward [58] to analyze the mean first passage time for a cluster of small traps may be fruitful. Thirdly, it would be interesting to formulate and analyze a related bulk-cell model where the chemical reactions occur on the boundaries of a collection of small compartments, rather than in the interior of the compartments. In this scenario, chemical species produced on the membrane can then detach and diffuse in the bulk medium. Such an extension is relevant for analyzing collective behavior that occurs for dynamically reactive solid pellets that are chemically coated and are coupled through a bulk diffusion field (cf. Taylor et al. [59], Taylor et al. [60], Tinsley et al. [61], and Tinsley et al. [62]). Finally, it would be worthwhile to extend our 2-D analysis to a 3-D setting. For a 3-D bounded domain that contains a collection of small spherical compartments, the analysis would be rather different than in 2-D since the free space Green's function has a rapid decay at infinity instead of a logarithmic growth. This would suggest that the inter-cell coupling effect would be, in general, much weaker in 3-D than in 2-D.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MP and MW analysis, conception, and writing of this article was done 50–50. All authors contributed to the article and approved the submitted version.
Funding
MW was supported by NSERC grant 81541.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2023.1110497/full#supplementary-material
References
1. Turing AM. The chemical basis of morphogenesis. Phil Trans Roy Soc B. (1952) 237:37–72. doi: 10.1098/rstb.1952.0012
2. Pearson J, Horsthemke W. Turing instabilities with nearly equal diffusivities. J Chem Phys. (1989) 90:1588. doi: 10.1063/1.456051
3. Baker RE, Gaffney EA, Maini PK. Partial differential equations for self-organization in cellular and developmental biology. Nonlinearity. (2008) 21:R251. doi: 10.1088/0951-7715/21/11/R05
4. Diambra L, Senthivel VR, Menendez DB, Isalan M. Cooperativity to increase Turing pattern space for synthetic biology. AVS Synthetic Biol. (2015) 4:177–86. doi: 10.1021/sb500233u
5. Lengyel I, Epstein IR. Modeling of Turing structures in the chlorite-iodide-malonic acid-starch reaction system. Science. (1991) 251:650. doi: 10.1126/science.251.4994.650
6. Dulos E, Boissonade J, Perraud JJ, Rudovics B, De Kepper P. Chemical morphogenesis: Turing patterns in an experimental chemical system. Acta Biotheor. (1996) 44:249. doi: 10.1007/BF00046531
7. Müller P, Rogers KW, You SR, Brand M, Schier AF. Morphogen transport. Development. (2013) 140:1621–39. doi: 10.1242/dev.083519
8. Rauch EM, Millonas MM. The role of trans-membrane signal transduction in Turing-type cellular pattern formation. J Theor Biol. (2004) 226:401–7. doi: 10.1016/j.jtbi.2003.09.018
9. Sozen B, Cornwall-Scoones J, Zernicka-Goetz M. The dynamics of morphogenesis in stem cell-based embryology: novel insights for symmetry breaking. Development. (2021) 474:82–90. doi: 10.1016/j.ydbio.2020.12.005
10. Pearson J. Pattern formation in a (2+1)-species activator-inhibitor immobilizer system. Physica A. (1992) 188:178–89. doi: 10.1016/0378-4371(92)90264-Q
11. Klika V, Baker RE, Headon D, Gaffney EA. The influence of receptor-mediated interactions on reaction-diffusion mechanisms of cellular self-organization. Bull Math Bio. (2012) 74:935–57. doi: 10.1007/s11538-011-9699-4
12. Korvasová K, A GE, K MP, A FM, Klika V. Investigating the Turing conditions for diffusion-driven instability in the presence of a binding immobile substrate. J Theor Biol. (2015) 367:286–95. doi: 10.1016/j.jtbi.2014.11.024
13. Marcon L, Diego X, Sharpe J, Müller P. High throughput mathematical analysis identifies Turing networks for patterning with equal diffusing signals. eLife. (2016) 5:e14022. doi: 10.7554/eLife.14022
14. Diego X, Marcon L, Müller P, Sharpe J. Key features of Turing systems are determined purely by network topology. Phys Rev X. (2018) 8:021071. doi: 10.1103/PhysRevX.8.021071
15. Landge A, Jordan BM, Diego X, Müller P. Pattern formation mechanisms of self-organizing reaction-diffusion systems. Dev Biol. (2020) 460:2–11. doi: 10.1016/j.ydbio.2019.10.031
16. Haas P, Goldstein R. Turing's diffusive threshold in random reaction-diffusion systems. Phys Rev Lett. (2021) 126:238101. doi: 10.1103/PhysRevLett.126.238101
17. Vanag VK, Epstein IR. Localized patterns in reaction-diffusion systems. Chaos. (2007) 17:037110. doi: 10.1063/1.2752494
18. Ward MJ. Spots, traps, and patches: asymptotic analysis of localized solutions to some linear and nonlinear diffusive processes. Nonlinearity. (2018) 31:R189. doi: 10.1088/1361-6544/aabe4b
19. Halatek J, Brauns F, Frey E. Self-organization principles of intracellular pattern formation. Phil Trans R Soc B. (2018) 373:20170107. doi: 10.1098/rstb.2017.0107
20. Halatek J, Frey E. Rethinking pattern formation in reaction-diffusion systems. Nat Phys. (2018) 14:507. doi: 10.1038/s41567-017-0040-5
21. Maini P, Painter K, Chau HNP. Spatial pattern formation in chemical and biological systems. J Chem Soc Faraday Trans. (1997) 93:3601–3610. doi: 10.1039/a702602a
22. Krause A, Gafney EA, Maini P, Klika V. Modern perspectives on near-equilibrium analysis of Turing systems. Phil Trans R Soc A. (2021) 379:20200268. doi: 10.1098/rsta.2020.0268
23. Pelz M, Ward MJ. The emergence of spatial patterns for compartmental reaction kinetics coupled by two bulk diffusing species with comparable diffusivities. Phil Trans Roy Soc A. (2022).
24. Gomez-Marin A, Garcia-Ojalvo J, Sancho JM. Self-sustained spatiotemporal oscillations induced by membrane-bulk coupling. Phys Rev Lett. (2007) 98:168303. doi: 10.1103/PhysRevLett.98.168303
25. Levine H, Rappel WJ. Membrane-bound Turing patterns. Phys Rev E. (2005) 72:061912. doi: 10.1103/PhysRevE.72.061912
26. Gou J, Li YX, Nagata W, Ward MJ. Synchronized oscillatory dynamics for a 1-D model of membrane kinetics coupled by linear bulk diffusion. SIAM J Appl Dyn Sys. (2015) 14:2096–137. doi: 10.1137/15M1039122
27. Gou J, Ward MJ. Oscillatory dynamics for a coupled membrane-bulk diffusion model with Fitzhugh-Nagumo kinetics. SIAM J Appl Math. (2016) 76:776–804. doi: 10.1137/15M1028297
28. Gou J, Chiang WY, Lai PY, Ward MJ, Li YX. A theory of synchrony by coupling through a diffusive chemical signal. Physica D. (2017) 339:1–17. doi: 10.1016/j.physd.2016.08.004
29. Paquin-Lefebvre F, Nagata W, Ward MJ. Weakly nonlinear theory for oscillatory dynamics in a one-dimensional PDE-ODE model of membrane dynamics coupled by a bulk diffusion field. SIAM J Appl Math. (2020) 80:1520–45. doi: 10.1137/19M1304908
30. Xu B, Bressloff P. A PDE-DDE model for cell polarization in fission yeast. SIAM J Appl Math. (2016) 76:1844–70. doi: 10.1137/16M1065458
31. Xu B, Jilkine A. Modeling the dynamics of Cdc42 oscillation in fission yeast. Biophysical J. (2018) 114:711–22. doi: 10.1016/j.bpj.2017.12.007
32. Gou J, Ward MJ. An asymptotic analysis of a 2-D model of dynamically active compartments coupled by bulk diffusion. J Nonlin Sci. (2016) 26:979–1029. doi: 10.1007/s00332-016-9296-7
33. Iyaniwura S, Ward MJ. Synchrony and oscillatory dynamics for a 2-D PDE-ODE model of diffusion-mediated communication between small signalling compartments. SIAM J Appl Dyn Sys. (2021) 20:438–99. doi: 10.1137/20M1353666
34. Ridgway W, Ward MJ, Wetton BT. Quorum-sensing induced transitions between bistable steady-states for a cell-bulk ODE-PDE model with Lux intracellular kinetics. J Math Bio. (2021) 84:1–2. doi: 10.1007/s00285-021-01705-z
35. Gomez D, Iyaniwura S, Paquin-Lefebvre F, Ward MJ. Pattern forming systems coupling linear bulk diffusion to dynamically active membranes or cells. Phil Trans Roy Soc A. (2021) 379:20200276. doi: 10.1098/rsta.2020.0276
36. Rätz A. Turing-type instabilities in bulk-surface reaction-diffusion systems. J Comp Appl Math. (2015) 289:142–52. doi: 10.1016/j.cam.2015.02.050
37. Elliott CM, Ranner T, Venkataraman C. Coupled bulk-surface free boundary problems arising from a mathematical model of receptor-ligand dynamics. SIAM J Math Anal. (2017) 49:360–397. doi: 10.1137/15M1050811
38. Madzvamuse A, Chung AHW, Venkataraman C. Stability analysis and simulations of coupled bulk-surface reaction-diffusion systems. Proc R Soc A. (2015) 471:20140546. doi: 10.1098/rspa.2014.0546
39. Madzvamuse A, Chung AHW. The bulk-surface finite element method for reaction-diffusion systems on stationary volumes. Finite Elem Anal Design. (2016) 108:9–21. doi: 10.1016/j.finel.2015.09.002
40. Paquin-Lefebvre F, Nagata W, Ward MJ. Pattern formation and oscillatory dynamics in a two-dimensional coupled bulk-surface reaction-diffusion system. SIAM J Appl Dyn Syst. (2019) 18:1334–90. doi: 10.1137/18M1213737
41. Cusseddu D, Edelstein-Keshet L, Mackenzie JA, Portet S, Madzvamuse A. A coupled bulk-surface model for cell polarisation. J Theor Biol. (2019) 481:119–35. doi: 10.1016/j.jtbi.2018.09.008
42. Rätz A, Röger M. Turing instabilities in a mathematical model for signaling networks. J Math Biol. (2012) 65:1215–44. doi: 10.1007/s00285-011-0495-4
43. Rätz A, Röger M. Symmetry breaking in a bulk-surface reaction-diffusion model for signalling networks. Nonlinearity. (2014) 27:1805. doi: 10.1088/0951-7715/27/8/1805
44. Stolerman LM, Getz M, Llewellyn Smith S, Holst M, Rangamani P. Stability analysis of a bulk-surface reaction model for membrane protein clustering. Bull Math Bio. (2020) 82:2. doi: 10.1007/s11538-020-00703-4
45. Paquin-Lefebvre F, Xu B, DiPietro KL, Lindsay AE, Jilkine A. Pattern formation in a coupled membrane-bulk reaction-diffusion model for intracellular polarization and oscillations. J Theor Biol. (2020) 497:110242. doi: 10.1016/j.jtbi.2020.110242
46. Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik. (1972) 12:30–39. doi: 10.1007/BF00289234
47. Güttel S, Tisseur F. The nonlinear eigenvalue problem. Acta Numerica. (2017) 26:1–94. doi: 10.1017/S0962492917000034
48. Betcke T, Highan NG, Mehrmann V, Schröder C, F T. NLEVP: a collection of nonlinear eigenvalue problems. ACM Trans Math Software. (2013) 39:7.1–7.28. doi: 10.1145/2427023.2427024
49. Betcke T, Highan NG, Mehrmann V, Porzio GMN, Schröder C, F T. NLEVP: a collection of nonlinear eigenvalue problems. In: Users' Guide. MIMS EPring 2011117. Manchester: The University of Manchester, UK (2019).
50. FlexPDE P. (2015). Solutions Inc. Available online at: http://www.pdesolutions.com.
51. Dhooge A, Govaerts W, Kuznetsov YA. MatCont: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans Math Software. (2003) 29:141–64. doi: 10.1145/779359.779362
52. Gierer A. Generation of biological patterns and form: some physical, mathematical, and logical aspects. Progr Biophys Mol Biol. (1981) 37:1–47. doi: 10.1016/0079-6107(82)90019-0
53. Bezanson J, Karpinski S, Shah VB, Edelman A. Julia: a fast dynamic language for technical computing. arXiv preprint arXiv:12095145. (2012). doi: 10.48550/arXiv.1209.5145
54. Tompkins N, Li N, Girabwe C, Fraden S. Testing Turing's theory of morphogenesis in chemical cells. Pro Natl Acad Sci USA. (2014) 111:4397–402. doi: 10.1073/pnas.1322005111
55. Epstein I, Xu B. Reaction-diffusion processes at the nano- and microscales. Nat Technol. (2016) 11:312–9. doi: 10.1038/nnano.2016.41
56. Budroni MA, Torbensen K, Ristori S, A AH, Rossi F. Membrane structure drives synchronization patterns in arrays of diffusively coupled self-oscillating droplets. J Phys Chem Lett. (2020) 11:2014–20. doi: 10.1021/acs.jpclett.0c00072
57. Iyaniwura S, Gou J, Ward MJ. Synchronous oscillations for a coupled cell-bulk PDE-ODE model with localized cells on ℝ2. J Eng Math. (2021) 127:24. doi: 10.1007/s10665-021-10113-7
58. Iyaniwura S, Ward MJ. Asymptotic analysis for the mean first passage time in finite or spatially periodic 2-D domains with a cluster of small traps. ANZIAM J. (2021) 63:1–22. doi: 10.21914/anziamj.v63.15976
59. Taylor AF, Tinsley M, Showalter K. Insights into collective cell behavior from populations of coupled chemical oscillators. Phys Chemistry Chem Phys. (2015) 17:20047–55. doi: 10.1039/C5CP01964H
60. Taylor AF, Tinsley M, Wang F, Huang Z, Showalter K. Dynamical quorum sensing and synchronization in large populations of chemical oscillators. Science. (2009) 323:614–017. doi: 10.1126/science.1166253
61. Tinsley MR, Taylor AF, Huang Z, Wang F, Showalter K. Dynamical quorum sensing and synchronization in collections of excitable and oscillatory catalytic particles. Physica D. (2010) 239:785–90. doi: 10.1016/j.physd.2009.08.001
Keywords: bulk diffusion, symmetry-breaking, nonlinear matrix eigenvalue problem, membrane reaction rate ration, Turing stability analysis
Citation: Pelz M and Ward MJ (2023) Symmetry-breaking bifurcations for compartmental reaction kinetics coupled by two bulk diffusing species with comparable diffusivities in 2-D. Front. Appl. Math. Stat. 9:1110497. doi: 10.3389/fams.2023.1110497
Received: 28 November 2022; Accepted: 16 January 2023;
Published: 09 February 2023.
Edited by:
Víctor F. Breña-Medina, Instituto Tecnológico Autónomo de México, MexicoReviewed by:
André H. Erhardt, Weierstrass Institute for Applied Analysis and Stochastics (LG), GermanyEdgar Knobloch, University of California, Berkeley, United States
Copyright © 2023 Pelz and Ward. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael J. Ward,  nredleaf22@gmail.com
nredleaf22@gmail.com
 Merlin Pelz
Merlin Pelz