Boxing-in of a blender in a Hénon-like family

Introduction: The extension of the Smale horseshoe construction for diffeomorphisms in the plane to those in spaces of at least dimension three may result in a hyperbolic invariant set referred to as a blender. The defining property of a blender is that it has a stable or unstable invariant manifold that appears to have a dimension larger than expected. In this study, we consider a Hénon-like family in ℝ³, which is the only explicitly given example of a system known to feature a blender in a certain range of a parameter (corresponding to an expansion or contraction rate). More specifically, as part of its hyperbolic set, this family has a pair of saddle fixed points with one-dimensional stable or unstable manifolds. When there is a blender, the closure of these manifolds cannot be avoided by one-dimensional curves coming from an appropriate direction. This property has been checked for the Hénon-like family by the method of computing extremely long pieces of global one-dimensional manifolds to determine the parameter range over which a blender exists.

Methods: In this study, we take the complimentary and local point of view of constructing an actual three-dimensional box (a parallelopiped) that acts as an outer cover of the hyperbolic set. The successive forward or backward images of this box form a nested sequence of sub-boxes that contains the hyperbolic set, as well as its respective local invariant manifold.

Results: This constitutes a three-dimensional horseshoe that, in contrast to the idealized affine construction, is quite general and features sub-boxes with curved edges. The initial box is defined in a parameter-dependent way, and this allows us to characterize properties of the hyperbolic set intuitively.

Discussion: In particular, we trace relevant edges of sub-boxes as a function of the parameter to provide additional geometric insight into when the hyperbolic set may or may not be a blender.

1. Introduction

We construct a three-dimensional horseshoe for the Hénon-like family of diffeomorphisms

$\begin{array}{ll}H(x,y,z)=(y,\mu +y^2+\beta x,\xi z+y),& (1)\end{array}$

which we introduced and studied in Hittmeyer et al. [1, 2]; see also Díaz et al. [3] for a Hénon-like endomorphism that motivated it. To date, the family H defined on ℝ³ is the only known example of a diffeomorphism with a blender given in explicit form, specifically by Equation (1). This means, in particular, that the properties of the invariant sets of H can be investigated not only theoretically but also with advanced numerical tools.

We now proceed by introducing the necessary theoretical concepts with specific reference to the family H in Equation (1). To do so, we begin with some basic properties. The map H has a skew-product structure: its restriction to the (x, y)-plane does not depend on z and is the Hénon map [4], written here in the form

$\begin{array}{ll}h(x,y)=(y,\mu +y^2+\beta x).& (2)\end{array}$

The z-coordinate of Equation (1) implements a shear with contraction factor ξ, which we take to be positive throughout.

We fix μ = −9.5 and β = 0.3, which ensures that the planar Hénon map h features a full Smale horseshoe; see Hittmeyer et al. ([2], Section 2). Hence, h has a hyperbolic set Λ_h in the form of a Cantor set that is topologically equivalent to a full shift on two symbols. In particular, Λ_h contains two saddle fixed points

$\begin{array}{l}{p}_h^{\pm }:=({\rho }^{\pm },{\rho }^{\pm }),\end{array}$

where

$\begin{array}{l}{\rho }^{\pm }:=\frac{1}{2}\left(1-\beta \pm \sqrt{{(1-\beta )}^2-4\mu }\right).\end{array}$

For our choice of μ = −9.5 and β = 0.3, the saddle points are

$\begin{array}{l}{p}_h^{-}\approx (-2.7520,-2.7520)\text{\hspace{1em}and\hspace{1em}}{p}_h^{+}\approx (3.4520,3.4520).\end{array}$

As for any full Smale horseshoe, the hyperbolic set Λ_h is transitive and, hence, arises as the closure of the intersection set of the stable and unstable manifolds of $p_h^{-}$ and $p_h^{+}$, that is, ${\Lambda }_h=\overline{W^s(p_h^{\pm })\cap W^u(p_h^{\pm })}$. It then also follows that the stable and unstable manifolds $W^s({\Lambda }_h)$ and $W^u({\Lambda }_h)$ of Λ_h are given as the closures of the manifolds $W^s(p_h^{\pm })$ and $W^u(p_h^{\pm })$, respectively.

Due to the skew-product structure of Equation (1), the hyperbolic set Λ_h of h lifts to a hyperbolic set Λ of H with similar properties. Namely, Λ is the closure of the intersection set of the stable and unstable manifolds W^s(p^±) and W^u(p^±) of two corresponding saddle fixed points

$\begin{array}{ll}{p}^{\pm }:=\left({\rho }^{\pm },{\rho }^{\pm },\frac{{\rho }^{\pm }}{1-\xi }\right)& (3)\end{array}$

of H; furthermore, $W^s(\Lambda )=\overline{W^s(p^{\pm })}$ and $W^u(\Lambda )=\overline{W^u(p^{\pm })}$. The dimensions of these manifolds depend on the contraction factor ξ ≠ 1, and we consider here the following two cases.

(1) ξ > 1, when there is expansion in the z-direction of H, which means that dim(W^s(p^±)) = 1 and dim(W^u(p^±)) = 2; and

(2) 0 < ξ < 1, when there is contraction in the z-direction of H, which means that dim(W^s(p^±)) = 2 and dim(W^u(p^±)) = 1.

Owing to the skew-product nature of Equation (1), for any ξ, the orthogonal projections of the global manifolds W^s(p^±) and W^u(p^±) of H onto the (x, y)-plane are the global manifolds $W^s(p_h^{\pm })$ and $W^u(p_h^{\pm })$ of the Hénon map h. In particular, the respective two-dimensional global manifolds, W^u(p^±) for ξ > 1 and W^s(p^±) for 0 < ξ < 1, are the direct products of ℝ (the z-direction) with $W^u(p_h^{\pm })$ and $W^s(p_h^{\pm })$, respectively.

In either case, for ξ sufficiently close to 1 the (transitive) hyperbolic set Λ is a blender [1, 2]. As mentioned in Hittmeyer et al. [1, 2], we use the definition of a blender from Díaz et al. [3] and Bonatti et al. [5] that says, colloquially speaking, that Λ is a blender if its one-dimensional global manifold—W^s(Λ) for ξ > 1 and W^u(Λ) for 0 < ξ < 1—acts geometrically as a set of dimension two. In more technical terms, the requirement is that there exists a C¹-open set of curve segments in the three-dimensional phase space that each intersect the respective one-dimensional manifold locally near Λ. Moreover, this property must be robust, that is, hold for the corresponding hyperbolic set of every sufficiently C¹-close diffeomorphism. We remark that the existence of a blender for some ξ > 1 does not automatically imply the existence of a corresponding blender for some 0 < ξ < 1. Indeed, the existence of a blender for the map H is determined by properties of W^s(Λ) for ξ > 1, but for 0 < ξ < 1 it is determined by properties of W^u(Λ). While W^u(Λ) can be considered as the stable manifold of Λ with respect to the inverse map H⁻¹, there is no known conjugacy between these two cases.

The concept of a blender was introduced by Bonatti and Díaz [6] to show that “wild” dynamics may occur C¹-robustly in (non-uniformly hyperbolic) systems [3, 5–15]. In particular, the construction of a blender is an important ingredient for showing that, subject to mild genericity conditions, the existence of a heterodimensional cycle is a C¹-robust property. Such a cycle consists of two hyperbolic fixed (or periodic) points of different index (dimensions of the unstable manifold), the stable and unstable manifolds of which intersect to form a heteroclinic cycle [5, 10, 16–18]. This requires a diffeomorphism with a phase space of dimension at least three, while a heterodimensional cycle in a vector field requires a phase space of dimension at least four; see Zhang et al. [19] and Mason et al. [20] for an example. Necessarily, one of the two connections of the heterodimensional cycle is structurally stable, while the other can be destroyed by a C¹-perturbation. This is why the robust existence of heterodimensional cycles is surprising, and a wild (not tame) property in the sense of Bonatti and Díaz [6]. Blenders are relevant in this context, because their stable (or unstable) manifold, while of too low dimension, can nevertheless not be avoided by the respective unstable (or stable) manifold of another periodic orbit.

We are motivated here by the questions: how can one check when a blender exists in a given system, and what are the required geometric properties? According to the definition from Hittmeyer et al. [1, 2], the hyperbolic set Λ of the map H is a blender if (when seen from an approriate direction) the one-dimensional manifold W^s(Λ) or W^u(Λ), respectively, looks like a surface—although it is a Cantor set of curves when viewed along the z-direction. We refer to this defining characteristic of a blender as the carpet property [1, 2]. Since the one-dimensional global manifolds, W^s(p^±) and W^u(p^±) of the fixed points p^± are dense in W^s(Λ) or W^u(Λ), respectively, the carpet property can be verified numerically for the family H by checking whether these one-dimensional global manifolds fill out an area in projection. This is achieved by considering the intersection points of W^s(p^±) or W^u(p^±) with a plane and showing, for a suitable projection, that the gaps between them converge to 0 as the arclength of the respective one-dimensional manifolds goes to infinity. The required very long one-dimensional global manifolds are computed as arclength-parametrized curves [21] after the phase space ℝ³ has been compactified to ${C}=\overline{𝔻}\times \left[-1,1\right]$; see Hittmeyer et al. [1, 2] for details. In this way, we showed over which range near ξ = 1 the hyperbolic set Λ of H is indeed a blender. We also explored numerically how the carpet property is lost when ξ deviates too far from 1 and found that this happens via the creation of infinitely many robust gaps as ξ is varied.

In this article, we focus on the complementary, local, and arguably “classical” perspective that the hyperbolic set Λ arises as the invariant set of a three-dimensional horseshoe construction. By this, we mean that there is a three-dimensional “box,” which is stretched and folded in such a way that its image and preimage intersect this box in a number of “sub-boxes”—two in the case of the Hénon family H. The hyperbolic set Λ and its respective local one-dimensional global manifolds are, hence, the limit of an infinite set of boxes intersecting boxes. Indeed, the question “What is …a blender?” is answered by Bonatti et al. [7] with an affine horseshoe construction, and the type of blender we find for the family H is also referred to as a blender-horseshoe [11, 22]. In complete analogy with Smale's horseshoe construction, the illustrations by Bonatti et al. [7] and Díaz and Pérez [11] show how a box in phase space should map back to itself such that a blender is created in the limit of this repeating process.

The affine blender-horseshoe construction by Bonatti et al. [7] is idealized in that the abstract map consists locally of linear scalings that align with the respective coordinate axes; hence, the initial box and all of its iterates are cuboids. While it still gives insight into the geometry of a blender when the central contraction or expansion rate is near 1, the affine construction is not sufficiently representative of how a box maps in an actual example. This is demonstrated here by considering a specific, more typical horseshoe construction. In particular, the nonlinear nature of the three-dimensional horseshoe turns out to be relevant when one is interested in the (dis)appearance of a blender as parameters change.

More specifically, for the Hénon-like family in Equation (1), we construct a parameter-dependent box in the form of a “tight” parallelopiped, meaning that the two sub-boxes that are its (pre)images extend to the boundary of the initial box. This is achieved separately for ξ > 1, for which one needs to consider backward images of the constructed box, and for 0 < ξ < 1, for which one needs to consider its forward images. Since the underlying horseshoe of the Hénon map is not symmetric under time reversal, these two cases show interesting differences in terms of how the constructed box maps under (pre)images of H to successive sub-boxes. In contrast to the affine construction, in both cases, these sub-boxes all have curved edges so that neither their “side” nor their “front” faces line up exactly with the initial box. These additional properties represent a more realistic case of a three-dimensional horseshoe, and they provide a more intuitive idea of how the respective one-dimensional local manifolds behave when the parameter ξ is varied. This will be illustrated in different ways: we present images that show (i) the initial box, its sub-boxes, and the relevant local manifolds inside the box in the three-dimensional phase space of H; and (ii) the intersection sets of these objects with a suitably chosen plane. We provide such illustrations for the two cases that the hyperbolic set Λ is a blender and that it is not, separately for both ξ > 1 and 0 < ξ < 1.

This allows us to identify and illustrate which edges are responsible for the opening and closing of gaps in a certain projection as the carpet property of the respective one-dimensional global manifolds is lost. This geometric insight is then used to trace out the locations of these edges in the parameter ξ, and they provide an outer approximation of the ξ-range over which a blender may exist. These results are complementary to earlier studies in Hittmeyer et al. [1, 2], which focused on the global (rather than local) one-dimensional manifolds as a means to identify blenders and study their (dis)appearance. In contrast, we show here that the non-affine nature of the box construction indeed matters, especially when one is interested in how the carpet property is lost and the hyperbolic set ceases to be a blender. More generally, knowledge of the nature of the three-dimensional horseshoe is useful if one wants to “continue” a blender in parameters and/or construct a computer-assisted proof of its existence by verifying topological properties, for example, based on methods by Zgliczyński and Gidea [23], Zgliczyński [24], and Kapela et al. [25] as applied by Capiński et al. [26].

The article is organized as follows. In Section 2, we construct a box ${B}$ for ξ > 1 that contains segments of W^s(Λ) in its successive preimages; we consider the properties of these preimages of ${B}$ for the two cases ξ = 1.2 when Λ is a blender and for ξ = 2.4 when it is not. Similarly, Section 3 presents and shows a box ${D}$ for 0 < ξ < 1 and its images under H, which contain segments of W^u(Λ); moreover, we show their properties when Λ is a blender and when it is not, for ξ = 0.8 and ξ = 0.4, respectively. Section 4, then, discusses for $\xi \in \left[\frac{1}{3},3\right]$ when successive (pre)images of boxes ${B}$ and ${D}$ overlap in the relevant direction of projection, and how this relates to the existence of a blender. In Section 5, we discuss our results and point out avenues of ongoing and future research.

2. Box and its preimages for ξ > 1

We first consider H with ξ > 1, in which case the stable manifolds W^s(p^±) and W^s(Λ) have dimension one. We consider the square [−Q, Q] × [−Q, Q] in the (x, y)-plane with the four points (±Q, ±Q), where

$\begin{array}{ll}Q:=\frac{1}{2}\left(1+\beta +\sqrt{{(1+\beta )}^2-4\mu }\right).& (4)\end{array}$

Note that this square only depends on the parameters β and μ of the Hénon map and that it always contains the two fixed points p^±; for our choice of μ = −9.5 and β = 0.3, we have Q = 3.8.

We now define for ξ > 1 the box ${B}$ in (x, y, z)-space as the parallelopiped given by the corner points

$\begin{array}{lll}\text{○}:& \left(\pm Q,-Q,-\frac{Q}{\xi -1}·\frac{2-\xi }{\xi }\right),& (5)\end{array}$

$\begin{array}{lll}◇:& \left(\pm Q,-Q,\frac{Q}{\xi -1}\right),& (6)\end{array}$

$\begin{array}{lll}\square :& \left(\pm Q,Q,-\frac{Q}{\xi -1}\right),& (7)\end{array}$

$\begin{array}{lll}△:& \left(\pm Q,Q,\frac{Q}{\xi -1}·\frac{2-\xi }{\xi }\right).& (8)\end{array}$

Hence, each of the symbols ○, ◇, □, and △ indicates a pair of corner points with the same y- and z-coordinates, and we will use these symbols also to denote the respective edges of ${B}$ between these points. The edges ○, ◇, □, and △ are given by x ∈ [−Q, Q] and, hence, are parallel to the x-axis.

By construction, ${B}$ has the following properties.

• ${B}$ projects in the z-direction onto the square [−Q, Q] × [−Q, Q].

• Each intersection of ${B}$ with a vertical plane of constant y is a rectangle with edges parallel to the x- and z-axes.

• Each intersection of ${B}$ with a vertical plane of constant x is a parallelogram with two vertical edges.

Moreover, box ${B}$ with Q as defined in Equation (4) is tight with respect to the action of the inverse H⁻¹. By this, we mean that its preimage satisfies the following statements, which can be checked directly from Equations (1), (4)–(8). Note here that, since ξ > 1, the x-direction of ${B}$ is expanded, while its y- and z-directions are contracted under H⁻¹.

• The three-dimensional horseshoe-like set $H^{-1}({B})$ intersects ${B}$ in two sub-boxes ${{B}}_{-}$ with negative y and ${{B}}_{+}$ with positive y. We will refer to ${{B}}_{-}$ and ${{B}}_{+}$ simply as the two (first) preimages of ${B}$.

• The preimages ${{B}}_{-}$ and ${{B}}_{+}$ intersect the boundary of ${B}$ only on its two faces with x = −Q and x = Q, respectively.

• Vertical edges (parallel to the z-axis) of ${B}$ map under H⁻¹ to vertical edges of $H^{-1}({B})$; hence, the sub-boxes ${{B}}_{\pm }$ have vertical edges that map to the vertical edges of ${B}$ under H.

• The outer vertical edges of ${{B}}_{-}$ and ${{B}}_{+}$ with x = −Q are subsets of the respective vertical edge of ${B}$; moreover, the two corner points $(\pm Q,Q,-\frac{Q}{\xi -1})$ of ${B}$ map as follows:

$\begin{array}{l}{H}^{-1}\left(Q,Q,-\frac{Q}{\xi -1}\right)=\left(-Q,Q,-\frac{Q}{\xi -1}\right)\text{ and}\\ H^{-1}\left(-Q,Q,-\frac{Q}{\xi -1}\right)=\left(-Q,-Q,-\frac{Q}{\xi -1}·\frac{2-\xi }{\xi }\right).\end{array}$

• The two (respective pieces of the) preimages of edge ◇ lie on the top face of ${B}$, and those of edge □ lie on the bottom face of ${B}$.

• The fixed points p⁻ and p⁺ lie on ${{B}}_{-}$ and ${{B}}_{+}$, respectively.

Figure 1 shows the parallelopiped ${B}$ for ξ = 1.2 together with its preimages ${{B}}_{-}$ and ${{B}}_{+}$; also shown is the diagonal plane Σ: = {(x, y, z)|x = y} containing the fixed points p^±, and the viewpoint is chosen such that the face of ${B}$ with x = Q is at the front of the image. Figure 1 illustrates the properties of box ${B}$ as well as of the preimages ${{B}}_{-}$ and ${{B}}_{+}$ inside ${B}$. Each of these boxes is represented by its edges with the faces colored and transparent. In particular, notice how ${{B}}_{-}$ and ${{B}}_{+}$ extend across ${B}$, meaning that they connect the faces of ${B}$ with x = ±Q; moreover, the edges of these sub-boxes form (approximate) parallelograms with straight sides but slightly curved tops and bottoms. Notice further that at x = −Q the outer vertical edges of ${{B}}_{-}$ and ${{B}}_{+}$ are indeed subsets of the vertical edges of ${B}$ and include the respective bottom corner point, while the inner vertical edges of ${{B}}_{-}$ and ${{B}}_{+}$ reach the upper edge of this face of ${B}$. The three-dimensional nature of Figure 1 is enhanced by the inclusion of the intersection sets of ${B}$ and ${{B}}_{\pm }$ with the diagonal section Σ, which are (approximate) parallelograms. Overall, this image shows that ${B}$ is indeed the tightest parallelopiped with a square “footprint” in the (x, y)-plane that yields a three-dimensional horseshoe, meaning that the sub-boxes ${{B}}_{\pm }\subset {B}$ intersect only the front and back faces with x = ±Q. We remark that if the value of Q in Equations (5)–(8) is increased from the one given in Equation (4) then one still has a three-dimensional horseshoe but it is no longer tight. However, if Q is decreased, the set $H^{-1}({B})$ no longer intersects ${B}$ as required to obtain a horseshoe.

FIGURE 1

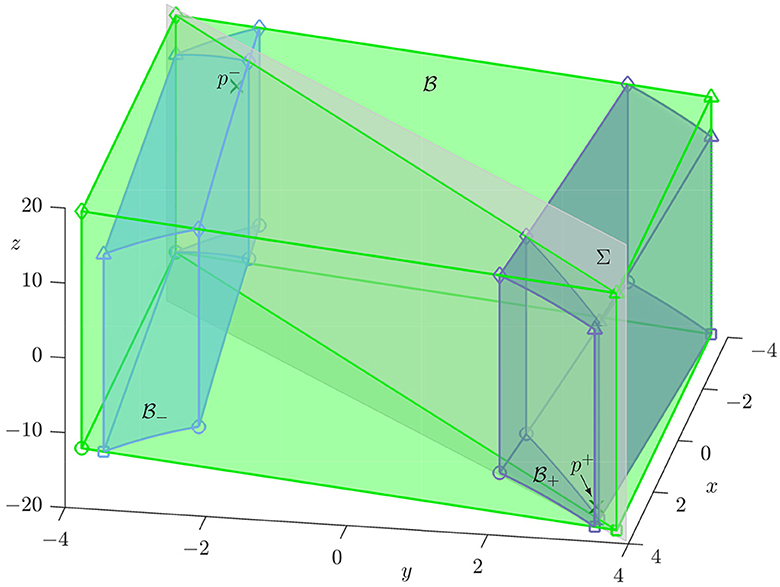
Figure 1. Box ${B}$ (green) and its preimages ${{B}}_{-}$ (light blue) and ${{B}}_{+}$ (dark blue) under H with ξ = 1.2. The x-aligned edges of ${{B}}_{\pm }$ are labeled ○, ◇, □, and △ by their corner points according to how they map under H to the respective edges of ${B}$ defined in Equations (5)–(8). Also shown are the saddle fixed points p^± (green crosses) contained in the diagonal plane Σ (gray); throughout μ = −9.5 and β = 0.3.

Figure 1 also shows how the respective edges and corner points of ${{B}}_{-}$ and ${{B}}_{+}$ inherit the labels ○, ◇, □, and △ from the respective x-aligned edges of ${B}$ that they map to. We refer to these labeled edges as the determining edges of each box because they are the ones that are expanded by H⁻¹ in the three-dimensional horseshoe construction. Owing to the nonlinear nature of map H, the determining edges of ${{B}}_{\pm }$ are no longer straight lines that are parallel to the x-axis. Nevertheless, they are still aligned with the x-axis, by which we mean that the angle between the tangent at any point of the edges ○, ◇, □, and △ with the vector (1, 0, 0) is small. In particular, the sub-boxes ${{B}}_{\pm }$ intersect the faces of ${B}$ with x = ±Q in (approximate) parallelograms; the same is true for any transverse plane, such as the diagonal plane Σ in Figure 1.

The overall geometry of the images of ${B}$ under H⁻¹ and H⁻² is shown in Figure 2. Figure 2A shows in (x, y, z)-space the box ${B}$, its first preimages ${{B}}_{-}$ and ${{B}}_{+}$, and its second preimages ${{B}}_{--},{{B}}_{-+}\subset {{B}}_{-}$ and ${{B}}_{+-},{{B}}_{++}\subset {{B}}_{+}$. These boxes are again represented by their edges with their faces colored and transparent; compare with Figure 1. In particular, the four sub-boxes ${{B}}_{\pm \mp }$ in Figure 2A also connect the faces of ${B}$ with x = ±Q, where they intersect in (approximate) parallelograms that are “steeper” and more sheared than those for ${{B}}_{\pm }$; by this, we mean that the angle of their non-vertical (slightly curved) edges with the y-direction is now larger. The top view in Figure 2B shows that these sub-boxes correspond to increasingly thinner strips in the (x, y)-plane for which the limit is the local stable manifold $W^s({\Lambda }_h)\cap \left(\left[-Q,Q\right]\times \left[-Q,Q\right]\right)$ of the hyperbolic set Λ_h of the Hénon map h; this set is a Cantor set of curve segments for our choice of the parameters. Figure 2A also shows the diagonal section Σ with the intersection sets of all boxes, and they are illustrated further in Figure 2C in a “front view” in projection onto the (y, z)-plane. Notice, in particular, how the parallelograms and, hence, the different boxes they represent become more sheared by taking successive preimages.

FIGURE 2

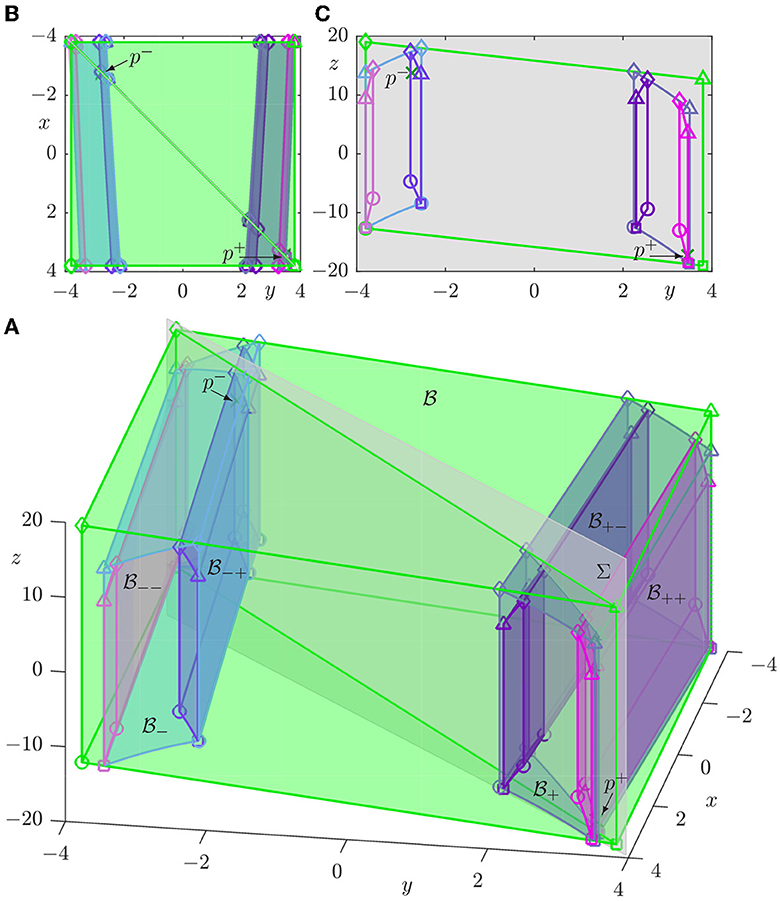
Figure 2. Box ${B}$ (green) for ξ = 1.2 with its two preimages ${{B}}_{-}$ (light blue) and ${{B}}_{+}$ (dark blue) and their four preimages ${{B}}_{--}$ (light magenta), ${{B}}_{-+}$ (light purple), ${{B}}_{+-}$ (purple), and ${{B}}_{++}$ (magenta). (A) shows these objects in (x, y, z)-space, together with p^± (green crosses) and the diagonal plane Σ (gray). (B) is the top view in the (x, y)-plane oriented as in (A), and (C) shows the intersecting (approximate) parallelograms in Σ; note that Σ is represented here by its projection onto the (y, z)-plane. Compare with Figure 1.

The affine three-dimensional blender-horseshoe construction [7, 11] is very special in that all edges remain parallel to the three axes. However, for the map H only the vertical edges remain parallel to the z-direction when taking preimages. Indeed, the determining edges ○, ◇, □, and △ of successive preimages of box ${B}$ are no longer straight lines parallel to the x-axis; moreover, we observe a shearing of the sub-boxes.

The box ${B}$ and its intersection set ${B}\cap \Sigma$, which is an exact parallelogram, are given explicitly from Equations (5)–(8) and their stated properties. The further sub-boxes and their intersection sets shown in Figure 2 are determined as follows. We represent the determining edges of ${B}$ by 30 evenly spaced points; the edges ○, ◇, □, and △ of ${{B}}_{-}$ and ${{B}}_{+}$ are then determined from the interpolation of the preimages of the respective 30 points. Due to the skew-product nature of H, this determines the side faces of these two sub-boxes. Their top and bottom faces are curved and determined in the same way by computing the respective pieces of the preimages of two sets of equidistant lines on the top and bottom surfaces of ${B}$, respectively, parallel to the determining edges, and each again represented by 30 points. Interpolation of this data is then used to compute the approximate parallelograms ${{B}}_{-}\cap \Sigma$ and ${{B}}_{+}\cap \Sigma$ and, in particular, the intersection points ○, ◇, □, and △ of their determining edges. The same procedure is then applied to determine ${{B}}_{--}$ and ${{B}}_{-+}$ from ${{B}}_{-}$, and ${{B}}_{+-}$ and ${{B}}_{++}$ from ${{B}}_{+}$. Despite the nonlinear nature of the sequence of sub-boxes in ${B}$, the limiting set

$\begin{array}{ll}{\displaystyle \underset{N\to \infty }{lim}}{\displaystyle \bigcap _{k=0}^N}{H}^{-k}({B})=W^s(\Lambda )\cap {B}& (9)\end{array}$

exists, and the question is whether it has the carpet property and, hence, whether the hyperbolic set Λ of H is a blender. Theory suggests that Λ is a blender when ξ > 1 is sufficiently close to 1, while it is not a blender when ξ is sufficiently large.

2.1. Carpet property for ξ = 1.2

According to our earlier results [1, 2], for ξ = 1.2 the one-dimensional manifold $W^s(\Lambda )=\overline{W^s(p^{\pm })}$ has the carpet property with respect to the y-direction and, hence, the hyperbolic set Λ of H is a blender. In the context of the three-dimensional horseshoe given by ${B}$ and its preimages, this can be understood by the fact that there is sufficient overlap between the sub-boxes at every level k ≥ 1 of Equation (9) when they are seen along the y-direction. To illustrate the carpet property and how it is connected to properties of the preimages of box ${B}$, Figure 3 illustrates how the stable manifolds W^s(p^±) intersect ${B}$ and its preimages. To achieve this, we compute the stable manifolds W^s(p⁻) and W^s(p⁺) as parametrized curves up to considerable arclength, from which we determine and show in Figure 3 the first 150 segments in ${B}$ of the repeated intersections for each branch of W^s(p^±). Specifically, these are both branches of W^s(p⁺) and one branch of W^s(p⁻) (its other branch goes straight to infinity and does not intersect ${B}$ again); see Hittmeyer et al. [1, 2] for more details of the global structure of W^s(p^±).

FIGURE 3

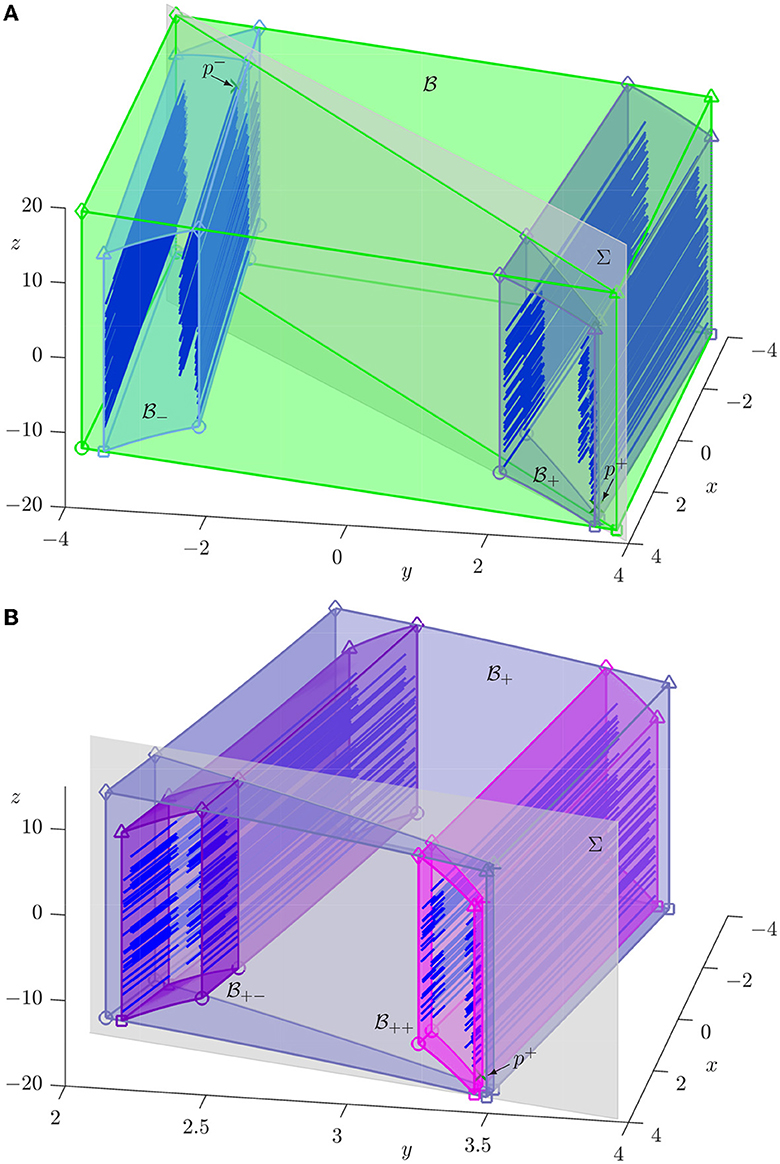
Figure 3. First 450 segments of $W^s(p^{\pm })\cap {B}$ (blue curves) for ξ = 1.2, shown in (A) inside ${B}$ (green), ${{B}}_{-}$ (light blue), and ${{B}}_{+}$ (dark blue), and in (B) inside ${{B}}_{+}$ (dark blue), ${{B}}_{+-}$ (purple), and ${{B}}_{++}$ (magenta); also shown are p^± (green crosses) and the diagonal plane Σ (gray).

Figure 3A shows the computed 450 segments in $W^s(p^{\pm })\cap {B}$ with ${B}$, ${{B}}_{-}$, and ${{B}}_{+}$, while Figure 3B is an enlargement near ${{B}}_{+}$ that also shows ${{B}}_{+-}$ and ${{B}}_{++}$. All segments in $W^s(p^{\pm })\cap {B}$ are aligned in the x-direction and connect the back and front faces of ${B}$, where x = ±Q; moreover, the segments can be seen to cluster successively in the sub-boxes ${{B}}_{-}$ and ${{B}}_{+}$, and ${{B}}_{+-}$ and ${{B}}_{++}$. By construction, when seen from the top along the z-direction, they form part of the Cantor set of curves $W^s({\Lambda }_h)\cap \left(\left[-Q,Q\right]\times \left[-Q,Q\right]\right)$. After taking k preimages of H, one can check in which sub-box a given segment lies to determine the symbolic sequence s ∈ {0, 1}^ℕ that represents its location in this Cantor set of curve segments. In turn, each symbolic sequence s ∈ {0, 1}^ℕ defines a unique one-dimensional segment of $W^s(\Lambda )\cap {B}$.

When viewed side-on, however, the 450 computed segments in Figure 3 seem to be very much distributed in their z-coordinate, and this suggests that $W^s(\Lambda )\cap {B}=\overline{W^s(p^{\pm })\cap {B}}$ acts as a surface. This is illustrated further in Figure 4 where we show the first 300 intersection points with Σ of each of the three repeatedly returning branches of W^s(p^±); here, Figure 4A shows the entirety of $\Sigma \cap {B}$, while Figures 4B1, B2 are enlargements near ${{B}}_{-}$ and ${{B}}_{+}$, respectively. Indeed, the 900 points shown look dense in projection onto the z-axes. We confirmed this observation [1, 2] by showing numerically that the (largest) gaps between the (finite number of) projected points W^s(p^±) ∩ Σ goes to zero as the number of points in W^s(p^±) ∩ Σ increases.

FIGURE 4

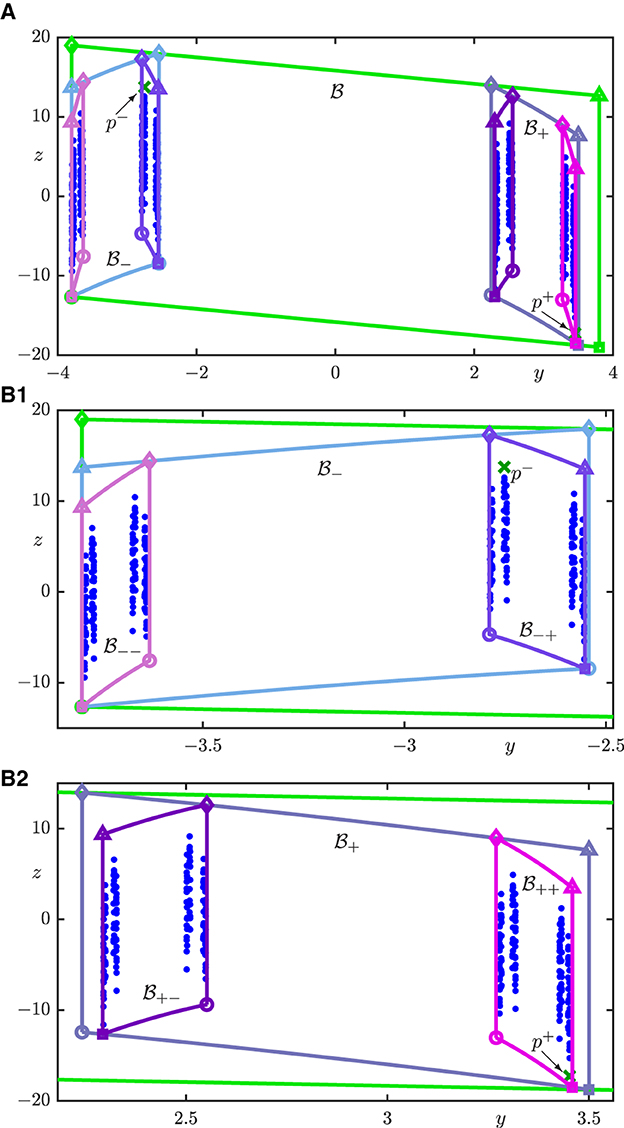
Figure 4. First 900 intersection points in W^s(p^±) ∩ Σ for ξ = 1.2 shown together with p^± and the intersection sets of ${B}$ (green), ${{B}}_{-}$ (light blue), ${{B}}_{+}$ (dark blue), ${{B}}_{--}$ (light magenta), ${{B}}_{-+}$ (light purple), ${{B}}_{+-}$ (purple), and ${{B}}_{++}$ (magenta). (A) shows all of $\Sigma \cap {B}$, and (B1, B2) are enlargements of ${{B}}_{-}$ and ${{B}}_{+}$, respectively.

Owing to the properties of the box ${B}$, the symbolic sequence of a particular segment can be determined from that of its intersection point with a transverse section; see Figure 4. Notice the self-similar nature of the construction in Equation (9) of taking the limit of successive preimages of ${B}$. In particular, note that each segment of W^s(Λ) ∩ Σ has a unique z-value. In more colloquial terms, and as Figure 3 illustrates, the set $W^s(\Lambda )\cap {B}=\overline{W^s(p^{\pm })\cap {B}}$ is a set of (infinitely many) spaghetti that look like a Cantor set from the top and like a surface when seen side-on. This is the geometric essence of the carpet property. Specifically, the orthogonal projection of W^s(p^±) ∩ Σ onto the y-axis is always the same Cantor set associated with the Hénon map—while the orthogonal projection of W^s(p^±) ∩ Σ onto the z-axis fills up an interval [1, 2].

2.2. Lack of the carpet property for ξ = 2.4

In contrast, when ξ = 2.4 the manifold W^s(Λ) does not have the carpet property according to the numerical convergence test for gaps in projection [1, 2]. Figure 5 shows the set $W^s(p^{+})\cap {B}$ and the boxes ${B}$, ${{B}}_{-}$, and ${{B}}_{+}$ for this case, in the same way as Figure 3A. While the top views of these two Figures are identical, Figure 5 now shows a much “thinner” set of spaghetti in ${B}$ that does not look like a surface. This is confirmed by the respective intersection sets with the diagonal plane Σ, as is illustrated further in Figure 6: the points W^s(p⁺) ∩ Σ now appear to have gaps in the z-coordinate. Notice how the segments in $W^s(p^{\pm })\cap {B}$ and points in W^s(p^±) ∩ Σ cluster strongly in ${{B}}_{-}$ and ${{B}}_{+}$, and successively in ${{B}}_{--}$ and ${{B}}_{-+}$, ${{B}}_{+-}$, and ${{B}}_{++}$. As a result, in Figure 6A the points in W^s(p^±) ∩ Σ are practically all obscured by the (approximate) parallelograms that are the intersection sets of ${{B}}_{--}$ and ${{B}}_{-+}$, ${{B}}_{+-}$ and ${{B}}_{++}$ with Σ. The set W^s(p^±) ∩ Σ is, however, visible in the enlargements in Figures 6B1, B2. The difference with the case ξ = 1.2 is that, for ξ = 2.4, the respective boxes no longer overlap fully: there is now a gap in the z-coordinate between the projections of ${{B}}_{-}$ and ${{B}}_{+}$, as well as of ${{B}}_{+-}$ and ${{B}}_{++}$; see Figures 6A, B2. This explains the visible gaps between points in W^s(p^±) ∩ Σ when seen in projection onto the z-coordinate. The boxes ${{B}}_{--}$ and ${{B}}_{-+}$ in Figure 6B1, however, still overlap.

FIGURE 5

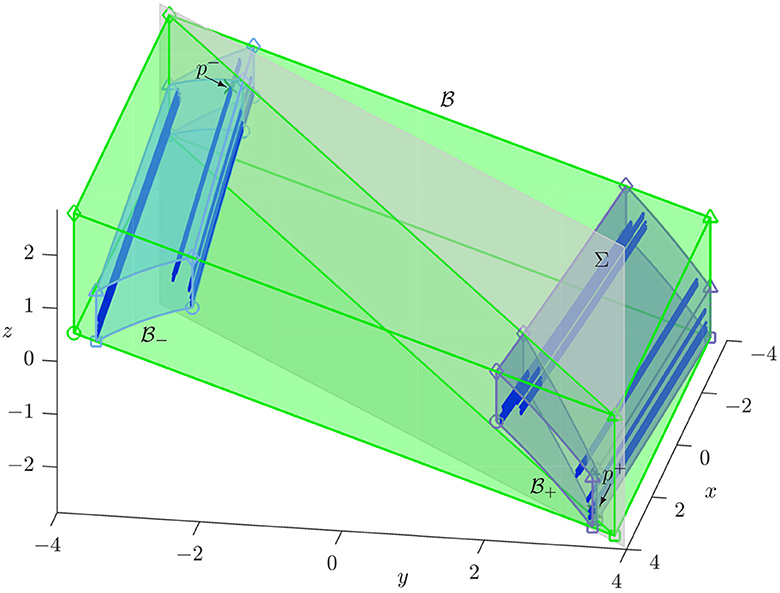
Figure 5. Stable manifolds W^s(p^±) (blue curves) of p^± (green crosses) for ξ = 2.4 inside the box ${B}$ (green) and its two preimages ${{B}}_{-}$ (light blue) and ${{B}}_{+}$ (dark blue); shown are the first 450 segments of $W^s(p^{\pm })\cap {B}$ in (x, y, z)-space together with p^± (green crosses) and the diagonal plane Σ (gray). Compare with Figure 3A.

FIGURE 6

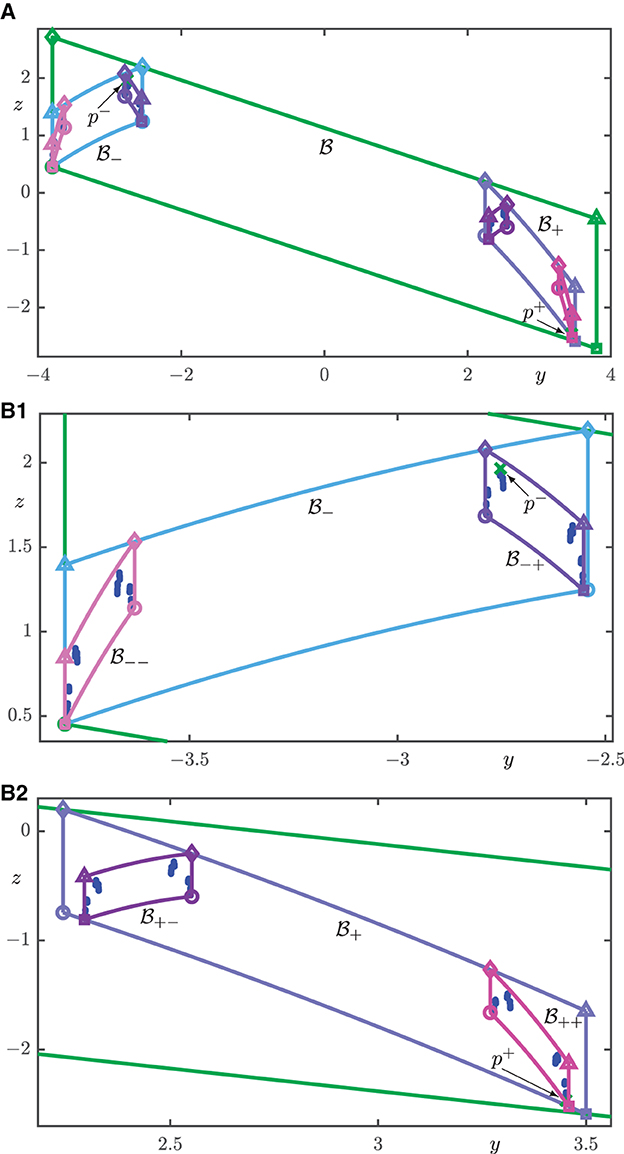
Figure 6. First 900 intersection points W^s(p^±) ∩ Σ for ξ = 2.4 from Figure 5 shown together with p^± and the intersection sets of ${B}$ (green), ${{B}}_{-}$ (light blue), ${{B}}_{+}$ (dark blue), ${{B}}_{--}$ (light magenta), ${{B}}_{-+}$ (light purple), ${{B}}_{+-}$ (purple), and ${{B}}_{++}$ (magenta). (A) shows all of $\Sigma \cap {B}$, and (B1, B2) are enlargements of ${{B}}_{-}$ and ${{B}}_{+}$, respectively.

3. Box and its preimages for 0 < ξ < 1

When 0 < ξ < 1 the unstable manifolds W^u(p^±) and W^u(Λ) are of dimension one, and we now consider images of a suitable box ${D}$ under H. This box is also defined over the square [−Q, Q] × [−Q, Q] in the (x, y)-plane with Q as in Equation (4), namely, as the parallelopiped given by the corner points

$\begin{array}{lll}\square :& \left(-Q,\pm Q,-\frac{Q}{1-\xi }\right),& (10)\end{array}$

$\begin{array}{lll}△:& \left(-Q,\pm Q,\frac{Q}{1-\xi }·\left(2\xi -1\right)\right),& (11)\end{array}$

$\begin{array}{lll}\text{○}:& \left(Q,\pm Q,-\frac{Q}{1-\xi }·\left(2\xi -1\right)\right),& (12)\end{array}$

$\begin{array}{lll}◇:& \left(Q,\pm Q,\frac{Q}{1-\xi }\right).& (13)\end{array}$

Therefore, the symbols ○, ◇, □, and △ again indicate the pairs of corner points and corresponding determining edges; these are now parallel to the y-axis, which is the expanding direction, while the x- and z-directions are contracted under H.

Figure 7 shows the parallelopiped ${D}$ (green) over the square [−Q, Q] × [−Q, Q] and its (forward) images ${{D}}_{-}$ and ${{D}}_{+}$; this illustrates that these boxes have the equivalent properties listed in Section 2 for ${B}$ and ${{B}}_{\pm }$, subject to the reversal of the roles of the x- and y-directions. Namely, the sub-boxes ${{D}}_{-}$ and ${{D}}_{+}$ intersect the boundary of ${D}$ only on the two faces given by y = −Q and y = Q, respectively. With Q as given in Equation (4), the box ${D}$ is tight with respect to the action of H, meaning that now the outer edges of ${{D}}_{\pm }$ are subsets of the outer edges of ${D}$ with y = Q; moreover, the two (respective pieces of the) images of the edges ◇ and □ lie on the top and bottom face of ${D}$, respectively. These properties follow from the expressions given by Equations (10)–(13) and the formula in Equation (1) for H. Figure 7 also shows the four images ${{D}}_{--}$, ${{D}}_{-+}$, ${{D}}_{+-}$, and ${{D}}_{++}$ of ${D}$ under H². Notice that these sub-boxes are very narrow in the x-direction and close to the respective boundaries of ${{D}}_{-}$ and ${{D}}_{+}$. This is due to the strong contraction of ${D}$ in the x-direction under H, which is considerably stronger than that of ${B}$ in the y-direction under H⁻¹; compare with Figure 2.

FIGURE 7

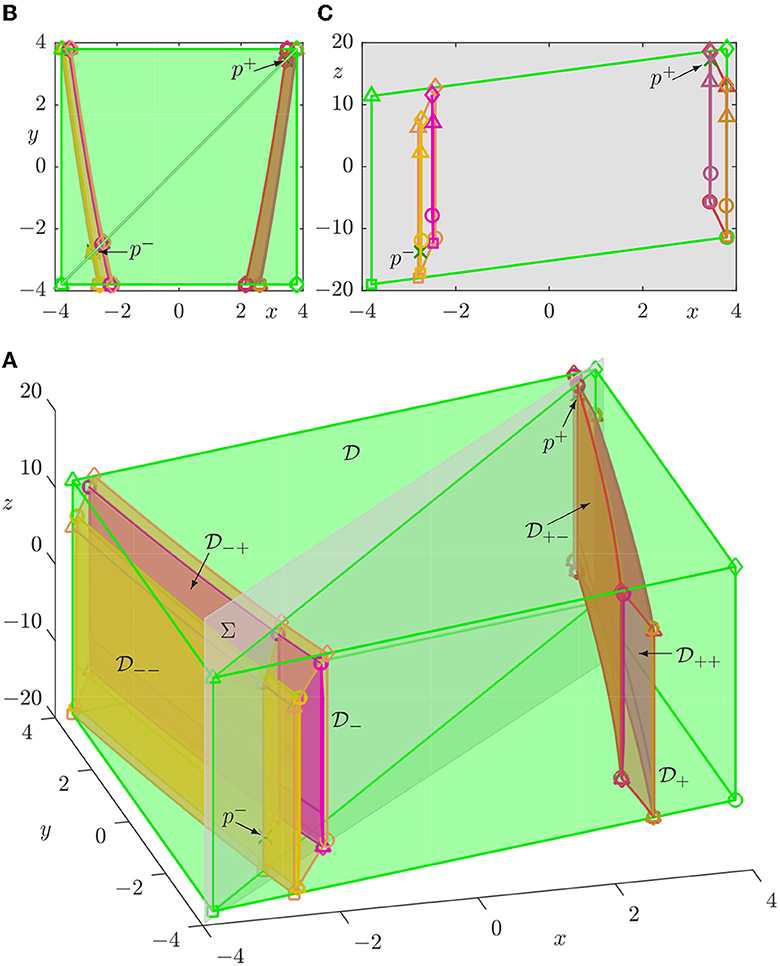
Figure 7. Box ${D}$ (green), its images ${{D}}_{-}$ (orange) and ${{D}}_{+}$ (red), and their images ${{D}}_{--}$ (yellow), ${{D}}_{-+}$ (magenta), ${{D}}_{+-}$ (dark magenta), and ${{D}}_{++}$ (light brown) under H with ξ = 0.8. (A) shows these objects in (x, y, z)-space together with p^± (green crosses) and diagonal Σ (gray). (B) is the top view in the (x, y)-plane, and (C) shows the intersecting parallelograms in Σ, which is represented by its projection onto the (x, z)-plane. The y-aligned determining edges are labeled □, △, ○, and ◇ by their respective corner points, as defined for ${D}$ in Equations (10)–(13). Compare with Figure 2.

As Figure 7 illustrates, the nested sub-boxes also constitute a three-dimensional horseshoe, now under the (forward) action of H, meaning that the limiting set

$\begin{array}{ll}{\displaystyle \underset{N\to \infty }{lim}}{\displaystyle \bigcap _{k=0}^N}{H}^k({D})=W^u(\Lambda )\cap {D}& (14)\end{array}$

exists and Λ is a blender when $W^u(\Lambda )\cap {B}$ has the carpet property. Moreover, Λ is expected to be a blender when 0 < ξ < 1 is sufficiently close to 1, while it is not a blender when ξ is sufficiently close to 0; see Hittmeyer et al. [1, 2].

3.1. Carpet property for ξ = 0.8

Figure 8 shows the unstable manifolds $W^u(p^{\pm })\cap {D}$ for ξ = 0.8 inside the box ${D}$ and its images ${{D}}_{-}$ and ${{D}}_{+}$ in Figure 8A, while Figure 8B illustrates the situation locally near ${{D}}_{-}$ with the second images ${{D}}_{--}$ and ${{D}}_{-+}$. We again compute the manifolds W^u(p^±) as curves and show the first 150 segments of the branches that intersect ${D}$ repeatedly, which are both branches of W^u(p⁻) and one branch of W^u(p⁺) (its other branch goes straight to infinity). As a result of the strong contraction of the x-direction under H, the segments $W^u(p^{\pm })\cap {D}$ are seen to cluster strongly near the boundaries of ${{D}}_{-}$ and ${{D}}_{+}$, and near ${{D}}_{--}$ and ${{D}}_{-+}$, respectively. As a result, the Cantor structure is much harder to recognize in Figure 8 compared to Figure 3.

FIGURE 8

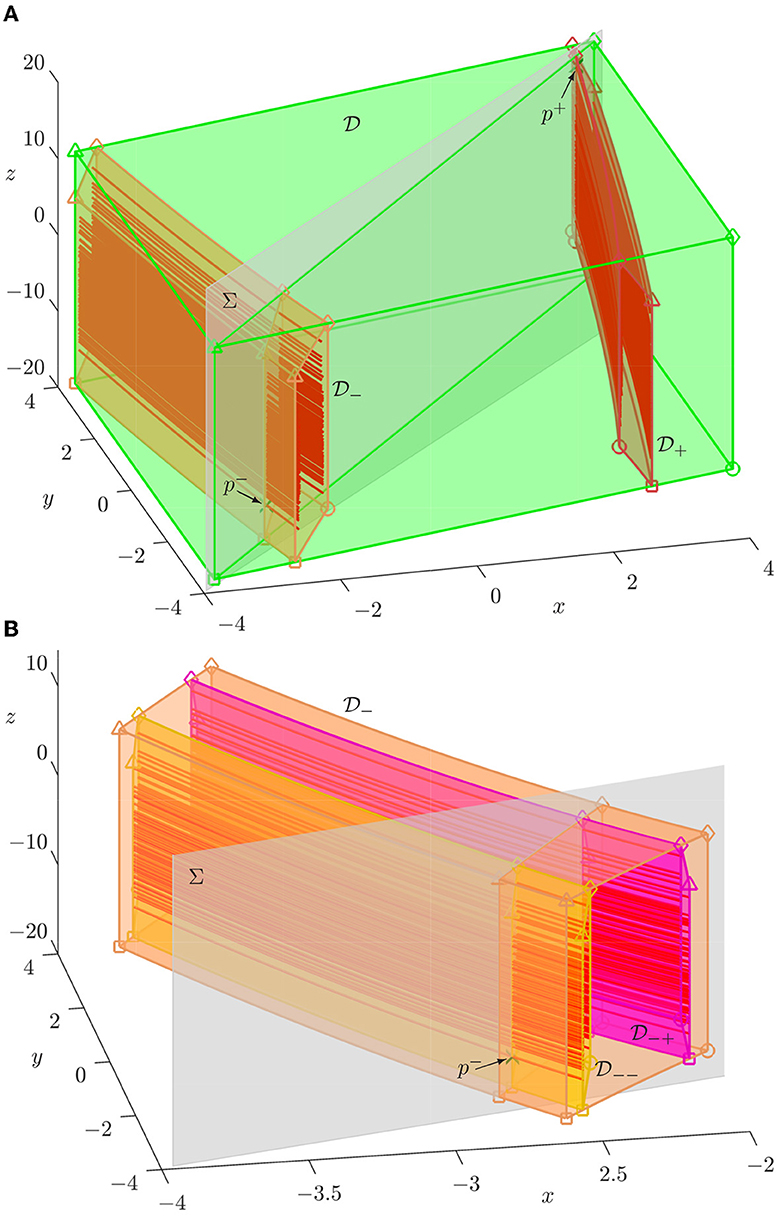
Figure 8. First 450 segments of $W^u(p^{\pm })\cap {D}$ (blue curves) for ξ = 0.8, shown in (A) inside ${D}$ (green), ${{D}}_{-}$ (orange), and ${{D}}_{+}$ (red), and in (B) inside ${{D}}_{-}$ (orange), ${{D}}_{--}$ (yellow), and ${{D}}_{-+}$ (magenta); also shown are p^± (green crosses) and the diagonal plane Σ (gray).

According to Hittmeyer et al. [1, 2], an orthogonal projection onto the z-coordinate for ξ = 0.8 shows gaps between the segments $W^u(p^{\pm })\cap {D}$ that converge to zero as more segments are added. Hence, W^u(Λ) has the carpet property and Λ is a blender. Indeed, the 450 segments computed for Figure 8 already give the impression that $W^u(p^{\pm })\cap {D}$ is dense in projection onto the (y, z)-plane. To illustrate this further, Figure 9 shows the first 300 intersection points with the diagonal plane Σ of each of the three repeatedly returning branches of W^u(p^±) together with the intersection sets of the sub-boxes from Figure 8; here Figure 9A shows all of ${D}$, while Figures 9B1, B2 are enlargements near ${{D}}_{-}$ and ${{D}}_{+}$, respectively. The 900 points of W^u(p^±) ∩ Σ do not appear to have any gaps between them (at this resolution) when projected onto the z-axis. This is because the sub-boxes ${{D}}_{-}$, and ${{D}}_{+}$, and ${{D}}_{--}$, ${{D}}_{-+}$, ${{D}}_{+-}$, and ${{D}}_{++}$ overlap sufficiently, meaning that they do not leave gaps when seen in projection onto the z-coordinate. Notice that ${{D}}_{--}$, ${{D}}_{-+}$, ${{D}}_{+-}$, and ${{D}}_{++}$ are so narrow that they would obscure W^u(p^±) ∩ Σ in Figure 9; this is why we now plot these points “on top” of the shown boundaries of these sub-boxes.

FIGURE 9

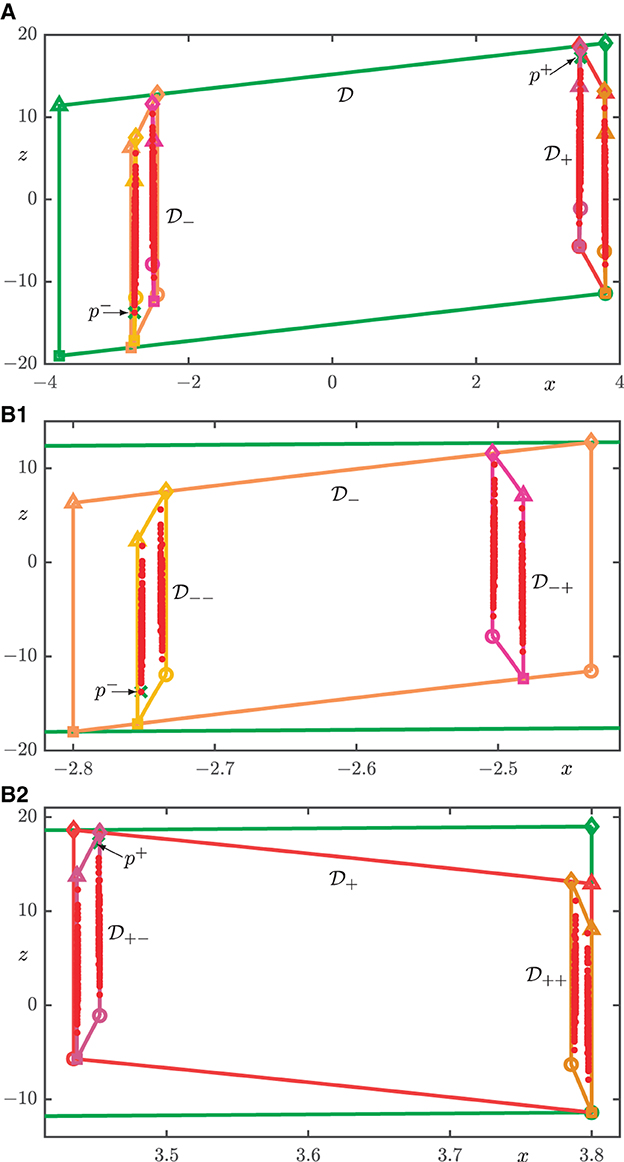
Figure 9. First 900 intersection points W^u(p^±) ∩ Σ for ξ = 1.2 from Figure 8 shown together with p^± and the intersection sets of ${D}$ (green), ${{D}}_{-}$ (orange), ${{D}}_{+}$ (red), ${{D}}_{--}$ (yellow), ${{D}}_{-+}$ (magenta), ${{D}}_{+-}$ (dark magenta), and ${{D}}_{++}$ (light brown). (A) shows all of $\Sigma \cap {D}$ and (B1, B2) are enlargements of ${{D}}_{-}$ and ${{D}}_{+}$, respectively.

3.2. Lack of the carpet property for ξ = 0.4

Figures 10, 11 illustrate that Λ is not a blender when ξ = 0.4 according to the convergence test in Hittmeyer et al. [1, 2]. When seen along the x-axis, the shown segments of $W^u(p^{\pm })\cap {D}$ in Figure 10 now appear to be a Cantor set of curves, which suggests that W^u(Λ) no longer has the carpet property. Figure 11 illustrates this further by showing how the points in W^u(p^±) ∩ Σ sit within the different sub-boxes. Notice in Figure 11A how narrowly spaced these points are in the very narrow ${{D}}_{--}$, ${{D}}_{-+}$, ${{D}}_{+-}$, and ${{D}}_{++}$, which lie near the boundaries of the sub-boxes ${{D}}_{-}$ and ${{D}}_{+}$. The enlargements in Figures 11B1, B2 show that, in turn, the points in W^u(p^±) ∩ Σ lie close to the boundaries of ${{D}}_{--}$, ${{D}}_{-+}$, ${{D}}_{+-}$, and ${{D}}_{++}$; specifically, in such a way that there are gaps in between these groups of points in terms of their z-coordinates. Notice from Figure 11 that the respective pairs of sub-boxes shown in each panel do not overlap in projection onto the z-axis, meaning that this projection of W^u(Λ) ∩ Σ is now also a Cantor set. This shows in a different way that Λ is indeed not a blender for ξ = 0.4.

FIGURE 10

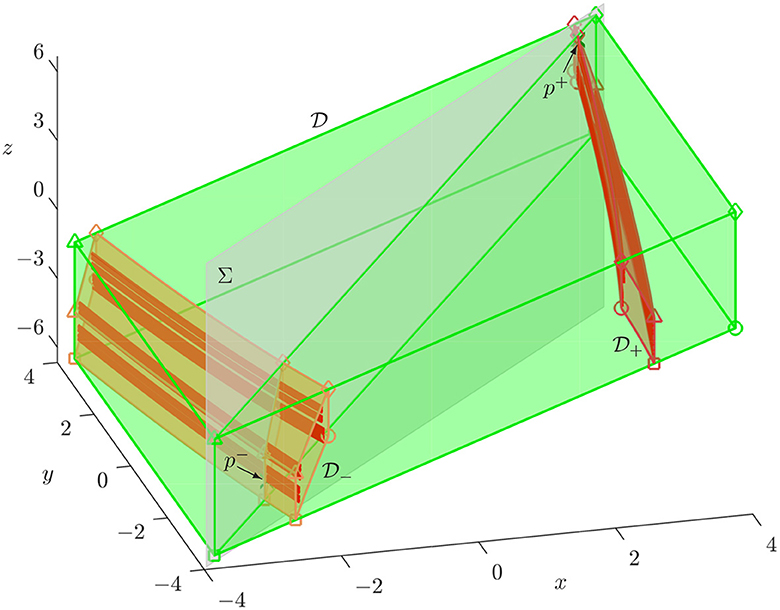
Figure 10. Unstable manifolds W^u(p^±) (red curves) of p^± (green crosses) for ξ = 0.4 inside the box ${D}$ (green) and its two preimages ${{D}}_{-}$ (orange) and ${{D}}_{+}$ (red); shown are the first 450 segments of $W^u(p^{\pm })\cap {B}$ in (x, y, z)-space together with the diagonal plane Σ (gray). Compare with Figure 8.

FIGURE 11

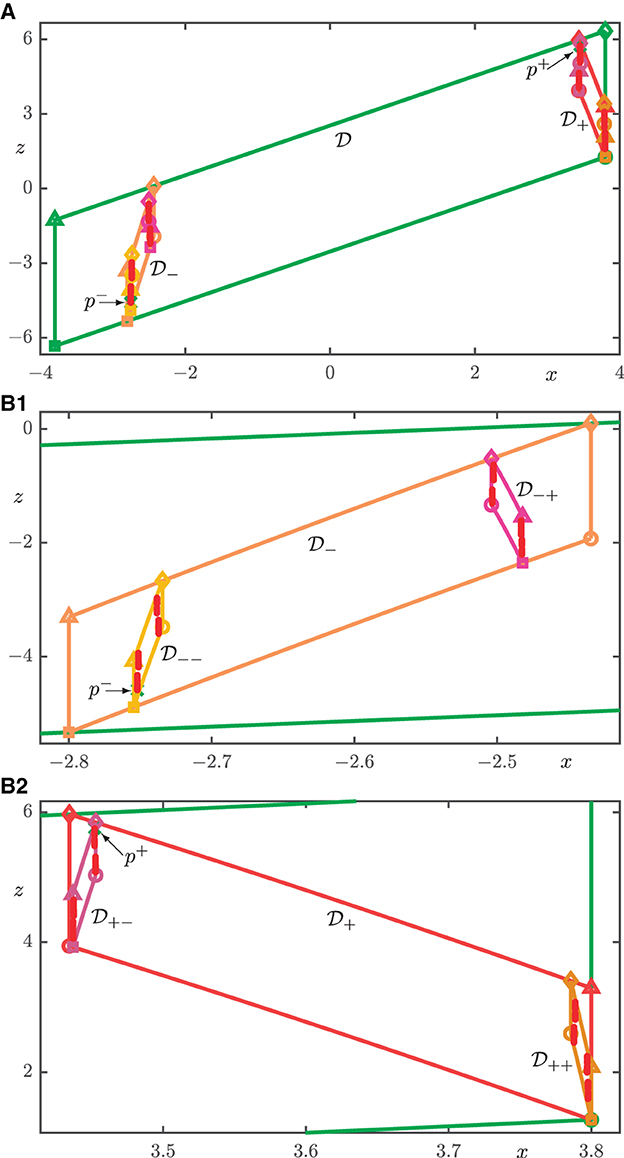
Figure 11. First 900 intersection points W^u(p^±) ∩ Σ for ξ = 0.4 from Figure 10 shown together with p^± and the intersection sets of ${D}$ (green), ${{D}}_{-}$ (orange), ${{D}}_{+}$ (red), ${{D}}_{--}$ (yellow), ${{D}}_{-+}$ (magenta), ${{D}}_{+-}$ (dark magenta), and ${{D}}_{++}$ (light brown). (A) shows all of $\Sigma \cap {D}$, and (B1, B2) are enlargements of ${{D}}_{-}$ and ${{D}}_{+}$, respectively.

4. Relative positions of determining edges

Figures 4, 6 of the intersection sets in the diagonal plane Σ illustrate that the carpet property of W^s(Λ) for ξ > 1 is associated with the overlap in the z-coordinate between sub-boxes in the sequence defining the limit set in Equation (9). Similarly and according to Figures 9, 11, the carpet property of W^u(Λ) for 0 < ξ < 1 is associated with the overlap in the z-coordinate between sub-boxes that generate the limit set in Equation (14). We now investigate further how the respective z-overlap between $H^{-k}({B})\cap \Sigma$ and $H^k({D})\cap \Sigma$ in the particular plane Σ of intersection relates to the properties of W^s(Λ) ∩ Σ and W^u(Λ) ∩ Σ, respectively. To this end, we consider how these objects change with the contraction rate ξ over the range $\left[\frac{1}{3},3\right]$. Since the corresponding z-ranges vary a lot with ξ, it is convenient to show the relevant information in the compactified coordinate $\bar{z}$, which is obtained by the transformation

$\begin{array}{ll}\bar{z}:=\frac{z}{1+\mid z\mid }\in \left[-1,1\right].& (15)\end{array}$

Moreover, for ease of comparison of the two cases 0 < ξ < 1 and ξ > 1, we transform the smaller interval $\left[\frac{1}{3},1\right]$ to the interval [−1, 1] so that it has length 2 as well; this is achieved by the transformation

$\begin{array}{ll}\xi \to -\frac{1}{\xi }+2.& (16)\end{array}$

Figure 12 shows the $\bar{z}$-values ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ of the intersection points with Σ of the determining edges of the pairs of sub-boxes ${{B}}_{\pm }$ and ${{D}}_{\pm }$ in Figure 12A, and of the four respective sub-boxes ${{D}}_{\pm \mp }$ and ${{B}}_{\pm \mp }$ in Figure 12B. These points form ξ-parametrized curves in the $(\xi ,\bar{z})$-plane, which are labeled by the respective symbols and have the color of the corresponding box as in previous figures. To obtain these curves, we consider 500 evenly spaced ξ-values in [0.001, 0.999] and 450 evenly spaced ξ-values in [1.01, 8.0], for which the intersection points of the respective determining edges with Σ are computed by interpolation from (pre)images of H as was explained in Section 2.

FIGURE 12

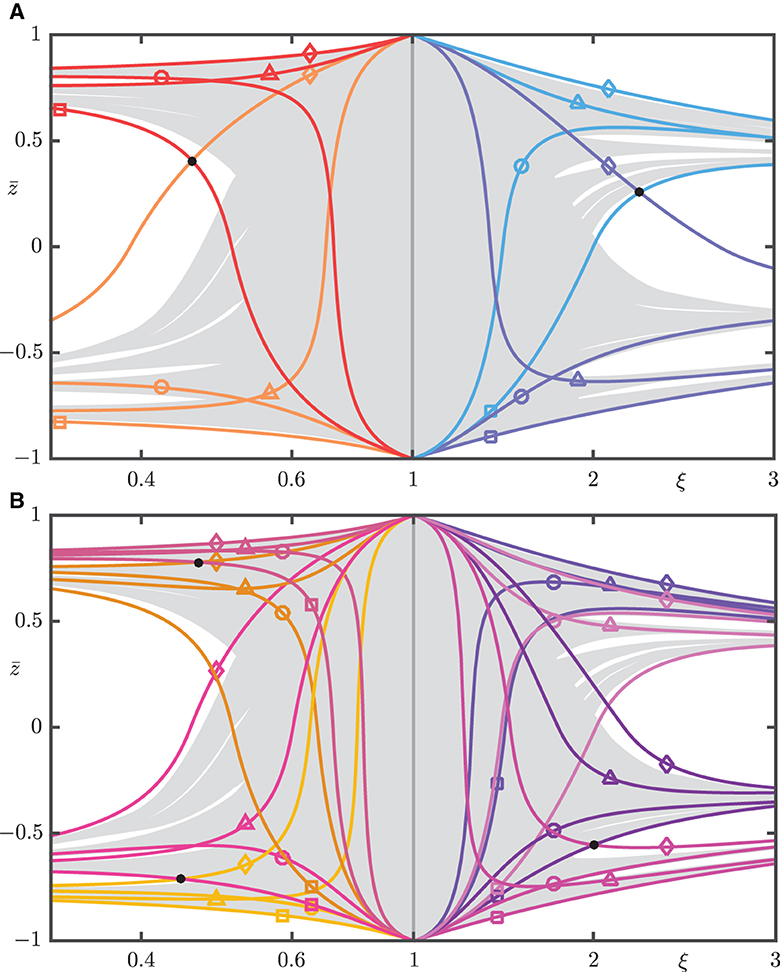
Figure 12. Curves ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ for the sub-boxes ${{B}}_{\pm }$ and ${{D}}_{\pm }$ in (A), and for the sub-boxes ${{D}}_{\pm \mp }$ and ${{B}}_{\pm \mp }$ in (B), shown in the $(\xi ,\bar{z})$-plane with $\left[\frac{1}{3},1\right]$ rescaled by Equation (16) to have width 2. Colors match those of the boxes in Figures 4, 6, 9, 11, and the gray background is formed by W^u(p^±) ∩ Σ for $\xi \in [\frac{1}{3},1)$ and W^s(p^±) ∩ Σ for ξ∈(1, 3]. Black dots mark the intersection points of ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$ of opposing sub-boxes, which indicate a gain/loss of overlap.

Figure 12 also shows the $\bar{z}$-values of the intersection sets W^u(p^±) ∩ Σ for 0 < ξ < 1 and W^s(p^±) ∩ Σ for ξ > 1. They form a gray background and consists of curves generated from computed intersection points. Specifically, the respective one-dimensional manifolds were computed for ξ∈{0.01,0.1,0.2,0.3,0.35,0.5, 0.6, 1.7, 1.8, 1.9, 2, 2.1, 2.4, 4.0, 10.0, 50.0, 100.0}; the first 1,000 intersection points for ξ ≤ 4 and the first 500 intersection points for ξ ≥ 4 were determined for each returning branch of a manifold. These points were then connected by using modified Akima interpolation in Matlab to obtain a set of gray ξ-parameterized curves over the ξ-range $\left[\frac{1}{3},3\right]$. Moreover, in the range ξ∈[0.6, 1.7], the area between the $\bar{z}$-values of p^± was gray-filled, since there are no visible gaps (in this projection) at the scale of these Figures; compare with Hittmeyer et al. ([2], Figure 8).

Notice in Figure 12 that the different curves ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ align quite well with the “boundaries” of W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ. It is noticeable that the curves for ${{D}}_{\pm \mp }$ and ${{B}}_{\pm \mp }$ in Figure 12B lie closer to W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ, respectively, than those for ${{B}}_{\pm }$ and ${{D}}_{\pm }$ in Figure 12A. In particular, intersection points between curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$ of pairs of sub-boxes correspond to changes in their overlap properties as identified in Figures 4, 6 for ξ > 1, and Figures 9, 11 for 0 < ξ < 1. As expected from these Figures, there are two intersection points in Figure 12A between the respective curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$. Namely, $(\xi ,\bar{z})\approx (0.4506,0.4061)$ marks the gain or loss of overlap between the sub-boxes ${{D}}_{-}$ and ${{D}}_{+}$, and $(\xi ,\bar{z})\approx (2.258,0.2566)$ marks that between ${{B}}_{-}$ and ${{B}}_{+}$.

Figure 12B shows the curves ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ for the sub-boxes ${{B}}_{\pm \mp }$ and ${{D}}_{\pm \mp }$. For 0 < ξ < 1, there are two intersection points between curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$, namely the point $(\xi ,\bar{z})\approx (0.4377,-0.7094)$ concerning the overlap between ${{D}}_{--}$ and ${{D}}_{-+}$, and the point $(\xi ,\bar{z})\approx (0.4566,0.7803)$ concerning overlap between ${{D}}_{+-}$ and ${{D}}_{++}$. The fact that both these points occur between ξ = 0.8 and ξ = 0.4 reflects the change in overlap observed in Figures 9, 11. For ξ > 1, Figure 12B shows only the intersection point $(\xi ,\bar{z})\approx (1.9883,-0.5498)$ between the respective curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$, which marks the change in overlap between ${{B}}_{+-}$ and ${{B}}_{++}$. Note that there is no intersection point between the curves ${◇}_{\bar{z}}(\xi )$ for ${{B}}_{--}$ and ${\square }_{\bar{z}}(\xi )$ for ${{B}}_{-+}$ in the shown ξ-range. Moreover, we did not find such an intersection point based on the data we computed in [1.01, 8.0]; so if it exists, this point will lie well beyond ξ = 8.0. In other words, ${{B}}_{--}$ and ${{B}}_{-+}$ remain in overlap, which agrees with the change observed in Figures 4, 6.

The curves ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ can be computed for further (pre)images, and Figure 13 shows them for the respective eight sub-boxes ${{D}}_{\pm \mp \pm }$ and ${{B}}_{\pm \mp \pm }$. Notice that these curves are now even closer to the boundaries of W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ, respectively. Moreover, we find further intersection points between curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$. For 0 < ξ < 1, we find all expected four intersection points in the shown ξ-range, namely $(\xi ,\bar{z})\approx (0.4410,-0.7928)$, $(\xi ,\bar{z})\approx (0.4396,-0.5639)$, $(\xi ,\bar{z})\approx (0.4024,0.7014)$, and $(\xi ,\bar{z})\approx (0.4740,0.8367)$, which correspond to changes in overlap between the pairs ${{D}}_{--\pm }$, ${{D}}_{-+\pm }$, ${{D}}_{+-\pm }$, and ${{D}}_{++\pm }$, respectively. For ξ > 1, however, Figure 13 shows only the three intersection points $(\xi ,\bar{z})\approx (1.92181,-0.70477)$, $(\xi ,\bar{z})\approx (2.07822,0.52975)$, and $(\xi ,\bar{z})\approx (2.51816,0.61039)$; they correspond to changes in overlap between the pairs ${{B}}_{--\pm }$, ${{B}}_{+-\pm }$, and ${{B}}_{++\pm }$, respectively. We did not find an intersection between the curves ${◇}_{\bar{z}}(\xi )$ for ${{B}}_{-+-}$ and ${\square }_{\bar{z}}(\xi )$ for ${{B}}_{-++}$ based on the data we computed for ξ ∈ [1.01, 8.0]. As was the case for ${{B}}_{--}$ and ${{B}}_{-+}$, this intersection point may well exist for values of ξ well beyond the ones considered here.

FIGURE 13

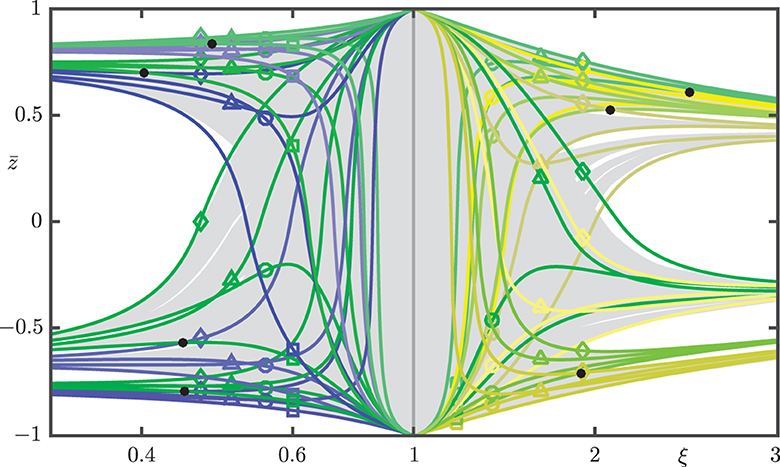
Figure 13. Curves ${\text{○}}_{\bar{z}}(\xi )$, ${◇}_{\bar{z}}(\xi )$, ${\square }_{\bar{z}}(\xi )$, and ${△}_{\bar{z}}(\xi )$ for the sub-boxes ${{D}}_{\pm \mp \pm }$ and ${{B}}_{\pm \mp \pm }$ shown with W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ as in Figure 12.

To summarize the discovered changes in overlap between successive sub-boxes, Figure 14 shows only the relevant curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$ for pairs of “opposite boxes” that generate the intersection points we identified in Figures 12, 13. Notice how the respective intersection points are reasonably close to the disappearance of the biggest $\bar{z}$-gaps of W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ, respectively. More specifically, the parts of the pairs of curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$ corresponding to non-overlapping of the respective pairs of sub-boxes, as well as the intersection points themselves, actually lie in the respective gap. This reflects the fact that the boxes ${B}$ and ${D}$, and their (pre)images provide an outer approximation of the local one-dimensional manifold of the hyperbolic set Λ. Hence, the ξ-values of the computed intersection points that represent a change in overlap, as well as those for further pairs of (pre)images of ${B}$ and ${D}$, provide an outer approximation of the ξ-interval around ξ = 1 where the carpet property holds and, hence, where Λ is a blender.

FIGURE 14

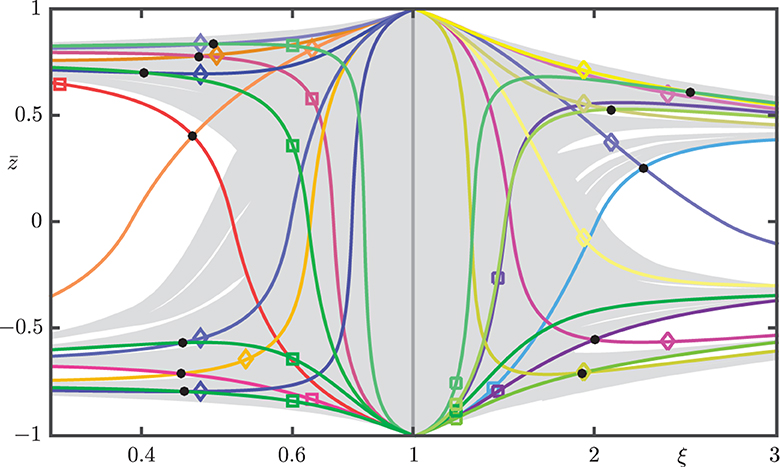
Figure 14. Curves ${◇}_{\bar{z}}(\xi )$ and ${\square }_{\bar{z}}(\xi )$ of opposing sub-boxes for ${{B}}_{\pm }$ and ${{D}}_{\pm }$, ${{D}}_{\pm \mp }$ and ${{B}}_{\pm \mp }$, and ${{B}}_{\pm \mp \pm }$ and ${{D}}_{\pm \mp \pm }$, shown with W^u(p^±) ∩ Σ and W^s(p^±) ∩ Σ as in Figures 12, 13.

5. Discussion and outlook

We have shown how to construct for the Hénon-like family H a parameter-dependent and tight linear box, a parallelopiped with forward images for 0 < ξ < 1 and backward images for ξ > 1 that intersect this box to yield a three-dimensional horseshoe containing the local one-dimensional (un)stable manifold of the underlying hyperbolic set Λ. As we illustrated, sufficient overlap of the corresponding sequence of sub-boxes, when viewed along the relevant direction, is directly associated with Λ being a blender. As the contraction/expansion rate ξ is varied away from ξ = 1, gaps are created between these boxes, again when viewed along the relevant direction, and eventually Λ ceases to be a blender.

Due to the nonlinear nature of map H, the (pre)images of the initial box deform in a non-affine way; here, we identified two different yet related general phenomena. First, while the determining edges of all sub-boxes are aligned with the expanding direction, they are nevertheless curved and so are not parallel to the determining edges of the initial parallelopiped. Second, the successive sub-boxes are sheared increasingly. Both these effects are relevant when one wants to decide whether there exists, or not, an overlap between sub-boxes when viewed from a given direction. In particular, the gaps between different pairs of sub-boxes, in a chosen transverse section and chosen direction, do not all open up for the same value of ξ. Moreover, when such gaps open depends on the section and not just on the chosen direction. This represents a typical scenario, and it shows that the disappearance of the blender via the vertical separation of the two “arms” of the three-dimensional horseshoe is a complicated and subtle process. While, as a first approximation, the affine construction provides a concise and persuasive explanation for the existence of blenders, it does not properly represent the details of their creation or disappearance.

Notwithstanding these issues, tracing the intersection points of the relevant determining edges of pairs of boxes with a transverse section provides an outer approximation of the ξ-range over which Λ should be expected to be a blender. Indeed, we observed that the successive gaps of the respective one-dimensional manifolds appear at values of ξ that are necessarily closer to ξ = 1 but still quite close to the ξ-values of the appearance of gaps between the corresponding boxes. This type of geometrical information should be useful also for subsequent investigations to determine an inner approximation of the ξ-range over which a blender exists. In particular, the presented box construction may inform and motivate a computer-assisted proof of the existence of a blender via rigorous computations based on interval arithmetic. This will require verifying that the (pre)image of the initial box satisfies topological as well as metric properties (expressed via cone conditions; see Díaz et al. [3] and Bonatti and Díaz [6]) required for a three-dimensional blender horseshoe. This may be achieved rigorously, for example, with the approach by Zgliczyński and Gidea [23], Zgliczyński [24], and Kapela et al. [25]; see Capiński et al. [26]. In a similar spirit, it should be possible to provide a computer-assisted proof that Λ is not a blender when ξ is sufficiently far from ξ = 1.

In the intermediate range, it is not so clear from a box construction whether a given hyperbolic set Λ is a blender or not. Namely, the mentioned distortion of iterates of the initial box, here under H or H⁻¹, is expected to play an important role. One observes an increasing, nonlinear distortion at deeper levels of the three-dimensional horseshoe construction, which is mainly due to the difference between the expanding rates in the strong unstable and the center stable directions. This implies that a guess derived from the affine systems may not be suitable when attempting to prove that a hyperbolic set is a blender. The issue of distortion in the generic setting is known to experts in the field; in particular, dealing with it is an important part of the proof by Bonatti and Díaz [6] that a blender exists, and it is dexterously circumvented in their work by combining the observations of forward and backward iterations.

This effect of distortion is pronounced near where the carpet property is lost. More precisely, both analytical as well as computer-assisted methods run into increasing difficulties with obtaining the required estimates at deeper levels as the overlap between boxes decreases. This suggests that other approaches should be used when one is interested in how a blender can disappear or be created as system parameters are changed. A specific example of an alternative approach is the computation of extremely long pieces of the respective one-dimensional manifolds. As we have shown in earlier [1, 2] for the Hénon-like family H, computing W^s(p^±) or W^u(p^±), respectively, as arclength-parametrized curves allows one to provide convincing numerical evidence (albeit in a non-rigorous way) that any gaps in projection converge to zero with increasing arclength. This constitutes a check that the carpet property is satisfied and, hence, Λ is a blender. Indeed, these one-dimensional manifolds exist for any value of ξ > 1 and of 0 < ξ < 1, respectively, so that the break-up of the blender via the emergence of gaps in the projection can be studied. The details of this transition—the bifurcation of the blender—are the subject of ongoing research.

As a concluding remark, we hope that this study will stimulate further investigations of blenders and their role for associated dynamics. As was already mentioned briefly in the introduction, there is a close connection between blenders and the C¹-robust existence of heterodimensional cycles [3, 5–15]. In the low-dimensional context of a diffeomorphism in ℝ³ as discussed here, a heterodimensional cycle is characterized by the existence of a quasi-transverse intersection of codimension one between the one-dimensional manifolds W^s(p) and W^u(q) of two saddle points p and q of different index; moreover, their two-dimensional manifolds W^u(p) and W^s(q) intersect transversely. Suppose now that p ∈ Λ, where Λ is a blender and W^u(q) approaches W^s(Λ) along the direction associated with the carpet property. Then there exists a (different) heteroclinic connection for any sufficiently small C¹-perturbation of the map. It is a challenging task to find or construct this geometric configuration in an explicitly given map or vector field. The Hénon family H is still the only explicit example of a diffeomorphism with a blender, and one approach of our ongoing work is to modify it in a suitable way to generate heterodimensional cycles. Alternatively, one may attempt to find blenders in systems that feature heterodimensional cycles. A few specific examples of such systems are known, including maps [18, 27] and vector fields [17, 19, 20], and the identification of a blender in any of them remains an interesting challenge.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SH generated the Figures with input from BK, HMO, and KS. A first draft of the paper was produced by BK. All authors devised and contributed equally to the research and contributed to editing and completing the writing. All authors contributed to the article and approved the submitted version.

Funding

KS was supported by the JSPS KAKENHI Grant 21K03320.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hittmeyer S, Krauskopf B, Osinga HM, Shinohara K. Existence of blenders in a Hénon-like family: geometric insights from invariant manifold computations. Nonlinearity. (2018) 31:R239–67. doi: 10.1088/1361-6544/aacd66

CrossRef Full Text | Google Scholar

2. Hittmeyer S, Krauskopf B, Osinga HM, Shinohara K. How to identify a hyperbolic set as a blender. Discr Cont Dynam Syst-A. (2020) 40:6815–36. doi: 10.3934/dcds.2020295

CrossRef Full Text | Google Scholar

3. Díaz LJ, Kiriki S, Shinohara K. Blenders in centre unstable Hénon-like families: with an application to heterodimensional bifurcations. Nonlinearity. (2014) 27:353–78. doi: 10.1088/0951-7715/27/3/353

CrossRef Full Text | Google Scholar

4. Hénon M. A two-dimensional mapping with a strange attractor. Comm Math Phys. (1976) 50:69–77. doi: 10.1007/BF01608556

CrossRef Full Text

5. Bonatti C, Díaz LJ, Viana M. Dynamics beyond uniform Hyperbolicity. In: A global geometric and probabilistic perspective. vol. 102 of Encylopaedia of Mathematical Sciences. Springer-Verlag: Berlin (2005).

Google Scholar

6. Bonatti C, Díaz LJ. Persistent nonhyperbolic transitive diffeomorphisms. Ann Math. (1996) 143:357–96. doi: 10.2307/2118647

CrossRef Full Text | Google Scholar

7. Bonatti C, Crovisier S, Díaz LJ, Wilkinson A. What is… a blender? Notices Amer Math Soc. (2016) 63:1175–8. doi: 10.1090/noti1438

CrossRef Full Text | Google Scholar

8. Bonatti C, Díaz LJ, Kiriki S. Stabilization of heterodimensional cycles. Nonlinearity. (2012) 25:931–60. doi: 10.1088/0951-7715/25/4/931

CrossRef Full Text | Google Scholar

9. Bonatti C, Díaz LJ. Abundance of C¹-robust homoclinic tangencies. Trans Amer Math Soc. (2012) 364:5111–48. doi: 10.1090/S0002-9947-2012-05445-6

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Díaz L. Robust nonhyperbolic dynamics and heterodimensional cycles. Ergod Theory Dyn Syst. (1995) 15:291–315. doi: 10.1017/S0143385700008385

CrossRef Full Text | Google Scholar

11. Díaz L, Pérez SA. Hénon-like families and blender-horseshoes at nontransverse heterodimensional cycles. Int J Bifurcat Chaos. (2019) 29:1930006. doi: 10.1142/S0218127419300064

CrossRef Full Text | Google Scholar

12. Díaz L, Pérez SA. Nontransverse heterodimensional cycles: stabilisation and robust tangencies. Trans Amer Math Soc. (2023) 376:891–944. doi: 10.1090/tran/8694

CrossRef Full Text | Google Scholar

13. Li D, Turaev D. Persistence of heterodimensional cycles. arXiv:210503739. (2021). doi: 10.48550/arXiv.2105.03739

CrossRef Full Text | Google Scholar

14. Avila A, Crovisier S, Wilkinson A. C¹ density of stable ergodicity. Adv Math. (2021) 379:107496. doi: 10.1016/j.aim.2020.107496

CrossRef Full Text

15. Biebler S. Almost blenders and parablenders. Ergodic Theory Dyn Syst. (2022) 2022:1–42. doi: 10.1017/etds.2022.16

CrossRef Full Text | Google Scholar

16. Bonatti C, Díaz L. Robust heterodimensional cycles and C¹-generic dynamics. J Inst Math Jussieu. (2008) 7:469–525. doi: 10.1017/S1474748008000030

CrossRef Full Text | Google Scholar

17. Li D. Homoclinic bifurcations that give rise to heterodimensional cycles near a saddle-focus equilibrium. Nonlinearity. (2017) 30:173–206. doi: 10.1088/1361-6544/30/1/173

CrossRef Full Text | Google Scholar

18. Kostelich EJ, Kan I, Grebogi C, Ott E, Yorke JA. Unstable dimension variability: a source of nonhyperbolicity in chaotic systems. Phys D. (1997) 109:81–90. doi: 10.1016/S0167-2789(97)00161-9

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhang W, Krauskopf B, Kirk V. How to find a codimension-one heteroclinic cycle between two periodic orbits. Discrete Contin Dyn Syst Ser A. (2012) 32:2825–51. doi: 10.3934/dcds.2012.32.2825

CrossRef Full Text | Google Scholar

20. Mason G, Hammerlindl A, Krauskopf B, Osinga HM. Determining the global manifold structure of a continuous-time heterodimensional cycle. J Comput Dynam. (2022) 9:393–419. doi: 10.3934/jcd.2022008

CrossRef Full Text | Google Scholar

21. Krauskopf B, Osinga HM. Growing 1D and quasi-2D unstable manifolds of maps. J Comput Phys. (1998) 146:404–19. doi: 10.1006/jcph.1998.6059

CrossRef Full Text | Google Scholar

22. Díaz LJ, Pérez SA. Blender-horseshoes in center-unstable Hénon-like families. In: Pacifico M, Guarino P, editors. New Trends in One-Dimensional Dynamics. vol. 285 of Springer Proceedings in Mathematics and Statistics. New York, NY: Springer (2019). p. 137–63.

PubMed Abstract | Google Scholar

23. Zgliczyński P, Gidea M. Covering relations for multidimensional dynamical systems. J Diff Equat. (2004) 202:32–58. doi: 10.1016/j.jde.2004.03.013

CrossRef Full Text | Google Scholar

24. Zgliczyński P. Covering relations, cone conditions and the stable manifold theorem. J Diff Equat. (2009) 246:1774–819. doi: 10.1016/j.jde.2008.12.019

CrossRef Full Text | Google Scholar

25. Kapela T, Mrozek M, Wilczak D, Zgliczyński P. CAPD::DynSys: a flexible C++ toolbox for rigorous numerical analysis of dynamical systems. Commun Nonlinear Sci Num Simulat. (2021) 101:105578. doi: 10.1016/j.cnsns.2020.105578

CrossRef Full Text | Google Scholar

26. Capiński MJ, Krauskopf B, Osinga HM, Zgliczyński P. Characterising blenders via covering relations and cone conditions. arXiv:221204861. (2022). doi: 10.48550/arXiv.2212.04861

CrossRef Full Text | Google Scholar

27. Gonchenko SV, Ovsyannikov II, Simó C, Turaev D. Three-dimensional Hénon-like maps and wild Lorenz-like attractors. Internat J Bifur Chaos Appl Sci Engrg. (2005) 15:3493–508. doi: 10.1142/S0218127405014180

CrossRef Full Text | Google Scholar