Pruning and optimization of optical neural network as a binary optical trigger

Optical neural networks implemented with Mach-Zehnder Interferometer (MZI) arrays are a promising solution to enable fast and energy-efficient machine learning inference, yet finding a practical application has proven challenging due to sensitivity to thermal noise and loss. To leverage the distinct advantages of integrated optical processors while avoiding its shortcomings given the current state of optical computing, we propose the binary optical trigger as a promising field of application. Implementable as small-scale application-specific circuitry on edge devices, the binary trigger runs binary classification tasks and output binary signals to decide if a subsequent energy intensive system should activate. Motivated by the limited task complexity, constrained area and power budgets of binary triggers, we perform 1) systematic, application-specific hardware pruning by physically removing specific MZIs, and 2) application-specific optimizations in the form of false negative reduction and weight quantization, as well as 3) sensitivity studies capturing the effect of imperfections in real optical components. The result is a customized MZI-mesh topology, MiniBokun Mesh, whose structure provides adequate performance and robustness for a targeted task complexity. We demonstrate in simulation that the pruning methodology achieves at least 50% less MZI usage compared to Clements and Reck meshes with the same input size, translating to at least between 4.6% and 24.2% savings in power consumption and a 40% reduction in physical circuitry footprint compared to other proposed unitary MZI topologies, sacrificing only 1%–2% drop in inference accuracy.

1 Introduction

Optical processors are known for their fast, efficient computation-by-propagation and high energy efficiency. Applying optical processing to machine learning is particularly promising: while optical processors are sensitive to noise, crosstalk, and optical signal attenuation, machine learning is error-tolerant by definition, and benefits substantially from the low-power matrix-vector multiplication (MVM) made possible by optical neural networks (ONNs) (McMahon, 2023).

Previous studies on ONN focused on implementing arbitrary weight matrices (Miller, 2013; Shen et al., 2017; Zhang et al., 2021; Banerjee et al., 2023) similar to the multi-layer perceptron (MLP) (Delashmit et al., 2005) implemented on a digital computer through singular value decomposition (SVD). This is achieved by inserting a diagonal matrix [$\mathbf{\Sigma }$, implemented by one column of Mach-Zehnder Interferometers (MZIs)] between two unitary rotation matrices ($\mathbf{U}$ and ${\mathbf{V}}^{*}$, each implemented by a unitary MZI-mesh). $\mathbf{T}\mathbf{U}\mathbf{\Sigma }$, a similar decomposition process proposed in Zhao et al. (2019) where $\mathbf{T}$ is a sparse matrix implemented by a tree-like mesh, reduces component usage by 15%–38%. However, challenges associated with scaling up the optical processors are significant (Al-Qadasi et al., 2022). A deep ONN, such as a three-layer decomposition-based structure, suffers from signal attenuation through the optical path and layer interfaces. This can be mitigated by using only one physical unitary mesh where one reprograms the network weight and loops back the signals to reuse the mesh during each inference. This approach, however, significantly increases the inference latency and compromises the main advantage of computation-by-propagation of an optical processor. On the other hand, a wide ONN with large matrix dimensions poses challenges in the calibration process, with error compounding along optical paths (Mojaver et al., 2023). A small ONN, on the other end, limits the dimension of the input vector and subsequently the potential field of application. For this reason, a tiled-based multiplier (Gu et al., 2020a; Feng et al., 2022) was proposed, where each multiplier with limited expressiveness implements one of the sub-matrices of the desired weight matrix. However, such approaches either require multiple copies of the multiplier or require iterations of weight reprogramming during inference when used for deep neural networks on complex multi-class classification tasks, suffering from similar hardware-reuse latency penalties.

To make the most of ONN’s low power operation while avoiding the above-mentioned caveats, using the ONN in some efficiency-demanding edge computing tasks is a promising application. Ideally, the task should have low complexity so that a small-scale ONN can be employed. For this reason, we propose using the ONN as an activation trigger for any subsequent energy-intensive system in an edge environment. Similar to the multi-stage architecture for facial recognition proposed in (Bong et al., 2018) but implemented using optical components, the optical processor will act as an ultra-lightweight neural network that responds to a particular input event (i.e., specific objects appearing in the input image), while being more sophisticated than a conventional motion- or proximity-based detector (Gazivoda and Bilas, 2022) to avoid unnecessary activation caused by any input fluctuation, such as newly present objects of noninterest in the monitoring area. For example, consider a smart door lock facing a busy pedestrian street: the system ignores passersby, and only activates an energy-intensive system (e.g., face recognition for authentication) when someone directly faces the sensor. By triggering the subsequent complex system only when it is needed, energy consumption can be dramatically reduced.

With the target application in mind, further efforts can be explored to construct a tailored ONN for the task. First, the edge execution environment would benefit tremendously from reduced active component usage and reduced control circuitry bit precision that is constantly drawing power. Second, trade-offs can be made between the rate of false activation and the rate of trigger miss, depending on the specific application. To reduce the number of active components, we explored a pruning approach inspired by machine learning, where low-saliency components with minimal impact on overall system performance are removed from an initially over-parametrized optical neural network while maintaining prediction accuracy. Regarding application-specific trade-offs, we examined methods for reducing false negatives and quantization for the proposed binary optical trigger.

In this paper, given the ONN’s fast and efficient computation ability yet with low scalability, we propose the binary optical trigger, a lightweight optical neural network designed for binary classification. The binary optical trigger has a structure similar to a traditional fully connected neural network but is composed of a mesh of MZIs, where the weight matrix is controlled by phase values programmed into the phase shifters. Our proposed ONN application and its associated optimizations diverge from previously reported efforts aimed at moderate classification tasks beyond MNIST, which often results in impractically large photonic circuits or extensive component reuse. Instead, our work focuses on binary classification tasks to trigger subsequent energy-intensive systems. Given the promising energy efficiency of ONNs, despite their early stage of development, this niche and innovative application effectively leverages their advantages in a practical, targeted manner. We then systematically explore the pruning of well-established unitary MZI topologies to optimize it as a trigger, leading to a new, application-specific topology named MiniBokun. Through simulation, we demonstrate that MiniBokun, when used as the binary optical trigger, prunes away at least 50% of the MZIs from a standard unitary at the cost of 1%–2% accuracy impairment—leading to a conservatively estimated power saving of 24% and an area reduction of 40%. The paper is structured as follows: we first cover the ONN background in Section 2. Our experimental setup, application-specific optimization, pruning approach, phase noise considerations, and estimations regarding a physical system (power, latency and area) are described in Section 3. The results, obtained through the methodology described in Section 3, are presented and analyzed in Section 4. Followed by the conclusion in Section 5.

2 Background

2.1 MZI basics

Our optical processor adheres to an MZI-based architecture, taking advantage of its capability of realizing signed, complex-valued weights (Mourgias-Alexandris et al., 2022). The MZI-based neural network accelerator consists of a mesh of $2\times 2$ reconfigurable MZI building blocks topologically arranged to form an optical processor unit, as shown at the top of Figure 1. Each building block splits the optical signal and adjusts the relative phase difference through the internal phase shifter ($\theta$, colored in orange). Next, the phase of the recombined optical signal is programmed through the external phase shifter ($\varphi$, colored in blue). The transformation matrix of a single MZI building block, $[D_{\text{MZI}}]$, mapped to the optical processor can be expressed as

$\left[D_{\text{MZI}}\right]=j{e}^{j\left(\frac{\theta }{2}\right)}\left[\begin{array}{cc}\hfill e^{j\varphi }\sin \left(\frac{\theta }{2}\right)\hfill & \hfill e^{j\varphi }\text{cos}\left(\frac{\theta }{2}\right)\hfill \\ \hfill \text{cos}\left(\frac{\theta }{2}\right)\hfill & \hfill -\sin \left(\frac{\theta }{2}\right)\hfill \end{array}\right],(1)$

with $\{\theta ,\varphi \}\in [\mathrm{0,2}\pi )$. The output field is expressed as the multiplication of the transformation matrix and the input field, i.e., a matrix-vector multiplication. Each processor behaves as one fully connected layer and an equal number of inputs and outputs, though only covering unitary or sub-unitary space as opposed to arbitrary linear space.

Figure 1

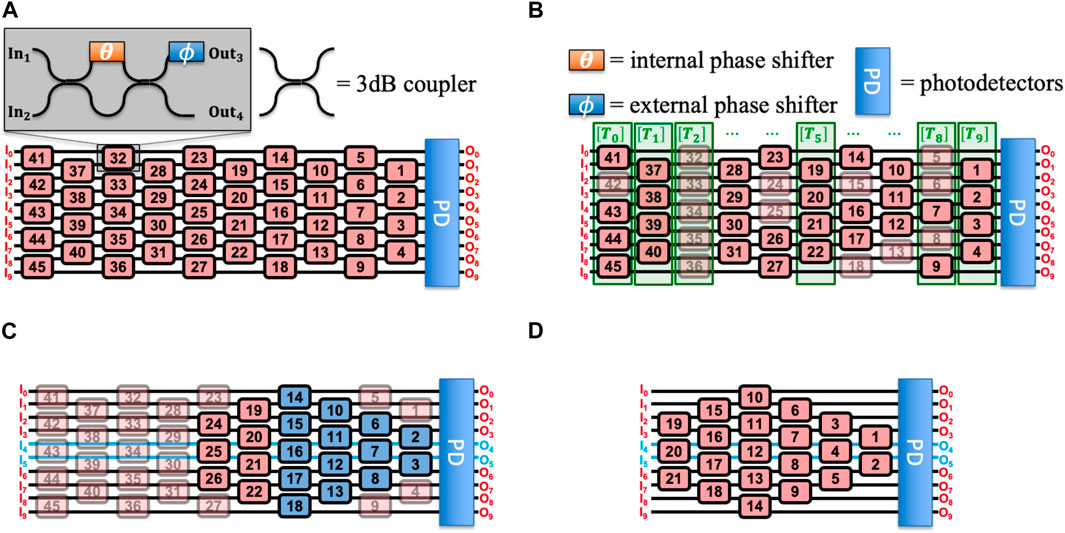
Figure 1. Structure of an MZI and MZI-based ONN. (A) A $10\times 10$ Clements Topology. (B) A random subset of the MZIs, shown in transparency, is pruned away from (A), forming a customized topology. (C) Specific Pruning of Clements to obtain MiniBokun Topology, for usage as a binary trigger. (D) MiniBokun Topology on its own with updated MZI numbering.

2.2 MZI-based optical processor topology and mathematical model

Larger transformation matrices can be realized by organizing these $2\times 2$ units in different topologies (one example is shown in Figure 1A) such that each $[D_{\text{MZI}}]$ in Equation 1 is multiplied and concatenated (Shokraneh et al., 2020). Well-established unitary topologies such as Reck (Reck et al., 1994), Clements (Clements et al., 2016), Diamond (Shokraneh et al., 2020) and Bokun (Mojaver et al., 2023) each have their advantage and drawback on physical footprint, calibration difficulty, and loss-balance properties (Mojaver et al., 2023).

Considering the specific topology, the transformation matrix, $\left[W_{\left(N\times N\right)}\right]$, represented by an ONN mesh of size $N\times N$, given the placement of the MZIs and the phase shifter value pair $(\theta ,\varphi )$ of each MZI in the mesh, can be defined by:

$\left[W_{\left(N\times N\right)}\right]={\left[D_{\text{MZI}}^{\left(K\right)}\right]}_{H_{N\times N}}\cdot {\left[D_{\text{MZI}}^{\left(K-1\right)}\right]}_{H_{N\times N}}\cdot \cdots \cdot {\left[D_{\text{MZI}}^{\left(i\right)}\right]}_{H_{N\times N}}\cdot \cdots \cdot {\left[D_{\text{MZI}}^{\left(2\right)}\right]}_{H_{N\times N}}\cdot {\left[D_{\text{MZI}}^{\left(1\right)}\right]}_{H_{N\times N}}(2)$

where,

${\left[D_{\text{MZI}}^{\left(i\right)}\right]}_{H_{N\times N}}={\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \cdots \hfill & \hfill ⋰\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \left[D_{\text{MZI}}^{\left(i\right)}\right]\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill ⋰\hfill & \hfill \cdots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]}_{N\times N},1\le i\le K(3)$

In Equation 2, $K$ is the total number of MZIs in the mesh (e.g., $K=\mathrm{45,21}$ in Figures 1A, D, respectively). The subscript $H_{N\times N}$ denotes that the MZI’s transformation matrix (i.e., Equation 1) occupies a 2-dimensional subspace within a $N\times N$ Hilbert space, as shown in Equation 3. As an example, MZI 11 in Figure 1A has its upper and lower branch aligned with waveguides 3 and 4, respectively, therefore, ${\left[D_{\text{MZI}}^{\left(11\right)}\right]}_{H_{N\times N}}$ is a matrix whose four entries located on row and column 3-4 are replaced by $\left[D_{\text{MZI}}^{\left(11\right)}\right]$, with 1s on the remaining diagonal entries and 0s elsewhere. Note that the waveguide number and matrix entries are zero-indexed.

At most $N^2-N$ tunable parameters (i.e., phase shifters) are used in representing $\left[W_{\left(N\times N\right)}\right]$. However, an arbitrary $N\times N$ complex matrix requires $2N^2$ parameters. Consequently, as indicated by the SVD process and mentioned in Section 2.1, $\left[W_{\left(N\times N\right)}\right]$ is a unitary or sub-unitary transformation matrix as opposed to a linear one. This implies that the entries in the matrix are not completely independent, and thus the weight matrix has a smaller learnable space than a conventional fully-connected layer (Miller, 2013).

Given an arbitrary mesh formed by the removal of a subset of MZIs from a full $N\times N$ mesh (i.e., Clements topology shown in Figure 1A), a more intuitive way of interpreting Equation 2 is to group MZIs into vertical columns, as shown in Figure 1B, the layer-wise transformation performed by MZI column $j$ is denoted by $\left[T_j\right]$. $\left[T_j\right]$ will be a matrix similar to ${\left[D_{\text{MZI}}^{\left(i\right)}\right]}_{H_{N\times N}}$, but with potentially more than one $2\times 2$ block on the diagonal being replaced by transformation matrices of the MZIs existing on that column. $\left[W_{\left(N\times N\right)}\right]$ can thus alternatively be written as:

$\left[W_{\left(N\times N\right)}\right]={\displaystyle \prod _{j=0}^{N-1}}\left[T_{N-1-j}\right](4)$

The interpretation in Equation 4 gives insight into the transformation performed by each MZI column while providing a clearer picture of how each MZI is ordered in Equation 2.

2.3 Signal basics

2.3.1 Phasor term

A phasor is a scalar, complex value sufficient to describe the steady state of a mono-frequency sinusoidal waveform. In the context of an optical signal, this represents the electric field component of the monochromatic laser. A phasor term takes the form of:

$E_i=E{e}^{j{\varphi }_i}(5)$

In Equation 5, $E_i$ is the phasor term for signal $i$, $E$ is its real amplitude, and ${\varphi }_i$ represents the incoming phase seen by the subsequent optical component on that signal’s path. The transformation matrices of size $n$, representing the effect of any combination of optical components, apply directly to the vector composed of $n$ incoming signals’ phasor. As an example, the incoming signal $I{n}_1$ and $I{n}_2$ to an MZI’s input ports will become $Ou{t}_1$ and $Ou{t}_2$ at the output ports, related by Equation 6:

$\left[\begin{array}{c}\hfill Ou{t}_1\hfill \\ \hfill Ou{t}_2\hfill \end{array}\right]=\left[D_{\text{MZI}}\right]\left[\begin{array}{c}\hfill I{n}_1\hfill \\ \hfill I{n}_2\hfill \end{array}\right](6)$

2.3.2 Value representation and importance of coherency

Due to difficulties of controlling the absolute phase of optical signal (Ip et al., 2008), the incoming data (i.e., feature vectors of each data sample) will be solely represented by the intensity $(P)$ of the signal, given by $P_i\propto |E_i{|}^2$, this implies that in an array of incoming signal represented as:

$\vec{E}=\left[\begin{array}{c}\hfill E_1\hfill \\ \hfill E_2\hfill \\ \hfill \dots \hfill \\ \hfill E_N\hfill \end{array}\right]=\left[\begin{array}{c}\hfill E_{\text{in}1}{e}^{j{\varphi }_1}\hfill \\ \hfill E_{\text{in}2}{e}^{j{\varphi }_2}\hfill \\ \hfill \dots \hfill \\ \hfill E_{\text{in}N}{e}^{j{\varphi }_N}\hfill \end{array}\right](7)$

In Equation 7, only the $E_{\text{in}i}$ terms vary across different data, and each ${\varphi }_i$ takes the same value in the range $[\mathrm{0,2}\pi )$ for all $i\in \left\{\mathrm{1,2},\dots ,N-1\right\}$. In theory, the zero phase difference ensures each MZI can split power to an arbitrary ratio between its two outputs $(\frac{P_{\mathit{out1}}}{P_{\mathit{out2}}}\in [0,\infty ])$. To achieve so, a layer of phase shifters is assumed to be present before the MZI mesh, albeit this is omitted in the diagram.

For the correct functioning of any trained network, not only the zero phase difference across input channels is required, but the absolute phase of each input signal should also remain constant throughout the network’s training and operation. As the MZI mesh works by the principle of interference, an incoherent or varying initial phase difference between signals will affect the intended splitting ratio learned from network training, making the resulting output signal array drastically different from the expectation.

2.4 Imperfect operation

The actual implementation of optical processors faces various aspects of imperfections, and the presence of imperfections significantly degrades the computation accuracy of ONNs (Shafiee et al., 2024; Gu et al., 2020b). In this work, our investigation of the impacts of imperfections focuses on two main sources, optical loss and phase value programming deviations.

2.4.1 Optical loss

During ONN inference, when light couples through the waveguide, the processor suffers from inherent propagation loss. The propagation loss eventually leads to a challenging optical power budget, limiting the signal-to-noise ratio at the photodetectors and reducing the classification accuracy of ONN. The linear loss values $(L_{\text{linear}})$, transformed from loss in dB-scale $(L_{\text{dB}})$ by $L_{\text{linear}}=10^{-L_{\text{dB}}/10}$, are applied to the ONNs and remain constant at a per MZI basis. The lossy transformation matrix can be expressed as

${\left[D_{\text{MZI}}\right]}_L=L_{\text{linear}}\cdot \left[D_{\text{MZI}}\right](8)$

2.4.2 Phase shifter programming deviation

The programmed phase shift can deviate from its intended value due to thermal crosstalk (Shafiee et al., 2024). When programming a targeted waveguide, the heat from resistive heaters can propagate to other waveguides, creating unintended phase changes. To capture these imperfections, we model the programmed phases with a Gaussian distribution $(\theta ,\varphi )\sim N((\widehat{\theta },\widehat{\varphi }),({\sigma }_{\theta }^2,{\sigma }_{\varphi }^2))$ where $\widehat{\theta },\widehat{\varphi }$ [rad] are phases obtained after training and quantization and $({\sigma }_{\theta }^2,{\sigma }_{\varphi }^2)$ are the phase variations due to thermal crosstalk.

2.5 Neural network pruning

In practice, pruning often implies the removal of neurons and weighted connections in a structured or unstructured fashion (Nagel et al., 2021). For neural networks (NNs) implemented by digital processors, network pruning has been known for its benefits of simplifying NN’s architecture, reducing computation workload and memory footprint, and subsequently improving inference speed and efficiency. ONNs, on the other hand, though composed of physically integrated photonics components (e.g., MZIs), benefit from an analogous set of advantages (Banerjee et al., 2023). First, pruning in the hardware context means the direct removal of photonic integrated circuit (PIC) components. The feasibility of the layout is not only subject to the number of on-chip components but also complicated by the requirement of a voltage supply line to each active component (e.g., for the thermo-optic phase shifter). As the number of components grows, this poses a significant challenge for the layout routability and manufacturability in a two-dimensional circuit board. The removal of PIC components immediately reduces layout complexity and manufacturing costs. Second, each component introduces loss to the propagating optical signal to various extents. Reducing the number of components on one optical path reduces the total amount of accumulated loss experienced by that signal, improving signal-to-noise ratio (SNR) at detection. Third, reducing the number of active components naturally leads to less power consumption during operation.

The pruning of MZI-based ONNs was explored in previous works. Banerjee et al. (2023) introduced a pruning algorithm and its variants targeting large-scale SVD-based ONNs for multi-class classification. The algorithm is demonstrated via simulation on networks comprising at least four unitary meshes connected by a non-linear activation function, with 64 as the minimum network width. In particular, their pruning is realized via power-gating or removal of phase shifters, not the entire MZI. This implies that imprecise beam splitters are still present in the actual physical system. Training-time structured pruning was also conducted in the tile-based ONN, such as the block-circulant unit in Gu et al. (2020a). However, to the best of our knowledge, no direct MZI-level pruning on well-established unitary meshes was explored. Specifically, we focused on removing entire MZIs from a unitary structure rather than power-gating active components in SVD-based setups or setups involving component reuse. Our pruning strategy enables a reduction in optical depth and insertion loss compared to these previous configurations. Though unitary meshes already have limited expressivity compared to an arbitrary linear weight matrix, our study showed that the application as a binary optical trigger allowed for an ultra-lightweight ONN that is pruned into deep sub-unitary space without significantly affecting classification accuracy.

3 Materials and methods

3.1 Neuroptica

We use Neuroptica (Bartlett et al., 2019) to evaluate the simulated performance of our ONN architectures. Neuroptica is a Python simulation platform for coherent optical neural networks built with integrated components, such as MZI. The platform allows one to explore ONN architecture design, ex-situ ONN training (Mojaver et al., 2023), and noise/loss robustness simulation of trained ONNs. In addition to the components simulated within the ONN mesh area, we assume the presence of a laser source and variable optical attenuators at the ONN’s input side to produce feature values for each data sample, though these components are not explicitly simulated.

3.1.1 Hyperparameter selection and training

We first evaluate networks with input sizes $(N)$ of 8, 16, 32, and 64 to understand the required network complexity given the two datasets under consideration (to be introduced in Section 3.2). We perform each simulation (training followed by evaluation with the test set) five times with five different random seeds. Each model with a random seed is trained for 50 epochs, and the phase values obtained from the epoch that gives the highest validation accuracy are kept for final tests. Except for special pruned cases, the first two output ports ($O_0$ and $O_1$ in Figure 1A) are used for final decision calculations. We use the test set to calculate each model’s test accuracy and F1 score. While test accuracy provides an overall measure of the model’s ability to classify test samples, the F1 score offers a balanced assessment of the model’s performance in correctly predicting both positive and negative classes in a binary classification task.

The limited size of the ONN we are evaluating and the resolution of the images in the selected datasets mean that data must first be compressed in some way prior to inference. Therefore, we use Principal Components Analysis (PCA) to perform dimensionality reduction. Mathematically, PCA maps $n$-dimensional data to a $k$-dimensional subspace $(k\ll n)$ by finding the eigenvectors that best represent the feature distributions in the data. These eigenvectors are decided by sorting their corresponding singular values obtained from SVD. The higher the singular value, the more variance in data points in the direction of the eigenvector, making the eigenvector more representative. The top-$k$ eigenvectors are combined and multiplied with the original data matrix to complete the transformation, resulting in $k$ features that are used as the input signal to the $k\times k$ ONN.

We make two assumptions about the input range of ONN based on laser power consumption. The first assumption assumes a fixed per-channel laser input range ($P_{\text{i}}\in [\mathrm{0,1}]$ mW per channel). This ensures the same input range to all channels regardless of the input feature size $(N)$ and the resultant overall laser power increases with $N$. On the other hand, the second assumption fixes the total laser power to 10 mW. For each input channel, $P_{\text{i}}\in [0,\frac{10}{N}]$ mW. As a result, the per-channel input range will decrease as $N$ increases.

With these training setups, training time ranged from two to three minutes for $8\times 8$ meshes to nearly half an hour for $64\times 64$ meshes on an Apple M2 Pro Processor (10 cores, 16 GB memory and 200 GB/s memory bandwidth).

3.2 Datasets

3.2.1 MNIST

The MNIST dataset (Deng, 2012) consists of $\mathrm{70,000}28\times 28$ grayscale images of handwritten digits 0-9. Given that our focus is binary classification, we modify the 10-class MNIST dataset by aggregating samples with labels $0-4$ and labels $5-9$ into samples with labels $[\mathrm{1,0}]$ and $[\mathrm{0,1}]$, respectively. Compared to using any two out of the 10 classes, this approach allows us to maximally utilize the available dataset and test the networks’ generalizability across diverse samples while avoiding biased task complexity caused by choosing two specific classes out of ten. The dataset is split $\mathrm{50,000}:\mathrm{10,000}:\mathrm{10,000}$ to form the training, validation, and test sets.

3.2.2 CIFAR-10

The CIFAR-10 dataset (Krizhevsky and Hinton, 2009) contains $32\times 32$ images in 10 classes (airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck), each with three colour channels (red, green, and blue). Similar to how we process the MNIST dataset, we rearrange the CIFAR-10 labels to make the classification binary by aggregating the original label of “airplanes”, “cars”, “ships”, and “trucks” into a new group called “vehicles”; “birds”, “cats”, “deer”, and “dogs” into a new group called “animals”. The images originally labelled as “frog” and “horse” are removed from the dataset to ensure the balance between data samples in the two classes. This reduces the total image number to 48,000 with 24,000 images in each category. The dataset is split $\mathrm{32,000}:\mathrm{8,000}:\mathrm{8,000}$ to form the training, validation, and test sets.

3.2.3 Task complexity and pruning efficacy

In both datasets, the original images have sufficient pixels to clearly depict the represented objects. This ensures that the complexity of any formulated task comes from the intrinsic difficulty of distinguishing objects across different classes rather than from low image resolution. Depending on the specific task complexity and the degree of over-parametrization in the network model, varying levels of pruning can be carried out. As a result, our aggregated classification tasks of both datasets provide meaningful task complexity and serve as effective benchmarks for evaluating the ONN capability and the efficacy of the pruning process.

3.3 Application-specific optimization

Apart from a grid search of hyperparameters, we consider the following application-specific optimization methods to further enhance the performance of the models. These optimization methods focus on actual implementation challenges and adapt the trained models to real-world conditions.

3.3.1 False negative reduction

The binary optical trigger structure is anticipated to be used in event-triggered structures, where the ONN activates the rest of a system when a pre-defined event takes place (e.g., a vehicle is detected by ONN after training on the CIFAR-10 dataset). A key challenge in the implementation of such a system is the optical trigger false negatives: the pre-defined event happens, but the ONN does not send a trigger signal, and the rest of the system fails by default. Therefore, one goal of our work is to minimize the number of False Negatives (FN) while maintaining the classification accuracy of ONN.

The FN reduction method considered in this work changes the weight assigned to each label class in the loss function. We penalize FN more severely, and the binary cross-entropy loss becomes

$L_{\text{BCE}}=-\beta y\cdot \text{log}\left(\widehat{y}\right)-\left(1-y\right)\text{log}\left(1-\widehat{y}\right)(9)$

where $\beta$ is a constant greater than 1, and $\widehat{y}$ is the output from classifier $(y)$ after Sigmoid activation. Consequently, the gradient of the loss function with respect to the network weight $(w)$ becomes

$\frac{\partial L_{\text{BCE}}}{\partial w}={\left(-\beta y+\left(\beta -1\right)\cdot y\widehat{y}+\widehat{y}\right)}^{*}\cdot z(10)$

where $z$ is the input to the ONN layer and the complex conjugate is taken for complex-valued neural networks.

During implementations in this work, in order to strike a trade-off between FN reduction and the classification performance, we train ONN models with different weights $(\beta \in [\mathrm{1,2}])$ assigned to the positive class and record their effects on the FN numbers and the test accuracy.

3.3.2 Post-training quantization (PTQ)

Programming the MZI-based building block of ONNs involves configuring their phase shifters to form a desired transfer matrix. In this work, we consider MZIs with phase shifters controlled by thermally changing the phase using resistive heaters tuned by a voltage supply (Masood et al., 2013). The relationship between the heater control voltage $(V_{\mathit{bias}})$ and the intended phase shift $(\theta ,\varphi )$ can be formulated as

$\left\{\theta ,\varphi \right\}=\gamma V_{\mathit{bias}}^2,(11)$

where $\gamma =\pi /V_{\pi }^2$ (Gu et al., 2020b) and $V_{\pi }$ refers to the required bias voltage for programming $\{\theta ,\varphi \}=\pi$ (Shokraneh et al., 2020).

Practical voltage sources have limited resolution, meaning they can be adjusted only to a finite number of discrete voltage levels equally spaced between the maximum and minimum values. A $b$-bit voltage supply has $2^b$ achievable voltage levels spaced apart by $V_{\text{res}}=V_{\text{max}}/(2^b-1)$ with the $i$-th voltage level being $V_i=i\cdot V_{\text{res}}$ volts. $V_{\text{max}}$ denotes the maximum supply voltage. As we require a phase setting range over $2\pi$ ($\{\theta ,\varphi \}\in [\mathrm{0,2}\pi )$), all the voltage levels beyond $V_{2\pi }$ are not used and the effective bit-resolution of the voltage supply further drops by $\lfloor {\text{log}}_2\left(\frac{V_{\text{max}}}{V_{2\pi }}\right)\rfloor$. The resultant quantized phases are obtained by mapping the sampled voltage levels $(V_i)$ back to $V_{\mathit{bias}}$ in Equation 11.

Models with selected hyperparameters from the previous steps are quantized by rounding the trained phase shifts to their nearest quantized phase values. We choose the least voltage resolution (in $[\mathrm{4,16}]$ bits) that enables the closest ONN test accuracy to those obtained from full resolution (32-bit) training settings.

3.4 Hardware pruning

In this section, we will use the $10\times 10$ Clements topology in Figure 1A as a running example to demonstrate a systematic way of performing pre-training pruning of MZI-based ONN. We begin with the Clements mesh, proven to be optimally unitary for its short optical depth and balanced path length (Clements et al., 2016). First, an important observation is that two output ports are sufficient for carrying out binary training and inferences. As indicated in Figure 1A, regardless of which two ports are used, certain MZIs will remain redundant, as they never receive backward propagating optical gradient signals at either output port, regardless of the states (cross or bar) of other MZIs in the mesh. We refer to these as redundant MZIs. The phase shifters in these MZIs remain at their initialization state and do not contribute to the classification process at all. This observation motivates two aspects for potential improvement: 1) the port choices, and 2) the removal of corresponding redundant MZIs. Given the importance of optical path balance, signals contributing to decision-making should propagate along paths with the same or similar number of MZIs. Typically, the longest optical path in an MZI mesh equals the number of MZI columns (i.e., signals go through one MZI in the current vertical column to arrive at the next column), and conversely, the shortest path “falls through” as many MZI layers without actually going through any MZIs as possible. In the case of the $10\times 10$ Clements, the shortest path lies on waveguide 0 and waveguide 9 $(shortest=5,longest=10)$, using any of the output ports on these waveguides will subject the signal to the maximally imbalanced condition. Furthermore, waveguides located at the edge of the network mesh have only one side for redirecting optical power (towards the center waveguides). In light of the above two considerations, using the central two output ports and pruning away corresponding redundant MZIs (MZI 1, 4, 5 and 9 in Figure 1C) achieves minimal path imbalance $([longest,shortest]=[\mathrm{7,10}])$ and unbiased utilization of the whole expressible space provided by the available optical components.

Upon deciding on port selection and pruning of redundant MZIs, we then perform layer-wise pruning. At each pruned step, we monitor the network performance by performing the same training and testing process and record the testing accuracy. The layer-wise pruning stops until we obtain a minimal network topology that still ensures all input signals are able to reach the center two waveguides. This topology consists of MZIs colored in blue in Figure 1C, which is a triangle mesh that marginally allows the diversion of optical power from top/bottom waveguides to the center waveguides, any further removal of MZIs on this topology will either result in wasted waveguide channels, or isolation between two-halves of the input vector causing unwanted dependence in the network’s decision making.

3.4.1 Expressivity study (fidelity analysis)

To gain insight into the trade-off between reducing component usage and disruption in network expressivity, we look for a suitable metric to evaluate the pruned mesh’s expressivity. In previous works, the concept of fidelity was employed (Feng et al., 2022; Zhang et al., 2021) for evaluating the similarity between two complex density matrices. Similar metrics include the Frobenius norm, cosine similarity, and correlation coefficients. However, we note the unsuitability of a simple similarity metric in our particular case, as the goal of pruning is not to produce an optical mesh capable of approximating the original unitary matrix. Rather, given the relative simplicity of the binary trigger task and monitoring of only two entries in the output vector, fully unitary ONNs are likely over-parameterized, and completely different sets of optimal weight may exist in the sub-unitary space that have little to no relation to the unitary weight matrices producing similar classification accuracy.

For this reason, we employ a sampling-based benchmark to evaluate the signal routing ability of $8\times 8$ sub-unitary meshes: 10,000 random sub-unitary weight matrices implemented by MiniBokun mesh are generated, each is provided with three sets of random input vectors (10 per set), plus an input vector whose power is equally distributed to all ports. Although random, the vectors in each of the three sets have distinct optical power concentrations at specific input ports (with the highest power at ports 0, 3, and 5, respectively). The input vectors are assumed to be coherent with an absolute phase of 0 rad, and the total input power is fixed at 10 mW. For each topology under test, the power distribution at each output port when subjecting the ONN to the aforementioned artificial input vectors is recorded. The expressivity of each topology can then be inferred based on the attained distribution.

3.5 Imperfection study (sensitivity analysis)

All the previous training and tuning of ONNs are conducted with the assumption of perfect operating conditions. However, in reality, ONNs suffer from various aspects of imperfections. To test the resilience of ONNs to imperfections, we inject and vary the magnitude of the optical loss and phase programming deviations to trained ONN models and check their response. The optical loss, defined at the dB-scale $(L_{\text{dB}})$, varies from 0 to 1 dB per MZI. It is converted to the linear scale and applied to the transfer matrices of the MZI using Equation 8. The phase programming deviations are defined as the phase deviations $(({\sigma }_{\theta },{\sigma }_{\varphi }))$ in Section 2.4.2, varying from 0 to 1 radian. We sample the deviated phase values from the normal distribution and recalculate transfer matrices with them. Next, the imperfect transfer matrices are applied to ONNs, and we obtain the ONNs’ test accuracy under imperfect conditions by re-performing the inference. To fully capture the models’ response to stochastic phase programming deviations, we sample 20 different $\theta$ and $\varphi$ values per phase deviation and took the average of the accuracy.

To quantify the tolerance of ONNs to imperfections, we define two Figures of Merits (FoMs) on two sets of imperfect scenarios. The first imperfect scenario assumes only phase programming deviations (Phi-Theta case), ${\sigma }_{\theta }$ and ${\sigma }_{\varphi }$ vary separately and $L_{\text{dB}}$ is kept at 0 dB. The first FoM is defined as the number of ${\sigma }_{\theta }$ and ${\sigma }_{\varphi }$ combinations that lead to a test accuracy greater than 60%, times the surface area covered by each ${\sigma }_{\theta }$ and ${\sigma }_{\varphi }$ combination in ${[\text{rad}}^2$]. This hard limit (60% test accuracy) is defined as our boundary of random guesses.

The second imperfect scenario (Loss-Phase Uncertainty case) considers both optical loss and phase deviations. We assume ${\sigma }_{\theta }={\sigma }_{\varphi }$ and compute a second FoM by multiplying the number of (${\sigma }_{\theta }={\sigma }_{\varphi }$, $L_{\text{dB}}$) combinations that lead to a test accuracy greater than 60% with the surface area covered by each combination in [rad$\cdot$dB].

3.6 Power, latency, and area estimations

The power consumption estimation of ONN takes into account power consumed by the laser, the memory for storing phase shifter values and input, the digital-to-analog and analog-to-digital conversions, optical input modulation, phase programming, and output optical-electrical signal conversion, as expressed in Equation 12.

$P_{\text{total}}=P_{\text{laser}}+P_{\text{mem}}+P_{\text{DAC}}+P_{\text{input\_mod}}+P_{\text{phase\_prog}}+P_{\text{O}-\text{E}}+P_{\text{comp}+\text{ADC}}(12)$

Similarly, the latency of one inference on ONN considers the time spent when the electrical and optical signal propagates through the system during one pass of calculation (or one inference). Assuming an always-on laser, the latency is expressed as:

$\begin{array}{c}\hfill t_{\text{total}}=max\left(t_{\text{input\_mem}}+t_{\text{DAC}}+t_{\text{input\_mod}},t_{\text{phase\_mem}}+t_{\text{DAC}}+t_{\text{phase\_prog}}\right)+\\ \hfill t_{\text{MZI}}+t_{\text{O}-\text{E}}+t_{\text{comp}+\text{ADC}}\end{array},(13)$

In Equation 13, $t_{\text{MZI}}$ is the time light travels through the MZIs in an optical mesh. The input modulation and phase programming steps can be parallelized as the data are fetched from different memory locations and there is no sharing of components along the data path. We keep the greater time spent by the two processes for latency calculation.

The area estimations focus on the layout area of the optical meshes, containing only the MZIs and their connecting waveguides. The length of the mesh is determined by the maximum number of MZIs and waveguide sections connected in series, and the width is the separation distance between waveguides times the number of gaps between input/output ports.

We account for a 10 dBm C-band laser with a wall plug efficiency of 10% (Al-Qadasi et al., 2022). This single laser source provides sufficient optical power to all input ports of ONNs while meeting the minimum required optical power sensitivity of the photodetector. The modulation of laser input (or the electrical-to-optical, EO conversion) is assumed to operate at approximately 20 fJ/bit with a rate of 2.5 Gb/s (Demirkiran et al., 2023).

The phase programming power estimation is divided into two scenarios: a conservative estimation using doped-Si heaters without insulation and an aggressive estimation considering heaters with thermal insulation trenches (formed by deep etching) (Masood et al., 2013). Without the insulation, the heaters consume $P_{\pi }\approx 21$ mW per $\pi$ phase shift with a stabilization time of less than 30 μs (Shokraneh et al., 2020); meanwhile, with the insulation, the heater responsivity improves to $P_{\pi }\approx 1.42$ mW per $\pi$ phase shift yet the settling time extends to more than 150 μs (Masood et al., 2013). We assume each $2\times 2$ MZI has a length of $\approx 300$ μm with phase shifters of 135 μm. (Shokraneh et al., 2020), and the waveguides are separated by 60 μm (Williamson et al., 2020). The effective index $(n_{\text{eff}})$ of MZIs is 2.8.

The input to ONN is fixed at 8-bit resolution while the phase value resolution will be determined by the post-training quantization. The estimations of digital-to-analog converters (DACs) power consumption patterns are also done in two ways: 1) a conservative FoM-based performance approximation which allows us to consider high-speed DACs (data rate = 10 GSamples/s) (Demirkiran et al., 2023), and 2) an aggressive performance estimation using established commercial products with low power consumption.

The optical-to-electrical (OE) circuit at each output port contains a photodetector with a responsivity of 1 A/W and a trans-impedance amplifier. Each channel of EO conversion consumes 100 mW of power with a group delay of 100 ps (Williamson et al., 2020). The subsequent comparator and analog-to-digital converter (ADC) circuit requires only binary resolution and consumes only 325 $\mathrm{\mu }$m of power with a propagation delay of 75 ns (Texas Instruments, 2018).

According to Al-Qadasi et al. (2022), the input to the ONN is stored in DRAMs while the phase values to be programmed are stored in SRAMs. The ONNs considered in this work are small, with each of them containing less than 256 bytes in total for both input and phase values. Despite this, we set the SRAM size to 16 KB and the DRAM size to 64 KB to sufficiently hold more than 100 copies of ONNs and a few thousand input samples after dimensionality reduction. The power and latency numbers are calculated based on modeling data from Cacti 7.0 (Thoziyoor et al., 2008).

4 Results and discussion

4.1 Architectural analysis of optical meshes

The architectural parameters of the three topologies are summarized in Table 1. Among the three topologies, the MiniBokun shown in Figure 1D, resulting from the pruning process, achieved minimum component usage while demonstrating a size-invariant path length difference of only two MZIs.

Table 1

Table 1. Architectural Parameters of Different Topologies of size $N$.

4.1.1 Pruning with accuracy monitoring

Following the method discussed in Section 3.4, the monitored average binary MNIST accuracy per $10\times 10$ network is shown in Figure 2. As indicated by the plateauing part of the curve, up to four MZIs columns can be pruned with less than $0.5\%$ accuracy drop, pruning six layers leads to the minimal triangle topology discussed in Section 3.4, in which significant accuracy degradation is observed. We thus restore two pruned columns, and remove the top and bottom MZIs in the left-most restored column (MZI $\mathrm{23,27}$ in Figure 1C, or equivalently, MZI $\mathrm{19,23}$ in Figure 2) to create diagonal access concerning paths $I_0\to O_4$ and $I_9\to O_5$ in practical chip-calibration (Mojaver et al., 2023). With the above steps, we obtain the MiniBokun Topology.

Figure 2

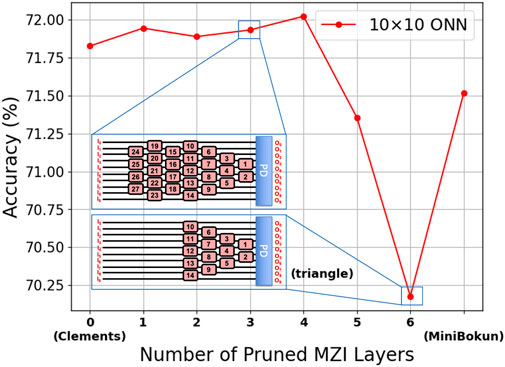
Figure 2. Accuracy Variation as the Clements topology is Pruned column by column, starting with the column closest to the input.

4.1.2 The MiniBokun topology

Similar to the full-size Bokun Mesh proposed in (Mojaver et al., 2023), MiniBokun provides diagonal access for all MZIs in the mesh for practical calibration consideration, yet with no MZI wasted due to being used solely for calibration purposes. Two simple observations can be made for a sufficient formal definition of MiniBokun topology, regardless of network size $N$:

• There are always two MZI columns before the widest column, each containing $\frac{N}{2}-1$ and $\frac{N}{2}-2$ MZIs.

• The last MZI column always contains two MZIs.

The placement of each MZI is thus well-defined, and the number of MZIs in a $N$-input MiniBokun mesh is $\frac{1}{8}(N^2-10N+32)$, as shown in Table 1.

4.1.3 Expressivity analysis

Using the benchmark method presented in Section 3.4.1. We perform statistical analysis on the collected power distribution at each output port for $8\times 8$ 1) Clements (Unitary), 2) Triangle (Over-Pruned) and 3) MiniBokun topologies, Reck topology is omitted as it covers the same unitary space as Clements. The box plot of the result is shown in Figure 3.

Figure 3

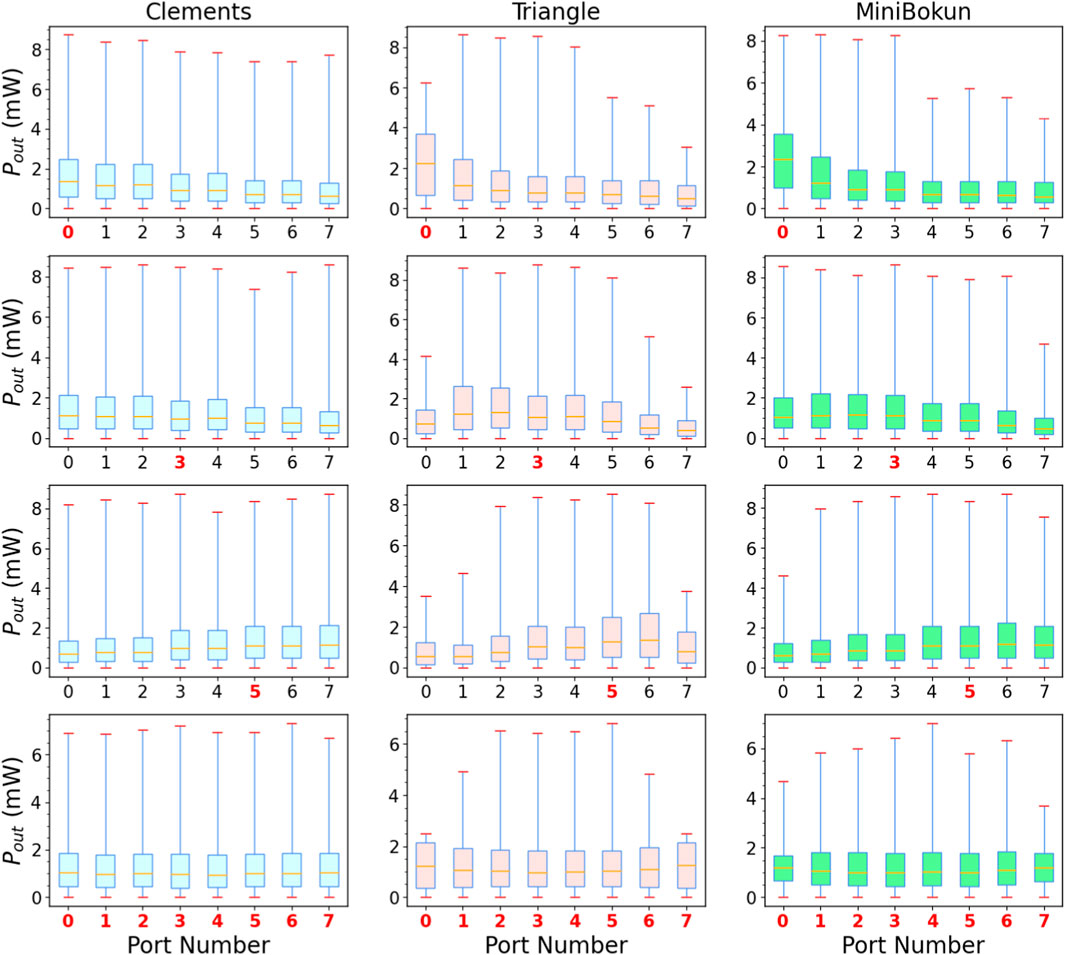
Figure 3. Expressivity of three different meshes. Blue, red and green box plots denote the registered power distribution at each of the eight output ports for Clements, Triangle and MiniBokun mesh. The port number in red indicates the corresponding input port had the highest optical power among all input ports, while the last row of figures denotes the case of equally distributed power among the input (at 1.25 mW per port). The whiskers on each box instance, from top to bottom, are: {max, third quartile, median, first quartile, min}.

As we are not assuming any loss, the average total output power, as expected, sums to 10 mW, which matches the total input power assumption. All tested topology-input combinations managed to achieve near 0 mW output in all output ports. The maximum registered maximum power difference among tested samples were 1.330, 6.205 and 4.080 mW for Clements (port 0), triangle (port 3) and MiniBokun (port 5), respectively. Unitary structures such as the Clements mesh provide full signal routing between any input-output waveguide pairs, thus giving a relatively uniform power distribution profile across each port, even when facing input with power concentrated on particular ports. On the other hand, sub-unitary topologies provide limited signal routing paths, in triangle topology, given the imbalanced number of MZI across different paths and the unbiased random phase setting, the biased weight space manifests as mismatching of maximum detected output power across different output, as well as the varying interquartile ranges. In particular, the low maximum power on edge ports (0, 7) indicates an impaired ability to discard unwanted power as part of the inference process. MiniBokun topology also shows such bias in its power distribution, but to a lighter extent, attributing to the two additional columns providing extra paths to disregard power from inputs 1 through 6, leading to a larger expressible space. This can be validated by the classification accuracy difference between a triangle mesh and a MiniBokun mesh in Figure 2.

4.2 Performance of optical meshes in ONN

4.2.1 Hyperparameter selection

We observe that topology sizes of $N=8$ and $N=16$ work best for the binary optical trigger, especially under the assumption of fixed input laser power.

Under the assumption of constant per-channel input power, all three metrics, the accuracy of each model on both validation and test set and the F1 score, increase as $N$ increases. As shown in Figure 4A, on average, the accuracy of the model prediction on the MNIST dataset improves by an absolute 6.9% as $N$ reaches 64. The models’ accuracy on the CIFAR-10 dataset, which is more complex than MNIST, only increases by an absolute 2.2%, as shown in Figure 4B.

Figure 4

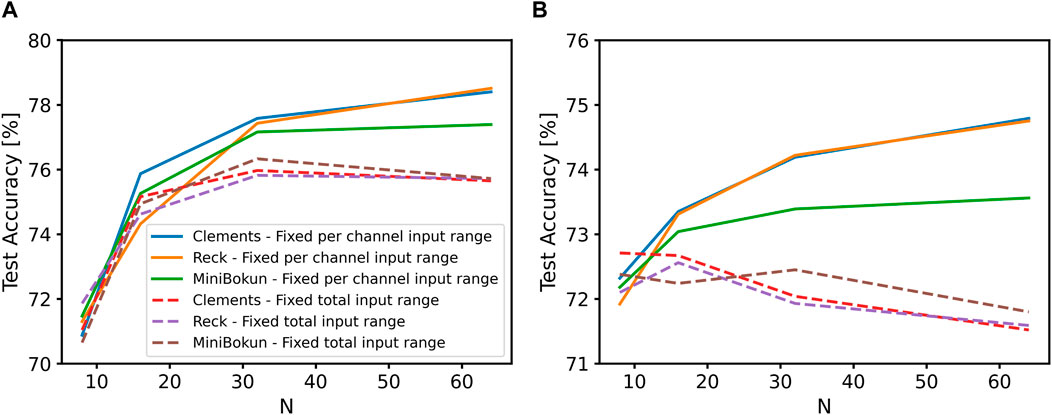
Figure 4. The variation in test accuracy of ONN models with different topology and input power assumptions trained on (A) MNIST dataset, and (B) CIFAR-10 dataset. The same set of legends is used in both figures.

When the assumption changes to fixed laser power, the actual per-channel input power range decreases as the optical mesh scales up. As $N$ grows from 8 to 64, the maximum input optical power $P_i$ to a channel drops from 1.25 mW to 0.16 mW. This input range reduction significantly undermines the ability of larger ONNs to learn. As seen in Figure 4, although the MNIST test accuracy increases with $N$, the magnitude of the growth in all models drops to an average maximum of 4.5%. On the CIFAR-10 dataset, model accuracy starts to drop after $N=16$ and eventually falls below the accuracy of $N=8$.

The increase in ONN classification accuracy with $N$ is subject to the perfect operating conditions assumed in the simulations. In reality, the optical loss of an ONN increases linearly with its size and becomes especially significant when $N\ge 32$ (Shafiee et al., 2024). Moreover, the power consumption of configuring the phase values increases quadratically with the optical mesh sizes (Al-Qadasi et al., 2022). Finally, under the fixed channel input power assumption, the laser input power obviously increases linearly with the number of input channels. Therefore, given our goal of finding a robust model that balances the overall accuracy and power efficiency, only ONNs of $N=8$ and $N=16$ trained with the fixed laser power assumption are considered.

4.2.2 Application-specific optimization

The weighted class method effectively reduces the number of FNs made by ONNs after training. As shown in Figures 5A, C, the FN count decreases from more than 1,000 to fewer than 10 as $\beta$ in Equations 9, 10 increases from 1 to 2. Increasing $\beta$ forces the model to make more positive predictions. Subsequently, there are more false positives, and the overall test accuracy drops, as shown in Figures 5B, D. In this case, sharp declines in overall test accuracy are observed for MNIST $(\beta >1.4)$ and CIFAR-10 $(\beta >1.2)$. To ensure a balance between the decrease in FN and the drop in accuracy, we finally selected $\beta \in [\mathrm{1,1.4}]$ for the rest of our discussions. Models trained with $\beta$ in this range achieve at most a 75% reduction in FN but less than a 5% drop in accuracy.

Figure 5

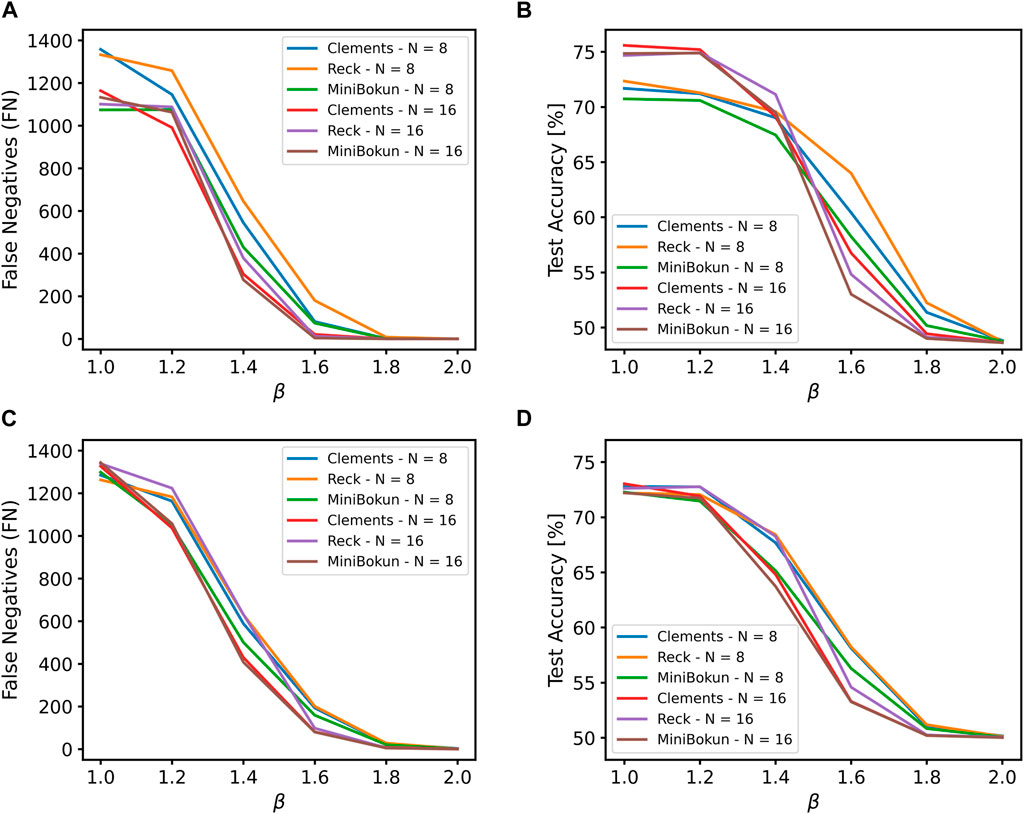
Figure 5. (A) The variation in false negative numbers and (B) the test accuracy of ONN models with different topology and input sizes on the MNIST dataset as a result of the weighted class method. (C) The variation in false negative numbers and (D) the test accuracy of ONN models with different topology and input sizes on the CIFAR-10 dataset as a result of the weighted class method.

We also find that an 8-bit voltage supply resolution is sufficient for models with the selected hyperparameters to achieve similar accuracy to those trained with full precision (32-bit), using a voltage supply setting of $V_{\text{max}}=4V,V_{\pi }=1.92V$ (Shokraneh et al., 2020). According to Figure 6, ONN accuracy increases significantly as the voltage supply resolution increases from 4 to 8 bits and gradually converges to the full-resolution test accuracy. At the 8-bit resolution point, most $8\times 8$ models show $<0.5\%$ deviation from the full-resolution accuracy while most $16\times 16$ models show $<0.8\%$ deviation. Therefore, we assume an 8-bit voltage supply resolution for the rest of our discussions.

Figure 6

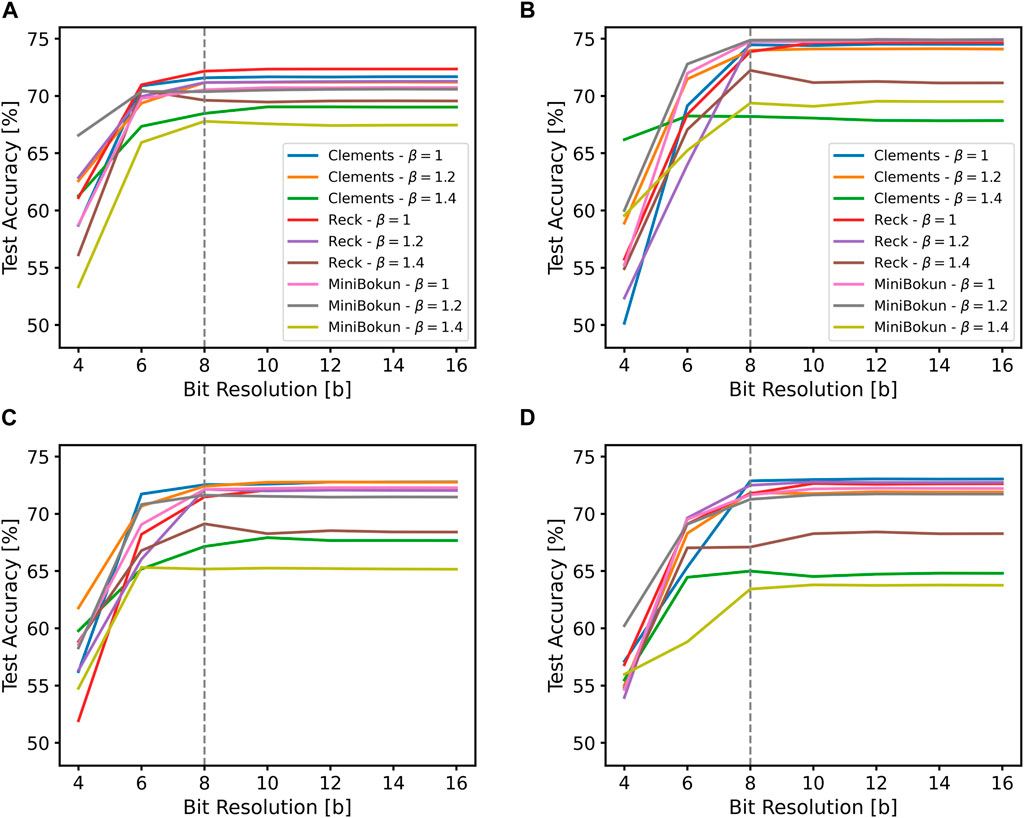
Figure 6. The change in test accuracy of ONN models as a result of post-training quantization (A) on the MNIST dataset with N = 8, (B) on the MNIST dataset with N = 16, and (C) on the CIFAR-10 dataset with N = 8, (D) on the CIFAR-10 dataset with N = 16. The same legend is kept across all four figures.

4.2.3 Impact of pruning on classification performance

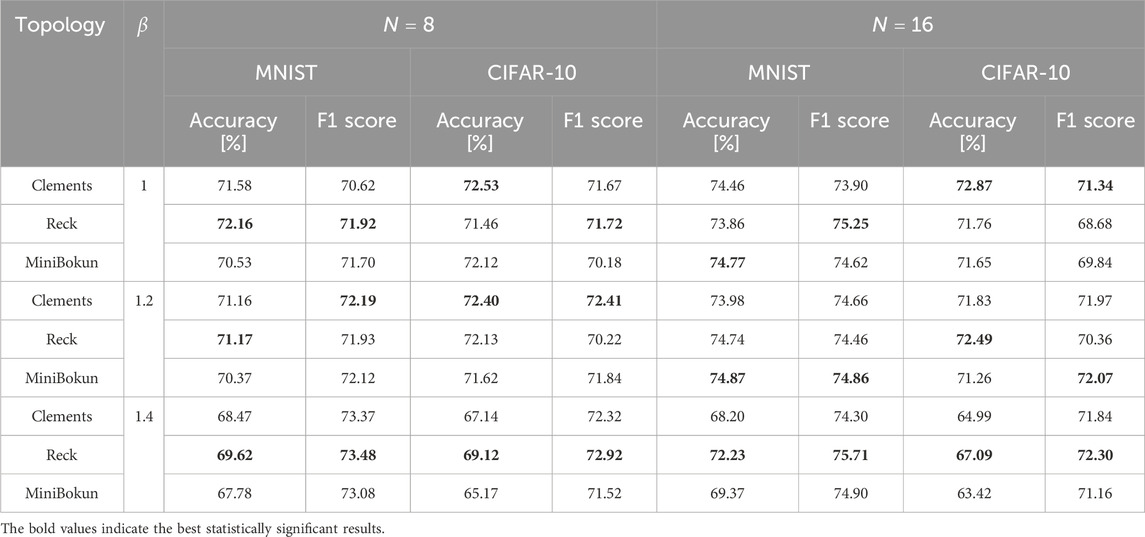
Based on the selected hyperparameters and optimization parameters, we summarized the accuracy and F1 score of all the models with different topologies in Table 2. The numbers labeled in bold are the best-performing topology in each category.

Table 2

Table 2. Test accuracy and F1 score of different topologies with different hyperparameters.

In the $N=8$ case, despite having fewer programmable phase shifters due to the small input size and the pre-training pruning performed, the MiniBokun mesh only experiences a 1.57% drop in accuracy and a 0.7% drop in F1 score on average compared with other meshes. Even with the slightly undermined learning ability, the performance gap between the best-performing model and MiniBokun is not large. MiniBokun mesh preserves a good balance in classifying both the positive and the negative classes of a dataset.

The performance gap between MiniBokun and the other meshes further closes when $N$ increases to 16. The average performance degradation drops to 1.42% in accuracy and 0.63% in F1 score. In certain cases, the MiniBokun mesh outperforms the other two in terms of both accuracy and F1 score.

4.3 Sensitivity analysis

Figure 7 shows the tolerance of investigated topologies towards phase shifter noise and propagation loss in optical components. The models subjected to the analysis are trained with an FN reduction factor $(\beta )$ of 1.2. The software-based FN reduction method does not alter the physical parameters of ONNs and hence does not impact the imperfection tolerance of an optical mesh with a certain topology and input size, thus the following observations remain consistent on models trained with $\beta =1$ or $\beta =1.4$.

Figure 7

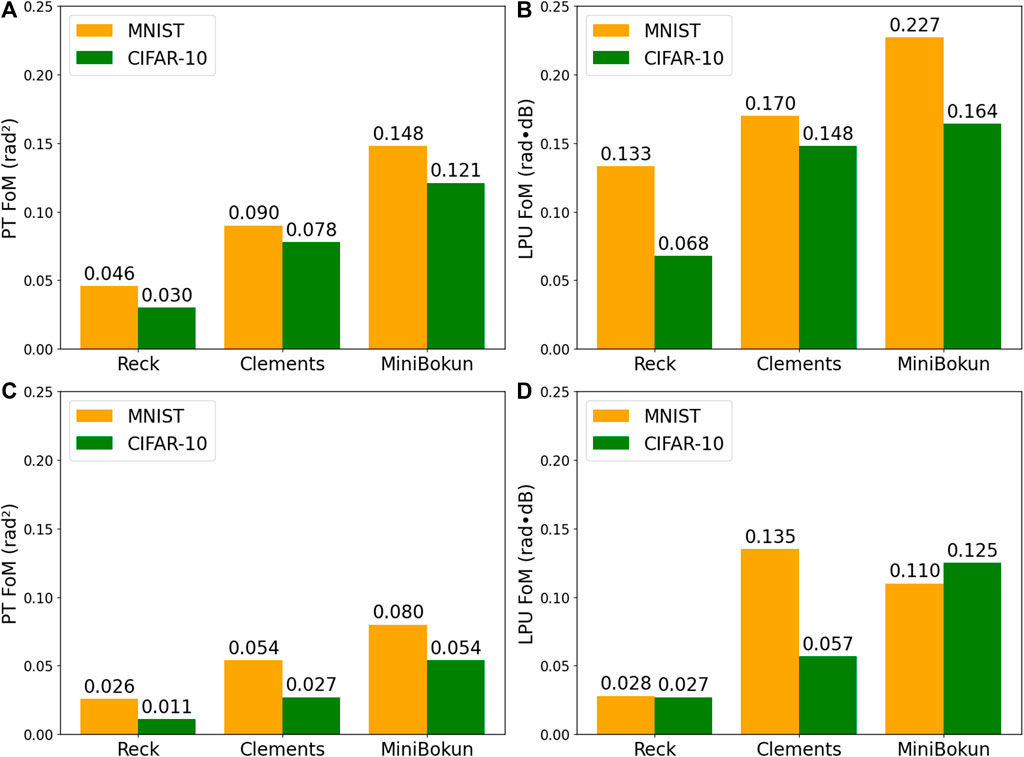
Figure 7. The FoMs of three network topologies: (A) $N=8$ ONNs, PT Plots, (B) $N=8$ ONNs, LPU Plots, (C) $N=16$ ONNs, PT Plots, (D) $N=16$ ONNs, LPU Plots.

In contrast to $8\times 8$ meshes, all $16\times 16$ meshes show weaker tolerance in both PT and LPU analysis due to the accumulation of phase error in longer optical paths. An average of 52.3% decrease in PT FoM area is observed over all topologies and both datasets when moving from $N=8$ to $N=16$, and a 49.4% decrease for LPU FoM.

In almost all cases except for the LPU analysis for $N=16$ network trained on the MNIST dataset, MiniBokun, thanks to the reduced number of components and balanced optical paths, shows greater tolerance of physical component imperfection. Overall, combining mesh sizes and datasets, MiniBokun’s average improvement to PT and LPU FoMs is 66.9% and 36.3% over Clements, respectively.

These improvements in the FoMs suggest that the increase in individual weight importance that comes naturally with a pruned neural network is negligible for topologies used in this study. The original network is over-parameterized enough for the pruning benefits to outweigh the errors imposed on the high-saliency phase shifter values.

4.4 Power, latency, and area estimations

Table 3 summarizes the power, latency, and area consumed by each topology with different sizes. Note that the estimation “conservative” and “aggressive” are subject to the overall power consumption. Both the ONN input and the phase value programming require 8-bit DACs (Texas Instruments, 2013) after PTQ.

Table 3

Table 3. Power, latency, and area estimations of different topologies and mesh sizes.

4.4.1 Power and latency consumption

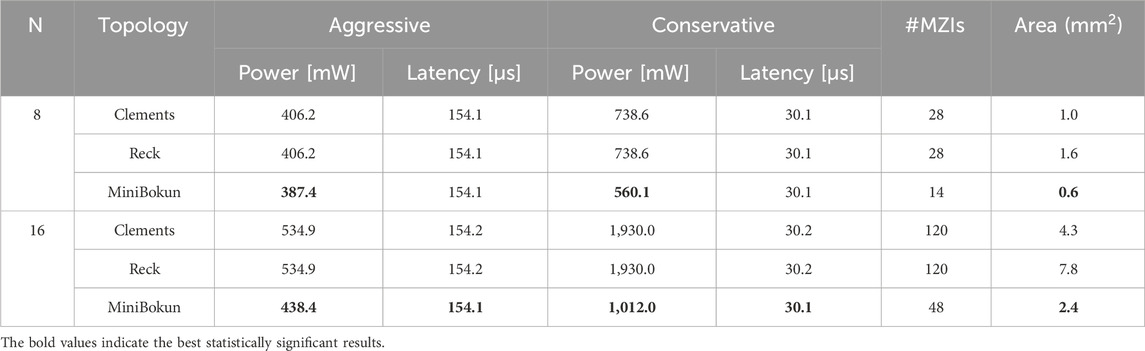
The pruned MiniBokun mesh has demonstrated a strong capability in reducing overall power consumption. Compared to the conventional Clements and Reck topology, the MiniBokun mesh saves 4.6% power in the aggressive case and 24.2% in the conservative case when $N=8$. These numbers further grow to 18.0% and 47.6% when $N$ increases to 16. On the other hand, the benefits of pruning in saving latency are insignificant, only up to 0.1 μs when $N=16$, as the latency of the slowest components (phase programming) is large per se and invariant to the topology.

If we take a closer look at the component-wise power and latency consumption, the phase value programming dominates both calculations. Assuming uniform phase distribution, the programming power is directly proportional to the number of MZIs in a mesh (Al-Qadasi et al., 2022). Without insulation (the “conservative” approach), the programming power can take up to 39.8% of the total power consumption in Reck and Clements topology when $N=8$ (as shown in Figure 8A), and this proportion continues to grow as the size of the optical mesh increases. Using the pruning strategy introduced in this work, we can effectively reduce the number of MZIs in the optical mesh by more than half. This subsequently relaxes the power requirement for programming the phase values and reduces the proportion it takes in the total power consumption, as shown in Figure 8B. The power savings by pruning becomes more evident when the optical meshes scale up, as indicated by the growing gap between the two lines in Figure 8C. Using insulated heaters with smaller $P_{\pi }$ (the “aggressive” approach) can effectively reduce the overall power consumption. However, this comes at a cost of $5\times$ more time spent on the programming stage.

Figure 8

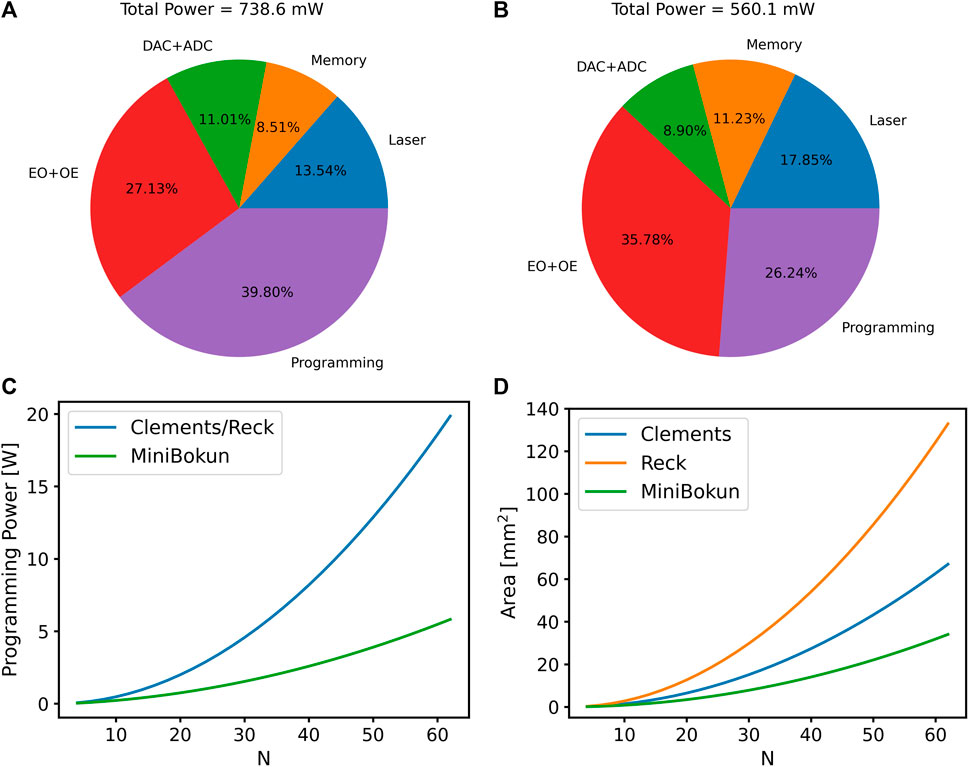
Figure 8. The power breakdown of (A) Clements/Reck topology, (B) the MiniBokun topology with $N=8$ and the “conservative” assumption. (C) The variation in programming power (Si-doped heater without insulation) with respect to the change in the optical mesh size. (D) The change in the layout area of optical meshes with respect to the change in the optical mesh size.

In the latency calculation, the pruned MiniBokun mesh effectively shortens the optical path length that light propagates through and lowers the number of memory read by reducing the number of phase values to be programmed. However, these savings ($\le 0.06$ μs in total) are comparatively negligible to the programming time itself ($[\mathrm{30,150}]$ μs). Disregarding the programming latency, the speed of the optical mesh computation is bottlenecked by the electrical ADCs and DAC. As the pruning technique does not alter the parameters of these devices, the speed of the MiniBokun mesh is still limited by them.

4.4.2 Layout area

The pruning strategy significantly reduces the area of the optical mesh by placing fewer MZIs horizontally along the optical path. As shown in Table 3, the MiniBokun mesh employs 50% fewer MZIs when $N=8$, and 60% fewer MZIs when $N=16$. Subsequently, the optical path length reduces from $2N-3$ in Reck mesh and $N$ in Clements mesh to $\frac{N}{2}+1$ in MiniBokun, bringing the total layout area down by at least 40%. As shown in Figure 8D, when the optical mesh size increases, the area of the MiniBokun mesh grows less rapidly than the other two topologies. When reaching the $N=64$ limit, it saves 73.6% and 48.4% layout area when compared to the Clements and Reck topologies.

For practical deployment, a typical smart lock uses a microcontroller comparable in size to an Arduino chip (Arduino, 2014), implying area constraints on the order of several square centimeters (Motwani et al., 2021). In contrast, modern smartphone processors, facing stricter area limitations, typically have a footprint of over 100 mm² (Yang et al., 2024). By comparison, our estimated mesh area is 2.4 mm² for the $16\times 16$ MiniBokun, which meets the area constraint of both of these target applications.

4.5 Limitations and future work

Imperfect operating conditions are obstacles to the deployment of proposed systems in real-world applications. In this work, we characterize the resilience of different topologies to two sources of error: optical loss and phase deviations. To achieve a more comprehensive evaluation of the model performance in the future, the model needs to take into account more factors, including the direct impact of fabrication non-uniformity (Mirza et al., 2022), input phase mismatch (Fang et al., 2019), and other sources of crosstalk (Shafiee et al., 2024).

The proposed pruning strategy is tested with well-established image classification datasets, and its performance is compared with existing optical mesh topologies. Although these datasets are sufficiently complex to provide insights into how the ONN trades off accuracy against power/area consumption, the comparisons lack real-world proximity. Future work will explore the use of datasets closer to the actual implementation of the binary optical trigger, for example, face recognition systems (Bong et al., 2018). These experiments can better reveal the benefits of the pruning strategy and the optical trigger structure itself when compared with existing digital electronic products.

Alternative pruning strategies, such as train-time or post-training pruning, consider parameter saliency before deciding which components to remove. However, further investigation is needed to assess these alternatives. Although these methods could offer comparable power savings while reducing the accuracy loss, they have the potential to create sparse network meshes with less clustered MZI removal and thus may provide limited area savings compared to the current pre-training pruning approach.

5 Conclusion

In this work, we propose a pre-training pruning strategy over established optical processor topology subject to the binary optical trigger structure. Motivated by the need for a low-power binary trigger to support machine learning at the edge of the Internet, the pruned structure, “MiniBokun” mesh, removed at least 50% of MZIs from a standard unitary topology and shortened the optical path length by half. The effect of pruning was tested with the binarized version of two benchmark datasets, MNIST and CIFAR-10, in which we only observed 1%–2% accuracy degradation and less than 1% drop in F1 score compared to the unpruned Clements and Reck topologies. In consideration of the practical deployment environment, the impact of limited voltage control precision and the robustness of ONNs toward component imperfections were investigated via weight quantization and a sensitivity study. The MiniBokun mesh showed $\ge 30\%$ and $\ge 60\%$ improvement in phase error and loss tolerance, respectively, while reducing the physical footprint of the mesh by $\ge 40\%$. With the removal of MZIs, an estimated $4.6\%-24.2\%$ power saving is achieved.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/Xoreus/neuroptica/tree/6c56736010dcfc271724b10a34c849fed349a598.

Author contributions

BZ: Conceptualization, Data curation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. XD: Data curation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing, Conceptualization. KR: Supervision, Writing–review and editing. BM: Supervision, Writing–review and editing. OL-L: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by Natural Science and Engineering Research Council of Canada (NSERC) through grants RGPIN-2018-05668 and RGPIN-2021-03480.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Qadasi, M., Chrostowski, L., Shastri, B., and Shekhar, S. (2022). Scaling up silicon photonic-based accelerators: challenges and opportunities. Apl. Photonics 7, 020902. doi:10.1063/5.0070992

CrossRef Full Text | Google Scholar

Arduino (2014). Nano 33 imu sensor. Monza, MB, Italy: Arduino s.r.l. [apparatus and software].

Google Scholar

Banerjee, S., Nikdast, M., Pasricha, S., and Chakrabarty, K. (2023). Pruning coherent integrated photonic neural networks. IEEE J. Sel. Top. Quantum Electron. 29, 1–13. doi:10.1109/JSTQE.2023.3242992

CrossRef Full Text | Google Scholar

Bartlett, B., Minkov, M., Hughes, T., and Williamson, I. A. D. (2019). Neuroptica: flexible simulation package for optical neural networks. Available at: https://github.com/fancompute/neuroptica.

Google Scholar

Bong, K., Choi, S., Kim, C., Han, D., and Yoo, H.-J. (2018). A low-power convolutional neural network face recognition processor and a cis integrated with always-on face detector. IEEE J. Solid-State Circuits 53, 115–123. doi:10.1109/JSSC.2017.2767705

CrossRef Full Text | Google Scholar

Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S., and Walsmley, I. A. (2016). Optimal design for universal multiport interferometers. Optica 3, 1460–1465. doi:10.1364/OPTICA.3.001460

CrossRef Full Text | Google Scholar

Delashmit, W., Missiles, L., and Manry, M. (2005). “Recent developments in multilayer perceptron neural networks,” in Proceedings of the seventh annual memphis area engineering and science conference, MAESC, 7, 33.

Google Scholar

Demirkiran, C., Eris, F., Wang, G., Elmhurst, J., Moore, N., Harris, N. C., et al. (2023). An electro-photonic system for accelerating deep neural networks. J. Emerg. Technol. Comput. Syst. 19, 1–31. doi:10.1145/3606949

CrossRef Full Text | Google Scholar

Deng, L. (2012). The mnist database of handwritten digit images for machine learning research [best of the web]. IEEE signal Process. Mag. 29, 141–142. doi:10.1109/msp.2012.2211477

CrossRef Full Text | Google Scholar

Fang, M. Y.-S., Manipatruni, S., Wierzynski, C., Khosrowshahi, A., and DeWeese, M. R. (2019). Design of optical neural networks with component imprecisions. Opt. express 27, 14009–14029. doi:10.1364/oe.27.014009

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, C., Gu, J., Zhu, H., Ying, Z., Zhao, Z., Pan, D. Z., et al. (2022). A compact butterfly-style silicon photonic–electronic neural chip for hardware-efficient deep learning. ACS Photonics 9, 3906–3916. doi:10.1021/acsphotonics.2c01188

CrossRef Full Text | Google Scholar

Gazivoda, M., and Bilas, V. (2022). Always-on sparse event wake-up detectors: a review. IEEE Sensors J. 22, 8313–8326. doi:10.1109/JSEN.2022.3162319

CrossRef Full Text | Google Scholar

Gu, J., Zhao, Z., Feng, C., Liu, M., Chen, R. T., and Pan, D. Z. (2020a). “Towards area-efficient optical neural networks: an fft-based architecture,” in 2020 25th asia and south pacific design automation conference (ASP-DAC), 476–481. doi:10.1109/ASP-DAC47756.2020.9045156

CrossRef Full Text | Google Scholar

Gu, J., Zhao, Z., Feng, C., Zhu, H., Chen, R. T., and Pan, D. Z. (2020b). “Roq: a noise-aware quantization scheme towards robust optical neural networks with low-bit controls,” in Date (IEEE), 1586–1589.

CrossRef Full Text | Google Scholar

Ip, E., Lau, A. P. T., Barros, D. J. F., and Kahn, J. M. (2008). Coherent detection in optical fiber systems. Opt. Express 16, 753–791. doi:10.1364/OE.16.000753

PubMed Abstract | CrossRef Full Text | Google Scholar

Krizhevsky, A., and Hinton, G. (2009). Learning multiple layers of features from tiny images.

Google Scholar

Masood, A., Pantouvaki, M., Lepage, G., Verheyen, P., Van Campenhout, J., Absil, P., et al. (2013). “Comparison of heater architectures for thermal control of silicon photonic circuits,” in 10th international conference on group IV photonics, 83–84.

Google Scholar

McMahon, P. L. (2023). The physics of optical computing. Nat. Rev. Phys. 5, 717–734. doi:10.1038/s42254-023-00645-5

CrossRef Full Text | Google Scholar

Miller, D. A. B. (2013). Self-configuring universal linear optical component [invited]. Phot. Res. 1, 1–15. doi:10.1364/PRJ.1.000001

CrossRef Full Text | Google Scholar

Mirza, A., Shafiee, A., Banerjee, S., Chakrabarty, K., Pasricha, S., and Nikdast, M. (2022). Characterization and optimization of coherent mzi-based nanophotonic neural networks under fabrication non-uniformity. IEEE Trans. Nanotechnol. 21, 763–771. doi:10.1109/TNANO.2022.3223915

CrossRef Full Text | Google Scholar

Mojaver, K. H. R., Zhao, B., Leung, E., Safaee, S. M. R., and Liboiron-Ladouceur, O. (2023). Addressing the programming challenges of practical interferometric mesh based optical processors. Opt. Express 31, 23851–23866. doi:10.1364/OE.489493

PubMed Abstract | CrossRef Full Text | Google Scholar

Motwani, Y., Seth, S., Dixit, D., Bagubali, A., and Rajesh, R. (2021). Multifactor door locking systems: a review. Mater. Today Proc. 46, 7973–7979. doi:10.1016/j.matpr.2021.02.708

CrossRef Full Text | Google Scholar

Mourgias-Alexandris, G., Moralis-Pegios, M., Tsakyridis, A., Simos, S., Dabos, G., Totovic, A., et al. (2022). Noise-resilient and high-speed deep learning with coherent silicon photonics. Nat. Commun. 13, 5572. doi:10.1038/s41467-022-33259-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagel, M., Fournarakis, M., Amjad, R. A., Bondarenko, Y., Van Baalen, M., and Blankevoort, T. (2021). A white paper on neural network quantization. arXiv preprint arXiv:2106.08295.

Google Scholar

Reck, M., Zeilinger, A., Bernstein, H., and Bertani, P. (1994). Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61. doi:10.1103/physrevlett.73.58

PubMed Abstract | CrossRef Full Text | Google Scholar

Shafiee, A., Banerjee, S., Chakrabarty, K., Pasricha, S., and Nikdast, M. (2024). “Analysis of optical loss and crosstalk noise in mzi-based coherent photonic neural networks,” in Journal of lightwave technology, 1–16.

Google Scholar

Shen, Y., Harris, N. C., Skirlo, S., Prabhu, M., Baehr-Jones, T., Hochberg, M., et al. (2017). Deep learning with coherent nanophotonic circuits. Nat. photonics 11, 441–446. doi:10.1038/nphoton.2017.93

CrossRef Full Text | Google Scholar

Shokraneh, F., Nezami, M. S., and Liboiron-Ladouceur, O. (2020). Theoretical and experimental analysis of a 4 × 4 reconfigurable MZI-based linear optical processor. J. Light. Technol. 38, 1258–1267. doi:10.1109/JLT.2020.2966949

CrossRef Full Text | Google Scholar

Texas Instruments (2013). DAC081S101 8-bit micro power digital-to-analog converter with rail-to-rail output. (Rev. C).

Google Scholar

Texas Instruments (2018). LMV7235 and LMV7239 75-ns, ultra low power, low voltage, rail-to-rail input comparator with open-drain and push-pull output. (Rev. O).

Google Scholar

Thoziyoor, S., Ahn, J. H., Monchiero, M., Brockman, J. B., and Jouppi, N. P. (2008). “A comprehensive memory modeling tool and its application to the design and analysis of future memory hierarchies,” in 2008 international symposium on computer architecture, 51–62. doi:10.1109/ISCA.2008.16

CrossRef Full Text | Google Scholar

Williamson, I. A. D., Hughes, T. W., Minkov, M., Bartlett, B., Pai, S., and Fan, S. (2020). Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Sel. Top. Quantum Electron. 26, 1–12. doi:10.1109/JSTQE.2019.2930455

CrossRef Full Text | Google Scholar

Yang, Z., Zhang, W., Ji, S., Zhou, P., and Jones, A. K. (2024). “Reducing smart phone environmental footprints with in-memory processing,” in International conference on hardware/software codesign and system synthesis (CODES+ISSS).

Google Scholar

Zhang, H., Thompson, J., Gu, M., Jiang, X. D., Cai, H., Liu, P. Y., et al. (2021). Efficient on-chip training of optical neural networks using genetic algorithm. ACS Photonics 8, 1662–1672. doi:10.1021/acsphotonics.1c00035

CrossRef Full Text | Google Scholar

Zhao, Z., Liu, D., Li, M., Ying, Z., Zhang, L., Xu, B., et al. (2019). “Hardware-software co-design of slimmed optical neural networks,” in Proceedings of the 24th asia and south pacific design automation conference (New York, NY, USA: Association for Computing Machinery), 705–710. ASPDAC ’19. doi:10.1145/3287624.3287720

CrossRef Full Text | Google Scholar