Analysis of the Solidification Process of Metal Alloys Under Microgravity Conditions

The solidification of metal alloys under low gravity conditions mainly deviates in four physical properties compared with samples solidified on earth. The coarseness of the structure and the solidification temperature increase. The latent heat and the solubility of alloying elements in solids are changed. Experimental results are presented and analyzed in order to find a unified theoretical understanding. The differences in the measured quantities between experiments performed in space and on earth were calculated and are presented in this article. Kinetic, thermodynamic, and thermophysical relations were used to analyze those values. The change in the melting point was found to be a result of an increase in the vibrational amplitude of the atoms in the solid. The increase in the latent heat results from an increase in the vibration of atoms in the liquid. The changes in the solubility are a result of an increase in heat of fusion of the alloying element. Furthermore, the increase in the coarseness of the structure is explained as an increase in the atom’s vibration. The analysis highlights that the atom’s vibration increases with decreasing gravity; especially, the amplitude will increase. The explanation for this is given by a decrease in the binding energy between the atoms with decreasing gravity. The decrease in binding energy for liquids is larger than for solids.

1 Introduction

Metals and their alloys mostly solidify by the formation of dendritic crystals. Since the early days, those crystals have been extensively investigated (Grignon, 1775). The aim to study the solidification of metals at reduced gravity was to analyze the effect of convection during the solidification process (Fredriksson, 1975). In the first rocket flight experiments about the solidification of metals, it was observed that the coarseness of the structure was changed with gravity (Carlberg et al., 1978). The researcher wanted to explain this as a result of a decrease in natural convection. This was used in the analysis of dendritic growth under reduced gravity by Glicksman et al. (1995) in their careful studies about dendritic growth in transparent materials under microgravity conditions. However, a number of differences were observed in those early experiments. One among many was changes in the solidification time (Carlberg et al., 1978; Carlberg, 1979). During that time, it was not easy to accept and explain. Later experiments showed that this is a result of a change in the latent heat (Dahlström, 1999; Fredriksson et al., 2001; Fredriksson, 2015). Furthermore, in the space experiment, a lower solidification undercooling and the composition in the crystals had changed despite the same experimental conditions.

During the Apollo missions, the astronauts performed some crystal growth experiments (Naumann and Herring, 1980). Those experiments showed that the crystals grown under microgravity conditions had a much lesser fraction of lattice defects. Experiments presented and performed in two PhD-thesis (Dahlström, 1999; Magnusson, 2006) investigated if the defects formed in the structure during solidification could explain the observed differences. However, it was found that the formation of lattice defects could not explain the difference in the experimental results between samples processed on earth and during microgravity conditions.

The truth must be found in the atomic structure in itself, such as a change in the binding energy or in the vibrations of the atoms. In this study, thermodynamic relations for phase transformations together with thermophysical relations were used, in order to see if such changings could explain the differences between the experimental results. An explanation is given related to the atom’s binding energies.

This article starts by presenting an overview of some earlier experimental results but only for the sake of theoretical analyze and more understandability. The results are from different microgravity opportunities selected from more than one hundred rocket or parabolic aircraft flights and two shuttle flights.

2 Experiments and Results

The structure formed during a solidification process is of most interest to describe and understand because it influences the properties of the material. Most metallic alloys solidify by the formation of dendrites, tree-like crystals. The structure can be characterized by its coarseness. Mostly, one selects a specific length in the structure to characterize the coarseness of the structure. For dendrites, such a length is the distance between the primary or secondary dendrite arms. Different laws are used to describe the formation of the coarseness as a tool to understand and design a material with the best structure. The laws used in analyzing a solidification process are heat flow and thermodynamic relations. Those laws are often used to analyze thermal analysis or unidirectional solidification experiments. During the thermal analysis, the heat of solidification and the solidification temperature, can be found. Mostly, it is interesting to measure how far below the equilibrium temperature the solidification starts and occurs. The composition of the crystals is also related to the solidification temperature by the phase diagram, and it will then be interesting to measure the concentration of the elements in the central part of dendrite arms as a function of the solidification temperature and relate the concentration to the phase diagram.

The theories presented in the literature (Kurz, 1989; Fredriksson and Åkerlind, 2012) about dendritic growth give a relation between growth rate and the growing dendrite tip radius squared. Secondary dendrite arms are formed behind the tip, and the distance between the secondary dendrite arms is directly related to the tip radius. One can simplify the relations and get the following equation:

$\mathit{V}= {\mathit{C}}_{\mathit{v}}/{\mathit{\lambda }}^{\mathbf{2}},(1)$

where $V$ is the growth rate of the dendrite tip, C_v is the constant, and $\lambda$ is the dendrite arm distance. The growth rate was not controlled in many of the experiments. Mostly, the cooling rate of the liquid prior to solidification was measured. The growth rate can, by a heat balance, be related to the cooling rate of the liquid, and instead of the growth rate one gets for experiments where the cooling rate was measured:

$\mathit{d}\mathit{T}/\mathit{d}\mathit{t}={\mathit{C}}_{\mathit{c}}/{\mathit{\lambda }}^{\mathbf{2}},(2)$

where $dT/dt$ is the cooling rate of the liquid prior to solidification, and $C_c$ is the constant, describing the relation between structure and cooling rate.

In the constants, C_v or $C_c$, a mass transfer coefficient in the liquid is included and is related to the diffusion coefficient. From the relation, one can then conclude that the smaller the diffusion rate is, the smaller will $\lambda$ be, and the finer will the structure be, or vice versa.

2.1 Texus 1

In the first rocket flight, one unidirectional experiment was performed (Carlberg et al., 1978) in one Al-6%Cu alloy and the structure was evaluated, the structure of growth rate was found, and the constant was evaluated using Eq. 1 and presented in Table 1 together with the reference result from the earth experiment.

TABLE 1

TABLE 1. Structure constant in the solidification rate experiment.

2.2 Gas

Another unidirectional experiment was performed in a Get Away Container in the shuttle. A special GAS container was constructed by the Swedish Space Cooperation. Four samples of lead-tin alloys were processed in a special graphite mold furnace for slowly directional solidification (Fredriksson and Wallin, 1993). Figure 1 shows the samples and graphite mold processed in the shuttle flight. The aim was to investigate the effect of the natural convection on the macro segregation (Shahani et al., 1992) and, at the same time, the structure coarseness was investigated. The solidification rate was evaluated from temperature measurements at the start and end of solidification. The sample structure was analyzed, and the dendrite arm space was evaluated (Figure 2). The characteristic constant was calculated, and the result is presented in Table 1. Also, in this case, the structure was coarser in the sample processed under microgravity conditions. It is to be noted that the relations between samples processed in the shuttle flights are close to the values found in the rocket flights and will be presented later.

FIGURE 1

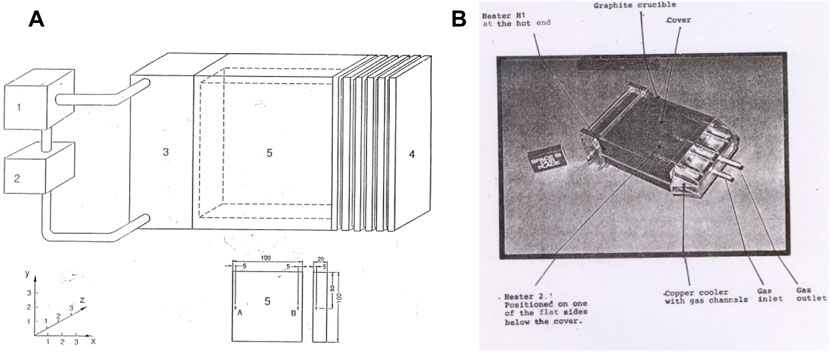
FIGURE 1. Sample holder for the Sn-Pb experiment in a GAS container processed in a shuttle flight. (A) Principal sketch, cooler to the left and heater to the right. Sample size marked with 5. (B) Flight holder (Fredriksson and Wallin, 1993).

FIGURE 2

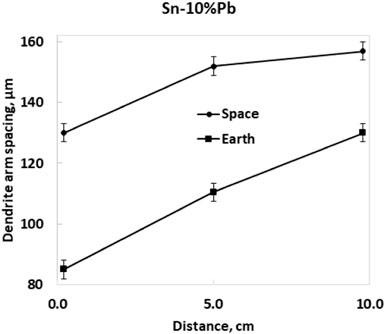
FIGURE 2. Dendrite arm space in the Sn-10% Pb sample (Fredriksson and Wallin, 1993).

2.3 Space Lab

One experiment with an Al-40%Sn alloy was performed in the isothermal heating facility (Shapland and Rycroft, 1984) in Space Lab (Figure 3). In the furnace, the alloy was heated and melted and then solidified under controlled cooling conditions. The cooling rate of the liquid prior to solidification was 0.045 °C/s. The structure has earlier been presented by Fredriksson (2015) and shows that the dendrite structure is coarser in the samples processed under microgravity conditions. The dendrite arm space was evaluated, and the result is presented as cooling rate multiplied by dendrite arm space squared according to Eq. (2). The result is presented in Table 2.

FIGURE 3

FIGURE 3. (A) Sample holder. (B) Sample processed in the isothermal heating facility in Space Lab.

TABLE 2

TABLE 2. Structure constant in the cooling rate experiment.

The difference in coarseness is described by factor 1.4, which is close to the factor found in unidirectional solidified samples (Table 1). Microprobe measurements of the composition in the central part of the dendrite arms were also performed. The average composition was found to be 0.090 wt% in the sample processed in space and 0.081 wt% in the samples processed on earth. It is interesting to note that the composition is 10% larger in the samples processed in space.

2.4 Parabolic Flights

If using the shuttle or rocket flights to perform experiments, the access time required is normally very long. The observations presented earlier need a number of experiments to be verified. This was possible to perform during parabolic aircraft flights. European Space Agency (ESA) has given those opportunities.

At the first Texus flight, a special type of mirror furnace was developed for thermal analysis of solidification (Figure 4) (Carlberg et al., 1978). The solidification process in those furnaces is given by the temperature–time curve. To analyze the solidification process, the cooling rate prior to and after the solidification was evaluated and related to the solidification time. In the first Texus flight, a thermal analysis of a eutectic AlSi alloy was performed, and surprisingly, it was found that the solidification time was 20% longer in the samples processed under microgravity conditions despite the same cooling rate prior to solidification (Figure 5). A heat balance between the cooling rate and solidification time gives that the latent heat should be larger in the samples processed under microgravity conditions.

FIGURE 4

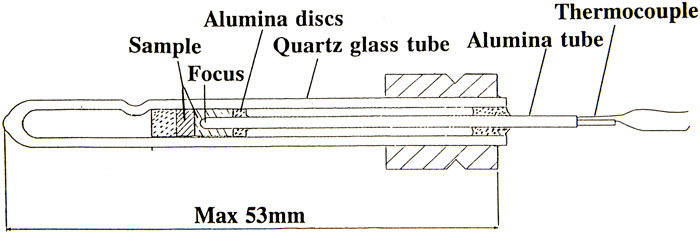
FIGURE 4. Mirror furnace (Lockowandt et al. 1992).

FIGURE 5

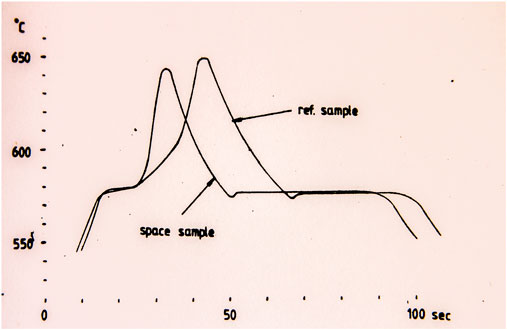
FIGURE 5. Temperature time curve of an Al-Si alloy (Carlberg, 1979; Fredriksson, 2015).

In this case, the mirror furnace, Figure 4, was reconstructed (Lockowandt et al., 1992) and used for thermal analysis experiments, and several hundred experiments were performed.

In the parabolic flights, a number of experiments with pure Al, Sn, and Pb were performed. In this case, the coarseness of the structure could not be evaluated. By analyzing the solidification time, the changings in latent heat could be indicated and verified from the Texus experiments, and an average value from several experiments could be presented. The average cooling rate was 50 °C/s. In some of the experiments, the cooling was interrupted after the solidification, and the samples were re-melted during the microgravity conditions.

The solidification temperature and the melting temperature were evaluated and presented as a difference between the measured value and the equilibrium value, which is defined as undercooling temperature. The results for pure Al are presented in Figure 6. The results show that the undercooling is lower in the samples solidified under microgravity conditions. Table 3 shows an average value of those temperatures for the three pure elements of Al, Sn, and Pb.

FIGURE 6

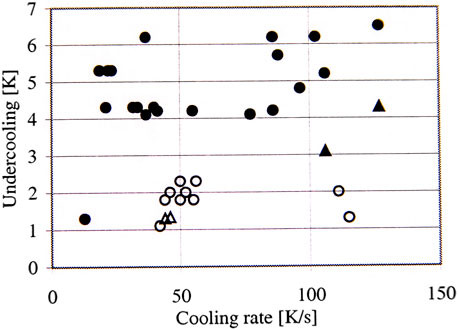
FIGURE 6. Growth undercooling in pure Al (Dahlström, 1999; Fredriksson et al., 2001).

TABLE 3

TABLE 3. Solidification undercooling and solidification latent heat for pure Sn, Pb, and Al.

A large number of Al base alloys were investigated at cooling rates around 50°C/s. In all samples, the growth undercooling was lower in the samples processed under microgravity conditions than in the samples processed on earth, and the latent heat also increased.

The coarseness of the structure followed the same observations as in the other experiments, and the result is presented in Table 4.

TABLE 4

TABLE 4. Composition in the solid.

The concentration in the central part of a dendrite arm was measured by microprobe measurements. It was found that the concentration in the dendrite arm was higher in the samples processed under microgravity conditions (Fredriksson et al., 2001). This was also observed in the Space Lab experiments. The result is presented in Table 4. The table shows that the value was 35% higher in alloys with 2 w-% Cu, 15% higher in alloys with 6w-% Cu, and 2% Si. It was10% higher in alloys with 40 w-% Sn.

3 Theoretical Analysis

The experimental results show that four main properties change when experiments are performed under microgravity conditions compared to experiments performed on earth. The four properties are as follows: structure coarseness, solidification temperature, latent heat, and composition of the dendrites. Those four properties are to be analyzed by kinetic or thermodynamic relations in order to find an explanation for the observed differences. Thermodynamic relations mostly describe equilibrium conditions. Here, the experiments are performed under nonequilibrium conditions. However, in this analysis, only the differences between the result given on earth with the one under microgravity conditions are discussed.

3.1 Melting Point

The solidification temperature increased with decreasing gravity. This can be explained in two different ways. The first is that the kinetics during the growth gives a lower undercooling as a result of a higher diffusion rate, as discussed earlier. The other one is that the melting temperature increases with decreasing gravity. The other observed experimental differences support the observations that the melting point is changed as a result of the gravity force changes, and this will be analyzed next.

The first one to discuss and propose a model to relate the melting point of different species to the frequency and amplitude of the atoms was Lindemann (1910). His model has then been extended and used to describe the melting points of different species over the years. The most well-known analyses are the ones by Gilvarry (1956), Grimvsall (1999), and Wallace (1991). The model says that when the amplitude of the vibrations supersedes a certain value, the bonds between the atoms are broken. The value of the amplitude has been evaluated and is in the range of 10–20 percent of the atomic distances and is not the same for different species.

Lindemann’s original idea was not to describe the melting points for different species as he wanted to discuss the vibrations of the specie with the help of the measured melting points. Here, those ideas have been used to compare the change of the amplitudes with the gravity. The relation given by Lindemann has been used and is given as follows:

${\mathit{T}}_{\mathit{m}}=\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}\mathit{m}{\mathit{C}}_{\mathit{L}}{\mathit{a}}^{\mathbf{2}}/{\mathit{k}}_{\mathit{B}},(3)$

where

$T_m$ is melting point, $m$ is mass of the specie, $a$ is atomic diameter, $k_B$ is Boltzmann’s constant, and $C_L$ is Lindemann’s constant.

The difference between earth results and microgravity results is given as follows:

${\mathit{T}}_{\mathit{m}\mathit{g}}-{\mathit{T}}_{\mathit{e}}=\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}\mathit{m}{\mathit{a}}^{\mathbf{2}}{\mathit{C}}_{\mathit{e}}\left({\mathit{C}}_{\mathit{m}\mathit{g}}/{\mathit{C}}_{\mathit{e}}-\mathbf{1}\right).(4)$

The subscripts $mg$ and $e$ refer to microgravity and earth conditions, respectively.

Since the melting temperature increases with the decreasing gravity, one can conclude that the maximum vibrational energy will increase in the species with decreasing gravity. Lindemann’s constant is directly related to the vibrations of the atoms, and by comparing with measured values of the solidification and melting temperature, our values give an increase of the atomic amplitude of around 0.5% or somewhat lesser.

3.2 Latent Heat

The experiments showed that the latent heat evolved in the samples processed under microgravity conditions is larger than in the samples processed on earth. At the melting point, one has an equilibrium between solid and liquid, and the enthalpy of fusion is equal to the entropy of fusion. In the experiments presented earlier, there is no equilibrium. However, in the following analysis, it is assumed that the values measured show the deviation from the equilibrium between the conditions under microgravity and on earth.

Lindemann’s theory describes the necessary changes of the atom’s movement in the solid to get the specie melted. The heat of fusion added during melting describes the change of the atom’s energy or their increase in vibrations and translation. There is a change in the kinetic and in the potential energy; both are a function of the amplitude and the frequency multiplied and squared. The following relation describes the changings in these relations:

$\mathbf{\Delta }{\mathit{H}}_{\mathit{m}\mathit{g}}^{\mathit{L}\to \mathit{S}}/\mathbf{\Delta }{\mathit{H}}_{\mathit{e}}^{\mathit{L}\to \mathit{S}}={\left({\mathit{v}}_{\mathit{m}\mathit{g}}\times {\mathit{\alpha }}_{\mathit{m}\mathit{g}}\right)}^{\mathbf{2}}\mathrm{/}{\left({\mathit{v}}_{\mathit{e}}\times {\mathit{\alpha }}_{\mathit{e}}\right)}^{\mathbf{2}},(5)$

where $\Delta H^{L\to S}$ is the measured value of heat of fusion, $v$ is the atomic frequency, $\alpha$ is the atoms amplitude, and the subscripts $mg$ and $e$ refer to microgravity condition and on earth, respectively. By using the measured values of heat of fusion and the solidification temperature, Table 2, one finds that the enthalpic of melting increases by around 10%, But the vibration time and the amplitude increase by around 4%. This is close to the same as the amplitude change in the solid. It is most likely that this increase is concentrated to the increase in the amplitude. Again, one can conclude that the binding force will decrease with decreasing gravity.

A similar conclusion can be found by using Richard’s rule. It is well known that the heat of fusion for metals follows Richard’s rule (Gaskell, 1981), which says that $\Delta H^{L\to S}$ for metals is equal to $R_x{T}_m$, where $R$ is the molar gas constant. $R_x{T}_m$ describes the entropy of fusion for pure metals. The heat capacity at high temperature is described by 3RT and is related to an increase in the vibrational energy with temperature. The conclusion is that the vibration is increased by RT at the melting of a metal. Defining RT as the entropy of fusion, one can calculate the entropy difference of melting metals at low gravity compared with melting on earth and get the following:

$\mathit{R}{\mathit{T}}_{\mathit{m}\mathit{g}}-\mathit{R}{\mathit{T}}_{\mathit{e}}=\mathit{R}\times {\mathit{T}}_{\mathit{e}}\left({\mathit{T}}_{\mathit{m}\mathit{g}}/{\mathit{T}}_{\mathit{e}}-\mathbf{1}\right),(6)$

where $R$ is gas constant, $T$ is solidification temperature for samples, and the subscripts $mg$ and $e$ refer to microgravity condition and on earth, respectively. The relation gives an increase in the vibrational energy of less than a half percent, which is close to the same as the one given by Lindemann’s relation and the heat of fusion experiments.

3.3 Partition Coefficient

The growth undercooling is related to the composition in the primary dendrite arm by the phase diagram. With the type of phase diagram relevant to the alloys investigated, one could expect a lower concentration in the dendrite arms with lower growth undercooling (Kurz, 1989). The experimental results showed that the growth undercooling was smaller in the space samples than in the samples processed on earth. One could thus expect a lower content of the alloying element in the dendrite arms in the samples processed under microgravity conditions. However, the opposite is observed (Table 4).

A chemical potentials analysis of the alloying element relates the solubility in the solid to the composition in the liquid and will be described by the following relation.

$\mathit{ln}{\mathit{x}}_{\mathit{S}}/{\mathit{x}}_{\mathit{L}}=\left(\left(-\mathbf{\Delta }{\mathit{H}}_{\mathit{A}\mathbf{1}}\right)-\mathit{T}\mathbf{\Delta }\mathit{S}\right)/\mathit{R}\mathit{T},(7)$

where

$x_S$ is the composition in the solid in equilibrium with liquid, $x_L$ the is composition in the liquid in equilibrium with solid, $\Delta H_{A1}$ is the heat of fusion of the alloying and the difference in the heat of mixing between the solid and liquid in the standard state under consideration, and $\Delta S$ is the entropy of fusion of the alloying elements in the given standard state and the difference in the entropy of mixing between the solid and liquid is included.

In this case, the analysis is based on the differences in the experimental data between the earth experiments and the microgravity ones. The liquid composition is the same in the two cases, the entropy is equal to R times temperature, and a constant, C_a1, is assumed to be constant. One gets the following relation:

${\mathit{x}}_{\mathit{m}\mathit{g}}/{\mathit{x}}_{\mathit{e}}=\mathit{exp}{\mathit{C}}_{\mathit{A}\mathbf{1}}\left(\left({\mathit{T}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{c}\mathit{e}}-{\mathit{T}}_{\mathit{e}\mathit{a}\mathit{r}\mathit{t}\mathit{h}}\right)/\mathit{T}\right)\mathit{exp}-\left(\mathbf{\Delta }{\mathit{H}}_{\mathit{e}\mathit{a}\mathit{r}\mathit{t}\mathit{h}}-\mathbf{\Delta }{\mathit{H}}_{\mathit{s}\mathit{p}\mathit{a}\mathit{c}\mathit{e}}\right)/\mathit{R}\mathit{T}.(\mathrm{7a})$

The first exponential term on the right-hand side will be close to one. The relation gives that the enthalpy of solidification for the alloying element is larger during solidification under microgravity conditions as for the base element. This supports the earlier conclusion that the vibrational energy will increase in all elements in the alloys.

3.4 Dendrite Coarseness

The constant C_v in Eq. (1) relates the difference in the coarseness of the structure to the experimental conditions and can be used to describe the difference in diffusion rate between the experiments performed on earth to the ones performed under microgravity conditions.

Very careful measurements of the diffusion rate in metal melts under microgravity conditions were performed during the Space Lab missions by Frohberg et al. (1987) and by NASA and presented in articles by Smith et al. (2000). The result shows that the diffusion rate is lower under microgravity conditions. One can then expect a finer crystal structure in the space processed samples than in the earth processed ones, but the opposite is observed. The diffusion process in the liquid is very complex and is not well understood. The simplest description is by a ring mechanism where the atoms move in small steps γ, and according to Swalin (1959), one gets the following:

$\mathit{D}={\mathit{D}}^{°}{\mathit{\gamma }}^{\mathbf{2}}\mathit{v},(8)$

where ${\mathit{D}}^{°}$ is constant, $\gamma$ is the atomic jump distance, and $v$ is the atomic frequency.

The thermodynamic analysis made earlier indicates that the frequencies increase with decreasing gravity. This then supports the observations that decrease in gravity increase the structure coarseness. Gamma is a jump distance. This is most probably related to the vibration amplitude which was observed to increase and it is also depending on the temperature which is observed to be squared by Frohberg et al. (1987). The experiments show that the diffusion rate is larger than the one on earth. This is against the observation by Frohberg et al. (1987) and Smith (2000). However, there is a strong indication from their experiments that one has an effect on the size of the test samples. The larger the size, the faster is the diffusion due to convection on earth.

4 Discussion

The analysis of the experimental results gives a change in the atomic vibrations and amplitude with limited percentages. However, it is difficult to find an alternative explanation, and the result of the analysis is supported by the fact that several different experimental results such as the differences in solidification temperature, latent heat, crystal composition, and crystal morphology between earth and microgravity are explained by these changings.

According to a Leonard-Jones treatment of the interaction between atoms, one finds a relation between a change in the atomic amplitude and the binding energy between atoms. An increase in the amplitude reflects a decrease in the binding energy. Thus, one can conclude that the binding energy decreases with decreasing gravity, and it is more for the liquid than for the solid. The first proposed experiments in this field were performed at the Apollo missions. If these results had been known at that time, one could, for instance, instead propose to look at evaporation of metals or spitting up of compounds but that might be for the future.

The conclusion about the binding energy decrease with the gravity has an interesting astronomic point of view and can lead to a new analysis of formation of different compounds in the space atmosphere. In those cases, one often uses theories based on a changing in the frequencies of the species but this study indicate that one should concentrate the studies more on energy balances.

An increase in the amplitude also gives a change in the molar volume, especially of the melt. Paradisa et al. (2008) measured the molar volume of liquid gold but did not get any difference between the measurements in space compared with the one made on earth. However, the results presented here gave a change in the amplitude, and this is in the range of the experimental faults. This type of measurement should be made on elements with lower binding energy where the effect of gravity is large.

According to Einstein’s general theory of gravity that light gets a redshift with increasing gravity, the gravitational redshift. Einstein also derived a law to describe the heat capacity of species. He assumed that the atomic vibration was quantified and followed the black body radiation law. By taking this into consideration, the assumption made in this study is valid that one could expect atomic vibration to increase with decreasing gravity. This has later been confirmed by atomic clock studies, where it is shown that the atomic vibrations increase with decreasing gravity. The studies of crystal frequencies also show, in the range of gravity force analyzed, very small changings in the frequencies and support the small variations found in this study. The measurements and the analysis presented in this article support that the atomic redshift is more generally and of importance at phase transformations.

The above-stated analysis might inspire further investigations and new discussions where temperature measurements together with heat balances will be the main tool. Within variable gravity force, the effect on the atomic structure is very small. There are some studies with X-ray by Matiesen (Murphy et al., 2016), but those experiments are similar to the Glicksmans experiments, but it was for metals. No similar experiments as the one presented here have been conducted over the years. Studies about the changes in phase transformations or the formation of compounds with gravity variations could open up new ways for research.

One could also add that we never expected to consider the effect of gravity the way used to explain the experimental results. If that had been our aim, we should have been much more careful in our analysis of the measured gravity vector. However, the experimental results are difficult to explain without assuming the atomic vibration amplitude increases with decreasing gravity and the atomic vibrations increase. Due to the isolation during the Corona pandemic, the necessary time was found to perform an analysis like this.

5 Concluding Remarks

The first experiments performed on the solidification process of metals under microgravity conditions gave some very confusing results. One observed a lower growth undercooling, a coarser dendrite structure, a higher alloying content in the dendrite arms and a higher value on the latent heat. Those observations were later confirmed by a series of experiments under many different conditions. Different theoretical models have been used over the years to explain these observations, but no explanation has been found. A new way has been chosen in this study. The difference in the measured values is explained by an increase in the materials’ vibration amplitude which is explained by a decrease in the binding energy between the atoms. This would be interesting to investigate further on in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials; further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication. The author has inititiated all the space experiments, and has been the supervisor to all the PhD students.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

A large number of researchers have been involved in those projects. Swedish Space Cooperation has constructed all the equipment and has also been responsible for the different flight missions. Among others, one finds Sven Grahn, Lars Stenmark, Kenneth Löth, Christian Lockowandt, and Sven Walin. The author is grateful to the company and their employers. They are also very grateful to all their PhD students over the years. The author thank Torbjörn Carlberg, Johan Dahlström, Jonas Fjellstedt, and Lena Magnussson for their work with the microgravity experiments and Abel Tadesse with the final manuscript presented here. They also express their gratitude to all personnel at NASA and ESA to do the flights.

References

Carlberg, T. (1979). Sloification of Composite Materials on Earth and Under Microgravity. (Stockholm: KTH, Casting of Metals). PhD thesis.

Carlberg, T., Fredriksson, H., Sunnerkranz, P., Grahn, S., and Stenmark, L. (1978). The Swedish Texas Experiment, a Technical Description and Some Preliminary Results. Paris: ESA Publication, 325–338. SP-135.

Google Scholar

Dahlström, J. (1999). On the Solidification of Al Alloys during Microgravity (Stockholm: KTH, Materials Processing). PhD thesis.

Fredriksson, H., and Åkerlind, U. (2012). Solidification and Crystallization Processing in Metals and Alloys. Chichester UK: J. Wiley and sons.

Google Scholar

Fredriksson, H., Dahlström, J., and Fjellstedt, J. (2001). “On the Solidification of Aluminium-Base Alloys under Different Gravity Conditions,” in International Conference on Solidification Science and Processing Bangalore. Bangalore, India.

Google Scholar

Fredriksson, H. (2015). “On the Solidification of Metal Alloys during Microgravity Conditions,” in Advances in the Science and Engineering of Casting Solidification. Editors L. Nastac, A. S. Sabau, H. Fredriksson, D. M. Maijer, and A. Sabau (TMS/Wiley).

CrossRef Full Text | Google Scholar

Fredriksson, H. (1975). Possible Dendrite Growth and Segragation Phenomena during Solidification of Alloys in Space. Paris: ESA Publication, 292–299. SP-114.

Google Scholar

Fredriksson, H., and Wallin, S. (1993). The Effect of Gravity in the Solidification Process inPb-Sn and Sn-Pb Alloys in AAIIA Conference (Reno, United States: NASA.

Frohberg, G., Kraatz, K. H., and Wever, H. (1987). Diffusion and Transport Phenomena in Liquids under Microgravity. Paris: ESA Publication, 585–591. SP-256.

Google Scholar

Gaskell, D. R. (1981). Metallurgical Thermodynamics. Bristol: Taylor & Francis.

Google Scholar

Gilvarry, J. J. (1956). The Lindemann and Grüneisen Laws. Phys. Rev. 102, 308–316. doi:10.1103/physrev.102.308

CrossRef Full Text | Google Scholar

Glicksman, M. E., Koss, M. B., Bushnell, L. T., Lacombe, J. C., and Winsa, E. A. (1995). Dendritic Growth of Succinonitrile in Terrestrial and Microgravity Conditions as a Test of Theory. ISIJ Int. 35, 604–610. doi:10.2355/isijinternational.35.604

CrossRef Full Text | Google Scholar

Grignon, M. (1775). Memoires de Physique sur Làrt de Fabriquerde de Fer. Paris.

Google Scholar

Grimvsall, G. (1999). Thermophysical Properties of Materials. North Holland: Amsterdam.

Google Scholar

Kurz, W. (1989). Fundamentals of Solidification. Switzerland: Trans. Tech. Publ.

Google Scholar

Lindemann, F. A. (1910). Yber die Berechnung molekulaer Eigenfrequenzen. Phys. Z. 11 (14), 609–614.

Google Scholar

Lockowandt, C., Löth, K., Ekbom, L., Eliasson, A., and Jarfors, A. (1992). The Seventh European Symposium on Materials and Fluid Science in Microgravity. Paris: ESA, 383–385. SP-333.

Google Scholar

Magnusson, L. (2006). On the Nucleation and Inoculation of Metals (Stockholm: KTH, Materials Processing). PhD thesis.

Murphy, A. G., Mathiesen, R. H., Houltz, Y., Li, J., Lockowandt, C., Henriksson, K., et al. (2016). Direct Observation of Spatially Isothermal Equiaxed Solidification of an Al-Cu Alloy in Microgravity on Board the MASER 13 Sounding Rocket. J. Cryst. Growth 454, 96–104. doi:10.1016/j.jcrysgro.2016.08.054

CrossRef Full Text | Google Scholar

Naumann, R. J., and Herring, H. W. (1980). Materials Processing in Space: Early Experiements. Alabama: NASA. Sp-441.

Google Scholar

Paradisa, P., Ishikawaa, T., and Koikeb, N. (2008). Density of Liquid Gold Measured by a Non-contact Technique. Gold Bull. 41, 242–245. doi:10.1007/bf03214876

CrossRef Full Text | Google Scholar

Shahani, H., Amberg, G., and Fredriksson, H. (1992). On the Formation of Macrosegregations in. Metall. Mater Trans. A 23, 2301–2311. doi:10.1007/bf02646023

CrossRef Full Text | Google Scholar

Shapland, D., and Rycroft, M. (1984). Spacelab. Cambridge: Cambridge University Press.

Google Scholar

Smith, R. W. (2000). “The Influence on G-Ji. Critter on the Measurement of Solute Diffusion in Dilute Liquid Metals in a Low Earth Orbiting Laboratory,” in Proc. Int Conference Space bound (Toronto: Canadian Space Agency).

Google Scholar

Swalin, R. A. (1959). On the theory of self-diffusion in liquid metals Sur la theorie de l'auto-diffusion dans les metaux liquides Über die theorie der selbstdiffusion in flüssigen metallen. Acta Met. 7 (11), 736–740. doi:10.1016/0001-6160(59)90179-8

CrossRef Full Text | Google Scholar

Wallace, D. C. (1991). Melting of Elements. Math. Phys. Sci. 433, 631–661.

Google Scholar