- 1Department of Orthopaedic Surgery, The Third Hospital of Hebei Medical University, Shijiazhuang, China
- 2Key Laboratory of Biomechanics of Hebei Province, Shijiazhuang, Hebei, China
- 3Cangzhou People's Hospital, Cangzhou City, Hebei, China
- 4NHC Key Laboratory of Intelligent Orthopaedic Equipment (The Third Hospital of Hebei Medical University), Shijiazhuang, Hebei, China
Objective: The purpose of this study was to evaluate the effect of residual varus/valgus deformity on the mechanical characteristics of the meniscus and cartilage after tibial shaft fracture.
Methods: A finite element model of the lower extremity of a healthy volunteer was constructed from CT and MRI images. The upper and middle tibial fracture models were modified to produce 3°, 5°, and 10° tibial varus/valgus models. For model validation, a patient-specific model with a 10° tibial varus deformity was constructed and simulated under the same boundary conditions.
Results: The contact area and maximum stress of the normal and modified deformity models were similar to those of the reported studies and a patient-specific model. The maximum stress, contact area, and contact force of the medial tibial cartilage in a normal neutral position were 0.64 MPa, 247.52 mm2, and 221.77 N, respectively, while those of the lateral tibial cartilage were 0.76 MPa, 196.25 mm2, and 146.12 N, respectively. From 10° of valgus to 10° of varus, the contact force, contact area, and maximum stress values of the medial tibial cartilage increased, and those of the lateral tibial cartilage gradually decreased. The maximum stress, contact area, and contact force of the medial tibial cartilage in the normal neutral position were 3.24 MPa, 110.91 mm2, and 62.84 N, respectively, while those of the lateral tibial cartilage were 3.45 MPa, 135.83 mm2, and 67.62 N, respectively. The maximum stress of the medial tibial subchondral bone in a normal neutral position was 1.47 MPa, while that of the lateral was 0.65 MPa. The variation trend of the medial/lateral meniscus and subchondral bone was consistent with that of the tibial plateau cartilage in terms of maximum stress, contact area, and contact force.
Conclusion: The residual varus/valgus deformity of the tibia has a significant impact on the mechanical loads exerted on the knee joint. This study provides a mechanical basis and references for the clinical evaluation of tibial fracture reduction and osteotomy for tibial deformity.
Introduction
Tibial fractures represent the most prevalent long bone fracture in clinical practice, accounting for approximately 2% of all cases of fractures (1–3). Tibial shaft fractures are frequently precipitated by high-energy trauma, resulting in extensive tissue damage. A variety of surgical techniques were proposed for the management of tibial fractures, including the use of intramedullary nails, plate fixation, and external fixation (4, 5). However, postoperative complications compromised the surgical outcomes, with reported non-union rates of up to 10% and malunion rates of up to 49% (5–7). Literature review showed that 29%–49% of tibial shaft fractures have an angle of greater than 5° after operation (6, 8). The residual tibial deformities undoubtedly change the normal load transmission of the lower limb, increasing the risk of knee pain and traumatic arthritis (TA) (9, 10). In addition to directly altering the biomechanical properties of the knee resulting in tissue damage, deformity healing can indirectly lead to muscle fatigue, ligament strains, and joint damage by affecting the tension balance in the surrounding muscles and ligaments (11, 12). Weinberg et al. (9) inspected 2,898 cadaveric skeletons and found that the specimens with coronal deformity greater than 5° had an increased incidence of knee arthritis.
A comprehensive grasp of the etiology of TA and an accurate assessment of the biomechanical impact of tibial deformity on the knee are essential prerequisites for the surgical management of tibial shaft fractures and the prevention of traumatic arthritis. However, the current literature is largely limited by epidemiological observational studies, as well as therapeutic studies, and there are few studies on the biomechanics of tibial deformity (13–15). Moreover, defining the deformity parameters largely (10°, 20°, 30°) may be a disadvantage in biomechanical study, as surgical treatment rarely leaves such a large deformity angle. Additionally, while the contact stress and contact area of the knee joint can be obtained in a biomechanical study, the above indicators are challenging to accurately measure the load condition of the knee joint.
Given the above, this study established a finite element model of the lower limb consisting of bone, meniscus, cartilage, and ligaments. The main purposes of this study are to (1) establish a finite element model of tibial varus/valgus deformities and (2) analyze the effect of residual varus or valgus deformity on the contact force, contact area, and stress distribution of the medial and lateral compartments of the knee joint after the middle and upper tibial shaft fracture.
Materials and methods
Finite element models
The experiments of this study were performed in accordance with all relevant guidelines and regulations and with the approval of the Institutional Review Board of The Third Hospital of Hebei Medical University. The use of these CT data in this investigation and the experimental protocol of the study were approved by the Third Hospital of Hebei Medical University. Written informed consent was obtained from the volunteers prior to the study commencement.
A healthy male volunteer (age, 30 years; height, 170 cm; body mass, 60 kg) and a male patient (age, 45 years; height, 172 cm; body weight, 60 kg) with tibial varus deformity were scanned by computed tomography (SOMATOM Definition AS Siemens, Germany) with slicing of 0.625 mm from hip joint to the ankle joint. The volunteers’ knee joints were scanned by MRI (MAGNETOM AVanto 1.5 T Siemens, Germany). CT images were used to obtain data on the femur, tibiofibular, and other bone tissues. MRI was used to obtain data on ligaments, menisci, and articular cartilage. The Mimics 21.0 software (Materialise, Leuven, Belgium) was utilized to segment the bone and soft tissue by setting the bone ash threshold to 226, thereby generating a three-dimensional model of the femur through a series of operations, including region growing, masking, segmentation, and smoothing. The three-dimensional model was imported into the Geomagic 2013 software to generate a solid femoral model by denoising and smoothing the surface.
Subsequently, the two-dimensional image data were transformed into a three-dimensional model using Mimics 21.0 software (Materialise, Leuven, Belgium). The apparent density (ρ), Young's modulus (E), and Poisson's ratio of each element were assigned based on the Hu value in the CT scans according to the following formula (16), which made a distinction between cancellous and cortical bone:
The geometry and surface were built and sampled by the Geomagic software. The normal lower extremity model was imported into UG NX 9.0 (Siemens Product Life Cycle Management Software, Inc., USA). The mechanical axis of the lower extremities was determined on the three-dimensional model according to the method proposed by Moreland et al. and Whiteside et al. (17, 18). The proximal and middle tibial fracture models were created and rotated 3°, 5°, and 10° medially or laterally, centered on the mechanical axis. There were six models of varus and valgus deformities, both each at 3°, 5°, or 10°. The normal lower extremity model was imported into Hypermesh 14.0 (Altair Engineering, Troy, MI, USA). The cartilage, meniscus, and bone models were constructed with C3D4 elements (Table 1). The models were exported to the finite analysis software Abaqus 6.14 (Simulia Corp., Providence, RI, USA).
Material properties and boundary conditions
We assumed that all models were homogeneous, isotropic, and linearly elastic. According to early scholars (19–21), articular cartilage, ligaments, and meniscus were assigned a Young's modulus (E) of 5 MPa, 215.3 MPa, and 59 MPa, respectively, and the Poisson's ratio was 0.46, 0.46, and 0.49, respectively. The anterior and posterior horns of the meniscus were connected with the tibial plateau by ten spring elements, and the spring stiffness was set at 200 N/mm (22).
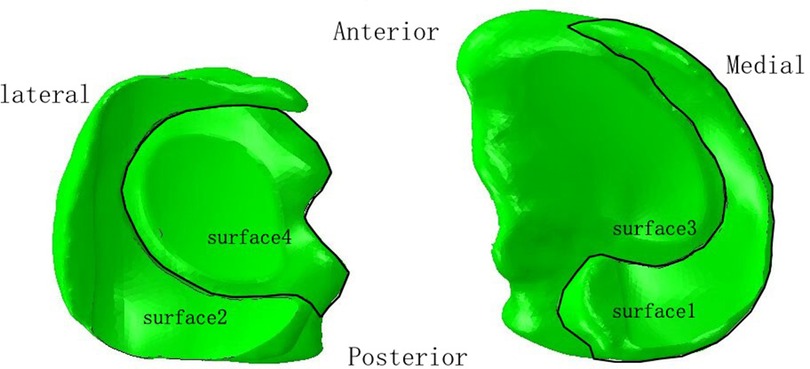
In the lower extremity model, four contact relationships were established. We defined the contact area between the medial femoral condylar cartilage and the medial meniscus, between the lateral femoral condylar cartilage and the lateral meniscus, between the medial femoral condylar cartilage and the medial tibial plateau cartilage, and between the lateral femoral condylar cartilage and the lateral tibial plateau cartilage as surface1, surface2, surface3 and surface4, respectively (Figure 1). The contact relationship was set as “hard contact between surface and surface” and “frictionless finite sliding,” which was used to simulate the finite sliding state of the knee joint. Ligaments and springs were bound to the corresponding regions. The tied relationships were used for malunited sites.
In this experiment, the lower extremity was loaded with a downward vertical force of 600 N (one-leg standing load force of 100% of the body weight; the gravitational acceleration, 10 m/s2) (23, 24). The distal tibiofibula was fixed in all degrees of freedom based on deformity extent (3°, 5°, and 10° at varus and valgus, respectively).
Validation of finite element models
The grid convergence calculations were tested by different sizes. The convergence criterion used was a change of <5%. To make a comparison with previous studies (25, 26), we applied a vertical load of 1,000 N and 2,400 N to the femoral head to obtain the contact area and maximum contact stress of the knee joint, respectively (Table 2). Furthermore, a patient-specific model with a 10° angle tibial varus was also created to validate the artificial deformed model. In this study, the maximum stress values and contact area of tibial cartilage and meniscus in neutral normal position were compared with the reported results (25, 26) and the patient-specific model to evaluate the effectiveness of modeling. The results of the comparison ensured that our modeling method was convincing and reliable (Figures 2, 3) (Table 2).
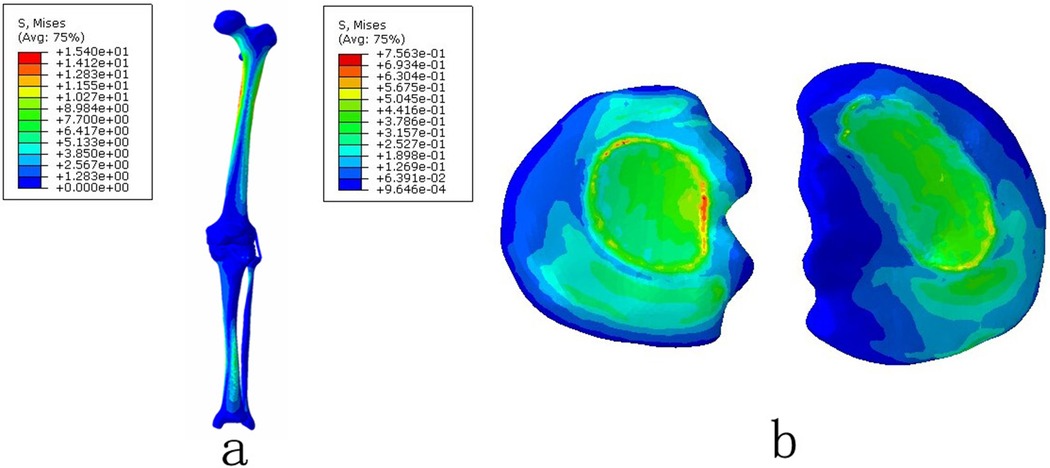
Figure 2. The von Mises stress distribution on the lower extremity under the normal natural position: (a) the complete lower extremity and (b) the tibial plateau cartilage.
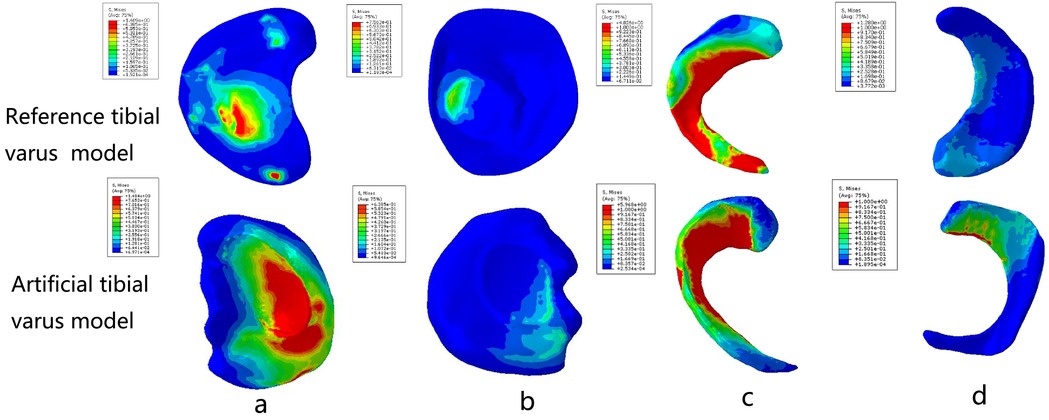
Figure 3. Comparison between the real varus tibial model and the artificial varus tibial model: (a) the medial tibial plateau cartilage; (b) the lateral tibial plateau cartilage; (c) the medial meniscus; and (d) the lateral meniscus.
Results
Stress distribution of the medial and lateral compartments of the knee joint under the tibial varus and valgus deformities
The maximum stress of medial tibial cartilage, tibial subchondral bone, and meniscus in a normal neutral position were 0.64 MPa, 0.65 MPa, and 3.24 MPa, while those of the lateral were 0.76 MPa, 1.47 MPa, and 3.45 MPa, respectively. From the neutral position to 10°of varus, the maximum stress of medial tibial cartilage, tibial subchondral bone, and meniscus increased to 1.48 MPa, 0.65 MPa, and 6.73 MPa, and those of the lateral gradually decreased to 0.62 MPa, 0.65 MPa, and 1.84 MPa, respectively. From the normal neutral position to 10°of valgus, the maximum stress of medial tibial cartilage, tibial subchondral bone, and meniscus gradually decreased to 0.55 MPa, 0.87 MPa, and 1.65 MPa, while those of the lateral increased to 1.63 MPa, 2.75 MPa, and 6.01 MPa, respectively (Figures 4 and 5).
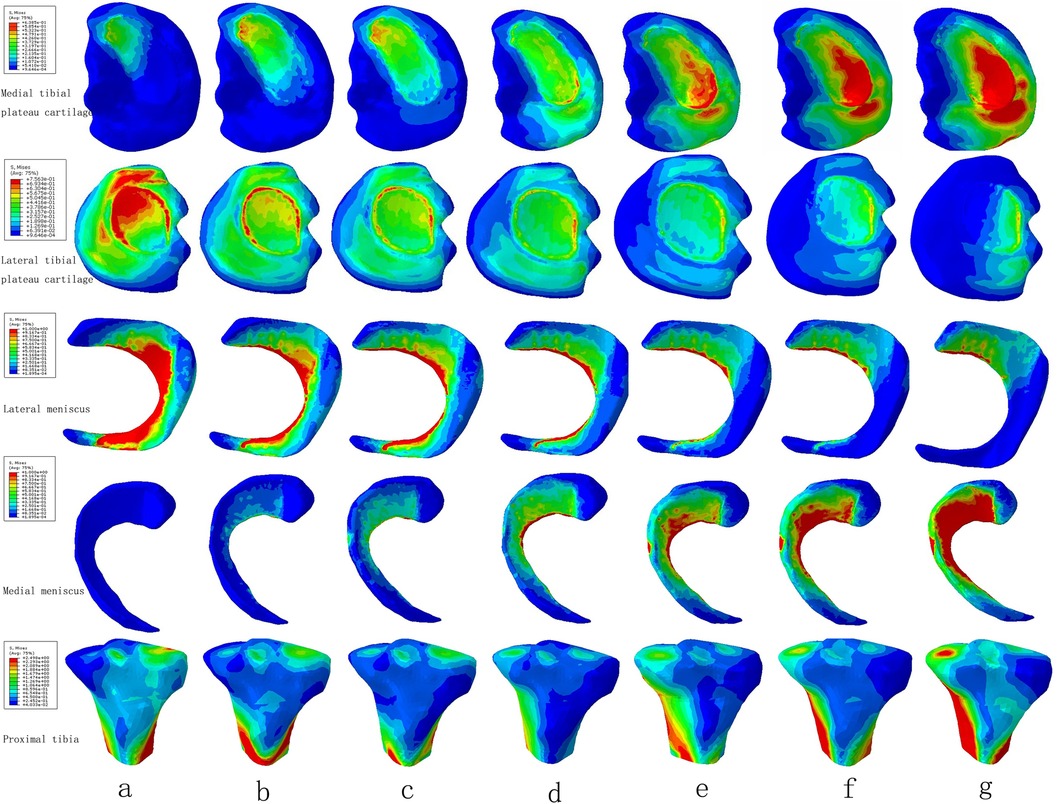
Figure 4. The von Mises stress distribution on the tibial plateau cartilage, meniscus, and proximal tibia under the condition of varus and valgus deformities of the tibia: (a) valgus 10°; (b) valgus 5°; (c) valgus 3°; (d) neutral position 0°; (e) varus 3°; (f) varus 5°; and (g) varus 10°.
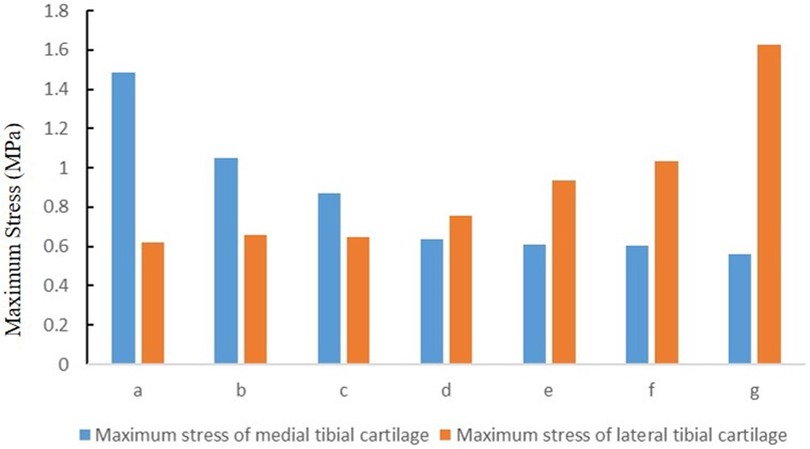
Figure 5. The stress distribution of cartilage under the condition of varus and valgus deformities of the tibia: (a) valgus 10°; (b) valgus 5°; (c) valgus 3°; (d) neutral position 0°; (e) varus 3°; (f) varus 5°; and (g) varus 10° (MPa).
The contact area of the medial and lateral compartments of the knee joint under the tibial varus and valgus deformities
The contact area of the medial tibial cartilage and meniscus in a normal neutral position was 247.52 mm2 and 110.91 mm2, while that of the lateral was 196.25 mm2 and 135.83 mm2, respectively. From the neutral position to 10°of varus, the contact area of medial tibial cartilage and meniscus increased to 250.12 mm2 and 139.46 mm2, and that of the lateral gradually decreased to 83.68 mm2 and 69.38 mm2, respectively. From the normal neutral position to 10°of valgus, the contact area of medial tibial cartilage and meniscus gradually decreased to 87.94 mm2 and 0 mm2, while that of the lateral increased to 205.51 mm2 and 146.87 mm2, respectively (Figure 6).
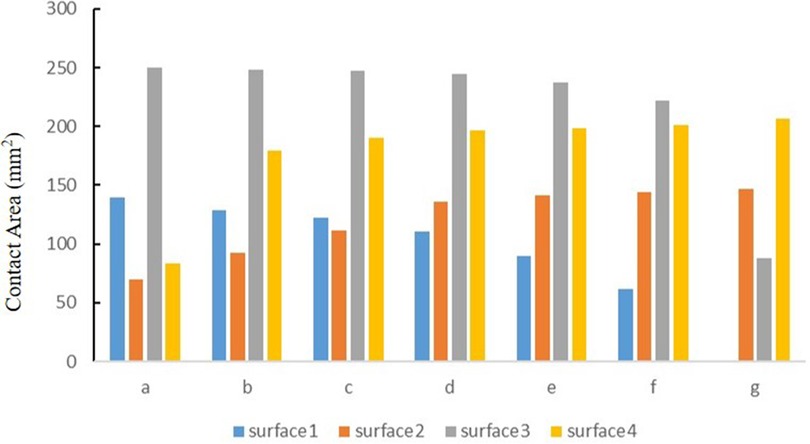
Figure 6. The contact area of four contact relationships under the condition of varus and valgus deformities of the tibia: (a) valgus 10°; (b) valgus 5°; (c) valgus 3°; (d) neutral position 0°; (e) varus 3°; (f) varus 5°; and (g) varus 10° (mm2).
The contact force of the medial and lateral compartments of the knee joint under the tibial varus and valgus deformities
The contact force of the medial tibial cartilage and meniscus in a normal neutral position was 221.77 N and 62.84 N, while that of the lateral was 146.12 N and 67.62 N, respectively. From the neutral position to 10°of varus, the contact force of medial tibial cartilage and meniscus increased to 351.55 N and 150.08 N, and that of the lateral gradually decreased to 40.71 N and 35.77 N, respectively. From the normal neutral position to 10°of valgus, the contact force of medial tibial cartilage and meniscus gradually decreased to 45.56 N and 0 N, while that of the lateral increased to 252.76 N and 140.91 N, respectively (Figure 7).
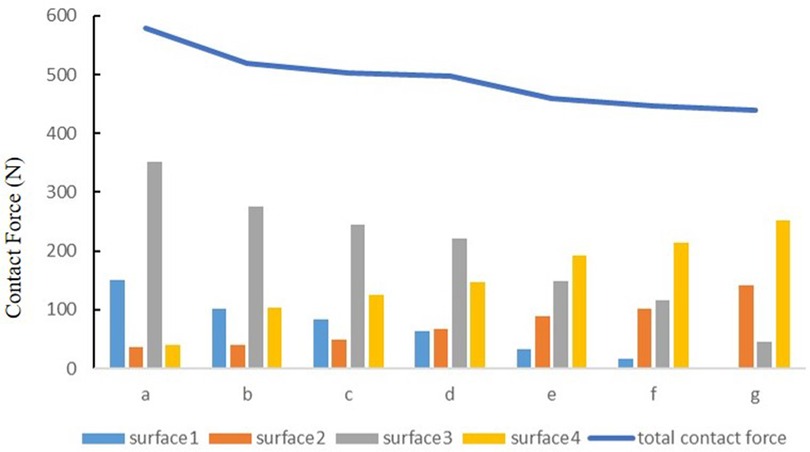
Figure 7. The contact force of four contact relationships under the condition of varus and valgus deformities of the tibia: (a) valgus 10°; (b) valgus 5°; (c) valgus 3°; (d) neutral position 0°; (e) varus 3°; (f) varus 5°; and (g) varus 10° (N).
Discussion
The varus/valgus deformity is a common complication after a tibial fracture. The tibial deformity is closely related to the occurrence and development of knee TA. Our findings demonstrate that the varus/valgus deformity of the tibia significantly alters the contact force, contact area, and stress of the knee's medial and lateral compartments, providing the biomechanical evidence to support the potential association between tibial deformity and knee TA.
The results demonstrate that the medial compartment exhibits a larger size than the lateral compartment with regard to both contact force and contact area. As the degree of varus deformity increases, the contact force, contact area, and stress peak value of the medial compartment gradually increase, while those of the lateral compartment gradually decrease. It is the opposite of valgus deformities. A tibial deformity alters the balance of the medial–lateral compartment of the normal neutral position by influencing the mechanical axis of the lower extremity, which may shift inward or outward. Varus and valgus deformities of the lower limb have increased the rate of knee arthritis, especially in obesity and overweight groups (9, 27, 28). Compared to previous studies (13, 15), the contact force of the meniscus and tibial cartilage is additionally recorded to reflect the load of the knee joint in the current study. However, the total contact force of normal and malunion models differs and is lower than 600 N. This is mainly caused by shorter tibial moments of the deformity and traction of ligaments around the knee joint. Moreover, the contact force of 10° of varus in the medial compartment is 1.76 times the normal values, and the contact force of 10° of valgus in the lateral compartment is 1.84 times the normal values. We suggest that tibial varus and valgus deformities have a symmetric effect on the knee joint in a finite element model of the lower limb. In this study, a finite element model of the lower limb was reconstructed, and the center of the femoral head to the center of the ankle joint was set as the lower limb of the mechanical axis, which avoided the deviation of the mechanical axis generated by a portion of the lower limb.
Tibial varus/valgus deformities alter the mechanical characteristics of the knee joint, thereby increasing the likelihood of knee arthritis. Firstly, for the injury mechanism of meniscus and tibial cartilage, tibial varus and valgus deformities caused an increase in the load and highly stressed zone of tibial cartilage and meniscus. According to the findings of a population baseline survey, the incidence of medial cartilage injury in individuals with varus malalignment is 3.59 times that observed in the normal population (29). Felson et al. (30) reported that valgus malalignment has a strong relation with lateral meniscal and cartilage damage. Furthermore, some studies have suggested that knee varus/valgus malalignment is an important risk factor for anterior cruciate ligament (ACL) injury (31, 32). Finally, subchondral osteosclerosis represents a significant clinical manifestation of knee arthritis, resulting from bone remodeling under conditions of excessive abnormal load. Bobinac et al. (33) suggested that subchondral bone morphological changes are even faster than cartilage changes in patients with knee arthritis. Tibial deformity has been demonstrated to significantly alter the stress distribution of the knee subchondral bone, which will ultimately lead to sclerosis of the knee subchondral bone.
The knee joint is composed of a variety of tissues, and damage to any tissue can affect the function and structure of other tissues as well. Damage to the ACL can result in tears to the meniscus, chronic knee instability, cartilage damage, and knee arthritis, due to alterations in the stability and alignment of the knee joint (31, 34, 35). Injuries to the meniscus can also lead to cartilage destruction and knee arthritis by changing the stability of the knee joint (36, 37). Additionally, sclerosis of the subchondral bone can result in a reduction of the cushioning force, leading to stress concentration in the cartilage and subsequent damage to the cartilage (38). The meniscus, cartilage, cruciate ligament, and subchondral bone of the knee joint are closely related to each other in tissue structure and function (39). Tibial varus and valgus deformities could cause damage to the normal structure of the knee joint, and various structures also interact, together leading to an increased incidence of knee arthritis for a long time. Therefore, early osteotomy can avoid the occurrence and progression of knee TA. To accurately construct soft tissue models, such as knee ligaments, we employed a knee brace to maintain the knee in a state of extension, thereby limiting the range of motion and reducing the discrepancy between CT and MRI images. Furthermore, this study also drew upon data reported in the literature and human anatomy to determine the initial and final points of the ligaments (40–42). The finite element model of the ligament was then constructed with precision through the aforementioned methods.
In addition to knee replacement, osteotomy is an important treatment to correct tibial varus and valgus deformities especially in the young population. However, correction goals for osteotomy are currently controversial. Coventry et al. (43) suggested that the intended tibiofemoral correction angles for varus knee was overcorrection to a lower limb anatomical axis of 8°–10° of valgus angulation. Hernigou et al. (44) recommended that a postoperative mechanical axis of 3°–6° of valgus angulation should be maintained. Jung et al. (45) demonstrated that cartilage regeneration in the medial compartment of knees with standard correction is superior to that observed with overcorrection and undercorrection, with respect to both cartilage regeneration and clinical outcomes. Nevertheless, some studies have indicated that there is no significant distinction in the impact of overcorrection and standard osteotomy on the knee joint (46, 47). Naudie et al. (47) posited that the intended mechanical axis of the lower limb should be maintained within the normal range. This study aimed to investigate the relationship between the magnitude of the deformity and the load in the medial and lateral compartments of the knee joint. This will enable the load in the medial and lateral compartments of the knee joint to be distributed quantitatively, thus providing an accurate reference for clinical osteotomy. Finally, the degree of osteotomy has not been quantified in the long-term prognosis of osteotomy. Future studies should still focus on the relationship between the overall survival time of osteotomy and loads.
This study has shown that tibial varus and valgus deformity can significantly affect the biomechanical properties of the knee joint. Therefore, our findings can provide clinical evidence on two aspects of tibial fracture management. Firstly, the reduction of the tibial shaft fracture should be kept in a clean alignment, and the fracture reduction should be more finely adjusted to keep the internal and external deformity angle less than 5°. Secondly, in view of the above evidence, the tibial internal and external deformity should be corrected aggressively for the deformity angle greater than 5° to prevent long-term complications such as arthritis.
Our study is not without limitations. First, this study simulates the human standing on one foot, ignoring the lower limb muscles, which may be different from the real load condition of the human body. Second, all models were assigned isotropy and homogeneity to simplify the model. However, the finite element model of the lower limb was validated with reported research, and the difference is within acceptable limits. Finally, the finite element model of the lower limb in this study does not include the foot, which may be different from the real lower limb.
In conclusion, tibial varus/valgus deformity has a significant influence on the contact force, contact area, and stress of the medial and lateral compartments of the knee joint. This study provides a mechanical basis and reference for clinical evaluation of tibial fracture reduction and osteotomy for tibial deformity.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Ethics statement
The experiments of this study were performed in accordance with all relevant guidelines and regulations and with the approval of the Institutional Review Board of The Third Hospital of Hebei Medical University. The use of these CT data in this investigation and the experimental protocol of the study were approved by the Third Hospital of Hebei Medical University. Written informed consent was obtained from the volunteers prior to the study commencement. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author contributions
KD: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing – original draft, Writing – review & editing. WL: Data curation, Formal Analysis, Investigation, Methodology, Writing – review & editing. DS: Methodology, Project administration, Writing – original draft, Writing – review & editing. YiZ: Investigation, Methodology, Writing – original draft, Writing – review & editing. CR: Conceptualization, Writing – original draft. XC: Software, Writing – review & editing. HW: Writing – original draft. YaZ: Writing – original draft, Writing – review & editing. XX: Investigation, Writing – review & editing. WC: Conceptualization, Investigation, Software, Validation, Writing – review & editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Support Program for the National Natural Science Foundation of China (Grant No. 82072447, 82272578) and the Hebei National Science Foundation-Outstanding Youth Foundation (Grant No. H2021206329). The funding source has no role in study design, conduction, data collection, or statistical analysis.
Acknowledgments
We thank Prof. Chen Wei for his help and support in the process of data analysis and article writing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Chen W, Lv H, Liu S, Liu B, Zhu Y, Chen X, et al. National incidence of traumatic fractures in China: a retrospective survey of 512 187 individuals. Lancet Glob Health. (2017) 5(8):e807–e17. doi: 10.1016/s2214-109x(17)30222-x
2. Court-Brown CM, Caesar B. Epidemiology of adult fractures: a review. Injury. (2006) 37(8):691–7. doi: 10.1016/j.injury.2006.04.130
3. Weiss RJ, Montgomery SM, Ehlin A, Al Dabbagh Z, Stark A, Jansson KA. Decreasing incidence of tibial shaft fractures between 1998 and 2004: information based on 10,627 Swedish inpatients. Acta Orthop. (2008) 79(4):526–33. doi: 10.1080/17453670710015535
4. Lin L, Liu Y, Lin C, Zhou Y, Feng Y, Shui X, et al. Comparison of three fixation methods in treatment of tibial fracture in adolescents. ANZ J Surg. (2018) 88(6):E480–e5. doi: 10.1111/ans.14258
5. Schmidt AH, Finkemeier CG, Tornetta P 3rd. Treatment of closed tibial fractures. Instr Course Lect. (2003) 52:607–22.12690886
6. van der Schoot DK, Den Outer AJ, Bode PJ, Obermann WR, van Vugt AB. Degenerative changes at the knee and ankle related to malunion of tibial fractures. 15-year follow-up of 88 patients. J Bone Joint Surg Br. (1996) 78(5):722–5. doi: 10.1302/0301-620X.78B5.0780722
7. Howard MW, Zinar DM, Stryker WS. The use of the lottes nail in the treatment of closed and open tibial shaft fractures. Clin Orthop Relat Res. (1992) 279:246–53. doi: 10.1097/00003086-199206000-00031
8. Milner SA, Davis TR, Muir KR, Greenwood DC, Doherty M. Long-term outcome after tibial shaft fracture: is malunion important? J Bone Joint Surg Am. (2002) 84(6):971–80. doi: 10.2106/00004623-200206000-00011
9. Weinberg DS, Park PJ, Liu RW. Association between tibial malunion deformity parameters and degenerative hip and knee disease. J Orthop Trauma. (2016) 30(9):510–5. doi: 10.1097/bot.0000000000000603
10. Kettelkamp DB, Hillberry BM, Murrish DE, Heck DA. Degenerative arthritis of the knee secondary to fracture malunion. Clin Orthop Relat Res. (1988) 234:159–69. doi: 10.1097/00003086-198809000-00029
11. Gao Z, Zhao L, Fekete G, Katona G, Baker JS, Gu Y. Continuous time series analysis on the effects of induced running fatigue on leg symmetry using kinematics and kinetic variables: implications for knee joint injury during a countermovement jump. Front Physiol. (2022) 13:877394. doi: 10.3389/fphys.2022.877394
12. Weber D, Weber M. Corrective osteotomies for malunited malleolar fractures. Foot Ankle Clin. (2016) 21(1):37–48. doi: 10.1016/j.fcl.2015.09.003
13. Li M, Chang H, Wei N, Chang W, Yan Y, Jin Z, et al. Biomechanical study on the stress distribution of the knee joint after tibial fracture malunion with residual varus-valgus deformity. Orthop Surg. (2020) 12(3):983–9. doi: 10.1111/os.12668
14. Kenawey M, Liodakis E, Krettek C, Ostermeier S, Horn T, Hankemeier S. Effect of the lower limb rotational alignment on tibiofemoral contact pressure. Knee Surg Sports Traumatol Arthrosc. (2011) 19(11):1851–9. doi: 10.1007/s00167-011-1482-4
15. Ding K, Yang W, Wang H, Zhan S, Hu P, Bai J, et al. Finite element analysis of biomechanical effects of residual varus/valgus malunion after femoral fracture on knee joint. Int Orthop. (2021) 45(7):1827–35. doi: 10.1007/s00264-021-05039-9
16. Reina-Romo E, Rodríguez-Vallés J, Sanz-Herrera JA. In silico dynamic characterization of the femur: physiological versus mechanical boundary conditions. Med Eng Phys. (2018) 23:S1350-4533(18)30090-0. doi: 10.1016/j.medengphy.2018.06.001
17. Moreland JR, Bassett LW, Hanker GJ. Radiographic analysis of the axial alignment of the lower extremity. J Bone Joint Surg Am. (1987) 69(5):745–9. doi: 10.2106/00004623-198769050-00016
18. Whiteside LA, Arima J. The anteroposterior axis for femoral rotational alignment in valgus total knee arthroplasty. Clin Orthop Relat Res. (1995) 321:168–72.
19. Li G, Lopez O, Rubash H. Variability of a three-dimensional finite element model constructed using magnetic resonance images of a knee for joint contact stress analysis. J Biomech Eng. (2001) 123(4):341–6. doi: 10.1115/1.1385841
20. LeRoux MA, Setton LA. Experimental and biphasic FEM determinations of the material properties and hydraulic permeability of the meniscus in tension. J Biomech Eng. (2002) 124(3):315–21. doi: 10.1115/1.1468868
21. McNulty AL, Guilak F. Mechanobiology of the meniscus. J Biomech. (2015) 48(8):1469–78. doi: 10.1016/j.jbiomech.2015.02.008
22. Donahue TL, Hull ML, Rashid MM, Jacobs CR. A finite element model of the human knee joint for the study of tibio-femoral contact. J Biomech Eng. (2002) 124(3):273–80. doi: 10.1115/1.1470171
23. Rudman KE, Aspden RM, Meakin JR. Compression or tension? The stress distribution in the proximal femur. Biomed Eng Online. (2006) 5:12. doi: 10.1186/1475-925x-5-12
24. Bai L, Zhang W, Guan S, Liu J, Chen P. Syndesmotic malreduction may decrease fixation stability: a biomechanical study. J Orthop Surg Res. (2020) 15(1):64. doi: 10.1186/s13018-020-01584-y
25. McKellop HA, Sigholm G, Redfern FC, Doyle B, Sarmiento A, Luck JV Sr. The effect of simulated fracture-angulations of the tibia on cartilage pressures in the knee joint. J Bone Joint Surg Am. (1991) 73(9):1382–91. doi: 10.2106/00004623-199173090-00014
26. Morimoto Y, Ferretti M, Ekdahl M, Smolinski P, Fu FH. Tibiofemoral joint contact area and pressure after single- and double-bundle anterior cruciate ligament reconstruction. Arthroscopy. (2009) 25(1):62–9. doi: 10.1016/j.arthro.2008.08.014
27. Yusuf E, Bijsterbosch J, Slagboom PE, Rosendaal FR, Huizinga TW, Kloppenburg M. Body mass Index and alignment and their interaction as risk factors for progression of knees with radiographic signs of osteoarthritis. Osteoarthritis Cartilage. (2011) 19(9):1117–22. doi: 10.1016/j.joca.2011.06.001
28. Brouwer GM, van Tol AW, Bergink AP, Belo JN, Bernsen RM, Reijman M, et al. Association between valgus and varus alignment and the development and progression of radiographic osteoarthritis of the knee. Arthritis Rheum. (2007) 56(4):1204–11. doi: 10.1002/art.22515
29. Sharma L, Chmiel JS, Almagor O, Felson D, Guermazi A, Roemer F, et al. The role of varus and valgus alignment in the initial development of knee cartilage damage by MRI: the most study. Ann Rheum Dis. (2013) 72(2):235–40. doi: 10.1136/annrheumdis-2011-201070
30. Felson DT, Niu J, Gross KD, Englund M, Sharma L, Cooke TD, et al. Valgus malalignment is a risk factor for lateral knee osteoarthritis incidence and progression: findings from the Multicenter Osteoarthritis Study and the Osteoarthritis Initiative. Arthritis Rheum. (2013) 65(2):355–62. doi: 10.1002/art.37726
31. Acevedo RJ, Rivera-Vega A, Miranda G, Micheo W. Anterior cruciate ligament injury: identification of risk factors and prevention strategies. Curr Sports Med Rep. (2014) 13(3):186–91. doi: 10.1249/jsr.0000000000000053
32. Price MJ, Tuca M, Cordasco FA, Green DW. Nonmodifiable risk factors for anterior cruciate ligament injury. Curr Opin Pediatr. (2017) 29(1):55–64. doi: 10.1097/mop.0000000000000444
33. Bobinac D, Spanjol J, Zoricic S, Maric I. Changes in articular cartilage and subchondral bone histomorphometry in osteoarthritic knee joints in humans. Bone. (2003) 32(3):284–90. doi: 10.1016/s8756-3282(02)00982-1
34. Harman MK, Markovich GD, Banks SA, Hodge WA. Wear patterns on tibial plateaus from varus and valgus osteoarthritic knees. Clin Orthop Relat Res. (1998) 352:149–58.
35. Rajgopal A, Noble PC, Vasdev A, Ismaily SK, Sawant A, Dahiya V. Wear patterns in knee articular surfaces in Varus deformity. J Arthroplasty. (2015) 30(11):2012–6. doi: 10.1016/j.arth.2015.05.002
36. Chambers HG, Chambers RC. The natural history of meniscus tears. J Pediatr Orthop. (2019) 39(Issue 6, Suppl 1 Suppl 1):S53–s5. doi: 10.1097/bpo.0000000000001386
37. Sharma L, Eckstein F, Song J, Guermazi A, Prasad P, Kapoor D, et al. Relationship of meniscal damage, meniscal extrusion, malalignment, and joint laxity to subsequent cartilage loss in osteoarthritic knees. Arthritis Rheum. (2008) 58(6):1716–26. doi: 10.1002/art.23462
38. Li G, Yin J, Gao J, Cheng TS, Pavlos NJ, Zhang C, et al. Subchondral bone in osteoarthritis: insight into risk factors and microstructural changes. Arthritis Res Ther. (2013) 15(6):223. doi: 10.1186/ar4405
39. Ziegler R, Goebel L, Seidel R, Cucchiarini M, Pape D, Madry H. Effect of open wedge high tibial osteotomy on the lateral tibiofemoral compartment in sheep. Part III: analysis of the microstructure of the subchondral bone and correlations with the articular cartilage and Meniscus. Knee Surg Sports Traumatol Arthrosc. (2015) 23(9):2704–14. doi: 10.1007/s00167-014-3134-y
40. Pache S, Aman ZS, Kennedy M, Nakama GY, Moatshe G, Ziegler C, et al. Posterior cruciate ligament: current concepts review. Arch Bone Jt Surg. (2018) 6(1):8–18.29430489
41. Park JG, Han SB, Lee CS, Jeon OH, Jang KM. Anatomy, biomechanics, and reconstruction of the anterolateral ligament of the knee joint. Medicina (Kaunas). (2022) 58(6):786. doi: 10.3390/medicina58060786
42. Zhang J, Hao D, Duan F, Yu T, Zhang C, Che J. The rotating stretched curved planar reconstruction of 3d-FIESTA MR imaging for evaluating the anterior cruciate ligament of the knee joint. Magn Reson Imaging. (2019) 55:46–51. doi: 10.1016/j.mri.2018.09.013
43. Coventry MB, Ilstrup DM, Wallrichs SL. Proximal tibial osteotomy. A critical long-term study of eighty-seven cases. J Bone Joint Surg Am. (1993) 75(2):196–201. doi: 10.2106/00004623-199302000-00006
44. Hernigou P, Medevielle D, Debeyre J, Goutallier D. Proximal tibial osteotomy for osteoarthritis with varus deformity. A ten to thirteen-year follow-up study. J Bone Joint Surg Am. (1987) 69(3):332–54. doi: 10.2106/00004623-198769030-00005
45. Jung WH, Takeuchi R, Chun CW, Lee JS, Ha JH, Kim JH, et al. Second-look arthroscopic assessment of cartilage regeneration after medial opening-wedge high tibial osteotomy. Arthroscopy. (2014) 30(1):72–9. doi: 10.1016/j.arthro.2013.10.008
46. Ziegler R, Goebel L, Cucchiarini M, Pape D, Madry H. Effect of open wedge high tibial osteotomy on the lateral tibiofemoral compartment in sheep. Part II: standard and overcorrection do not cause articular cartilage degeneration. Knee Surg Sports Traumatol Arthrosc. (2014) 22(7):1666–77. doi: 10.1007/s00167-013-2410-6
Keywords: tibial fractures, varus/valgus deformity, knee joint, mechanical characters, finite element analysis
Citation: Ding K, Liu W, Sun D, Zhang Y, Ren C, Cheng X, Wang H, Zhu Y, Xing X and Chen W (2024) Residual coronary malformation after tibial shaft fracture alters the contact status of the meniscus and cartilage in the knee joint: a computational study. Front. Surg. 11:1325085. doi: 10.3389/fsurg.2024.1325085
Received: 20 October 2023; Accepted: 29 August 2024;
Published: 13 September 2024.
Edited by:
Xiaofei Hu, Army Medical University, ChinaReviewed by:
Zixiang Gao, Eötvös Loránd University, HungaryYunfeng Yang, Shanghai Jiao Tong University, China
Ionel Șerban, Transilvania University of Brașov, Romania
Copyright: © 2024 Ding, Liu, Sun, Zhang, Ren, Cheng, Wang, Zhu, Xing and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xin Xing, eHg5ODMxNUAxMjYuY29t; Wei Chen, ZHJjaGVud2VpMUAxNjMuY29t
†These authors have contributed equally to this work
 Kai Ding
Kai Ding Wei Liu3,†
Wei Liu3,† Yifan Zhang
Yifan Zhang Yanbin Zhu
Yanbin Zhu Wei Chen
Wei Chen