Evolution of the flux tube instability parameters in plasma injections at saturnian magnetosphere

The evolution of the flux tube stability parameters in plasma injections at the Saturnian magnetosphere is reviewed. Plasma injections result from an imbalance in the centrifugal, total pressure gradient, and magnetic tension forces acting on plasma in the magnetosphere. Plasma originating from Enceladus tends to move outward due to centrifugal forces while reconnected flux tubes that are depleted of plasma collapse because of the magnetic tension leading to plasma injections. As the flux tube moves inward and contracts, the ambient density and pressure increase sufficiently to resist further collapse and the injected flux tube brakes. During this process the flux tube may also lose its integrity due to particle drifts, which allow exchange of plasma with adjacent flux tubes so as to bring the flux tube closer to equilibrium and stability so that it is indistinguishable from adjacent plasma. Stability parameters using this energy approach are defined and examined. The results show that the net forces push the plasma moves inward for L > 11 and outward for L < 8.5, while equilibrium is generally reached for 8.5 < L < 11, where L is the equatorial magnetic field crossing measured in Saturnian radii. The evolution of the stability parameters can also apply to Jovian and other fast rotating planetary magnetospheres.

1 Introduction

In the study of the Saturnian magnetosphere, the radially inward plasma transport or plasma injection has long been a fascinating and confounding topic. The plasma injection in the inner magnetosphere is often characterized by a sudden incursion of plasma having higher temperature and lower density than the ambient plasma (Burch et al., 2005; Azari et al., 2018; Thomsen, 2013). The injected plasma or flux tube has been observed to be nearly in pressure balance with the ambient plasma and hence there is often an accompanying sudden increase or decrease in the magnetic field strength and pressure (André et al., 2005; 2007; Azari et al., 2018; Wing et al., 2022). As the injected hot plasma moves radially inward, the ions and electrons execute an energy dependent curvature and gradient azimuthal drift, leading to an energy dispersion signature from which the age and location of the injection can be estimated (Burch et al., 2005; Chen and Hill, 2008; Yin et al., 2023; Thomsen, 2013). Hill et al. (2005) reported that injections have typical ages <11 h and azimuthal widths <1 Rs in a sample of 48 events. Azari et al. (2018), Azari et al. (2019) found that plasma injections rarely reach r < 6 Rs in observations gathered by Cassini spacecraft. Paranicas et al. (2020) found that the inflow speeds of the energetic particle injections range from 0 to 50 km s^–1 in 20 events. The flux-tube interchange injections have been associated with electron cyclotron harmonic (ECH), whistler mode, and upper-hybrid waves (Kennelly et al., 2013; Long et al., 2023; Menietti et al., 2008) and periodic 5 kHz narrowband radio wave emissions (Mitchell et al., 2009; Mitchell et al., 2015; Menietti et al., 2016; Wing et al., 2020). A comprehensive review of the plasma injections at the Saturnian magnetosphere can be found in Thomsen (2013) and Achilleos et al. (2015).

Two key factors contribute to the complexity of the plasma injections: (1) Saturn rotates on its axis rapidly with a periodicity of about 10–11 h (Azari et al., 2019) and (2) Enceladus, a moon located at r ∼ 4 Rs where Rs = Saturn radius ∼60,268 km, continuously sources cold plasma at the rate of 12–250 kg s^–1 in the magnetosphere (Bagenal and Delamere, 2011). Thus, many or most studies considered the effective gravity or Rayleigh-Taylor like instability as the mechanism for plasma injections where hot tenuous flux tube moves in and replaces the cold dense flux tube that moves out (e.g., Hill, 1976; Chen and Hill, 2008; Sittler et al., 2008; Bagenal and Delamere, 2011; Liu and Hill, 2012; Thomsen et al., 2013; Azari et al., 2019; Ma et al., 2016; Stauffer et al., 2019; Thomsen and Coates, 2019). Liu et al. (2010) simulated this process using Rice Convection Model (RCM) showing narrow radial fingers of hot tenuous inflowing plasma adjacent to fingers of cold dense outflowing plasma.

At Earth where the planet rotates more slowly and its moon does not source plasma, observations and simulations have shown that flux tube entropy instability where injected flux tube having depleted flux tube entropy (S) resulting from magnetotail reconnection can move inward until its S reaches the same value as that of the ambient plasma (e.g., Birn et al., 2006; 2009; Pontius and Wolf, 1990; Wing and Johnson, 2009; Johnson and Wing, 2009; Dubyagin et al., 2010). Ma et al. (2019) investigated the role of the flux tube entropy instability in the plasma injections at Saturnian magnetosphere, but they did not consider the effective gravity. Nonadiabatic plasma heating such as turbulent heating can increase flux tube entropy and hence can affect the plasma injection (Saur, 2004; Neupane et al., 2021; Wing et al., 2014).

Plasma in the rotating magnetosphere is affected by the centrifugal force that tends to push plasma outward, magnetic tension that resists stretching of field lines, and total pressure, which tends to push plasma outward. Dense plasma originating at Enceladus in the inner magnetosphere is pushed outward by the centrifugal force, while flux tubes that are depleted by reconnection in the magnetotail collapse under the magnetic tension leading to plasma injections. Southwood and Kivelson (1987) developed an energy-based formalism for the stability requirement of an inward moving flux tube that includes both the effective gravity (centrifugal force + gravity) and the flux tube entropy instabilities in fast rotating magnetosphere (cf., Ferrière et al., 2001). Based on the Southwood and Kivelson (1987) formalism, Wing et al. (2022) examined the roles of the effective gravity and flux tube entropy in seven plasma injection events observed by Cassini spacecraft in the Saturnian magnetosphere.

The present paper reviews the above studies of the plasma injections at the Saturnian magnetosphere, but narrowly focuses on the following two questions: (1) What roles do the effective gravity and flux tube entropy play in the Saturnian plasma injections? Which term is dominant? and (2) Why do injections rarely reach r < 6 Rs as reported in Azari et al. (2018), Azari et al. (2019)?

2 Flux tube instability parameters

The stability requirement for the inward moving flux tube interchange for a fast rotating magnetosphere is given in Equation 1 (Southwood and Kivelson, 1987):

$\left[\frac{K\left(\frac{\partial S}{\partial X_p}\right)}{V^{\gamma }}–\left(\frac{m{g}_{e}h}{V}\right)\left(\frac{\partial N}{\partial X_p}\right)\right]<0(1)$

where $K=\left[2\left(B^2/{\mu }_o\right)\left(hc\right)+nmhg\right]/P_{\gamma }$, n = plasma density, N = flux-tube content, $P_{\gamma }=\left(\gamma p+B^2/{\mu }_o\right)$, p = flux-tube averaged plasma pressure, γ = polytropic index = 5/3, B = magnitude of the magnetic field, X_p = the displacement of the interchange motion, h = Lamé coefficient along X_p, m = average ion mass, μ_o = magnetic field permeability constant, c = component of the magnetic field curvature in the X_p direction, S = flux-tube or total entropy = pV^γ, V = flux-tube volume, and g_e = effective gravity given by Equation 2,

$g_e=r{\mathrm{\Omega }}^2–g(2)$

where g = gravity, Ω = planet angular velocity and r = radial distance.

The first term of Equation 1 tends toward instability when the entropy gradient is negative radially outward given that the curvature is negative. In this case, an outward perturbation of plasma governed by an adiabatic pressure law would have a higher entropy than the flux tube it displaced and therefore a higher pressure. The increased pressure would push the perturbed plasma further outward leading to instability. On the other hand, if the entropy gradient were positive, the displaced flux tube would have a lower pressure than the flux tube it displaced. In this case, the JxB force would push the low pressure flux tube back toward its original position and the configuration is stable. The second term of Equation 1 tends toward instability when the gradient of the flux tube content is negative outwards. In this case an outward displacement of a flux tube increases the outward force it exerts relative to that of the displaced plasma leading to instability. On the other hand, a positive outward gradient of the flux tube content is stable because the total outward force exerted by the flux tube decreases relative to the displaced flux tube and therefore the surrounding flux tubes will push it back toward the original position. At the Saturnian magnetosphere, Enceladus provides a steady plasma source and therefore the overall profile of the flux tube content is generally decreasing in the radial direction at r > 5–6 Rs, and such a configuration is unstable to centrifugal interchange.

Based on Equation 1, Wing et al. (2022) considered the stability of the inner and outer edges of the injected flux tube and derived a Total Stability (TS) parameter, which quantifies the conditions for which flux tubes are unstable to inward and outward displacement. Additionally, in order to study the roles of the flux tube entropy and the effective gravity separately, they separated the TS parameter into its two components as shown in Equation 3:

$TS=E_t+G_t(3)$

where the first term is the entropy term (Equation 4),

$E_t=V^{–\gamma }∆S(4)$

and the second term is the effective gravity term (Equation 5),

$G_t=\left(-1\right)K^{-1}\left(\frac{m{g}_{e}h}{V}\right)\left(∆N\right).(5)$

If TS = 0, the condition predicts that the flux-tube is in equilibrium, but if TS < 0 or TS > 0, it would describe the flux tube instability condition for inward and outward moving flux tube, respectively. If TS > 0, the net force would push the flux tube outward and conversely, if TS < 0, the net force would push the flux tube inward. If the effective gravity is negligible, i.e., G_t = 0, then TS = E_t, which is similar to the formalism for the flux tube interchange developed for Earth (e.g., Erickson and Wolf, 1980; Pontius and Wolf, 1990; Birn et al., 2006; Birn et al., 2009).

3 Evolution of the stability parameters TS, E_t, and G_t in the plasma injection

The Cassini spacecraft orbited Saturn 2004 to 2017 and carried Cassini Magnetospheric Imaging Instrument (MIMI), Cassini Plasma Spectrometer (CAPS), and Dual Technique Magnetometer (MAG) instruments. The CAPS instrument observed ions with energy range 1 eV/q–50 keV/q and electrons with energy range 1 eV–30 keV (Young et al., 2004). CAPS ion moments (density, temperature, flow velocity) have been calculated by numerical integration over the observed distribution (Thomsen et al., 2010) while the CAPS electron moments are computed as described by Lewis et al. (2008). The CHarge Energy Mass Spectrometer (CHEMS) is part of the MIMI instrument suite and observed ions with energy range 3–220 keV/q (Krimigis et al., 2004). The MAG instrument detected magnetic fields up to 44,000 nT (Dougherty et al., 2004).

Wing et al. (2022) used CAPS, CHEMS, and MAG data, which are publicly available at the NASA Planetary Data System (PDS) Planetary Plasma Interaction (PPI) node (https://pds-ppi.igpp.ucla.edu/index.jsp). The Wing et al. (2022) study selected 7 plasma injections from previously published injection events in Thomsen et al. (2014); (events 1, 2, 3), Mitchell et al. (2015); (events 4, 5, 6), and Rymer et al. (2009); (event 7). These events were selected because they have clear injection signatures and CAPS, CHEMS, and MAG have good data. The 7 events, which range from L ∼ 14 to 7, are given in Table 1 in Wing et al. (2022). The L-value gives the distance in planetary radii where the magnetic field intersects the equatorial plane (McIlwain, C. E., 1961) and is computed using Achilleos et al. (2010) magnetic field model. For completeness, these 7 events are listed here in quintuplets.

(event number, time (UT), location SZS (X, Y, Z) Rs, L, Latitude (degree)):

{(1, 2010–06–02 12:20:00, (−8.9, 7.6, 2.4), 14.2, 11.6),

(2, 2007–05–27 14:38:00, (9.2, −0.46, −2.2), 11.3, −13.4),

(3, 2007–10–24 19:27:30, (5.7, −6.1, 0.5), 8.5, 3.4),

(4, 2006–03–21 05:15:53, (−2.5, 7.2, 4.0e-2), 7.6, 0.3),

(5, 2006–03–21 04:44:25, (−2.2, 7.1, 3.0e-2), 7.4, 0.2),

(6, 2006–03–21 04:23:05, (−1.9, 7.0, 3.0e-2), 7.3, 0.2),

(7, 2005–10–30 07:34:48, (−6.9, 1.4, 5.0e-2), 7.0, 0.4)}.

Flux tube entropy, S, and content, N, were calculated from the Cassini (CAPS, CHEMS, MAG) observations, the pressure and density scale height parameters obtained from a method developed in Thomsen et al. (2010), and Achilleos magnetic field model (Achilleos et al., 2010). S and N were calculated inside and outside (ambient) the injected flux tubes with the assumption that the injected flux tube plasma is isotropic and outside is anisotropic. This assumption is perhaps more similar to old injections (Mitchell et al., 2015) and to the selected events.

Figure 1 shows TS, E_t, and G_t for the 7 injected events. At large L (L > 11), E_t < 0, G_t < 0, and hence TS < 0. Apparently, the entropy and effective gravity terms work in tandem to destabilize flux tube to move inward. As the plasma moves inward, the ambient flux tube entropy (S_a) becomes smaller, which allows G_t to become more positive. At some point, at 8.5 < L < 11, E_t > 0, G_t < 0, |E_t| = |G_t|, and hence TS = 0, and equilibrium is reached. At L < 8.5, with the exception of one event (Event 6), E_t > 0 and |E_t| > |G_t|, which causes TS > 0. A possible interpretation is that the injection may overshoot the equilibrium and oscillate around equilibrium as observed at Earth (Wolf et al., 2012; Panov et al., 2013; Merkin et al., 2019; Yang et al., 2019). Thus, at L < 8.5, if the flux tube is not moving outward, its inward motion is decelerating.

Figure 1

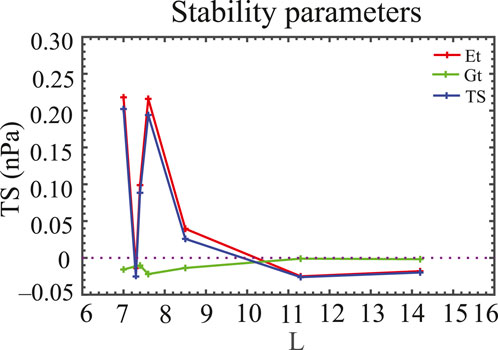
Figure 1. The evolution of the stability parameters TS, E_t, and G_t. The red, green, and blue curves correspond to E_t, G_t, and TS, respectively (from Wing et al., 2022).

It is worth noting that in all cases but one, |E_t| dominates |G_t|. G_t is negative in all cases. If the plasma injection stops, it is because of the E_t term. In other words, the entropy term, E_t, acts to brake the injections at L < 11.

Wing et al. (2022) repeated the stability calculations using dipole and Khurana et al. (2006) magnetic field models. They found that qualitatively the results are similar to those obtained using Achileos et al. (2010) magnetic field model (plotted in Figure 1). However, the results obtained from using Khurana et al. (2006) and Achileos et al. (2010) models are closer to each other than those obtained using dipole magnetic field.

Ma et al. (2019) found that based on the flux tube entropy alone, plasma injections resulting from magnetodisk reconnections at r = 22.5–27.5 Rs, should reach equilibrium at r = 8.8–10.5 Rs. As shown in Figure 1, E_t < 0 at L ∼ 11.3 and E_t > 0 at L = 8.5 (the red curve in Figure 1), suggesting that based on the consideration of the flux tube entropy alone, equilibrium should be reached somewhere between 8.5 and 11.3. This result is similar to the equilibrium positions obtained in Ma et al. (2019).

4 Conclusion and summary

Wing et al. (2022) examined the stability parameters (TS, E_t, G_t) in 7 injection events ranging from L ∼ 14 to 7. Figure 1 plots these parameters.

Figure 2 shows a schematic diagram that can help illustrate the evolution of TS, E_t, G_t as plasma injection moves inward. In the left panels (panels A, B, and C), the magenta curve shows the ambient flux tube content N_a while in the right panels (panels D, E, and F), the blue curve shows the ambient flux tube entropy S_a. N_a has an outward negative gradient whereas S_a has a positive gradient. These opposite gradients have an impact on the evolution of the plasma injection as it moves inward, as discussed next.

Figure 2

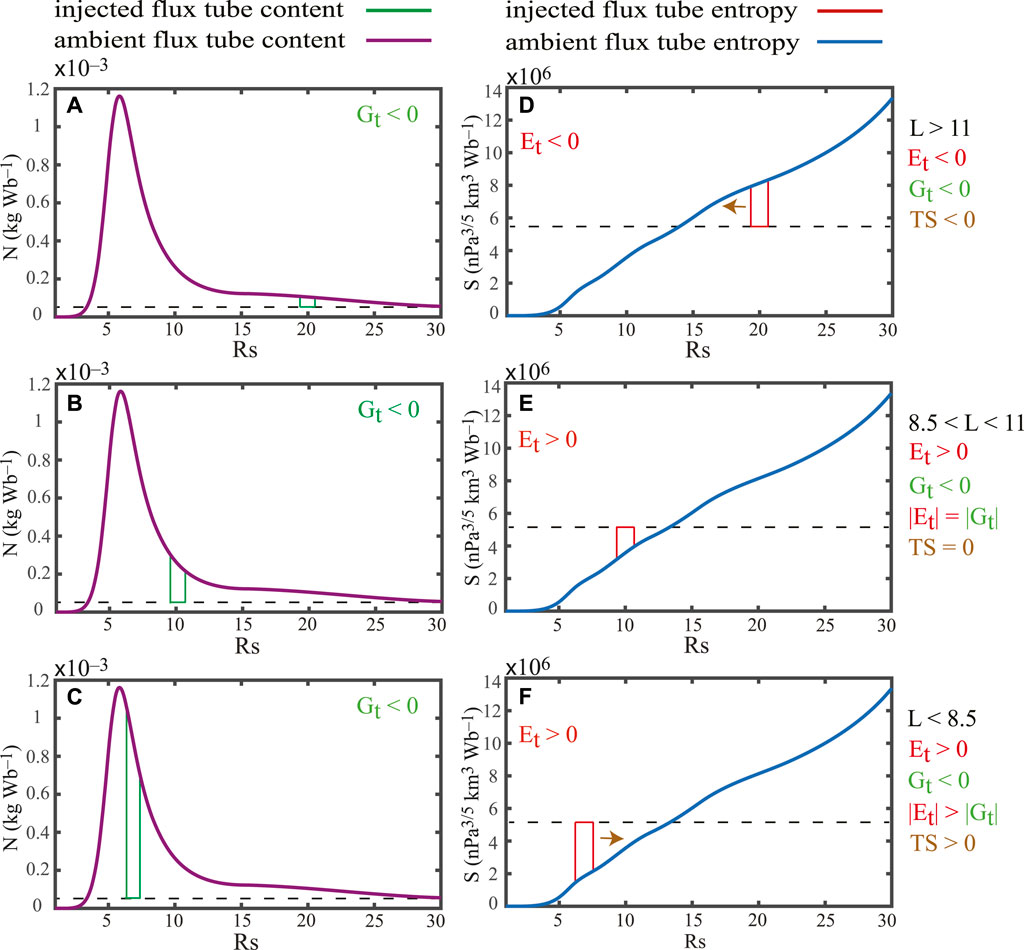
Figure 2. Schematic diagram illustrating the evolutions of TS, E_t, and G_t as the plasma injection moves inward based on Wing et al. (2022). The magenta curve on the left panels (panels A–C) show the ambient flux tube content (N_a) whereas the blue curve on the right panels (panels D–F) show the ambient flux tube entropy (S_a). In panels (A–C), the green tube is an injected flux tube content, which has lower N than N_a. The red tube is an injected flux tube entropy, which has lower S than S_a in panel (D), but higher S than S_a in panels (E, F). N_a and S_a are based on the Cassini measurements [CAPS (Thomsen et al., 2010) and CHEMS (Wing et al., 2022) moment data products] and a steady-state magnetic field model [i.e., the Saturn version of Caudal model (Caudal, 1986), see details in Ma et al. (2019)].

The evolution of G_t is illustrated in Figure 2 panels A, B, and C. The injected flux tube is characterized as having lower density (Chen and Hill, 2008; Liu et al., 2010; Thomsen et al., 2014; Thomsen et al., 2016; Azari et al., 2018) and flux tube content (Thomsen and Coates, 2019) relative to those of ambient plasma (depicted with a green tube in Figure 2). As a result, at L > 11, G_t < 0 and based on N alone, the flux tube should move inward (panel A). The centrifugal force pushes the flux tube with higher content outward while the flux tube with lower content moves inward. The flux tube that has G_t < 0 would continue having G_t < 0 as the injection moves inward because the ambient flux tube content N_a has negative gradient (panels B and C). As the injection moves inward, the difference between N_a and N_i (injected flux tube content) becomes larger and as a result, G_t becomes more negative as shown by the green tube in Figure 1 panels A–C.

However, E_t evolves differently. At large L, L > 11, the injected flux tube (depicted by the red tube in Figure 2) has lower flux tube entropy S_i relative to that of the ambient plasma S_a (panel D) and hence E_t < 0. Thus, at large L, TS < 0 because E_t < 0 and G_t < 0 (panel A) and hence, plasma moves inward. The reconnected flux tube with lower plasma density and content collapses and moves inward due to the magnetic tension force. Here, the centrifugal and the magnetic tension forces work in tandem to push the flux tube inward. As the injection moves inward, the ambient flux tube entropy S_a gets smaller, but the pressure increases, which would tend to resist further collapse of the injected flux tube. As a result, E_t becomes more positive. At some point at 8.5 < L < 11, the injected flux tube entropy S_i is slightly larger than that of the ambient plasma S_a, E_t is slightly positive, G_t remains negative (panel B), |E_t| = |G_t|, TS = 0, the net force is zero, and equilibrium is reached (panel E). However, the injection may overshoot and oscillate around the equilibrium as seen in observations and simulations at Earth (e.g., Wolf et al., 2012; Panov et al., 2013; Merkin et al., 2019; Yang et al., 2019). So, at L < 8.5, the injected flux tube entropy S_i is much larger than that of the ambient plasma S_a, E_t > 0 (panel F), G_t < 0 (panel C), but because E_t dominates G_t, TS > 0 (panel f). The ambient pressure force, which dominates other forces, pushes the injected flux tube outward. If the flux tube is not actually moving outward, its inward motion should be decelerating at this point. While the injected flux tube moves inward, it can lose integrity as plasma from the injected flux tube drifts out while the ambient plasma drifts in, which can also help stabilize the injection. After a while, the injected flux tube would be indistinguishable from the background or ambient plasma.

The schematic diagram depicted in Figure 2 is constructed using only the 7 events in the Wing et al. (2022) study. Even with the small number events, the equilibrium locations obtained from the consideration of flux tube entropy alone (E_t) are remarkably similar to those obtained statistically in Ma et al. (2019). Nonetheless, the exact L or region where the equilibrium is reached (TS = 0) can be expected to vary slightly from one event to another, depending on magnetospheric activity and other conditions. With more data points, one can perhaps determine statistically the region where the transitions from TS < 0 to TS = 0 and to TS > 0 occur, which may differ from those shown in Figure 2. However, the basic description of the evolution of TS, E_t, and G_t parameters as the plasma moves inward should still apply.

It is interesting to compare the roles of E_t and G_t in plasma injections at the terrestrial and Saturnian magnetospheres. At Earth, E_t plays a significant role in moving plasma injection inward and braking the injection (Birn et al., 2006; 2009; Pontius and Wolf, 1990; Wing and Johnson, 2009; Wing and Johnson, 2010; Wing et al., 2014; Johnson and Wing, 2009; Dubyagin et al., 2010). The G_t term is negligible. The injection reaches equilibrium when E_t = 0. At Saturn, the picture is more complicated. E_t and G_t work in tandem to move the injection inward at L > 11. The G_t term is always negative because of the negative gradient of the ambient flux tube content. As the injection gets closer to the planet (L < 11), the E_t term becomes positive and acts to oppose that of G_t. Because E_t dominates G_t, E_t acts to brake the injection.

Azari et al. (2018), Azari et al. (2019) found that statistically, plasma injections rarely reach r < 6 Rs. The stability analysis presented in Wing et al. (2022) and reviewed herein can be seen as consistent with the observations.

Author contributions

SW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. JRJ: Formal Analysis, Investigation, Methodology, Writing–review and editing, Conceptualization. MFT: Formal Analysis, Investigation, Methodology, Writing–review and editing, Data curation. XM: Data curation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. We acknowledge the support of NASA grants 80NSSC22K0310, 80NSSC20K0704, 80NSSC22K0515, 80NSSC19K0899, 80NSSC23K0904, 80NSSC20K1279 and NSF grant 2131013.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achilleos, N., André, N., Blanco-Cano, X., Brandt, P. C., Delamere, P. A., and Winglee, R. (2015). 1. Transport of mass, momentum and energy in planetary magnetodisc regions. Space Sci. Rev. 187 (1–4), 229–299. doi:10.1007/s11214-014-0086-y

CrossRef Full Text | Google Scholar

Achilleos, N., Guio, P., and Arridge, C. S. (2010). A model of force balance in Saturn’s magnetodisc. Mon. Notices R. Astronomical Soc. 401 (4), 2349–2371. doi:10.1111/j.1365-2966.2009.15865.x

CrossRef Full Text | Google Scholar

André, N., Dougherty, M. K., Russell, C. T., Leisner, J. S., and Khurana, K. K. (2005). Dynamics of the Saturnian inner magnetosphere: first inferences from the Cassini magnetometers about small-scale plasma transport in the magnetosphere. Geophys. Res. Lett. 32, L14S06. doi:10.1029/2005GL022643

CrossRef Full Text | Google Scholar

André, N., Persoon, A. M., Goldstein, J., Burch, J. L., Louarn, P., Lewis, G. R., et al. (2007). Magnetic signatures of plasma-depleted flux tubes in the Saturnian inner magnetosphere. Geophys. Res. Lett. 34, L14108. doi:10.1029/2007GL030374

CrossRef Full Text | Google Scholar

Azari, A. R., Jia, X., Liemohn, M. W., Hospodarsky, G. B., Provan, G., Ye, S.-Y., et al. (2019). Are Saturn's interchange injections organized by rotational longitude? J. Geophys. Res. Space Phys. 124, 1806–1822. doi:10.1029/2018JA026196

CrossRef Full Text | Google Scholar

Azari, A. R., Liemohn, M. W., Jia, X., Thomsen, M. F., Mitchell, D. G., Sergis, N., et al. (2018). Interchange injections at Saturn: statistical survey of energetic H⁺ sudden flux intensifications. J. Geophys. Res. Space Phys. 123, 4692–4711. doi:10.1029/2018JA025391

CrossRef Full Text | Google Scholar

Bagenal, F., and Delamere, P. A. (2011). Flow of mass and energy in the magnetospheres of Jupiter and Saturn. J. Geophys. Res. 116, A05209. doi:10.1029/2010JA016294

CrossRef Full Text | Google Scholar

Birn, J., Hesse, M., and Schindler, K. (2006). Entropy conservation in simulations of magnetic reconnection. Phys. Plasmas 13, 092117. doi:10.1063/1.2349440

CrossRef Full Text | Google Scholar

Birn, J., Hesse, M., Schindler, K., and Zaharia, S. (2009). Role of entropy in magnetotail dynamics. J. Geophys. Res. 114, A00D03. doi:10.1029/2008JA014015

CrossRef Full Text | Google Scholar

Burch, J. L., Goldstein, J., Hill, T. W., Young, D. T., Crary, F. J., Coates, A. J., et al. (2005). Properties of local plasma injections in Saturn's magnetosphere. Geophys. Res. Lett. 32, L14S02. doi:10.1029/2005GL022611

CrossRef Full Text | Google Scholar

Caudal, G. (1986). A self-consistent model of Jupiter's magnetodisc including the effects of centrifugal force and pressure. J. Geophys. Res. 91 (A4), 4201–4221. doi:10.1029/JA091iA04p04201

CrossRef Full Text | Google Scholar

Chen, Y., and Hill, T. W. (2008). Statistical analysis of injection/dispersion events in Saturn's inner magnetosphere. J. Geophys. Res. 113, A07215. doi:10.1029/2008JA013166

CrossRef Full Text | Google Scholar

Dougherty, M. K., Kellock, S., Southwood, D. J., Balogh, A., Smith, E. J., Tsurutani, B. T., et al. (2004). The Cassini magnetic field investigation. Space Sci. Rev. 114, 331–383. doi:10.1007/978-1-4020-2774-1_4

CrossRef Full Text | Google Scholar

Dubyagin, S., Sergeev, V., Apatenkov, S., Angelopoulos, V., Nakamura, R., McFadden, J., et al. (2010). Pressure and entropy changes in the flow-braking region during magnetic field dipolarization. J. Geophys. Res. 115, A10225. doi:10.1029/2010JA015625

CrossRef Full Text | Google Scholar

Erickson, G. M., and Wolf, R. A. (1980). Is steady convection possible in the Earth’s magnetotail? Geophys. Res. Lett. 7, 897–900. doi:10.1029/GL007i011p00897

CrossRef Full Text | Google Scholar

Ferrière, K. M., Zimmer, C., and Blanc, M. (2001). Quasi-interchange modes and interchange instability in rotating magnetospheres. J. Geophys. Res. 106 (A1), 327–343. doi:10.1029/2000JA000133

CrossRef Full Text | Google Scholar

Hill, T. W. (1976). Interchange stability of a rapidly rotating magnetosphere. Planet. Space Sci. 24, 1151–1154. doi:10.1016/0032-0633(76)90152-5

CrossRef Full Text | Google Scholar

Hill, T. W., Rymer, A. M., Burch, J. L., Crary, F. J., Young, D. T., Thomsen, M. F., et al. (2005). Evidence for rotationally driven plasma transport in Saturn's magnetosphere. Geophys. Res. Lett. 32, L14S10. doi:10.1029/2005GL022620

CrossRef Full Text | Google Scholar

Johnson, J. R., and Wing, S. (2009). Northward interplanetary magnetic field plasma sheet entropies. J. Geophys. Res. 114, A00D08. doi:10.1029/2008JA014017

CrossRef Full Text | Google Scholar

Kennelly, T. J., Leisner, J. S., Hospodarsky, G. B., and Gurnett, D. A. (2013). Ordering of injection events within Saturnian SLS longitude and local time. J. Geophys. Res. Space Phys. 118, 832–838. doi:10.1002/jgra.50152

CrossRef Full Text | Google Scholar

Khurana, K. K., Arridge, C. S., Schwarzl, H., and Dougherty, M. K. (2006). A model of Saturn's magnetospheric field based on latest Cassini observations. Eos Trans. AGU 87 (36).

Google Scholar

Krimigis, T., Mitchell, D. G., Hamilton, D. C., Livi, S., Dandouras, J., Jaskulek, S., et al. (2004). Magnetosphere imaging instrument (MIMI) on the Cassini mission to saturn/titan. Space Sci. Rev. 114, 233–329. doi:10.1007/s11214-004-1410-8

CrossRef Full Text | Google Scholar

Lewis, G. R., Andre, N., Arridge, C. S., Coates, A. J., Gilbert, L. K., Linder, D. R., et al. (2008). Derivation of density and temperature from the Cassini-Huygens CAPS electron spectrometer. Planet. Space Sci. 56, 901–912. doi:10.1016/j.pss.2007.12.017

CrossRef Full Text | Google Scholar

Liu, X., and Hill, T. W. (2012). Effects of finite plasma pressure on centrifugally driven convection in Saturn’s inner magnetosphere. J. Geophys. Res. 117, A07216. doi:10.1029/2012JA017827

CrossRef Full Text | Google Scholar

Liu, X., Hill, T. W., Wolf, R. A., Sazykin, S., Spiro, R. W., and Wu, H. (2010). Numerical simulation of plasma transport in Saturn’s inner mag-netosphere using the Rice Convection Model. J. Geophys. Res. 115, A12254. doi:10.1029/2010JA015859

CrossRef Full Text | Google Scholar

Long, M., Cao, X., Gu, X., Ni, B., Qu, S., Lou, Y., et al. (2023). Excitation of Saturnian ECH waves within remote plasma injections: Cassini observations. Geophys. Res. Lett. 50, e2022GL101969. doi:10.1029/2022GL101969

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P. A., and Otto, A. (2016). Plasma transport driven by the Rayleigh-Taylor instability. J. Geophys. Res. Space Phys. 121, 5260–5271. doi:10.1002/2015JA022122

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P. A., Thomsen, M. F., Otto, A., Neupane, B., Burkholder, B. L., et al. (2019). Flux tube entropy and specific entropy in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 124, 1593–1611. doi:10.1029/2018JA026150

CrossRef Full Text | Google Scholar

McIlwain, C. E. (1961). Coordinates for mapping the distribution of magnetically trapped particles. J. Geophys. Res. 66 (11), 3681–3691. doi:10.1029/JZ066i011p03681

CrossRef Full Text | Google Scholar

Menietti, J. D., Santolik, O., Rymer, A. M., Hospodarsky, G. B., Persoon, A. M., Gurnett, D. A., et al. (2008). Analysis of plasma waves observed within local plasma injections seen in Saturn's magnetosphere. J. Geophys. Res. 113, A05213. doi:10.1029/2007JA012856

CrossRef Full Text | Google Scholar

Menietti, J. D., Yoon, P. H., Písa, D., Ye, S.-Y., Santolík, O., Arridge, C. S., et al. (2016). Source region and growth analysis of narrowband Z-mode emission at Saturn. J. Geophys. Res. Space Phys. 121 (11), 929–1011. doi:10.1002/2016JA022913

CrossRef Full Text | Google Scholar

Merkin, V. G., Panov, E. V., Sorathia, K., and Ukhorskiy, A. Y. (2019). Contribution of bursty bulk flows to the global dipolarization of the magnetotail during an isolated substorm. J. Geophys. Res. Space Phys. 124, 8647–8668. doi:10.1029/2019JA026872

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitchell, D. G., Brandt, P. C., Carbary, J. F., Kurth, W. S., Krimigis, S. M., Paranicas, C., et al. (2015). “Injection, interchange, and reconnection,” in Magnetotails in the solar System. Editors A. Keiling, C. M. Jackman, and P. A. Delamere (Hoboken, NJ: John Wiley and Sons, Inc). doi:10.1002/9781118842324.ch19

CrossRef Full Text | Google Scholar

Mitchell, D. G., Krimigis, S., Paranicas, C., Brandt, P., Carbary, J., Roelof, E., et al. (2009). Recurrent energization of plasma in the midnight-to-dawn quadrant of Saturn's magnetosphere, and its relationship to auroral UV and radio emissions. Planet. Space Sci. 57, 1732–1742. doi:10.1016/j.pss.2009.04.002

CrossRef Full Text | Google Scholar

Neupane, B. R., Delamere, P. A., Ma, X., Ng, C.-S., Burkholder, B., and Damiano, P. (2021). On the nature of turbulent heating and radial transport in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 126, e2020JA027986. doi:10.1029/2020JA027986

CrossRef Full Text | Google Scholar

Panov, E. V., Kubyshkina, M. V., Nakamura, R., Baumjohann, W., Angelopoulos, V., Sergeev, V. A., et al. (2013). Oscillatory flow braking in the magnetotail: THEMIS statistics. Geophys. Res. Lett. 40, 2505–2510. doi:10.1002/grl.50407

CrossRef Full Text | Google Scholar

Paranicas, C., Thomsen, M. F., Kollmann, P., Azari, A. R., Bader, A., Badman, S. V., et al. (2020). Inflow speed analysis of interchange injections in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 125, e2020JA028299. doi:10.1029/2020JA028299

CrossRef Full Text | Google Scholar

Pontius, D. H., and Wolf, R. A. (1990). Transient flux tubes in the terrestrial magnetosphere. Geophys. Res. Lett. 17 (1), 49–52. doi:10.1029/gl017i001p00049

CrossRef Full Text | Google Scholar

Rymer, A. M., Mauk, B., Hill, T., André, N., Mitchell, D., Paranicas, C., et al. (2009). Cassini evidence for rapid interchange transport at Saturn. Planet. Space Sci. 57, 1779–1784. doi:10.1016/j.pss.2009.04.010

CrossRef Full Text | Google Scholar

Saur, J. (2004). Turbulent heating of Jupiter’s middle magnetosphere. Astrophysical J. Lett. 602, L137–L140. doi:10.1086/382588

CrossRef Full Text | Google Scholar

Sittler, E. C., André, N., Blanc, M., Burger, M., Johnson, R. E., Coates, A., et al. (2008). Ion neutral sources and sinks within Saturn’s inner magnetosphere: Cassini results. Planet. Space Sci. 54 (1). doi:10.1016/j.pss.2007.06.006

CrossRef Full Text | Google Scholar

Southwood, D. J., and Kivelson, M. G. (1987). Magnetospheric interchange instability. J. Geophys. Res. 92 (A1), 109–116. doi:10.1029/JA092iA01p00109

CrossRef Full Text | Google Scholar

Stauffer, B. H., Delamere, P. A., Ma, X., Neupane, B. R., and Burkholder, B. L. (2019). Hybrid simulations of magnetodisc transport driven by the Rayleigh-taylor instability. J. Geophys. Res. Space Phys. 124 (7), 5107–5120. doi:10.1029/2018JA026420

CrossRef Full Text | Google Scholar

Thomsen, M. F. (2013). Saturn's magnetospheric dynamics. Geophys. Res. Lett. 40, 5337–5344. doi:10.1002/2013GL057967

CrossRef Full Text | Google Scholar

Thomsen, M. F., and Coates, A. J. (2019). Saturn's plasmapause: signature of magnetospheric dynamics. J. Geophys. Res. Space Phys. 124, 8804–8813. doi:10.1029/2019JA027075

CrossRef Full Text | Google Scholar

Thomsen, M. F., Reisenfeld, D. B., Delapp, D. M., Tokar, R. L., Young, D. T., Crary, F. J., et al. (2010). Survey of ion plasma parameters in Saturn's magnetosphere. J. Geophys. Res. 115, A10220. doi:10.1029/2010JA015267

CrossRef Full Text | Google Scholar

Thomsen, M. F., Coates, A. J., Roussos, E., Wilson, R. J., Hansen, K. C., Lewis, G. R., et al. (2016). Suprathermal electron penetration into the inner magnetosphere of Saturn. J. Geophys. Res. Space Phy. 121, 5436–5448. doi:10.1002/2016JA022692

CrossRef Full Text | Google Scholar

Thomsen, M. F., Reisenfeld, D. B., Wilson, R. J., Andriopoulou, M., Crary, F. J., Hospodarsky, G. B., et al. (2014). Ion composition in interchange injection events in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 119, 9761–9772. doi:10.1002/2014JA020489

CrossRef Full Text | Google Scholar

Thomsen, M. F., Wilson, R. J., Tokar, R. L., Reisenfeld, D. B., and Jackman, C. M. (2013). Cassini/CAPS observations of duskside tail dynamics at Saturn. J. Geophys. Res. Space Phys. 118, 5767–5781. doi:10.1002/jgra.50552

CrossRef Full Text | Google Scholar

Wing, S., Brandt, P. C., Mitchell, D. G., Johnson, J. R., Kurth, W. S., and Menietti, J. D. (2020). Periodic narrowband radio wave emissions and inward plasma transport at saturn’s magnetosphere. Ap J. 159, 249. doi:10.3847/1538-3881/ab818d

CrossRef Full Text | Google Scholar

Wing, S., and Johnson, J. R. (2009). Substorm entropies. J. Geophys. Res. 114, A00D07. doi:10.1029/2008JA013989

CrossRef Full Text | Google Scholar

Wing, S., and Johnson, J. R. (2010). Introduction to special section on entropy properties and constraints related to space plasma transport. J. Geophys. Res. 115, A00D00. doi:10.1029/2009JA014911

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Chaston, C. C., Echim, M., Escoubet, C. P., Lavraud, B., et al. (2014). Review of solar wind entry into and transport within the plasma sheet. Space Sci. Rev. 184, 33–86. doi:10.1007/s11214-014-0108-9

CrossRef Full Text | Google Scholar

Wing, S., Thomsen, M. F., Johnson, J. R., Mitchell, D. G., Allen, R. C., Ma, X., et al. (2022). The roles of flux tube entropy and effective gravity in the inward plasma transport at Saturn. Astrophysical J. 937 (1), 42. doi:10.3847/1538-4357/ac85b2

CrossRef Full Text | Google Scholar

Wolf, R. A., Chen, C. X., and Toffoletto, F. R. (2012). Thin filament simulations for Earth's plasma sheet: interchange oscillations. J. Geophys. Res. 117, A02215. doi:10.1029/2011JA016971

CrossRef Full Text | Google Scholar

Yang, J., Wolf, R., Toffoletto, F., Sazykin, S., Wang, W., and Cui, J. (2019). The inertialized rice convection model. J. Geophys. Res. Space Phys. 124, 10294–10317. doi:10.1029/2019JA026811

CrossRef Full Text | Google Scholar

Yin, Z.-F., Sun, Y.-X., Zhou, X.-Z., Pan, D.-X., Yao, Z.-H., Yue, C., et al. (2023). Trapped and leaking energetic particles in injection flux tubes of Saturn's magnetosphere. Geophys. Res. Lett. 50, e2023GL105687. doi:10.1029/2023GL105687

CrossRef Full Text | Google Scholar

Young, S., Berthelier, J. J., Blanc, M., Burch, J. L., Coates, A. J., Goldstein, R., et al. (2004). Cassini plasma spectrometer investigation. Space Sci. Rev. 114, 1–112. doi:10.1007/978-1-4020-2774-1_1

CrossRef Full Text | Google Scholar