Bayesian inference: more than Bayes’s theorem

Bayesian inference gets its name from Bayes’s theorem, expressing posterior probabilities for hypotheses about a data generating process as the (normalized) product of prior probabilities and a likelihood function. But Bayesian inference uses all of probability theory, not just Bayes’s theorem. Many hypotheses of scientific interest are composite hypotheses, with the strength of evidence for the hypothesis dependent on knowledge about auxiliary factors, such as the values of nuisance parameters (e.g., uncertain background rates or calibration factors). Many important capabilities of Bayesian methods arise from use of the law of total probability, which instructs analysts to compute probabilities for composite hypotheses by marginalization over auxiliary factors. This tutorial targets relative newcomers to Bayesian inference, aiming to complement tutorials that focus on Bayes’s theorem and how priors modulate likelihoods. The emphasis here is on marginalization over parameter spaces—both how it is the foundation for important capabilities, and how it may motivate caution when parameter spaces are large. Topics covered include the difference between likelihood and probability, understanding the impact of priors beyond merely shifting the maximum likelihood estimate, and the role of marginalization in accounting for uncertainty in nuisance parameters, systematic error, and model misspecification.

1 Introduction

The Bayesian approach to statistical inference and other data analysis tasks gets its name from Bayes’s theorem (BT). BT specifies that a posterior probability for a hypothesis concerning a data generating process may be computed by multiplying a prior probability and a likelihood function (and normalizing):

$\text{posterior}\propto \text{prior}\times \text{likelihood}.(1)$

Tutorials on Bayesian methods often focus on how BT adjusts the likelihood function to account for base rates of hypotheses about members of a population, using simple examples like binary classification (e.g., disease/no-disease; guilty/not-guilty; star/galaxy) based on binary diagnostic data (e.g., a positive or negative test or evidentiary result). At the iid 2022: Statistical Methods for Event Data meeting that is the topic of this special issue of Frontiers, a charming and insightful tutorial along these lines was presented by Torsten Enßlin; see his “Bayes Basics” presentation at the meeting’s website.

In this tutorial contribution to the issue we address readers familiar with (and perhaps already using) Bayesian methods, to make the case that a focus on Bayes’s theorem risks overlooking a more fundamental and crucial aspect of Bayesian inference. We consider a key distinguishing feature of Bayesian inference to be is its use of the law of total probability (LTP), directing one to compute probabilities for composite hypotheses by marginalizing over the hypothesis or parameter space.

We do not consider this a new or controversial insight. The first author came to appreciate it as a student of the work of Jeffreys (1961), Jaynes (2003), Zellner (1971), and other mid-20th-century pioneers of modern Bayesian inference, and through the work of the second author and Jim Berger (Berger and Wolpert (1988), especially §§ 3.5 and 5.3). We have highlighted this in the past (e.g., in Loredo (1992; 1999; 2013); Berger et al. (1999), and in lectures at the Penn State Summer School in Statistics for Astronomers). But we feel this aspect of Bayesian analysis is underappreciated, especially by newcomers and non-experts. With the growing importance of high-dimensional models in statistics and machine learning (ML) there is new motivation for highlighting it. In particular, ML relies heavily on optimization over large parameter spaces, where, from a Bayesian perspective, marginalization may instead be the right operation. Recent research demonstrates that the performance of some ML models can be significantly enhanced by replacing optimization with marginalization (even approximately), particularly in settings were good uncertainty quantification is important. Andrew Wilson’s Bayesian machine learning group has done particularly notable work in this direction (Wilson, 2020; Wilson and Izmailov, 2020). It seems to us the crucial importance of the LTP and marginalization deserves amplification, particularly for newcomers to Bayesian methods.

In this tutorial, we start by establishing notation and informally reviewing BT, the LTP, and the Bayesian interpretation of probability. Then we explore the role of marginalization in Bayesian inference in the context of the following topics:

$•$ Likelihood vs. probability: We review Fisher’s introduction of likelihood as a complement to probability, and the use of BT to “flip the conditional” and create a posterior distribution from a likelihood function. Newcomers to Bayesian inference who use the term “likelihood of the data” will find a corrective here.

$•$ Priors are not (merely) penalties: A prior distribution does more than just shift the peak of the likelihood function; it converts the likelihood to a quantity that can be meaningfully integrated. In even modest-dimension spaces, so-called “curses of dimensionality” and related ideas imply that integrated probability can pile up in unexpected ways, away from the peak of the likelihood function.

$•$ Marginalization vs. optimization over nuisance parameters: Most data analysis problems in astronomy rely on models that include both parameters of direct scientific interest, and nuisance parameters—parameters (e.g., describing backgrounds) that are necessary for linking the interesting parameters to the data. Bayesian methods marginalize (average) over nuisance parameters to account for their uncertainty. We contrast marginalization with a popular alternative approach relying on optimization instead. We also discuss so-called measurement error problems (a statistics term of art), where the differences between marginalization and optimization can be amplified.

$•$ Marginalization and systematic error: We briefly describe recent and ongoing work using marginalization to describe and propagate systematic error in settings where standard “propagation of error” (the statisticians’ “delta method”) fails or is inapplicable. A Supplementary Appendix provides more details on some of this work.

2 Notation and basic concepts

We adopt notation similar to that of Jeffreys, Cox, and Jaynes, who view Bayesian inference as a generalized logic (Cox, 1946; Jeffreys, 1961; Jaynes, 2003). Whereas deductive logic provides a calculus for truth and falsity in settings where we can reason with certainty (e.g., with truth and falsity represented by 1 and 0 in Boolean algebra), probability theory provides a calculus for degrees of entailment, or argument strength, in settings where we must quantify uncertainty (with probabilities taking values over the real interval, [0,1]). We use $P(A|B)$ to denote the probability that the truth of statement $A$ follows from taking statement $B$ to be true (whether $B$ is known to be true or just assumed to be true). We call this the conditional probability for $A$ given $B$. Interpreting probability as a measure of entailment or argument strength means that all probabilities are necessarily conditional. The argument of a probability symbol is the whole expression inside the parentheses—$A|B$ here—understood as the statement that the truth of $A$ follows from the truth $B$. In logic, such a statement is called an argument, so we may say that the argument of a (Bayesian) probability symbol is, well, an argument. The conditioning statements comprise the premises for the argument (the “givens”).

We will often be computing a collection of probabilities that share common conditions that will not be questioned (i.e., they never appear to the left of the conditioning bar), at least for the duration of a specific calculation. We often denote such conditioning information by $\mathcal{C}$, the context for the calculation. Some contextual information may represent secure knowledge (e.g., basic physical principles that firmly justify some probability distributions appearing in an analysis). Other contextual information may represent less secure, provisional assumptions, adopted “for the sake of the argument,” to enable us to compute probabilities required in the course of an analysis; such assumptions ideally should be reassessed in a later stage of analysis¹.

Complex statements may be built by combining simpler statements. For example, we use $(A,B)$ to denote “$A$ and $B$ are both true,” and $(A\vee B)$ to denote “$A$ is true, or $B$ is true, or both.” Two important basic rules of probability are the conjunction rule (the “and” or “product” rule):

$\begin{array}{ll}\hfill P\left(A,B|\mathcal{C}\right)& =P\left(A|\mathcal{C}\right)P\left(B|A,\mathcal{C}\right)\hfill \\ \hfill & =P\left(B|\mathcal{C}\right)P\left(A|B,\mathcal{C}\right),\hfill \end{array}(2)$

and the disjunction rule (the “or” or “sum” rule):

$P\left(A\vee B|\mathcal{C}\right)=P\left(A|\mathcal{C}\right)+P\left(B|\mathcal{C}\right)-P\left(A,B|\mathcal{C}\right).(3)$

We presume the reader is familiar with these basics; they are here to establish notation and terminology.

We often compute probabilities for collections of statements labeled by an integer or a real-valued parameter (or vector of parameters). In such cases we use a lower-case $p$ (or another letter) to denote the appropriately labeled probabilities. For discrete cases, the probabilities comprise a probability mass function (PMF), such as $p_i=P(A_i|\mathcal{C})$ (for $i$ an integer over some specified range). For continuous cases, we instead use a probability density function (PDF), defined so that for a parameter $\theta$ the probability assigned to an interval of size $d\theta$ is $p(\theta )d\theta =P({\theta }_{\ast }\in [\theta ,\theta +d\theta ]|\mathcal{C})$, where ${\theta }_{\ast }$ is the (uncertain) true value of the parameter. So the argument of a probability symbol is an argument (comprised of statements comprising premises and a conclusion), and the argument or index of a PMF or PDF symbol is a number.

When conditioning information is common to all probability symbols in a formula it can be distracting to display it explicitly. We sometimes suppress symbols for common conditions for clarity, when the conditions are clear from the context. When we do want to display a common dependence, we adopt clever notation introduced by John Skilling (the “Skilling conditional”), showing the shared information with a double bar beside the equations, as here:

$P\left(A,B\right)=P\left(A\right)P\left(B|A\right)\Vert \mathcal{C}.(4)$

In what follows we will focus on Bayesian inference—computing probabilities for hypotheses of interest given data and other information, including modeling assumptions. Bayesian inference is the core of Bayesian data analysis (BDA), comprising the use of Bayesian probability for a broader variety of tasks, including making decisions (Bayesian decision theory), designing experiments (Bayesian experimental design), and addressing tasks where there is not enough structure for formal inference (e.g., Bayesian model checking and Bayesian exploratory data analysis). Marginalization plays a key role in all of these data analytical activities. The book Bayesian Data Analysis (Gelman et al., 2014a) provides comprehensive coverage of many topics comprising BDA. An emerging term of art, Bayesian workflow, refers to best practices for integrating diverse Bayesian techniques (including methods fusing Bayesian and frequentist considerations) into robust data analysis pipelines that include model checking and refinement steps. Gelman et al. (2020) provide a broad discussion of Bayesian workflow; Tak et al. (2018) and Eadie et al. (2023) discuss key components of sound Bayesian workflow in astrostatistics.

3 Bayes’s theorem and interpreting probability

If we equate the two factorizations on the right hand side of Equation 2 and solve for $P(A|B,\mathcal{C})$, we get Bayes’s theorem,

$P\left(A|B\right)=\frac{P\left(A\right)P\left(B|A\right)}{P\left(B\right)}\Vert \mathcal{C},(5)$

provided that $P(B)\ne 0$². We can view BT as showing how adding statements to the premises in an argument should change the degree of entailment for the conclusion. Here the initial argument is that $A$ follows from $\mathcal{C}$ (the argument of the first factor in the numerator), and the argument of the probability on the left hand side asserts that $A$ follows from the combined statement $(B,\mathcal{C})$, i.e., $B$ has been added to the premises.

To get BT in a form useful for data analysis, let $H_i$ denote statements asserting rival hypotheses specifying a data generating process (DGP), indexed by $i$; let $D_{\text{\hspace{0.17em}obs}}$ denote a statement asserting the values of observed data; and let $\mathcal{C}$ denote all other information at hand, including a description of how the hypotheses and data are connected. Rewrite BT, taking $A=H_i$ and $B=D_{\text{\hspace{0.17em}obs}}$, giving

$P\left(H_i|D_{\text{\hspace{0.17em}obs}}\right)=\frac{P\left(H_i\right)P\left(D_{\text{\hspace{0.17em}obs}}|H_i\right)}{P\left(D_{\text{\hspace{0.17em}obs}}\right)}\Vert \mathcal{C}.(6)$

With these choices for the statements, the factors in this equation have names:

$•$ $P(H_i|D_{\text{\hspace{0.17em}obs}})$ is the posterior probability for hypothesis $H_i$ (given $D_{\text{\hspace{0.17em}obs}}$). Considered as a function of $i$ it is a posterior PMF. “Posterior” here refers to “after taking into account the observed data.”

$•$ $P(H_i)$ is the prior probability for $H_i$, also a PMF when considered as a function of $i$. “prior” here refers to “Prior to accounting for the observed data.”

$•$ $P(D_{\text{\hspace{0.17em}obs}}|H_i)$ is the likelihood for hypothesis $H_i$, or, considered as a function of $i$, the likelihood function. The term “likelihood” is meant to indicate it is not a probability for $H_i$, since $H_i$ is on the wrong side of the bar (in particular, ${\sum }_{i}P(D_{\text{\hspace{0.17em}obs}}|H_i)$ need not equal unity). We discuss the relationship between probability and likelihood further in § 5.

$•$ $P(D_{\text{\hspace{0.17em}obs}})$ is the prior predictive probability, the probability with which one would predict the observed data without specifying which of the $H_i$ is true.

If we are considering a continuum of hypotheses labeled by a continuous parameter $\theta$, then one may derive an analogous result involving PDFs:

$p\left(\theta |D_{\text{\hspace{0.17em}obs}}\right)=\frac{p\left(\theta \right)p\left(D_{\text{\hspace{0.17em}obs}}|\theta \right)}{p\left(D_{\text{\hspace{0.17em}obs}}\right)}\Vert \mathcal{C}(7)$

(where we have mildly overloaded our notation, using $\theta$ and $D_{\text{\hspace{0.17em}obs}}$ to denote variables for the scalar or vector parameter and data quantities when to the left of the bar, and statements asserting values for those quantities when to the right). The factors have analogous names, e.g., $p(\theta |D_{\text{\hspace{0.17em}obs}})$ is the posterior PDF for $\theta$.

There is nothing controversial in BT as an uninterpreted mathematical result. But a problem arises in its use for data analysis if one insists on adopting a frequentist interpretation of probability. Such interpretations assert that probabilities can be meaningfully assigned and manipulated only for statements about quantities that take on diverse values in some kind of replication setting; such statements are called events³. In such settings, the probability for an event is the fraction of the time the event happens (the statement is true) among replications, as the number of replications tends to infinity⁴. The frequentist view is significantly restrictive. It allows us to say, “the probability for heads is $1/2$,” interpreted as a property of an ensemble of flips of a coin. But it does not allow us to say, “the probability for heads on the next flip is $1/2$,” if we are about to flip a coin just once.

More importantly, the frequentist interpretation does not permit assigning or computing probabilities for hypotheses about fixed but uncertain properties of a physical system. For example, in the 1800s Laplace famously used Bayesian probability (the historically original notion of probability) to analyze detailed but noisy observations of Saturn’s orbit to estimate the ratio of Saturn’s mass to the Sun’s mass. He estimated the ratio to be within $\pm 1\%$ of $2.847\times 10^{-4}$, with a probability of 0.99991. (The modern convention would fix the probability at some convenient target like 0.95 and find the associated range; Laplace did the reverse. The current estimate is $2.858\times 10^{-4}$, comfortably inside Laplace’s range.) Such a probability makes no sense if one adopts a frequentist interpretation. The true mass of Saturn either is or is not in that interval, and it would be either in it or outside of it for every replication of the observations. The frequentist probability for Saturn’s mass being in that interval is either 0 or 1—but we have no way of knowing which it is.

One sometimes hears a complaint from a scientist only familiar with the frequentist interpretation that they can follow the Bayesian math, but stumble at the idea that a parameter value should be considered to be “random,” a random variable taking on a distribution of values. This reflects an error in interpretation. Figure 1 is our attempt at depicting the different interpretations for a PDF for some real-valued quantity $x$ (the interpretations differ regardless of whether $x$ refers the value of a parameter or a datum). The left panel depicts the frequentist interpretation of $p(x)$; the PDF describes an infinite collection of replications, across which $x$ takes on many values, whose limiting histogram is $p(x)$. The right panel depicts the Bayesian interpretation; the PDF describes uncertainty about the value of $x$ in a single case-at-hand by distributing probability over the values $x$ may take (depicted by the shading along the $x$ axis). In the frequentist interpretation, it is the $x$ in $p(x)$ that is distributed (across replications). In the Bayesian interpretation, it is the $p$ in $p(x)$ that is distributed (across possible values $x$ may take in the case at hand). A Bayesian PDF is analogous to a matter density, $\rho (x)$, in classical mechanics; it is the matter that is distributed, not values of $x$.

Figure 1

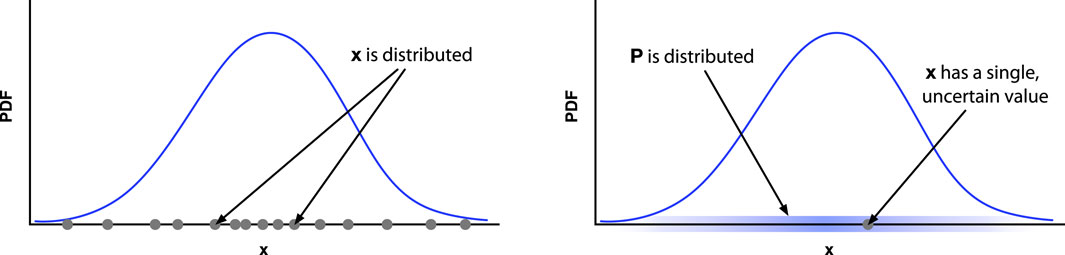
Figure 1. Frequentist and Bayesian interpretations of a PDF (blue curve) for a real-valued quantity $x$. Left: Frequentist interpretation as a (limiting) histogram of values $x$ takes across replications; the values of $x$ are distributed according to the PDF. Right: Bayesian interpretation as $x$ taking a single fixed (but uncertain) value in the case at hand (dot on the $x$ axis), with probability distributed over the possible values (depicted via the shading along the $x$ axis).

4 The law of total probability and marginalization

BT followed from the conjunction (“and”) rule. The LTP follows from application of both the conjunction and disjunction (“or”) rules to problems where a statement of interest may be true or false depending on what is true about auxiliary details in the problem. As simple example, consider rolling a die, and a hypothesis about the outcome of a single roll, $H=$ “The number of dots on the top face is a prime.” Let the auxiliary detail be the actual number that comes up, with $B_i=$ “The side with $i$ dots is up.” Here $H$ is true when any of $B_2$, $B_3$, or $B_5$ is true, and false otherwise. Note also that only one of the $B_i$ statements may be true. We say that $H$ is a composite hypothesis: there are multiple ways it may be true or false, given the nature of the problem (the context). Here the $B_i$ comprise an exclusive, exhaustive set of statements—a collection of statements such that our contextual information asserts one of them must be true, but only one. Downey (2021) dubs such a set a suite, terminology we like that is not yet widely used.

In such settings, the joint probability (“and”) for $H$ and one of the $B_i$ may be factored as $P(H,B_i)=P(H)P(B_i|H)$. Now sum this over $i$, noting that $P(H)$ does not depend on $i$ and so may be taken out of the sum:

${\displaystyle \sum _i}P\left(H,B_i\right)=P\left(H\right){\displaystyle \sum _i}P\left(B_i|H\right)=P\left(H\right)\Vert \mathcal{C},(8)$

where for the final equation we used repeated application of the “or” rule and the suite property to show that ${\sum }_{i}P(B_i|H,\mathcal{C})$ is unity. We thus have the LTP:

$\begin{array}{ll}\hfill P\left(H\right)& ={\displaystyle \sum _i}P\left(H,B_i\right)\hfill \\ \hfill & ={\displaystyle \sum _i}P\left(B_i\right)P\left(H|B_i\right)\Vert \mathcal{C},\hfill \end{array}(9)$

where the last line uses the alternative factorization of $P(H,B_i)$. The summing over auxiliary details is called marginalization, after the practice of collecting values of a joint probability in a table and listing sums across rows and columns in the margins of the table. The LTP is a kind of “decomposition/recomposition” result that is used in two ways.

First, if we have a problem where both $H$ (or a set of alternatives, $H_j$) and $B_i$ are present from the start, so $P(H,B_i)$ is available, the top line of Equation 9 tells us how to compute the probability for $H$ if it alone is of interest: sum the joint over the ways $H$ may be true.

Second, if we have a problem where initially only $H$ is present but we do not immediately see how to compute or assign $P(H)$, the second line of Equation 9 suggests doing something reminiscent of a basis expansion: identify some additional detail that, if known, would let you compute the probability for $H$; that is, find a suite, $B_i$, so that $P(H|B_i)$ is known. Then sum over the possible choices of auxiliary details, weighting the terms by the probabilities for each choice. This has been called “extending the conversation” (Lindley et al., 1978). Harvard statistician Joseph Blitzstein offers a different term in one of his YouTube lectures (see “Statistics 110, Lecture 6: Monty Hall, Simpson’s Paradox,” slightly paraphrased here):

In most mathematical subjects, if you have a problem and you’re stuck, saying “I wish I knew this or that” does not help you. In probability theory, thinking “I wish I knew this” gives you a hint at what you should condition on. Then you condition on it, act as if you did know it, and then average over those possibilities.

I did not name the law of total probability, but if I had, I would have just called it wishful thinking: what do I wish I knew?

In continuous-parameter settings where uncertainty may be quantified by PDFs, the LTP instructs us to integrate over those parameters specifying choices of auxiliary details.

In a typical Bayesian data analysis application, one will begin by using BT to define a posterior distribution, but then use that distribution by applying the LTP to address diverse tasks. Here are several such tasks:

$•$ Normalizing posterior PDFs: The posterior predictive probability in the denominator of BT in Equation 7 appears to play the role of a normalization constant, in that it does not depend on $\theta$. We can show this explicitly using the “wishful thinking” version of the LTP:

$p\left(D_{\text{\hspace{0.17em}obs}}\right)=\int \mathrm{d}\theta p\left(\theta \right)p\left(D_{\text{\hspace{0.17em}obs}}|\theta \right).(10)$

Since the integrand is just the numerator of Equation 7, the LTP has both verified that the prior predictive probability is a normalization constant, and shown us how to compute it. It is also the source of the more common name for this quantity, the marginal likelihood (for the model as a whole), i.e., the weighted integral of the likelihood function.

$•$ Credible regions: Calculating the probability in a credible region, $R$, for $\theta$ may be done similarly:

$p\left(\theta \in R|D_{\text{\hspace{0.17em}obs}}\right)={\int }_{R}d\theta p\left(\theta \in R|\theta \right)p\left(\theta |D_{\text{\hspace{0.17em}obs}}\right).(11)$

There may be many regions that have a desired target amount of probability. The smallest such region is typically unique, with density higher in $R$ than outside it, and it is called a highest posterior density (HPD) credible region.

$•$ Marginalizing over nuisance parameters: Most real-life data analysis problems in astronomy have nuisance parameters: parameters required for modeling the data, but not directly interesting. Perhaps the most common such parameters are those describing backgrounds contaminating the measurement of a signal. Let $\psi$ denote the interesting (signal) parameters, and $\eta$ the nuisance (background) parameters. The uncertainty in $\psi$ (with the $\eta$ uncertainty fully propagated) is quantified by the marginal posterior PDF,

$p\left(\psi |D_{\text{\hspace{0.17em}obs}}\right)=\int d\eta p\left(\psi ,\eta |D_{\text{\hspace{0.17em}obs}}\right).(12)$

If the posterior is explored via posterior sampling (say, via MCMC), this integral may be approximated by simply making a histogram of the $\psi$ component of the posterior samples of $(\psi ,\eta )$. A popular way to handle nuisance parameters in astronomy and physics is via profile likelihood, which optimizes rather than averages over the nuisance parameters. We discuss the relationship between marginalization and optimization (profiling) at some length in § 7.

$•$ Propagation of uncertainty: Suppose we have computed a posterior PDF for a model’s parameters, $\theta$, but we are interested, not directly in $\theta$, but in a quantity $f=F(\theta )$ for a known function $F(\theta )$. This is the setting for standard “propagation of errors” techniques (known as the “delta method” in statistics), but these rely on approximations that presume the posterior is Gaussian. We can propagate uncertainty more thoroughly and accurately using the LTP to compute a marginal posterior for $f$:

$\begin{array}{ll}\hfill p\left(f|D,M\right)& =\int d\theta p\left(f,\theta |D_{\text{\hspace{0.17em}obs}},M\right)=\int \mathrm{d}\theta p\left(\theta |D_{\text{\hspace{0.17em}obs}},M\right)p\left(f|\theta ,M\right)\hfill \\ \hfill & =\int d\theta p\left(\theta |D_{\text{\hspace{0.17em}obs}},M\right)\delta \left[f-F\left(\theta \right)\right].\hfill \end{array}(13)$

If the posterior is explored via posterior sampling, this integral may be approximated by simply making a histogram of $F(\theta )$ evaluated over the posterior samples of $\theta$.

$•$ Prediction: In the context of a model with parameters $\theta$ for observed data $D_{\text{\hspace{0.17em}obs}}$, where we want to make predictions about future data we may obtain (say, for experimental design purposes), we can use the LTP to compute a posterior predictive distribution. Denoting future data by $D^{\prime }$, the posterior predictive PDF is

$p\left(D^{\prime }|D_{\text{\hspace{0.17em}obs}}\right)=\int d\theta p\left(D^{\prime }|\theta \right)p\left(\theta |D_{\text{\hspace{0.17em}obs}}\right),(14)$

with the integration accounting for parameter uncertainty in the prediction, weighting possible choices of $\theta$ by the posterior PDF.

$•$ Model comparison: To compare rival parametric models defined by contexts $M_i$ (each with parameters ${\theta }_i$), we compute posterior odds or Bayes factors. These require computation of each model’s marginal likelihood⁵

$p\left(D_{\text{\hspace{0.17em}obs}}|M_i\right)=\int d{\theta }_{i}p\left({\theta }_i|M_i\right)p\left(D_{\text{\hspace{0.17em}obs}}|{\theta }_i,M_i\right)\Vert M_1\vee M_2\dots .(15)$

This is just the normalization constant for the posterior PDF for a particular model’s parameters. This says that the likelihood for a model (as a whole, i.e., accounting for uncertainty in its parameters) is the average of the likelihood function for that model’s parameters⁶.

$•$ Model averaging: Consider again a setting with rival parametric models with contexts $M_i$, but where all models share some interesting parameters, $\varphi$, but supplement them with different sets of nuisance parameters, ${\eta }_i$. An example from cosmology is estimating the curvature and size of the universe, accounting for uncertainty in the choice of cosmological models (e.g., whether dark energy is due to a cosmological constant or is instead evolving, thus possibly requiring additional parameters for the dark energy equation of state; see Vardanyan et al., 2011). In settings where no particular model is strongly preferred over its rivals, we would like to account for model uncertainty in estimation of $\varphi$. Let $\mathcal{C}$ here denote an overall context, collecting all rival models. Model averaging uses the LTP to propagate both model and nuisance parameter uncertainty as follows:

$\begin{array}{cc}\hfill p\left(\varphi |D,\mathcal{C}\right)=& {\displaystyle \sum _i}p\left(M_i|D,\mathcal{C}\right)p\left(\varphi |D,M_i\right)\hfill \\ \hfill & \propto {\displaystyle \sum _i}p\left(D_{\text{\hspace{0.17em}obs}}|M_i\right)\int d{\eta }_{i}p\left(\varphi ,{\eta }_i|D,M_i\right),\hfill \end{array}(16)$

where for the last line we presume the models are considered equally probable a priori, so that the probability for each model is proportional to its marginal likelihood, $p(D_{\text{\hspace{0.17em}obs}}|M_i)$.

This is not an exhaustive list, but surely is long enough to make the case for the powerful role the LTP plays in Bayesian inference.

5 Likelihood vs probability

A parametric model for data specifies how one may predict or simulate hypothetical data, $D$, as a function of a fixed-dimension parameter vector, $\theta$. That is, a parametric model is a collection of sampling distributions, a bivariate function of hypothetical values of the parameter, and hypothetical values of the data:

$p\left(D|\theta \right)=f\left(D;\theta \right).(17)$

Each sampling distribution is a probability disribution for data.

The likelihood function fixes $D=D_{\text{\hspace{0.17em}obs}}$, yielding a function only of $\theta$:

$\mathcal{L}\left(\theta \right)\equiv p\left(D_{\text{\hspace{0.17em}obs}}|\theta \right)=f\left(D_{\text{\hspace{0.17em}obs}};\theta \right).(18)$

The likelihood function is not a probability distribution for $\theta$ ($\theta$ is on the wrong side of the bar). Strictly speaking, any positive multiple of $p(D_{\text{\hspace{0.17em}obs}}|\theta )$ may serve as the likelihood function. The multiplier may be constant or a function of $D_{\text{\hspace{0.17em}obs}}$; such factors do not change the dependence of $\mathcal{L}(\theta )$ on $\theta$, which is what governs inference (Berger and Wolpert, 1988). Any such factor would also appear in the prior predictive probability, $p(D_{\text{\hspace{0.17em}obs}})$, and thus cancel in BT.

In Figure 2 we depict the relationship between the sampling distribution and the likelihood function for estimation of the probability of a binary outcome from data counting the number of successes in a sequence of trials or tests—think of counting the number of heads in flips of coins, or the number of stars in a sequence of star/galaxy separation tests in image data. This is a case where the sample space is discrete (and so the sampling distribution is a PMF), and the parameter space is continuous (so the likelihood function is continuous). The blue histogram shows the binomial distribution giving the probability for seeing $n$ successes in $N$ total trials with a success probability specified by the real-valued parameter $\theta$,

$p\left(n|\theta ,\mathcal{C}\right)=\frac{N!}{n!\left(N-n\right)!}{\theta }^n{\left(1-\theta \right)}^{N-n},(19)$

where the context includes specification of the total number of trials, $N$; the histogram is for θ = 0.5. The black curves show potential likelihood functions corresponding to different numbers of successes, $n$. Once $n=13$ is observed, the particular curve highlighted in red is identified as the likelihood function relevant for inference.

Figure 2

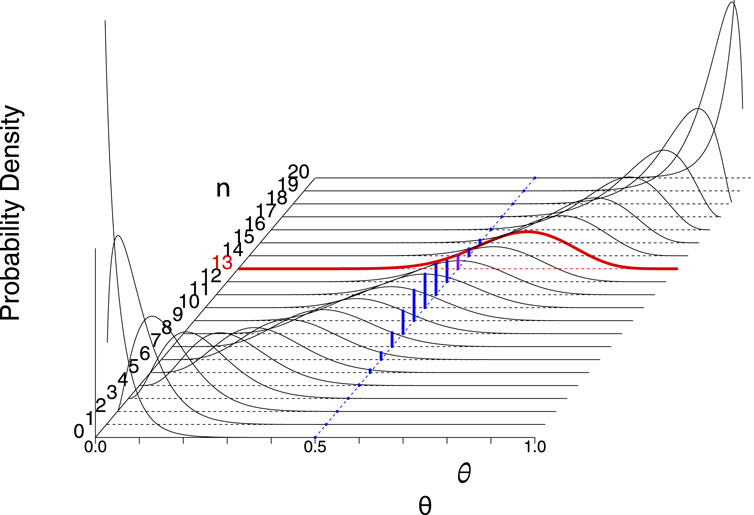
Figure 2. The relationship between the sampling distribution and likelihood functions for estimation of the success probability parameter, $\alpha$, specifying a binomial distribution for the number of successes, $n$, expected in $N=20$ trials. The blue histogram shows the binomial PMF as a function of $n$ for one particular choice of $\mathit{\theta }$ (0.5). The black curves show potential likelihood functions corresponding to different numbers of successes, $n$. Once an observed value, $n=13$, is available, the actual likelihood is identified as the red curve.

Figure 3 shows a complementary case, where both the sample space and the parameter space are continuous, and the sample space is two-dimensional. It depicts the relationship between the sampling distributions for a model with a parameter $\mu$ determining predictions for 2-dimensional data $(x_1,x_2)$. Here $\mu$ is the common mean of two independent normal distributions for $(x_1,x_2)$ (with known standard deviation $\sigma$, specified in $\mathcal{C}$), so

$p\left(x_1,x_2|\mu ,\mathcal{C}\right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\left(x_1-\mu \right)}^2}{2{\sigma }^2}\right]\times \frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\left(x_2-\mu \right)}^2}{2{\sigma }^2}\right].(20)$

Figure 3

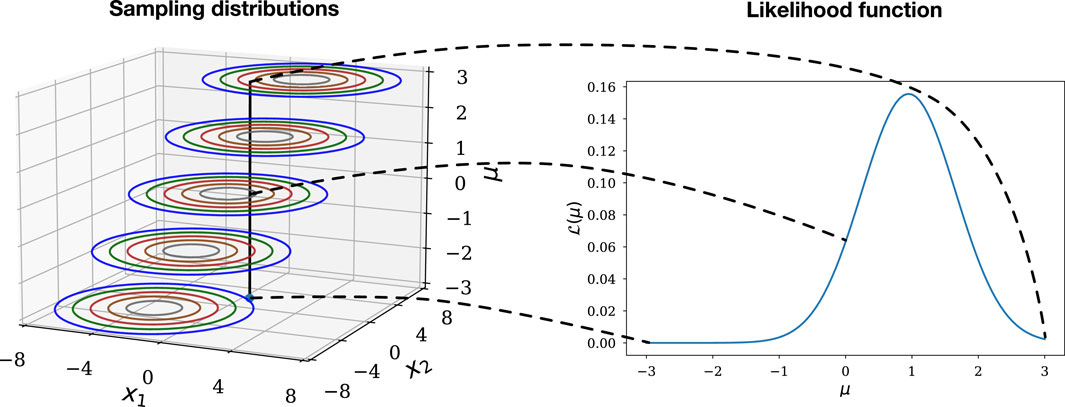
Figure 3. The relationship between the collection of sampling distributions comprising a parametric model for 2-dimensional continuous data (left) and the likelihood function (right).

For each choice of $\mu$ (vertical axis), the model specifies a 2-dimensional normalized PDF for $(x_1,x_2)$, depicted via sets of contours in $(x_1,x_2)$ space for each of five values of $\mu$. Once data are observed, we fix $(x_1,x_2)$ to those observed values and evaluate the sampling distribution as a function only of $\mu$. This corresponds to slicing through the sampling distributions along the vertical black line. (See Box (1980) for a similar figure showing how the posterior PDF relates to the joint distribution for data and parameters.)

The likelihood function quantifies how well each of the candidate sampling distributions—labeled by the parameter $\mu$ in the last example—predicts the observed values of the data, $(x_1,x_2)$. Note that a statistical model specifies sampling distributions for data, and a likelihood function for parameters. “Likelihood for the data” is incorrect usage—it entirely misses the point of introducing the likelihood terminology. Sir Ronald Fisher introduced the term specifically to make a distinction between probability and this measure of prediction quality:

If we need a word to characterise this relative property of different values of $p$ [a parameter], I suggest that we may speak without confusion of the likelihood of one value of $p$ being thrice the likelihood of another, bearing always in mind that likelihood is not here used loosely as a synonym of probability, but simply to express the relative frequencies with which such values of the hypothetical quantity $p$ would in fact yield the observed sample (Fisher (1922), emphasis added).

Alas, colloquially “probability” and “likelihood” are synonyms, inviting misuse. The clash between the terminology and colloquial use is unfortunate; “predictive” or “prognostic” might have been better names for this function.

Fisher goes on:

Likelihood also differs from probability in that it is a differential element, and is incapable of being integrated: it is assigned to a particular point of the range of variation, not to a particular element [interval] (Fisher (1922), emphasis added).

He used stronger language earlier: “…the integration with respect to $m$ [a parameter] is illegitimate and has no definite meaning … ” (Fisher (1912), a paper written when he was a third-year undergraduate at Cambridge!).

The posterior PDF is closely related to the likelihood function, obtained simply by multiplying by a prior PDF and normalizing:

$p\left(\theta |D_{\text{\hspace{0.17em}obs}}\right)\propto p\left(\theta \right)\times \mathcal{L}\left(\theta \right).(21)$

The posterior PDF is a probability distribution over $\mathit{\theta }$, whose integrals over θ are meaningful.

6 Priors are not (merely) penalties

The distinction between likelihood and probability points to the dual role of prior probabilities in Bayesian inference. Bayesian tutorials typically focus on priors as adjusters of the likelihood to account for base rates, parameter constraints (such as positivity), or results from prior experiments. This is indeed an important capability. But more fundamentally, the role of the prior is to “flip the conditional,” that is, to get us from likelihood to probability. With a probability distribution in hand, we are then able to use the LTP to address a myriad of questions involving consideration of composite hypotheses. In this section we elaborate on the role of priors in Bayesian inference, beyond the usually emphasized role of “modulating” the likelihood to account for prior information.

6.1 Intensive vs extensive quantities in inference

For an audience of physical scientists, a thermodynamic analogy may be illuminating. In thermodynamics, temperature is an intensive quantity. It is meaningful to talk about the temperature, $T(x)$, at a point in space, $x$, but not about the “total temperature” for a volume of space; temperature does not add or integrate across space. Heat, on the other hand, is an extensive quantity; in mathematical parlance, it may be described by a measure (a cumulative mapping from sets or regions, rather than points, to a real number). The two quantities are related; the heat in a volume $V$ is given by

$Q={\int }_{V}dx\left[\rho \left(x\right)c\left(x\right)\right]T\left(x\right),(22)$

where $\rho (x)$ is the matter density and $c(x)$ is the specific heat capacity. The product $\rho c$ is extensive, and serves as a kind of conversion factor between temperature and heat.

Priors play a similar role in Bayesian inference, not just modulating the likelihood function, but, more fundamentally, converting intensive likelihood to extensive probability. In thermodynamics, a region with a high temperature may have a small amount of heat if its volume is small, or if, despite having a large volume, $\rho c$ is small throughout. In Bayesian inference, a region of parameter space with high likelihood may have a small probability if its volume is small, or if the prior PDF assigns low probability to the region. Approaches that rely exclusively on likelihood focus on particular hypotheses that are “hot” (e.g., with maximum likelihood), while Bayesian inference focuses on sets of hypotheses with the most “heat” (i.e., with large probability).

6.2 Typical vs optimal parameter values

Frequentist statistics includes penalized maximum likelihood methods that multiply the likelihood by a penalty function, $r(\theta )$ (e.g., a regularizer), and then locate the maximum of the product:

$\tilde{\theta }\equiv \arg \underset{\theta }{\max }r\left(\theta \right)\mathcal{L}\left(\theta \right).(23)$

The penalty function shifts the location of the maximum. It looks like a prior, in that it multiplies the likelihood function, but because Bayesian calculations integrate rather than maximize over parameter space, the prior can do much more than shift the location of the mode (the location of the peak of the posterior) with respect to the maximum likelihood location.

A number of concepts from different areas of mathematics can help us understand the consequences of having a (summable/integrable) measure and not just a preference ordering over a parameter space:

$•$ Curses of dimensionality observed in high-dimensional geometry, perhaps best known for their impact on numerical computation. An well-known example is the accumulation of volume close to the edges of a hypercube as dimension grows.

$•$ Concentration of measure in measure theory, showing that volume in a high-dimensional space (with a kind of symmetry) can concentrate in a surprising way in a small region of the space.

$•$ Typical sets in information theory, indicating that the mode of a discrete PMF or a continuous PDF can be highly unrepresentative of typical samples from the distribution (Cover and Thomas, 2006; Betancourt, 2017).

We will give a sense of how these notions can help us understand the impact of integrating vs optimizing with two simple examples.

Consider $N=\mathrm{1000}$ flips of a coin with $\alpha \equiv P(\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{s})=\mathrm{0.8}$, with the goal being to predict the number of heads. The sequence of outcomes with the highest probability is the sequence with 1,000 heads. Despite that, students of probability theory (and probably many less educated!) would predict $\approx 800\pm 28$ heads. How can we reconcile this discrepancy? The sequence with 1,000 heads is ${\left(\frac{\alpha }{1-\alpha }\right)}^{200}\approx 2\times 10^{120}$ times more probable than any sequence with 800 heads; that is, it is hugely more probable. But there are many, many sequences with $\approx 800$ heads ($\sim 10^{217}$ within one standard deviation of 800 heads); the probability of that so-called typical set is $\sim 1$. A typical random sequence of flips does not at all resemble the most probable sequence.

This phenomenon is not unique to discrete spaces. Consider now curve fitting with $N=1000(x_i,y_i)$ datapoints, modeled with $y_i=f(x_i)+{ϵ}_i$, for some known parametric function $f(x)$, and with standard normal errors ${ϵ}_i$ (denoted collectively as $\overrightarrow{ϵ}$). The most probable sample has ${ϵ}_i=0$ for all 1000 samples. But those familiar with weighted least squares (minimum ${\chi }^2$) fitting know that we expect ${\chi }^2$, the sum of squared residuals, to be $\approx N\pm \sqrt{2N}$ (i.e., ${\chi }^2$ should be nearly equal to the “degrees of freedom”). Note that ${\chi }^2$ is just the squared length of the (estimated) $\overrightarrow{ϵ}$ vector. The familiar degrees of freedom result is telling us that a set of random $\overrightarrow{ϵ}$ vectors will point to locations in a thin shell far from the origin when $N$ is large, even though the probability density for $\overrightarrow{ϵ}$ is much higher near the origin than in that shell (one of the “curses of high dimensionality”). This is true even though the PDF for the errors has its peak at the origin. The density of points is maximized at the origin, but volume grows so quickly with radius in high dimensions that a typical random vector will point far from the origin.

The left panel of Figure 4 shows this quantitatively for $N=30$. The orange curve shows the PDF of the absolute value of a single ${ϵ}_i$ coordinate, peaking at the origin. The green curve shows how the surface area (hypervolume) of a 29-dimensional sphere (and thus volume in a shell of constant thickness) grows with distance from the origin, $\chi$ (the square root of ${\chi }^2$). The blue curve shows the PDF for distance, proportional to the product of the area curve and the 30 normal coordinate PDFs. The shaded region shows the central 90% region of the $\chi$ PDF; the lengths of typical $\overrightarrow{ϵ}$ vectors will lie in this region. That is, typical points in the 30-dimensional ${ϵ}_i$ space lie in a shell about 5.4 standard deviations from the origin. The right panel of Figure 4 highlights that such intuitively appealing statements do not fully capture the truly non-intuitive nature of distributions in high-dimensional spaces. We drew $10^5$ samples from a 30-dimensional standard normal, computed the lengths of those vectors, and formed a histogram estimate of the lengths as the blue histogram. It empirically duplicates the $\chi$ PDF from the left panel. The brown histogram shows the distribution of the maximum absolute value of the coordinates in each vector. It reveals that no single coordinate value in this large sample ever gets a value near the typical values of $\chi$; put differently, none of the $10^5$ 30-dimensional vectors is close to a coordinate axis. In the low-dimensional world where our intuition has been trained, these distributions strongly overlap.

Figure 4

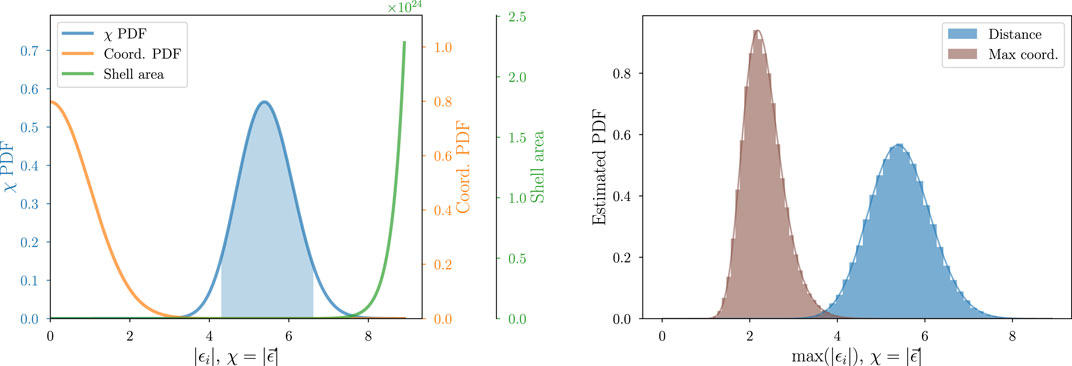
Figure 4. Elucidation of the nature of the typical set for a 30-dimensional standard normal distribution with coordinates ${ϵ}_i$ and coordinate vector distance $\chi =|\overrightarrow{ϵ}|$ (the square root of ${\chi }^2$). Left: Orange curve (against first right ordinate) shows the PDF for a single coordinate value, with highest density at the origin. Green curve (against the second right ordinate) shows the area of a 29-dimensional hyperspherical surface as a function of $\chi$. Blue curve (against the left ordinate) shows the PDF for $\chi$, proportional to the product of area curve and the 30 normal coordinate PDFs. There is 90% probability for $\chi$ lying in the shaded region; i.e., typical $\overrightarrow{ϵ}$ draws from a 30-dimensional standard normal will lie in a shell $\approx 5.4$ standard deviations from the origin. Right: PDFs for $\chi$ (blue) and $\max |{ϵ}_i|$ (brown), the maximum size of one of the coordinates, estimated with histograms of $10^5$ draws of $\overrightarrow{ϵ}$ vectors (curves show analytical PDFs). The blue histogram empirically duplicates the $\chi$ PDF from the left panel.

The lesson of these examples is that for high-dimensional spaces, the mode of a distribution is likely to be very atypical, in the sense that random draws from the distribution are unlikely to resemble the mode (in terms of the values of the PMF or PDF for the draws). These examples looked at properties of familiar sampling distributions, but the math does not care if we call a variable “data” or “parameter”—the notion of typical sets applies to distributions over large parameter spaces as well as to distributions over large sample spaces.

6.3 Example: histogram-based density estimation

As an example of these ideas at work in a parameter estimation setting, consider estimating a PDF for some continuous observable quantity via histogram data—say, galaxy fluxes grouped into a few dozen flux bins (a “number-counts” or “$\log N$ – $\log S$” number-size distribution). We may model the histogram counts with a multinomial distribution, with probabilities $f_k$ for objects to fall in each of $K$ bins $({\sum }_k{f}_k=1)$. The likelihood function associated with a set of observed counts $n_k$ is then

$\mathcal{L}\left(f_1,\dots ,f_K\right)=\frac{N!}{{\prod }_k{n}_k!}\prod _k{f}_k^{n_k},(24)$

where $N={\sum }_k{n}_k$ is the total number of objects counted. It is straightforward to show that the maximum likelihood estimates (MLEs) are ${\widehat{f}}_k=n_k/N$, an intuitively appealing result.

For a Bayesian analysis, a tempting choice of prior, intending to be uninformative about the $f_i$ parameters, is a flat or uniform prior over the simplex ${\sum }_k{f}_k=1$; intuitively, that would seem to be noncommittal. What does such a distribution say about our prior expectations for $\{f_i\}$?

Figure 5 tries to build insight into this question by looking at random samples from the prior. The left panel shows a stack of 10 random $f_i$ vectors from a flat prior for $K=5$ bins. The samples show a reasonable amount of diversity, with some samples appearing roughly flat, and some samples having one or more large-$f_i$ bins. The right panel shows another stack of 10 random vectors, but now for $K=30$. Perhaps surprisingly, there is now little diversity; all of the samples are nearly flat.

Figure 5

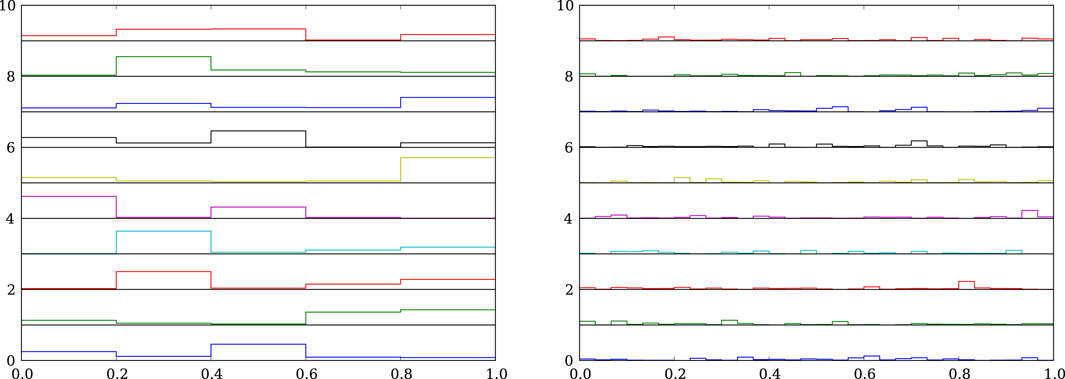
Figure 5. 10 samples of $f_i$ vectors from a flat prior distribution on the probability simplex, plotted as distributions for a quantity binned over the unit interval. Left: Samples from a distribution for $K=5$ bins. Right: Samples from a distribution for $K=30$ bins.

A bit of analytical work confirms the visual impression (see Frigyik et al., 2010 for a tutorial covering the math). We can compute the marginal PDF for a particular $f_k$ (marginalizing over all of the other $f_k$ values). For $K=2$, this marginal PDF is flat over the unit interval, but as $K$ increases, it increasingly concentrates near $f_k=0$, with a skew distribution whose expectation value is $1/K$ and whose variance becomes increasingly small. The random draws and analytical work are telling us that, as dimension grows, most of the volume of a simplex is in the region where all of the $f_k$ are nearly equal to each other, near the middle of the simplex. (Notably, this is different from the better-known “curse of dimensionality” behavior of hypercubes, where volume accumulates at the boundary.)

How might we fix this? Consider the family of symmetric Dirichlet priors, of the form

$p\left(f_1,\dots ,f_K\right)\propto \delta \left(1-{\displaystyle \sum _k}{f}_k\right)\prod _k{f}_k^{\alpha -1}(25)$

(the $\delta$-function imposes the normalization constraint on the $f_k$ parameters). Note that the $f_k$ dependence is a product of powers of each $f_k$—the same form of dependence that is in the likelihood function, Equation 24. This prior has a single (scalar) “hyperparameter,” $\alpha >0$, that we can experiment with to control its behavior (it is called the concentration parameter or the flattening parameter for the symmetric Dirichlet). For $\alpha =1$, the symmetric Dirichlet becomes a flat (uniform) prior. For other values, the net effect of the prior on the likelihood function is to add $\alpha -1$ to each count, $n_k$; crudely speaking, the prior is adding $\alpha -1$ “a priori counts” to the likelihood function. Finally, this prior is analytically tractable, and produces analytically tractable posteriors. (This is thanks to conjugacy—a Dirichlet prior (symmetric or not), multiplying the multinomial likelihood function, produces a Dirichlet posterior.)

How to set $\alpha$? One appealing idea recognizes that the binning can be done in different ways, and seeks some kind of consistency across different binning choices, e.g., different choices of $K$. Consider in particular aggregation consistency: devise a rule for choosing $\alpha$ such that applying that rule for $K=10$, say, and then aggregating adjacent pairs of bins to produce a 5-bin model, yields the same prior as one would get by applying the $\alpha$ rule directly for $K=5$. It is not hard to show that setting $\alpha =C/K$ for any constant $C$ satisfies aggregation consistency (for any $K$ and any kind of aggregated binning), while a constant value—like $\alpha =1$, corresponding to the uniform prior used for Figure 5—does not. (Perks, 1947 appears to have offered the first argument along these lines.).

Figure 6 shows samples from an aggregation-consistent prior with $C=2$, so $\alpha =2/K$. For $K=2$ bins, this becomes a flat prior, which we saw has acceptable behavior for small $K$. The figure shows prior samples for $K=30$, to be compared with the right panel in Figure 5. The prior samples no longer are all flat; in most samples, one or more bins may have significantly larger values of $f_i$ than other bins.

Figure 6

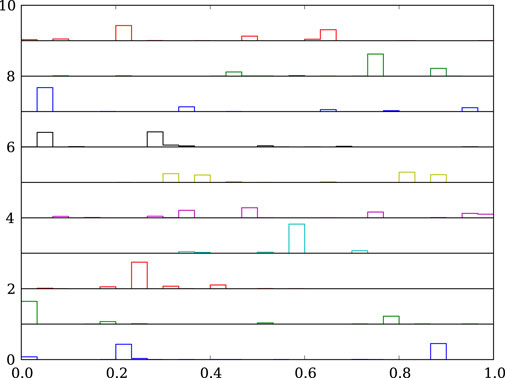
Figure 6. As in Figure 5, but with samples drawn from an aggregation-consistent symmetric Dirichlet distribution for $K=30$ bins, with $\alpha =2/K$.

We have focused on the prior; what is the impact on the posterior? For estimating all $K$ bin heights $f_i$ jointly, the impact is negligible if there are at least a few counts per bin; the new prior effectively subtracts $C/K-1$ from each $n_k$ counts value, which is not much of a change compared to use of the uniform prior. However, if we are interested in just one or few bins, and so will marginalize over many other $f_k$ parameters, the difference can be dramatic. Finally, if we want to do model comparison, comparing models with different numbers of bins via their marginal likelihoods (thus marginalizing over all $f_i$ parameters), then the two priors can lead to very different results. See Loredo (2012) for further discussion and examples.

A lesson of this section is that we should be cautious and skeptical of our intuition when attempting inference in high-dimensional parameter spaces (Genovese et al. (2004) have urged similar caution from a frequentist perspective). Prior probabilities let us get something integrable from likelihood functions, enabling diverse useful calculations when we are interested in composite hypotheses. But the “extensive” (summable) nature of prior and posterior distributions means that parameter space volume effects can have surprising impacts on inference. If we think of priors merely as modulating or penalizing the likelihood function, it would seem that a uniform prior would not divert attention from the peak of the likelihood function. But the notion of typical sets, and the behavior of uniform priors in multinomial inference, alert us that even flat priors may divert attention from the maximum likelihood region when the parameter space is high-dimensional. On the one hand, this is a warning that optimization can be misleading; it can focus attention on parts of parameter space that are very atypical. On the other hand, it is also a warning against relying on low-dimension intuition, like equating prior uniformity with being noncommittal or uninformative. A practical lesson is to always look at samples from the prior, particularly when working in high-dimensional parameter spaces.

7 Nuisance parameters: marginalization vs optimization

Of the many tasks using the LTP listed in SS 4, one of the most important is marginalizing over nuisance parameters. It is very common (in our experience, essentially ubiquitous) for a data modeling problem to require introducing parameters that are not of direct scientific interest, but that are necessary for describing how the data relate to the quantities of interest. Estimation of the interesting quantities has to somehow account for the uncertainty in the uninteresting “nuisance” quantities. In this section we elaborate on how marginalization over nuisance parameters accomplishes this, in particular the role of parameter space volume in the behavior of marginal posterior PDFs.

A frequently-arising nuisance parameter setting is analysis of measurements contaminated by uncertain backgrounds or foregrounds. A somewhat more subtle but also prevalent setting is estimating population distributions (density estimation) or correlations and scaling laws for a population (regression), when the properties of members of the population are measured with uncertainty—so-called measurement error problems (statisticians use this term for density estimation with noisy measurements, or regression with noise in both the measured predictors/covariates ($X$s) and the dependent/response variables ($Y$s); see Carroll et al., 2006). Examples of density estimation with measurement error (and possibly also with selection effects) include: estimating luminosity functions of star, galaxy, and transient object populations; estimating joint distributions of exoplanet properties such as orbital period and planet size; estimating distributions of minor planet sizes based on brightness measurements; and estimating the distribution of binary black hole system parameters from gravitational wave measurements of masses and spins. Examples of regression with measurement error include estimating correlations between galaxy properties (as in the Tully-Fisher and fundamental plane “luminosity indicator” relations, or gas density–star formation rate relationships like the Kennicutt-Schmidt relation), and calibrating the Type Ia supernova luminosity vs light curve shape relation.

In a Bayesian treatment of such measurement error problems (and in many frequentist formulations), the unknown true properties for each object formally appear as latent parameters, estimated with uncertainty. For inference about a population as a whole, the latent parameters are nuisance parameters, and their uncertainty must be propagated into population inferences. Importantly, in measurement error problems the number of latent parameters grows with sample size; as a result, even small inaccuracies in accounting for measurement error per-object can accumulate and lead to incorrect population-level inferences (Loredo, 2004). Hierarchical Bayesian (HB) models handle measurement error by marginalizing over the latent parameters. Some entry points into the rapidly growing literature on HB demographic modeling in astronomy include: Loredo (2004); Kelly (2012); Mandel (2012); Loredo (2013); Andreon and Hurn (2013); Hsu et al. (2018); Loredo and Hendry (2019); Mandel et al. (2019); Vitale (2020).

7.1 Understanding marginalization

Given the prevalence and importance of nuisance parameter problems in astronomy, it is worth building insight into how marginalization accounts for nuisance parameter uncertainty. To do so, we will consider the signal-plus-background setting, with interesting signal parameter, $s$, and background nuisance parameter, $b$. We suppose the available data provides useful information about $b$, so the joint posterior PDF, $p(s,b|D_{\text{\hspace{0.17em}obs}},\mathcal{C})$, exhibits some dependence between $s$ and $b$. For example, $D_{\text{\hspace{0.17em}obs}}$ may include independent data about $b$ from an off-source measurement at a location away from a candidate source in an image analysis setting. In such “on/off” settings, the on-source data provide a noisy measurement of $s+b$, and the off-source data provide a separate noisy measurement of $b$. The joint likelihood function for $(s,b)$ then typically resembles the left panel of Figure 7, exhibiting a negative correlation (the larger $b$ may be, the smaller $s$ is likely to be).

Figure 7

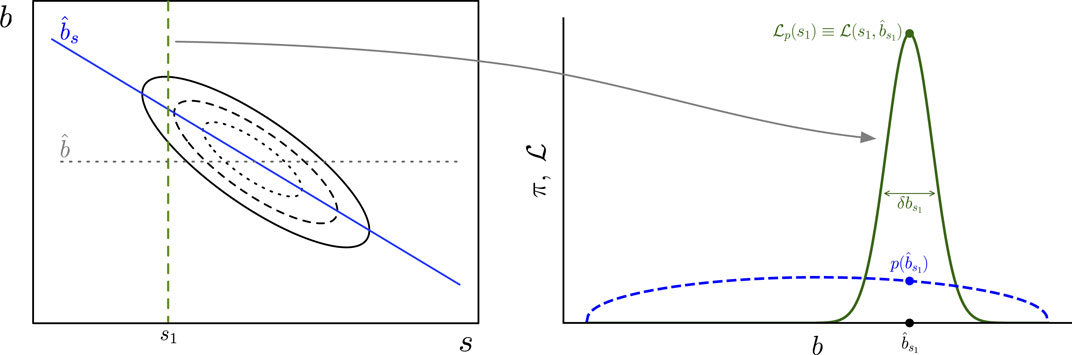
Figure 7. Left: An example joint likelihood function for $(s,b)$ in a signal-plus-background setting with on/off data that produces a bivariate Gaussian likelihood function. Gray dotted horizontal line shows $\widehat{b}$, the global MLE for $b$. Blue line shows ${\widehat{b}}_s$, the MLE for $b$ when $s$ is given; it crosses contours of the joint likelihood function where they become vertical. Vertical green dashed line indicates slice of the joint likelihood function at $s=s_1$ displayed in right panel. Right: Ingredients for approximating the marginal likelihood function for $s$. Green curve shows a slice of the joint likelihood function at $s_1$, as a function of $b$. Blue dashed curve shows the (conditional) prior PDF for $b$. See text for symbols.

Specifying the value of one parameter in a multiparameter problem is a composite hypothesis: specifying just $s$ in a problem with parameters $(s,b)$ corresponds to saying that, for the given $s$, some parameter choice in the set $\{(s,b):b\in [b_l,b_u]\}$ holds, though we do not know which (here $[b_l,b_u]$ denotes the range of allowed $b$ values, e.g., $[0,\infty ]$).

To summarize implications for $s$, accounting for $b$ uncertainty, we compute the marginal posterior PDF for $s$,

$\begin{array}{ll}\hfill p\left(s|D_{\text{\hspace{0.17em}obs}},\mathcal{C}\right)& =\int dbp\left(s,b|D_{\text{\hspace{0.17em}obs}},\mathcal{C}\right)\hfill \\ \hfill & \propto \int dbp\left(s,b|\mathcal{C}\right)\mathcal{L}\left(s,b\right),\hfill \end{array}(26)$

where the second line uses the numerator of BT, with likelihood function $\mathcal{L}(s,b)$ and a joint prior PDF $p(s,b|\mathcal{C})$.

Now factor that joint prior as the prior for $s$, $p(s|\mathcal{C})$, times a conditional prior for $b$ given $s$, $p(b|s,\mathcal{C})$. In many settings there may be no contextual information linking $b$ and $s$ a priori, making this factor independent of $s$; to simplify the notation, we assume such independence, so the $b$ prior factor is simply $p(b|\mathcal{C})$.

Since the marginalization integral is over $b$, the $s$ prior can be taken out of the integral:

$\begin{array}{ll}\hfill p\left(s|D_{\text{\hspace{0.17em}obs}}\right)& \propto p\left(s\right)\int dbp\left(b\right)\mathcal{L}\left(s,b\right)\Vert \mathcal{C}\hfill \\ \hfill & \propto p\left(s\right){\mathcal{L}}_m\left(s\right)\hfill \end{array}(27)$

where we have defined the marginal likelihood function for $s$ as

${\mathcal{L}}_m\left(s\right)\equiv \int dbp\left(b\right)\mathcal{L}\left(s,b\right)(28)$

(where we suppress $\mathcal{C}$ henceforth to simplify the notation). Since the integration underlying marginalization is isolated to the marginal likelihood function, we will focus henceforth on ${\mathcal{L}}_m(s)$.

To build insight into what marginalization accomplishes, we approximate the integral over $b$ in two steps (the ingredients for this approximation are depicted in the right panel of Figure 7):

1. Assume the data are informative, so the prior PDF for $b$ is nearly constant in the region where the integrand in Equation 28 has most of its area. This lets us pull the $p(b)$ factor out of the integral, setting it equal to its value at the location of the peak of the sliced likelihood function.

2. Approximate the remaining integral of $\mathcal{L}(s,b)$ over $b$—the area under the likelihood function in the nuisance parameter dimension—as the product of the height of the likelihood function and some convenient measure of its width (in the $b$ dimension).

We need some notation to implement these steps. Let ${\widehat{b}}_s$ denote the value of $b$ that maximizes the likelihood function when $s$ is fixed, i.e., along a vertical slice on the left panel of Figure 7 (the depicted slice has $s=s_1$):

${\widehat{b}}_s=\arg \underset{b}{\max }\mathcal{L}\left(s,b\right).(29)$

Graphically, ${\widehat{b}}_s$ as a function of $s$ traces the points where tangents to the contours of $\mathcal{L}(s,b)$ become vertical. The uninformative prior assumption of Step 1 implies

$\int dbp\left(b|s\right)\mathcal{L}\left(s,b\right)\approx p\left({\widehat{b}}_s|s\right)\int db\mathcal{L}\left(s,b\right).(30)$

The integral over $b$ gives the area under the likelihood function curve. Let $\delta b_s$ denote some convenient measure of the width of the sliced likelihood function. Approximate the integral as the product of the height and width of the sliced likelihood function,

$\int db\mathcal{L}\left(s,b\right)\approx \mathcal{L}\left(s,{\widehat{b}}_s\right)\delta b_s(31)$

The first factor is the joint likelihood function maximized over $b$ for each $s$. This is a function solely of $s$; it is called the profile likelihood function for $s$,

${\mathcal{L}}_p\left(s\right)\equiv \mathcal{L}\left(s,{\widehat{b}}_s\right).(32)$

It corresponds to looking at the 3D $\mathcal{L}(s,b)$ surface along the $b$ direction, producing a 2D projection or profile of the surface.

Assembling these results, we have this helpful approximation for the marginal likelihood function for $s$:

${\mathcal{L}}_m\left(s\right)\approx p\left({\widehat{b}}_s\right){\mathcal{L}}_p\left(s\right)\delta b_s.(33)$

The last two factors are the data-dependent factors. Much of the work done by marginalization is captured in the profile likelihood factor. A naive approach to handling a nuisance parameter would be to fix it at its best-fit value. This would correspond to slicing $\mathcal{L}(s,b)$ horizontally along the gray dotted line (through the global MLE point, $(\widehat{s},\widehat{b})$). The profile likelihood function instead slices $\mathcal{L}(s,b)$, accounting for the fact that a choice of $s$ implies a different “best” choice for $b$ than the global MLE. But the marginal likelihood function includes the additional factor, $\delta b_s$, that accounts for how the uncertainty in the nuisance parameter may change as a function of the interesting parameter. Essentially, marginalization is saying to start by profiling (rather than just using the best-fit nuisance parameter), but then adjust the profile likelihood, weighting regions where the nuisance parameter uncertainty is large more heavily than regions where it is small.

Figure 7 depicts a joint likelihood function that is a bivariate Gaussian function. Recall that a bivariate Gaussian may be written as the product of a Gaussian for one variable (say, $s$ here) and a Gaussian for the second variable with mean related linearly to the first one (the ${\widehat{b}}_s$ line in the figure), and constant standard deviation in the second dimension. This implies that $\delta b_s$ is constant with respect to $s$ here: the marginal likelihood function is proportional to the profile likelihood function. But that is a special property of multivariate Gaussians that does not hold in general.

Figure 8 shows two scenarios where marginal and profile likelihood functions may noticeably differ (here $s$ and $b$ denote generic interesting and nuisance parameters). The top left panel shows a “flaring” two-variable likelihood function, with the uncertainty in $b$ changing significantly as a function of $s$. The bottom left panel indicates how the flaring shifts the marginal likelihood function away from the joint peak, reflecting that the larger $b$ uncertainty to the right makes it more likely the true parameter values are to the right of the MLE point. The top right panel shows a “banana-shaped” two-variable likelihood function. These arise commonly in settings where predictions depend on the parameters via power laws (so predictions vary more weakly along a curve than orthogonal to it). Here the $\delta b_s$ weighting of the profile likelihood function arises because as the likelihood contours tilt upward with increasing $s$, the uncertainty in $b$ increases.

Figure 8

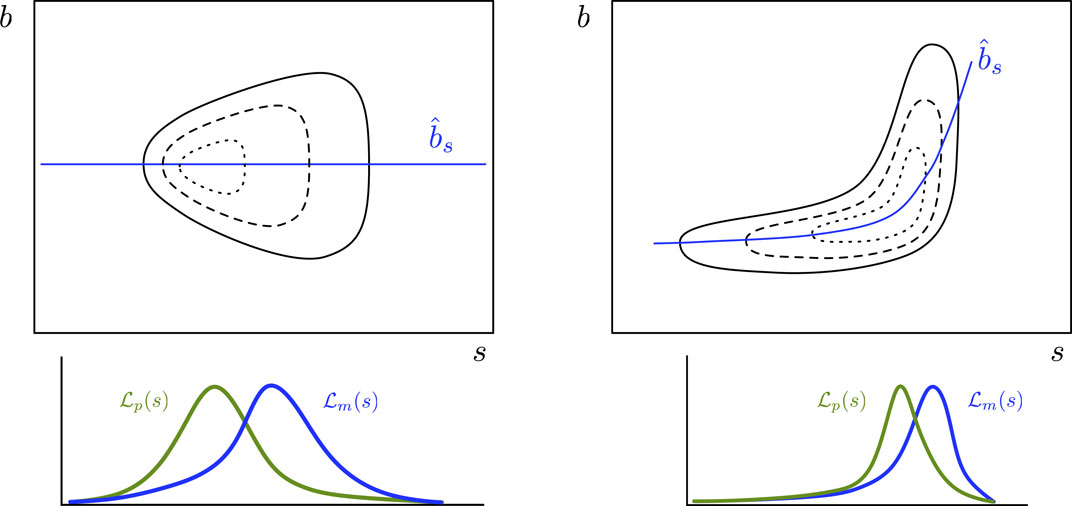
Figure 8. Illustration of two-parameter likelihood function geometries where marginalization and profile likelihood may lead to significantly different inferences. Top panels show joint likelihood functions for parameter of interest $s$ and nuisance parameter $b$. Blue curves show ${\widehat{b}}_s$, the MLE for $b$ when $s$ is given, the path defining the profile likelihood function. Bottom panels show profile (green) and marginal (blue) likelihood functions for $s$. Left: A likelihood function with “flaring” contours, with the nuisance parameter uncertainty varying significantly as a function of the interesting parameter. Right: A likelihood function with “banana-shaped” contours, with nuisance parameter uncertainty varying because of the curvature of the profile path.

7.2 Measurement error problems—handling many nuisance parameters

It is often the case that the nuisance parameter volume correction is noticeable in a single measurement, but not hugely significant; it may shift the profile likelihood function by only a fraction of its width. But the effect tends to be in a similar direction for similar measurements. When combining information across many measurements, the systematic effect from the nuisance parameter volume factor can accumulate, and ignoring it can corrupt aggregated inferences, such as demographic inferences.

Figure 9 illustrates this with a somewhat contrived but illuminating example⁷. For each of a set of $N$ objects, we make a pair of measurements of some object property, ${\mu }_i$ for object $i$, with an instrument that provides measurements with additive Gaussian noise with zero mean and fixed but unknown standard deviation, $\sigma$. Denote the pair of measurements by $x_i$ and $y_i$. For object $i$, there is a likelihood function for its ${\mu }_i$ and the shared $\sigma$ parameter that is the product of two normal distributions,

${\ell }_i\left({\mu }_i,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\left(x_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right]\times \frac{1}{\sigma \sqrt{2\pi }}\exp \left[-\frac{{\left(y_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right].(34)$

From a single pair of measurements, there is substantial uncertainty in both ${\mu }_i$ and $\sigma$. The left panel in Figure 9 displays this; it shows contours of ${\ell }_i({\mu }_i,\sigma )$ for the pair of measurements depicted as dots along the ordinate. Notably, this is an example of a flaring likelihood function, which we see is not an unusual phenomenon; it is relevant even for the familiar normal distribution when there is uncertainty, not just in its mean, but also in its standard deviation.

Figure 9

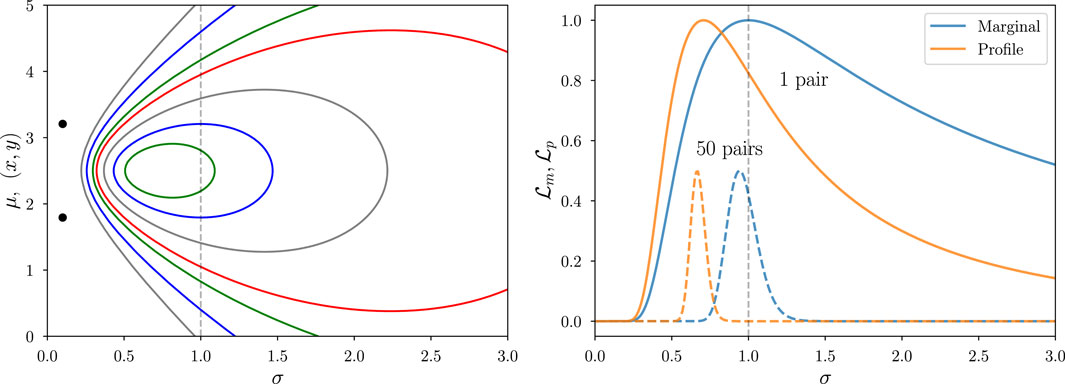
Figure 9. Joint, marginal, and profile likelihood functions for the normal pairs (Neyman-Scott) problem. Left: Joint likelihood function for the standard deviation $\sigma$, and the mean $\mu$ of a normal distribution, inferred using a pair of samples (depicted as dots adjacent to the $\mu$ axis). Vertical dashed line shows the true value of $\sigma$ for the ensemble of pairs of which this pair is a member. Contours bound approximate 25%, 50%, 75%, 90%, 95%, 99%, and 99.9% confidence regions. Right: Likelihood functions for $\sigma$ based on a single pair (solid curves, scaled to unit height) or a set of measurements of 50 pairs (dashed curves, scaled to height 0.5 for visibility). Blue curves are marginal likelihood functions, orange curves are profile likelihood functions. Vertical dashed line shows the true value of $\sigma$ for the ensemble of pairs.

We should be able to improve inference by pooling information across many pairs of measurements. Each pair brings in more information about $\sigma$, letting us calibrate the noise level of the instrument. That combination of $\sigma$ information should then let us measure each ${\mu }_i$ more precisely, as if $\sigma$ became known. The right panel of Figure 9 shows ingredients for inferring $\sigma$ from the pooled data. The solid curves show the profile (orange) and marginal (blue) likelihood functions from a single pair of measurements (for the marginal, a uniform prior was used for ${\mu }_i$). The behavior illustrated in Figure 8 is apparent here; the peak of the marginal is shifted to the right of the peak of the profile curve. Moreover, the marginal curve is considerably broader. That said, the two curves have substantial overlap. From a single pair measurement, inferences based on the two curves would differ noticeably, but perhaps not strongly.

The dashed curves in the right panel of Figure 9 show what happens when we accumulate information across multiple paired measurements (here drawn from a broad, uniform distribution, though the findings described here do not depend on this choice). Formally, we do this by computing a likelihood function for the full dataset that is the product of the likelihood functions for the pairs,

$\mathcal{L}\left(\vec{\mu },\sigma \right)=\prod _{i=1}^N{\ell }_i\left({\mu }_i,\sigma \right),(35)$

where $\vec{\mu }$ denotes the collection of ${\mu }_i$ parameters. We can again summarize the implications for $\sigma$ by profiling or marginalizing over ${\mu }_i$—but now over $N\text{of}\text{the}{\mu }_i$ parameters. The dashed curves show the resulting profile and marginal likelihood functions. Both are becoming usefully narrow. But the profile likelihood function is converging away from the true value ($\sigma =1$ here). One can show that the MLE is in fact an inconsistent estimator for $\sigma$ in this setting—it converges to the wrong value as $N\to \infty$ (this remains the case even if more than two measurements are made per object, provided the number of per-object measurements is finite). In the first (frequentist) treatment of this problem, Neyman and Scott (Neyman and Scott, 1948) noted that a useful estimate for $\sigma$ could be obtained by averaging unbiased moment-based point estimates of $\sigma$ from the pairs. But they commented that “This is undoubtedly true but beside the point” that such problems expose a problem with maximum likelihood estimation that has no general solution. (Bayesian methods were uncommon in statistics at that time, and they did not explore marginalization.)

To make the point that such problems are not uncommon in astronomy, Figure 10 shows likelihood functions from simulated data for isolated dim point sources observed with a CCD camera with a critically-sampled Gaussian PSF (the calculations are based on the description of the Hyper Suprime-Cam pipeline in Bosch et al., 2018). The left panel is for a $\approx 6\sigma$ source whose true position is in the middle of a pixel. Contours are in the space of flux, $F$, and one of the direction coordinates, $x$ (position on the CCD; the other coordinate is fixed at its best-fit value). The contours exhibit flaring; they are nearly symmetric in $x$, but are very asymmetric in $F$, showing the significant flux-direction dependence: positions away from the best-fit position, in either direction, imply lower flux estimates. The growth of area in the contours with decreasing flux means that the marginal likelihood for flux gets shifted downward from the joint best-fit flux. The shift is at the percent level, much smaller than in the paired measurement problem above. But, as in that problem, the shift is systematic, in the same direction and of similar scale for all $6\sigma$ sources; it impacts accuracy (bias), more than precision, and would dominate statistical errors in analyses averaging over a few hundred sources. The right panel shows likelihood contours for a $\approx 3\sigma$, sub-threshold measurement of a source with a quarter-pixel offset. It shows that the likelihood function rapidly becomes more complicated for sources dimmer than $\approx 5\sigma$, amplifying the need to thoroughly account for nuisance parameter uncertainty when studying the flux distribution of dim sources (e.g., via forced photometry).

Figure 10

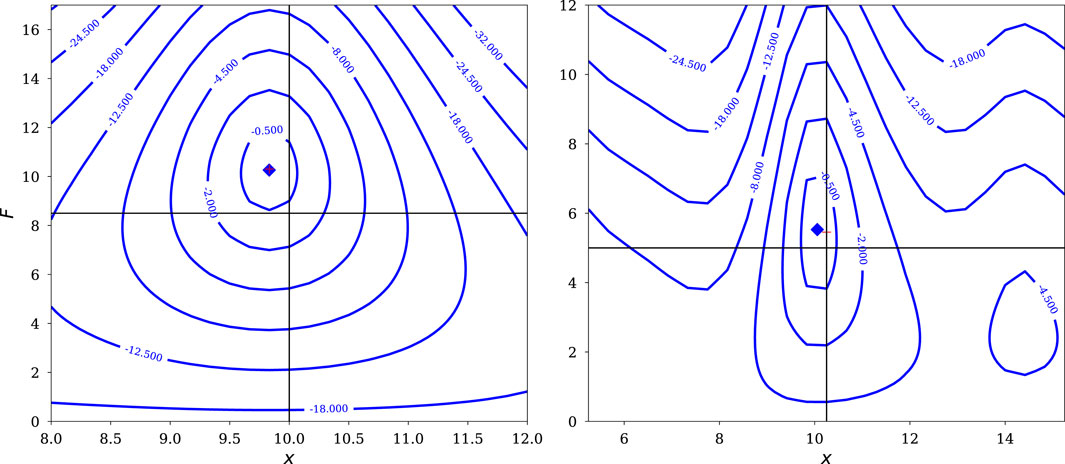
Figure 10. Likelihood functions as a function of flux, $F$, and one position coordinate, $x$ for dim point sources in an astronomical image. Crosshairs show the true $(x,F)$; diamonds shows maximum likelihood estimates. Contours have nominal $1\sigma$ spacing. Left: Likelihood for a source that would just pass a $6\sigma$ detection threshhold. Left: Likelihood for a source that would just pass a $3\sigma$ detection threshhold.

For those requiring a frequentist solution to measurement error problems, there is a large and growing literature presenting numerous techniques specialized to specific problem settings. From a Bayesian perspective, specialized inference techniques are unnecessary; marginalization over latent parameters handles such problems generally and flexibly (though the resulting computational challenges can demand nontrivial computational algorithms specialized to different settings). Notably, even statisticians who generally favor frequentist methods recommend Bayesian approaches that marginalize over latent parameters in complicated settings, particularly for nonlinear modeling of data with heteroscedastic measurement error (i.e., with measurements that have differing standard deviations); see Carroll et al. (2006). Astronomical data commonly has heteroscedastic measurement error, and the ability of marginalization to flexibly accommodate this complication has been a strong motivation for the spread of Bayesian methods for measurement error problems in astronomy.

8 Systematic error and model misspecification

A well-known aphorism attributed to George Box motivates our final marginalization application area: “All models are wrong, but some are useful” (Box and Draper, 1987; see also Box, 1976). In some data analysis settings, we may be largely secure about our model, but still want to explore the possibility that inference may be corrupted by potential influences omitted from the model. In other settings we may knowingly adopt an approximate model, and want to account for the lack of fidelity to the data when we make inferences about salient features of the model. Here we briefly describe the role composite hypotheses and marginalization can play to improve uncertainty quantification in such settings. We consider two settings: first, where systematic error arises due to model selection uncertainty (i.e., whether to include terms for anticipated corrupting effects), and second, where a model aims to account only for salient features of a phenomenon, and we want to account for uncertainty in deliberately unmodeled details.

8.1 Systematic error and model selection uncertainty

A fairly common way astronomers try to account for systematic error from identified potential corrupting effects is to use a classical null hypothesis significance test (NHST) to see if there is significant evidence in the data for the effects. A statistic is devised to test for the presence of a potential effect; if the null hypothesis of no effect is not rejected, analysis proceeds assuming no effect is present. A significant issue with this approach is that failure to reject a null hypotheses need not correspond to a strong preference for the null over the alternative (see, e.g., Berger, 2003; Wasserstein and Lazar, 2016; Greenland et al., 2016; Wasserstein et al., 2019). Ideally we would like to take into account potential systematic effects, weighted in a way that measures the strength of evidence for or against their presence.

Marginal likelihoods can provide such a weighting (see the brief description of model averaging above). However, marginal likelihoods typically are more sensitive to the choice of prior than are parameter estimates—in particular, to the ranges of the parameter spaces considered for rival models—and one must be cautious about using them to account for systematic error.

An example of systematic error quantification using marginal likelihoods and Bayes factors is the work of Drell et al. (2000) (DLW00) exploring the potential impact of systematic error from source evolution on early analyses of the evidence for dark energy from measurements of Type Ia supernova (SN Ia) light curves (“SN cosmology”). The dark energy discovery papers found no significant evidence for SN Ia source evolution (dependence of light curve properties on redshift), and so assumed there was exactly zero evolution in their analyses. DLW00 computed Bayes factors indicating the data were equivocal regarding the presence of evolution. An important aspect of the calculation was consideration of a variety of priors for parameters in evolution models, to ensure the findings were robust. Allowing for plausibly small levels of evolution, and marginalizing over its impact, significantly weakened the strength of the evidence for dark energy, unless one assumed a flat cosmology, which was not justified at the time. Fortunately, within a few years accumulating evidence from other cosmological phenomena honed in on flat cosmologies. From the perspective of the DLW00 systematic error analysis, it was only in the context of this later evidence that the discovery of dark energy became secure.

8.2 Systematic error, overdispersion, and model discrepancy

In astronomy we often knowingly use models that capture only the salient features of a phenomenon. This is particularly true when first exploring a frontier area, where learning such features can provide significant insight, even if the salient feature model overlooks details. Examples include counting pulses in gamma-ray burst prompt light curves (where we may care only about the number of pulses and their time scales, not every minor wiggle), or modeling luminosity functions with broken power laws (where we would like to estimate a power law slope and a break luminosity, irrespective of minor bumps in the distribution). Simply adopting the salient feature model and ignoring model misspecification can corrupt inferences, in particular by providing artificially tight constraints on the salient model parameters.

One approach to handling this is to simply inflate sampling distributions. For example, in the statistics literature analyzing count data, it is common to adopt negative binomial (NB) rather than Poisson distributions at the outset, since the NB distribution has an extra parameter that can be used to overdisperse the predictive distribution for counts, and it includes the Poisson distribution as a special case (see, e.g., Hilbe 2011; de Souza et al. (2015) for an application in astronomy; see the Supplementary Appendix for a brief discussion of the NB distribution and its use for modeling overdispersion). Bonamente (2023) has adapted this idea to account for systematic error in astronomical data analysis of Poisson data in the regime where ${\chi }^2$ fitting is nominally accurate, devising a new overdispersed ${\chi }^2$ distribution.

We are developing complementary methods for salient feature modeling of Poisson count and point process data that are closely tied to use of NB distributions. But we do not adopt overdispersed distributions outright. In contrast to most applications of the Poisson distribution in the statistics literature, in many astrophysical applications there is a strong physical basis for adopting a Poisson distribution as the description of the repeated-sampling variability expected in the data—the so-called aleatoric uncertainty (from the Latin aleator for “dice player”). We use overdispersion to reflect a combination of aleatoric and epistemic sources of uncertainty (with the epistemic component capturing the systematic errors that may not vary randomly across replications).

We construct overdispersed distributions via representations that tie them to the underlying aleatoric sampling distribution via a plausible discrepancy mechanism (adapting the notion of additive discrepancy functions from Gaussian process emulation of computer models; see the Supplementary Appendix). We consider the actual intensity function (event rate) for the Poisson process governing the data to be the product of the parametric salient model rate that we wish to estimate, and a nonnegative discrepancy factor. Figure 11 illustrates the construction for a model for photon counts from a time-varying source, binned in time, used to estimate parameters of a salient light curve model. The blue histogram depicts the predictions of a Poisson model for the photon counts in bins, as expectation values, ${\lambda }_i$. These are from the salient feature model, an idealized description of the true light curve that captures key features of scientific interest (e.g., location, duration, amplitude). To predict the observed counts in a bin, $n_i$, we multiply each intensity, ${\lambda }_i$, by an uncertain discrepancy factor, ${\alpha }_i$, drawn from a distribution with positive support and unit mean, shown in the inset. We use a gamma distribution for ${\alpha }_i$; with the mean fixed to one, there is only a single parameter, the shape parameter, $\beta$, controlling the variance. In the fitting process, we marginalize over all of the ${\alpha }_i$ factors, and treat $\beta$ as an uncertain parameter, estimated from the data.

Figure 11

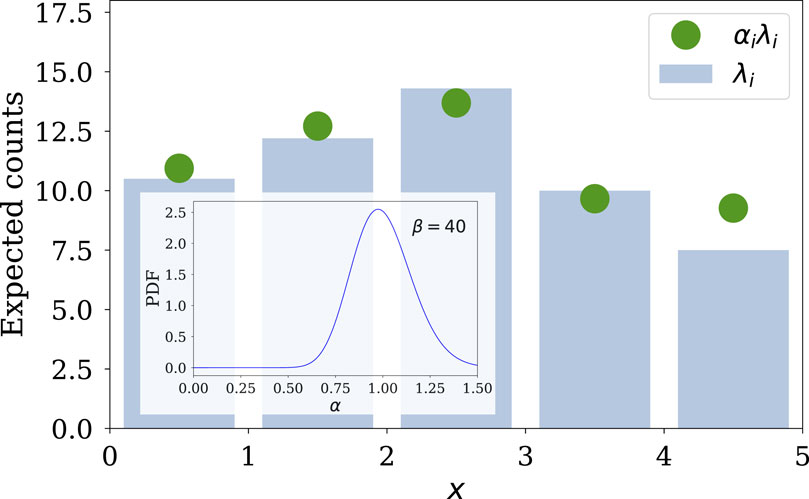
Figure 11. Depiction of the multiplicative discrepancy approach. Blue histogram shows the Poisson distribution PMF from a salient feature model. Green dots depict the PMF resulting from multiplying the Poisson expectation values by draws from a gamma distribution discrepancy process. Inset shows the unit-mean gamma distribution for the discrepancy factors.

The choice of a gamma distribution enables analytic marginalization over the discrepancy factors, producing a predictive PMF for the counts that is NB, with a variance that may be inflated with respect to that of a Poisson distribution. (See the Supplementary Appendix for further details.) More deeply, the gamma choice lets us introduce discrepancy in a manner that preserves aggregation consistency in a sense analogous to what we described above regarding Dirichlet priors for histograms. This framework explicitly acknowledges that the actual count variability distribution is expected to be Poisson. It also points toward generalizations that can apply to point data, and that can account for bin-to-bin correlations in the discrepancy. Details for specific astrophysical applications will be reported elsewhere.

9 More than Bayes’s theorem

The theme of this tutorial has been that BT and the LTP are partners in Bayesian inference—arguably unequal partners, with the LTP carrying much of the burden in analysis and computation. This is because of how common composite hypotheses are in astrophysical data analysis. We hope we have made a strong case that the role of the LTP and marginalization should be highlighted more prominently in the Bayesian astrostatistics literature, particularly in pedagogical presentations.

Python and R code producing figures from this paper are available at https://github.com/tloredo/MoreThanBT2024-Figures.

Data availability statement

The datasets presented in this article are not readily available because only small simulated datasets were used, for didactic purposes. Requests to access the datasets should be directed to bG9yZWRvQGFzdHJvLmNvcm5lbGwuZWR1.

Author contributions

TL: Conceptualization, Methodology, Writing–original draft, Writing–review and editing. RW: Conceptualization, Methodology, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the National Science Foundation under Grants No. DMS-2015386 and AST-2206339 (for TL), and DMS-2015382 (for RW).

Acknowledgments

We gratefully acknowledge the organizers and participants of the $\mathit{iid}$2022 workshop for helpful interactions on the topic of this paper. We are also grateful to the issue editor and two reviewers for helpful feedback that we believe significantly improved this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1326926/full#supplementary-material

Footnotes

¹John Tukey—best known for his work on the fast Fourier transform and exploratory data analysis—observed: “No body of data tells us all we need to know about its own analysis” (Tukey, 1977). Data do not “speak for themselves” in scientific arguments; data analysis considers the implications of data within some context. In this sense, data analysis (Bayesian or frequentist) is necessarily subjective and provisional, and a virtue of the Jeffreys/Cox/Jaynes notation is its recognition that all probabilities are conditional, at least depending on the context, $\mathcal{C}$ (whose components should be explicitly identified). For further discussion of subjectivity in statistical data analysis we recommend perspective papers by Berger and Berry (1988), Lindley (2000), and Gelman and Hennig (2017) (the latter including wide-ranging remarks by many invited discussants).

²In settings where the alternatives are labeled by a continuous parameter, $\theta$, $B$ would represent a statement about the value of $\theta$, i.e., that it is positive, or lies in a specified interval. When the probability $P(B)$ can be computed using a continuous PDF, $p(\theta )$, the probability that $\theta$ takes a specified value ${\theta }_{\ast }$, $P(B:\theta ={\theta }_{\ast })$, formally vanishes (it is equal to $p(\theta )\mathit{d}\theta$ in the limit as $\mathit{d}\theta \to 0$). In such settings, it can be possible to condition on $\theta ={\theta }_{\ast }$ even though $P(B)=0$, by considering a limit, or more generally, via measure-theoretic arguments. See Marin and Robert (2010) for discussion of this and its potential relevance for Bayesian model comparison.

³A statement $D_{\text{obs}}$ asserting values for observed data—e.g., “The number of heads in 10 flips was 7”, or “The photon count in bin 1 is 11, the photon count in bin 2 is 15 … ”—can typically be considered an event in this sense, interpreting the sampling distribution as a distribution for repeated sampling.

⁴This idea is notoriously difficult to define rigorously; arguably there is not yet a sound definition. For an exceptionally accessible overview of the difficulties see Diaconis and Skyrms (2018).

⁵Readers new to model comparison should note that in the astronomy literature and some machine learning literature it is popular to use the term evidence for the marginal likelihood. (Bayesian evidence also appears, awkwardly implying there are Bayesian vs non-Bayesian forms of evidence.) We eschew this terminology. The data (and possibly additional contextual information) comprise the evidence, and in the Bayesian philosophy of science literature it has long been common to use $E$ and “evidence” where we have used $D_{\text{obs}}$ and “data.” Unsurprisingly, “evidence” is used in the same way in the literature on statistics in jurisprudence. Using “evidence” for marginal likelihood obscures that there are just two types of hypothesis-dependent quantities in Bayesian inference, the probability for a hypothesis (with the hypothesis to the left of the bar) and the likelihood for a hypothesis (with the hypothesis to the right of the bar). The marginal likelihood works just like the more familiar parameter likelihood function; “marginal” merely specifies how it is computed. Jack Good has noted that marginal likelihoods operate just like likelihood functions, calling them Bayesian likelihoods. He used weight of evidence for the logarithm of the ratio of marginal likelihoods for two hypotheses (i.e., the logarithm of the Bayes factor), providing an additive (rather than multiplicative) measure of how much the available evidence favors one hypothesis over the other; the terminology originates with Alan Turing (Good, 1950; 1985).

⁶The values of marginal likelihoods depend more sensitively on properties of prior distributions than do posterior PDFs for parameters; in particular, they are roughly inversely proportional to the prior ranges of parameters. As a result, formal Bayesian model comparison and model averaging are best reserved for problems where the analyst can strongly motivate priors (especially prior ranges), or quantitatively study how results depend on properties of priors. Good entry points to the literature on this (in both astronomy and statistics) include: Volinsky et al. (1999); Clyde and George (2004); Clyde et al. (2007); Trotta (2012). For a Bayesian perspective on model selection relying on measures of anticipated out-of-sample predictive performance (vs a priori prediction of the observed sample, as measured by marginal likelihood), see Gelman et al. (2014b).

⁷Statisticians know this problem as the Neyman-Scott problem, a well-known counterexample to maximum likelihood estimation (Neyman and Scott, 1948). Neyman and Scott did important work on statistics in astronomy. Although the Neyman-Scott problem was first described in an econometrics journal, they posed it in terms of measuring “some physical constant such as the radial velocity of a star or the velocity of light.” They noted the connection to measurement error problems, and described several settings in astronomy where the issues they addressed potentially arise. Our discussion here expands on a shorter treatment in Loredo (2004).

References

Andreon, S., and Hurn, M. (2013). Measurement errors and scaling relations in astrophysics: a review. Stat. Analysis Data Min. ASA Data Sci. J. 9 (1), 15–33. doi:10.1002/sam.11173

CrossRef Full Text | Google Scholar

Berger, J. O. (2003). Could Fisher, Jeffreys and neyman have agreed on testing? Stat. Sci. 18, 1–32. doi:10.1214/ss/1056397485

CrossRef Full Text | Google Scholar

Berger, J. O., and Berry, D. A. (1988). Statistical analysis and the illusion of objectivity. Am. Sci. 76, 159–165.

Google Scholar

Berger, J. O., Liseo, B., and Wolpert, R. L. (1999). Integrated likelihood methods for eliminating nuisance parameters. Stat. Sci. 14, 1–28. doi:10.1214/ss/1009211804

CrossRef Full Text | Google Scholar

Berger, J. O., and Wolpert, R. L. (1988). The likelihood principle. No. 6 in IMS lecture notes monogr. Ser. (SPIE). doi:10.1214/lnms/1215466210

CrossRef Full Text | Google Scholar

Betancourt, M. (2017). A conceptual introduction to Hamiltonian Monte Carlo. arXiv:1701.02434 [stat] ArXiv: 1701.02434.

Google Scholar

Bonamente, M. (2023). Systematic errors in the maximum-likelihood regression of Poisson count data: introducing the overdispersed X² distribution. Mon. Notices R. Astronomical Soc. 522, 1987–2001. doi:10.1093/mnras/stad463

CrossRef Full Text | Google Scholar

Bosch, J., Armstrong, R., Bickerton, S., Furusawa, H., Ikeda, H., Koike, M., et al. (2018). The Hyper Suprime-Cam software pipeline. Publ. Astronomical Soc. Jpn. 70, S5. doi:10.1093/pasj/psx080

CrossRef Full Text | Google Scholar

Box, G. E. P. (1976). Science and statistics. J. Am. Stat. Assoc. 71, 791–799. doi:10.1080/01621459.1976.10480949

CrossRef Full Text | Google Scholar

Box, G. E. P. (1980). Sampling and Bayes’ inference in scientific modelling and robustness. J. R. Stat. Soc. Ser. A General. 143, 383–430. Publisher: [Royal Statistical Society, Wiley]. doi:10.2307/2982063

CrossRef Full Text | Google Scholar

Box, G. E. P., and Draper, N. R. (1987) “Empirical model-building and response surfaces,” in Wiley series in probability and mathematical statistics. New York: Wiley.

Google Scholar

Carroll, R. J., Ruppert, D., Stefanski, L. A., and Crainiceanu, C. M. (2006) “Measurement error in nonlinear models: a modern perspective, vol. 105 of Monographs on Statistics and Applied Probability,”. second edn. Boca Raton, FL: Chapman and Hall/CRC. Available at: https://www.routledge.com/Measurement-Error-in-Nonlinear-Models-A-Modern-Perspective-Second-Edition/Carroll-Ruppert-Stefanski-Crainiceanu/p/book/9781584886334.doi:10.1201/9781420010138

CrossRef Full Text | Google Scholar

Clyde, M., and George, E. I. (2004). Model uncertainty. Inst. Math. Statistics 19, 81–94. doi:10.1214/088342304000000035

CrossRef Full Text | Google Scholar

Clyde, M. A., Berger, J. O., Bullard, F., Ford, E. B., Jefferys, W. H., Luo, R., et al. (2007). “Current challenges in bayesian model choice,”. Statistical challenges in modern astronomy IV. Editors G. J. Babu, and E. D. Feigelson, 371, 224.

Google Scholar

Cover, T. M., and Thomas, J. A. (2006). Elements of information theory. 2nd ed edn. Hoboken, N.J.: Wiley-Interscience. doi:10.1002/047174882X

CrossRef Full Text | Google Scholar

Cox, R. T. (1946). Probability, frequency and reasonable expectation. Am. J. Phys. 14, 1–13. doi:10.1119/1.1990764

CrossRef Full Text | Google Scholar

[Dataset] Wilson, A. G. (2020). The case for bayesian deep learning

Google Scholar

de Souza, R. S., Hilbe, J. M., Buelens, B., Riggs, J. D., Cameron, E., Ishida, E. E. O., et al. (2015). The overlooked potential of generalized linear models in astronomy - III. Bayesian negative binomial regression and globular cluster populations. Mon. Notices R. Astronomical Soc. 453, 1928–1940. doi:10.1093/mnras/stv1825

CrossRef Full Text | Google Scholar

Diaconis, P., and Skyrms, B. (2018). Ten great ideas about chance. Princeton: Princeton University Press. OCLC: ocn983825018.

Google Scholar

Downey, A. B. (2021). Think Bayes: bayesian statistics in Python. second edition edn. Beijing Boston Farnham Sebastopol Tokyo: O’Reilly.

Google Scholar

Drell, P. S., Loredo, T. J., and Wasserman, I. (2000). Type IA supernovae, evolution, and the cosmological constant. Astrophysical J. 530, 593–617. doi:10.1086/308393

CrossRef Full Text | Google Scholar

Eadie, G. M., Speagle, J. S., Cisewski-Kehe, J., Foreman-Mackey, D., Huppenkothen, D., Jones, D. E., et al. (2023). Practical guidance for bayesian inference in astronomy. ArXiv:2302.04703. [astro-ph, stat]. doi:10.48550/arXiv.2302.04703

CrossRef Full Text | Google Scholar

Fisher, R. A. (1912). On an absolute criterion for fitting frequency curves. Messenger Mathmatics 41, 155–160. doi:10.1214/ss/1029963260

CrossRef Full Text | Google Scholar

Fisher, R. A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Trans. R. Soc. Lond. Ser. A, Contain. Pap. a Math. or Phys. Character 222, 309–368. Publisher: The Royal Society. doi:10.1098/rsta.1922.0009

CrossRef Full Text | Google Scholar

Frigyik, B. A., Kapila, A., and Gupta, M. R. (2010) “Introduction to the dirichlet distribution and related processes,” in Tech. Rep. UWEETR-2010-0006. Seattle, WA: University of Washington.

Google Scholar

Gelman, A. (2020). Bayesian workflow. doi:10.48550/arXiv.2011.01808

CrossRef Full Text | Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014a) “Bayesian data analysis,” in Chapman and Hall/CRC texts in statistical science. third edition edn. Boca Raton: CRC Press.

Google Scholar

Gelman, A., and Hennig, C. (2017). Beyond subjective and objective in statistics. J. R. Stat. Soc. Ser. A Statistics Soc. 180, 967–1033. doi:10.1111/rssa.12276

CrossRef Full Text | Google Scholar

Gelman, A., Hwang, J., and Vehtari, A. (2014b). Understanding predictive information criteria for Bayesian models. Statistics Comput. 24, 997–1016. doi:10.1007/s11222-013-9416-2

CrossRef Full Text | Google Scholar

Genovese, C. R., Miller, C. J., Michol, R. C., Arjunwadkar, M., and Wasserman, L. (2004). Nonparametric inference for the cosmic microwave background. Stat. Sci. 19, 308–321. doi:10.1214/088342304000000161

CrossRef Full Text | Google Scholar

Good, I. J. (1950). Probability and the weighing of evidence. London: Charles Griffin and Co.). Google-Books-ID: k9g0AAAAMAAJ.

Google Scholar

Good, I. J. (1985). Weight of evidence: a brief survey. In Bayesian statistics 2, eds. J. M. Bernardo, M. H. DeGroot, D. V. Lindley, and A. F. M. Smith (Amsterdam: Elsevier Science Publishers). 249–269.

Google Scholar

Greenland, S., Senn, S. J., Rothman, K. J., Carlin, J. B., Poole, C., Goodman, S. N., et al. (2016). Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur. J. Epidemiol. 31, 337–350. doi:10.1007/s10654-016-0149-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hilbe, J. M. (2011) “Negative binomial regression,”. Cambridge University Press. doi:10.1017/CBO9780511973420

CrossRef Full Text | Google Scholar

Hsu, D. C., Ford, E. B., Ragozzine, D., and Morehead, R. C. (2018). Improving the accuracy of planet occurrence rates from kepler using approximate bayesian computation. Astronomical J. 155, 205. doi:10.3847/1538-3881/aab9a8

CrossRef Full Text | Google Scholar

Jaynes, E. T. (2003). Probability theory: the logic of science. Cambridge University Press, 1. doi:10.1017/CBO9780511790423

CrossRef Full Text | Google Scholar

Jeffreys, H. (1961). Theory of probability. Oxford classic texts in the physical sciences (Clarendon Press ; Oxford University Press), 3rd ed edn.

Google Scholar

Kelly, B. C. (2012). “Measurement error models in astronomy,” in Statistical challenges. Lecture notes in statistics. Editors V. Modern Astronomy, E. D. Feigelson, and G. J. Babu (Springer New York), 147–162.

CrossRef Full Text | Google Scholar

Lindley, D. V. (2000). The philosophy of statistics. J. R. Stat. Soc. Ser. D (The Statistician) 49, 293–337. doi:10.1111/1467-9884.00238

CrossRef Full Text | Google Scholar

Lindley, D. V., Barndorff-Nielsen, O., Elfving, G., Harsaae, E., Thorburn, D., Hald, A., et al. (1978). The bayesian approach [with discussion and reply]. Scandinavian Journal of Statistics 5, 1–26. Publisher: [Board of the Foundation of the Scandinavian Journal of Statistics, Wiley].

Google Scholar

Loredo, T. J. (1992). The promise of bayesian inference for astrophysics. In Statistical challenges in modern astronomy, eds. E. D. Feigelson, and G. J. Babu (New York, NY: Springer). 275–297. doi:10.1007/978-1-4613-9290-3_31

CrossRef Full Text | Google Scholar

Loredo, T. J. (1999). “Computational technology for bayesian inference,”. Astronomical data analysis software and systems VIII. Editors D. M. Mehringer, R. L. Plante, and D. A. Roberts, 172, 297.

Google Scholar

Loredo, T. J. (2004). Accounting for source uncertainties in analyses of astronomical survey data. AIP Conference Proceedings (AIP Publishing) 735, 195–206. doi:10.1063/1.1835214

CrossRef Full Text | Google Scholar

Loredo, T. J. (2012). “Rotating stars and revolving planets: bayesian exploration of the pulsating sky * - oxford scholarship,” in Bayesian statistics 9. Editors J. M. Bernardo, M. J. Bayarri, J. O. Berger, A. P. Dawid, D. Heckerman, A. F. M. Smithet al. (Valencia, Spain: Oxford University Press), 361–392. doi:10.1093/acprof:oso/9780199694587.003.0012

CrossRef Full Text | Google Scholar

Loredo, T. J. (2013). “Bayesian astrostatistics: a backward look to the future,” in Astrostatistical challenges for the new astronomy. Editor J. M. Hilbe (Springer New York. Springer Series in Astrostatistics), 15–40. doi:10.1007/978-1-4614-3508-2_2

CrossRef Full Text | Google Scholar

Loredo, T. J., and Hendry, M. A. (2019). Multilevel and hierarchical Bayesian modeling of cosmic populations. arXiv e-prints 1911, arXiv1911, 12337.

Google Scholar

Mandel, I., Farr, W. M., and Gair, J. R. (2019). Extracting distribution parameters from multiple uncertain observations with selection biases. Monthly Notices of the Royal Astronomical Society 486, 1086–1093. doi:10.1093/mnras/stz896

CrossRef Full Text | Google Scholar

Mandel, K. S. (2012). “Hierarchical bayesian models for type Ia supernova inference,”. Statistical Challenges in Modern Astronomy V. Editors E. D. Feigelson, and G. J. Babu (New York: Springer), 902, 209–218. Conference Name: Statistical Challenges in Modern Astronomy V ADS Bibcode: 2012LNS…902.209M. doi:10.1007/978-1-4614-3520-4_20

CrossRef Full Text | Google Scholar

Marin, J.-M., and Robert, C. P. (2010). On resolving the Savage–Dickey paradox. Electronic Journal of Statistics 4, 643–654. doi:10.1214/10-EJS564

CrossRef Full Text | Google Scholar

Neyman, J., and Scott, E. L. (1948). Consistent estimates based on partially consistent observations. Econometrica 16, 1–32. Publisher: [Wiley, Econometric Society]. doi:10.2307/1914288

CrossRef Full Text | Google Scholar

Perks, W. (1947). Some observations on inverse probability including a new indifference rule. Journal of the Institute of Actuaries (1886-1994) 73, 285–334. doi:10.1017/s0020268100012270

CrossRef Full Text | Google Scholar

Tak, H., Ghosh, S. K., and Ellis, J. A. (2018). How proper are Bayesian models in the astronomical literature? Monthly Notices of the Royal Astronomical Society 481, 277–285. doi:10.1093/mnras/sty2326

CrossRef Full Text | Google Scholar

Trotta, R. (2012). Recent advances in cosmological bayesian model comparison. In Astrostatistics and data mining, eds. L. M. Sarro, L. Eyer, W. O’Mullane, and J. De Ridder (New York, NY: Springer). 3–15. doi:10.1007/978-1-4614-3323-1_1

CrossRef Full Text | Google Scholar

Tukey, J. W. (1977) “Exploratory data analysis,” in Addison-Wesley series in behavioral science. Reading, Mass: Addison-Wesley Pub. Co.

Google Scholar

Vardanyan, M., Trotta, R., and Silk, J. (2011). Applications of Bayesian model averaging to the curvature and size of the Universe. Monthly Notices of the Royal Astronomical Society 413, L91–L95. doi:10.1111/j.1745-3933.2011.01040.x

CrossRef Full Text | Google Scholar

Vitale, S. (2020). One, No one, and one hundred thousand – inferring the properties of a population in presence of selection effects. arXiv2007.05579 [astro-ph, physicsgr-qc] ArXiv

Google Scholar

Volinsky, C. T., Raftery, A. E., Madigan, D., and Hoeting, J. A. (1999). Bayesian model averaging: a tutorial (with comments by M. Clyde, David Draper and E. I. George, and a rejoinder by the authors). Statistical Science 14, 382–417. doi:10.1214/ss/1009212519

CrossRef Full Text | Google Scholar

Wasserstein, R. L., and Lazar, N. A. (2016). The ASA statement on p-values: context, process, and purpose. The American Statistician 70, 129–133. 00–00doi. doi:10.1080/00031305.2016.1154108

CrossRef Full Text | Google Scholar

Wasserstein, R. L., Schirm, A. L., and Lazar, N. A. (2019). Moving to a world beyond “p < 0.05”. The American Statistician 73, 1–19. doi:10.1080/00031305.2019.1583913

CrossRef Full Text | Google Scholar

Wilson, A. G., and Izmailov, P. (2020). “Bayesian deep learning and a probabilistic perspective of generalization,”. Advances in neural information processing systems. Editors H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, and H. Lin (Curran Associates, Inc.), 33, 4697–4708.

Google Scholar

Zellner, A. (1971). An introduction to bayesian inference in econometrics. New York: J. Wiley.

Google Scholar