- 1Analytics Ventures, San Diego, CA, United States
- 2AlphaTrai, Inc., San Diego, CA, United States
- 3NASA Goddard Space Flight Center, Greenbelt, MD, United States
A major challenge facing scientists using conventional approaches for solving PDEs is the simulation of extreme multi-scale problems. While exascale computing will enable simulations of larger systems, the extreme multiscale nature of many problems requires new techniques. Deep learning techniques have disrupted several domains, such as computer vision, language (e.g., ChatGPT), and computational biology, leading to breakthrough advances. Similarly, the adaptation of these techniques for scientific computing has led to a new and rapidly advancing branch of High-Performance Computing (HPC), which we call neural-HPC (NeuHPC). Proof of concept studies in domains such as computational fluid dynamics and material science have demonstrated advantages in both efficiency and accuracy compared to conventional solvers. However, NeuHPC is yet to be embraced in plasma simulations. This is partly due to general lack of awareness of NeuHPC in the space physics community as well as the fact that most plasma physicists do not have training in artificial intelligence and cannot easily adapt these new techniques to their problems. As we explain below, there is a solution to this. We consider NeuHPC a critical paradigm for knowledge discovery in space sciences and urgently advocate for its adoption by both researchers as well as funding agencies. Here, we provide an overview of NeuHPC and specific ways that it can overcome existing computational challenges and propose a roadmap for future direction.
1 Introduction
Over the years there have been many techniques trumpeted as having great disruptive potential, which were eventually found to have muted applicability. It is rare that a technology comes along that is truly disruptive and is adopted across wide areas of science and engineering. Modern artificial intelligence (AI) is a rare technology where those claims are not overblown. In what follows, we will use the terms “machine learning” and “artificial intelligence” interchangeably.
One of the authors (HK) was an early advocate of the use of AI and computer vision in space sciences with applications in event detection/classification (e.g., Karimabadi et al., 2009), knowledge discovery in simulations and in-situ-visualization (e.g., Karimabadi et al., 2011a; Karimabadi et al., 2011c; 2012; 2013a), and derivation of equations from data (Karimabadi et al., 2007). The impetus for this effort was based on the vision that as our ability to generate data continues to grow exponentially, data driven science would become an indispensable field of scientific knowledge discovery. This vision has since come to pass, but the rate and scale with which this has happened has exceeded all expectations.
Despite the promising results and utility of those early works, including applications of simple neural nets to spacecraft data (e.g., Newell et al., 1991; Boberg et al., 2000), the techniques were not widely adopted. At the time, the field of AI was in a nascent stage in which artificial neural networks (ANNs) had been largely abandoned in favor of “lighter weight” techniques such as support vector machines. These algorithms had limited learning capacity, and relied heavily on hand engineered features, requiring a top-down agent to act as a “God outside the machine” to tell the models which attributes of the world to focus on, rather than allowing the algorithms to learn what is and is not relevant bottom-up, from the data and the model’s objective function. Another factor that limited their utility was their lack of universality. One had to devise special algorithms for problems in computer vision, speech, and audio, among others.
Everything changed in 2012 when AlexNet, a GPU implemented convolutional network (CNN), won ImageNet’s image classification competition by a wide margin. This seemingly overnight success was built upon 7 decades of slowly evolving research in deep learning (see the Supplementary Material for definition of deep learning). The field had to wait for the accessibility of large data sets and the development of GPUs, a widely available relatively inexpensive device with a special kind of massively parallel computational power, before its potential could be realized.
Since AlexNet, advances in AI have fueled adoption of neural algorithms across a myriad of industries and sciences. The first applications of AI in space sciences have been in analysis of spacecraft data (e.g., Camporeale, 2019; Breuillard et al., 2020; Li et al., 2020; Hu et al., 2022) where off-the-shelf AI techniques can be readily applied. However, application of AI in NeuHPC offers a greater opportunity with the potential to qualitatively change the field. The remainder of this article focusses on NeuHPC.
Partial differential equations (PDEs) often lead to extreme multi-scale behavior which makes the resolution of all scales in one simulation impossible. While exascale computing will enable simulations of larger systems (e.g., Xiao et al., 2021; Ji et al., 2022), the extreme multiscale nature of many problems in space sciences requires new techniques. In the global magnetosphere, there are 107 degrees of separation in spatial and temporal scales, putting it beyond the conventional techniques even at exascale. Also, round-off error in time-stepped solvers is severely limiting. Further, exascale simulations present other challenges, from knowledge discovery to the massive datasets, to efficient checkpointing and data management. We consider AI as a core technology and its adoption as critical for meaningful advancement in scientific computing. This belief is based on unique features of neural nets and the rapid and promising advancements of their use in scientific computation.
Table 1 summarizes key features of ANNs that make them especially suitable for overcoming the current HPC challenges by enabling new capabilities not possible with conventional approaches. While in-depth discussion of each topic is beyond the scope of this paper, relevant references are provided for interested reader to learn more. First, automated differentiation (see the Supplementary Material for more details) enables accurate computation of derivatives of arbitrary order (spatial and temporal) to working precision. This mesh-free operation, resulting in mesh invariant solutions, is advantageous over numerical differentiation methods (e.g., finite differencing) which suffer from discretization error with increasing cost and error in higher derivatives. As an example, one can solve the heat equation ∂u/∂t = Δ(u) where the function u is represented as a neural net and the spatial and temporal derivatives are calculated using the chain rule.
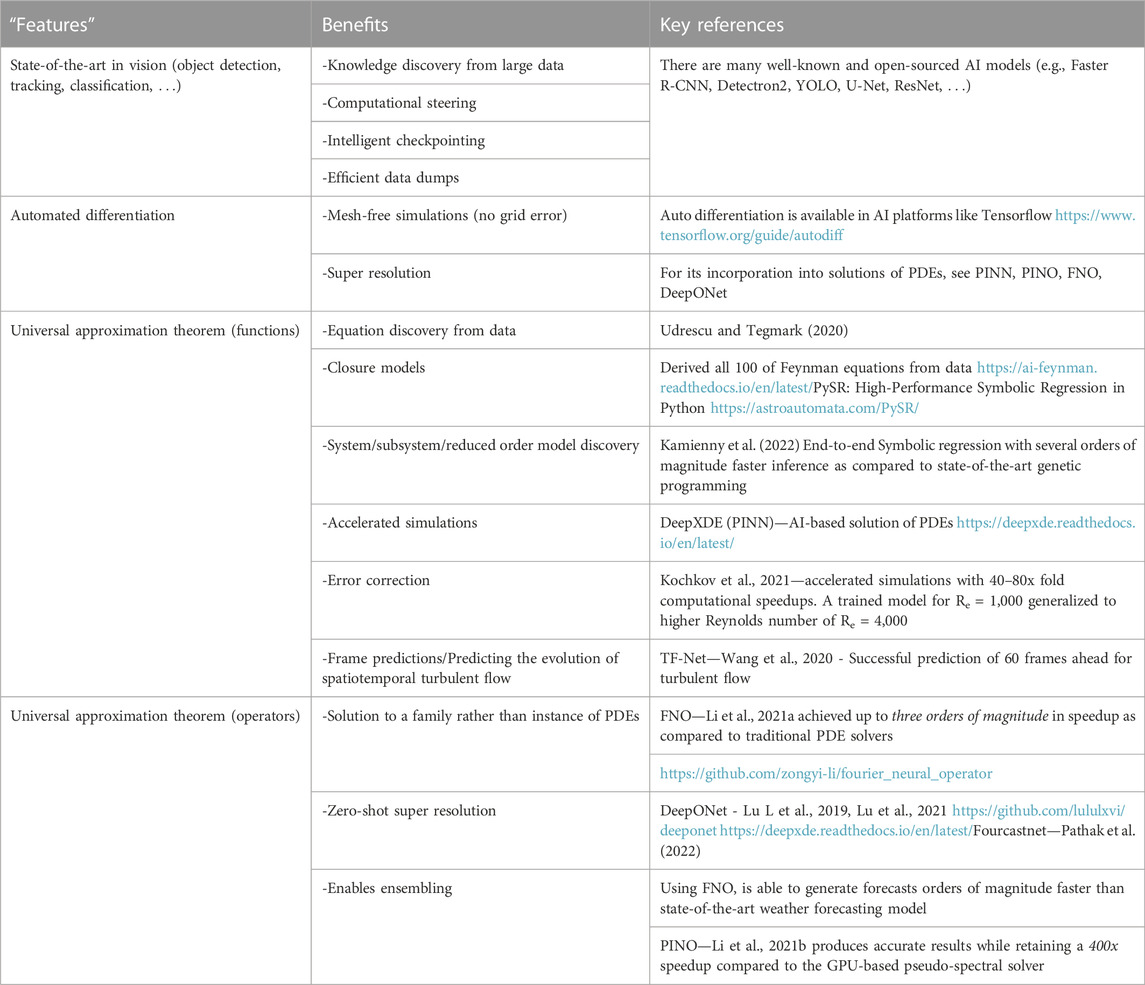
TABLE 1. Summary of key features of ANNs that enable new capabilities in HPC. References to some recent work that have gone beyond the proof of concept stage are also provided.
Second, the universal approximation theorem (Hornik et al., 1989) implies that ANNs can accurately approximate any function. In contrast to fixed-shaped approximators that have no internal parameters (e.g., polynomials), neural networks consist of parameterized functions, allowing them to take on a variety of different shapes.
Less known but as important is the universal approximation theorem for operators (Chen and Chen, 1995) which states that a neural net with a single hidden layer can accurately approximate any non-linear continuous operator (Lu et al., 2021). The operator can be explicit such as derivatives (e.g., Laplacian), integrals (e.g., Laplace transform) or implicit such as solution operators of a PDE. This offers a unique capability where the network can learn the solution to an entire family of PDEs rather than an instance of a PDE, as in the conventional approaches. Once the model is trained, inference to obtain solutions for different parameters of the PDE is very fast. This can lead to orders of magnitude speedup and enables efficient exploration of the solution space and ensemble modeling which may be prohibitively expensive otherwise.
These capabilities open the door to zero-shot learning, i.e., the operator can be trained on a lower resolution and evaluated at a higher resolution, without seeing any higher resolution data. To this end, Li et al. (2021a) developed the first network (FNO) with zero-shot learning that successfully learns the resolution-invariant solution operator for the family of Navier-Stokes equations in the turbulent regime. This feature of transferring the solution between the meshes works well on both the spatial and temporal domain (Kovachki et al., 2021). We refer the reader to Kim et al. (2021) for discussion and differences of super-resolution reconstruction for paired versus unpaired data. Another useful feature of AI-based solvers is transfer learning. For example, Li et al. (2021b) used a pre-trained model on the Kolmogorov flow to transfer it to different Reynolds numbers.
A wide variety of solutions have been proposed to leverage ANNs in computations across domains such as CFD, material science, and weather forecasting. A detailed review is beyond the scope of the present work. Our goal is simply to bring awareness to promising advances in NeuHPC and provide a starting point for further exploration. Although our focus is NeuHPC, techniques such as system identification can also be applied to spacecraft data either in isolation or in combination with simulation data.
2 Proof of concepts and beyond
2.1 Quantitative data analysis
We demonstrate the utility of AI for analysis of simulation data by addressing the challenging problem of automated detection and measurement of scales of individual current sheets formed in plasma turbulence. Previous works, limited to two snapshots of MHD simulations, were based on phenomenological approach, utilizing insights on MHD physics (e.g., Uritsky et al., 2010; Zhdankin et al., 2013). We time-boxed ourselves to 2 days to see whether we can significantly reduce time-to-solution using existing AI techniques. We used the magnitude of current density (507 timeslices) from simulations of Karimabadi et al. (2013b). Figure 1 shows the results for one time slice, where lengths of only a few current sheets are displayed. Visual comparison with the raw image of the current sheets shows generally good agreement and demonstrates the utility of AI. Details including the code and videos of results over 507 slices are provided in the Supplementary Material.
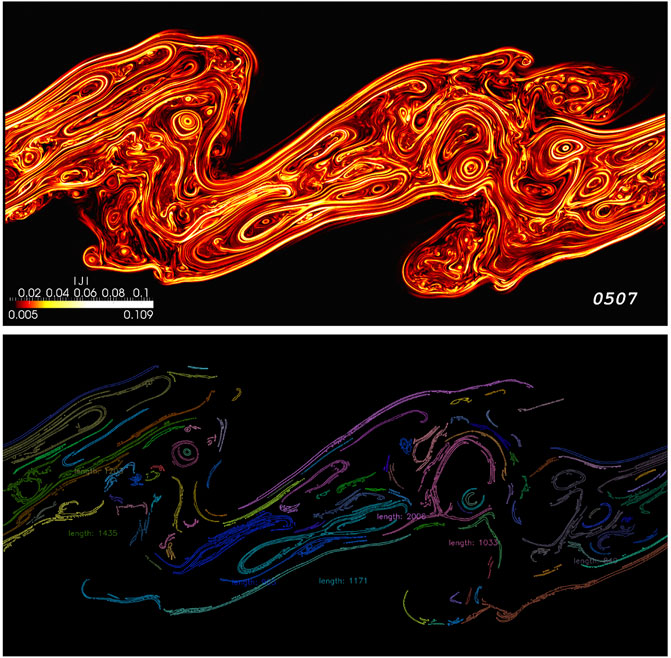
FIGURE 1. (A) Intensity plot of current density, (B) Automated detection and length measurements of current sheets.
2.2 Derivation of equations and operators from data
Deriving closed form, compact and understandable analytical equations from data is at the core of scientific discovery. In the following, we provide an overview of the recent ML techniques aimed at turning machine models to scientific knowledge. Such knowledge discovery can come in different forms: a) derivation of algebraic equation (e.g., law of gravity), b) derivation of ODE or PDE (e.g., the diffusion equation), and c) the derivation of the unknown parameters of a known equation (the so-called inverse problem).
2.2.1 Algebraic equations
Symbolic regression is an ML technique that searches the space of mathematical expressions to find the best data-feeding model. The goal is to strike a balance between model accuracy and model complexity. The common benchmark to compare the efficacy of different models is the Symbolic Regression database (https://space.mit.edu/home/tegmark/aifeynman.html) which contains 120 symbolic regression mysteries and answers. Most (100) of the equations are from Feynman Lectures on Physics and 20 more difficult equations are sourced from other physics books. See La Cava et al. (2021) for additional benchmarks.
Symbolic regression has been commonly carried out using generic programming and evolutionary algorithms, and there are several open source and commercially available libraries such as Eureqa (Schmidt and Lipson, 2009). Their main drawback is that, due to the combinatorial nature of the problem, genetic programming does not scale well to high dimensional systems. In contrast, ANNs are highly efficient at learning in high-dimensional space, and this has led to a flurry of activity in their adaptation to address the combinatorial challenge of symbolic regression. The blackbox nature of neural nets seems at first to be at odds with the goals of symbolic regression. Various approaches differ in how they overcome this issue and have been of two general varieties. In one approach, neural nets are used as an aid to reduce the search space of genetic programming techniques (e.g., Cranmer et al., 2020; Petersen et al., 2020; Udrescu et al., 2020; Udrescu and Tegmark, 2020). In AI-Feynman (Udrescu & Tegmark, 2020), the neural nets are used to find hidden simplicity such as symmetry in the data. Using this approach, they were able to derive all 100 of Feynman equations versus 71 using previous techniques.
The second class of solutions adapt the architecture of the neural nets for symbolic regression. The two key modifications required are to enable ANN to have access to a vocabulary of functions/primitives and to impose sparsity to reduce model complexity while maintaining high accuracy. Martius & Lampert (2016) proposed a simple feedforward ANN where standard activation functions are replaced with symbolic building blocks corresponding to functions common in science and engineering. These activation functions are analogous to the primitive functions in symbolic regression. Sahoo et al. (2018) extended the work to include division. In the Supplementary Material, we construct another type of ANN which, unlike standard ANNs, has a variety of synapses and cell body types. We show that it can derive law of gravity from data. Another approach involves adaptation of language models/transformers to the symbolic regression problem. Kamienny et al. (2022) developed an end-to-end transformer-based model that uses both symbolic tokens for the operators and variables, and numeric tokens for the constants. It shows a significant jump in accuracy compared to previous ANN-based approaches, with several orders of magnitude faster inference as compared to state-of-the-art genetic programming.
2.2.2 Unknown PDEs
In cases where the underlying PDEs are not known, scientists want i) accurate solvers that generalize well, ii) fast solvers which would be faster than traditional solvers in test cases where the PDE is known, iii) accurate symbolic extraction. Studies with their prime focus on symbolic extraction follow similar approaches as those for algebraic equations (see below). However, there are innovative breakthroughs in the development of solvers that address objectives i)-ii). This is accomplished through approaches that learn PDE solution operators. This includes DeepONet (Lu et al., 2019; Lu et al., 2021) and FNO (Li et al., 2021a, Kovachki et al., 2021) which are open source. See the latter for additional references and a useful literature review. Li et al. (2021a) showed successful experiments on Burger’s equation, Darcy flow, and the Navier-Stokes equations and achieved up to three orders of magnitude in speedup compared to traditional PDE solvers. Another important proof point and real-world application for FNO came from its adaptation for weather forecasting (FourCastNet) by Pathak et al. (2022). In a head-to-head comparison with a state-of-the-art forecasting system (IFS), FourCastNet was found to have generally comparable accuracy as IFS but with higher accuracy for small-scale variables, including precipitation. In addition, FourCastNet can generate forecasts (less than 2 s for a week-long forecast) orders of magnitude faster than IFS. This enables creation of fast large-ensemble forecasts which are out of reach of traditional techniques.
While DeepONet and FNO were not focused on symbolic extraction, one can always add symbolic extraction to the models. The basic ideas for discovery of PDEs from data in symbolic form are like those for algebraic data and can be cast into three categories. One category (e.g., sparse identification of non-linear dynamics (SINDy)) consists of construction of a candidate library of partial derivatives which is then used by a sparse regression technique to obtain a parsimonious model (Rudy et al., 2017; Champion et al., 2019). In case of PDEs, neural nets offer the added advantage of accurate differentiation. As a result, a second category of solutions combine neural nets with genetic algorithms where the derivatives are calculated by neural nets and genetic algorithms are used for search (Xu et al., 2020; Desai and Strachan, 2021). A third class is purely neural net based and includes the use of symbolic networks (Long et al., 2019).
2.3 Solutions when the form of the PDE is known
Here, we discuss three class of AI based approaches when the form of the PDE is known. As mentioned earlier, the so-called inverse problem is not discussed here (see Camporeale et al., 2022 for an application in space physics).
2.3.1 AI solvers
Conventional solvers (e.g., FDM) discretize the domain into a grid and advance the simulation using time-stepped methodology or discrete-event based time advance (e.g., Omelchenko and Karimabadi, 2022). The so-called Physics-Informed Neural Network (PINN)-type methods (Raissi et al., 2019; Jagtap and Karniadakis, 2020) overcome discretization issues of conventional solvers by taking advantage of auto-differentiation to compute the exact, mesh-free derivatives. They also offer several advantages over other deep learning approaches. PINN requires less training data since the underlying equation is already known. And having the prior knowledge of the physical/conservation laws enables their incorporation into the neural network design which in turn reduces the space of admissible solutions.
A notable study is that of Li et al. (2021b) who combined operator learning (FNO) with function optimization (PINN). This integrated technique (PINO) outperforms previous ML methods including both PINN and FNO, while retaining the significant speedup of FNO compared to instance-based solvers. In the challenging problem of long temporal transient flow of Navier-Stokes equation, where the solution builds up from near-zero velocity to a velocity where the system reaches ergodic state, PINO produces accurate results while retaining a 400x speedup compared to the GPU-based pseudo-spectral solver.
2.3.2 Closure models
A common approach to deal with the extreme multi-scale solution to PDEs is using subgrid closure models. Given the utility of neural networks for extracting equations from data, there has been significant work, especially in the CFD domain, on their use for development of closure models (Kurz and Beck, 2022 and references therein). Here we refer the reader to several review articles on this topic (e.g., Taghizadeh et al., 2020; Sofos et al., 2022).
2.3.3 Error correction
Another approach has been to use AI to correct errors at each time step in under-resolved simulations (Kochkov et al., 2021 and references therein). This approach requires training a coarse resolution solver with high resolution ground truth simulations. Promising results were obtained in solution to Navier-Stokes by Kochkov et al. (2021). Results were as accurate as baseline solvers with 8–10x finer resolution in each spatial dimension, resulting in 40–80x fold computational speedups. The model exhibited good stability over long simulations and showed surprisingly good generalization to Reynolds numbers outside of the flows where it is trained.
3 Discussion and proposed roadmap for NeuHPC in space physics
We advocate for the following changes: a) make funding NeuHPC a priority, b) adapt the funding to the pace of AI developments. This means a short leash on grants and strong focus on results measured by well-established benchmarks (see examples of benchmarks below). c) Promotion of interdisciplinary collaboration with AI experts in industry and academia to overcome the fact that most plasma physicists do not have deep expertise in AI.
Given AI’s prowess in predictions, we suggest as starting point proof-of-concept (POC) studies focused on video prediction and error correction:
• Video prediction: Apply off-the-shelf spatio-temporal deep learning models for video prediction (e.g., U-net, ResNet) to simulations. This would create a benchmark (Wang et al., 2020) for comparison with follow up studies using PDE centric AI approaches like PINO or FNO. We suggest 2D hybrid simulations (e.g., KHI) where many training cases can be generated for videos of current density, mixing (see Supplementary Material), among others.
• Grid error correction: Assess the viability of error correction in a coarse grid hybrid simulation, against an equivalent high-resolution simulation. DES hybrid (Omelchenko and Karimabadi, 2022) is particularly useful since it remains stable even when the grid scale is significantly larger than the ion inertial length.
• PIC noise error correction: Since noise level goes down only as the square root of number of particles, an AI-based correction would enable running a simulation with a low number of particles (e.g., 5 particles/cell) but reproducing results of a simulation with a much higher number of particles/cell (e.g., 500), a major breakthrough.
Other POCs of interest that target multi-scale problems include:
• Closure models: Explore derivation of closure models for the island coalescence problem (Karimabadi et al., 2011b).
• PDE derivation: Explore derivation of an equation that describes the temporal evolution of the island coalescence problem.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number (s) can be found in the article/Supplementary Material.
Author contributions
HK conceived of the idea for the paper and wrote the first draft. JW wrote the codes and produced the results for the two POCs in the Supplementary Material. All authors discussed and edited the final version of the manuscript.
Funding
Two of the authors (HK and JW) did not receive any external funding for their work. DAR is supported by NASA's Heliophysics Digital Resource Library.
Acknowledgments
The authors express their gratitude to Vadim Roytershteyn for obtaining the simulation data and making it available. They also acknowledge the valuable feedback from the reviewers that helped improve the manuscript. Additionally, the authors appreciate the constructive discussions with Hudson Cooper, Yuri Omelchenko, and William Daughton.
Conflict of interest
HK was employed by Analytics Ventures, JW was employed by AlphaTrai, Inc.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1120389/full#supplementary-material
References
Boberg, F., Peter, W., and Lundstedt, H. (2000). Real time Kp predictions from solar wind data using neural networks. Phys. Chem. Earth, Part C Sol. Terr. Planet. Sci. 254, 275–280. doi:10.1016/s1464-1917(00)00016-7
Breuillard, H., Dupuis, R., Retino, A., Le Contel, O., Amaya, J., and Lapenta, G. (2020). Automatic classification of plasma regions in near-earth space with supervised machine learning: Application to magnetospheric multi scale 2016–2019 observations. Front. Astronomy Space Sci. 7, 55. doi:10.3389/fspas.2020.00055
Camporeale, E., Wilkie, G. J., Drozdov, A. Y., and Bortnik, J. (2022). Data-driven discovery of fokker-planck equation for the earth's radiation belts electrons using physics-informed neural networks. J. Geophys. Res. Space Phys. 127, e2022JA030377. doi:10.1029/2022ja030377
Camporeale, E. (2019). The challenge of machine learning in space weather nowcasting and forecasting. Space Weather. 17, 1166–1207. doi:10.1029/2018SW002061
Champion, K., Lusch, B., Kutz, J. N., and Brunton, S. L. (2019). Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. 116, 22445–22451. doi:10.1073/pnas.1906995116
Chen, T., and Chen, H. (1995). Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Networks 6, 911–917. doi:10.1073/pnas.1906995116
Cranmer, M., Sanchez-Gonzalez, A., Battaglia, P., Xu, R., Cranmer, K., Spergel, D., et al. (2020). Discovering symbolic models from deep learning with inductive biases. Adv. Neural Inf. Process Syst. 33, 17429–17442.
Desai, S., and Strachan, A. (2021). Parsimonious neural networks learn interpretable physical laws. Sci. Rep. 11 (1), 12761–12769. doi:10.1038/s41598-021-92278-w
Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Netw. 2, 359–366. doi:10.1016/0893-6080(89)90020-8
Hu, A., Camporeale, E., and Swiger, B. (2022). Multi-hour ahead dst index prediction using multi-fidelity boosted neural networks. arXiv:2209.12571.
Jagtap, A. D., and Karniadakis, G. E. (2020). Extended physics-informed neural networks (xpinns): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 28 (5), 2002–2041. doi:10.4208/cicp.OA-2020-0164
Ji, H., Daughton, W., Jara-Almonte, J., Le, A., Stanier, A., and Yoo, J. (2022). Magnetic reconnection in the era of exascale computing and multiscale experiments. Nat. Rev. Phys. 4, 263–282. doi:10.1038/s42254-021-00419-x
Kamienny, P.-A., d’Ascoli, S., Lample, G., and Charton, F. (2022). End-to-end symbolic regression with transformers. arXiv preprint arXiv:2204.10532.
Karimabadi, H., Sipes, T., White, H., Marinucci, M., Dmitriev, A., Chao, J., et al. (2007). Data mining in space physics: Minetool algorithm. J. Geophys. Res. 112, A11215. doi:10.1029/2006JA012136
Karimabadi, H., Sipes, T., Wang, Y., Lavraud, B., and Roberts, A. (2009). A new multivariate time series data analysis technique: Automated detection of flux transfer events using Cluster data. J. Geophys. Res. 114, A06216. doi:10.1029/2009JA014202
Karimabadi, H., Vu, H. X., Loring, B., Omelchenko, Y., Sipes, T., Roytershteyn, V., et al. (2011a). “Petascale kinetic simulation of the magnetosphere,” in Proceeding of the TeraGrid Conference, Salt Lake City, UT, July 2011. Article No. 5. doi:10.1145/2016741.2016747
Karimabadi, H., Dorelli, J., Roytershteyn, V., Daughton, W., and Chacón, L. (2011b). Flux pileup in collisionless magnetic reconnection: Bursty interaction of large flux ropes. Phys. Rev. Lett. 107, 025002. doi:10.1103/PhysRevLett.107.025002
Karimabadi, H., Loring, B., Vu, H. X., Omelchenko, Y., Tatineni, M., Majumdar, A., et al. (2011c). Petascale global kinetic simulations of the magnetosphere and visualization strategies for analysis of very large multi-variate data sets. San Francisco: Astronomical Soc Pacific, 281–291.
Karimabadi, H., Yilmaz, A., and Sipes, T. (2012). “Recent advances in analysis of large datasets,” in Numerical modeling of space PlasmaFlows:ASTRONUM-2011. ASP conference series. Editors N. V. Pogorelov, J. A. Font, E. Audit, and G. P. Zank (San Francisco: Astronomical Society of the Pacific), 459, 371–377.
Karimabadi, H., O’Leary, P., Loring, B., Majumdar, A., Tatineni, M., and Geveci, B. (2013a). “In-situ visualization for global hybrid simulations,” in Proceeding of the Conference on Extreme Science and Engineering Discovery Environment: Gateway to Discovery (XSEDE ’13), July 2013 (San Diego: Association for Computing Machinery).
Karimabadi, H., Roytershteyn, V., Wan, M., Matthaeus, W. H., Daughton, W., Wu, P., et al. (2013b). “Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys. Plasmas 20 (1), 012303.
Kim, H., Kim, J., Won, S., and Lee, C. (2021). Unsupervised deep learning for super-resolution reconstruction of turbulence. J. Fluid Mech. 910, A29. doi:10.1017/jfm.2020.1028
Kochkov, D., Smith, J. A., Alieva, A., Wang, Q., P Brenner, M., and Hoyer, S. (2021). Machine learning accelerated computational fluid dynamics. arXiv preprint arXiv:2102.01010.
Kovachki, N., Li, Z., Liu, B., Azizzadenesheli, K., Bhattacharya, K., Stuart, A., et al. (2021). Neural operator: Learning maps between function spaces. arXiv preprint arXiv:2108.08481.
Kurz, M., and Beck, A. (2022). A machine learning framework for LES closure terms. Electron. Trans. Numer. Analysis 56, 117–137. doi:10.1553/etna_vol56s117
La Cava, W., Orzechowski, P., Burlacu, B., de Franca, F. O., Virgolin, M., Jin, Y., et al. (2021). “Contemporary symbolic regression methods and their relative performance,” in Advances in neural information processing systems — datasets and benchmarks track.
Li, X., Zheng, Y., Wang, X., and Wang, L. (2020). Predicting solar flares using a novel deep convolutional neural network. Astrophysical J. 891, 10. doi:10.3847/1538-4357/ab6d04
Li, Z., Kovachki, N. B., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A. M., et al. (2021a). “Fourier neural operator for parametric partial differential equations,” in Proceeding of the 9th International Conference on Learning Representations, ICLR 2021, Austria, May 2021 (Vienna: Virtual Event).
Li, Z., Zheng, H., Kovachki, N., Jin, D., Chen, H., Liu, B., et al. (2021b). Physics-informed neural operator for learning partial differential equations. arXiv preprint arXiv:2111.03794.
Long, Z., Lu, Y., and Dong, B. (2019). PDE-net 2.0: Learning PDEs from data with a numeric-symbolic hybrid deep network. J. Comput. Phys. 399, 108925. doi:10.1016/j.jcp.2019.108925
Lu, L., Jin, P., Pang, G., Zhang, Z., and Karniadakis, G. E. (2021). Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 3, 218–229. doi:10.1038/s42256-021-00302-5
Lu, L., Meng, X., Mao, Z., and Karniadakis, G. E. (2019). DeepXDE: A deep learning library for solving differential equations. arXiv preprint arXiv:1907.04502.
Martius, G., and Lampert, C. H. (2016). Extrapolation and learning equations. [Online]. Available: http://arxiv.org/abs/1610.02995.
Newell, P. T., Wing, S., Meng, C. I., and Sigillito, V. (1991). The auroral oval position, structure, and intensity of precipitation from 1984 onward: An automated on-line data base. J. Geophys. Res. Space Phys. 96, 5877–5882. doi:10.1029/90ja02450
Omelchenko, Y. A., and Karimabadi, H. (2022). Emaps: An intelligent agent-based technology for simulation of multiscale systems. Space and astrophysical plasma simulation. Editor J. Büchner Ch. 13 (in print). doi:10.1007/978-3-031-11870-8_13
Pathak, J., Subramanian, S., Harrington, P., Raja, S., Chattopadhyay, A., Mardani, M., et al. (2022). Fourcastnet: A global data-driven high-resolution weather model using adaptive fourier neural operators. arXiv preprint arXiv:2202.11214.
Petersen, B. K., Larma, M. L., Mundhenk, T. N., Santiago, C. P., Kim, S. K., and Kim, J. T. (2020). Deep symbolic regression: Recovering mathematical expressions from data via risk-seeking policy gradients. In Proceeding of the International Conference on Learning Representations, Sept 2020.
Raissi, M., Perdikaris, P., and E Karniadakis, G. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045
Rudy, S. H., Brunton, S. L., Proctor, J. L., and Kutz, J. N. (2017). Data-driven discovery of partial differential equations. Sci. Adv. 3, 1602614. doi:10.1126/sciadv.1602614
Sahoo, S. S., Lampert, C. H., and Martius, G. (2018). Learning equations for extrapolation and control. arXiv preprint arXiv:1806.07259.
Schmidt, M., and Lipson, H. (2009). Distilling free-form natural laws from experimental data. science 324 (5923), 81–85. doi:10.1126/science.1165893
Sofos, F., Stavrogiannis, C., Exarchou-Kouveli, K. K., Akabua, D., Charilas, G., and Karakasidis, T. E. (2022). Current trends in fluid research in the era of artificial intelligence: A review. A Rev. Fluids 7, 116. doi:10.3390/fluids7030116
Taghizadeh, S., Witherden, F., and Girimaji, S. (2020). Turbulence closure modeling with data-driven techniques: Physical compatibility and consistency considerations. New J. Phys. 22, 093023. doi:10.1088/1367-2630/abadb3
Udrescu, S-M., Tan, A., Feng, J., Neto, O., Wu, T., and Tegmark, M. (2020). AI Feynman 2.0: Pareto-optimal symbolic regression exploiting graph modularity. arXiv:2006.10782.
Udrescu, S-M., and Tegmark, M. (2020). AI feynman: A physics-inspired method for symbolic regression. arXiv:1905.11481, [physics.comp-ph].
Uritsky, V. M., Pouquet, A., Rosenberg, D., Mininni, P. D., and Donovan, E. F. (2010). Structures in magnetohydrodynamic turbulence: Detection and scaling. Phys. Rev. E 82, 326. doi:10.1103/physreve.82.056326
Wang, R., Kashinath, K., Mustafa, M., Albert, A., and Yu, R. (2020). “Towards physics-informed deep learning for turbulent flow prediction,” in Proceedings of the 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ’20), Virtual Event, CA, USA, August 2020 (ACM), 1457–1466. New York, NY, USA. doi:10.1145/3394486.3403198
Xiao, J., Chen, J., Zheng, J., An, H., Huang, S., Yang, C., et al. (2021). “Symplectic structure-preserving particle-in-cell whole-volume simulation of tokamak plasmas to 111.3 trillion particles and 25.7 billion grids,” in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, November 2021 (IEEE), 1–13.
Xu, H., Chang, H., and Zhang, D. (2020). DLGA-PDE: Discovery of PDEs with incomplete candidate library via combination of deep learning and genetic algorithm. J. Comput. Phys. 418, 109584. doi:10.1016/j.jcp.2020.109584
Keywords: AI1, PDE2, HPC3, Neural Nets4, Symbolic Regression5, closure Model6, error Prediction7
Citation: Karimabadi H, Wilkes J and Roberts DA (2023) The need for adoption of neural HPC (NeuHPC) in space sciences. Front. Astron. Space Sci. 10:1120389. doi: 10.3389/fspas.2023.1120389
Received: 09 December 2022; Accepted: 23 January 2023;
Published: 21 February 2023.
Edited by:
Joseph E Borovsky, Space Science Institute, United StatesReviewed by:
Enrico Camporeale, University of Colorado Boulder, United StatesCopyright © 2023 Karimabadi, Wilkes and Roberts. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Homa Karimabadi, aG9tYWthckBnbWFpbC5jb20=
 Homa Karimabadi
Homa Karimabadi Jason Wilkes2
Jason Wilkes2 D. Aaron Roberts
D. Aaron Roberts