Solar Wind Turbulence Outlined Through Magnetic Islands and Nonlinear Waves

Various space missions and observations over the past decades have provided unexampled details about the nature of solar wind, the acceleration mechanism, and different nonlinear phenomena responsible for energy transfer and turbulence in the interplanetary space. This review focuses on the role of Alfvénic fluctuations—both kinetic Alfvén wave (KAW) and dispersive Alfvén wave (DAW)—in driving solar wind turbulence and magnetic reconnection at 1 AU. The process of filamentation has been studied through a nonlinear coupling system of KAW/IAW (ion acoustic wave) and relatively high-frequency pump KAW (HKAW, i.e., frequency less than ion cyclotron frequency) in the presence of LKAW (low-frequency KAW, i.e., frequency very much less then ion cyclotron frequency) perturbation by formulating their dynamical equations in the presence of ponderomotive force and using the numerical results for the same. A simplified model is presented to have a deeper insight into the evolution pattern using the results of simulation. The formation of coherent structures and current sheets using a numerical and semi-analytical approach is elaborated near the magnetic reconnection sites. In addition to this, the relevance of the generated turbulence is also depicted through the energy spectrum by examining the spectral index which is noticeable in determining the energy cascade down to smaller scales.

Introduction

Solar wind predominantly permeates the whole heliosphere, providing an indispensable medium to study collisionless plasma. It develops a strong turbulent character on expansion, and for decades, intensive efforts have been directed to understand solar wind and its turbulent nature through various space missions like SOHO (Solar Heliospheric Observatory), Ulysses, Voyager, Helios, Yohkoh, FREJA, POLAR, FAST, Cluster, and TRACE (Transition Region and Coronal Explorer). Emanating from the solar corona and expanding outward into space (Parker, 1958), solar wind acts as a natural laboratory (Bruno and Carbone, 2013) for in situ spacecraft measurements to investigate solar wind turbulence. To understand the turbulent system and perform multipoint measurements, the NASA MIDEX mission HelioSwarm is in a Phase-A study (Klein, 2019; Spence, 2019; Hautaluoma and Fox, 2020). The latest NASA mission, the Parker Solar Probe, is designed to probe the mechanisms leading to acceleration of solar wind. At the closest approach to the Sun, the Parker Solar Probe has progressed one step toward reaching the Sun to explore the mysteries of the evolution of the Sun and provide deeper insights into the flow of energy from the solar corona to the accelerating solar wind. The evolution of astrophysical environments is significantly affected by the turbulent cascade of energy and, so to identify with the dynamics of energy dissipation, is therefore of cardinal importance to the astrophysics communities.

In a turbulent medium like solar wind, the magnetic field lines constantly break and reconnect at some scales (Franci et al., 2017; Mallet et al., 2017; Vech et al., 2018), making magnetic reconnection an inherent part of a turbulent cascade. This process is associated with the release of large amount of energy and is responsible for the transfer of energy between different length scales, thereby leading to the acceleration of particles in solar wind (Lazarian et al., 2020). This review presents an outline of the solar wind plasma portraying the influence of the nonlinear wave–wave interactions (Kraichnan, 1965; Howes & Nielson, 2013; Iroshnikov P.S., 1964; Pezzi et al., 2017a, 2017b; Roberts et al., 2017; Narita, 2018; Roberts et al., 2022) and their role in understanding the nature of turbulence through the transfer of energy from large scales to smaller scales. The understanding of mechanisms which play a decisive part in creation of astrophysical environments through the dissipation of turbulent energy to heat has always been an issue of debate. Different schools of thought have structured this debate. In the first, Alfvénic turbulence is considered one of the processes responsible for the transfer of energy (Coleman, 1968; Isenberg and Hollweg, 1982; Tu et al., 1984; Hu et al., 2000; Isenberg, 2004). Being low-frequency magnetohydrodynamic (MHD) modes and difficult to dissipate, they are able to permeate the whole solar atmosphere and are ubiquitously present in the solar wind. An illustrative characteristic of magnetized turbulence is the propensity to form sheets of current density that are liable to magnetic reconnection (Matthaeus & Lamkin, 1986; Biskamp & Welter, 1989; Dmitruk & Matthaeus, 2006; Retinò et al., 2007; Servidio et al., 2009; Comisso and Sironi, 2019). These reconnecting current sheets are typical sites of particle acceleration and magnetic energy dissipation (Dmitruk et al., 2004). Concurrently, it has long been known that particles can gain energy through random scattering by turbulence fluctuations (Kulsrud & Ferrari, 1971). Therefore, turbulence fluctuations and magnetic reconnection work in alliance, and for a comprehensive understanding of the physics in a turbulent surrounding we need to have a detailed examination of their interplay.

The solar wind is inhabited by Alfvénic fluctuations spanning from fraction of a second to several hours. Their presence in the astrophysical plasma is endorsed by various observational evidences (Belcher and Davis, 1971; Cirtain et al., 2007; He et al., 2009; Okamoto et al., 2007). The restoring force and inertia for the Alfvén wave are provided by the magnetic tension and the ion mass, respectively. Ideal MHD equations administer the propagation of this non-dispersive Alfvén wave which is now called the shear Alfvén wave. The Alfvénic wave disturbance moves with no attenuation with distance along the background magnetic field, and this remarkable property has important ramifications for the transport of energy in plasma fluids. The nonlinear phenomena are of prominent interest to properly assess the acceleration and transportation of the particles in the solar wind. Alfven waves may come across instabilities and may convert into other dispersive modes which may provide a pathway to carry large amounts of energy and then dissipate it as heat (Bogdan et al., 2003).

When the Alfven waves attain wavelengths comparable to the ion gyroradius in the direction perpendicular to the background magnetic field, they are known as kinetic Alfvén waves (KAWs) (Podesta, 2013; Narita et al., 2020). KAWs are believed to play an indispensable role in particle heating and acceleration mechanisms (Wu, 2003; Wu and Chao, 2004). The transfer of energy from MHD scales to kinetic scales is also possible through the interaction of KAWs with large-scale MHD waves (Zhao et al, 2011). The in situ measurements in the solar wind back up the idea of an Alfvén wave turbulent cascade in the perpendicular direction at the ion or electron scales producing the KAWs (Howes et al., 2008a, Howes et al., 2008b, Howes et al., 2011; Alexandrova et al., 2013; Sahraoui et al., 2009; Zhao et al., 2013). KAWs are also dominating at proton kinetic scales (He et al., 2009; Roberts et al., 2017) and also shorter scales (Chen et al., 2010a). In addition, they can also couple with high-frequency modes (Zhao et al., 2013). The shear and kinetic Alfvén waves account for various nonlinear effects like parametric processes such as three-wave decay interactions, modulational instability, and the background plasma number density being modified by the ponderomotive force of the Alfvén wave. The nonlinear interaction of the KAW and shear Alfvén wave has been intensively studied by many authors and energy transfer processes so as to interpret the observations to have a deeper insight into the turbulent cascade of energy (Zhao et al., 2013). With the finite frequency correction, i.e., when the frequency of the Alfven wave becomes comparable to but less than the ion cyclotron frequency, we get circularly polarized dispersive Alfven waves (DAWs). This dispersion of the wave also occurs when the wavelength is around the ion inertial length, which many authors (Meyrand & Galtier, 2012; Ghosh, et al., 1996) consider the Hall term, and this Hall term contributes significantly to the transfer of energy over and across the small scales as well as has an important role in the increased reconnection rate (Shay et al., 2001; Smith et al., 2004). The interaction of these dispersive Alfvén waves undergoing filamentation with the pre-existing chain of magnetic islands may also contribute toward the turbulent cascade of energy in the solar wind.

Nonlinear processes being dominant in the transfer of energy from long wavelength magnetic fluctuations to shorter wavelengths, the study of the frequency spectrum is of utmost importance to unravel the nature of turbulent plasma. The energy spectrum depicting the turbulence scaling comprises the energy injection scales followed by the energy-containing scale, known as the forcing range or injective range, marking the energy source. Next, the “inertial range,” also called the intermediate range, marks the energy transfer process to smaller scales. This range is often described as the “dissipation range,” “dispersion range,” or the “scattering range.” In this range, the fluctuations are converted to thermal energy, thereby causing the heating of particles. For magnetic fluctuations at very large scales (i.e. f ≤ 10–⁴ Hz), the power spectra go as k ⁻¹. This range is the energy reservoir feeding the turbulent cascade and so called the 1/f range (Matthaeus and Goldstein 1986; Chandran 2018; Matteini et al., 2018). Various measurements account for the Kolmogorov k^−5/3 spectrum in the inertial range (10⁻³ Hz ≤ f ≤ 10⁻¹Hz) followed by steepening at ion kinetic scales. A spectral break appears around kρ_s >1 (where ρ_s is the ion gyroradius), and the spectral index lies between -2 and -5 (Bale et al., 2005; Shaikh and Shukla, 2009; Sahraoui et al., 2009). Between the ion scales and the electron scales, a small scale turbulent cascade is established (Alexandrova 2009). As the turbulent cascade crosses the ion scales and before reaching the electron scales (i.e. 3 ≤ f ≤ 30 Hz), the magnetic spectra follow ∼ k^−2.8 (Alexandrova et al., 2009; Chen et al., 2010a; Sahraoui et al., 2010). The spectral index is conspicuous of the energy transfer phenomena. Many pioneering works have been carried out to understand the dynamics and the different nonlinear processes responsible for this steepening (Leamon et al., 2000; Sahraoui et al. 2010; Rudakov et al., 2011).

The prime candidates contributing to the spectral properties and the steepening of the spectra are the various nonlinear processes like transverse collapse or filamentation due to KAW, its interaction with other wave modes, and/or the formation of coherent (magnetic) structures resulting from the current sheets. In the literature, the analysis of the field fluctuations from the proton to the electron scales shows the presence of current sheets or possible coherent structures of sub-proton scales which are possible sites of magnetic reconnection and energy dissipation (Perri et al., 2012). The current sheets may be formed self-consistently from the Alfven wave-driven turbulence as discussed by Tanbarge & Howes, (2013). These coherent structures play an important role in driving the nonlinear transfer of energy to the smaller scales as they make some additional self-consistent energy injection available (Ma et al., 1995; Sturrock et al., 1999) and thus support the continuation of the turbulence over the smaller scales (Cerri & Califano, 2017). Therefore, it is required to further examine if this turbulent energy transfer across and below the ion scales takes place as a result of instabilities or some other mechanism such as magnetic reconnection that causes the formation of coherent/localized structures or if it is both. A plethora of studies show that instabilities such as those driven by the temperature anisotropy (Gary and Lee, 1994; Verscharen et al., 2014), stream-shear-driven instabilities (Roberts et al., 1992), and parametric instabilities (Longtin and Sonnerup, 1986; Brodin and Stenflo, 1988; Viñas and Goldstein, 1991; Stenflo and Shukla, 2007; Primavera et al., 2019) such as filamentation, all may possibly lead to the dissipation of solar wind turbulence. At the same time, observations also show that reconnection can typically cause turbulence in the solar wind (Vörös et al., 2014). The spectral scaling of these fluctuations driven by the reconnection flow (obtained using the WIND spacecraft data) bears resemblance with the observations in the inertial and dispersive regime of the solar wind. Thus, these two processes, that is, turbulence and magnetic reconnection, work in alliance, and an associative study is required to be carried out.

Here, we revisit the nonlinear effects caused by dispersive Alfvén waves and KAWs to comprehend the dynamics of solar wind turbulence. Part A discusses the nonlinear effects and the turbulence due to the KAW presenting the effect of initial conditions on the spectra and the detailed explanation governing the evolution pattern through a simplified model. In part B, we study the nonlinear evolution of dispersive Alfvén waves in the vicinity of pre-existing chains of magnetic islands. The wave becomes dispersive due to the wave frequency which is finite but less than the ion cyclotron frequency.

A. Turbulence due to the Kinetic Alfvén Wave

Many simulations backed up with observations have led to a deeper understanding of turbulence at 1 AU (Howes and Quataert, 2010; Sahraoui et al., 2010; Narita et al., 2020) unwinding the energy transfer processes. This section predominantly focuses on the role of KAWs in understanding the dissipation of energy through different nonlinear processes. One of the processes leading to energy transfer is filamentation or transverse collapse which has been widely investigated. The sensitivity of the nonlinear coupling of KAWs/IAWs resulting in the transverse collapse on different initial conditions is addressed. Considering the wave propagation in the x–z plane and background field $B_0\widehat{z}$ and using a two-fluid model, the following system of equations is derived in the dimensionless form (Gaur and Sharma, 2015):

$\begin{array}{l}i\frac{\partial B_y}{\partial t}+i\frac{\partial B_y}{\partial z}+2i{c}_1\frac{\partial B_y}{\partial x}+\frac{{\partial }^2{B}_y}{\partial x^2}+c_2\frac{{\partial }^2{B}_y}{\partial z^2}+n{B}_y=0,\\ \frac{{\partial }^{2}n}{\partial t^2}-\frac{{\partial }^2}{\partial t^2}\frac{{\partial }^{2}n}{\partial x^2}-\beta \frac{{\partial }^{2}n}{\partial z^2}=-\frac{{\partial }^2}{\partial t^2}\frac{{\partial }^2}{\partial x^2}{\left|B_y\right|}^2-\beta \frac{{\partial }^2}{\partial z^2}{\left|B_y\right|}^2.\end{array}(1)$

The localized structures of KAWs with the magnetic field $B_y$ in the transverse direction are studied at 1 AU under different initial conditions by performing numerical simulation of this set of equations. Here, $c_1=k_{0x}{\rho }_s$, $c_2=k_{0x}^2{\rho }_s^2/4$, and $\beta =c_s^2/V_A^2$. The equation is normalized using the parameters $x_n={\rho }_s$, $z_n=2/k_{0z}$, $t_n=\left(2\omega /V_A^2{k}_{0z}^2\right)$, $n_n=n_0$, and $B_n={\left[\left\{1-\eta \left(1+\delta \right)\right\}{V}_A^2{k}_{0z}^2/16\pi n_{0}T{\omega }^2\right]}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$. Here, $\eta =\frac{{\omega }^2}{{\omega }_{ci}^2}$ and $\delta =\frac{m_e{k}_{0x}^2}{m_i{k}_{0z}^2}$, and $T_e+T_i=T,k_{0x}$ is the perpendicular wave vector component and $k_{0z}$ is the parallel wave vector component to $\widehat{z}{B}_0$, where $\omega$ refers to the KAW frequency, $c_s$ is the acoustic speed, $V_A$ is the Alfvén speed, and ${\rho }_s$ is the ion acoustic gyroradius. Three different perturbations imposed on a uniform plane KAW are periodic perturbation (IC-1), Gaussian perturbation (IC-2), and the third random perturbation (IC-3):

$\text{IC}-1B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon \cos \left({\alpha }_{x}x\right)\right)\left(1+\epsilon \cos \left({\alpha }_{z}z\right)\right)\mathrm{and}n\left(x,z,0\right)={\left|B_y\left(x,z,0\right)\right|}^2$

$\text{IC}-2B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon \exp \left(\frac{-x^2}{r_{01}^2}\right)\right)\left(1+\epsilon \exp \left(\frac{-z^2}{r_{02}^2}\right)\right)$

$\text{IC}-3B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon \exp \left(2\pi i\theta \left(x\right)\right)\right)\left(1+\epsilon \exp \left(2\pi i\theta \left(z\right)\right)\right)$

Here, the initial amplitude of the main KAW is $B_{y0}=1$, $\epsilon =0.1$ is the magnitude of the perturbation, $r_{01}$ (normalized by $x_n$) is the transverse scale size of the perturbation, $r_{02}$ (normalized by $z_n$) is the longitudinal scale size of the perturbation, and $\theta \left(x\right)$ and $\theta \left(z\right)$ are the random variables uniformly distributed on [0,1] (Sharma et al., 1996). The random value for theta is attributed at each grid point in the x–z plane. A seed value was initially provided, and random variables were generated and uniformly distributed on [0,1] in the x–z plane.

Figures 1A–3A,C present the simulation results indicating the splitting of pump KAW at different instances of time with periodic, Gaussian, and random perturbation forms, respectively, in real space alongside contour plots in the Fourier space, i.e., Figures 1B–3B,D. The figures demonstrate that there is no regularity in the filament formation with the formation of the most intense structures at the early time and an increase in complexity at later times. The contour plot shows the dependence of $|B_{yk}{|}^2$ on Fourier modes. As is noticeable in these figures, the filamentary structures obtained have different intensities and patterns. Also, there is a varied scale size of the structures under the three initial conditions ($\approx 0.3{\rho }_s$ with periodic, $\approx 1.6{\rho }_s$ with Gaussian, and $\approx 0.5{\rho }_s$ with random perturbation). For β $>$ $\frac{m_e}{m_i}$, the transverse size of Alfvén vortex tubes is of the order of ${\rho }_s$ (Chmyrev et al., 1988).

FIGURE 1

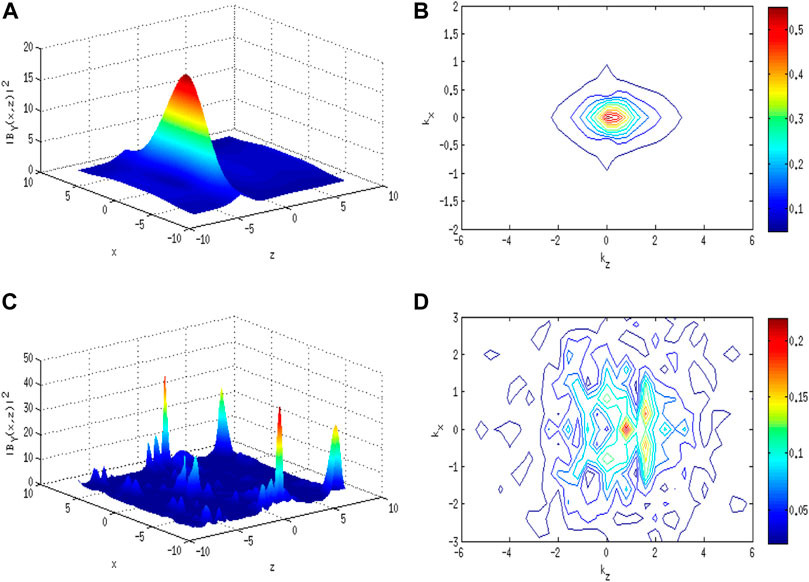
FIGURE 1. With IC-1. (A) Normalized intensity profile of the KAW magnetic field ($\left|B_y^2\right|/B_n^2$) at normalized t = 6 (t normalized by $t_n=\left(2\omega /V_A^2{k}_{0z}^2\right)$) in a normalized x–z plane (x normalized with $x_n={\rho }_s$, and z normalized by $z_n=2/k_{0z}$). (B) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 6. (C) Normalized intensity profile of the KAW magnetic field $\left(\left|B_y^2\right|/B_n^2\right)$ at normalized t = 13. (D) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 13. “Reproduced from [(Gaur and Sharma, 2014), Astrophys Space Sci (2014) 350, https://doi.org/10.1007/s10509-013-17701], with the permission of Springer Publishing.”

FIGURE 2

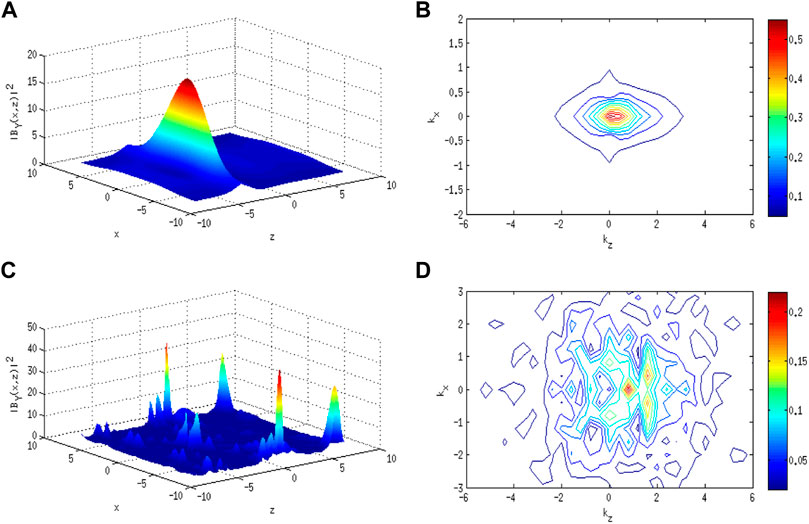
FIGURE 2. With IC-2. (A) Normalized intensity profile of the KAW magnetic field $\left(\left|B_y^2\right|/B_n^2\right)$ at normalized t = 6 (t normalized by $t_n=2\omega /V_A^2{k}_{0z}^2$) in a normalized x–z plane (x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$). (B) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 6. (C) Normalized magnetic field intensity profile of KAW at t = 13. (D) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 13. “Reproduced from [(Gaur and Sharma, 2014), Astrophys Space Sci (2014) 350, https://doi.org/10.1007/s10509-013-17701], with the permission of Springer Publishing.”

FIGURE 3

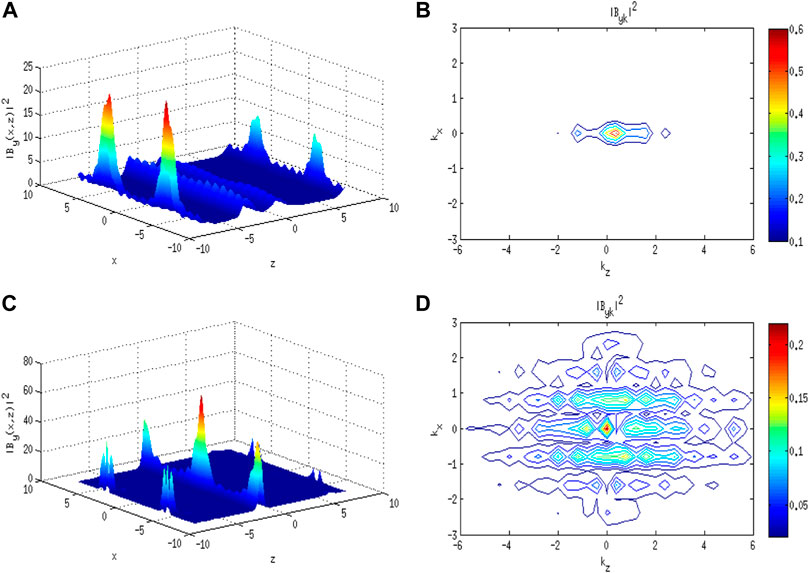
FIGURE 3. With IC-3. (A) Normalized intensity profile of the KAW magnetic field $\left(\left|B_y^2\right|/B_n^2\right)$ at normalized t = 6 (t normalized by $t_n=2\omega /V_A^2{k}_{0z}^2$) in a normalized x–z plane (x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$). (B) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 6. (C) Normalized magnetic field intensity profile of KAW at t = 13. (D) Contours of normalized ${\left|B_{yk}\right|}^2$ against Fourier modes of KAW at t = 13. “Reproduced from [Gaur et al. (2014), Astrophys Space Sci (2014) 350, https://doi.org/10.1007/s10509-013-17701], with the permission of Springer Publishing.”

Figure 4 illustrates the effect of formation of localized structures on the wave number spectrum. In the power spectra obtained by plotting ${\left|B_k\right|}^2$ against $k$, $k_x=0$, the scaling law approaches $k^{-5/3}$ for $k<1$ followed by a spectral break at around $k\approx 1$. The scaling index for $k>1$ shows dependence on the initial conditions being $k^{-2.6}$ for periodic, $k^{-2.2}$ for Gaussian, and $k^{-2.6}$ for the random forms of perturbation.

FIGURE 4

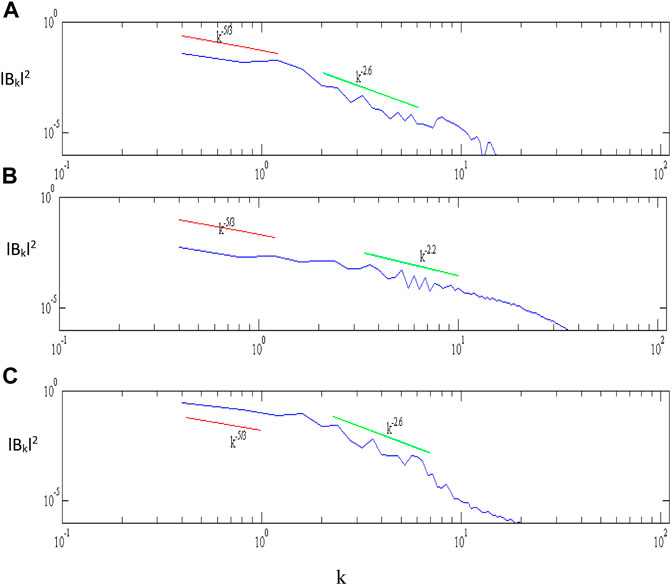
FIGURE 4. Power spectrum of normalized magnetic field fluctuations $\raisebox{1ex}{${\left|B_k\right|}^2$}\!\left/ \!\raisebox{-1ex}{$B_n^2$}\right.$ against$\text{k}\left({\text{normalized with ρ}}_{\text{s}}\right)$. (A) With IC-1 at t = 15. (B) With IC-2 at t = 17. (C) With IC-3 at t = 15. “Reproduced from [Gaur et al. (2014), Astrophys Space Sci (2014) 350, https://doi.org/10.1007/s10509-013-17701], with the permission of Springer Publishing.”

A Simplified Model: A Deeper Insight Into the Evolution Pattern of Kinetic Alfvén Wave

Implementing the conditions ${\partial }_x{B}_y$ >>$k_{0x}{B}_y$ and ${\partial }_z{B}_y$ <<$k_{0z}{B}_y$ on the aforementioned system of equations in the un-normalized form (Sharma et al., 2011a), the dynamics of the evolution are studied in an extended paraxial regime semi-analytically. As elaborately discussed by Sharma et al. (2014), the equation for dimensionless beam width parameter $f_0$ is obtained as (using normalization distance $\xi =R_d$, where $R_d=k_{0z}{r}_0^2$):

$\frac{{\partial }^2{f}_0}{\partial {\xi }^2}=\frac{1}{a^2{f}_0^3}\left(1-2a_0^2-2a_0+6a_1\right)-\frac{R_d^2\gamma B_{00}^2}{a{r}_0^2{f}_0^2}\left(1+a_0\right)-\frac{R_d^2{f}_0{\alpha }^2}{2!}{\displaystyle \sum _{m=1}^{64}{n}_m{m}^2}.(\mathrm{a})$

In the RHS of the aforementioned equation, the finite transverse size of the KAW accounted by the first term causes diffraction, and the nonlinearity is marked by the last three terms. The equation represents the interplay of diffraction, and nonlinear terms indicate the divergence less travel of the wave when these terms balance each other. The equation for $S_{02}$ is obtained as:

$\frac{\partial S_{02}}{\partial \xi }=-\frac{{\rho }_s^2}{2r_0^2{f}_0^6}\left(11a_0{a}_1-2a_0^3-2a_0^2+4a_1\right)+\frac{\gamma B_{00}^2}{4f_0^5}+\frac{a_1\gamma B_{00}^2}{2f_0^5}-\frac{a_0\gamma B_{00}^2}{2f_0^5}+\frac{r_0^4{\alpha }^4{n}_1}{2\left(4!\right)}{\displaystyle \sum _{m=1}^{64}{n}_m{m}^4}.(\mathrm{b})$

The Equations for $a_0$ and $a_1$ are expressed as:

$\frac{\partial a_0}{\partial \xi }=-\frac{12S_{02}{f}_0^2}{a{r}_0^2},(\mathrm{c})$

$\frac{\partial a_1}{\partial \xi }=\left(8-20a_0\right)\frac{S_{02}{f}_0^2}{a{r}_0^2}.(\mathrm{d})$

Here, $B_{00}$ is the initial wave field at z = 0, $a_0$ and $a_1$ are the coefficients of x² and x⁴, respectively, $S_{00}$ is the slowly varying functions of x and z, $r_0$ is the transverse scale size of the wave, and $\gamma =1/B_n^2$ is the normalization factor. The system of coupled equations (a)-(d) is numerically solved using the fourth-order Runge–Kutta method for a plane wave front under initial conditions being $f_{0 }$ = 1 and $\raisebox{1ex}{$d{f}_0$}\!\left/ \!\raisebox{-1ex}{$dz$}\right.=0$ at z = 0 and $a_0=a_1=0$ at z = 0.

As illustrated in Figure 5. The wave intensity becomes high when the parameter $f_0$ takes a minimum value and vice versa. The time dependence in the model is consolidated through the dependency of $n$ on time (using simulation results). As time progresses, the intensity and localization pattern of the KAW changes through the change in density harmonics.

FIGURE 5

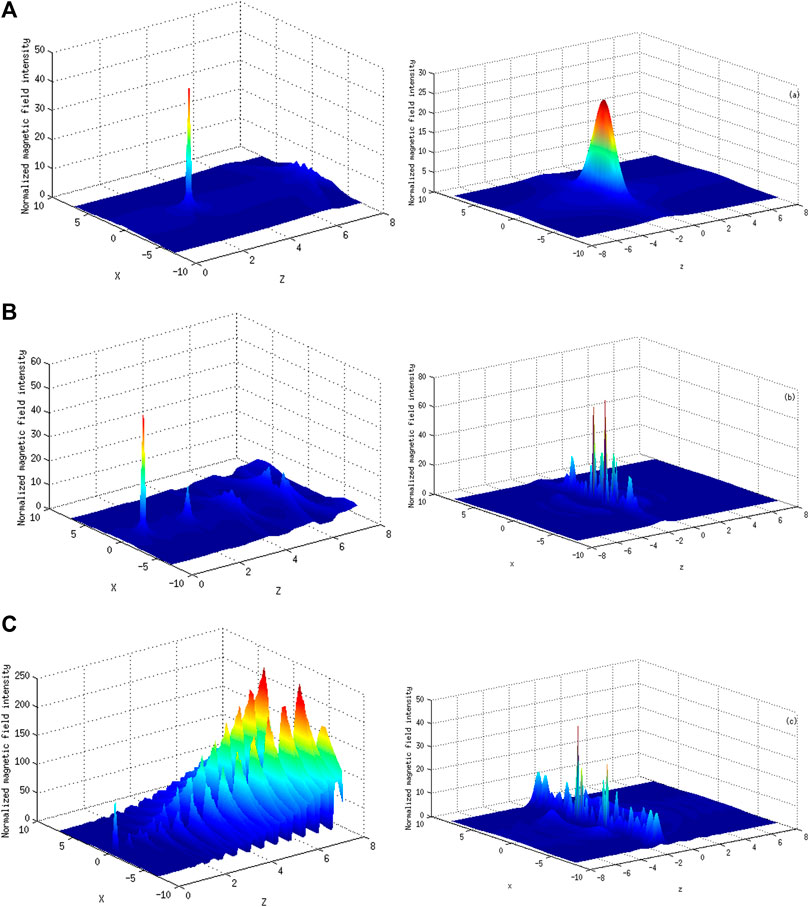
FIGURE 5. Normalized magnetic field intensity distribution $\left(\left|B_y^2\right|/B_n^2\right)$ of the wave from the (1) Simplified model and (2) Numerical simulation in a normalized x–z plane ((x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$), at (A) t = 9, (B) t = 11, and (C) t = 12. “Reproduced from [(Sharma and Gaur, 2014), Physics of Plasmas, 21, 042,302, http://dx.doi.org/10.1063/1.4870500], with the permission of AIP Publishing.”

Nonlinear Effects due to KAW

Various wave modes interact with KAW to comprehend the turbulence in the space plasma. Other wave modes are excited by the ponderomotive force of KAW which leads to modification in density resulting in the nonlinear dynamics of KAW. Low-frequency KAW (LKAW) is also one of the wave modes present in the plasma, and its excitation by the ponderomotive force of relatively high-frequency, high-power pump KAW is analyzed to study its effect on the solar wind turbulence. With cold plasma assumption and two fluid models (separate ion and electron motions) in the solar wind regime, the dynamical equations are formulated and solved numerically to study the KAW evolution and the power spectra at 1 AU [ Gaur, N and R.P Sharma, 2014]:

$i\frac{\partial B_y}{\partial t}+i\frac{\partial B_y}{\partial z}+2i{c}_1\frac{\partial B_y}{\partial x}+\frac{{\partial }^2{B}_y}{\partial x^2}+c_2\frac{{\partial }^2{B}_y}{\partial z^2}+n{B}_y=0,$

$\frac{{\partial }^{2}n}{\partial t^2}-c_3\frac{{\partial }^{4}n}{\partial t^2\partial x^2}+c_4\frac{{\partial }^{4}n}{\partial x^2\partial z^2}-c_5\frac{{\partial }^{2}n}{\partial z^2}=-c_1\frac{{\partial }^4}{\partial x^2\partial z^2}{\left|B_y\right|}^2-c_2\frac{{\partial }^4}{\partial z^3\partial x}{\left|B_y\right|}^2.$

This system of equations is solved under the following initial conditions (ICs) for the magnetic field and density perturbation:

$B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{x}x\right)\right)\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{z}z\right)\right)\text{and }n\left(x,z,0\right)=a_1\cos \left({\alpha }_{mx}x+{\alpha }_{mz}z\right),$(IC-1)

$B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{x}x\right)\right)\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{z}z\right)\right)\text{and }n\left(x,z,0\right)=a_1\left(\exp \left(-r_x{x}^2/r_{01}^2\right)\right)\left(\exp \left(-r_z{z}^2/r_{02}^2\right)\right),$(IC-2)

$B_y\left(x,z,0\right)=B_{y0}\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{x}x\right)\right)\left(1+\epsilon e^{i\theta }\cos \left({\alpha }_{z}z\right)\right)\text{and }n\left(x,z,0\right)=a_1\left(\exp \left(-x^2/r_{01}^2\right)\right)\left(exp\left(-z^2/r_{02}^2\right)\right).$(IC-3)

The initial amplitude of the pump wave is $B_{y0}=1{\text{, a}}_1=\text{0}\text{.}1$ for density perturbation at t = 0, and $\epsilon$ represents the magnitude of the perturbation. The normalized transverse and longitudinal scale size of the perturbation is $r_{01}$ and $r_{02}$, respectively. Here, $r_x$ and $r_z$ are the random variables uniformly distributed on [0,1].

The filamentation process giving rise to strong magnetic filaments parallel to the ambient field is demonstrated under three initial conditions. The effect of the perturbation wave number is shown in the Figures 6–8 under different initial conditions. It exemplifies the dependence of nonlinear evolution patterns on the values of ${\alpha }_x,{\alpha }_z$, and as shown, the structures become highly irregular and random with increased values of the perturbation wave number.

FIGURE 6

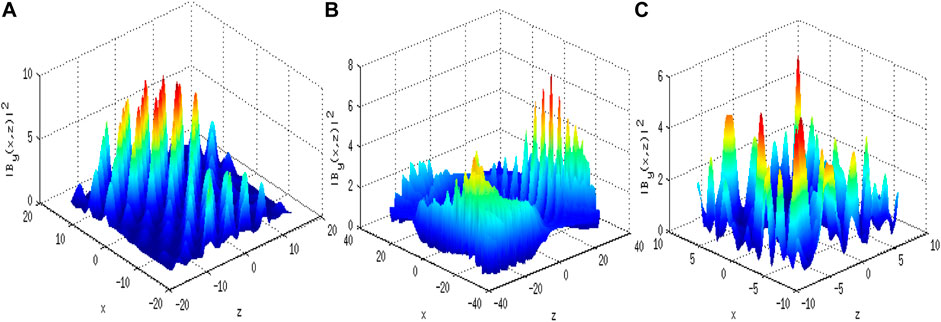
FIGURE 6. Normalized magnetic field intensity of wave $\left|B_y^2\right|/B_n^2$ in a normalized x–z plane (x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$ with IC-1 for (A) ${\alpha }_x,{\alpha }_z=0.2$, (B) ${\alpha }_x,{\alpha }_{z }=0.1$, and (C) ${\alpha }_x,{\alpha }_z=0.4$. “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.”

FIGURE 7

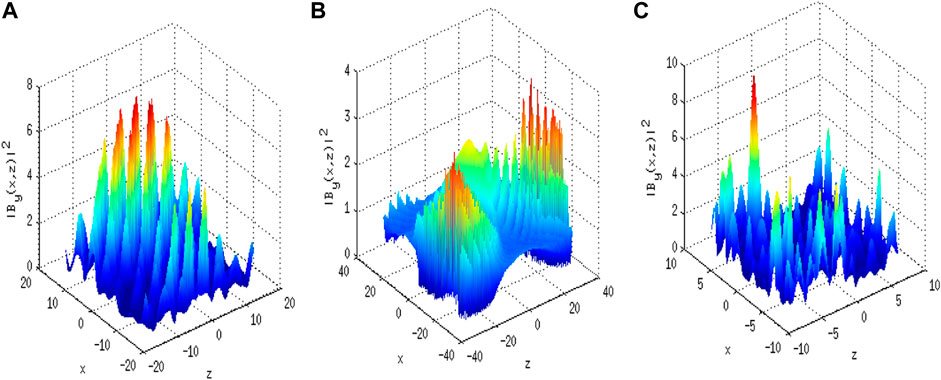
FIGURE 7. Normalized magnetic field intensity of wave $\left|B_y^2\right|/B_n^2$ $\text{in}$ a normalized x–z plane (x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$) with IC-2 for (A) ${\alpha }_x,{\alpha }_z=0.2$, (B) ${\alpha }_x,{\alpha }_z=0.1$, and (C) ${\alpha }_x,{\alpha }_z=0.4$. “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.”

FIGURE 8

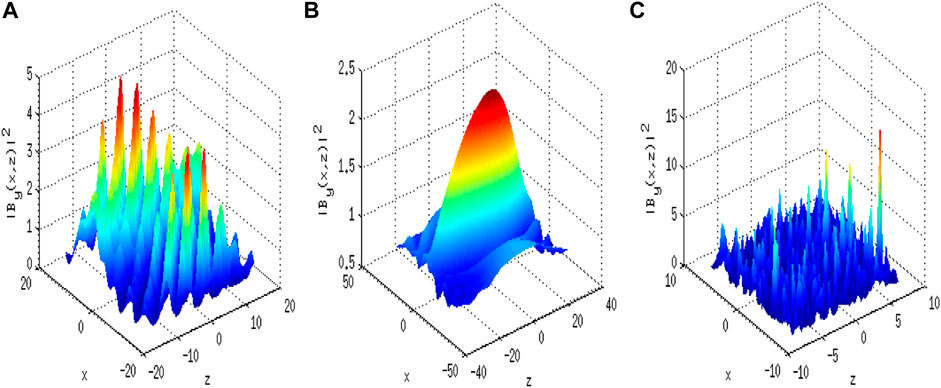
FIGURE 8. Normalized magnetic field intensity of wave $\left(\left|B_y^2\right|/B_n^2\right)$ in a normalized x–z plane (x normalized with $x_n={\rho }_s$ and z normalized by $z_n=2/k_{0z}$) with IC-3 for (A) ${\alpha }_x,{\alpha }_z=0.2$, (B) ${\alpha }_x,{\alpha }_z=0.1$, and (C) ${\alpha }_x,{\alpha }_z=0.4$. “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.”

The energy distribution is further illustrated in the contour plots of $B_{yk}$ in the $\left(k_x,k_z\right)$ Fourier space in Figure 9 which clearly highlight the confinement of energy to low $k_x\text{, }{k}_z$ wave numbers at initial times and its distribution to higher wave numbers at later times (energy flow from larger scales to smaller scales).

FIGURE 9

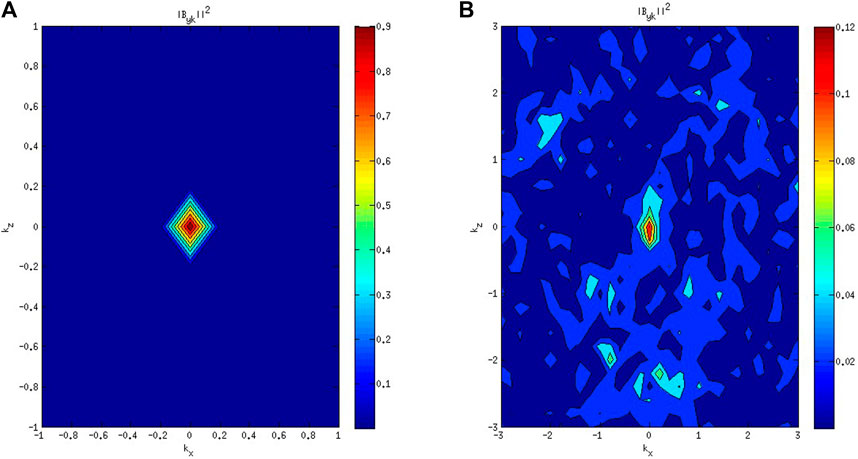
FIGURE 9. Contours of normalized ${\left|B_{yk}\right|}^2$ in $k_{x }, k_z$ space for pump KAW at (A) t = 20 and (B) t = 32. “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.”

Finally, the averaged power spectra for all the three initial conditions are also shown to analyze the energy transfer through the localization process in Figure 10A with IC-1 and Figure 10B with IC-2 and IC-3. For $k<1$, the power spectrum nearly follows the Kolmogorov scaling, and for $k>1$, the power spectrum shows steepening (for reference, the green line with a spectral index of nearly -2.6 is shown, indicating that this nonlinear interaction may lead to the distribution of energy at k > 1 (Saharoui, 2012).

FIGURE 10

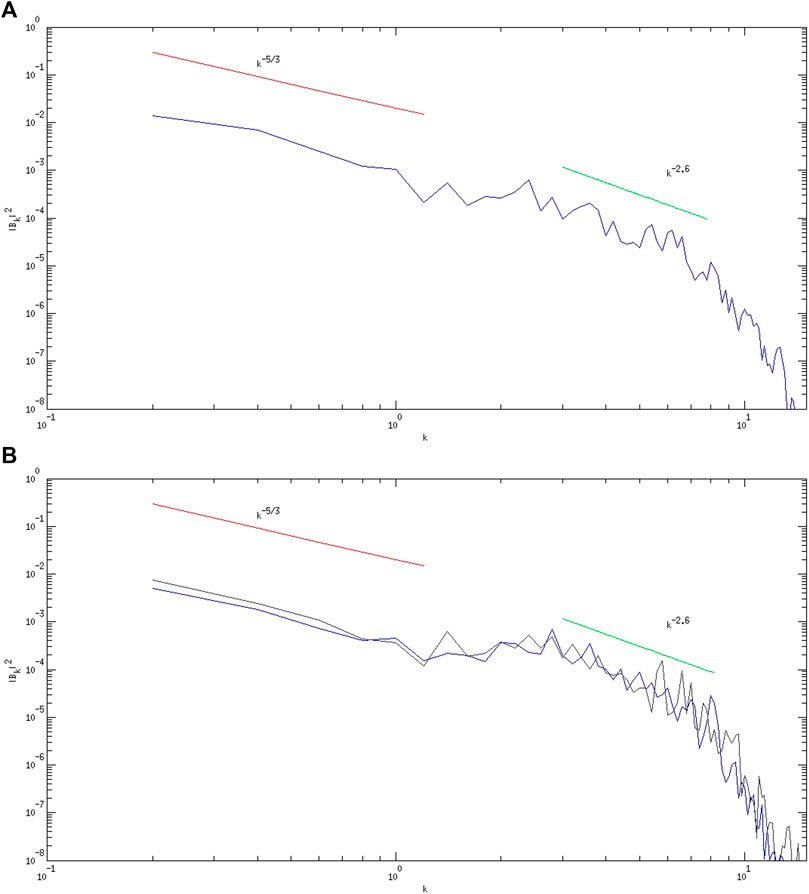
FIGURE 10. (A) Ensemble averaged normalized wave number spectrum of pump KAW $\raisebox{1ex}{${\left|B_k\right|}^2$}\!\left/ \!\raisebox{-1ex}{$B_n^2$}\right.$ against $\text{ k }\left({\text{normalized with ρ}}_{\text{s}}\right)$. “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.” (B) Ensemble averaged normalized wave number spectrum of pump KAW $\raisebox{1ex}{${\left|B_k\right|}^2$}\!\left/ \!\raisebox{-1ex}{$B_n^2$}\right.$ against $\text{k }\left({\text{normalized with ρ}}_{\text{s}}\right)$ obtained in a quasi-steady state with IC-2 (black line) and IC-3 (blue line). “Reproduced from [(Gaur and Sharma, 2015), J. Geophys. Res. Space Physics, 120, 2,397–2,408, doi:10.1002/2014JA020771], with the permission of AGU Publishing.”

The role of kinetic Alfvén turbulence in collisionless high beta-plasmas is well documented, and the present model may be a step further to understand the turbulence in the solar wind (Boldyrev and Perez, 2012; Howes et al., 2008b).

B. Magnetic Island-Based Dispersive Alfvén Wave Model

Since turbulence and magnetic reconnection work in alliance, therefore for a comprehensive study, it is important to examine their interplay. For this, we consider the existence of a fully developed pre-existing chain of magnetic islands in the background of the parallel propagating dispersive Alfvén wave. The dispersion in the wave is considered due to the wave frequency which is finite but less than the ion cyclotron frequency. For the study, a uniform background magnetic field ($B_{0z}$) is considered in the z direction, and the magnetic field ($\delta B_y$) as a result of the magnetic islands is assumed along the y direction. Therefore, our wave (DAW) subjected to a transverse instability or filamentation is propagating in the vicinity of the total magnetic field, ${\overrightarrow{\mathit{B}}}_0={\mathit{B}}_{0z}\widehat{\mathit{z}}+\delta {\mathit{B}}_y(x,y)\widehat{y}$. The wave dynamical equation in terms of dimensionless flux function is obtained using a two-fluid model as follows (Sharma et al., 2020):

$i\frac{\partial {\tilde{A}}_1}{\partial z}+c_1\left(\frac{{\partial }^2{\tilde{A}}_1}{\partial x^2}+\frac{{\partial }^2{\tilde{A}}_1}{\partial y^2}\right)-2\left(-\frac{{\left(x+x_{01}\right)}^2}{2}-\frac{{\left(x-x_{02}\right)}^2}{2}+b_{01}\cos \left(k_1^{\prime }y\right)+b_{02}\cos \left(k_2^{\prime }y\right)\right){\tilde{A}}_1+{\left|{\tilde{A}}_1\right|}^2{\tilde{A}}_1=0.$

In the aforementioned equation, ${\tilde{A}}_1$ is the right circularly polarized DAW amplitude, $c_1=\frac{1}{2k_{-}^2{\lambda }_i^2}\left(1+\frac{{\epsilon }_{-00}}{{\epsilon }_{0zz}}\right)$ is constant, ${\lambda }_i=c/{\omega }_{pi}$ is the ion inertial length, ${\rho }_s=c_s/{\omega }_{ci}$ is the ion gyroradius, $k_{-}=\frac{{\omega }_0}{c}{\epsilon }_{-00}^{1/2}$ is the wave number of propagation, ${\epsilon }_{-00}=\frac{{\omega }_{pe}^2}{{\omega }_{ce}\left({\omega }_0+{\omega }_{ci}\right)}$ is the linear part of dielectric, and ${\omega }_0$ is the frequency of DAW. Here, $x_{01}=x_{02}=0.1,k_1^{\prime }=k_2^{\prime }=0.2,b_{01}=0.5and{b}_{02}=0.3$ are the magnetic island parameters with $b_{01},b_{02}$ as the magnitude of the perturbation and $k_1^{\prime },k_2^{\prime }$ is the wave number of perturbation of the magnetic island. The normalization parameters are: $x_n=y_n={\lambda }_i,z_n\approx 2/k_{-},n_n=n_0,A_n=0.1/\sqrt{{\alpha }_0},$ where ${\alpha }_0=\frac{{\omega }_{pi}^2{\omega }_0^2}{32\pi n_0{c}^{2}T\left({\omega }_{ci}^2-{\omega }_0^2\right)}\left(1-\frac{{\omega }_0}{{\omega }_{ci}}\right)$. The last two terms of the aforementioned equation are the fluctuations attributable to the existence of magnetic islands and density perturbations, respectively.

For typical solar wind parameters, ${\text{B}}_{\text{0}}\approx 6.2\text{×}{10}^{-5}\text{ G}$, ${\text{T}}_{\text{e}}\approx 1\text{.}4\text{×}{10}^5\text{ K}$, ${\text{T}}_{\text{i}}\approx 5\text{.}8\text{×}{10}^5\text{ K}$, and ${\text{n}}_{\text{0}}\approx 3{\text{ cm}}^{-3}$ (Wilson et al., 2018), the dynamical equation is solved numerically under the following initial condition:

${\tilde{A}}_1\left(x,y,z=0\right)=\cos \left(2x+2.3\right)+\cos \left(y+4.1\right).$

The numerical value of the wave parameters is calculated as ${\omega }_{ci}\approx 0.594Hz$, $V_A\approx 7.815\times {10}^{6}cm/s$, $c_s\approx 7.713\times {10}^{6}cm/s$, ${\omega }_{pe}\approx 9.767\times {10}^{4}Hz$, ${\rho }_s=1.298\times {10}^{7}cm$, and ${\lambda }_i=1.315\times {10}^{7}cm$. For the wave with frequency, ${\omega }_{\text{0}}\approx 0.8{\omega }_{ci}$, the wave number is $k_{-}=4.531\times {10}^{-8}c{m}^{-1}$.

The results depict that the fluctuations in the field occurring due to the existence of the chain of magnetic islands may induce localization, and the amplitude of these localized structures increases with z as shown in Figure 11. As clearly visible from the contour plot in Figure 11, the symmetry in the patterns is maintained only at the early stages, and as we evolve along z, this symmetry is broken, and highly irregular structures are obtained. The characteristic scale size of these coherent/localized structures is of the order of ion inertial length scales. For DAW propagating under the influence of both the factors, that is, density fluctuations as well as magnetic islands, these localized structures seem to be more intense and well evolved (Figure 12) compared to the case when DAW was propagating under the influence of magnetic islands only. Thus, these results clearly depict that nonlinearity supports the formation of localized structures, thereby aiding the generation of turbulence.

FIGURE 11

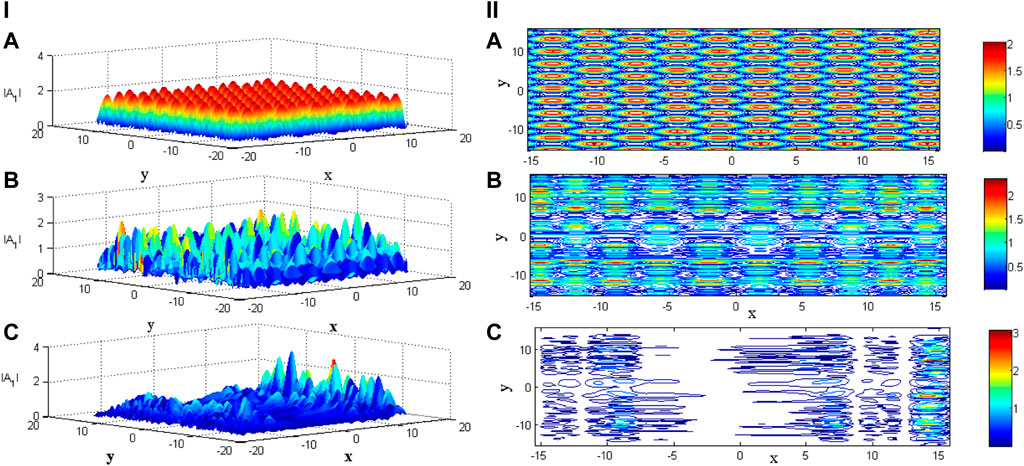
FIGURE 11. (I) DAW localization (normalized magnetic vector potential $\left|A_1\right|/A_n$) and (II) contour of DAW-normalized magnetic vector potential $\left(\left|A_1\right|/A_n\right)$ in a normalized x–y plane (x and y axis is normalized by ${\lambda }_i$) at three snapshots of normalized z (normalization constant $z_n\approx 2/k_{-}$), (A) z = 0, (B)z = 4, and (C) z = 8, respectively, when only magnetic islands are present. “Reproduced from [(Sharma et al., 2020), Physics of Plasmas, 27, https://doi.org/10.1063/1.5142893], with the permission of AIP Publishing.”

FIGURE 12

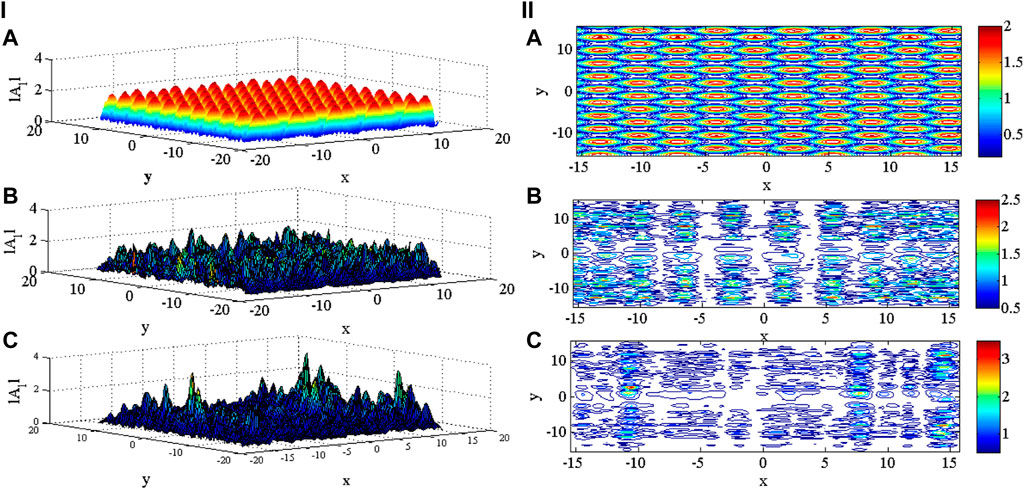
FIGURE 12. (I) DAW localization (normalized magnetic vector potential $\left|A_1\right|/A_n$) and (II) contour of DAW-normalized magnetic vector potential ($\left|A_1\right|/A_n$) in a normalized x–y plane (x and y axis is normalized by ${\lambda }_i$) at three snapshots of normalized z (normalization constant $z_n\approx 2/k_{-}$), (A) z = 0, (B)z = 4, and (C) z = 8, respectively, when magnetic islands and perturbation in the background density are present. “Reproduced from [(Sharma et al., 2020), Physics of Plasmas, 27, https://doi.org/10.1063/1.5142893], with the permission of AIP Publishing.”

The localized structures unveil the turbulent behavior that may further result in the development of current sheets. The current density plot of DAW as shown in Figure 13 explains that in the beginning, there is a symmetrical distribution of current in the x–y plane, but for larger z, it grows into several asymmetric and irregular structures. The size of these current sheets is found to be of the order of sub-ion scale length.

FIGURE 13

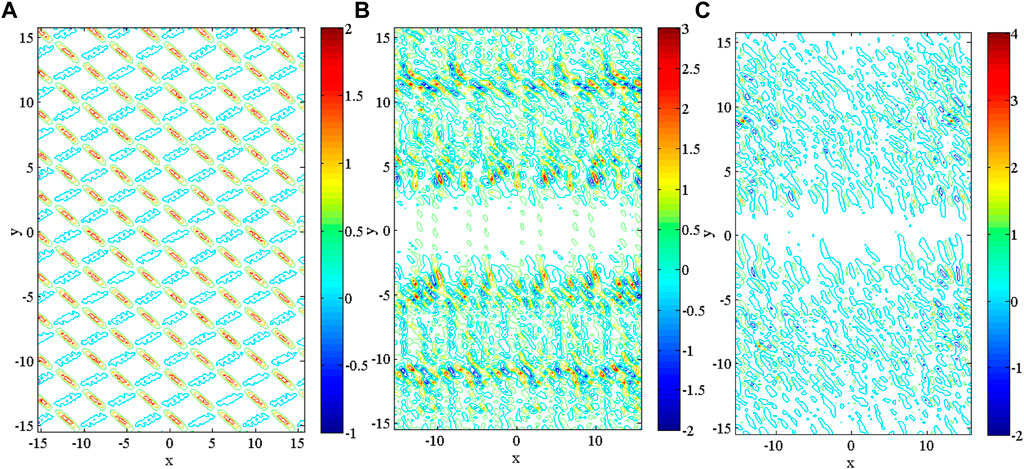
FIGURE 13. DAW-normalized current density for different z, (A) z = 0, (B) z = 2, and (C) z = 5 when the magnetic islands and perturbation in the background density are present. “Reproduced from [(Sharma et al., 2020), Physics of Plasmas, 27, https://doi.org/10.1063/1.5142893], with the permission of AIP Publishing.”

The power spectrum of DAW (Figure 14) shows that the energy distribution takes place from larger length scales to smaller length scales. For $k{\lambda }_i\approx 1$, the fluctuations start deviating from the typical Kolmogorov’s scaling, and the spectra go steeper beyond the ion inertial length $(k{\lambda }_i>>1)$. The observed scaling exponents bear resemblance with the observations in the inertial and dispersive regime in the solar wind (Alexandrova et al., 2008; Voros et al., 2014). Although the study is restricted to limited dispersion of the wave and nonlinear evolution of the perturbation, it does provide an assessment of the turbulent energy transfer and coherent structures/current sheet formation in the vicinity of magnetic islands and the ponderomotive nonlinearity which is useful for future studies.

FIGURE 14

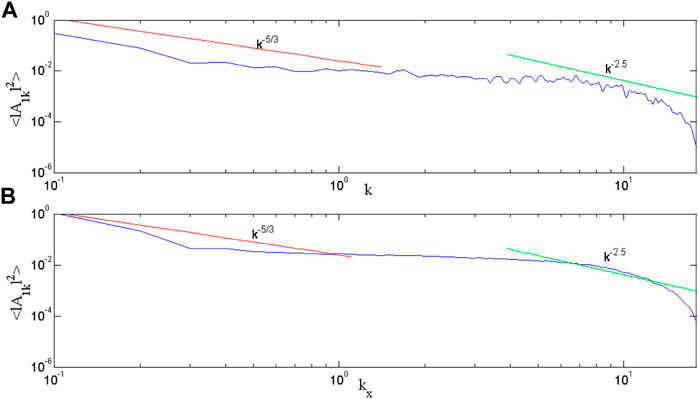
FIGURE 14. Normalized saturated average wave number spectrum of DAW showing the distribution of energy over length scales when magnetic islands and background density perturbations are existing. In the figure, we plot (A) $\langle {\left|A_{1k}\right|}^2\rangle /A_n^2$ versus $k=\sqrt{k_x^2+k_y^2}$ (here k_x and k_y are normalized by ${\lambda }_i$ ) using nine spectra, i.e., between z = 24 and z = 32 and (B) $\langle {\left|A_{1k}\right|}^2\rangle /A_n^2$ versus the wave number k_x (normalized by ${\lambda }_i$) using seven spectra, i.e., between z = 25 and z = 31. “Reproduced from [(Sharma et al., 2020), Physics of Plasmas, 27, https://doi.org/10.1063/1.5142893], with the permission of AIP Publishing.”

Semi-Analytical Method

For a better insight into the development of coherent structures and to determine their scale size, a semi-analytical approach is adopted for the aforementioned model equation as discussed by Sharma et al., 2020. Within the paraxial limit $\left(x<<r_{01}^{}{f}_{1}andy<<r_{02}^{}{f}_2\right)$, where $r_{01}^{}and{r}_{02}^{}$ are the transverse scale size of the DAW, following Akhmanov et al. (1967), the dimensionless beam width parameters $f_{1}and{f}_2$ can be obtained as:

$\frac{d^2{f}_1}{d{z}^2}=\frac{1}{4}{\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)}^2\left(\frac{1}{f_1^3}-\frac{4R_{d1}^2{\lambda }_i^2{f}_1}{{\left({\lambda }_i{\rho }_s\right)}^2\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)}-\frac{2={\left|E_{00}\right|}^2{R}_{d1}^2{\alpha }_0}{r_{01}^2{f}_1^2{f}_2\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)}\exp \left(\frac{{\alpha }_0{\left|E_{00}\right|}^2}{f_1{f}_2}\right)\right),$

$\frac{d^2{f}_2}{d{z}^2}=\frac{1}{4}{(1+{\epsilon }_{-00}/{\epsilon }_{0zz})}^2\left(\frac{1}{f_2^3}-\frac{4\times 0.04R_{d2}^2{\lambda }_i^2\left(b_{01}+b_{02}\right)f_2}{{\left({\lambda }_i{\rho }_s\right)}^2\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)}-\frac{2{\left|E_{00}\right|}^2{R}_{d2}^2{\alpha }_0}{r_{02}^2{f}_2^2{f}_1\left(+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)}\exp \left(\frac{{\alpha }_0{\left|E_{00}\right|}^2}{f_1{f}_2}\right)\right),$

where $R_{d1}^{}=k_{-}{r}_{01}^{2}and{R}_{d2}^{}=k_{-}{r}_{02}^2$ and $E_{00}$ is the amplitude of the wave. The aforementioned equations are solved using the Runge–Kutta method under the initial conditions $\frac{d{f}_1}{dz}=\frac{d{f}_2}{dz}=0atz=0and{f}_1=f_2=1atz=0$.

On the right-hand side of the aforementioned equations, the opposite sign between the first and last two terms indicates that they behave contrary. The first term is the diffraction due to DAW, and the last two terms show convergence due to nonlinearity and magnetic islands. A competition between them goes on until the converging effects dominate the divergence leading to the localization of DAW. The result in Figure 15 shows that the localization of the wave occurs in both the planes, but the distribution of these structures is uneven due to different rates of diffraction and nonlinearity.

FIGURE 15

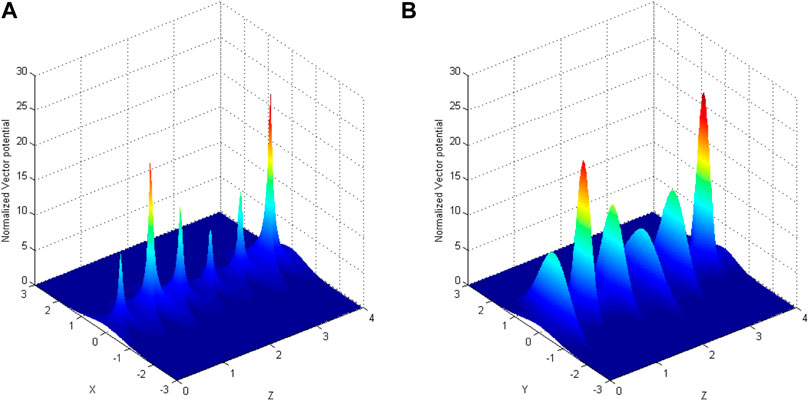
FIGURE 15. DAW normalized vector potential in the presence of magnetic islands as well as perturbation in the density in the (A) x–z plane (fixed y) and (B)y–z plane (fixed x) obtained using a semi-analytical model. “Reproduced from [(Sharma et al., 2020), Physics of Plasmas, 27, https://doi.org/10.1063/1.5142893], with the permission of AIP Publishing.”

To calculate the critical scale size, we equate the diffraction and convergence term and when only magnetic islands are present, it is found to be: $r_{01}={\left({\rho }_s^2\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)/4k_{-}^2\right)}^{1/4}=1.195\times {10}^{7}cm:r_{02}={\left({\rho }_s^2\left(1+{\epsilon }_{-00}/{\epsilon }_{0zz}\right)/4\times 0.04\left(b_{01}+b_{02}\right)k_{-}^2\right)}^{1/4}$ $=2.827\times {10}^{7}cm$. If we plot the critical scale size versus DAW field strength, we see that with the DAW field, the scale size also varies. Thus, the coherent structures ranging from few proton scales to sub-proton scales may be formulated by changing the strength of DAW. In a similar manner, we can find out the critical scale size when ponderomotive nonlinearity as well as magnetic islands are present.

Summary and Conclusion

In this review, we have discussed the role of kinetic Alfvén waves and dispersive Alfvén waves interacting with the surrounding, nonlinearities, other low-frequency modes, and pre-existing chain of magnetic islands in the evolution of solar wind turbulence. Amongst the different validated processes for explaining the small-scale physics, emphasis is given on the en route generated coherent or localized structures which lead to the turbulent behavior and transfer of energy along and across the ion scales. The background vicinity and initial conditions affect the evolution of these structures, but the energy transfer continues to occur from larger length scales to smaller length scales. Although some variation in the spectral index is observed due to these effects, it lies within the observed spectral range of the solar wind turbulence, that is, ∼1.41.7 for large scales and ∼2.62.8 for small scales. As indicated by the observations, a reconnection flow can also generate turbulence in the solar wind, and the magnetic reconnection (magnetic island sites) may customize the plasma conditions such that several dissipation mechanisms may contribute to the evolution of the solar wind (Voros et al., 2014). Thus, solar wind turbulence is a result of various nonlinear processes like transverse collapse or localization due to KAW, its interaction with other wave modes, and/or the formation of coherent (magnetic) structures resulting from the current sheets, and all these processes gives solar wind turbulence the structure it is found in.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work is supported by the Rashtriya Uchchatar Shiksha Abhiyan (RUSA 2.0), India, under Grant No. F. 35-532/PP/2021/1244. The work is partially supported by Indian Space Research organization (ISRO), Department of Science and Technology (DST) and Council of Scientific and Industrial Research (CSIR) India.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Authors thank Melvyn Goldstein from the NASA Goddard Space Flight Centre for useful discussions during the course of original publications from where material for the present review has been taken.

References

Akhmanov, S. A., Sukhorukov, A. P., and Khokhlov, R. V. (1967). Self-focusing and Diffraction of Light in a Nonlinear Medium. Usp. Fiz. Nauk. 93 (9), 19–70. doi:10.3367/ufnr.0093.196709c.0019

CrossRef Full Text | Google Scholar

Alexandrova, O., Carbone, V., Veltri, P., and Sorriso Valvo, L. (2008). Small Scale Energy Cascade of the Solar Wind Turbulence. Astrophysical J. 674 (2), 1153–1157. doi:10.1086/524056

CrossRef Full Text | Google Scholar

Alexandrova, O., Chen, C. H. K., Bale, S. D., Sorriso-Valvo, L., and Horbury, T. S. (2013). Solar Wind Turbulence and the Role of Ion Instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S. J., et al. (2009). Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys. Rev. Lett. 103, 165003. doi:10.1103/PhysRevLett.103.165003

PubMed Abstract | CrossRef Full Text | Google Scholar

Bale, S. D., Kellogg, P. J., Mozer, F. S., Horbury, T. S., and Reme, H. (2005). Measurement of the Electric Fluctuation Spectrum of Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 94, 215002. doi:10.1103/PhysRevLett.94.215002

PubMed Abstract | CrossRef Full Text | Google Scholar

Belcher, J. W., and Davis, L. (1971). Large-amplitude Alfvén Waves in the Interplanetary Medium, 2. J. Geophys. Res. 76 (16), 3534–3563. doi:10.1029/JA076i016p03534

CrossRef Full Text | Google Scholar

Biskamp, D., and Welter, H. (1989). Dynamics of Decaying Two Dimensional Magnetohydrodynamic Turbulence. Phys. Fluids B Plasma Phys. 1 (10), 1964–1979. doi:10.1063/1.859060

CrossRef Full Text | Google Scholar

Bogdan, T. J., Hansteen, M. C. V., McMurry, A., Rosenthal, C. S., Johnson, M., Petty Powell, S., et al. (2003). Waves in the Magnetized Solar Atmosphere. II. Waves from Localized Sources in Magnetic Flux Concentrations. ApJ 599, 626–660. doi:10.1086/378512

CrossRef Full Text | Google Scholar

Brodin, G., and Stenflo, L. (1988). Parametric Instabilities of Finite Amplitude Alfvén Waves. Phys. Scr. 37, 89–92. doi:10.1088/0031-8949/37/1/013

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 10, 2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Cerri, S. S., and Califano, F. (2017). Reconnection and Small-Scale Fields in 2D-3V Hybrid-Kinetic Driven Turbulence Simulations. New J. Phys. 19 (2), 025007. doi:10.1088/1367-2630/aa5c4a

CrossRef Full Text | Google Scholar

Chandran, B. D. G. (2018). Parametric Instability, Inverse Cascade and the Range of Solar-Wind Turbulence. J. Plasma Phys.f range solar-wind Turbul. 84, 905840106. doi:10.1017/s0022377818000016

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, C. H. K., Horbury, T. S., Schekochihin, A. A., Wicks, R. T., Alexandrova, O., and Mitchell, J. (2010a). Anisotropy of Solar Wind Turbulence between Ion and Electron Scales. Phys. Rev. Lett. 104, 255002. doi:10.1103/PhysRevLett.104.255002

PubMed Abstract | CrossRef Full Text | Google Scholar

Chmyrev, V. M., Bilichenko, S. V., Pokhotelov, O. A., Marchenko, V. A., Lazarev, V. I., Streltsov, A. V., et al. (1988). Alfvén Vortices and Related Phenomena in the Ionosphere and the Magnetosphere. Phys. Scr. 38, 841–854. doi:10.1088/0031-8949/38/6/016

CrossRef Full Text | Google Scholar

Cirtain, J. W., Golub, L., Lundquist, L., Van Ballegooijen, A., Savcheva, A., Shimojo, M., et al. (2007). Evidence for Alfven Waves in Solar X-Ray Jets. Science 318 (5856), 1580–1582. doi:10.1126/science.1147050

PubMed Abstract | CrossRef Full Text | Google Scholar

Coleman, P. J. J. (1968). Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma. ApJ 153, 371. doi:10.1086/14967

CrossRef Full Text | Google Scholar

Comisso, L., and Sironi, L. (2019). The Interplay of Magnetically Dominated Turbulence and Magnetic Reconnection in Producing Nonthermal Particles. ApJ 886 (2), 122. doi:10.3847/1538-4357/ab4c33

CrossRef Full Text | Google Scholar

Dmitruk, P., Matthaeus, W. H., and Seenu, N. (2004). Test Particle Energization by Current Sheets and Nonuniform Fields in Magnetohydrodynamic Turbulence. ApJ 617 (1), 667–679. doi:10.1086/425301

CrossRef Full Text | Google Scholar

Dmitruk, P., and Matthaeus, W. H. (2006). Structure of the Electromagnetic Field in Three-Dimensional Hall Magnetohydrodynamic Turbulence. Phys. Plasmas 13 (4), 042307. doi:10.1063/1.2192757

CrossRef Full Text | Google Scholar

Franci, L., Cerri, S. S., Califano, F., Landi, S., Papini, E., Verdini, A., et al. (2017). Magnetic Reconnection as a Driver for a Sub-ion-scale Cascade in Plasma Turbulence. ApJ 850 (1), L16. doi:10.3847/2041-8213/aa93fb

CrossRef Full Text | Google Scholar

Gary, S. P., and Lee, M. A. (1994). The Ion Cyclotron Anisotropy Instability and the Inverse Correlation between Proton Anisotropy and Proton Beta. J. Geophys. Res. 99, 11297. doi:10.1029/94ja00253

CrossRef Full Text | Google Scholar

Gaur, N., and Sharma, R. P. (2015). Nonlinear Effects Associated with Kinetic Alfvén Wave. J. Geophys. Res. Space Phys. 120, 2397–2408. doi:10.1002/2014JA020771

CrossRef Full Text | Google Scholar

Gaur, N., and Sharma, R. P. (2014). Nonlinear Evolution of Kinetic Alfvén Wave and Turbulent Spectra: Effect of Initial Conditions. Astrophys. Space Sci. 350, 573–578. doi:10.1007/s10509-013-1770-1

CrossRef Full Text | Google Scholar

Ghosh, S., Siregar, E., Roberts, D. A., and Goldstein, M. L. (1996). Simulation of High-Frequency Solar Wind Power Spectra Using Hall Magnetohydrodynamics. J. Geophys. Res. 101 (A2), 2493–2504. doi:10.1029/95ja03201

CrossRef Full Text | Google Scholar

Hautaluoma, G., and Fox, K. (2020). NASA Space Weather Release, 20–083.Available from: https://www.nasa.gov/press-release/nasa-selects-proposalsfor- new-space-environment-missions.

Google Scholar

He, J. S., TuMarsch, C. Y. E., Guo, L.-J., Yao, S., and Tian, H. (2009). Upward Propagating High Frequency Alfvén Waves as Identified from Dynamic Wave like Spicules Observed by SOT on Hinode. Astron. Astrophys. 497, 525. doi:10.1051/0004-6361/200810777

CrossRef Full Text | Google Scholar

Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A. (2008a). A Model of Turbulence in Magnetized Plasmas: Implications for the Dissipation Range in the Solar Wind. J. Geophys. Res. 113, A05103. doi:10.1029/2007JA012665

CrossRef Full Text | Google Scholar

Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E. A., Schekochihin, A. A., et al. (2008b). Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas. Phys. Rev. Lett. 100, 065004. doi:10.1103/PhysRevLett.100.065004

PubMed Abstract | CrossRef Full Text | Google Scholar

Howes, G. G., and Nielson, K. D. (2013). Alfvén Wave Collisions, the Fundamental Building Block of Plasma Turbulence. Asymptotic Solution. Phys. Plasmas 20 (7), 072302. doi:10.1063/1.4812805

CrossRef Full Text | Google Scholar

Howes, G. G., and Quataert, E. (2010). On the Interpretation of Magnetic Helicity Signatures in the Dissipation Range of Solar Wind Turbulence. ApJ 709, L49–L52. doi:10.1088/2041-8205/709/1/L49

CrossRef Full Text | Google Scholar

Howes, G. G., Tenbarge, J. M., and Dorland, W. (2011). A Weakened Cascade Model for Turbulence in Astrophysical Plasmas. Phys. Plasmas 18, 102305. doi:10.1063/1.3646400

CrossRef Full Text | Google Scholar

Hu, Y. Q., Esser, R., and Habbal, S. R. (2000). A Four-Fluid Turbulence-Driven Solar Wind Model for Preferential Acceleration and Heating of Heavy Ions. J. Geophys. Res. 105, 5093–5111. doi:10.1029/1999JA900430

CrossRef Full Text | Google Scholar

Iroshnikov, P. S. (1964). Turbul. a conducting fluid a strong magnetic field 7 (4).

Isenberg, P. A. (2004). Correction to "The Kinetic Shell Model of Coronal Heating and Acceleration by Ion Cyclotron Waves: 3. The Proton Halo and Dispersive Waves". J. Geophys. Res. 109, 3101. doi:10.1029/2004JA010524

CrossRef Full Text | Google Scholar

Isenberg, P. A., and Hollweg, J. V. (1982). Finite Amplitude Alfvén Waves in a Multi-Ion Plasma: Propagation, Acceleration, and Heating. J. Geophys. Res. 87, 5023–5029. doi:10.1029/JA087iA07p05023

CrossRef Full Text | Google Scholar

Klein, K. G. (2019). Multipoint Measurements of the Solar Wind : A Proposed Advance for Studying Magnetized Turbulence. Plasma 2020 Decadal. Available at: https://arxiv.org/abs/1903.05740v2.

Google Scholar

Kraichnan, R. H. (1965). Inertial-range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 8 (7), 1385–1387. doi:10.1063/1.1761412

CrossRef Full Text | Google Scholar

Kulsrud, R. M., and Ferrari, A. (1971). The Relativistic Quasilinear Theory of Particle Acceleration by Hydromagnetic Turbulence. Astrophys. Space Sci. 12 (2), 302–318. doi:10.1007/BF00651420

CrossRef Full Text | Google Scholar

Lazarian, A., Eyink, G. L., Jafari, A., Kowal, G., Li, H., Xu, S., et al. (2020). 3D Turbulent Reconnection: Theory, Tests, and Astrophysical Implications. Phys. Plasmas 27 (1), 012305–012394. doi:10.1063/1.5110603

CrossRef Full Text | Google Scholar

Leamon, R. J., Matthaeus, W. H., Smith, C. W., Zank, G. P., Mullan, D. J., and Oughton, S. Mhd-driven Kinetic Dissipation in the Solar Wind and Corona. Astrophys. J. 537, 1054. doi:10.1086/309059

CrossRef Full Text | Google Scholar

Longtin, M., and Sonnerup, B. U. Ö. (1986). Modulation Instability of Circularly Polarized Alfvén Waves. J. Geophys. Res. 91, 6816. doi:10.1029/ja091ia06p06816

CrossRef Full Text | Google Scholar

Ma, Z. W., Lee, L. C., and Otto, A. (1995). Generation of Field Aligned Currents and Alfvén Waves by 3D Magnetic Reconnection. Geophys. Res. Lett. 22 (13), 1737–1740. doi:10.1029/95GL01430

CrossRef Full Text | Google Scholar

Mallet, A., Schekochihin, A. A., and Chandran, B. D. G. (2017). Disruption of Alfvénic Turbulence by Magnetic Reconnection in a Collisionless Plasma. J. Plasma Phys. 83 (6). doi:10.1017/S0022377817000812

CrossRef Full Text | Google Scholar

Matsumoto, Y., Amano, T., Kato, T. N., and Hoshino, M. (2015). Stochastic Electron Acceleration during Spontaneous Turbulent Reconnection in a Strong Shock Wave. Science 347 (6225), 974–978. doi:10.1126/science.1260168

PubMed Abstract | CrossRef Full Text | Google Scholar

Matteini, L., Stansby, D., Horbury, T. S., and Chen, C. H. K. (2018). On the 1/f Spectrum in the Solar Wind and its Connection with Magnetic Compressibility. Astrophysical J. Lett. 869 (6pp), L32. doi:10.3847/2041-8213/aaf573

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Goldstein, M. L. (1986). Low-Frequency1fNoise in the Interplanetary Magnetic Field. Phys. Rev. Lett. 57, 495–498. doi:10.1103/physrevlett.57.495

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Lamkin, S. L. (1986). Turbulent Magnetic Reconnection. Phys. Fluids 29 (8), 2513. doi:10.1063/1.866004

CrossRef Full Text | Google Scholar

Meyrand, R., and Galtier, S. (2012). Spontaneous Chiral Symmetry Breaking of Hall Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 109 (19), 9–13. doi:10.1103/PhysRevLett.109.194501

CrossRef Full Text | Google Scholar

Narita, Y., Roberts, O. W., Vörös, Z., and Hoshino, M. (2020). Transport Ratios of the Kinetic Alfvén Mode in Space Plasmas. Front. Phys. 8, 166. doi:10.3389/fphy.2020.00166

CrossRef Full Text | Google Scholar

Narita, Y. (2018), Space-time Structure and Wavevector Anisotropy in Space Plasma Turbulence, Living Rev. Sol. Phys. 15. doi:10.1007/s41116-017-0010-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Okamoto, T. J., Tsuneta, S., Berger, T. E., Ichimoto, K., Katsukawa, Y., Lites, B. W., et al. (2007). Coronal Transverse Magnetohydrodynamic Waves in a Solar Prominence. Science 318, 1577–1580. doi:10.1126/science.1145447

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, E. N. (1958). Dynamics of the Interplanetary Gas and Magnetic Fields. ApJ 128, 664. doi:10.1086/146579

CrossRef Full Text | Google Scholar

Perez, J. C., Mason, J., Boldyrev, S., and Cattaneo, F. (2012). On the Energy Spectrum of Strong Magnetohydrodynamic Turbulence. Phys. Rev. X 2, 041005. doi:10.1103/PhysRevX.2.041005

CrossRef Full Text | Google Scholar

Perri, S., Goldstein, M. L., Dorelli, J. C., and Sahraoui, F. (2012). Detection of Small-Scale Structures in the Dissipation Regime of Solar-Wind Turbulence. Phys. Rev. Lett. 109 (19), 1–5. doi:10.1103/PhysRevLett.109.191101

CrossRef Full Text | Google Scholar

Pezzi, O., Parashar, T. N., Servidio, S., Valentini, F., Vásconez, C. L., Yang, Y., et al. (2017a). Colliding Alfvénic Wave Packets in Magnetohydrodynamics, Hall and Kinetic Simulations. J. Plasma Phys. 83 (1). doi:10.1017/S0022377817000113

CrossRef Full Text | Google Scholar

Pezzi, O., Parashar, T. N., Servidio, S., Valentini, F., Vásconez, C. L., Yang, Y., et al. (2017b). Revisiting a Classic: the Parker-moffatt Problem. ApJ 834 (2), 166. doi:10.3847/1538-4357/834/2/166

CrossRef Full Text | Google Scholar

Podesta, J. J. (2013). Evidence of Kinetic Alfvén Waves in the Solar Wind at 1 AU. Sol. Phys. 286 (2), 529–548. doi:10.1007/s11207-013-0258-z

CrossRef Full Text | Google Scholar

Primavera, L., Malara, F., Servidio, S., Nigro, G., and Veltri, P. (2019). Parametric Instability in Two-Dimensional Alfvénic Turbulence. ApJ 880 (2), 156. doi:10.3847/1538-4357/ab29f5

CrossRef Full Text | Google Scholar

Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M., and Owen, C. J. (2007). In Situ evidence of Magnetic Reconnection in Turbulent Plasma. Nat. Phys. 3 (4), 235–238. doi:10.1038/nphys574

CrossRef Full Text | Google Scholar

Roberts, D. A., Goldstein, M. L., Matthaeus, W. H., and Ghosh, S. (1992). Velocity Shear Generation of Solar Wind Turbulence. J. Geophys. Res. 97, 17115. doi:10.1029/92ja01144

CrossRef Full Text | Google Scholar

Roberts, O. W., Narita, Y., Nakamura, R., Vörös, Z., and Verscharen, D. (2022). The Kinetic Alfvén-like Nature of Turbulent Fluctuations in the Earth's Magnetosheath: MMS Measurement of the Electron Alfvén Ratio. Phys. Plasmas 29, 012308. doi:10.1063/5.0068828

CrossRef Full Text | Google Scholar

Roberts, O. W., Narita, Y., Li, X., and Laakso, H. (2017). Multipoint Analysis of Compressive Fluctuations in the Fast and Slow Solar Wind. J. Geophys. Res. Space Phys. 122, 6940–6963. doi:10.1002/2016JA023552

CrossRef Full Text | Google Scholar

Rudakov, L., Mithaiwala, M., Ganguli, G., and Crabtree, C. (2011). Linear and Nonlinear Landau Resonance of Kinetic Alfvén Waves: Consequences for Electron Distribution and Wave Spectrum in the Solar Wind. Phys. Plasmas 18, 012307. doi:10.1063/1.3532819

CrossRef Full Text | Google Scholar

Sahraoui, F., Belmont, G., and Goldstein, M. L. (2012). New Insight into Short-Wavelength Solar Wind Fluctuations from Vlasov Theory. ApJ 748, 100. doi:10.1088/0004-637X/748/2/100

CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L. (2010). Three Dimensional AnisotropickSpectra of Turbulence at Subproton Scales in the Solar Wind. Phys. Rev. Lett. 105, 131101. doi:10.1103/PhysRevLett.105.131101

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Robert, P., and Khotyaintsev, Y. V. (2009). Evidence of a Cascade and Dissipation of Solar-Wind Turbulence at the Electron Gyroscale. Phys. Rev. Lett. 102, 231102. doi:10.1103/physrevlett.102.231102

PubMed Abstract | CrossRef Full Text | Google Scholar

Servidio, S., Matthaeus, W. H., Shay, M. A., Cassak, P. A., and Dmitruk, P. (2009). Magnetic Reconnection in Two-Dimensional Magnetohydrodynamic Turbulence. Phys. Rev. Lett. 102 (11), 1–4. doi:10.1103/PhysRevLett.102.115003

CrossRef Full Text | Google Scholar

Shaikh, D., and Shukla, P. K. (2009). 3D Simulations of Fluctuation Spectra in the Hall-MHD Plasma. Phys. Rev. Lett. 102, 045004. doi:10.1103/PhysRevLett.102.045004

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, R. P., and Gaur, N. (2014). Nonlinear Simplified Model to Study Localization of Kinetic Alfvén Wave. Phys. Plasmas 21, 042302. doi:10.1063/1.4870500

CrossRef Full Text | Google Scholar

Sharma, R. P., Kumar, S., Sharma, N., Singh, H. D., and Kumar, S. (2011a). Numerical Simulations to Study Solar Wind Turbulence. Phys. Plasmas 18, 022904. doi:10.1063/1.3556676

CrossRef Full Text | Google Scholar

Sharma, R. P., Stubbe, P., and Verga, A. D. (1996). Numerical Simulation of a Zakharov-Boussinesq System of Equations to Study Langmuir Turbulence in the Ionosphere. J. Geophys. Res. 101, 10995–11003. doi:10.1029/96JA00043

CrossRef Full Text | Google Scholar

Sharma, S., Sharma, R. P., Mishra, M. K., and Uma, R. (2020). Nonlinear Evolution of Dispersive Alfvén Waves and the Effect of Magnetic Islands in the Solar Wind Plasmas. Phys. Plasmas 27 (July 2020), 072903–072910. doi:10.1063/1.5142893

CrossRef Full Text | Google Scholar

Shay, M. A., Drake, J. F., Rogers, B. N., and Denton, R. E. (2001). Alfvénic Collisionless Magnetic Reconnection and the Hall Term. J. Geophys. Res. 106, 3759–3772. doi:10.1029/1999ja001007

CrossRef Full Text | Google Scholar

Smith, D., Ghosh, S., Dmitruk, P., and Matthaeus, W. H. (2004). Hall and Turbulence Effects on Magnetic Reconnection. Geophys. Res. Lett. 31 (2), 3–6. doi:10.1029/2003GL018689

CrossRef Full Text | Google Scholar

Spence, H. E. (2019). “HelioSwarm: Unlocking the Multiscale Mysteries of Weakly Collisional Magnetized Plasma Turbulence and Ion Heating,” in Fall Meeting of the American Geophysical Union. Abstract SH11B-04.

Google Scholar

Stenflo, L., and Shukla, P. K. (2007). “Nonlinear Processes in Space Plasmas,” in Handbook of the Solar- Terrestrial Environment. Editors Y. Kamide, and A. C. L. Chian.

Google Scholar

Sturrock, P. A., Roald, C. B., and Wolfson, R. (1999). Chromospheric Magnetic Reconnection and its Implication for Coronal Heating. Astrophysical J. 524 (1), L75–L78. doi:10.1086/312301

CrossRef Full Text | Google Scholar

Tenbarge, J. M., and Howes, G. G. (2013). Current Sheets and Collisionless Damping in Kinetic Plasma Turbulence. ApJ 771 (2), L27–7. doi:10.1088/2041-8205/771/2/L27

CrossRef Full Text | Google Scholar

Vech, D., Mallet, A., Klein, K. G., and Kasper, J. C. (2018). Magnetic Reconnection May Control the Ion-Scale Spectral Break of Solar Wind Turbulence. ApJ 855 (2), L27. doi:10.3847/2041-8213/aab351

CrossRef Full Text | Google Scholar

Verscharen, D., Bourouaine, S., and Chandran, B. D. G. (2014). Instabilities Driven by the Drift and Temperature Anisotropy of Alpha Particles in the Solar Wind. Astrophys. J. 773, 163.

Google Scholar

Viñas, A. F., and Goldstein, M. L. (1991). Parametric Instabilities of Circularly Polarized Large-Amplitude Dispersive Alfvén Waves: Excitation of Obliquely-Propagating Daughter and Side-Band Waves. J. Plasma Phys. 46, 129–152. doi:10.1017/s0022377800015993

CrossRef Full Text | Google Scholar

Vörös, Z., Sasunov, Y. L., Semenov, V. S., Zaqarashvili, T. V., Bruno, R., and Khodachenko, M. (2014). Reconnection Outflow Generated Turbulence in the Solar Wind. ApJ 797 (1), L10–L15. doi:10.1088/2041-8205/797/1/L10

CrossRef Full Text | Google Scholar

Wilson III, L. B., Stevens, M. L., Kasper, J. C., Klein, K. G., Maruca, B. A., Bale, S. D., et al. (2018). The Statistical Properties of Solar Wind Temperature Parameters Near 1 au. ApJS 236 (2), 41. doi:10.3847/1538-4365/aab71c

CrossRef Full Text | Google Scholar

Wu, D. J., and Chao, J. K. (2004). Recent Progress in Nonlinear Kinetic Alfvén Waves. Nonlin. Process. Geophys. 11 (5–6), 631–645. doi:10.5194/npg-11-631-2004

CrossRef Full Text | Google Scholar

Wu, D. J. (2003). Model of Nonlinear Kinetic Alfvén Waves with Dissipation and Acceleration of Energetic Electrons. Phys. Rev. E 67 (2), 4. doi:10.1103/PhysRevE.67.027402

CrossRef Full Text | Google Scholar