- Department of Mathematical Sciences, Bodoland University, Kokrajhar, Assam, India
Anisotropic cloud string cosmological models has been investigated in the context of five dimensional Kaluza- Klein space time. In this paper the energy momentum tensor is generated by rest energy density and tension density of the string with particle density attached to them. To obtained the exact solutions of the Einstein field equations we assumed a scale factor
Introduction
Now a day, string cosmology has attracted lots of attention, because of its significant role in the study of the origin and evaluation of the Universe before the creation of particles. It is a fascinating field for cosmologists to study and discover the mysterious phenomena that have yet to be observed and explore the unseen information of our Universe. As a result, cosmologists are extremely interested in learning more about the past, present, and future evolution of the Universe. But, as of now, we lack strong evidence to make a conclusive statement about its origin and evolution. So, further investigation is required to discover the mysterious phenomena of the entire universe. Stachel (1980) and Letelier (1983) was started the study of string in the context of general relativity. Because the string is extremely appropriate in describing the early phase of the evolution of our Universe. Many eminent authors are interested to work in the field of cosmic strings within the context of general relativity (Kibble, 1976; 1983), and it is thought that strings cause density perturbations that lead to the formation of massive scale structures in the Universe (Zel’dovich et al., 1974; Zel’dovich, 1980).
Strings are stable topological structures that formed during the early universe phase transition due to a drop in temperature below certain critical temperatures. Observations of our universe using contemporary technical tools also suggest that in the early stages of our Universe, there existed a massive scale network of strings. Geometric strings and massive strings are two types of strings that contain stress-energy. The presence of strings is responsible for the universe is anisotropy; nevertheless, strings are no longer visible. These strings are not damaging the cosmological models, instead, they can lead to a variety of fascinating astrophysical results. Strings can also be used to describe the nature and essential arrangement of the early Universe. String theory describes the early stage of evolution of the Universe in terms of (vibrating) strings instead of particles and gives us a single theoretical structure in which all matter and forces are unified. Because strings play such an important role in describing the evolution of the early stages of our Universe. Several authors have recently focused their attention on string cosmological models. According to GUT (grand unified theories), after the big-bang explosion, there is a symmetry flouting during the phase transition of the early stages of the Universe, and these strings appear when the cosmic temperature descends below certain critical temperatures (Everett, 1981; A. Vilenkin, 1981a,b).
The study of Kaluza-Klein (KK) (Kaluza, 1921; Klein, 1926) theory is a model that sought to integrate Einstein’s theory of gravity and Maxwell’s electromagnetism theory, which revolves around the concept of the fifth dimension, beyond the four dimensions of space and time. The study of KK cosmology became popular because of its illustrious history and some interesting features to revolutionize the study of the universe. This allows the universe to expand early and study its evolution and behavior, adding extra dimensions to Einstein’s field equations as seen nowadays. It is becoming very fascinating to study string cosmology in higher-dimensional space-time in the context of general relativity. Several researchers like Chodos and Detweiler (1980), Appelquist et al. (1987) have investigated a homogeneous higher dimensional cosmological model with massive string in general relativity. Naidu et al. (2013) and Reddy and Lakshmi (2014) have explored the possibility of higher dimensional space-time in the field of cosmology. Jain and Shyamsunder (2015), Khadekar and Patki (2008), Sharif and Khanum (2011), Venkateswarlu and Kumar (2006), Khadekar and Vaishali (2010), Samanta and Dhal (2013), Raut et al. (2015) have discussed five-dimensional KK cosmological models with different matters. Adhav et al. (2008) and Yilmaz (2006) have investigated KK cosmic solutions are examined in higher dimensions for quark matter along with string cloud and domain walls in the context of general relativity. Reddy et al. (2007) and Reddy and Naidu (2007) have investigated a higher-dimensional string cosmological model in different theories of gravitation. Khadekar et al. (2008) investigated string dust cosmological models with particles attached to them by considering three different forms of variable Λ in the context of five-dimensional KK space-time. Khadekar et al. (2007) studied a string cosmological model with bulk viscosity in higher dimensional space-time. Nimkar (2017) discussed String cosmological model with the electromagnetic field in general relativity. Pawar et al. (2018) discussed KK string cosmological model in f (R, T) theory of gravity. Krori et al. (1994) have investigated a higher dimensional Bianchi type-I cosmological model with string and they found that matter and string coexist throughout the evolution of the universe. Mohanty et al. (2002), Sahoo et al. (2017) have investigated the anisotropic cosmological model universe in Bianchi type-I space-time. Venkateswarlu and Pavankuma (2005) have investigated a string cosmological model in higher dimensional space-time with scale covariant theory of gravitation. Rahaman et al. (2003) obtained the exact solutions of the field equations for the higher dimensional space time in the framework of Lyra manifold when the source of gravitational field is a massive string. Kandalkar et al. (2012) constructed Bianchi type-III string cosmological models in presence of magnetic field in the context of general relativity and obtained exact solution of the field equations by using the condition that the sum of the energy density and tension density is zero. Mohanty and Samanta (2009) have investigated a five dimensional axially symmetry string cosmological models in general theory of relativity in presence of bulk viscous fluid. Samanta and Debata (2011) constructed Bianchi type-I five dimensional string cosmological model in the framework of Lyra manifold. Choudhury (2017), Tripathi et al. (2021), Dubey et al. (2018), Tiwari et al. (2019), Ram and Verma (2019), Mollah et al. (2019) and Singh and Baro (2020) are some of the eminent authors who studied different string cosmological models in higher dimensional space time in the contexts of the general relativity. Recently Mollah and Singh (2021) and Baro et al. (2021) constructed higher dimensional Bianchi type-III string cosmological in the framework of general relativity.
In this article, we discuss anisotropic cloud string cosmological models with particles attached to them in the five-dimensional KK space-time. This article is prepared as follows: Sec.2 is devoted to the metric and Einstein’s field equations. In Sec. 3 we presented the solutions of the field equations. The geometrical and physical interpretation of the results is given in sec. 4. In the last section, we give the conclusions.
Metric and field equations
The five-dimensional KK metric is given by
where A and B are functions of cosmic time t only and the fifth coordinate ϕ is taken to be extended space like coordinate.
Einstein’s field equation is given by
where Rij is the Ricci tensor R is the Ricci scalar gij is the metric tensor and Tij is the energy-momentum tensor for a cloud string respectively.
Thus the energy-momentum tensor for a cloud string is given by
where νi and xi satisfy the conditions
Here ρ is the rest energy density for a cloud of strings with particles attached to them. ρ = ρp + λ, ρp being the rest energy density of particles attached to the strings and λ the tension density of the strings. Here p and ρ are a function of cosmic time t only. xi is a unit space-like vector instead of the direction of strings so that x2 = x3 = x4 = 0 and x1 ≠ 0.
The energy-momentum tensor Tij in co-moving coordinates for could string is given by
The field Eq 2 for the line-element (1) with the help of Eqs. 3–5 can be written explicitly as
An over dot indicates a derivative with respect to cosmic time t.
The spatial volume for the model (1) is given by
The generalized signify Hubble parameter for Kaluza-Klein space time is given by
The directional Hubble parameters Hx, Hy, Hz and Hϕ in the direction of x, y, z and ϕ respectively for the Kaluza-Klein metric are
and
The scalar expansion θ and shear scalar σ2 are given by
The expansion of signify anisotropic parameter (Δ) is given by
where ΔHi = Hi − H and Hi = 1, 2, 3, 4 represent the directional Hubble parameters in Hx, Hy, Hz and Hϕ directions respectively.
Solutions of the field equations
The set of linearly independent field Eqs 6–9 with five unknown A, B, ρ, λ and ρp.
To solve the system of equations we consider deceleration parameter (q) as a linear function of hubble parameter (Tiwari et al., 2015; Tiwari et al., 2018; Sharma et al., 2019):
Here α and β arbitrary constants.
For α = −1 in Eq 15
which yields the following differential equation
After integration Eq 16 we get
where c is an integrating constant.
Collins et al. (1980) have exposed that for a spatially homogeneous metric, a large class of solutions that can satisfy the condition
where n is constant and n ≠ 1.
From Eqs. 10, 17, 18 the metric component are
and
Therefore the metric (1) reduce to
Eq. 21 represents Five-Dimensional KK Cosmological Models with variable deceleration parameter.
Physical properties of the model
We have obtained the cosmological model (21), the directional Hubble parameters Hx, Hy, Hz and Hϕ, the physical quantities such as Hubble parameter H, spatial volume V, signify anisotropy parameter Δ, expansion scalar θ, shear scalar σ2, energy density ρ, particles density ρp and tension density of the string λ are obtained as follows:
The directional Hubble parameters Hx, Hy, Hz and Hϕ are
and
For Kaluza-Klein space-time, the signify Hubble parameter(H) is given by
The spatial volume(V) is given by
The expansion of signify anisotropic parameter (Δ) is given by
The expansion scalar (θ) is given by
The shear scalar (σ2) is given by
The energy density ρ is given by
The tension density λ for the string is given by
The particles density ρp is obtained by
The deceleration parameter (q) is given by
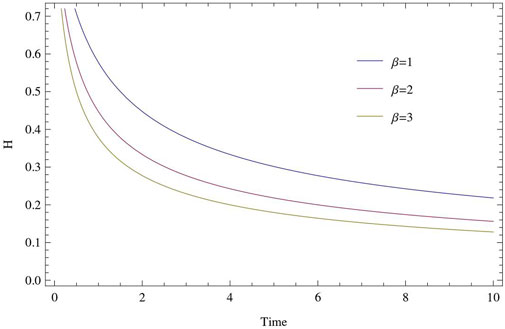
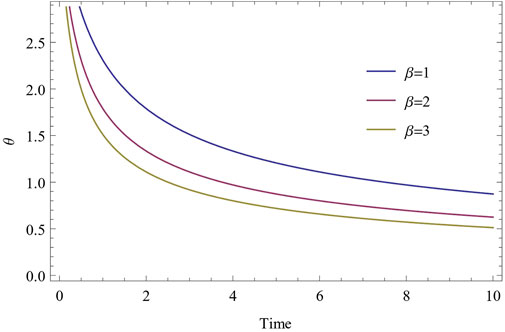
It can be seen that from Eqs. 22, 25, both the Hubble parameter (H) and expansion scalar (θ) is a positive and decreasing function of cosmic time t. The Hubble parameter (H) and expansion scalar (θ) tend to infinity as t → 0 and tend to a finite value as t → ∞ are shown in Figures 1, 3 which are agrees with established theories. Figure 2 shows variation of spatial volume w.r.t. time. We have also noticed that
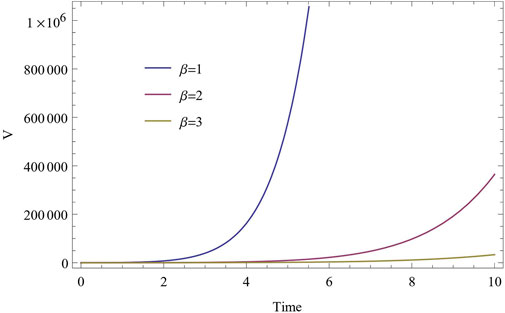
From Eq. 23 shows that at t = 0 the spatial volume is finite and thereafter increases continuously when cosmic time t is increasing. Figure 3 depicts the nature of variations of V versus t.
From Eq. 31 it is observed that the deceleration parameter q > 0 for
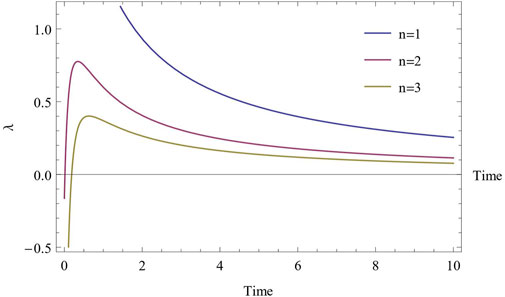
The expansion of signify anisotropic parameter Δ ≠ 0 (constant) for n ≠ 1 and Δ = 0 for n = 1. We also observed from Eq. 27 that
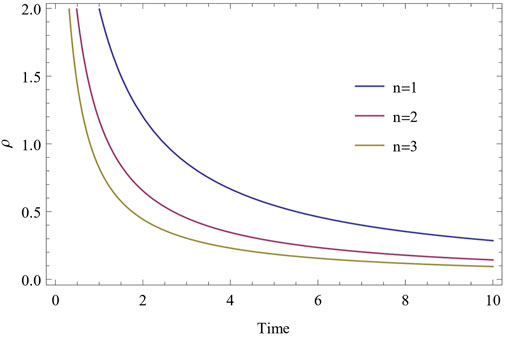
From Eq. 28 it is seen that the expansion for rest energy density ρ is a decreasing function of cosmic time t. This shows that the rest energy density is positive and satisfies the condition of energy ρ ≥ 0 for all n ≥ −1. Also from Figure 4, it is seen that the rest energy density ρ is decreasing when time t is increasing and initially ρ → ∞ when t → 0, thus has an initial singularity.
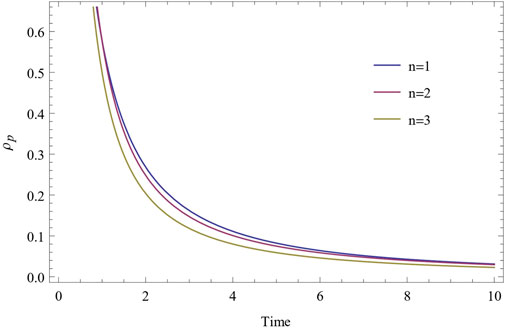
It is seen from Figures 5, 6 that both the string tension density λ and particle density ρp are positive, decreasing function of cosmic time t, and become zero as t → ∞. Also, we observed that initially both the string tension density λ and particle density ρp tend to infinity when t tends to zero which suggests that the universe began with big bang and as time progresses, both the string tension density λ and particle density ρp decreases with the expansion of the universe.
Conclusion
In the present article, we have investigated the behavior of anisotropic cloud string cosmological models in five-dimensional KK space-time to describe the mysterious phenomena of the entire universe. To get the exact solutions of the Einstein field equations, we assumed a scale factor
Data availability statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author contributions
All of the authors listed have contributed a significant, direct, and intellectual contribution to the work and have given their permission for it to be published.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adhav, K. S., Nimkar, S., and Dawande, M. (2008). String cloud and domain walls with quark matter in n-dimensional kaluza-klein cosmological model. Int. J. Theor. Phys. 47, 2002–2010. doi:10.1007/s10773-007-9644-3
Amendola, L. (2003). Acceleration at z >1? Mon. Not. R. Astron. Soc. 342, 221–226. doi:10.1046/j.1365-8711.2003.06540.x
Appelquist, T., Chodos, A., and Freund, P. G. O. (1987). Morden kaluza-klein theories. Boston: Addison-Wesley.
Baro, J., Singh, P. K., and Singh, T. A. (2021). Mathematical analysis on anisotropic Bianchi type-III inflationary string cosmological models in Lyra geometry. Indian J. Sci. Technol. 14, 46–54. doi:10.17485/IJST/v14i1.1705
Chodos, A., and Detweiler, S. (1980). Where has the fifth dimension gone. Phys. Rev. D. 21, 2167–2170. doi:10.1103/physrevd.21.2167
Choudhury, S. (2017). Bianchi type I universe in braneworld scenario with non-zero weyl tensor of the bulk. Eur. Phys. J. C 77, 619–622. doi:10.1140/epjc/s10052-017-5175-0
Collins, C. B., Glass, E. N., and Wilkinson, (1980). Exact spatially homogeneous cosmologies. Gen. Relativ. Gravit. 12, 805–823. doi:10.1007/BF00763057
Dubey, R. K., Shukla, B. V., and Yadav, N. (2018). On mathematical analysis for Bianchi type-I string cosmological model in modified theory of relativity. Phys.Astron. Int.J. 2, 143–146. doi:10.15406/paij.2018.02.00058
Everett, A. (1981). Cosmic strings in unified gauge theories. Phys. Rev. D. 24, 858–868. doi:10.1103/physrevd.24.858
Jain, N., and Shyamsunder, S. (2015). Kaluza-Klein bulk viscous cosmological model with time dependent gravitational constant and cosmological constant. Int. J. Theor. Phys. (Dordr). 54, 2991–3003. doi:10.1007/s10773-015-2538-x
Kaluza, T. (1921). Zum unitätsproblem in der physik. Sitzungsber. Preuss. Akad. Wiss. Berl. Math. Phys. K1 1921, 966–972. doi:10.1142/S0218271818700017
Kandalkar, S. P., and Samdurkar, S. (2015). LRS Bianchi type-I cosmological model with bulk viscosity in Lyra geometry. Bulg. J. Phys. 42, 42–52.
Kandalkar, S. P., Samdurkar, S. W., and Gawande, S. (2012). Bianchi type-III string cosmological models in the presence of magnetic field in general relativity. Int. J. Sci.Eng. Res. 3, 1–7.
Khadekar, G. S., and Patki, V. (2008). Kaluza-klein type robertson walker cosmological model with dynamical cosmological term λ. Int. J. Theor. Phys. 47, 1751–1763. doi:10.1007/s10773-007-9617-6
Khadekar, G. S., Patki, V., and Radha, R. (2007). String cosmological model with bulk viscosity in higher dimensional space time. J. Dyn. Syst. Geometric Theor. 5, 117–123. doi:10.1080/1726037X.2007.10698531
Khadekar, G. S., and Vaishali, K. (2010). Higher dimensional cosmological model of the universe with variable equation of state parameter in the presence of g and λ. Rom. J. Phys. 55, 871–880.
Khadekar, G. S., Vrishali, K., Patki, V., and Radha, R. (2008). Higher dimensional string cosmological model with dynamical cosmological term λ. J. Dyn. Syst. Geometric Theor. 6, 61–73. doi:10.1080/1726037X.2008.10698545
Kibble, T. W. B. (1983). Some implications of a cosmological phase transition. Phys. Rep. 28, 183–199. doi:10.1016/0370-1573(80)90091-5
Kibble, T. W. B. (1976). Topology of cosmic domains and strings. J. Phys. A Math. Gen. 9, 1387–1398. doi:10.1088/0305-4470/9/8/029
Klein, O. (1926). On the unification problem in physics, preuss. akad. wiss. berlin. Z. Phys. 32, 895–906. doi:10.1007/bf01397481
Krori, K. D., Chaudhuri, T., and Mahanta, C. R. (1994). Strings in some bianchi type cosmologies. Gen. Relativ. Gravit. 26, 265–274. doi:10.1007/BF02108006
Mohanty, G., Sahoo, P., and Mishra, B. (2002). On Bianchi type-I mesonic cosmological model in bimetric theory. Astrophys. Space Sci. 281, 609–612. doi:10.1023/A:1015868106122
Mohanty, G., and Samanta, G. C. (2009). Five dimensional axially symmetric string cosmological models with bulk viscous fluid. Int. J. Theor. Phys. 48, 2311–2318. doi:10.1007/s10773-009-0020-3
Mollah, M. R., and Singh, K. P. (2021). Behaviour of viscous fluid in string cosmological models in the framework of Lyra geometry. New Astron. 88, 101611. doi:10.1016/j.newast.2021.101611
Mollah, M. R., Singh, K. P., and Singh, P. S. (2019). Bianchi type-III cosmological model with quadratic EoS in Lyra geometry. Int. J. Geom. Methods Mod. Phys. 15, 1850194–194. doi:10.1142/S0219887818501943
Naidu, R. L., Naidu, K. D., Babu, K. S., and Reddy, D. R. K. (2013). A five dimensional Kaluza-Klein bulk viscous string cosmological model in Brans-Dicke scalar-tensor theory of gravitation. Astrophys. Space Sci. 347, 197–201. doi:10.1007/s10509-013-1498-y
Nimkar, A. S. (2017). String cosmological model with electromagnetic field in general relativity. Int. J. Sci. Res. 6, 2227.
Padmanabhan, T., and Choudhury, T. R. (2003). A theoretician’s analysis of the supernova data and the limitations in determining the nature of dark energy. Mon. Not. R. Astron. Soc. 344, 823–834. doi:10.1046/j.1365-8711.2003.06873.x
Pawar, D. D., Bhuttampalle, G. G., and Agrawal, P. K. (2018). Kaluza–klein string cosmological model in f(r, t) theory of gravity. New Astron. 65, 1–6. doi:10.1016/j.newast.2018.05.002
Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R. A., Nugent, P., Castro, P. G., et al. (1999). Measurements of ω and λ from 42 high-redshift supernovae. Astrophys. J. 517, 565–586. doi:10.1086/307221
Rahaman, F., Chakraborty, S., Das, S., Hossain, M., and Bera, J. (2003). Higher-dimensional string theory in Lyra geometry. Pramana -. J. Phys. 60, 453–459. doi:10.1007/BF02706151
Ram, S., and Verma, M. K. (2019). Spatially homogeneous Bianchi type I mesonic models in two-fluid cosmology. Presp. J. 10, 293–300.
Raut, V. B., Adhav, K. S., Wankhade, R. P., and Gawande, S. M. (2015). Kaluza-klein cosmological models with anisotropic dark energy and special form of deceleration parameter. Int. J. Sci. Eng. Res. 6, 2229.
Reddy, D., and Lakshmi, G. (2014). Five dimensional radiating model in brans-dicke theory of gravitation. Astrophys. Space Sci. 354, 633–636. doi:10.1007/s10509-014-2112-7
Reddy, D. R. K., and Naidu, R. L. (2007). Five dimensional string cosmological models in a scalar-tensor theory of gravitation. Astrophys. Space Sci. 307, 395–398. doi:10.1007/s10509-007-9387-x
Reddy, D. R. K., Naidu, R. L., Rao, S. A., and Devi, K. N. (2007). A higher-dimensional string cosmological model in brans–dicke theory of gravitation. Astrophys. Space Sci. 310, 177–180. doi:10.1007/s10509-007-9490-z
Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116, 1009–1038. doi:10.1086/300499
Sahoo, P. K., Sahoo, P., and Bishi, B. K. (2017). Anisotropic cosmological models in f(R, T) gravity with variable deceleration parameter. Int. J. Geom. Methods Mod. Phys. 14, 1750097. doi:10.1142/s0219887817500979
Samanta, G. C., and Dhal, S. N. (2013). Higher dimensional cosmological models filled with perfect fluid in f(r, t) theory of gravity. Int. J. Theor. Phys. 52, 1334–1344. doi:10.1007/s10773-012-1449-3
Samanta, G., and Debata, S. (2011). Five dimensional Bianchi type-I string cosmological models in Lyra manifold. J. Mod. Phys. 3, 180–183. doi:10.4236/jmp.2012.32024
Sharif, M., and Khanum, F. (2011). Kaluza-klein cosmology with varying g and λ. Astrophys. Space Sci. 334, 209–214. doi:10.1007/s10509-011-0711-0
Sharma, U. K., Zia, R., Pradhan, A., and Beesham, A. (2019). Stability of LRS Bianchi type-I cosmological modelsin f(r, t) gravity. Res. Astron. Astrophys. 19, 055. doi:10.1088/1674–4527/19/4/55
Singh, K. P., and Baro, J. (2020). Bulk viscous fluid Bianchi type-I string cosmological model with negative constant deceleration parameter. Adv. Math. Sci. J. 9, 4907–4916. doi:10.37418/amsj.9.7.55
Stachel, J. (1980). Thickeningthe string. I. the string perfect dust. Phys. Rev. D. 21, 2171–2181. doi:10.1103/physrevd.21.2171
Tiwari, K. R., Beesham, A., and Shukla, B. K. (2018). Scenario of two fluid dark energy models in Bianchi type-III universe. Int. J. Geom. Methods Mod. Phys. 15, 1850189. doi:10.1142/S021988781850189X
Tiwari, R. K., Shukl, B. K., and Mishra, S. (2019). Bianchi type-III string cosmological model in f(rt) modified gravity theory. Presp. J. 10, 306–315.
Tiwari, R. K., Singh, R., and Shukla, B. K. (2015). A cosmological model with variavle deceleration parameter. Afr. Rev. Phys. 10, 0048.
Tripathi, B. R., Tyagi, A., and Parikh, S. (2021). Bianchi type-I inhomogeneous string cosmological model with electromagnetic field in general relativity. Presp. J. 8, 474–483.
Venkateswarlu, R., and Kumar, K. (2006). Higher dimensional frw cosmological models in self-creation theory. Astrophys. Space Sci. 301, 73–77. doi:10.1007/s10509-006-7304-3
Venkateswarlu, R., and Pavankuma, K. (2005). Higher dimensional string cosmologies in scale-covariant theory of gravitation. Astrophys. Space Sci. 298, 403–408. doi:10.1007/s10509-005-5830-z
Vilenkin, A. (1981b). Gravitational field of vacuum domain walls and strings. Phys. Rev. D. 23, 852–857. doi:10.1103/physrevd.23.852
Yilmaz, I. (2006). String cloud and domain walls with quark matter in 5-d kaluza–klein cosmological model. Gen. Relativ. Gravit. 38, 1397–1406. doi:10.1007/s10714-006-0322-1
Zel’dovich, Y. B. (1980). Cosmological fluctuations produced near a singularity. Mon. Not. R. Astron. Soc. 192, 663–667. doi:10.1093/mnras/192.4.663
Keywords: kaluza-klein space time, string tension density, particle density, variable deceleration parameter, cloud string
Citation: Ray PK and Roy Baruah R (2022) Anisotropic cloud string cosmological model with five-dimensional kaluza-klein space-time. Front. Astron. Space Sci. 9:869020. doi: 10.3389/fspas.2022.869020
Received: 03 February 2022; Accepted: 21 July 2022;
Published: 11 October 2022.
Edited by:
Maxim Yurievich Khlopov, Southern Federal University, RussiaReviewed by:
Kazuharu Bamba, Fukushima University, JapanGoverdhan Sakharam Khadekar, Rashtrasant Tukadoji Maharaj Nagpur University, India
Copyright © 2022 Ray and Roy Baruah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rajshekhar Roy Baruah, cnNyb3liYXJ1YWgwMDdAZ21haWwuY29t
 Pranjal Kumar Ray
Pranjal Kumar Ray Rajshekhar Roy Baruah
Rajshekhar Roy Baruah