- 1Soft Kinetic Group, Engineering Sciences Department, Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland
- 2Locomotion in Biorobotic and Somatic Systems Group, Max Planck Institute for Intelligent Systems, Stuttgart, Germany
- 3Department of Electronic Engineering, University of Rome Tor Vergata, Rome, Italy
- 4Laboratory for Computational Engineering, Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland
- 5Institute for NeuroInformatics, ETH and University of Zürich, Zürich, Switzerland
Soft bio-mimetic robotics is a growing field of research that seeks to close the gap with animal robustness and adaptability where conventional robots fall short. The embedding of sensors with the capability to discriminate between different body deformation modes is a key technological challenge in soft robotics to enhance robot control–a difficult task for this type of systems with high degrees of freedom. The recently conceived Linear Repetitive Learning Estimation Scheme (LRLES)–to be included in the traditional Proportional–integral–derivative (PID) control–is proposed here as a way to compensate for uncertain dynamics on a soft swimming robot, which is actuated with soft pneumatic actuators and equipped with soft sensors providing proprioceptive information pertaining to lateral body caudal bending akin to a goniometer. The proposed controller is derived in detail and experimentally validated, with the experiment consisting of tracking a desired trajectory for the bending angle envelope while continuously oscillating with a constant frequency. The results are compared vis a vis those achieved with the traditional PID controller, finding that the PID endowed with the LRLES outperforms the PID controller (though the latter has been separately tuned) and experimentally validating the novel controller’s effectiveness, accuracy, and matching speed.
1 Introduction
The last 2 decades accelerated a paradigm shift in experimental robotics, driven in part by computational advances as well as by the comparative analysis of biological systems. This shift has catalyzed the development of sophisticated robots that are borrowed from general principles of biomechanics and neurocontrol of living organisms, as delineated in the foundational works of (Dickinson et al., 2000; Ijspeert, 2020). Despite remarkable progress in crafting robots that mirror the form and function of biological entities, a significant gap remains in replicating the adaptability and resilience inherent in natural locomotion. This disparity is particularly evident in areas such as sensory perception and adaptive response mechanisms. The unparalleled dexterity of animals, exemplified by geckos maneuvering on water surfaces (Nirody et al., 2018), crocodiles in their prey-capture patterns (Fish et al., 2007), and the enduring resilience of migratory fish (Crossin et al., 2004), underscores the profound complexity and efficiency of biological systems. This gap primarily arises from animals’ flexible anatomies combined with integrated sensing, which grants them an ability termed ‘morphological intelligence’ (Woodward and Sitti, 2018; Martinez-Hernandez et al., 2019).
The objectives of bio-mimetic robotics encompass a triad of goals: to decode and understand fundamental natural mechanisms, to replicate biological components, and ultimately, to engineer robotic systems that exhibit parallel functionalities. Recent strides in soft robotics have been pivotal in emulating the functionality of natural systems through the use of bio-mimetic materials (Coyle et al., 2018; Sachyani Keneth et al., 2021). These soft robotic systems offer distinct advantages, including ease of fabrication, inherent safety, and the ability to interact delicately with their environment or navigate through complex terrains (Shepherd et al., 2011; Shintake et al., 2018). Various modes of actuation such as elastomeric actuators, hydrogels, shape memory alloys (SMA), and electroactive polymers (EAP) have emerged as the mainstay in these systems (Appiah et al., 2019; Banerjee et al., 2021).
The study of aquatic locomotion is a focal point in soft robotics due to its potential for advancing our knowledge of efficient, adaptable movement in complex fluid environments. By understanding the fundamental biological principles of aquatic locomotion (Lighthill, 1975) and nature’s remarkable agility and efficiency (Lauder et al., 2007), soft robotics aims to develop robots that mimic those capabilities, enhancing our ability to design and control machines for efficient navigation and operation in water-based settings.
Fish in particular are renowned for their swift and efficient movement through dynamically changing aquatic environments (see Supporting Video 1), a trait that enables them to undertake strenuous tasks such as upstream migration during fasting periods (Crossin et al., 2004). The key to their exceptional energy efficiency lies in their ability to modulate the amplitude and frequency of their body undulations, leveraging the stiffness of their structure (McHenry et al., 1995; Lauder et al., 2011). By synchronizing body undulation frequency with the flow, fish swim efficiently, harnessing energy from the fluid and converting it into propulsion (Beal et al., 2006; Akanyeti et al., 2016; Liao and Akanyeti, 2017). The oscillation of the caudal fin emerges as one of the most efficient propulsion modes in terms of transport costs (Rayner, 1986; Ludeke and Iwasaki, 2019), and underwater speeds are enhanced significantly (Block et al., 1992), resulting in passive propulsion even in deceased fish specimens (Liao et al., 2003).
Research into fish locomotion have spawned a plethora of soft robotic designs capable of aquatic movement (Struebig et al., 2020; Nguyen and Ho, 2021). These designs range from robots that mimic the motion of tuna, surpassing their predatory speeds (Barrett, 1996; Zhu et al., 2019), to platforms that execute rapid ‘C-start’ maneuvers similar to carangiform fish (Marchese et al., 2014), and even robots capable of three-dimensional acoustic maneuvering (Hsieh et al., 2016; Katzschmann et al., 2018). Additionally, lateral body motions and reflex-based jumping capabilities have been integrated into robotic designs (Fan et al., 2005; Kim et al., 2020; Zhao et al., 2020; Yang et al., 2021). The intricacies of fish locomotion, particularly the interplay between active and passive stiffness control and the internal dynamics, offer a rich terrain for bio-mimetic technology transfer (Low and Chong, 2010; Low et al., 2010). Although fully passive fin systems have been developed to mimic fish propulsion, challenges arise in adjusting thrust output and drag in response to variations in flow velocity or frequency (Jayne and Lauder, 1996; Yun et al., 2011; Yun et al., 2015). To emulate the fish’s ability to adaptively modulate swimming body undulations and utilize soft surfaces, a sensory-driven control mechanism becomes essential.
This research resides at the intersection of bio-inspired and bio-mimetic robotics (Kim et al., 2013; Hammond et al., 2023). We seek to emulate the intricate locomotion observed in aquatic life, contributing to the field’s evolution from leveraging general biological principles to the precise replication of specific functions. Our exploration of aquatic locomotion mechanisms enhances our understanding of the way soft robotic designs can mimic biological systems, offering innovative solutions for navigating and interacting within fluid environments. This approach not only advances robotics but also provides biologists with tools to test hypotheses that may be impractical with living specimens, thereby serving as invaluable assets in bio-mechanical research (Siddall et al., 2021; Chellapurath et al., 2022).
In our exploration of aquatic locomotion, we examine the biomechanics of fish such as the bluegill sunfish to inform the design of our robotic fish (Schwalbe et al., 2019). Our robot utilizes a flexible plastic foil to emulate the structural foundation of a fish’s spine and is equipped with soft pneumatic actuators to mimic the nuanced muscular movements, particularly in the tail region, enabling realistic fish-like bending. The undulation frequency selected for our robot is designed to represent a spectrum of fish swimming behaviors, optimizing the system’s ability to mimic a variety of natural locomotive strategies. The actuation mechanism facilitates lateral body caudal bending, a key feature of efficient aquatic propulsion. Furthermore, the choice of Dragon Skin™ silicone for the actuators is informed by the need to replicate the natural flexural stiffness observed in aquatic organisms, ensuring a balance between flexibility and rigidity crucial for effective movement. This biomimetic approach, inspired by the dynamic stiffness modulation strategies identified in aquatic species, aims to capture the essence of efficient propulsion mechanisms in fish, contributing to the advancement of soft robotics in simulating natural aquatic locomotion.
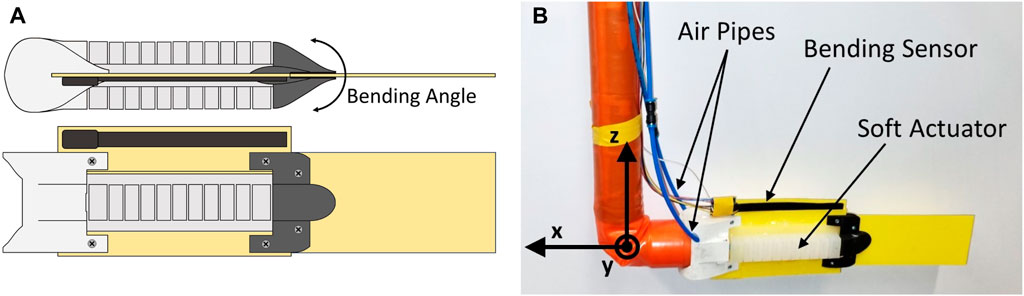
Now, utilizing such a soft robotic fish platform equipped with pneumatically actuated soft actuators and a soft bending sensor, as illustrated in Figure 1, we aim to advance the understanding and application of bio-mimetic robotics. The soft bending sensor enables real-time monitoring and control of the bending amplitude of the robotic fishtail during oscillation. This setup, in which the body caudal fin undulation of the soft robotic fish exhibits repetitive features, is particularly suited for testing Repetitive Learning Controllers (RLC) (Xu and Yan, 2006; Marino et al., 2012; Verrelli, 2016; 2022) or learning inverse kinematics (Zhao et al., 2023). Indeed, the most suitable control design is one that solves an output tracking control problem for uncertain nonlinear systems characterized by unstructured uncertainties (that is when no parameterization of the uncertainties is available) and by output reference signals that belong to the family of general periodic time functions with a known period (piece-wise constant references or sinusoidal references are special cases). RLCs are required (Marino et al., 2012; Verrelli, 2016; Verrelli, 2022), since they are not model-based and aim at performing a dynamic system inversion just through the feedback, with the output tracking error being reduced without increasing the feedback control gains (as happens for the typical robust adaptive approach; the reader is also referred to the discussion on the gains of the PID control of the subsequent Section 2.3). On the other hand, the non-structured periodic disturbance constituted by the reference input, whose effect has to be nullified by the RLC, is highly uncertain and is very complex in general, due to the nonlinearities of the system making traditional resonant PID controllers be non-effective. Nevertheless, finite memory implementations of control laws are needed in practice. They should involve the use of a finite number of stored values or be finite-dynamic-order controls. This is the case of the linear repetitive learning control of (Verrelli et al., 2015) (see theoretical foundations in (Tomei and Verrelli, 2015), in which the delay involved within the repetitive learning estimation scheme is approximated by Padé theory-based rational proper functions, so as to approximate a delay-based infinite-dimensional system by a finite-dimensional one. Owing to the dynamic linearity of Padé approximants and the use of a stabilizing filter, the resulting Linear Repetitive Learning Estimation Scheme (LRLES) generalizes the classical integral action (typically used within the PID control for robotic systems, with no “zeros” and relative degree two) to the case of periodic (non-constant) references. The resulting learning scheme is constituted by a transfer function with all its poles having a negative real part, with the typical long-term instability issues of classical RLCs, due to high-frequency disturbance noises, thus being avoided.
This study thus presents an original comparative analysis of trajectory tracking for a desired fishtail bending angle envelope under constant oscillating frequency, using the innovative PID-LRLES in comparison with the typically used PID controller.
The remainder of this manuscript is organized as follows: Section 2 outlines the experimental setup, the PID controller, and the PID-LRLES, along with the experimental procedures; Section 3 presents our experimental findings; and Section 4 discusses the implications of this work and outlines future research directions.
2 Materials and methods
2.1 Experimental setup
2.1.1 Soft robotic fish platform
The soft robotic fish platform used in this work (Figure 1) consists of a flexible plastic foil, representing the backbone of the animal, to which two soft pneumatic actuators are glued to provide bending actuation. A frontal cuff (3D-printed, ABS) serves as an attachment point to the fixed mast, while another flexible tail cuff (3D-printed, TPU A95) holds the passive caudal fin. The cuffs also help streamline the overall fish profile. The main body is made following a similar method as described by Jusufi et al. (2017) and based on the work of Mosadegh et al. (2014). The flexible backbone foil (0.52 mm thick shim stock: Artus, Inc.) has a flexural stiffness comparable to that of a fish (9.9e-4 [Nm2] Jusufi et al. (2017)), and the actuators, made using a silicone-based elastomer (Dragon Skin™ 20, Smooth-On Inc.), are glued using a dedicated silicone adhesive (Dowsil 734 Flowable Sealant, DOW). A soft capacitive sensor (1-Axis Soft Flex Sensor, Nitto Bend Technologies) is affixed to a flexible foil extension above the midline to measure the bending angle while the fish is actuated. Care is taken to have both ends of the sensor rest above both cuffs to measure the bending angle across the actuators to have a more precise control. Thanks to the sensor’s narrow build and its softer stiffness compared to both the plastic and the silicone parts of the robot, the effect of the sensor on the structural rigidity of the fish-like robot is minimal and can be neglected, not significantly altering the robot’s overall flexibility or movement dynamics. Previous work from Wright et al. (2019) employed resistive eutectic gallium-indium (eGaIn) sensors to estimate the bending angle. As those sensors cannot measure both positive and negative angle values alone, two units, one on each side of the fish, have to be combined to extract a complete measurement. Additionally, for the bending to create sufficient stretching of the eGaIn sensors, they have to be placed at a distance from the midline. The capacitive sensor, on the other hand, can measure both positive and negative angles accurately, can be placed directly on the midline, and requires less calibration effort. For these reasons, and because the resistive sensors are also more fragile, the capacitive sensor was selected in the end.
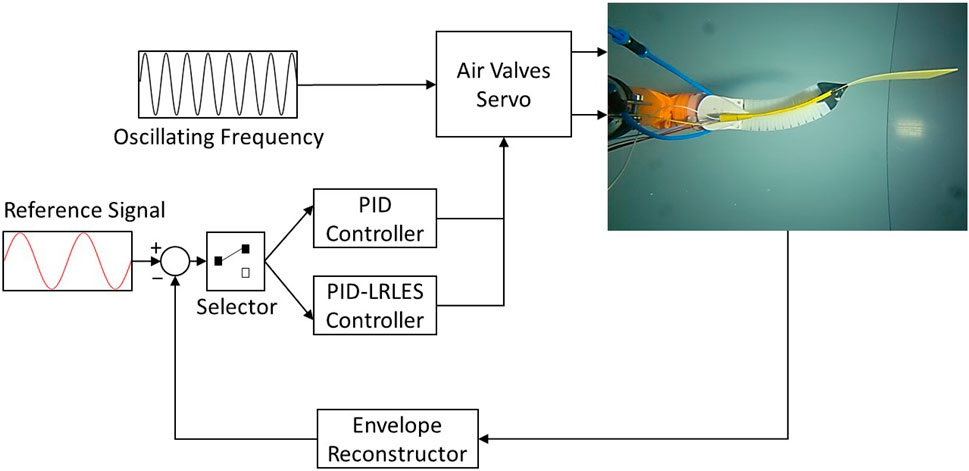
The pressure network system used to power the soft actuators is illustrated in Figure 2. A digital pressure regulator (ITV0050-3BS, SMC) supplies between 0.7 and 2.5 bar (actuator working range) of compressed air to the system in a controlled fashion. Each actuator is governed by two solenoid valves (SYJ7320-5LOU-01F-Q, SMC) that either connect it to the pressure system controlled by the regulator, or the atmosphere. An air tank allows to store some pressure during actuation and helps mitigate the variations created by the release of actuator pressure in the atmosphere. A real-time microcontroller (myRIO-1900, National Instruments) acts as the Control Unit of the robotic platform. It samples the bending sensor via I2C at 1 kHz and runs the control loop at the same frequency, generating the actuating signals to the valves and control signal to the pressure regulator as displayed in Figure 3.
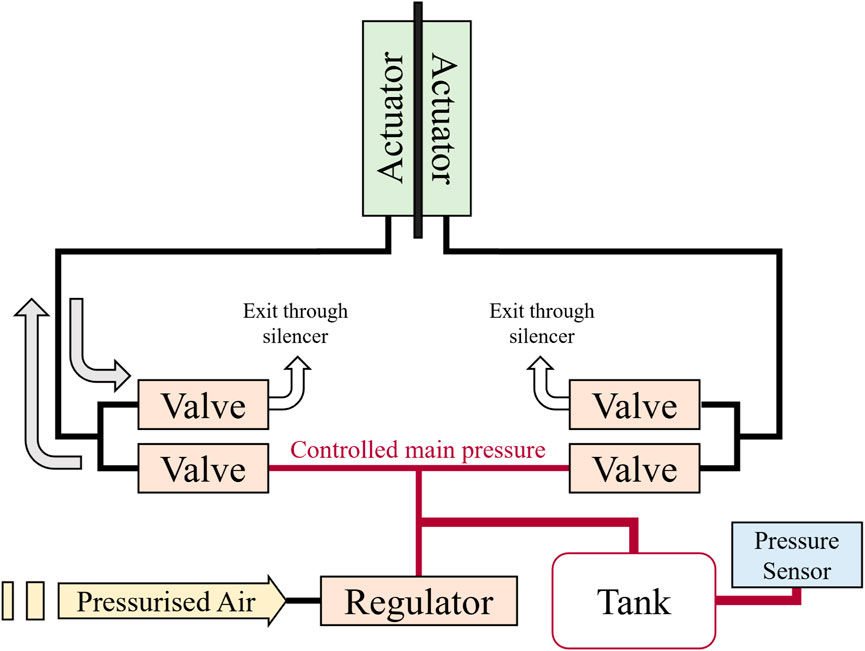
Figure 2. Schematic of the soft fish platform’s pneumatic actuation circuit. The external pressurized air source provides the regulator with a stable 2.5 bar input. For each actuator at any point in time, one of the two connected solenoid valves is opened to either fill the actuator at the controlled main pressure (0.7–2.5 bar) or release it to atmospheric pressure.
2.1.2 Test rig
Experiments were conducted within a large water tank located at the Swiss Federal Laboratories for Material Science (Empa) with a cross-sectional area measuring 0.6 × 1 m2, accommodating a fully transparent test section extending up to 6 m in length (Figure 4A).
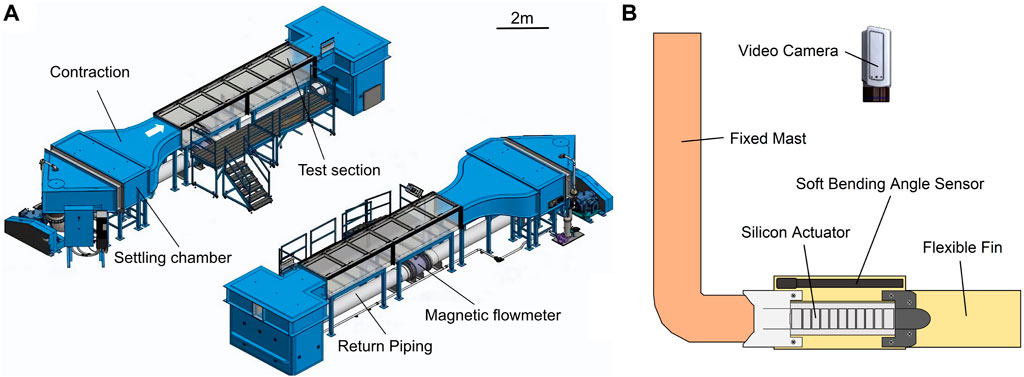
Figure 4. Experimental setup for the soft robotic swimming experiments. (A) General setup of the water tank. (B) Schematic of the robotic platform placed in the water tank.
The soft robotic fish platform was suspended in the center of the test section and secured in place by two extra aluminum beams on both sides of the mast for stability. A video camera was placed above the platform to capture the robotic fish’s midline kinematics (Figure 4B). To avoid waves and reflections at the water surface, the recording was made through a Plexiglas tray in contact with the water at all times.
2.2 From PID control to PID-LRLES
The control of the tethered soft robotic platform aims at developing a general control strategy that can be also deployed on an untethered underwater robot, mimicking the size and behavioral traits of living fish. Controlling robotic fish plays a pivotal role in achieving bio-mimetic swimming performance, ultimately leading to a system that closely resembles its natural counterparts. While various model-based control approaches can potentially be applied to soft robotic systems akin to other robotic platforms, the lumped nature of soft-system models–with internal states just being representative of complex neglected dynamics and parameters that are uncertain–limits the applicability of certain theories and algorithms that require more than the knowledge of the structural properties of the model, such as relative degree, high-frequency gain, and minimum-phase. Controlling soft robots thus presents a significant challenge, necessitating the exploration of viable and optimally effective control strategies capable of managing the soft body and leveraging its intrinsic intelligence.
In our model, the primary control objective revolves around regulating the pressure within the soft actuators. This pressure modulation dynamically influences the entire robotic fish system by altering thrust and side force, generating torque at each joint, ultimately impacting the final bending angle of the tail, considered as an end-effector of the robot.
Owing to the repetitive features of the body caudal fin undulation of the soft robotic fish, the linear repetitive learning control strategy of (Verrelli et al., 2015) is here adopted: the dynamic linearity of Padé approximants and the use of a stabilizing filter make the LRLES generalize the classical integral action to the case of periodic (non-constant) references. In particular, a LRLES of such a type (referred to as
is defined by the (possibly filtered) linear combination
2.2.1 PID control
The
with transfer function
was initially employed for the control of a soft robotic fish by (Lin et al., 2021). Controller (2) is referred to as
in terms of the proportional, integral, and derivative gains
This controller is widely used in diverse dynamic systems, including industrial, robotic, and biological applications and stands as the first viable candidate due to its robust performance. The PID controller operates by continuously calculating the error value from the difference between a desired setpoint and the measured process variable. It incorporates a proportional and a derivative term–each with the corresponding gain–to stabilize the error system, along with an integral term to reconstruct the constant reference input that guarantees perfect output regulation to any constant output reference.
An amplitude control system, prototyped in Simulink, incorporating sensor noise effects, was designed and tested (Lin et al., 2021). This control system extracts the maximum amplitude within each half period from the oscillating strain signal. The PID controller demonstrates robust behavior against sensor noise, exhibiting fluctuations around the step point under noises. Furthermore, periodic references, though piece-wise constant, repeatedly induce transient error behaviors.
2.2.2 PID-LRLES
The RLC idea comes from the observation that animals can enhance task execution through repeated trials. In contrast to non-learning controllers, the repetitive learning mechanism utilizes the error signal coming from p previous executions
Following (Tomei and Verrelli, 2015), let the [m, m]-Padé approximant of e−sT being given by
with
Then, define the proper transfer function
which approximates the Laplace transform
in which:
•
•
• μ and αi, 1 ≤ i ≤ p, are positive design parameters with αi satisfying
• b = α1 + 2α2 + ⋯ + pαp and j* = min{j: αj > 0}.
Such a learning estimation scheme relies on a weighted sum of the information stored in the p previous executions: the weights αi, 1 ≤ i ≤ p are extra degrees of freedom that allow the control design to take into account the whole available information about the past to improve the performance of a periodic system. If
When the action of the saturation function is neglected and
which satisfies
in the Laplace domain. On the other hand, if ξ*0(t) denotes the function which is equal to ξ*(t) on the set [0, T) while being zero outside it, then we can write
which plays the role of an infinite-dimensional exosystem reproducing the time T-periodicity of ξ*(t). The initial function ξ*0(t) (just like the initial condition for a finite-dimensional exosystem) is the only unknown quantity to the controller to be dealt with by means of the feedback action
where the signal σ(t) can be obtained by comparison. Then, we design the (1 + p ⋅ m)-finite-dimensional approximation of the exosystem as (
where (Ap, Bp, Cp, Dp) is a minimal realization of the proper transfer function P(s). Here, Ap is a Hurwitz matrix, dp(s) is a p ⋅ m-order polynomial whereas α ∈ [0, 1), β ∈ (0, 1] are assumed to guarantee that the polynomial
has all the roots belonging to
to have a transfer function
with all the poles belonging to
The incorporation of the (α, β)-filter is necessary for this purpose since, when α = 0 and β = 1, s = 0 is a root of qπ(s) according to
Notice that, for α = 0, β < 1 and α1 = 1, αj = 0 (j = 2, … , p), the equivalent exosystem
becomes
where the solution of
evaluated at any t = t* + kT (t* ∈ [0, T), k = 0, 1, … ) constitutes a decreasing sequence converging to zero. The preceding equation can be rewritten as
in which the second term on the right-hand-side (with β − 1 sufficiently small) plays a stabilizing role, which leads to a bounded-input bounded-output estimation law without the use of saturation functions or projection algorithms.
2.3 Experimental protocol
The experiment consists of tracking a desired trajectory for the envelope containing the amplitude of the bending angle of the robotic fish. The platform is actuated at a constant frequency (called flapping frequency) and 0.55 duty cycle (5% co-contraction). The experiment is performed three times, each time with a different flapping frequency; the tested frequencies are 0.8, 1.0, and 1.2 Hz, and the controllers have been tuned to the case of a flapping frequency of 1.2 Hz. The envelope is used to obtain a positive, smoother signal. The desired profile of the envelope is described by a sine wave with period T = 30 s, an amplitude of 0.1 rad, and a 0.6 offset. The experimental procedure compares the tracking performance of the PID controller and the PID-LRLES depicted in Figure 5. Both controllers have been separately tuned manually to signals with the same frequency during preliminary experiments (through a trial and error tuning procedures), with the PID controller gains resulting in Kp = 3, Ki = 0.28, and Kd = 0.15 (look at the corresponding step response in Figure 6 (c)) and the PID-LRLES gains resulting in m = 7, p = 3, α1 = 0.3, α2 = 0.2, α3 = 0.5, γ = 4, β = 0.99, μ = 0.4950, ki = 0.3 and kp = 0.01. Notice that the PID controller, which does not contain the learning estimation scheme, has to increase its proportional and derivative gains–compared to the ones within the PID-LRLES (recall (5 leading to Kp = 0.34, Ki = 1.2, and Kd = 0.01)–and decrease the integral gain in order to exhibit a comparable–though worse–closed-loop behavior. This is further illustrated by Figure 6 presenting the comparative tracking results (a-b) with respect to the PID with equivalent gains, namely, with Kp = 0.34, Ki = 1.2, and Kd = 0.01: a largely worse performance is obtained for the PID control, highlighting the advantageous learning features of the LRLES. It is worth recalling that the midline motion of the fish is primarily captured using built-in soft sensors, providing real-time control feedback. At the same time, the external camera is used to capture the swimming swing of the whole fish spine, both active backbone and passive tail, and reconstruct it offline to have a qualitative understanding of the fish’s undulatory motion, see Figures 6D–F.
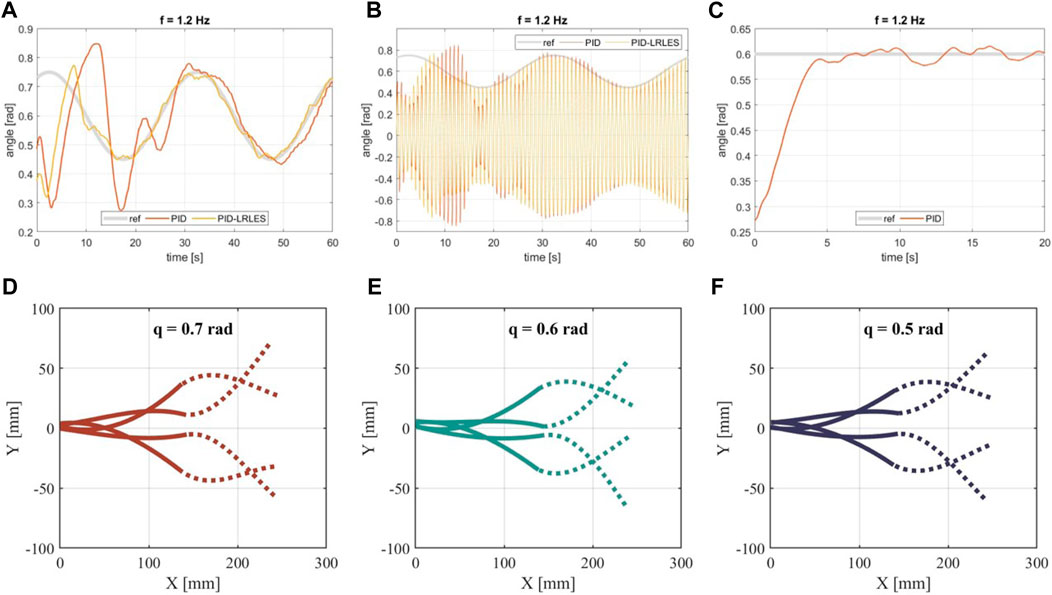
Figure 6. Bending angle (A) and its envelope (B) with the PID controller under equivalent gains (namely, Kp =0.34, Ki =1.2, and Kd =0.01) while tracking ref =0.6+0.15 sin (2π t/30); (C) step response of the PID controller with gains Kp =3, Ki =0.28, and Kd =0.15; the flapping frequency is 1.2 Hz; (D, E, F) illustrate the midline motion pattern of the fish’s foil during a complete swimming swing captured with the external camera. They display variations in oscillation magnitude while tracking signals with different bending amplitude envelopes q. The thick lines indicate the backbone of the fish, which corresponds to the bending angle measured with the bending sensor, while the dashed lines represent the passive movement of the tail. The leading edges are on the left.
All experiments start with the fish oscillating in an open loop, meaning that the actuation chambers are inflated alternatively for a fixed and predefined amount of time. After some iterations, the amplitude of the bending angle envelope reaches a steady state, and at that moment, the desired controller is turned on, allowing the robotic fish to track the desired trajectory for the amplitude of the bending angle envelope.
3 Results
The experimental procedure compares the PID controller’s and the PID-LRLES’s performance in tracking different periodic desired trajectories of the fishtail bending angle envelope. In particular, Figure 7 and Figure 8 show the tracking accuracy during the experiments with reference signals ref = 0.6 + 0.15 sin (2π t/30) and ref = 0.6 + 0.05 sin (2π t/30) + 0.05 sin (2π t/15) + 0.05 sin (2π t/10), respectively. The PID-LRLES performs better than the PID controller in tracking the desired trajectories (though the PID controller was separately tuned, as aforementioned), being at the same time faster and more accurate, regardless of the value of the flapping frequency. The root mean square error (RMSE), calculated over an oscillation period of the reference trajectory (20–50 s) for Figures 7, 60–90 for Figure 8, is in fact summarized in Table 1: the PID-LRLES outperforms the PID controller, with lower RMSEs in all the experiments. Nevertheless, Figures 7D–F illustrates the fish kinematics by plotting the mid-line kinematics of the fish backbone (solid line) and tail (dashed line) in three different moments of the experiments, with the fish tracking respectively the minimum, the medium, and the maximum tracked values for the bending angle envelopes q = 0.5, q = 0.6 and q = 0.7 rad.
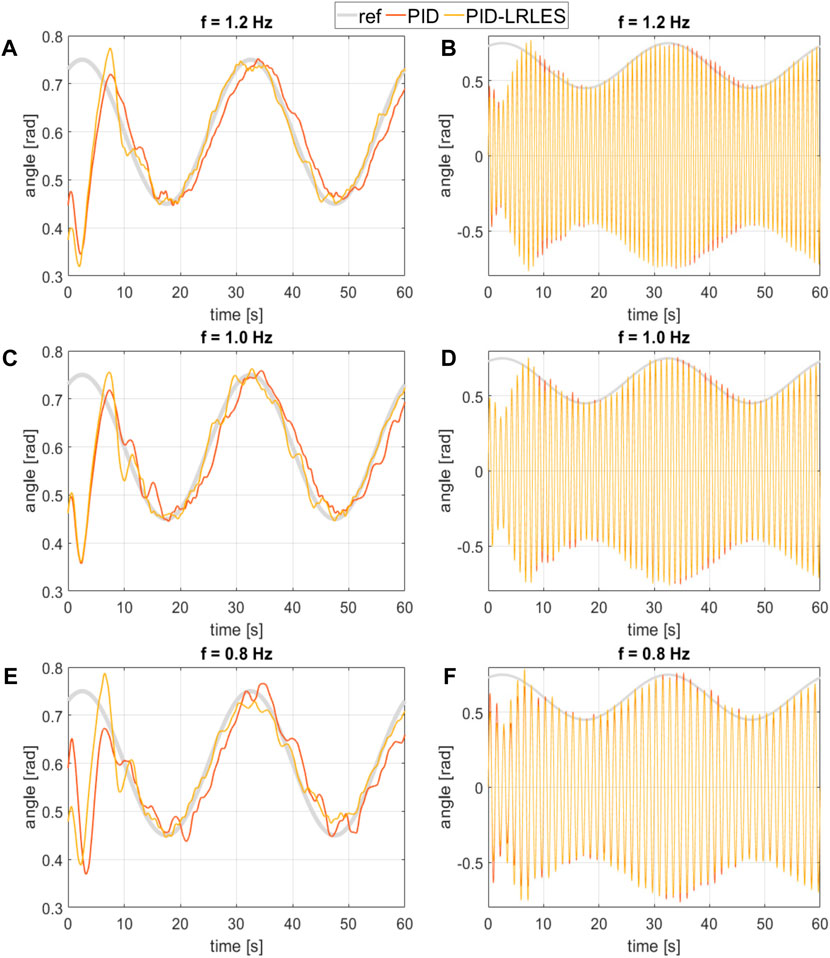
Figure 7. The extract analyzes the tracking accuracy of a soft robotic fish platform, specifically comparing the bending angle (A,C, E) and its envelope (B,D, F) under different control conditions, flapping frequency f=1.2, f=1.0, f=0.8 Hz and a reference signal ref =0.6+0.15 sin (2π t/30). Both controllers are tuned with a flapping frequency of f = 1.2 Hz ‘ref’ denotes the target amplitude envelope for the tail oscillation. ‘PID’ represents the data measured using the Proportional-Integral-Derivative (PID) controller with gains Kp =3, Ki =0.28, and Kd =0.15. ‘PID-LRLES’ refers to measurements obtained using a separately tuned PID controller augmented with the Linear Repetitive Learning Estimation Scheme (LRLES) method.
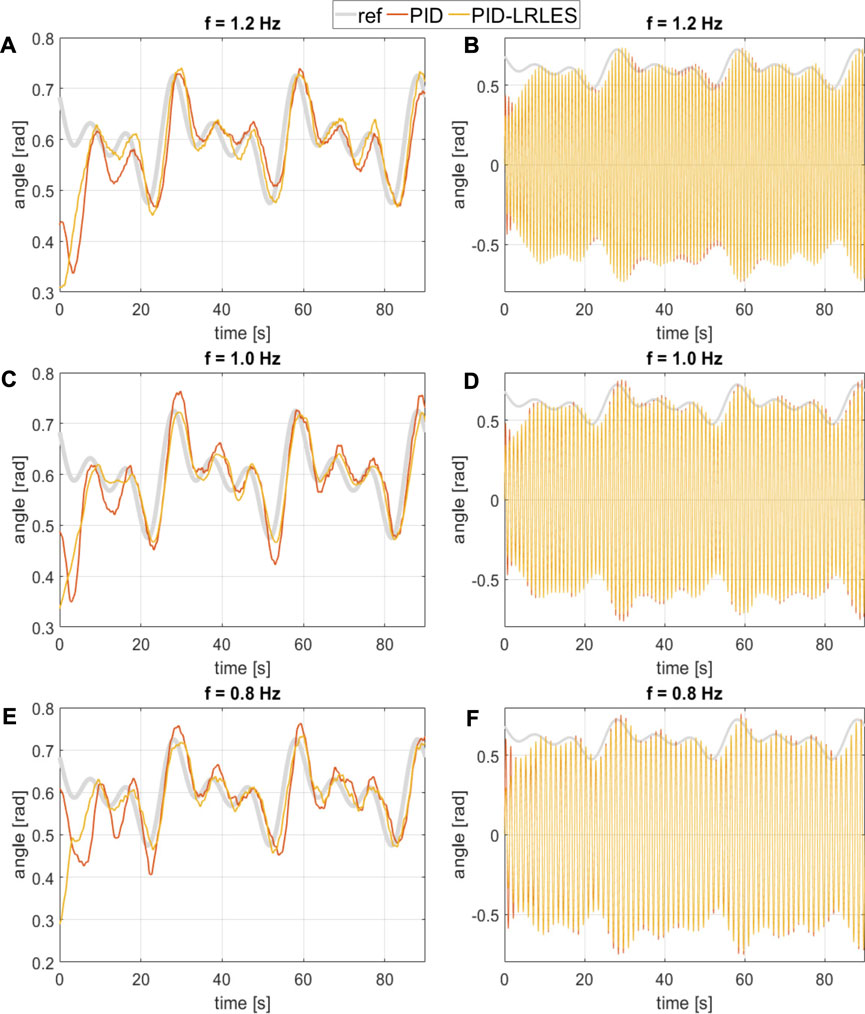
Figure 8. The extract analyzes the tracking accuracy of a soft robotic fish platform, specifically comparing the bending angle (A,C, E) and its envelope (B,D, F) under different control conditions, flapping frequency f=1.2, f=1.0, f=0.8 Hz and a reference signal ref =0.6+0.05 sin (2π t/30)+0.05 sin (2π t/15)+0.05 sin (2π t/10). Both controllers are tuned with a flapping frequency of f = 1.2 Hz ‘ref’ denotes the target amplitude envelope for the tail oscillation. ‘PID’ represents the data measured using the Proportional-Integral-Derivative (PID) controller with gains Kp =3, Ki =0.28, and Kd =0.15. ‘PID-LRLES’ refers to measurements obtained using a separately tuned PID controller augmented with the Linear Repetitive Learning Estimation Scheme (LRLES) method.
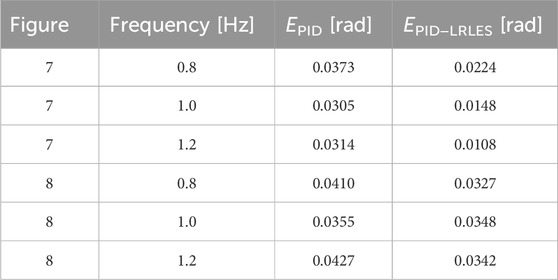
Table 1. Root Mean Square Error (RMSE) over an oscillation period of the reference trajectory (20–50 s) of Figure 7 and (60–90 s) of Figure 8 with different flapping frequencies. RMSEs are respectively EPID for the PID and EPID-LRLES for the separately tuned PID-LRLES controller. Both controllers are tuned with a flapping frequency f = 1.2 Hz.
The high-frequency oscillations in Figure 7 (b-d-f) are at flapping frequency. We attribute this behavior to the abrupt changes in the oscillatory direction that happen when the control system switches the active actuator, causing the 3D-printed support to rattle in its location (see accompanying video). Both controllers proved to be robust to unmodeled disturbance at a price of small oscillations.
4 Discussion and future work
In this study, we have successfully developed and implemented a Proportional-Integral-Derivative with a Linear Repetitive Learning Estimation Scheme (PID-LRLES) controller on a soft robotic fish platform. This novel controller demonstrates a significant improvement in performance over the traditional PID controller in tracking periodic signals. Its success is particularly notable in the context of soft robotic systems, which often contend with uncertain parameters and unmodeled dynamics. This advancement is not just a technical achievement but also a critical step forward in the field of soft robotics, showcasing the potential of advanced control methods in managing complex dynamic systems.
Our work builds upon and extends our previous foundational studies (Jusufi et al., 2017; Lin et al., 2021; Schwab et al., 2021; 2022). While Jusufi et al. focused on open-loop control experiments without feedback on the oscillating tail’s position, and Lin et al. limited their exploration to a PID controller for single step-response tracking, our approach achieves faster and more accurate tracking. This progress is attributed to both the innovative PID-LRLES controller and enhancements in the mechanical structure of the robotic fish. However, the pioneering work by Lin et al. remains a valuable reference, especially in their use of eutectic gallium-indium (eGaIn) stretch sensors for bending angle measurements.
While our controller’s performance in environments with incoming water flow (that is able to change the dynamics of the system by adding an apparent fluid stiffness) remains untested due to unforeseen constraints, we hypothesize that the PID-LRLES controller could effectively estimate and compensate for periodic components of drag variations caused by flow. This capability would mark a significant advancement in robustness compared to classical control methods. Future research will focus on employing resistive soft sensors in place of the capacitive sensors used in this work to test this hypothesis. Resistive sensors are expected to mitigate the electromagnetic disturbances encountered in the flow tank and refine the process of bending angle measurement.
Looking ahead, our aim is to refine current tail design limitations for enhanced bio-mimicry while further developing the soft robotic fish platform, with a specific focus on water pressurization to remove the buoyancy effect and experimental validation in flow tank conditions. Indeed, the next phase of research will involve integrating the flow regime into the control structure of the PID-LRLES, aiming for a more holistic and responsive control system. This approach promises to open new avenues in the design and control of soft robotic systems, contributing to our understanding of bio-mimetic robotics and its application in dynamic aquatic environments. Furthermore, even though the significance of the passive tail, extending from the midpoint to the tail end, is implicitly considered as its movement results from the actuation of the front portion, we also aim at focusing, in future work, on specific fluid motion and criteria analysis–including the Strouhal number (Schwab et al., 2022) that correlates with vortex shedding dynamics–for enhancing the accuracy of fish performance replication. Finally, our study focused on dynamics primarily in forward motion rather than upstream, where extreme disturbances in dynamics might pose challenges beyond the compensation capabilities of any controller type. Regarding the response speed, Figure 6, Figure 7, Figure 8 have shown that the PID-LRLES achieves a more satisfactory convergence to the reference profiles compared to the traditional PID controller (though with significantly larger proportional and derivative gains in Figure 7; Figure 8), indicating its superior performance in terms of faster reaction (besides the steady-state behaviour). The development of an autonomous swimming robot and the redesign for optimal shape and hydrodynamics indeed represent the next steps and challenges for our future work. Finally, it is worth mentioning that PID-LRLES, whose compensation strategy also mimics a learning action that has to face periodic external disturbances, might even be successfully adopted in the case in which periodic waves influence the motion of the fish robot.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author contributions
FS: Conceptualization, Investigation, Supervision, Writing–original draft, Writing–review and editing, Data curation, Formal Analysis, Methodology, Project administration, Software, Validation, Visualization. ME: Writing–review and editing, Formal Analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization. SR: Formal Analysis, Methodology, Writing–review and editing. HS: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Validation, Visualization, Writing–original draft. FA: Data curation, Formal Analysis, Methodology, Software, Validation, Visualization, Writing–review and editing. CM: Writing–review and editing, Formal Analysis, Methodology, Visualization. IL: Resources, Writing–review and editing. CV: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Writing–review and editing. AJ: Visualization, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by fundamental science grants from the Swiss National Science Foundation (to AJ) and the Cyber Valley Max Planck Research Board Fund [CyVy-RF-19-08 to AJ].
Acknowledgments
We thank the Central Service Station for Robotics at the Max Planck Institute for Intelligent Systems for practical support. We thank Bingcheng Wang of Soft Kinetic Group for the kinematics analysis of undulatory body caudal fin swimming. We thank Roger Vonbank of the Laboratory for Multiscale Studies in Building Physics for his support with the experimental setup. Finally, we are indebted to the reviewers for providing insightful comments, which allowed us to definitely improve the quality of our paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akanyeti, O., Thornycroft, P. J., Lauder, G. V., Yanagitsuru, Y. R., Peterson, A. N., and Liao, J. C. (2016). Fish optimize sensing and respiration during undulatory swimming. Nat. Commun. 7, 11044–11048. doi:10.1038/ncomms11044
Appiah, C., Arndt, C., Siemsen, K., Heitmann, A., Staubitz, A., and Selhuber-Unkel, C. (2019). Living materials herald a new era in soft robotics. Adv. Mater. 31, 1807747. doi:10.1002/adma.201807747
Banerjee, H., Kalairaj, M. S., Ren, H., and Jusufi, A. (2021). Strong, ultrastretchable hydrogel-based multilayered soft actuator composites enhancing biologically inspired pumping systems. Adv. Eng. Mater. 25. doi:10.1002/adem.202300405
Barrett, D. S. (1996). Propulsive efficiency of a flexible hull underwater vehicle. Ph.D. thesis. Cambridge: Massachusetts Institute of Technology.
Beal, D. N., Hover, F. S., Triantafyllou, M. S., Liao, J. C., and Lauder, G. V. (2006). Passive propulsion in vortex wakes. J. Fluid Mech. 549, 385. doi:10.1017/s0022112005007925
Block, B., Booth, D., and Carey, F. (1992). Direct measurement of swimming speeds and depth of blue marlin. J. Exp. Biol. 166, 267–284. doi:10.1242/jeb.166.1.267
Chellapurath, M., Khandelwal, P., Rottier, T., Schwab, F., and Jusufi, A. (2022). Morphologically adaptive crash landing on a wall: soft-bodied models of gliding geckos with varying material stiffnesses. Adv. Intell. Syst. 4. doi:10.1002/aisy.202200120
Coyle, S., Majidi, C., LeDuc, P., and Hsia, K. J. (2018). Bio-inspired soft robotics: material selection, actuation, and design. Extreme Mech. Lett. 22, 51–59. doi:10.1016/j.eml.2018.05.003
Crossin, G. T., Hinch, S., Farrell, A., Higgs, D., Lotto, A., Oakes, J., et al. (2004). Energetics and morphology of sockeye salmon: effects of upriver migratory distance and elevation. J. Fish Biol. 65, 788–810. doi:10.1111/j.0022-1112.2004.00486.x
Dickinson, M. H., Farley, C. T., Full, R. J., Koehl, M., Kram, R., and Lehman, S. (2000). How animals move: an integrative view. science 288, 100–106. doi:10.1126/science.288.5463.100
Fan, R., Yu, J., Wang, L., Xie, G., Fang, Y., and Hu, Y. (2005). “Optimized design and implementation of biomimetic robotic dolphin,” in 2005 IEEE International Conference on Robotics and Biomimetics - ROBIO, Hong Kong, China, 05-09 July 2005, 484–489.
Fish, F., Bostic, S., Nicastro, A., and Beneski, J. (2007). Death roll of the alligator: Mechanics of twist feeding in water. J. Exp. Biol. 210, 2811–2818. doi:10.1242/jeb.004267
Hammond, M., Cichella, V., and Lamuta, C. (2023). Bioinspired soft robotics: state of the art, challenges, and future directions. Curr. Robot. Rep. 4, 65–80. doi:10.1007/s43154-023-00102-2
M. A. Hsieh, O. Khatib, and V. Kumar (2016). Hydraulic autonomous soft robotic fish for 3D swimming experimental robotics (Cham: Springer International Publishing).
Ijspeert, A. J. (2020). Amphibious and sprawling locomotion: from biology to robotics and back. Annu. Rev. Control, Robotics, Aut. Syst. 3, 173–193. doi:10.1146/annurev-control-091919-095731
Jayne, B. C., and Lauder, G. V. (1996). New data on axial locomotion in fishes: how speed affects diversity of kinematics and motor patterns. Am. Zool. 36, 642–655. doi:10.1093/icb/36.6.642
Jusufi, A., Vogt, D. M., Wood, R. J., and Lauder, G. (2017). Undulatory swimming performance and body stiffness modulation in a soft robotic fish-inspired physical model. Soft Robot. 4, 202–210. doi:10.1089/soro.2016.0053
Katzschmann, R., DelPreto, J., MacCurdy, R., and Rus, D. (2018). Exploration of underwater life with an acoustically controlled soft robotic fish. Sci. Robot. 3, eaar3449. doi:10.1126/scirobotics.aar3449
Kim, S., Laschi, C., and Trimmer, B. (2013). Soft robotics: a bioinspired evolution in robotics. Trends Biotechnol. 31, 287–294. doi:10.1016/j.tibtech.2013.03.002
Kim, T., Lee, S., Hong, T., Shin, G., Kim, T., and Park, Y.-L. (2020). Heterogeneous sensing in a multifunctional soft sensor for human-robot interfaces. Sci. Robotics 5, eabc6878. doi:10.1126/scirobotics.abc6878
Lauder, G. V., Anderson, E., Tangorra, J., and Madden, P. (2007). Fish biorobotics: kinematics and hydrodynamics of self-propulsion. J. Exp. Biol. 210, 2767–2780. doi:10.1242/jeb.000265
Lauder, G. V., Lim, J., Shelton, R., Witt, C., Anderson, E., and Tangorra, J. L. (2011). Robotic models for studying undulatory locomotion in fishes. Mar. Technol. Soc. J. 45, 41–55. doi:10.4031/mtsj.45.4.8
Liao, J. C., and Akanyeti, O. (2017). Fish swimming in a kármán vortex street: kinematics, sensory biology and energetics. Mar. Technol. Soc. J. 51, 48–55. doi:10.4031/mtsj.51.5.8
Liao, J. C., Beal, D. N., Lauder, G. V., and Triantafyllou, M. S. (2003). The kármán gait: novel body kinematics of rainbow trout swimming in a vortex street. J. Exp. Biol. 206, 1059–1073. doi:10.1242/jeb.00209
Lighthill, S. J. (1975). Mathematical biofluiddynamics. Society for Industrial and Applied Mathematics.
Lin, Y.-H., Siddall, R., Schwab, F., Fukushima, T., Banerjee, H., Baek, Y., et al. (2021). Modeling and control of a soft robotic fish with integrated soft sensing. Adv. Intell. Syst. 5, 2000244. doi:10.1002/aisy.202000244
Low, K. H., and Chong, C. W. (2010). Parametric study of the swimming performance of a fish robot propelled by a flexible caudal fin. Bioinspiration Biomimetics 5, 046002. doi:10.1088/1748-3182/5/4/046002
Low, K. H., Chong, C. W., and Zhou, C. (2010). Performance study of a fish robot propelled by a flexible caudal fin. IEEE Int. Conf. Robotics Automation, 2010, 90–95. doi:10.1109/ROBOT.2010.5509848
Ludeke, T., and Iwasaki, T. (2019). Exploiting natural dynamics for gait generation in undulatory locomotion. Int. J. Control 93, 307–318. doi:10.1080/00207179.2019.1569763
Marchese, A. D., Onal, C., and Rus, D. (2014). Autonomous soft robotic fish capable of escape maneuvers using fluidic elastomer actuators. Soft Robot. 1, 75–87. doi:10.1089/soro.2013.0009
Marino, R., Tomei, P., and Verrelli, C. M. (2012). Learning control for nonlinear systems in output feedback form. Syst. control Lett. 61, 1242–1247. doi:10.1016/j.sysconle.2012.07.011
U. Martinez-Hernandez, V. Vouloutsi, A. Mura, M. Mangan, M. Asada, T. J. Prescottet al. (2019). Heads or tails? Cranio-caudal mass distribution for robust locomotion with biorobotic appendages composed of 3D-printed soft materials (Cham: Springer).
McHenry, M. J., Pell, C. A., and Long, J. H. (1995). Mechanical control of swimming speed: stiffness and axial wave form in undulating fish models. J. Exp. Biol. 198, 2293–2305. doi:10.1242/jeb.198.11.2293
Mosadegh, B., Polygerinos, P., Keplinger, C., Wennstedt, S., Shepherd, R. F., Gupta, U., et al. (2014). Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 24, 2163–2170. doi:10.1002/adfm.201303288
Nguyen, D. Q., and Ho, V. A. (2021). Anguilliform swimming performance of an eel-inspired soft robot. Soft Robot. 9, 425–439. doi:10.1089/soro.2020.0093
Nirody, J. A., Jinn, J., Libby, T., Lee, T. J., Jusufi, A., Hu, D. L., et al. (2018). Geckos race across the water’s surface using multiple mechanisms. Curr. Biol. 28, 4046–4051. doi:10.1016/j.cub.2018.10.064
Rayner, J. M. (1986). Pleuston: animals which move in water and air. Endeavour 10, 58–64. doi:10.1016/0160-9327(86)90131-6
Sachyani Keneth, E., Kamyshny, A., Totaro, M., Beccai, L., and Magdassi, S. (2021). 3d printing materials for soft robotics. Adv. Mater. 33, 2003387. doi:10.1002/adma.202003387
Schwab, F., Lunsford, E. T., Hong, T., Wiesemüller, F., Kovac, M., Park, Y.-L., et al. (2021). Body caudal undulation measured by soft sensors and emulated by soft artificial muscles. Integr. Comp. Biol. 61, 1955–1965. doi:10.1093/icb/icab182
Schwab, F., Wiesemüller, F., Mucignat, C., Park, Y.-L., Lunati, I., Kovac, M., et al. (2022). Undulatory swimming performance explored with a biorobotic fish and measured by soft sensors and particle image velocimetry. Front. Robotics AI 8, 791722. doi:10.3389/frobt.2021.791722
Schwalbe, M., Boden, A., Wise, T., and Tytell, E. (2019). Red muscle activity in bluegill sunfish lepomis macrochirus during forward accelerations. Sci. Rep. 9, 8088. doi:10.1038/s41598-019-44409-7
Shepherd, R. F., Ilievski, F., Choi, W., Morin, S. A., Stokes, A. A., Mazzeo, A. D., et al. (2011). Multigait soft robot. Proc. Natl. Acad. Sci. 108, 20400–20403. doi:10.1073/pnas.1116564108
Shintake, J., Cacucciolo, V., Floreano, D., and Shea, H. (2018). Soft robotic grippers. Adv. Mater. 30, 1707035. doi:10.1002/adma.201707035
Siddall, R., Byrnes, G., Full, R. J., and Jusufi, A. (2021). Tails stabilize landing of gliding geckos crashing head-first into tree trunks. Commun. Biol. 4, 1020. doi:10.1038/s42003-021-02378-6
Struebig, K., Bayat, B., Eckert, P., Looijestijn, A., Lueth, T. C., and Ijspeert, A. J. (2020). Design and development of the efficient anguilliform swimming robot—mar. Bioinspiration Biomimetics 15, 035001. doi:10.1088/1748-3190/ab6be0
Tomei, P., and Verrelli, C. (2015). Linear repetitive learning controls for nonlinear systems by padé approximants. Int. J. Adapt. Control Signal Process. 29, 783–804. doi:10.1002/acs.2507
Verrelli, C. M. (2016). A larger family of nonlinear systems for the repetitive learning control. Automatica 71, 38–43. doi:10.1016/j.automatica.2016.04.021
Verrelli, C. M. (2022). Pi-generalizing saturated repetitive learning control for a class of nonlinear uncertain systems: robustness wrt relative degree zero or one. Syst. Control Lett. 164, 105248. doi:10.1016/j.sysconle.2022.105248
Verrelli, C. M., Pirozzi, S., Tomei, P., and Natale, C. (2015). Linear repetitive learning controls for robotic manipulators by padé approximants. IEEE Trans. Control Syst. Technol. 23, 2063–2070. doi:10.1109/tcst.2015.2396012
Woodward, M., and Sitti, M. (2018). Morphological intelligence counters foot slipping in the desert locust and dynamic robots. Proc. Natl. Acad. Sci. 115, E8358–E8367. doi:10.1073/pnas.1804239115
Wright, B., Vogt, D. M., Wood, R. J., and Jusufi, A. (2019). “Soft sensors for curvature estimation under water in a soft robotic fish,” in 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Korea (South), 14-18 April 2019, 367–371. doi:10.1109/ROBOSOFT.2019.8722806
Xu, J.-X., and Yan, R. (2006). On repetitive learning control for periodic tracking tasks. IEEE Trans. Automatic Control 51, 1842–1848. doi:10.1109/tac.2006.883034
Yang, B., Baines, R., Shah, D., Patiballa, S., Thomas, E., Venkadesan, M., et al. (2021). Reprogrammable soft actuation and shape-shifting via tensile jamming. Sci. Adv. 7, eabh2073. doi:10.1126/sciadv.abh2073
Yun, D., Kim, K., Kim, S., Kyung, J., and Lee, S. (2011). Actuation of a robotic fish caudal fin for low reaction torque. Rev. Sci. Instrum. 82, 075114. doi:10.1063/1.3611002
Yun, D., Kim, K.-S., and Kim, S. (2015). Thrust characteristic of a caudal fin with spanwise variable phase. Ocean. Eng. 104, 344–348. doi:10.1016/j.oceaneng.2015.04.089
Zhao, G., Szymanski, F., and Seyfarth, A. (2020). Bio-inspired neuromuscular reflex based hopping controller for a segmented robotic leg. Bioinspiration Biomimetics 15, 026007. doi:10.1088/1748-3190/ab6ed8
Zhao, J., Monforte, M., Indiveri, G., Bartolozzi, C., and Donati, E. (2023). Learning inverse kinematics using neural computational primitives on neuromorphic hardware. npj Robot. 1 (1), 1. doi:10.1038/s44182-023-00001-w
Keywords: bio-mimicry, soft robotics, repetitive learning, robotic fish, locomotion, swimming, soft sensor, experimental validation
Citation: Schwab F, El Arayshi M, Rezaei S, Sprumont H, Allione F, Mucignat C, Lunati I, Verrelli CM and Jusufi A (2024) Learning control for body caudal undulation with soft sensory feedback. Front. Sens. 5:1367992. doi: 10.3389/fsens.2024.1367992
Received: 09 January 2024; Accepted: 29 March 2024;
Published: 24 April 2024.
Edited by:
Edoardo Milana, University of Freiburg, GermanyReviewed by:
Ahmet Fatih Tabak, Istanbul Commerce University, TürkiyePaolo Roberto Massenio, Politecnico di Bari, Italy
Copyright © 2024 Schwab, El Arayshi, Rezaei, Sprumont, Allione, Mucignat, Lunati, Verrelli and Jusufi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ardian Jusufi, YXJkaWFuLmp1c3VmaUBlbXBhLmNo
 Fabian Schwab
Fabian Schwab Mohamed El Arayshi
Mohamed El Arayshi Seyedreza Rezaei
Seyedreza Rezaei Hadrien Sprumont
Hadrien Sprumont Federico Allione
Federico Allione Claudio Mucignat
Claudio Mucignat Ivan Lunati4
Ivan Lunati4 Cristiano Maria Verrelli
Cristiano Maria Verrelli Ardian Jusufi
Ardian Jusufi