
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Water, 01 October 2024
Sec. Environmental Water Quality
Volume 6 - 2024 | https://doi.org/10.3389/frwa.2024.1456647
The temporal dynamics of solute export from catchments are challenging to quantify and model due to confounding hydrological and biogeochemical processes and sparse measurements. Conventionally, the concentration-discharge relationship (C-Q) and statistical approaches to describe it, such as the Weighted Regressions on Time, Discharge and Seasons (WRTDS), have been widely used. Recently, deep learning (DL) approaches, especially Long-Short-Term-Memory (LSTM) models, have shown predictive capability for discharge, temperature, and dissolved oxygen. However, it is not clear if such advances can be expanded to water quality variables driven by complex subsurface biogeochemical processes. This work evaluates the performance of LSTM and WRTDS for 20 water quality variables across ~500 catchments in the continental US. We find that LSTM does not markedly outperform WRTDS in our dataset, potentially limited by the current measurement capabilities of water quality across CONUS. Both models present similar performance patterns across water quality variables, with the LSTM displaying better performance for nutrients compared to weathering-derived solutes. Additionally, the LSTM does not benefit from flexibility in the inputs. For example, incorporation of climate data that constrains streamflow generation, does not significantly improve the LSTM performance. We also find that data availability is not a straightforward predictor of LSTM model performance, although higher availability tends to stabilize performance. To fully assess the potential of the LSTM model, it may be necessary to use a higher frequency dataset across the CONUS, which does not exist today. To evaluate the dynamics of C-Q patterns relative to model performance, we introduce a “simplicity index” considering both the seasonality in the concentration pattern and the linearity in the C-Q relationship, or the C-Q-t pattern. The simplicity index is strongly correlated with model performance and differentiates the underlying controls on water quality dynamics. Further DL experiments and model-intercomparison highlight the strengths and deficiencies of existing frameworks, pointing to the need for further hydrogeochemical theories that are amenable to complex basins and solutes.
• Two models for water quality prediction were developed and applied to 20 water quality variables across 482 basins.
• Despite the additional inputs provided, a deep learning model could not outperform a traditional statistical model for most variables.
• The simplicity index, a measure of the dependence of concentrations on discharge and season, explains model performances.
Chemical export from catchments provides a comprehensive measure of how water travels through and interacts with the subsurface, is influenced by human activities, and modified within the stream network. However, distinguishing between biogeochemical processes and catchment characteristics, including the role of topography, subsurface structure and composition, stream routing, land use/land cover, and climate as controls on chemical export is complicated by underlying correlations that create non-unique relationships (Anderson et al., 1997; Moatar et al., 2017; Roelandt et al., 2010; Li et al., 2021). As a result, simulating dynamic chemical export requires detailed representation of processes unfolding across a watershed — from how rainfall or snow becomes streamflow, to geochemical reactions happening along the flow paths and in the stream. To date, only a few spatially explicit multi-component reactive transport models have been applied at the catchment scale, and only for small domains and limited reaction networks (Bao et al., 2017; Li et al., 2017). Despite advancements in reactive transport modeling of solute export, direct simulation at scale and across diverse catchments remains an outstanding problem (Maher and Navarre-Sitchler, 2019; Xu et al., 2022).
To diagnose chemical export, relationships between concentration and discharge (C-Q) are used to infer the underlying processes (Godsey et al., 2009; Johnson et al., 1969; Langbein and Dawdy, 1964; Thompson et al., 2011; Torres and Baronas, 2021). In general, the slope of the C-Q relationship indicates the extent to which concentration is a function of discharge, based on the premise that discharge is itself a variable that integrates across multiple auxiliary characteristics (e.g., climate, subsurface heterogeneity, land use, etc.). Myriad different approaches have been used to examine C-Q relationships, including power law models (e.g., Godsey et al., 2009), a piecewise approach based on segmentation of the hydrograph (e.g., Meybeck and Moatar, 2012), and a hyperbolic approach based on concentration thresholds (e.g., Maher, 2011; Maher and Chamberlain, 2014; Ibarra et al., 2016; Wymore et al., 2017). As an extension of the approaches above, statistical methods, such as the WRTDS (Weighted Regressions on Time, Discharge and Season), provide accurate regressions of solute concentrations based on C-Q relationships (Hirsch et al., 2010; Hirsch, 2014). However, a limitation to all these methods is that they cannot capture the full dynamics of solute behavior, particularly for parameters with substantial coefficients of variation (Godsey et al., 2009; Hirsch et al., 2010; Musolff et al., 2015; Knapp et al., 2020; Ebeling et al., 2021). Currently, the reasons for high variance in C-Q relationships remain poorly understood, limiting the widespread use of data-driven models. Furthermore, auxiliary characteristics whose temporospatial heterogeneity are difficult to quantify, such as human impacts from land use or water management, are difficult to integrate into data-driven models.
Diagnosing the auxiliary characteristics that drive chemical export, in addition to discharge, would thus improve our ability to build parsimonious yet effective models of solute export and identify underlying processes that control water quality. The development of both process models and data products to support large-scale water quality models would benefit from increased knowledge of how watershed auxiliary characteristics interact with the hydrologic, biogeochemical and anthropogenic processes that collectively drive water quality dynamics. For example, conceptual approaches, including INCA (Wade et al., 2002), SimplyP (Jackson-Blake et al., 2017), and HYPE (Lindström et al., 2010) simplify the catchment system into lumped parameters and fixed spatial domains. These models also rely extensively on parameter calibration, which limits their use across multiple solutes and a broad geographic distribution of basins. Although land use, especially agricultural practices, are known to partly control export of P and N species (Basu et al., 2010; Thompson et al., 2011; Ebeling et al., 2021), for other elements the link to auxiliary characteristics are not established but may contribute to the high variance observed in C-Q relationships. Establishing connections between watershed characteristics and solute dynamics may guide development and application of existing water quality models to a wider range of water quality variables.
An alternative approach to modeling water quality may leverage recent advances in hydrological modeling using deep learning (DL) approaches. In particular, long-short-term memory (LSTM) is shown to be a powerful tool in modeling watershed-scale streamflow (Kratzert et al., 2018; Kratzert et al., 2019a; Feng et al., 2020; Nearing et al., 2021). These results suggest that LSTM models are capable of linking rainfall or snowfall to streamflow generation, which is also a fundamental control on solute export. Hence, as recently summarized by Varadharajan et al. (2022), DL approaches like LSTM are expected to advance our capability in modeling water quality, not only by connecting streamflow and solute generating processes, but also by identifying auxiliary characteristics. Indeed, recent work demonstrates the advantage of LSTM for modeling stream water temperature (Rahmani et al., 2021) and dissolved oxygen (Zhi et al., 2021) over hundreds of basins. However, both dissolved oxygen and temperature in streams are strongly linked to local temperature (Edinger et al., 1968), whereas other solutes are more strongly linked to subsurface processes, from weathering (e.g., Ca, Mg, Na, K, Gaillardet et al., 1999) to biogeochemical reactions (e.g., N, P, Basu et al., 2010). For those solutes, applications of LSTM or other DL approaches are limited to sites along a river (Liu et al., 2019; Baek et al., 2020; Yan et al., 2020), or single variables across nearby basins (Jung et al., 2020; Saha et al., 2023). Although these authors highlight the promising performance of DL models, the potential to capture complex and spatially heterogeneous linkages has not been evaluated. These linkages include both intra-element dependencies on catchment attributes, such as slope, lithology, as well as element-element linkages that constrain the system of solutes. The DL models also have not been evaluated against commonly used data-driven approaches across variable environmental conditions. Given the difficulty of measuring water quality parameters, the potential for the LSTM to draw connections across a range of solutes would be advantageous. On the other hand, data density is low for most parameters, potentially limiting the LSTM capabilities. Although neither model explicitly models processes, model intercomparisons between LSTM and WRTDS may further indicate additional controls on solute generation.
Here, we develop and evaluate two promising models for water quality modeling and prediction: (1) an LSTM that integrates auxiliary characteristics into water quality prediction, and (2) a WRTDS model that uses time, discharge and seasonality as additional weighting functions, but does not allow for the model to build relationships to auxiliary catchment characteristics. Hence, the LSTM model is trained to retain knowledge of the catchment attributes while also learning the signals inherent in the temporal variations in climate forcings, discharge and 20 analytes. The data used to test the models comprises data for ~500 catchments across the continental U.S. (CONUS), covering a broad range of climatic and geological provinces. A series of experiments is used to further refine the application of the LSTM to continental-scale data sources. The objectives are to (1) evaluate the capability of the LSTM relative to the conventional WRTDS model across diverse environments, (2) determine the statistical indicators that explain both the similarity and differences between modeled analyte behaviors; and (3) provide guidance for future applications of DL methods based on the model performance.
We trained LSTM and WRTDS models to predict 20 stream water quality analytes on a daily basis using 36 years of observations on 482 sites across the CONUS with relatively complete water quality records (see 2.1.1). The input data are aggregated according to the contributing catchment of the water quality sites, including the time series for runoff, atmospheric forcing, vegetation indexes and rainfall chemistry, as well as static geographic attributes of those catchments, as described below.
Our training targets, daily water quality measurements, are extracted from the U.S. Geological Survey’s (USGS) National Water Information System (NWIS) database. To provide a comprehensive overview of water quality, we selected 20 analytes which are important to understanding biogeochemical processes and are regularly measured by USGS (Table 1). The selected water quality analytes are associated with different underlying controls and hence reflect a wide variety of dynamics. We use the following groupings (Moatar et al., 2017):
(1) stream water quality: temperature (Temp), dissolved oxygen (DO),
(2) weathering processes: silica (SiO2), sodium (Na), calcium (Ca), and magnesium (Mg),
(3) nutrients derived from agricultural and urban land use or nutrient utilization, such as nitrate (NO3), unfiltered total nitrogen (TN), unfiltered organic nitrogen (N-org), orthophosphate (PO), unfiltered total phosphorous (TP), non-particulate organic carbon (NPOC), and
(4) mixed behavior, or analytes that are influenced by multiple factors, including (1), (2) and (3): potassium (K+), chloride (Cl−), sulfate (SO42−), suspended sediment concentration (SSC) and conductivity (Cond). Stream pH and total dissolved CO2 are also included here.
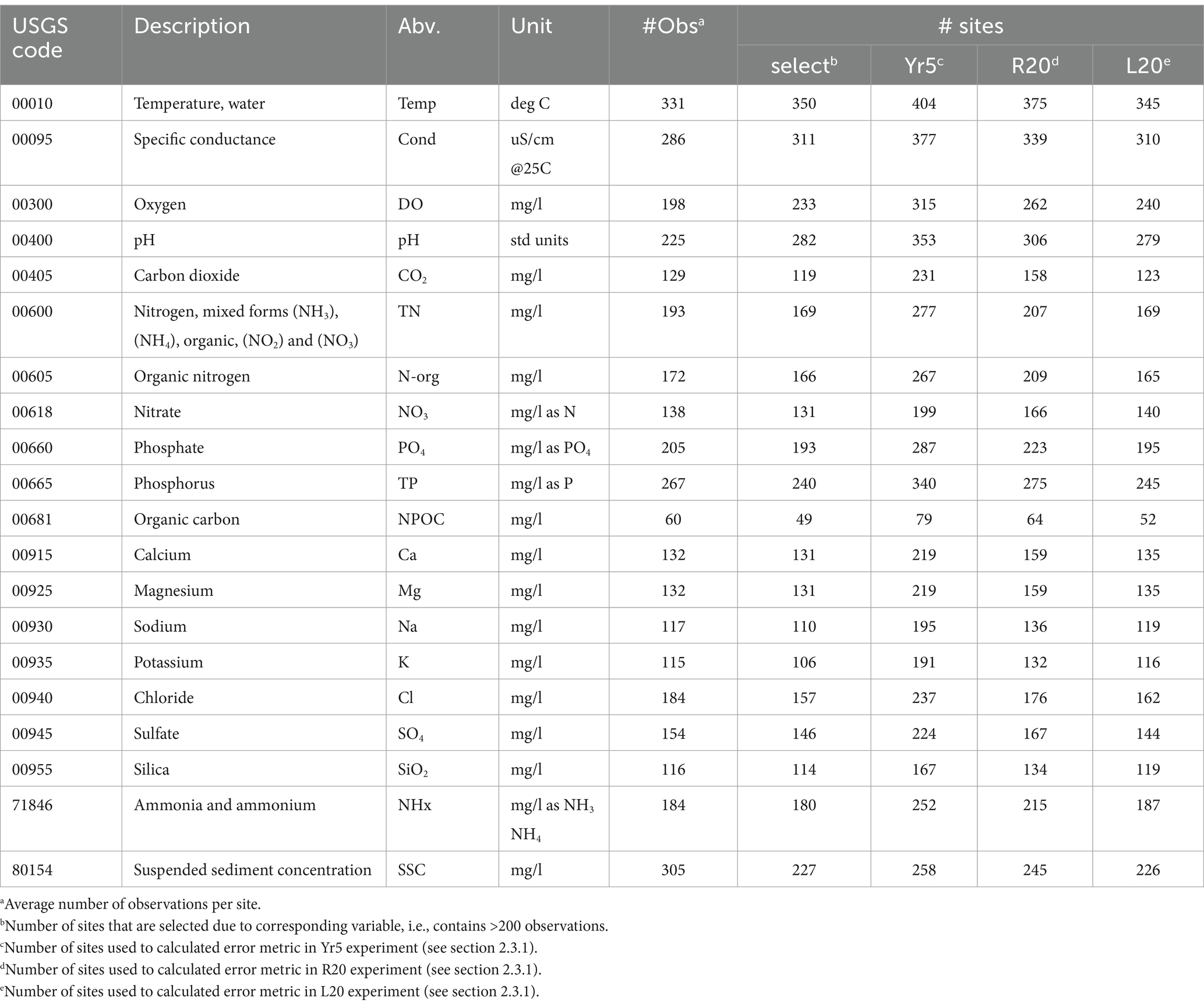
Table 1. selected water quality variables, average number of observations from 1982 to 2018 and count of sites that meet screening standard.
As a side note, other variables that are of wide interest, e.g., alkalinity, dissolved inorganic carbon (DIC) and HCO3, are not included in this work as their measurements were not adequately represented in the NWIS database. Additionally, we removed flagged measurements, including those below the detection limit. Measurements are treated as daily water quality data in this work without considering the diurnal variation, as the measuring time is generally consistent.
We focused on the water quality dynamics spanning a 36-year period, from 1982/01/01 to 2018/12/31, during which the inputs are relatively complete (see the section 2.1.2). We selected 482 basins following a sequential screening method: (1) the basin is included in GAGES-II database (Falcone, 2011), which is used to extract basin boundaries; (2) the site contains more than 200 dates where at least one of the selected variables is measured; (3) from basins identified in (2), we then removed the sites that only measured water temperature and specific conductance. Specifically, we found that more than ~1,000 sites meet the first two rules, but ~500 only measured water temperature and specific conductance. After the screening process, 482 basins were selected for model training and evaluation.
We chose input predictors that could potentially affect chemical export at watershed scales, including streamflow, climatic forcing, vegetation, rainfall chemistry, basin geographic structures, and land use descriptors. We then preprocessed the data to provide informative predictors on basin scale. The time series are extracted and preprocessed from four data sources:
(1) Streamflow for each basin (labelled as “Q”), which is the daily mean discharge measured by USGS (code 00060 in cubic feet per second). For the LSTM we also provided the daily runoff, which is the streamflow divided by basin area in [m/d]. Missing streamflow is filled by an invalid label (−1).
(2) Daily climate forcing data (labelled as “F”) was extracted from the gridMET product (Abatzoglou, 2013), which contains precipitation, temperature, humidity, radiation, and reference evapotranspiration, on a daily basis from 1982/01/01 to 2018/12/31, with a spatial resolution of 1~/24 degree. For each targeted USGS site, we extracted the gridMET maps clipped by the drainage boundaries from GAGES-II database, and linearly aggregated the data for each date.
(3) Daily remote sensing vegetation indexes (labelled as “V”) including leaf area index (LAI), net primary production (NPP) and fraction of absorbed photosynthetically active radiation (FAPAR) from Global Land Surface Satellite (GLASS) dataset (Liang et al., 2013). GLASS products provide 8-day estimates with 0.05° spatial resolution. These data were temporally interpolated to daily time series using cubic splines. Also, as done for climatic forcings described in (2), the vegetation indexes are spatially aggregated by basin boundary. The raw data of (2) and (3) are spatially distributed, and we aggregated them according to watershed boundaries, such that the spatial gradients within the basins are lost, particularly for large basins. In addition, any errors in the basin boundary (e.g., inter-basin transfer or errors in watershed delineation) will be inherited by those spatially aggregated inputs. This preprocessing is similar to that used for CAMELS (Newman et al., 2015), which is widely used for LSTM experiments in predicting hydrological variables (see, e.g., Kratzert et al., 2018; Zhi et al., 2019). Although CAMELS contains ~600 basins, most of them do not record water quality variables.
(4) Chemical composition of precipitation (labelled as “P”) was extracted from the National Trends Network (NTN), which contains the average wet concentration of Ca, Mg, Na, K, SO4, NO3, Cl, NH4 in [mg/L], and pH, at approximately weekly intervals. Estimating the rainfall concentrations at basin scale is challenging due to the quality of NTN data – there are <200 NTN stations across CONUS, and most are characterized by substantial and irregular gaps in the dates. In addition, those NTN stations started to operate in different decades, and their weekly measurements respond to different weekdays. Hence, we used a new strategy following two steps: (1) for each NTN site, we downscale the weekly data to daily by assigning the weekly average value to each day and also record the number of days from the starting day of this week as an additional input; (2) for each basin at each date, we used the measurement from the nearest operating NTN site as input. We also record the distance between the basin center and corresponding NTN site as additional input predictors. As a result, each basin is assigned 11 time series from the proximal NTN site with available data for that time period – concentrations for nine variables, plus two additional time series of observation date and distance of site. Ultimately, at each date we only provide the nearest measurement rather than multiple of them, as we found that the precipitation chemical data is not of significant importance for most basins (see section 4.4).
The rationale for simplifying the precipitation inputs is to provide the LSTM model the most comprehensive inputs and then train it to utilize that information automatically given the spatial and temporal averaging described above. Previous studies have highlighted the capability of LSTM-based models in spatial–temporal interpolation, especially for air quality data (Ma et al., 2019; Le et al., 2020). Hence, we assume that the LSTM model is capable of aggregating measurements from proximal stations into basin averages if given the distance.
Other than time series inputs, we selected 17 static geographic attributes from GAGES-II database that may impact weathering and biogeochemical processes. Those variables describe the watershed-aggregated geological and hydrological structures, land use, ecological classes, soil properties etc., as listed in Supplementary Table S1.
LSTM is a widely used model in the family of Recurrent Neural Network (RNN) models, which makes use of sequential information to predict target time series. The basic RNN is not capable of appreciating long-term dependencies as the network gradient would decrease exponentially through time steps, which is also known as the vanishing gradient issue. LSTM introduces a memory mechanism, where “memory states” units and “gates” decide when and what to remember or forget (Hochreiter and Schmidhuber, 1997).
In this work we used the LSTM model implemented by pyTorch (Paszke et al., 2019) library, version 1.8.0. The model is of two LSTM layers, with 256 hidden size and 0.5 dropout rate. The sequence length is 365 days and minibatch size is 500. The model is trained for 500 epochs, in which the chance that each observation date is included during one epoch is greater than 99%. We have tested different hyperparameters, including hidden size, sequence length and training epochs (part of the results are presented in Supplementary Figure S1), and the model with selected hyperparameters presents decent performance. Models trained with longer sequence length or hidden size may report slightly higher testing correlation for some water quality variables, yet lower for others, resulting in a similar general performance pattern. The model was optimized using ADADELTA (Zeiler, 2012) which adaptively adjusts the learning rate from 0.01 during the training. The loss function is defined as root-mean-square error (RMSE).
Weighted Regressions on Time, Discharge, and Season (WRTDS) model (Hirsch et al., 2010) has been widely used as an interpolation approach for water quality dynamics (e.g., Zhang, 2018; Stackpoole et al., 2019; Newcomer et al., 2021). Previous studies have shown WRTDS to provide among the most accurate estimates compared to other common methods (Hirsch, 2014; Park et al., 2021).
The WRTDS estimates concentrations by weighted fitting of the following equation:
where C is solute concentrations, Q is streamflow, and T is the time as decimal year. Each of the terms in Equation (1) describes the linear C-Q relationship, seasonality, and long-term trend correspondingly. This equation is fitted by weighted least squares (WLS), and the weights are defined as differences between observation and target date for streamflow, seasonality and time. For detailed steps, please refer to tS1 in Supporting Information or Hirsch et al. (2010). Noting that weights are assigned to each input date based on the target date, hence the regressed model values (i.e., ) for each target date are different. We reconstructed the algorithm in python using the same hyper parameters following EGRET (Hirsch and Cicco, 2015), which is the R-package used by almost all WRTDS related applications (Hirsch et al., 2010). Here we focus on predictive capability over relatively long periods of missing data (see Section 2.3.1). Therefore, we did not assimilate observations close to the testing date to further improve performance, as done in Zhang and Hirsch (2019) and Park et al. (2021) for WRTDS, or in Fang and Shen (2020) and Feng et al. (2020) for LSTM. Additionally, such assimilation frameworks would be problematic in predicting water quality at CONUS scale due to the significant and irregular temporal gaps between water quality observations.
The data set considered here includes water quality, streamflow and climate forcing data for 482 basins from 1982/01/01 to 2018/01/01. The models were trained on 4 out of every 5 years and tested on the remaining years, i.e., we masked out observations for 1985, 1990, 1995, 2000, 2005, 2010 and 2015 and used these as the testing data. We did not include a validation set considering the low frequency of target samples.
We focused on above-mentioned training strategy (referred as “Yr5”) for two reasons: (1) most water quality sites across CONUS contain measurement gaps extending up to several years, and this model can be used to fill those gaps; and (2) the testing dates are orderly ranked, which makes the testing time series easier to decipher. In addition, we also explored two conventional experiments: “R20,” trained on random 80% of the dates with observations; and “L20,” trained on first 80% of observation dates for each site. We found that those three experiments result in similar patterns of model performance, while the model performance for Yr5 is generally between R20 and L20. The design and result from R20 and L20 experiment are detailed in Supplementary Text S1 and Supplementary Figure S2.
Model performance is evaluated by temporal generalization experiments, i.e., the error metrics between observations and predictions on testing dates. To evaluate individual model performance for different water quality variables, we report the Pearson correlation coefficient (R). The R values are calculated for each variable on each site separately. The R values for LSTM and WRTDS are referred to as and , correspondingly. As R values only account for model performance with respect to temporal variance, we also report the Kling-Gupta efficiency (KGE) scores as:
where R is the Pearson correlation coefficient above, β is the bias term, or the ratio between , and α is the variation error defined as the ratio between the standard deviations of prediction and observation, i.e., std(P)/std(O).
We choose R and KGE (Equation (2)) as the error metrics because the magnitude of the differences in water quality values across individual variables, as well as across basins for the same variable, is substantial. Statistics affected by the value scale, e.g., root-mean-square error (RMSE) or bias, cannot be used to compare the model performance between variables, and will neglect basins with relatively small concentrations. In addition, as observed concentrations are not normally distributed, the Nash–Sutcliffe coefficient (NSE), as well as the β term in KGE, are also problematic. For instance, when dealing with numerous measurements at or near the lower measuring limit, NSE and β lose their interpretability. However, we also present our model results for long-term bias and the above-mentioned alternative error metrics in Supplementary Figures S4–S6 for comparison.
To compare performance differences between the LSTM and WRTDS, we report the L2 norm of R and L1 norm of KGE as:
The signed difference, rather than a ratio, is used in Equation (3) to avoid assigning a specific model to the denominator and to enable straightforward linear comparisons. The L2 norm of R indicates the models’ varying abilities to capture temporal variance. While the difference in KGE lacks a specific interpretative meaning, L1 norm was chosen for its simplicity and to minimize confusion. We further use the Wilcoxon signed-rank test to examine if the performance difference is significant, as this work explores whether one model outperforms another on each basin, rather than the average performance.
In addition, to obtain robust error metrics, we need to guarantee that the metrics are calculated from sites that contain adequate training and testing samples for corresponding water quality variables. Although all selected sites contain more than 200 observation dates (section 2.1.1), counts of samples of each water quality variable could be much smaller than 200. Here when calculating the error metrices, we only included sites with at least 80 training samples and 20 testing samples. Also, as the WRTDS model requires streamflow observations as input, water quality measurements without same-day streamflow observation are also excluded during model evaluation to guarantee a fair comparison.
To train LSTM efficiently, we need to normalize data of different ranges of magnitudes into a balanced scale. In comparison, it is not necessary to normalize the data for WRTDS. Based on the distribution of data, we chose min-max or log-min-max normalization approaches, which will linearly convert data to roughly [−1,1] based on their 10 and 90% percentiles:
where refers to a variable and is the normalized value that is used to train LSTM models, and refer to the function for finding the 10th and 90th percentile. The min-max strategy of Equations (4) and (5) is more stable than standardization when data density is low. The choice of log preprocess was decided by the histograms of data variables. Most water quality and rainfall chemistry variables (except for Temp, pH and DO), precipitation, and runoff are approximately log-normally distributed and are normalized by log min-max approach. Other variables are normalized using min-max approach.
In contrast, WRTDS does not require the above-mentioned normalization steps. During the weight calculation of WRTDS (detailed in section 2.2.2), the parameters that are assigned to each predictor resolve the magnitude difference so the weighted regression will not be affected by normalization of data.
In comparison to the WRTDS approach, we trained a single LSTM model to simulate 20 water quality variables simultaneously, rather than training independent models for each. There are two reasons to choose this pooling strategy: (1) the model could discover the hidden relationships among variables, particularly for strongly correlated measurements of nitrogen and phosphorous species. Although inter-species correlation may also introduce potential bias to the model, our experiments suggest that the multiple-target LSTM is better able to predict selected variables compared to independent models (see Supplementary Figure S3); and (2) The pooling strategy is much more computationally efficient. As the computational cost to train an LSTM with multiple targets is of the same magnitude as the single ones, the pooling strategy will reduce the computation time roughly by 20 times for 20 target variables.
To explore the differences in model performance between basins and between variables, we develop an additional set of indexes that characterize the dominant signals associated with concentrations. Concentration-discharge dynamics are extremely complex, with many different patterns noted (e.g., Maher, 2011; Moatar et al., 2017; Musolff et al., 2015; Thompson et al., 2011). Accordingly, numerous methods have been developed to characterize C-Q relationships including the exponent, b, of the power law describing the relationship between discharge and concentration (e.g., Godsey et al., 2009), the ratio of coefficients of variation for concentration and discharge (CVC/CVQ) (Thompson et al., 2011), thresholds in C-Q slopes (Moatar et al., 2017) and combinations of the above (Musolff et al., 2015). Although some studies have binned the data according to characteristic intervals (Fazekas et al., 2021), in general these methods do not capture the temporal patterns embedded in C-Q relationships, which is important for evaluating model approaches (Kirchner and Neal, 2013). To provide a metric for model intercomparison, we introduce a simplicity index (referred as simplicity in the following), to quantify the extent to which water quality signals can be explained by a linear C-Q relationship and annual cycle. The simplicity index is computed from a least square linear regression for each water quality time series using (1) streamflow (Q), (2) sine and cosine day of year as predictor:
where C is solute concentrations, Q is streamflow, and t is the time as decimal year. The coefficient of determination (R2) from Equation (6) is reported as the simplicity index. Similarly, we also report the R2 using only streamflow, or sine and cosine of date separately, and refer them as linearity and seasonality, respectively, as per the following two equations:
Linearity from Equation (7) is equivalent to the coefficient of determination of Q to concentrations, and seasonality from Equation (8) is equivalent to the signal power of the one-year frequency, which is found to be the dominating frequency for water quality dynamics (Kirchner and Neal, 2013).
By combining linearity and seasonality, the simplicity index describes the proportion of variance of a water quality dynamic that can be explained by the linear C-Q relationship and annual cycle, i.e., C-Q-t. For example, high simplicity could be characterized by a strongly seasonal and linear C-Q relationship (Figure 1A), low linearity but high seasonality (Figure 1B) and high linearity but low seasonality (Figure 1C). Thus, water quality constituents that show a general lack of structure with respect to discharge or time of year typically have high ratio between the coefficient of variation of C over Q (or CVC/CVQ, following Thompson et al., 2011), resulting in an inverse correlation between simplicity and CVC/CVQ. We also present the map of simplicity, linearity and seasonality of each water quality variable across selected sites in Supplementary Figures S8–S10.
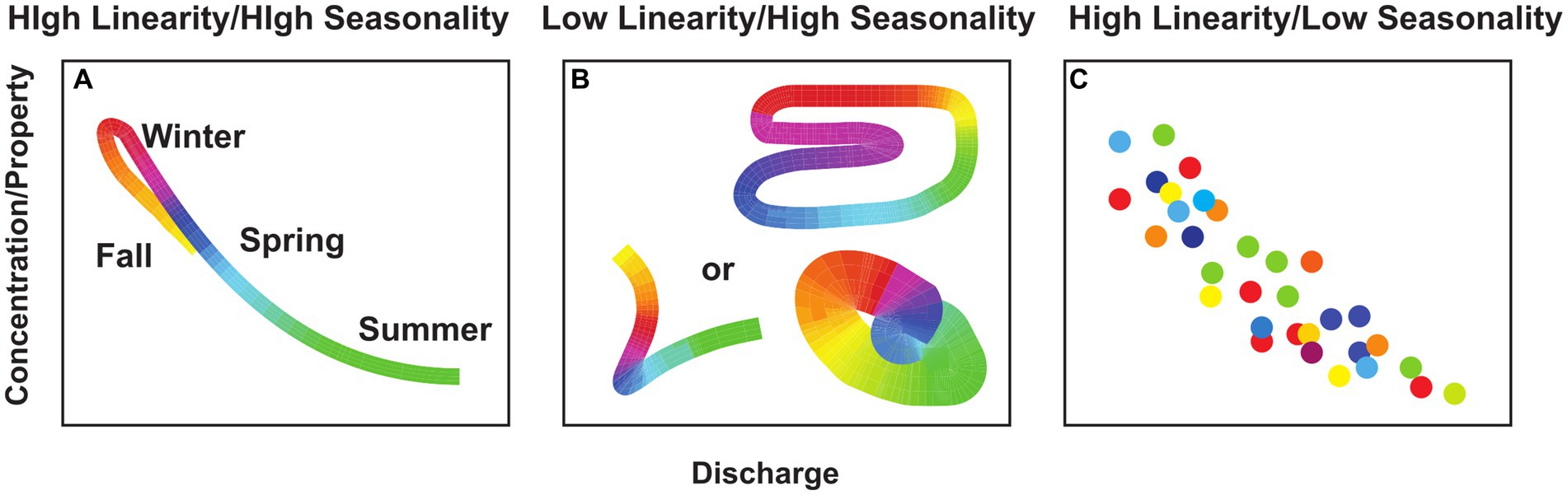
Figure 1. Examples of variations in a concentration or property (e.g., temperature) as a function of discharge corresponding to different combinations that result in high simplicity. The color scale is indicated in (A) with red corresponding to winter months, spring as blue, summer as green and fall as orange and the width of the lines approximates the scatter observed in individual measurements. (A) High simplicity case of a strongly linear and seasonal C-Q pattern, (B) examples of different characteristic patterns that result in low linearity but strong seasonality, and (C) high linearity but low seasonality. All of these patterns result in high to moderate simplicity.
As noted above (section 2.3.3) the underlying distributions of water quality analytes are variable and thus various alternative indices were considered. Here, we do not log-transform any variables based on both the underlying distributions and to maintain consistency across variables but note that in certain circumstances log transformation of C and inclusion of an additional time-dependency term may be warranted. For instance, a simplicity index defined using log-transformed C rather than C increases the correlation with model performance for nutrient variables, but weakens the correlation with model performance for other variables. Also, a simplicity index that includes a time term to capture long-term trends provides more power in estimating model performance. However, the contribution to simplicity from such long-term predictors is minor compared to linearity and seasonality, and introduces an additional analysis dimension. For this work, we adhere to the simplest form of the simplicity index. In practice, especially when focusing on a smaller subset of C variables and catchments, alternative simplicity index should be considered based on the underlying distribution and long-term trend of C.
The performances of the LSTM and WRTDS are highly correlated across water quality variables (Yr5 experiment in Figure 2, R20 and L20 in Supplementary Figure S2) indicating an analyte that is well predicted by LSTM will also be similarly predicted by WRTDS, and vice versa. In general, model performances are better for variables that tend to be dominated by in-stream processing (Temp, DO) and weathering processes (e.g., Ca, Mg, Na, and SiO2). On the other hand, analytes that are affected by agriculture, nutrient utilization, or municipal wastewater, such as TN, TP, PO4, NO3, are challenging for both models. By comparison with WRTDS, LSTM performance is on par or worse than WRTDS for weathering solutes but is generally better for biogeochemically cycled species. Out of 20 variables, significant differences are observed in nine variables for R, and eight variables for KGE, based on a p-value below 0.01 in the Wilcoxon test. Those two numbers rise to 13 given p < 0.05 (see Supplementary Table S2 for details). In general, it is not apparent that one model demonstrably outperforms the other, considering all the selected variables.
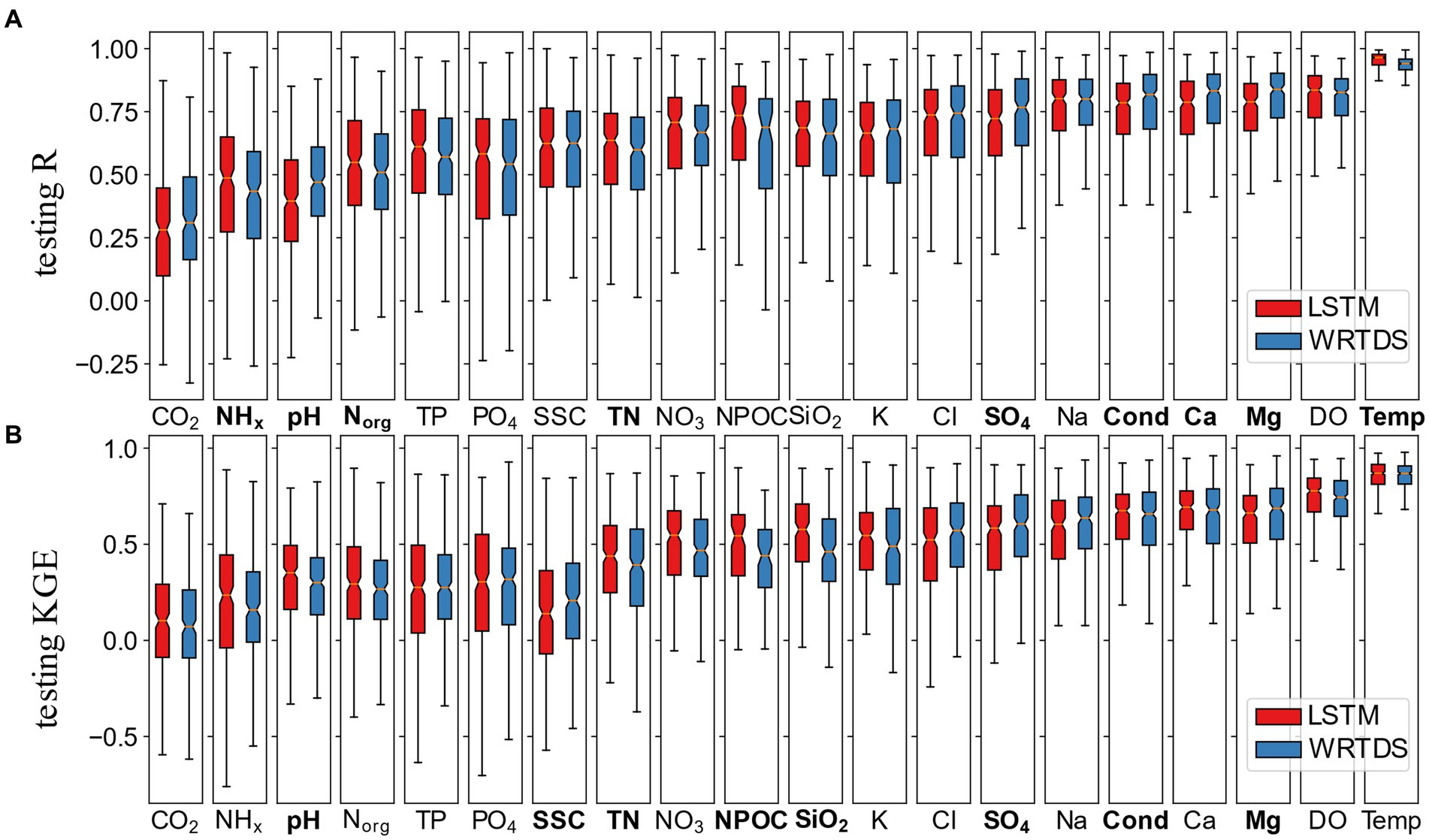
Figure 2. Testing R (A) and KGE (B) of LSTM and WRTDS model for 20 selected water quality variables. Ordered by median simplicity index. Variables with significant performance difference (p < 0.01) between LSTM and WRTDS are bolded.
The simplicity indices (see section 2.4) manifest a clear and interesting pattern among the models (Figure 3). In general, the simplicity index increases from nutrient variables to weathering variables to those dominated by in-stream processes. This trend is reflected in the performances of both LSTM and WRTDS, which increase with simplicity for all variables (Figures 2, 3). Across the range of variables, the correlation between the median simplicity and the respective performance metrics (R, KGE) are notable, with values of 0.88 and 0.98 for LSTM, and 0.90 and 0.95 for KGE with respect to WRTDS. Consequently, these findings suggest that simplicity can serve as a reference index to assess the relative difficulty level of modeling different variables.
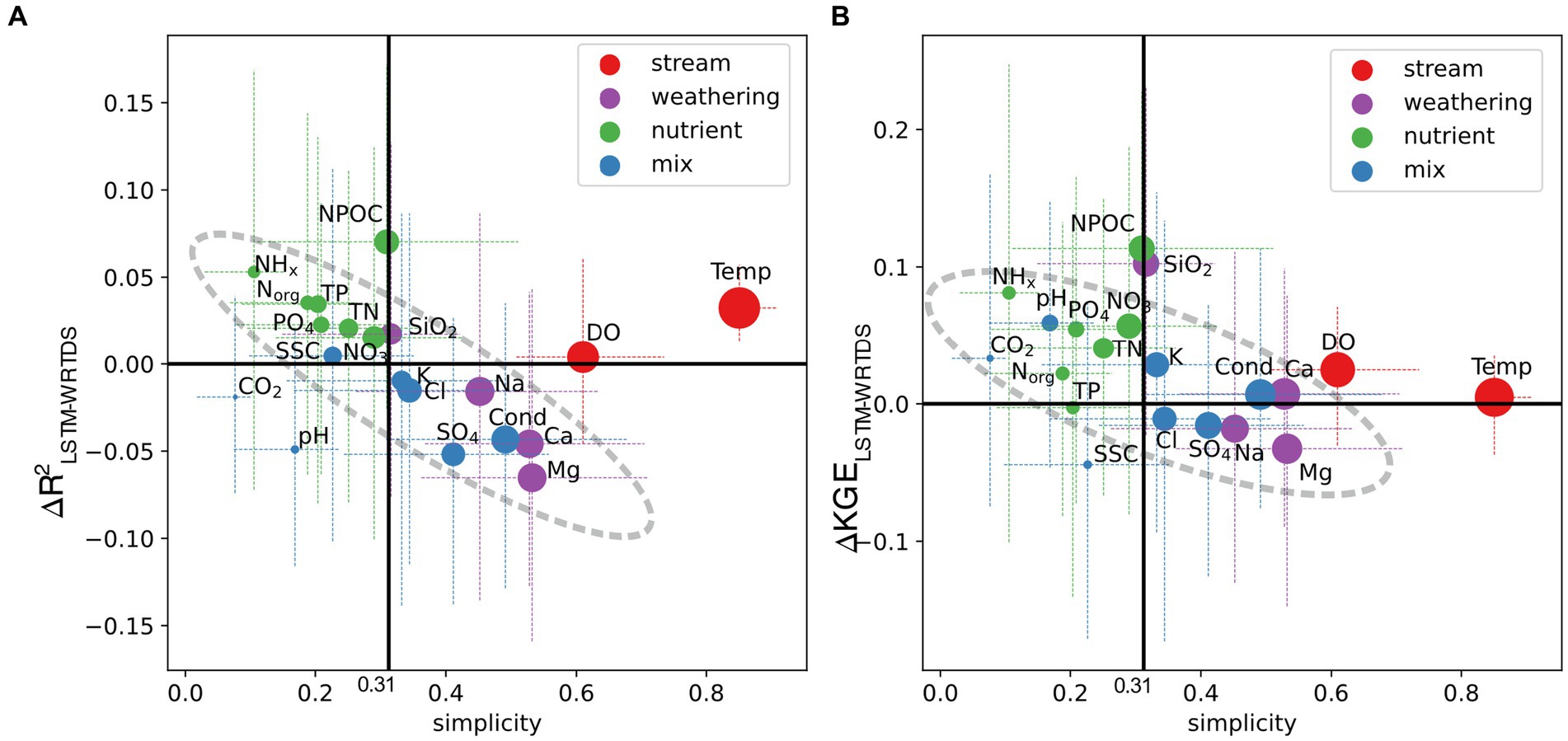
Figure 3. Comparison between simplicity and ΔR2LSTM-WRTDS (A) and ΔKGELSTM-WRTDS (B) for each element. The locations of bubbles represent the mean of corresponding data, and the line segments are from the 25 to 75%. The bubble size is proportional to average LSTM testing R (A) and KGE (B) of each element. The line at simplicity = 0.31 is the median simplicity of 20 variables.
Concurrently, the advantage of LSTM over WRTDS generally diminishes as the simplicity of variables increases (Figure 3). This general trend exhibits strong consistency across most variables (highlighted in Figure 3), with correlation of 0.88 for ∆R2LSTM-WRTDS. In the case of ∆KGELSTM-WRTDS, this trend is less pronounced with a correlation of 0.71 and appears to reveal two distinct groups of variables exhibiting parallel trends. Notably, there are more variables with a positive ∆KGELSTM-WRTDS compared to ∆R2LSTM-WRTDS, highlighting LSTM’s advantage in capturing long-term variance and mean. Nevertheless, there are exceptions to this overarching trend, including DO, Temp, NPOC, as well as CO2 and pH for R, and SiO2 and SSC for KGE. Noting that DO and Temp, CO2 and pH form pairs of variables with strong interconnections. For DO, Temp, NPOC and SiO2, LSTM presents an exceptionally strong performance relative to the general trend. However, LSTM fails to capture the dynamic variance of CO2 and pH and suffers from significant bias in SSC prediction (Supplementary Figure S4). These outcomes highlight the use of simplicity index not only as an initial estimate of model performance but also as a guide in selecting the appropriate modeling approach. LSTM, a relatively complex model, may overfit weathering variables that show a simple dilution pattern (as detailed in 3.3) but can identify hidden connections between nutrient dynamics and additional input features (as detailed in Section 3.4).
Below, we present the basin-level results for each group of analytes as illustrated in Figures 2, 3. To examine model behaviors, we will present and discuss time series of typical sites where (1) both LSTM and WRTDS perform well; (2) LSTM outperforms WRTDS; (3) WRTDS outperforms LSTM. We only selected sites with median data availability to rule out the effects of data density (which will be discussed in section 4.2). See Supplementary Figure S7 for the detailed selection procedure.
Water temperature (Temp) and DO, which are predominantly associated with in-stream processes, correspond to the strongest model performance for both LSTM and WRTDS. Across individual basins, Temp and DO are strongly dominated by seasonal cycles: the seasonality is over 0.8 for 80% of basins for Temp, and over 0.5 for 75% of basins for DO (Figures 4A, 5A). When the seasonality is strong, both models show promise in predicting the Temp and DO (Figures 4A, 5A).
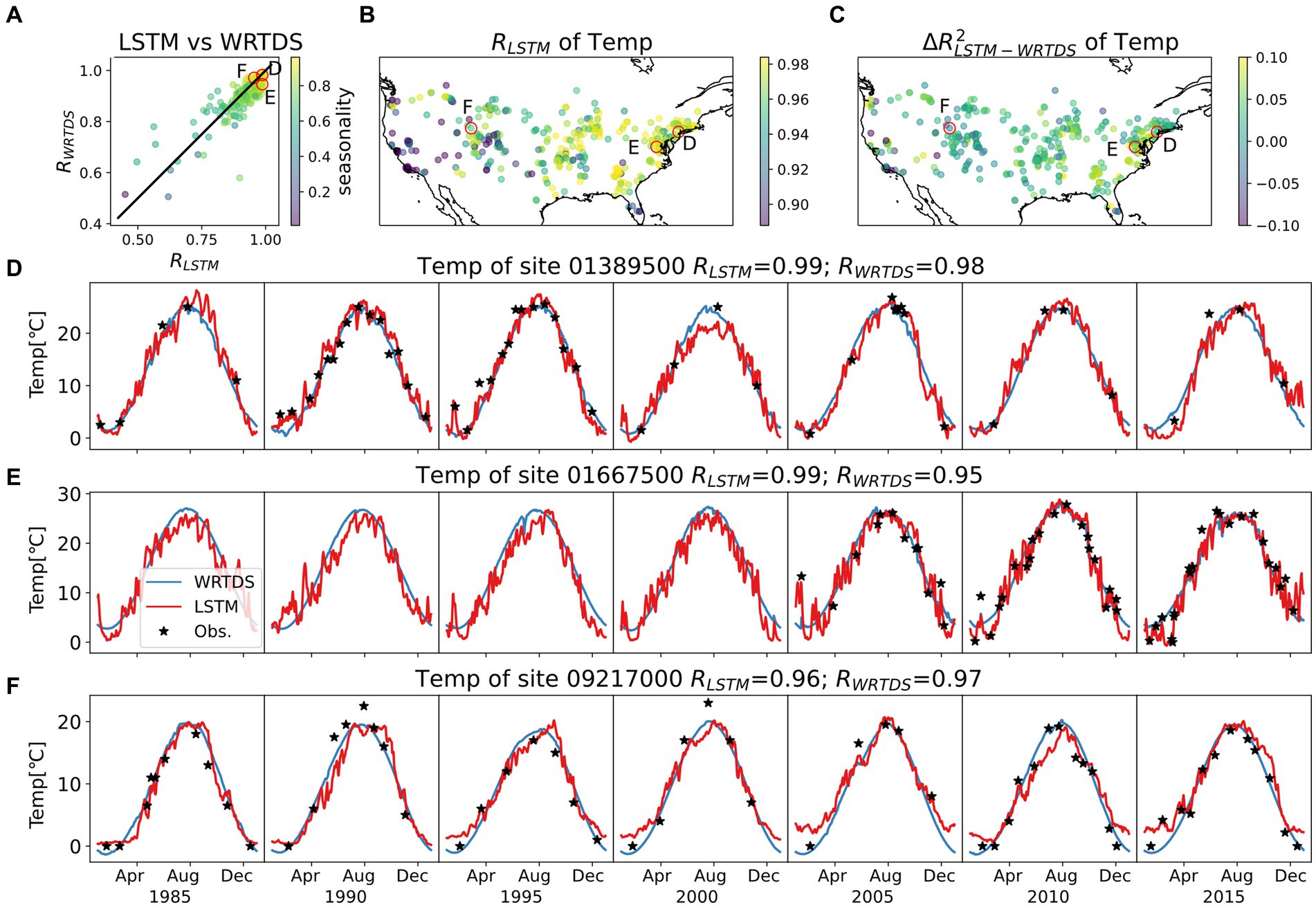
Figure 4. Model behaviors of Temp. The top three panels show (A) R comparison between LSTM and WRTDS for each basin, colored by seasonality; (B) map of RLSTM; (C) map of ΔR2LSTM-WRTDS. Three typical basins are selected as both LSTM and WRTDS perform well (D), or one significantly outperforms the other (E,F). Their locations are circled in top three panels and their time series for the testing period are presented in (D–F). Selecting procedure are detailed in Supplementary Figure S3. Note the variation in scale for temperature.
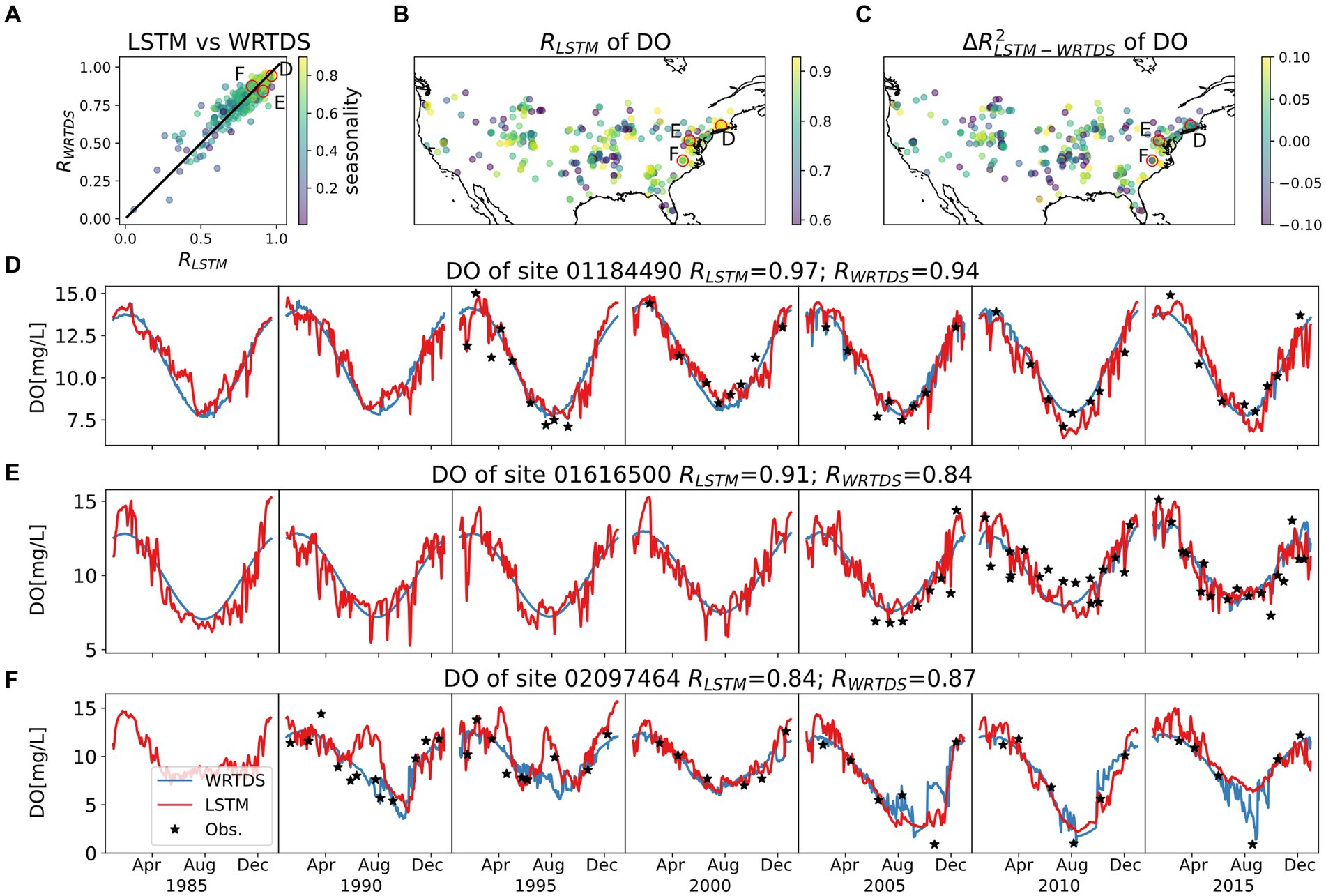
Figure 5. Model behaviors of DO, with same style as Figure 4. The top three panels show (A) R comparison between LSTM and WRTDS for each basin, colored by seasonality; (B) map of RLSTM; (C) map of ΔR2LSTM-WRTDS. Three typical basins are circled in top three panels and their time series for the testing period are presented in (D–F).
For Temp, both models capture the observed temperature patterns across a large number of basins, with better model performance as seasonality increases (Figure 4A) and slightly better performance for the LSTM as seasonality decreases. The seasonality for Temp is strong for most basins across CONUS, but weaker along the western coast of CONUS (Supplementary Figure S10), a trend that is mirrored in the model performance (Figure 4B). For basins with high seasonality, both models can capture the sine-shaped curve, but the LSTM model typically predicts greater short-term fluctuations (e.g., Figure 4D). The average RLSTM of 0.94 and median of 0.96 compares to values of 0.94 and 0.92 for WRTDS, a difference which is significant (p-value = 3e-40 in a Wilcoxon test).
The behaviors of LSTM and WRTDS depart when the seasonality of Temp is low (Figure 4A). Both models can capture the seasonal trends of Temp. However, deviations from these trends lead to divergent model performances. For example, the basin shown in Figure 4E experiences an unusual Temp spike in February. LSTM captures this anomaly, whereas WRTDS does not. Conversely, in Figure 4F, where there are significant year-to-year magnitude differences, LSTM incorrectly predicts a time shift rather than a magnitude shift. Overall, LSTM generally outperforms WRTDS across the northeastern US but is slightly worse than WRTDS along the west coast and in Florida (Figure 4C).
The LSTM and WRTDS predictions for DO also show a strong dependence on seasonality (Figure 5A) resulting in similar pattern to Temp. In basins with strongly seasonal DO, both LSTM and WRTDS can reproduce the DO with high correlations (Figures 5B,C), while LSTM predicts more frequent fluctuations along the smooth cosine curve reported by WRTDS (Figure 5D). When seasonality is weaker, the behavior of LSTM and WRTDS departs and their performances decrease (e.g., Figures 5E,F). It is not apparent why model performance decreases on some basins, although there is an apparent shift away from purely sinusoidal DO patterns that may reflect increased biogeochemical processing (Zhi et al., 2021).
In summary, stream water Temp and DO dynamics are strongly seasonal and well described by both modeling approaches, even though WRTDS was not designed to model Temp. When the seasonal Temp pattern is complex, such as the bimodal pattern in Figure 4E, the LSTM tends to better capture the dynamics. For DO, both models have difficulty capturing sites with low seasonality. In agreement with prior studies (Rahmani et al., 2021; Zhi et al., 2021), the capability of LSTM in modeling Temp and DO is confirmed by this experiment, although LSTM performance is only slightly better than WRTDS for Temp and nearly identical for DO.
In this section, we examine the prediction of solutes that are predominantly associated with weathering processes, including Ca, Mg, Na, and SiO2, and those partly controlled by weathering processes, including K, Cl, SO4, and Cond. These variables are characterized by a relatively strong linear C-Q relationship (linearity) and median seasonality (Supplementary Figures S9, S10). Both LSTM and WRTDS achieve relatively high R and KGE, with the LSTM generally underperforming compared to WRTDS (Figure 2). Among those variables, RLSTM is only higher than RWRTDS for SiO2, and the difference is not significant. KGELSTM is significantly higher than KGEWRTDS for SiO2 and Cond, but lower for Mg and SO4.
Across the weathering solutes, model performance is best for Ca, with half of the basins of an R higher than 0.7 for both LSTM and WRTDS models. Model performance is correlated with linearity (Figure 6A), although to a weaker extent than observed between Temp and DO and seasonality. As a result, the spatial gradient in model performances (Figures 6B,C) generally agrees with the simplicity (Supplementary Figure S8), with high R values in the central Rocky Mountains and northeastern coast. For those mountainous and snowmelt-dominated basins, for example Figure 6D, LSTM predicts a temporal pattern that is nearly identical to WRTDS, especially during high streamflow events. Across the Mississippi River Basin, especially downstream parts of Arkansas basin (HUC11) and upper Mississippi (HUC07), many sites report low linearity. The C-Q relationship may be confounded by mixing of tributaries upstream and agricultural/land use practices, leading to more variable model performance across the central US.
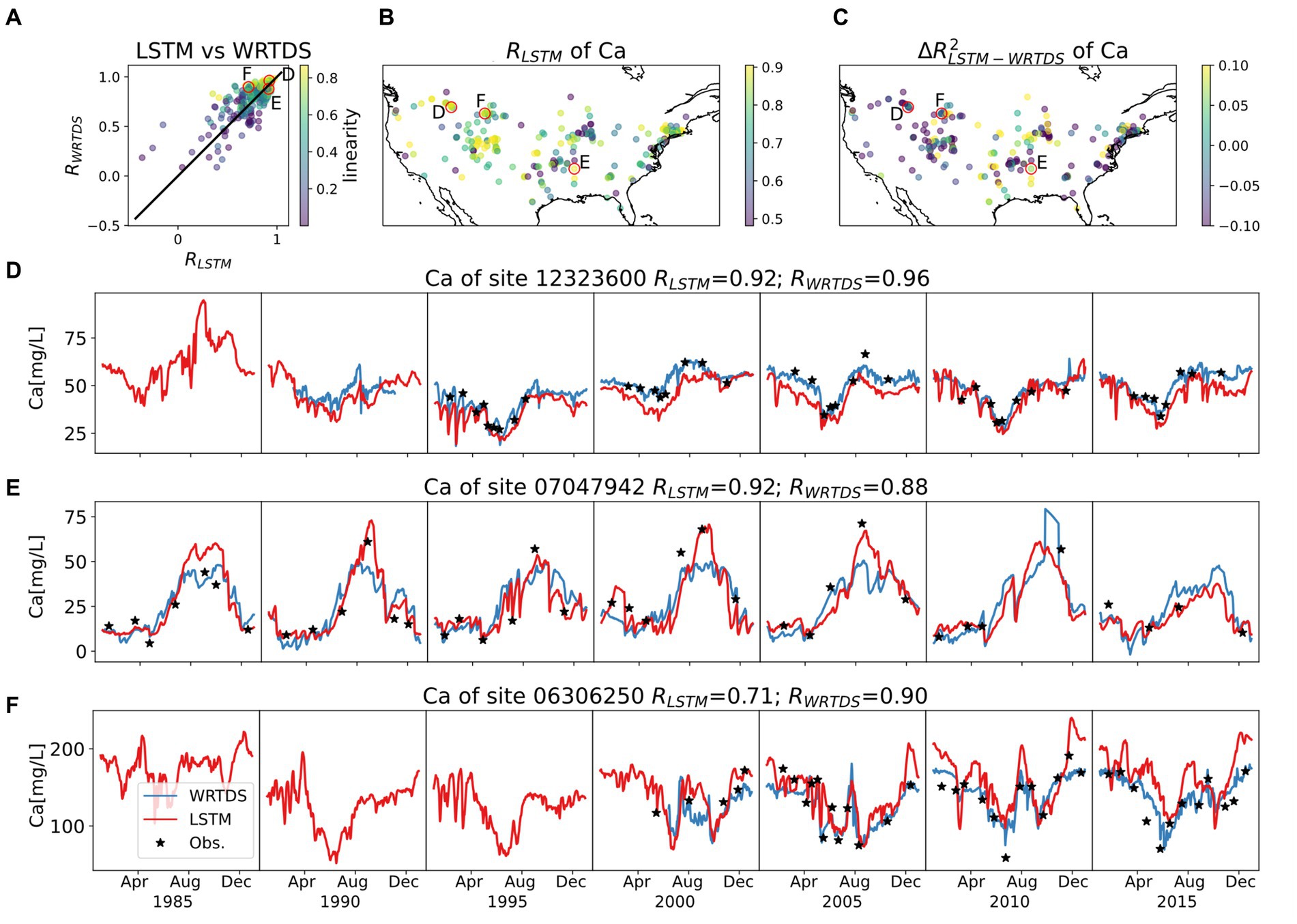
Figure 6. Model behaviors of Ca, with same style as Figure 4. The top three panels show (A) R comparison between LSTM and WRTDS for each basin, colored by linearity; (B) map of RLSTM; (C) map of ΔR2LSTM-WRTDS. Three typical basins are circled in top three panels and their time series of testing period are presented in (D–F). Note the variation in scale for concentrations.
In analyses of basins with median data availability, WRTDS outperforms LSTM at more sites, as shown in Supplementary Figure S7. LSTM’s primary advantage lies in its ability to capture the peaks in Ca concentrations more accurately, such as Figure 6E. These peaks are reflective of low flow hysteresis within a generally linear C-Q pattern (Figure 1A), indicating that LSTM is adept at identifying outliers within a linear context. However, in simpler basins where a strong linear C-Q relationship exists, LSTM tends to predict a shifted pattern, which significantly reduces its performance. For instance, in Figure 6F, LSTM predicts an increasing long-term trend, leading to an overestimation of Ca concentrations in 2010 and 2015. Additionally, at the same basin, LSTM incorrectly predicts that drops in Ca concentration will occur days after high-flow events —a prediction not made by WRTDS or other statistical models that rely on direct C-Q relationships. Overall, both models demonstrate limited effectiveness in the absence of both seasonality and linearity in the C-Q-t relationship. WRTDS better describes the linear C-Q pattern, while LSTM more effectively identifies non-linear outliers.
To further examine the importance of linearity for modeling of the weathering variables, we equally divided basins into “linear” or “non-linear” groups based on the median linearity index for each solute, and separately plotted model performances for each group (Figure 7). On “linear” basins, WRTDS is significantly better (p < 0.05) for most weathering variables except for K and SiO2, which have the lowest median linearity among selected variables. On the other hand, LSTM outperforms WRTDS (p < 0.05) on “non-linear” basins for most variables except for Cond and SO4. For basins with high linearity, the weathering solute concentrations are strongly affected by dilution at high discharge. In contrast, low linearity indicates relatively complex solute generating processes, e.g., seasonal flow paths or more chemostatic behavior. Thus, when the C-Q pattern results from dilution from baseflow concentrations, LSTM is likely to be less skillful at predicting the variations. However, when the solute generating process is too complex to be captured by a linear C-Q relationship, the advantage of LSTM over WRTDS is highlighted. Arguably, the weathering solute generation process typically unfolds over decades or even centuries, greatly exceeding the LSTM model’s training sequence length. In addition, the extent of weathering is linked to variations in water age and mixing, which may complicate temporal dynamics (as reviewed in Maher and Navarre-Sitchler, 2019). As a result, trying to map the dilution process from a relatively short sequence of historical forcings may perplex the LSTM model, leading to overfitting rather than accurate predictions.
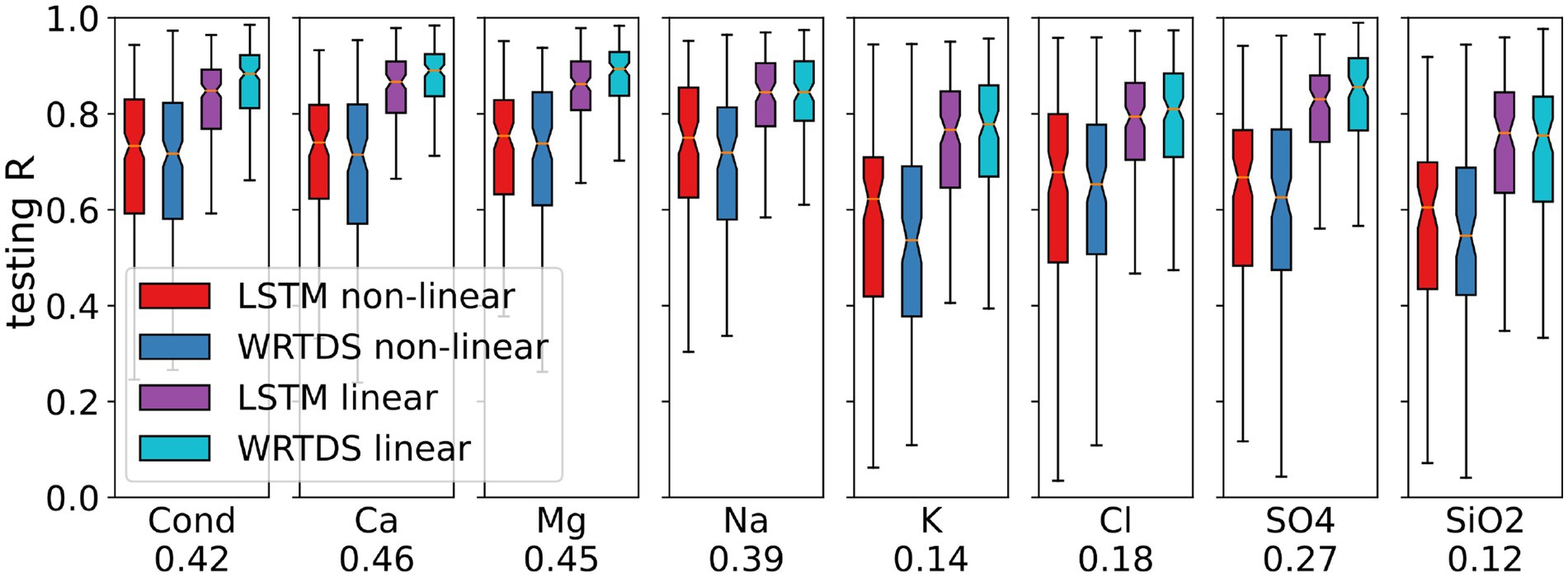
Figure 7. LSTM and WRTDS performance of weathering and mixed variables. The median linearity of each variable is presented under the variable name, which separates the basins into linear and non-linear groups for plotting.
For most nutrient variables, including NPOC, NO3, TN, N-org, NHx, TP and PO4, LSTM outperforms WRTDS. These variables are affected by biogeochemical processes and human activities like land use practices and agricultural inputs, and both LSTM and WRTDS predictions are characterized by relatively low R and KGE values. CO2 and pH are particularly challenging for both approaches (Figure 2), with LSTM generally worse than WRTDS. Unlike Temp, DO or weathering solutes, most basins are characterized by low simplicity, i.e., nutrient dynamics are not determined by strong seasonality or a linear C-Q relationship.
For NO3, the overall simplicity index is still strongly correlated with model performance (Figure 8A)—a trend also observed at other nutrient variables. The LSTM outperforms WRTDS, achieving a median R of 0.71 compared to 0.67 for WRTDS (p = 1.4E-02). There is also minimal spatial structure in model performance as basins with relative high RLSTM and ΔR2LSTM-WRTDS are clustered together (Figures 8B,C). However, we did not find any single geophysical attribute controlling this spatial pattern.
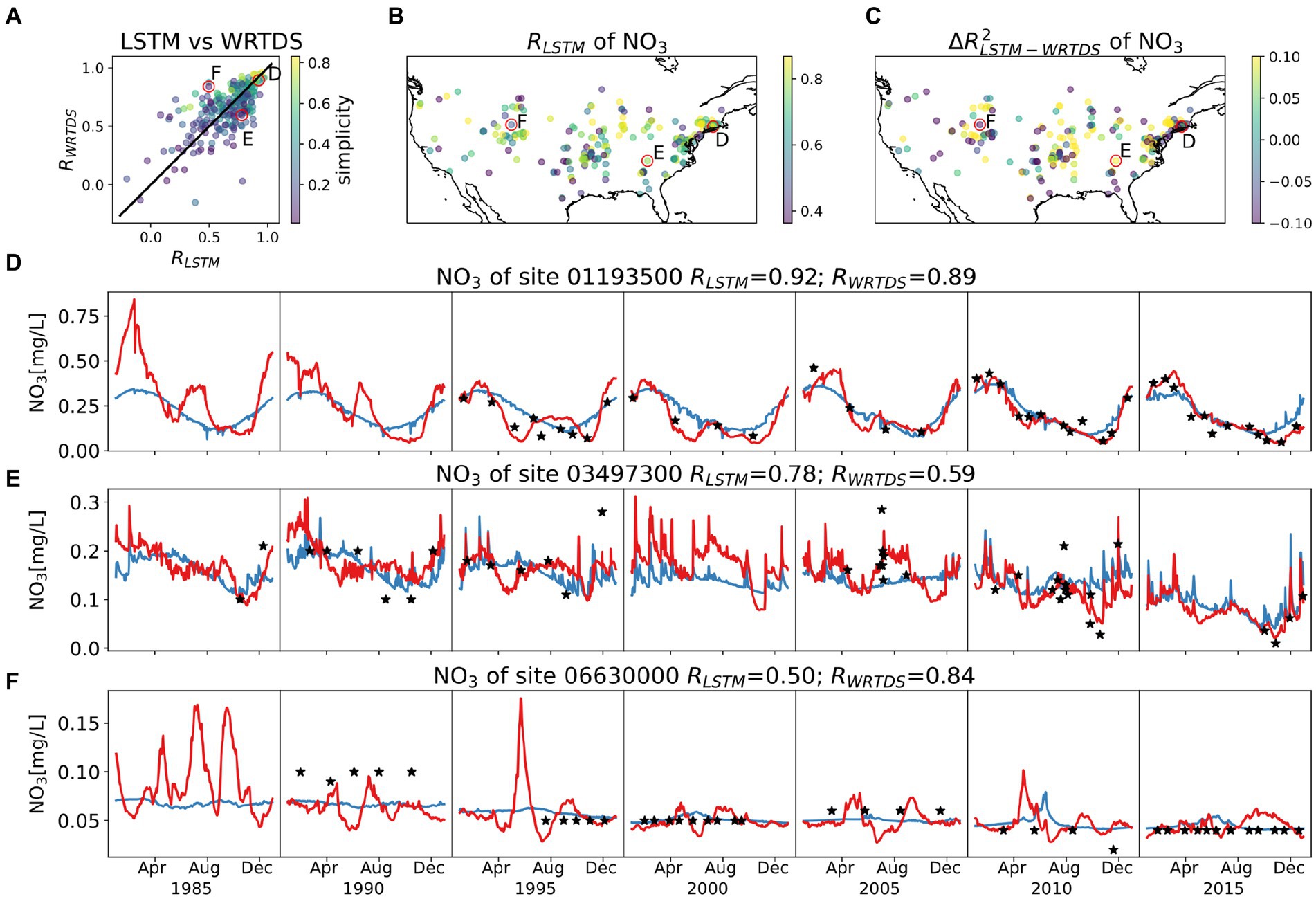
Figure 8. Model behaviors of NO3, with same style as Figure 4. The top three panels show (A) R comparison between LSTM and WRTDS for each basin, colored by simplicity; (B) map of RLSTM; (C) map of ΔR2LSTM-WRTDS. Three typical basins are circled in top three panels and their time series of testing period are presented in (D–F). Note the variation in scale for concentrations.
LSTM and WRTDS models predict markedly different NO3 dynamics, even in basins with a high simplicity index where both models perform well—a divergence not seen in previously presented stream and weathering variables. For instance, in the basin presented in Figure 8D, although both models achieve high performance, the LSTM model reveals an evolving seasonal pattern while WRTDS does not. LSTM predicts a shift from pronounced early fluctuations with transient peaks to a more uniform declining trend in recent years. This pattern is noticeable during the training period; however, due to the limited data from those early years, we cannot fully confirm this trend. In cases where LSTM significantly outperforms WRTDS, such as the one shown in Figure 8E, its advantage comes from accurately capturing extreme events, notably the peak of summer 2005 and the trough of autumn 2010. Conversely, WRTDS tends to outperform LSTM at sites with data density concerns, such as those illustrated in Figure 8F, which show constant readings indicative of a potential measurement issue. A notable number of sites (~10) suffer from this data quality issue, yet because they lack corresponding quality flags we cannot exclude them without subjective data manipulation. In these instances, while LSTM displays a tendency to overfit these consistently flat measurements, WRTDS is more adept at approximating them.
Below we examine the associations among seasonality, linearity, and simplicity, and among basin characteristics and model performance. In addition, we explore the differences and commonalities among LSTM models trained with different strategies and predictors in order to (1) understand basic drivers of LSTM performance and (2) provide a practical guide for future model use and development in water quality prediction.
By comparing results from two different data-driven modeling approaches, LSTM and the WRTDS, we find that both approaches show similar performance across a broad spectrum of analytes (Figure 9). The most challenging variables for the models are the nutrients, followed by weathering-derived solutes, and then Temp and DO.
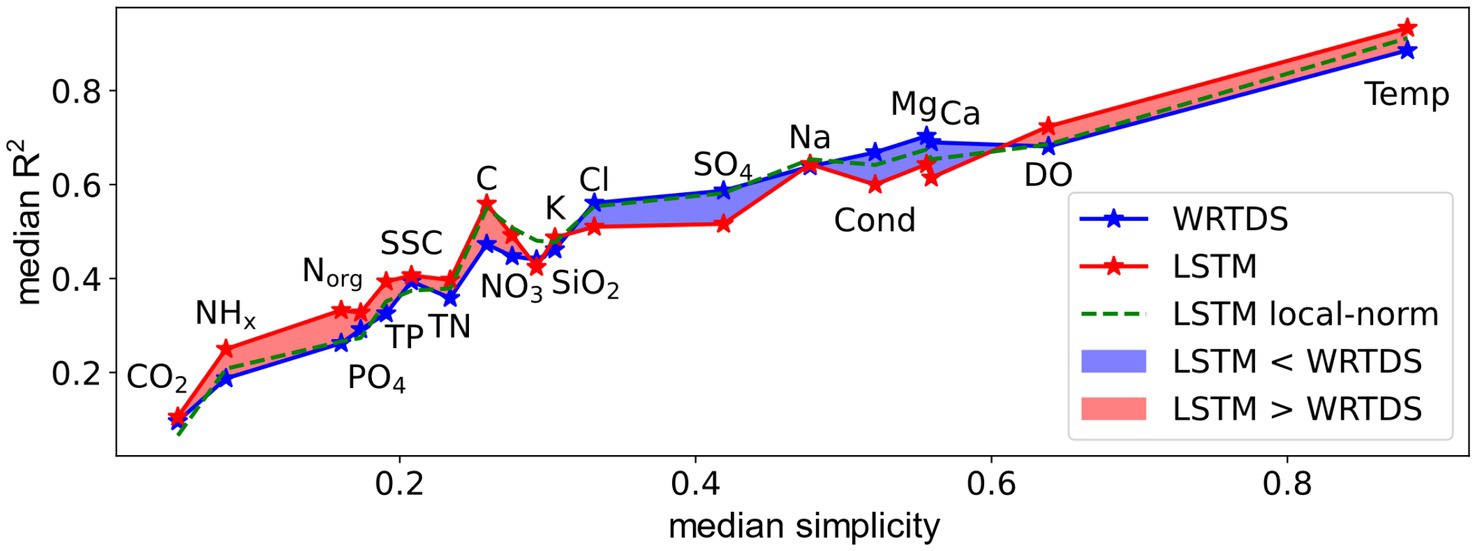
Figure 9. Median testing R2 of LSTM model vs. similarity index for selected water quality variables. Blue line present WRTDS R2 and red line is LSTM. The green dash line shows the performance of LSTM model with local normalization discussed in section 4.2.
For Temp and DO, WRTDS achieved decent performance although it is not designed to model them. LSTM results for Temp and DO agree with prior work that found strong model performance for a smaller set of data-rich and dam-free basins (Rahmani et al., 2021; Zhi et al., 2021; Sadler et al., 2022), performance that generally exceeds that of statistical stream temperature models (e.g., Gallice et al., 2015). Similarly, we also observe the performance of the WRTDS and LSTM to decrease at low seasonality and/or for non-sinusoidal DO patterns. Overall, the strong performance of both model types for Temp and DO can be explained by the representation of seasonal patterns, supplemented by discharge dependencies.
In contrast to Temp and DO, the weathering solutes are characterized by linearity over seasonality and lower overall simplicity. Both models perform moderately well on these analytes, with WRTDS significantly better for Ca, Mg, and SO4 (Supplementary Table S2). Although numerous models have been presented for these patterns, including WRTDS (and related variants), no studies have yet to apply LSTMs to predict a range of water quality variables across heterogeneous catchments. However, LSTMs have shown considerable promise for modeling water stable isotopes (Sahraei et al., 2021), urban discharge (Zhang et al., 2022), and individual water quality time series (Jung et al., 2020). Hence, the lack of distinction in LSTM performance relative to WRTDS is surprising.
All nutrient variables are characterized by complex C-Q-t patterns (low simplicity), and poor model performances. The inherent complexity of nutrient C-Q patterns is well established. The complexity is evidenced both in the decline of CVC/CVQ with increasing export load (Thompson et al., 2011), lower power law exponents (Musolff et al., 2015) and positive precipitation anomalies (Fazekas et al., 2021). Thompson et al. (2011) attributed decreasing CVC/CVQ to an increasingly homogeneous distribution of mass stores within the catchment due to anthropogenic inputs, also resulting in more chemostatic tendencies. Here, we do not see a consistent relationship between nutrient CVC/CVQ and model performance. Although CVC/CVQ is weakly anti-correlated with simplicity (Supplementary Figure S11), it does not consider the coherence of the seasonal pattern, which is an important component of the overall behavior for nutrients (Figure 8).
The strong correlation between simplicity and model performance also indicates that we have not captured all of the drivers of C-Q-t behavior. Even though we provided more comprehensive predictors to the LSTM, including climate forcing, vegetation dynamics and numerous catchment attributes from GAGES-II, in general the LSTM does not outperform the WRTDS (Figure 2). However, temporally and spatially resolved human inputs, such as fertilizer applications and point source loads, were not available as additional predictors. We also did not find strong relationships between the simplicity index and the non-climatic basin attributes (Supplementary Figure S10), except in a few instances discussed below. The inability of the LSTM to gain an advantage indicates that the connection between those additional predictors and target dynamic is either less important compared to the C-Q-t relationship, or extremely hard to quantify with existing predictors.
Collectively, our results present a paradox: a model architecture (LSTM) designed to inherently detect hidden patterns performs similarly to a statistical model built on assumptions of the dominant patterns (WRTDS), and their performance strongly agrees with trends revealed by the simplicity index. At the same time, in complex basins the LSTM shows slightly better performance suggesting that it may have established “auxiliary characteristics,” or temporal dynamics not directly provided in the inputs. Below (section 4.4), we examine several instances that may explain these additional “hidden” inputs.
The availability of water quality observations is surely a limiting factor in the performance of both LSTM and WRTDS models; however, the correlation is complex (Figure 10, see Supplementary Figure S12 for all 20 variables). When the number of training samples is relatively small, the testing R exhibits considerable variability, with some sites showing strong performance even in spite of low data availability. As the number of training samples increases, the scatter in performance values contracts to relatively high and consistent values suggesting that adequate training samples will result in relatively consistent model performance across most sites. In general, this stabilization of performance is guaranteed when the size of training samples is larger than 500, which includes, unfortunately, less than 4% of the sites. This pattern suggests that as the data quality increases, the performance of LSTM tends to approach a relatively high and stable level. However, given the scarcity of sites with frequent observations, the question of whether this pattern will hold for even larger data sizes remains unclear. For the same reason, the execution of a leave-samples-out experiment to validate this inference is also challenging.
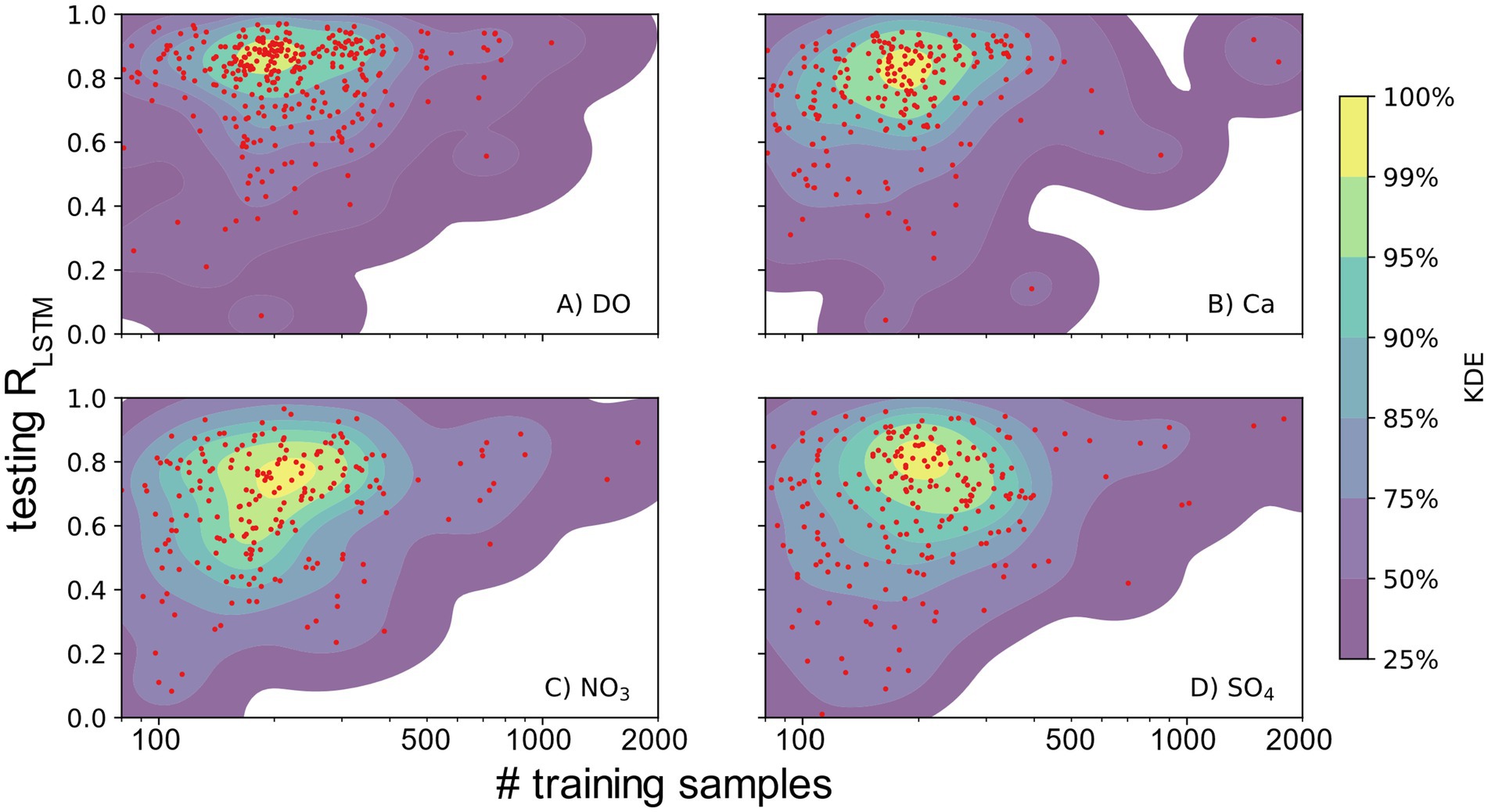
Figure 10. Number of training samples vs. testing R for (A) DO, (B) Ca, (C) NO3, and (D) SO4. Each red point represents a basin. The gaussian kernel density estimation (KDE) colored based on percentiles of z-values represents the density of points.
While an increased number of training samples significantly reduces performance variations, the overall median performance remains relatively constant or exhibits a mild upward trend. The slopes of testing R and KGE with respect to number of training samples are generally small for most variables. Agricultural variables, such as K, NO3, PO4, and NPOC, are exceptions, presenting a notable surge in model performance as the number of training samples increases. This observation implies that the LSTM model benefits from a more frequent sampling to effectively capture the intricate patterns arising from human activities. Expanding the collection of water quality samples has the potential to enhance the stability of model performance, as supported by previous work with local but high frequency measurements (Saha et al., 2023). Yet it remains uncertain whether an increase in data alone could effectively address the challenges presented by basins characterized by lower levels of simplicity.
In summary, there is no clear evidence to conclude that the size of the training sample is a dominant control on model performance, evidenced by the close to zero correlation between training sample size and testing R or KGE. On the other hand, the correlation between simplicity and model performance is much stronger. Nevertheless, the overall count of training samples only partly indicates the quality of training data. For example, some sites exhibit a high frequency of water sample collection but for only a limited number of years or months. This situation results in a relatively dense yet low-count training data scenario. For a more comprehensive understanding of data quality, a thorough analysis of the distribution of the measuring time stamp is needed.
Given the apparent uniqueness of water quality behavior across basins, we further explore model assumptions to determine their impact on model performance. In the model experiments described above, we used a global normalization strategy (see section 2.3.3), which normalizes target variables based on pooled values across all basins. Hence, the local temporal dynamics of water quality are dampened. Accordingly, we tested an alternative local normalization strategy on water quality targets that exaggerates local variations while relegating inter-basin connections. For each basin, we standardize each water quality variable by:
where is water quality observation at site k, with mean and standard derivation (std) calculated using only data from the training set. The mean and std for each site and each variable as per Equation (9) are recorded and provided to the LSTM model as additional static inputs. Noting that we did not log transform as the site-wise concentrations are not log-distributed for most sites and variables.
We found that local normalization affects weathering variables and nutrient variables in opposite ways (Figure 9, green line). For weathering variables, local normalization substantially improves the model performance, minimizing the difference between the LSTM and WRTDS models and overall higher testing correlations for K and SiO2, on par for Na, Cl and SO4, and worse for Ca, Mg and Cond. However, for all water quality variables where LSTM outperforms WRTDS, local normalization decreases LSTM performance. In short, local normalization results in greater similarity between the LSTM and WRTDS.
Local normalization transforms water quality measurements into a relatively uniform distribution; hence the LSTM model can more easily fit the target values compared to global normalization. At the same time, the information on the magnitude difference between basins is missing, preventing the model from learning universal rules across different sites. Therefore, the effect of local normalization may indicate how LSTM learns the water quality dynamics. In general, such cross-site information could be leveraged by LSTM to predict nutrient and in-stream dynamics but would undermine predictions of weathering variables. This finding may indicate controls on water quality variables, where nutrient analytes are determined by a common set of factors and the generation of weathering solutes is partly determined by local geology. The latter limits the ability of the model to transfer knowledge among basins. However, such correlations are not straightforward to perceive from the existing attributes in our database when compared to the simplicity for each parameter. For example, Ca simplicity shows an inverse correlation with the fineness of soil texture, whereas Na simplicity does not (Supplementary Figure S13). Other studies have found stronger correlations between C-Q metrics and catchment attributes across Germany, within a much tighter geographic and climatic range (Ebeling et al., 2021).
The experiment of local normalization is also useful from a practical standpoint: when using LSTM to simulate water quality dynamics, local normalization is preferable for weathering variables but not for others. This preprocessing step could remedy the weakness of LSTM in the prediction of weathering variables, and result in an enhanced LSTM model that mostly outperforms WRTDS, even if we do not have a clear statistical explanation for the effect of local normalization.
To determine if additional inputs could improve simulations of water quality dynamics, we investigated the contribution of additional predictors, including climatic forcing, precipitation chemistry and vegetation index. We used a sequence of labels to represent models of different inputs, as detailed in section 2.1.2. For example, an experiment labelled “QFPV-C” means the input of the model contains drainage basin runoff (Q), climatic forcings (F), precipitation chemistry (P) and vegetation indexes (V), while the target is water quality dynamics (C). We compare the behaviors of QFPV-C, model with full inputs; QFP-C, model without vegetation indexes; QFV-C, model without rainfall chemistry; Q-C, model only using streamflow (same inputs as WRTDS); and FPV-QC, which simulates streamflow and water quality simultaneously.
In general, additional input data does not significantly improve the performance of LSTM, as the experiments with additional input variables (QFPV-C, QFV-C and QFP-C) did not significantly outperform the model with only streamflow (Q-C) (Figure 11). However, there are some exceptions. Climatic forcings do improve prediction of Temp and DO; vegetations indexes improve nutrient variables, including NO3, PO4 and NHx. Although the model with most comprehensive inputs (QFPV-C) reported the highest correlation, the differences to other LSTM models with fewer predictors are not significant in Wilcoxon test for most variables. The small effect is surprising as the connection between those additional variables (i.e., climate forcing, rainfall chemicals, and vegetation characteristics) have been assumed to influence C-Q patterns.
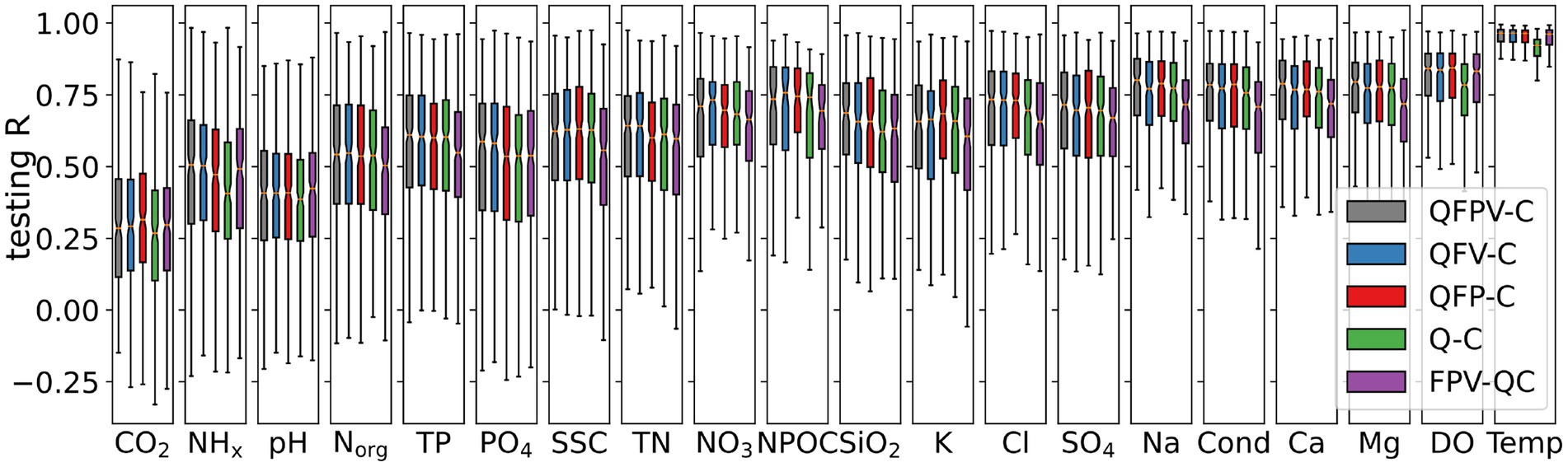
Figure 11. comparison of LSTM testing performance with different input and target, for 20 selected water quality variables ordered by their median simplicity index. QFPV-C (black) is the reference model that is trained with complete inputs.
We found that the insignificant performance difference introduced by additional inputs is due to tradeoffs in model performance. For example, we compare the SO4 predictions between model QFPV-C and QFV-C (i.e., LSTM with precipitation chemistry and without), on a northeastern basin that is substantially impacted by acid rain (USGS ID is 01349150). As Figure 12 shows, precipitation chemical data improved the LSTM predictions of the fall peaks in SO4 in 1995 and 2005, but then overestimated in 1995 spring and 2015 fall. As a result, QFPV-C and QFV-C models reported the same testing R (0.93). Although SO4 can be strongly affected by the legacy of acid rain as well as marine aerosol inputs, rainfall chemistry can both improve and diminish the performance of the LSTM model in predicting SO4, which is also evidenced by the small improvement from QFV-C to QFPV-C model (SO4 in Figure 11, median correlation from 0.7 to 0.72). This example highlights both the potential advantage and disadvantage of using DL approaches – although more data can be utilized, they may have no effect, or worse negatively influence predictions. Compared with C-Q relationships, the relationship between those additional flux and water quality metrics are less straightforward and cannot be fully captured by LSTM in our experiment. It is not clear whether this issue can be mitigated by adding more data, including both comprehensive inputs and adequate target observations; or if we need more advanced DL models with skillful regulation techniques or embedded coupling to physical rules.
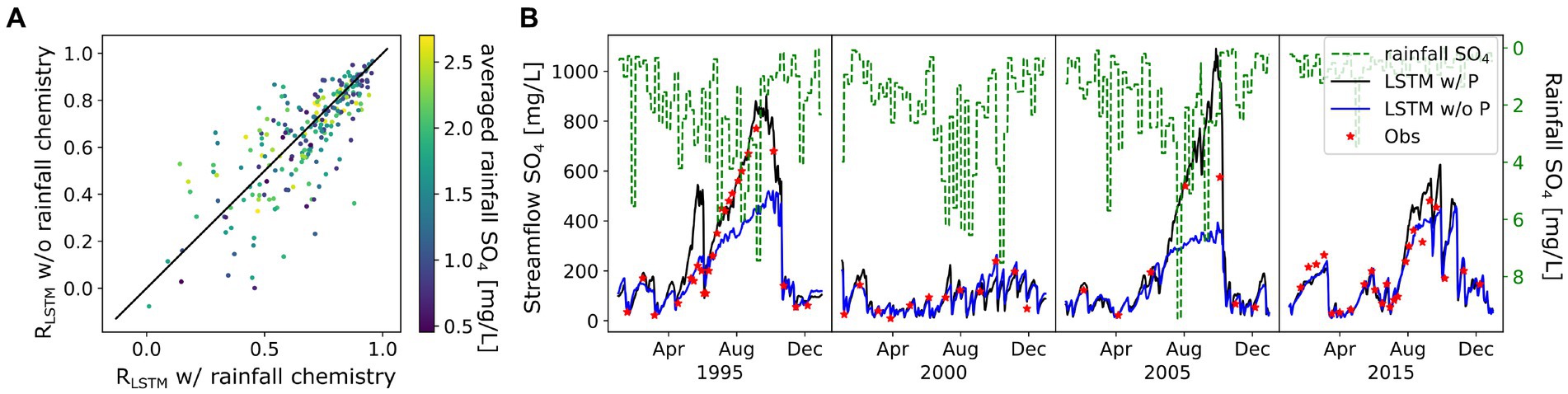
Figure 12. The affect of rainfall chemical input on LSTM prediction of SO4. (A) comparison between the testing correlation of LSTM models with and without rainfall chemistry (labeled as P) as inputs, colored by long-term averaged rainfall SO4 concentration. (B) example time series on basin 01349150.
In the above experiment, we found that the FPV-QC model, in which the LSTM is trained to simulate Q and C simultaneously, results in a decline in model performance compared to the other experiments where streamflow is used as input (e.g., FQPV-C) (Figure 11). Previous studies have shown that LSTM is a promising method for simulating streamflow (Feng et al., 2020; Kratzert et al., 2019a; Kratzert et al., 2018; Gholizadeh et al., 2023). As solute export is highly linked to streamflow generation, we would expect an LSTM model that is trained to predict streamflow and water quality at the same time to identify and benefit from such relationships. This inability of the LSTM to utilize the learned streamflow-generating behavior to model water quality dynamics is thus surprising. For weathering variables, the FPV-QC model is even worse than the model using only streamflow as input (Q-C). On one hand, the FPV-QC model presumably uses hidden parameters to successfully predict streamflow and to simulate water quality. Those hidden parameters are assumed to be a promising representation of the streamflow generating process. The streamflow prediction from FPV-QC model is close to the rainfall-runoff LSTM model (i.e., F-Q model), which is the state-of-art streamflow simulator (Kratzert et al., 2019b). On the other hand, the Q-C model does not know how the Q is generated but was provided accurate Q as inputs. Surprisingly the latter advantage overrides the former one.
We argue that in applications to water quality, the LSTM model works as a statistical model extracting the C-Q-t relationship, rather than a representation of catchment function as asserted for LSTM models of streamflow (Nearing et al., 2021). More specifically, the LSTM model cannot extract the flow path and travel time distributions of water, then couple the physical and chemical processes to predict the dynamics of weathering solutes. This deficiency may result from the lack of frequent observations of water quality, although our dataset does not contain high-frequency water quality observation to investigate thresholds. While streamflow is commonly measured daily, solute concentrations are usually measured bi-weekly or monthly, and on the outlet of a much smaller number of basins. Nevertheless, data-driven models are likely to learn the most straightforward relationship between concentrations and streamflow. Our results indicate that the underlying internal processes are not easily identified by a direct implementation of an LSTM.
On many catchments, LSTM outperforms WRTDS, possibly by capturing auxiliary characteristics that affect the solute dynamics, beyond seasonality and linear C-Q. Unfortunately, as the LSTM is a black-box model, it is hard to interpret LSTM weights as readable auxiliary characteristics: those auxiliary characteristics are hidden inside the LSTM and hard to extract. To interrogate those hidden controls, we examined the relationship between and environment conditions. Such analyses provide an indication of potential auxiliary characteristics that contribute to the water quality variations, and by extension, the means by which LSTM gains an advantage. These insights may also inform future modeling efforts.
For example, the LSTM substantially outperforms WRTDS for NHx when the basins are heavily affected by agricultural practices. Comparison of the nitrogen addition (via fertilizer and manure, estimated by Ruddy et al., 2006) to the results in a triangular array (Figure 13). When the nitrogen input is more than 5,000 kg/km2, the average R value for LSTM NHx is 0.66, while the WRTDS is 0.48. On the other hand, when the basin is not heavily fertilized, LSTM only slightly outperforms WRTDS, with R of 0.5. A similar pattern is found for the NO3 models: when agriculture occupies more than 25% of the riparian zones, the average R value for NO3 prediction by LSTM model is 0.71, which is substantially higher than for WRTDS (R = 0.63) or LSTM on other basins (R = 0.65) (not shown). For PO4, the LSTM correlation reaches 0.70 on basins whose phosphorus input is higher than 1,200 kg/km2, while correlation for WRTDS on those basins is 0.62, and LSTM on other basins is 0.60 (not shown). These examples indicate that LSTM may capture the temporal dynamics of agricultural practices, which substantially affect nutrient concentrations and exports (Basu et al., 2010), contributing to the advantage of LSTM in modeling nutrient dynamics. In general, LSTM achieves higher R on fertilized basins over unfertilized ones, which implies that the nutrient dynamics produced by human activities are easier to model compared to natural biogeochemical processes.
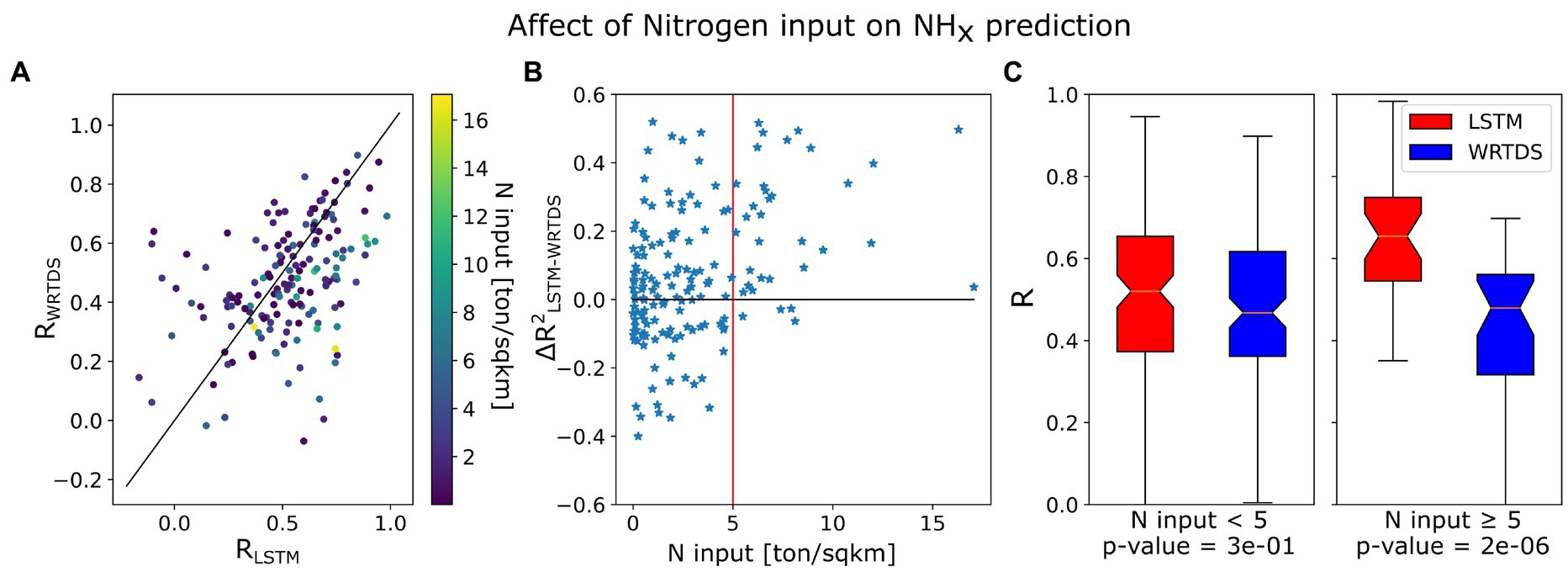
Figure 13. The relation between estimated Nitrogen input and model performance of NHx. (A) comparison between LSTM and WRTDS testing correlation colored by N input; (B) comparison between model performance difference and N input; (C) testing correlation of LSTM and WRTDS on heavily fertilized basins and others.
Noting that the agricultural input to the model is constant rather than dynamic, reflecting a long-term average, it is more likely that the daily inputs of climate and vegetation provided to the LSTM contribute to the improved model performance in heavily fertilized basins. The improvement of the LSTM in human-impacted basins may also reflect the accumulation of mass stores within the catchment, resulting in reduced variance in concentrations throughout the year (Thompson et al., 2011). Accumulation of P, N and SO4 from excess inputs is well established for many catchments (Basu et al., 2010; Green et al., 2014; Zhang, 2018; Stackpoole et al., 2019) and may underlie some of the broader trends seen across our results. Detailed information on anthropogenic chemical inputs to watersheds (e.g., time series of fertilizer or manure applied) could greatly improve LSTM model performance. However, nutrient input data, typically derived from county-level surveys (e.g., Falcone, 2021), require extensive work to be integrated into catchment-scale inputs. Despite the recent effort integrating nutrient input into HUC8 scale (e.g., Sabo et al., 2019, 2021), the variability in catchment sizes associated with USGS gages introduces significant uncertainty. Moreover, nutrient input data are generally reported annually, making them incompatible with training a daily-based DL model. The future work should consider developing a new deep learning architecture capable of directly handling these spatial and temporal discrepancies, which would be more effective than attempting to create a daily basin-level product for model input.
Other studies have correlated catchment attributes with C-Q behavior. In a study of nine European catchments, Musolff et al. (2015) found that the fraction of drained arable land, available water capacity in the root zone, and baseflow, were the most important variables for predicting the slope b, although the dominant attributes varied across solutes. For CVC/CVQ, the topographic gradient and base flow index were most important. Our results point to a similar pattern of element-specific correlations in catchment attributes, wherein simplicity is correlated with a unique set of attributes (Supplementary Figure S10). We also show here that seasonality is an important attribute for the nutrient analytes. Furthermore, land use practices may not be reflected adequately in the climate and vegetation dynamics (as provided to the LSTM here), at least for lower land use intensities.
Even with the increased number of inputs and the capability to model nonlinear behaviors, we find that the LSTM architecture does not capture the diversity of C-Q-t patterns, particularly for basins/variables of low simplicity. Our results highlight the need to focus on understanding and modeling low simplicity analytes and watersheds, as it is clear the predictive power of existing models is already substantial for basins that rank highly in simplicity. In contrast, complex basins defy predictability, even when paired with other assumed drivers (vegetation, climate, land use and basin attributes), presenting an outstanding challenge for our understanding of water quality. Water quality measurements at the scales considered here are also too sparse to evaluate underlying signals, such as fractal scaling indicative of multi-scale dispersive mixing processes (Kirchner and Neal, 2013). In addition, the correspondence between low simplicity and poor LSTM performance for highly reactive nutrients may arise from inadequate representation of complex reaction networks within the LSTM model. Future model frameworks will need to account for both dispersive mixing and complex reaction networks.
Our findings above also provide a practical guide for the future use of LSTMs to interpolate or forecast water quality dynamics. Although the LSTM shows promise for simple parameters (DO and Temp), as well as for human-impacted systems, it also is more computationally expensive during the training stage, currently more labor-intensive, and less interpretable compared to WRTDS. In addition, our experiment used 20 variables for nearly 500 basins across CONUS, whereas an LSTM model focused on a smaller number of basins would likely suffer from overfitting, as suggested by streamflow LSTM modeling (Fang et al., 2022), and require careful hyper-parameter tuning. Hence, for many applications WRTDS and related products may provide practical advantages over LSTMs, especially when engaging with a relatively small dataset. Yet, the spatial gradients of difference between LSTM and WRTDS are highly variable, and LSTM may provide superior performance on selected local basins. The proposed simplicity index provides intuition about the level of performance prior to training either model. One important difference is that LSTM can estimate water quality on ungauged basins (using the FPV-QC model presented in Figure 11), while WRTDS cannot.
Ultimately, we argue that using deep learning approaches to simulate water quality is more challenging than for streamflow, for the following reasons: (1) the processes generating and/or transforming solutes are more complex, (2) observations of water quality may be inadequate compared to streamflow observations, (3) the necessary forcings required to improve LSTM performance are missing or remain to be discovered. As a result of these limitations, it is a challenge for LSTM to learn the patterns of all but the simplest water quality dynamics. We acknowledge that, despite exhaustive efforts, the LSTM model has yet to attain its maximum learning potential. Enhanced performance could potentially be realized through training with high-frequency water quality samples, fine-tuning of hyperparameters, or incorporation of supplementary input features that are distinct from those typical of streamflow generating processes. Nevertheless, within the scope of our testing, such endeavors are unlikely to induce a dramatical shift in the reported gradient across sites and variables, suggesting that data availability is not the only limitation.
Considering that forthcoming work concerning large-scale water quality dynamics will likely continue to be constrained by the low frequency of observations, future studies should consider ways to constrain DL by existing theories about solute generation (Zhi et al., 2024), for example, travel time distributions and storage selection functions (Benettin and Bertuzzo, 2018; Harman, 2019; Torres and Baronas, 2021) or consideration of the potential for reaction networks involving multiple species and the subsurface minerals and solids. As noted in Varadharajan et al. (2022), considering the scale, complexity and data availability of water quality problems, integrating process knowledge into model design is necessary to unlock the potential of DL models in handling complex water quality dynamics. Additionally, DL models demonstrate promise for modeling of variables affected by human activities, even with only static inputs describing long-term average inputs. To better model these variables, future work should consider incorporating human input data by addressing the current spatial and temporal discrepancies. Future work could also consider factors related to the water samples, e.g., instruments used, the timing of measurements, and the quality of samples. Based on our analysis of the model performance relative to the simplicity metric, it will also be important to focus on complex basins rather than those that are characterized by high seasonality and/or linearity, as the latter do not present an outstanding challenge for either DL or statistical models.
We find that the capability of the LSTM to model water quality is comparable to the conventional WRTDS model. Both models perform poorly for solutes and basins that classify as low simplicity, an indication that high C-Q variance is not directly attributable to catchment characteristics or the climate, vegetation and precipitation forcings as provided. The differences in performance between the models are subtle, with LSTM advantageous for modeling Temp and several nutrient analytes (e.g., TN, NO3, TP and PO4) and WRTDS advantageous for modeling many weathering analytes (Ca, Mg, SO4). Targeted experiments reveal additional information underlying inter-model differences. A local normalization strategy alleviates the deficiency of the LSTM for weathering variables relative to WRTDS, but also negatively impacts performance for nutrient variables. Removing climate, vegetation and precipitation or moving Q to the prediction have an insignificant impact on the LSTM predictions, suggesting the LSTM is not able to extract additional information in those forcings beyond seasonality and C-Q relationships.
Catchment attributes (e.g., fertilizer additions) are correlated with thresholds in model behavior, suggesting that LSTM may detect auxiliary characteristics. However, in many cases poor model performance cannot be attributed to any single or collective set of attributes, suggesting that underlying drivers, potentially including subsurface properties, complex reaction networks, tributary mixing, and/or human factors, were not captured by the input or training data. Collectively, we conclude that to harness the power of DL and statistical models for water quality will require consideration of the low simplicity end-members in C-Q-t space and less reliance on simple basins and water quality constituents, which are robustly modeled by both the DL architecture and a comprehensive statistical approach.
The raw data supporting the conclusions of this article are shared on Hydroshare with DOI https://doi.org/10.4211/hs.8da6ebf2ee9a491490bb09a6349e70fe.
KF: Writing – original draft, Writing – review & editing. JC: Writing – original draft, Writing – review & editing. KM: Writing – original draft, Writing – review & editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project was supported by funding from the U.S. Department of Energy BER award DE-SC0018155, National Science Foundation Grant No. NSF-2132007, and the Human-Centered AI (HAI) program at Stanford University. Computing for this project was performed on the Sherlock cluster, provided by Stanford University and the Stanford Research Computing Center.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2024.1456647/full#supplementary-material
Abatzoglou, J. T. (2013). Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 33, 121–131. doi: 10.1002/joc.3413
Anderson, S. P., Dietrich, W. E., Torres, R., Montgomery, D. R., and Loague, K. (1997). Concentration-discharge relationships in runoff from a steep, unchanneled catchment. Water Resour. Res. 33, 211–225. doi: 10.1029/96WR02715
Baek, S.-S., Pyo, J., and Chun, J. A. (2020). Prediction of water level and water quality using a CNN-LSTM combined deep learning approach. Water 12:3399. doi: 10.3390/w12123399
Bao, C., Li, L., Shi, Y. N., and Duffy, C. (2017). Understanding watershed hydrogeochemistry: 1. Development of RT-Flux-PIHM. Water Resour. Res. 53, 2328–2345. doi: 10.1002/2016WR018934
Basu, N. B., Destouni, G., Jawitz, J. W., Thompson, S. E., Loukinova, N. V., Darracq, A., et al. (2010). Nutrient loads exported from managed catchments reveal emergent biogeochemical stationarity. Geophys. Res. Lett. 37:L23404. doi: 10.1029/2010GL045168
Benettin, P., and Bertuzzo, E. (2018). Tran-SAS v1.0: a numerical model to compute catchment-scale hydrologic transport using StorAge selection functions. Geosci. Model Dev. 11, 1627–1639. doi: 10.5194/gmd-11-1627-2018
Ebeling, P., Kumar, R., Weber, M., Knoll, L., Fleckenstein, J. H., and Musolff, A. (2021). Archetypes and controls of riverine nutrient export across German catchments. Water Resour. Res. 57:e2020WR028134. doi: 10.1029/2020WR028134
Edinger, J., Duttweiler, D., and Geyer, J. (1968). The response of water temperature to meteorological conditions. Water Resour. Res. 5, 1137–1143. doi: 10.1029/WR004i005p01137
Falcone, J. A. (2011). GAGES-II: geospatial attributes of gages for evaluating streamflow. U.S. Geological Survey data release.
Falcone, J. A., (2021). Estimates of county-level nitrogen and phosphorus from fertilizer and manure from 1950 through 2017 in the conterminous United States (no. 2020–1153), Open-File Report. U.S. Geological Survey.
Fang, K., Kifer, D., Lawson, K., Feng, D., and Shen, C. (2022). The data synergy effects of time-series deep learning models in hydrology. Water Resour. Res. 58:e2021WR029583. doi: 10.1029/2021WR029583
Fang, K., and Shen, C. (2020). Near-real-time forecast of satellite-based soil moisture using long short-term memory with an adaptive data integration kernel. J. Hydrometeorol. 21, 399–413. doi: 10.1175/JHM-D-19-0169.1
Fazekas, H. M., McDowell, W. H., Shanley, J. B., and Wymore, A. S. (2021). Climate variability drives watersheds along a transporter-transformer continuum. Geophys. Res. Lett. 48:e2021GL094050. doi: 10.1029/2021GL094050
Feng, D. P., Fang, K., and Shen, C. P. (2020). Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 56:e2019WR026793. doi: 10.1029/2019wr026793
Gaillardet, J., Dupré, B., Louvat, P., and Allègre, C. J. (1999). Global silicate weathering and CO2 consumption rates deduced from the chemistry of large rivers. Chem. Geol. 159, 3–30. doi: 10.1016/S0009-2541(99)00031-5
Gallice, A., Schaefli, B., Lehning, M., Parlange, M. B., and Huwald, H. (2015). Stream temperature prediction in ungauged basins: review of recent approaches and description of a new physics-derived statistical model. Hydrol. Earth Syst. Sci. 19, 3727–3753. doi: 10.5194/hess-19-3727-2015
Godsey, S. E., Kirchner, J. W., and Clow, D. W. (2009). Concentration–discharge relationships reflect chemostatic characteristics of US catchments. Hydrol. Process. 23, 1844–1864. doi: 10.1002/hyp.7315
Gholizadeh, H., Zhang, Y., Frame, J., Gu, X., and Green, C. T. (2023). Long short-term memory models to quantify long-term evolution of streamflow discharge and groundwater depth in Alabama. Sci. Tot. Env. 901:165884. doi: 10.1016/j.scitotenv.2023.165884
Green, C. T., Bekins, B. A., Kalkhoff, S. J., Hirsch, R. M., Liao, L., and Barnes, K. K. (2014). Decadal surface water quality trends under variable climate, land use, and hydrogeochemical setting in Iowa, USA. Water Resour. Res. 50, 2425–2443. doi: 10.1002/2013WR014829
Harman, C. J. (2019). Age-ranked storage-discharge relations: a unified description of spatially lumped flow and water age in hydrologic systems. Water Resour. Res. 55, 7143–7165. doi: 10.1029/2017WR022304
Hirsch, R. M. (2014). Large biases in regression-based constituent flux estimates: causes and diagnostic tools. J. Am. Water Resour. Assoc. 50, 1401–1424. doi: 10.1111/jawr.12195
Hirsch, R. M., and Cicco, L. A. D. (2015). User guide to exploration and graphics for RivEr trends (EGRET) and dataRetrieval: R packages for hydrologic data (version 2.0, February 2015): U.S. Geological Survey Techniques and Methods Book 4, Chap. A10, 93 p., doi: 10.3133/tm4A10
Hirsch, R. M., Moyer, D. L., and Archfield, S. A. (2010). Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river Inputs1: weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river inputs. J. Am. Water Resour. Assoc. 46, 857–880. doi: 10.1111/j.1752-1688.2010.00482.x
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735
Ibarra, D. E., Caves, J. K., Moon, S., Thomas, D. L., Hartmann, J., Chamberlain, C. P., et al. (2016). Differential weathering of basaltic and granitic catchments from concentration–discharge relationships. Geochim. Cosmochim. Acta 190, 265–293. doi: 10.1016/j.gca.2016.07.006
Jackson-Blake, L. A., Sample, J. E., Wade, A. J., Helliwell, R. C., and Skeffington, R. A. (2017). Are our dynamic water quality models too complex? A comparison of a new parsimonious phosphorus model, simply P, and INCA-P: over-complexity in water quality models. Water Resour. Res. 53, 5382–5399. doi: 10.1002/2016WR020132
Johnson, N. M., Likens, G. E., Bormann, F. H., Fisher, D. W., and Pierce, R. S. (1969). A working model for variation in stream water chemisty at Hubbard brook experimental Forest, New Hampshire. Water Resour. Res. 5, 1353–1363. doi: 10.1029/WR005i006p01353
Jung, K., Um, M.-J., Markus, M., and Park, D. (2020). Comparison of long short-term memory and weighted regressions on time, discharge, and season models for nitrate-N load estimation. Sustain. For. 12:5942. doi: 10.3390/su12155942
Kirchner, J. W., and Neal, C. (2013). Universal fractal scaling in stream chemistry and its implications for solute transport and water quality trend detection. Proc. Natl. Acad. Sci. 110, 12213–12218. doi: 10.1073/pnas.1304328110
Knapp, J. L. A., von Freyberg, J., Studer, B., Kiewiet, L., and Kirchner, J. W. (2020). Concentration–discharge relationships vary among hydrological events, reflecting differences in event characteristics. Hydrol. Earth Syst. Sci. 24, 2561–2576. doi: 10.5194/hess-24-2561-2020
Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M. (2018). Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 22, 6005–6022. doi: 10.5194/hess-22-6005-2018
Kratzert, F., Klotz, D., Herrnegger, M., Sampson, A. K., Hochreiter, S., and Nearing, G. S. (2019a). Toward improved predictions in ungauged basins: exploiting the power of machine learning. Water Resour. Res. 55, 11344–11354. doi: 10.1029/2019wr026065
Kratzert, F., Klotz, D., Shalev, G., Klambauer, G., Hochreiter, S., and Nearing, G. (2019b). Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 23, 5089–5110. doi: 10.5194/hess-23-5089-2019
Langbein, W. B., and Dawdy, D. R. (1964). Occurrence of dissolved solids in surface waters in the United States (Report) : U.S. Geological Survey Professional Paper 501-D.
Le, V.-D., Bui, T.-C., and Cha, S.-K., (2020). Spatiotemporal deep learning model for citywide air pollution interpolation and prediction, In: 2020 IEEE international conference on big data and smart computing (BigComp). Presented at the 2020 IEEE international conference on big data and smart computing (BigComp), IEEE, Busan, Korea (South), pp. 55–62.
Li, L., Bao, C., Sullivan, P. L., Brantley, S., Shi, Y. N., and Duffy, C. (2017). Understanding watershed hydrogeochemistry: 2. Synchronized hydrological and geochemical processes drive stream chemostatic behavior. Water Resour. Res. 53, 2346–2367. doi: 10.1002/2016wr018935
Li, L., Sullivan, P. L., Benettin, P., Cirpka, O. A., Bishop, K., Brantley, S. L., et al. (2021). Toward catchment hydro-biogeochemical theories. WIREs Water 8:e1495. doi: 10.1002/wat2.1495
Liang, S., Zhao, X., Liu, S., Yuan, W., Cheng, X., Xiao, Z., et al. (2013). A long-term global LAnd surface satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 6, 5–33. doi: 10.1080/17538947.2013.805262
Lindström, G., Pers, C., Rosberg, J., Strömqvist, J., and Arheimer, B. (2010). Development and testing of the HYPE (hydrological predictions for the environment) water quality model for different spatial scales. Hydrol. Res. 41, 295–319. doi: 10.2166/nh.2010.007
Liu, P., Wang, J., Sangaiah, A. K., Xie, Y., and Yin, X. (2019). Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustain. For. 11:2058. doi: 10.3390/su11072058
Ma, J., Ding, Y., Cheng, J. C. P., Jiang, F., and Wan, Z. (2019). A temporal-spatial interpolation and extrapolation method based on geographic long short-term memory neural network for PM2.5. J. Clean. Prod. 237:117729. doi: 10.1016/j.jclepro.2019.117729
Maher, K. (2011). The role of fluid residence time and topographic scales in determining chemical fluxes from landscapes. Earth Planet. Sci. Lett. 312, 48–58. doi: 10.1016/j.epsl.2011.09.040
Maher, K., and Chamberlain, C. P. (2014). Hydrologic regulation of chemical weathering and the geologic carbon cycle. Science 343, 1502–1504. doi: 10.1126/science.1250770
Maher, K., and Navarre-Sitchler, A. (2019). Reactive transport processes that drive chemical weathering: from making space for water to dismantling continents. Rev. Mineral. Geochem. 85, 349–380. doi: 10.2138/rmg.2018.85.12
Meybeck, M., and Moatar, F. (2012). Daily variability of river concentrations and fluxes: indicators based on the segmentation of the rating curve. Hydrol. Process. 26, 1188–1207. doi: 10.1002/hyp.8211
Moatar, F., Abbott, B. W., Minaudo, C., Curie, F., and Pinay, G. (2017). Elemental properties, hydrology, and biology interact to shape concentration-discharge curves for carbon, nutrients, sediment, and major ions. Water Resour. Res. 53, 1270–1287. doi: 10.1002/2016WR019635
Musolff, A., Schmidt, C., Selle, B., and Fleckenstein, J. H. (2015). Catchment controls on solute export. Adv. Water Resour. 86, 133–146. doi: 10.1016/j.advwatres.2015.09.026
Nearing, G. S., Kratzert, F., Sampson, A. K., Pelissier, C. S., Klotz, D., Frame, J. M., et al. (2021). What role does hydrological science play in the age of machine learning? Water Resour. Res. 57:e2020WR028091. doi: 10.1029/2020wr028091
Newcomer, M. E., Bouskill, N. J., Wainwright, H., Maavara, T., Arora, B., Siirila-Woodburn, E. R., et al. (2021). Hysteresis patterns of watershed nitrogen retention and loss over the past 50 years in United States hydrological basins. Glob. Biogeochem. Cycles 35:e2020GB006777. doi: 10.1029/2020GB006777
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., et al. (2015). Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Syst. Sci. 19, 209–223. doi: 10.5194/hess-19-209-2015
Park, D., Um, M.-J., Markus, M., Jung, K., Keefer, L., and Verma, S. (2021). Insights from an evaluation of nitrate load estimation methods in the Midwestern United States. Sustain. For. 13:7508. doi: 10.3390/su13137508
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). PyTorch: an imperative style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 32, 8024–8035.
Rahmani, F., Shen, C. P., Oliver, S., Lawson, K., and Appling, A. (2021). Deep learning approaches for improving prediction of daily stream temperature in data-scarce, unmonitored, and dammed basins. Hydrol. Process. 35:e14400. doi: 10.1002/hyp.14400
Roelandt, C., Goddéris, Y., Bonnet, M.-P., and Sondag, F. (2010). Coupled modeling of biospheric and chemical weathering processes at the continental scale. Glob. Biogeochem. Cycles 24:3420. doi: 10.1029/2008GB003420
Ruddy, B. C., Lorenz, D. L., and Mueller, D. K. (2006). County-level estimates of nutrient inputs to the landsurface of the conterminous United States, 1982-2001 (USGS numbered series no. 2006–5012), county-level estimates of nutrient inputs to the landsurface of the conterminous United States, 1982-2001, scientific investigations report. Reston, VA: U.S. Geological Survey.
Sabo, R. D., Clark, C. M., Bash, J., Sobota, D., Cooter, E., Dobrowolski, J. P., et al. (2019). Decadal shift in nitrogen inputs and fluxes across the contiguous United States: 2002–2012. J. Geophys. Res. Biogeosciences 124, 3104–3124. doi: 10.1029/2019JG005110
Sabo, R. D., Clark, C. M., Gibbs, D. A., Metson, G. S., Todd, M. J., LeDuc, S. D., et al. (2021). Phosphorus inventory for the conterminous United States (2002–2012). J. Geophys. Res. Biogeosci. 126:e2020JG005684. doi: 10.1029/2020JG005684
Sadler, J. M., Appling, A. P., Read, J. S., Oliver, S. K., Jia, X., Zwart, J. A., et al. (2022). Multi-task deep learning of daily streamflow and water temperature. Water Resour. Res. 58:e2021WR030138. doi: 10.1029/2021WR030138
Saha, G. K., Rahmani, F., Shen, C., Li, L., and Cibin, R. (2023). A deep learning-based novel approach to generate continuous daily stream nitrate concentration for nitrate data-sparse watersheds. Sci. Total Environ. 878:162930. doi: 10.1016/j.scitotenv.2023.162930
Sahraei, A., Houska, T., and Breuer, L. (2021). Deep learning for isotope hydrology: the application of long short-term memory to estimate high temporal resolution of the stable isotope concentrations in stream and groundwater. Front. Water 3:44. doi: 10.3389/frwa.2021.740044
Stackpoole, S. M., Stets, E. G., and Sprague, L. A. (2019). Variable impacts of contemporary versus legacy agricultural phosphorus on US river water quality. Proc. Natl. Acad. Sci. 116, 20562–20567. doi: 10.1073/pnas.1903226116
Thompson, S. E., Basu, N. B., Lascurain, J., Aubeneau, A., and Rao, P. S. C. (2011). Relative dominance of hydrologic versus biogeochemical factors on solute export across impact gradients: hydrology controls solute export. Water Resour. Res. 47:W00J05. doi: 10.1029/2010WR009605
Torres, M. A., and Baronas, J. J. (2021). Modulation of riverine concentration-discharge relationships by changes in the shape of the water transit time distribution. Glob. Biogeochem. Cycles 35:e2020GB006694. doi: 10.1029/2020GB006694
Varadharajan, C., Appling, A. P., Arora, B., Christianson, D. S., Hendrix, V. C., Kumar, V., et al. (2022). Can machine learning accelerate process understanding and decision-relevant predictions of river water quality? Hydrol. Process. 36:e14565. doi: 10.1002/hyp.14565
Wade, A. J., Durand, P., Beaujouan, V., Wessel, W. W., Raat, K. J., Whitehead, P. G., et al. (2002). A nitrogen model for European catchments: INCA, new model structure and equations. Hydrol. Earth Syst. Sci. 6, 559–582. doi: 10.5194/hess-6-559-2002
Wymore, A. S., Brereton, R. L., Ibarra, D. E., Maher, K., and McDowell, W. H. (2017). Critical zone structure controls concentration-discharge relationships and solute generation in forested TROPICAL montane watersheds: TROPICAL C-Q RELATIONSHIPS. Water Resour. Res. 53, 6279–6295. doi: 10.1002/2016WR020016
Xu, Z., Molins, S., Özgen-Xian, I., Dwivedi, D., Svyatsky, D., Moulton, J. D., et al. (2022). Understanding the Hydrogeochemical response of a mountainous watershed using integrated surface-subsurface flow and reactive transport modeling. Water Resour. Res. 58:e2022WR032075. doi: 10.1029/2022WR032075
Yan, J., Gao, Y., Yu, Y., Xu, H., and Xu, Z. (2020). A prediction model based on deep belief network and least squares SVR applied to cross-section water quality. Water 12:1929. doi: 10.3390/w12071929
Zeiler, M. D. (2012). ADADELTA: an adaptive learning rate method. arXiv 1212:5701. doi: 10.48550/arXiv.1212.5701
Zhang, Q. (2018). Synthesis of nutrient and sediment export patterns in the Chesapeake Bay watershed: complex and non-stationary concentration-discharge relationships. Sci. Total Environ. 618, 1268–1283. doi: 10.1016/j.scitotenv.2017.09.221
Zhang, Q., and Hirsch, R. M. (2019). River water-quality concentration and flux estimation can be improved by accounting for serial correlation through an autoregressive model. Water Resour. Res. 55, 9705–9723. doi: 10.1029/2019WR025338
Zhang, Y., Li, C., Jiang, Y., Sun, L., Zhao, R., Yan, K., et al. (2022). Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model. J. Clean. Prod. 354:131724. doi: 10.1016/j.jclepro.2022.131724
Zhi, W., Appling, A. P., Golden, H. E., Podgorski, J., and Li, L. (2024). Deep learning for water quality. Nat. Water 2, 228–241. doi: 10.1038/s44221-024-00202-z
Zhi, W., Feng, D., Tsai, W.-P., Sterle, G., Harpold, A., Shen, C., et al. (2021). From hydrometeorology to river water quality: can a deep learning model predict dissolved oxygen at the continental scale? Environ. Sci. Technol. 55, 2357–2368. doi: 10.1021/acs.est.0c06783
Keywords: water quality, biogeochemial processes, deep learning—artificial intelligence, WRTDS, LSTM, concentration-discharge models
Citation: Fang K, Caers J and Maher K (2024) Modeling continental US stream water quality using long-short term memory and weighted regressions on time, discharge, and season. Front. Water. 6:1456647. doi: 10.3389/frwa.2024.1456647
Received: 28 June 2024; Accepted: 05 September 2024;
Published: 01 October 2024.
Edited by:
Qian Zhang, University of Maryland, United StatesReviewed by:
Christopher Green, United States Department of the Interior, United StatesCopyright © 2024 Fang, Caers and Maher. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: K. Fang, a3VhaWZhbmdAc3RhbmZvcmQuZWR1; K. Maher, a21haGVyQHN0YW5mb3JkLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.