- DeFrees Hydraulics Laboratory, School of Civil & Environmental Engineering, Cornell University, Ithaca, NY, United States
The use of image based velocimetry methods for field-scale measurements of river surface flow and river discharge have become increasingly widespread in recent years, as these methods have several advantages over more traditional methods. In particular, image based methods are able to measure over large spatial areas at the surface of the flow at high spatial and temporal resolution without requiring physical contact with the water. However, there is a lack of tools to understand the spatial uncertainty in these methods and, in particular, the sensitivity of the uncertainty to parameters under the implementer's control. We present a tool specifically developed to assess spatial uncertainty in remotely sensed, obliquely captured, quantitative images, used in surface velocimetry techniques, and selected results from some of our measurements as an illustration of the tool's capabilities. The developed software is freely available via the public repository GitHub. Uncertainty exists in the coordinate transformation between pixel array coordinates (2D) and physical coordinates (3D) because of the uncertainty related to each of the inputs to the calculation of this transformation, and additionally since the transformation itself is generally calculated in a least squares sense from an over determined system of equations. In order to estimate the uncertainty of the transformation, we perform a Monte Carlo simulation, in which we perturb the inputs to the algorithm used to find the coordinate transformation, and observe the effect on the results of transformations between pixel- and physical- coordinates. This perturbation is performed independently a large number of times over a range of the input parameter space, creating a set of inputs to the coordinate transformation calculation, which are used to calculate a coordinate transformation, and predict the physical coordinates of each pixel in the image. We analyze the variance of the physical position corresponding to each pixel location across the set of transformations, and quantify the sensitivity of the transformation to changes in each of the inputs across the field of view. We also investigate the impact on uncertainty of ground control point (GCP) location and number, and quantify spatial change in uncertainty, which is the key parameter for calculating uncertainty in velocity measurements, in addition to positions. This tool may be used to plan field deployments, allowing the user to optimize the number and distribution of GCPs, the accuracy with which their position must be determined, and the camera placement required to achieve a target level of spatial uncertainty. It can also be used to estimate the uncertainty in image-based velocimetry measurements, including how this uncertainty varies over space within the field of view.
1. Introduction
Image based velocimetry methods have great utility, as they allow continuous, non-contact, measurements of velocity over two-dimensional areas. Particle image velocimetry (PIV) and particle tracking velocimetry (PTV) methods, which have been used extensively in the laboratory (e.g., Adrian, 1991; Cowen and Monismith, 1997), have also been extended for use in field scale settings (e.g., Fujita et al., 1998; Creutin et al., 2003; Kim et al., 2008). These methods are based on tracking images of particles or patterns, as they are digitized on an array of pixels, as they are advected by the flow, and inferring the flow velocity based on a transformation of these pixel displacement to physical dimensions of length, and knowledge of the time over which they occurred.
Field scale image velocimetry applications can use algorithms adapted from laboratory applications, however, in recent years a large number of methods have been developed specifically for use with field-scale imagery, including Space-Time Image Velocimetry (STIV; Fujita et al., 2007), Kanade-Lucas-Tomasi feature tracking (KLT; Perks et al., 2016), Optical Tracking Velocimetry (OTV; Tauro et al., 2018b), Surface Structure Image Velocimetry (SSIV; Leitāo et al., 2018), Infrared Quantitative Image Velocimetry (IR-QIV; Schweitzer and Cowen, 2021), and others. These methods have been used with cameras both in fixed positions or mounted on mobile platforms such as unoccupied aerial systems (UASs) (Detert and Weitbrecht, 2015; Detert et al., 2017; Lewis et al., 2018; Eltner et al., 2020). Image-based surface velocimetry methods have been used utilizing images captured in various spectral ranges, including the visible light spectral range, and the infrared spectral range (Chickadel et al., 2011; Puleo et al., 2012; Legleiter et al., 2017; Eltner et al., 2021; Schweitzer and Cowen, 2021).
Although image-based surface velocimetry methods span a range of analysis methods, camera configurations, and imaged wavelengths, they all share the need for georeferencing, which involves a transformation between a three dimensional coordinates system in physical space and the two dimensional coordinates of an array of pixels in an image. Several methods of finding a transformation between these two coordinate systems exist, all of which depend, implicitly or explicitly, on the camera's position and orientation, and on resolving distortion introduced by the image acquisition system. Any uncertainty associated with the determination of the parameters used to calculate the coordinate transformation will create uncertainty in the transformation, which will carry over and lead to uncertainty in the resulting velocity measurements.
Literature discussing uncertainty in field-scale, image-based velocimetry (e.g., Hauet et al., 2008; Muste et al., 2008), generally focuses on discharge estimation, and combines uncertainty stemming from multiple sources: surface seeding and illumination, selection of interrogation area size, estimation of water column velocity from the surface velocity (velocity index, or α), cross-channel bathymetry, and georeferencing. In recent years, with technological advances allowing for small, high quality cameras, and the flexibility to deploy cameras from drones and other platforms, image-based velocimetry methods have increasingly been used for applications requiring more detailed measurements than estimating bulk parameters such as mean velocity and discharge. An early example of this is Fujita et al.'s (2004) work on flow over and around spur dykes, and more recently, the study of river confluences (Lewis and Rhoads, 2018), fish diversion structures (Strelnikova et al., 2020), and instantaneous velocity measurements at the surface of rivers (Schweitzer and Cowen, 2021).
These high-fidelity surface measurement applications require a more nuanced approach to uncertainty analysis, and in particular benefit from analysis of the spatial distribution of uncertainty between different regions of the field of view field of view (FOV). However, specific discussion of uncertainty resulting from georeferencing remains lacking in the surface velocimetry literature. The accuracy of georeferencing depends on performing appropriate intrinsic and extrinsic calibrations of cameras used for surface velocimetry, however, as reported by Detert (2021), these fundamental steps are often neglected or overly simplified by making assumptions about camera parameters and viewing angles. When used in a laboratory or similar setting the camera can often be set up with a view normal to the plane of the image, in which case the transformation between pixel coordinates and physical dimensions of length is straightforward (e.g., Cowen and Monismith, 1997). In field settings the camera is often oriented at an oblique angle to the surface being imaged, which introduces perspective distortion in the image (i.e., the physical distance between the locations described by two adjacent pixels will change based on their position within the image). Even if the camera is orientation approximately normal to the water surface, such as from an aerial platform or a bridge, small deviations from nadir view can have a significant impact on velocimetry results. For example, Detert (2021) showed that incomplete camera calibration can lead to errors in velocity estimation on the order of 20% or more. This article presents a method of estimating uncertainty related to georeferencing by quantifying the sensitivity of the results of the transformation to stochastic changes in the inputs, using a Monte Carlo simulation technique.
Recently published analyses of uncertainty in image based surface velocimetry include that of Rozos et al. (2020), who used a Monte Carlo simulation method to analyze the effects of interrogation area dimensions on uncertainty in large scale particle image velocimetry (LSPIV), and of Le Coz et al. (2021) who used Bayesian methods and a Markov Chain Monte Carlo sampler to conduct an in-depth analysis of uncertainty related to georeferencing, and to reduce uncertainty in velocity and discharge LSPIV measurements, by combining available knowledge of GCP coordinates and of the camera's position and orientation. The strength of Le Coz et al.'s (2021) method is that it utilizes a combination of explicit information about the camera's position and orientation, and implicit information in the form of ground control point (GCP) coordinates. However, the method described in that article does not address spatial variance of uncertainty within a particular FOV, and one of its conclusions is that a need exists additional other methods to quantify uncertainty due to camera model errors and GCP real-world coordinate errors, two topics which are discussed in this article.
In contrast to the Bayesian approach of Le Coz et al. (2021), our approach examines the variance of spatial uncertainty across the FOV, as a result of either explicit or implicit georeferencing methods (separately, but not combined), and can be used as a straightforward tool to optimize camera and GCP positioning at the site of a planned study.
Our method allows in depth examination of not only the general uncertainty in georeferencing a particular FOV, but also how it varies from place to place within the FOV. Understanding the spatial variance of this uncertainty is key to quantifying the uncertainty of velocity measurements, since they will be affected by changes in the accuracy of the georeferencing transformation along the path over which a parcel of water is tracked. In addition, the method described in this article provides tools to explore the potential impact of modifying specific parameters, such as the position and location of GCPs, or improving the accuracy with which GCP positions are determined.
The structure of this article is as follows: in Section 2 we present an overview of georeferencing methods, and of our Monte Carlo method of estimating uncertainty. In Section 3 we present an example from a large scale velocity measurement conducted by the authors using IR-QIV. Discussion is provided in the remaining sections.
The uncertainty analysis tools described in this article were developed by the authors using the Julia programming language. Julia is an open source, high level, high performance, scientific computing language (Bezanson et al., 2017). The code for the camera calibration and uncertainty analysis tools described in this article is publicly available at https://github.com/saschweitzer/camera-calibration.
2. Methods
2.1. Georeferencing Method
Georeferencing involves a transformation between two-dimensional image (pixel) coordinates (u, v) and three-dimensional physical coordinates (x, y, z). In general, this transformation requires precise knowledge of the camera's position and orientation (known as extrinsic camera calibration parameters), as well as optical characteristics, including magnification and any distortion that might exist due to the optical or electronic image acquisition path (known as intrinsic calibration parameters). When all of the camera calibration parameters are known it is possible to transform between 3D physical coordinates and 2D pixel coordinates. The inverse transformation, from pixel to physical coordinates, requires an additional piece of information, namely the distance between the camera and the object visible in the image. In surface velocimetry applications this is often found from the difference between the camera's elevation and the water surface elevation (WSE). Other methods of determining the distance from the camera, such as multiscopic views, are not discussed in this article, however, the uncertainty analysis method described here remains valid, with the appropriate modifications to inputs, regardless of the method used.
If the camera calibration parameters are known a-priori an explicit, or direct georeferencing, transformation can be calculated. This is often done if the camera can be assumed to be oriented normal to the water surface (i.e., at a nadir view), e.g., if the camera is mounted on an aerial platform. The camera's orientation may also be measured directly, e.g., by using an inertial measurement unit (IMU). In the more general case where the camera's position and orientation are not known these parameters may be calculated from the collected images, by relating the coordinates of features visible in the image in the two coordinate systems. These features are known as ground control points (GCPs, sometimes referred to as ground reference points, GRPs), and can be either naturally occurring or placed by the practitioner. Good GCPs must be clearly identifiable both in the field and in images so that their coordinates can be unambiguously determined in the two coordinate systems. This type of calculation is known as implicit georeferencing.
Most camera calibration methods can be categorized as explicit or implicit (Holland et al., 1997). Explicit methods use an iterative algorithm that minimizes a set of non-linear, or in some cases linearized, equations to estimate all the camera calibration parameters and uses them to calculate the coordinate transformation. Implicit methods, such as the Direct Linear Transformation (DLT) method of Abdel-Aziz et al. (1971), use intermediate parameters to calculate the coordinate transformation. The parameters are calculated based on a closed-form solution to a linear set of equations. Two-step methods solve for combinations of implicit and explicit methods for the various camera calibration parameters, such as Holland et al.'s (1997) method, which itself is a modified version of Tsai's (1987) method.
In this manuscript, we follow the georeferencing method developed by Holland et al. (1997), which is a two-step method in which the intrinsic camera properties (coordinates of the image center, horizontal and vertical magnification coefficients, and radial distortion) are determined before deploying the camera, so that only the extrinsic properties of the camera must be determined in the field. The extrinsic parameters include the camera's coordinates (xc, yc, zc), orientation angles (azimuth, ϕ, tilt, τ, and roll, σ), and the focal length (f). Focal length is technically an intrinsic characteristic of the camera, but it can vary with lens focus and with changes in the camera temperature (e.g., Elias et al., 2020), so it is advantageous to determine it in the field after positioning the camera. While it is possible to determine both the intrinsic and extrinsic camera parameters in the field using GCPs, separating the process into two steps reduces the number of GCPs required, while increasing the accuracy of the intrinsic calibration by using a calibration target in a controlled environment. The intrinsic camera parameters only change if the camera's hardware is modified (e.g., changing the lens), so it only needs to be performed once, whereas the extrinsic calibration must be repeated any time the camera is moved.
There are seven unknowns (xc, yc, zc, ϕ, τ, σ, f) to be solved for in the extrinsic calibration. Each GCP yields a pair of equations (one each for the u and v pixel coordinates), so a minimum of four GCPs are required, although in theory it is possible to reduce this number if other information is available, such as the position of the camera (xc, yc, zc). If more than the minimum number of GCPs are available the system of equations is overdetermined and it is typical solved in a least-squares sense. Once the intrinsic and extrinsic camera calibration parameters have been found they are used to calculate the coefficients of the DLT, which transforms between pixel coordinates and physical coordinates.
Other georeferencing methods for velocimetry applications exist in the literature. These include, among others, a coplanar-GCP method that requires all the GCPs to be placed in a plane parallel to the plane of the water surface, first described by Fujita et al. (1997, 1998) and used by others, e.g., Creutin et al. (2003), Jodeau et al. (2008), and a method that requires a minimum of six non-coplanar GCPs that solves for all 11 calibration parameters from GCPs in the field without separating intrinsic and extrinsic calibration steps, described by, for example, Muste et al. (2008).
In velocimetry methods based on images collected from aerial platforms an assumption is sometimes made that the camera is oriented at a normal angle to the water surface, and, therefore, the transformation between pixel and physical coordinate systems is only a matter of magnification based on the camera's focal length and distance from the water surface, and rotation (e.g., relative to the north) (Streßer et al., 2017; Tauro et al., 2018a). However, while this type of assumption simplifies the analysis required for velocimetry, neglecting to perform careful intrinsic and extrinsic calibration can lead to significant reduction in the accuracy of velocimetry results (Detert, 2021).
All of the above methods are based on a pinhole camera model, which assumes no distortion in the optical path. Radial distortion (i.e., barrel, pincushion, or a combination of the two) can be present in cameras used for velocimetry applications, and can lead to significant errors if not corrected for, especially when using short focal length lenses. The effects are increased near the edges of the image, and exist even if there is little perspective distortion due to a nadir view (Detert, 2021). Radial distortion must, therefore, be accounted for before performing georeferencing. The radial distortion of a camera is often modeled as a polynomial, the coefficients of which can be found by imaging a regular grid target such as a checkerboard, and fitting a curve to the change in distance between grid points in the image as a function of distance from the image center. Similar methods are used to remove radial distortion when using infrared (IR) images, however printed checkerboards may not be the best calibration target in this case. Alternate targets may be preferable, such as the emissivity contrast target described in Schweitzer and Cowen (2021). In georeferencing methods that involve only a field (i.e., GCP) step, without a separate intrinsic calibration step, radial distortion is sometimes addressed using a grid of reference points in the field, covering a subset of the FOV (e.g., Lewis and Rhoads, 2018), or using image processing software that makes assumptions of the distortion based on the camera and lens model (e.g., Tauro et al., 2018b). However, these methods may not completely eliminate the effects of radial distortion (Detert, 2021).
2.2. Georeferencing Sensitivity Simulation
We quantify the general georeferencing uncertainty, and the sensitivity of the georeferencing transformation to uncertainty in its inputs, by way of a Monte Carlo simulation. Regardless of the method used, georeferencing consists of using a set of inputs to calculate a transformation between pixel and physical coordinates, which is then used to calculate the physical coordinates of the center of pixels in the image. Our approach is to perturb the inputs to the calculation, and observe the effect on the transformed coordinate set. By perturbing one or more of the inputs by a randomly selected amount, repeated a significant number of times with a range of perturbations, we calculate statistics of the sensitivity of the output of the coordinate transformation to perturbations in its inputs. We select a distribution of input perturbations that is similar to our estimates of a reasonable distribution of error in the inputs in a real measurements, e.g., the x, y, z coordinates of a GCP may be perturbed by random values corresponding to the uncertainty of the survey method used to determine its location.
This methodology is similar to the more basic version described in Schweitzer and Cowen (2021), expanded here to illustrate the effects of correcting for, or neglecting, radial lens distortion, comparing oblique (e.g., camera installed on the river bank), and nadir (such as from an aerial platform) viewing angles, and to consider the effects of the distribution of GCPs within the images, which can be a useful planning tool. Additionally, we simulate the uncertainty related to using a direct georeferencing system, which is based on directly measuring, or estimating, the position and orientation of the camera (e.g., using an IMU), without utilizing GCPs.
The steps of the simulation are:
Create a reference set of coordinates: Define a reference camera installation geometry, and use it to calculate a reference set of (x, y) pixel ground footprint coordinates from each pixel's (u, v) coordinates. This will be used as a baseline to compare the results of the perturbed simulations. The reference geometry can be defined either by directly defining the camera's position (xc, yc, zc), orientation (ϕ, τ, σ), and focal length (f), or by using a set of GCPs and performing a georeferencing calculation. In the second case the input parameters can be the surveyed or estimated GCP coordinates from an existing measurement, or they can be arbitrarily assigned, e.g., as the design parameters for a planned surface velocity measurement. Since this reference set of coordinates is used only for simulations, and not for rectifying actual images, we can reduce computational costs by considering only a subset of pixels (e.g., every 6th row and column of pixels).
Generate a random set of input perturbations: After generating the reference coordinates, we randomly select multiple sets of perturbations to apply to simulate uncertainty. Each of these sets are either a combination of perturbations to the WSE and the GCP's pixel and physical coordinates, or direct perturbations of camera's position and orientation. Alternatively, the location of GCPs to be used may be randomly selected to analyze the sensitivity to GCP placement. In this case the GCP coordinates may be selected either in the pixel or the physical coordinate systems. We can also simulate radial distortion in the image, to test sensitivity of the velocimetry results to the effects of not performing a correction for radial distortion.
Use the input perturbations to calculate a simulated set of coordinates: Using each set of input perturbations separately, perform the extrinsic calibration, and calculate the simulated (x, y) coordinates of the pixels from the reference set. The error distance between the reference and simulated coordinates is then calculated at each point, and interpolated over a regular grid for each set of simulation inputs. The interpolation step is important especially when the camera is oriented at an oblique viewing angle because the corresponding (x, y) distance between adjacent (u, v) pixel coordinates is not uniform, so a regular grid in pixel coordinates will result in a concentration of grid points close to the camera in physical coordinates. Interpolating the error distance over a regular grid eliminates sampling biases when calculating statistics of error across the FOV.
Finally, calculate uncertainty statistics for each pixel: At the end of n iterations, we will have a set of n different (x, y) coordinates corresponding to each pixel in the reference set. We can now calculate statistics of the range of values at each point. Note that uncertainty in the intrinsic calibration stage, most notably related to removal of radial distortion, is included in the simulation implicitly in the form of uncertainty in identifying the pixel (u, v) coordinates of the GCPs, however, it is also possible to explicitly introduce this as an additional uncertainty parameter in the Monte Carlo simulation.
2.3. Uncertainty Range for Georeferencing Inputs
The simulated data set is generated by adding random perturbations with a user-defined distribution to each of the inputs of the georeferencing calculation. We assume that when conducting a field measurement the errors in these inputs are random and unbiased, and, therefore, select perturbations from a normal distribution with zero mean, and standard deviation selected based on our assumptions of accuracy of each input parameter. We note that while the perturbations are selected randomly, based on the assumption of random and unbiased error to actual inputs, the effect of a set of perturbed inputs is to introduce a bias error into the georeferencing results, i.e., for a given set of input perturbations, errors in the georeferenced results will be fixed and not random.
The distributions from which perturbations of each of the georeferencing inputs are randomly selected may be defined by the user of the software tool, to match the camera being used or other constraints of a particular measurement. In the following we describe the distributions used in the simulations presented in Section 3.
We estimate a standard deviation of 3 cm for the surveyed x, y, z coordinates of GCPs. The uncertainty of the position of a single survey measurement may be much smaller, on the order of 1 cm or less depending on the equipment used and the skill of the operator. However, the precision with which the measurement location on the face of the GCP targets is determined must also be taken into account. Likewise, when identifying the u, v (pixel) coordinates for GCPs within images, the accuracy is a combination of operator skill, the relative size of pixel footprints and the GCP target being identified, as well as factors such as radial and perspective distortion. We generally use 0.5 pixels as the standard deviation for this perturbation.
We estimate the WSE uncertainty as having a standard deviation of 3 cm. This uncertainty includes a combination of uncertainty from a number of sources, including the measurement uncertainty of the sensor tracking the WSE, the accuracy with which the sensor's position is determined, and variations in WSE across the FOV due to ripples or other surface effects.
In direct georeferencing we use standard deviations of 0.8° for heading, 0.1° for roll and pitch, and 5 cm for position. These values are based on manufacturer specifications of typical IMU systems (e.g., the one used by Eltner et al., 2021). We note, however, that in practice there are additional challenges to account for when considering direct georeferencing uncertainty, including offsets between the IMU and camera coordinate systems, and temporal synchronization of image capture and IMU readings. Also, images acquired from a mobile platform, such as a UAS, often require digital image stabilization, which may introduce additional spatial uncertainty (Ljubičić et al., 2021). Therefore, it is likely that in many cases the uncertainty estimates for direct georeferencing used here are not highly conservative, especially for images acquired from mobile platforms, and we expect the actual uncertainty when using direct georeferencing to at times be significantly higher.
Radial lens distortion can optionally be added to the analysis. We introduce radial distortion as a way to simulate the result of neglecting to correct for radial distortion when acquiring images. Radial distortion is often modeled as a polynomial function of distance from the image center (e.g., Holland et al., 1997). We use a polynomial of the form , where r is the distance (in pixels) from the image center and Δr represents the pixel displacement due to distortion, with the coefficients , calculated from an intrinsic calibration of the camera described in Schweitzer and Cowen (2021).
Since velocimetry applications such as LSPIV use the distance a parcel of water has been advected over some finite amount of time to calculate velocity, it is important to know not only what is the uncertainty at any point within an image, but how the uncertainty changes throughout the image. If the start and end locations over which a parcel of water is displaced have the same bias (or fixed) uncertainty error, this constant offset will not affect the relative distance between the two coordinates. In order to estimate the effects of spatial uncertainty on velocity measurements we, therefore, calculate the spatial gradient of uncertainty at each point within the image. If the gradient of uncertainty is small at any position within the image, it follows that the uncertainty of a velocity measurement at that location will also be relatively low. This is illustrated in Section 3.1.
3. Results and Discussion
Here, we present examples of spatial uncertainty analysis from two field setups, one with the camera oriented at an oblique viewing angle, the second simulating an unoccupied aerial vehicle (UAV) with a vertically oriented camera. The oblique view setup used here is based on the one described in Schweitzer and Cowen (2021), in which a camera was installed at an elevation of approximately 25 m above the water surface, oriented to view across a 50 m wide channel. In that study an infrared camera was used, but the uncertainty analysis is the same regardless of the operating wavelength of the camera (i.e., infrared or visible light).
Analysis of uncertainty is presented for these two setups both for the case of GCP-based georeferencing and direct georeferencing. Additional plots describe the uncertainty under similar conditions, but in the presence of uncorrected radial distortion in the lens system. In all plots the distances indicated are horizontal distances in the plane of the water surface, measured from directly beneath the camera. We report the results as contours of uncertainty. We calculate, at each pixel location within the FOV, the distance between the nominal x, y position of the reference set of coordinates and the position calculated in each of n simulations. We then take the 95th percentile of this set at each pixel location, and use this to plot the contours.
In the GCP-based georeferencing cases presented here a total of four GCPs were used, in positions selected at random from a 50 × 50 pixel region in each corner of the image. The position of the GCPs are plotted as red dots in the figures. The GCP coordinates are not identical in all plots, since each plot describes a distinct set of simulations, and each set used a separate, randomly selected, collection of GCPs. However, in each case GCP coordinates were selected using the same constraint on distance from the corners of the image. The plotted position of the GCPs corresponds to the reference set of coordinates, as described in the first step of the simulation process (Section 2.2).
This distribution of GCPs was selected to illustrate the uncertainty analysis tool, and the resulting uncertainty when using this near-optimal distribution of GCPs. However, the number of GCPs to use, and constraints on their placement, are input parameters that may be defined by a user of the software tool in accordance with any desired experimental setup.
Figure 1A shows contours of the 95th percentile of uncertainty at each location within the FOV, using GCP-based georeferencing. Figure 1B is similar, but is calculated using direct georeferencing. In this oblique view scenario, direct georeferencing has significantly more uncertainty than GCP-based georeferencing, up to approximately a factor of five (for this camera and setup geometry) when assuming the same level of uncertainty in the inputs to the georeferencing calculation. In Figure 2A, the GCP-based analysis is repeated, but without correcting for radial distortion from the camera lens. The corresponding direct georeferencing case is shown in Figure 2B. If radial distortion is not accounted for, the spatial uncertainty can increase by as much as a factor of five, even when using a GCP-based calculation.
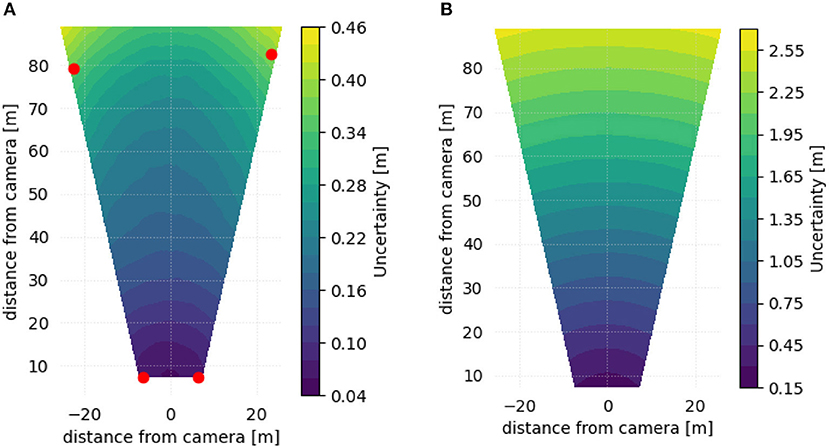
Figure 1. Contours of the 95th percentile of spatial uncertainty estimated at each pixel footprint in an oblique view camera setup, after correcting the images for radial distortion. (A) Using 4 GCPs located near the corners of the FOV (red dots). (B) Using direct georeferencing.
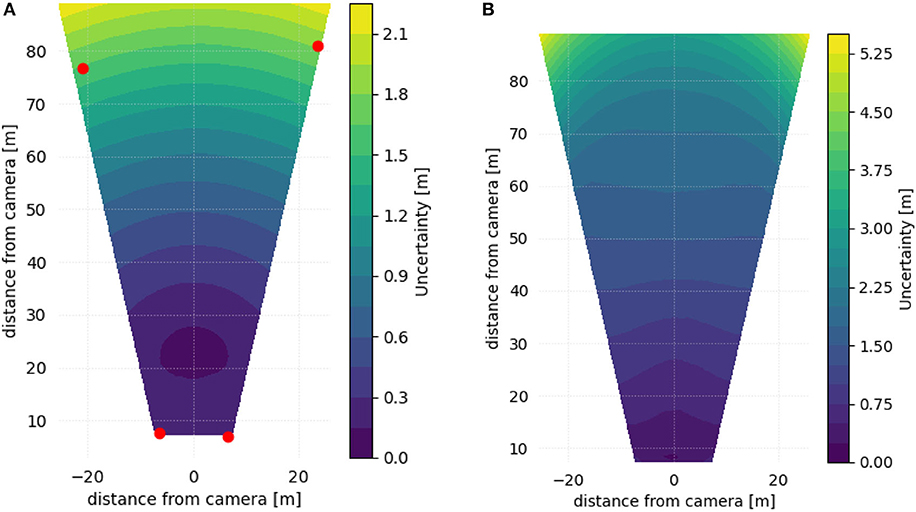
Figure 2. Contours of the 95th percentile of spatial uncertainty estimated at each pixel footprint in an oblique view camera setup, without correcting the images for radial distortion. (A) Using 4 GCPs located near the corners of the FOV (red dots). (B) Using direct georeferencing.
Radial distortion violates the assumption of collinearity between the camera's optical center (xc, yc, zc), pixel coordinates (u, v), and physical coordinates (x, y, z); that a straight line drawn between the camera's optical center and an object in space will extend through the (u, v) coordinate in the pixel array where the object is observed in an image (Holland et al., 1997). As a result, uncorrected (u, v) pixel coordinates identified in an image that is affected by radial distortion will have an offset from their coordinates in a distortion-free system, which impacts georeferencing in two ways. First, in the case of GCP-based georeferencing, failing to account for radial distortion will lead to the use of inaccurate GCP pixel coordinates during the extrinsic calibration step, resulting in an incorrect georeferencing transformation. Second, for both GCP-based and direct georeferencing, even if the position and orientation of the camera were perfectly determined and an error-free coordinate transformation was found, using pixel coordinates that are not corrected for radial distortion as inputs will lead to errors in the transformed x, y coordinates. Uncorrected radial distortion will, therefore, lead to an increase in uncertainty, since it will magnify georeferencing errors in regions of the image affected by radial distortion.
Figures 3A,B show 95th percentile uncertainty contours in a nadir view camera setup, such as might be collected from a UAS. The estimated uncertainty is again on the order of five times or more larger when using direct georeferencing relative to the GCP-based method, especially in regions not directly beneath the camera (i.e., in locations where the viewing angle becomes relatively oblique).
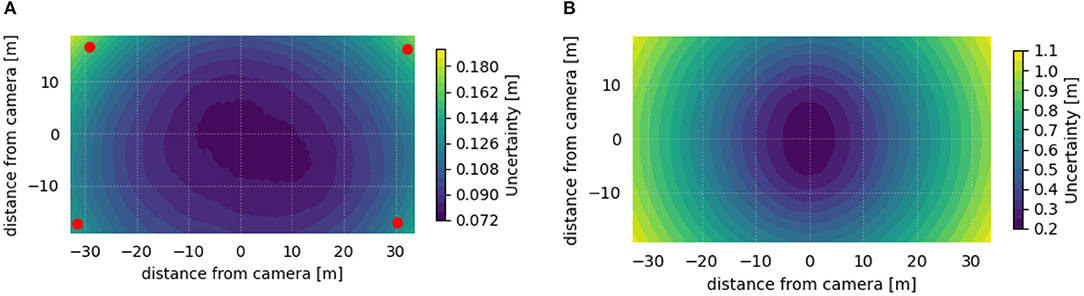
Figure 3. Contours of the 95th percentile of spatial uncertainty estimated at each pixel footprint in a nadir view camera setup, after correcting the images for radial distortion. (A) Using 4 GCPs located near the corners of the FOV (red dots). (B) Using direct georeferencing.
Figures 4A–C illustrate the effect of introducing perturbations to only one of the georeferencing inputs. In the setup described here, and with the selected distribution of input perturbations, it is clear that the primary source of uncertainty in georeferencing in this setup is due to uncertainty in determining the correct x, y, z coordinates of the GCPs, as the uncertainty introduced by perturbing only this input is larger by 50% or more than the uncertainty introduced by perturbing the u, v pixel coordinates or the WSE.
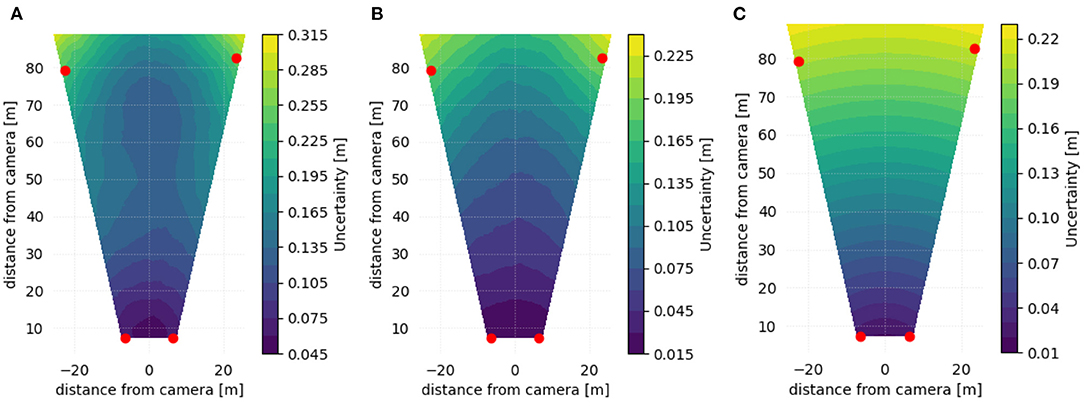
Figure 4. 95th percentile contours of spatial uncertainty, resulting from perturbing only one input to the georeferencing calculation. Red dots indicate positions of GCPs. (A) Perturbations applied only to the physical (x, y, z) coordinates of each GCP. (B) Perturbations applied only to the pixel (u, v) coordinates of each GCP. (C) Perturbations applied only to the water surface elevation.
The setup described here, with GCPs distributed near each corner of the FOV, leads to minimal uncertainty. This is a near ideal distribution of GCPs within the FOV that an experimental plan might attempt to achieve, and it simplifies comparisons of different sources of uncertainty. In practice, it might not be possible to achieve this type of distribution of GCPs. When the camera's viewing angle is oblique, uncertainty grows as a function of distance from the camera (due to increasingly oblique viewing angles at larger distances), and distance from the GCPs. This is illustrated in Figure 5 in which 6 GCPs are distributed unevenly throughout the FOV. The uncertainty in this case is approximately four times higher than observed in Figure 4C (in both of these figures uncertainty is calculated considering perturbations only to the water surface elevation).
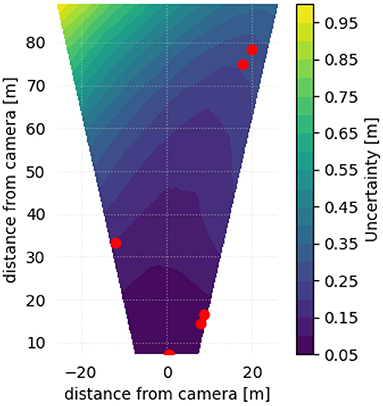
Figure 5. 95th percentile contours of spatial uncertainty, with 6 GCPs (red dots) distributed unevenly within the FOV, resulting from perturbing only the water surface elevation.
The software tool allows us to simulate a range of possible FOV configurations, and either select locations to position each GCP, or randomly assign them to specific regions of the FOV, in order to optimize an experimental plan.
3.1. Gradients in Spatial Uncertainty
The analysis described previously allows us to quantify the positioning uncertainty at any point within the camera's FOV, that is, to quantify the uncertainty of the conversion between pixel and physical coordinates. However, when considering the uncertainty of a velocity measurement we need to consider how this uncertainty changes over space. Velocity calculations are based on finding the distance between the origin and final locations over which a parcel of water has been advected over a known period of time. If the error in calculating the origin and final locations is the same it will not affect the velocity calculation, even though it will lead to an error in the location to which that velocity measurement is assigned. To extend the uncertainty analysis to uncertainty of velocity measurements, we, therefore, calculate the gradient of uncertainty at each point in the FOV. Velocity calculations in regions of the image where this gradient is small will have low velocimetry uncertainty, whereas regions with a larger gradient will correspondingly have a higher uncertainty in the velocity calculation, since a larger gradient indicates increased likelihood of different georeferencing error at the origin and final positions over which a parcel of water has been advected over a given period of time.
Similar to the analysis presented in the previous section, we calculate spatial gradients in uncertainty independently for each of n simulations, and calculate statistics on this set of simulations at each point (e.g., the 95th percentile at a certain pixel- or physical-coordinate). Figure 6 illustrates gradients in uncertainty within an oblique-view FOV, using GCP-based (Figure 6A) and direct- (Figure 6B) georeferencing. The gradients are presented as the non-dimensional, absolute value of the ratio of length change in local uncertainty per length change in distance from the camera. Uncertainty in the direct georeferencing case is on the order of 5 times greater than the GCP-based case. Figure 7 shows similar gradients of uncertainty calculated in a normal-view case. Figure 7A shows GCP-based georeferencing, with correction for radial distortion in the images, whereas in Figure 7B direct georeferencing is presented without correcting for radial distortion. In this case, the estimated gradient in spatial uncertainty, and hence the expected uncertainty in the velocimetry calculation, is on the order of 10 times larger throughout much of the FOV, and even greater in regions near the corners of the image.
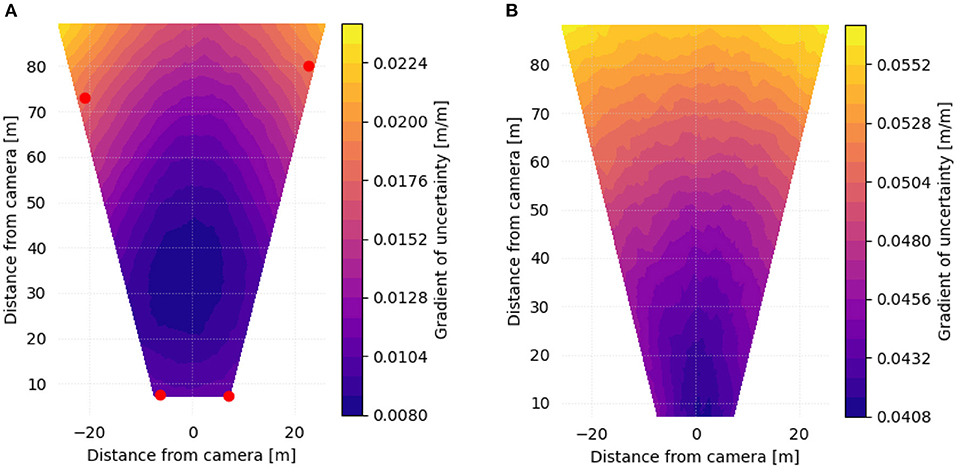
Figure 6. Contours of the 95th percentile of the gradient of spatial uncertainty estimated at each pixel footprint in an oblique view camera setup, after correcting the images for radial distortion. (A) Using 4 GCPs located near the corners of the FOV (red dots). (B) Using direct georeferencing.
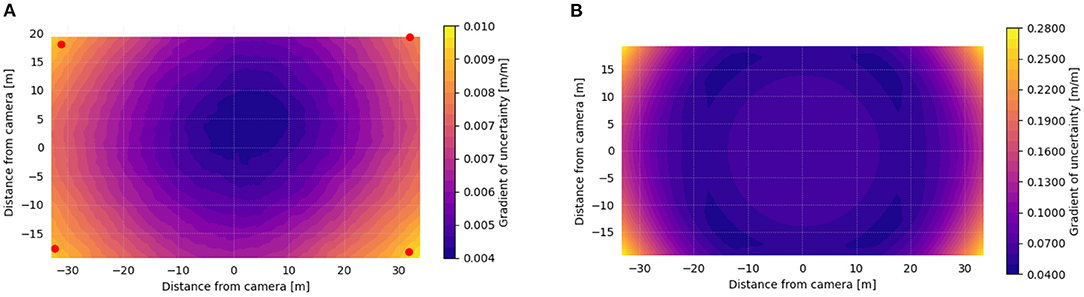
Figure 7. Contours of the 95th percentile of the gradient of spatial uncertainty estimated at each pixel footprint in a normal view (UAV) camera. (A) Using 4 GCPs located near the corners of the FOV (red dots), and correcting for radial distortion. (B) Using direct georeferencing, without correcting for radial distoriton.
4. Conclusion
We have presented a methodology and software tool used for analysis of spatial uncertainty in image based surface flow velocimetry. The tool is based on a Monte Carlo simulation of changes to the calculated, georeferenced x, y, z coordinates of pixels in the camera's FOV, as a function of perturbations of the input parameters used to find the georeferencing coordinate transformation. These input perturbations were selected from distributions corresponding to the estimated uncertainty of each of the respective inputs (GCP coordinates in physical and pixel space, or camera position and orientation angles when using direct georeferencing, and WSE in either case), and hence the Monte Carlo simulation estimates the level of uncertainty expected in the georeferenced coordinates. This tool can be used as a planning aide before making a measurement, or to bound the uncertainty after images are collected.
For the example experimental setups presented here, GCP-based georeferencing methods were shown to be significantly more accurate than direct georeferencing methods, with uncertainty reduced by a factor of five or more. In addition, the presented results illustrate the importance of correcting radial distortion in the optical path.
The effects of spatial uncertainty on velocity measurements were also examined by analyzing spatial gradients in georeferencing uncertainty. With oblique camera views, uncertainty in velocity measurements associated with direct georeferencing was found to be five times larger than when using GCP-based georeferencing. In nadir-view camera orientation, velocimetry uncertainty was found to be ten times larger when using direct georeferencing without considering radial distortion than when using GCP-based georeferencing corrected for radial distortion.
The software tool can be easily adapted to explore other factors affecting spatial uncertainty in this type of image, such as the number of GCPs used, and their distribution within the FOV. The authors have made this software tool freely available to the community.
Data Availability Statement
The computer code for the camera calibration and uncertainty analysis tools described in this article is publicly available at https://github.com/saschweitzer/camera-calibration, further inquiries can be directed to the corresponding author/s.
Author Contributions
SAS conceived the idea for this software tool, developed the computer code and algorithms, drafted the paper, and generated the plots. EAC provided scientific and editorial guidance and leadership, obtained funding, supervised the development of the methods and manuscript, and participated in writing the manuscript. Both authors contributed to the article and approved the submitted version.
Funding
This work was funded by the California Department of Water Resources (DWR), contract numbers 4600010495 and 4600012347.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://github.com/saschweitzer/camera-calibration
References
Abdel-Aziz, Y. I., and H. M. Karara (1971). “Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry.” in Symposium on Close-Range Photogrammetry. American Society of Photogrammetry. (Falls Church, VA), 1–19.
Adrian, R. J. (1991). Particle-imaging techniques for experimental fluid mechanics. Ann. Rev. Fluid Mech. 23, 261–304. doi: 10.1146/annurev.fl.23.010191.001401
Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B. (2017). Julia: a fresh approach to numerical computing. SIAM Rev. 59, 65–98. doi: 10.1137/141000671
Chickadel, C. C., Talke, S. A., Horner-Devine, A. R., and Jessup, A. T. (2011). Infrared-based measurements of velocity, turbulent kinetic energy, and dissipation at the water surface in a tidal river. IEEE Geosci. Remote Sens. Lett. 8, 849–853. doi: 10.1109/LGRS.2011.2125942
Cowen, E. A., and Monismith, S. G. (1997). A hybrid digital particle tracking velocimetry technique. Exp. Fluids 22, 199–211.
Creutin, J., Muste, M., Bradley, A., Kim, S., and Kruger, A. (2003). River gauging using PIV techniques: a proof of concept experiment on the Iowa River. J. Hydrol. 277, 182–194. doi: 10.1016/S0022-1694(03)00081-7
Detert, M. (2021). How to avoid and correct biased riverine surface image velocimetry. Water Resour. Res. 57, e2020WR027833. doi: 10.1029/2020WR027833
Detert, M., Johnson, E., and Weitbrecht, V. (2017). Proof-of-concept for low-cost and non-contact synoptic airborne river flow measurements. J. Hydraulic Res. 53, 532–539. doi: 10.1080/01431161.2017.1294782
Detert, M., and Weitbrecht, V. (2015). A low-cost airborne velocimetry system: proof of concept. J. Hydraulic Res. 53, 532–539. doi: 10.1080/00221686.2015.1054322
Elias, M., Eltner, A., Liebold, F., and Maas, H.-G. (2020). Assessing the influence of temperature changes on the geometric stability of smartphone- and raspberry pi cameras. Sensors 20, 643. doi: 10.3390/s20030643
Eltner, A., Mader, D., Szopos, N., Nagy, B., Grundmann, J., and Bertalan, L. (2021). Using thermal and RGB UAV imagery to measure surface flow velocities of rivers. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. XLIII-B2-2021, 717–722. doi: 10.5194/isprs-archives-XLIII-B2-2021-717-2021
Eltner, A., Sardemann, H., and Grundmann, J. (2020). Technical Note: Flow velocity and discharge measurement in rivers using terrestrial and unmanned-aerial-vehicle imagery. Hydrol. Earth Syst. Sci. 24, 1429–1445. doi: 10.5194/hess-24-1429-2020
Fujita, I., Muste, M., and Kruger, A. (1998). Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraulic Res. 36, 397–414.
Fujita, I., Muto, Y., Shimazu, Y., Tsubaki, R., and Aya, S. (2004). Velocity measurements around nonsubmerged and submerged spur dykes by means of large-scale particle image velocimetry. J. Hydrosci. Hydraulic Eng. 22, 51–61.
Fujita, I., and S. Aya, T. Deguchi (1997). “Surface velocity measurement of river flow using video images of an oblique angle,” in Environmental and Coastal Hydraulics: Protecting the Aquatic Habitat, Proceedings of Theme B, vols 1 & 2, Water For a Changing Global Community. 27th Congress of the International-Association-for-Hydraulic-Research, Vol. 27. eds S. Wang, and T. Carstens (New York, NY: Amer Soc Civil Engineers), 227–232.
Fujita, I., Watanabe, H., and Tsubaki, R. (2007). Development of a non-intrusive and efficient flow monitoring technique: The space-time image velocimetry (stiv). Int. J. River Basin Manag. 5, 105–114. doi: 10.1080/15715124.2007.9635310
Hauet, A., Creutin, J.-D., and Belleudy, P. (2008). Sensitivity study of large-scale particle image velocimetry measurement of river discharge using numerical simulation. J. Hydrol. 349, 178–190. doi: 10.1016/j.jhydrol.2007.10.062
Holland, K., Holman, R., Lippmann, T., Stanley, J., and Plant, N. (1997). Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean. Eng. 22, 81–92. doi: 10.1109/48.557542
Jodeau, M., Hauet, A., Paquier, A., Coz, J. L., and Dramais, G. (2008). Application and evaluation of LS-PIV technique for the monitoring of river surface velocities in high flow conditions. Flow Meas. Instrum. 19, 117–127. doi: 10.1016/j.flowmeasinst.2007.11.004
Kim, Y., Muste, M., Hauet, A., Krajewski, W. F., Kruger, A., and Bradley, A. (2008). Stream discharge using mobile large-scale particle image velocimetry: a proof of concept. Water Resour. Res. 44, W09502. doi: 10.1029/2006WR005441
Le Coz, J., Renard, B., Vansuyt, V., Jodeau, M., and Hauet, A. (2021). Estimating the uncertainty of videobased flow velocity and discharge measurements due to the conversion of field to image coordinates. Hydrol. Process. 35, e14169. doi: 10.1002/hyp.14169
Legleiter, C. J., Kinzel, P. J., and Nelson, J. M. (2017). Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 554, 490–506. doi: 10.1016/j.jhydrol.2017.09.004
Leitāo, J. P., Pen̄a-Haro, S., Lüthi, B., Scheidegger, A., and Moy de Vitry, M. (2018). Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry. J. Hydrol. 565, 791–804. doi: 10.1016/j.jhydrol.2018.09.001
Lewis, Q. W., Lindroth, E. M., and Rhoads, B. L. (2018). Integrating unmanned aerial systems and lspiv for rapid, cost-effective stream gauging. J. Hydrol. 560, 230–246. doi: 10.1016/j.jhydrol.2018.03.008
Lewis, Q. W., and Rhoads, B. L. (2018). LSPIV measurements of two-dimensional flow structure in streams using small unmanned aerial systems: 2. hydrodynamic mapping at river confluences. Water Resour. Res. 54,7981–7999. doi: 10.1029/2018WR022551
Ljubičić, R., Strelnikova, D., Perks, M. T., Eltner, A. Pen̄a-Haro, S., Pizarro, A., et al. (2021). A comparison of tools and techniques for stabilising UAS imagery for surface flow observations. Hydrol. Earth Syst. Sci. Discus. 1–42. doi: 10.5194/hess-2021-112
Muste, M., Fujita, I., and Hauet, A. (2008). Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 44. doi: 10.1029/2008WR006950
Perks, M. T., Russell, A. J., and Large, A. R. G. (2016). Technical note: advances in flash flood monitoring using unmanned aerial vehicles (uavs). Hydrol. Earth Syst. Sci. 20, 4005–4015.
Puleo, J. A., T. E. McKenna, K. T. Holland, and J. Calantoni (2012). Quantifying riverine surface currents from time sequences of thermal infrared imagery. Water Resour Res. 48. doi: 10.1029/2011WR010770
Rozos, E., Dimitriadis, P., Mazi, K., Lykoudis, S., and Koussis, A. (2020). On the uncertainty of the image velocimetry method parameters. Hydrology 7, 65. doi: 10.3390/hydrology7030065
Schweitzer, S. A., and Cowen, E. A. (2021). Instantaneous river-wide water surface velocity field measurements at centimeter scales using infrared quantitative image velocimetry. Water Resour. Res. 57, e2020WR029279. doi: 10.1029/2020WR029279
Strelnikova, D., Paulus, G., Käfer, S., Anders, K.-H., Mayr, P., Mader, H., et al. (2020). Drone-based optical measurements of heterogeneous surface velocity fields around fish passages at hydropower dams. Remote Sens. 12, 384. doi: 10.3390/rs12030384
Streßer, M., Carrasco, R., and Horstmann, J. (2017). Video-based estimation of surface currents using a low-cost quadcopter. IEEE Geosci. Remote Sens. Lett. 14, 2027–2031. doi: 10.1109/LGRS.2017.2749120
Tauro, F., Petroselli, A., and Grimaldi, S. (2018a). Optical sensing for stream flow observations: a review. J. Agricul. Eng. 49, 199–206. doi: 10.4081/jae.2018.836
Tauro, F., Tosi, F., Mattoccia, S., Toth, E., Piscopia, R., and Grimaldi, S. (2018b). Optical tracking velocimetry (otv): leveraging optical flow and trajectory-based filtering for surface streamflow observations. Remote Sens. 10, 2010. doi: 10.3390/rs10122010
Keywords: LSPIV, IR-QIV, river flow, turbulence, hydrodynamics, uncertainty analysis, UAV, UAS
Citation: Schweitzer SA and Cowen EA (2022) A Method for Analysis of Spatial Uncertainty in Image Based Surface Velocimetry. Front. Water 4:744278. doi: 10.3389/frwa.2022.744278
Received: 20 July 2021; Accepted: 04 February 2022;
Published: 04 April 2022.
Edited by:
Matthew Perks, Newcastle University, United KingdomReviewed by:
Evangelos Rozos, National Observatory of Athens, GreeceRyota Tsubaki, Nagoya University, Japan
Copyright © 2022 Schweitzer and Cowen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Seth A. Schweitzer, c2V0aC5zY2h3ZWl0emVyQGNvcm5lbGwuZWR1
 Seth A. Schweitzer
Seth A. Schweitzer Edwin A. Cowen
Edwin A. Cowen