Surface Flow Velocities From Space: Particle Image Velocimetry of Satellite Video of a Large, Sediment-Laden River

Conventional, field-based streamflow monitoring in remote, inaccessible locations such as Alaska poses logistical challenges. Safety concerns, financial considerations, and a desire to expand water-observing networks make remote sensing an appealing alternative means of collecting hydrologic data. In an ongoing effort to develop non-contact methods for measuring river discharge, we evaluated the potential to estimate surface flow velocities from satellite video of a large, sediment-laden river in Alaska via particle image velocimetry (PIV). In this setting, naturally occurring sediment boil vortices produced distinct water surface features that could be tracked from frame to frame as they were advected by the flow, obviating the need to introduce artificial tracer particles. In this study, we refined an end-to-end workflow that involved stabilization and geo-referencing, image preprocessing, PIV analysis with an ensemble correlation algorithm, and post-processing of PIV output to filter outliers and scale and geo-reference velocity vectors. Applying these procedures to image sequences extracted from satellite video allowed us to produce high resolution surface velocity fields; field measurements of depth-averaged flow velocity were used to assess accuracy. Our results confirmed the importance of preprocessing images to enhance contrast and indicated that lower frame rates (e.g., 0.25 Hz) lead to more reliable velocity estimates because longer capture intervals allow more time for water surface features to translate several pixels between frames, given the relatively coarse spatial resolution of the satellite data. Although agreement between PIV-derived velocity estimates and field measurements was weak (R² = 0.39) on a point-by-point basis, correspondence improved when the PIV output was aggregated to the cross-sectional scale. For example, the correspondence between cross-sectional maximum velocities inferred via remote sensing and measured in the field was much stronger (R² = 0.76), suggesting that satellite video could play a role in measuring river discharge. Examining correlation matrices produced as an intermediate output of the PIV algorithm yielded insight on the interactions between image frame rate and sensor spatial resolution, which must be considered in tandem. Although further research and technological development are needed, measuring surface flow velocities from satellite video could become a viable tool for streamflow monitoring in certain fluvial environments.

1. Introduction

Regular, reliable monitoring of streamflow is crucial for a number of management applications including water supply forecasting, flood hazard assessment, habitat conservation, and provision of recreational opportunities. However, obtaining basic information on river discharge can be difficult and costly, particularly in remote, inaccessible locations. For example, although the state of Alaska features over 1,200,000 km of rivers and streams, the U.S. Geological Survey (USGS) streamgage network consists of only 111 continuous monitoring locations, a density of coverage far less than in the contiguous U.S. (Conaway et al., 2019). One reason so many Alaskan waterways remain ungaged is the logistical challenge associated with making periodic streamflow measurements and performing maintenance operations. For example, because many gages are located in roadless areas, these sites must be accessed by helicopter, which places hydrographers at risk. The USGS is actively seeking to improve safety, increase efficiency, and expand the streamgage network by developing non-contact methods for measuring streamflow. Remotely sensed data used for this purpose can be acquired from a range of platforms including: (1) near-field, bridge-mounted sensors (Legleiter et al., 2017; Fulton et al., 2020b); (2) small uncrewed aircraft systems (sUAS, or drones; e.g., Kinzel and Legleiter, 2019; Bandini et al., 2021; Fulton et al., 2020a); (3) fixed-wing aircraft and helicopters (Legleiter and Kinzel, 2020); and (4) satellites, both existing (e.g., Bjerklie et al., 2018) and yet to be launched (e.g., Altenau et al., 2019). Most current approaches to estimating river discharge from space involve images that represent a single point in time and have relatively coarse pixel sizes on the order of 30 m or more and are based on various hydraulic approximations (e.g., Gleason and Durand, 2020). In this study we explore an alternative strategy focused on inferring one component of discharge, flow velocity, from high spatial resolution satellite video that captures dynamic water surface features and thus enables particle image velocimetry (PIV).

PIV and related optical flow and particle-tracking algorithms are increasingly applied to natural channels, where the technique is often referred to as large-scale PIV to distinguish these outdoor settings from laboratory investigations (e.g., Muste et al., 2008; Tauro et al., 2016; Eltner et al., 2020; Pearce et al., 2020; Strelnikova et al., 2020; Tosi et al., 2020). Many of these studies make use of image data acquired from bridge- or bank-mounted cameras or sUAS and in some cases the flow must be seeded with artificial tracers to facilitate particle detection and tracking under low flow conditions. This approach is not well-suited to large rivers where introducing a sufficient quantity of tracers would be impractical and restrictions on sUAS flying height preclude imaging the entire channel width. Thermal imaging is a different type of remote sensing that does not require seeding and has proven effective in small rivers (e.g., Kinzel and Legleiter, 2019; Lin et al., 2019) but is subject to several other constraints. For example, thermal features are expressed at the water surface as subtle differences in temperature that are most readily detected by highly sensitive, cooled mid-wave infrared cameras, although Fujita (2017) reported a successful application in which an uncooled, long-wave infrared camera was used to acquire images at night. Even with such sophisticated (and expensive) instrumentation, the method is contingent upon the air-water temperature contrast and can be affected by the exhaust emitted by some airborne platforms.

Although seeding the flow is not feasible for large Alaskan rivers, the use case that is our primary concern, and we also found thermal PIV to be problematic in this setting, our previous research demonstrated the potential to infer surface flow velocities from standard RGB (red, green, blue) video (Legleiter and Kinzel, 2020). For rivers that drain glaciated terrain and convey large quantities of sediment in suspension, turbulence within the water column produces sediment boil vortices that are manifested at the surface as differences in water color and can thus be detected and tracked via PIV. In a recent study on the Tanana River, we used video acquired from a helicopter hovering above the channel to produce continuous, two-dimensional, high spatial resolution surface velocity fields that agreed closely (R² up to 0.99) with depth-averaged velocities measured directly in the field. While, this approach is only applicable when and where rivers have high concentrations of suspended sediment, it has the important advantage of using a natural tracer, sediment, rather than artificially seeded material. The purpose of the investigation reported herein was to assess the potential to adapt this framework to video acquired from a satellite platform.

Inferring surface flow velocities from space has a strong precedent in the literature. For example, Kääb et al. (2019) used near-simultaneous images, separated by approximately 90 s, from a constellation of optical cubesats to track river ice floes and thus estimate water surface velocities with a high degree of accuracy. In addition to the issues associated with cloud cover that are inherent to any spaceborne imaging system, this approach also is limited by the fact that near-simultaneous swath overlaps within the constellation cover only a small fraction of the Earth's surface. This type of data can thus only be acquired opportunistically for a small number of locations defined by the cubsesat orbital trajectories. Furthermore, for the two northern rivers evaluated by Kääb et al. (2019), velocity mapping was sensitive to timing, as ice forming in the fall was easier to track over longer time periods than ice breaking up in the spring. Previously, Kääb and Leprince (2014) described a variety of applications of motion detection from near-simultaneous images but also highlighted the potential for errors introduced by imaging geometry and target elevation. Although their review mentioned tracking suspended sediment to estimate surface flow velocities and presented some compelling illustrations of this approach, the examples were selectively drawn from confluence zones where sediment-laden and relatively clear rivers converge. Even in these unique settings, only a few velocity vectors could be inferred within the mixing zone itself.

This study builds upon previous research by pursuing an approach to spaceborne mapping of river velocities that differs from prior work in several important respects. For example, using video collected from satellites that have off-nadir pointing capabilities and can thus be tasked to acquire data from user-specified locations provides greater flexibility and more extensive, continuous coverage than relying upon near-simultaneous images from a few areas where swaths fortuitously overlap. Such tasking could facilitate both as needed situational response to hydrologic events and routine operational monitoring via recurring collections. In addition, PIV of satellite video can yield higher spatial resolution surface velocity fields by tracking sediment boil vortices that are present throughout the channel, rather than discrete, isolated objects like the ice floes used by Kääb et al. (2019), which might be unevenly distributed when they are present at all. More specifically, Kääb et al. (2019) produced a velocity field with a grid node spacing of 75 m by tracking ice floes ranging from 3 to 300 m in size on the Amur River in Siberia, whereas this study presents PIV output on a 30 m grid for the sediment-laden Tanana River in central Alaska. Similarly, while large, bright, particle-like features such as ice floes are relatively easy to detect and track, discerning the motion of more subtle, continuous, and deforming features of the water surface itself presents a much greater image processing challenge.

The novel contribution of this work is the extension of PIV techniques typically applied to remotely sensed data from various near-field or airborne platforms to video acquired by satellites in orbit far above the Earth. The primary objectives of this investigation include the following:

1. Test the feasibility of inferring surface flow velocities in a large, sediment-laden river under natural, unseeded flow conditions by applying a PIV algorithm to remotely sensed data acquired from space.

2. Outline a modular, spatially explicit workflow for producing surface velocity fields from satellite video.

3. Examine the effects of image preprocessing and image frame rate on PIV analyses.

4. Assess the accuracy of PIV-based velocity estimates via comparison to field measurements of velocity.

5. Evaluate the potential to infer bulk flow characteristics, such as cross-sectional mean and maximum velocities, from PIV-derived velocity fields.

2. Materials and Methods

The satellite video and in situ field observations upon which this study was based are available in Legleiter and Kinzel (2021). The parent landing of Legleiter and Kinzel (2021) page provides an overview and links to separate child pages for three individual data sets, all from our study site on the Tanana River in central Alaska, USA: (1) field measurements of flow velocity; (2) orthophotos used as a base for geo-referencing; and (3) video acquired from a satellite, along with the image frames that were extracted therefrom and used to perform the PIV analyses described herein.

2.1. Study Area

Alaska is the largest state in the USA but remains relatively sparsely gaged, in part because many Alaskan rivers are located in remote, inaccessible terrain (Conaway et al., 2019). These circumstances imply a compelling need for alternative remote sensing techniques for measuring streamflow and this study sought to advance the development of such non-contact methods by focusing on a large, sediment-laden river typical of Alaska, the Tanana. More specifically, we examined a reach near Nenana, southwest of the city of Fairbanks in the central part of the state (Figure 1). This site also features a USGS gaging station (#15515500) at which the drainage area is 66,200 km²; the river's water surface slope is 0.00014. A discharge of 1,770 m³/s was recorded at the time the satellite video was acquired on 14 July 2020, slightly higher than the median value of 1,710 m³/s for this date based on 58 years of record. The field measurements of flow velocity described below were obtained at a nearly identical discharge of 1,781 m³/s on 24 July 2019. Although the field and remotely sensed data were separated by nearly a year's time, our experience at this site suggests that no significant channel changes occurred in the interim and we assumed that the field observations were representative of the flow conditions captured by the video.

FIGURE 1

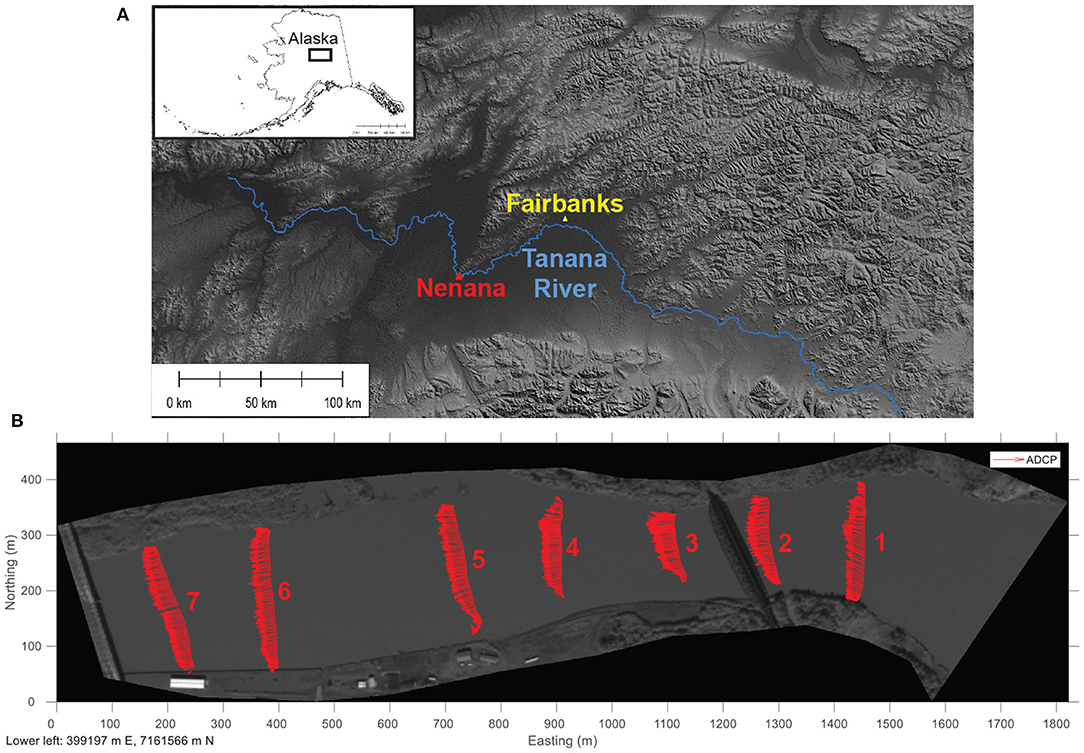
Figure 1. (A) Overview map showing location of the study area within the state of Alaska and the study reach at Nenana in relation to the city of Fairbanks and the course of the Tanana River. (B) Example image frame extracted from the satellite video with velocity vectors measured in the field with an acoustic Doppler current profiler (ADCP) overlain. Cross section numbers are indicated.

Much of the Tanana's watershed is glaciated, providing a steady supply of outwash that results in consistently high concentrations of suspended sediment (Wada et al., 2011). For example, a suspended sediment concentration of 2,309 mg/L was estimated on the day the satellite video was acquired based on a power function relating concentration to discharge (Legleiter and Kinzel, 2020). Our previous research on the Tanana demonstrated that this abundance of suspended material enables surface flow velocities to be inferred via PIV under natural, ambient flow conditions. The premise of this approach is that turbulence within the water column produces sediment boil vortices that are expressed at the water surface as variations in color and brightness that can be tracked from frame to frame through an image sequence as these distinct but deformable features are advected downstream by the flow. Importantly, the presence of these water surface features allowed velocities to be estimated in a large river where seeding the flow with artificial tracer particles would have been impractical (Legleiter and Kinzel, 2020).

2.2. Remotely Sensed Data

The primary objective of this investigation was to assess the potential for mapping continuous, two-dimensional, high resolution surface flow velocity fields from space. We pursued this goal using video acquired by a satellite orbiting 450 km above Earth's surface as part of the Planet Labs SkySat constellation (Table 1). This imaging system consists of a telescope with a 3.6 m focal length and three 5.5 megapixel detectors comprising a common focal plane. SkySats can acquire multispectral images, but the video data consist of a single panchromatic band. Although durations of up to 120 s are possible, a 60 s video acquired at a frame rate of 30 Hz was obtained for this study. Data delivered by Planet Labs included an MP4 video file, a TIFF image for each of the 1,800 individual frames, a frame index file, and supporting metadata. A cross-sensor non-uniformity correction was applied but the data were not radiometrically calibrated, nor was any kind of atmospheric correction performed; the TIFF images consisted of 16-bit digital numbers.

TABLE 1

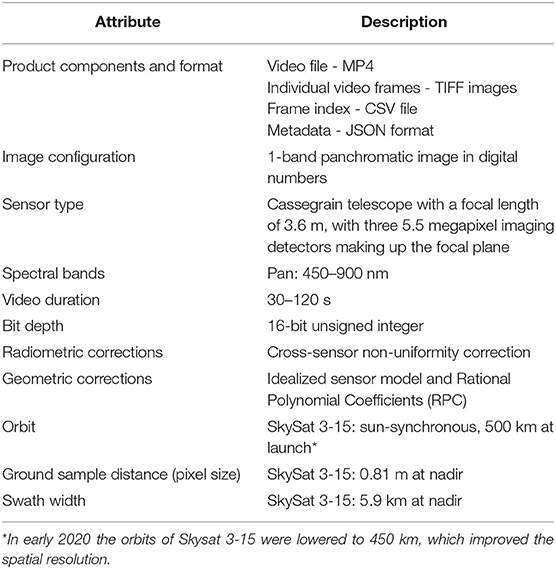
Table 1. Planet SkySat video product information and sensor specifications (European Space Agency, 2020; Planet Labs, Inc., 2020).

The video was acquired at an off-nadir view angle and had a nominal mean ground sampling distance (i.e., pixel size) of 1 m. The metadata included a rational polynomial coefficients (RPC) model for geometric correction, but we used a simpler image-to-image registration approach to spatially reference the video to a projected coordinate system (UTM Zone 6, NAD83). An orthophoto of the Tanana River acquired from a helicopter on 24 July 2019 and described in more detail by Legleiter and Kinzel (2020) served as the base for geo-referencing.

Due to the passage of clouds during the video, we retained only a 17 s subset during which the river was not obscured. To evaluate the effects of image frame rate, we sub-sampled this video clip to frame rates of 1, 0.5, and 0.25 Hz by retaining only every 30th, 60th, and 120th frame, respectively, from the original 30 Hz time series. For the limited, cloud-free subset of the video, this procedure resulted in sequences consisting of 17, 9, and 5 images, respectively.

2.3. Field Measurements

Although direct, in situ observations of flow velocity coincident with the satellite video were not available, we used field data acquired at a similar discharge (section 2.1) to assess the accuracy of image-derived velocity estimates and thus guide the selection of appropriate image preprocessing techniques and frame rates. This field data set was acquired using a TDRI RiverRay acoustic Doppler current profiler (ADCP) (Teledyne Marine, 2020) equipped with a Hemisphere A101 differential Global Navigation Satellite System (GNSS) receiver with a horizontal precision of 0.6 m (Hemisphere GNSS, 2020). The ADCP was deployed from a small, custom-fitted catamaran towed behind a boat with an outboard motor while traversing the channel on a series of transects oriented perpendicular to the primary flow direction. The cloud-free subset of the video encompassed seven of these cross sections, each consisting of a single pass across the river. During data collection, the RiverRay was controlled from within the boat using the TRDI WinRiver II software package, which enabled real-time visualization of the velocity field throughout the water column as the boat moved across the river. The ADCP data were post-processed in WinRiver II and then imported into the USGS Velocity Mapping Toolbox (VMT) (Parsons et al., 2013). We used VMT to post-process the original, individual ADCP measurement points into a set of seven cross sections (XS) arranged from upstream to downstream along the channel (Figure 1B). Each of these transects was obtained by fitting a line to the original boat track, projecting the individual ADCP measurements onto this line, and smoothing the data both horizontally and vertically to provide a mean cross section consisting of depth-averaged flow velocities at 1 m distance increments from the left bank; depth-averaged velocities were obtained by averaging over the entire depth of flow at each point. We then used an export tool within VMT to produce text files consisting of projected spatial coordinates and depth-averaged velocities for all of the points along each of the smoothed mean cross sections generated via VMT. Although we visually inspected ADCP- and PIV-based velocity vectors, our quantitative accuracy assessment of the PIV output was based on velocity magnitudes.

In addition to the ADCP data, we also used measurements from an RQ-30 radar gage manufactured by Sommer Messtechnik that was mounted on a bridge over the Tanana River located at the downstream end of our study area and is described in greater detail by Fulton et al. (2020a,b). As discussed by these authors, velocity radars use the Doppler effect to translate radar frequencies into surface flow velocities. Observations from the radar gage thus provided an independent, non-contact measurement of surface velocity for assessing the accuracy of PIV-based estimates derived from the satellite video, whereas the ADCP data consisted of depth-averaged velocities. Another advantage of the radar gage is that this sensor operates continuously to monitor streamflow, which allowed us to query the record and identify a measurement made within 15 min of when the satellite video was acquired. However, a complicating factor in comparing this radar gage observation to the PIV-based velocity estimates was the difference in spatial resolution between the radar gage footprint (an ellipse with a long axis of approximately 5.15 m) and the 1 m pixel size of the satellite image frames. In addition, the exact location of the radar beam on the water surface was not known precisely. We accounted for these issues by extracting the three PIV output vectors closest to the presumed location of the radar gage measurement and averaging the magnitudes of these three PIV vectors.

2.4. Velocity Index Calculations

Whereas the field measurements obtained with an ADCP and processed with VMT were depth-averaged flow velocities, the velocities inferred from the satellite video were assumed to represent the water surface. To enable comparison of ADCP- and PIV-derived velocities for accuracy assessment, the remotely sensed surface flow velocities thus had to be converted to depth-averaged velocities (e.g., Le Coz et al., 2010). This conversion is typically achieved by defining a velocity index α as the ratio of the depth-averaged velocity U_d to the surface velocity U_s (e.g., Smart and Biggs, 2020):

$\begin{array}{ll}\alpha =\frac{U_d}{U_s}& (1)\end{array}$

In this study, we used the Qrev software package developed by the USGS (Mueller, 2013, 2016a,b) to obtain site-specific, calibrated α values for each of the seven transects across the Tanana River shown in Figure 1B. The “extrap” module within Qrev aggregated all of the vertical velocity profiles (i.e., ensembles) recorded by the ADCP during each traverse of the channel, standardized the profiles, and averaged them to produce a single, normalized velocity profile representative of the cross section. However, these profiles did not extend up to the water surface due to the blanking distance between the ADCP transducer and the first cells measured on the vertical profiles; gaps also occurred between the lowest cells measured and the streambed. The extrap tool provided a means of extrapolating from the central, measured portion of the water column up to the surface and down to the bottom. More specifically, assuming that the vertical velocity profile was described by a power law of the form

$\begin{array}{ll}U(z)=a{z}^m,& (2)\end{array}$

where U(z) is the flow velocity at a height z above the streambed, a is a coefficient, and m is an exponent, extrap identified the exponent that yielded the optimal fit to the ADCP data. As shown by Legleiter et al. (2017), integrating Equation (2) over the entire depth of flow and dividing by the depth d yields an expression for the depth-averaged velocity U_d. Dividing this result by the velocity at the water surface U_s, obtained by evaluating Equation (2) for z = d, leads to the following relation for the velocity index:

$\begin{array}{ll}\alpha =\frac{U_d}{U_s}=\frac{\frac{a{d}^{m+1}}{d(m+1)}}{a{d}^m}=\frac{1}{m+1}& (3)\end{array}$

The Qrev output is summarized in Figure 2, which depicts the normalized velocity profile and power law fits for each of the seven Tanana River cross sections. Also shown for each transect are the optimal value of the power law exponent m and the corresponding velocity index α, calculated via Equation (3). α values varied over a narrow range from 0.85 to 0.91, with a mean of 0.88, consistent with the widely used default value of 0.85 that corresponds to a power law with m = 1/6, which is equivalent to Manning's equation (Smart and Biggs, 2020). These cross section-specific α values were used to convert PIV-derived surface flow velocities to depth-averaged velocities comparable to the field measurements recorded by the ADCP and processed in VMT.

FIGURE 2

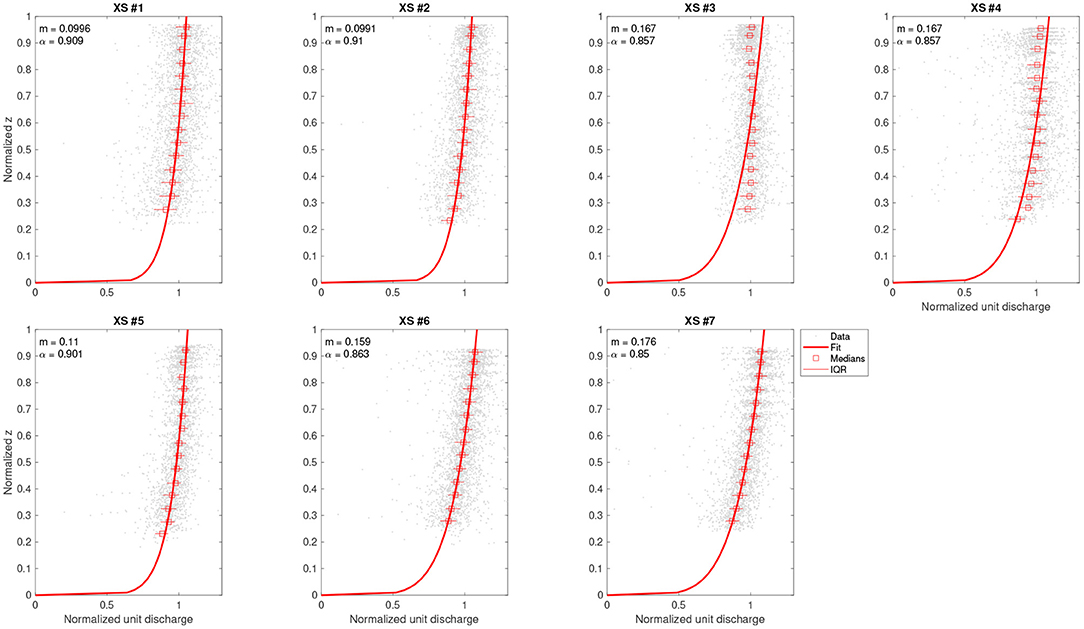
Figure 2. Velocity profiles measured with an ADCP and fit using the Qrev software program. The power law exponent m and the corresponding velocity index α used to convert PIV-derived surface flow velocities to depth-averaged velocities is indicated for each cross section. The gray dots represent individual ADCP data points along the normalized profile, the red curve is the best-fit power law, and the red squares and horizontal lines are the median and interquartile range (IQR) of normalized velocities within a series of vertical bins. See Mueller (2016a,b) for further details on Qrev.

2.5. Particle Image Velocimetry (PIV) Workflow

To perform PIV analyses for this study, we built upon a modular workflow established through previous research on the Tanana River based on image sequences acquired from a helicopter hovering above the channel (Legleiter and Kinzel, 2020). Although some of these procedures were applicable to the satellite data as well, certain components were not relevant and other new features were added as we continued to refine the approach. The analysis was conducted primarily within MATLAB, with the widely used PIVlab add-in developed by Thielicke and Stamhuis (2014; 2019) serving as the core PIV algorithm, but also involved image preprocessing tools from the open source FIJI software suite (FIJI-ImageJ, 2020). The workflow applied in this study is depicted graphically in Figure 3 and summarized below.

1. The process of inferring surface flow velocities from space begins with the acquisition of a video or sequence of still images from a satellite platform in orbit above the river of interest. These data must encompass the same area of the river for a period of at least a few seconds so that the features detected on the water surface have sufficient time to translate a measurable distance. The first user input to be specified is the frame rate to retain for PIV analysis.

2. Once the remotely sensed data have been collected and sub-sampled to obtain the desired frame rate, the individual image frames must be stabilized relative to one another and then geo-referenced to an established coordinate system. Aligning the images is essential so that any detected motion of surface features can be attributed to advection by the flow rather than motion of the imaging platform. In this study, we performed image stabilization using the TrakEM2 plugin to the FIJI image processing software package (Cardona et al., 2012). The first image in the resulting, stabilized sequence is then geo-referenced to a suitable base by selecting image-to-image tie points. These tie points are used to parameterize an affine transformation from image (column, row) to spatial (easting, northing) coordinates. The resulting transformation is applied to each frame to project the entire, aligned sequence into the same real world coordinate system.

3. The resulting stack of stabilized, geo-referenced images is then output as a series of individual image files stored in a directory. Preparing these images for PIV involves filtering and contrast adjustment; we performed these tasks by calling a FIJI macro programatically from within MATLAB. The macro uses FIJI functions for finite Fourier transform (FFT) bandpass filtering and histogram equalization contrast enhancement. The images output from this preprocessing routine are imported back into MATLAB.

4. Next, the spatial footprint of each frame is defined by outlining the boundary of the non-zero pixels in the image. The resulting polygon highlights the area of actual image data and thus can be irregular in shape and orientation, whereas a simple rectangular bounding box might include large areas of no data for an image that was rotated during the stabilization and/or geo-referencing phases of the workflow.

5. The footprints from all of the images in the stack are then overlain and displayed so that the user can determine the area of common coverage throughout the entire sequence and then digitize a region of interest (ROI) accordingly. This ROI also can serve as a water-only mask or be intersected with an existing water mask to highlight the channel proper. This step ensures that only portions of the river captured by all of the images in the sequence are included in the ROI used for PIV.

6. To focus the analysis on this area, all of the images in the stack are cropped to a common bounding box based on the digitized ROI. In addition, a raster mask corresponding to the digitized ROI is applied to each image to obtain a series of co-registered water-only images suitable for PIV. Performing these cropping and masking operations prior to PIV reduces storage requirements and computing time in subsequent stages of the workflow.

7. The PIV analysis itself is conducted by calling an ensemble correlation algorithm, included in the latest version (2.37, published 4 December 2020) of PIVlab, programatically from within MATLAB. The ensemble correlation method is well-suited to PIV applications where the seeding density (the number of tracer particles per unit area in an image sequence) is low and/or trackable features are not evenly distributed, as is the case in river flows. Whereas standard PIV algorithms operate sequentially on successive frame pairs, ensemble correlation involves averaging correlation matrices over the entire image sequence before identifying the correlation peak. This approach results in more robust velocity estimates, particularly for sequences consisting of a large number of images (Strelnikova et al., 2020). Key user inputs to the PIV algorithm include the size of the interrogation area (IA), which specifies the area (in pixels) within which features are tracked by computing correlations between successive images. The step size parameter controls the spacing of the PIV output vectors and was set to half the IA. Although PIVlab allows for multiple passes, we found that accuracy did not improve with additional passes and so used only a single pass in this study.

8. The PIV workflow employed in this study diverged from that implemented in our previous research (Legleiter and Kinzel, 2020) at this stage. Whereas the prior version did not post-process the PIV output, the workflow now includes filtering and interpolation steps to refine the original vectors. Filters include a minimum velocity threshold set to the product of one pixel and the frame rate, discarding outliers beyond three standard deviations from the mean velocity magnitude, and a normalized median check based on that implemented in PIVlab. Similarly, we incorporated a linear interpolation routine from PIVlab to fill gaps in the PIV output grid that were created by applying the various filters. In addition, the updated workflow extracts the correlation matrix for each IA produced by the ensemble correlation algorithm so that this information also can be used to assess the quality of the PIV output.

9. Once the PIV analysis is complete, the vectors are converted from units of pixels/frame to m/s. This step involves using the spatial referencing information for the image stack to establish the image scale (i.e., the number of pixels per meter) and then multiplying by the user-specified frame rate in units of Hz. The geo-referencing information also is used to transform the PIV-derived velocity vectors to the same real world coordinate system as the images.

10. Finally, the vectors inferred via PIV are overlain on the first image in the sequence to enable visualization of the flow field and the accuracy of the PIV output is evaluated via comparison with field measurements of flow velocity.

FIGURE 3

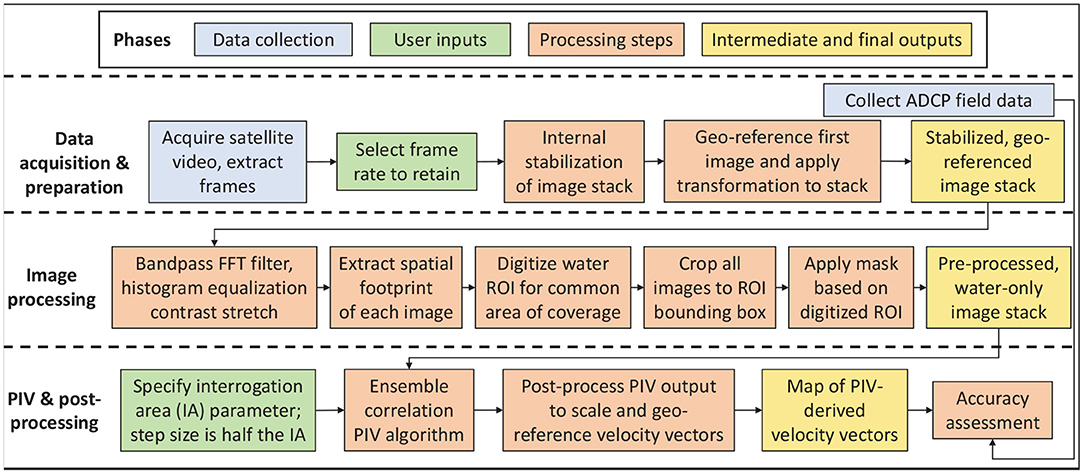
Figure 3. Flowchart illustrating the data requirements, user inputs, processing steps, and intermediate and final outputs involved in estimating surface flow velocities from satellite video using PIV.

2.6. Accuracy Assessment

We evaluated the accuracy of remotely sensed flow velocities by comparing the PIV output to direct field measurements of depth-averaged flow velocity obtained with an ADCP and post-processed with VMT as described above. We extracted surface flow velocity estimates from the PIV output grids derived from various image sequences for each of the seven cross sections. The PIV output was then interpolated to provide a remotely sensed velocity estimate for each point on each of the mean cross sections produced by VMT. Finally, the PIV-derived surface velocities were multiplied by velocity indices specific to each of the cross sections to convert them to depth-averaged velocities comparable to the ADCP measurements.

Having paired velocities inferred via PIV with those measured by the ADCP thusly, we quantified the accuracy of the remotely sensed flow velocities in terms of several metrics. We used the root mean squared error (RMSE) as an index of the precision of PIV estimates and the mean bias as an index of absolute accuracy. Bias was calculated as the difference between the ADCP-measured and PIV-derived velocity magnitudes, such that a positive value of the mean bias implied under-prediction of the ADCP-measured velocity by the PIV algorithm on average. Conversely, a negative value of the mean bias indicated that velocities inferred from the satellite video tended to be greater than those observed in the field. We also normalized the RMSE and mean bias by the mean of the ADCP measurements upon which the comparison was based to express each metric as a percentage of the reach-averaged mean velocity.

Observed (ADCP) vs. predicted (PIV) (OP) regressions were performed and the OP regression R²-value used to summarize correspondence between flow velocities recorded in the field by the ADCP and those inferred from the video via PIV. The slope and intercept terms of the OP regressions provided further information on the performance of the PIV algorithm. A slope of 1 and an intercept of 0 would indicate perfect agreement, but any deviation from these values would imply that the PIV-derived velocities were not scaled correctly (i.e., a slope coefficient less than or greater than 1) and/or were biased (i.e., a non-zero intercept) relative to the ADCP measurements (Pineiro et al., 2008). In addition, we visually inspected maps of the velocity estimation error to identify spatial variations in predictive capability.

2.7. Evaluating the Effects of Image Preprocessing and Frame Rate

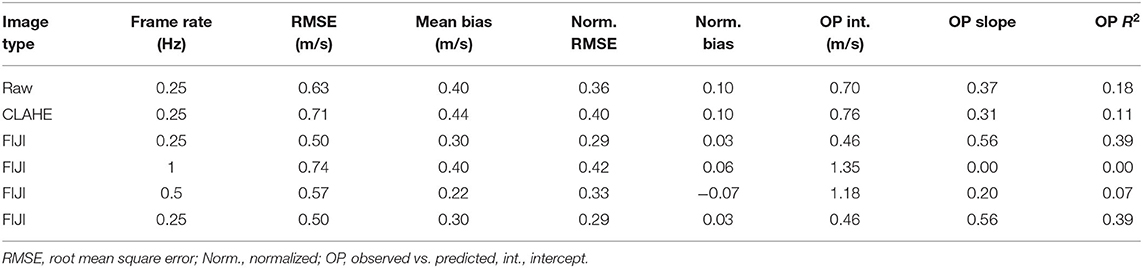
We used satellite video from the Tanana River to examine the influence of various image preprocessing approaches and frame rates on surface flow velocity estimates inferred via PIV. First, the 0.25 Hz image sequence was used as the base frame rate for evaluating the effects of three different preprocessing strategies: (1) using the raw image data directly; (2) applying the contrast limited adaptive histogram equalization (CLAHE) technique implemented in PIVlab; and (3) using a FIJI macro to apply a FFT bandpass filter and histogram equalization contrast stretch. We made this assessment by performing PIV for each of these image types, which we refer to as raw, CLAHE, and FIJI. The resulting PIV output was then compared in terms of the error metrics listed in section 2.6, OP regressions based on ADCP field measurements of flow velocity, and visual inspection of velocity fields inferred from the various image types.

Similarly, to examine the influence of image frame rate on the accuracy of PIV-based velocity estimates, we used the FIJI technique as the base case image preprocessing approach and performed PIV for image sequences extracted from the original video at frame rates of 1, 0.5, and 0.25 Hz. These capture intervals correspond to an image every second, every other second, and every fourth second, respectively. We compared the PIV output generated for each of these three frame rates by computing error metrics, performing OP regressions, and mapping the remotely sensed surface flow velocity fields.

3. Results

3.1. Image Stabilization and Geo-Referencing

Two important preparatory steps in the workflow outlined above were stabilization and geo-referencing of the image sequence prior to PIV analysis. Both of these processes involved some degree of error that could have affected the level of agreement between the remotely sensed flow velocities and the direct field measurements made with the ADCP. To account for motion of the satellite platform during video acquisition, we used the TrakEM2 FIJI plugin to bring the extracted frames into alignment with one another. A frame from the middle of the stack was designated as the reference and all of the other images were registered to this base using a scale-invariant feature transform (SIFT) algorithm that identified distinct features such as bridges and buildings that remained stationary throughout the video. We set the maximum alignment error parameter in TrakEM2 to five pixels and used an affine transformation specific to each frame to align all of the frames extracted from the 17 s subset of the original video that was free of cloud cover. In addition to the stabilized image sequence, output from TrakEM2 also included a report of the minimum, mean, and maximum displacement errors associated with the stabilization: 0.225, 0.310, and 0.394 pixels, respectively. Because these errors were all less than the size of a single image pixel, which is the smallest feature translation between successive frames that could be detected by the PIV algorithm, stabilization error was not a significant source of uncertainty in the inferred velocity fields.

Once the image sequence was internally stabilized, we next geo-referenced the first image in the stack to enable comparison of the PIV-derived velocities with ADCP field measurements. This phase of the workflow was performed in the Global Mapper software package (Global Mapper - All-in-one GIS Software, 2020) using a 2019 orthophoto as a base (Legleiter and Kinzel, 2020). We identified 11 distinct, stationary features, such as buildings, visible in both the satellite image and orthophoto and used these tie points to parameterize an affine transformation between the row, column image coordinates and the easting and northing coordinates of the projected real world coordinate system. Applying this transformation to the satellite image resulted in a geo-referenced image with a ground sampling distance (i.e., pixel size) of 0.927 m. The transformation matrix also was used to predict the locations of the tie points from their image coordinates. Comparing these predictions to the actual locations of the tie points on the orthophoto lead to a geo-referencing RMSE of 1.48 m. This error was uniform throughout the image sequence because all of the individual frames had been stabilized relative to one another and the same transformation matrix was applied to each frame to geo-reference the entire stack. The geo-referencing error did not influence the PIV-derived velocity vectors because within our workflow these velocity estimates were based on relative displacements of water surface features between successive frames in the stabilized sequence.

The absolute geo-referencing error could have introduced some degree of uncertainty into the comparison of PIV-derived and ADCP-measured velocities used for accuracy assessment. However, the PIV- and ADCP-based velocities were linked to one another at a spatial resolution set by the spacing of the PIV output vectors, which is set by the step size parameter , and the lateral distance increment used to generate smoothed mean cross sections from the ADCP data via VMT. In this study, the step size was held constant at 32 pixels, corresponding to a spatial distance of 29.6 m, and the cross sections output from VMT had a 1 m spacing between points. A typical geo-referencing error of 1.48 m was thus only 5% of the spacing between PIV output vectors, implying that incorrectly pairing an ADCP measurement with a PIV-based estimate was very unlikely.

3.2. Effects of Image Preprocessing

To isolate the effects of image preprocessing on PIV-derived velocity estimates, we held the frame rate fixed at 0.25 Hz and used raw, CLAHE-, and FIJI-preprocessed images as input to the ensemble correlation PIV algorithm. An example of each input image type is shown in Figure 4. Distinct water surfaces were difficult, if not impossible, to discern in the raw image (Figure 4A) and the CLAHE technique did not yield any significant improvement (Figure 4B). More distinct tonal patterns became evident when an FFT bandpass filter and histogram equalization-based contrast adjustment were applied using the FIJI macro; such highlighting of water surface features facilitated tracking their displacement from frame to frame. Comparing the PIV output derived from each image type to ADCP field measurements quantified the improvement provided by the FIJI approach (Table 2). The OP regression R² increased from 0.18 and 0.11 for the raw and CLAHE-preprocessed images, respectively, to 0.39 for the images prepared for PIV via FIJI; the normalized RMSE and bias also were reduced for the image sequences preprocessed with FIJI.

FIGURE 4

Figure 4. Example frames for each image type: (A) Raw, (B) CLAHE preprocessed, and (C) FIJI preprocessed.

TABLE 2

Table 2. Error metrics for various combinations of image preprocessing type and frame rate.

3.3. Effects of Image Frame Rate

In this study, we examined the effect of image frame rate on remotely sensed surface flow velocities by applying the FIJI-based image preprocessing approach outlined above to sequences extracted from the original satellite video at frame rates of 1, 0.5, and 0.25 Hz. These capture intervals correspond to 1, 2, and 4 s of elapsed time between frames, with the lower frame rates allowing for greater displacement of surface features between successive images. For the highest frame rate, a water surface feature would translate by a distance barely exceeding the pixel size, making its motion difficult to detect by a correlation-based PIV algorithm. Halving the frame rate would improve the situation by giving such a feature 2 s to move a greater distance during the time interval between successive frames in an image sequence. A further two-fold reduction in the frame rate would allow a full 4 s for the pattern to advect by a distance of several pixels, which could facilitate recognition of the offset.

To evaluate the influence of frame rate on PIV-derived velocity estimates, we used the 1, 0.5, and 0.25 Hz image sequences to produce maps of surface flow velocity, assess accuracy via comparison with ADCP field measurements, and examine spatial patterns of error. The velocity fields inferred from the three image sequences are illustrated in Figure 5, with vectors overlain on a raster representation of the flow field in which the color represents the surface velocity magnitude and darker blues indicate higher velocity. For the highest frame rate, depicted in Figure 5A, the vectors were consistently oriented in the proper, downstream direction, with a few exceptions along the north bank in the middle of the reach, but the relatively uniform, mid-blue tone suggested a homogeneous flow field that lacked a high velocity core or slower flow along the banks. For the 0.5 Hz image sequence (Figure 5B), erratic vectors were less common and velocities varied to a greater degree across the channel, including areas of higher velocity toward the north bank where the Tanana exits a large meander bend and begins to flow to the west just upstream of the satellite image footprint. For the lowest frame rate we considered, the inferred flow field represented in Figure 5C exhibited greater heterogeneity, with more pronounced differences in velocity both across and along the channel. However, the PIV output based on the 0.25 Hz sequence also featured some clearly erroneous vectors, including a few oriented upstream, even after applying the filters incorporated into our refined workflow.

FIGURE 5

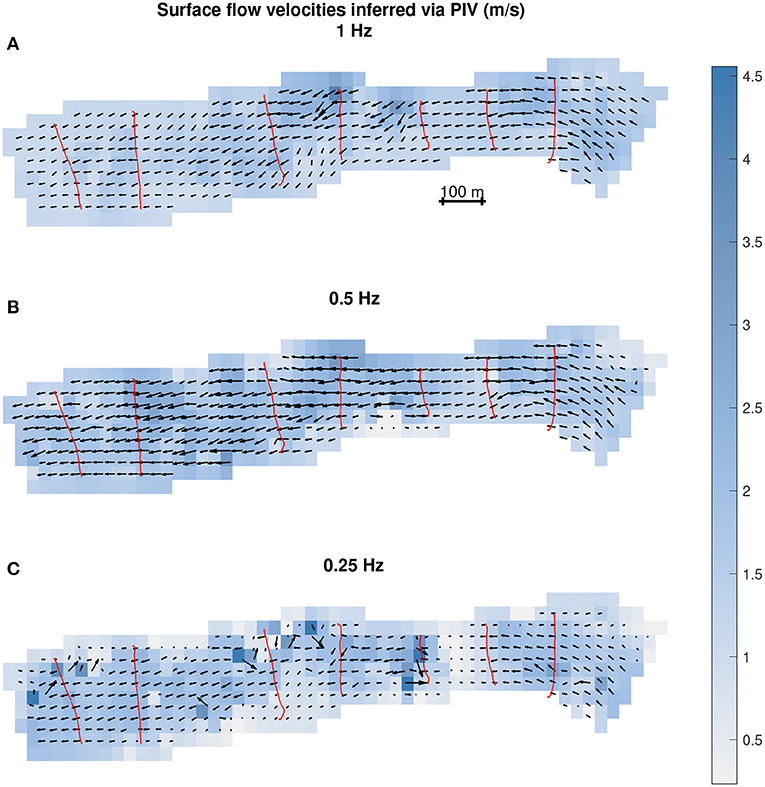
Figure 5. Maps of PIV-derived surface flow velocities for different frame rates: (A) 1 Hz, (B) 0.5 Hz, and (C) 0.25 Hz. The locations of the ADCP velocity measurements used for accuracy assessment are shown in red.

The results of this analysis are summarized quantitatively in Table 2, which lists several error metrics by frame rate, and Figure 6, which consists of OP regression scatter plots for the 1, 0.5, and 0.25 Hz image sequences. Whereas agreement between PIV-derived velocity estimates and field measurements from the ADCP was very weak for the 1 and 0.5 Hz frame rates, with OP R²-values near 0, the OP R² improved to a still modest 0.39 for the lowest frame rate we considered, 0.25 Hz. The normalized RMSE, which can be interpreted as a measure of precision expressed as a percentage of the reach-averaged mean flow velocity measured in the field, was reduced from 42 and 33% for the 1 and 0.5 Hz sequences, respectively, to 29% for the 0.25 Hz data set. Similarly, the normalized mean bias, an index of absolute accuracy relative to the field observations, decreased by a factor of two for the 0.25 Hz sequence, to 3%. However, even for the lowest frame rate that yielded the strongest agreement with the ADCP measurements, the dimensional version of the RMSE was 0.5 m/s, indicating that PIV of the satellite video failed to provide precise estimates of surface flow velocity on a point-by-point basis at high spatial resolution.

FIGURE 6

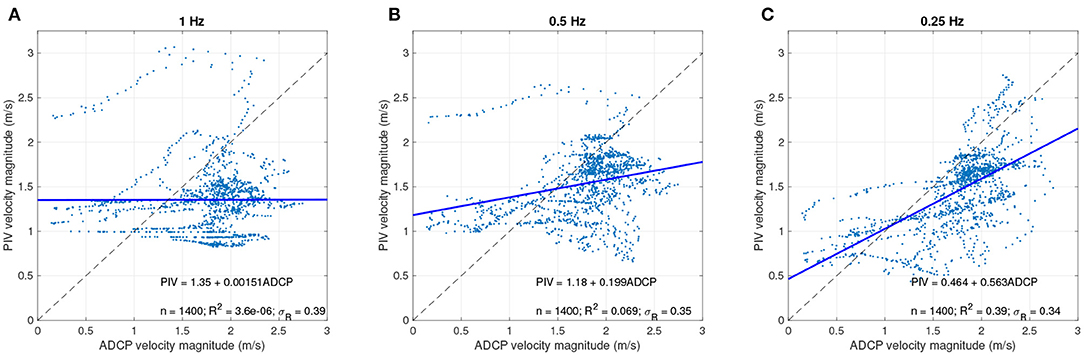
Figure 6. Observed (ADCP) vs. predicted (PIV) regressions for the entire study area (i.e., aggregated over all seven cross sections) for different frame rates: (A) 1 Hz, (B) 0.5 Hz, and (C) 0.25 Hz.

The maps presented in Figure 7 summarize the spatial pattern of these velocity estimation errors for each frame rate. Defined as the difference between the depth-averaged velocity magnitudes observed in the field and inferred from remotely sensed data, errors were positive (red tones) where PIV under-estimated the velocity relative to the field data and negative (blue tones) where PIV yielded a velocity estimate greater than that measured in the field. Closer agreement is represented by neutral, near-white colors, which were most extensive for the lowest frame rate we considered. Velocity errors tended to be large and negative, implying over-estimates, near the banks, particularly for the 1 and 0.5 Hz image sequences. In the along-channel direction, the largest errors occurred at the fourth cross section downstream, in the middle of our study area, but to a lesser degree for the lowest frame rate. Overall, this analysis confirmed that although PIV-based velocity estimates were not very reliable on a point-by-point basis for any of the image sequences we extracted from the satellite video, that with the lowest frame rate, 0.25 Hz, yielded the strongest agreement with the field data.

FIGURE 7

Figure 7. Differences between depth-averaged velocities measured by an ADCP and surface velocity estimates inferred via PIV for different frame rates: (A) 1 Hz, (B) 0.5 Hz, and (C) 0.25 Hz.

3.4. Comparison of Bulk Flow Characteristics Inferred via PIV and Measured in the Field

Although the accuracy assessment summarized in the preceding section indicated that flow velocities inferred from satellite video did not correspond closely with ADCP-based field measurements when considered on a point-by-point basis, we also evaluated whether larger-scale bulk flow characteristics could be estimated reliably from a spaceborne platform. As one component of this analysis, we compared velocities derived from the video to measurements from a radar gage mounted on a bridge at the downstream end of our study area. Importantly, this radar sensor provided a true surface flow velocity that was more directly comparable to the PIV output than the ADCP data, which consisted of velocities that were vertically averaged over the full depth of the water column (except for blanking distances immediately below the surface and near the bed that cannot be measured by an ADCP; Mueller, 2013). Because the radar gage was mounted on a bridge and oriented at an oblique but nearly vertical angle, the instrument observed an area of the river very close to the bridge itself. This proximity to the bridge forced us to use PIV output derived from the 0.5 Hz image sequence because the vectors produced from the 0.25 Hz sequence included obvious edge effects associated with the bridge. In addition, because the location of the radar gage footprint was not known exactly, we averaged the three PIV-based velocity estimates closest to the approximate location of the radar measurement. The radar gage recorded a surface flow velocity of 1.58 m/s at the time (within 15 min) the satellite video was acquired, whereas the mean of the three surface velocity estimates extracted from the PIV output was 1.72 m/s. The velocity inferred from the spaceborne sensor thus agreed with the bridge-mounted radar gage to within 8.65%. This result implied that video acquired from space could yield surface flow velocities consistent with those obtained by another type of non-contact but near-field streamflow measurement instrument.

We also assessed the degree to which satellite video might yield reliable velocity information on a cross-sectional basis. A comparison of velocities measured in the field with an ADCP and processed with VMT and inferred from satellite video via PIV is summarized in Figure 8, which shows, in general, a strong agreement between the PIV-based velocity estimates and the post-processed field observations, particularly for XS 1, 6, and 7. For XS 2 and 5, PIV underestimated the depth-averaged flow velocity across much of the channel whereas overestimates occurred near the banks on XS 4 and in the middle of XS 3.

FIGURE 8

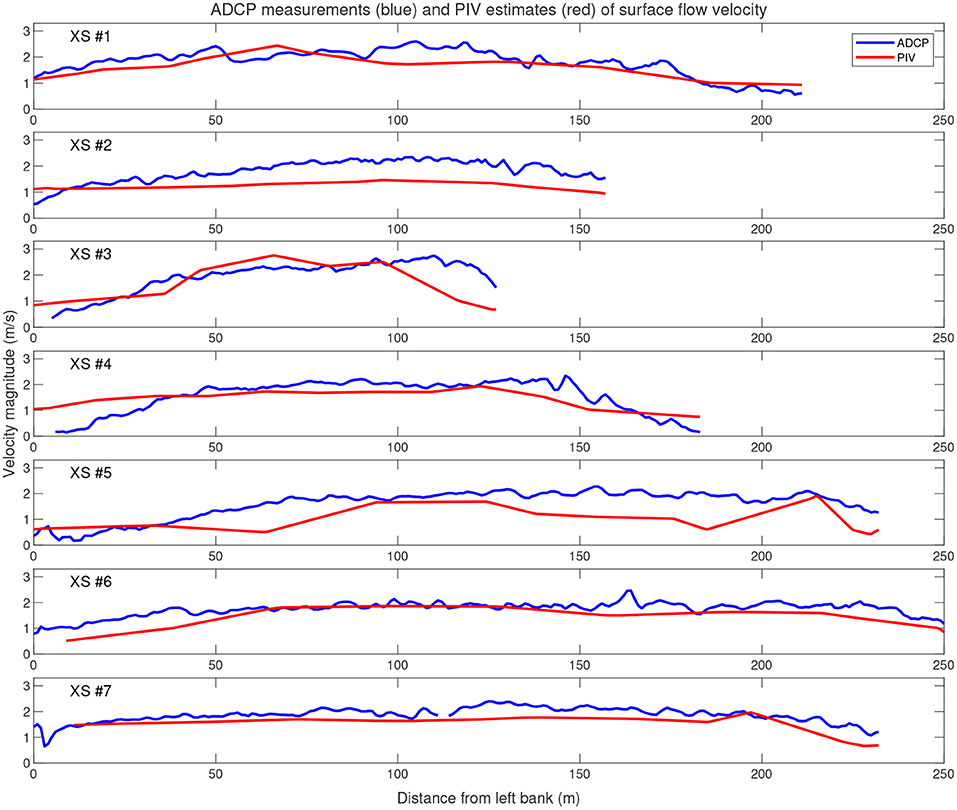
Figure 8. ADCP field measurements of depth-averaged flow velocity and PIV-based estimates of surface flow velocity derived from the 0.25 Hz image sequence for seven cross sections along the Tanana River.

To quantify this comparison, we performed an observed (ADCP) vs. predicted (PIV) (OP) regression for each cross section. The resulting scatter plots, best-fit OP regression lines, and one-to-one lines of perfect agreement for the seven transects are compiled in Figure 9. OP R²-values varied from 0.34 to 0.64 and tended to be greater where the field observations spanned a greater range of velocity. A high R² did not necessarily imply reliable velocity estimates, however, and considering the intercept and slope of the OP regression lines also was important. For example, whereas XS 7 had a relatively high R² of 0.56 and an intercept near 0 and slope near 1, indicating unbiased velocity estimates, XS 4 had an identical R²-value but an intercept greater than 1 and a slope of only 0.441, implying that PIV tended to overestimate the flow velocities that were observed in the field and post-processed in VMT. A similar scenario occurred at XS 2, where the R² of 0.6 was primarily due to the homogeneity of the PIV-based estimates, which lead to an OP regression slope of only 0.233, well below the ideal value of 1 for a line of perfect agreement. Overall, however, the OP regression results for the individual VMT-generated mean cross sections were superior to those based on the reach-aggregated ADCP measurement points (Figure 6), suggesting that satellite video could yield reasonably accurate velocity estimates at the cross-sectional scale. We also evaluated the potential to infer two key summaries of cross-sectional hydraulics from satellite video by computing the mean and maximum of both the PIV-based velocity estimates and the VMT-processed ADCP measurements for each of the seven cross sections and comparing these values via OP regressions. Figure 10 indicates that whereas the cross-sectional average velocities estimated via PIV did not correspond closely with those calculated from the field data (R² = 0.42), the remotely sensed data yielded much stronger agreement with the maximum velocities observed at each cross section, with an OP regression R² of 0.76.

FIGURE 9

Figure 9. Observed (ADCP) vs. predicted (PIV) regressions for seven cross sections along the Tanana River. PIV-based velocity estimates were derived from the 0.25 Hz image sequence.

FIGURE 10

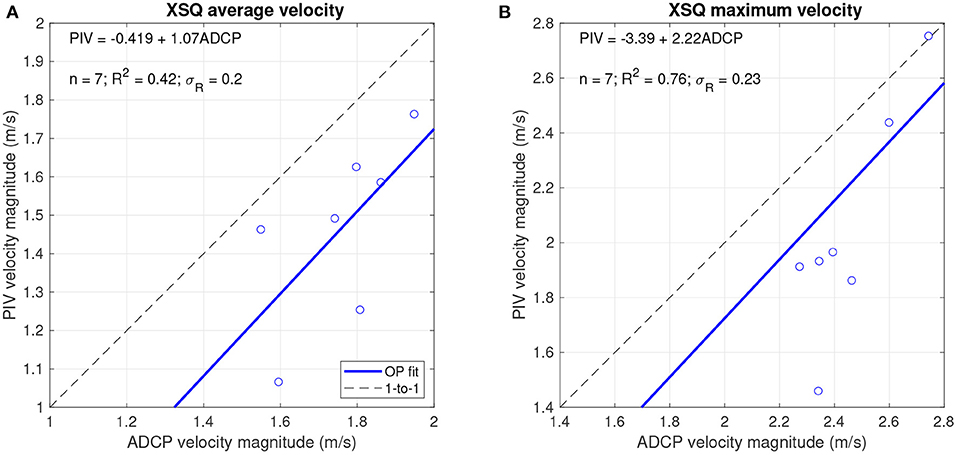
Figure 10. Observed (ADCP) vs. predicted (PIV) regressions for cross-sectional (A) average and (B) maximum surface flow velocities for seven cross sections along the Tanana River.

The distributions of the cross-sectional average and maximum velocity values derived from the field observations and satellite video across the seven transects are summarized in Figure 11. PIV yielded a broader range of mean velocities than the ADCP measurements, with median values (red lines in the box plots) that were less than the field observations after applying the cross section-specific velocity indices to convert surface flow velocities to depth-averaged velocities (Figure 11A). Similarly, the range of cross-sectional maximum velocities was much wider for the remotely sensed estimates and had a lower median value than the ADCP data. For neither the cross-sectional average nor maximum velocities did the interquartile range (blue box) for the PIV estimates encompass that of the ADCP data.

FIGURE 11

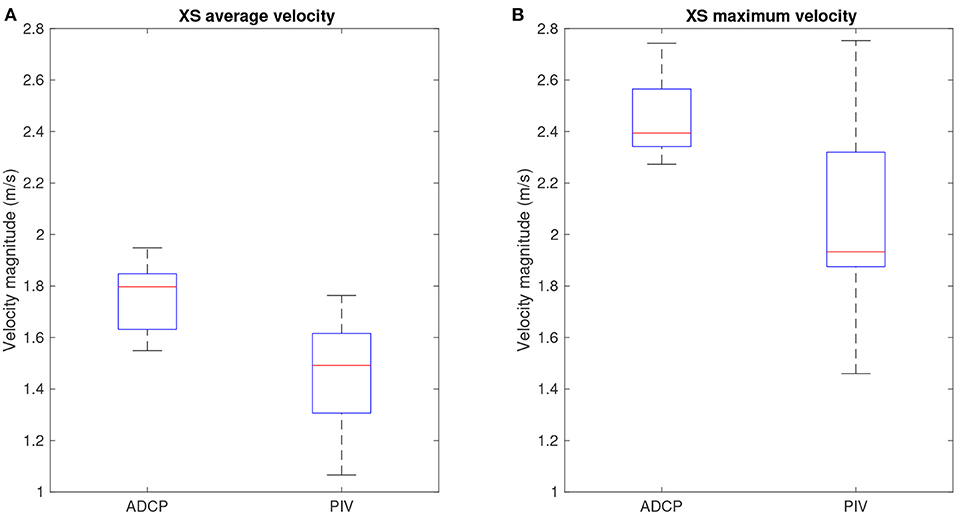
Figure 11. Box plots comparing ADCP- and PIV-based cross-sectional (A) average and (B) maximum surface flow velocities for seven cross sections along the Tanana River.

We also compared the cross-sectional mean and maximum velocities from the ADCP and the satellite video by computing mean errors, normalizing them by the reach-averaged cross-sectional mean and maximum velocities, and performing statistical hypothesis tests. For the cross-sectional mean velocity, the mean error averaged over the seven cross sections was 0.29 m/s, or 16.7% of the mean of the cross-sectional averaged velocities. The standard deviation of these errors provided a metric of precision and was 0.18 m/s, or 10.2% of the mean of the cross-sectional average velocities. A two-sample t-test comparing the ADCP- and PIV-based velocities resulted in a p-value of 0.005 and we rejected the null hypothesis that the means of the cross-sectional average velocities measured by the ADCP and inferred via PIV were equal. The results for the cross-sectional maximum velocities were similar. The mean error averaged over the seven cross sections was 0.40 m/s, equivalent to 16.5% of the mean of the cross-sectional maximum velocities. The standard deviation of these errors was 0.29 m/s, 11.8% of the mean of the cross-sectional maximum velocities. A two-sample t-test yielded a p-value of 0.01 and we thus rejected the null hypothesis that the means of the cross-sectional maximum velocities measured by the ADCP and inferred via PIV were equal. These results implied that video acquired from space could provide reasonably precise but biased (i.e., under-estimated relative to ADCP measurements) information on bulk flow characteristics in a large, sediment-laden river.

4. Discussion

4.1. The Role of Image Preprocessing and Image Frame Rate in PIV

The results summarized in section 3.2 highlighted the importance of effective image preprocessing, consistent with our past experience with many other data sets. Preparing images for input to PIV by enhancing water surface features proved essential both in this study, based on satellite video, and in our previous work using image sequences acquired from a bridge (Legleiter et al., 2017) or a helicopter (Legleiter and Kinzel, 2020). For example, we found that enhancing raw images with an FFT bandpass filter and histogram equalization contrast stretch facilitated tracking of water surface features via PIV and thus lead to more accurate velocity estimates. Although many alternative approaches to image preprocessing are available, we incorporated FIJI into our workflow because this freely available, open source software package provides a wide range of image processing tools and is conducive to scripting, batch processing, and external, programmatic access from other programs such as MATLAB. Regardless of the details of implementation, this study provided further evidence of the importance of preprocessing image sequences so as to allow PIV algorithms to more readily detect the advection of water surface features.

Selecting an appropriate frame rate is another critical step in any effort to infer surface flow velocities from remotely sensed data. In essence, PIV algorithms compare pairs of images acquired sequentially over time to infer the displacement of either discrete particles, as in the laboratory settings where the technique was first developed (Raffel et al., 2007), or distinct features on the surface of larger-scale flows in natural channels, where various image-based velocimetry techniques are increasingly applied (e.g., Muste et al., 2008; Bandini et al., 2021; Eltner et al., 2020). For a given flow velocity, the time interval between images dictates the amount of displacement that can occur between frames and, along with the image pixel size, thus imposes a fundamental constraint on the range of velocities that can be inferred. For example, in a river with a surface flow velocity of 1 m/s and an image sequence consisting of 1 m pixels, any frame rate higher than 1 Hz would not allow sufficient time between frames for surface features to advect by a distance greater than 1 pixel, which is the minimum offset from the first to the second image that could be detected by a correlation-based algorithm. Although most PIV implementations allow for sub-pixel peak-finding, such functionality is intended to refine velocity estimates and does not influence the correlation calculation upon which the inference is based. In general, the lowest velocity detectable via PIV, denoted by v_min, is the product of the pixel size p in m and the frame rate f in Hz: v_min = p × f. For the satellite video used in this study, which was acquired at a high temporal resolution, with a native frame rate of 30 Hz, but relatively coarse spatial resolution, with a ground sampling distance of 0.927 m after geo-referencing, our results suggest that the image pixel size was a key limitation on the range of velocities that could be inferred via PIV, as well as the accuracy and precision of those estimates.

To gain insight regarding the impact of image frame rate on PIV-based velocity estimates, we extracted correlation matrices generated as an intermediate output by the PIVlab algorithm for each node of the PIV output grid. Conceptually, the correlation matrix summarizes the similarity or overlap between the textural patterns present in two sequential images when the first is offset relative to the second by various lags. The location of the correlation peak indicates the number of rows and columns by which the first image must be translated to produce the strongest match with the second and is assumed to represent the magnitude and direction by which features are advected by the flow during the time period between frames. Although the corresponding velocity estimate is based on the peak, inspecting the full correlation matrix can provide an indication of the quality of this estimate (Raffel et al., 2007; Le Coz et al., 2010). For example, the height of the peak relative to the other offsets represented within the correlation matrix can be interpreted as an index of signal to noise. Raffel et al. (2007) suggested that this metric, defined as the ratio of the height of the correlation peak to the mean correlation value for the entire matrix, could be used to assess the validity of velocity estimates but also cautioned that mismatched images or stationary background features can produce high correlations. An advantage of this approach is that normalizing correlation values, which depend on image brightness, allows for comparison of correlation matrices from various image data sets.

In this study, we extracted correlation matrices from the PIV output grids generated from the 1, 0.5, and 0.25 Hz image sequences for a common, fixed location to help inform our analysis of the effects of image frame rate (Figure 12). In addition, as a point of comparison, we also included the correlation matrix from the same position in the Tanana River derived from video acquired via helicopter in July 2019 that lead to very strong agreement between PIV-based velocity estimates and the same ADCP field measurements used in this study (Legleiter and Kinzel, 2020). Importantly, although the helicopter data had a frame rate of 1 Hz, equivalent to the highest frame rate retained from the satellite video, these images had a pixel size of approximately 15 cm, one-sixth that of the satellite images. For the 1 Hz satellite sequence, a single, moderately high peak occurred near the center of the matrix (Figure 12A), indicating a very small displacement of the textural pattern from one frame to the next and suggesting that water surface features did not have sufficient time to advect a measurable distance (i.e., multiple pixels) between frames. For the 0.5 Hz satellite sequence (Figure 12B), the peak is offset from the origin of the matrix to a greater degree and in a direction (to the left) consistent with the known flow direction (to the west) of the Tanana River. Further reducing the frame rate to 0.25 Hz resulted in a more diffuse, lower correlation peak, as well as several other offsets with correlations nearly as high, that was farther from the center of the matrix, suggesting that although the pattern match between frames was weak, it was maximized at a more realistic position (Figure 12C). Finally, the correlation matrix for the 2019 helicopter data, in contrast, was dominated by a much stronger, clearly defined peak well-separated from the origin (Figure 12D), implying a more reliable velocity estimate. We attribute this improvement to the smaller pixel size of the airborne, rather than spaceborne, data.

FIGURE 12

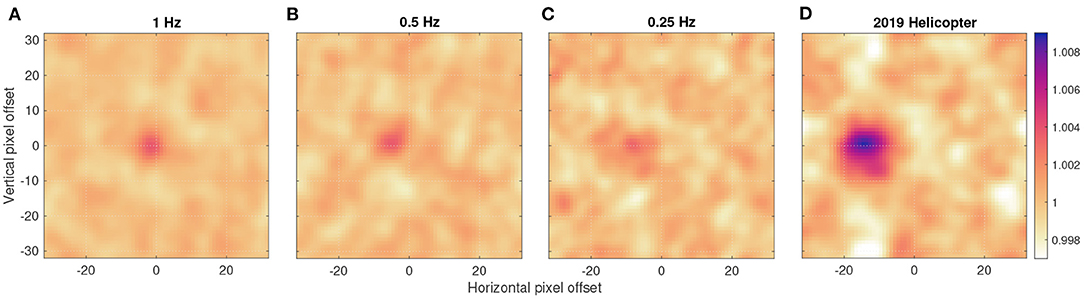
Figure 12. Correlation matrices for the same location in the channel for satellite video resampled to three different frame rates, (A) 1 Hz, (B) 0.5 Hz, and (C) 0.25 Hz, and (D) video acquired from a helicopter in 2019 at a frame rate of 1 Hz and with a pixel size of 0.15 m, in contrast to the 0.93 m pixels of the satellite video. To enable comparison, each correlation matrix is normalized by its mean value.

Further information on the reliability of PIV-derived velocity estimates can be obtained by mapping the peak correlation values, one for each node in the PIV output grid, spatially throughout the region of interest (Figure 13). In general, the peak correlation is inversely proportional to the displacement. In the trivial, limiting case of an image pair containing only stationary features, a single correlation spike with a value of 1 would occur at a pixel offset of 0. In the context of a river, smaller displacements and thus higher correlations would be expected in lower-velocity areas along the margins of the channel, as observed along the south bank of the Tanana for all three frame rates extracted from the satellite video as well as the 2019 helicopter data. Closer inspection of the correlation maps in Figure 13, for which the satellite data were subset to match the smaller spatial footprint of the helicopter-based image sequence, also indicated that correlations were higher throughout the channel proper for satellite image sequences with greater frame rates. Because in this context stronger correlations correspond to smaller, even negligible, displacements of surface features from frame to frame, the more extensive warm, saturated tones in the correlation map produced from the 1 Hz sequence (Figure 13A) than in the maps for the 0.5 or 0.25 Hz sequences (Figures 13B,C) indicate smaller translations for the higher frame rate, implying less reliable velocity estimates. For the helicopter data with six-fold finer pixels, this effect was even more evident, as the map of peak correlation values in Figure 13D consists primarily of very low, even negative correlations due to the greater displacements, in units of pixels, from frame to frame, even though the images were separated by only 1 s. These results imply that whereas a frame rate of 1 Hz was excessive for the relatively coarse pixels of the satellite data, the same capture interval was appropriate for the smaller ground sampling distance of the images acquired from the helicopter. The effects of image frame rate are thus closely intertwined with those of image pixel size—an imaging system's temporal and spatial resolution must be considered in tandem. This analysis suggests that, given the limited spatial resolution achievable via satellite video, relatively low frame rates might lead to more reliable velocity estimates.

FIGURE 13

Figure 13. Maps of peak correlation values for satellite video resampled to three different frame rates, (A) 1 Hz, (B) 0.5 Hz, and (C) 0.25 Hz, and (D) video acquired from a helicopter in 2019 at a frame rate of 1 Hz and with a pixel size of 0.15 m, in contrast to the 0.93 m pixels of the satellite video.

4.2. Potential Applications, Persistent Limitations, and Directions for Future Research

In practice, many streamflow monitoring applications, most notably discharge measurement, rely upon data from individual channel cross sections, not continuous, two-dimensional flow fields such as those that can be produced from remotely sensed data via PIV. For this reason, we assessed the degree to which satellite video could provide velocity information of acceptable accuracy on a cross-sectional basis. Moreover, if the objective is to measure river discharge, further aggregation of PIV-derived velocity fields could be sufficient; a discharge calculation can be as simple as the product of the channel's cross-sectional area and the mean flow velocity for the cross section. Similarly, the probability concept described by Fulton et al. (2020a,b) provides a means of estimating discharge based on the maximum surface velocity for a cross section, as well as an independent source of information on cross-sectional area. In either case, the error in the calculated discharge is directly proportional to the error in the mean or maximum velocity for the cross section, implying that if reliable estimates of these bulk flow characteristics could be derived from satellite video, this approach could become a viable tool for non-contact streamflow measurement.

In this study, we observed stronger agreement between PIV-based estimates and field observations for cross-sectional maximum velocities than for cross-sectional mean velocities. This result was consistent with our analysis of the effects of image frame rate: higher velocities were more reliably inferred from the 0.25 Hz image sequence because greater displacement of surface features between frames occurred in areas of faster flow. Using the maximum rather than the mean cross-sectional velocity is advantageous in this context because this approach focuses on the high velocity core of the channel and avoids lower velocity zones near the banks where small frame-to-frame displacements might not be detectable at the spatial resolution of the satellite video, even at a low frame rate. Improving the ground sampling distance that can be achieved from space thus emerges as a key technical requirement for remote sensing of river discharge. Two additional limitations are the need to: (1) convert surface velocities inferred via PIV to depth-averaged velocities for calculating discharge, typically by assuming or calibrating a velocity index (Mueller, 2013); and (2) obtain an independent source of information on channel cross-sectional area, either surveyed in the field or obtained via non-contact methods. The latter issue is particularly challenging because standard approaches to mapping river bathymetry from remotely sensed data, such as spectrally based depth retrieval and bathymetric lidar (e.g., Legleiter and Harrison, 2019), are not well-suited to the large, turbid rivers where flow velocities can be inferred by tracking sediment boil vortices. A crucial objective for future research is thus to develop new, complementary technologies for observing both velocity and depth and design multi-sensor payloads accordingly.

Although this study demonstrated the potential for remote sensing of surface flow velocities from space to contribute to non-contact streamgaging programs, our work also called attention to several important limitations of this approach, beyond the general environmental and imaging system considerations described by Legleiter and Kinzel (2020). First, the ~1 m pixel size of currently available satellite video is relatively large in comparison to image data acquired from an airborne platform such as a helicopter or, to an even greater degree, sUAS. Because coarser pixels dictate that more time must pass between successive images for frame-to-frame feature displacements to be detectable, lower frame rate image sequences must be provided as input to PIV algorithms. A potentially important question raised by the use of lower frame rates is the persistence of the sediment boil vortices that were tracked by the PIV algorithm, which allowed us to avoid seeding the flow with artificial tracers. For example, if the water surface features associated with these vortices are very short-lived, capturing an image only once every four seconds might be inadequate to detect their movement. Our initial results implied that frame rates as low as 0.25 Hz might be sufficient, but further research on the dynamics of sediment boil vortices, building upon earlier work by Fujita and Komura (1994), Fujita and Hino (2003), Chickadel et al. (2009), and Talke et al. (2013) is needed. Another consequence of using a lower frame rate (e.g., 0.25 Hz) is a reduction in the number of images retained for a given video duration. The resulting limited sample size could lead to less accurate velocity estimates because the performance of ensemble correlation PIV improves with the number of images (Strelnikova et al., 2020). In this study, the original 60 s video had to be truncated due to cloud cover and we were left with only a handful of images for analysis: five for the 0.25 Hz sequence. If imaging conditions were more favorable, a longer dwell time might yield more reliable velocity estimates for a given frame rate. Future research could examine the sensitivity of PIV output to image sequence duration for different frame rates, similar to the analysis we performed for helicopter data (Legleiter and Kinzel, 2020). Another constraint imposed by the relatively coarse pixels of satellite video and the resulting inability to resolve small frame-to-frame feature displacements is the need to filter out low velocity estimates that fail to satisfy the v_min = p × f criterion. Applying this threshold could bias calculations of cross-sectional mean velocities and exclude low velocity zones that might be of primary interest for applications such as habitat assessment and contaminant transport characterization.

Because the relatively coarse pixel sizes of satellite video dictate the use of frame rates two orders of magnitude smaller than the 30 Hz at which the video are acquired, one instead might consider using still images acquired in rapid succession. For example, the Planet Labs SkySat constellation can acquire panchromatic video with 1 m pixels or multispectral images with 0.5 m pixels, which would allow lower velocities to be resolved for a given capture interval. In addition, the spectral information provided by the still images could facilitate feature detection and tracking. Planet Labs already offers a rapid revisit product that provides coverage up to nine times per day, but the ability of the current configuration to acquire multiple images over much shorter time periods has not been tested. In principle, a stereo acquisition could take advantage of the off-nadir pointing capability of a single SkySat to provide four images acquired on the same pass and separated in time by a few seconds. Such an approach would build upon the work of Kääb et al. (2019) in northern rivers by providing higher spatial and temporal resolution and greater flexibility in site selection and image acquisition. Although spaceborne platforms are subject to cloud cover that helicopters, fixed-wing aircraft, and sUAS can fly beneath, satellites offer some distinct advantages, such as safety, efficiency, ease of tasking, and potentially cost, that could make them more conducive to operational streamflow monitoring. Similarly, high-altitude, long-endurance (HALE) UAS capable of observing a particular location of interest for extended periods of time represent another intriguing prospect. Further technological development and additional research effort, including coordinated acquisition of remotely sensed data and field measurements across a broader range of river environments, are needed to explore these possibilities.

5. Conclusion

Large rivers in remote, inaccessible locations, including much of the state of Alaska, pose significant challenges for field-based streamgaging operations. In an ongoing effort to improve safety, reduce cost, and expand coverage, this study explored the possibility of estimating surface flow velocities from satellite video, building upon previous work based on near-simultaneous (~ 90 s capture interval) acquisition of satellite still images (Kääb et al., 2019) and video acquired from a helicopter (Legleiter and Kinzel, 2020). Current spaceborne imaging systems can collect 60 s of panchromatic video at 30 Hz with a pixel size of approximately 1 m and their orbital perspective ensures a broad field of view encompassing both banks, which is critical for image stabilization and geo-referencing. This type of data could thus play a central role in non-contact streamgaging programs and provide spatially distributed velocity information to support a number of other riverine applications. As in the helicopter-based study, which focused on the same sediment-laden river in central Alaska, we exploited naturally occurring sediment boil vortices to perform PIV analyses, avoiding the need to seed the flow with artificial tracers. Although the coarse pixel size of the satellite video relative to airborne images dictated the use of low frame rates and precluded detection of velocities less than ~1 m/s, this study demonstrated the potential to infer surface flow velocities from space. Salient outcomes of this investigation include the following principal conclusions:

1. The individual frames extracted from the satellite video were successfully stabilized relative to one another, with sub-pixel maximum displacement errors.

2. Similarly, the first frame of the stabilized image stack was accurately geo-referenced to an orthophoto base, with a typical error of 1.48 m that did not influence velocity estimates based on feature displacements from frame to frame and allowed us to confidently associate these PIV-derived estimates with field measurements to assess their accuracy.

3. Preprocessing images to enhance the detection and tracking of water surface features is an essential prerequisite to effective PIV and was achieved in this study by applying an FFT bandpass filter and histogram equalization contrast stretch implemented within open source image processing software.

4. The strongest agreement between PIV-derived surface flow velocities and field measurements of depth-averaged velocity occurred for the lowest frame rate we considered, 0.25 Hz, but remained weak (R² = 0.39). Only at such a low frame rate did water surface features have sufficient time to advect a distance equivalent to several pixels between successive image frames. The normalized mean bias and normalized RMSE of the velocities inferred from the 0.25 image sequence were 3% and 29%, respectively, of the reach-averaged velocity measured in the field.

5. The surface flow velocity inferred from satellite video matched an independent measurement from a bridge-mounted radar gage to within 8.65%.

6. Aggregating the PIV-derived velocities to the cross-sectional scale improved agreement with seven mean cross sections produced by post-processing the field data, with R²-values as high as 0.64, although biases were observed for some of the transects.

7. Two key summary metrics of cross-sectional hydraulics, the mean and maximum velocity, were estimated reliably from satellite video, with an R² of 0.76 for the cross-sectional maximum velocity. However, comparing the distributions of these two channel attributes via statistical hypothesis tests indicated that the mean values of the cross-sectional mean and maximum velocities derived via PIV and computed from the field data were significantly different from one another. Multiplying the original PIV-derived surface flow velocities by a cross section-specific velocity index tended to yield underestimates of the depth-averaged flow velocity.

8. Examining the correlation matrices produced as an intermediate output by PIV algorithms can yield insight on the interactions between image frame rate and spatial resolution, which must be considered in tandem. This analysis helped to explain the superior performance of the lower, 0.25 Hz frame rate image sequence as a consequence of the ~1 m pixel size of the satellite data.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: The datasets used in this study can be found in Legleiter and Kinzel (2021).

Author Contributions

Field data collection in Alaska and video acquisition by Planet Labs, Inc., were coordinated by CL and PK. CL was the primary developer of the code for implementing the image processing and PIV workflow described herein, with conceptual contributions from PK. Data analysis and accuracy assessment was performed by CL. CL prepared the initial draft of the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

Funding for this study was provided by the U.S. Geological Survey Water Mission Area.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared research group with one of the author CL.

Acknowledgments

Heather Best and Karenth Dworsky of the USGS Alaska Science Center obtained field measurements of flow velocity from the Tanana River. Dominic Filiano and Carl Green of the U.S. Army Corps of Engineers Cold Regions Research and Engineering Laboratory acquired and processed the helicopter- and field-based data used to produce the orthophoto. The USGS Groundwater and Streamflow Information Program provided financial support. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Abbreviations

ADCP, Acoustic Doppler Current Profiler; CLAHE, Contrast Limited Adaptive Histogram Equalization; FFT, Finite Fourier Transform; HALE, High Altitude Long Endurance; IA, Interrogation Area; GNSS, Global Navigation Satellite System; OP, Observed vs. Predicted; PIV, Particle Image Velocimetry; RGB, Red, Green, Blue; RMSE, Root Mean Squared Error; ROI, Region Of Interest; RPC, Rational Polynomial Coefficients; SIFT, Scale Invariant Feature Transformation; sUAS, small Uncrewed Aircraft System; USGS, United States Geological Survey; VMT, Velocity Mapping Toolbox; XS, Cross Section.

References

Altenau, E. H., Pavelsky, T. M., Moller, D., Pitcher, L. H., Bates, P. D., Durand, M. T., et al. (2019). Temporal variations in river water surface elevation and slope captured by AirSWOT. Remote Sens. Environ. 224, 304–316. doi: 10.1016/j.rse.2019.02.002

CrossRef Full Text | Google Scholar

Bandini, F., Lüthi, B., Peña-Haro, S., Borst, C., Liu, J., Karagkiolidou, S., et al. (2021). A drone-borne method to jointly estimate discharge and manning's roughness of natural streams. Water Resour. Res. 57, e2020WR028266. doi: 10.1029/2020WR028266

CrossRef Full Text | Google Scholar

Bjerklie, D. M., Birkett, C. M., Jones, J. W., Carabajal, C., Rover, J. A., Fulton, J. W., et al. (2018). Satellite remote sensing estimation of river discharge: application to the Yukon River Alaska. J. Hydrol. 561, 1000–1018. doi: 10.1016/j.jhydrol.2018.04.005

CrossRef Full Text | Google Scholar

Cardona, A., Saalfeld, S., Schindelin, J., Arganda-Carreras, I., Preibisch, S., Longair, M., et al. (2012). TrakEM2 software for neural circuit reconstruction. PLoS ONE 7:e38011. doi: 10.1371/journal.pone.0038011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chickadel, C. C., Horner-Devine, A. R., Talke, S. A., and Jessup, A. T. C. L. (2009). Vertical boil propagation from a submerged estuarine sill. Geophys. Res. Lett. 36:L10601. doi: 10.1029/2009GL037278

CrossRef Full Text | Google Scholar

Conaway, J., Eggleston, J., Legleiter, C., Jones, J., Kinzel, P., and Fulton, J. (2019). Remote sensing of river flow in Alaska–New technology to improve safety and expand coverage of USGS streamgaging. U.S. Geol. Surv. Fact Sheet 2019:4. doi: 10.3133/fs20193024

CrossRef Full Text | Google Scholar

Eltner, A., Sardemann, H., and Grundmann, J. (2020). Technical note: flow velocity and discharge measurement in rivers using terrestrial and unmanned-aerial-vehicle imagery. Hydrol. Earth Syst. Sci. 24, 1429–1445. doi: 10.5194/hess-24-1429-2020

CrossRef Full Text | Google Scholar

European Space Agency (2020). SkySat Mission | Earth Online. Available online at: https://earth.esa.int/eogateway/missions/skysat (accessed November 23, 2020).

FIJI-ImageJ (2020). FIJI. Available online at: https://imagej.net/Fiji (accessed December 8, 2020).

Fujita, I. (2017). Discharge measurements of snowmelt flood by space-time image velocimetry during the night using far-infrared camera. Water 9:269. doi: 10.3390/w9040269

CrossRef Full Text | Google Scholar

Fujita, I., and Hino, T. (2003). Unseeded and seeded PIV measurements of river flows videotaped from a helicopter. J. Visual. 6, 245–252. doi: 10.1007/BF03181465

CrossRef Full Text | Google Scholar

Fujita, I., and Komura, S. (1994). Application of video image analysis for measurements of river-surface flows. Proc. Hydraul. Eng. 38, 733–738. doi: 10.2208/prohe.38.733

CrossRef Full Text | Google Scholar

Fulton, J. W., Anderson, I. E., Chiu, C.-L., Sommer, W., Adams, J. D., Moramarco, T., et al. (2020a). QCam: sUAS-based Doppler radar for measuring river discharge. Remote Sens. 12:3317. doi: 10.3390/rs12203317

CrossRef Full Text | Google Scholar

Fulton, J. W., Mason, C. A., Eggleston, J. R., Nicotra, M. J., Chiu, C.-L., Henneberg, M. F., et al. (2020b). Near-field remote sensing of surface velocity and river discharge using radars and the probability concept at 10 U.S. Geological Survey Streamgages. Remote Sens. 12:1296. doi: 10.3390/rs12081296

CrossRef Full Text | Google Scholar

Gleason, C. J., and Durand, M. T. (2020). Remote sensing of river discharge: a review and a framing for the discipline. Remote Sens. 12:1107. doi: 10.3390/rs12071107

CrossRef Full Text | Google Scholar

Global Mapper - All-in-one GIS Software (2020). Available online at: https://www.bluemarblegeo.com/products/global-mapper.php (accessed December 10, 2020).

Hemisphere GNSS (2020). Hemisphere GNSS A101 Smart Antenna User Guide. Available online at: https://www.hemispheregnss.com/wp-content/uploads/2019/01/hemispheregnss_a101_userguide_875-0324-000_b1.pdf (accessed December 8, 2020).

Kääb, A., Altena, B., and Mascaro, J. (2019). River-ice and water velocities using the Planet optical cubesat constellation. Hydrol. Earth Syst. Sci. 23, 4233–4247. doi: 10.5194/hess-23-4233-2019

CrossRef Full Text | Google Scholar

Kääb, A., and Leprince, S. (2014). Motion detection using near-simultaneous satellite acquisitions. Remote Sens. Environ. 154, 164–179. doi: 10.1016/j.rse.2014.08.015

CrossRef Full Text | Google Scholar

Kinzel, P., and Legleiter, C. (2019). sUAS-based remote sensing of river discharge using thermal particle image velocimetry and bathymetric lidar. Remote Sens. 11:2317. doi: 10.3390/rs11192317

CrossRef Full Text | Google Scholar

Le Coz, J., Hauet, A., Pierrefeu, G., Dramais, G., and Camenen, B. (2010). Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 394, 42–52. doi: 10.1016/j.jhydrol.2010.05.049

CrossRef Full Text | Google Scholar

Legleiter, C., and Harrison, L. R. (2019). Remote sensing of river bathymetry: evaluating a range of sensors, platforms, and algorithms on the Upper Sacramento River, California, USA. Water Resour. Res. 55, 2142–2169. doi: 10.1029/2018WR023586

CrossRef Full Text | Google Scholar

Legleiter, C., and Kinzel, P. (2021). Satellite Video and Field Measurements of Flow Velocity Acquired from the Tanana River in Alaska and Used for Particle Image Velocimetry (PIV). U.S. Geological Survey data release.

Legleiter, C., and Kinzel, P. J. (2020). Inferring surface flow velocities in sediment-Laden Alaskan rivers from optical image sequences acquired from a helicopter. Remote Sens. 12:1282. doi: 10.3390/rs12081282

CrossRef Full Text | Google Scholar

Legleiter, C. J., Kinzel, P. J., and Nelson, J. M. (2017). Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 554(Suppl. C), 490–506. doi: 10.1016/j.jhydrol.2017.09.004

CrossRef Full Text | Google Scholar

Lin, D., Grundmann, J., and Eltner, A. (2019). Evaluating image tracking approaches for surface velocimetry with thermal tracers. Water Resour. Res. 55, 3122–3136. doi: 10.1029/2018WR024507

CrossRef Full Text | Google Scholar

Mueller, D. S. (2013). extrap: software to assist the selection of extrapolation methods for moving-boat ADCP streamflow measurements. Comput. Geosci. 54, 211–218. doi: 10.1016/j.cageo.2013.02.001

CrossRef Full Text | Google Scholar

Mueller, D. S. (2016a). QRev – Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements – Technical Manual for Version 2.8. U S Geological Survey Open-File Report 2016–1068. doi: 10.3133/ofr20161068

CrossRef Full Text | Google Scholar

Mueller, D. S. (2016b). QRev – Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements – User's Manual for Version 2.8. U S Geological Survey Open-File Report 2016–1052. doi: 10.3133/ofr20161052

CrossRef Full Text | Google Scholar

Muste, M., Fujita, I., and Hauet, A. (2008). Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 44:W00D19. doi: 10.1029/2008WR006950

CrossRef Full Text | Google Scholar

Parsons, D. R., Jackson, P. R., Czuba, J. A., Engel, F. L., Rhoads, B. L., Oberg, K. A., et al. (2013). Velocity Mapping Toolbox (VMT): a processing and visualization suite for moving-vessel ADCP measurements. Earth Surface Process. Landforms 38, 1244–1260. doi: 10.1002/esp.3367

CrossRef Full Text | Google Scholar

Pearce, S., Ljubičić, R., Peña-Haro, S., Perks, M., Tauro, F., Pizarro, A., et al. (2020). An evaluation of image velocimetry techniques under low flow conditions and high seeding densities using unmanned aerial systems. Remote Sens. 12:232. doi: 10.3390/rs12020232

CrossRef Full Text | Google Scholar

Pineiro, G., Perelman, S., Guerschman, J. P., and Paruelo, J. M. (2008). How to evaluate models: observed vs. predicted or predicted vs. observed? Ecol. Modell. 216, 316–322. doi: 10.1016/j.ecolmodel.2008.05.006

CrossRef Full Text | Google Scholar

Planet Labs, Inc. (2020). Planet Imagery Product Specifications. Available online at: https://assets.planet.com/docs/Planet_Combined_Imagery_Product_Specs_letter_screen.pdf (accessed November 23, 2020).

Raffel, M., Willert, C., Wereley, S., and Kompenhans, J. (2007). Particle Image Velocimetry: A Practical Guide, 2nd Edn. Berlin; Heidelberg: Springer-Verlag. doi: 10.1007/978-3-540-72308-0

CrossRef Full Text | Google Scholar

Smart, G. M., and Biggs, H. J. (2020). “Remote gauging of open channel flow: estimation of depth averaged velocity from surface velocity and turbulence,” in Proceedings of River Flow 2020 (Delft), 1–10. doi: 10.1201/b22619-145

CrossRef Full Text | Google Scholar

Strelnikova, D., Paulus, G., Käfer, S., Anders, K.-H., Mayr, P., Mader, H., et al. (2020). Drone-based optical measurements of heterogeneous surface velocity fields around fish passages at hydropower dams. Remote Sens. 12:384. doi: 10.3390/rs12030384

CrossRef Full Text | Google Scholar

Talke, S. A., Horner-Devine, A. R., Chickadel, C. C., and Jessup, A. T. (2013). Turbulent kinetic energy and coherent structures in a tidal river. J. Geophys. Res. Oceans 118, 6965–6981. doi: 10.1002/2012JC008103

CrossRef Full Text | Google Scholar

Tauro, F., Porfiri, M., and Grimaldi, S. (2016). Surface flow measurements from drones. J. Hydrol. 540, 240–245. doi: 10.1016/j.jhydrol.2016.06.012

CrossRef Full Text | Google Scholar

Teledyne Marine (2020). RiverRay ADCP. Available online at: http://www.teledynemarine.com/riverray-adcp?ProductLineID=13 (accessed December 8, 2020).

Thielicke, W., and Stamhuis, E. J. (2014). PIVlab - towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2:e30. doi: 10.5334/jors.bl

CrossRef Full Text | Google Scholar

Thielicke, W., and Stamhuis, E. J. (2019). PIVlab v2.37 - Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB. Figshare Dataset. doi: 10.6084/9.figshare.1092508.v12

CrossRef Full Text

Tosi, F., Rocca, M., Aleotti, F., Poggi, M., Mattoccia, S., Tauro, F., et al. (2020). Enabling image-based streamflow monitoring at the edge. Remote Sens. 12:2047. doi: 10.3390/rs12122047

CrossRef Full Text | Google Scholar

Wada, T., Chikita, K. A., Kim, Y., and Kudo, I. (2011). Glacial effects on discharge and sediment load in the subarctic Tanana River Basin, Alaska. Arctic Antarct. Alpine Res. 43, 632–648. doi: 10.1657/1938-4246-43.4.632

CrossRef Full Text | Google Scholar