Bi-modal contrastive learning for crop classification using Sentinel-2 and Planetscope

Remote sensing has enabled large-scale crop classification for understanding agricultural ecosystems and estimating production yields. In recent years, machine learning has become increasingly relevant for automated crop classification. However, the existing algorithms require a huge amount of annotated data. Self-supervised learning, which enables training on unlabeled data, has great potential to overcome the problem of annotation. Contrastive learning, a self-supervised approach based on instance discrimination, has shown promising results in the field of natural as well as remote sensing images. Crop data often consists of field parcels or sets of pixels from small spatial regions. Additionally, one needs to account for temporal patterns to correctly label crops. Hence, the standard approaches for landcover classification cannot be applied. In this work, we propose two contrastive self-supervised learning approaches to obtain a pre-trained model for crop classification without the need for labeled data. First, we adopt the uni-modal contrastive method (SCARF) and, second, we use a bi-modal approach based on Sentinel-2 and Planetscope data instead of standard transformations developed for natural images to accommodate the spectral characteristics of crop pixels. Evaluation in three regions of Germany and France shows that crop classification with the pre-trained multi-modal model is superior to the pre-trained uni-modal method as well as the supervised baseline models in the majority of test cases.

1 Introduction

Crop classification is a method of identifying agricultural plant types at particular locations using remote sensing data. This process is crucial for optimizing farming practices, assessing damages, and increasing yields. It relies on information from public landcover satellite missions such as Sentinel-2 (Drusch et al., 2012) and Landsat¹, which provide global coverage at regular intervals. Crops exhibit distinct temporal signatures due to their phenological traits, reflecting growth stages from seed to ripening (Meier et al., 2009).

The availability of extensive satellite data facilitates large-scale crop mapping suitable for machine learning applications. However, traditional supervised learning methods face significant challenges. Labeling crops is time-consuming and requires skilled human effort, often limiting studies to small regions with few crop fields. Conventional methods like random forests generate good results for specific fields but fail to generalize across different geographical properties (Račič et al., 2020) or at different time periods (Hütt et al., 2020).

Unsupervised learning algorithms such as K-means clustering and K-Nearest Neighbor (KNN) do not require labels but are only effective for low-dimensional data, making them less suitable for high-dimensional remote sensing time series. This limitation has led to the development of advanced deep learning techniques, particularly self-supervised learning.

tSelf-supervised learning enables pre-training of models using large amounts of unlabeled data, with subsequent transfer learning for related tasks with limited annotations. This approach has shown improvements over randomly initialized models (Yang et al., 2020). Among self-supervised methods, contrastive learning (Liu et al., 2021) has demonstrated promising results. Contrastive learning aims to align outputs from different viewpoints of the data sample while pushing away outputs from other data samples. It typically uses alternative loss functions like InfoNCE (van den Oord et al., 2018) to avoid trivial solutions. The method relies on data augmentation to maximize mutual information shared between a sample and its augmented version.

However, applying contrastive learning to remote sensing time series data poses unique challenges. Standard image transformations assume static images covering large spatial neighborhoods, which is unsuitable for crop analysis characterized by small field sizes and significant temporal changes. Moreover, the lack of field boundary information makes it harder to adapt the existing self-supervised approach for crops. This can be overcome by using spectral information of individual pixels instead of relying on crop field boundaries. This approach is justified because the variance of spectral patterns among pixels belonging to one field is quite low. The variance distribution plots of spectral measurements for four field parcels can be found in the Supplementary materials.

To address the challenges of augmentation for remote sensing time-series data, we propose a novel bi-modal contrastive learning approach (Yuan et al., 2021). Instead of relying on standard augmentation techniques, our method obtains the augmented version of Sentinel-2 data directly from another source, specifically Planetscope. This innovative strategy serves a dual purpose: it not only provides an alternative to traditional augmentation but also combines the complementary strengths of both data sources—Sentinel-2’s superior spectral resolution and Planetscope’s finer spatial resolution. Further, it enables the development of a bi-modal self-supervised pre-trained model that can be applied even when only one data source is available for downstream tasks.

In this work, we designed a strategy to develop a bi-modal self-supervised pre-trained model, thus combining the higher spectral resolution of Sentinel-2 with the finer spatial resolution of Planetscope. Although both Sentinel-2 and Planetscope are used for pre-training, the pre-trained model can be applied to problems, where only data from one source is available. To evaluate this, we demonstrate crop classification using only Sentinel-2 data as our downstream tasks. In this paper, we demonstrate with our experiment setup that the proposed bi-modal contrastive self-supervised pre-training improves crop classification accuracy compared to the uni-modal contrastive self-supervised model. The remainder of this paper is structured as follows: Section 22 discusses the related work in the field, providing context and background for existing methods. Section 3 details the methods employed in our study, explaining our approach and techniques. Section 4 describes the datasets used in our experiments, including their sources and characteristics. Section 5 outlines our experimental setup and procedures. Section 6 presents the results of our experiments and analyses. Section 7 offers conclusions drawn from our findings. Finally, Section 8 provides a discussion of the implications of our results, limitations of the study, and potential directions for future research.

2 Related work

Recent studies have explored contrastive self-supervised learning in remote sensing. SeCo (Mañas et al., 2021) demonstrated that their pre-trained model outperformed Imagenet (Russakovsky et al., 2014) pre-trained models on several landcover classification benchmarks. Some studies have implemented multi-modal contrastive learning approaches in remote sensing images, aligning optical (Sentinel-2) with radar (Sentinel-1) images (Scheibenreif et al., 2022; Liu et al., 2022).

In the realm of time series tasks for remote sensing, limited work has been done on contrastive learning. The work from (Yuan et al., 2023) is one such study that focuses on developing pre-trained a model for crop classification using only the field parcel boundaries to identify similar pairs.

For tabular data in contrastive machine learning, there exist methods such as SCARF (Bahri et al., 2021), SAINT (Somepalli et al., 2021), and VIME (Yoon et al., 2020). SCARF uses random feature corruption techniques for augmentation. SAINT modifies Tabtransformer (Huang et al., 2020) to handle both categorical and continuous data, using Cutmix (Yun et al., 2019) and Mixup (Zhang et al., 2017) for augmentation. VIME is another self-supervised method for tabular data, using feature corruption and masking instead of contrastive learning.

When it comes to various loss functions similar to SimCLR, there exists loss functions such as MoCo (He et al., 2019), BYOL (Grill et al., 2020), DiNo (Caron et al., 2021), and Barlow twins (Zbontar et al., 2021). Each has its own advantages and disadvantages.

3 Methods

3.1 Bi-modal self-supervised learning

Figure 1 illustrates the experiment setup of our bi-modal contrastive learning method. The most common choice for tabular data is a fully connected network (MLP). Inspired by the skip connection mechanism of ResNets (He et al., 2015), we use ResMLP as our backbone. ResMLP is a standard MLP with additional skip connections to the previous layers. The ResMLP employed in this work is an 8-layer network with approximately 550K parameters. Two different networks are employed for contrastive learning. The backbone network serves as the feature extractor, producing representations from the input data, while the projector network is responsible for optimizing the contrastive loss function, which aligns similar representations and separates dissimilar ones. In the bi-modal contrastive approach, the networks are not shared between the two modalities due to the different input dimensions of both sources, thus two different networks are used for each modality. In our case, we denote the backbone network for Sentinel-2 by $E_s:{\mathbb{R}}^{12}\to {\mathbb{R}}^{256}$ and the network for Planetscope by $E_p:{\mathbb{R}}^{36}\to {\mathbb{R}}^{256}$. Similarly, the projector network is denoted by $P_s:{\mathbb{R}}^{256}\to {\mathbb{R}}^{256}$ and $P_p:{\mathbb{R}}^{256}\to {\mathbb{R}}^{256}$ for Sentinel-2 and Planetscope, respectively. Here, 12 refers to 12 spectral bands of Sentinel-2, and 36 refers to 4 spectral bands of $3\times 3$ Planetscope pixels flattened to a 36-dimensional vector. Equation 1 provides a mathematical formulation of the SimCLR loss function (Chen et al., 2020) used in our work. For the pre-training, we adapt the SimCLR loss to our bi-modal setup:

$l_{x_{is},x_{ip}}=-\log \frac{r_{\mathit{iisp}}}{{\displaystyle \sum _{k=1,k\ne i}^N}{r}_{\mathit{ikss}}+{\displaystyle \sum _{m=1,m\ne i}^N}{r}_{\mathit{imsp}}}(\mathrm{1a})$

where

$r_{\mathit{ijsp}}=\exp \left(\frac{sim\left(z_{is},z_{jp}\right)}{\tau }\right)(\mathrm{1b})$

and

$sim\left(z_{is},z_{jp}\right)=\frac{z_{is}^T{z}_{jp}}{‖z_{is}‖‖z_{jp}‖}.(\mathrm{1c})$

Figure 1

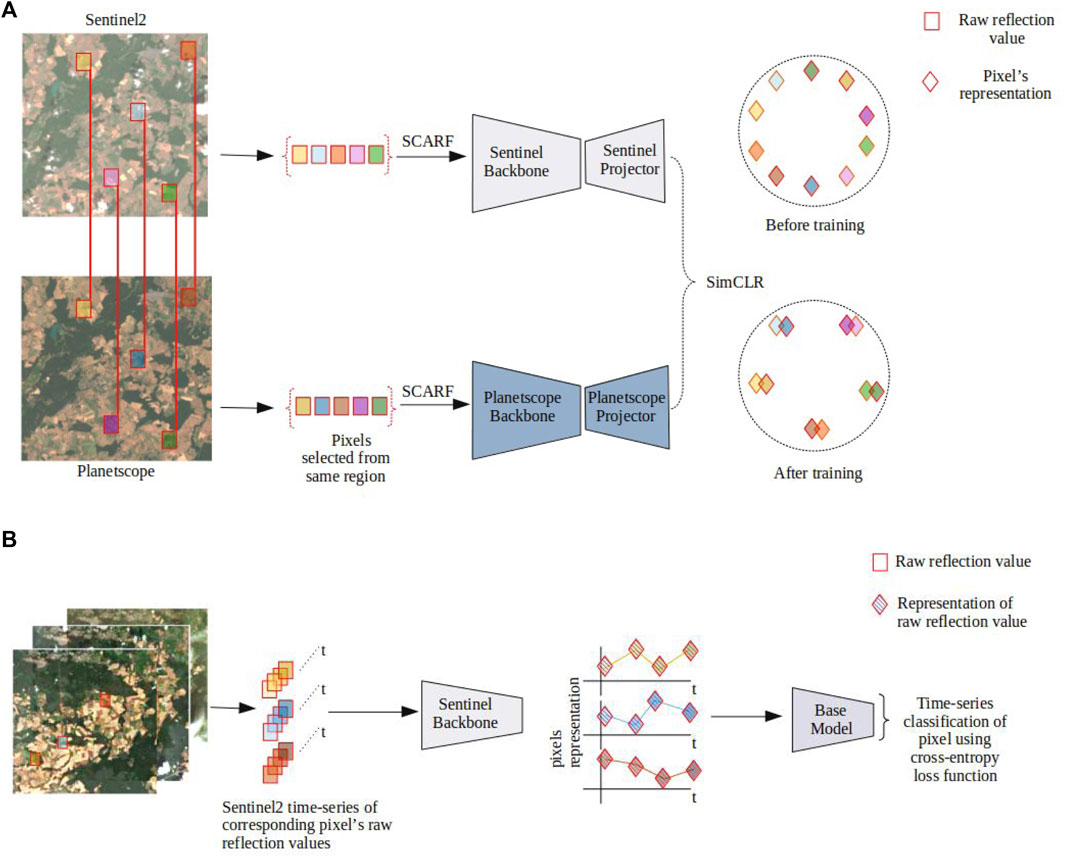
Figure 1. Schematic setup of our bi-modal self-supervised experiment. (A) The top part illustrates the bi-modal setup, where corresponding pixels indicated by red bordered colored boxes are randomly selected. Sentinel-2 and Planetscope data are passed through their respective backbone and projector networks. The outputs are aligned by optimizing the contrastive loss to attract similar and repel dissimilar pairs. Two spherical diagrams on the right side show how the projection of the data is randomly distributed before and after training. The similar pairs get aligned simultaneously maintaining uniformity in the latent hypersphere space. A sample of pixel collection is shown for one timestamp as an example. Similarly, data for pre-training are collected from other timestamps. (B) The bottom part shows the training of a downstream task, where raw Sentinel-2 data is fed through the pre-trained Sentinel-2 backbone. The output is then fed to different base models for conventional supervised learning, optimizing the standard cross entropy loss for multi-class classification. (A) Setup of pre-training the network using Sentinel-2 and Planetscope data (B) Setup of downstream experiment Sentinel-2 data.

Here, $x_{is}$ represents the $i^{th}$ Sentinel-2 data sample, and $z_{is}$ represents the output obtained after passing through the encoder and projector components of the Sentinel-2 network. Similarly, $x_{ip}$ represents the $i^{th}$ Planetscope data sample, and $z_{ip}$ represents the output obtained after passing through the encoder and projector components of the Planetscope network. The parameter $\tau$ denotes the temperature that controls the sensitivity of the loss function. In the original SimCLR equation (Chen et al., 2020), there is only one network and two augmented views share the same model. In contrast, in our bi-modal case, there are separate networks for different views. The term $r_{\mathit{ikss}}$ in the denominator of Equation 1a denotes the cosine distance between a Sentinel-2 data sample to other Sentinel-2 data samples in the batch, while $r_{\mathit{imsp}}$ denotes the cosine distance between the Sentinel-2 data sample and the other Planetscope data samples in the batch.

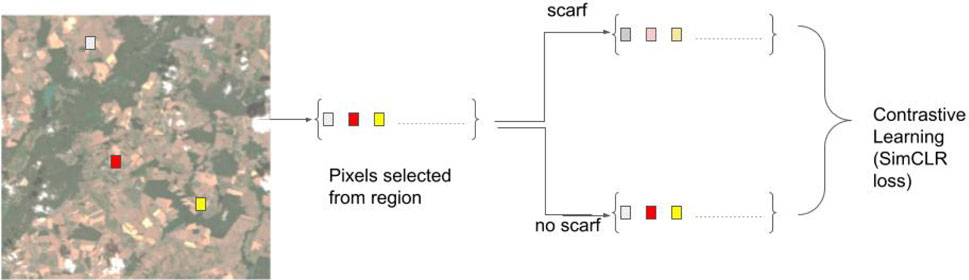
We employ the random feature corruption technique from SCARF (Bahriet al., 2021) as a transformation on both sources in our bi-modal self-supervised learning setup, illustrated in Figure 1A. The random feature corruption, with a given corruption rate $c$, randomly replaces $c$% of the features in the data by the empirical marginal distribution of the corresponding features. Figure 2 provides a schematic diagram of the random feature corruption technique.

Figure 2

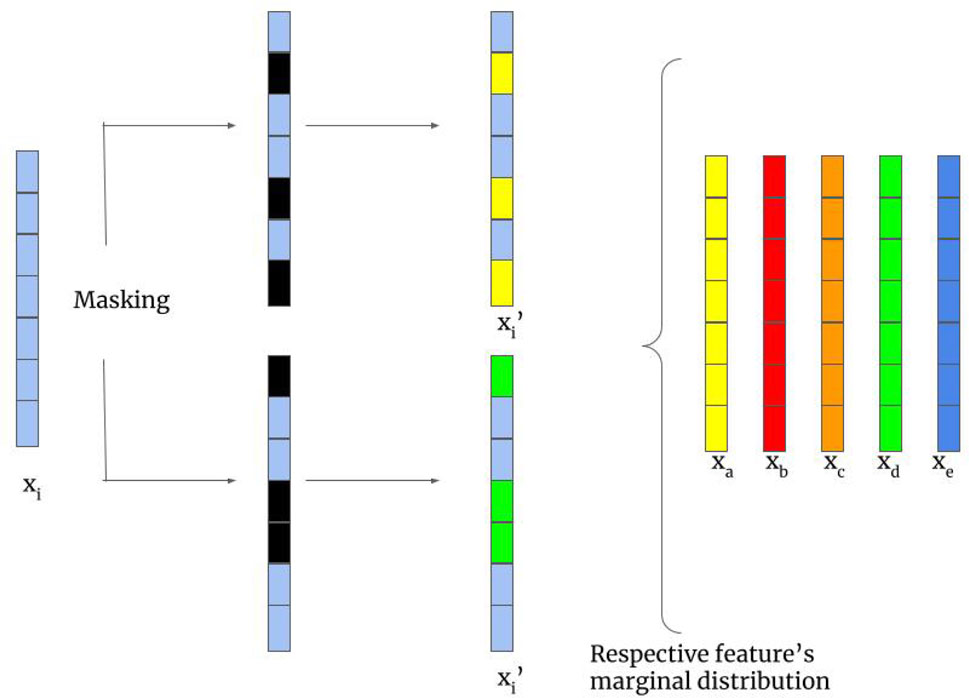
Figure 2. Random feature corruption mechanism in SCARF (Bahri et al., 2021). Entries of a feature vector $x_i$ are masked, indicated by black cells. These masked features are then replaced by features from other samples in the batch, denoted by $x_a$, …, $x_e$. This results in two corrupted feature vectors $(x_i^{\prime })$. The two corrupted feature vectors build a positive pair.

3.2 Downstream tasks

The downstream tasks, each slightly different from the others, allow us to test the generalizability of the pre-trained model. The first task involves data from the same region (Brandenburg) as the pre-training data. The second task uses data from a different region in Brandenburg but from a distinct year. The third task encompasses data from the Brittany region in France. In these downstream tasks, the time series of pre-trained features is fed to a temporal network for classification, which we call base model.

Figure 1B illustrates how the pre-trained Sentinel-2 backbone is used for the downstream task of crop classification. For each pixel, 144 timestamps are passed through the pre-trained model to obtain an abstract pixel representation. The time series formed with the representations of each timestamp serves as an input to a base model. As base models, we investigate three standard deep learning architectures: Bi-LSTM (Cornegruta et al., 2016), inception time (Fawaz et al., 2019), and position encoded transformers (Vaswani et al., 2017). An overview of these models can be found in the supplementary materials. As bi-modal pre-training implicitly learns a mapping from Planetscope to Sentinel-2 data, it is sufficient to input only Sentinel-2 data into the model for the downstream classification task. Thereby, users can implicitly take advantage of Planetscope’s finer spatial resolution.

4 Datasets

In this work, we use Sentinel-2 and Planetscope as two different sources for bi-modal contrastive learning. Sentinel-2 is an ESA satellite mission. Its multi-spectral instrument (MSI) consists of 12 bands, spanning from visible to thermal and infrared bands ($400\mathrm{n}\mathrm{m}$ to $2190\mathrm{n}\mathrm{m}$). For Sentinel-2 with a spatial resolution of $10\mathrm{m}$, each pixel covers an area of $100{\mathrm{m}}^{\mathrm{2}}$. Data are publicly available and can be accessed either through the Copernicus API or Google Earth Engine (Gorelick et al., 2017). Despite the availability of cloud masks, obtaining cloud-free images for a particular region can be challenging. In contrast, Planetscope, a commercial satellite mission, provides higher pixel resolution at $3\mathrm{m}/\mathrm{p}\mathrm{x}$. The instrument takes multiple snapshots of a particular region and uses the “best scene on top” algorithm². Planetscope ensures images with minimal cloud, haze, and other disturbances. However, it has a limitation in spectral resolution, providing only 4 channels (R, G, B, and NIR).

In this work, we utilize the training and validation sts of the DENETHOR dataset (Kondmann et al., 2021) to create a custom dataset for bi-modal self-supervised learning experiments. DENETHOR is a publicly available crop type classification dataset that provides high-resolution remote sensing data from Planetscope, Sentinel-2, and Sentinel-1. It is developed for near real-time monitoring of agricultural growth cycles in Northern Germany. By leveraging multiple satellite sources, DENETHOR enhances the data for accurate crop classification. DENETHOR provides both training and validation sets. The dataset provides both training and validation sets, with the latter being at different temporal and geographical location, thereby allowing the development of models that are robust to such variations.

DENETHOR’s training dataset covers a $24\times 24k{m}^2$ region in the state of Brandenburg, Germany. For our work, we utilize data from Sentinel-2 and Planetscope. The training data covers the entire year 2018. In our work, we perform pixel-wise analysis. There are pixels which are not associated with crops. These pixels are discarded for our work. As the pixel resolution of Sentinel-2 is $10\mathrm{m}/\mathrm{p}\mathrm{x}$ and $3\mathrm{m}/\mathrm{p}\mathrm{x}$ for Planetscope, the dimensions of the measurement scenes are represented as $2400\times 2400$ and $8000\times 8000$, respectively. The training set is used for generating data for pre-training experiments and data for downstream task1. For both Sentinel-2 and PlanetScope, we utilize the same 144 timestamps for each year. It is important to note that although Sentinel-2 has a revisit time of 5 days, there are certain areas such as the one used in DENETHOR where two corresponding swaths overlap. As a result, we obtain double the amount of data in those regions. DENETHOR’s validation dataset also covers a $24\times 24\mathrm{k}{\mathrm{m}}^{\mathrm{2}}$ in the state of Brandenburg, but from a different region. Furthermore, the validation dataset is from 2019 and similarly, the pixels not associated to any crops are discarded. The validation set is used to generate data for downstream task2.

The training set comprises 2,534 field parcels, while the validation set comprises 2064 field parcels. They are distributed across 9 different crop types. In both sets, there are locations where no crops are grown, and the pixels associated with these locations are masked.

The use of multiple downstream tasks serves to evaluate the generalizability of a pre-trained model. This is done by evaluation of test data from a different time and region. Figure 3 shows a visual representation of our splitting strategy. Subsection 4.1 details the generation of the pre-training data and Subsection 4.2 offers an overview of the data generated for the downstream tasks.

Figure 3

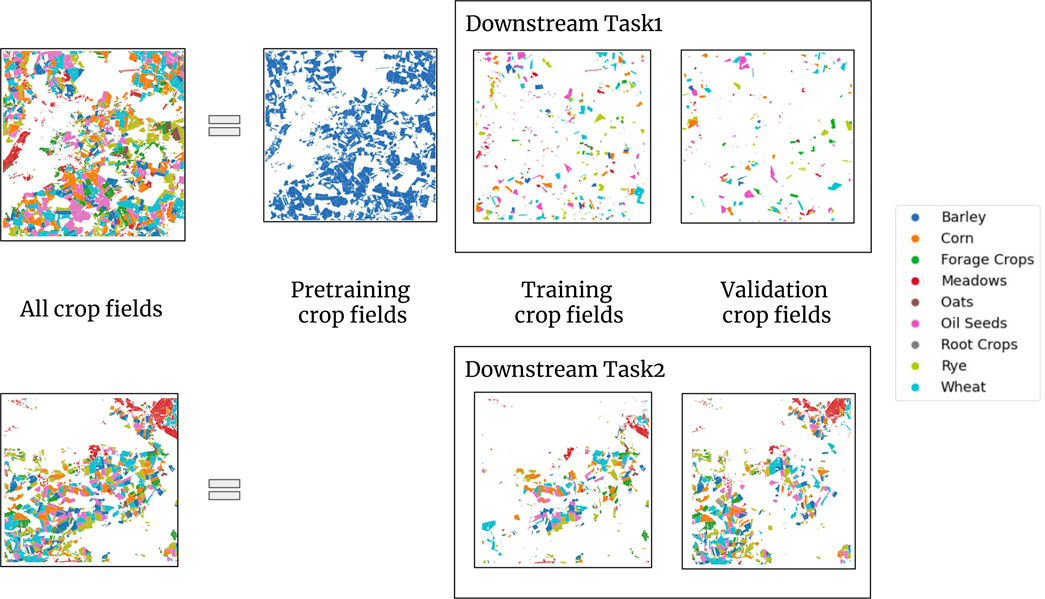
Figure 3. Dataset for the bi-modal self-supervised learning experiment. The top row of the figure illustrates the splitting applied to DENETHOR’s training dataset. The top image shows all crop fields in the training dataset, divided into three parts. The first part is used for pre-training and is represented by blue crop fields. The blue color represents unlabeled data. The other two parts are training and validation data for our downstream task1. The bottom row shows the validation dataset for DENETHOR. In the case of downstream task2, we split the validation data into training and validation for our downstream task2. The downstream task2 is trained using the pre-trained model obtained from the same pre-training dataset, allowing us to assess its performance when region and time period are changed. We refer to (Rußwurm et al., 2019) for the dataset of downstream task3.

4.1 Data for pre-training

For pre-training, we utilize unlabeled data. To acquire this, we use 70% of the random crop fields following the 70-21-9 split. We do not use the crop labels. For our pre-training dataset, we iterate through each of the 144 Sentinel-2 timestamps and randomly select 100,000 pixels from the 70% split, resulting in 14,400,000 data samples for our bi-modal self-supervised experiment. Since the samples are randomly chosen, the pre-training dataset is not balanced. The 14,400,000 data samples are independent. So, the negatives for a Sentinel-2 pixel include other pixels as well as the same pixel in the same location at a different time stamp. Given one pixel of Sentinel-2 covers $100{\mathrm{m}}^{\mathrm{2}}$ while a Planetscope pixel covers $9{\mathrm{m}}^{\mathrm{2}}$, we align a Sentinel-2 pixel to $3\times 3$ pixels of Planetscope, as illustrated in Figure 4.

Figure 4

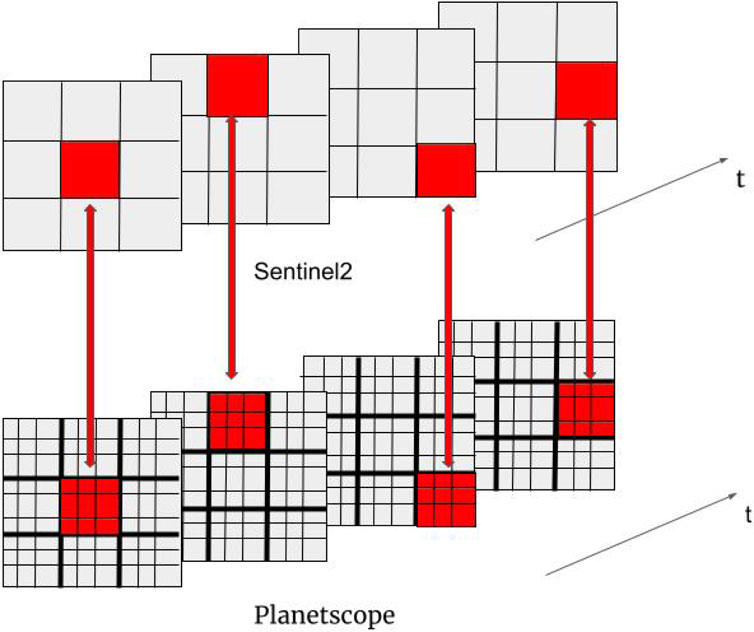
Figure 4. Description of data alignment for bi-modal self-supervised learning. The top and the bottom rows display a spatial region of the same geographical area captured by Sentinel-2 and Planetscope, respectively. For each timestamp, pixels are randomly selected from Sentinel-2. The pixel data is aligned to $3\times 3$ pixels from the same corresponding region for the same timestamp from Planetscope.

4.2 Data for downstream tasks

The pre-trained model is tested on three different sets of Sentinel-2 data (two from DENETHOR and one from Breizhcrop) to assess its generalizability. We establish two crop classification downstream tasks using DENETHOR’s training and validation dataset. For downstream task1, we use 21% and 9% of the data, as per the given 70-21-9 split of DENETHOR’s training dataset, to separate training and validation field parcels. To ensure a balanced dataset, 5,000 pixels are randomly selected for each of the 9 crop types from their field parcels. Similarly, for the validation set of downstream task1, we create a balanced dataset by randomly selecting 1,000 pixels for each crop from the validation field parcels. A 70-30 split is applied on DENETHOR’s validation set to separate training and validation field parcels for downstream task2. We follow a similar procedure to generate a balanced dataset for our second crop classification downstream task. Figure 3 visually illustrates the two downstream tasks.

The downstream task 3 is added to assess the performance of the pre-trained model in a region located further away from the region used for pre-training. We use a subset of the Breizhcrop dataset (Rußwurm et al., 2019), containing 2018 data from the Brittany region in France. The dataset provides aggregated spectral measurements per field parcel. We specifically use data from field parcels with spectral measurements for more than 142 time stamps. There are 9 crop types in the original dataset (permanent meadows, temporary meadows, corn, wheat, rapeseed, barley, orchards, sunflower, and nuts). We discard data from orchards, sunflowers, and nuts as there are fewer field parcels for these crop types. We create a balanced dataset from the remaining crop. For training subsets, we collect 9,000 data samples from each of the six crop types, and for the validation subset, we collect 1,000 data samples. The final task is crop classification with 54,000 training samples and 6,000 validation samples.

5 Experiments

To evaluate the performance of our new bi-modal, self-supervised, contrastive method, we conducted supervised experiments and uni-modal self-supervised experiments as competitors. All experiments were performed on a 16 GB NVIDIA Tesla V100 GPU.

5.1 Supervised experiments

We use 10 different models for each category of base models. To obtain these 10 models, we define the range or definite sets for each hyperparameter. We randomly generated 10 different models for each category. This random generation of 10 models for each category is done using Optuna hyperparameter tuner (Akiba et al., 2019) on a defined hyperparameter grid. It is important to note that, in this case, we do not use the tuner to find the best model rather we use all 10 models for our analysis.

For bi-directional LSTM, the hyperparameter space is defined as follows: dimensions of the hidden layer as one of [32,64,128,256], number of layers between 2 and 6, and learning rate in the range from $10^{-5}$ to $10^{-3}$. For inception time, the hyperparameter space is specified as follows: number of layers as either 2, 4, or 8, dimension of hidden layer as one of [128,256,512,1024], kernel size as one of [40,80,120,136], and learning rate between $10^{-5}$ and $10^{-3}$. The hyperparameter space for transformers is defined as follows: the dimension of the model is either 32, 64, or 128, the number of attention heads as one of [2,4,8], the number of layers between 2 and 6, and the learning rate ranges between $10^{-5}$ and $10^{-3}$. In all supervised experiments, we train the network for 20 epochs. We use the initial learning rate of $10^{-3}$ with the linear scheduler.

5.2 Uni-modal self-supervised experiments

This is our second set of experiments. With these experiments, we intend to compare our proposed bi-modal self-supervised models to the self-supervised models trained using one source. In this experiment setup, we use uni-modal contrastive learning, employing only Sentinel-2 data during pre-training. The absence of transformation processes such as cropping, and color jittering for tabular data makes it difficult to obtain augmented samples for Sentinel-2. Therefore, we use the random feature corruption technique SCARF (Bahri et al., 2021) to facilitate contrastive learning for tabular data with a single source. The experiment setup is illustrated in the Figure 5. In our uni-modal self-supervised experiment setup, we obtain the pre-trained model by applying contrastive learning on pre-training data. We run the pre-training for 100 epochs. We use a SimCLR loss function with a temperature of 0.07. The learning rate is set to $10^{-3}$. Given that a contrastive loss requires a higher batch size to generalize effectively, we opt for a batch size of 2048. We obtain two pre-trained models, one with a random feature corruption rate of 20% and the other with 60%.

Figure 5

Figure 5. Uni-modal contrastive learning experiment setup.

5.3 Bi-modal self-supervised experiments

This is the new experimental setup proposed in this study. In contrast to the uni-modal setup, the bi-modal self-supervised model uses data from two sources i.e., Sentinel-2 and Planetscope, to obtain pairs of matching samples.

The Sentinel-2 and Planetscope data are processed with different networks for pre-training and the pretext task consists of aligning the representation obtained from spectral signatures of both input data streams. We run the pre-training for 100 epochs. Similar to the uni-modal self-supervised experiment setup, we set the initial learning to $10^{-3}$. The temperature parameter for the bi-modal SimCLR loss is set to 0.07. In addition, we use the random feature corruption for each source. Similar to the uni-modal setting, we pre-train two models, one with a corruption rate of $20\%$ and another one with $60\%$. Experiments without corruption are also conducted, but the models with feature corruption yield better results. Therefore, we are reporting the results for models pre-trained with 20% and 60% corruption rates.

For evaluating • different experiments, We adopt the protocol from SCARF (Bahri et al., 2021), which involves a win-matrix plot and a box plot to compare different models on a number of test datasets. In the win-matrix plot, each cell’s value represents the ratio of experiments mentioned in the row outperforming the one in the column, as formulated in Equation 2; where $i$ and $j$ are competing methods, and $N$ is the total number of experiments.

$W_{ij}=\frac{{\displaystyle \sum _{i=1}^N}\mathbb{I}\left(val\text{\_}ac{c}_i>val\text{\_}ac{c}_j\right)}{N}(2)$

We provide separate results for each downstream task, as well as a distinct evaluation for the three base models. To evaluate the performance, we compare bi-modal self-supervised against uni-modal pre-trained models on the same corruption rate with corruption rates of 20% and 60%, respectively. The results are discussed in the next section.

6 Results

For each downstream task, we use 10 different models from each category with varying hyperparameters. For supervised learning, we report the mean scores for these 10 models. In order to evaluate the pre-trained model, we fed the representation obtained from our pre-trained model to these 10 models with the same hyperparameters. We report the mean relative gain of the self-supervised model over the corresponding supervised model with the same architecture and training parameters. We show our win-matrix and relative gain plot for 20 scores (10 results each for corruption coefficient of 20% and 60%, respectively). We report the mean gain (min and max value inside the parenthesis) for the self-supervised models. In some cases, the uni-modal self-supervised models show inferior results compared to the supervised and bi-modal methods. These are shown with negative values.

Figure 6 shows the win-matrix and relative gain box plot for ResMLP pre-trained models on downstream task1. The bi-modal self-supervised model outperforms uni-modal self-supervised and supervised models. The random feature corruption technique, which demonstrated improved results on OPENML tabular data (Bischl et al., 2021) in the case of uni-modal contrastive learning pre-trained models, does not yield promising results for time-series crop classification data. Upon comparing the bi-modal self-supervised ResMLP model with the supervised setup for downstream task1, the win-ratios are $17/20$, $19/20$, and $20/20$ for LSTM, inception, and transformer, respectively. This indicates that bi-modal self-supervised learning during the pre-training stage gains knowledge about crops. On comparing to the uni-modal self-supervised ResMLP model, the bi-modal self-supervised win-ratios are $19/20$ for LSTM and $20/20$ for the other base models.

Figure 6

Figure 6. Win-matrix and box plot for ResMLP backbone model on downstream task 1. Plots (A), (C), and (E) show the win-matrix for LSTM, inception, and transformer, respectively. Panels (B), (D), and (F) correspond to box plots showing a relative gain for both uni-modal and bi-modal self-supervised compared to the supervised experiments for LSTM, inception, and transformer, respectively.

The mean classification accuracies of supervised models are $66.7\%\pm 2.53\%$, $25.84\%\pm 4.65\%$, and $71.39\%\pm 4.54\%$ for LSTM, inception, and transformer, respectively. The corresponding box plot shows the range of gain over the supervised setup. For LSTM, the mean gain over the supervised experiment is −2.26% (min: −16.33%, max: 3.87%) for uni-modal self-supervised and 3.75% (−9.38%, 9.14%) for bi-modal self-supervised. In the case of inception, the mean gain is −10.43% (−14.8%, −2.87%) for uni-modal self-supervised, while for bi-modal self-supervised, the mean gain is 8.92% (−2.26%, 19.02%). For transformers, the mean gain is 3.36% (−18.81%, 11.76%) for uni-modal self-supervised, whereas for bi-modal, the mean gain is 8.78% (0.66%, 17.68%).

Figure 7 presents the results for downstream task2. The objective of downstream task2 is to assess how the models behave when they are applied to data from a different year and at a different geographical region with relatively similar characteristics compared to the region used for training. We find that the uni-modal self-supervised model’s performance is inferior for all three baseline models. Similar to downstream task1, the bi-modal self-supervised model outperforms the uni-model self-supervised model in all experiments. When comparing the bi-modal self-supervised ResMLP model with the supervised base model, the win-ratios are $20/20$, $17/20$, and $10/20$ for LSTM, inception, and transformer, respectively. In comparison with the uni-modal self-supervised model, the win-ratios of bi-modal self-supervised are $17/20$, $20/20$, and $19/20$ for LSTM, inception, and transformer, respectively. The mean classification accuracies of the supervised models are $59.31\%\pm 5.75\%$, $20.43\%\pm 3.98\%$, and $80.83\%\pm 2.69\%$ for LSTM, inception, and transformer, respectively. The box plots in Figure 7 show the range of gain over the supervised experiment. For LSTM, the mean gain is −0.11% (min: −10.27%, max: 12.12%) for uni-modal self-supervised, and the mean gain is 5.62% (0.46%, 19.18%) for bi-modal self-supervised. In the case of inception, the mean gain is −5.78% (−9.75%, −1.01%) for uni-modal self-supervised, whereas the mean gain is 1.77% (−1.39%, 5.62%) for bi-modal self-supervised. For transformers, the mean gain is −4.63% (−11.56%, 3.37%) for uni-modal self-supervised, and the mean gain is −0.25% (−6.76%, 5.82%) for bi-modal self-supervised.

Figure 7

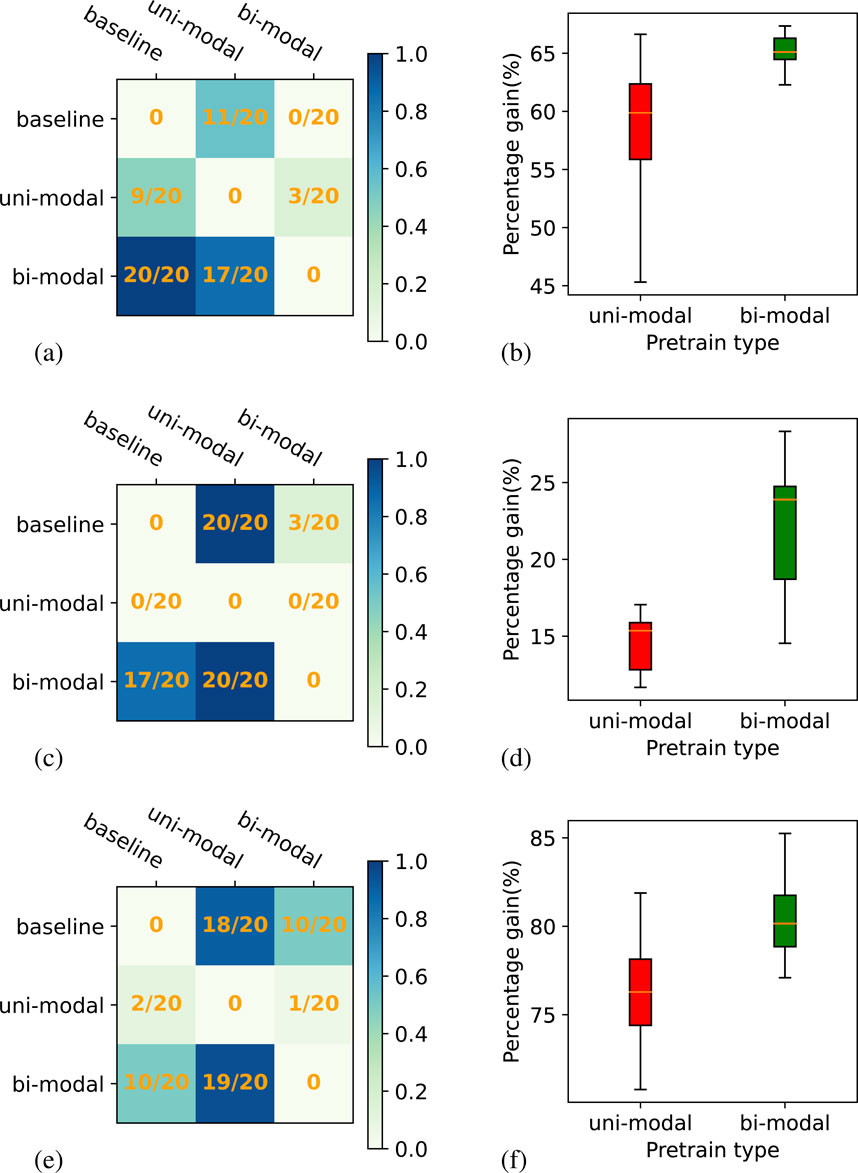
Figure 7. Win-matrix and box plot for ResMLP backbone model on downstream task 2. Plots (A), (C), and (E) show the win-matrix for LSTM, inception, and transformer, respectively. Panels (B), (D), and (F) correspond to box plots showing a relative gain for both uni-modal and bi-modal self-supervised compared to the supervised experiments for LSTM, inception, and transformer, respectively.

Figure 8 presents the results for downstream task3. The objective of downstream task3 is to assess how the models behave when they are tested on data from a region that is far away from the Brandenburg region of Germany, from where our pre-training data is taken. The test data of this experiment is from Brittany, France. Consistent with the results from the previous two downstream tasks, the bi-modal self-supervised model outperforms the uni-model self-supervised model across all experiment setups. When comparing the bi-modal self-supervised ResMLP model with the base model, the win-ratios are $20/20$, $9/20$, and $18/20$ for LSTM, inception, and transformer, respectively. When bi-modal is compared with uni-modal, the win-ratios are $20/20$, $15/20$, and $19/20$ for LSTM, inception, and transformer, respectively. The classification accuracies for supervised models are $33.19\%\pm 5.19\%$, $16.15\%\pm 3.38\%$, and $19.92\%\pm 4.46\%$ for LSTM, inception, and transformer, respectively. In the case of LSTM, the mean gain is 1.4% (min: −0.17%, max: 2.78%) for uni-modal self-supervised, and for bi-modal self-supervised, the mean gain is 3.17% (1.82%, 4.6%). For inception, the mean gain is −3.2% (−23.59%, 11.73%) for uni-modal self-supervised, whereas for bi-modal self-supervised, the mean gain is 0.42% (−8.88%, 11.35%). For transformers, the mean gain is −2.09% (−10.04%, 1.47%) for uni-modal self-supervised and 1.56% (−1.70%, 3.55%) for bi-modal self-supervised.

Figure 8

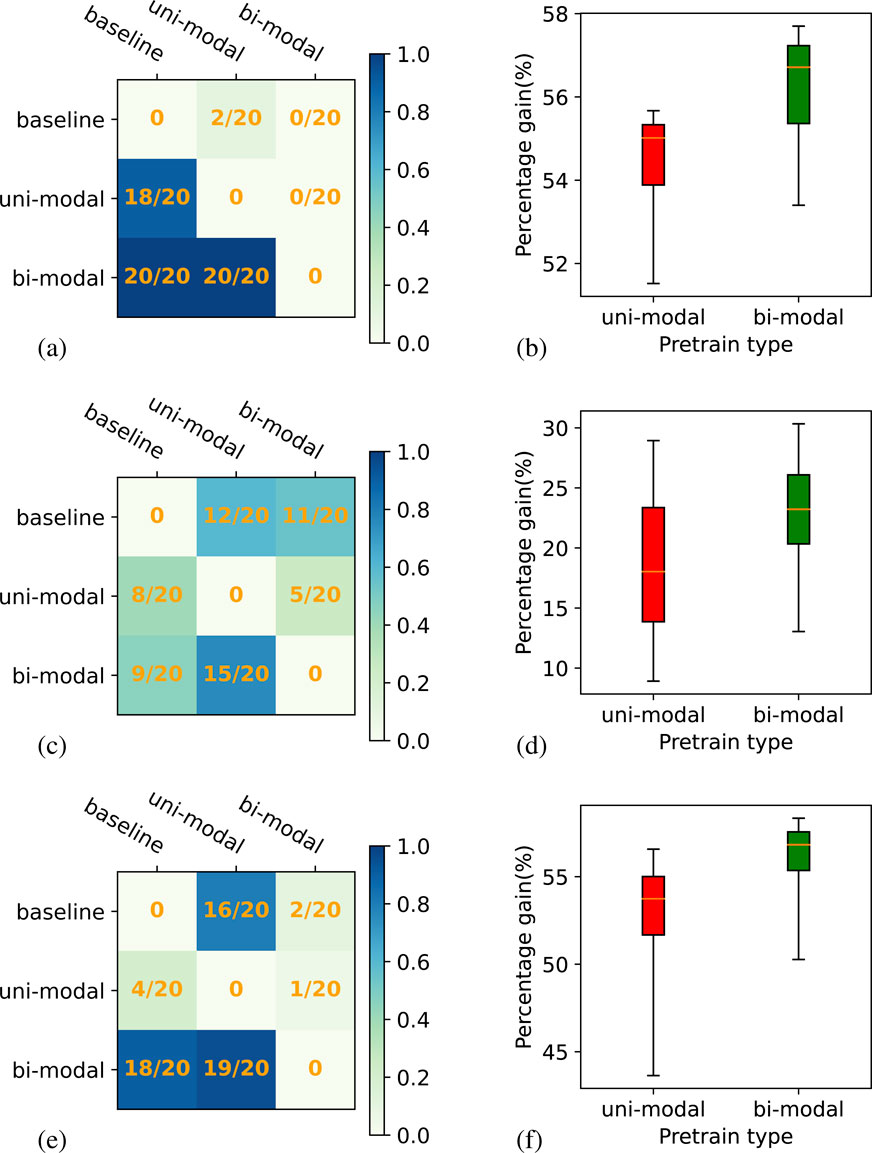
Figure 8. Win-matrix and box plot for ResMLP backbone model on downstream task 3. Plots (A), (C), and (E) show the win-matrix for LSTM, inception, and transformer, respectively. Panels (B), (D), and (F) correspond to box plots showing a relative gain for both uni-modal and bi-modal self-supervised compared to the supervised experiments for LSTM, inception, and transformer, respectively.

Table 1 shows the supervised accuracy and gain for both uni-modal and bi-modal self-supervised learning for all downstream tasks. We present per-class results for 6 selected experiment sets in the Appendix.

Table 1

Table 1. Accuracy of the supervised setup and relative gain of uni-modal and bi-modal self-supervised pre-training for the three different downstream tasks.

7 Conclusion

In this work, we presented a new bi-modal, self-supervised contrastive learning method for pixel-wise crop classification from satellite images. The method uses Sentinel-2 and Planetscope data together with a feature corruption technique for pre-training and employs various networks to learn the temporal patterns of the pixel spectra of different crop types. After the pre-training, the model can be applied with one data source only. We compared our bi-modal contrastive learning to uni-modal self-supervised learning using only Sentinel-2 data. We used ResMLP as the backbone model for pre-training and evaluated the pre-trained representation using it as input for three different base models for crop classification, i.e., bi-directional LSTM, inception time, and position encoded transformers.

In summary, we conclude that contrastive learning using the feature corruption technique to generate positive sample pairs on Sentinel-2 is unable to learn an expressive representation for crop classification. On the other hand, when we use bi-modal contrastive self-supervised learning with Sentinel-2 and Planetscope, we find a relative gain in performance for most of the test cases. For the bi-directional LSTM, we find a higher gain for all the downstream tasks. The gains are smaller for inception in the case of downstream task3 and for one test case, i.e., transformer network for downstream task2, there was no positive gain. Given the improvement found in most test cases, we can conclude that bi-modal contrastive learning helps in learning an expressive representation for crop classification. In the bi-modal setting, the network has learned to take into account finer-scale features from the higher-resolution Planetscope data during pre-training. As a result, the classification accuracy increases even when only Sentinel-2 data are fed into the pre-trained network. All our test cases are pixel-wise crop classification. The new method can, however, be transferred to other downstream tasks like a prediction of crop yield or identification of the nutritional value of the crop at a location.

8 Discussion

We have shown the benefits of our method but there are many points to be discussed. We have already highlighted some of the existing methods and SimCLR-like loss functions in Section 2. Our approach differs from existing methods in several key aspects. Unlike SeCo (Mañas et al., 2021), which used only Sentinel-2 data and classical image transformations, we align two optical remote sensing sources (Sentinel-2 and Planetscope) with different properties for contrastive learning. While some studies (Scheibenreif et al., 2022; Liu et al., 2022) have implemented multi-modal contrastive learning approaches in remote sensing by aligning optical (Sentinel-2) with radar (Sentinel-1) images, our method focuses on pixel-level analysis rather than whole images. This pixel-wise approach is particularly beneficial for crop classification and eliminates the need for field boundary information, making it fully self-supervised. While SCARF (Bahri et al., 2021), SAINT (Somepalli et al., 2021), and VIME (Yoon et al., 2020) utilize various augmentation techniques for tabular data, our approach employs SimCLR (Chen et al., 2020) contrastive loss on distinct data sources. Our methods leverage the availability of multiple sources in the field of remote sensing. Although several competitive loss functions exist, we found that SimCLR outperforms others like Barlow twins (Zbontar et al., 2021) in our bi-modal setup, aligning with findings from SCARF authors on OPENML-CC18 (Bischl et al., 2021) data. The other loss functions, MoCo (He et al., 2019), BYOL (Grill et al., 2020; Caron et al., 2021) are not feasible for bi-modal contrastive experimental setups as the training with loss functions employs two networks with similar architecture but the weights are not shared between them. So, our proposed method offers a novel approach to crop classification using contrastive self-supervised learning, thereby advancing the fields of remote sensing and agricultural monitoring.

Using a single 16 GB NVIDIA Tesla V100 GPU, we can obtain the pre-trained model in just 6 h. The model architecture consists of an 8-layer ResMLP, which is relatively small and allows for larger batch sizes. This is particularly advantageous because SimCLR is not parallelizable. However, increasing the number of layers will lead to longer pre-training times. Once pre-trained, the model can utilize either LSTM or transformer architectures as its base. While LSTMs are inefficient during training due to backpropagation through time, they run sequentially during deployment with a computational complexity of $O(1)$. In contrast, the attention mechanism in transformers has a computational complexity of $O(n^2)$. The Sentinel-2 time series data for 1 year contains a maximum of 144 timestamps, which is significantly less than the data typically handled in generative tasks performed by GPT models. This limited number of timestamps has minimal impact on computational time when using modern GPUs. During training for 20 epochs, both models averaged less than 20 min for the datasets in downstream tasks 1 and 2. When scaling to millions of pixels, parallelization becomes necessary during deployment. Since this application is not real-time, we find our approach to be practical in large-scale implementations.

There are some limitations of the network architecture in our approach. ResMLP is still not a state-of-the-art network. The recently proposed Spectral MAMBA network (Yao et al., 2024) has shown promising results on hyperspectral image classification. It is worth noting the feasibility of such a model as a substitute for ResMLP. The second limitation is that our work assumes that a landcover classification model is available that can detect the croplands in arbitrary satellite scenes. Pre-training on all types of landcover might result in a representation that is less suitable for crop classification. Furthermore, the method only considers the spectral component and does not consider the potential information coming from neighboring pixels. Extending our method to include the spatial context might improve the results further. In future work, we aim to leverage the capabilities of transformer networks like UTAE (Sainte Fare Garnot and Landrieu, 2021) and TSViT (Tarasiou et al., 2023), with a particular emphasis on handling remote sensing time series data to address the aforementioned limitations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Validation, Writing–original draft, Writing–review and editing. SS: Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing–review and editing. MS: Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing. JG: Investigation, Methodology, Resources, Supervision, Validation, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was funded by German Federal Ministry for the Environment, Nature Conservation, and Nuclear Safety under grant no 67KI2043 (KISTE). Computing time for this study was kindly provided by the Juelich Supercomputing Centre under project DeepACF. JG is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - SFB 1502/1-2022 - Projektnummer:450058266.

Acknowledgments

We acknowledge the support from Lukas Leufen and Michael Langguth in proofreading the paper. I would like to recognize the standard version of the Perplexity GenAI tool, which was utilized for rephrasing sentences and detecting grammatical errors.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1480101/full#supplementary-material

Footnotes

¹https://landsat.gsfc.nasa.gov/appendix/references/

²https://developers.Planet.com/docs/data/visual-basemaps/

References

Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M. (2019). “Optuna: a next-generation hyperparameter optimization framework,” in Optuna: a next-generation hyperparameter optimization framework, 19. New York, NY, USA: Association for Computing Machinery, 2623–2631. doi:10.1145/3292500.3330701

CrossRef Full Text | Google Scholar

Bahri, D., Jiang, H., Tay, Y., and Metzler, D. (2021). SCARF: self-supervised contrastive learning using random feature corruption. Corr. abs/2106 (15147). doi:10.48550/arXiv.2106.15147

CrossRef Full Text | Google Scholar

Bischl, B., Casalicchio, G., Feurer, M., Gijsbers, P., Hutter, F., Lang, M., et al. (2021). Openml: a benchmarking layer on top of openml to quickly create, download, and share systematic benchmarks. NeurIPS.

Google Scholar

Caron, M., Touvron, H., Misra, I., Jégou, H., Mairal, J., Bojanowski, P., et al. (2021). “Emerging properties in self-supervised vision transformers,” in Proceedings of the international conference on computer vision (ICCV).

CrossRef Full Text | Google Scholar

Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. E. (2020). A simple framework for contrastive learning of visual representations. CoRR, 05709. abs/2002. doi:10.48550/arXiv.2002.05709

CrossRef Full Text | Google Scholar

Cornegruta, S., Bakewell, R., Withey, S., and Montana, G. (2016). “Modelling radiological language with bidirectional long short-term memory networks,” in Proceedings of the seventh international workshop on health text mining and information analysis (Auxtin, TX: Association for Computational Linguistics), 17–27. doi:10.18653/v1/W16-6103

CrossRef Full Text | Google Scholar

Drusch, M., Del Bello, U., Carlier, S., Colin, O., Fernandez, V., Gascon, F., et al. (2012). Sentinel-2: esa’s optical high-resolution mission for gmes operational services. Remote Sens. Environ. 120, 25–36. The Sentinel Missions - New Opportunities for Science. doi:10.1016/j.rse.2011.11.026

CrossRef Full Text | Google Scholar

Fawaz, H. I., Lucas, B., Forestier, G., Pelletier, C., Schmidt, D. F., Weber, J., et al. (2019). Inceptiontime: finding alexnet for time series classification. CoRR. abs/1909.04939. doi:10.48550/arXiv.1909.04939

CrossRef Full Text | Google Scholar

Gorelick, N., Hancher, M., Dixon, M., Ilyushchenko, S., Thau, D., and Moore, R. (2017). Google earth engine: planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 202, 18–27. doi:10.1016/j.rse.2017.06.031

CrossRef Full Text | Google Scholar

Grill, J.-B., Strub, F., Altché, F., Tallec, C., Richemond, P. H., Buchatskaya, E., et al. (2020). “Bootstrap Your Own Latent: a new approach to self-supervised learning,” in Neural information processing systems (montréal, Canada).

Google Scholar

He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. B. (2019). Momentum contrast for unsupervised visual representation learning. Corr. abs/1911, 05722. doi:10.48550/arXiv.1911.05722

CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep residual learning for image recognition. Corr. abs/1512, 03385. doi:10.48550/arXiv.1512.03385

CrossRef Full Text | Google Scholar

Huang, X., Khetan, A., Cvitkovic, M., and Karnin, Z. S. (2020). Tabtransformer: tabular data modeling using contextual embeddings. Corr. abs/2012, 06678. doi:10.48550/arXiv.2012.06678

CrossRef Full Text | Google Scholar

Hütt, C., Waldhoff, G., and Bareth, G. (2020). Fusion of sentinel-1 with official topographic and cadastral geodata for crop-type enriched lulc mapping using foss and open data. ISPRS Int. J. Geo-Information 9, 120. doi:10.3390/ijgi9020120

CrossRef Full Text | Google Scholar

Kondmann, L., Toker, A., Rußwurm, M., Camero, A., Peressuti, D., Milcinski, G., et al. (2021). “DENETHOR: the dynamicearthNET dataset for harmonized, inter-operable, analysis-ready, daily crop monitoring from space,” in Thirty-fifth conference on neural information processing systems datasets and benchmarks track (round 2).

Google Scholar

Liu, C., Sun, H., Xu, Y., and Kuang, G. (2022). Multi-source remote sensing pretraining based on contrastive self-supervised learning. Remote Sens. 14, 4632. doi:10.3390/rs14184632

CrossRef Full Text | Google Scholar

Liu, X., Zhang, F., Hou, Z., Mian, L., Wang, Z., Zhang, J., et al. (2021). Self-supervised learning: generative or contrastive. IEEE Trans. Knowl. Data Eng., 1–1doi. doi:10.1109/tkde.2021.3090866

CrossRef Full Text | Google Scholar

Mañas, O., Lacoste, A., Giró-i-Nieto, X., Vázquez, D., and Rodríguez, P. (2021). Seasonal contrast: unsupervised pre-training from uncurated remote sensing data. Corr. abs/2103 (16607), 9394–9403. doi:10.1109/iccv48922.2021.00928

CrossRef Full Text | Google Scholar

Meier, U., Bleiholder, H., Buhr, L., Feller, C., Hack, H., Heß, M., et al. (2009). The bbch system to coding the phenological growth stages of plants-history and publications. J. für Kulturpflanzen 61, 41–52. doi:10.5073/JfK.2009.02.01

CrossRef Full Text | Google Scholar

Račič, M., Oštir, K., Peressutti, D., Zupanc, A., and Čehovin Zajc, L. (2020). Application of temporal convolutional neural network for the classification of crops on sentinel-2 time series. ISPRS - Int. Archives Photogrammetry, Remote Sens. Spatial Inf. Sci. XLIII-B2-2020, 1337–1342. doi:10.5194/isprs-archives-XLIII-B2-2020-1337-2020

CrossRef Full Text | Google Scholar

Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., et al. (2014). Imagenet large scale visual recognition challenge. Corr. abs/1409 (0575). doi:10.48550/arXiv.1409.0575

CrossRef Full Text | Google Scholar

Rußwurm, M., Lefèvre, S., and Körner, M. (2019). Breizhcrops: a satellite time series dataset for crop type identification. Corr. abs/1905, 11893. doi:10.48550/arXiv.1905.11893

CrossRef Full Text | Google Scholar

Sainte Fare Garnot, V., and Landrieu, L. (2021). Panoptic segmentation of satellite image time series with convolutional temporal attention networks. ICCV. doi:10.48550/arXiv.2107.07933

CrossRef Full Text | Google Scholar

Scheibenreif, L., Hanna, J., Mommert, M., and Borth, D. (2022). “Self-supervised vision transformers for land-cover segmentation and classification,” in IEEE/CVF Conference on computer Vision and pattern recognition workshops, CVPR workshops 2022, New Orleans, LA, USA, june 19-20, 2022 (IEEE), 1421–1430. doi:10.1109/CVPRW56347.2022.00148

CrossRef Full Text | Google Scholar

Somepalli, G., Goldblum, M., Schwarzschild, A., Bruss, C. B., and Goldstein, T. (2021). SAINT: improved neural networks for tabular data via row attention and contrastive pre-training. Corr. abs/2106, 01342. doi:10.48550/arXiv.2106.01342

CrossRef Full Text | Google Scholar

Tarasiou, M., Chavez, E., and Zafeiriou, S. (2023). “Vits for sits: vision transformers for satellite image time series,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), 10418–10428.

CrossRef Full Text | Google Scholar

van den Oord, A., Li, Y., and Vinyals, O. (2018). Representation learning with contrastive predictive coding. Corr. abs/1807, 03748. doi:10.48550/arXiv.1807.03748

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all you need,”. Advances in neural information processing systems. Editors I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathanet al. (Curran Associates, Inc.), 30.

Google Scholar

Yang, X., He, X., Liang, Y., Yang, Y., Zhang, S., and Xie, P. (2020). Transfer learning or self-supervised learning? A tale of two pretraining paradigms. Corr. abs/2007, 04234. doi:10.48550/arXiv.2007.04234

CrossRef Full Text | Google Scholar

Yao, J., Hong, D., Li, C., and Chanussot, J. (2024). Spectralmamba: efficient mamba for hyperspectral image classification

Google Scholar

Yoon, J., Zhang, Y., Jordon, J., and van der Schaar, M. (2020). “Vime: extending the success of self- and semi-supervised learning to tabular domain,”. Advances in neural information processing systems. Editors H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin (Curran Associates, Inc.), 33, 11033–11043.

Google Scholar

Yuan, X., Lin, Z., Kuen, J., Zhang, J., Wang, Y., Maire, M., et al. (2021). Multimodal contrastive training for visual representation learning. Corr. abs/2104, 12836. doi:10.48550/arXiv.2104.12836

CrossRef Full Text | Google Scholar

Yuan, Y., Lin, L., Zhou, Z.-G., Jiang, H., and Liu, Q. (2023). Bridging optical and sar satellite image time series via contrastive feature extraction for crop classification. ISPRS J. Photogrammetry Remote Sens. 195, 222–232. doi:10.1016/j.isprsjprs.2022.11.020

CrossRef Full Text | Google Scholar

Yun, S., Han, D., Oh, S. J., Chun, S., Choe, J., and Yoo, Y. (2019). Cutmix: regularization strategy to train strong classifiers with localizable features. Corr. abs/1905, 04899. doi:10.48550/arXiv.1905.04899

CrossRef Full Text | Google Scholar

Zbontar, J., Jing, L., Misra, I., LeCun, Y., and Deny, S. (2021). Barlow twins: self-supervised learning via redundancy reduction. Corr. abs/2103, 03230. doi:10.48550/arXiv.2103.03230

CrossRef Full Text | Google Scholar

Zhang, H., Cissé, M., Dauphin, Y. N., and Lopez-Paz, D. (2017). mixup: beyond empirical risk minimization. Corr. abs/1710, 09412. doi:10.48550/arXiv.1710.09412

CrossRef Full Text | Google Scholar