
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Remote Sens. , 08 January 2024
Sec. Multi- and Hyper-Spectral Imaging
Volume 4 - 2023 | https://doi.org/10.3389/frsen.2023.1295855
This article is part of the Research Topic Optical Radiometry and Satellite Validation View all 22 articles
The primary ocean color product is the spectrum of remote sensing reflectance RRS that allows the quantification of in-water optically significant constituents and all ocean color applications. The determination of its uncertainties is thus key to the creation of comprehensive uncertainty budgets for all derived ocean color products. The assessment of satellite RRS uncertainties has largely relied on corresponding field measurements but this process is solid only if these field measurements are in turn fully characterized. Uncertainty budgets have therefore been defined and reported for the radiometric measurements collected in the framework of the Ocean Color component of the Aerosol Robotic Network (AERONET-OC). The contemporaneous deployment of two autonomous systems for 5.5 years on the Acqua Alta Oceanographic Tower (AAOT) located in the northern Adriatic Sea led to the collection of 4,449 pairs of coincident observations (collected with a time difference lower than 10 min) distributed over 659 days of data acquisitions that can be used to verify reported uncertainty values. The comparison of matched pairs showed a good agreement for RRS (with differences of typically 2%–3% between 412 and 560 nm), as well as for the aerosol optical thickness τa (3%–6%). Differences between data from the two systems appear generally consistent with their stated uncertainties, indicating that they are metrologically compatible and that uncertainties reported for AERONET-OC data are usually trustworthy (with possible exceptions depending on the level of error correlation between measurements from the two systems). Using uncertainty cone diagrams, this result holds across the range of uncertainty values with few exceptions. Independent uncertainty estimates associated with non-systematic error contributions were obtained using a collocation framework allowing for error correlation between measurements from the two systems. The resulting uncertainties appeared comparable with the reported values for τa and RRS. The related mathematical development also showed that the centered root-mean-square difference between data collected by two systems is a conservative estimate of the uncertainty associated with these data (excluding systematic contributions) if these data show a good agreement (expressed by a slope of method II regression close to 1) and if their uncertainties can be assumed similar with errors moderately correlated (typically lower than 0.5).
Ocean color products derived from data of water-leaving radiance LW or remote sensing reflectance RRS offer an extensive array of applications (IOCCG, 2008), including environmental monitoring or climate science, in the context of which LW is listed as an Essential Climate Variable (ECV) (GCOS, 2011). But the use of ocean color remote sensing is only trustworthy if these products are accompanied by uncertainty estimates (IOCCG, 2019), a requirement increasingly recognized in explicit terms in related projects (Donlon et al., 2012; Hollmann et al., 2013; Ahmad et al., 2019). Much of what is known about uncertainties of ocean color data relies on comparison with field measurements, a process termed validation. In the context of climate studies, validation activities are actually required by the Global Climate Observing System (GCOS) for the generation of ECV products (GCOS, 2010). Among the field data used for validation activities, Fiducial Reference Measurements (FRM) have a central role to play as data of particularly high quality; they must fulfill some criteria on measurement and quality control protocols, uncertainty characterization, and traceability to standards (Ruddick et al., 2019; Donlon et al., 2014; Fahy et al., 2022). However, the validity of uncertainty estimates associated with FRMs should also be verified, a process that can rely on inter-comparison exercises (Donlon et al., 2014). Even though such exercises have proved useful for an improved characterization of radiometric measurements and associated uncertainties (e.g., Hooker and Maritorena, 2000; Hooker et al., 2002; Zibordi et al., 2004; Vabson et al., 2019; Alikas et al., 2020; Tilstone et al., 2020), they have often been limited to short periods of time.
Since 2002, the Ocean Color (OC) component of the Aerosol Robotic Network (Holben et al., 1998), AERONET-OC (Zibordi et al., 2021), has provided standardized radiometric measurements collected by autonomous Sun photometers operating from offshore structures in coastal regions or lakes. AERONET-OC radiometric measurements have been extensively used for the validation of satellite radiometric products (normalized water leaving radiance LWN or RRS) from a variety of satellite missions (e.g., Zibordi et al., 2009a; Zibordi et al., 2022b; Mélin et al., 2011; Mélin et al., 2012; Pahlevan et al., 2021; McCarthy et al., 2023) as well as for other applications such as the assessment of detection methods for specific types of phytoplankton (Cazzaniga et al., 2021; Cazzaniga et al., 2023), the testing of multi-mission merging techniques (Mélin and Zibordi, 2007; Mélin et al., 2009) or system vicarious calibration (Mélin and Zibordi, 2010). They benefit from a calibration traceable to standards (Johnson et al., 2021) and a comprehensive set of quality control procedures (Zibordi et al., 2022a; D’Alimonte and Zibordi, 2006; Giles et al., 2019). Studies by Gergely and Zibordi (2014) and Cazzaniga and Zibordi (2023) also described an approach to compute uncertainty estimates for each AERONET-OC LWN record.
In October 2017, the AERONET-OC system operating on the Acqua Alta Oceanographic Tower (AAOT), located in the northern Adriatic Sea (45.314°N, 12.508°E), was updated with the installation of a CE-318T Sun photometer with enhanced capabilities but the previous CE-318 instrument was kept in operation till March 2023, which has provided 5.5 years of simultaneous measurements from similar instruments. This dual configuration and the resulting large body of data offer a unique opportunity to assess the AERONET-OC observations and their uncertainty budget by analysing if the differences observed between measurements of two instruments are compatible with their associated uncertainties. The first objective of this study is thus to verify the uncertainty estimates reported for the AAOT AERONET-OC data as well as to validate the approach devised to compile these uncertainties. The second objective is more methodological, i.e., to present a metrologically sound approach for such an assessment that could be applied to other cases of simultaneous observations.
The Acqua Alta Oceanographic Tower (AAOT) in the northern Adriatic Sea has been hosting a SeaWiFS1 Photometer Revision for Incident Surface Measurements (SeaPRISM or simply PRS hereafter) CE-318 system since 2002 and is the precursor site for AERONET-OC. This site is characterized by a large variability in bio-optical quantities since located in a transition region between open sea and coastal waters affected by the input from several rivers (Zibordi et al., 2009a). The aerosol type is mostly continental, occasionally maritime (Mélin and Zibordi, 2005; Mélin et al., 2006).
In October 2017, a more recent SeaPRISM system (CE-318T, Zibordi et al., 2021) was additionally deployed on AAOT. The two instruments were located a short distance apart (∼65 cm) and observed the same portion of the sea (see Zibordi et al., 2021, for a view of the setting). The two systems (hereafter called PRS0 and PRS1 for CE-318T and CE-318, respectively) operated simultaneously from October 2017 to March 2023. CE-318 and CE-318T differ mainly in the number of measurement sequences performed and the number of the center-wavelengths at which measurements are acquired, which are both higher for PRS0 (CE-318T). Every hour, whereas CE-318 instruments perform two sequences of measurements, CE-318T instruments perform two triplets of measurement sequences. Each triplet is composed of three complete measurement sequences typically completed within 10 min.
CE-318 acquires measurements at eight bands with nominal center-wavelengths at 412.5, 442.5, 490.0, 532.0, 551.0, 667.0, 870.0 and 1,020.0 nm, while CE-318T acquires measurements at 11 bands with nominal center-wavelengths matching those of the Ocean and Land Colour Imager (OLCI, Donlon et al., 2012), at 400.0, 412.5, 442.5, 490.0, 510.0, 560.0, 620.0, 665.0, 779.0, 865.0, and 1,020.0 nm. Exact center-wavelengths actually vary with each deployment, with a maximum deviation of 4.4 nm for CE-318 (maximum in the range 551–555 nm) and 0.3 nm for CE-318T. In the considered observation period (Oct. 2017-March 2023), 2 and 5 instruments were alternatively deployed for PRS0 and PRS1, respectively. These instruments were regularly substituted for maintenance and re-calibration: the considered period was associated with seven deployments for PRS0 and 8 deployments for PRS1, so that the pair of instruments in operation varied at irregular intervals. Even though comparison statistics may somewhat vary from one pair of instruments to another (Zibordi et al., 2021), the observations collected by successive deployments of CE-318T and CE-318 were considered as a single time-series covering the whole period for PRS0 and PRS1, respectively, which is consistent with the way the respective data sets are distributed through the AERONET-OC portal2 for the “AAOT” and “Venice” sites.
The water-leaving radiance LW at wavelength λ is quantified by PRS measurements in the following way (Zibordi et al., 2021, and references therein):
where LT is the total radiance measured by the instrument pointed at the sea surface with the geometry defined by the zenith viewing angle θ (fixed at 40°) and relative azimuth with respect to the solar plane ϕ (fixed at 90°) with a solar zenith angle θ0, and Li is the sky radiance collected with a viewing angle θ′ = 180°-θ. The sea-surface reflectance factor ρ is computed as a function of geometry and sea state represented by wind speed w (Mobley, 1999; Mobley, 2015). For each measurement sequence, 11 measurements of LT and 3 measurements of Li are performed. Selected values of LT and Li are then obtained by averaging all Li measurements and the lowest 2 out of 11 measurements of LT, aiming at minimizing the impact of wave perturbations, as described in Zibordi et al. (2021) and in D’Alimonte et al. (2021).
The conversion from LW to the normalized water-leaving radiance LWN is performed through:
where d is the inverse normalized Earth-Sun distance, and td is the diffuse atmospheric transmittance (Deschamps et al., 1983). The remote sensing reflectance RRS is simply defined as LWN/E0, where E0 is the mean extra-terrestrial solar irradiance (Thuillier et al., 2003). In effect, the product d2cos θ0E0td normalizes LW by the incident downward irradiance. CQ is a factor correcting for bidirectional effects associated for non-nadir illumination and observation conditions. It is here modeled as a function of geometry, wind speed and the optical properties of the water (labeled OP), represented either by chlorophyll-a concentration (Chl) according to Morel et al. (2002) or by Inherent Optical Properties (IOP) according to Lee et al. (2011). Both correction methods are provided for AERONET-OC data and corresponding RRS values are hereafter referred to as
As indicated above, wavelengths associated with any two systems differ slightly. This could be corrected with a band-shift correction such as that described in Zibordi et al. (2009a) and applied to LWN. This shift includes a correction for E0 (which is here embedded in the conversion to RRS) and a component modeling spectral changes in IOPs of the water, themselves computed with LWN with a regional algorithm. This part of the correction may be associated with significant uncertainties (Mélin and Sclep, 2015; Salem et al., 2023) that are not easily quantified for all records. Thus, considering that differences in wavelengths are relatively small and that comparison statistics actually do not improve when applying the correction, it is not applied here.
For completeness, it is recalled that AERONET-OC sites also function as generic AERONET sites for the determination of the aerosol optical thickness τa using direct solar irradiance measurements (Holben et al., 1998; Smirnov et al., 2000). Reported uncertainties for τa measurements are typically decreasing with wavelength from the blue to the near-infrared (NIR) in the interval 0.010–0.015 (Eck et al., 1999; Schmid et al., 1999). In the comparison between τa collected by instruments at different wavelengths, a band-shifting procedure is applied by modeling the spectrum of τa as a second-order polynomial (in log-space) (O’Neill et al., 2001; Mélin et al., 2007; Mélin et al., 2013).
In this work, only Level 2.0 AERONET-OC data, i.e., measurements that passed the highest level of quality control (QC), were used. A first automated QC process, fully described in Zibordi et al. (2022a), discarded measurements potentially affected by clouds, high aerosol load, high variability in both illumination and water surface conditions. Additionally, until March 2023, data were qualified as Level 2.0 after an expert-based quality control procedure. For more recent data, an automated comprehensive QC procedure was instead applied, which included former automated checks and mimicked the expert analysis during the final QC of AERONET-OC data.
The measurement function associated with the AERONET-OC systems and its related error sources is displayed in an uncertainty analysis diagram (also called uncertainty tree) following Mittaz et al. (2019) (Figure 1). In the works by Gergely and Zibordi (2014) and Cazzaniga and Zibordi (2023), the combined standard uncertainty (with a coverage factor k = 1) associated with AERONET-OC LW data, u(LW,j) for record j, was expressed by the law of uncertainty propagation applying a first-order Taylor series development to Eq. 1 (Ku, 1966; GUM, 2008) leading to (omitting the spectral dependence for simplicity):
where u%(LT) and u%(Li) are LT and Li relative uncertainty values, respectively, which include the uncertainty affecting instrument calibration, the decay of instrument sensitivity during a deployment and the short-term environmental perturbations uenv(LT) and uenv(Li) (Figure 1) (the notation u% will indicate relative uncertainties in % throughout the manuscript). Since only PRS0 systems provide triplets of measurements, used to estimate uenv(LT) and uenv(Li), u%(Li) and u%(LT) were calculated as in Cazzaniga and Zibordi (2023) only for PRS0 time series, and their average values were applied too when calculating PRS1 uncertainties. For those PRS1 center-wavelengths which were not available from PRS0, these average values were interpolated spectrally. Finally, u%,j(ρ), relative uncertainty for ρ, was calculated for each LW,j value as in Cazzaniga and Zibordi (2023). It is acknowledged that Eq. 3 does not include error correlation terms that are deemed insufficiently characterized.
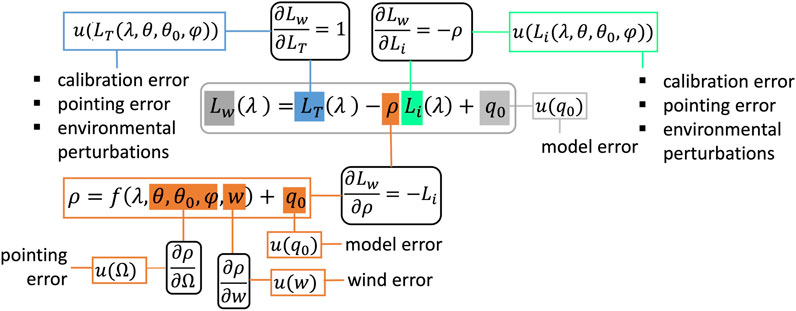
FIGURE 1. Uncertainty tree diagram for the AERONET-OC LW measurement function (associated with Eq. 3). The measurement function is in the grey rectangle, expressing the measurand as a function of its influence quantities (or input quantities). For each input, the associated error sources are traced with various colors to their contributing factors. Rounded black rectangles indicate the sensitivity factors (expressed as partial derivatives), i.e., the extent to which an error in an input impacts the measurand. For all equations in the diagram, q0 is a generic notation indicating a possible model error. Ω is a short notation for the geometry of observation and illumination.
The conversion from LW to the normalized water-leaving radiance LWN or, equivalently, to the remote sensing reflectance RRS (LWN and RRS merely differ by the factor E0, Eq. 2) is illustrated by the uncertainty tree diagram of Figure 2. For each record j, the combined standard uncertainty for LWN, u(LWN,j), was calculated from u(LW,j) and the law of uncertainty propagation applied to Eq. 2, according to (also ignoring correlated terms):
where

FIGURE 2. Uncertainty tree diagram for the conversion from LW to RRS (associated with Eq. 4). Its construction is similar to Figure 1. Bold notations indicate a spectrum of values for RRS or for optical properties OP. td,r, td,a, and td,o are transmittance associated with air molecules (Rayleigh), aerosol and ozone. τr is the Rayleigh optical thickness (dependent on tabulated values at the standard atmospheric pressure and the actual atmospheric pressure).
For each day of operation of PRS0 and for each measurement, the data collected by PRS1 were searched for the record with the closest time of acquisition, and the pair of coincident measurements was selected for comparison if the time difference was smaller than Δt. From the data set of N pairs of matched data
where the overbar indicates an average value. Δ, the root-mean-square (RMS) difference between x0 and x1 (Eq. 5), can be expressed as the sum (in quadratic form) of the average difference (also called bias), δ, and the centered RMS difference Δc.
Acknowledging that there was no reason to consider one measurement better than the other, relative differences were quantified using their unbiased (or symmetric) form, i.e., taking the average of x0 and x1 as a reference (at the denominator) (e.g., Hooker and Morel, 2003; Mélin and Franz, 2014).
The “median” operator was adopted to reduce the possible impact of outliers; |ψu|m is the median unbiased absolute relative difference (here “absolute” refers to the use of the modulus operator | |, Eq. 8) and ψu,m is the median unbiased relative difference (Eq. 9).
The Pearson correlation coefficient r between coincident PRS0 and PRS1 measurements (RRS or τa) was also computed.
Going beyond simple comparison statistics, collocation analysis underpinned by an error model can provide more elaborate statistics characterizing uncertainties (Stoffelen, 1998; Toohey and Strong, 2007). Here the following error model was adopted for the records
where t is a reference value and the ϵ′s are zero-mean random error terms. The term t that serves as a link between x0 and x1 can be related to the true value and is not impacted by non-systematic effects that are captured by ϵ. Additive and multiplicative biases, α and β, respectively, further relate x0 and x1. Besides systematic effects, uncertainties of x0 and x1 could be characterized by the standard deviation of the associated
This framework was adopted to investigate uncertainties of satellite values (Mélin, 2010; Mélin et al., 2016; Mélin, 2021; Mélin, 2022) with the assumption that the ϵ terms were uncorrelated with t and with each other. Considering that the simultaneous determination of RRS by the 2 PRS systems share some elements (Figures 1, 2), this assumption is not warranted here and the framework was extended to the case where ϵ0 and ϵ1 are correlated with a coefficient rϵ. Writing the variance and covariance terms associated with x0 and x1 in that case leads to:
where σ0 and σ1 are the standard deviation of x0 and x1, respectively, and σϵ0 and σϵ1 the standard deviation of ϵ0 and ϵ1, respectively.
This system can be rewritten by removing σt from Eqs 12, 14 using Eq. 13:
This system with two equations and four unknowns can be solved if the ratio σϵ1/σϵ0, noted η, and rϵ are known. This leads to a second-order polynomial with the solution:
The case rϵ = 0 reduces β to the slope of the model II regression, and to the slope of a simple major-axis regression if additionally η = 1 (Legendre and Legendre, 1998).
The value of β finally leads to σϵ0 and σϵ1 that are considered as the uncertainties associated with x0 and x1 (excluding systematic effects).
During the common period of operations (∼5.5 years), PRS0 produced Level 2.0 data over 1,112 days totaling 14,700 records, while data were collected by PRS1 in 811 days (3,059 records). The difference in the number of acquisitions is mostly explained by the higher frequency of observation granted by the CE-318T system (PRS0).
Figure 3 shows the median values for RRS and associated median uncertainty u(RRS) for both terms
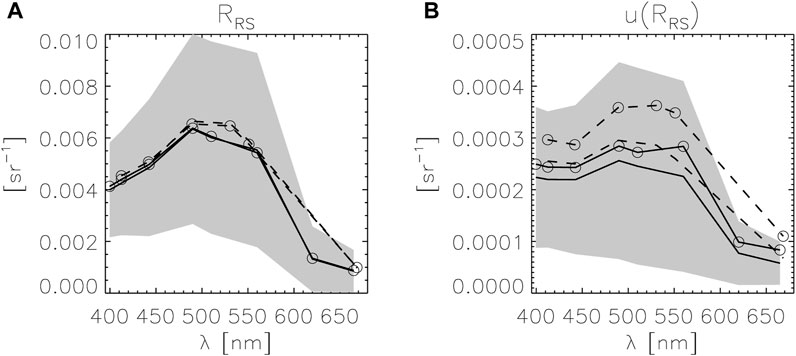
FIGURE 3. Overall average statistics: (A) Spectrum of median RRS for PRS0 (line) and PRS1 (dashed line), for
The overall median aerosol optical thickness τa decreases from 0.167 (standard deviation, s.d., 0.133) at 412 nm to 0.054 (s.d. 0.051) at 865 nm for PRS0, and from 0.166 (s.d. 0.143) at 412 nm to 0.055 (s.d. 0.056) at 869 nm for PRS1. The median Ångström exponent [computed with a log-transformed linear regression for bands between 412 and 869 nm, Ångström, (1964)] is equal to 1.55 (s.d. 0.30) and 1.52 (s.d. 0.31) for PRS0 and PRS1, respectively. These values are also typical for the site and representative of the continental aerosols encountered in the region (Mélin and Zibordi, 2005; Mélin et al., 2006; Clerici and Mélin, 2008).
Focusing on the uncertainties of RRS (calculated assuming uncorrelated inputs, see Section 2.2), Figure 4 shows the distribution functions of
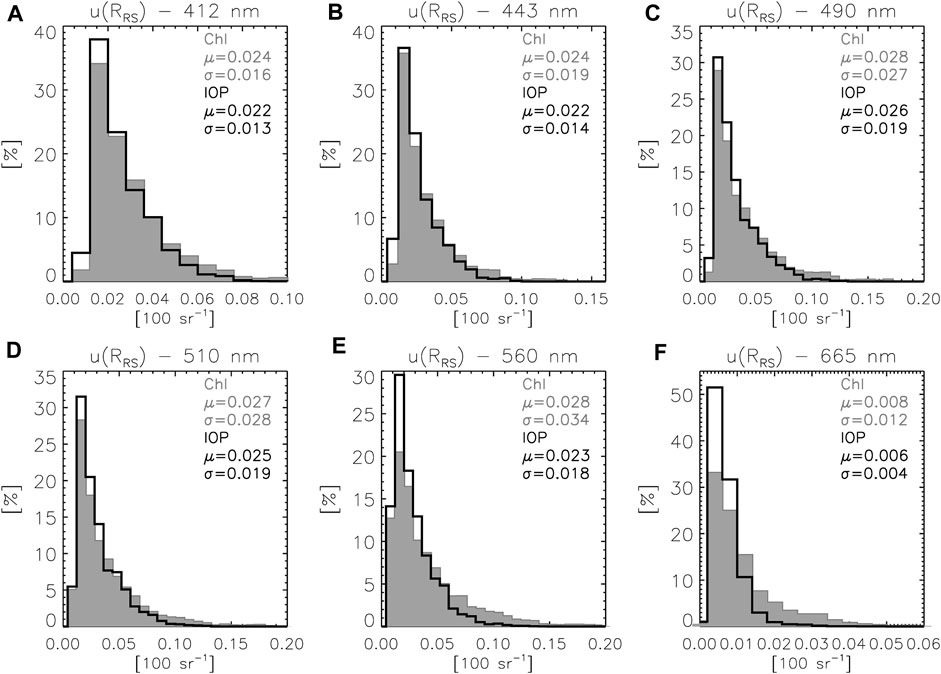
FIGURE 4. Normalized distribution functions of the uncertainties u(RRS) for PRS0 at (A) 412 nm, (B) 443 nm, (C) 490 nm, (D) 510 nm, (E) 560 nm and (F) 665 nm. Grey histogram and statistics are associated with
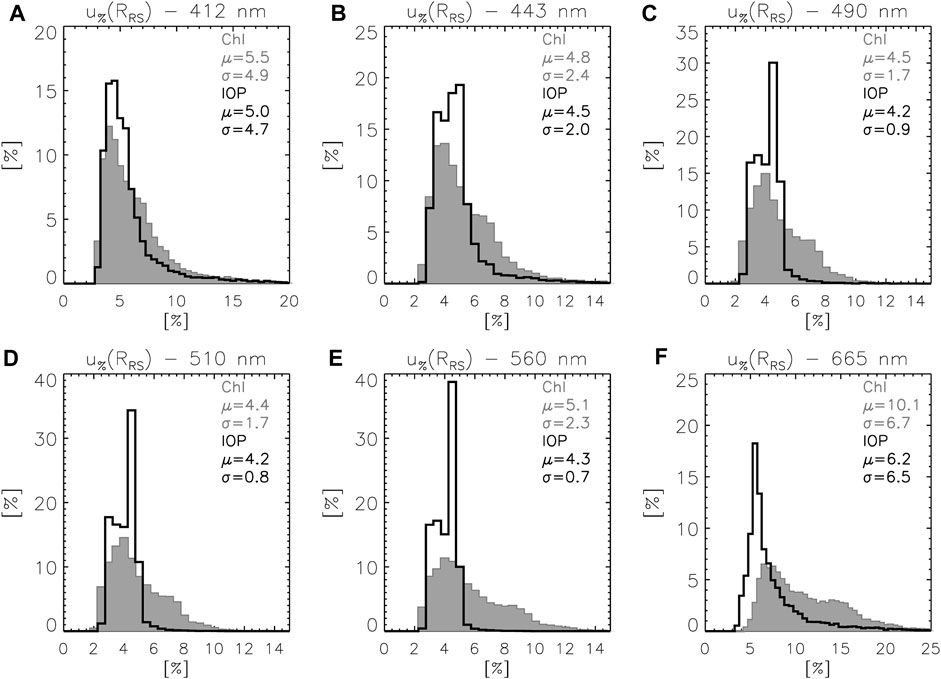
FIGURE 5. Normalized distribution functions of the relative uncertainties u%(RRS) for PRS0 at (A) 412 nm, (B) 443 nm, (C) 490 nm, (D) 510 nm, (E) 560 nm and (F) 665 nm. Grey histogram and statistics are associated with
Selecting a maximum time difference Δt of 10 min, 659 days have at least one pair of matching observations, amounting to a total of 4,449 pairs. This short time difference is associated with similar conditions of illumination, with a mean absolute difference of 0.49° for the solar zenith angle and 1.9° for the solar azimuth angle. In this matching exercise, several members of each PRS0 triplet (up to 3) can be associated with the same PRS1 record. Enforcing the occurrence of the PRS1 data in one matching pair only would reduce the number of matching pairs by half: it would exclude some members of the associated PRS0 triplet and ultimately a considerable number of valid observations in an arbitrary way. The option adopted here is to consider all PRS0 data as valid independent observations to be compared to PRS1 observations. Importantly, besides a lower number of match-ups, results are not affected by this choice.
The comparison between τa from PRS0 and PRS1 shows a remarkable agreement with a determination coefficient r2 decreasing from 0.994 at 412 nm to 0.977 at 865 nm, maximum RMS differences Δ of ∼0.01 in the spectral range 412–560 nm, and median unbiased absolute relative differences |ψu|m lower than 5% (6.5% at 865 nm) (see Table 1 and Figure 6). There are very few outliers that might be associated with cases of rapid changes in the atmosphere. For instance on 25 February 2020 (the case associated with the highest τa in Figure 6), PRS0 detected three values of τa (412) in a hour, 1.26, 1.25 and 1.67, while PRS1 recorded only one value (1.38) 6 min before the third PRS0 record.

TABLE 1. Comparison statistics for τa with determination coefficient r2, RMS difference Δ, median unbiased absolute relative difference |ψu|m and median unbiased relative difference ψu,m. Positive values indicate that τa from PRS1 is higher than from PRS0.
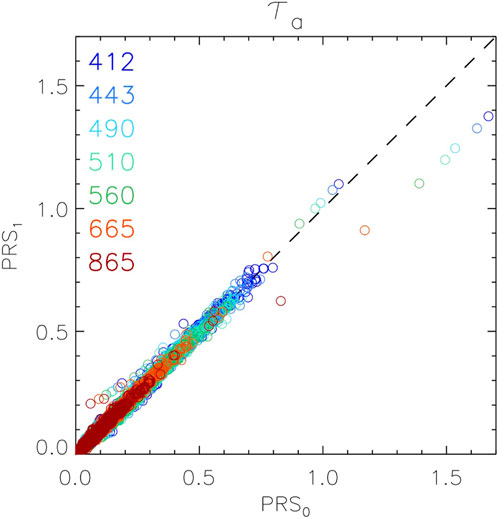
FIGURE 6. Scatter plot of τa between PRS0 and PRS1 for the indicated wavelengths. Statistics of comparison are given in Table 1.
The RRS data from the two systems also agree very well with very few outliers (Figure 7) in agreement with preliminary results found in Zibordi et al. (2021). This is true for both
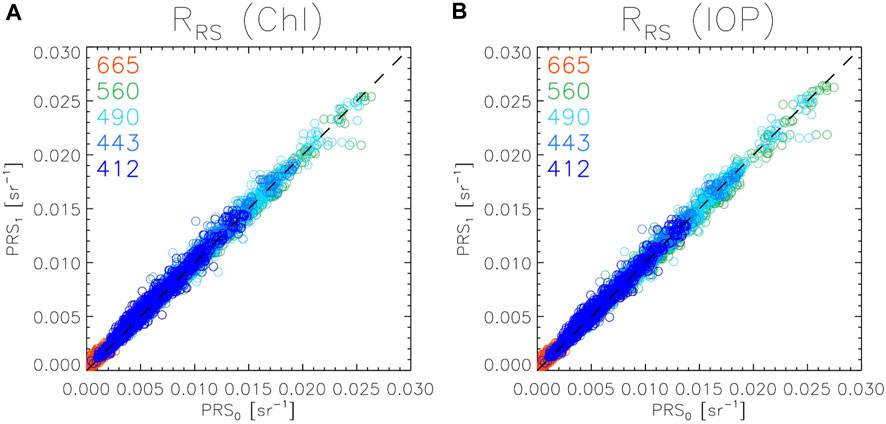
FIGURE 7. Scatter plots comparing (A)
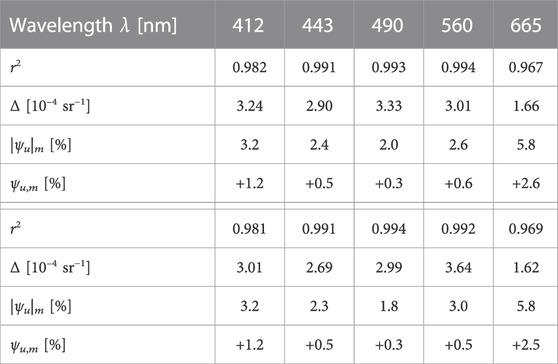
TABLE 2. Comparison statistics for
Considering the similar conditions of observations associated with the matched data and the common method to derive uncertainty estimates, u(RRS) from PRS0 and PRS1 are expected to be close, which is indeed verified by Figure 8. For both
The uncertainty estimates should now be related to the differences between coincident records of RRS from PRS0 and PRS1 documented in the previous Section 3.2. The uncertainty associated with the difference RRS,1 − RRS,0 can be expressed with (Mélin, 2021):
where r(e(RRS,0), e(RRS,0)) is the correlation between the errors associated with RRS,0 and RRS,1. If this correlation is null in Eq. 20, the uncertainty associated with the difference is the sum of the uncertainties (in quadratic form) [e.g., Immler et al. (2010)]. The following inequality may then be introduced (Kacker et al., 2010; Mélin, 2021):
where k is the so-called coverage factor. With a normal hypothesis, this inequality would be true in 68% of cases with a coverage factor k = 1. Strictly speaking, this reasoning is valid for a hypothetical situation where multiple measurements are repeated in identical conditions; it was here extended to the current match-up data set where RRS (and their uncertainties) are associated with varying conditions experienced during years of operations. No estimate is readily available to quantify the term associated with error correlation (see further on for discussion on this issue) and four cases were considered (with the correlation coefficient assumed constant across the data set): no correlation, low correlation (0.2), moderate correlation (0.5) and high correlation (0.7). The percentage κ of records where Eq. 21 is true appears much higher than 68% for
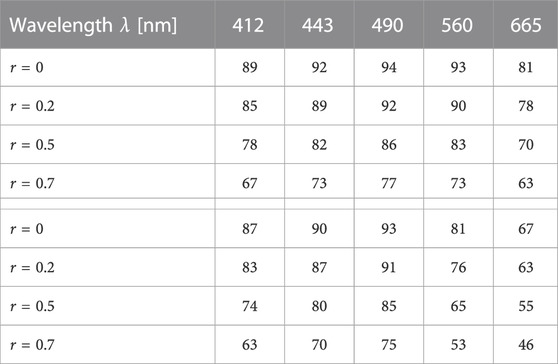
TABLE 3. Fractions κ (given in %) of records where Eq. 21 is verified for
The previous analysis was conducted with statistics compiled over the whole data set; taking advantage of the amount of data available, it can be completed by a more detailed analysis along the range of uncertainties. The set of uncertainties u(RRS) was split into 20 bins of equal sample size for which the average value was computed. Then, the centered RMS difference Δc (Eq. 7) and average difference δ (Eq. 6) between RRS from PRS0 and PRS1 were computed using the records associated with each bin.
Results for
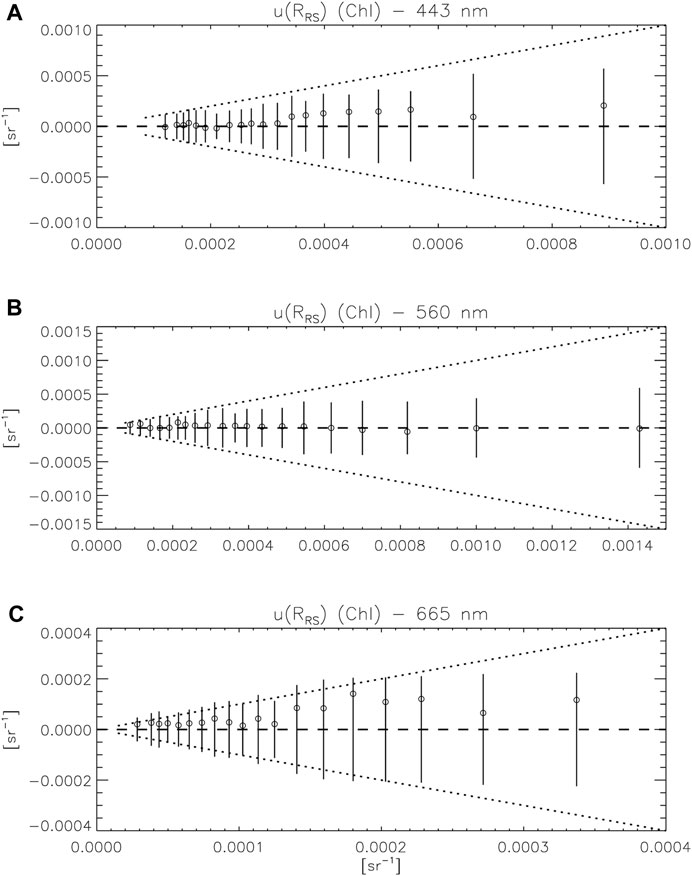
FIGURE 9. Comparison between uncertainty estimates
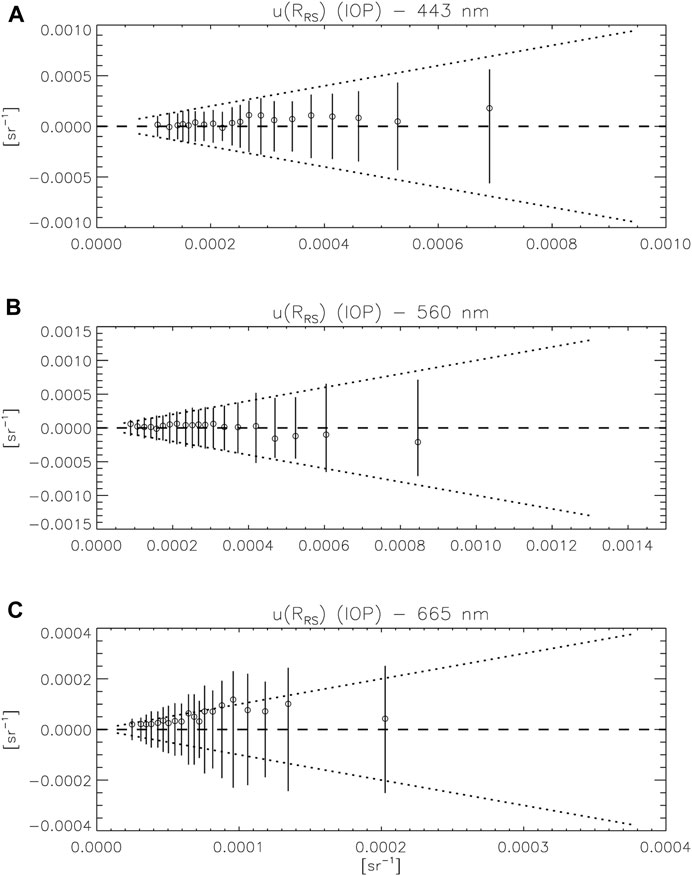
FIGURE 10. Comparison between uncertainty estimates
At almost all wavelengths and across the range of reported uncertainties, the average differences δ between RRS,0 and RRS,1 is well below the uncertainty (circles in the dotted cone in Figures 9, 10), the exception being the case of
The collocation approach was first applied to the aerosol optical thickness data τa. Considering the agreement of the τa data from PRS0 and PRS1 (Figure 6), the choice of η = 1 (ratio of the σϵ’s) appears justified. A value for the error correlation is also required and four cases are again considered with rϵ equal to 0, 0.2, 0.5 and 0.7. For the case of rϵ = 0, the value of β varies between 0.996 and 1.011 (at 865 nm) (Table 4), values that are barely affected by the choice of rϵ. σϵ tends to decrease with wavelength, e.g., from 0.0072 at 412 nm to 0.0053 at 865 nm for rϵ = 0. Contrary to β, σϵ increases with rϵ (following Eqs. 18, 19), from 0.0072 for rϵ = 0 to 0.0131 for rϵ = 0.7 at 412 nm, or from 0.0053 to 0.0096 at 865 nm. These results are mostly lower than reported uncertainties (Eck et al., 1999; Schmid et al., 1999) of 0.01–0.015 (in the interval 412–865 nm, decreasing with wavelength) but are very close in the case of rϵ = 0.7. Similar inputs in environmental variables used in τa retrieval, such as atmospheric pressure for the determination of the Rayleigh optical depth or ozone concentration and properties, would result in an error correlation for two instruments functioning simultaneously, whereas effects such as instrument noise would not. While determining the relative weights of correlated and uncorrelated effects in τa retrievals is out of the scope of this work, it can be said that, unless the contribution to the uncertainty budget from environmental variables is dominant, leading to the upper value of the error correlation, σϵ is found somewhat lower than reported uncertainty values; but it is also stressed that σϵ does not contain contributions from systematic effects (these would be captured by α and β in Eqs. 10, 11), which can be significant (Giles et al., 2019). For completeness, it is noted that the median difference between τa from PRS0 and PRS1 varies (in modulus) between 0.0010 and 0.0033. Overall, collocation statistics appear consistent with reported uncertainty values for τa.
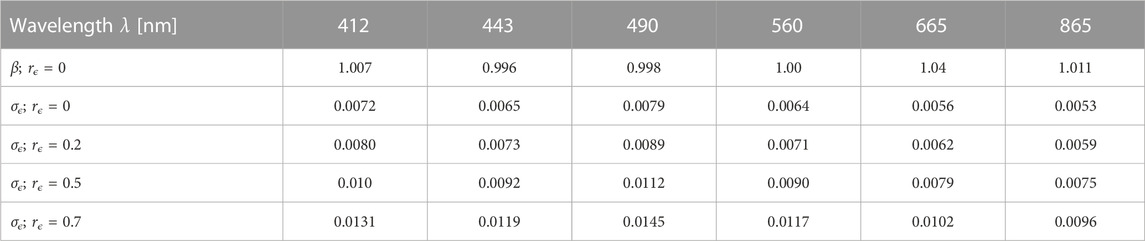
TABLE 4. Collocations statistics: regression slope β for rϵ = 0, and σϵ for τa for four cases of error correlation rϵ.
A similar analysis was conducted with RRS with results reported in Table 5 for the same four cases of error correlation rϵ (this time relative to RRS), again under the assumption of η = 1 considering the agreement in RRS illustrated in Figures 7, 8. The value of β is only given for rϵ = 0 since it hardly varies with rϵ (with values very close to 1). As for τa and according to Eqs 18, 19, σϵ increases with rϵ for both
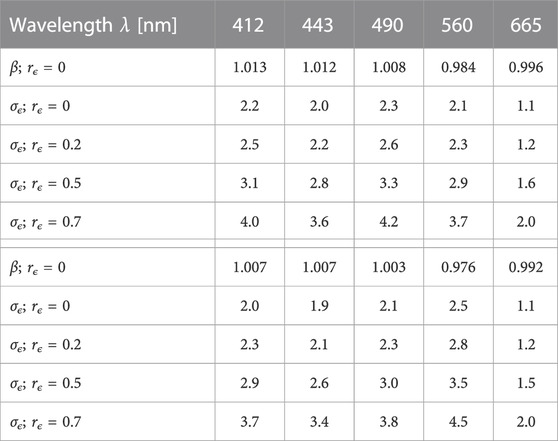
TABLE 5. Collocations statistics β for rϵ = 0, and σϵ (in 10–4 sr−1) for
Values of σϵ can eventually be compared with other statistics presented in the previous sections, the median uncertainty estimate u(RRS) (for both PRS0 and PRS1, computed with the common records of the match-up data set) and the RMS difference between RRS from PRS0 and PRS1 in its centered form Δc since σϵ does not include systematic contributions (the average difference δ is also illustrated for completeness and comparison with non-systematic terms). In agreement with Section 2.1 and Figure 4, the median
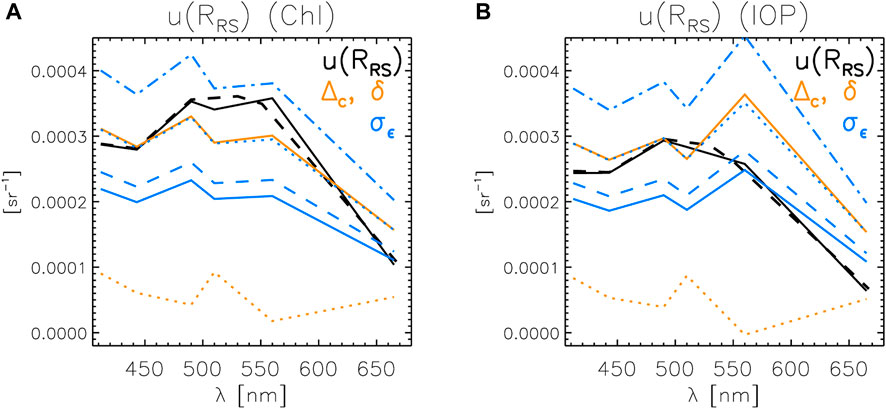
FIGURE 11. Spectra of the median reported uncertainty u (RRS) (black line for PRS0 and black dashed line for PRS1) computed for coincident measurements, spectra of centered RMS differences Δc (orange line) and average differences δ (orange dotted line), and spectra of σϵ for rϵ = 0 (blue line), 0.2 (blue dashed line), 0.5 (blue dotted line) and 0.7 (blue dashed-dotted line). Results are given for (A)
The relation between Δc and σϵ can be further discussed by relating Δc with terms of variance and covariance of
In the case where η ∼1, if β → 1, then
The issue of the correlation of the errors associated with the matched RRS data from PRS0 and PRS1 has appeared in the previous analyses, when comparing reported uncertainty estimates and comparison statistics (Section 3.3; Eq. 21) and when computing collocation statistics (Section 3.5). Admittedly, additional analyses would be required to quantify the level of correlation between errors affecting simultaneous measurements of RRS. It could change with observation conditions and would certainly vary with wavelength as the weights of different contributing factors in the uncertainty budget varies spectrally (Cazzaniga and Zibordi, 2023). The following discussion attempts to provide an approximate range of values for the error correlation between LWN (or RRS) data from PRS0 and PRS1 by defining informed guesses on the error correlation associated with these contributing factors. Cazzaniga and Zibordi (2023) detail five major contributions to the overall uncertainty budget for LWN, the uncertainties due to: i) the calibration of the sensor, ucal, ii) the sea surface reflectance factor ρ, uρ, iii) the normalization term for downwelling irradiance CA = 1/(d2μ0td) (Eq. 2),
Starting with the measurement function of LW (Figure 1), evaluating the correlation of errors due to the calibration of the instruments would require assumptions on the behavior of specific calibration lamps or plaques and on the aging of the sensors, while instrument noise that could additionally affect LT and Li would not introduce correlated errors. As a guess for the associated error correlation rcal, the triplet [0, 0.1, 0.3] is proposed. Environmental perturbations may affect the terms of the measurement function LT, Li and ρ in a similar way for the two systems but quantifying this relationship is not straightforward and only an arbitrary choice for the associated error correlation renv is selected here, [0, 0.1, 0.3]. The case of ρ can be further discussed, particularly with respect to wind (input to the expression of ρ, Figure 1). In the processing of AERONET-OC data, wind speed is provided by re-analysis products of coarse temporal and spatial resolutions and would have virtually the same value for two measurements collected at short time intervals. If the local wind can be assumed constant for the matched measurements (i.e., in a time interval shorter than 10 min), then the error associated with the use of the re-analysis product will be identical for the two measurements, suggesting a high error correlation affecting ρ for PRS0 and PRS1. However, parameterizing the state of the air-sea interface at a precise moment as a function of wind speed is a simplification (represented by the term of model error q0 in Figure 1). The two instruments are looking at virtually the same small spot on the sea surface (with a full-angle field of view of
Error correlations may be more easily identified in relation to the conversion from LW to LWN (or RRS) (Figure 2), introduced by quantities depending on common environmental variables such as the transmittance td or CQ (as well as by E0). The modeling of the term CQ contributes significantly to the overall uncertainty budget to an extent that varies with wavelength and water type (Talone et al., 2018; Cazzaniga and Zibordi, 2023). Considering that RRS provided by the two systems are very close (Figure 7), the derived IOPs and Chl used to calculate CQ will also be very similar with correlated errors with respect to the actual IOPs and Chl (errors that would depend on the bio-optical model and on RRS). In addition, CQ models representing the correction for bidirectional effects as a function of IOPs or Chl are imperfect [e.g., Gleason et al. (2012); Talone et al. (2018)], which is again represented by the term q0 associated with CQ in Figure 2; considering that the same CQ model was adopted when comparing data from PRS0 and PRS1, error correlations
For each system PRSj (j = 0 or 1), the error ϵj of a given measurement can be written as the sum of errors associated with the contributions discussed above:
As said for the uncertainty contributions, it is stressed that the terms of Eq. 24 are representing error contributions to the final value of RRS errors and not errors of the single quantities (e.g., ϵρ is not the error on ρ but the error on RRS that ultimately depends on an error on ρ). Assuming that the errors from different contributions are uncorrelated between PRS0 and PRS1 (e.g., that the errors due to environmental variability for PRS0 are uncorrelated with errors due to CQ for PRS1), a calculation of the covariance
where, e.g.,
where u0 and u1 are the combined standard uncertainties for PRS0 and PRS1 data while the u0 and u1 terms on the right-hand side are associated with the contributions indicated in subscript (Cazzaniga and Zibordi, 2023).
Eq. 26 is applied for the three scenarios (low, medium and high values of the triplets) to calculate an informed guess of the error correlation associated with RRS from PRS0 and PRS1 (Figure 12). With the various cases considered, the resulting error correlation could take values in the broad interval 0.2–0.8 with the medium case in the interval of approximately 0.4–0.6. By assuming error correlation coefficients spectrally constant for each type of contribution, the overall correlation is seen to increase from the blue to 560 nm, which can be related to the larger weight of
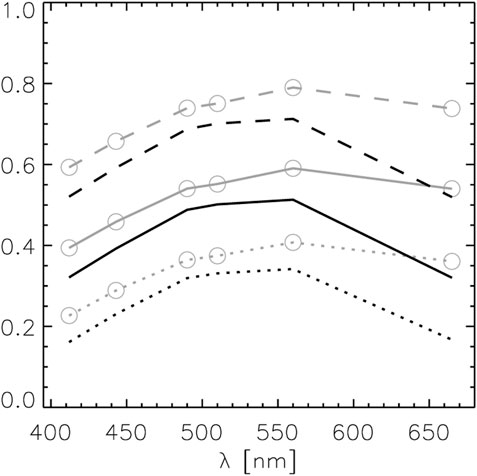
FIGURE 12. Spectra of the error correlation coefficient obtained with Eq. 26 associated with
Looking back at Figure 11A,
This study has taken advantage of a large body of radiometric data collected simultaneously by two instruments to assess uncertainty estimates reported for RRS (and secondarily τa). The first objective was to verify these uncertainty estimates for the specific case of the AERONET-OC data collected at AAOT. τa and RRS collected by the two systems appear very close (Figures 6, 7; Tables 1 and 2) and measurements generally agree within their stated uncertainties (Section 3.3), i.e., they are metrologically compatible (Kacker et al., 2010). Actually the analysis comparing uncertainty estimates u(RRS) with comparison statistics suggested that u(RRS) could be slightly too high in some cases (but too low for
The second objective was more methodological, aiming at applying a metrology-sound protocol to verify uncertainty estimates using simultaneous measurements, while identifying related challenges and limitations. The construction of uncertainty tree diagrams (Mittaz et al., 2019) appears very valuable for a comprehensive view of all error sources affecting a measurement system. Strictly speaking, the measuring system under study here is one quantifying the difference between RRS observed by two instruments (i.e., RRS,1 − RRS,0) but for ease of illustration, uncertainty tree diagrams were given for an individual PRS system (Figures 1, 2). Uncertainty cone diagrams (Figures 9, 10) provided a mean to compare uncertainty estimates u(RRS) with comparison statistics across their range of values. Collocation statistics also proved valuable by providing an independent method of verification. These methods could be applied to other cases where a sufficient number of coincident measurements from different systems are available, starting with the AAOT site that is regularly hosting other instruments (Vansteenwegen et al., 2019; Tilstone et al., 2020; Brando and Vilas, 2023).
The collocation framework used in previous comparison analyses (e.g., Mélin, 2021; Mélin, 2022) was here extended to cases allowing correlation between errors associated with non-systematic effects (leading to a revised expression for the slope of the model II regression, Eq. 17). This approach is powerful to verify uncertainty estimates but has also limitations. To be solved, the system of Eqs 15, 16 requires assumptions on the ratio η of uncertainties σϵ and the error correlation rϵ. The first assumption (on the value of η) is not a major limitation as long as the σϵ can be assumed comparable since the results are not strongly dependent on η (for instance η = 1.21 would multiply σϵ,1 by 1.1 and σϵ,0 by 0.91). As shown by Figure 11, the choice of rϵ has a stronger impact on σϵ, and its actual value should be better characterized as acknowledged in Section 3.6. Another limitation of the collocation approach is that it provides only one general value for the whole data set (even though the current data set is actually large enough to permit computing collocation statistics on subsets of increasing RRS) and therefore allows only the verification of average statistics of the reported uncertainties u(RRS).
The collocation analysis has also led to a practical result, i.e., that the centered root-mean-square difference Δc between data collected by two systems can directly serve to quantify the uncertainty associated with these data (excluding systematic contributions); this is valid if these data show a good agreement (expressed by a slope of method II regression close to 1) and if their uncertainties are comparable (η not largely different from 1) with moderate error correlation. If the error correlation is negligible, Δc is actually twice the uncertainty, while it happens to be a good estimate of the uncertainty for an error correlation of 0.5. For highly correlated errors, Δc would be an underestimate of the uncertainty.
As more data sets come with documented uncertainties, and new observing networks emerge (e.g., for field radiometric measurements, Brown et al., 2007; Białek et al., 2020; Goyens et al., 2021; Lin et al., 2022; Cazzaniga and Zibordi, 2023), appropriate metrologically-based methods will be required to verify uncertainty estimates and ensure that they are trustworthy for validation activities. This work illustrates how the simultaneous operation of multiple systems can help in that regard, but also that a comprehensive understanding of the contributing factors to the uncertainty budget is required for a solid interpretation of differences between matching observations.
Publicly available datasets were analyzed in this study. This data can be found here: https://aeronet.gsfc.nasa.gov/new_web/ocean_color.html.
FM: Conceptualization, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. IC: Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. PS: Data curation, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Partial funding was given by the EMPIR grant 19ENV07 associated with the MetEOC-4 project under the EMPIR programme. Additional funding was provided by DG DEFIS, i.e., the European Commission Directorate-General for Defence Industry and Space, and by DG JRC (Joint Research Centre).
This work was supported by the MetEOC-4 project through the EURAMET European Metrology Programme for Innovation and Research (EMPIR) under Grant 19ENV07. The EMPIR programme is co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. The support provided by DG DEFIS, i.e., the European Commission Directorate-General for Defence Industry and Space, and the Copernicus Programme is also gratefully acknowledged. G. Zibordi and B. Bulgarelli are thanked for their contribution to the operation of the AAOT AERONET-OC site.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1standing for Sea-viewing Wide Field-of-view Sensor
2https://aeronet.gsfc.nasa.gov/new_web/ocean_color.html
Ahmad, Z., Cetinić, I., Franz, B., Karaköylü, E., McKinna, L., Patt, F., et al. (2019). “Data product requirements and error budgets consensus document,” in NASA technical memorandum 2018-219027. NASA goddard space flight center. Editors I. Cetinić, C. McClain, and P. Werdell (Greenbelt, Maryland), 6. of PACE Technical Report Series. 55pp.
Alikas, K., Vabson, V., Ansko, I., Tilstone, G., Dall’Olmo, G., Nencioli, F., et al. (2020). Comparison of above-water Seabird and TriOS radiometers along an atlantic meridional transect. Remote Sens. 12, 1669. doi:10.3390/rs12101669
Ångström, A. (1964). The parameters of atmospheric turbidity. Tellus 26, 64–75. doi:10.1111/j.2153-3490.1964.tb00144.x
Białek, A., Vellucci, V., Gentili, B., Antoine, D., Gorroño, J., Fox, N., et al. (2020). Monte Carlo-based quantification of uncertainties in determining ocean remote sensing reflectance from underwater fixed-depth radiometry measurements. J. Atmos. Ocean. Tech. 37, 177–196. doi:10.1175/JTECH–D–19–0049.1
Brando, V., and Vilas, L. G. (2023). Initial sample of HYPERNETS hyperspectral water reflectance measurements for satellite validation from the VEIT site (Italy). Zenodo. doi:10.5281/zenodo.8057531
Brown, S., Flora, S., Feinholz, M., Yarbrough, M., Houlihan, T., Peters, D., et al. (2007). “The Marine Optical BuoY (MOBY) radiometric calibration and uncertainty budget for ocean color satellite vicarious calibration,” in Proc. SPIE 6744, Sensors, Systems, and Next-Generation Satellites XI (Florence, Italy: SPIE Remote Sensing 2007), 67441M.
Cazzaniga, I., and Zibordi, G. (2023). AERONET-OC LWN uncertainties: revisited. J. Atmos. Ocean. Tech. 40, 411–425. doi:10.1175/jtech-d-22-0061.1
Cazzaniga, I., Zibordi, G., and Mélin, F. (2021). Spectral variations of the remote sensing reflectance during coccolithophore blooms in the western Black Sea. Remote Sens. Environ. 264, 112607. doi:10.1016/j.rse.2021.112607
Cazzaniga, I., Zibordi, G., and Mélin, F. (2023). Spectral features of ocean colour radiometric products in the presence of cyanobacteria blooms in the Baltic Sea. Remote Sens. Environ. 287, 113464. doi:10.1016/j.rse.2023.113464
Clerici, M., and Mélin, F. (2008). Aerosol direct radiative effect in the Po Valley region derived from AERONET measurements. Atmos. Chem. Phys. 8, 4925–4946. doi:10.5194/acp-8-4925-2008
D’Alimonte, D., Kajiyama, T., Zibordi, G., and Bulgarelli, B. (2021). Sea-surface reflectance factor: replicability of computed values. Opt. Exp. 29, 25217–25241. doi:10.1364/oe.424768
D’Alimonte, D., and Zibordi, G. (2006). Statistical assessment of radiometric measurements from autonomous systems. IEEE Trans. Geosci. Remote Sens. 44, 719–728. doi:10.1109/tgrs.2005.862505
Deschamps, P.-Y., Herman, M., and Tanré, D. (1983). Modeling of the atmospheric effects and its application to the remote sensing of ocean color. Appl. Opt. 22, 3751–3758. doi:10.1364/ao.22.003751
Donlon, C., Berruti, B., Buongiorno, A., Ferreira, M.-H., Féménias, P., Frerick, J., et al. (2012). The global monitoring for environment and security (GMES) Sentinel-3 mission. Remote Sens. Environ. 120, 37–57. doi:10.1016/j.rse.2011.07.024
Donlon, C., Wimmer, W., Robinson, I., Fisher, G., Ferlet, M., Nightingale, T., et al. (2014). A second-generation blackbody system for the calibration and verification of seagoing infrared radiometers. J. Atmos. Oceano. Tech. 31, 1104–1127. doi:10.1175/jtech-d-13-00151.1
Eck, T., Holben, B., Reid, J., Dubovik, O., Smirnov, A., O’Neill, N., et al. (1999). The wavelength dependence of the optical depth of biomass burning, urban and desert dust aerosols. J. Geophys. Res. 104, 31333–31350. doi:10.1029/1999JD900923
Fahy, J., Fox, N., Gardiner, T., Green, P., Hunt, S., Mittaz, J., et al. (2022). General guidance on a metrological approach to fundamental data records (FDR), thematic data products (TDPS) and fiducial reference measurements (FRMs) - Metrology theoretical basis. (QA4EO).
GCOS (2010). Guideline for the geenration of datasets and products meeting GCOS requirements. GCOS-143).
GCOS (2011). Systematic observation requirements for satellite-based products for climate. (GCOS-154, Supplemental details to the satellite-based component of the “Implementation plan for the Global Observing System for Climate in Support of the UNFCC”).
Gergely, M., and Zibordi, G. (2014). Assessment of AERONET-OC LWN uncertainties. Metrologia 51, 40–47. doi:10.1088/0026-1394/51/1/40
Ghent, D., Veal, K., Trent, T., Dodd, E., Sembhi, H., and Remedios, J. (2019). A new approach to defining uncertainties for MODIS land surface temperature. Remote Sens. 11, 1021. doi:10.3390/rs11091021
Giles, D., Sinyuk, A., Sorokin, M., Schafer, J., Smirnov, A., Slutsker, I., et al. (2019). Advancements in the Aerosol Robotic Network (AERONET) Version 3 database - automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos. Meas. Tech. 12, 169–209. doi:10.5194/amt-12-169-2019
Gleason, A., Voss, K., Gordon, H., Twardowski, M., Sullivan, J., Trees, C., et al. (2012). Detailed validation of the bidirectional effect in various Case I and Case II waters. Opt. Exp. 20, 7630–7645. doi:10.1364/oe.20.007630
Goyens, C., Vis, P. D., and Hunt, S. (2021). “Automated generation of hyperspectral fiducial reference measurements of water and land surface reflectance for the HYPERNETS networks,” in Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, July 11-16, 2021 (Brussels, Belgium: IGARSS). 4pp. doi:10.1109/IGARSS47720.2021.9553738
GUM (2008). Evaluation of measurement data – guide to the expression of uncertainty in measurements, JCGM 100 (Joint Committee for Guides in Metrology, Bureau International des Poids et Mesures).
Holben, B., Eck, T., Slutsker, I., Tanré, D., Buis, J., Setzer, A., et al. (1998). AERONET - a federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 66, 1–16. doi:10.1016/s0034-4257(98)00031-5
Hollmann, R., Merchant, C., Saunders, R., Downy, C., Buchwitz, M., Cazenave, A., et al. (2013). The ESA climate change initiative: satellite data records for essential climate variables. Bull. Am. Meteorol. Soc. 94, 1541–1552. doi:10.1175/bams-d-11-00254.1
Hooker, S., Lazin, G., Zibordi, G., and McLean, S. (2002). An evaluation of above- and in-water methods for determining water-leaving radiances. J. Atmos. Ocean. Tech. 19, 486–515. doi:10.1175/1520-0426(2002)019<0486:aeoaai>2.0.co;2
Hooker, S., and Maritorena, S. (2000). An evaluation of oceanographic radiometers and deployment methodologies. J. Atmos. Ocean. Tech. 17, 811–830. doi:10.1175/1520-0426(2000)017<0811:aeoora>2.0.co;2
Hooker, S., and Morel, A. (2003). Platform and environmental effects on above-water determinations of water-leaving radiances. J. Atmos. Ocean. Tech. 20, 187–205. doi:10.1175/1520-0426(2003)020<0187:paeeoa>2.0.co;2
Immler, F., Dykema, J., Gardiner, T., Whiteman, D., Thorne, P., and Vömel, H. (2010). Reference quality upper-air measurements: guidance for developing GRUAN data products. Atmos. Meas. Tech. 3, 1217–1231. doi:10.5194/amt-3-1217-2010
IOCCG (2008)., No. 7. Dartmouth, Canada: IOCCG. of Reports of the International Ocean Colour Coordinating Group.Why Ocean colour? The societal benefits of ocean-colour technology
IOCCG (2019). Uncertainties in ocean Colour remote sensing, No. 18. Dartmouth, Canada: IOCCG. of Reports of the International Ocean Colour Coordinating Group.
Johnson, B., Zibordi, G., Brown, S., Feinholz, M., Sorokin, M., Slutsker, I., et al. (2021). Characterization and absolute calibration of an AERONET-OC radiometer. Appl. Opt. 60, 3380–3392. doi:10.1364/ao.419766
Kacker, R., Kessel, R., and Sommer, K.-D. (2010). Assessing differences between results determined according to the guide to the expression of uncertainty in measurement. J. Res. Natl. Inst. Stand. Technol. 115, 453–459. doi:10.6028/jres.115.031
Ku, H. (1966). Notes on the use of propagation of error formulas. J. Res. Natl. Bureau Stand. 70C, 263–273. doi:10.6028/jres.070c.025
Lee, Z.-P., Du, K., Voss, K., Zibordi, G., Lubac, B., Arnone, R., et al. (2011). An inherent-optical-property-centered approach to correct the angular effects in water-leaving radiance. Appl. Opt. 50, 3155–3167. doi:10.1364/AO.50.003155
Lin, J., Dall’Olmo, G., Tilstone, G., Brewin, R., Vabson, V., Ansko, I., et al. (2022). Derivation of uncertainty budgets for continuous above-water radiometric measurements along an Atlantic Meridional Transect. Opt. Exp. 30, 45648–45675. doi:10.1364/oe.470994
McCarthy, S., Crawford, S., Wood, C., Lewis, M., Jolliff, J., Martinolich, P., et al. (2023). Automated atmospheric correction of nanosatellites using coincident ocean color radiometer data. J. Mar. Sci. Eng. 11, 660. doi:10.3390/jmse11030660
Mélin, F. (2010). Global distribution of the random uncertainty associated with satellite derived Chla. IEEE Geosci. Remote Sens. Lett. 7, 220–224. doi:10.1109/lgrs.2009.2031825
Mélin, F. (2021). From validation statistics to uncertainty estimates: application to VIIRS ocean color radiometric products at European coastal locations. Front. Mar. Sci. 8, 1790948. doi:10.3389/fmars.2021.790948
Mélin, F. (2022). Validation of ocean color remote sensing reflectance data: analysis of results at European coastal sites. Remote Sens. Environ. 280, 113153. doi:10.1016/j.rse.2022.113153
Mélin, F., Clerici, M., Zibordi, G., and Bulgarelli, B. (2006). Aerosol variability in the Adriatic Sea from automated optical field measurements and sea-viewing Wide field-of-view sensor (SeaWiFS). J. Geophys. Res. 111, D22201. 2006JD007226. doi:10.1029/2006jd007226
Mélin, F., and Franz, B. (2014). “Assessment of satellite ocean colour radiometry and derived geophysical products,” in Optical radiometry for oceans climate measurements. Experimental methods in the physical sciences. Editors G. Zibordi, C. Donlon, and A. Parr (San Diego: Academic Press), 47, 609–638.
Mélin, F., and Sclep, G. (2015). Band-shifting for ocean color multi-spectral reflectance data. Opt. Exp. 23, 2262–2279. doi:10.1364/oe.23.002262
Mélin, F., Sclep, G., Jackson, T., and Sathyendranath, S. (2016). Uncertainty estimates of remote sensing reflectance derived from comparison of ocean color satellite data sets. Remote Sens. Environ. 177, 107–124. doi:10.1016/j.rse.2016.02.014
Mélin, F., and Zibordi, G. (2005). Aerosol variability in the Po Valley analyzed from automated optical measurements. Geophys. Res. Lett. 32, L03810. doi:10.1029/2004gl021787
Mélin, F., and Zibordi, G. (2007). Optically based technique for producing merged spectra of water-leaving radiances from ocean color remote sensing. Appl. Opt. 46, 3856–3869. doi:10.1364/ao.46.003856
Mélin, F., and Zibordi, G. (2010). Vicarious calibration of satellite ocean color sensors at two coastal sites. Appl. Opt. 49, 798–810. doi:10.1364/ao.49.000798
Mélin, F., Zibordi, G., and Berthon, J.-F. (2012). Uncertainties in remote sensing reflectance from MODIS-Terra. IEEE Geosci. Remote Sens. Lett. 9, 432–436. doi:10.1109/lgrs.2011.2170659
Mélin, F., Zibordi, G., Berthon, J.-F., Bailey, S., Franz, B., Voss, K., et al. (2011). Assessment of MERIS reflectance data as processed with SeaDAS over the European seas. Opt. Exp. 19, 25657–25671. doi:10.1364/oe.19.025657
Mélin, F., Zibordi, G., and Djavidnia, D. (2009). Merged series of normalized water leaving radiances obtained from multiple satellite missions for the Mediterranean Sea. Adv. Space Res. 43, 423–437. doi:10.1016/j.asr.2008.04.004
Mélin, F., Zibordi, G., and Djavidnia, S. (2007). Development and validation of a technique for merging satellite derived aerosol optical depth from SeaWiFS and MODIS. Remote Sens. Env. 108, 436–450. doi:10.1016/j.rse.2006.11.026
Mélin, F., Zibordi, G., and Holben, B. (2013). Assessment of the aerosol products from the SeaWiFS and MODIS ocean color missions. IEEE Geosci. Remote Sens. Lett. 10, 1185–1189. doi:10.1109/lgrs.2012.2235408
Mittaz, J., Merchant, C., and Woolliams, E. (2019). Applying principles of metrology to historical Earth observations from satellites. Metrologia 56, 032002. doi:10.1088/1681–7575/ab1705
Mobley, C. (1999). Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 38, 7442–7455. doi:10.1364/ao.38.007442
Mobley, C. (2015). Polarized reflectance and transmittance properties of windblown sea surfaces. Appl. Opt. 54, 4828–4849. doi:10.1364/ao.54.004828
Morel, A., Antoine, D., and Gentili, B. (2002). Bidirectional reflectance of oceanic waters: accounting for Raman emission and varying particle scattering phase function. Appl. Opt. 41, 6289–6306. doi:10.1364/ao.41.006289
O’Neill, N., Eck, T., Holben, B., Smirnov, A., Dubovik, O., and Royer, A. (2001). Bimodal size distribution influences on the variation of Ångström derivatives in spectral and optical depth space. J. Geophys. Res. 106, 9787–9806. doi:10.1029/2000jd900245
Pahlevan, N., Mangin, A., Balasubramanian, S., Smith, B., Alikas, K., Arai, K., et al. (2021). ACIX-Aqua: a global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers and coastal waters. Remote Sens. Environ. 258, 112366. doi:10.1016/j.rse.2021.112366
Ruddick, K., Voss, K., Boss, E., Castagna, A., Frouin, R., Gilerson, A., et al. (2019). A review of protocols for fiducial reference measurements of water-leaving radiance for validation of satellite remote-sensing data over water. Remote Sen. 11, 2190. doi:10.3390/rs11192198
Salem, S., Higa, H., Ishizaka, J., Pahlevan, N., and Oki, K. (2023). Spectral band-shifting of multispectral remote-sensing reflectance products: insights for amtchup and cross-mission consistency assessments. Remote Sens. Environ. 299, 113486. doi:10.1016/j.rse.2023.113846
Schmid, B., Michalsky, J., Halthore, R., Beauharnois, M., Harrison, L., Livingston, J., et al. (1999). Comparison of aerosol optical depth from four solar radiometers during the Fall 1997 ARM intensive observation period. Geophys. Res. Lett. 26, 2725–2728. doi:10.1029/1999gl900513
Smirnov, A., Holben, B., Eck, T., Dubovik, O., and Slutsker, I. (2000). Cloud screening and quality control algorithms for the AERONET database. Remote Sens. Environ. 73, 337–349. doi:10.1016/s0034-4257(00)00109-7
Stoffelen, A. (1998). Toward the true near-surface wind speed: error modeling and calibration using triple collocation. J. Geophys. Res. 103, 7755–7766. doi:10.1029/97jc03180
Talone, M., Zibordi, G., and Lee, Z.-P. (2018). Correction for the non-nadir viewing geometry of AERONET-OC above water radiometry data: an estimate of uncertainties. Opt. Exp. 26, A541–A561. doi:10.1364/oe.26.00a541
Thuillier, G., Hersé, M., Labs, D., Foujols, T., Peetermans, W., Gillotay, D., et al. (2003). The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 214, 1–22. doi:10.1023/A:1024048429145
Thuillier, G., Hersé, M., Simon, P., Labs, D., Mandel, H., Gillotay, D., et al. (1998). The visible solar spectral irradiance from 350 to 850 nm as measured by the SOLSPEC spectrometer during the ATLAS I mission. Sol. Phys. 177, 41–61. doi:10.1023/a:1004953215589
Tilstone, G., Dall’Olmo, G., Hieronymi, M., Ruddick, K., Beck, M., Ligi, M., et al. (2020). Field intercomparison of radiometer measurements for ocean colour validation. Remote Sens. 12, 1587. doi:10.3390/rs12101587
Toohey, M., and Strong, K. (2007). Estimating biases and error variances through the comparison of coincident satellite measurements. J. Geophys. Res. 112, D13306. doi:10.1029/2006JD008192
Vabson, V., Kuusk, J., Ansko, I., Vendt, R., Alikas, K., Ruddick, K., et al. (2019). Field intercomparison of radiometers used for satellite validation in the 400-900 nm range. Remote Sens. 11, 1129. doi:10.3390/rs11091129
Vansteenwegen, D., Ruddick, K., Cattrijsse, A., Vanhellemont, Q., and Beck, M. (2019). The pan-and-tilt hyperspectral radiometer system (PANTHYR) for autonomous satellite validation measurements—prototype design and testing. Remote Sens. 11, 1360. doi:10.3390/rs11111360
Zibordi, G., Berthon, J.-F., Mélin, F., D’Alimonte, D., and Kaitala, S. (2009a). Validation of satellite ocean color primary products at optically complex coastal sites: northern Adriatic Sea, Northern Baltic Proper and Gulf of Finland. Remote Sens. Environ. 113, 2574–2591. doi:10.1016/j.rse.2009.07.013
Zibordi, G., D’Alimonte, D., and Kajiyama, T. (2022a). Automated quality control of AERONET-OC LWN data. J. Atmos. Ocean. Technol. 39, 1961–1972. doi:10.1175/jtech–d–22–0029.1
Zibordi, G., Holben, B., Slutsker, I., Giles, D., D’Alimonte, D., Mélin, F., et al. (2009b). AERONET-OC: a network for the validation of ocean color primary products. J. Atmos. Ocean. Tech. 26, 1634–1651. doi:10.1175/2009JTECHO654.1
Zibordi, G., Holben, B., Talone, M., D’Alimonte, D., Slutsker, I., Giles, D., et al. (2021). Advances in the Ocean Color component of the Aerosol Robotic Network (AERONET-OC). J. Atmos. Ocean. Technol. 38, 725–746. doi:10.1175/jtech–d–20–0085.1
Zibordi, G., Kwiatkowska, E., Mélin, F., Talone, M., Cazzaniga, I., Dessailly, D., et al. (2022b). Assessment of OLCI-A and OLCI-B radiometric data products across European seas. Remote Sens. Environ. 272, 112911. doi:10.1016/j.rse.2022.112911
Keywords: ocean color, optical radiometry, uncertainty, metrology, AERONET-OC
Citation: Mélin F, Cazzaniga I and Sciuto P (2024) Verification of uncertainty estimates of autonomous field measurements of marine reflectance using simultaneous observations. Front. Remote Sens. 4:1295855. doi: 10.3389/frsen.2023.1295855
Received: 17 September 2023; Accepted: 11 December 2023;
Published: 08 January 2024.
Edited by:
Kevin Ruddick, Royal Belgian Institute of Natural Sciences, BelgiumReviewed by:
Peng-Wang Zhai, University of Maryland, Baltimore County, United StatesCopyright © 2024 Mélin, Cazzaniga and Sciuto. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frédéric Mélin, ZnJlZGVyaWMubWVsaW5AZWMuZXVyb3BhLmV1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.