qCLUE: a quantum clustering algorithm for multi-dimensional datasets

Clustering algorithms are at the basis of several technological applications, and are fueling the development of rapidly evolving fields such as machine learning. In the recent past, however, it has become apparent that they face challenges stemming from datasets that span more spatial dimensions. In fact, the best-performing clustering algorithms scale linearly in the number of points, but quadratically with respect to the local density of points. In this work, we introduce qCLUE, a quantum clustering algorithm that scales linearly in both the number of points and their density. qCLUE is inspired by CLUE, an algorithm developed to address the challenging time and memory budgets of Event Reconstruction (ER) in future High-Energy Physics experiments. As such, qCLUE marries decades of development with the quadratic speedup provided by quantum computers. We numerically test qCLUE in several scenarios, demonstrating its effectiveness and proving it to be a promising route to handle complex data analysis tasks – especially in high-dimensional datasets with high densities of points.

1 Introduction

Clustering is a data analysis technique that is crucial in several fields, owing to its ability to uncover hidden patterns and structures within large datasets (Gopalakrishnan et al., 2024). It is essential for simplifying complex data, improving data organization, and enhancing decision-making processes (Oyelade et al., 2019; Gu and Hübschmann, 2022; Caruso et al., 2018; Wu et al., 2021). For instance, clustering has been applied in marketing (Huang et al., 2007; Punj and Stewart, 1983), where it helps segment customers for targeted advertising (Wu et al., 2009), and in biology, for classifying genes and identifying protein interactions (Dutta et al., 2020; Au et al., 2005; Wang et al., 2010; Asur et al., 2007). In the realm of computer science and artificial intelligence, it is invaluable for speech recognition (Kishore Kumar et al., 2018; Chang et al., 2017), image segmentation (Coleman and Andrews, 1979), as well as for recommendation systems (Shepitsen et al., 2008; Schickel-Zuber and Faltings, 2007) used for personalizing user content. Finally, clustering techniques are pivotal for Event Reconstruction (ER), where data points that originated from the same “event” are to be grouped together. In High-Energy Physics, for instance, clustering algorithms are used to reconstruct the trajectories of subatomic particles in collider experiments. High volumes of data are expected at the endcap High Granularity CALorimeter (HGCAL) (Didier and Austin, 2017) which is currently being built for the CMS detector at the High Luminosity Large Hadron Collider (HL-LHC). This must be tackled by new generations of clustering algorithms such as CLUE (Rovere et al., 2020). The discovery of the Higgs boson (Aad et al., 2012), awarded the Nobel prize in 2012, was made possible by such algorithms.

ER enables the interpretation of data obtained from particle collision events, including those occurring at the Large Hadron Collider (LHC) at CERN. Several clustering algorithms like DBScan, K-Means, and Hierarchical Clustering among others (Amaro et al., 2023; Dalitz et al., 2019; Rodenko et al., 2019) can be employed for ER. Our work is based on CERN’s CLUstering of Energy (CLUE) algorithm (Rovere et al., 2020; CMS Collaboration, 2022), which is adopted by the CMS collaboration (Hayrapetyan et al., 2023; Hayrapetyan et al., 2024; Tumasyan et al., 2023). It is designed for the future HGCAL detector due to the limitations of the currently employed algorithms. Despite these limitations, such algorithms are already at the basis of several discoveries, such as the doubly charged tetraquark (Aaij et al., 2023), the study of rare B meson decays to two muons (Tumasyan et al., 2023) and the observation of four-top quark production in proton-proton collisions (Hayrapetyan et al., 2023).

The efficiency of clustering algorithms, as illustrated by the CLUE algorithm (Rovere et al., 2020), is crucial for handling large datasets. Initially designed for two-dimensional datasets, CLUE reduces the search complexity from $O(n^2)$ to $O(mn)$ through the use of local density and a tiling procedure, where $n$ $(m)$ represents the (average) number of points (per tile).

In the context of CLUE, where the datasets in question are limited to two dimensions, $m$ is small, making this approach to ER particularly effective. However, as the dimensionality of the dataset is incremented, the value of $m$ generally increases exponentially. This is highlighted by Figure 1A, where for a $\mathbb{d}$-dimensional lattice with $a$ points per edge, $m$ follows the relation $m=a^{\mathbb{d}}$. This is a serious challenge to CLUE and classical clustering algorithms in general.

Figure 1

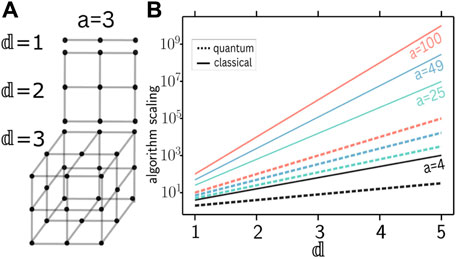
Figure 1. Scaling of point density and complexities of classical and quantum algorithms for the unstructured search problem with dimension$\mathbb{d}$. In (A), different $\mathbb{d}$-dimensional lattices for$\mathbb{d}=\mathrm{1,2,3}$ and $a=3$ points per edge. In (B), best-known classical (solid lines) and quantum (dashed lines) algorithmic scaling for the Unstructured Search Problem (Lov, 1996) applied to square $\mathbb{d}$-dimensional lattices with the values of $a$ reported in the plot. Classically, the cost $O(m)$ reflects the need to iterate through all the $m$ points to find the desired one. Grover achieves the same in $O(\sqrt{m})$ steps, providing a quadratic advantage. This advantage increases with the density of points in the considered dataset, which grows exponentially with respect to the dimension $\mathbb{d}$ according to $m=a^{\mathbb{d}}$.

A first step towards extending CLUE to more dimensions is 3D-CLUE (Rovere et al., 2020; Brondolin, 2022). In this work, data points from different detector layers are first projected onto a single$\mathbb{d}=2$ surface, where clustering is then performed. However, this projection from the original $\mathbb{d}=3$ dataset to a$\mathbb{d}=2$ surface comes at the cost of a slower algorithm since $m$ becomes effectively larger. The solid lines in Figure 1B show the increase in average points per tile in $\mathbb{d}$-dimensional datasets made of the lattices in panel (a). While the improved performance of 3D-CLUE in ER tasks (Rovere et al., 2020; Brondolin, 2022) justifies the increased computational overhead, extending this enhancement to higher dimensions and larger datasets is challenging. Finding practical approaches to deal with datasets where $\mathbb{d}$ is large is therefore extremely important, not only for ER tasks, but also in other fields such as gene analysis in bioinformatics (Karim et al., 2020) and market segmentation in business (Zhou et al., 2020).

Quantum computers provide a route to mitigate the complexity blow-up arising from higher-dimensional datasets. Wei et al. (2020) addresses the task of jet clustering in High-Energy Physics, while Kerenidis and Landman (2021) targets spectral clustering, which itself uses the efficient quantum analogue of $k$-means clustering (Kerenidis et al., 2019). Gong et al. (2024a); Zhou et al. (2021) provide $k$-Nearest-Neighbors based approaches for image classification, a common machine learning task. Other approaches include quantum $k$-medians clustering (Aïmeur et al., 2007) and a quantum algorithm for density peak clustering (Duarte et al., 2023). Gong et al. (2022); Gong et al. (2024b); Gong C. et al. (2024) also present interesting quantum solutions to a wide number of common machine learning tasks.

In this work we develop qCLUE, a CLUE-inspired quantum algorithm. Similarly to other quantum algorithms (Nicotra et al., 2023; Tüysüz et al., 2020), qCLUE leverages the advantage provided by Grover Search (Lov, 1996). A comparison of classical and quantum (Grover) runtimes is presented in Figure 1B, where the solid [dashed] lines refer to the classical $O(m)$ [quantum $O(\sqrt{m})$] scaling. As can be seen, the complexity advantage that Grover search provides can be substantial, particularly for large values of $\mathbb{d}$ or $a$.

Overall, we find that qCLUE performs well in a wide range of scenarios. With ER-inspired datasets as a specific example, we demonstrate that clusters are correctly reconstructed in typical experimental settings. Similar to other quantum approaches to clustering that rely on Grover Search (Aïmeur et al., 2007; Pires et al., 2021; Magano et al., 2022), qCLUE showcases a quadratic speedup compared to classical algorithms. Magano et al. (2022) is especially interesting as it provides a detailed computational complexity analysis to a related problem within ER. Specifically, this approach tackles a subsequent task compared to qCLUE, namely the creation of so-called tracksters from hits (CMS Collaboration, 2022). It also demonstrates that the quantum algorithm has a quadratic advantage if compared to the classical one in physically relevant scenarios. We mention here the significance of variational solutions (Zlokapa et al., 2021; Tüysüz et al., 2021) to the ER reconstruction problem but note that these do not have predictable runtimes or error bound guarantees.

The specific advantages of qCLUE are its CLUE-inspired approach to cluster reconstruction (which demonstrated to be extremely successful (CMS Collaboration, 2022; Hayrapetyan et al., 2023; Tumasyan et al., 2023; CMS Collaboration, 2024)), and its consequent seamless integration with the classical framework currently employed by the CMS collaboration (Rovere et al., 2020; Brondolin, 2022; CMS Collaboration, 2023).

This paper is structured as follows. In Section 2, we describe our algorithm qCLUE. Specifically, we provide a general overview of its subroutines – namely the Compute Local Density, Find Nearest Higher, and the Find Seeds, Outliers and Assign Clusters steps. We describe the results of our simulated version of qCLUE on a classical computer in Section 3. In more detail, we explain the scoring metrics we use to quantify our results, and describe qCLUE performance when the dataset is subject to noise and different clusters overlap. Conclusions and outlook are finally presented in Section 4.

2 qCLUE

qCLUE is a quantum adaptation of CERN’s CLUE and 3D-CLUE algorithms (Rovere et al., 2020; Brondolin, 2022), that is specifically developed for ER, yet it is suitable to work with any (high dimensional) dataset. The main advantage of qCLUE stems from employing Grover’s algorithm, which provides a quadratic speedup for the Unstructured Search Problem (Lov, 1996). While qCLUE is designed to work in arbitrary dimensions, for clarity we restrict ourselves to $\mathbb{d}=2$. This simplifies the following discussions and allows us to simulate qCLUE with meaningful datasets on a classical computer. Generalizations to higher dimensions can be done following the steps outlined below. Furthermore, to provide a better connection with CLUE and 3D-CLUE, we employ a similar notation.

In Section 2.1, we offer an overview of the algorithm and its different subroutines. Section 2.2 is dedicated to the first subroutine of qCLUE, namely, calculating the Local Density. We then explain how to determine the Nearest Highers $({\mathcal{N}}_j)$, Seeds, and Outliers in Section 2.3. Finally, Section 2.4 delves into the conclusive Cluster Assignment subroutine, where the points in the dataset are effectively heirarchically clustered.

2.1 Overview and setting

As for CLUE and 3D-CLUE (Rovere et al., 2020; Brondolin, 2022), we consider a dataset with spatial coordinates and an weight for every point. Similar datasets can also be found in medical image analysis and segmentation (Qaqish et al., 2017; Ng et al., 2006), in the analysis of asteroid reflectance spectra and hyperspectral astronomical imagery in astrophysics (Galluccio et al., 2008; Gaffey, 2010; Gao et al., 2021) and in gene analysis in bioinformatics (Karim et al., 2020; Oyelade et al., 2016).

In $\mathbb{d}=2$ dimensions, the spatial coordinates $X_j$ for point $j$ are $X_j=\left[x_{j,1},x_{j,2}\right]$, that are promptly generalized for larger values of$\mathbb{d}$. Both CLUE and qCLUE first perform tiling over the dataset to reduce the search and therefore enhance the efficiency of the algorithm. Tiling is the process of partitioning the dataset into a grid of rectangular tiles ${\square }_k$, where $k$ is the tile index (see Figure 2). Therefore, our input dataset comprises of point and tile indices $j$ and $k$, respectively, the coordinates $X_j$, and a parameter $E_j$ associated to each point. Following CLUE’s notation, we call $E_j$ the weight, yet this should be considered as a label that can be employed to improve the clustering quality for any given dataset. The tiling procedure of qCLUE and CLUE enables searching only over Search Spaces $\mathcal{S}$ marked by the tiles in green in Figure 2A as opposed to the full dataset. In case of CLUE, this allowed for an improvement in scaling from $O(n^2)$ to $O(mn)$. The scaling of qCLUE is investigated below.

Figure 2

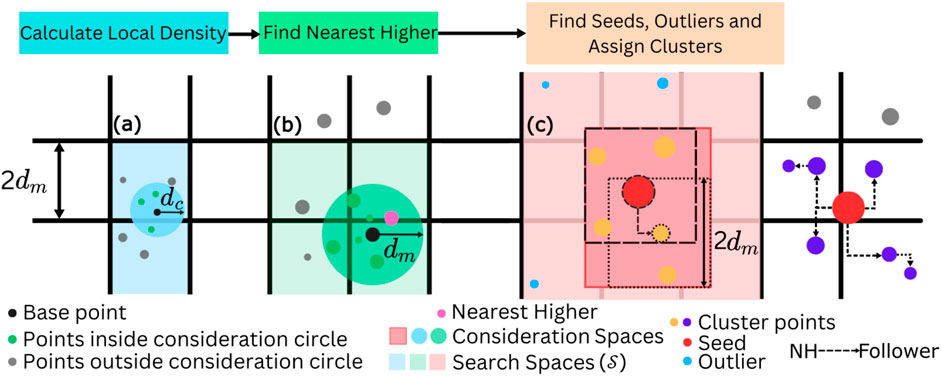
Figure 2. Pictorial representation of the main subroutines of qCLUE. In (A), the Local Density computation subroutine is represented. The consideration circle of radius $d_{\text{c}}$ (light blue) centered at the base point $j$ (black) contains all points (green) that satisfy $d_{i,j}\le d_{\text{c}}$. This consideration circle intersects 2 tiles ${\square }_k$ (indexed by tile index $k$), highlighted in blue, that form the search space $\mathcal{S}$. As per Equation 2, the Local Density computation step determines the set of green points from all points in the search space (green and grey) and then computes the local density. In (B), we pictorially present the Find Nearest Higher $({\mathcal{N}}_j)$ subroutine. The consideration circle (green) around base point $j$ (black) has radius $d_{\text{m}}$. This consideration circle, containing the green points as well as the Nearest Higher ${\mathcal{N}}_j$ (pink), intersects the 4 tiles highlighted in green, which form the search space $\mathcal{S}$. In (C), we describe the Find Seeds, Outliers and Assign Clusters subroutines. The seeds (red) and outliers (blue) are determined via Grover search on the dataset. In this specific example there are two clusters in the dataset whose non-seed points are in orange and purple, respectively. Followers (see main text) in these clusters are connected by dashed arrows. The Cluster Assignment subroutine is shown to be working on the orange cluster where the cluster $\mathcal{C}$ currently consists of the seed (red, dashed border) and the first of its followers (orange, dotted border). Followers are being found within the Dynamic Search Space (DSS, light red box with solid red border). The DSS is formed as the set of tiles ${\square }_k$ covered partially or fully by the minimum bounding box of the square windows that contains all the search spaces $\mathcal{S}$ of the points within $\mathcal{C}$.

In this work, we employ a qRAM to store and access data, which is an essential building block for quantum computers. Following Giovannetti et al. (2008), we therefore assume that we can efficiently prepare the state.

${\displaystyle \sum _j}\left|j\right.⟩\stackrel{\mathrm{q}\mathrm{R}\mathrm{A}\mathrm{M}}{\to }\left|j\right.⟩\left|D_j\right.⟩,(1)$

where $D_j$ is the data associated with a given index $j$, e.g., the $j^{\text{th}}$ point in the database. As explained in Giovannetti et al. (2008), the cost of preparing the dataset for qRAM is $O(n)$, which has to be done once. Subsequent accesses cost $O(\log n)$. This makes this step more efficient than the other subroutines within qCLUE. For convenience, here, in Equation 1, and throughout this paper we do not explicitly write the normalization factors of quantum states.

The qCLUE algorithm consists of the following steps:

2.1.1 Local density

The first step is to calculate the local density ${\rho }_j$ of all points $j$ [e.g., black point in Figure 2A] that is defined by

${\rho }_j=E_j+\frac{1}{2}{\displaystyle \sum _{d_{i,j}<d_{\text{c}}}}{E}_i(2)$

and it is indicative of the weight in a neighborhood of point $j$. As can be seen from Equation 2; Figure 2A, ${\rho }_j$ is a weighted sum over the weights $E_i$ of all points $i$ whose distance $d_{i,j}=\sqrt{{\sum }_{\alpha =1}^{\mathbb{d}}{(x_{i,\alpha }-x_{j,\alpha })}^2}$ from the base point $j$ is within a user-specified critical radius $d_{\text{c}}$ that characterizes the consideration circle for the Local Density computation subroutine (light blue circle in the figure). As such, $E_i$ is the weight of the $i^{\text{th}}$ point which is $d_{i,j}$ away from point $j$. The choice of weight factor $1/2$ for $E_j$ in the definition of ${\rho }_j$ in Equation 2 is empirically found to yield better performances for CLUE (Rovere et al., 2020).

2.1.2 Find nearest higher

After calculating the local densities, we determine the nearest highers. The Nearest Higher ${\mathcal{N}}_j$ of a point $j$ is the point nearest to $j$ with a higher local density ${\rho }_{{\mathcal{N}}_j}>{\rho }_j$. As better explained in Section 2.4, the Nearest Higher are used to heirarchically cluster points together in the Cluster Assignment process at the end of qCLUE. In Figure 2B, the Nearest Higher ${\mathcal{N}}_j$ of the base point $j$ (black point) is the pink point.

2.1.3 Find seeds, outliers and assign clusters

As schematically represented in Figure 2C, seeds (red points) are the points whose distance $d_{j,{\mathcal{N}}_j}$ from their Nearest Higher ${\mathcal{N}}_j$ and whose local density ${\rho }_j$ are lower bounded by user defined thresholds. Outliers (blue points) are the points whose distance from Nearest Higher is similarly lower bounded but whose Local Density has an upper threshold. As such a point $j$ is

$\text{a}seed\text{if}{d}_{{\mathcal{N}}_j,j}>d_{\text{c}}\text{\hspace{0.17em}and\hspace{0.17em}}{\rho }_j>\tilde{\rho },(\mathrm{3a})$

$\text{an}outlier\text{if\hspace{0.17em}}{d}_{{\mathcal{N}}_j,j}>\delta d_{\text{c}}\text{\hspace{0.17em}and\hspace{0.17em}}{\rho }_j<\tilde{\rho }.(\mathrm{3b})$

Here, $\delta$ is the Outlier Delta Factor that determines the upper bound on the allowed local density for outliers. Furthermore, $\tilde{\rho }$ is the critical density threshold – the lowest local density a point can have to be classified as a seed. Both $\delta$ and $\tilde{\rho }$ are user-specified and can be varied to enhance the quality of the output. Seeds are generally located in areas of high weight density, and will be employed as starting points to build clusters. Outliers are points that are likely to be noise in the dataset and are therefore discarded.

Once seeds and outliers are determined, the clusters are constructed. From the seeds, we iteratively combine “followers.” If point ${\mathcal{N}}_j$ is the Nearest Higher of point $j$, then point $j$ is termed as ${\mathcal{N}}_j$’s follower. The follower of a point is most likely generated by the same process as the point itself (in the context of ER, by the same particle), and as such shall be included in the same cluster. In Figure 2C, the orange and purple points form two different clusters, and the followers of the points in the purple one are indicated by arrows.

2.2 Local density computation

In this section, we describe the subroutine (schematically represented in Figure 3) that computes the Local Density ${\rho }_j$ of the point $j$, as defined in Equation 2. To perform the computation, all points $i$ whose distance $d_{i,j}$ from point $j$ is smaller than the threshold $d_{\text{c}}$ need to be determined from the search space $\mathcal{S}$. This search space is the smallest set of tiles ${\square }_k$ required to cover the $d_{i,j}<d_{\text{c}}$ consideration circle. In Figure 2A, $\mathcal{S}$ is highlighted in light blue.

Figure 3

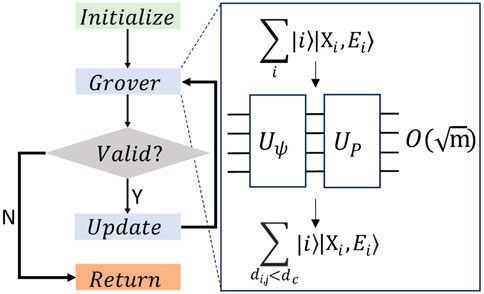
Figure 3. Algorithm flow for Local Density computation and for Assigning Clusters. The quantum state is initialized in the green “Initialize” box. For Local Density Computation (Cluster Assignment), it comprises all points in the DSS $\mathcal{S}$ (in the DSS). The “Grover” (light blue) block performs $U_{\psi }$ and $U_P$ in succession $O(\sqrt{m})$ times, and returns all points satisfying the required condition. The inset considers the case of Local Density computation where the condition is $d_{i,j}<d_{\text{c}}$. For the cluster assignment step, we check if points in the DSS are followers of the points in the cluster $\mathcal{C}$ (see Section 2.4). The output of the Grover subroutine is then measured to yield an index that is checked for validity in the grey “Valid?” diamond. If the point satisfies the chosen condition, the $Y$ branch is executed. Within the “Update” (light blue) step this point is then removed from either $\mathcal{S}$ or the DSS and stored to be returned in the “Return” orange box. Once all points are found, the “Valid?” condition triggers the $N$ branch to terminate the algorithm. Depending on the chosen subroutine, the returned indices are employed to compute the Local Density from Equation 2, or to construct $\mathcal{C}$.

We shall refer to $\mathcal{S}$ as the local dataset that, as explained above, can be efficiently prepared with the qRAM (Giovannetti et al., 2008). To do so, we only require determining the tiles ${\square }_k$ that are in the search space, which can be done efficiently classically (Rovere et al., 2020). The initial state of this subroutine, after being prepared via the qRAM, is therefore

${\displaystyle \sum _{k\in \mathcal{S}}}{\displaystyle \sum _{i\in {\square }_k}}\left|i\right.⟩\stackrel{\text{qRAM}}{\to }{\displaystyle \sum _{k\in \mathcal{S}}}{\displaystyle \sum _{i\in {\square }_k}}\left|i\right.⟩\left|X_i,E_i\right.⟩,(4)$

where the index $i$ is unique for each point in $\mathcal{S}$. $i\in {\square }_k$ indicate all indices within tile $k$ [either of the light blue squares in Figure 2A]. Ancillary qubits, omitted for clarity in Equation 4, are employed within the Grover search (for more information, see Supplementary Appendix SA).

At this stage, we must find the points $i$ [green dots in Figure 2A] that are within a radius of $d_{\text{c}}$ from the base point $j$ [black point in Figure 2A]. As shown in Figure 3, we perform Grover Search Brassard et al. (2002) to prepare.

${\displaystyle \sum _i}\left|i\right.⟩\left|X_i,E_i\right.⟩\stackrel{\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}}{\to }{\displaystyle \sum _{d_{i,j}<d_{\text{c}}}}\left|i\right.⟩\left|X_i,E_i\right.⟩.(5)$

Here, the first register of the Grover output contains all points characterized by indices $i$ such that $d_{i,j}<d_{\text{c}}$. As shown in the inset of the figure, the Grover Search consists of $O(\sqrt{m})$ repetitions (where $m$ is the number of points in $\mathcal{S}$) of the $U_{\psi }$ and $U_P$ operators. $U_P$ is the diffusion operator and $U_{\psi }$ is the unitary associated with the oracle of Grover Search (Lov, 1996). Further details regarding Grover Search and the unitaries we use for our algorithm can be found in Supplementary Appendix SA.

When the algorithm is run, measurement either yields a point that satisfies this distance condition, or (if there are no valid indices left) an index that does not satisfy this condition. This is verified by the grey “Valid?” diamond in Figure 3. The branched logic following this block ensures that the algorithm loops until all the required points are returned by the algorithm in the “Return” block.

Once we have obtained all indices $i$ of points satisfying the distance condition $(d_{i,j}<d_{\text{c}})$, we perform the summation in Equation 2. This is computed and stored in the original dataset for each point. The database is now updated using qRAM with local density values for all points where the $j^{\text{th}}$ point in the database has the corresponding computed local density ${\rho }_j$.

The scaling of the subroutine that determines the local density of a single point is given by the number of points in the blue consideration circle in Figure 2A such that $d_{i,j}<d_{\text{c}}$. If we say this number is $p$, $O(p)$ runs are required. This is therefore a $O(p\sqrt{m})$ algorithm as opposed to the $O(m)$ classical iterative algorithm for the Unstructured Search Problem.

As a final remark, we highlight that it is in principle possible to design a unitary that computes the Local Density directly and stores the output in a quantum register. This unitary would remove the requirement of finding individually the indices $i$ such that $d_{i,j}<d_{\text{c}}$, thus removing the overhead of $p$ in $O(p\sqrt{m})$. However, designing this circuit is non-trivial and its depth may be large. This is therefore left for future investigations.

2.3 Find nearest higher

Here, we describe qCLUE’s subroutine for finding the Nearest Highers $({\mathcal{N}}_j)$ introduced in Section 2.1. As a reminder, ${\mathcal{N}}_j$ is the nearest point to the base point $j$ whose local density ${\rho }_{{\mathcal{N}}_j}$ is more than the local density ${\rho }_j$ of the base point, see Equation 3a.

Similar to the initialization carried out for the Local Density Computation step, we use qRAM to initialize the quantum state

${\displaystyle \sum _{k\in \mathcal{S}}}{\displaystyle \sum _{i\in {\square }_k}}\left|i\right.⟩\stackrel{\text{qRAM}}{\to }{\displaystyle \sum _{k\in \mathcal{S}}}{\displaystyle \sum _{i\in {\square }_k}}\left|i\right.⟩\left|X_i\right.⟩\left|{\rho }_i\right.⟩.(6)$

Here, the indices $i$ are within the tiles ${\square }_k$, as in Equation 4, and $\mathcal{S}$ is the considered search space, schematically represented by the light green box in Figure 2B. This search space is determined from $d_{\text{m}}$ as opposed to $d_{\text{c}}$, which is the user-defined threshold that is set to be $\delta d_{\text{c}}$. Note that the weight $E_i$, employed for determining the densities ${\rho }_i$ in Section 2.2, is hereon not required.

To find the Nearest Higher, we use a Grover-Enhanced Binary Search (GEBS) where each search step is enhanced by Grover’s algorithm (Equation 5). The output of every Grover run,

${\displaystyle \sum _{\begin{array}{c}{d}_{\text{L}}<d_{i,j}<d_{\text{t}},\\ {\rho }_i>{\rho }_b\end{array}}}\left|i\right.⟩\left|X_i,{\rho }_i\right.⟩,(7)$

is a superposition over all points $i$ whose distance $d_{i,j}$ from the base point $j$ lies between the thresholds $d_{\text{L}}$ and $d_{\text{t}}$. Furthermore, their local density ${\rho }_i$ should be higher than that of the base ${\rho }_j$. At each step, $d_{\text{L}}$ and $d_{\text{t}}$ are updated based on whether a point satisfying the conditions in the grey diamond of Figure 4A is found. Ancilla registers are used here as detailed in Supplementary Appendix SA.

Figure 4

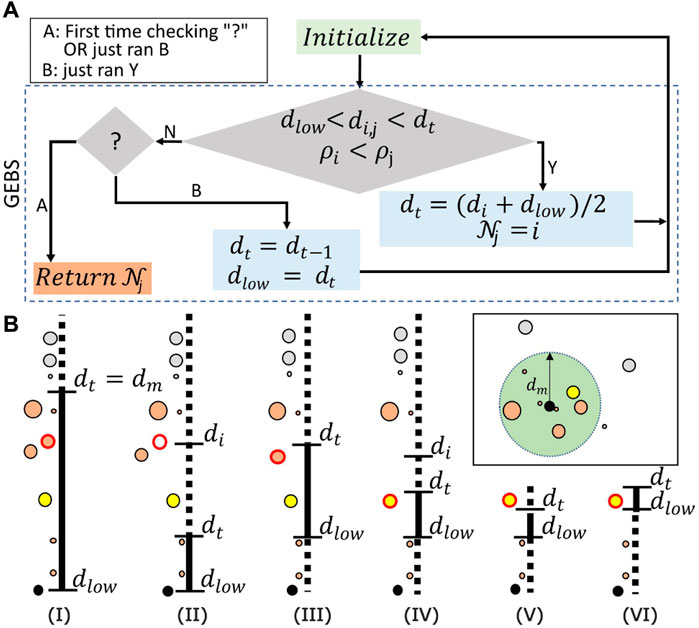
Figure 4. (A) Diagrammatic representation of the algorithm. GEBS determines successive candidates for the “Nearest Higher” until the proper one is found. The quantum state in Equation 6 is prepared in the “Initialize” step (green box). Grover Search (larger diamond) is then performed to find the points satisfying $d_{\text{L}}<d_{i,j}<d_{\text{t}},{\rho }_i<{\rho }_j$. If this condition is satisfied (“$Y$” branch), $d_{\text{t}}$ is updated and Grover run again. If not (“$N$” branch), control flows to the “?” diamond. The branch $A$ is entered if the “?” condition is being checked for the first time or if branch $B$ was just run. Branch $B$ is entered if branch $Y$ was just run. (B) The algorithm’s working is shown step-by-step (numbers at the bottom) for the search space $\mathcal{S}$ in the inset in the top right corner. The points are mapped to a line where the height represents the distance $d_{i,j}$ from the base point $j$ (black dot at the bottom). The grey (orange) points are outside (inside) the green consideration circle with radius $d_{\text{m}}$ [see also Figure 2B]. At each step of GEBS, the thresholds $d_{\text{L}}$ and $d_{\text{t}}$ are updated according to the logic in panel (A). The dot with the red border indicates the current candidate for ${\mathcal{N}}_j$; when filled (empty) it is (not) found by Grover Search at that step. The yellow point is the Nearest Higher $\mathcal{N\_\{j\}}$ that is found at the end of GEBS.

To better understand the algorithm, we provide a step-by-step walkthrough of the example in Figure 4B. The search space $\mathcal{S}$ is schematically represented by the inset in the right hand side, where each dot represents a point with a size that is proportional to its local density. The consideration circle (light green, dotted border) highlights all points within a radius $d_{\text{m}}=\delta d_{\text{c}}$. In this work, we set the outlier delta factor $\delta$ to 2. The consideration circle in the inset corresponds to $d_L=0$ and $d_{\text{t}}=d_{\text{m}}$, shown in step (I). In the main panel, vertical lines refers to the steps (I–VI) of GEBS that are reported below, and schematically represent the distances of all points (coloured dots) from the base point $j$ (black one at the bottom).

GEBS starts with the higher threshold set as $d_{\text{t}}=d_{\text{m}}$ and the lower threshold $d_{\text{L}}=0$ as shown in vertical line (I) of Figure 4B. Following the probabilistic nature of quantum mechanics, assume that the point with a red border indexed $i$ is found after measuring the output of the Grover Search in Equation 7. This triggers the updates in the $Y$ branch in the diagram of Figure 4A, such that we assign ${\mathcal{N}}_j=i$ and update $d_{\text{t}}\mapsto (d_{i,j}+d_{\text{L}})/2$. The point indexed $i$ is then removed from the search space, as can be seen in (II). Now, since no point satisfies the conditions in the diamond of the flow diagram [see (II)] and $d_{\text{t}}$ was just set to $(d_{i,j}+d_{\text{L}})/2$, the $B$ branch is carried out. This updates the thresholds $d_{\text{t}}$ and $d_{\text{L}}$ for the next iteration of the algorithm, see (III).

Now, assume that the new point with a red border is found [step (III)]. Updates in the $Y$ branch of Figure 4A are carried out again with a new index $i$ and the search region is reduced to contain a single point. In the next step (IV), that point (yellow) is found and, for the third and last time, the nearest higher and the thresholds are triggered according to the $Y$ branch. Next, since no point is found in (V), qCLUE executes the updates in the $B$ branch of the diagram. In the last iteration (VI), no points satisfy the desired conditions. The parameter $d_{\text{t}}$ was just set to $d_{\text{t}-1}$, i.e., the subroutine just ran $B$ which means that the $A$ branch is now executed and ${\mathcal{N}}_j$ is returned.

The runtime complexity of the GEBS procedure, with $m$ points in the search space $\mathcal{S}$, is $O(\alpha \sqrt{m})$ as opposed to $O(m)$ classically. The $\alpha$ term is due to the binary search procedure and depends on the size of the quantum register used to encode the distance. Specifically, for a chosen precision $2^{-\mathrm{\Delta }}$ used for the positions of the points in the datasets, $\alpha =\mathrm{\Delta }$.

2.4 Find seeds, outliers, and assign clusters

Once the Nearest Highers ${\mathcal{N}}_j$ are determined for all points $j$ in the dataset, Seeds and Outliers are found via another Grover Search over all points in the dataset. As per the definition in Equation 3a, Seeds [red points in Figure 2C] are the points with highest local density within a neighbourhood. Outliers [blue points in Figure 2C] are mathematically described by Equation 3b, are most likely noise, and therefore do not belong to any cluster.

Similar to the previous subroutines, the quantum registers for these procedures are initialized via qRAM. Seeds and outliers are then determined based on the corresponding conditions via Grover Search. Two quantum registers, the first marking whether a point is an outlier and the second to store the seed number – which is also the cluster number – are added to the quantum database.

The final subroutine of qCLUE is the assignment of points to clusters. At this stage, outliers have been removed from the input dataset, as they have been already identified. The algorithm flow is the same as that of the Local Density step in Figure 3. For a chosen seed $s$, we define $\mathcal{C}$ to be the set containing the indices of all points determined to be in the associated cluster at the end of this subroutine. To assign points to $\mathcal{C}$, we follow a procedure similar to that of the Local Density step in Figure 3. In the “Initialize” step, $\mathcal{C}$ is initialized to $\{s\}$ and the quantum registers are initialized via qRAM to the state.

${\displaystyle \sum _{i\in \text{DSS}}}\left|i\right.⟩\stackrel{\mathrm{q}\mathrm{R}\mathrm{A}\mathrm{M}}{\to }{\displaystyle \sum _i}\left|i\right.⟩\left|{\mathrm{V}}_i\right.⟩,(\mathrm{8a})$

$\left|{\mathrm{V}}_i\right.⟩=\left|X_i,{\rho }_i,d_{{\mathcal{N}}_i,i},X_{{\mathcal{N}}_i}\right.⟩.(\mathrm{8b})$

In the “Grover” block, we search over a superposition of points in the dataset which we call the Dynamic Search Space (DSS) created by qRAM as shown in Equations 8a, 8b. The DSS differs from the search space $\mathcal{S}$ in the Local Density step as it is dynamic. This is because it depends on the points in $\mathcal{C}$, which are updated at each iteration. In Figure 2C, for instance, the red seed and the orange point both with black borders are the elements of the current $\mathcal{C}$. To find the DSS, a square window of edge $2d_{\text{m}}$ is first opened for every point in $\mathcal{C}$ (in the figure, the squares with the same border style as the corresponding points). A rectangular region (red box) is then obtained by finding the axis-aligned minimum bounding box for these windows. The set of tiles ${\square }_k$ covered partially or fully by this minimum bounding box is the DSS. For example, in Figure 2C, it comprises the 9 tiles highlighted in light red.

With a similar procedure as for the Local Density subroutine, the “Grover” block now systematically identifies all followers of all points within set $\mathcal{C}$. Here, in the “Update” step in Figure 3, as the point found by the “Grover” block has passed the “Valid” condition, it is appended to $\mathcal{C}$. Once no more points are found, the “Return” block yields $\mathcal{C}$, following the same flow as the Local Density computation subroutine.

The complexity of the Cluster Assignment step is similar to the one of the Local Density Computation subroutine. The quantum advantage stems from the quadratic speedup provided by the Grover algorithm, which allows determining the follower faster if compared to CLUE. If there are $f$ points in a cluster $\mathcal{C}$ and $m$ points in the corresponding DSS, the classical complexity of the Cluster Assignment step is $O(m)$, while the quantum algorithm has a runtime of $O(f\sqrt{m})$.

3 Results

In this section, we test qCLUE in multiple scenarios, each designed to investigate its performance for different settings. In Section 3.1, we introduce the scoring metrics used for our analysis. In Section 3.2, we describe the performance of the algorithm applied on a single cluster in a uniform noisy environment. In Section 3.3, we study the performance on overlapping clusters. Finally, in Section 3.4, we study the performance of qCLUE on non-centroidal clusters with and without a weight profile.

3.1 Scoring metrics: homogeneity and completeness scores

It is more important to correctly classify high-weight points such as seeds as compared to low-weight points such as outliers. Since we would like our metric to be cognizant to this, we use modified, weight-aware versions (Jekaterina, 2023) of the Homogeneity $({\mathcal{F}}_H)$ and Completeness $({\mathcal{F}}_C)$ scores (Rosenberg and Hirschberg, 2007). These metrics are defined in terms of the predicted cluster labels ${\mathcal{C}}_{\text{p}}$ obtained from qCLUE, and the true cluster labels ${\mathcal{C}}_{\text{t}}$ of the generated dataset. ${\mathcal{F}}_H$ and ${\mathcal{F}}_C$ are based on the weight aware (Jekaterina, 2023) mutual information $I({\mathcal{C}}_{\text{p}}:{\mathcal{C}}_{\text{t}})$, the Shannon entropy $H({\mathcal{C}}_{\text{t}})$, and the joint Shannon entropy $H({\mathcal{C}}_{\text{t}},{\mathcal{C}}_{\text{p}})$ (Nielsen and Chuang, 2010):

${\mathcal{F}}_H=\frac{I\left({\mathcal{C}}_{\text{p}}:{\mathcal{C}}_{\text{t}}\right)}{H\left({\mathcal{C}}_{\text{t}}\right)}\text{\hspace{0.17em}and\hspace{0.17em}}{\mathcal{F}}_C=\frac{I\left({\mathcal{C}}_{\text{p}}:{\mathcal{C}}_{\text{t}}\right)}{H\left({\mathcal{C}}_{\text{p}}\right)},(\mathrm{9a})$

$H\left({\mathcal{C}}_{\text{p}}\right)=-{\displaystyle \sum _a}\frac{E_a}{E}{\log }_2\frac{E_a}{E},(\mathrm{9b})$

$H\left({\mathcal{C}}_{\text{t}}\right)=-{\displaystyle \sum _b}\frac{E_b}{E}{\log }_2\frac{E_b}{E},(\mathrm{9c})$

$H\left({\mathcal{C}}_{\text{p}},{\mathcal{C}}_{\text{t}}\right)=-{\displaystyle \sum _a}{\displaystyle \sum _b}\frac{E_{a,b}}{E}{\log }_2\frac{E_{a,b}}{E},(\mathrm{9d})$

$I\left({\mathcal{C}}_{\text{p}}:{\mathcal{C}}_{\text{t}}\right)=H\left({\mathcal{C}}_{\text{p}}\right)+H\left({\mathcal{C}}_{\text{t}}\right)-H\left({\mathcal{C}}_{\text{p}},{\mathcal{C}}_{\text{t}}\right).(9e)$

As discussed in (Jekaterina, 2023), $E_a$ is the weight aggregated over all points that qCLUE classifies into cluster $a$. $E_b$ is the weight aggregated over all points in cluster $b$ in the true dataset. $E_{a,b}$ is the sum of weights of all points in cluster $b$ in the true dataset that are also assigned to cluster $a$ by qCLUE. $E$ is the accumulated weight of all points in the dataset. We remark that for unit weights, Equations 9a, Equations 9e, reduce to the more common form presented in Rosenberg and Hirschberg (2007).

qCLUE applied to an input dataset yields homogeneity ${\mathcal{F}}_H=1$ if all of the predicted clusters only contain data points that are members of a single true cluster. On the other hand, ${\mathcal{F}}_C=1$ is obtained if all the data points that are members of a given true cluster are elements of the same reconstructed cluster. Therefore, these metrics are better suited to different scenarios. The impacts of noise and cluster overlap investigated in Sections 3.2, 3.3 are better captured by ${\mathcal{F}}_H$. Indeed, if qCLUE incorrectly classifies noise points into predicted clusters, ${\mathcal{F}}_C$ is unaffected. On the other hand, ${\mathcal{F}}_C$ shall be employed when studying non-centroidal clusters in Section 3.4, since ${\mathcal{F}}_H=1$ if one true cluster is divided by qCLUE into many sub-clusters.

3.2 Noise

Here, we study the performance of qCLUE for a single cluster in a noisy environment. We vary the number $N_N$ of noise points sampled from a uniform distribution over a square region of fixed size. A cluster of $N_C$ points with coordinates $X_j=\left[x_{j,1},x_{j,2}\right]$ is sampled from the multivariate Gaussian distribution.

$pdf\left(X_j\right)=\frac{e^{-\frac{1}{2}{\left(X_j-{\mu }_j\right)}^T{\mathrm{\Sigma }}^{-1}\left(X_j-{\mu }_j\right)}}{{\left(2\pi \right)}^{\frac{n}{2}}|\mathrm{\Sigma }{|}^{\frac{1}{2}}},(10)$

where $\mu ={\left[{\mu }_{x_1},{\mu }_{x_2}\right]}^T$ is the mean of the distribution (set to ${[\mathrm{0,0}]}^T$ in our case) and $\mathrm{\Sigma }$ the covariance matrix. Here, we choose $\mathrm{\Sigma }=\sigma \mathcal{I}$, with $\mathcal{I}$ being the identity matrix and $\sigma$ a positive real number.

Examples of the generated clusters (in orange) and noise (in blue) are given in Figures 5A, B for $N_N/N_C=0.33$ at $\sigma =32$ and $N_N/N_C=1$ at $\sigma =10$, respectively. The weight assigned to each point $X_j$ in the cluster is given by $A\times pdf(X_j)$ [see Equation 10] with $A=5\times 10^2$. The weight of each noise point is randomly sampled between zero and one. This choice resembles the typical scenarios in ER tasks for which CLUE (Rovere et al., 2020) was designed.

Figure 5

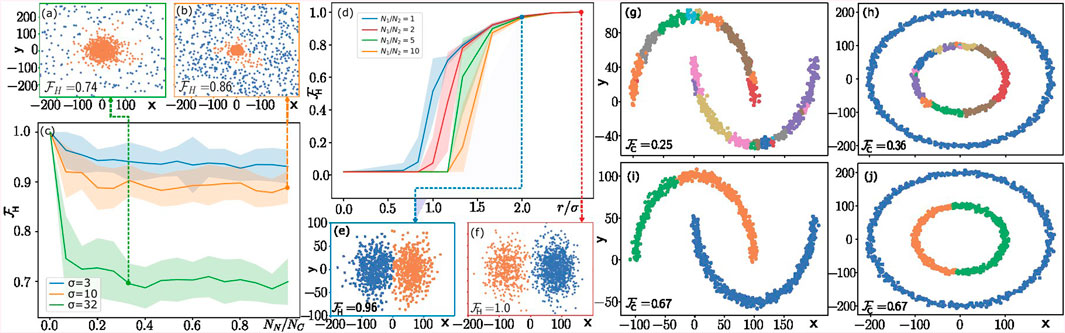
Figure 5. Numerical results from qCLUE simulated on a classical machine. (A–C) qCLUE’s performance in noisy environments. The dataset generated for these experiments and visualized in panels (A, B) consists of a cluster (noise) with $N_C=750$ $(N_N)$ points sampled from the Gaussian distribution in Equation 10 (uniform distribution) over a square of size 500. The weight of noise points is sampled uniformly between zero and one, while each cluster point is assigned a weight that is the probability of being sampled multiplied by a factor $A=500$. (A, B) Computed clusters at $N_N/N_C=0.33,\sigma =32$, and $N_N/N_C=1,\sigma =10$, respectively. In (C), ${\mathcal{F}}_H$ is plotted against $N_N/N_C$ for the $\sigma$ in the legend. (D–F) Performance for overlapping clusters. In (D), ${\mathcal{F}}_H$ vs. $r/\sigma$ is shown for $\sigma =30$ and different ratios $N_1/N_2$. Here, $r$ is the distance between the centers of two clusters with $N_1=500$ and $N_2$ points, and we assign to each point a weight that is equal to its sampling probability in Equation 10. (E, F) Computed clusters at $r/\sigma =2.0,N_1/N_2=1$, and $r/\sigma =2.67,N_1/N_2=2$, respectively. The shadowed regions in (C, D) represent the standard deviations of ${\mathcal{F}}_H$ over 30 iterations. (G–J) Performance over non-centroidal clusters of 500 points each generated from $scikit-learn$ (Pedregosa et al., 2018). In (G, H) the points’ weight profile is uniform, while in (I, J) is varied linearly with respect to the distance such that each cluster has a single, most energetic point (see Section 3.4). For all experiments, $d_{\text{c}}$ was set to 20 and $\tilde{\rho }$ was set to 25. (A–F) use the weight-aware metric in Equation 9a, Equation 9e, while in (G–J), since the weight profile is assigned by the user and is not part of the dataset itself, in the scoring process we set all points to have the same weight.

In Figure 5C, we show the variation of homogeneity score ${\mathcal{F}}_H$ with respect to the ratio $N_N/N_C$. We employ the values of $\sigma$ reported in the legend, associated to different colors in the plot. As can be seen, the clustering performance is inversely proportional to both $N_N/N_C$ and $\sigma$. When these parameters are small, the typical distance between cluster points is much smaller than that between noise points, and ${\mathcal{F}}_H$ approaches unity. With a higher chance of labeling noise points as within the cluster, however, ${\mathcal{F}}_H$ is lowered. As such, the degradation of ${\mathcal{F}}_H$ is proportional to the probability of a noise point being in the cluster region, which increases with both $\sigma$ and $N_N/N_C$.

3.3 Overlap

Here, we consider the case of two circular clusters with $N_1$ and $N_2$ points respectively, each sampled from the multivariate Gaussian distribution in Equation 10 and with $\mathrm{\Sigma }=\sigma \mathcal{I}$. The weight profile is determined by $pdf(X_j)$ for coordinates $X_j$. The centers ${\mu }_1$ and ${\mu }_2$ (two instances of $\mu$) are chosen to be $(r/\mathrm{2,0})$ and $(-r/\mathrm{2,0})$, respectively, such that the distance between the cluster centers is $r$.

In Figure 5D, we study the variation of homogeneity score ${\mathcal{F}}_H$ as a function of $r/\sigma$ for several values of $N_2/N_1$. The computed clusters for $r/\sigma =2$ at $N_2/N_1=1$ and $r/\sigma =2.67$ at $N_2/N_1=2$ are shown in panels (e) and (f), respectively, to showcase the typical scenarios considered here.

For all $N_1/N_2$, ${\mathcal{F}}_H$ is zero for low $r/\sigma$ (high overlap). There is then a region where ${\mathcal{F}}_H$ increases with $r/\sigma$ and then saturates at unity for high $r/\sigma$ (little to no overlap). When the two clusters are too close, i.e., $r/\sigma \ll 1$, they are in fact indistinguishable and qCLUE labels all points together. Increasing the ratio $r/\sigma$ makes the clusters move away from each other and thus qCLUE can discern them. This behavior can be observed in Figures 5E, F. Importantly, large values of ${\mathcal{F}}_H$ are already attained when the clusters still have a significant overlap. In this scenario, employing the weight labels and the weight density considerably contributes to accurate cluster assignment. In fact, the nearest higher points are more likely to connect the points near or on the decision boundary with the more energetic core, thus separating the clusters better.

The performance of qCLUE is also affected by the ratio $N_1/N_2$. When one cluster contains more points than the other, it is more likely to “capture” points from the smaller. The resulting loss in homogeneity score ${\mathcal{F}}_H$ for low $r/\sigma$ ratios is evident from Figure 5D, where it can be seen that clusters of similar sizes are better distinguished from each other.

3.4 Non-centroidal clusters

Finally, we study the performance of qCLUE on non-centroidal clusters. For this purpose, we use the Moons and Circles datasets in Figures 5G–J, generated using $scikit-learn$ (Pedregosa et al., 2018). Two settings are considered - one where a uniform weight profile is applied over the points [panels (g, h)] and one where a linear gradient weight profile is employed [panels (i, j)].

In the latter case, we assign the highest value of the weight for each cluster to a single point and lower the weights of all other points proportionally to their $x_2$ coordinate. In the case of the moon dataset, $E=x_2$ for the upper moon (so the top point of the upper moon has the maximum weight in the cluster) and $E=60-x_2$ for the lower moon (so the bottom point has the highest weight in the cluster). For the circles, $E=|x_2-200|/10$ for the inner circle and $E=|x_2+100|/5$ for the outer one.

Since these datasets are noiseless and well separated, ${\mathcal{F}}_H$ is always one and we employ ${\mathcal{F}}_C$ to characterize the performance of qCLUE. As in Figures 5G, H the weight profile is uniform, and several points satisfy the seed condition. Therefore, qCLUE groups each circle into several clusters, such that we obtain limited values for ${\mathcal{F}}_C$. On the contrary, cases with a weight profile assigned [Figures 5I, J] results in fewer seeds that are better recognized by qCLUE, and the completeness score ${\mathcal{F}}_C$ is considerably enhanced.

4 Conclusion and outlook

We introduced qCLUE, a novel quantum clustering algorithm designed to address the computational challenges associated with high-dimensional datasets. qCLUE’s significance lies in its potential to efficiently cluster data by effectively leveraging quantum computing, mitigating the escalating computational complexity encountered by classical algorithms upon increasing dimensionality of datasets. The algorithm’s ability to navigate high-dimensional spaces is particularly promising on datasets with high point density, where local searches become too demanding for classical computers. Therefore, qCLUE will be beneficial in multiple scenarios, ranging from quantum-enhanced machine learning (Haug et al., 2023; Zeguendry et al., 2023) to complex data analysis tasks (Sinayskiy et al., 2015).

According to our numerical results, qCLUE works well and its performance is significantly enhanced when a weight profile is assigned. Specifically, we study qCLUE in noisy environments, on overlapping clusters, and on non-centroidal datasets that are commonly used to benchmark clustering algorithms (Fujita, 2021; Tiwari et al., 2020). In scenarios that are typically encountered in ER tasks, qCLUE correctly reconstructs the true clusters to a high level of accuracy as it matches the performance of CERN’s CLUE on a given dataset. On the other hand, a weight profile can significantly boost qCLUE performance as we have seen in the case of non-centroidal clusters. Our numerical results, backed up by the well-studied CLUE and by the quadratic speedup stemming from Grover search, make qCLUE a promising candidate for addressing high-dimensional clustering problems (Wei et al., 2020; Kerenidis and Landman, 2021; Duarte et al., 2023).

As a first outlook, we identify the implementation of qCLUE on NISQ hardware (Celi et al., 2020; Labuhn et al., 2016; Bernien et al., 2017; Lanyon et al., 2011; Arute et al., 2019; Córcoles et al., 2015; Debnath et al., 2016). This requires a comprehensive consideration of real device constraints. Aspects such as circuit optimization (Nash et al., 2020), and the impact of noise will be critical and must be carefully addressed. Second, it is possible to improve the scaling of qCLUE by devising a unitary that mitigates the need for repeating Grover’s algorithm for each point satisfying the search condition and thereby eliminating the factors of $p$, $\alpha$, and $f$ in the scaling of the subroutines outlined in Sections 2.2–2.4 respectively. We finally note that it is worth investigating variations of qCLUE that improve the quality of clustering in different scenarios. For instance, one can devise more sophisticated criteria for the Nearest Higher or Local Density computation steps. Performance on a given dataset can also be improved by performing exhaustive hyperparameter searches or via hyperparameter optimization algorithms (Wu et al., 2019).

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://zenodo.org/records/12655189.

Author contributions

DG: Writing–original draft, Writing–review and editing. LD: Writing–original draft, Writing–review and editing. AD: Writing–original draft, Writing–review and editing. WR: Writing–original draft, Writing–review and editing. FP: Writing–original draft, Writing–review and editing. MM: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. CERN Quantum Initiative. Wolfgang Gentner Programme of the German Federal Ministry of Education and Research (grant no. 13E18CHA). EPSRC quantum career development grant EP/W028301/1. NTT PHI Lab. Government of Canada through Innovation, Science and Economic Development Canada (ISED). Province of Ontario through the Ministry of Colleges and Universities.

Acknowledgments

We thank the CERN Quantum Initiative, Fabio Fracas for creating the fertile ground for starting this project and Andrew J. Jena as well as Priyanka Mukhopadhyay for theoretical support. WR acknowledges the Wolfgang Gentner Programme of the German Federal Ministry of Education and Research (grant no. 13E18CHA). LD acknowledges the EPSRC quantum career development grant EP/W028301/1. DG and MM acknowledge the NTT PHI Lab for funding. Research at IQC is further supported by the Government of Canada through Innovation, Science and Economic Development Canada (ISED). Research at Perimeter Institute is supported in part by the Government of Canada through ISED and by the Province of Ontario through the Ministry of Colleges and Universities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2024.1462004/full#supplementary-material

References

Aad, G., Abajyan, T., Abbott, B., Abdallah, J., Abdel Khalek, S., Abdelalim, A., et al. (2012). Observation of a new particle in the search for the standard model higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716 (1), 1–29. doi:10.1016/j.physletb.2012.08.020

CrossRef Full Text | Google Scholar

Aaij, R., Abdelmotteleb, A., Abellan Beteta, C., Abudinén, F., Ackernley, T., Adeva, B., et al. (2023). First observation of a doubly charged tetraquark and its neutral partner. Phys. Rev. Lett. 131 (4), 041902. doi:10.1103/PhysRevLett.131.041902

PubMed Abstract | CrossRef Full Text | Google Scholar

Aïmeur, E., Brassard, G., and Gambs, S. (2007). “Quantum clustering algorithms,” in Proceedings of the 24th International Conference on Machine Learning. ICML ’07, Corvalis, Oregon, June 20–24, 2007 (New York, NY: Association for Computing Machinery), 1–8. doi:10.1145/1273496.1273497

CrossRef Full Text | Google Scholar

Amaro, F. D., Antonietti, R., Baracchini, E., Benussi, L., Bianco, S., Borra, F., et al. (2023). Directional iDBSCAN to detect cosmic-ray tracks for the CYGNO experiment. Meas. Sci. Technol. 34 (12), 125024. doi:10.1088/1361-6501/acf402

CrossRef Full Text | Google Scholar

Arute, F., Arya, K., Babbush, R., Bacon, D., Bardin, J. C., Barends, R., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Asur, S., Ucar, D., and Srinivasan, P. (2007). An ensemble framework for clustering protein–protein interaction networks. Bioinformatics 23.13, i29–i40. doi:10.1093/bioinformatics/btm212

PubMed Abstract | CrossRef Full Text | Google Scholar

Au, W.-H., Chan, K. C. C., Wong, A. K. C., and Wang, Y. (2005). Attribute clustering for grouping, selection, and classification of gene expression data. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2 (2), 83–101. doi:10.1109/TCBB.2005.17

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernien, H., Schwartz, S., Keesling, A., Levine, H., Omran, A., Pichler, H., et al. (2017). Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584. doi:10.1038/nature24622

PubMed Abstract | CrossRef Full Text | Google Scholar

Brassard, G., Høyer, P., Mosca, M., and Tapp, A. (2002). Quantum amplitude amplification and estimation. arxiv 53, 74. doi:10.1090/conm/305/05215

CrossRef Full Text | Google Scholar

Brondolin, E. (2022). CLUE a clustering algorithm for current and future experiments. Tech. Rep. doi:10.1088/1742-6596/2438/1/012074

CrossRef Full Text | Google Scholar

Caruso, G., Antonio Gattone, S., Fortuna, F., and Di Battista, T. (2018). “Cluster analysis as a decision-making tool: a methodological review,” in Decision economics: in the tradition of herbert A. Simon’s heritage. Editors E. Bucciarelli, S.-H. Chen, and J. M. Corchado (Cham: Springer International Publishing), 48–55.

CrossRef Full Text | Google Scholar

Celi, A., Vermersch, B., Viyuela, O., Pichler, H., Lukin, M. D., and Zoller, P. (2020). Emerging two-dimensional gauge theories in rydberg configurable arrays. Phys. Rev. X 10 (2), 021057. doi:10.1103/PhysRevX.10.021057

CrossRef Full Text | Google Scholar

Chang, J., Wang, L., Meng, G., Xiang, S., and Pan, C. (2017). “Deep adaptive image clustering,” in Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, October 22–29, 2017 (ICCV).

CrossRef Full Text | Google Scholar

CMS Collaboration (2022). The TICL (v4) reconstruction at the CMS phase-2 high granularity calorimeter endcap.

Google Scholar

CMS Collaboration (2023). Development of the CMS detector for the CERN LHC run.

Google Scholar

CMS Collaboration (2024). Review of top quark mass measurements in CMS.

Google Scholar

Coleman, G. B., and Andrews, H. C. (1979). Image segmentation by clustering. Proc. IEEE 67 (5), 773–785. doi:10.1109/PROC.1979.11327

CrossRef Full Text | Google Scholar

Córcoles, A. D., Magesan, E., Srinivasan, S. J., Cross, A. W., Steffen, M., Gambetta, J. M., et al. (2015). Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6 (1), 6979. doi:10.1038/ncomms7979

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalitz, C., Ayyad, Y., Wilberg, J., Aymans, L., Bazin, D., and Mittig, W. (2019). Automatic trajectory recognition in Active Target Time Projection Chambers data by means of hierarchical clustering. Comput. Phys. Commun. 235, 159–168. doi:10.1016/j.cpc.2018.09.010

CrossRef Full Text | Google Scholar

Debnath, S., Linke, N. M., Figgatt, C., Landsman, K. A., Wright, K., and Monroe, C. (2016). Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66. doi:10.1038/nature18648

PubMed Abstract | CrossRef Full Text | Google Scholar

Didier, C., and Austin, B. (2017). The phase-2 upgrade of the CMS endcap calorimeter. CERN LHC Experiments Committee. doi:10.17181/CERN.IV8M.1JY2

CrossRef Full Text | Google Scholar

Duarte, M., Buffoni, L., and Omar, Y. (2023). Quantum density peak clustering. Quantum Mach. Intell. 5 (1), 9. doi:10.1007/s42484-022-00090-0

CrossRef Full Text | Google Scholar

Dutta, P., Saha, S., Pai, S., and Kumar, A. (2020). A protein interaction information-based generative model for enhancing gene clustering. Sci. Rep. 10 (1), 665. doi:10.1038/s41598-020-57437-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujita, K. (2021). Approximate spectral clustering using both reference vectors and topology of the network generated by growing neural gas. PeerJ Comput. Sci. 7, e679. doi:10.7717/peerj-cs.679

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaffey, M. J. (2010). Space weathering and the interpretation of asteroid reflectance spectra. Icarus 209(2), 564–574. doi:10.1016/j.icarus.2010.05.006

CrossRef Full Text | Google Scholar

Galluccio, L., Michel, O., Bendjoya, P., Slezak, E., and Bailer-Jones, C. A. (2008). “Unsupervised clustering on astrophysics data: asteroids reflectance spectra surveys and hyperspectral images,” in Classification and discovery in large astronomical surveys. Editor C. A. L. Bailer-Jones (American Institute of Physics Conference Series), 1082, 165–171. doi:10.1063/1.3059034

CrossRef Full Text | Google Scholar

Gao, A., Rasmussen, B., Kulits, P., Scheller, E. L., Greenberger, R. N., and Ehlmann, B. L. (2021). “Generalized unsupervised clustering of hyperspectral images of geological targets in the near infrared,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Nashville, TN, June 19–25, 2021, 4294–4303.

CrossRef Full Text | Google Scholar

Giovannetti, V., Lloyd, S., and Maccone, L. (2008). Quantum random access memory. Phys. Rev. Lett. 100, 160501. doi:10.1103/physrevlett.100.160501

PubMed Abstract | CrossRef Full Text | Google Scholar

Gong, C., Zhou, N., Xia, S., and Huang, S. (2024). Quantum particle swarm optimization algorithm based on diversity migration strategy. Future Gener. comput. Syst. 157.C, 445–458. doi:10.1016/j.future.2024.04.008

CrossRef Full Text | Google Scholar

Gong, L.-H., Ding, W., Li, Z., Wang, Y.-Z., and Zhou, N.-R. (2024a). Quantum K-nearest neighbor classification algorithm via a divide-and-conquer strategy. Adv. Quantum Technol. 7.6, 2300221. doi:10.1002/qute.202300221

CrossRef Full Text | Google Scholar

Gong, L.-H., Pei, J.-J., Zhang, T.-F., and Zhou, N.-R. (2024b). Quantum convolutional neural network based on variational quantum circuits. Opt. Commun. 550, 129993. doi:10.1016/j.optcom.2023.129993

CrossRef Full Text | Google Scholar

Gong, L.-H., Xiang, L.-Z., Liu, S.-H., and Zhou, N.-R. (2022). Born machine model based on matrix product state quantum circuit. Phys. A Stat. Mech. its Appl. 593, 126907. doi:10.1016/j.physa.2022.126907

CrossRef Full Text | Google Scholar

Gopalakrishnan, D., Dellantonio, L., Di Pilato, A., Redjeb, W., Pantaleo, F., and Mosca, M. (2024). QLUE-algo/qlue: frontiers-paper. Version frontiers-paper. doi:10.5281/zenodo.12655189

CrossRef Full Text | Google Scholar

Gu, Z., and Hübschmann, D. (2022). SimplifyEnrichment: a bioconductor package for clustering and visualizing functional enrichment results. Genomics, Proteomics Bioinforma. 21 (1), 190–202. doi:10.1016/j.gpb.2022.04.008

CrossRef Full Text | Google Scholar

Haug, T., Self, C. N., and Kim, M. S. (2023). Quantum machine learning of large datasets using randomized measurements. Mach. Learn. Sci. Technol. 4 (1), 015005. doi:10.1088/2632-2153/acb0b4

CrossRef Full Text | Google Scholar

Hayrapetyan, A., Tumasyan, A., Adam, w., Andrejkovic, J. W., Bergauer, T., Chatterjee, S., et al. (2024). Search for new physics with emerging jets in proton-proton collisions at √s=13\TeV. JHEP 07, 142. doi:10.1007/JHEP07(2024)142

CrossRef Full Text | Google Scholar

Hayrapetyan, A., Tumasyan, A., Adam, W., Andrejkovic, J., Bergauer, T., Chatterjee, S., et al. (2023). Observation of four top quark production in proton-proton collisions at √s=13TeV. Phys. Lett. B 847, 138290. doi:10.1016/j.physletb.2023.138290

CrossRef Full Text | Google Scholar

Huang, J.-J., Tzeng, G.-H., and Ong, C.-S. (2007). Marketing segmentation using support vector clustering. Expert Syst. Appl. 32.2, 313–317. doi:10.1016/j.eswa.2005.11.028

CrossRef Full Text | Google Scholar

Jekaterina, J. (2023). A new trackster linking algorithm based on graph neural networks for the CMS experiment at the large Hadron collider at CERN. Present. 14 Jul 2023. Prague, Tech. U.

Google Scholar

Karim, M. R., Beyan, O., Zappa, A., Costa, I. G., Rebholz-Schuhmann, D., Cochez, M., et al. (2020). Deep learning-based clustering approaches for bioinformatics. Briefings Bioinforma. 22 (1), 393–415. doi:10.1093/bib/bbz170

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerenidis, I., and Landman, J. (2021). Quantum spectral clustering. Phys. Rev. A 103 (4), 042415. doi:10.1103/PhysRevA.103.042415

CrossRef Full Text | Google Scholar

Kerenidis, I., Landman, J., Luongo, A., and Prakash, A. (2019). “q-means: a quantum algorithm for unsupervised machine learning”. in Advances in neural information processing systems. Editor H. Wallachet al. (Red Hook, New York: Curran Associates, Inc.), 32

Google Scholar

Kishore Kumar, R., Birla, L., and Sreenivasa Rao, K. (2018). A robust unsupervised pattern discovery and clustering of speech signals. Pattern Recognit. Lett. 116, 254–261. doi:10.1016/j.patrec.2018.10.035

CrossRef Full Text | Google Scholar

Labuhn, H., Barredo, D., Ravets, S., de Léséleuc, S., Macrì, T., Lahaye, T., et al. (2016). Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models. Nature 534.7609, 667–670. doi:10.1038/nature18274

PubMed Abstract | CrossRef Full Text | Google Scholar

Lanyon, B. P., Hempel, C., Nigg, D., Müller, M., Gerritsma, R., Zähringer, F., et al. (2011). Universal digital quantum simulation with trapped ions. Science 334, 57–61. doi:10.1126/science.1208001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lov, K. G. (1996). “A fast quantum mechanical algorithm for database search,” in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing. STOC ’96, Philadelphia, Pennsylvania, USA, May 22–24, 1996 (New York, NY: Association for Computing Machinery), 212–219. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

Magano, D., Kumar, A., Kālis, M., Locāns, A., Glos, A., Pratapsi, S., et al. (2022). Quantum speedup for track reconstruction in particle accelerators. Phys. Rev. D. 105 (7), 076012. doi:10.1103/PhysRevD.105.076012

CrossRef Full Text | Google Scholar

Nash, B., Gheorghiu, V., and Mosca, M. (2020). Quantum circuit optimizations for NISQ architectures. Quantum Sci. Technol. 5.2, 025010. doi:10.1088/2058-9565/ab79b1

CrossRef Full Text | Google Scholar

Ng, H. P., Ong, S. H., Foong, K. W. C., Goh, P. S., and Nowinski, W. L. (2006). “Medical image segmentation using K-means clustering and improved watershed algorithm,” in 2006 IEEE Southwest Symposium on Image Analysis and Interpretation, Denver, CO, March 26–28, 2006, 61–65. doi:10.1109/SSIAI.2006.1633722

CrossRef Full Text | Google Scholar

Nicotra, D., Lucio Martinez, M., de Vries, J., Merk, M., Driessens, K., Westra, R., et al. (2023). A quantum algorithm for track reconstruction in the LHCb vertex detector. J. Instrum. 18, P11028. doi:10.1088/1748-0221/18/11/p11028

CrossRef Full Text | Google Scholar

Nielsen, M. A., and Chuang, I. L. (2010). Quantum computation and quantum information. 10th Anniversary Edition. Cambridge, England: Cambridge University Press.

Google Scholar

Oyelade, J., Isewon, I., Oladipupo, F., Aromolaran, O., Uwoghiren, E., Ameh, F., et al. (2016). Clustering algorithms: their application to gene expression data. Bioinform. Biol. 10 BBI.S38316. doi:10.4137/BBI.S38316

PubMed Abstract | CrossRef Full Text | Google Scholar

Oyelade, J., Isewon, I., Oladipupo, O., Emebo, O., Omogbadegun, Z., Aromolaran, O., et al. (2019). “Data clustering: algorithms and its applications,” in 2019 19th International Conference on Computational Science and Its Applications (ICCSA), St. Petersburg, Russia, July 01–04, 2019, 71–81. doi:10.1109/ICCSA.2019.000-1

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2018). Scikit-learn: machine learning in Python. Research Gate.

Google Scholar

Pires, D., Bargassa, P., Seixas, J., and Omar, Y. (2021). A digital quantum algorithm for jet clustering in high-energy physics. Research Gate. doi:10.48550/arXiv.2101.05618

CrossRef Full Text | Google Scholar

Punj, G., and Stewart, D. W. (1983). Cluster analysis in marketing research: review and suggestions for application. J. Mark. Res. 20 (2), 134–148. doi:10.1177/002224378302000204

CrossRef Full Text | Google Scholar

Qaqish, B. F., O’Brien, J. J., Hibbard, J. C., and Clowers, K. J. (2017). Accelerating high-dimensional clustering with lossless data reduction. Bioinformatics 33.18, 2867–2872. doi:10.1093/bioinformatics/btx328

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodenko, S. A., Mayorov, A. G., Malakhov, V. V., and Troitskaya, I. K.on behalf of PAMELA collaboration (2019). Track reconstruction of antiprotons and antideuterons in the coordinate-sensitive calorimeter of PAMELA spectrometer using the Hough transform. J. Phys. Conf. Ser. 1189 (1), 012009. doi:10.1088/1742-6596/1189/1/012009

CrossRef Full Text | Google Scholar

Rosenberg, A., and Hirschberg, J. (2007). “V-measure: a conditional entropy-based external cluster evaluation measure,” in Proceedings of the 2007 joint conference on empirical methods in natural language processing and computational natural language learning (EMNLP-CoNLL), Prague, Czech Republic, June 28–30, 2007, 410–420.

Google Scholar

Rovere, M., Chen, Z., Di Pilato, A., Pantaleo, F., and Seez, C. (2020). CLUE: a fast parallel clustering algorithm for high granularity calorimeters in high-energy physics. Front. Big Data 3, 591315. doi:10.3389/fdata.2020.591315

PubMed Abstract | CrossRef Full Text | Google Scholar

Schickel-Zuber, V., and Faltings, B. (2007). “Using hierarchical clustering for learning theontologies used in recommendation systems,” in Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’07, San Jose, California, USA, August 12–15, 2007 (New York, NY: Association for Computing Machinery), 599–608. doi:10.1145/1281192.1281257

CrossRef Full Text | Google Scholar

Seidel, R., Tcholtchev, N., Bock, S., Kai-Uwe Becker, C., and Hauswirth, M. (2021). Efficient floating point arithmetic for quantum computers. Research Gate.

Google Scholar

Shepitsen, A., Gemmell, J., Mobasher, B., and Burke, R. (2008). “Personalized recommendation in social tagging systems using hierarchical clustering,” in Proceedings of the 2008 ACM Conference on Recommender Systems. RecSys ’08, Lausanne, Switzerland, October 23–25, 2008 (New York, NY: Association for Computing Machinery), 259–266. doi:10.1145/1454008.1454048

CrossRef Full Text | Google Scholar

Sinayskiy, I., Schuld, M., and Petruccione, F. (2015). An introduction to quantum machine learning. Contemp. Phys. 56.2, 172–185. doi:10.1080/00107514.2014.964942

CrossRef Full Text | Google Scholar

Tiwari, P., Dehdashti, S., Karim Obeid, A., Melucci, M., and Bruza, P. (2020). Kernel method based on non-linear coherent state. Quantum Physics. doi:10.48550/arXiv.2007.07887

CrossRef Full Text | Google Scholar

Tumasyan, A., Adam, W., Andrejkovic, J., Bergauer, T., Chatterjee, S., Damanakis, K., et al. (2023). Measurement of the $B_s^0\to {\mu }^{+}{\mu }^{-}$ decay properties and search for the $B^0\to {\mu }^{+}{\mu }^{-}$ decay in proton-proton collisions at √s=13TeV. Phys. Lett. B 842, 137955. doi:10.1016/j.physletb.2023.137955

CrossRef Full Text | Google Scholar

Tüysüz, C., Carminati, F., Demirköz, B., Dobos, D., Fracas, F., Novotny, K., et al. (2020). “Particle track reconstruction with quantum algorithms” in The European Physical Journal Conferences. Editor C. Doglioni, 09013.

Google Scholar

Tüysüz, C., Rieger, C., Novotny, K., Demirköz, B., Dobos, D., Potamianos, K., et al. (2021). Hybrid quantum classical graph neural networks for particle track reconstruction. Quantum Mach. Intell. 3.2, 29. doi:10.1007/s42484-021-00055-9

CrossRef Full Text | Google Scholar

Wang, J., Li, M., Deng, Y., and Pan, Yi (2010). Recent advances in clustering methods for protein interaction networks. BMC Genomics 11 (3), S10. doi:10.1186/1471-2164-11-S3-S10

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, A. Y., Naik, P., Harrow, A. W., and Thaler, J. (2020). Quantum algorithms for jet clustering. Phys. Rev. D. 101 (9), 094015. doi:10.1103/PhysRevD.101.094015

CrossRef Full Text | Google Scholar

Wu, J., Chen, X.-Y., Zhang, H., Xiong, L.-D., Lei, H., and Deng, S.-H. (2019). Hyperparameter optimization for machine learning models based on bayesian optimizationb. J. Electron. Sci. Technol. 17.1, 26–40. doi:10.11989/JEST.1674-862X.80904120

CrossRef Full Text | Google Scholar

Wu, T., Liu, X., Qin, J., and Herrera, F. (2021). Balance dynamic clustering analysis and consensus reaching process with consensus evolution networks in large-scale group decision making. IEEE Trans. Fuzzy Syst. 29 (2), 357–371. doi:10.1109/TFUZZ.2019.2953602

CrossRef Full Text | Google Scholar

Wu, X., Yan, J., Liu, N., Yan, S., Chen, Y., and Chen, Z. (2009). “Probabilistic latent semantic user segmentation for behavioral targeted advertising,” in Proceedings of the Third International Workshop on Data Mining and Audience Intelligence for Advertising. ADKDD ’09, Paris, France, June 28, 2009 (New York, NY: Association for Computing Machinery), 10–17. doi:10.1145/1592748.1592751

CrossRef Full Text | Google Scholar

Zeguendry, A., Jarir, Z., and Mohamed, Q. (2023). Quantum Machine Learning: A Review and Case Studies. Entropy (Basel) 25. 287. doi:10.3390/e25020287

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, J., Zhai, L., and Pantelous, A. A. (2020). Market segmentation using high-dimensional sparse consumers data. Expert Syst. Appl. Expert Syst. Appl. 145, 113136. doi:10.1016/j.eswa.2019.113136

CrossRef Full Text | Google Scholar

Zhou, N.-R., Liu, X.-X., Chen, Y.-L., and Du, N.-S. (2021). Quantum K-Nearest-Neighbor image classification algorithm based on K-L transform. Int. J. Theor. Phys. 60 (3), 1209–1224. doi:10.1007/s10773-021-04747-7

CrossRef Full Text | Google Scholar

Zlokapa, A., Anand, A., Vlimant, J. R., Duarte, J. M., Job, J., Lidar, D., et al. (2021). Charged particle tracking with quantum annealing optimization. Quantum Mach. Intell. 3 (2), 27. doi:10.1007/s42484-021-00054-w

CrossRef Full Text | Google Scholar