- 1Beijing Advanced Innovation Center for Materials Genome Engineering, Beijing Information Science and Technology University, Beijing, China
- 2Laboratory of Data Science and Information Studies, Beijing Information Science and Technology University, Beijing, China
- 3State Key Laboratory of High-efficiency Coal Utilization and Green Chemical Engineering, College of Chemistry and Chemical Engineering, Ningxia University, Yinchuan, China
- 4State Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, Shanxi, China
- 5Beijing Key Laboratory of Internet Culture and Digital Dissemination Research, Beijing Information Science and Technology University, Beijing, China
- 6Synfuels China Co. Ltd.—SynCat@Beijing, Beijing, China
- 7Hong Kong Quantum AI Laboratory, Ltd., Hong Kong, Hong Kong SAR, China
Many have reported the use of quantum chemistry approaches for evaluating the catalytic properties of iron carbide clusters. Unfortunately, structural energy calculations are computationally expensive when using density functional theory. The computational cost is prohibitive for high-throughput simulations with large length and time scales. In this paper, we generate data from 177 k clusters and choose state-of-the-art machine learning models within physical chemistry to train the features of this data. The generated potential gives a very high prediction accuracy on the order of the structure stability and achieves better adaptability/tolerance to poor structures of clusters. In addition, we use the machine learning potential to assist in high-throughput data collection and the prediction of hydrogen adsorption sites on cluster surfaces. We achieve more stable adsorption locations of the hydrogen atom more rapidly compared with traditional quantum chemical calculations.
1 Introduction
Iron-based catalysts have been widely adopted in many chemical processes such as ammonia synthesis (Emmett and Brunauer, 1934; Emmett and Brunauer, 1937), Fischer–Tropsch synthesis (FTS) (Fischer and Tropsch, 1923; Fischer and Tropsch, 1926), CO oxygenation (Li et al., 2003; Qiao et al., 2011), and propane dehydrogenation (Sun et al., 2015; Tan et al., 2016). Among them, iron carbides are commonly utilized within the catalyst systems. Particularly, in FTS, which converts syngas to hydrocarbons, iron carbides (ε-Fe2C, ε′-Fe2.2C, χ-Fe5C2, θ-Fe3C, and Fe7C3) (de Smit and Weckhuysen, 2008; de Smit et al., 2009; Liu et al., 2017) are usually regarded as the active phases. However, under practical conditions, the catalysts are usually present as mixture phases and exhibit a wide range of nanocluster size distributions (Herranz et al., 2006; Chang et al., 2018). Iron particles are also active as catalysts for carbon nanotube preparation, which is a highly promising material for application as catalyst substrates or energy conversion systems (Baughman et al., 2002; Kumar and Ando, 2010; Pant et al., 2021).
For the bulk iron carbides, the structures are usually observed as a distorted metal lattice, with the carbon atoms located at interstitial sites determined by geometric and electronic factors (Oyama, 1992). In θ-Fe3C (cementite), χ-Fe5C2 (Hägg carbide), and Fe7C3, carbon atoms are in the trigonal prismatic interstices (de Smit and Weckhuysen, 2008), while ε-Fe2C and ε′-Fe2.2C possess structures with carbon atoms occupying the octahedral interstices. For small FexCy clusters [e.g., FeC, FeC2, FeCn (n = 3–6), and FenCm (n = 1, 2, 3 and m = 2–8)], extensive experimental work has found a variety of compositions, structures, and even catalytic properties from the mass spectra and gas phase ion chromatograph (Fan and Wang, 1994; Drechsler et al., 1995; von Helden et al., 1994; Steglich et al., 2014; Pilgrim and Duncan, 1993). Computationally, the detailed structures and bond strength of iron carbide clusters are determined by energetic calculations (Nash et al., 1996; Tzeli and Mavridis, 2002; Gutsev and Bauschlicher, 2003; Noya et al., 2003; Ryzhkov et al., 2005; Ryzhkov et al., 2008; Largo et al., 2009; Ryzhkov and Delley, 2012; Li et al., 2013; Chen and Xie, 2014). For example, the ground states for FeC2∼4 are fan-like structures, while linear and cyclic geometries are more stable structures for FeC5 and FeC6∼10, respectively (Zhu and Li, 2009). Zheng et al. (2016) investigated FexCy (x ≤ 8; y ≤ 8) clusters combining structure searching and optimization by density functional theory and found that carbon chains are energetically preferred in carbon rich clusters. In addition, the catalytic reaction mechanisms on the clusters are also estimated with calculated energies (Li et al., 2015). However, in various catalysis systems, a huge class of iron carbides with varying element numbers and configurations should be calculated to fully represent the potential structures that exist, especially in FTS where thousands of possible elementary reactions and complex catalyst components occur. Fast and accurate methods are desperately needed to reduce the expensive structural explorations. The community needs an advanced high-throughput calculator to explore metal carbide/oxide cluster systems.
Machine learning (ML) has emerged as a powerful new tool in chemistry (Butler et al., 2018; Xie and Grossman, 2018; Ye et al., 2018), driven in part by the advent of large material datasets from high-throughput electronic structure calculations. To the best of our knowledge, differently from some famous benchmarks in molecules (such as QM9, with 134 k molecules) and crystals (such as MatBench, which contains many datasets, with 132 k samples at most), no cluster benchmark has been published for iron carbides. Therefore, we must first develop a cluster dataset to provide the necessary exploration framework.
The scientific community has developed a wide variety of molecular representation methods for machine learning approaches to structure optimization—for example, SIFF (Structural Information Filtered Features) developed by Lewis et al. (Zeledon et al., 2020), SMILES (Simplified Molecular Input Line Entry Specification) (Weininger et al., 1989), SOAP (Smooth Overlap of Atomic Positions) (Bartók et al., 2013), CM (Coulomb Matrix) (Rupp et al., 2012), pymatgen (Python Materials Genomics) (Ong et al., 2013), and others. As an integral part of the ML architecture, the representation or defined features of molecular entities play a vital role in how accurately the ML model predicts the desired properties. Many machine learning approaches have been developed with an aim toward drug discovery (Yang et al., 2019; Chen et al., 2019; Feinberg et al., 2018; Schütt et al., 2018). Many approaches have focused on organic molecules, which mainly contain C, H, O, and N. However, for heterogeneous catalysis, we need representations that are appropriate for clusters containing transition metal atoms. Therefore, we evaluate the performance on cluster prediction using state-of-the-art machine learning models such as graph networks, MEGNet (Chen et al., 2019), or the continuous-filter convolutional neural network SchNet (Schütt et al., 2018).
In this work, we use the structure generation software combined with a first-principles calculator to search the structure of iron carbide clusters. We generate an Fe-C machine learning potential that is data driven from the high-throughput calculations of many clusters. There are several advantages of machine learning potentials compared to purely traditional quantum chemistry calculations for cluster structure optimization. The relative energy will determine the thermodynamic stability of different structures, and the equilibrium geometric configurations are found more rapidly using machine learning potentials. There is a demonstrated significant improvement in calculation speed for machine learning algorithms. Our work was released as an open-source code within a GitHub repository located at https://github.com/tony-dd/FeC_prediction.
2 Computational methodology
2.1 Clusters generation
In our dataset, we generate iron carbide clusters using the Crystal Structure Analysis by Particle Swarm Optimization (CALYPSO) code (Lv et al., 2012; Wang et al., 2012). The geometry optimization and energy calculations come from the Vienna Ab-initio Simulation Package (VASP) (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). Within these calculations, the electron–ion interactions are described from projector augmented wave (PAW) (Blöchl, 1994; Kresse and Joubert, 1999) potentials, and the electron exchange and correlation energy are treated by the Perdew–Burke–Ernzerhof (PBE) function, including spin polarization (Perdew et al., 1996). All calculations are performed within a box size of 15 Å to simulate a cluster calculation The cut-off energy of 400 eV and Gaussian smearing with the width of 0.1 eV with the Gamma k-point sampling ensure accurate energies for the Fe-C clusters.
2.2 Clusters energy prediction
We have generated over 177 thousand structures and divided the entire dataset into nine parts according to the stoichiometric count of the iron atoms within the cluster. Detailed distributions of each group within the dataset are provided in Table 1.
MEGNet and SchNet are proven to work well with the QM9, MD17, and ISO17 datasets; hence, we choose these methods to predict our Fe-C clusters. The molecular representation, or features, of MEGNet is in the pymatgen format. We label the molecular representation of SchNetPack as ‘SchNet’, because SchNetPack does not report the format of its molecular representation. We first use the ASE package to process each cluster structure and then fit structural representations of all the clusters to the two different feature representations—pymatgen and SchNet. During the training of our data, we use the default parameters that are found within MEGNet and SchNetPack. A cross-validation training strategy yields the best results by randomly shuffling and training all but one of the nine datasets and testing on the final dataset. This approach reduces the influence of the data proximity and thereby generalizes the performance of the models. The validation error is monitored, and the training is stopped when the validation error does not improve for 20 consecutive epochs. The models are trained on Nvidia RTX 3080 GPUs. Most models reach convergence within 500 epochs. On average, the training process takes 50 s and 80 s per epoch for each model, respectively. All chemistry structure calculations are handled using the Atomic Simulation Environment (ASE) (Larsen et al., 2017). Finally, we get nine trained models, and we develop the average predicted results to fit the final potential function.
2.3 Hydrogen adsorption prediction
The machine learning models need retraining from a new dataset when modeling the location of hydrogen absorption on the Fe-C clusters. We apply the SchNet model to assist VASP in optimizing structures to generate a new dataset, which reduces a lot of the computing and time cost. More specifically, we select two structures with the largest variation in shape for each stoichiometry of the FexCy structure. The variation is defined by comparing the proportions of the long and short axes of the cluster. Figure 1 shows the calculation of the long and short axes of one structure. The convex hulls of the selected structures are calculated using SciPy. We introduce hydrogen atoms randomly on the planes parallel to the convex hulls and at 1 Å, as shown in Figure 2. The potentials of Fe and C are trained from the previous models, so the machine learning models can be used to optimize iron and carbon atoms in the new Fe-C clusters. The models optimize the structures, which significantly shortens the optimization calculation time. Finally, the structures processed by the models are optimized by VASP to obtain the final dataset.
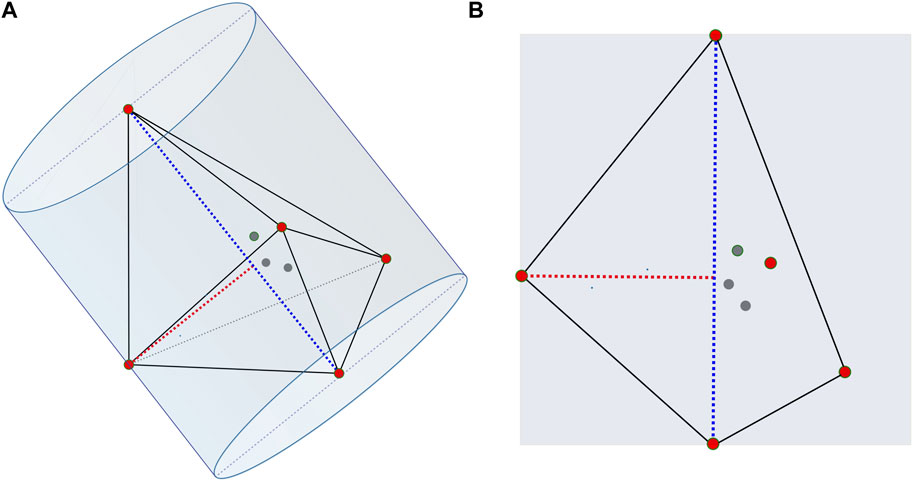
FIGURE 1. Long and short axes calculation of a certain Fe4C4. The blue dotted line, the long axis, is the farthest distance between the two atoms. The red dotted line, the short axis, is the farthest distance from the atom to the long axis. The central axis of the cylinder is the long axis, and the short axis is the radius. (B) is a cross-section of (A).
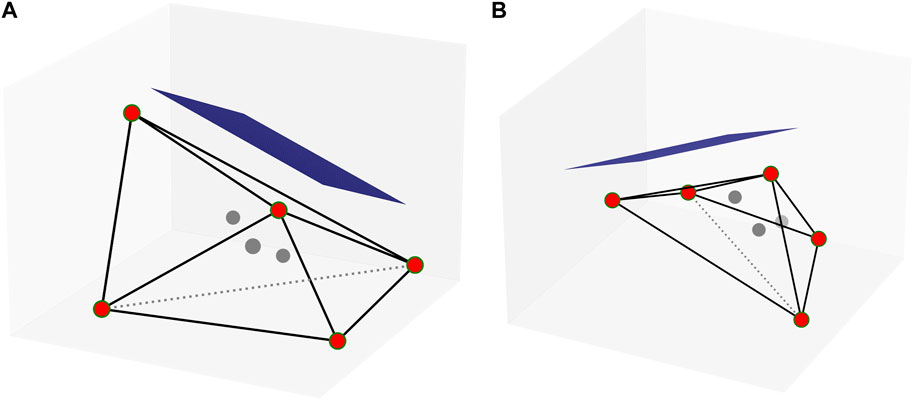
FIGURE 2. Convex hull of a certain Fe4C4 from two perspectives. The red circles are on the convex hull, and the gray circle is inside the convex hull. The blue planes are parallel to the surfaces of the convex hull, and the quantity is equal to the number of convex hull surfaces. The hydrogen atoms are randomly selected on the blue planes.
The final trained models from the new datasets will predict the adsorption position of hydrogen atoms on the surface of the Fe-C clusters. As a demonstration of our approach, we have selected a stable Fe5C2 cluster from our initial dataset and randomly introduced a hydrogen atom on the surface. Fixing iron and carbon atoms in the structure, we conduct the following computational steps:
(I) Optimize the hydrogen absorption by VASP.
(II) Optimize it next by SchNet and VASP and use the conjugate gradient method for SchNet local optimization.
(III) Optimize it also by SchNet and VASP but use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm and SchNet local optimization
We utilize both the conjugate gradient and BFGS to show the influence of different optimization algorithms on the results.
3 Results and discussion
The distribution of the difference between the predicted values and actual values will provide an evaluation of the predicted accuracy of our machine learning models. We plot these results in Figure 3. The different colors represent the different testing sets. The average errors between the predicted values and the actual value are within 0.5 eV. In addition to the absolute values of prediction, the relative order accuracy (ROA) of the results represents a more significant evaluation of the model accuracy. The relative order accuracy evaluates the final optimized structure directly by using energy as a convergence condition. We sort the test data according to the DFT calculated values, shown in Figure 3, and assign each dataset an identifier: m1, m2, …, etc. We reorder the test data according to the potential energy predicted by the model and calculate the inversion number I of each set and rearrange each set according to the inversion number (as discussed in the Supplementary Material).
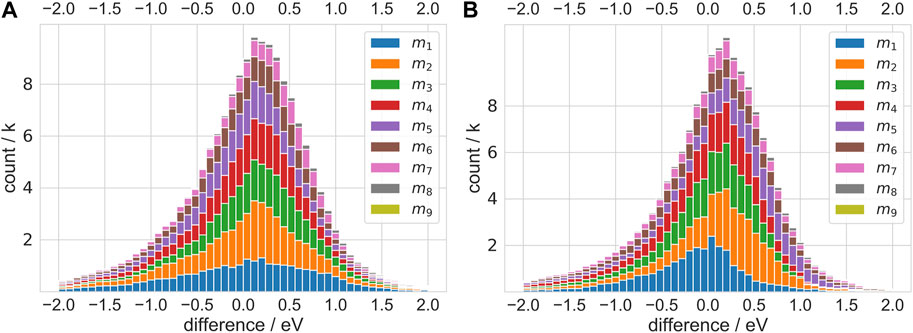
FIGURE 3. Error distribution histogram. The difference refers to the difference between the predicted value and the DFT calculated values for each structure. The mi (1 ≤ i ≤ 9) means FeiCy for test and others for training.
Table 2 shows the comparison of the prediction results with the DFT calculated values, including the mean absolute errors (MAEs) and ROAs for MEGNet and SchNet. The average MAEs of the results are below 0.8 eV, and the average ROAs of prediction are above 95%. It can be seen that the ability of machine learning models to predict the ROA is excellent, which can ensure the reliability of the structural optimization. It is interesting that potential energy prediction MAE of m3 is the smallest. We suggest the deviation of potential energy prediction is related to the average atoms count in the test and the coverage of the training set on the test set. In mi (i ≤ 3), we output the intermediate vectors predicted by MEGNet to verify the relationship between the MAEs and the coverage of the training set on the test set. Figure 4 shows the results after the intermediate vector dimension reduction. Through comparison, we find that the coverage of m3 training data on the test data exceeds m1 significantly, which can explain the previous observation to a certain extent. In mj (j ≥ 4), the deviation of potential energy prediction increases with the average number of atoms. When the average number of atoms in the test set exceeds 8, the MAEs are mainly affected by that.
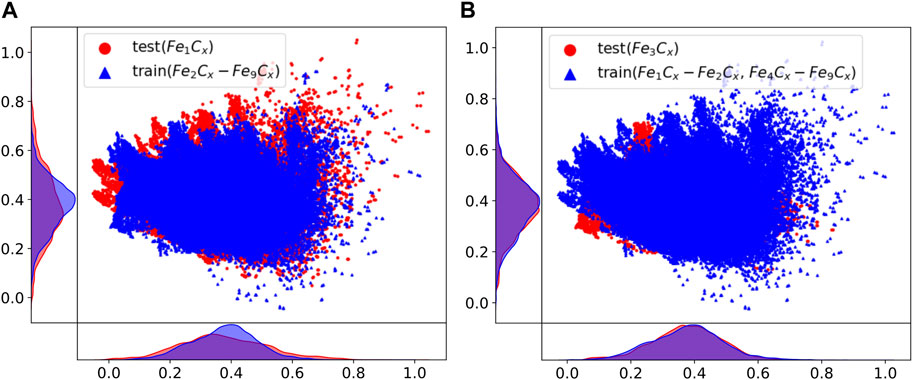
FIGURE 4. Structural information coverage projected onto two-dimensional space after dimension reduction. Scatter points in the test set are drawn first, and information on the training set is drawn on the upper layer. More exposure to the test points means less coverage of the training dataset.
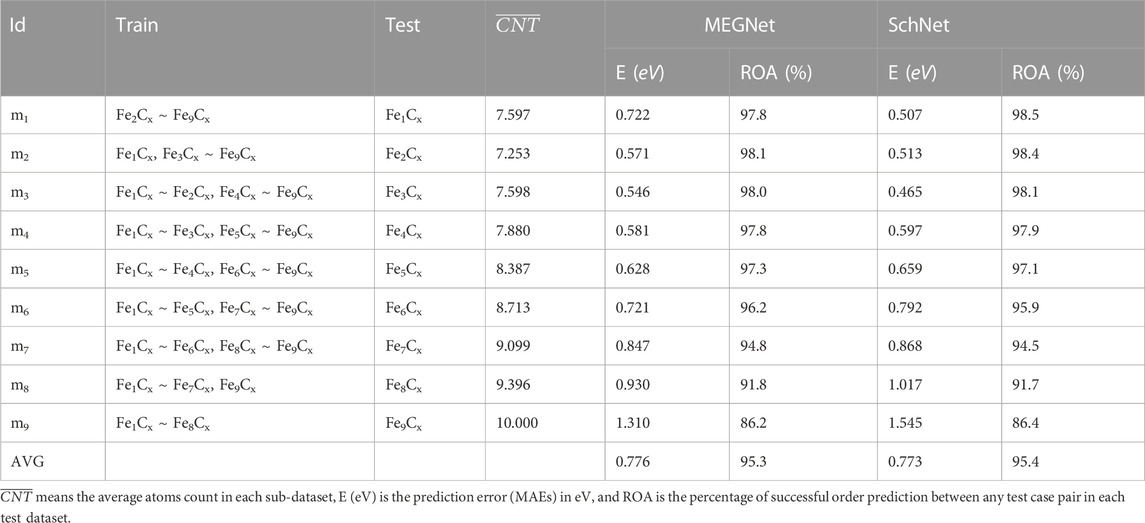
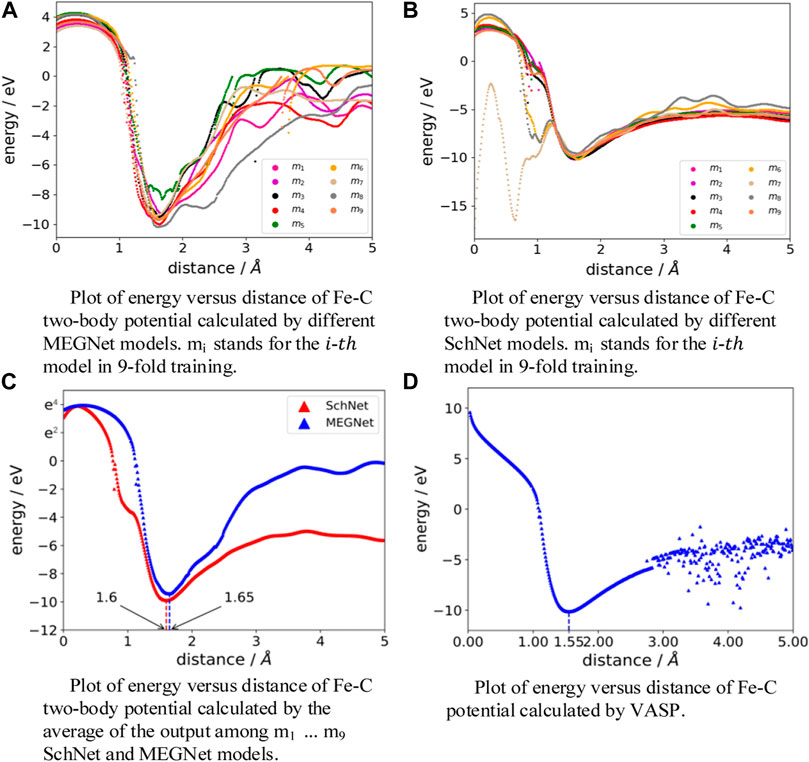
The high accuracy of the relative order shows that machine learning models have excellent performance in judging structural stability. To further demonstrate this point, we apply models to predict the relationship between the potential energy and the Fe-C distances, comparing the results with the calculation results of VASP. Detail information is shown in Figure 5. The distance between Fe and C is 0–5 Å, and the step length is 0.01 Å. Therefore, there are 500 points in each curve that show the relationship between the Fe-C distance and the potential energy. We focus on the trend of the curves and the lowest points representing the most stable distances. The trend and the lowest points of the curves predicted by MEGNet and SchNet are roughly the same throughout Figures 5A, B. We average the results of the MEGNet and SchNet models and visualize this average in Figure 5C. The result of the VASP calculation is shown in Figure 5D as a reference. According to the calculation of VASP, the change of the potential energy is no longer apparently regular when the distance of Fe-C exceeds 3 Å. The most stable distance of Fe-C predicted by MEGNet and SchNet differs from VASP by 0.1 Å and 0.05 Å, respectively, as observed in Figures 5C, D.
We randomly generate 100 Fe5C5 poor initial structures to investigate the adaptability of models in structural optimization. These initial structures are considered poor in that VASP cannot optimize these structures. Traditional quantum chemical calculators such as VASP can effectively predict cluster geometries with a high level of accuracy. However, poor guesses from the user will add costly computational cycles in the performance, and these quantum chemistry tools struggle with out-of-the-box initial geometries. We test these 100 Fe5C5 poor initial structures so that we can obtain an understanding of the performance of VASP in extreme cases and compare them with our machine learning approach. We also generate several typical Fe5C5 clusters to verify the performance of the structure optimization of the SchNet machine learning models. The SchNet model is treated as a ‘calculator’ of ASE, and BFGSLineSearch is used for local optimization. After about 100 steps of optimization, the potential energy of structures decreases rapidly by more than 10 eV while each step takes less than one second (as seen in Supplementary Figure S4). We find stable structures in a short time without expensive first-principles calculations.
Based on this, we generate 10 k new FexCyH data by the method in Section 2.3 and use VASP to perform a single point calculation for most of these structures with the same parameters as Section 2.1. We continue to train previous machine learning models with the new dataset to predict the adsorption position of hydrogen atoms. Table 3 shows the results of structural optimization of the hydrogen absorption calculations with iron and carbon atoms fixed in Section 2.3. In (Ⅰ), the potential energy of the structure is reduced by 1.62 eV. In (Ⅱ), the SchNet model can more rapidly reduce the potential energy of the structure by more than three times in less than 1% optimization time compared with VASP. In (Ⅱ) and (Ⅲ), the difference of the final structural potential energy is within 1 eV after VASP optimization to convergence. As a result, different local optimization algorithms have little effect on the results. Meanwhile, our results show that the model will optimize the structure to a more stable state than VASP in a much shorter time, and SchNet can also assist VASP in finding the most stable adsorption position by improving the initial guesses.
4 Conclusion
To conclude, we use CALYPSO and VASP for iron carbide cluster generation and apply state-of-the-art molecular properties prediction networks to the potential energy prediction of clusters and structural optimization. Although there are errors between machine learning models and DFT calculation methods in cluster potential energy prediction, the performance of models in judging structural stability is excellent. As a result, machine learning models can provide reliable structural optimization. In terms of cluster structure optimization, the machine learning models can obtain a more stable structure than VASP in a shorter time. Further, they can be used to assist VASP in finding the most stable adsorption position on the cluster surface in the catalytic process. This work is helpful in exploring the essential control factors of catalytic reaction activity and selectivity and realizing the regulation of catalyst activity and selectivity.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. All authors contributed to the article and approved the submitted version.
Funding
This project was supported by the National Natural Science Foundation of China (No. 22002008), National Key R&D Program of China (No. 2021YFB2600600), and the Ningxia Key Research and Development Project (No. 2022BEE03002). Additional funding was provided to the Institute of Data Science for promoting the development of universities for key research and cultivation projects (No. 2121YJPY225) and for building innovation capacity for scientific research institutions.
Conflict of interest
Author JL was employed by Synfuels China Co. Ltd.—SynCat@Beijing and Author JL was employed by Hong Kong Quantum AI Laboratory, Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frqst.2023.1190522/full#supplementary-material
References
Bartók, A. P., Kondor, R., and Csányi, G. (2013). On representing chemical environments. Phys. Rev. B 87 (18), 184115. doi:10.1103/physrevb.87.184115
Baughman, R. H., Zakhidov, A. A., and De Heer, W. A. (2002). Carbon nanotubes--the route toward applications. science 297 (5582), 787–792. doi:10.1126/science.1060928
Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50 (24), 17953–17979. doi:10.1103/physrevb.50.17953
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O., and Walsh, A. (2018). Machine learning for molecular and materials science. Nature 559 (7715), 547–555. doi:10.1038/s41586-018-0337-2
Chang, Q., Zhang, C., Liu, C., Wei, Y., Cheruvathur, A. V., Dugulan, A. I., et al. (2018). Relationship between iron carbide phases (ε-Fe2C, Fe7C3, and χ-Fe5C2) and catalytic performances of Fe/SiO2 Fischer–Tropsch catalysts. ACS Catal. 8 (4), 3304–3316. doi:10.1021/acscatal.7b04085
Chen, C., Ye, W., Zuo, Y., Zheng, C., and Ong, S. P. (2019). Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31 (9), 3564–3572. doi:10.1021/acs.chemmater.9b01294
Chen, Z.-H., and Xie, Z. (2014). The geometries, electronic structures and magnetic properties of TM doped cn (TM= Fe, Co, Ni, n= 9–15) clusters: A density functional theory investigation. Eur. Phys. Journal-Applied Phys. 67 (1), 10403. doi:10.1051/epjap/2014140121
de Smit, E., Beale, A. M., Nikitenko, S., and Weckhuysen, B. M. (2009). Local and long range order in promoted iron-based fischer–tropsch catalysts: A combined in situ X-ray absorption spectroscopy/wide angle X-ray scattering study. J. Catal. 262 (2), 244–256. doi:10.1016/j.jcat.2008.12.021
de Smit, E., and Weckhuysen, B. M. (2008). The renaissance of iron-based fischer–tropsch synthesis: On the multifaceted catalyst deactivation behaviour. Chem. Soc. Rev. 37 (12), 2758. doi:10.1039/b805427d
Drechsler, G., Bäßmann, C., Boesl, U., and Schlag, E. (1995). Structure analysis of high reactive metal catalysts intermediates by a combination of mass spectrometry and photodetachment-ZEKE-photoelectron spectroscopy. J. Mol. Struct. 348, 337–340. doi:10.1016/0022-2860(95)08657-h
Emmett, P., and Brunauer, S. (1934). The adsorption of nitrogen by iron synthetic ammonia catalysts. J. Am. Chem. Soc. 56 (1), 35–41. doi:10.1021/ja01316a011
Emmett, P. H., and Brunauer, S. (1937). The use of low temperature van der Waals adsorption isotherms in determining the surface area of iron synthetic ammonia catalysts. J. Am. Chem. Soc. 59 (8), 1553–1564. doi:10.1021/ja01287a041
Fan, J., and Wang, L.-S. (1994). A study of FeC2 and FeC2H by anion photoelectron spectroscopy. J. Phys. Chem. 98 (46), 11814–11817. doi:10.1021/j100097a002
Feinberg, E. N., Sur, D., Wu, Z., Husic, B. E., Mai, H., Li, Y., et al. (2018). PotentialNet for molecular property prediction. ACS central Sci. 4 (11), 1520–1530. doi:10.1021/acscentsci.8b00507
Fischer, F., and Tropsch, H. (1926). Die Erdölsynthese bei gewöhnlichem Druck aus den Vergasungsprodukten der Kohlen. Brennst. Chem. 7, 97.
Fischer, F., and Tropsch, H. (1923). Uber die Herstellung synthetischer olgemische (Synthol) durch Aufbau aus Kohlenoxyd und Wasserstoff. Brennst. Chem. 4, 276.
Gutsev, G. L., and Bauschlicher, C. W. (2003). Interaction of carbon atoms with Fen, Fen−, and Fen+ clusters (n= 1–6). Chem. Phys. 291 (1), 27–40. doi:10.1016/s0301-0104(03)00157-5
Herranz, T., Rojas, S., Pérez-Alonso, F. J., Ojeda, M., Terreros, P., and Fierro, J. L. G. (2006). Genesis of iron carbides and their role in the synthesis of hydrocarbons from synthesis gas. J. Catal. 243 (1), 199–211. doi:10.1016/j.jcat.2006.07.012
Kresse, G., and Furthmüller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6 (1), 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. b 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758
Kumar, M., and Ando, Y. (2010). Chemical vapor deposition of carbon nanotubes: A review on growth mechanism and mass production. J. Nanosci. Nanotechnol. 10 (6), 3739–3758. doi:10.1166/jnn.2010.2939
Largo, L., Barrientos, C., and Redondo, P. (2009). Small iron doped carbon clusters: A comparison with early and late first-row transition metal doped clusters. J. Chem. Phys. 130 (13), 134304. doi:10.1063/1.3095423
Larsen, A. H., Mortensen, J. J., Blomqvist, J., Castelli, I. E., Christensen, R., Dułak, M., et al. (2017). The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 29 (27), 273002. doi:10.1088/1361-648x/aa680e
Li, H.-F., Li, Z.-Y., Liu, Q.-Y., Li, X.-N., Zhao, Y.-X., and He, S.-G. (2015). Methane activation by iron-carbide cluster anions FeC6. J. Phys. Chem. Lett. 6 (12), 2287–2291. doi:10.1021/acs.jpclett.5b00937
Li, P., Miser, D. E., Rabiei, S., Yadav, R. T., and Hajaligol, M. R. (2003). The removal of carbon monoxide by iron oxide nanoparticles. Appl. Catal. B Environ. 43 (2), 151–162. doi:10.1016/s0926-3373(02)00297-7
Li, R., Peverati, R., Isegawa, M., and Truhlar, D. G. (2013). Assessment and validation of density functional approximations for iron carbide and iron carbide cation. J. Phys. Chem. A 117 (1), 169–173. doi:10.1021/jp3079106
Liu, X.-W., Cao, Z., Zhao, S., Gao, R., Meng, Y., Zhu, J.-X., et al. (2017). Iron carbides in Fischer–Tropsch synthesis: Theoretical and experimental understanding in epsilon-iron carbide phase assignment. J. Phys. Chem. C 121 (39), 21390–21396. doi:10.1021/acs.jpcc.7b06104
Lv, J., Wang, Y., Zhu, L., and Ma, Y. (2012). Particle-swarm structure prediction on clusters. J. Chem. Phys. 137 (8), 084104. doi:10.1063/1.4746757
Nash, B. K., Rao, B., and Jena, P. (1996). Equilibrium structure and bonding of small iron–carbon clusters. J. Chem. Phys. 105 (24), 11020–11023. doi:10.1063/1.472901
Noya, E., Longo, R., and Gallego, L. (2003). Density-functional calculations of the structures, binding energies, and spin multiplicities of Fe–C clusters. J. Chem. Phys. 119 (21), 11130–11134. doi:10.1063/1.1622378
Ong, S. P., Richards, W. D., Jain, A., Hautier, G., Kocher, M., Cholia, S., et al. (2013). Python materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319. doi:10.1016/j.commatsci.2012.10.028
Oyama, S. T. (1992). Preparation and catalytic properties of transition metal carbides and nitrides. Catal. today 15 (2), 179–200. doi:10.1016/0920-5861(92)80175-m
Pant, M., Singh, R., Negi, P., Tiwari, K., and Singh, Y. (2021). A comprehensive review on carbon nano-tube synthesis using chemical vapor deposition. Mater. Today Proc. 46, 11250–11253. doi:10.1016/j.matpr.2021.02.646
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865
Perdew, J. P., and Wang, Y. (1992). Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45 (23), 13244–13249. doi:10.1103/physrevb.45.13244
Pilgrim, J., and Duncan, M. (1993). Metallo-carbohedrenes: Chromium, iron, and molybdenum analogs. J. Am. Chem. Soc. 115 (15), 6958–6961. doi:10.1021/ja00068a065
Qiao, B., Wang, A., Yang, X., Allard, L. F., Jiang, Z., Cui, Y., et al. (2011). Single-atom catalysis of CO oxidation using Pt1/FeO x. Nat. Chem. 3 (8), 634–641. doi:10.1038/nchem.1095
Rupp, M., Tkatchenko, A., Müller, K.-R., and Von Lilienfeld, O. A. (2012). Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108 (5), 058301. doi:10.1103/physrevlett.108.058301
Ryzhkov, M., and Delley, B. (2012). Geometry, electronic structure, and magnetic ordering of iron–carbon nanoparticles. Theor. Chem. Accounts 131, 1144. doi:10.1007/s00214-012-1144-8
Ryzhkov, M., Ivanovskii, A., and Delley, B. (2008). Geometry, electronic structure and energy barriers of all possible isomers of Fe 2 C 3 nanoparticle. Theor. Chem. Accounts 119, 313–318. doi:10.1007/s00214-007-0385-4
Ryzhkov, M. V., Ivanovskii, A. L., and Delley, B. T. (2005). Electronic structure and geometry optimization of nanoparticles Fe2C, FeC2, Fe3C, FeC3 and Fe2C2. Chem. Phys. Lett. 404 (4-6), 400–408. doi:10.1016/j.cplett.2005.01.114
Schütt, K., Kessel, P., Gastegger, M., Nicoli, K., Tkatchenko, A., and Müller, K.-R. (2018). computation. SchNetPack: A deep learning toolbox for atomistic systems. J. Chem. theory 15 (1), 448.
Steglich, M., Chen, X., Johnson, A., and Maier, J. P. (2014). UV spectra of iron-doped carbon clusters FeCn n= 3–6. Int. J. mass Spectrom. 365, 351–355. doi:10.1016/j.ijms.2014.02.006
Sun, Y., Wu, Y., Shan, H., Wang, G., and Li, C. (2015). Studies on the promoting effect of sulfate species in catalytic dehydrogenation of propane over Fe 2 O 3/Al 2 O 3 catalysts. Catal. Sci. Technol. 5 (2), 1290–1298. doi:10.1039/c4cy01163e
Tan, S., Hu, B., Kim, W.-G., Pang, S. H., Moore, J. S., Liu, Y., et al. (2016). Propane dehydrogenation over alumina-supported iron/phosphorus catalysts: Structural evolution of iron species leading to high activity and propylene selectivity. ACS Catal. 6 (9), 5673–5683. doi:10.1021/acscatal.6b01286
Tzeli, D., and Mavridis, A. (2002). Theoretical investigation of iron carbide, FeC. J. Chem. Phys. 116 (12), 4901. doi:10.1063/1.1450548
von Helden, G., Gotts, N. G., Maitre, P., and Bowers, M. T. (1994). The structures of small iron-carbon cluster anions. Linear to planar to three-dimensional. Chem. Phys. Lett. 227 (6), 601–608. doi:10.1016/0009-2614(94)00871-x
Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). Calypso: A method for crystal structure prediction. Comput. Phys. Commun. 183 (10), 2063–2070. doi:10.1016/j.cpc.2012.05.008
Weininger, D., Weininger, A., Weininger, J. L., and Sciences, C. (1989). SMILES. 2. Algorithm for generation of unique SMILES notation. J. Chem. Inf. 29 (2), 97–101. doi:10.1021/ci00062a008
Xie, T., and Grossman, J. C. (2018). Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120 (14), 145301. doi:10.1103/physrevlett.120.145301
Yang, K., Swanson, K., Jin, W., Coley, C., Eiden, P., Gao, H., et al. (2019). Analyzing learned molecular representations for property prediction. J. Chem. Inf. 59 (8), 3370–3388. doi:10.1021/acs.jcim.9b00237
Ye, W., Chen, C., Wang, Z., Chu, I.-H., and Ong, S. P. (2018). Deep neural networks for accurate predictions of crystal stability. Nat. Commun. 9 (1), 3800. doi:10.1038/s41467-018-06322-x
Zeledon, J. A. H., Romero, A. H., Ren, P., Wen, X., Li, Y., and Lewis, J. P. (2020). The structural information filtered features (SIFF) potential: Maximizing information stored in machine-learning descriptors for materials prediction. J. Appl. Phys. 127 (21), 215108. doi:10.1063/5.0002252
Zheng, L., Liu, X., Meng, Y., Zhou, Y., Guo, W., Peng, Q., et al. (2016). How far away are iron carbide clusters from the bulk? Phys. Chem. Chem. Phys. 18 (48), 32944–32951. doi:10.1039/c6cp06224e
Keywords: iron carbide clusters, machine learning potentials, adsorbate prediction, cluster optimization, high-throughput data analysis
Citation: Diao E, He Y, Liu X, Tong Q, Yang T, Liu X and Lewis JP (2023) First principles data-driven potentials for prediction of iron carbide clusters. Front. Quantum Sci. Technol. 2:1190522. doi: 10.3389/frqst.2023.1190522
Received: 21 March 2023; Accepted: 25 April 2023;
Published: 25 May 2023.
Edited by:
Abolfazl Alizadeh Sahraei, Laval University, CanadaReviewed by:
Bhupesh Mishra, Dera Natung Government College, IndiaKaterine Paredes Gil, Metropolitan University of Technology, Chile
Copyright © 2023 Diao, He, Liu, Tong, Yang, Liu and Lewis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James P. Lewis, amFtZXMucC5sZXdpcy5waGRAZ21haWwuY29t
†These authors have contributed equally to this work
 Enhu Diao
Enhu Diao Yurong He1,3,4†
Yurong He1,3,4† James P. Lewis
James P. Lewis