Detection of infrared light through stimulated four-wave mixing process

Infrared optical measurement has a wide range of applications in industry and science, but infrared light detectors suffer from high costs and inferior performance than visible light detectors. Four-wave mixing (FWM) process allows detection in the infrared range by detecting correlated visible light. We experimentally investigate the stimulated FWM process in a hot ⁸⁵Rb atomic vapor cell, in which a weak infrared signal laser at 1,530 nm induces the FWM process and is amplified and converted into a strong FWM light at 780 nm, the latter can be detected more easily. We find the optimized single- and two-photon detunings by studying the dependence of the frequency of input laser on the generated FWM light. What’s more, the power gain increases rapidly as the signal intensity decreases, which is consistent with our theoretical analysis. As a result, the power gain can reach up to 500 at a signal laser power of 0.1 μW and the number of detected photons increased by a factor of 250. Finally, we experimentally prove that our amplification process can work in a broad band in the frequency domain by exploring the response rate of our stimulated FWM process.

1 Introduction

Infrared optical measurement is an important technique for applications in scientific research and industrial production. However, infrared light detectors in infrared optical devices have higher dark count rates, lower specific detectivities, and higher cost than the detector in the visible range, and often need to be cooled (Griffiths and de Haseth, 2007). For this dilemma, researchers correlate infrared light with visible light through nonlinear optical phenomena, and measure infrared light by detecting visible light with visible light detectors (Kalashnikov et al., 2016; Paterova et al., 2018). Four-wave mixing (FWM) is a common method for generating high-power visible light (Lavoute et al., 2010) and converting infrared light to visible light (Ding et al., 2012a, d, e), the latter is investigated in our work.

Four-wave mixing process is one of the prominent nonlinear optical phenomena (Yariv and Pepper, 1977) and originates from the third-order optical nonlinear effects in the interaction of optical fields with a nonlinear medium. In atomic system, the FWM process has been explored extensively due to its wide applications such as observing optical parametric amplification in the process of degenerate stimulated four-photon interaction (Carman et al., 1966) and optical precursors phenomena (Ding et al., 2015); generating non-classical correlated photon pairs (Ding et al., 2012c; Liu et al., 2012; Dong et al., 2017; Yu et al., 2018) via the spontaneous FWM process for use in long-distance quantum communication (Duan et al., 2001) and optical quantum information processing (Zhang et al., 2020a); observing squeezed light (Slusher et al., 1985) and strong relative intensity squeezing (McCormick et al., 2007); exhibiting localized entanglement of twin images (Boyer et al., 2008); and converting frequency of the optical field (Radnaev et al., 2010; Ding et al., 2012b). The FWM process has been realized in atomic system with various energy-level configurations such as double-ladder type (Lee et al., 2016; Lee and Moon, 2017a), double-lambda type (Ding et al., 2013b; Zhang et al., 2018; Yu et al., 2020), diamond type (Ding et al., 2013a; Shi et al., 2020) and inverted-Y type (Wen et al., 2008). In this paper, we focus on a four-level system with a diamond-type configuration.

The stimulated FWM process with a four-level atomic system is an extensively researched topic in a double-ladder or diamond configuration. This phenomenon requires the interaction of three optical fields with the atoms in which two strong fields excite the atoms to a higher excited state (such as 5D or 4D state in rubidium atomic system) and a weak seed (driving) field induces the atoms to generate a strong FWM field. This process is also referred to as seeded FWM in some works (Zhang et al., 2020b). To date, the stimulated FWM process in a ladder-type atomic system has been studied to investigate the effects of atomic coherence on the FWM spectrum (Lee and Moon, 2016) or the relationship between three-photon electromagnetically induced absorption and FWM (Lee and Moon, 2017b). The biphoton spectral wave form of photon pairs emitted from a cascade-type atomic ensemble also can be measured by using the stimulated FWM process (Jeong et al., 2019). Recently, the amplified spontaneous emission induced self-stimulated FWM process and the stimulated FWM process have been exploited in the diamond-type atomic system (Zhang et al., 2020b), and the stimulated nondegenerate FWM phenomenon without amplified spontaneous emission has been realized in cesium atoms with a power of the generated FWM light up to 1.2 mW (Wu et al., 2022). The stimulated FWM process has also been investigated in rubidium atoms via Rydberg states (Kölle et al., 2012). To put it briefly, the stimulated FWM is generally utilized to explore precision spectroscopic measurements, atomic coherence, and efficient generation of FWM light.

In this paper, we report on an experimental exploration of the stimulated FWM process in a diamond-type ⁸⁵Rb atomic ensemble. Realizing the amplified detection of the infrared laser by converting the weak infrared signal light into the strong visible FWM light. In this work, the atoms are excited and populated in the upper state by inputting two strong pump lasers and we make an infrared beam as a seed light to induce atoms to efficiently generate the FWM light. Specifically, we find that we can achieve the purpose of amplifying and detecting the infrared signal by detecting the strong visible FWM signal which is induced by this infrared signal. In addition, in order to investigate the response properties of the amplifier, we compare the waveforms between the input signal and the output signal for various rising edge cases.

2 Experimental setup

We experimentally realized the amplified detection of infrared signal through a stimulated FWM process in hot ⁸⁵Rb atomic vapor with a four-levels diamond configuration as shown in Figure 1A. It consists of one ground state |1⟩ (5S_1/2(F = 2)), one excited state |4⟩ (4D_3/2(F′′ = 3)), and two intermediate states |2⟩ and |3⟩ (5P_1/2(F′ = 2) and 5P_3/2(F′ = 3)). The pump1 (795 nm) and pump2 (1,475 nm) lasers excite the atoms from |1⟩ to |2⟩ and |2⟩ to |4⟩ respectively, then the atoms decay into the ground state |1⟩ through the intermediate state |3⟩. Since the difference between the spontaneous decay rates (Γ₄₃) from |4⟩ to |3⟩ and the spontaneous decay rates (Γ₃₁) from |3⟩ to |1⟩ satisfies the relation Γ₄₃ = 0.1Γ₃₁, the populations of |4⟩ and |3⟩ are not significantly inversed and the FWM process cannot occur obviously in the absence of the signal laser (Zhang et al., 2020b). So that we input the signal (1,530 nm) laser which interacts with the |3⟩ − |4⟩ transition to induce the FWM, and the FWM (780 nm) light can be generated strongly in the transition from |3⟩ to |1⟩ under the phase-matching condition of wave-vector conservation and energy conservation. Through this stimulated FWM process, a weak signal laser can be converted into a strong FWM light to achieve the amplification of the infrared signal laser. The detuning frequencies of the pump1, pump2, and signal lasers correspond to Δ₁, Δ₂ and Δ₃ respectively.

FIGURE 1

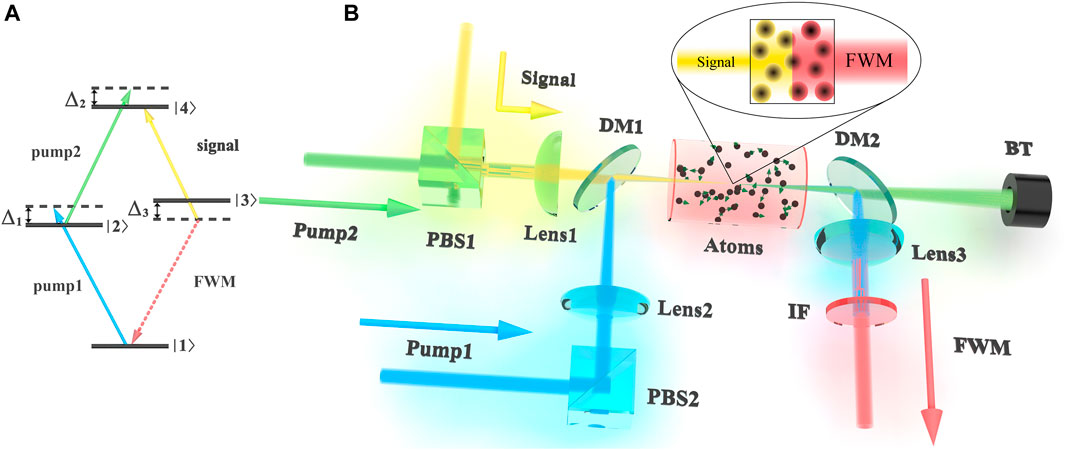
FIGURE 1. (color online) (B) Schematic diagram of the experimental setup. PBS1, PBS2: polarizing beam splitter; DM: dichroic mirror; Lens: planoconvex lens (the focal length of Lens1, Lens2 and Lens3 are 150, 300, and 150 mm respctively); IF: Interference filter; BT: beam traps. (A) Energy-level diagram of diamond configuration.

The experimental setup is schematically depicted in Figure 1B, where pump 1, pump2 and signal lasers are continuous waves (CW) and overlap in a 5-cm-long ⁸⁵Rb cell that is heated to 140°C. The horizontally polarized pump2 beam and vertically polarized signal beam are focused into the center of the cell with the same diameter of 126 μm. The vertically polarized pump1 beam is superimposed with the pump2 beam and the signal beam through a dichromatic mirror (DM1), and has a diameter of 141 μm in the focal spot. The strong pump2 laser and signal laser are filtered out by the DM2, and the pump1 laser is blocked by a subsequent interference filter (IF). A photomultiplier tube (PMT) with an adjustable attenuation collects the generated FWM light in the direction which is colinear with the pump1 laser in our system.

3 Experimental results and theoretical analysis

A critical metric to characterize the performance of our system is the power gain (G = I_F/I_s) defined as the ratio of the FWM light power (I_F) and the signal laser power (I_s). Figure 2 shows the variation of the power gain (three black curves) with the detuning frequencies of pump1, pump2, and signal lasers (Δ₁, Δ₂ and Δ₃), where the powers of the signal, pump1 and pump2 lasers are 10 μW, 110 and 110 mW respectively. In Figure 2A, the power gain are measured when we scan the detuning frequency of pump1 Δ₁ laser and the detuning frequency of pump2 Δ₂ (signal Δ₃) laser is fixed at 475 × 2π MHz (−190, ×, 2π MHz). The maximum power gain approaches 30 when the Δ₁ is equal to 0, ×, 2π MHz, and the blue curve is the saturated absorption spectrum (SAS) of the pump1 field. We can find that the power gain has two peaks when the pump1 laser is resonant with the |1⟩ − |2⟩ transition and the frequency of the signal laser is satisfied with Δ₃ = −190, ×, 2π MHz, as shown in Figure 2B. It is due to another two peaks which are corresponded to the transitions of 5S_1/2(F = 2) − 5P_1/2(F′ = 3) − 4D_3/2(F′′ = 3) and 5S_1/2(F = 2) − 5P_1/2(F′ = 2) − 4D_3/2(F′′ = 3) in the normalized two photons spectrum (TPS) of pump2 laser (green curve) and the maximum power gain occurs at the condition of Δ₂ = 475 × 2π MHz. Figure 2C displays the power gain and the normalized TPS of the signal laser (yellow curve) when we scan the Δ₃ of the signal laser under the conditions of Δ₁ = 0, ×, 2π MHz and Δ₂ = 475 × 2π MHz. It is obvious from Figure 2 that the single-photon detunings of pump and signal fields significantly affect the value of the power gain. The maximum point of the power gain reaches 30 when the Δ₁, Δ₂, and Δ₃ are fixed at 0, ×, 2π MHz, 475 × 2π MHz, and −190, ×, 2π MHz respectively.

FIGURE 2

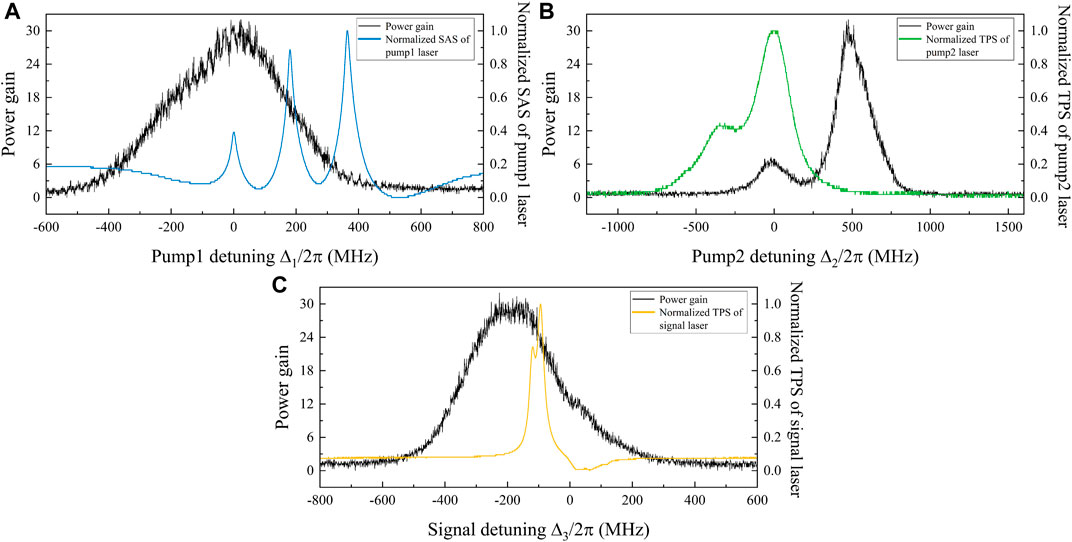
FIGURE 2. (color online) (A) Power gain (black curve) and normalized SAS of the pump1 laser (blue curve) against the detuning of the pump1 laser. (B) Power gain (black curve) and normalized SAS of the pump2 laser (green curve) against the detuning of the pump2 laser. (C) Power gain (black curve) and normalized TPS of the signal laser (yellow curve) against the detuning of the signal laser.

In Figure 3, we plot the power gain as a function of the signal power I_s under the optimal experimental conditions we mentioned above, and the power is measured with a power meter instead of the PMT. Due to the strong pump1 and pump2 lasers, the atoms are mostly populated at the state |4⟩ via two-photon excitation. Meanwhile, the weak signal laser is converted and amplified into a strong FWM light. We can fetch the information from Figure 3 that the power gain increases rapidly with the decrease of the signal power. Figure 3A indicates that the power gain exceeds 100 when the power of the signal laser is less than 2 μW, and the power gain can be reached up to 500 in the case of I_s = 0.1 μW. The amplification effect exhibits a tendency to saturation when the signal power intensity is beyond 1 mW, which is illustrated in Figure 3B. We also can defined the photon-number gain (or detection gain) G_photon in this amplification process as the ratio of the number of output visible photons to the number of input infrared photons. Considering that the energy of a photon is inversely proportional to its wavelength, we can obtain the relationship G_photon = 0.5G between photon-number gain and power gain. Similarly, the photon-number gain can reach 250 at the case of I_s = 0.1 μW according to Figure 3B, which means that the number of photons detected by a detector is increased from 1 to 250.

FIGURE 3

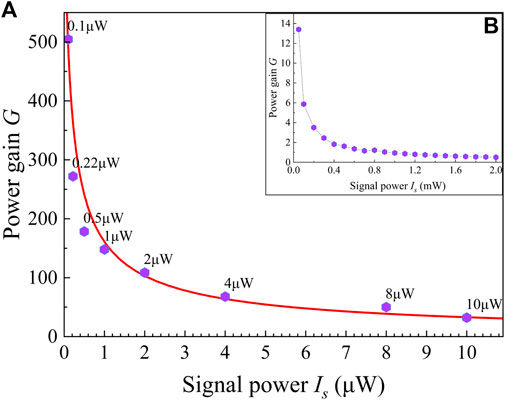
FIGURE 3. (color online) Power gain G between FWM light and signal laser against the power of the signal laser. (A) Experimental datas (purple dots) and theoretical fitting (red curve) of signal power I_s from 0.1 to 10 μW. (B) Experimental datas (purple dots) of signal power I_s from 0.05 to 2 mW.

To explain the amplification of signal laser in the stimulated FWM process, we theoretically calculate the relation between power gain and signal power in an atomic diamond-type energy-level system. The equation of motion can be described as (Boyd, 2003).

$\frac{\partial {\rho }_{ij}}{\partial t}=-\frac{i}{\hslash }{\displaystyle \sum _k}\left[H_{ik}{\rho }_{kj}-{\rho }_{ik}{H}_{kj}\right]-{\mathrm{\Gamma }}_{ij}{\rho }_{ij}-{\gamma }_{ij}{\rho }_{ij}(1)$

where ρ_ij is the density-matrix element and H_ij is the effective interaction Hamiltonian. The subscript indices i and j indicate the |i⟩ and |j⟩ states respectively. Γ_ij denotes the population spontaneous relaxation rate from state |i⟩ to state |j⟩ while γ_ij = (Γ_ii + Γ_jj)/2 denotes the relaxation rates of the coherences. For ⁸⁵Rb, the spontaneous decay rates are Γ₃₃ = 6 × 2π MHz, Γ₂₂ = Γ₃₃, Γ₄₄ = 0.35Γ₃₃, Γ₄₃ = 0.1Γ₃₃, and Γ₄₂ = 0.25Γ₃₃. The matrix of the effective interaction Hamiltonian $\widehat{H}$ can be represented as

$\widehat{H}=\frac{\hslash }{2}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill {\mathrm{\Omega }}_{21}^{\ast }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\mathrm{\Omega }}_{21}\hfill & \hfill -2{\mathrm{\Delta }}_1\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{42}^{\ast }\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\left({\mathrm{\Delta }}_3-{\mathrm{\Delta }}_2-{\mathrm{\Delta }}_1\right)\hfill & \hfill {\mathrm{\Omega }}_{43}^{\ast }\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Omega }}_{42}\hfill & \hfill {\mathrm{\Omega }}_{43}\hfill & \hfill -2\left({\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2\right)\hfill \end{array}\right)(2)$

where Ω₂₁, Ω₄₂ and Ω₄₃ are the Rabi frequency of pump1, pump2, and signal laser respectively. We can then deduce the steady-state optical coherence ρ₁₃ from Eqs 1, 2 as (Sun et al., 2004):

${\rho }_{31}=-\frac{i{\mathrm{\Omega }}_{21}{\mathrm{\Omega }}_{42}{\mathrm{\Omega }}_{43}^{\ast }}{\left[2i{\mathrm{\Delta }}_1-{\gamma }_{21}\right]\left[2i\left({\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2\right)-{\gamma }_{41}\right]\left[2i\left({\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2-{\mathrm{\Delta }}_3\right)-{\gamma }_{31}\right]}.(3)$

The amplitude of the FWM light wave E_FWM is proportional to the third-order optical polarization $P_{\mathit{FWM}}^{(3)}$ (Parniak and Wasilewski, 2015):

$E_{\mathit{FWM}}\propto P_{\mathit{FWM}}^{\left(3\right)}=N{\mu }_{31}^{\ast }{\rho }_{31}+\mathrm{H}.\mathrm{c}.(4)$

where N is the number density of atoms and ${\mu }_{31}^{\ast }$ is the transition dipole moment between states |1⟩ and |3⟩. In our system, the third-order optical polarization can be represented as $E_{\mathit{FWM}}\propto P_{\mathit{FWM}}^{(3)}={ϵ}_0{\chi }^{(3)}{E}_{p1}{E}_{p2}{E}_s^{*}$, where χ⁽³⁾ denotes the third-order susceptibility; ϵ₀ is the vacuum permittivity; E_p1, E_p2 and E_s are amplitudes of the pump1, pump2 and the signal electric fields, respectively. We can obtain the power conversion efficiency $\eta \propto E_{\mathit{FWM}}^2/E_s^2$ between signal light and FWM light by calculating χ⁽³⁾.

Considering the stimulated amplified process of signal light, we treat the state |3⟩ and the state |4⟩ equivalents as a simple two-level atomic system for the signal field. The stimulated emission from the interaction between this two-level atomic system and signal field can enhance the input signal light with a gain factor of G_factor = I_sout/I_s (I_sout is the power of the amplified signal light), and G_factor is satisfied by the following equation which is described in references (Riehle, 2004; Pan et al., 2018):

$I_s\left(G_{\mathit{factor}}-1\right)+2A\ln G_{\mathit{factor}}=\frac{1}{2}B.(5)$

with $A=\pi {\omega }_s^2{I}_{\mathit{sat}}\frac{{\mathrm{\Delta }}_3^2+{\mathrm{\Gamma }}_{43}^2}{{\mathrm{\Gamma }}_{43}^2}$ and $B=\alpha N\pi {\omega }_s^{2}h\nu L$, where ω_s is the waist of signal light, ν is the frequency of the signal light at 1530nm, L is the length of the ⁸⁵Rb vapor cell, I_sat = πhcΓ₄₃/(3λ³) is the saturation intensity, and α = 1/τ_cyc represents the pumping rate with ${\tau }_{\mathit{cyc}}=\frac{1}{{\mathrm{\Omega }}_{43}}+\frac{1}{{\mathrm{\Gamma }}_{43}}+\frac{1}{{\mathrm{\Gamma }}_{31}}$ being the atomic cycling time (Zhang et al., 2013). We obtain the power gain

$G=\eta G_{\mathit{factor}}(6)$

by considering that the stimulated FWM process consists of an amplification process and a frequency conversion process, where η is a constant and G_factor is a function of I_s. We then fit our experimental data with the deduced function and the result is shown in Figure 3A. The theoretical analysis agrees with our experimental results.

Finally, for amplified detection of an infrared signal, we should also pay attention to the response rate in this conversion process. As illustrated in Figure 4, we replace the CW signal laser with a pulsed signal laser. Figures 4A–D compare the signal pulse with the generated FWM pulse at a rising time of 1 μs, 500 ns, 100 ns and 60 ns, respectively. It can be concluded that the rising time of the input signal light and output FWM light are almost identical and the response time of this conversion process is faster than 60 ns. The study of higher response rate is mainly restricted by the shortest achievable rising time of the acoustic optical modulator (AOM) in our setup, which is 55 ns.

FIGURE 4

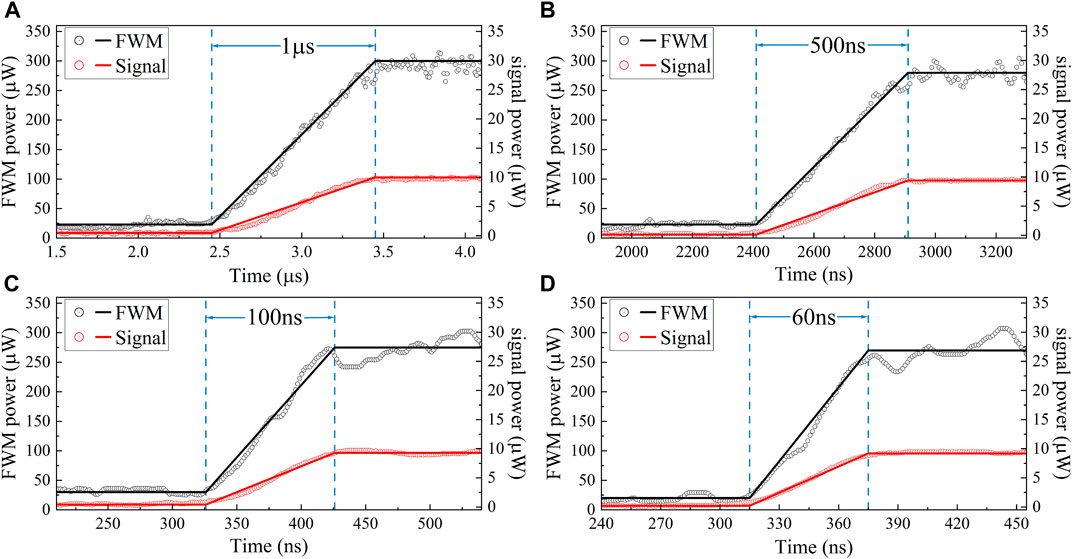
FIGURE 4. (color online) The measured wavefroms of the input pulsed infrared signal laser (red curve) and the output pulsed FWM laser (black curve) with a rising time of (A) 1 μs, (B) 500 ns, (C) 100 ns, (D) 60 ns.

4 Conclusion

In conclusion, we have demonstrated the amplified detection of an infrared signal via a stimulated FWM process based on an atomic diamond-type configuration. What’s more, the generated FWM light is in the visible range, which can be detected more efficiently. We find that the power gain increases sharply as the power of the signal laser decreases, and the experimental data is in good agreement with our theoretical fitting. We also investigate the dependence of power gain on the detunings of the three input lasers. Simultaneously, we experimentally confirm that the response rate of the FWM process is faster than 60 ns, therefore it can be applied to the detection of the weak infrared signals in specific situations.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

D-SD and B-SS coordianted the research project. W-HZ peformed the experimental fabrication, measurments and analyzed the data. All authors discussed the manuscript.

Funding

We acknowledge funding from National Natural Science Foundation of China (Grant Nos. U20A20218, 61525504, and 11934013), Youth Innovation Promotion Association of the Chinese Academy of Sciences (Grant No. 2018490) and the Major Science and Technology Projects in Anhui Province (Grant No. 202203a13010001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boyd, R. W. (2003). Nonlinear optics. Rochester, NY: Elsevier.

Google Scholar

Boyer, V., Marino, A. M., Pooser, R. C., and Lett, P. D. (2008). Entangled images from four-wave mixing. Science 321, 544–547. doi:10.1126/science.1158275

PubMed Abstract | CrossRef Full Text | Google Scholar

Carman, R., Chiao, R., and Kelley, P. (1966). Observation of degenerate stimulated four-photon interaction and four-wave parametric amplification. Phys. Rev. Lett. 17, 1281–1283. doi:10.1103/physrevlett.17.1281

CrossRef Full Text | Google Scholar

Ding, D.-S., Jiang, Y. K., Zhang, W., Zhou, Z.-Y., Shi, B.-S., and Guo, G.-C. (2015). Optical precursor with four-wave mixing and storage based on a cold-atom ensemble. Phys. Rev. Lett. 114, 093601. doi:10.1103/physrevlett.114.093601

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Huang, W., Shi, B.-S., Zou, X.-B., and Guo, G.-C. (2012a). Experimental up-conversion of images. Phys. Rev. A . Coll. Park. 86, 033803. doi:10.1103/physreva.86.033803

CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., and Guo, G.-C. (2013b). Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 4, 2527–7. doi:10.1038/ncomms3527

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., and Shi, B.-S. (2013a). Slow light via four-wave mixing in a hot rubidium vapour. Chin. Phys. B 22, 114203. doi:10.1088/1674-1056/22/11/114203

CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., and Zou, X.-B. (2012b). Efficient infrared upconversion via a ladder-type atomic configuration. J. Mod. Opt. 59, 1768–1771. doi:10.1080/09500340.2012.743608

CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., Zou, X.-B., and Guo, G.-C. (2012c). Generation of non-classical correlated photon pairs via a ladder-type atomic configuration: Theory and experiment. Opt. Express 20, 11433–11444. doi:10.1364/oe.20.011433

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., Zou, X.-B., and Guo, G.-C. (2012d). Image transfer through two sequential four-wave-mixing processes in hot atomic vapor. Phys. Rev. A . Coll. Park. 85, 053815. doi:10.1103/physreva.85.053815

CrossRef Full Text | Google Scholar

Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., Zou, X.-B., and Guo, G.-C. (2012e). Linear up-conversion of orbital angular momentum. Opt. Lett. 37, 3270–3272. doi:10.1364/ol.37.003270

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, M.-X., Zhang, W., Shi, S., Wang, K., Zhou, Z.-Y., Liu, S.-L., et al. (2017). Two-color hyper-entangled photon pairs generation in a cold ^85Rb atomic ensemble. Opt. Express 25, 10145–10152. doi:10.1364/oe.25.010145

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, L.-M., Lukin, M. D., Cirac, J. I., and Zoller, P. (2001). Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418. doi:10.1038/35106500

PubMed Abstract | CrossRef Full Text | Google Scholar

Griffiths, P. R., and de Haseth, J. A. (2007). Fourier transform infrared spectrometry. Vol. 171. Hoboken, NJ, USA: John Wiley & Sons.

Google Scholar

Jeong, T., Park, J., and Moon, H. S. (2019). Stimulated measurement of spontaneous four-wave mixing from a warm atomic ensemble. Phys. Rev. A . Coll. Park. 100, 033818. doi:10.1103/physreva.100.033818

CrossRef Full Text | Google Scholar

Kalashnikov, D. A., Paterova, A. V., Kulik, S. P., and Krivitsky, L. A. (2016). Infrared spectroscopy with visible light. Nat. Photonics 10, 98–101. doi:10.1038/nphoton.2015.252

CrossRef Full Text | Google Scholar

Kölle, A., Epple, G., Kübler, H., Löw, R., and Pfau, T. (2012). Four-wave mixing involving rydberg states in thermal vapor. Phys. Rev. A . Coll. Park. 85, 063821. doi:10.1103/physreva.85.063821

CrossRef Full Text | Google Scholar

Lavoute, L., Knight, J. C., Dupriez, P., and Wadsworth, W. J. (2010). High power red and near-ir generation using four wave mixing in all integrated fibre laser systems. Opt. Express 18, 16193–16205. doi:10.1364/oe.18.016193

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-S., Lee, S. M., Kim, H., and Moon, H. S. (2016). Highly bright photon-pair generation in Doppler-broadened ladder-type atomic system. Opt. Express 24, 28083–28091. doi:10.1364/oe.24.028083

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-S., and Moon, H. S. (2016). Atomic coherence effects in four-wave mixing process of a ladder-type atomic system. Opt. Express 24, 10723–10732. doi:10.1364/oe.24.010723

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-S., and Moon, H. S. (2017a). Doppler-free three-photon coherence in Doppler-broadened diamond-type atomic system. Opt. Express 25, 5316–5326. doi:10.1364/oe.25.005316

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y.-S., and Moon, H. S. (2017b). Doppler-free three-photon coherence in Doppler-broadened diamond-type atomic system. Opt. Express 25, 5316–5326. doi:10.1364/oe.25.005316

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Wu, J., Ding, D., Shi, B., and Guo, G. (2012). Bichromatic field generation from double-four-wave mixing in a double-electromagnetically induced transparency system. New J. Phys. 14, 073047. doi:10.1088/1367-2630/14/7/073047

CrossRef Full Text | Google Scholar

McCormick, C., Boyer, V., Arimondo, E., and Lett, P. (2007). Strong relative intensity squeezing by four-wave mixing in rubidium vapor. Opt. Lett. 32, 178–180. doi:10.1364/ol.32.000178

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, D., Shi, T., Luo, B., Chen, J., and Guo, H. (2018). Atomic optical stimulated amplifier with optical filtering of ultra-narrow bandwidth. Sci. Rep. 8, 6567. doi:10.1038/s41598-018-24895-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Parniak, M., and Wasilewski, W. (2015). Interference and nonlinear properties of four-wave-mixing resonances in thermal vapor: Analytical results and experimental verification. Phys. Rev. A . Coll. Park. 91, 023418. doi:10.1103/physreva.91.023418

CrossRef Full Text | Google Scholar

Paterova, A., Yang, H., An, C., Kalashnikov, D., and Krivitsky, L. (2018). Measurement of infrared optical constants with visible photons. New J. Phys. 20, 043015. doi:10.1088/1367-2630/aab5ce

CrossRef Full Text | Google Scholar

Radnaev, A., Dudin, Y., Zhao, R., Jen, H., Jenkins, S., Kuzmich, A., et al. (2010). A quantum memory with telecom-wavelength conversion. Nat. Phys. 6, 894–899. doi:10.1038/nphys1773

CrossRef Full Text | Google Scholar

Riehle, F. (2004). Frequency standars: Basics and applications. Berlin: Wiley VCH.

Google Scholar

Shi, S., Dong, M.-X., Yu, Y.-C., Ye, Y.-H., Zhang, W., Wang, K., et al. (2020). Entangled qutrits generated in four-wave mixing without post-selection. Opt. Express 28, 11538–11547. doi:10.1364/oe.383378

PubMed Abstract | CrossRef Full Text | Google Scholar

Slusher, R., Hollberg, L., Yurke, B., Mertz, J., and Valley, J. (1985). Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 55, 2409–2412. doi:10.1103/physrevlett.55.2409

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., Zuo, Z., Mi, X., Yu, Z., Jiang, Q., Wang, Y., et al. (2004). Two-photon resonant four-wave mixing in a dressed atomic system. Phys. Rev. A . Coll. Park. 70, 053820. doi:10.1103/physreva.70.053820

CrossRef Full Text | Google Scholar

Wen, J., Du, S., Zhang, Y., Xiao, M., and Rubin, M. H. (2008). Nonclassical light generation via a four-level inverted-y system. Phys. Rev. A . Coll. Park. 77, 033816. doi:10.1103/physreva.77.033816

CrossRef Full Text | Google Scholar

Wu, J., Guo, M., Zhou, H., Liu, J., Li, J., and Zhang, J. (2022). Experimental realization of efficient nondegenerate four-wave mixing in cesium atoms. Opt. Express 30, 12576–12585. doi:10.1364/oe.452790

PubMed Abstract | CrossRef Full Text | Google Scholar

Yariv, A., and Pepper, D. M. (1977). Amplified reflection, phase conjugation, and oscillation in degenerate four-wave mixing. Opt. Lett. 1, 16–18. doi:10.1364/ol.1.000016

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Y.-C., Ding, D.-S., Dong, M.-X., Shi, S., Zhang, W., and Shi, B.-S. (2018). Self-stabilized narrow-bandwidth and high-fidelity entangled photons generated from cold atoms. Phys. Rev. A . Coll. Park. 97, 043809. doi:10.1103/physreva.97.043809

CrossRef Full Text | Google Scholar

Yu, Y.-C., Dong, M.-X., Ye, Y.-H., Guo, G.-C., Ding, D.-S., and Shi, B.-S. (2020). Experimental demonstration of switching entangled photons based on the rydberg blockade effect. Sci. China Phys. Mech. Astron. 63, 110312–110317. doi:10.1007/s11433-020-1602-1

CrossRef Full Text | Google Scholar

Zhang, K., Wang, W., Liu, S., Pan, X., Du, J., Lou, Y., et al. (2020a). Reconfigurable hexapartite entanglement by spatially multiplexed four-wave mixing processes. Phys. Rev. Lett. 124, 090501. doi:10.1103/physrevlett.124.090501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, T., Wang, Y., Zang, X., Zhuang, W., and Chen, J. (2013). Active optical clock based on four-level quantum system. Chin. Sci. Bull. 58, 2033–2038. doi:10.1007/s11434-013-5877-0

CrossRef Full Text | Google Scholar

Zhang, W., Dong, M.-X., Ding, D.-S., Shi, S., Wang, K., Zhou, Z.-Y., et al. (2018). Interfacing a two-photon noon state with an atomic quantum memory. Phys. Rev. A . Coll. Park. 98, 063820. doi:10.1103/physreva.98.063820

CrossRef Full Text | Google Scholar

Zhang, Y., Wu, J., He, Y., Zhang, Y., Hu, Y., Zhang, J., et al. (2020b). Observation of the interplay between seeded and self-seeded nondegenerate four-wave mixing in cesium vapor. Opt. Express 28, 17723–17731. doi:10.1364/oe.393032

PubMed Abstract | CrossRef Full Text | Google Scholar