
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Robot. AI , 13 August 2024
Sec. Biomedical Robotics
Volume 11 - 2024 | https://doi.org/10.3389/frobt.2024.1439427
This article is part of the Research Topic Intelligent Micro- and Nanorobotic Systems for Enhanced Medical Procedures View all 6 articles
Microparticles are increasingly employed as drug carriers inside the human body. To avoid collision with environment, they reach their destination following a predefined trajectory. However, due to the various disturbances, tracking control of microparticles is still a challenge. In this work, we propose to use an Adaptive Nonlinear PID (A-NPID) controller for trajectory tracking of microparticles. A-NPID allows the gains to be continuously adjusted to satisfy the performance requirements at different operating conditions. An in-vitro study is conducted to verify the proposed controller where a microparticle of 100
Microrobots have considerable potential to revolutionize the treatment of several diseases that are currently considered difficult to cure (Nelson et al., 2010). Due to their small size, they can navigate through hard-to-access regions inside the human body, and precisely deliver drug doses to target lesions in a minimal-invasive and effective manner Abbott et al. (2007); Sitti (2009); (Nelson et al., 2010); Khalil et al. (2012a); Scheggi and Misra (2016). This precision delivery means that a higher concentration of the drug will arrive at the most beneficial site, and that the risk of potential side effects is minimized because the drug is much less likely to diffuse to the surrounding tissue. However, to reach their destination, microparticles have to navigate through a complex network of blood vessels with multiple forks and narrow paths Belharet et al. (2012); Coene et al. (2015). Steering the particle in such environment can be realized by means of a teleoperation device i.e. joystick which allows the operator to remotely guide the particle towards the targeted goal. The operator can get his feedback about the particle position through an artificial image reconstructed from the slices obtained from MRI. However, this procedure is very difficult and stressful even for a skilled operator, mostly because of the reduced workspace, the high precision required, the lack of haptic perception and the complexity induced by artificial vision feedback. Alternatively, closed-loop control system allows microparticles to autonomously reach their target position following an obstacle-free trajectory without the intervention of the operator. For this purpose, a path planning algorithm has to be firstly used to generate a reference trajectory that avoids the collision with the surrounding environment.Several path-planning algorithms have been presented in the literature for autonomous navigation of mobile robots such as A* algorithm Lin et al. (2017), Dijkstra algorithm Wang et al. (2011), RRT algorithm Gong et al. (2014), probabilistic roadmaps (PRM) Amato and Wu (1996); Kavraki et al. (1996), genetic algorithm Liu et al. (2004), ant colony algorithm Wang et al. (2018), and artificial potential field algorithm Qi et al. (2008). However, navigation inside the human body is more challenging task as several constraints and physiological issues have to be considered. For instance, the path planning algorithm must ensure that the ratio between the diameter of the microparticle and the diameter of blood vessel satisfies a specific range, and the microparticle can counteract the reciprocal blood flow which is typically higher in larger diameter blood vessels Sabra et al. (2005).
A comparative study was conducted in Sabra et al. (2005) between a group of path planning algorithms to find the best trajectory to be followed by a microparticle to reach a goal in the cardiovascular system. The study took into consideration the exclusive features of the blood circulatory system beside the other constraints that are associated with the navigation inside the human body. The criteria for the best algorithm were computation time, memory usage, local minima handling, and the capability of determining multiple paths. Among nine algorithms, the Artificial Potential Filed (APF) was found one of the most appropriate. Recently, another experimental comparison between six path planning algorithms when applied to the motion control of paramagnetic microparticles was presented in Scheggi and Misra (2016). The comparison was conducted based on three metrics i.e., computation time, trajectory length, and elapsed time. The experimental results revealed equivalence between almost all the considered planners in terms of trajectory length and completion time while the artificial potential field and A* with quadtree achieved the best performances regarding the computation time. The APF algorithm was also presented in other several studies as in Khalil et al. (2012a) where an untethered microrobot was wirelessly controlled to reach its destination with obstacle avoidance. Motivated by the satisfactory performance of the APF algorithm in the previous studies, it is selected in this work to generate a collision-free path for the microparticle while flowing in a an open fluidic resvoir with virtual narrow vessel-like channel and static obstacles.To ensure accurate trajectory tracking of the microparticle, a closed-loop control system is indispensable. Several control logarithms have been presented in the literature for the position tracking of magnetically actuated microparticles. For instance, in Khamesee et al. (2002) the PID controller was applied to the microrobot position, but its performance was unsatisfactory as practically, the microrobot is a complicated system with high nonlinearity and uncertainty. In addition, at microscale, the external disturbances and dynamic uncertainties may have a greater influence on the motion of microparticles Jiang et al. (2022). This makes classic linear controllers like PID inadequate for such a control task. Thus, more advanced model-based nonlinear control strategies have been reported to improve the position tracking performance Piepmeier et al. (2014); Mellal et al. (2016). However, their performance were still insufficient to achieve position tracking due to the lack of accurate mathematical models describing the dynamic effects Zhang et al. (2013). Other adaptive, robust and optimal control algorithms could demonstrate ability to respect the performance measures under high model uncertainties and environmental disturbances Marino et al. (2014); Ma et al. (2017); Meng et al. (2020).
In this work, an adaptive-nonlinear PID control algorithm is proposed for trajectory tracking of microparticles. The proposed controller allows the gains to be adjusted online in order to satisfy the performance requirements at different operating conditions Das and Sengupta (2018), Li and Yuan (2020). The A-NPID algorithm has been used in the literature with various applications but to the best of our knowledge it has never been tested with micro-sized agents which exhibit high sensitivity to environmental variables Liu et al. (2020); Rithirun et al. (2021). Moreover, the paramagnetic microparticles employed in this research are magnetically driven in a very small workspace adding an additional challenge due to the water concave meniscus formed near the wall of the reservoir. The proposed controller is investigated through conducting a complete study that aims to ensure successful navigation and control of a microparticle flowing in an open fluidic resvoir with virtual narrow vessel-like channel and static obstacles. As such, in this study, we achieve the following.
The remainder of this article is organized as follows: Section 2 presents the description of the electromagnetic system and its dynamic model derivation. Section 3 presents the development of the Artificial Potential Field path planning algorithm. Section 4 presents the implementation of the adaptive-nonlinear PID controller in addition to the simulation results. Section 5 presents the experimental verification. Finally, section 6 concludes this article and provides directions for future work.
The system consists mainly of four equally sized coils with metal cores used to generate the magnetic field needed to move the particle (see Figure 1). Each coil has 1,400 turns of 0.7 mm round copper wire coated with enamel. The inner radius of the coil
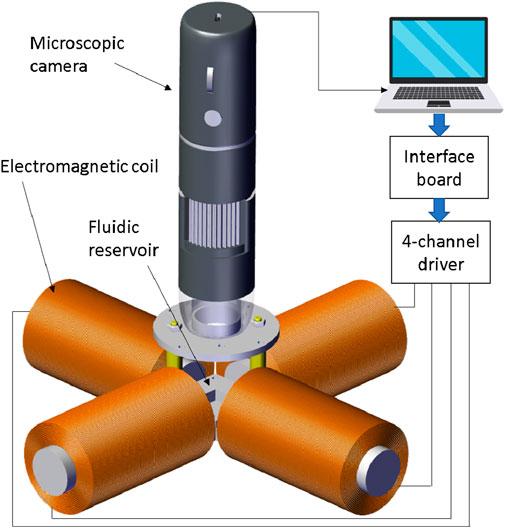
Figure 1. Electromagnetic system for autonomous navigation and control of microparticles. The setup consists of four lateral coils placed in a symmetrical perpendicular configuration. A microscopic camera is positioned properly above the workspace to detect the particle position.
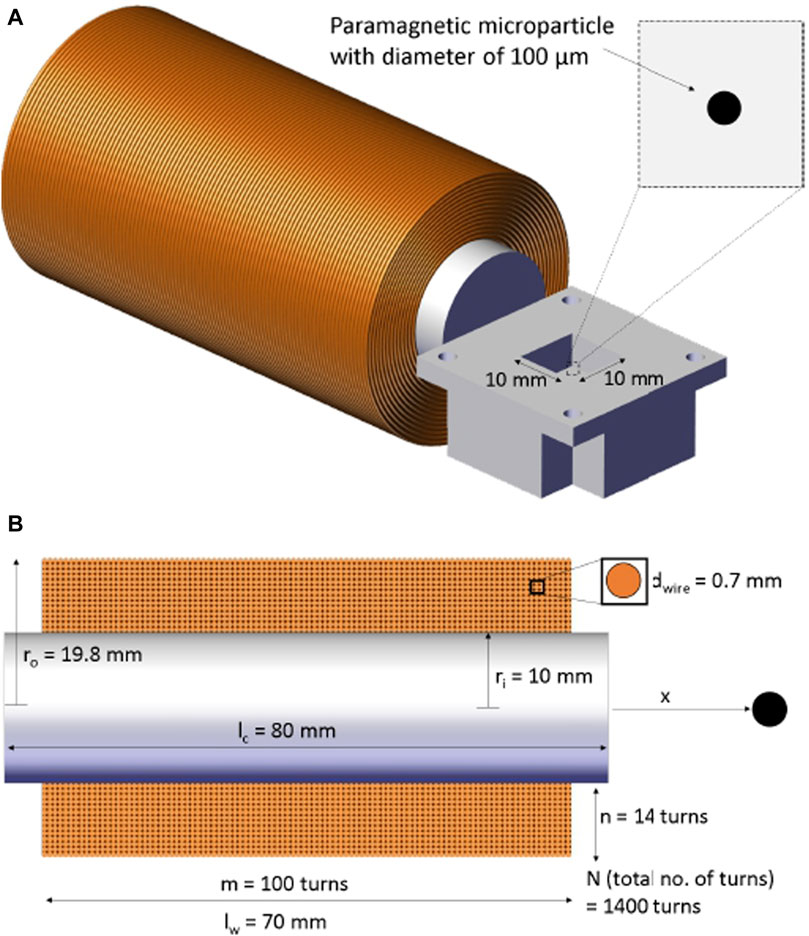
Figure 2. Schematic of the employed electromagnetic coil showing its dimensions and number of turns. (A) The microparticle is allowed to move within a workspace of 10 × 10 mm yet the region of interest is only about 3 × 3 mm. (B) A cross-section view of the coil shows number of turns in lateral and axial directions.
The average series resistance of each coil is measured to be around 6
In order to reduce the coupling effect between the coils, the current direction in all coils should be the same. Having different directions of the current showed that the coupling effect significantly reduces the generated magnetic field.
Microparticles move in the fluid under the influence of two main forces; the external magnetic force, and drag force. Firstly, the formula of each of these two forces are found. Then, the equation that governs the motion of the particle is derived.
The magnetic force
where
where
Combining Equation 1 and Equation 3 results in:
The magnetic field
where
Substituting Equation 6 in Equation 4 yields
Assuming the windings of our coil are perfectly stacked, the field-current relation can be theoretically found by the following formula:
where
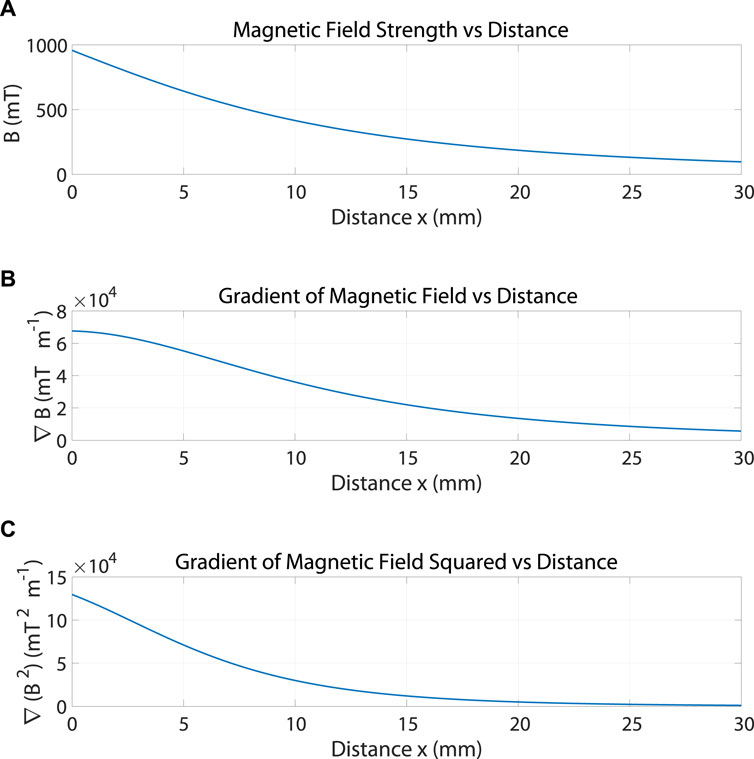
Figure 3. (A) The magnetic field
The term multiplied by the current
Substituting Equation 9 in Equation 7 yields
It can be shown from Equation 10 that the generated force is a function of the microparticle size and geometry, the distance between the particle and the coil, and the applied current. The force current map Equation 10 is used to determine whether the generated magnetic force would overcome the viscous drag force
where
Following the derivation presented in Khalil et al. (2012b), the motion equation of the microparticle can be given as following:
where

Figure 4. The estimated gradient of the squared magnetic field in x direction is represented using a polynomial of third order system obtained from curve fitting operation.
This section presents the APF algorithm that generates an obstacle-free path through which the microparticle can reach its destination without collision with the surrounding environment. The microparticle is represented as a point moving under the influence of an attractive potential field generated by the goal and repulsive potential field generated by the obstacles. The direction of the motion of the particle is decided based on the negative gradient of the generated global potential field. The resultant force that drives the particle will be the additive sum of all forces existed due to the gradient of the potential fields. In our case, the particle is assumed to be navigating inside a virtual fluidic channel with a set of obstacles inspired from blood vessels with embolus as shown in Figures 5, 6. To avoid the singularity associated with the canonical form, the attractive potential field of the goal is represented by the quadratic form in Equation 15:
where
where
On the other side, the repulsive potential field that represents the obstacles can be estimated using the following formula of Equation 18:
where
The total potential field under which the particle is moving can be obtained by summing the attractive potential of the goal and repulsive potential of the obstacles as following in Equation 20:
In our case, the equation of the total potential field has to take into consideration the multiple repulsive potentials due to the three circular obstacles and two edges. The new equation of the total potential can be formulated as following in Equation 21:
where
where
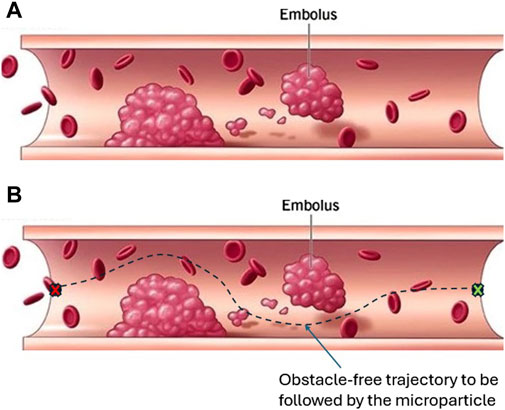
Figure 5. This blood vessel with embolus inspired us to assume a virtual fluidic channel with static obstacles augmented with the open fluidic reservoir as a working environment. (A) A vessel with embolus that can block or affect blood circulation. Such an embolus has to be avoided by microparticle when flowing through the blood-vessel. (B) For autonomous control, a path planning algorithm is used to generate an obstacle-free trajectory to be tracked by the microparticle Clinic, 2021.
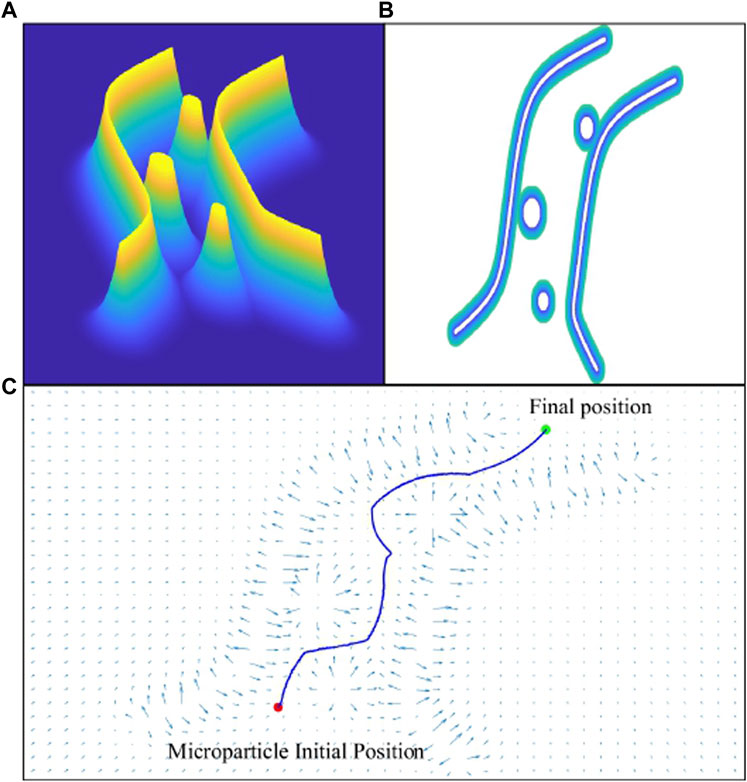
Figure 6. The virtual fluidic channel is represented by a field of attractive and repulsive forces using artificial potential field algorithm. (A) Graph of the repulsive potential field. (B) 2D view of the fluidic channel and blood clots i.e., obstacles. (C) The generated collision-free path from the initial position to final destination of the particle.
Model Reference Adaptive Controller (MRAC) acts as a servo system with desired performance expressed in form of a reference model. In this work, the NPID control parameters will be adjusted online using the model reference adaptive technique Valluru et al. (2018); Gambier and Yunazwin Nazaruddin (2018); Sirsode et al. (2019). Figure 7 shows the block diagram of the whole system in presence of the proposed control scheme. The reference model is designed such that its output satisfies the performance requirements of our system. In real time, the difference between the ideal output of the reference model and the actual output of the system is sent to an adjustment mechanism that calculates the new gains of the NPID controller as described hereafter, Shamseldin et al. (2022); Shamseldin (2023a); Shamseldin (2023b).The proposed form of the NPID control scheme is given by Equation 23 as following:
where
Therefore, the adaptive control law Equation 23 has six adaptation gains that have to be continuously estimated using the adjustment mechanism namely
where
where
where
where
The error
To find the derivative of the adaptation gain
Following Equation 26, the derivative of the adaptation gain
Similarly, we can find the adaptation gains
The adaptation weights
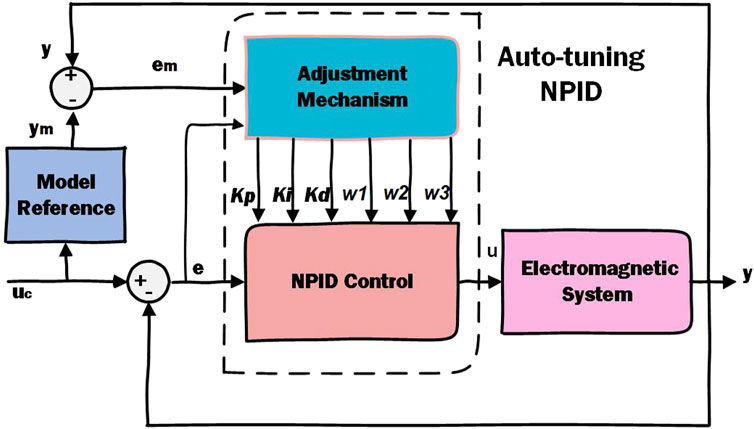
Figure 7. Block diagram of the proposed adaptive nonlinear PID control system. The gains of the A-NPID controller are continuously adjusted by the adaptation mechanism. The equations and parameters of the adaptation mechanism are estimated based on the performance requirements represented by the reference model.
Figure 8 shows the simulation results in which the tracking performance of the microparticle is evaluated. Three tests are conducted at different sets of gains and different sampling rates of the reference data which in turn affects the average velocity of the particle. The collision-free path generated by the artificial potential field planning algorithm in Section 2.3 is used as a reference trajectory. The gains of two tests were selected randomly and then tuned manually. While the gains of the third test were obtained using an optimization algorithm. Figure 8A shows that when the particle is moving fast with an average velocity of 1 mm/s neither the position tracking nor the steady-state error are satisfying. Figure 8D shows the particle tracking in the first test in x-axis and y-axis where the integral of squared error (ISE) between the reference and actual trajectory in x-axis is 0.21
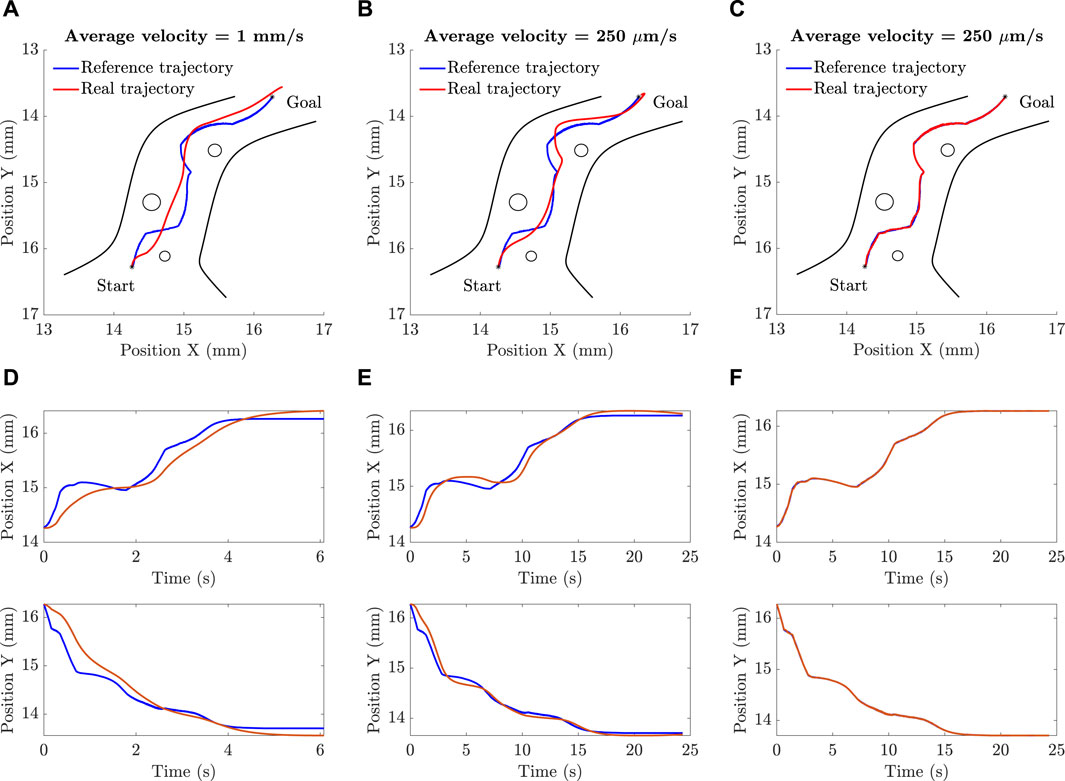
Figure 8. The simulation results show successful navigation of microparticle at different sets of controller parameters. The performance is highly improved when the parameters are estimated using an optimization technique: (A), (D) The parameters in this case are selected by trial and error. The time graphs of the x and y positions are created such that the average velocity of the microparticle is 1 mm/s. (B), (E) The parameters in this case are selected by trial and error but the average velocity was reduced to 250
The experimental setup consists of four identical electromagnetic coils placed in x-y plane. In order to reduce the coupling effect between the coils, the current direction in all coils should be the same. Having different directions of the current showed that the coupling could significantly reduce the generated magnetic field. Each coil has 1,400 turns of 0.7 mm round copper wire coated with enamel. The inner radius of the coil

Figure 9. The experimental setup shown in (A) has been used to test the proposed A-NPID controller practically. The setup consists of a set of electromagnets, a microscopic camera, two 2-channels drivers,a power supply, an arduino board and PC running a labview VI representing the proposed controller. The arduino board is used as a data acquisition card to send the control signals to the motor drivers. (B) The microscopic camera is positioned properly over the target. (C) The microparticle is magnified while flowing on the surface of the water in the reservoir.
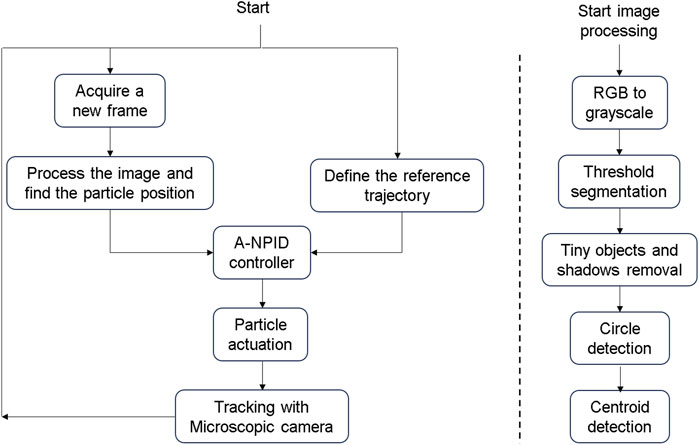
Figure 10. The flowchart on the left-hand side represents the closed loop control system. The controller receives the required and current positions of the particle from the path-planning algorithm and microscopic camera respectively. A control action is taken by the A-NPID and sent to the coils to actuate the particle. The flowchart on the right-hand side represents the operations applied on the image acquired from the microscopic camera to detect the particle position.
On the right hand side of Figure 10, there exist another flowchart about the steps of the process of the image processing. After defining the region of interest (ROI), the acquired RGB image is converted into a greyscale image. In the second step, a threshold value is used to get a binary image where the contrast between the particle and background is clear. In the third step the tiny objects that has smaller diameters than the particle are removed along with the shadows near the edges of the image. In the fourth step, the outer circumference of the particle is recognized as a circle. Then, its radius is estimated in pixels and compared with the previously known diameter of 100

Figure 11. The image acquired from the microscopic camera is processed to detect the particle position. Firstly, the RGB image is converted into a greyscale image. Secondly, a threshold is used to obtain a binary image showing the particle on a black background. Afterwards, the noise is removed and the particle center is detected.
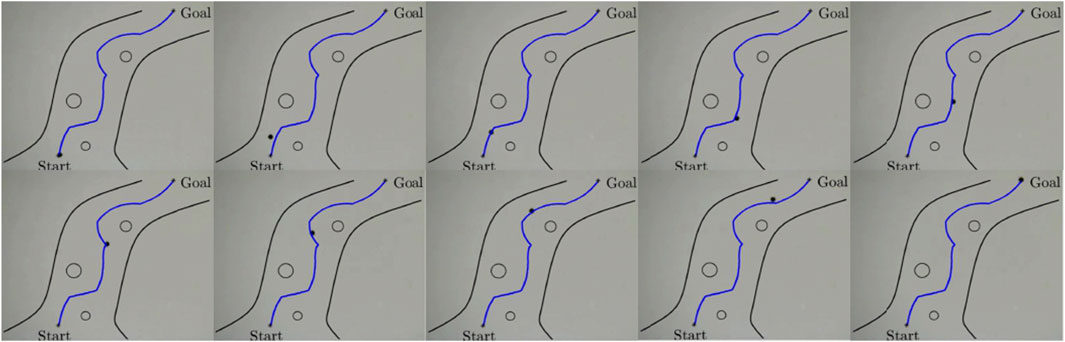
Figure 12. Selected frames from the real experiments augmented with the generated collision-free trajectory along with the virtual fluidic channel and obstacles. The experiment shows successful navigation and arrival at the targeted position. In this example the average velocity of the microparticle is 35
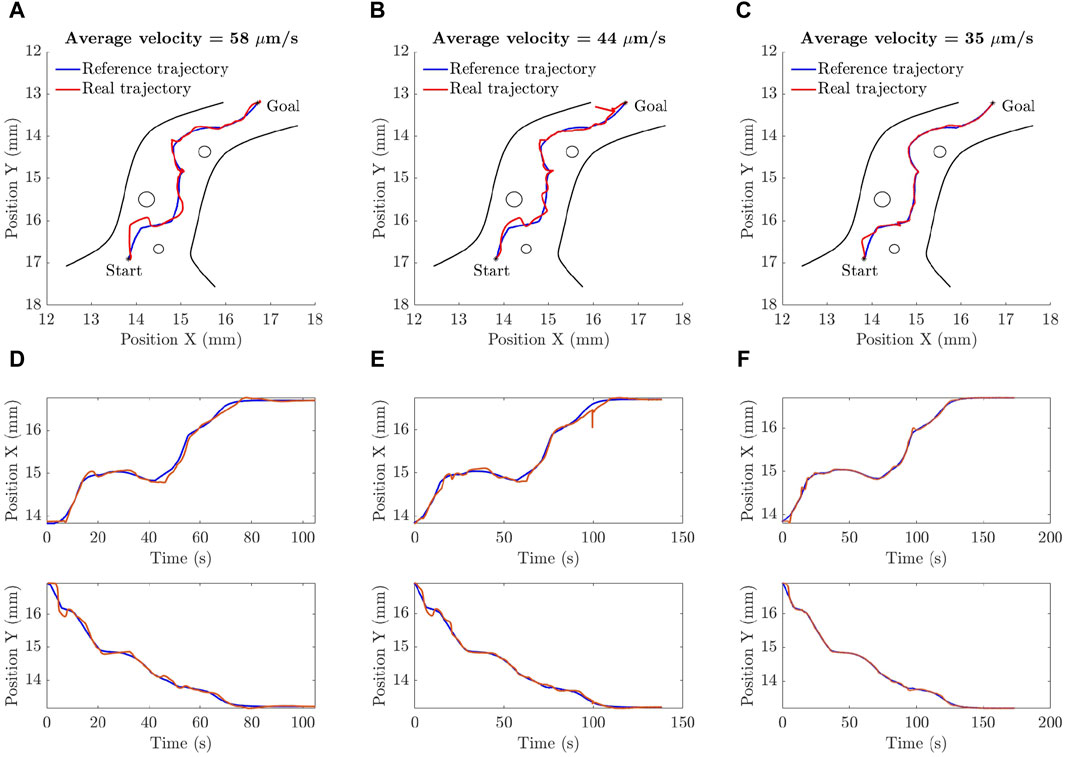
Figure 13. The experimental results verify the ability of the proposed A-NPID controller to drive the microparticle along the required trajectory at different operating conditions. Three tests were conducted at the same set of parameters but with different sampling rate. In all cases, the particle reached its targeted position but deviation that depends on the desired average velocity. (A), (D) The particle is moving with an average velocity of 58
The same tests were repeated in absence of the adaptive terms of the A-NPID control law as only the PID gains were left. The results showed that the PID controller allowed the particle to track the reference trajectory with obstacles collision avoidance but with significant deviation and steady state error. The reason behind such a degradation in the performance is that the final destination is near the edge of the reservoir where the surface of the water is not as flat as in the middle of the reservoir. Figure 14 depicts this phenomenon of concave meniscus which takes place due to the surface tension and adhesion force between the water and reservoir. Such a parabolic inclination represents different environmental conditions that requires tuning the gains of the controller. Since the linear PID control law has fixed gains, the performance was degraded when the particle approached the inclined surface. Figure 15 compares the performance of both controllers, A-NPID and PID, in terms of steady state error. The graph shows superiority of A-NPID due to its adaptation mechanism that allows the gains to be continuously adjusted in order to satisfy the performance requirements represented by the model reference. It is shown that at all operating conditions, the steady-state error was as small as 4
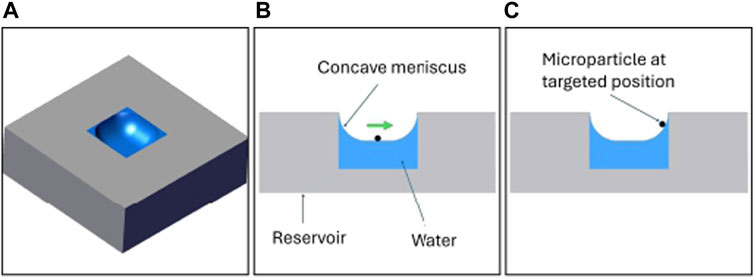
Figure 14. A concave meniscus occurs when the molecules of the water are attracted to those of the container. The operating conditions changes from the middle of the reservoir than the right side of the reservoir due to the inclination of the water surface.
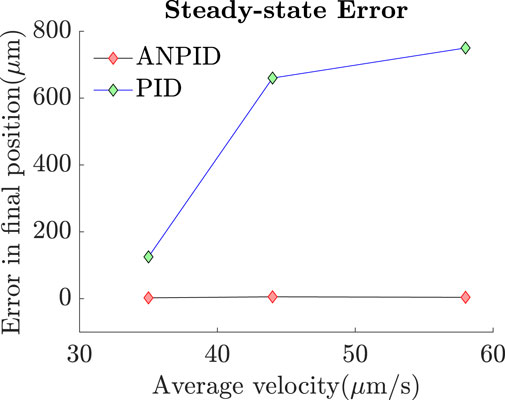
Figure 15. The A-NPID controller allowed the microparticle to reach its targeted position with minimal steady-state error even in presence of concave meniscus. However, in case of using the PID controller in absence of the adaptation terms, the particle could successfully track the trajectory but failed to reach its final destination with minimal steady-state error due to the sudden inclination of water surface.
In this work, an adaptive nonlinear PID control scheme was proposed for autonomous navigation and control of microparticles. The proposed controller allowed the gains to be continuously adjusted to cope with the varying operating conditions and to satisfy the performance requirements. The results showed that the A-NPID was able to drive the microparticle successfully to follow a collision-free trajectory and reach its destination with minimal steady-state error of about 4
In future studies, the motion control presented in this paper will be put in comparison with other advanced control algorithms such as Model Predictive Control (MPC), Fuzzy Logic Control, or Reinforcement Learning-based controllers. This would highlight the relative strengths and weaknesses of the proposed approach. In addition, exploring adaptive mechanisms to further tune the controller parameters in real-time based on the changing dynamics of the environment should be considered. It is also necessary to employ a variety of test scenarios for more comprehensive evaluation of the proposed controller’s robustness.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
MS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MSh: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. FF: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research leading to these results has been partially supported by the BRIEF “Biorobotics Research and Innovation Engineering Facilities” project (Project identification code IR0000036) funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 3.1 of Italian Ministry of University and Research funded by the European Union NextGenerationEU.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbott, J. J., Nagy, Z., Beyeler, F., and Nelson, B. J. (2007). Robotics in the small, part i: microbotics. IEEE Robotics Automation Mag. 14, 92–103. doi:10.1109/MRA.2007.380641
Amato, N., and Wu, Y. (1996) “A randomized roadmap method for path and manipulation planning,”. Minneapolis, MN, USA: IEEE, 113–120. doi:10.1109/ROBOT.1996.503582Proceedings of IEEE International Conference on Robotics and Automation
Belharet, K., Folio, D., and Ferreira, A. (2012). Untethered microrobot control in fluidic environment using magnetic gradients. In , 2012 International Symposium on Optomechatronic Technologies (ISOT 2012). 1–5. doi:10.1109/ISOT.2012.6403290
Clinic, C. (2021). How thrombosis can lead to a blocked blood vessel. Available at: https://my.clevelandclinic.org/health/diseases/22242-thrombosis ( (March 4, 2024).
Coene, A., Crevecoeur, G., and Dupré, L. (2015). Robustness assessment of 1-d electron paramagnetic resonance for improved magnetic nanoparticle reconstructions. IEEE Trans. Biomed. Eng. 62, 1635–1643. doi:10.1109/TBME.2015.2399654
Das, N., and Sengupta, A. (2018). A comparison between adaptive pid controller and pid controller with derivative path filter based on bacterial foraging optimization algorithm. In , 2018 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE). 1–6. doi:10.1109/EPETSG.2018.8659329
Gambier, A., and Yunazwin Nazaruddin, Y. (2018). Nonlinear pid control for pitch systems of large wind energy converters. In , 2018 IEEE Conference on Control Technology and Applications (CCTA). 996–1001. doi:10.1109/CCTA.2018.8511531
Gong, L., Zhang, Y., and Cheng, J. (2014). Coordinated path planning based on rrt algorithm for robot. Appl. Mech. Mater. 494-495, 1003–1007.
Jiang, J., Yang, Z., Ferreira, A., and Zhang, L. (2022). Control and autonomy of microrobots: recent progress and perspective. Adv. Intell. Syst. 4. doi:10.1002/aisy.202100279
Kavraki, L., Svestka, P., Latombe, J.-C., and Overmars, M. (1996). Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robotics Automation 12, 566–580. doi:10.1109/70.508439
Khalil, I. S. M., Keuning, J. D., Abelmann, L., and Misra, S. (2012a). Wireless magnetic-based control of paramagnetic microparticles. In , 2012 4th IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics. 460–466. doi:10.1109/BioRob.2012.6290856
Khalil, I. S. M., Metz, R. M. P., Abelmann, L., and Misra, S. (2012b) “Interaction force estimation during manipulation of microparticles,”. Vilamoura-Algarve, Portugal: IEEE, 950–956. doi:10.1109/IROS.2012.6386184IEEE/RSJ International Conference on Intelligent Robots and Systems
Khamesee, M., Kato, N., Nomura, Y., and Nakamura, T. (2002). Design and control of a microrobotic system using magnetic levitation. IEEE/ASME Trans. Mechatronics 7, 1–14. doi:10.1109/3516.990882
Li, J., and Yuan, Y. (2020) “A nonlinear proportional integral derivative-incorporated stochastic gradient descent-based latent factor model,”. Toronto, ON, Canada: IEEE, 2371–2376. doi:10.1109/SMC42975.2020.92833442020 IEEE International Conference on Systems, Man, and Cybernetics (SMC)
Lin, M., Yuan, K., Shi, C., and Wang, Y. (2017) “Path planning of mobile robot based on improved a* algorithm,”. Chongqing, China: IEEE, 3570–3576. doi:10.1109/CCDC.2017.79791252017 29th Chinese Control And Decision Conference (CCDC)
Liu, S., Tian, Y., and Liu, J. (2004) “Multi mobile robot path planning based on genetic algorithm,”. Hangzhou, China: IEEE, 4706–4709. doi:10.1109/WCICA.2004.1342412Fifth World Congress on Intelligent Control and Automation (IEEE Cat. No.04EX788)
Liu, T., Chen, Y., Chen, Z., Wu, H., and Cheng, L. (2020) “Adaptive fuzzy fractional order pid control for 6-dof quadrotor,”. Shenyang, China: IEEE, 2158–2163. doi:10.23919/CCC50068.2020.91886772020 39th Chinese Control Conference (CCC)
Ma, W., Li, J., Niu, F., Ji, H., and Sun, D. (2017). Robust control to manipulate a microparticle with electromagnetic coil system. IEEE Trans. Industrial Electron. 64, 8566–8577. doi:10.1109/TIE.2017.2701759
Marino, H., Bergeles, C., and Nelson, B. J. (2014). Robust electromagnetic control of microrobots under force and localization uncertainties. IEEE Trans. Automation Sci. Eng. 11, 310–316. doi:10.1109/TASE.2013.2265135
Mathieu, J.-B., and Martel, S. (2010). Steering of aggregating magnetic microparticles using propulsion gradients coils in an mri scanner. Magnetic Reson. Med. 63, 1336–1345. doi:10.1002/mrm.22279
McNeil, R., Ritter, R., Wang, B., Lawson, M., Gillies, G., Wika, K., et al. (1995). Characteristics of an improved magnetic-implant guidance system. IEEE Trans. Biomed. Eng. 42, 802–808. doi:10.1109/10.398641
Mellal, L., Folio, D., Belharet, K., and Ferreira, A. (2016) “Optimal control of multiple magnetic microbeads navigating in microfluidic channels,”. Stockholm, Sweden: IEEE, 1921–1926. doi:10.1109/ICRA.2016.74873382016 IEEE International Conference on Robotics and Automation (ICRA)
Meng, K., Jia, Y., Yang, H., Niu, F., Wang, Y., and Sun, D. (2020). Motion planning and robust control for the endovascular navigation of a microrobot. IEEE Trans. Industrial Inf. 16, 4557–4566. doi:10.1109/TII.2019.2950052
Nelson, B. J., Kaliakatsos, I. K., and Abbott, J. J. (2010). Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 12, 55–85. doi:10.1146/annurev-bioeng-010510-103409
Piepmeier, J. A., Firebaugh, S., and Olsen, C. S. (2014). Uncalibrated visual servo control of magnetically actuated microrobots in a fluid environment. Micromachines 5, 797–813. doi:10.3390/mi5040797
Qi, N., Ma, B., Liu, X., Zhang, Z., and Ren, D. (2008). “A modified artificial potential field algorithm for mobile robot path planning,” in 2008 7th world congress on intelligent control and automation, 2603–2607. doi:10.1109/WCICA.2008.4593333
Rithirun, C., Charean, A., and Sawaengsinkasikit, W. (2021). Comparison between pid control and fuzzy pid control on invert pendulum system. In , 2021 9th International Electrical Engineering Congress (iEECON). 337–340. doi:10.1109/iEECON51072.2021.9440344
Sabra, W., Khouzam, M., Chanu, A., and Martel, S. (2005). Use of 3d potential field and an enhanced breadth-first search algorithms for the path planning of microdevices propelled in the cardiovascular system. In , 2005, 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference. 3916–3920. doi:10.1109/IEMBS.2005.1615318
Scheggi, S., and Misra, S. (2016). An experimental comparison of path planning techniques applied to micro-sized magnetic agents. In , 2016 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS). 1–6. doi:10.1109/MARSS.2016.7561695
Shamseldin, M. A. (2021). Optimal covid-19 based pd/pid cascaded tracking control for robot arm driven by bldc motor. WSEAS Trans. Syst. 20, 217–227. doi:10.37394/23202.2021.20.24
Shamseldin, M. A. (2023a). Design of auto-tuning nonlinear pid tracking speed control for electric vehicle with uncertainty consideration. World Electr. Veh. J. 14, 78. doi:10.3390/wevj14040078
Shamseldin, M. A. (2023b). Real-time inverse dynamic deep neural network tracking control for delta robot based on a covid-19 optimization. J. Robotics Control 4, 643–649. doi:10.18196/jrc.v4i5.18865
Shamseldin, M. A., Khaled, E., Youssef, A., Mohamed, D., Ahmed, S., Hesham, A., et al. (2022). A new design identification and control based on ga optimization for an autonomous wheelchair. Robotics 11, 101. doi:10.3390/robotics11050101
Sirsode, P., Tare, A., and Pande, V. (2019). Design of robust optimal fractional-order pid controller using salp swarm algorithm for automatic voltage regulator (avr) system. In , 2019 Sixth Indian Control Conference (ICC). 431–436. doi:10.1109/ICC47138.2019.9123188
Valluru, S. K., Singh, M., Goel, A., Kaur, M., Dobhal, D., Kartikeya, K., et al. (2018). Design of multi-loop l-pid and nl-pid controllers: an experimental validation. In , 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES). 1228–1231. doi:10.1109/ICPEICES.2018.8897368
Wang, H., Yu, Y., and Yuan, Q. (2011). Application of dijkstra algorithm in robot path-planning. In 2011 Second International Conference on Mechanic Automation and Control Engineering. 1067–1069. doi:10.1109/MACE.2011.5987118
Wang, T., Zhao, L., Jia, Y., and Wang, J. (2018). “Robot path planning based on improved ant colony algorithm,” in 2018 WRC symposium on advanced robotics and automation (WRC SARA), 70–76. doi:10.1109/WRC-SARA.2018.8584217
Keywords: magnetic control, drug delivery, path planning, paramagnetic microparticle, ANPID
Citation: Sallam M, Shamseldin MA and Ficuciello F (2024) Autonomous navigation and control of magnetic microcarriers using potential field algorithm and adaptive non-linear PID. Front. Robot. AI 11:1439427. doi: 10.3389/frobt.2024.1439427
Received: 27 May 2024; Accepted: 26 July 2024;
Published: 13 August 2024.
Edited by:
Van Du Nguyen, Chonnam National University, Republic of KoreaReviewed by:
Barış Can Yalçın, University of Luxembourg, LuxembourgCopyright © 2024 Sallam, Shamseldin and Ficuciello. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohamed Sallam, bW9oYW1lZGFiZGVsZ2hhbnkuc2FsbGFtQHVuaW5hLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.