Language task-based fMRI analysis using machine learning and deep learning

Introduction: Task-based language fMRI is a non-invasive method of identifying brain regions subserving language that is used to plan neurosurgical resections which potentially encroach on eloquent regions. The use of unstructured fMRI paradigms, such as naturalistic fMRI, to map language is of increasing interest. Their analysis necessitates the use of alternative methods such as machine learning (ML) and deep learning (DL) because task regressors may be difficult to define in these paradigms.

Methods: Using task-based language fMRI as a starting point, this study investigates the use of different categories of ML and DL algorithms to identify brain regions subserving language. Data comprising of seven task-based language fMRI paradigms were collected from 26 individuals, and ML and DL models were trained to classify voxel-wise fMRI time series.

Results: The general machine learning and the interval-based methods were the most promising in identifying language areas using fMRI time series classification. The geneal machine learning method achieved a mean whole-brain Area Under the Receiver Operating Characteristic Curve (AUC) of $0.97\pm 0.03$, mean Dice coefficient of $0.6\pm 0.34$ and mean Euclidean distance of $2.7\pm 2.4$ mm between activation peaks across the evaluated regions of interest. The interval-based method achieved a mean whole-brain AUC of $0.96\pm 0.03$, mean Dice coefficient of $0.61\pm 0.33$ and mean Euclidean distance of $3.3\pm 2.7$ mm between activation peaks across the evaluated regions of interest.

Discussion: This study demonstrates the utility of different ML and DL methods in classifying task-based language fMRI time series. A potential application of these methods is the identification of language activation from unstructured paradigms.

1 Introduction

Individual variation in functional representation in the cerebral cortex (1, 2) and the potential for re-organisation in the setting of neurological disorders (3, 4) make it crucial to accurately localise eloquent areas of the cortex when surgery that may impinge on these areas is contemplated. Accurate localization plays a key role in guiding the decision to proceed with surgery and in intra-operative surgical guidance aiming to minimize the risk of post-operative neurological deficits. Functional Magnetic Resonance Imaging (fMRI) is a non-invasive method of functional brain mapping that measures the blood oxygen level dependent (BOLD) signal changes in the brain due to changes in regional cerebral blood flow during brain activation (5, 6). It is commonly used for non-invasive pre-surgical mapping across a range of functional domains, including the key domain of language (7–11).

Task-based language fMRI is a conventional approach for presurgical language mapping. It achieves language lateralization and localization that is concordant with gold standard methods, such as direct cortical stimulation and the Wada test (12–14). In task-based language fMRI, the subject completes a specific language task arranged in a paradigm comprising of blocks with task performance interleaved with blocks during which a control or baseline task is performed, (11, 15). Such designs facilitate statistical analysis using the General Linear Model to identify brain areas activated during the performance of the language task (16, 17). In these areas, the time course of the fMRI signal resembles the temporal profile predicted from the structure of the task (i.e., the task regressor). Clinical application of task-based fMRI requires the patient to understand and perform the task paradigm, potentially hampering its use in patient groups such as young children or those with deficits in comprehension, memory or attention that interfere with task performance.

This limitation of task-based paradigms can be overcome by using unstructured, continuous paradigms such as naturalistic fMRI (18–22). Naturalistic paradigms are less demanding in terms of patient compliance and mimic everyday activities insofar as they may only involve passive viewing of a movie or video (18, 20). However, unlike task-based fMRI, naturalistic fMRI has no obvious task regressor of interest. In previous studies, regressors have been defined by manually labelling the movie stimulus to identify features that are considered a priori to engage specific cognitive processes (23, 24). The labelling procedure is subjective and likely to vary with the expertise of the reviewer. A more direct alternative approach would be to extract the regressor(s) of interest from the temporal profiles of already-defined functional systems. One way to investigate the feasibility of this approach is to validate extracted temporal profiles using task-based paradigms in which the temporal profiles are known.

Machine Learning (ML) and Deep Learning (DL) methods have already been applied to fMRI analysis [See (25) for a general review of the applications of ML and DL in fMRI data analysis]. ML and DL methods are data-driven and their potential use for the classification of fMRI time series in keeping with their ability to classify time series in other application domains (26–28). However, the application of ML/DL methods to voxel-wise time series fMRI data (i.e., 1D data) have not been considered to date. The best ML/DL approach for learning task regressors are also yet to be determined.

To answer these questions, we first investigated the ability of different ML and DL algorithms to detect language activation by task-based language fMRI paradigms in individuals. We evaluated different types of ML and DL algorithms using a range of clinically relevant performance metrics including Area Under the Receiver Operating Characteristic curve (AUC), the Dice coefficient and the Euclidean distances between corresponding activation peaks identified by the ML or DL methods and those identified by the gold standard, the General Linear Model. This approach enabled us to determine the ML/DL methods that identify areas of language activation corresponding to the gold standard. This result serves as the foundation for future work to extract the task regressors from naturalistic paradigms using ML/DL methods.

2 Materials and methods

2.1 Participants

The study was approved by the Royal Brisbane and Women’s Hospital Human Research Ethics Committee. All participants provided written informed consent. The study comprised of 26 individuals (20 healthy participants and 6 epilepsy patients; mean age 40, range 21–71 years, 13 females). Head motion for each individual across each language language paradigm was accessed using Framewise Displacement (FD) (29). Framewise Displacement for the 26 participants across all language paradigms were found to be within the acceptable range (Mean FD $=0.12\pm 0.06$ mm, maximum FD less than 0.4 mm). All participants’ primary language was English and handedness was assessed using the Edinburgh Handedness Inventory (EHI) Questionnaire.

2.2 Task design

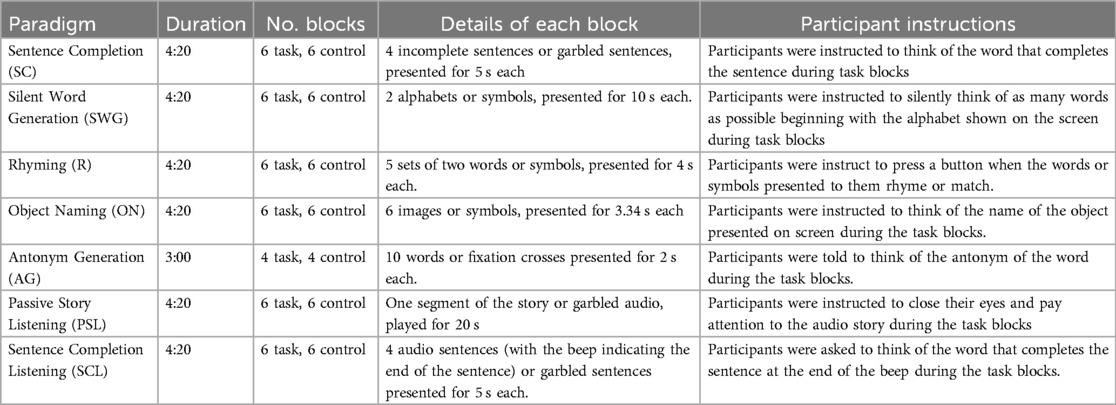
All participants underwent seven task-based language fMRI scans in a single session. The paradigms utilized a block design with task blocks interleaved with control blocks. Participants were provided with training for each task before the scanning session and at the beginning of each task, instructions were presented on screen followed by 10 s of dummy scans, during which a black screen was presented. Dummy scans were excluded from the analysis. At the end of each task, a black screen was also presented for 10 s to allow for signal stabilisation. See Table 1 for more information.

Table 1

Table 1. Task paradigms.

For each task, participants were instructed to respond covertly during the task blocks (i.e., to think of the responses and not to speak out loud) and to fixate on a fixation point presented on the screen during control blocks.

Task stimuli were presented with E-prime 3.0 software (Psychology Software Tools Inc., version 3.0) and participants were given MRI-safe active noise-cancelling headphones. Participants who required vision correction were encouraged to wear contact lenses or MRI-safe vision correction lenses were used.

2.3 Image acquisition

Data were collected using a Siemens Magnetom 3T Prisma scanner (Siemens Healthcare, Erlangen, Germany). BOLD Functional images were acquired using an Echo Planar (EPI) sequence and standard 64 channel head coil. (TR $=$ 2,000 ms, TE $=$ 23 ms, Flip angle $=$ 90 Degrees, FoV $=$ 210 mm, Resolution $=70\times 70$, 42 Axial Slices, Voxel size $=3\times 3\times 3$ mm). Whole brain T1 MPRAGE structural images were also acquired (TR $=$ 1,900 ms, TE $=$ 256 mm, Flip Angle $=$ 9 Degrees, FoV $=$ 256 mm, Resolution $=256\times 256$, 192 Axial Slices, Voxel size $=1\times 1\times 1$ mm).

2.4 Pre-processing of fMRI data

Data were analysed using Statistical Parametric Mapping SPM12 software (30, 31). The steps included slice timing correction, realignment (realigning images to the mean image functional image across all tasks for each participant), co-registration to structural T1 image, spatial normalization to Montreal Neurological Institute (MNI) space (re-sampled to $3\times 3\times 3$ mm) and smoothing using a full-width half maximum (FWHM) Gaussian kernel of 6 mm.

2.5 Task-based language fMRI activation

For each participant, first-level task-based language activation maps were derived for each of the seven tasks. Pre-processed voxel-wise fMRI time series data were modeled with the General Linear Model using SPM12 software. General linear modelling was performed with defined task regressors and covariates. The former were obtained by convolving the box-car stimulus function (contrasting task and control conditions) of each task with the canonical Haemodynamic Response Function (HRF). Covariates or nuisance regressors were the six motion parameters from the motion correction step during pre-processing. High pass filtering with a cut off of 128s and a first-level autoregressive model, i.e., AR(1) were employed.

A threshold of $p<0.001$, uncorrected for multiple comparisons, was applied to the $t$-statistic images to generate language activation maps which were binarised (activated vs non-activated) for machine learning analysis. The process of deriving task-based language activation maps is illustrated in Figure 1.

Figure 1

Figure 1. Illustrated are the steps to obtain task-based language activation maps. Task paradigm stimulus function was convolved with the hemodynamic response function to get task regressors. Raw fMRI images were preprocessed, and together with task and nuisance regressors activation maps are produced using Genearl Linear modelling.

2.6 Training and test pipeline

Data analysis with machine learning and deep learning comprises of training and testing stages. A set of carefully curated training data is first provided to ML or DL algorithms, allowing patterns to be extracted from the data, resulting in a trained model. Test set(s) are then used to evaluate the performance of the ML/DL model.

2.6.1 Training set

To construct the training set, pre-processed fMRI voxel time series of 14 healthy participants across 6 tasks (SC, SWG, R, ON, PSL, SCL) were extracted and labelled as activated (label 1) or non-activated (label 0) to yield binarised activation maps for each paradigm. The classification problem to be solved by the ML/DL methods was therefore to classify whether a fMRI voxel time series was activated or non-activated. The process of extracting voxel-wise fMRI time series and labelling is illustrated in Figure 2. Data from the AG tasks were excluded from the training set because the length of the voxel time series differed from that of the other tasks; however, the AG task was included in the test set, see Section 2.6.2).

Figure 2

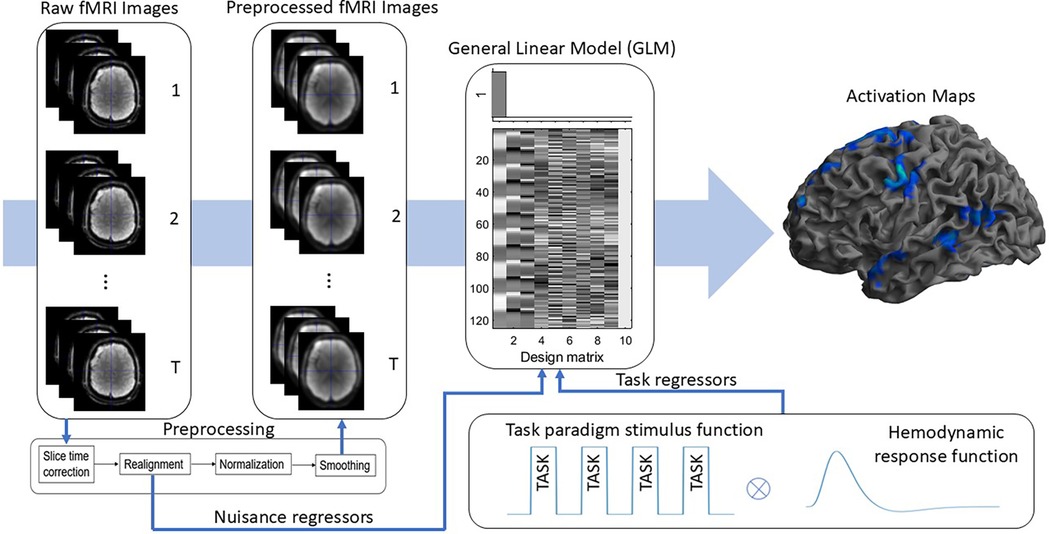
Figure 2. Illustrated are the steps to extract voxel time series data and corresponding binary labels. Task-based language activation maps were used to define the 0 and 1 labels.

Reflecting individual variation in brain function, the number of activated and non-activated fMRI voxel time series varied across participants and tasks. To balance the training set so that the numbers of activated and non-activated time series was equal, and to equalize the contribution of samples from each participant and each task, the participant and task paradigm with the smallest number of activated voxels was identified, which corresponded to 29 fMRI time series samples. The number of activated fMRI voxel time series and non-activated voxel time series for the remaining participants and tasks was randomly sampled, without replacement, to match the smallest number of activated voxels (i.e., resulting in 58 samples from each task paradigm for each participant, with the number of activated voxel time series and non-activated voxel time series from each participant totaling up to 348).

The resulting training set had 4,872 samples, of which 2,436 samples were labelled 1 and 2,436 samples were labelled 0.

2.6.2 Test set

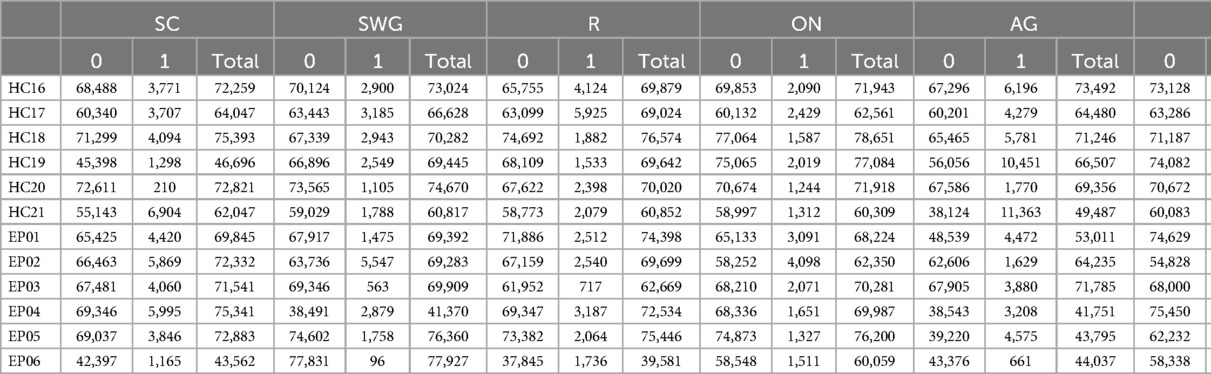
For the test set, time series from all brain voxels in 6 healthy and 6 epilepsy patients for 6 tasks (SC, SWG, R, AG, ON, SCL) were extracted and labelled according to the binarised language activation maps. A combination of healthy participants and epilepsy patients were included in the test set to ensure diversity in the test data. The PSL task was excluded from analysis because there was little activation in most participants. To determine whether the trained models could be used to analyse unseen data with fMRI time series of different lengths, the time series for the AG task was padded with the final time point in the fMRI time series to match the length of fMRI time series of other tasks.

An average of 66,036 samples was extracted from each task in each participant. The voxel locations of each sample were saved and later used to reconstruct ML/DL activation maps. See Table A1 in Appendix (Section A) for the number of samples that were extracted for each participant and each task.

2.6.3 Choice of machine learning and deep learning algorithms

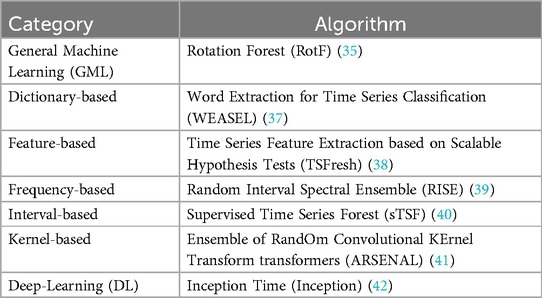
Several types of machine learning and deep learning algorithms have been proposed for time series classification. They can be categorised into general machine learning, dictionary-based, distance-based, feature-based, frequency-based, interval-based, kernel-based, shapelet-based, hybrid or ensemble-based and deep learning methods. The different ML/DL categories and methods can be found in the SKTIME library (version 13.4) (32, 33). A separate category was defined, namely the general machine learning (GML) category which includes ML methods that were conventionally developed to solve non-time series problems. These methods can be found in the Scikit-Learn library and the Rotation Forest algoritm falls into this category (34, 35).

A representative algorithm from each category is chosen based on the literature and evaluated to determine whether a particular category of classification algorithms was more suited to task-based language fMRI analysis. Table 2 shows the algorithms from each category. Default hyper-parameters were used to evaluate each of the chosen algorithms. While hyper-parameter tuning is largely discussed in the machine learning community, Probst et al. (36) evaluated the impact of hyper-parameter tuning on six different ML algorithms and showed that AUC at most improves by 10% by optimizing of hyper-parameters. Default hyper-parameters are also useful starting points to ML algorithm evaluation and generally work well across different problems (35). The use of default parameters also ensures reproducibility of results.

Table 2

Table 2. Algorithms evaluated from different categories.

To choose the algorithms to be tested, we first identified the most recent algorithms to be developed in each category. The literature was then reviewed to determine their performance in comparison with algorithms previously used to benchmark time series classification performance in terms of accuracy and computational efficiency (28). The algorithms chosen for comparison from each category were trained on high performance computing clusters with different memory requirements depending on the algorithm. Algorithms that required more than 24 h or 128 GB of memory on a single core for training were excluded from selection. Because long test times can be overcome by testing multiple batches of data in parallel, we did not consider this in algorithm selection. See Appendix (Section A) for further details on the justification of machine learning algorithm choices.

This study focused on time series classification methods that build on traditional machine learning methods because of their proven success in other application domains involving time series datasets (See (28) for more). While deep learning methods have great success in many domains, DL-based methods often require more data to train and run the risk of over-fitting. Deep learning networks are also more complex, which often makes interpretation challenging.

2.6.4 Performance evaluation

Measures used to assess algorithm performance were Area Under the Receiver Operating Characteristic Curve (AUC), Dice coefficient and Euclidean distance(s) between activation peaks identified with SPM and ML/DL. These were calculated for each participant according to language paradigm and ML/DL algorithm.

AUC was calculated for the whole brain and both the Dice coefficient and Euclidean distance were calculated using 12 language-related regions from both left and right hemispheres defined using parcellations from (43). Of the 12 language-related regions of interest, those for which at least one test participant showed $>50$ percent overlap between the region and the area of task-based activation were selected, yielding 25 regions across 6 language paradigms.

AUC values were calculated from Receiver Operating Characteristic (ROC) curves which plot the True Positive Rate vs. False Positive Rate for each test participant and task at different probability thresholds. The Dice coefficient was calculated using: $Dice=\frac{2|A\cap B|}{|A|+|B|}$ , where A corresponds to activated voxels identified by SPM and B corresponds to ML/DL activated areas. AUC and Dice coefficient values range from 0 to 1, with 1 indicating that a ML/DL algorithm performs perfectly in classifying test samples (i.e., full overlap between ML/DL and task-based activation maps. We categorised a Dice coefficient of 0.00–0.19 as low overlap, 0.20–0.39 as low-moderate overlap, 0.40–0.59 as moderate overlap, 0.60–0.79 as moderate-high overlap and 0.80–1.00 as high overlap, in keeping with categories defined by (44).

The Euclidean distance between peaks within language-related regions was also evaluated as peak location is of potential clinical importance in neurosurgical decision-making. In each selected language-related region, the distance between the highest SPM activation peak and every ML/DL activation peak was calculated and the shortest distance reported in millimeters (mm). We also assessed whether the peaks identified by ML/DL and by SPM were in the same or different gyri by co-registering the activation maps to each participant’s T1 MPRAGE structural image.

A Kruskal-Wallis test with post hoc pairwise comparisons using the Dunn test ($p$-value corrected for multiple comparisons using the Holm–Bonferroni method) were performed to identify if there were significant differences between the mean AUC, Dice coefficient and Euclidean distance between peaks for different ML/DL methods. The threshold for statistical significance was set at $p<0.05$.

3 Results

3.1 Activation maps

To illustrate how well each method performs, Figure 3 shows the overlap between activation areas found by SPM and each ML/DL algorithm studied for the Sentence Completion (SC) task in two test participants ($p<0.001$ uncorrected). The black areas denote the overlap between SPM and ML/DL activation, yellow areas denote activated areas found only by SPM and red areas denote activated areas only found by each ML/DL methods. Activated areas identified by SPM are shown in the upper left row of the figure. Reflecting the expressive and receptive language components of the SC task, activation can be seen in frontal and temporal lobes in both participants; bilateral activation was observed.

Figure 3

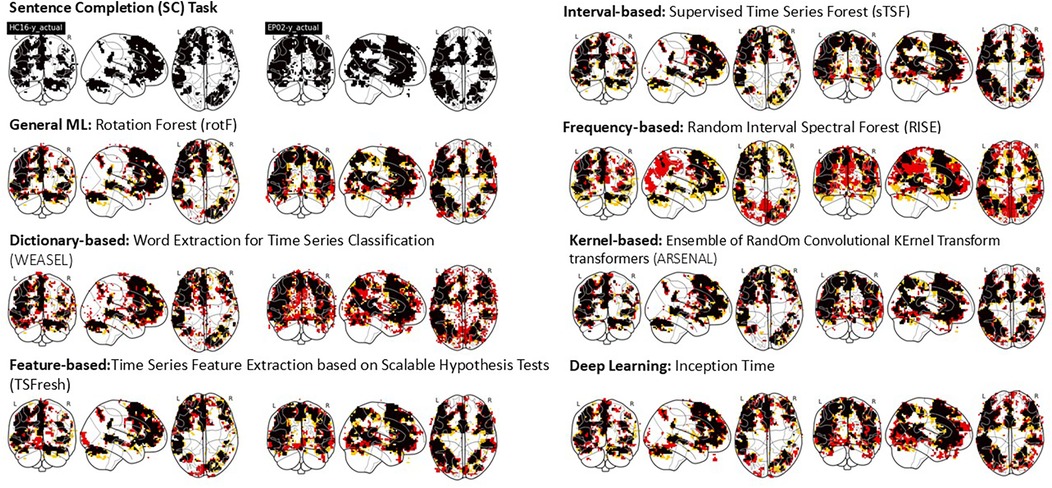
Figure 3. This figure shows the overlap between SPM activation maps vs. evaluated ML/DL activation maps of two test participants (A healthy participant, LHS under each algorithm title and an epilepsy patient, RHS under each algorithm title) for a single single language task - Sentence Completion (SC). Black - Overlap, yellow - SPM activation, Red - ML/DL activation.

Activated voxels identified by the ML/DL algorithms occurred in clusters and a qualitatively good level of overlap (as indicated by the ratio of black areas compared to red and yellow areas) was observed for most methods except for the frequency-based and dictionary-based methods. The frequency-based method shows areas that are not found to be activated by SPM (red areas in the posterior brain, including occipital and parietal areas). A number of scattered small activated areas were identified by the dictionary-based method, although the main activation clusters were still identified.

3.2 Whole-brain AUC

The scatter plot in Figure 4 shows the mean whole-brain AUC values across test participants of different ML/DL categories and language paradigms. The violin plots show the distribution of AUC values across test participants for the best and worse performing ML/DL categories of each language paradigm. Blue violin plots show the distribution of AUC values for the best performing ML/DL method and orange violin plots show the distribution of AUC values for the worst performing ML/DL method. Table 3 shows the values associated with the scatter plot in Figure 4.

Figure 4

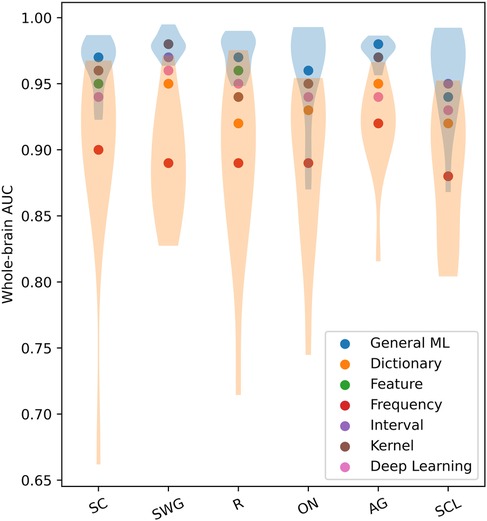
Figure 4. Mean whole-brain AUC values across test participants of different ML/DL categories, by language paradigm (as a scatter plot with violin plots showing the distribution of AUC values for the best and worse performing ML/DL methods for each language paradigm. Blue - best, Orange - worst).

Table 3

Table 3. Table of mean whole-brain AUC values across test participants by language paradigm, associated with scatter plot in Figure 4.

Mean whole-brain AUC values for different ML/DL categories and language paradigms exceeded 0.8 with the GML method achieving the highest AUC values for 5 of 6 of the language paradigms (highlighted in blue in Table 3). For the SWG paradigm, both the GML and kernel-based methods achieved the highest AUC value of 0.98. AUC values for the GML method ranged between 0.94 to 0.98, with values being highest for SWG and AG (0.98). The highest mean AUC value across language paradigms was achieved by the GML method ($0.97\pm 0.03$; Table 3). The frequency-based method consistently ranked the lowest in whole-brain AUC values, with values ranging from 0.93 to 0.96 (Mean AUC: $0.89\pm 0.06$; Table 3).

The mean AUC differed significantly between ML categories (Kruskal-Wallis Test, $H(6)=131.1$, $p=7.34\times {10}^{-26}$). On post hoc testing, the mean AUC of the GML method was found to be significantly higher than that of the dictionary, frequency and DL-based methods. The mean AUC of the frequency-based method was found to be significantly lower than that of all other evaluated methods.

When evaluated across the healthy participant and epilepsy patient groups, the GML method consistently ranks the top three when evaluated across the different language paradigms. This occurs in 89% of cases for healthy participant group and 72% for the epilepsy patient group. The GML method ranks the top two in 75% of cases for healthy participant group and 64% for the epilepsy patient group, and ranks the highest for 50% of cases for healthy participant group and 42% for the epilepsy patient group. In contrast, the frequency-based method ranks lowest among both groups, with 83% of cases for healthy participants and 86% for epilepsy patients across the evaluated language paradigms. This suggests consistent performance of ML/DL methods between healthy participants and epilepsy patients.

3.3 Dice coefficients of language regions

Figure 5 shows the mean Dice coefficients (across test participants) for each ML/DL category in different language-related regions. The violin plots show the distribution of Dice coefficients across test participants for the best and worse performing ML/DL categories of each language region of interest. Blue violin plots show the distribution of Dice coefficients for the best performing ML/DL method and orange violin plots show the distribution of Dice coefficient values for the worst performing ML/DL method. Table 4 shows the values associated with Figure 5.

Figure 5

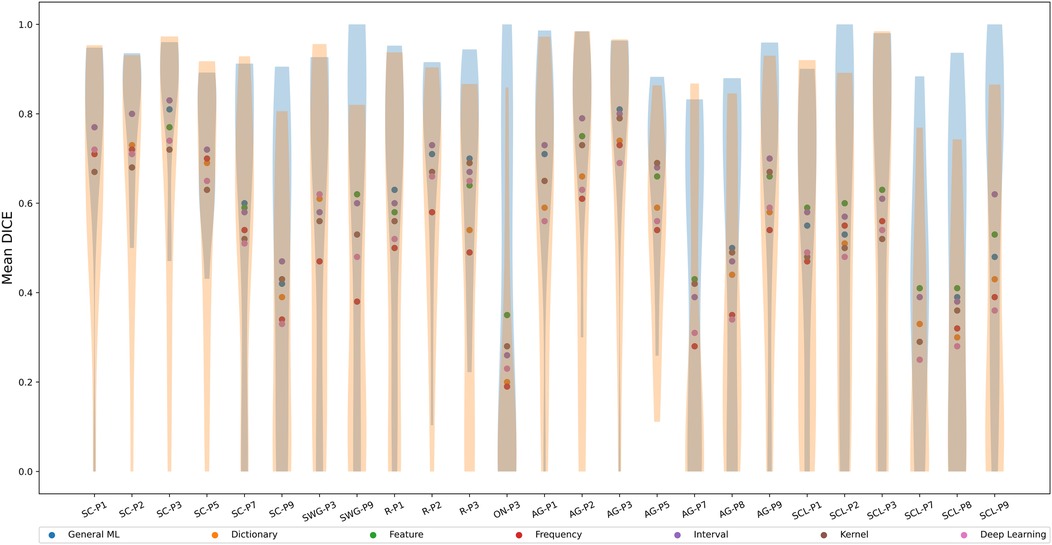
Figure 5. Mean Dice coefficient across test participants of different ML/DL categories, by language regions of interest (as a scatter plot with violin plots denoting the distribution of Dice coefficient values for the best and worse performing ML/DL methods for each language paradigm. Blue - best, Orange - worst).

Table 4

Table 4. Table of mean Dice coefficient across test participants by language language regions of interest, associated with Figure 5.

The interval-based method has the highest mean Dice coefficient values ($0.61\pm 0.33$) across evaluated language region and ranks highest for 10 out of the 25 language-related regions (highlighted in blue in Table 4). Mean Dice coefficient values for the interval-based method range from 0.26 (ON-P3) to 0.83 (SC-P3), with mean values larger or equal than 0.6 for most language-related regions except SC-P7, SC-P9, SWG-P3, ON-P3, AG-P7, AG-P8, SCL-P1, SCL-P2, SCL-P7, SCL-P8, indicating at least a moderate to high level of overlap between activated voxels identified by SPM and by the interval-based method. However, a high overlap (0.8-1.0) between activated voxels identified by SPM and by the interval-based method was only observed in 3 language-related regions (SC-P2, SC-P3, AG-P3). The frequency-based method had the lowest mean Dice coefficient ($0.5\pm 0.35$) across the evaluated language regions and ranked the lowest for 13 out of 25 language-related regions. The frequency-based method achieved a mean Dice coefficient of larger than 0.6 in only 7 regions (SC-P1, SC-P2, SC-P3, SC-P5, AG-P1, AG-P2, AG-P3), with a high level of overlap not being observed in any of the language regions.

The mean Dice coefficient differed significantly between ML Categories (Kruskal-Wallis Test, $H(6)=41.8$, $p=2.00\times {10}^{-7}$). The post hoc Dunn test revealed that the mean Dice coefficient of the interval-based method was significantly larger than that of the dictionary, frequency and DL-based methods but not significantly different from that of the remaining methods. The mean Dice coefficient for the frequency-based method was significantly lower than that of the GML, feature and interval-based methods but not significantly different from that of the remaining methods.

3.4 Euclidean distance between peaks

The scatter plot in Figure 6 shows the mean Euclidean distance (across test participants) between peaks in different language-related regions identified by SPM vs. peaks identified by the ML/DL methods in millimeters (mm). The violin plots show the distribution of Euclidean distances between peaks across test participants and ML/DL methods in different language-related regions. Table 5 shows the values associated with Figure 6.

Figure 6

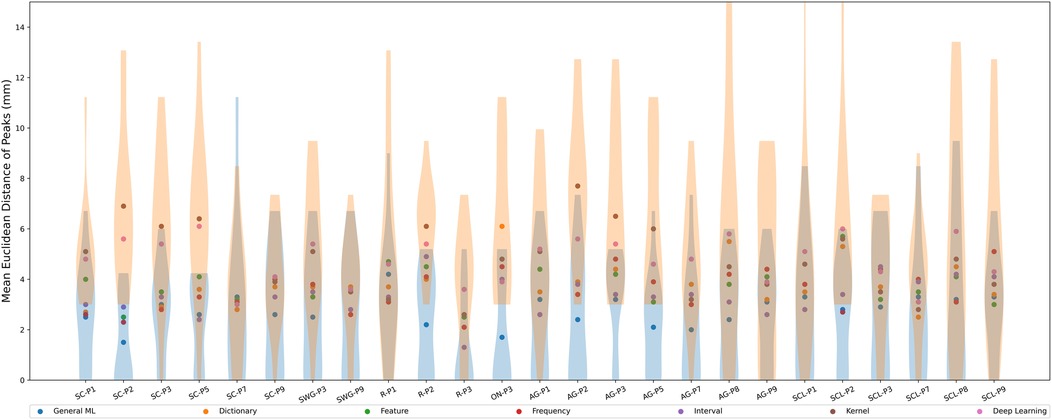
Figure 6. Mean Euclidean distance between activation peaks across test participants of different ML/DL categories and SPM, by language regions of interest (as a scatter plot with violin plots denoting the distribution of Euclidean distances for the best and worse performing ML/DL methods for each language paradigm. Blue - best, Orange - worst).

Table 5

Table 5. Table of mean Euclidean distance values across test participants by language regions of interest, associated with Figure 6.

Euclidean distances ranged from 1.3 mm (R-P3, interval-based method) to 7.7 mm (AG-P2, kernel-based method) across different ML/DL categories. The GML method had the shortest average distance between SPM peaks and GML peaks for 13 out of 25 regions (highlighted in blue in Table 5), with distances ranging from 1.5 mm (SC-P2) to 4.2 mm (R-P1). The mean Euclidean distances between the peaks for the GML method was $2.7\pm 2.4$ mm. The DL and kernel-based methods ranked the lowest for 9 out of 25 and 8 out of 25 regions respectively. Euclidean distance for the DL-based method ranged from 3.0 mm (SC-P7) to 6.1 mm (SC-P5) and for the kernel-based method it ranged from 2.6 mm (R-P3) to 7.7 mm (AG-P2). The mean Euclidean distances for the DL and kernel-based method were $4.8\pm 3.1$ mm and $4.7\pm 3.1$ mm respectively.

The mean Euclidean distance differed significantly between ML categories (Kruskal-Wallis Test, $H(6)=130.4$, $p=1.04\times {10}^{-}25$). On post hoc testing, the mean Euclidean distance for the GML method was significantly smaller than that of all other evaluated methods. The mean Euclidean distances for the kernel and DL-based methods did not significantly differ from each other but were significantly larger than that of all other evaluated methods.

Qualitative assessment of peaks was performed on the activation maps corresponding to the two most promising categories of methods (GML and interval-based). GML method identified peaks which were either in the same or adjacent gyrus to 80% of the peaks identified by SPM across the regions of interest. The interval-based method identified peaks in the same or adjacent gyrus to 60% of the peaks identified by SPM. (Note that in each participant, we only included language regions with at least 50% overlap and consequently the number of language regions of interest varied between test participants).

4 Discussion

We aimed to identify ML/DL methods for classification of language activation in fMRI time series. This was motivated by the challenges of analysing naturalistic fMRI data, where regressors are often difficult to define. fMRI data from seven language tasks were acquired. Experiments using task-based language activation data i.e., structured fMRI time series data, allowed us to understand how the ML/DL methods classify. We considered ML/DL methods for univariate time series classification from seven categories, namely general ML, DL, dictionary, feature, frequency, interval, and kernel. fMRI time series voxel data from 14 healthy participants were used for training (4,872 1D time series samples). Data from 12 participants including 6 healthy and 6 epilepsy patients were chosen for test. There were around 720,000 total 1D samples per language paradigm - see Appendix (Section A) for exact number of test samples. ML/DL models were trained on labelled data, using participant-specific SPM activation maps as the ground truth. The ML/DL methods were quantitatively evaluated using three different performance measures: whole-brain AUC, Dice coefficient and Euclidean distance between of activation peaks identified ML/DL and by SPM.

The GML and interval-based methods showed good correspondence with SPM activation (refer to Figure 3). Quantitatively, the GML method had the highest mean AUC values across the different ML/DL methods ($0.97\pm 0.03$). Interestingly, whole-brain AUC values were high for all the evaluated ML/DL methods and the mean AUC values for the GML, feature, interval and kernel-based methods were not significantly different. The interval-based method achieved the highest mean Dice coefficient (i.e., $0.61\pm 0.33$). The GML method produced the smallest mean Euclidean distance for more than half the evaluated language regions, as well as the smallest mean distance ($2.7\pm 2.4$ mm, superior by at least 0.5 mm compared to other ML/DL methods) when all of the evaluated language regions were considered. The GML and interval-based methods located peaks that were qualitatively similar in location to those identified by SPM for 80% (GML) and 60% of the (interval-based) evaluated peaks. The mean Euclidean distance for the GML method was significantly lower than for other evaluated methods. The DL and frequency-based methods rank lowest across evaluation metrics. While the frequency-based method showed excess areas of activation not corresponding to task activation, the DL-based method did predict reasonable activation. The methods associated with the other categories produced varied results, with no apparent trend in the metrics evaluated. Additionally, there was also no noticeable difference in results between healthy participants and epilepsy patients.

The results here suggest that the classification methods perform dissimilarly. Methods involving decision trees (GML and interval-based) outperform all other types of methods. Worst performing methods appeared to be those incorporating frequency information in one way or another into the features used for classification. The frequency-based method uses spectral features, and the DL-based method apply convolution operations (essentially a product operation in the frequency domain). Their inability to classify frequency features from the 1D time series information may be because the brain response during the task varies across time in a distinct, non-periodic, way (45). GML and the interval-based method rely on many decision trees chosen across the time series, essentially allowing selection of specific time points. The feature method also considers the time series features of the entire time series (38), which results in worse performance than GML and interval-based methods. Although not considered here, this suggests potential opportunities for reducing the length of the time series data without sacrificing classification accuracy.

A previous study using resting state fMRI data suggested that locations of abnormal brain activity could be predicted from 1D fMRI time series using a Convolutional Neural Network (CNN) (i.e., DL-based method) (46) and raised the possibility that DL-based methods can inform design of naturalistic fMRI stimuli. Our findings suggest that GML and interval-based methods may provide additional utility for 1D fMRI time series analysis and task design.

To our best knowledge, specific comparisons between methods categorised in the manner described here have not been performed to date, but comparisons of specific ML/DL methods in different research domains have been reported. Findings by Cabello et al. (40) on different types of time series data such as electrocardiographic recordings, stock market prices, seismic data, power demand over time, and other 1D time series data from the UCR database (47), suggest that the interval-based method sTSF is superior to TSF in terms of critical difference ranking (compared against 100+ datasets from the UCR database). This study informed our choice of sTSF in our study. Whilst not reported here, we did implement TSF and found sTSF to produce better results for time series fMRI data. In previous work, Bagnall et al. compared TSF with Rotation Forest (our GML method) and found TSF to be the best time series classification method (28), which were not concordant with our findings. In a subsequent study by Bagnall et al., the inception time approach, a DL algorithm and ROCKET, a kernel-based approach, sometimes did not perform well (48), perhaps because of over-fitting during training of these algorithms. This agrees with our finding that the DL-based method was inferior in classification performance to the others that we considered.

Our analyses indicate that, machine learning classification methods can be used to identify brain activation from fMRI time series data. The highlight the potential for ML/DL methods to identify activation in fMRI studies without pre-specified task regressors and in cognitive domains other than language.

4.1 Limitations and future work

Our study focused on comparing different ML/DL methods for the classification of task-based language fMRI time series but an analogous approach should be applicable to fMRI time series with a similar block design. We used default hyper-parameters for training the ML/DL methods and fMRI time series across different language tasks of similar block design and length were used (or the time series modified to ensure uniform length, such as padding for the AG task). Further work should examine how these methods generalize to other block designs or tasks (and fMRI time series without block designs such as naturalistic fMRI). This may involve identification of which time frame or combination of time frames within the fMRI time series contribute most to the classification resulting from the ML/DL method.

5 Conclusions

Our study involved seven routinely used fMRI language activation tasks. We evaluated the utility of different ML/DL methods from different time series classification algorithm categories in predicting which task-based language fMRI 1D time series data are activated by stimuli. The GML and interval-based method were able to best identify language areas and shows promise for use in fMRI data analysis. Our findings may lead to other work where the potential of machine learning approaches for 1D fMRI time series analysis are considered under different paradigms, such as visual and motor activation.

Data availability statement

The datasets presented in this article are not readily available as the data and code for this article is not publicly available due to patient privacy and ethical limitations. Requests to access the datasets should be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by Royal Brisbane and Women’s Hospital Human Research Ethics Committee. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

EK: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing – original draft, Writing – review & editing; VV: Conceptualization, Investigation, Methodology, Supervision, Validation, Writing – review & editing; JP: Data curation, Resources, Writing – original draft; KO: Conceptualization, Funding acquisition, Writing – review & editing; AH: Funding acquisition, Writing – original draft; DR: Conceptualization, Funding acquisition, Methodology, Resources, Supervision, Validation, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work has been supported by the Australian Research Council Training Centre for Innovation Biomedical Imaging Technology (IC170100035) funded by the Australian Government. The authors acknowledge the the facilities of the National Imaging Facility at the Centre for Advanced Imaging (CAI) and Herston Imaging Research Facility (HIRF).

Conflict of interest

KO and AH were employed by Siemens Healthcare Pty Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Seghier ML, Lazeyras F, Pegna AJ, Annoni J-M, Zimine I, Mayer E, et al. Variability of fMRI activation during a phonological and semantic language task in healthy subjects. Hum Brain Mapp. (2004) 23(3):140–55. doi: 10.1002/hbm.20053

PubMed Abstract | Crossref Full Text | Google Scholar

2. Knecht S, Jansen A, Frank A, van Randenborgh J, Sommer J, Kanowski M, et al. How atypical is atypical language dominance? Neuroimage. (2003) 18(4):917–27. doi: 10.1016/S1053-8119(03)00039-9

PubMed Abstract | Crossref Full Text | Google Scholar

3. Berl MM, Zimmaro LA, Khan OI, Dustin I, Ritzl E, Duke ES, et al. Characterization of atypical language activation patterns in focal epilepsy. Ann Neurol. (2014) 75(1):33–42. doi: 10.1002/ana.24015

PubMed Abstract | Crossref Full Text | Google Scholar

4. Powell HR, Parker GJ, Alexander DC, Symms MR, Boulby PA, Wheeler-Kingshott CA, et al. Abnormalities of language networks in temporal lobe epilepsy. Neuroimage. (2007) 36(1):209–21. doi: 10.1016/j.neuroimage.2007.02.028

PubMed Abstract | Crossref Full Text | Google Scholar

5. Ogawa S, Lee T-M, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci. (1990) 87(24):9868–72. doi: 10.1073/pnas.87.24.9868

PubMed Abstract | Crossref Full Text | Google Scholar

6. Kim S-G, Ogawa S. Biophysical and physiological origins of blood oxygenation level-dependent fMRI signals. J Cereb Blood Flow Metab. (2012) 32(7):1188–206. doi: 10.1038/jcbfm.2012.23

PubMed Abstract | Crossref Full Text | Google Scholar

7. Orringer DA, Vago DR, Golby AJ. Clinical applications and future directions of functional MRI. In: Seminars in Neurology. Vol. 32. New York, NY: Thieme Medical Publishers (2012). pp. 466–75.

Google Scholar

8. Benjamin CF, Gkiatis K, Matsopoulos GK, Garganis K. Presurgical language fMRI in epilepsy: an introduction. Transl Neurosci Speech Lang Disord. (2020): 205–39. doi: 10.1007/978-3-030-35687-3_10

Crossref Full Text | Google Scholar

9. Manan HA, Franz EA, Yahya N. Utilization of functional MRI language paradigms for pre-operative mapping: a systematic review. Neuroradiology. (2020) 62:353–67. doi: 10.1007/s00234-019-02322-w

PubMed Abstract | Crossref Full Text | Google Scholar

10. Bookheimer S. Pre-surgical language mapping with functional magnetic resonance imaging. Neuropsychol Rev. (2007) 17:145–55. doi: 10.1007/s11065-007-9026-x

PubMed Abstract | Crossref Full Text | Google Scholar

11. Black D, Vachha B, Mian A, Faro S, Maheshwari M, Sair H, et al. American society of functional neuroradiology–recommended fMRI paradigm algorithms for presurgical language assessment. Am J Neuroradiol. (2017) 38(10):E65–E73. doi: 10.3174/ajnr.A5345

PubMed Abstract | Crossref Full Text | Google Scholar

12. Bizzi A, Blasi V, Falini A, Ferroli P, Cadioli M, Danesi U, et al. Presurgical functional MR imaging of language and motor functions: validation with intraoperative electrocortical mapping. Radiology. (2008) 248(2):579–89. doi: 10.1148/radiol.2482071214

PubMed Abstract | Crossref Full Text | Google Scholar

13. Binder JR, Swanson SJ, Hammeke TA, Morris GL, Mueller WM, Fischer M, et al. Determination of language dominance using functional MRI: a comparison with the Wada test. Neurology. (1996) 46(4):978–84. doi: 10.1212/WNL.46.4.978

PubMed Abstract | Crossref Full Text | Google Scholar

14. Roux F-E, Boulanouar K, Lotterie J-A, Mejdoubi M, LeSage JP, Berry I. Language functional magnetic resonance imaging in preoperative assessment of language areas: correlation with direct cortical stimulation. Neurosurgery. (2003) 52(6):1335–47. doi: 10.1227/01.NEU.0000064803.05077.40

PubMed Abstract | Crossref Full Text | Google Scholar

15. Agarwal S, Sair HI, Gujar S, Pillai JJ. Language mapping with fMRI: current standards and reproducibility. Top Magn Reson Imaging. (2019) 28(4):225–33. doi: 10.1097/RMR.0000000000000216

PubMed Abstract | Crossref Full Text | Google Scholar

16. Lindquist MA. The statistical analysis of fMRI data. Statist Sci. (2008) 23(4):439–64. doi: 10.1214/09-STS282

Crossref Full Text | Google Scholar

17. Kiebel SJ, Holmes AP. The general linear model. In: Penny WD, Friston KJ, Ashburner JT, Kiebel SJ, Nichols TE, editors. Statistical Parametric Mapping: The Analysis of Functional Brain Images. San Diego, CA and London: Elsevier (2007). p. 101–25.

Google Scholar

18. Sonkusare S, Breakspear M, Guo C. Naturalistic stimuli in neuroscience: critically acclaimed. Trends Cogn Sci (Regul Ed). (2019) 23(8):699–714. doi: 10.1016/j.tics.2019.05.004

PubMed Abstract | Crossref Full Text | Google Scholar

19. Hasson U, Malach R, Heeger DJ. Reliability of cortical activity during natural stimulation. Trends Cogn Sci (Regul Ed). (2010) 14(1):40–8. doi: 10.1016/j.tics.2009.10.011

PubMed Abstract | Crossref Full Text | Google Scholar

20. Eickhoff SB, Milham M, Vanderwal T. Towards clinical applications of movie fMRI. NeuroImage. (2020) 217:116860. doi: 10.1016/j.neuroimage.2020.116860

PubMed Abstract | Crossref Full Text | Google Scholar

21. Finn ES, Bandettini PA. Movie-watching outperforms rest for functional connectivity-based prediction of behavior. NeuroImage. (2021) 235:117963. doi: 10.1016/j.neuroimage.2021.117963

PubMed Abstract | Crossref Full Text | Google Scholar

22. Jääskeläinen IP, Sams M, Glerean E, Ahveninen J. Movies and narratives as naturalistic stimuli in neuroimaging. NeuroImage. (2021) 224:117445. doi: 10.1016/j.neuroimage.2020.117445

Crossref Full Text | Google Scholar

23. Çelik E, Dar SUH, Yılmaz Ö, Keleş Ü, Çukur T. Spatially informed voxelwise modeling for naturalistic fMRI experiments. NeuroImage. (2019) 186:741–57. doi: 10.1016/j.neuroimage.2018.11.044

PubMed Abstract | Crossref Full Text | Google Scholar

24. Ylipaavalniemi J, Savia E, Malinen S, Hari R, Vigário R, Kaski S. Dependencies between stimuli and spatially independent fMRI sources: towards brain correlates of natural stimuli. NeuroImage. (2009) 48(1):176–85. doi: 10.1016/j.neuroimage.2009.03.056

PubMed Abstract | Crossref Full Text | Google Scholar

25. Rashid M, Singh H, Goyal V. The use of machine learning and deep learning algorithms in functional magnetic resonance imaging—a systematic review. Expert Syst. (2020) 37(6):e12644. doi: 10.1111/exsy.12644

Crossref Full Text | Google Scholar

26. Bock C, Moor M, Jutzeler CR, Borgwardt K. Machine learning for biomedical time series classification: from shapelets to deep learning. Artif Neural Netw. (2021) 2190:33–71. doi: 10.1007/978-1-0716-0826-5_2

PubMed Abstract | Crossref Full Text | Google Scholar

27. Ismail Fawaz H, Forestier G, Weber J, Idoumghar L, Muller P-A. Deep learning for time series classification: a review. Data Min Knowl Discov. (2019) 33(4):917–63. doi: 10.1007/s10618-019-00619-1

Crossref Full Text | Google Scholar

28. Bagnall A, Bostrom A, Large J, Lines J. The great time series classification bake off: an experimental evaluation of recently proposed algorithms. extended version. arXiv [Preprint]. arXiv:1602.01711 (2016).

Google Scholar

29. Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. (2012) 59(3):2142–54. doi: 10.1016/j.neuroimage.2011.10.018

PubMed Abstract | Crossref Full Text | Google Scholar

30. SPM - statistical parametric mapping. Available online at: https://www.fil.ion.ucl.ac.uk/spm/ (accessed December 19, 2023).

Google Scholar

31. Ashburner J, Barnes G, Chen C-C, Daunizeau J, Flandin G, Friston K, et al. SPM12 manual. Wellc Trust Centre Neuroimaging Lond UK. (2014) 2464(4):19–78. https://www.fil.ion.ucl.ac.uk/spm/doc/spm12_manual.pdf

Google Scholar

32. Löning M, Bagnall A, Ganesh S, Kazakov V, Lines J, Király FJ. sktime: a unified interface for machine learning with time series. arXiv [Preprint]. arXiv:1909.07872 (2019).

Google Scholar

33. Time series classification; sktime documentation. Available online at: https://sktime-backup.readthedocs.io/en/v0.13.4/api_reference/classification.html. (accessed December 19, 2023).

Google Scholar

34. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in python. J Mach Learn Res. (2011) 12:2825–30. http://jmlr.org/papers/v12/pedregosa11a.html

Google Scholar

35. Rodriguez JJ, Kuncheva LI, Alonso CJ. Rotation forest: a new classifier ensemble method. IEEE Trans Pattern Anal Mach Intell. (2006) 28(10):1619–30. doi: 10.1109/TPAMI.2006.211

PubMed Abstract | Crossref Full Text | Google Scholar

36. Probst P, Boulesteix A-L, Bischl B. Tunability: Importance of hyperparameters of machine learning algorithms. J Mach Learn Res. (2019) 20(53):1–32. http://jmlr.org/papers/v20/18-444.html

Google Scholar

37. Schäfer P, Leser U. Fast and accurate time series classification with weasel. In: Proceedings of the 2017 ACM on Conference on Information and Knowledge Management (2017). pp. 637–46.

Google Scholar

38. Christ M, Braun N, Neuffer J, Kempa-Liehr AW. Time series feature extraction on basis of scalable hypothesis tests (tsfresh–a python package). Neurocomputing. (2018) 307:72–7. doi: 10.1016/j.neucom.2018.03.067

Crossref Full Text | Google Scholar

39. Lines J, Taylor S, Bagnall A. Time series classification with hive-cote: the hierarchical vote collective of transformation-based ensembles. ACM Trans Knowl Discov Data (TKDD). (2018) 12(5):1–35. doi: 10.1145/3182382

Crossref Full Text | Google Scholar

40. Cabello N, Naghizade E, Qi J, Kulik L. Fast and accurate time series classification through supervised interval search. In: 2020 IEEE International Conference on Data Mining (ICDM). IEEE (2020). pp. 948–53.

Google Scholar

41. Middlehurst M, Large J, Flynn M, Lines J, Bostrom A, Bagnall A. Hive-cote 2.0: a new meta ensemble for time series classification. Mach Learn. (2021b) 110(11-12):3211–43. doi: 10.1007/s10994-021-06057-9

Crossref Full Text | Google Scholar

42. Ismail Fawaz H, Lucas B, Forestier G, Pelletier C, Schmidt DF, Weber J, et al. Inceptiontime: Finding alexnet for time series classification. Data Min Knowl Discov. (2020) 34(6):1936–62. doi: 10.1007/s10618-020-00710-y

Crossref Full Text | Google Scholar

43. Fedorenko E, Hsieh P-J, Nieto-Castañón A, Whitfield-Gabrieli S, Kanwisher N. New method for fMRI investigations of language: defining ROIs functionally in individual subjects. J Neurophysiol. (2010) 104(2):1177–94. doi: 10.1152/jn.00032.2010

PubMed Abstract | Crossref Full Text | Google Scholar

44. Wilson SM, Bautista A, Yen M, Lauderdale S, Eriksson DK. Validity and reliability of four language mapping paradigms. NeuroImage: Clin. (2017) 16:399–408. doi: 10.1016/j.nicl.2016.03.015

PubMed Abstract | Crossref Full Text | Google Scholar

45. Handwerker DA, Gonzalez-Castillo J, D’esposito M, Bandettini PA. The continuing challenge of understanding and modeling hemodynamic variation in fMRI. Neuroimage. (2012) 62(2):1017–23. doi: 10.1016/j.neuroimage.2012.02.015

PubMed Abstract | Crossref Full Text | Google Scholar

46. Wu Y-Y, Hu Y-S, Wang J, Zang Y-F, Zhang Y. Toward precise localization of abnormal brain activity: 1D CNN on single voxel fMRI time-series. Front Comput Neurosci. (2022) 16:399–408. doi: 10.3389/fncom.2022.822237

Crossref Full Text | Google Scholar

47. Dau HA, Bagnall A, Kamgar K, Yeh C-CM, Zhu Y, Gharghabi S, et al. The UCR time series archive. IEEE/CAA J Autom Sin. (2019) 6(6):1293–305. doi: 10.1109/JAS.2019.1911747

Crossref Full Text | Google Scholar

48. Bagnall A, Flynn M, Large J, Lines J, Middlehurst M. A tale of two toolkits, report the third: on the usage and performance of hive-cote v1.0. arXiv [Preprint]. arXiv:2004.06069 (2020).

Google Scholar

49. Abanda A, Mori U, Lozano JA. A review on distance based time series classification. Data Min Knowl Discov. (2019) 33(2):378–412. doi: 10.1007/s10618-018-0596-4

Crossref Full Text | Google Scholar

50. Middlehurst M, Large J, Cawley G, Bagnall A. The temporal dictionary ensemble (TDE) classifier for time series classification. In: Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2020, Ghent, Belgium, September 14–18, 2020, Proceedings, Part I. Springer (2021). pp. 660–76.

Google Scholar

51. Lines J, Taylor S, Bagnall A. Hive-cote: the hierarchical vote collective of transformation-based ensembles for time series classification. In: 2016 IEEE 16th International Conference on Data Mining (ICDM) (2016). pp. 1041–6. doi: 10.1109/ICDM.2016.0133.

Crossref Full Text | Google Scholar

52. Bagnall A, Flynn M, Large J, Lines J, Middlehurst M. On the usage and performance of the hierarchical vote collective of transformation-based ensembles version 1.0 (hive-cote v1.0). In: Advanced Analytics and Learning on Temporal Data: 5th ECML PKDD Workshop, AALTD 2020, Ghent, Belgium, September 18, 2020, Revised Selected Papers 6. Springer (2020). p. 3–18.

Google Scholar

53. Dempster A, Petitjean F, Webb GI. Rocket: exceptionally fast and accurate time series classification using random convolutional kernels. Data Min Knowl Discov. (2020) 34(5):1454–95. doi: 10.1007/s10618-020-00701-z

Crossref Full Text | Google Scholar

54. Middlehurst M, Large J, Bagnall A. The canonical interval forest (CIF) classifier for time series classification. In: 2020 IEEE International Conference on Big Data (Big Data). IEEE (2020). p. 188–95.

Google Scholar

55. Deng H, Runger G, Tuv E, Vladimir M. A time series forest for classification and feature extraction. Inf Sci (Ny). (2013) 239:142–53. doi: 10.1016/j.ins.2013.02.030

Crossref Full Text | Google Scholar

Appendix

A.1 Test set size for different participant and tasks

Refer to Table A1 for test set sizes of the various fMRI language tasks.

Table A1

Table A1. Test set size for different participants and tasks.

A.2 Further justification of ML/DL choice

Authors in (28) suggest that on data that has never been evaluated before to start with Random Forest (RF), Rotation Forest (RotF) or Dynamic Time Warping (DTW) as a basic sanity check. Although DTW is known to be one of the more accurate algorithms, like other distance-based methods it is known to be slow and hard to scale (49) (For this reason the distance-based category was also excluded from further analysis). Hence, for the general ML category, RF and RotF were evaluated and RotF was retained due to its strong performance. For the dictionary-based category, two algorithms were short-listed, Temporal Dictionary Ensemble (TDE) and Word Extraction for Time Series Classification (WEASEL) (50). While TDE is built on the advantages of other dictionary-based algorithms such as Bag of Symbolic-Fourier Approximation (BOSS), Contractable Bag of Symbolic-Fourier Approximation (cBOSS) and Word Extraction for Time Series Classification (WEASLE)), TDE is known to be more accurate but also memory intensive (50). Authors in (50) also suggest that for faster prediction to use WEASLE. It was found that TDE indeed was memory intensive and took a long time to train, hence WEASLE was chosen instead. The Hierarchical Vote Collective of Transformation-Based Ensembles (HIVE-COTE) (51, 52) algorithm is an ensemble of 4 different algorithms (Shapelet Transform Classifier (STC), Time Series Forest (TSF), Random Interval Spectral Forest (RISE) and Contractable Bag of Symbolic-Fourier Approximation (cBOSS)) and was the early benchmark time series classifier with high accuracy. However, it had the disadvantage of long training and test times (28). It was since super-seeded by the Kernal-based method, RandOm Convolutional KErnel Transform (ROCKET) (53) algorithm (which was faster and more scalable) and subsequently HIVE-COTE version 2 (41). However, we found that the version 2 (v2) of HIVE-COTE (41) still has long training time and is also memory intensive, and was excluded from our analysis. The ROCKET algorithm fails to produce prediction probabilities, and ARSENAL which is an ensemble of ROCKET(s) was evaluated instead. The RISE algorithm (39) remains the only algorithm in the frequency-based category and was the only algorithm evaluated within the category. Several feature-based algorithms were also evaluated and the best performing algorithm, the Time Series Feature Extraction based on Scalable Hypothesis Tests (TSFresh) (38) method was retained. Several interval-based algorithms including Canonical Interval Forest (CIF) (54), Diverse Representation Canonical Interval Forest (DrCIF) (41) Time Series Forest (TSF) (55) and supervised Time Series Forest (sTSF) (40) were evaluated as task-based fMRI time series is block-designed and is known to have repetitive intervals. The best performing algorithm i.e., sTSF was retained. The shapelet based method, Shapelet Transform Classifier, was unable to generate prediction probabilities, and was excluded from further analysis. Deep learning algorithms have had great success in the image classification domain and efforts have been made to adapt these algorithms for time series classification. We found that Inception time performed well for time series classification compared to two other methods, Residual Neural Network (ResNet) and Fully Convolutional Network (FCN) and Inception Time was retained.