
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Public Health , 23 October 2024
Sec. Injury Prevention and Control
Volume 12 - 2024 | https://doi.org/10.3389/fpubh.2024.1453788
This article is part of the Research Topic Road Traffic Injury Prevention and Control View all 12 articles
Introduction: Emergency medical service (EMS) serves as a pivotal role in linking injured road users to hospitals via offering first aid measures and transportation. This paper aims to investigate the effect of emergency medical service (EMS) response time on the fatality risk of freeway crashes.
Methods: Crash injury severity data from Kaiyang Freeway, China in 2014 and 2015 are employed for the empirical investigation. A Bayesian random parameters spatial logistic model is developed for analyzing crash severity.
Results: Bayesian inference of the random parameters spatial logistic model demonstrates the importance of reducing EMS response time on minimizing the fatality risk of freeway crashes. Fatality odds would increase by 2.6% for 1 min increase in EMS response time. Additionally, vehicle type, crash type, time of day, horizontal curvature, vertical grade, and precipitation are also found to have significant effects on the fatality probability of freeway crashes.
Conclusion: It is crucial to reduce EMS response time to decrease the fatality likelihood of freeway crashes. Some countermeasures have been proposed to shorten EMS response time.
Given the huge emotional and economic burden imposed by roadway crashes on the society, identifying contributing factors to crash occurrence and injury severity and quantifying their effects have long been a research focus in the research field of traffic safety (1). Most of existing studies (2–5) explored contributing factors to crash occurrence (pre-crash factors) and those to injury severity during the crash event from human, vehicle, and environmental factors. On the other hand, post-crash factors, such as those pertaining to emergency medical services (EMS), have been relatively less investigated, due to data availability and reliability.
After the crash occurrence, EMS serves as a pivotal role in linking injured road users to hospitals via offering first aid measures and transportation (6). EMS response time, herein defined as the time that elapses from the notification of a traffic crash until EMS personnel arrives at the crash scene (7), is an important indicator of the time for patients to be treated and the performance of dispatching EMS resources (8). Many safety researchers (9–11) acknowledge the significant impact of EMS response time on the fatality likelihood of traffic crashes, especially in cases of victims sustaining severe injury. This opinion is reasonable, because a proportion of crash deaths would be evitable, from the clinical perspective, if timely medical treatments were provided to the severely injured victims, particularly those with brain/heart trauma (12) or in need of haemorrhage controls or open airways (13, 14).
Despite of sparseness, there is a small quantity of studies that have investigated the effect of EMS response time on the injury severity of traffic crashes, using discrete outcome models. For example, based on a binary probit regression analysis of a dataset with over 1,400 traffic crashes in Spain, Sánchez-Mangas et al. (11) concluded that a 10-min reduction of EMS response time is expected to result in the fatality likelihood decreasing by 33%. Using a dataset from the Fatality Analysis Reporting System (FARS) in the U.S., Ma et al. (15) investigated the smooth relationship between crash fatality probability and EMS response time and found that 17 min is the gold time for crash rescues. Lee et al. (6) developed a random effects ordered probit model for analyzing crash injury severity, and incorporated crash-reporting time, response time, and transport time into the analysis. Their results indicate that longer response time and transport time are linked to more severe injury outcomes. Hosseinzadeh and Kluger (16) also adopted a random effects ordered probit model for uncovering the association between crash injury severity and EMS response time and on-scene time, as well as crash-related factors. They found that shorter response time and longer on-scene time is helpful to decrease the severity level of entire-body injuries. Zeng et al. (17) proposed a spatial generalized ordered probit model for the analysis of freeway crash severity, where EMS response time is included as an explanatory variable. The results also suggested that is lower crash severity is associated with a shorter EMS response time. Although the above studies have all demonstrated the significant impact of EMS response time on crash injury severity, a distinct difference lies in them: the former two studies categorized crash severity into two levels (i.e., fatal and non-fatal) and assumed that EMS response time has a considerable effect on fatality likelihood, and the latter three studies categorized crash severity into more than two levels (e.g., KABCO has five severity levels) and implied that EMS response time may have significant effects on the likelihoods of other severity levels, such as no injury. Obviously, the former assumption is more reasonable and consistent to the findings from clinic medicine. To accurately quantify the effect of EMS response time on the fatality likelihood of freeway crashes, in this research, the injury severity will be divided into fatal and non-fatal, as in Sánchez-Mangas et al. (11) and Ma et al. (15). Our research focuses on freeway crashes, as they are more likely to result in human deaths than traffic crashes on other types of roadways, such as urban roads. Besides, the unique built environment (e.g., far from hospitals) and roadway conditions (e.g., the existence of emergency lane and no intersection) may make the EMS response time for freeway crashes different from that for crashes on other roadways.
Analytic method is also important to analyze crash injury severity. Given the binary categorization, statistically, binary logit or probit models have been most frequently used. In the recent decade, accounting for the unobserved heterogeneity and spatial correlation is prevalent when modeling crash severity (18, 19). Random parameters (20), latent class/finite mixture (21), and Markov switching approaches (22) are typical methods capable of capturing the unobserved heterogeneity. Among them, random parameters approaches are most widely used. To accommodate spatial correlation, various spatial structures, including spatial lag (23, 24), spatial error (23), intrinsic conditional autoregressive (CAR) (25, 26), and Leroux CAR (17), have been incorporated into the formulation of discrete outcome models. Zeng et al. (17) found that the Leroux CAR is superior to other alternatives. In this research, we propose a random parameters spatial logistic model with Leroux CAR for analyzing freeway crash severity, which can simultaneously capture the unobserved heterogeneity and spatial correlation in it.
The rest of the article is organized into four sections. The freeway crash-severity data used for the empirical analysis are introduced in Section 2. We specify the formulation of the random parameters spatial logistic model in Section 3. The Bayesian estimation results of the proposed model are summarized and interpreted in Section 4. In the last section, we draw conclusions from the research and offer guidance for future research.
Crash data of 2 years in 2014 and 2015 were collected from Kaiyang Freeway in Guangdong, China, which were acquired from the Highway Maintenance and Administration Management System maintained by Guangdong Transportation Group. Excluding the crash records with incomplete information, 1,414 crash records were used for the empirical analysis. In the original crash records, injury severity is categorized into four levels: no injury, slight injury, severe injury, and fatality. As mentioned earlier, the paper focuses on quantifying the effect of EMS response time on the fatality likelihood of freeway crashes versus that of non-fatality. Thus, the injury severity in the analysis was contracted into two levels: non-fatality (combining no injury, slight injury, and severe injury) and fatality. Among the observations, 1,378 crashes’ severity levels are of non-fatality and 36 crashes’ are of fatality.
In the crash records, in addition to injury severity, some information pertaining to EMS, involved vehicle(s) and accident configuration is also documented, including: EMS response time, vehicle type (passenger car, coach, truck, and others) and license number (which is used to distinguish if a vehicle is local or not), crash time (morning, afternoon, evening, and before dawn), crash date (weekday and weekend), crash type (single-vehicle crash, rear-end crash, and angle crash), and crash location (which is expressed as kilometers marker of the freeway). As the key factor under investigation, the distribution of EMS response time in the dataset is shown in Figure 1.
We obtain the geometry design materials on Kaiyang Freeway from Guangdong Province Communication Planning and Design Institute Co., Ltd. Four roadway attributes, including horizontal curvature, vertical grade, and if the crash site is near a ramp or on a bridge, are extracted from the materials and matched with each crash according to their location information. To capture the spatial effects in the crashes, the freeway is segmented into 154 sections based on the criterion of homogeneity in horizontal curvature and vertical grade, which is line with the roadway segmentation methods used in the past studies (17, 27).
We collect the real-time weather data along the freeway from the Meteorological Information Management System. The system is administrated by the Guangdong Climate Centre, an official meteorological organization. The data on wind speed, precipitation, visibility, temperature, and humidity are observed and recorded in each hour by three weather stations: Enping Weather Station, Kaiping Weather Station, and Yangjiang Weather Station. We match each crash under investigation with the hourly meteorological information from the nearest weather station through the crash time and location.
Table 1 displays the definitions and descriptive statistics of crash injury severity and its potential influence factors for the empirical analysis. We conduct Pearson correlation test and multi-collinearity diagnoses for the factors in SPSS software and find that there is no significant correlation or multi-collinearity among them.
We propose a random parameters spatial logistic model for investigating the crash injury severity with binary outcomes (fatality and non-fatality). To justify the superiority of the proposed model, we compare it with traditional logistic model and spatial logistic model. In the section, the formulations of these models are clearly specified in the order of model complexity (Section 3.1); and then the implementation processes of Bayesian estimation and performance assessment criterion for the models are introduced (Section 3.2).
Logistic model (i.e., binary logit model) is one of the most extensively used methods for the analysis of crash injury severity divided into two levels (1). As suggested in Table 1, denote fatal crash = 1 and non-fatal crash = 0. For any crash , a latent variable is set. It is assumed that there is a linear association between and the covariates. If is positive, the injury severity of crash is fatal; otherwise, it is non-fatal. The model equation is shown in Equations 1 and 2:
where is the observed value of the th covariate, , in crash , and is the coefficient corresponding to . is a constant term. and are the numbers of covariates and crashes in the dataset. is a residual term and is assumed to have a logistic distribution. Its cumulative distribution function is expressed as Equation 3:
According to the model formulation, the probabilities of crash resulting in fatality and non-fatality (represented by and respectively), can be calculated as Equations 4 and 5:
Accordingly, the odds of fatality crash are calculated as Equation 6:
To quantify the effect of a certain factor on crash injury severity, its odds ratio is usually computed and reported (28). For any covariate , its odds ratio is defined as Equation 7:
Some unobserved/unobservable factors may have similar effects on the injury severities of crashes in close proximity, resulting in spatial correlation/dependency across them (17). To account for the spatial dependency, a spatial logistic model is developed, by adding a random error term with CAR prior into the formulation of . Different from the intrinsic CAR prior adopted in the previous studies (25, 26), the Leroux CAR prior which is able to flexibly capture the strength of spatial correlation (29), is specified in the spatial logistic model. Specifically, for crash occurring in freeway section can be calculated by Equations 8 and 9:
where and represent the spatial effects of crashes in freeway sections and . represents the degree of the proximity between sections and . The first order adjacency-based rule which is widely used in spatial modeling, is employed to define the proximity degrees: if freeway sections and share a common end, ; otherwise, . is an estimable parameter which measures the strength of spatial correlation. A higher value of indicates stronger spatial correlation. implies that no spatial correlation exists among the injury severities of observed crashes. (equivalent to the intrinsic CAR prior) suggests that the injury severities of adjacent crashes are fully correlated. is a hyper-parameter related to the variance of spatial correlation.
There may be unobserved heterogeneities in the effects of certain factors on crash injury severity (18). To simultaneously account for unobserved heterogeneity and spatial correlation, a random parameters spatial logistic model is proposed. Specifically, the coefficient in Equation 8 is switched to random parameters which can vary across crashes. Although there are a number of applicable forms of random parameters, the commonest one is adopted in the study as shown in Equation 10:
in which is the mean of . is a normally distributed random term as shown in Equation 11:
where denotes the standard deviation of .
Given the complex structure of CAR prior, the above models are estimated by Bayesian inference method. It necessitates specifying a prior distribution for each parameter or hyper-parameter, which reveals the researchers’ prior knowledge on it. In the case of no available prior knowledge, as in the previous studies (17, 25, 26), non-informative distributions are adopted. Specifically, a diffused normal distribution, , is set as the prior of and ; a uniform distribution, , is set as the prior of ; and a uniform distribution, , is set as the prior of and .
The Bayesian estimation is implemented in the WinBUGS software (30), in which Gibbs sampling algorithms and Markov chain Monte Carlo (MCMC) simulation techniques are embedded to infer the posterior distributions of parameters. For each model, a chain of MCMC simulation is run, and 100,000 simulation iterations are set, with the first 50,000 iterations acting as burn-in. To judge if the MCMC simulations are converged, we visually inspect the history plots for the parameters (such as that for EMS response time in the random parameters model as shown in Figure 2) and monitor whether the ratio between the Monte Carlo simulation error for each parameter and its posterior standard deviation is less than 5%. In the random parameters spatial logistic model, if the posterior variance is not statistically significant at the 95% Bayesian credibility level, it is transformed to a fixed parameter.
The deviance information criterion (DIC), which is the most popular criterion for assessing Bayesian models, is used for comparing the comprehensive performance of the above crash severity models. As a Bayesian generalization of Akaike’s information criterion, the DIC provides a hybrid measure of model fitting and complexity. According to Spiegelhalter et al. (31), its calculation equation is expressed as Equation 12:
where and are the posterior mean deviance and the effective number of parameters respectively, which are used to measure the model fitting and complexity accordingly. Generally, a lower DIC value means a better overall performance. As suggested by Lunn et al. (30), we can conclude that a model with a lower DIC is considerably superior if the DIC difference with another one is greater than 10.
The results of Bayesian estimation and performance assessment for the three models are summarized in Table 2. Only the covariates whose parameters are significant at least at the 90% credibility level are included in the table. We can find that the value of the spatial logistic model is lower than that of the logistic model with the difference over 20. It indicates that the spatial logistic model performs substantially better than the logistic model in fitting the association between crash severity and EMS response time as well as other factors. Although the lower value of the logistic model implies that it is more parsimonious, the 16 points of DIC lower for the spatial logistic model suggest its superior overall performance. These findings are in line with the previous studies (17, 23, 25, 26): accounting for spatial correlation among adjacent crashes by CAR prior can effectively reduce model misspecification and improve model estimation. The reasonableness of the spatial logistic model with Leroux CAR prior can also be demonstrated by the Bayesian estimates of and , which are both significant at the 95% credibility level. Additionally, the posterior mean of is 0.62. It implies that the spatial correlation in the crash severity is medium, that cannot be figured out by the intrinsic CAR prior applied in Xu et al. (26) and Meng et al. (25).
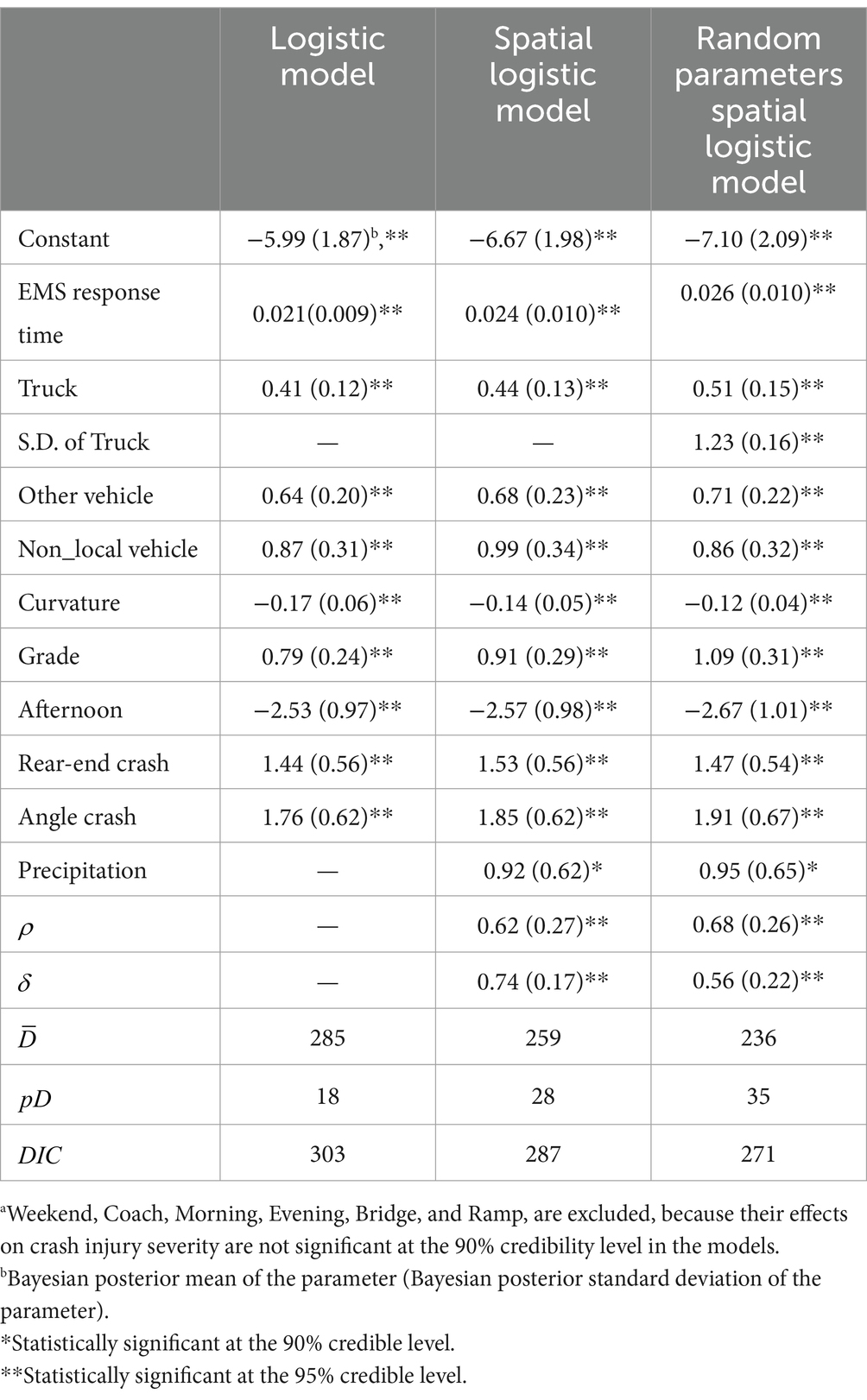
Table 2. Results of Bayesian parameter estimation and performance assessment for the models.a
The random parameters spatial logistic model yields the lowest values of and DIC. We may conclude that accounting for the unobserved heterogeneities in the effects of certain covariates by allowing their parameters to vary across observations can further improve model fitting performance, given the consideration of spatial correlation. Similar results can be found in the research conducted by Zeng et al. (32). In the random parameters spatial logistic model, the posterior mean of is a little higher than the counterpart in the spatial logistic model. That is, the strength of spatial correlation is slightly increased due to the accommodation of random parameters. Besides, the posterior mean of is significantly lower in the random parameters model. This is reasonable, as a proportion of the structure spatial effects may be derived from the unobserved heterogeneity which has been captured by the random parameter.
The effects of EMS response time and other significant variables on the fatality probability of freeway crashes are interpreted based on the parameter estimation in the random parameters spatial logistic model, since it outperforms the other two models.
According to the Bayesian modeling estimation results summarized in Table 2, the parameter for EMS response time is statistically significant with a positive coefficient at the 95% credibility level, which indicates that a longer EMS response time is expected to increase the probability of fatality crash. The odds ratio for EMS response time is estimated to be 1.026 (=exp.(0.026)), i.e., the odds of resulting in fatality crash would be increased by 2.6% for per one-minute increase of EMS response time. The findings are generally consistent with those in most of the previous studies (6, 11, 17) and experiences from clinic medicine and transportation engineering: rapid response of EMS personnel is able to prevent the death of certain traffic crash victims suffered from severe trauma injuries, but are different from those in some others. For example, Ma et al. (15) found that the effect of EMS response time on fatality risk is non-monotonic, such that EMS response time may be negatively associated with the odds of fatality in some cases. These phenomena are originated from the urgency level of a crash and EMS dispatch priority (15, 33–35). Nevertheless, we did not find such phenomena from the current study. It is possible because freeway crashes in China usually have the high priority for EMS dispatch, given their more severe outcomes than those on other types of roadways (17). Besides, the average marginal effect of 10-min EMS response time on fatality crash is estimated to be 0.00231. That is, 0.23 less fatality crash per every 100 crashes is expected for a 10-min reduction in EMS response time. The marginal effect is significantly lower than that (=0.024) estimated by Sánchez-Mangas et al. (11), which may be attributed to lower fatality rate of our crash data and the differences in EMS level between China and Spain.
To make the EMS personnel and vehicles arrive at crash scenes as soon as possible, the following countermeasures may be effective (1): Installing sufficient EMS facilities near freeways. Once a freeway crash is reported or detected, the emergency management agencies usually dispatch rescue personnel and vehicles from the nearest EMS facility to the crash scene. More EMS facilities can reduce the expected distance between them and crash locations (2).; Optimizing the traveling path to crash scenes (as shown in Figure 3), according to the real-time traffic data collected by various detection techniques and transmitted by 5G communication technology. There may be several alternative traveling paths from a EMS facility to the crash scene. The travel time of each path is depended on the traffic conditions which is usually influenced by the traffic crash. If the traffic conditions on each path is detected, transmitted, and predicted in real-time, we can find the one with shortest travel time (3). Strict enforcement against illegal occupancy of emergency lanes on freeways. The occurrence of traffic crash may bring about traffic congestion. A rescue vehicle can travel on emergency lanes to avoid the adverse impacts of traffic congestion on its travel speed. However, emergency lanes may also be illegally occupied by other vehicles. Thus, strict enforcement against the illegal occupancy is also helpful to reduce the arrival time of EMS vehicles.
Truck is the only covariate that has a heterogeneous effect on crash injury severity. The estimated mean and standard deviation of the random parameter for truck are 0.51 and 1.23 respectively, which indicate that about 66% of truck involved crashes are more likely to result in fatality. It is reasonable, because trucks usually possess larger mass and higher structural rigidity which impose greater harm on the occupants in other vehicles involved in the same collision, i.e., higher crash aggressivity defined in Huang et al. (36). Meanwhile, the rest 34% of truck involved crashes are less likely to result in fatality. In this research, a proportion of truck’s effect on crash severity may be derived from truck drivers’ driving behavior which is not observed in the crash data. Considerable variability in truck drivers’ behavior when occurring a crash may explain the heterogeneous effect.
Other_vehicle is found to have a significant and homogeneous effect on crash severity. According to the Bayesian estimates, the fatality odds of crashes involving other type vehicles (e.g., towed vehicles) are 2.03 [=exp(0.71)] times of that of crashes involving passenger cars only, with all other factors equal. Similar to trucks, other type vehicles also possess higher crash aggressivity than passenger cars, thus more likely to resulting in fatalities.
It is interesting to find that non_local vehicle has a significantly positive effect on crash severity. That is, involving non-local vehicles (i.e., those not registered in the province where the crash happened) would increase the crash fatality risk. Specifically, the fatality odds are expected to increase by 136% [=exp(0.86)−1], if there is one or more non-local vehicle involved in a crash. We can find similar results in the research conducted by Zeng et al. (17). They argued that the drivers of non-local vehicles are usually less familiar with the roadway environment, and thus may not have enough time to take proper actions before crashes.
Regarding roadway geometric attributes, curvature and grade are significantly associated with crash injury severity. The negative sign of the parameter for curvature suggests that crashes on freeway sections with smaller horizontal curve radius are less likely to result in fatalities. The crash fatality odds would decrease by 11% [=1−exp(−0.12)] for a 0.1 km−1 increase in horizontal curvature. It is possible, because drivers tend to reduce speed and become more cautious to avoid vehicles out of control when driving on small radius curves (37, 38). The estimated mean of the parameter for grade is 1.09. It indicates that the odds of crash fatality would increase by 197% [=exp(1.09)−1] for a 1% increase in vertical grade. High grade would reduce sight distance (2, 5). Thereby, less time is retained for drivers to appropriately respond to upcoming crashes.
For the time of day, the parameter for afternoon on crash injury severity is negative at the 95% credibility level. It is anticipated, as the vision of drivers is usually clearer in afternoon than before dawn (the reference case), and thus more time is available for them to take defensive actions when encountered with emergency. In addition, because of the light traffic and human circadian rhythmicity respectively, we may observe more frequent speeding and fatigue/drowsy driving before dawn, which probably result in severe traffic accidents (4).
With regard to crash type, the estimation results suggest that rear-end crashes and angle crashes are more prone to lead to fatalities than single-vehicle crashes (the reference type). Particularly, the fatality odds of rear-end crashes and angle crashes are 4.35 and 6.75 times of that of single-vehicle crashes, respectively. The results are generally in line with the findings of Zeng et al. (17), and may be attributed to that more casualties usually exist in multiple-vehicle crashes (covering rear-end crashes, angle crashes, and others) than in single-vehicle crashes.
Precipitation is the weather-related variable with a significant effect on crash injury severity. According to its estimated parameter, heavier precipitation is associated with higher probability of fatality crash. The results are consistent with the previous research (39, 40) and engineering intuitions: because of rainfall, roadway surfaces would become slippery and their skidding resistance would be reduced. Accordingly, vehicles would collide at higher speeds which were prone to bring about severer injury severity outcomes. Additionally, during the processes of precipitation, drivers’ vision might be impaired which results in reduced reaction time available to drivers.
This research empirically investigated the effect of EMS response time and the fatality risk of freeway crashes, using a two-years crash injury severity dataset from Kaiyang Freeway, China. A Bayesian random parameters spatial logistic model was advocated for the empirical investigation. The advocated model simultaneously accounted for the spatial correlation across adjacent crashes and unobserved heterogeneities in effects of the observed factors.
The values of DIC indicated that the overall performance of the random parameters spatial logistic model is substantially better than the logistic model and spatial logistic model. The parameter estimation results in the random parameters spatial model revealed that EMS response time has a significantly positive effect on crash injury severity. One minute increase in EMS response time would increase the crash fatality odds by 2.6%. Three countermeasures were suggested to reduce the EMS response time. They are: (1) establishment of EMS facilities near freeways at the optimized location; (2) optimization of path to the crash location based on real-time traffic data; and (3) strict enforcement against illegal occupancy of emergency lanes.
In addition, the estimation results show that truck has a heterogeneous effect on crash injury severity. Fatalities are more likely to occur in crashes involving other vehicles, non-local vehicles, on freeway sections with smaller horizontal curvature and greater vertical grade, in weather conditions with more precipitation, and before dawn. The fatality risk of rear-end crashes and angle crashes is higher than that of single-vehicle crashes.
While the significant effect of EMS response time on crash fatality risk and the superiority of the advocated Bayesian random parameters spatial logit model were demonstrated, there are some limitations to the current research. For instance, only the crash data from one freeway are used in the model development, and the attributes related to drivers are not included. It will be necessary to further validate the safety effect of EMS response time if comprehensive crash injury severity data are available in the future.
The data are available from the corresponding authors upon reasonable request. Requests to access these datasets should be directed to Qiang Zeng, emVuZ3FpYW5nQHNjdXQuZWR1LmNu.
PH: Validation, Resources, Project administration, Investigation, Writing – original draft. SO: Resources, Formal analysis, Conceptualization, Writing – original draft. HY: Writing – review & editing, Conceptualization, Funding acquisition. XW: Writing – review & editing, Software, Project administration, Methodology, Data curation. JL: Writing – review & editing. QZ: Writing – review & editing, Supervision, Software, Methodology.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was jointly supported by the Natural Science Foundation of Guangdong Province (No. 2022A1515011974), the National Natural Science Foundation of China (No. 51878297), and the Foundation of Guangdong Communication Planning & Design Institute Group Co., Ltd. (No. 20221615). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
PH, SO, and HY were employed by Guangzhou Expressway Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Savolainen, PT, Mannering, FL, Lord, D, and Quddus, MA. The statistical analysis of highway crash-injury severities: a review and assessment of methodological alternatives. Accid Anal Prev. (2011) 43:1666–76. doi: 10.1016/j.aap.2011.03.025
2. Christoforou, Z, Cohen, S, and Karlaftis, MG. Vehicle occupant injury severity on highways: an empirical investigation. Accid Anal Prev. (2010) 42:1606–20. doi: 10.1016/j.aap.2010.03.019
3. Eluru, N, Bhat, CR, and Hensher, DA. A mixed generalized ordered response model for examining pedestrian and bicyclist injury severity level in traffic crashes. Accid Anal Prev. (2008) 40:1033–54. doi: 10.1016/j.aap.2007.11.010
4. Huang, H, Chin, HC, and Haque, MM. Severity of driver injury and vehicle damage in traffic crashes at intersections: a Bayesian hierarchical analysis. Accid Anal Prev. (2008) 40:45–54. doi: 10.1016/j.aap.2007.04.002
5. Yu, R, and Abdel-Aty, M. Analyzing crash injury severity for a mountainous freeway incorporating real-time traffic and weather data. Saf Sci. (2014) 63:50–6. doi: 10.1016/j.ssci.2013.10.012
6. Lee, J, Abdel-Aty, M, Cai, Q, and Wang, L. 2018. Effects of emergency medical services times on traffic injury severity: a random effects ordered probit approach. Traffic Inj Prev. (2018) 19:577–81. doi: 10.1080/15389588.2018.1468889
7. Meng, Q, and Weng, J. 2013. Uncertainty analysis of accident notification time and emergency medical service response time in work zone traffic accidents. Traffic Inj Prev. (2013) 14:150–8. doi: 10.1080/15389588.2012.708886
8. Amorim, M, Ferreira, S, and Couto, A. Road safety and the urban emergency medical service (uEMS): strategy station location. J Transp Health. (2017) 6:60–72. doi: 10.1016/j.jth.2017.04.005
9. Gonzalez, RP, Cummings, GR, Phelan, HA, Mulekar, MS, and Rodning, CB. Does increased emergency medical services prehospital time affect patient mortality in rural motor vehicle crashes? A statewide analysis. Am J Surg Jan. (2009) 197:30–4. doi: 10.1016/j.amjsurg.2007.11.018
10. Li, MD, Doong, JL, Chang, KK, Lu, TH, and Jeng, MC. Differences in urban and rural accident characteristics and medical service utilization for traffic fatalities in less-motorized societies. J Saf Res. (2008) 39:623–30. doi: 10.1016/j.jsr.2008.10.008
11. Sánchez-Mangas, R, García-Ferrrer, A, de Juan, A, and Arroyo, AM. The probability of death in road traffic accidents. How important is a quick medical response? Accid Anal Prev. (2010) 42:1048–56. doi: 10.1016/j.aap.2009.12.012
12. MacLeod, JB, Cohn, SM, Johnson, EW, and McKenney, MG. Trauma deaths in the first hour: are they all unsalvageable injuries? Am J Surg. (2007) 193:195–9. doi: 10.1016/j.amjsurg.2006.09.010
13. Bakke, HK, and Wisborg, T. The trauma chain of survival - each link is equally important (but some links are more equal than others). Injury. (2017) 48:975–7. doi: 10.1016/j.injury.2017.04.001
14. Oliver, GJ, Walter, DP, and Redmond, AD. Are prehospital deaths from trauma and accidental injury preventable? A direct historical comparison to assess what has changed in two decades. Injury. (2017) 48:978–84. doi: 10.1016/j.injury.2017.01.039
15. Ma, L, Zhang, H, Yan, X, Wang, J, Song, Z, and Xiong, H. Smooth associations between the emergency medical services response time and the risk of death in road traffic crashes. J Transp Health. (2019) 12:379–91. doi: 10.1016/j.jth.2018.08.011
16. Hosseinzadeh, A, and Kluger, R. Do EMS times associate with injury severity? Accid Anal Prev. (2021) 153:106053. doi: 10.1016/j.aap.2021.106053
17. Zeng, Q, Wang, Q, Wang, F, and Sze, NN. Revisiting spatial correlation in crash injury severity: a Bayesian generalized ordered probit model with Leroux conditional autoregressive prior. Transportmetrica A Transp Sci. (2022) 18:1084–102. doi: 10.1080/23249935.2021.1922536
18. Mannering, FL, and Bhat, CR. Analytic methods in accident research: methodological frontier and future directions. Anal Methods Accid Res. (2014) 1:1–22. doi: 10.1016/j.amar.2013.09.001
19. Mannering, FL, Shankar, V, and Bhat, CR. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal Methods Accid Res. (2016) 11:1–16. doi: 10.1016/j.amar.2016.04.001
20. Milton, JC, Shankar, VN, and Mannering, FL. Highway accident severities and the mixed logit model: an exploratory empirical analysis. Accid Anal Prev. (2008) 40:260–6. doi: 10.1016/j.aap.2007.06.006
21. Yasmin, S, Eluru, N, Bhat, CR, and Tay, R. A latent segmentation based generalized ordered logit model to examine factors influencing driver injury severity. Anal Methods Accid Res. (2014) 1:23–38. doi: 10.1016/j.amar.2013.10.002
22. Malyshkina, NV, and Mannering, FL. Markov switching multinomial logit model: an application to accident-injury severities. Accid Anal Prev. (2009) 41:829–38. doi: 10.1016/j.aap.2009.04.006
23. Castro, M, Paleti, R, and Bhat, CR. A spatial generalized ordered response model to examine highway crash injury severity. Accid Anal Prev. (2013) 52:188–203. doi: 10.1016/j.aap.2012.12.009
24. Prato, CG, Kaplan, S, Patrier, A, and Rasmussen, TK. Considering built environment and spatial correlation in modeling pedestrian injury severity. Traffic Inj Prev. (2018) 19:88–93. doi: 10.1080/15389588.2017.1329535
25. Meng, F, Xu, P, Wong, SC, Huang, H, and Li, YC. Occupant-level injury severity analyses for taxis in Hong Kong: a Bayesian space-time logistic model. Accid Anal Prev. (2017) 108:297–307. doi: 10.1016/j.aap.2017.08.010
26. Xu, X, Xie, S, Wong, SC, Xu, P, Huang, H, and Pei, X. Severity of pedestrian injuries due to traffic crashes at signalized intersections in Hong Kong: a Bayesian spatial logit model. J Adv Transp. (2016) 50:2015–28. doi: 10.1002/atr.1442
27. Ahmed, M, Huang, H, Abdel-Aty, M, and Guevara, B. Exploring a Bayesian hierarchical approach for developing safety performance functions for a mountainous freeway. Accid Anal Prev. (2011) 43:1581–9. doi: 10.1016/j.aap.2011.03.021
28. Washington, S, Karlaftis, MG, Mannering, F, and Anastasopoulos, P. Statistical and econometric methods for transportation data analysis. New York: CRC Press (2020).
29. Lee, D. A comparison of conditional autoregressive models used in Bayesian disease mapping. Spat Spatiotemporal Epidemiol. (2011) 2:79–89. doi: 10.1016/j.sste.2011.03.001
30. Lunn, DJ, Thomas, A, Best, N, and Spiegelhalter, D. WinBUGS-A Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput. (2000) 10:325–37. doi: 10.1023/A:1008929526011
31. Spiegelhalter, DJ, Best, NG, Carlin, BP, and Van Der Linde, A. Bayesian measures of model complexity and fit. J R Stat Soc. (2002) 64:583–639. doi: 10.1111/1467-9868.00353
32. Zeng, Q, Wen, H, Huang, H, and Abdel-Aty, M. A Bayesian spatial random parameters Tobit model for analyzing crash rates on roadway segments. Accid Anal Prev. (2017) 100:37–43. doi: 10.1016/j.aap.2016.12.023
33. Shah, MN, Bishop, P, Lerner, EB, Fairbanks, RJ, and Davis, EA. Validation of using EMS dispatch codes to identify low-acuity patients. Prehosp Emerg Care. (2005) 9:24–31. doi: 10.1080/10903120590891651
34. Bandara, D, Mayorga, ME, and McLay, LA. Priority dispatching strategies for EMS systems. J Oper Res Soc. (2014) 65:572–87. doi: 10.1057/jors.2013.95
35. Alter, SM, Infinger, A, Swanson, D, and Studnek, JR. Evaluating clinical care in the prehospital setting: is rapid emergency medicine score the missing metric of EMS? Am J Emerg Med. (2017) 35:218–21. doi: 10.1016/j.ajem.2016.10.047
36. Huang, H, Siddiqui, C, and Abdel-Aty, M. Indexing crash worthiness and crash aggressivity by vehicle type. Accid Anal Prev. (2011) 43:1364–70. doi: 10.1016/j.aap.2011.02.010
37. Kim, JK, Ulfarsson, GF, Shankar, VN, and Mannering, FL. A note on modeling pedestrian-injury severity in motor-vehicle crashes with the mixed logit model. Accid Anal Prev. (2010) 42:1751–8. doi: 10.1016/j.aap.2010.04.016
38. Aziz, HM, Ukkusuri, SV, and Hasan, S. Exploring the determinants of pedestrian-vehicle crash severity in New York City. Accid Anal Prev. (2013) 50:1298–309. doi: 10.1016/j.aap.2012.09.034
39. Naik, B, Tung, LW, Zhao, S, and Khattak, AJ. Weather impacts on single-vehicle truck crash injury severity. J Saf Res. (2016) 58:57–65. doi: 10.1016/j.jsr.2016.06.005
40. Zeng, Q, Huang, H, Pei, X, Wong, SC, and Gao, M. Rule extraction from an optimized neural network for traffic crash frequency modeling. Accid Anal Prev. (2016) 97:87–95. doi: 10.1016/j.aap.2016.08.017
Keywords: emergency medical service, response time, fatality risk, freeway crash, random parameters spatial logistic model
Citation: Huang P, Ouyang S, Yan H, Wang X, Lee JJ and Zeng Q (2024) Effect of emergency medical service response time on fatality risk of freeway crashes: Bayesian random parameters spatial logistic approach. Front. Public Health. 12:1453788. doi: 10.3389/fpubh.2024.1453788
Received: 24 June 2024; Accepted: 09 October 2024;
Published: 23 October 2024.
Edited by:
Qingfeng Li, Johns Hopkins University, United StatesReviewed by:
Taesik Lee, Korea Advanced Institute of Science and Technology (KAIST), Republic of KoreaCopyright © 2024 Huang, Ouyang, Yan, Wang, Lee and Zeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaofei Wang, eGlhb2ZlaXdAc2N1dC5lZHUuY24=; Qiang Zeng, emVuZ3FpYW5nQHNjdXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.