
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Psychol., 19 May 2022
Sec. Emotion Science
Volume 13 - 2022 | https://doi.org/10.3389/fpsyg.2022.880322
In the context of the COVID-19 pandemic, a large amount of information is gathered on Internet platforms, through which people express their opinions and vent their emotions. Emotional guidance of netizens has become an important part of social governance during turbulences caused by a so-called “infodemic”. This study focuses on the evolution and interaction of netizens' emotions after the occurrence of network public opinion events. First, the transfer model of netizens' emotions is constructed, and the significance of each parameter in the model is studied through simulation. Then, based on the model, we put forward the optimization method and quantitative method of guidance strategy of netizens' emotions. Finally, the empirical study proves the effectiveness of the model, which can provide a theoretical basis for the emotional guidance strategies after the outbreak of network public opinion events.
Emotional contagion is common in the crowd. Each individual acts as an emotional sensor to affect others' emotions, and then affect others' judgment and behavior (Barsade, 2002). Under the COVID-19 pandemic, the characteristics of emotional contagion have been different from those in the normal environment. The global pandemic of COVID-19 has caused a lot of anxiety. In the face of the epidemic, some people were more vulnerable to experiencing anxiety and other mental health symptoms (Wheaton et al., 2021). Due to the segregated environments, people's cognition of happiness was significantly reduced, while their cognition of negative emotions was significantly improved (Meléndez et al., 2020), and the expectation of “return to normal” was a strong emotion under the pandemic (Slaughter et al., 2021). In short, compared with pre-pandemic, people's physical and psychological conditions have decreased significantly, and the important factor causing this decline was that it was difficult for people to describe and regulate emotions (Panayiotou et al., 2021). COVID-19 not only affected emotional infection but also changed people's social communication mode. In the context of the popularity of COVID-19, the control of governments restricts people's offline communication to a certain extent, and more social activities have moved online. Research showed that posting through social networks could also affect people's emotions and achieve large-scale transmission (Kramer et al., 2014), which provided an efficient way for emotional contagion. In addition, even without deliberately manipulating the posting of content in social networks, due to individual differences, netizens would show positive or negative emotions after receiving information (Ferrara and Yang, 2015), which showed that the dissemination of emotions on the Internet does not need deliberate behavior, but a spontaneous process. At the same time, because the Internet could efficiently spread information, emotional contagion was also accelerated on social networks, and the emotional synchronization of netizens may be strengthened (Coviello et al., 2014), which objectively strengthened the emotional contagion among netizens. It can be seen that emotional contagion among netizens is widespread, with the characteristics of large-scale and high-speed transmission, and this process is not limited by region.
It can be seen from the above analysis that under the COVID-19 pandemic and the prevalence of social networks when a focus event occurs in society, a large number of netizens' comments about the event will be posted on the social platform, which implies the emotional tendency of netizens—favorable comments often imply positive emotions and negative ones imply negative emotions. This process is also accompanied by emotional contagion among netizens. Therefore, the analysis of netizens' comment information essentially involves the analysis of netizens' emotions. Identifying and classifying the implicit emotion in the comment text is the basis of analyzing the emotion of netizens, and a large number of studies focus on it. Traditional machine learning methods such as SVM and Naive Bayes have been applied to multi-classification and prediction of text emotion (Kirange and Deshmukh, 2012; Krishnan et al., 2017). The development of artificial neural networks also promotes the research in this field and the language processing models such as RNN, LSTM, transformer, and Bert have been widely used (Zhang Q. et al., 2020; Banothu et al., 2021; Nemes and Kiss, 2021; Yang et al., 2021). On the basis of text emotion recognition and classification, some studies have begun to pay attention to the interaction between individual emotion and group emotion (Zeng and Zhu, 2019), the promotion of different emotions in information dissemination (Zhang L. et al., 2020), and the evolution and prediction of netizens' emotions (Jin and Yang, 2018; Ren et al., 2019). LDA model has been applied to study the relationship between topic words evolution (Tan et al., 2021), event topic (Zhou and Zhang, 2017), and netizen emotion. In addition, the mathematical models represented by SIR, SIS, SEIR model, and their improved model were also used to study the emotional contagion among netizens. Fang et al. constructed the S-SEIR Epidemic model based on netizens' emotions. This model considered the text's emotion and the transmission law of the text. The simulation experiment showed that text emotion could affect the transmission behavior of information (Fang et al., 2019). Considering the popularity of social media, Xu et al. constructed the time-varying SIR model to study the impact of social media on COVID-19 dissemination. The study found that the negative emotions on Twitter are related to a lower transmission rate of the corresponding susceptible compartment (Xu et al., 2021). Hill et al. (2010) assessed the spread of emotions in social networks through the SISa model and proved that both positive and negative emotions can exist in social networks for a long time like infectious diseases. The research on the spread of emotions in the crowd is also worthy of reference. Xiang et al. paid attention to the emotional contagion in dynamic people and simulated the emotional interaction in the process of crowd aggregation by the SIR model (Xiang et al., 2017a,b). Liu et al. focused on the factors that affect the values of emotions in the process of emotional contagion and constructed the SOSa–SPSa model. The simulation results showed that the values of positive emotion and negative emotion are positively correlated with spontaneity and contagion, and negatively correlated with recovery (Liu et al., 2014). Yi et al. studied the influence of emotion on information diffusion in online social networks (Yi et al., 2019).
The above studies generally focus on the following aspects: (1) identifying and classifying netizens' emotions through natural language processing technology; (2) research on the relationship between netizens' emotions and other elements such as public topics and Internet rumors; and (3) through mathematical modeling (most of them are based on SIR model and its improved model), studying the communication states of netizens' emotions, the factors affecting emotional contagion, and the impact of emotions on the dissemination of other information. However, few studies pay attention to the changes in netizens' emotions and the interaction between different emotions from the perspective of event evolution. By improving the logistic model, we studied the continuous evolution and interaction mechanism of netizens' emotions under a network public opinion event. The contributions of the model are as follows: (1) describing the evolution law of a single emotion over time when there is an interaction between multiple emotions; (2) different emotional interaction modes are simulated by changing the table of parameters; and (3) providing a quantitative way of netizens' emotional guidance and guidance effect, and carry out empirical research on the basis of the theoretical model, which proves the rationality of the theory proposed in this article.
In this section, first, we explain the modeling method of the emotional information based on the logistic model. Then, we construct a logistic model considering the transfer of emotion and giving the meaning of each parameter and the solution of the equilibrium point. Finally, we explain the method of estimating model parameters by constructing difference equations and multiple linear regression analysis.
The trend of network public opinion propagation can be expressed by the number of comments, forum posts, and messages written on social networking platforms. Figure 1 shows the real data of the above information of three different public opinion events. At the same time, this information can be represented in different moods and the curve of the amount of emotional information is also similar to the curve in Figure 1. This article regards the accumulation value of emotional information as a continuous variable that monotonously increases with time and describes the curve with the logistic model. The formula is as follows:
The natural growth rate of emotional information is r (r > 0). The initial value is x0. And the upper growth limit of the emotional information quantity is K.
In the processing of public opinion propagation, some netizens will influence other netizens' views on issues and change their emotions about these issues when they make comments and share their opinions, thus resulting in emotional transfer. To simulate this situation, we assume that X1, X2, X3, …, Y are different emotions and x1 = x1(t), x2 = x2(t), x3 = x3(t), …, xn = xn(t), y = y(t) represent the emotional information quantity of them, respectively.
Emotion is the potential driving force of information dissemination in society (Stieglitz and Dang, 2013). When a focus event occurs in society, a large number of netizens' comments on the event are collected on the social platform, which implies the emotional tendency of netizens. The dissemination of information is essentially the dissemination of emotions. When the information on the social platform spreads from one netizen to another, the emotion attached to the information also spreads with the information. Because the transmission process of information is unidirectional and independent, we believe that the transmission of emotion is also unidirectional and independent. Therefore, we propose the following hypotheses to simplify the model:
Hypothesis 1: In the real scene, there are complex cases of mutual transfer between multiple emotions, but this model only considers the case of transfer from N emotions to a single emotion.
Hypothesis 2: The direction of emotion transfer is unidirectional, and there is no reverse transfer process.
Hypothesis 3: In the process of emotion transfer, each emotion is independent of the other and does not affect each other.
Based on the above hypotheses, there are n emotions (X1, X2, X3, …, Xn) that transfer to one emotion (Y). First, the emotion information transferred from the ith emotion is , and bi(0< bi < 1) is conversion proportion, which describes the proportion of the transferred emotion information amount to the original emotion information amount. After this process, the remaining space of xi converts from to (Figure 2, process ①). Then, we define transfer coefficient ai(0< ai < 1). The emotional information which is a part of , transfers into y. The remaining space of y converts from to (Figure 2, process ②). Based on the above two processes, the transfer model of netizens' emotions is constructed as:
where the initial values are x10,x20,x30,…,xn0,y0, the natural growth rates of emotional information are r1,r2,r3,…,rn,r, and the upper growth limits of the emotional information quantity are K1,K2,K3,…,Kn,K (Table 1).
This model has no analytic solutions, but the stability of this model can be studied by calculating its equilibrium points. Set , get equilibrium points. Considering x1, x2, x3, …, xn, y are continuous variables that are non-zero and monotonously increase with time, this model has the one and the only one non-zero equilibrium point .
The parameters to estimate in this model include Ki, K, ri, r, ai, and bi. We estimate the parameters by constructing difference equations and multiple linear regression. From Equation (2), we can get:
According to the definition of differential and difference in mathematics, Δt = dt, Δxn = dxn + O(Δt),y = dy + O(Δt). When the unit time is taken (i.e., t = dt = 1), the differential equation model is constructed as:
where Δxi(k) = xi(k) − xi(k − 1) and Δy(k) = y(k) − y(k − 1)(k = 1, 2, 3…, i = 1, 2, 3, …, n). The values of xi(k) and y(k) can be obtained by collecting real-time data on online public opinion. We can see that there is a linear relationship between the left side of the equations and the variables on the right side of the equations in Equation (3). Therefore, all parameters can be calculated using multiple linear regression analysis with real-time data as input.
Some major public crisis events often attract the attention of netizens on social networks, which causes netizens to have negative emotions such as anger and form a negative emotional scenario. In this case, relevant management departments need to adopt some guiding strategies to guide netizens to make positive comments and reduce negative words, so that neutral and negative emotions in the emotional scenario can be transferred to positive emotions (Figure 3). Under the effect of the guiding strategy, neutral emotion and negative emotion will decrease by a certain proportion. This proportion is represented by bi, which represents the guiding strength of guiding strategy. At the same time, due to the influence of various factors, only part of the reduced neutral and negative emotions will be transformed into positive emotions. This proportion is represented by ai, which represents the guiding efficiency of the guidance strategy.
This study simulates the influence of transfer coefficient and conversion proportion on transfer of emotions in the above scenario. The three variables x1(t), x2(t), and y(t) are defined to represent the amount of negative, neutral, and positive emotion information, respectively. The mathematical model is as follows:
Three factors are studied in the simulation: (1) The influence of the transfer coefficient is studied when the value of conversion proportion is fixed. (2) The influence of conversion proportion is studied when the value of the transfer coefficient is fixed. (3) The influence of transfer coefficient and conversion proportion on the upper growth limit of positive emotion information is studied by setting different value combinations.
Considering the negative emotional scenario and the control effect of management departments, this study sets a small growth rate for negative emotional information, but a large upper growth limit. The specific parameters' information is shown in Table 2.
Setting b1 = b2 = 0.9 and changing the values of a1 and a2, which are a1 = 0.1, a1 = 0.2, …, a1 = 0.9 and a2 = 0.9, a2 = 0.8, …, a2 = 0.1. Table 3 shows the values and proportions of the three emotions at the equilibrium point under different parameter values and Figure 4 shows the evolution trend of the proportions of the three emotions when a1 equals 0.1, 0.5, and 0.9, respectively.
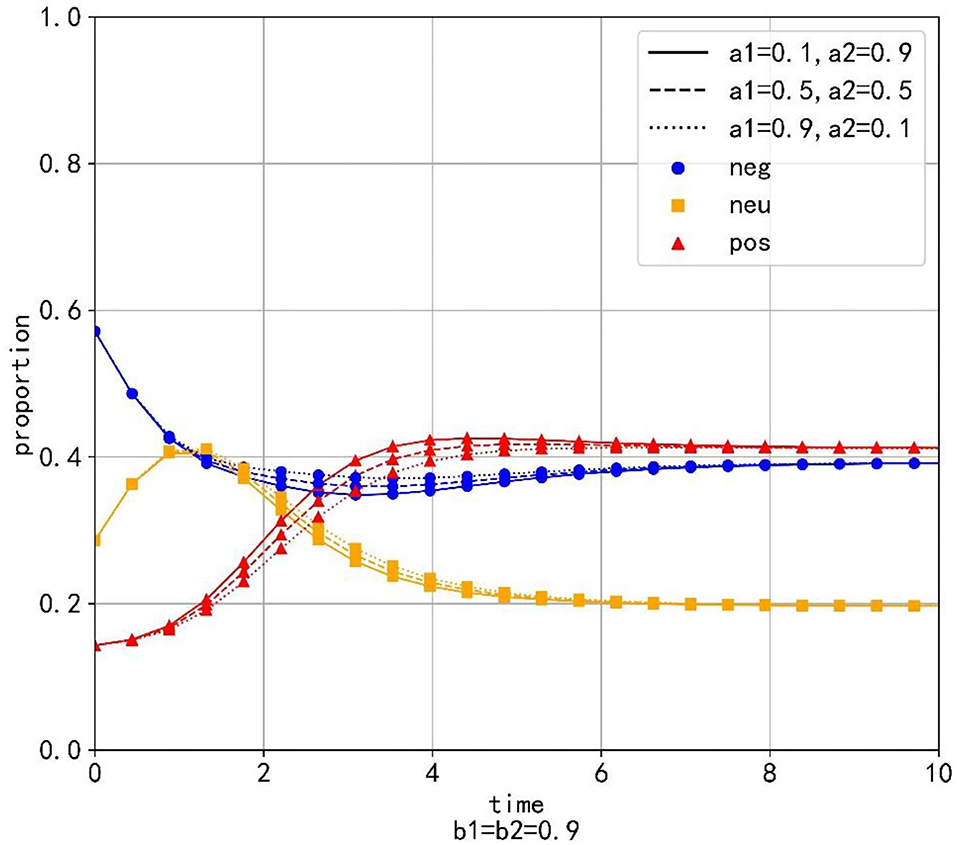
Figure 4. The evolution trend of the proportion of three emotions under the condition of changing the transfer coefficient.
As is shown in Table 3, when the equilibrium point is reached, the proportion of positive emotion is higher than that of neutral emotion and negative emotion with any parameter values. Besides, with the increase of a1, the value and proportion of positive emotion decrease gradually, while the proportions of neutral emotion and negative emotion increase gradually at the equilibrium point. It can be seen that neutral emotion has a larger intrinsic growth rate than the negative emotion. Therefore, under the condition of constant conversion proportion, the larger a2 is, the more emotional information is transferred into positive emotion and the value and proportion of the positive emotion will be larger at the equilibrium point.
As is shown in Figure 4, different values of the transfer coefficients have no significant effect on the evolution trend of the three emotions. Because neutral emotion has a large intrinsic growth rate, the proportion of neutral emotion does not decrease immediately when emotion transfers out, but displays the tendency to rise at beginning and decline later. On the contrary, the intrinsic growth rate of negative emotion is small, so its proportion decreases immediately when the emotion transfer occurs. At the same time, with the decrease of a2, the proportion of positive emotion decreases, but the proportions of neutral emotion and negative emotion increase, which indicates that in the evolution process of emotion evolution, the emotion transferred out with a higher growth rate is the main factor determining the proportion of emotion transferred in.
As can be seen from the above simulation results, when relevant departments implement public opinion guidance, the guiding strength of guidance strategy is the primary factor determining the final guidance effect, while the efficiency of guidance strategy is only a secondary factor. Therefore, relevant departments should invest enough force to make neutral emotion and negative emotion transfer out in a large proportion as far as possible. At the same time, when certain guiding strength is applied, we should first consider improving the guiding efficiency of the emotion with a higher growth rate, so that the transferring part of the emotion is transferred to positive emotion in a larger proportion, which will be more conducive to obtaining good guiding effect.
Setting a1 = a2 = 0.5 and changing the values of b1 and b2, which are b1 = 0.1, b1 = 0.2, …, b1 = 0.9 and b2 = 0.9, b2 = 0.8, …, b2 = 0.1. Table 4 shows the values and proportions of the three emotions at the equilibrium point under different parameter values and Figure 5 shows the evolution trend of the proportions of the three emotions when b1 equals 0.1, 0.5, and 0.9, respectively.
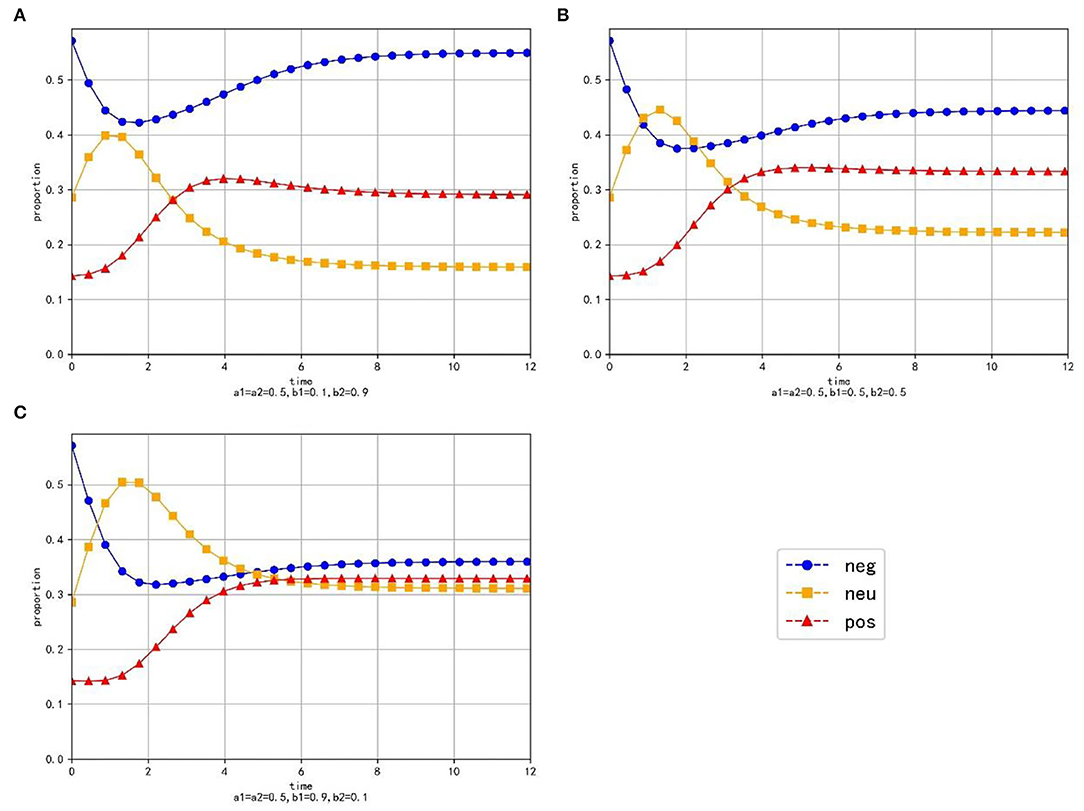
Figure 5. The evolution trend of the proportion of three emotions under the condition of changing the conversion proportion. (A) When a1 = a2 = 0.5, b1 = 0.2 and b2 = 0.9. (B) When a1 = a2 = 0.5, b1 = 0.5 and b2 = 0.5. (C) When a1 = a2 = 0.5, b1 = 0.9 and b2 = 0.1.
As is shown in Table 4, at the equilibrium point, the proportions and values of neutral emotion and negative emotion are inversely proportional to their conversion proportions, respectively. When b1 increases and b2 decreases, the value and proportion of neutral emotion gradually increase, the value and proportion of negative emotion gradually decrease, while the value and proportion of positive emotion first increase then decrease (the evolution law of positive emotion is specifically discussed in Section The Influence of Transfer Coefficient and Conversion Proportion on Positive Emotion).
As is shown in Figure 5, the proportion of neutral emotion has a trend of rising first and falling with time. With the decrease of b2, the peak value of negative emotion curve increases obviously and the rate of decline gradually slows down. Since the growth rate of negative emotion is small, the proportion of negative emotion decreases at the beginning, however, as time goes by, the information transferred from negative emotion decreases gradually and the negative information that grows naturally is enough to make up for the amount of information transferred out, then the proportion of negative emotion increases in the later period. With the increase of b1, the minimum value of the curve of negative emotion becomes smaller and the ascending process of the curve gradually becomes less obvious. The proportion of positive emotion increases at the beginning, but in the later period, the emotional information transferred from negative emotion and neutral emotion decreases, which leads to a decrease in the proportion of positive emotion. With the increase of b1, the downward trend of positive emotion gradually becomes gentle in the later period.
The simulation results show that when the guiding efficiency of the guiding strategy is certain, the change of the guiding strength greatly affects the final guiding effect of public opinion, which further confirms the view that the guiding force is the primary consideration for relevant departments to implement public opinion guidance. In addition, for the emotion with a large growth rate, its proportion cannot be inhibited in the early stage under a certain guiding strength. This shows once again that the emotion with a large growth rate is the focus of guidance, and it needs to be guided vigorously for a long time to effectively reduce its proportion and get a better guidance effect.
As can be seen from Equation (4), the value of y at the equilibrium point is related to parameters a1, a2, b1, and b2, and the simulation results in Table 4 show that, when the transfer coefficient is fixed, the value of y at the equilibrium point increases first and then decreases with the increase of b1 and the decrease of b2, which is not directly or inversely proportional to the value of conversion proportion. In simulations 3.1 and 3.2, the influence of a1 and a2 (or b1 and b2) on the value of positive emotion at the equilibrium point was explored only when the values of b1 and b2 (or a1 and a2) were fixed, which cannot comprehensively display the change trend of positive emotion value at the equilibrium point when a1, a2, b1, and b2 change continuously at the same time. Therefore, this study designed four groups of simulation experiments, corresponding to four different scenarios of neutral and negative emotion transfer to positive emotion. Calculating the value of positive emotion at the equilibrium point under different values of each parameter, the values of parameters a1, a2, b1, and b2 in each simulation are as follows:
Simulation 1: Set a2 = a1, b2 = b1, where a1 values 0.1, 0.2, 0.3, …, 0.9 in turn. For each value of a1, b1 values 0.1, 0.2, 0.3, …, 0.9.
Simulation 2: Set a2 = a1, b2 = 1 − b1, where a1 values 0.1, 0.2, 0.3, …, 0.9 in turn. For each value of a1, b1 values 0.1, 0.2, 0.3, …, 0.9.
Simulation 3: Set a2 = 1 − a1, b2 = b1, where a1 values 0.1, 0.2, 0.3, …, 0.9 in turn. For each value of a1, b1 values 0.1, 0.2, 0.3, …, 0.9.
Simulation 4: Set a2 = 1 − a1, b2 = 1 − b1, where a1 values 0.1, 0.2, 0.3, …, 0.9 in turn. For each value of a1, b1 values 0.1, 0.2, 0.3, …, 0.9.
Taking the simulation 1 as an example, the values of a1, a2, b1 and b2 are as follows (Table 5):
In the scenario of simulation 1, it is assumed that relevant government departments have sufficient resources to implement guidance strategies and can efficiently guide both neutral emotion and negative emotion. Therefore, parameters a1, a2, b1, and b2 can increase synchronously. This scenario is the most ideal guiding scenario. When a1 = a2 = b1 = b2=0.9, the optimal guiding effect can be achieved, the value of positive emotion quantity y is 555.789, and the proportion of emotion quantity is 0.4680938 (Figure 6). It can be seen from the simulation results that the change rates of the surface along the direction a1 and b1 are similar, that is to say, the changes of a and b have similar effects on the changes of y. When a1 and b1 increase synchronously, it has great benefit to improving the guiding effect.
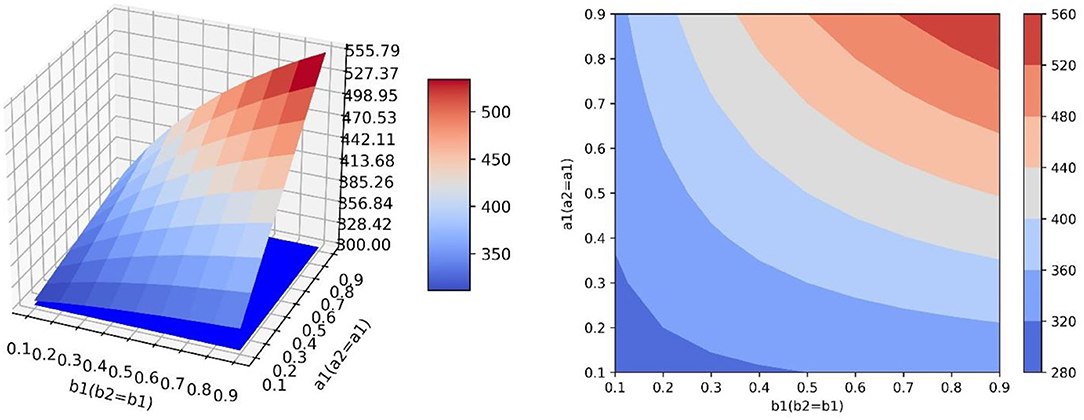
Figure 6. In the scene of simulation 1, the value of positive emotion at the equilibrium point: surface graph and surface projection.
In the scenario of simulation 2, it is assumed that relevant government departments do not have sufficient resources to guide both neutral emotion and negative emotion. When one emotion is guided with great strength, the other emotion is guided with little strength. Therefore, for b1 and b2, when the value of one of them increases, the value of the other one decreases. However, in this scenario, the two emotions can be guided with high efficiency at the same time, so a1 and a2 can increase synchronously (Figure 7). It can be seen that since a1 and a2 can increase synchronously, the change rate of the surface along the a1 direction is larger. In this scenario, compared with increasing the value of b1, increasing the value of a1 is more beneficial for improving the guidance effect. By analyzing changes along the b1 axis, it can be seen that when a1 has a constant value and b1 = b2 = 0.5, the local optimal value of y can be obtained. At this point, the value of y will decrease regardless of increasing or decreasing the value of b1 (Figure 8). This is because when the value of one of b1 and b2 increases, the value of the other will decrease. Only when the value of the two parameters is considered comprehensively (the guiding strength of neutral emotion and negative emotion is considered comprehensively in the implementation of guidance), and the maximum value of b2 can be achieved, the better guidance effect can be achieved.
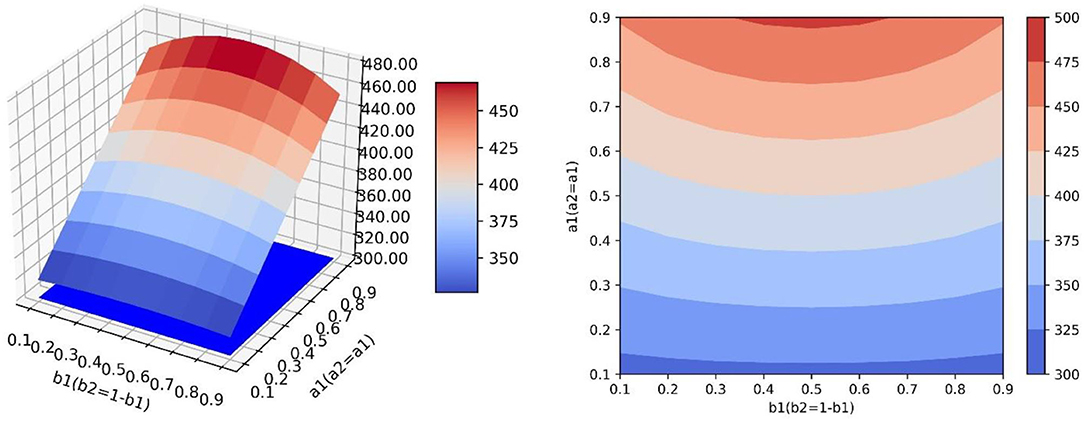
Figure 7. In the scene of simulation 2, the value of positive emotion at the equilibrium point: surface graph and surface projection.
In the scenario of simulation 3, it is assumed that relevant government departments have sufficient resources to guide both neutral and negative emotions, therefore, parameters b1 and b2 can increase synchronously. However, in this scenario, the guidance efficiency of the guidance strategy is not high, and it cannot have high guidance efficiency for two emotions at the same time, and the values of one of a1 and a2 show that one increases and the other decreases (Figure 9). This scenario is contrary to the scenario of simulation 2. Changing the value of a1 does not influence the improvement of the guidance effect, while increasing the value of b1 has great benefits on the improvement of the guidance effect.
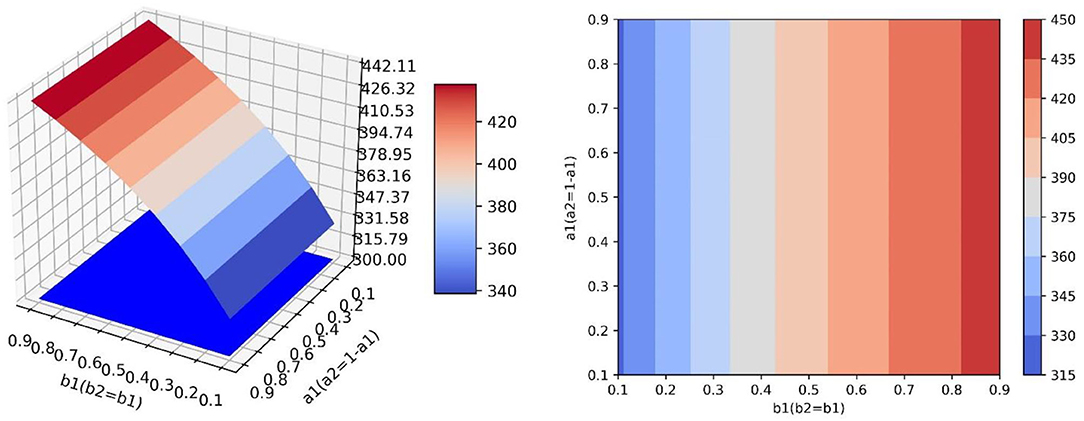
Figure 9. In the scene of simulation 3, the value of positive emotion at the equilibrium point: surface graph and surface projection.
In the scenario of simulation 4, it is assumed that relevant government departments neither have sufficient resources to guide both neutral and negative emotions at the same time (parameters b1 and b2 cannot increase synchronously), nor can they have high guidance efficiency for both emotions at the same time (parameters a1 and a2 cannot increase synchronously) (Figure 10). In this scenario, there is a saddle point PS on the surface, and the influence of the values of parameters on the value of y needs to be discussed separately. When the position of point PL is lower than the saddle point, the value of a1 should be increased and the value of b1 should be decreased to improve the guiding effect. However, when the position of point PH is lower than the saddle point, the values of a1 and b1 need to be increased simultaneously to improve the guiding effect (Figure 11).
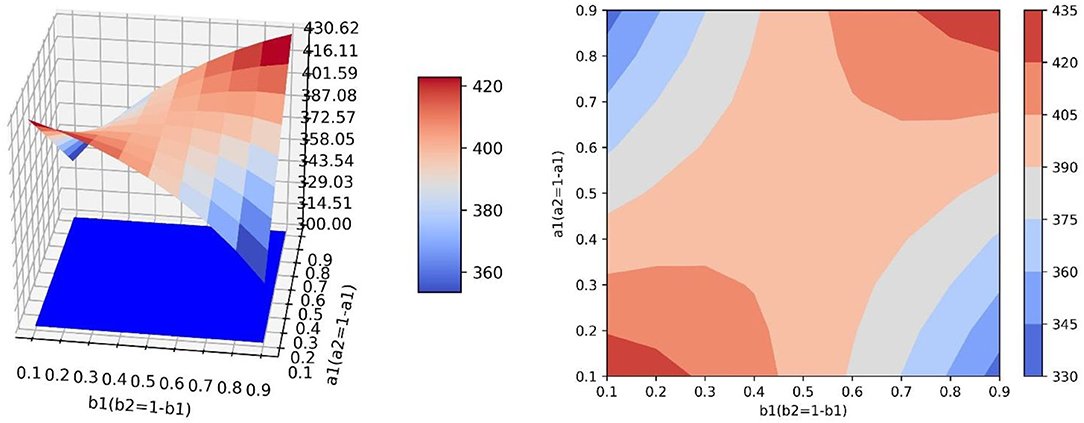
Figure 10. In the scene of simulation 4, the value of positive emotion at the equilibrium point: surface graph and surface projection.
It can be concluded from the above four simulation results that different guidance strategies need to be adopted in different scenarios to improve the guidance effect, which cannot be qualitatively generalized. Therefore, it is necessary to put forward a quantitative optimization method for guiding strategies in different scenarios to effectively deal with them. The next section presents the specific approach to this problem.
The analysis in Section The Influence of Transfer Coefficient and Conversion Proportion on Positive Emotion is only a qualitative analysis by observing simulation results. To quantitatively analyze how to take optimal steps to optimize the current guidance strategy in actual guidance scenarios, this section takes simulation 1 as an example and makes the following definitions (Figure 12): point P0 represents the guidance effect under the current guidance strategy, at this point, the quantity of positive emotional information y = yP0, and . We define the values of the parameters as a guidance strategy, represented by a five-tuple:
To achieve a more ideal guiding effect , it is necessary to adjust the parameter values so that the guidance policy is adjusted to the better guidance policy . As shown in Figure 12, there are multiple paths from P0 to P1 on the surface. Paths R1, R2, and R3 are defined as policy paths which are the directions that each parameter should be adjusted under the current guidance policy. It can be seen that although the P1 point can be reached along different policy paths, the policy path R2 has a shorter path distance and can reach P1 point faster than the other two paths which need to go through the intermediate nodes and , and it takes less time in implementing the guidance strategy. Therefore, it is a better path.
Mathematically, there are infinite directional derivatives at any point on a smooth three-dimensional surface, and the value of the function increases fastest along the gradient direction. Therefore, the gradient direction is the optimal direction to select the strategic path under the current guidance strategy, and the problem of finding the optimal strategic path is transformed into the problem of finding the gradient direction. We can find the optimal strategy path by the gradient ascent method. Assuming y = f(a1, b1) is a binary function of a1 and b1, which has first-order continuous partial derivative. So for every point P(a1, b1), we get a vector and the gradient of function f(a1, b1) at point P(a1, b1) is ∇f(a1, b1). In order to find the gradient at any point on the surface, 81 sets of simulation data are used to fit the surface by the least square method. The surface equation in simulation 1 is and the gradient of the surface at any point is .
After obtaining the gradient equation, the optimal strategy path can be obtained by iterating Equation (5).
In Equation (5), γ(γ > 0) is step length which defines how much the current parameter vector changes along the gradient direction. Figure 13 shows the formation of the optimal policy path.
After natural disasters, accident disasters, social security incidents, and other emergencies, people's emotions tend to be negative. Effective positive guidance of people's emotions is an important content of social governance. Under the background of COVID-19 pandemic, people's emotional guidance in emergencies is facing new situations and challenges: First, the double superposition of epidemic risk and event risk has strengthened the breeding and dissemination of negative emotions among the people. In addition, due to the epidemic prevention and control, a large number of people's social activities and information dissemination have been transferred online, and guiding netizens' emotions through network channels has become a significant problem.
Since July 19, 2021, Zhengzhou City, Henan Province, was hit by rainstorms for many days, resulting in an urban flood, and the impact of the disaster continued until early August. During the same period, Zhengzhou was also in the normalization stage of epidemic prevention and control. At the end of July, new local COVID-19 cases appeared again in Zhengzhou, and then the number of cases continued to increase. In the context of the spread of the epidemic, the sudden rainstorm disaster had a secondary impact on people's normal life, and a large number of negative emotions gathered and spread on the Internet.
In the early stage of the flood situation, most netizens expressed anxiety about the extreme rainfall and concerns about the spread of the epidemic. Negative emotional information was dominant on the Internet. In response to this situation, relevant government departments took emergency measures in time to publish flood information and the situation of epidemic prevention and control, and actively guided online public opinion to reduce negative emotional information on the Internet. This study obtains emotional data through the network public opinion monitoring platform (https://www.gsdata.cn), which uses the natural language processing model (NLP) to divide the text information published by netizens into different emotions and publish the results on the platform. Therefore, we used this platform to collect the statistical data of positive information, neutral information, and negative information on the Internet from 19 July to 30 July with “Zhengzhou rainstorm” as the key word. It can be seen from Figure 14 that in the first 5 days, the amount of negative information and neutral information is far more than that of positive information. Starting on the fifth day, the amount of positive information began to outnumber the amount of negative and neutral information. This is a typical scene of emotion transfer from negative emotion and neutral emotion to positive emotion, indicating that the emergency guidance measures of relevant government departments played a positive role. Therefore, based on the collected data, we carried out an experiment.
In the model, variables x1, x2, and y represent the amount of negative information, neutral information, and positive information, respectively. Various parameters of the model can be calculated by regression analysis introduced in Section Parameters Estimation (Table 6).
The fitting result of the model is tested by R2, VIFs, and F-values. The results are as follows:
Plug parameters into the model and draw the graph of theoretical Transfer Model, Original Model, and actual data (Figure 15). It can be seen from the graph and R-Square that the theoretical model fits well and has research value. At the equilibrium point, the amount of negative emotion information decreased from 1,570,565.10101 to 1,088,345.87043, decreasing by 30.7%, the amount of neutral emotion information decreased from 2,245,255.63158 to 1,498,893.23150, decreasing by 33.2%, and the amount of positive emotion information increased from 909,502.33298 to 987,878.46469, increasing by 7.9%. According to the analysis of the data, the increase of positive emotion information is not large, which is far less than the decrease in negative emotion and neutral emotion. Relevant government departments need to adjust the guidance strength and efficiency to improve the guidance effect.
The three-dimensional surface of positive emotional information is fitted by the least square method in four scenarios. The ŷ is the amount of positive emotional information and n is the number of iterations.
Scenario 1:
Scenario 2:
Scenario 3:
Scenario 4:
After n iterations of the gradient ascent method, the optimal policy path in each scenario can be obtained. In each scenario, the amount of positive emotional information at the balance point gradually increases along the strategy path (Figure 16), which obtains a better guidance effect and proves the effectiveness of the optimization strategy.
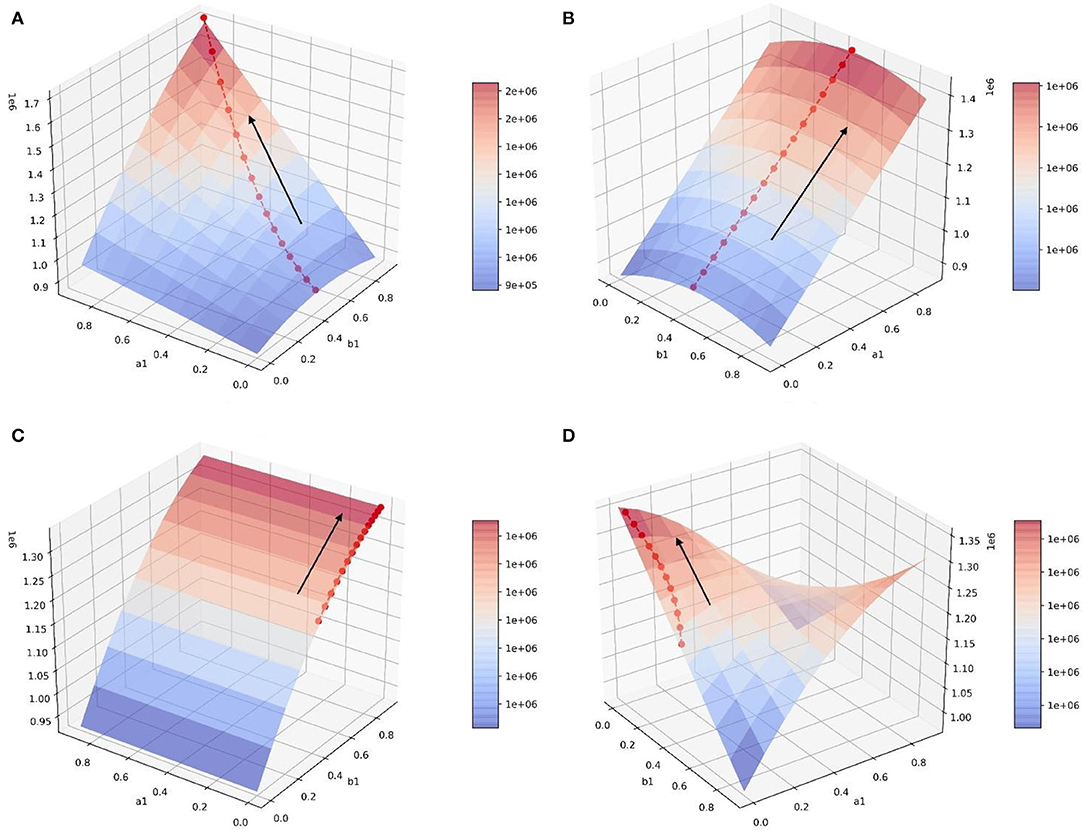
Figure 16. Optimal policy paths in four scenarios. (A) Optimal policy path in scenario 1. (B) Optimal policy path in scenario 2. (C) Optimal policy path in scenario 3. (D) Optimal policy path in scenario 4.
Due to the constraint of the numerical relationship between a1, a2, b1, and b2 in four hypothetical scenarios, we need to select a scenario that is more consistent with the data of this case. On the premise that the values of r1, r2, r, K1, K2, K, a1, b1 are fixed, let n = 0, and based on the transfer model, calculating the evolution values of positive emotional information in each scenario with and without the constraint of a1, a2,b1, and b2, drawing the evolution curve (Figure 17) and calculating the Euclidean distance between the two sets of data, as shown in Table 7.
In scenario 1 and scenario 2, the Euclidean distance is smaller, indicating that this case is more applicable to scenario 1 and scenario 2. By further analyzing the value changes of a1, b1, and ŷ in this case under two scenarios (Tables 8, 9) could be obtained:
By analyzing Figures 16A,B and Tables 8, 9, it can be seen that in the process of gradient rise, the change rate of a1 in both scenarios is greater than that of b1, indicating that in this case, improving the guidance efficiency is the key to improving the guidance effect. The relevant government departments have invested enough force in the guidance process but ignored the efficiency in the implementation process. This results in the Barrel Effect, which makes the increase of positive emotional information much smaller than the decrease of negative emotion and neutral emotion. What is more, in scenario 1, since b1 and b2 can increase synchronously, a better guidance effect is finally achieved compared with scenario 2, which indicates that attention should be paid to both neutral and negative emotional people and the neglect of one kind of people will also cause a poor guidance effect.
We discussed the emotion transfer mechanism of netizens, and established the emotion transfer model through a differential equation:
This article defines two key parameters: transfer coefficient and conversion proportion. In the practical application of the model, the value of the transfer coefficient represents the guiding efficiency of relevant government departments in netizens' emotion guidance, and the value of conversion proportion represents the guiding strength. This study qualitatively discussed the influence of transfer coefficient and conversion proportion on the process of emotion transfer. The simulation results mainly support the following three conclusions:
First, when the guidance strength is certain, the adjustment of guiding efficiency can only change the final guiding effect to a small extent. At the same time, when the guiding efficiency of emotions with a larger intrinsic growth rate is higher, the guiding effect also tends to be better, which shows that the relevant government departments should pay more attention to the emotion with a higher intrinsic growth rate when guiding the netizens' emotions. Second, when the guidance efficiency is certain, the change of guidance strength has a great impact on the guidance effect, which shows that it is the key to investing enough force in the emotional guidance of netizens. Finally, the research shows that the adjustment of guidance efficiency and guidance strength is not blind, which needs to be discussed according to the situation. This article discusses four scenarios. In the ideal situation of scenario 1 (Figure 6), the guidance effect will be better with the improvement of guidance efficiency and guidance strength. However, in scenario 2 (Figure 8), blindly increasing the guidance strength of one of the emotions may bring a worse guidance effect. Similarly, in scenario 3 (Figure 9), blindly changing the guidance efficiency will not have a significant impact on the guidance effect. It can be seen that in the above two scenarios (scenarios 2 and 3), the aimless adjustment of guidance efficiency and guidance strength will make the investment unable to get a better reward. Saddle points appear in scenario 4 (Figure 11), which makes the situation more complex. It is difficult to give the adjustment of guidance efficiency and guidance strength through intuitive judgment. In order to solve the above problem, this study innovatively puts forward the optimization method of guidance strategy based on the gradient ascent algorithm, which theoretically shows that the guidance effect and guidance strategy are quantifiable.
In the subsequent empirical research, the theoretical model was fitted through the actual data to verify the rationality of the above theory and the feasibility of the method. The empirical study showed three aspects of the public opinion event. First, the discussion about this event tended to be negative. The model showed that the upper growth limit and intrinsic growth rate of netizens' negative emotion (r1 = 1.56996, K1 = 1570565.10101) were greater than those of netizens' positive emotion (r = 1.16771, K = 909502.33298). Negative emotion gathered in netizens, so it was urgent to guide netizens' emotions. Second, the guidance work of relevant government departments played a positive role in the emotional transfer of netizens, and from the fifth day after the occurrence of this public opinion event, the growing amount of positive emotional information in 1 day began to be more than that of the other two emotions. The equilibrium point of the model showed the effect of the work of relevant government departments. When the amount of information on the three emotions tended to be stable, the amount of positive emotional information increased by 7.9% and the amount of negative emotional information decreased by 30.7%. Finally, the analysis of the guidance strategy optimization showed that the guidance effect of this event was not in the best state, and left a lot to be desired. It also showed that the efficiency of relevant government departments in emotional guidance was low, which made the transfer coefficient of negative emotion (a1 = 0.01) and neutral emotion (a2 = 0.25) in the model obtain small values and affected the final guidance effect.
In future research, we will improve the model and apply it to more complex scenarios. First, the emotion transfer model in this article only describes the scene of a one-way transfer from multiple emotions to one emotion, but in reality, there will be a situation where a single emotion will be transferred to a variety of emotions or the transfer between multiple emotions. Therefore, it is necessary to change the value range of parameters in the model (allowing the values of ai and bi to be <0) or introduce new parameters to make the model better describe the emotion transfer process in complex scenes. In addition, in the simulation of this article, it is a relatively simple way to divide emotion into positive emotion, neutral emotion, and negative emotion. In the existing fine-grained research, emotion is divided into 5 types and 7 types. Therefore, it is necessary to introduce more variables into the equation system and carry out simulation research on n kinds of emotion (n > 3).
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
YX was involved in the theoretical research, model construction, and the reviewing of the manuscript. ZW was involved in the data collection, data analysis, and the writing of the manuscript. ML was involved in the reviewing and revising of the manuscript. YL helped to build the mathematical model in his paper. All authors contributed to the article and approved the submitted version.
This work was supported by the National Social Science Fund of China (Grant No. 20BXW074).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank all those who helped write this article and the editors and typesetters for their efforts to improve the quality of this article.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2022.880322/full#supplementary-material
Banothu, S., Akula, S., Akarapu, V., and Rao, T. R. L. (2021). “Emotion extraction and classification from twitter text,” in Proceedings of the International Conference on IoT Based Control Networks and Intelligent Systems - ICICNIS 2021. Kottayam.
Barsade, S. G. (2002). The tipple effect: emotional contagion and its influence on group behavior. Administrative Science Quarterly. 47:644–675. doi: 10.2307/3094912
Coviello, L., Sohn, Y., Kramer, A. D. I., Marlow, C., Franceschetti, M., Christakis, N.A., et al. (2014). Detecting emotional contagion in massive social networks. PLoS ONE. 9, e90315. doi: 10.1371/journal.pone.0090315
Fang, M., Li, L., and Yang, L. (2019). Social network public opinion research based on S-SEIR epidemic model. IEEE Int. Conf. Cloud Comput. Technol. Sci. (CloudCom). 2019, 374–379. doi: 10.1109/CloudCom.2019.00064
Ferrara, E., and Yang, Z. (2015). Measuring emotional contagion in social media. PLoS ONE. 10, e0142390. doi: 10.1371/journal.pone.0142390
Hill, A. L., Rand, D. G., Nowak, M. A., and Christakis, N. A. (2010). Emotions as infectious diseases in a large social network: the SISa model. Proc. R. Soc. B. 277, 3827–3835. doi: 10.1098/rspb.2010.1217
Jin, X., and Yang, H. (2018). Research on evolution mechanism and sentiment analysis of emergency network public opinion. Int. J. Comput. Commun. Eng. 7, 8–19. doi: 10.17706/IJCCE.2018.7.2.8-19
Kirange, D. K., and Deshmukh, R. R. (2012). Emotion classification of news headlines using SVM. Asian J. Comp. Sci. Inform. Technol. 2, 104–106.
Kramer, A. D. I., Guillory, J. E., and Hancock, J. T. (2014). Experimental evidence of massive-scale emotional contagion through social networks. Proc. Natl. Acad. Sci. 111, 8788–8790. doi: 10.1073/pnas.1320040111
Krishnan, H., Elayidom, M. S., and Santhanakrishnan, T. (2017). Emotion detection of tweets using naïve bayes classifier. Int. J. Eng. Technol. Sci. Res. 4, 457–462.
Liu, Z., Zhang, T., and Lan, Q. (2014). An extended SISa model for sentiment contagion. Discrete Dynam. Nat. Soc. 2014, 262384. doi: 10.1155/2014/262384
Meléndez, J. C., Satorres, E., Olmedo, M. R., Delhom, I., Real, E., and Lora, Y. (2020). Emotion recognition changes in a confinement situation due to COVID-19. J. Environ. Psychol. 72, 101518. doi: 10.1016/j.jenvp.2020.101518
Nemes, L., and Kiss, A. (2021). Social media sentiment analysis based on COVID-19. J. Inform. Telecommun. 5, 1–15. doi: 10.1080/24751839.2020.1790793
Panayiotou, G., Panteli, M., and Leonido, C. (2021). Coping with the invisible enemy: the role of emotion regulation and awareness in quality of life during the COVID-19 pandemic. J. Contex. Behav. Sci. 19, 17–27. doi: 10.1016/j.jcbs.2020.11.002
Ren, Z., Zhang, P., Liu, J., and Lan, Y. (2019). Research on netizens' emotion evolution in emergency based on machine learning. Sci. Rep. 1419, 012004. doi: 10.1088/1742-6596/1419/1/012004
Slaughter, J. E., Gabriel, A. S., Ganster, M. L., Vaziri, H., and MacGowan, R. L. (2021). Getting worse or getting better? Understanding the antecedents and consequences of emotion profile transitions during COVID-19-induced organizational crisis. J. Appl. Psychol. 106, 1118–1136. doi: 10.1037/apl0000947
Stieglitz, S., and Dang, X. L. (2013). Emotions and information diffusion in social media—sentiment of microblogs and sharing behavior. J. Manag. Inform. Syst. 29, 217–248. doi: 10.2753/MIS0742-1222290408
Tan, X., Zhuang, M., Lu, X., and Mao, T. (2021). An analysis of the emotional evolution of large-scale Internet public opinion events based on the BERT-LDA hybrid model. IEEE Access. 9, 15860–15871. doi: 10.1109/ACCESS.2021.3052566
Wheaton, M. G., Prikhidko, A., and Messner, G. R. (2021). Is fear of COVID-19 contagious? The effects of emotion contagion and social media use on anxiety in response to the coronavirus pandemic. Front. Psychol. 11, 567379. doi: 10.3389/fpsyg.2020.567379
Xiang, N., Zhou, Z., and Pan, Z. (2017a). “Dynamic crowd aggregation simulation using SIR model based emotion contagion,” in International Conference on Virtual Reality and Visualization (ICVRV). (Zhengzhou),352–353.
Xiang, N., Zhou, Z., and Pan, Z. (2017b). Using SIR model to simulate emotion contagion in dynamic crowd aggregation process. Int. J. Performability Eng. 14, 134–143. doi: 10.23940/ijpe.18.01.p14.134143
Xu, Y., Huang, T., Zuo, Z., and Wang, X. (2021). “Social media sentiment and COVID-19 transmission: results from a Time-varying SIR model,” in PACIS 2021 Proceedings, 31. Available online at: https://aisel.aisnet.org/pacis2021/31 (accessed March 08, 2022).
Yang, M., Xu, J., Luo, K., and Zhang, Y. (2021). Sentiment analysis of Chinese text based on Elmo-RNN model. J. Phys. Conf. Series. 1748, 022033. doi: 10.1088/1742-6596/1748/2/022033
Yi, Y., Lu, L., and Meng, Y. (2019). The impact of emotion on the information diffusion model in online social network. IOP Conf. Series Earth Environ. Sci. 234, 020100. doi: 10.1088/1755-1315/234/1/012100
Zeng, R., and Zhu, D. (2019). A model and simulation of the emotional contagion of netizens in the process of rumor refutation. Sci. Rep. 9, 14164. doi: 10.1038/s41598-019-50770-4
Zhang, L., Wei, J., and Boncella, R. J. (2020). Emotional communication analysis of emergency microblog based on the evolution life cycle of public opinion. Inform. Discov. Deliv. 48, 151–163. doi: 10.1108/IDD-10-2019-0074
Zhang, Q., Gao, T., Liu, X., and Zheng, Y. (2020). Public environment emotion prediction model using LSTM network. Sustainability. 12, 1665. doi: 10.3390/su12041665
Keywords: netizens' emotion, transfer model, guidance strategy, optimization, post-pandemic
Citation: Wen Z, Xia Y, Liu M and Lan Y (2022) The Transfer Model and Guidance Strategy of Netizens' Emotions. Front. Psychol. 13:880322. doi: 10.3389/fpsyg.2022.880322
Received: 22 February 2022; Accepted: 14 April 2022;
Published: 19 May 2022.
Edited by:
Yizhang Jiang, Jiangnan University, ChinaReviewed by:
Simone Belli, Complutense University of Madrid, SpainCopyright © 2022 Wen, Xia, Liu and Lan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yixue Xia, cmNvZm5wb2dAMTI2LmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.