Xiujie Yang
Xiangzhi Meng- 1Faculty of Psychology, Beijing Normal University, Beijing, China
- 2School of Psychological and Cognitive Sciences, Beijing Key Laboratory of Behavioral and Mental Health, Peking University, Beijing, China
- 3PekingU-PolyU Center for Child Development and Learning, Beijing, China
The main purpose of the present study was to investigate whether visual processing uniquely contributed to character reading and early mathematics in Chinese children. Eighty-two Chinese kindergarteners at K3 (mean age = 68 months, SD = 0.30) were followed up to grade one (mean age = 82 months, SD = 0.35) with an interval of 14 months. Nonverbal intelligence, inhibitory control, sustained attention, character reading, and mathematics were measured at kindergarten. Character reading and mathematics were assessed again at grade one. Results showed visual processing at kindergarten significantly predicted character reading at grade one after controlling for prior reading performance, inhibitory control, sustained attention, age, gender, and nonverbal IQ. Similarly, visual processing at kindergarten explained unique variance in early mathematics at grade one when prior mathematics performance and other covariates at kindergarten were controlled. These findings suggest that visual processing should serve as a domain-general precursor of children’s performance in character reading and early mathematics and an important cognitive factor for later academic learning.
Introduction
Visual processing is the procedure of organizing and interpreting visual information (Siok and Fletcher, 2001; McGrew, 2009). It reflects the ability of attending to and distinguishing a figure’s features and details, such as shape, orientation, color, and size (Kulp et al., 2004; Yang et al., 2013). In the past decades, evidence has shown that poor performance in visual processing might explain learning difficulties in reading and mathematics (Barrett, 1965; O’Neill and Stanley, 1976; Corballis et al., 1985; Boden and Brodeur, 1999). For example, children who have deficits in visual perception often cannot efficiently distinguish words printed in different sizes or colors (Fischer et al., 2000; Visser et al., 2004). Students suffering from visual perception impairment usually exhibit reversals and misaligning of horizontal series of digits, and weak math visualization (Willows et al., 2012). People with visual processing deficits are often diagnosed with dyslexia (e.g., Talcott et al., 2000; Amitay et al., 2002; Ramus et al., 2003) and/or dyscalculia (O’hare et al., 1991; Emmons and Anderson, 2005).
Reading and mathematics abilities are important for future academic success (Jordan et al., 2009; Cooper et al., 2014). Besides, there are at least three additional reasons for investigating the effect of visual processing on reading acquisition and early mathematics. First, previous researchers have found high overlaps between visual skills and domain-general cognitive skills (e.g., sustained attention, nonverbal reasoning, and inhibitory control) (Buckley et al., 2018; Yang et al., 2019a), as well as RAN (Yang et al., 2019b). However, it remains unclear whether visual processing will uniquely contribute to reading and mathematics when these general cognitive abilities are taken into consideration. Second, even among those existing studies, very few provided longitudinal evidence among kindergarten children about the predictive effect of visual processing on their future Chinese reading (e.g., Huang and Hanley, 1995, 1997; Ho, 1997; McBride-Chang et al., 2005) and mathematics (e.g., Zhang and Lin, 2015). Third, as is known, the transition of early reading and early mathematics from kindergarten to primary school could be problematic for children who fall behind in basic cognitive abilities (LeFevre et al., 2010; Gunderson et al., 2012; Yang et al., 2019a). If visual processing can uniquely contribute to reading and mathematics, perhaps educators and parents would pay more attention to children’s visual skills and identify children at risk of learning difficulties as early as possible.
The role of visual skills in early reading development may be stronger for Chinese readers than for readers of alphabetic languages. That is because many Chinese characters are visually similar but are usually pronounced differently. Meanwhile, they convey different meanings, for example, “±” (tu3, means “earth”) and “±” (shi4, means “soldier”). Moreover, Chinese characters also feature nonlinear visual processing; they involve more complex spatial configuration processing, e.g., left–right, up–down, inside–outside, enclosed, semi-enclosed, and within stroke patterns. Szwed et al. (2014) have found that Chinese reading involves enhanced engagement of intermediate visual areas compared to alphabetic reading. Compared to alphabetic readers, Chinese readers tend to be more likely to make use of the visual symbols as the basis of orthographic knowledge in Chinese characters (Luo et al., 2013; Zhou et al., 2015). Metalinguistic skills, such as phonological awareness, morphological awareness, and orthographic knowledge, are found to be associated with visual processing (McBride-Chang et al., 2005; Martens and de Jong, 2006; Chung et al., 2008; Luo et al., 2013). Indeed, Chinese children are found to rapidly distinguish the visual–orthographic characteristics from their similar counterparts and match them with the phonological representations stored in long-term memory (e.g., McBride-Chang et al., 2005; Luo et al., 2013). Otherwise, children might exhibit difficulties in visually distinguishing similar characters because there are more diverse spatial patterns among strokes compared to English (Ding et al., 2002). For example, Chinese primary school children with dyslexia usually struggle to distinguish “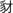
” (jackal) and “
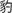” (leopard) and have difficulty in identifying whether “lonely” should be written as “
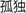” or “
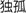” (the former is correct) (Ding et al., 2002).
In addition, McBride (2016) proposed that Chinese characters’ visual distinctiveness may lead children to foster categorization strategies in recognizing characters (McBride, 2016). Indeed, there has been evidence showing that Chinese beginning learners at the age of 3 acquire character reading abilities using a visual strategy of discriminating the graphic feature in the character, given that Chinese characters are composed of radicals with complicated spatial structures (Ho and Bryant, 1997). Therefore, we believe that visual processing should be more essential in Chinese character recognition. However, among a relatively small body of literature with different conclusions (e.g., Huang and Hanley, 1995, 1997; Ho, 1997; McBride-Chang et al., 2005), most studies were conducted in Hong Kong and Taiwan, where traditional Chinese is used. Mainland Chinese children learn simplified characters, while children in Hong Kong and Taiwan learn traditional Chinese characters (McBride, 2016). The semantic and phonetic radicals in characters facilitate readers’ pronouncing and understanding the meanings of these characters. Simplified characters are more difficult to recognize than traditional characters because the radical clues have been cut down (Cui et al., 2019). Mainland Chinese children have to rely more on visual processing to carefully recognize the remaining radical clues in each character. Based on the findings on traditional Chinese reading (Chen and Yuen, 1991; McBride, 2016; Cui et al., 2019), we hypothesized that visual processing also would be important for simplified Chinese reading.
With regard to early mathematics, we propose that visual processing, along with early numeracy knowledge, such as counting, number sense, and number knowledge (Jordan et al., 2010; Garon-Carrier et al., 2018), and general cognitive skills, such as sustained attention, nonverbal reasoning, and inhibitory control (LeFevre et al., 2010), are essential in its development. To acquire calculation and number comparison skills, individuals need to visually recognize number words and transform number symbols into quantities, at least among young children (Geary, 2004; Krajewski and Schneider, 2009a, b). According to Dehaene’s triple-code model, the visual system is one of the most important systems of number representation, and numbers can be encoded as Arabic numerals (Dehaene, 1992; Dehaene and Cohen, 1995). Indeed, visual skills can facilitate mathematics problem solving by forming an accurate “mental blackboard” to organize the interrelations between numerical quantities (Tartre, 1990; Zhang et al., 2014; Zhang and Lin, 2015). Children with high visual–spatial skills tended to translate more math problems into pictorial and spatial descriptions and demonstrated better flexibility in changing a formed word problem into an arithmetic problem, abstracting arithmetic formulas from applied word problems, and mentally processing number relationships (Talcott et al., 2000; Sigmundsson et al., 2010; Zhang and Lin, 2015). In contrast, children with inadequate visual processing had difficulty in breaking an arithmetic formula into a spatial mental process (Fennema and Tartre, 1985; Zhang et al., 2017). Indeed, children with disabilities in arithmetic exhibited lower visual–spatial abilities (Rourke and Finlayson, 1978; Sigmundsson et al., 2010). Neuroimaging evidence also indicates that proficient math performers tended to make use of spatial-based strategies that are associated with parietal regions (Rivera et al., 2005). Importantly, Tosto et al. (2014) have suggested a strong genetic overlap between mathematical ability and visual–spatial processing, indicating the important role of visual processing in children’s mathematics development.
In contrast to mature math learners who use fact retrieval strategies, kindergarten children often use mental counting to solve arithmetic problems (Geary et al., 1993). They usually transform a mathematics problem into a mental spatial format that represents how numbers are correlated to each other (Yang et al., 2019a). For example, to solve an addition problem (e.g., 5 + 6), children might turn it into a visual finger counting or mental counting process. These abilities of abstracting and classifying characteristics of objects during counting with mental spatial skills usually play important roles in mathematics learning. As such, we hypothesize that visual processing is essential for spatial mental activity and proficient mathematics problem solving, and the development of visual processing would predict later mathematics performance of Chinese children. However, some studies solely considered visual processing as part of intelligence, suggesting that age and verbal ability may moderate the relationships between visual–spatial ability, reading, and mathematics (Huang and Hanley, 1995, 1997; Buckley et al., 2018; Frick, 2018). Moreover, there are relatively few Chinese studies investigating relations of spatial abilities and mathematics development apart from general cognitive abilities (Zhou et al., 2015; Zhang, 2016), especially among mainland Chinese kindergarten children who are beginning to learn mathematics.
The Present Study
In the past decades, there has been a debate on whether visual processing contributes to reading acquisition (Kavale, 1982; Stanovich, 1992; Huang and Hanley, 1995, 1997; Ho and Bryant, 1997, 1999; Hu and Catts, 1998; Siok and Fletcher, 2001; McBride-Chang and Kail, 2002; McBride-Chang et al., 2005) and mathematics learning (Zhou et al., 2015; Cui et al., 2019). Meanwhile, there is a scarcity of research investigating reading and mathematics simultaneously to identify their common underlying factors among Chinese young children.
The present study intended to investigate the potentially simultaneous role of visual processing in reading acquisition and early mathematics among mainland Chinese young children. We chose children at kindergarten and followed them up to grade one, since this is the period when children go from receiving informal education to formal education, and there was a high possibility to find out those children’s improvements in reading and mathematics performance (Yang et al., 2019a, c). Visual processing was measured by the orientation discrimination task, which distinguishes orientation differences between two separated lines (O’Neill and Stanley, 1976; Wang et al., 2014). The task required rapid visual processing to identify the orientation of the two lines and to perceive whether a line was tilted clockwise or anticlockwise. Spatial orientation has been consistently shown as the one of the most important visual perceptual/processing abilities among all visual–spatial abilities (Silver and Hagin, 1970; O’Neill and Stanley, 1976; Yilmaz, 2009; Wang et al., 2014; Zhang, 2016). People have found that the spatial orientation threshold between the two lines is higher in children with dyslexia than in typically developed children (O’Neill and Stanley, 1976). Therefore, we hypothesized that visual processing would simultaneously contribute to children’s reading and mathematics performance concurrently and longitudinally. Specifically, children who were higher in the orientation discrimination thresholds were expected to achieve lower scores in reading and mathematics.
Some researchers proposed that the contribution of visual processing to reading and mathematics performance could be explained by general cognitive abilities such as intelligence (e.g., Olson and Datta, 2002). More researchers indicated that the effects of visual processing on reading and mathematics still existed even when general cognitive abilities were controlled (Kavale, 1982; Talcott et al., 2000). Therefore, further research is necessary to include other general cognitive abilities to clarify the unique relations of visual processing with reading and mathematics. Considering that visual processing was highly associated and shared much variance with inhibition and sustained attention (Buckley et al., 2018; Yang et al., 2019a), along with general intelligence (Olson and Datta, 2002; Cui et al., 2019), we assessed them with the Flanker task, the Continuous Performance Task (CPT), and the Combined Raven’s Test (CRT). The current study set out to provide evidence for the unique role of visual processing in children’s reading and mathematics acquisitions in their early years, in turn contributing to the screening and remediation of children at risk of dyslexia, dyscalculia, or both.
Materials and Methods
Participants
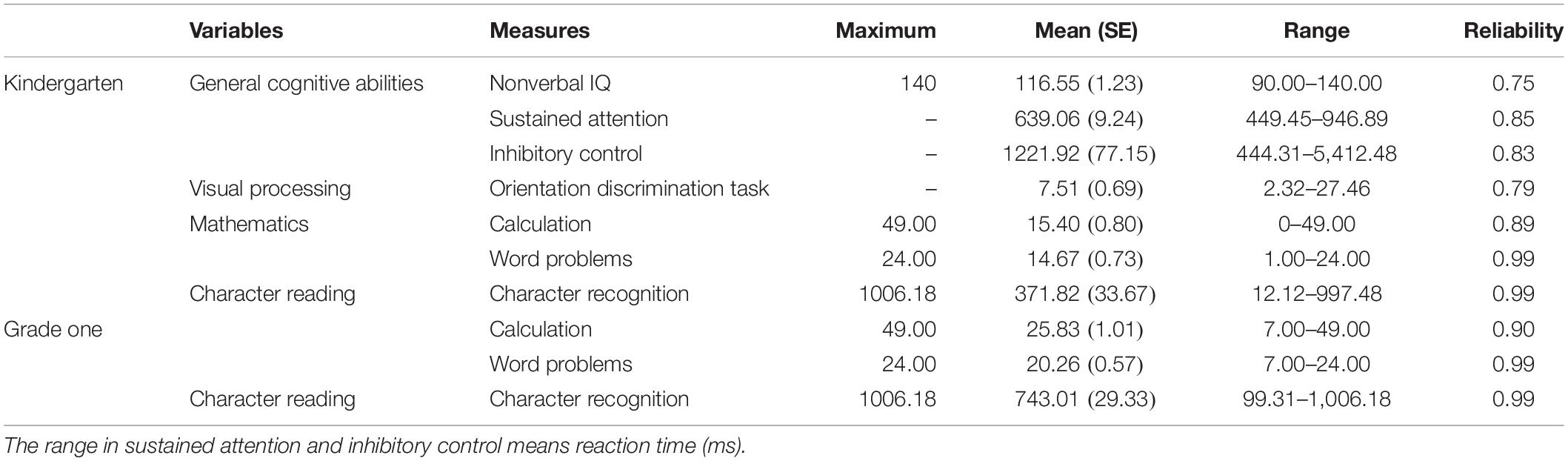
The study began with 108 Chinese kindergarteners (63 boys and 45 girls) who attended their last year at senior kindergarten. They were followed up to grade one after 14 months. Informed consent was obtained from the headmaster and the children’s parents. Ethics approval was sought from the Survey and Behavioral Research Ethics Committee of Peking University. All children had no auditory or visual deficits. Vision or correct vision was normal. The sample size dropped to 82 by the second measurement because some children were not enrolled in the same school or had moved away. Thus, the dropout rate was approximately 24%. We conducted an independent T-test and found no significant differences in all measures between the dropout children and the remaining children (all p > 0.05). At the beginning of the study, the children’s average age was 5 years and 8 months (SD = 0.30); at grade one, the children’s average age was 6 years and 10 months (SD = 0.35). All of these children were fluent in Mandarin.
Measures
Character Reading
This measure was revised from a standardized Chinese character recognition test (Wang and Tao, 1996). It involved 142 Chinese characters that were divided into 10 sets based on their levels of difficulty. Children were required to read the Chinese characters aloud when they were in senior kindergarten and grade one. The experimenter recorded the total number of characters that children read correctly. The correct answer was transformed into children’s character reading performance based on the norm.
Mathematics
We used calculation and word problems to assess children’s mathematics abilities. The calculation task was adapted from Butterworth (2003) and Rodic et al. (2015), in which 50 simple calculation problems (e.g., 6 + 2) were presented on a computer screen one by one, and the administrator would, meanwhile, orally present them. Children needed to choose between two candidate choices to get the correct answer as quickly and accurately as possible. The total test time was 2 min. To reduce the guessing effect in this timed task, we used the correction formula S = R − W/(n − 1) to calculate the total score, where S stands for the adjusted score, R refers to the number of correct responses, W represents the number of incorrect responses, and n is the number of alternative responses to each item (Guilford, 1936). In the word problems, children were asked to compare the result of one calculation task with one specific number in some context (Wei et al., 2012). For example, the experimenter stated one story in Chinese: “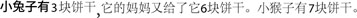
[A rabbit has three cookies, and her mother gave her another six cookies. A monkey has seven cookies].” And then the experimenter asked: “ 
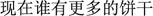[Now who has more cookies]?” As such, children needed to comprehend the context and compute the involved numbers in order to get the answer. The test was stopped when three consecutive errors were made. The total score is 24, with 1 point for one correctly answered item.
Visual Processing
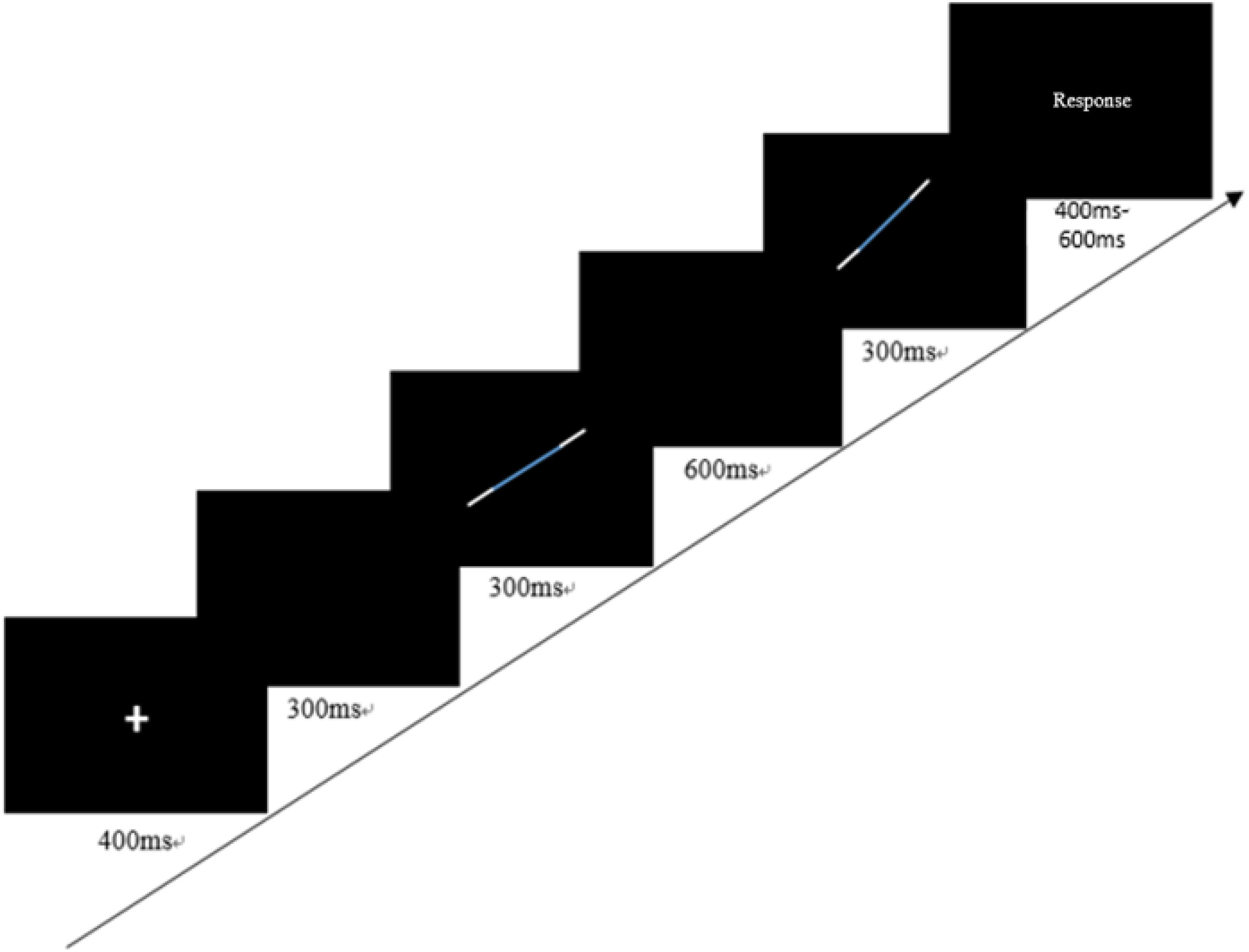
An orientation discrimination task was adopted to assess children’s sensitivity in discriminating orientation differences between two segments (Wang et al., 2014). In the task, children were asked to determine which direction the second segment turned compared to the first segment (clockwise/anticlockwise). Therefore, children needed to understand the representation of the segment and the spatial relations between the two segments. On each trial, the order of being clockwise or anticlockwise was randomly determined. To adapt to children’s ability, we changed the original pure lines and pure dots into a bicolor segment based on the pilot study. This is easier than the original task because children had more cues to judge if the segment shifted clockwise or anticlockwise. The segment was 6° length presented in the first quartile. A three-down-one-up self-adaptive rule was used, and the step size was 1.0715°. That is to say, when the orientation differences between the two segments started from 10.239°, it would decrease 1.0715° when the children answered correctly three times in succession but rose 1.0715° when the children answered incorrectly once.
The task had two blocks with 10 reversals in each block. The reversal occurred when the orientation differences changed between the two segments. The orientation discrimination threshold was the indicator of the visual processing task, which was calculated with the mean of the angle differences between the two solid segments. To help children adapt to the task, and to avoid fatigue, we only used the mean of the angle differences in the middle six reversals as the orientation discrimination threshold. The lower the threshold, the higher the visual processing ability. To keep the visual angle consistent, children were required to sit 80 cm away from the central screen. The concrete procedure for each trial is shown in Figure 1.
Figure 1. A trial of the orientation discrimination task.
Sustained Attention
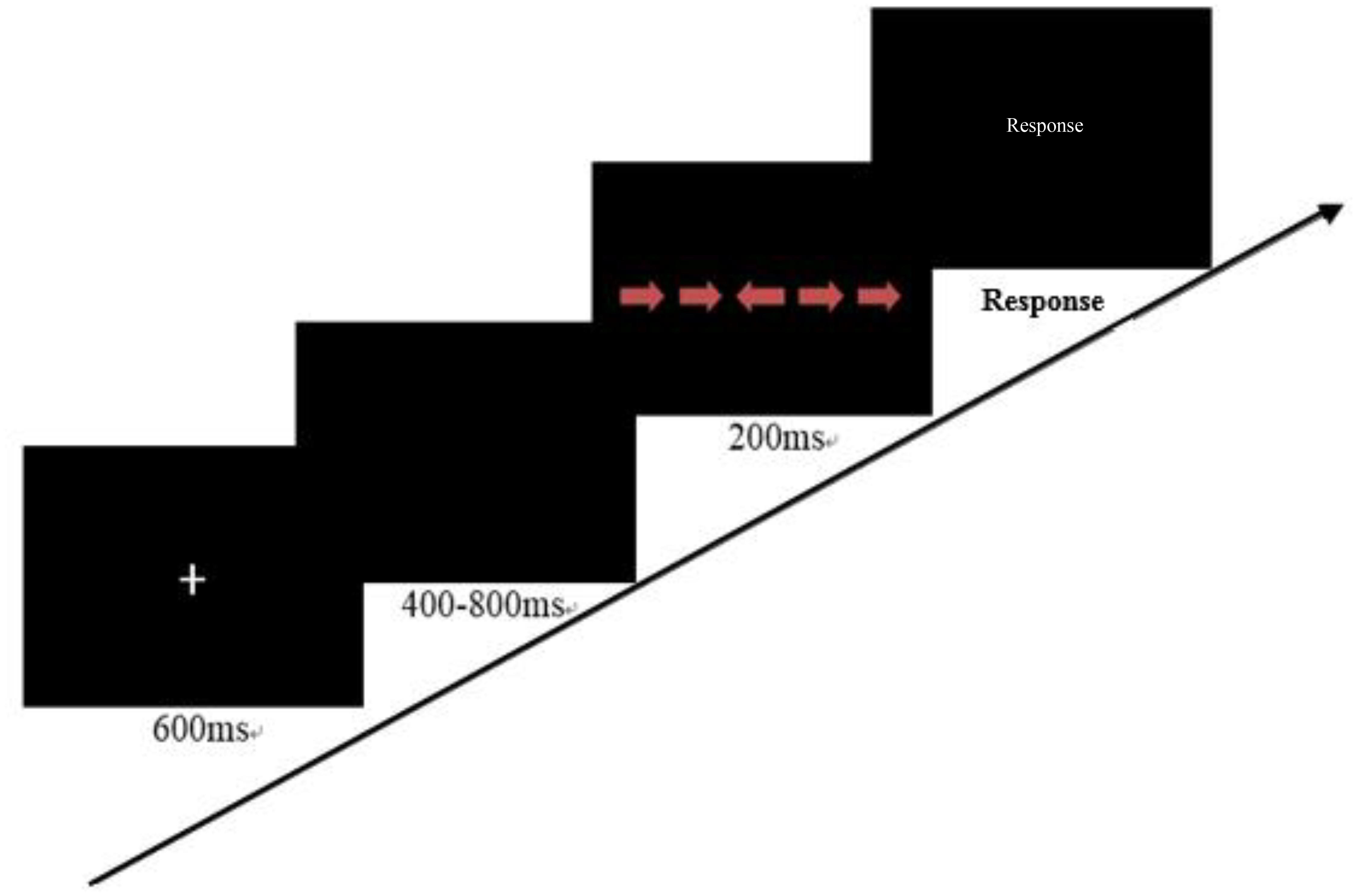
The CPT is typically conceptualized as an assessment of sustained attention (Gardner-Neblett et al., 2014). There were 16 types of figures (□, ○, △, and ✩, colored red, yellow, blue, or green), each presented on the screen in the center of the computer screen for 200 ms one at a time. The interval time between two stimuli was randomly distributed to 1,500, 2,000, 2,500, or 3,000 ms. During the task, the child was required to press the left key when the red square appeared on the screen but ignore other stimuli (Figure 2). Ten practice trials would first appear, followed by 120 test trials.
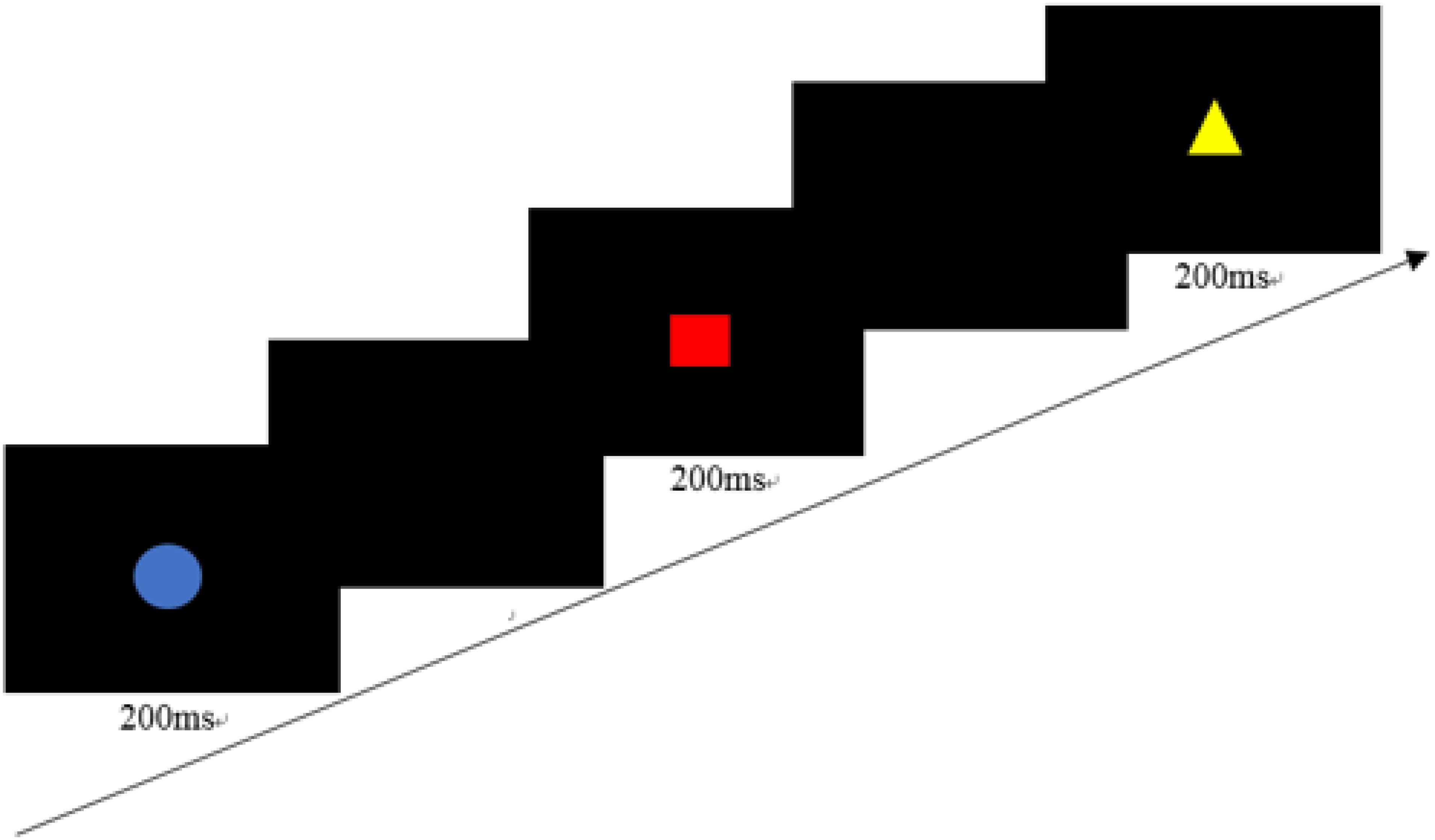
Figure 2. A trial of the Continuous Performance Task (the interval time is 1,500, 2,000, 2,500, or 3,000 ms).
Inhibitory Control
We used an adapted version of the Flanker task to test children’s inhibitory control ability (Ridderinkhof and van der Molen, 1995; Miller and Cohen, 2001). In this task, the child was told a story that a young princess was lost in the forest, and there were some arrow marks to assist her home. Only the arrow laying in the central position is the correct direction. In the incongruent condition, arrows pointed to the direction opposite the central one; in the congruent condition, all of the arrows pointed to the same direction. The instructor asked the child to point out the direction by pressing the left or right key. Ten practice trials were first presented and were followed by 40 experimental trials. The procedure is shown in Figure 3.
Figure 3. A trial of the Flanker task (there is no time limit for response).
Nonverbal IQ
The CRT was used to measure children’s nonverbal IQ (Li et al., 1989). This test has 72 matrices with sets A, AB, B, C, D, and E of increasing difficulty. For set A, children were required to identify the missing element to fill the blanks of an incomplete picture. For the next four sets, children needed to select one element that was suitable in a matrix that met a certain rule. Children had to stop after 20 min, or when they made three consecutive errors in the row of C, D, or E. We converted the total number of matrices solved correctly to a standard score based on the CRT norm from urban China for children aged 5 to 16 years.
Procedure
Children completed a battery of measures as in the above description along with some others as part of a large-scale longitudinal study. For the kindergarten assessments, children were tested individually on several consecutive days. Nonverbal IQ, sustained attention, inhibitory control, orientation discrimination task, calculation, word problems, and character recognition were conducted. After 14 months, as when children entered grade one, calculation, word problems, and character recognition measures were conducted. Each session was administered in a quiet room at school within 30 min to avoid fatigue.
Results
Preliminary Analyses
The means, standard errors, skewness, kurtosis, and reliabilities for all variables assessed at senior kindergarten and grade one are included in Table 1. All data are presented as raw scores. Specifically, sustained attention is presented as reaction time in the CPT in which children responded to the target stimulus, and inhibitory control is presented as reaction time in the Flanker task in the incongruent condition.
Table 1. Descriptive statistics for variables measured at senior kindergarten and grade one.
In order to investigate how children developed from kindergarten to grade one, we had their mathematics (calculation and word problems) and character reading abilities as the dependent variables with a paired-sample T-test. Results showed that, for character reading, t(1, 80) = 12.81, p < 0.001; for calculation, t(1, 72) = 10.79, p < 0.001; for word problems, t(1, 75) = 6.60, p < 0.001. Therefore, children had significant improvements in mathematics and character reading from kindergarten to grade one. Because we had multiple measures for early numerical processing and mathematics, we used principal component analysis to create factor scores to index early numerical processing (rapid digit naming, number identification, and numerical reasoning) and mathematics (calculation and word problems).
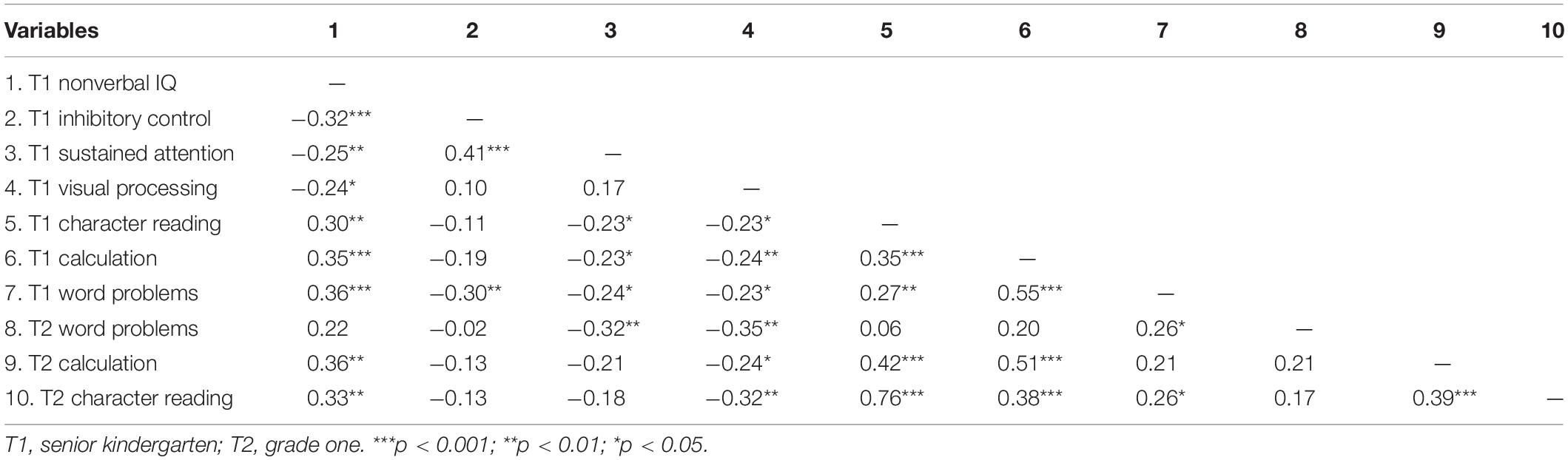
Table 2 displays the correlations among visual processing and general cognitive abilities at kindergarten, character reading, and mathematics at kindergarten and grade one. Considering that the reaction time and accuracy in the sustained attention task were correlated with each other (trade-off effect: r = −0.33, p < 0.01), we performed a formula S = RT × (1 + 2 × error) to correct the result, in which RT stands for correct reaction time in the hit condition and error indicates the false negative alarm rate (children did not respond when the target appeared, when they should have). The formula has been widely used before to handle trade-off measures (e.g., Lyons et al., 2014). Similarly, for inhibitory control, the Flanker task also demonstrated a trade-off effect (r = −0.31, p < 0.01), and we employed the same formula dealing with the problem. In the Flanker task, RT and error were from the incongruent condition. Table 2 demonstrates that visual processing was significantly related with mathematics and character reading either at senior kindergarten or at grade one.
Table 2. Correlations among all variables at kindergarten and grade one.
Regression Analyses
To further investigate how visual processing was associated with character reading, we performed hierarchical regression for character reading and mathematics, controlling for gender, age, nonverbal IQ, sustained attention, and inhibitory control. R2, R2 change, standardized beta coefficients, and t scores are reported in Table 3 for character reading and mathematics, respectively. In order to estimate the risk of multicollinearity, we checked the tolerance and the variance inflation factor (VIF) values of the predictors calculationally. In this analysis, the tolerance values were all larger than 0.50, and VIF values were all smaller than 2.0, indicating that there was no multicollinearity in the current analysis. Table 3 demonstrates that, when gender and age were statistically controlled, general cognitive factors, including nonverbal IQ, attention, and inhibitory control, significantly explained 18% of the variance in character reading. Interestingly, after initial character reading at senior kindergarten was further controlled, visual processing still significantly explained 4% of the variance in character reading. As regards mathematics, we conducted univariate hierarchical regression analysis to see whether visual processing would account for it. Table 3 indicates that, when gender and age were statistically controlled, general cognitive factors significantly explained 17% of the variance in mathematics. Interestingly, after initial mathematics at senior kindergarten was further controlled, visual processing still significantly explained 7% of the variance in mathematics. The tolerance values were all larger than 0.54, and VIF values were all smaller than 1.80, indicating that there was no multicollinearity in the current analysis. We also controlled metalinguistic awareness in order to spell out their effects (see Supplementary Table S1).
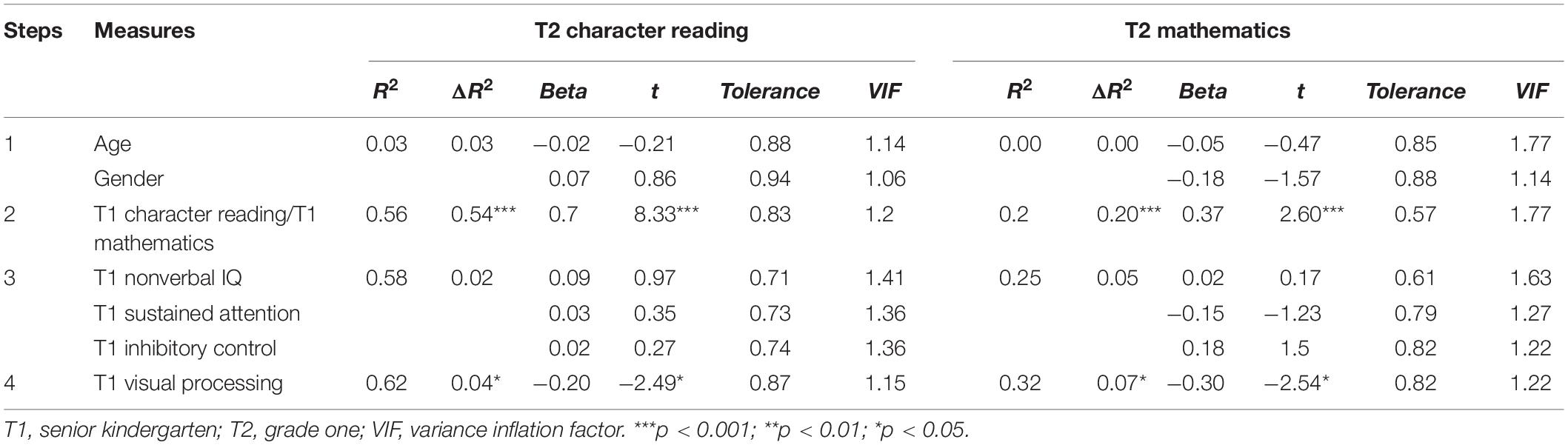
Table 3. Hierarchical regression analysis of first grade character reading with visual processing, general cognitive abilities, and initial character reading controlled.
Overall, after all general cognitive factors, age, gender, and initial reading and mathematics performance were controlled, visual processing at senior kindergarten still significantly accounted for the variance in character reading and mathematics at grade one.
Discussion
In the present study, we investigated whether and how visual processing predicted young Chinese children’s reading and mathematics performance, including character reading and mathematics abilities. To achieve this goal, we tested kindergarten children’s visual processing, reading, and mathematics performance, and followed up 14 months later. We found that visual processing was concurrently and longitudinally associated with character reading and early mathematics. To rule out possible confounding factors, we also assessed three important cognitive skills, including intelligence, attention, and inhibitory control. Results showed that visual processing still significantly explained variance in future character reading and mathematics abilities, even when children’s age, gender, these general cognitive abilities, initial reading, and initial mathematics performance were controlled for.
Visual processing is a required step for discriminating letters, characters, symbols, and written numbers (McBride-Chang et al., 2005; Meng et al., 2011). As prior work showed, all visual reading and mathematics development should involve basic visual processing (Zhou et al., 2015). In line with the arguments from alphabetic languages (Franceschini et al., 2012, 2013), to recognize characters, Chinese children need to develop a visual strategy of discriminating the visual graphic features and their relations within the character (Ho and Bryant, 1997). For example, the Chinese characters “±” (means “earth”) and “±” (means “solider”) are quite similar visually. When seeing the two characters clearly, one will visually notice that their difference lies in whether the upper horizontal line in the characters is longer than the lower horizontal line. Many children with reading disabilities often show difficulties in distinguishing one from the other. For example, the spatial orientation difference threshold between the two straight lines is higher in children with dyslexia than in typically developed children (O’Neill and Stanley, 1976). This is also consistent with English studies that showed that the left fusiform visual word form area explained the maximum effect of mirror priming (e.g., “b” vs. “d”) in children with reading disabilities (Dehaene et al., 2010).
Furthermore, visual processing shapes the way visual information is extracted from print (Aghababian and Nazir, 2000). Specifically, visual processing might be important for Chinese children to reduce an indecipherable character into simple character radicals (McBride-Chang et al., 2005; Luo et al., 2013). For example, the Chinese character “
” (means “win”) can be visually divided into five Chinese characters (“
”), making it easier for young children to recognize the character. As we have argued, the Chinese writing system is heavily orthographically based, which is different from English, which is phonologically based (e.g., Chen and Kao, 2002; Shu et al., 2003; Hsiao and Shillcock, 2006). Chinese children with higher visual processing exhibit greater ease at acquiring the visual–orthographic knowledge in characters, which in turn facilitates character recognition (Siok and Fletcher, 2001). In other words, during reading, the quality of the visual–orthographic form mapped onto the lexical representation could affect children’s performance (Perfetti and Hart, 2002). Although previous literature has indicated conflicting relations of reading and visual processing among children in Taiwan and Hong Kong (e.g., Huang and Hanley, 1995, 1997; Ho, 1997), mainland kindergartners who spoke Mandarin and learned the simplified script usually developed stronger visual discrimination skills than their counterparts in Hong Kong (Peng et al., 2010; Luo et al., 2013) and demonstrated stronger relations of visual processing with Chinese character reading (McBride-Chang et al., 2005).
Similarly, the current findings support that visual processing promotes children’s development of mathematics skills. The present study examined calculation via addition and subtraction and word problems via story problem solving. Visual processing expertise may contribute to gains in these mathematics subskills through the following ways. First, visual processing may influence an individual’s calculation ability through his/her capacity of representing number words and obtaining quantity information (Simon et al., 1998). Supporting evidence is that, when children learn to count objects, they need to distinguish the quantity from the visual features of each object (e.g., color, size). For example, to count apples one by one, young children need to visually figure out the corresponding quantity of each apple setting aside the volume or color of each apple. Second, visual perception reflects children’s understanding, recognizing, and interpreting relationships between object stimuli. In order to fulfill the orientation discrimination of the present study, children needed to distinguish the location of each segment and the spatial relations between the two segments; this is similar to solving math problems orally presented, and children needed to represent the addition and subtraction problem and manipulate the numerals mentally. Third, visual processing is particularly important in accurately distinguishing quantities and representing relations between number words mentally (Dehaene and Cohen, 1995; Kulp et al., 2004). In addition to calculation, word problem solving requires children to mentally present the numerals and quantity information to figure out which of the two numbers is larger. Visual processing might therefore support the representations of quantity information via a mental number line (Dehaene, 2003) and might help to form and hold mental representations of the numerals (Tartre, 1990; Geary et al., 1993; Robert and LeFevre, 2013). Consistent with this claim, Gunderson et al. (2012) revealed that children’s visual–spatial skill predicted their performance on calculation and that this relation was mediated by children’s knowledge of linear number line estimation. In sum, visual processing is necessary for young children to mentally represent number words from calculation problems and story problems, do calculations mentally, and compare quantities in story problems mentally (Fennema and Tartre, 1985; Assel et al., 2003; Landerl et al., 2004; Vaidya, 2004; Sigmundsson et al., 2010).
The current study demonstrated insignificant correlations between inhibitory control and reading and early mathematics (except for word problems at kindergarten). This might be because the cognitive workload of our assessments was relatively low. For example, we assessed single character reading rather than long words, and simple addition rather than four arithmetic operations. More reading and mathematics measures should be included to investigate how measure types might moderate the associations of visual processing with reading and mathematics. In addition, although the results provide relatively straightforward evidence for the association among visual processing, character reading, and mathematics performance, intervention studies to investigate the causality of visual processing in reading and mathematics are still needed. Moreover, the orientation discrimination task administered in this study is only one kind of visual discrimination, but visual processing demonstrates various abilities to identify features and details of stimuli, including shape, orientation (the present study), color, and size (Ho and Bryant, 1999; Kulp et al., 2004; Rohde, 2008). Therefore, it is important for future studies to include various visual processing components and test their associations with Chinese character reading. Finally, longitudinal studies examining visual processing, reading, and mathematics at multiple time points are needed given that there might be a bidirectional association between visual processing and reading acquisition in the early years (e.g., Goswami, 2015). Reading Chinese might even show a stronger effect on visual skills than reading some alphabetic languages (Demetriou et al., 2005). The association of visual processing with mathematics was similar to that with reading (e.g., Sigmundsson et al., 2010).
Altogether, this research is among the first to follow Chinese children from kindergarten to first grade and to investigate whether and to what extent visual processing predicted later reading and mathematics competence. Particularly, we included both Chinese character reading and early mathematics, which are the most important foundations of children’s later academic success. Our findings demonstrated that visual processing served as a domain-general indicator that contributed to organizing information to help solve different types of academic problems, in spite of nonverbal intelligence, inhibitory control, and attention. The present results showed potential implications for education and practice. Specifically, educators, psychologists, and parents should pay more attention to how visual processing might affect children’s early learning (Basch, 2011). For example, standardized assessments of visual processing can be developed in the future to screen children at risk of reading and mathematics difficulties. Moreover, systematic visual processing training, including spatial relations, visual perceptions, and orientation discriminations, along with Chinese radicals and written numbers, might be conducted among children to assist them in learning characters and early mathematics knowledge.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the Ethics Committee of School of Psychology, Peking University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
XY designed the experiments, collected, and analyzed the data, and wrote the manuscript. XM designed the experiments interface, discussed the data analyses, and commented on the manuscript. Both authors gave the final approval of the version to be published.
Funding
This work was supported by grants from the National Natural Science Foundation of China (NSFC: 31971039 and 81371206).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We sincerely appreciate all children, parents, and the kindergartens for their participation and cooperation in our study.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2020.00462/full#supplementary-material
References
Aghababian, V., and Nazir, T. A. (2000). Developing normal reading skills: aspects of the visual processes underlying word recognition. J. Exp. Child Psychol. 76, 123–150. doi: 10.1006/jecp.1999.2540
Amitay, S., Ben Yehudah, G., Banai, K., and Ahissar, M. (2002). Disabled readers suffer from visual and auditory impairments but not from a specific magnocellular deficit. Brain 125, 2272–2285. doi: 10.1093/brain/awf231
Assel, M. A., Landry, S. H., Swank, P., Smith, K. E., and Steelman, L. M. (2003). Precursors to mathematical skills: Examining the roles of visual-spatial skills, executive processes, and parenting factors. Appli. Dev. Sci. 7, 27–38. doi: 10.1207/S1532480XADS0701_3
Barrett, T. C. (1965). The relationship between measures of pre-reading visual discrimination and first grade reading achievement: A review of the literature. Read. Res. Q. 1, 51–76. doi: 10.2307/746973
Basch, C. E. (2011). Vision and the achievement gap among urban minority youth. J. Sch. Health 81, 599–605. doi: 10.1111/j.1746-1561.2011.00633.x
Boden, C., and Brodeur, D. A. (1999). Visual processing of verbal and nonverbal stimuli in adolescents with reading disabilities. J. Learn. Disabil. 32, 58–71. doi: 10.1177/002221949903200106
Buckley, J., Seery, N., Canty, D., and Gumaelius, L. (2018). Visualization, inductive reasoning, and memory span as components of fluid intelligence: implications for technology education. Int. J. Educ. Res. 90, 64–77. doi: 10.1016/j.ijer.2018.05.007
Chen, M. J., and Yuen, J. C. K. (1991). Effects of pinyin and script type on verbal processing: comparisons of China, Taiwan, and Hong Kong experience. Int. J. Behav. Dev. 14, 429–448. doi: 10.1177/016502549101400405
Chen, X., and Kao, H. S. R. (2002). “Visual–spatial properties and orthographic processing of Chinese characters,” in Cognitive Neuroscience Studies of the Chinese Language, eds H. S. R. Kao, C. Leong, and D. Gao, (Hong Kong: Hong Kong University Press), 175–194.
Chung, K. K. H., McBride-Chang, C., Wong, S. W. L., Cheung, H., Penney, T. B., and Ho, C. S.-H. (2008). The role of visual and auditory temporal processing for Chinese children with developmental dyslexia. Ann. Dyslexia 58:15. doi: 10.1007/s11881-008-0015-4
Cooper, B. R., Moore, J. E., Powers, C. J., Cleveland, M., and Greenberg, M. T. (2014). Patterns of early reading and social skills associated with academic success in elementary school. Early Educ. Dev. 25, 1248–1264. doi: 10.1080/10409289.2014.932236
Corballis, M. C., Macadie, L., Crotty, A., and Beale, I. L. (1985). The naming of disoriented letters by normal and reading−disabled children. J. Child Psychol. Psychiatry 26, 929–938. doi: 10.1111/j.1469-7610.1985.tb00607.x
Cui, J., Zhang, Y., Wan, S., Chen, C., Zeng, J., and Zhou, X. (2019). Visual form perception is fundamental for both reading comprehension and arithmetic computation. Cognition 189, 141–154. doi: 10.1016/j.cognition.2019.03.014
Dehaene, S. (1992). Varieties of numerical abilities. Cognition 44, 1–42. doi: 10.1016/0010-0277(92)90049-N
Dehaene, S. (2003). The neural basis of the Weber–Fechner law: a logarithmic mental number line. Trends Cogn. Sci. 7, 145–147. doi: 10.1016/S1364-6613(03)00055-X
Dehaene, S., and Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathemat. Cogn. 1, 83–120.
Dehaene, S., Nakamura, K., Jobert, A., Kuroki, C., Ogawa, S., and Cohen, L. (2010). Why do children make mirror errors in reading? Neural correlates of mirror invariance in the visual word form area. Neuroimage 49, 1837–1848. doi: 10.1016/j.neuroimage.2009.09.024
Demetriou, A., Kui, Z. X., Spanoudis, G., Christou, C., Kyriakides, L., and Platsidou, M. (2005). The architecture, dynamics, and development of mental processing: greek, Chinese, or universal? Intelligence 33, 109–141. doi: 10.1016/j.intell.2004.10.003
Ding, D., Liu, X. P., Li, L., Zhao, H., Yao, J., and Tian, T. (2002). A study on Features of being literate in reading disabled children. Psychol. Dev. Educ. 18, 64–67. [
. (2002). 
, 18(2), 64-67.].
Emmons, P., and Anderson, L. (2005). Understanding Sensory Dysfunction: Learning, Development and Sensory Dysfunction in Autism Spectrum Disorders, ADHD, Learning Disabilities and Bipolar Disorder. London: Jessica Kingsley Publishers.
Fennema, E., and Tartre, L. A. (1985). The use of spatial visualization in mathematics by girls and boys. J. Res. Mathemat. Educ. 16, 184–206. doi: 10.2307/748393
Fischer, B., Hartnegg, K., and Mokler, A. (2000). Dynamic visual perception of dyslexic children. Perception 29, 523–530. doi: 10.1068/p2666b
Franceschini, S., Gori, S., Ruffino, M., Pedrolli, K., and Facoetti, A. (2012). A causal link between visual spatial attention and reading acquisition. Curr. Biol. 22, 814–819. doi: 10.1016/j.cub.2012.03.013
Franceschini, S., Gori, S., Ruffino, M., Viola, S., Molteni, M., and Facoetti, A. (2013). Action video games make dyslexic children read better. Curr. Biol. 23, 462–466. doi: 10.1016/j.cub.2013.01.044
Frick, A. (2018). Spatial transformation abilities and their relation to later mathematics performance. Psychol. Res. 83, 1465–1484. doi: 10.1007/s00426-018-1008-5
Gardner-Neblett, N., DeCoster, J., and Hamre, B. K. (2014). Linking preschool language and sustained attention with adolescent achievement through classroom self-reliance. J. Appl. Dev. Psychol. 35, 457–467. doi: 10.1016/j.appdev.2014.09.003
Garon-Carrier, G., Boivin, M., Lemelin, J. P., Kovas, Y., Parent, S., Séguin, J. R., et al. (2018). Early developmental trajectories of number knowledge and math achievement from 4 to 10 years: Low-persistent profile and early-life predictors. J. Sch. Psychol. 68, 84–98. doi: 10.1016/j.jsp.2018.02.004
Geary, D. C. (2004). Mathematics and learning disabilities. J. Learn. Disabil. 37, 4–15. doi: 10.1177/00222194040370010201
Geary, D. C., Bow-Thomas, C. C., Fan, L., and Siegler, R. S. (1993). Even before formal instruction, Chinese children outperform American children in mental addition. Cogn. Dev. 8, 517–529. doi: 10.1016/S0885-2014(05)80007-3
Goswami, U. (2015). Sensory theories of developmental dyslexia: three challenges for research. Nat. Rev. Neurosci. 16, 43–54. doi: 10.1038/nrn3836
Guilford, J. P. (1936). The determination of item difficulty when chance success is a factor. Psychometrika 1, 259–264. doi: 10.1007/BF02287877
Gunderson, E. A., Ramirez, G., Beilock, S. L., and Levine, S. C. (2012). The relation between spatial skill and early number knowledge: the role of the linear number line. Dev. Psychol. 48, 1229–1241. doi: 10.1037/a0027433
Ho, C. S., and Bryant, P. (1999). Different visual skills are important in learning to read English and Chinese. Educ. Child Psychol. 16, 4–14. doi: 10.1177/0022219409345016
Ho, C. S.-H. (1997). The importance of phonological awareness and verbal short-term memory to children’s success in learning to read Chinese. Psychol. Int. J. Psychol. Orient 40, 211–219.
Ho, C. S.-H., and Bryant, P. (1997). Phonological skills are important in learning to read Chinese. Dev. Psychol. 33, 946–951. doi: 10.1037//0012-1649.33.6.946
Hsiao, J. H. W., and Shillcock, R. (2006). Analysis of a Chinese phonetic compound database: implications for orthographic processing. J. Psychol. Res. 35, 405–426. doi: 10.1007/s10936-006-9022-y
Hu, C.-F., and Catts, H. W. (1998). The role of phonological processing in early reading ability: what we can learn from Chinese. Sci. Stud. Reading 2, 55–79. doi: 10.1207/s1532799xssr0201_3
Huang, H. S., and Hanley, J. R. (1995). Phonological awareness and visual skills in learning to read Chinese and English. Cognition 54, 73–98. doi: 10.1016/0010-0277(94)00641-W
Huang, H. S., and Hanley, J. R. (1997). A longitudinal study of phonological awareness, visual skills, and Chinese reading acquisition among first-graders in Taiwan. Int. J. Behav. Dev. 20, 249–268. doi: 10.1080/016502597385324
Jordan, N. C., Glutting, J., and Ramineni, C. (2010). The importance of number sense to mathematics achievement in first and third grades. Learn. Individ. Diff. 20, 82–88. doi: 10.1016/j.lindif.2009.07.004
Jordan, N. C., Kaplan, D., Ramineni, C., and Locuniak, M. N. (2009). Early math matters: kindergarten number competence and later mathematics outcomes. Dev. Psychol. 45, 850–867. doi: 10.1037/a0014939
Kavale, K. (1982). Meta-analysis of the relationship between visual perceptual skills and reading achievement. J. Learn. Disabil. 15, 42–51. doi: 10.1177/002221948201500110
Krajewski, K., and Schneider, W. (2009a). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: findings from a four-year longitudinal study. Learn. Instruct. 19, 513–526. doi: 10.1016/j.learninstruc.2008.10.002
Krajewski, K., and Schneider, W. (2009b). Exploring the impact of phonological awareness, visual–spatial working memory, and preschool quantity–number competencies on mathematics achievement in elementary school: findings from a 3-year longitudinal study. J. Exp. Child Psychol. 103, 516–531. doi: 10.1016/j.jecp.2009.03.009
Kulp, M. T., Earley, M. J., Mitchell, G. L., Timmerman, L. M., Frasco, C. S., and Geiger, M. E. (2004). Are visual perceptual skills related to mathematics ability in second through sixth grade children? Focus Learn. Prob. Math. 26, 44–57.
Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8–9-year-old students. Cognition 93, 99–125. doi: 10.1016/j.cognition.2003.11.004
LeFevre, J. A., Fast, L., Skwarchuk, S. L., Smith−Chant, B. L., Bisanz, J., Kamawar, D., et al. (2010). Pathways to mathematics: longitudinal predictors of performance. Child Dev. 81, 1753–1767. doi: 10.1111/j.1467-8624.2010.01508.x
Li, D., Chen, G. P., and Jin, Y. (1989). Combined Raven’s Matrices Test (CRT): Handbook of Chinese (Revised ed.). (in Chinese). Shanghai: East China Normal University Press.
Luo, Y. C., Chen, X., Deacon, S. H., Zhang, J., and Yin, L. (2013). The role of visual processing in learning to read Chinese characters. Sci. Stud. Read. 17, 22–40. doi: 10.1080/10888438.2012.689790
Lyons, I. M., Price, G. R., Vaessen, A., Blomert, L., and Ansari, D. (2014). Numerical predictors of arithmetic success in grades 1–6. Dev. Sci. 17, 714–726. doi: 10.1111/desc.12152
Martens, V. E., and de Jong, P. F. (2006). The effect of visual word features on the acquisition of orthographic knowledge. J. Exp. Child Psychol. 93, 337–356. doi: 10.1016/j.jecp.2005.11.003
McBride, C. (2016). Is Chinese special? Four aspects of Chinese literacy acquisition that might distinguish learning Chinese from learning alphabetic orthographies. Educ. Psychol. Rev. 28, 523–549. doi: 10.1007/s10648-015-9318-2
McBride-Chang, C., Chow, B. W., Zhong, Y., Burgess, S., and Hayward, W. G. (2005). Chinese character acquisition and visual skills in two Chinese scripts. Read. Writ. 18, 99–128. doi: 10.1007/s11145-004-7343-5
McBride-Chang, C., and Kail, R. V. (2002). Cross-cultural similarities in the predictors of reading acquisition. Child Dev. 73, 1392–1407. doi: 10.1111/1467-8624.00479
McGrew, K. S. (2009). CHC theory and the human cognitive abilities project: standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37, 1–10. doi: 10.1016/j.intell.2008.08.004
Meng, X., Cheng-Lai, A., Zeng, B., Stein, J. F., and Zhou, X. (2011). Dynamic visual perception and reading development in Chinese school children. Ann. Dyslex. 61, 161–176. doi: 10.1007/s11881-010-0049-2
Miller, E. K., and Cohen, J. D. (2001). An integrative theory of prefrontal cortex function. Ann. Rev. Neurosci. 24, 167–202. doi: 10.1146/annurev.neuro.24.1.167
O’hare, A. E., Brown, J. K., and Aitken, K. (1991). Dyscalculia in children. Dev. Med. Child Neurol. 33, 356–361.
Olson, R., and Datta, H. (2002). Visual-temporal processing in reading-disabled and normal twins. Read. Writ. 15, 127–149. doi: 10.1023/A:1013872422108
O’Neill, G., and Stanley, G. (1976). Visual processing of straight lines in dyslexic and normal children. Br. J. Educ. Psychol. 46, 323–327. doi: 10.1111/j.2044-8279.1976.tb02329.x
Peng, G., Minett, J. W., and Wang, W. S. Y. (2010). Cultural background influences the liminal perception of Chinese characters: an ERP study. J. Neuroling. 23, 416–426. doi: 10.1016/j.jneuroling.2010.03.004
Perfetti, C. A., and Hart, L. (2002). “The lexical quality hypothesis,” in Precursors of Functional Literacy, eds L. Vehoeven, C. Elbro, and P. Reitsma, (Amsterdam: John Benjamins), 67–86.
Ramus, F., Rosen, S., Dakin, S. C., Day, B. L., Castellote, J. M., White, S., et al. (2003). Theories of developmental dyslexia: Insights from a multiple case study of dyslexic adults. Brain 126, 841–865. doi: 10.1093/brain/awg076
Ridderinkhof, K. R., and van der Molen, M. W. (1995). A psychophysiological analysis of developmental differences in the ability to resist interference. Child Dev. 66, 1040–1056. doi: 10.1111/j.1467-8624.1995.tb00921.x
Rivera, S. M., Reiss, A. L., Eckert, M. A., and Menon, V. (2005). Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cort. 15, 1779–1790. doi: 10.1093/cercor/bhi055
Robert, N. D., and LeFevre, J.-A. (2013). Ending up with less: the role of working memory in solving simple subtraction problems with positive and negative answers. Res. Math. Edu. 15, 165–176. doi: 10.1080/14794802.2013.797748
Rodic, M., Tikhomirova, T., Kolienko, T., Malykh, S., Bogdanova, O., Zueva, D. Y., et al. (2015). Spatial complexity of character-based writing systems and arithmetic in primary school: a longitudinal study. Front. Psychol. 6:333. doi: 10.3389/fpsyg.2015.00333
Rohde, T. E. (2008). An Examination of How Visual Perception Abilities Influence Mathematics Achievement. (Doctoral. dissertation, Case Western Reserve University, Cleveland, OH).
Rourke, B. P., and Finlayson, M. A. J. (1978). Neuropsychological significance of variations in patterns of academic performance: Verbal and visual-spatial abilities. J. Abnorm. Child Psychol. 6, 121–133. doi: 10.1007/bf00915788
Shu, H., Chen, X., Anderson, R. C., Wu, N., and Xuan, Y. (2003). Properties of school Chinese: implications for learning to read. Child Dev. 74, 27–47. doi: 10.1111/1467-8624.00519
Sigmundsson, H., Anholt, S. K., and Talcott, J. B. (2010). Are poor mathematics skills associated with visual deficits in temporal processing? Neurosci. Lett. 469, 248–250. doi: 10.1016/j.neulet.2009.12.005
Silver, A. A., and Hagin, R. A. (1970). “Visual perception in children with reading disabilities,” in Early Experience and Visual Information Processing in Perceptual and Reading Disorders, ed. F. A. Young, (Washington, D.C: National Academy of Sciences), 445–456.
Simon, T. J., Peterson, S., Patel, G., and Sathian, K. (1998). Do the magnocellular and parvocellular visual pathways contribute differentially to subitizing and counting? Percept. Psychophys. 60, 451–464. doi: 10.3758/BF03206866
Siok, W. T., and Fletcher, P. (2001). The role of phonological awareness and Visual-orthographic skills in Chinese reading acquisition. Dev. Psychol. 37, 886–899. doi: 10.1037/0012-1649.37.6.886
Stanovich, K. E. (1992). Developmental reading disorder. Dev. Dis. Diagn. Criteria Clin. Assess. 173–208.
Szwed, M., Qiao, E., Jobert, A., Dehaene, S., and Cohen, L. (2014). Effects of literacy in early visual and occipitotemporal areas of Chinese and French readers. J. Cogn. Neurosci. 26, 459–475. doi: 10.1162/jocn_a_00499
Talcott, J. B., Witton, C., McLean, M. F., Hansen, P. C., Rees, A., Green, G. G., et al. (2000). Dynamic sensory sensitivity and children’s word decoding skills. Proc. Natl. Acad. Sci. U.S.A. 97, 2952–2957. doi: 10.1073/pnas.040546597
Tartre, L. A. (1990). Spatial orientation skill and mathematical problem solving. J. Res. Math. Educ. 21, 216–229. doi: 10.2307/749375
Tosto, M. G., Hanscombe, K. B., Haworth, C. M. A., Davis, O. S. P., Petrill, S. A., Dale, P. S., et al. (2014). Why do spatial abilities predict mathematical performance? Dev. Sci. 17, 462–470. doi: 10.1111/desc.12138
Visser, T. A., Boden, C., and Giaschi, D. E. (2004). Children with dyslexia: evidence for visual attention deficits in perception of rapid sequences of objects. Vis. Res. 44, 2521–2535. doi: 10.1016/j.visres.2004.05.010
Wang, X. L., and Tao, B. P. (1996). Chinese Character Recognition Test Battery and Assessment Scale for Primary School Children, Chap. Shanghai. Shanghai Education Press.
Wang, Z., Cheng-Lai, A., Song, Y., Cutting, L., Jiang, Y., Lin, O., et al. (2014). A perceptual learning deficit in Chinese developmental dyslexia as revealed by visual texture discrimination training. Dyslexia 20, 280–296. doi: 10.1002/dys.1475
Wei, W., Lu, H., Zhao, H., Chen, C., Dong, Q., and Zhou, X. (2012). Gender differences in children’s mathematics performance are accounted for by gender differences in language abilities. Psychol. Sci. 32, 320–330. doi: 10.1177/0956797611427168
Willows, D. M., Kruk, R., and Corcos, E. (2012). Visual Processes in Reading and Reading Disabilities. Abingdon: Routledge.
Yang, L. Y., Guo, J. P., Richman, L. C., Schmidt, F. L., Gerken, K. C., and Ding, Y. (2013). Visual skills and Chinese reading acquisition: a meta-analysis of correlation evidence. Educ. Psychol. Rev. 25, 115–143. doi: 10.1007/s10648-013-9217-3
Yang, X., Chung, K. K. H., and McBride, C. (2019a). Longitudinal contributions of executive functioning and visual-spatial skills to mathematics learning in young Chinese children. Educ. Psychol. 39, 678–704. doi: 10.1080/01443410.2018.1546831
Yang, X., McBride, C., Ho, C. S. H., and Chung, K. K. H. (2019b). Longitudinal associations of phonological processing skills, Chinese word reading, and arithmetic. Read. Writ. 1–21. doi: 10.1007/s11145-019-09998-9
Yang, X., Peng, P., and Meng, X. (2019c). How do metalinguistic awareness, working memory, reasoning, and inhibition contribute to Chinese character reading of kindergarten children? Inf. Child Dev. 28:e2122. doi: 10.1002/icd.2122
Yilmaz, H. B. (2009). On the development and measurement of spatial ability. Int. Electron. J. Element. Educ. 1, 83–96.
Zhang, X. (2016). Linking language, visual-spatial, and executive function skills to number competence in very young Chinese children. Early Child. Res. Q. 36, 178–189. doi: 10.1016/j.ecresq.2015.12.010
Zhang, X., Koponen, T., Räsänen, P., Aunola, K., Lerkkanen, M. K., and Nurmi, J. E. (2014). Linguistic and spatial skills predict early arithmetic development via counting sequence knowledge. Child Dev. 85, 1091–1107. doi: 10.1111/cdev.12158
Zhang, X., and Lin, D. (2015). Pathways to arithmetic: the role of visual-spatial and language skills in written arithmetic, arithmetic word problems, and nonsymbolic arithmetic. Contem. Educ. Psychol. 41, 188–197. doi: 10.1016/j.cedpsych.2015.01.005
Zhang, X., Räsänen, P., Koponen, T., Aunola, K., Lerkkanen, M. K., and Nurmi, J. E. (2017). Knowing, applying, and reasoning about arithmetic: roles of domain-general and numerical skills in multiple domains of arithmetic learning. Dev. Psychol. 53, 2304–2318. doi: 10.1037/dev0000432
Keywords: visual processing, Chinese reading, mathematics performance, kindergarten children, longitudinal study
Citation: Yang X and Meng X (2020) Visual Processing Matters in Chinese Reading Acquisition and Early Mathematics. Front. Psychol. 11:462. doi: 10.3389/fpsyg.2020.00462
Received: 27 September 2019; Accepted: 27 February 2020;
Published: 01 April 2020.
Edited by:
Duo Liu, The Education University of Hong Kong, Hong KongReviewed by:
Li Yin, Tsinghua University, ChinaWilliam Choi, The Education University of Hong Kong, Hong Kong
Copyright © 2020 Yang and Meng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiangzhi Meng, bWVuZ3h6aEBwa3UuZWR1LmNu