
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Psychol. , 03 February 2012
Sec. Perception Science
Volume 3 - 2012 | https://doi.org/10.3389/fpsyg.2012.00023
 Cyril R. Pernet1* and Pascal Belin2
Cyril R. Pernet1* and Pascal Belin2
Voice gender perception can be thought of as a mixture of low-level perceptual feature extraction and higher-level cognitive processes. Although it seems apparent that voice gender perception would rely on low-level pitch analysis, many lines of research suggest that this is not the case. Indeed, voice gender perception has been shown to rely on timbre perception and to be categorical, i.e., to depend on accessing a gender model or representation. Here, we used a unique combination of acoustic stimulus manipulation and mathematical modeling of human categorization performances to determine the relative contribution of pitch and timbre to this process. Contrary to the idea that voice gender perception relies on timber only, we demonstrate that voice gender categorization can be performed using pitch only but more importantly that pitch is used only when timber information is ambiguous (i.e., for more androgynous voices).
How humans categorize the world is a fundamental question in cognitive sciences (Murphy, 2004). Of particular interest is the categorization of socially and culturally relevant stimuli such as faces and voices. There is indeed strong social pressure to categorize gender accurately even in conditions of degraded or less than complete sensory input as, e.g., evidenced by our embarrassment when mistaking the gender of an interlocutor over the phone. Fortunately such mistakes are rare as gender is easily and accurately perceived through the voice alone (Whiteside, 1998), even in brief non-speech vocalizations such as laughter or sighs (Childers and Wu, 1991; Wu and Childers, 1991; Kreiman, 1997). In this article, we investigated the ability of human subjects to categorize vocal sounds as male or female.
There is an important sexual dimorphism in the vocal apparatus of male and female adults, affecting both the source and filter aspects of voice production (Titze, 1994). These anatomo-physiological differences result in a number of acoustical differences between the voices of male and female adult speakers and in particular the mean fundamental frequency of phonation (F0) and formant frequencies (Childers and Wu, 1991). The fundamental frequency (related to the perceived pitch) is a variable of sounds that can be easily identified. In general, the fundamental frequency of a sound is inversely proportional to the size of the source, that is, adults males tend to have voices with a low F0 or low pitch, and adult females tend to have voices with a high F0 or high pitch. However, this simple relationship does not always hold. For instance, Rendall et al. (2005) showed that although men, on average, have a larger body-size and lower mean voice F0 and formant frequencies than females, F0 and subjects’ gender cannot be predicted from body-size. Prediction of subjects’ gender is more accurate when considering the vocal track size (Titze, 1994) but again, the intra-subject variability is so large (∼100–200 Hz for males vs. ∼120–350 Hz for females – Titze, 1994) that gender categorization cannot rely on pitch alone. Thus, voice gender categorization is not a straightforward pitch categorization task, but a higher-level auditory cognitive ability, that could be restricted to the sound category of human voices – a “voice cognition” ability (Belin et al., 2004). This voice cognition ability is supported by evidences of the existence of perceptual representation(s) of voice gender in the listener’s brain. Such representations were first investigated behaviorally by means of a selective adaptation paradigm and a synthetic male–female continuum (Mullennix et al., 1995). Recent behavioral adaptations effects (shifts in the male–female labeling function) showed that gender perception is influenced by previously heard voices but not by F0-matched pure tone (Schweinberger et al., 2008).
Another distinct variable responsible for the perceived “quality” of sounds is the timbre, which somehow reflects the mixture of harmonics and their relative height. Indeed, timbre is “the psycho-acoustician’s multidimensional wastebasket category for everything that cannot be qualified as pitch or loudness” (McAdams and Bregman, 1979). Thus, timbre is what allows differentiating two sounds that can have the same perceived pitch and loudness. The ability to perceive gender can therefore be mediated by vocal acoustical properties such as the fundamental frequency of phonation (F0) but also formant values (F1, F2, F3), glottal function, and spectral slope (Coleman, 1976; Klatt and Klatt, 1990; Mullennix et al., 1995; Whiteside, 1998; Hanson and Chuang, 1999; Lavner et al., 2000).
Based on this literature, several hypotheses can be proposed: (1) voice perception compared to other categories should be “special” (Schweinberger et al., 2008); in particular we hypothesized that differences between pairs of stimuli should be enhanced for voices compared to other stimuli with similar pitch and energy but a non-vocal timbre; (2) pitch is not required to perform gender categorization (Titze, 1994), i.e., the perception of differences in pairs of pitch equalized voice stimuli (i.e., with timbre cues alone) should be comparable to that of stimuli in which both pitch and timbre differ; and (3) since pitch is likely to be analyzed when present, pitch should help categorical perception at least for ambiguous stimuli.
Thirty-three subjects (17 females 24.3 ± 4.7 years old, 16 males 26.8 ± 6.8 years old) participated to this study. All subjects were healthy volunteer and did not report known auditory problem.
Subjects had to perform an auditory categorization task on four types of stimuli: bass clarinet/oboe morphed sounds, male/female morphed voices, male/female morphed voices equalized in pitch, male/female morphed voices equalized in timbre.
Male and female stimuli were the average voice of 16 adult speakers uttering the syllables “had,” taken from the database of American-English vowels (Hillenbrand et al., 1995). Averaging, pitch manipulation, and morphing were performed using STRAIGHT (Kawahara, 2003, 2006) running under Matlab®. STRAIGHT performs an instantaneous pitch-adaptive spectral smoothing for separation of source from filter (spectral distribution) contributions to the signal. Anchor points, i.e., time–frequency landmarks, were identified in each individual sound based on easily recognizable features of the spectrograms. Temporal anchors were defined as the onset, offset, and initial burst of the sounds. Spectro-temporal anchors were the first and second formants at onset of phonation, onset of formant transition, and end of phonation. Using the temporal landmarks, each continuum was equalized in duration (39.2 ms long, i.e., 17289 data points at 44100 Hz). Morphed stimuli were then generated by re-synthesis based on a linear interpolation of female and male anchor templates and spectrogram level in steps of 10%. We thus obtained a continuum of 11 voices ranging from 100% male (re-synthesized male stimulus) to 100% female (re-synthesized female stimulus) with nine gender-interpolated voices (90% male–10% female; 80% male–20% female; …; 10% male–90% female). It should be noted that the interpolated voices sounded natural, i.e., as if produced by a real human being, because of the independent interpolation and re-synthesis of the source and filter components. A similar approach was used to morph the bass clarinet and oboe. Note that prior morphing, F0 of all four stimuli were manipulated so that male/bass clarinet F0 were equal to 110 Hz and female/clarinet F0 were equal to 220 Hz. This procedure was performed automatically since STRAIGHT separates source from filter.
To create voices with the same pitch, we moved up the F0 of the male stimulus from 110 to 165 Hz whilst moving down the F0 of the female stimulus from 220 to 165 Hz. These two new stimuli were subsequently morphed as describe above, creating a continuum male/female where the pitch (165 Hz) is held constant. Categorization of these stimuli thus relied on timber information only. For the timbre equalized voices, we started from the 50% male 50% female stimulus with the pitch at 165 Hz from the pitch equalized continuum and changed the pitch in both directions: down to 110 Hz and up to 220 Hz. This created a continuum male/female in which the timbre (50% male/50% female) was constant but F0 varied (Figure 1). Categorization of these stimuli thus relied on pitch information only. We further controlled the stimulus space by equating energy levels across all stimuli, i.e., a root mean square normalization of amplitude levels was performed after all stimuli were created.
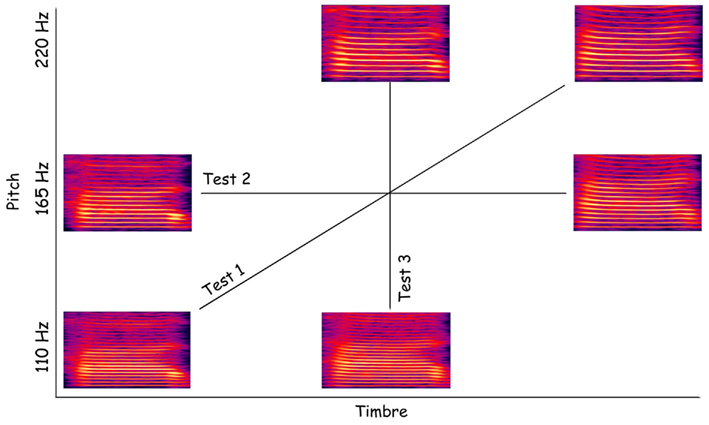
Figure 1. Spectrogram representation of the morphed voices. In the diagonal are represented the original male (lower left) and female (upper right) stimuli. From these stimuli a continuum of nine male/female voices were generated. Similar continua were created along the pitch and timbre dimensions.
Subjects answered by key press and a total of 110 sounds were presented per continuum (10 times 11 sounds). Instructions were as follow: “You will hear a series of sounds. You have to decide for each of these sounds whether it is more male (clarinet) or more female (oboe). Here is an example of each of these two categories [the male/bass clarinet followed by the female/oboe stimuli were played]. If the sounds you will hear is closer to the male (clarinet) sound, answer with the key “A”; if the sound is closer to the female (oboe) sound answer with the key “L.” Do you understand?” If subjects did not understand, examples were replayed (only once) and the last sentence repeated. The order in which the participants categorized continua was counterbalanced across all subjects and stimulus order in each continuum was random.
Three sets of analyses were conducted. The first set analyses aimed at characterizing how subjects perceived each sound along the various continua by testing for differences in the percentage of female/oboe response curves. The second set of analyses aimed at characterizing perceived changes among each pair of sounds along the continua. Finally, the third analysis aimed at testing if voice perception can be seen as a mixture of pitch and timbre rather than timbre alone.
The first set of analyses relied on percentages of female/oboe responses computed at each step of the continua and for each subject. First, to test for possible shifts of the categorical boundaries, two bootstrap MANOVAs were performed on the point of subjective equality (PSE). MANOVAs using Hotelling T2 were used as a mean to estimate repeated measurements and account for sphericity (Rencher, 2002). Bootstrap was performed under H0 by centering the data in each condition and resampling these data 1000 to obtain an empirical F distribution. The p values were computed by comparing the observed F values against this empirical distribution (Wilcox, 2005). Data from each subject were modeled using a cumulative Weibull function and the 50% of female response was estimated. For the first MANOVA, PSE for original male/female sounds vs. bass clarinet/oboe sounds were compared, with the condition (musical instruments/voices) as the repeated measure and the participants’ gender (male/female) as the independent measure. For the second MANOVA, PSE for the different variants of the male/female stimuli were compared, with the condition (original vs. same pitch vs. same timbre) as the repeated measure and the participant’s gender (male/female) as the independent measure. Two similar separate ANOVA were next computed within the generalized linear model framework to compare the whole response curves, i.e., data count across all subjects were modeled using a binomial distribution and a logit link function. The model included the conditions and the participant’s gender as dummy variables and the continuum (1–11) as a continuous regressor. Parameters were fitted using a weighted least square with the weights being the inverse of the variance computed across all subjects for each condition and steps along the continua. A restricted parameterized approach (i.e., full rank design matrix) was used such as effects were estimated using a t-test on the regression parameters. Finally, reaction times (RTs) were also analyzed using a bootstrap MANOVA with the condition and continuum as the repeated measure and the participant gender as the independent variable.
For the second set of analyses, the perceptual distances d′ and response bias c were computed between each stimulus pair of the continua using signal detection theory, i.e., responses were classified as correct or false alarm for each successive pair of stimuli and their z ratio and difference computed (Macmillan and Creelman, 2005). Bootstrap MANOVAs were conducted on d′ and c with the condition and pairs as repeated measures, and participant gender as independent variable. Using d′ is more sensitive than employing percentages because it reflects perceptual distances among stimuli rather than the performance on each stimulus itself. Thus, while differences in percentages indicate an effect of the variable of interest along the continua, differences in d′ allow a direct comparison between perceptual and physical distances. For all analyses (first and second set), post hoc tests were performed using bootstrap percentile t-tests on the differences (Wilcox, 2005). Effect sizes (i.e., differences) are reported with their 95% confidence intervals adjusted for multiple comparisons. Note that using bootstrap under H0 for the ANOVA, assumption of normality were relaxed whilst post hoc test were performed on differences and were non-parametric.
For the third set of analyses, the perceptual response d′ to original voices were modeled as a function of the timbre and pitch. In specific terms for our experiment, this can be described as:
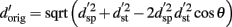
with 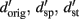 the d prime values for original, same pitch and same timbre voices, and θ the angle between pitch and timbre equalized vectors. The analysis was performed on 23 subjects for whom all of the data followed a sigmoid shape response as identified by the Weibull fit. First, the distribution of original d′ was modeled for each stimulus pair using d′ from pitch equalized and timbre equalized voices and angles between 0° and 180°. Second, the mean squared differences (mean square error, MSE) between modeled and observed data were computed for each pair and each angle. Third, angles that minimized the mean squared error were recorded. At this stage, a percentile bootstrap on the differences between the data and the model for each pairs was computed. This allowed the goodness of fit of the model to be tested. The above steps were then repeated 1000 times resampling (with replacement) subjects, giving bootstrap estimates of best angles of each pair and their dispersion. The median of these best angles were compared using a Friedman ANOVA, effectively testing for differences in the mixture pitch/timbre among pairs.
the d prime values for original, same pitch and same timbre voices, and θ the angle between pitch and timbre equalized vectors. The analysis was performed on 23 subjects for whom all of the data followed a sigmoid shape response as identified by the Weibull fit. First, the distribution of original d′ was modeled for each stimulus pair using d′ from pitch equalized and timbre equalized voices and angles between 0° and 180°. Second, the mean squared differences (mean square error, MSE) between modeled and observed data were computed for each pair and each angle. Third, angles that minimized the mean squared error were recorded. At this stage, a percentile bootstrap on the differences between the data and the model for each pairs was computed. This allowed the goodness of fit of the model to be tested. The above steps were then repeated 1000 times resampling (with replacement) subjects, giving bootstrap estimates of best angles of each pair and their dispersion. The median of these best angles were compared using a Friedman ANOVA, effectively testing for differences in the mixture pitch/timbre among pairs.
Point of subjective equality values were estimated using cumulative Weibull functions for each condition and subject separately. Most of the data showed a good fit (Figures 2–5). However, some subjects had to be removed, as their performances did not allow modeling. Overall, only 12 of the 122 set of responses recorded were discarded: 16.66% of the subjects for the clarinet/oboe condition, 3.12% of the subjects for the male/female condition, 10.34% of the subjects for the male/female equalized in pitch condition, and 10% of the subjects for the male/female equalized in timbre condition.
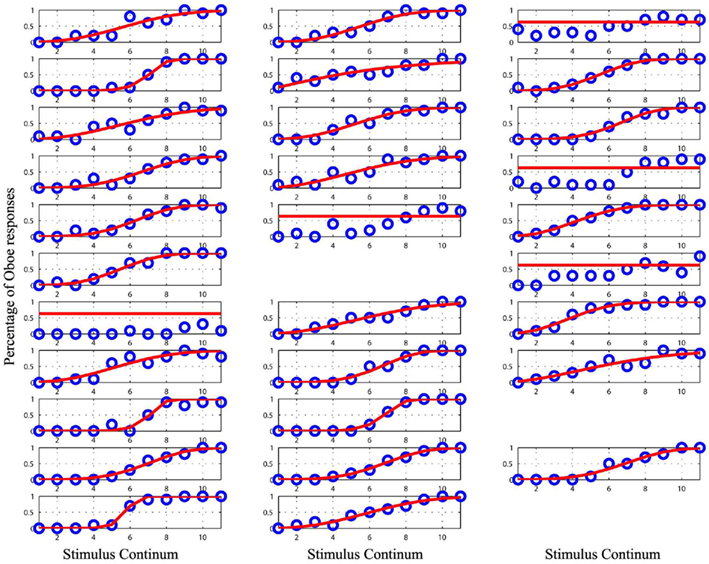
Figure 2. Plot of the raw data (blue circles) and the cumulative Weibull function (red lines) for each subject in the bass clarinet/oboe condition. Empty spaces mark missing data for subject 17, 27, and 33. Data from the subject 3, 12, 14, 18, and 19 were removed from the analyses as they could not be modeled.
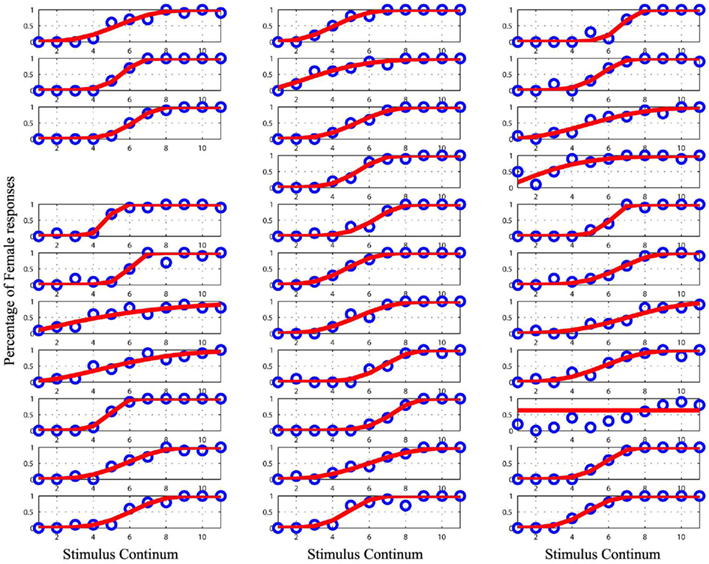
Figure 3. Plot of the raw data (blue circles) and the cumulative Weibull function (red lines) for each subject in the original male/female condition. The empty space marks missing data for subject 10. Data from the subject 27 was removed from the analyses as it could not be modeled.
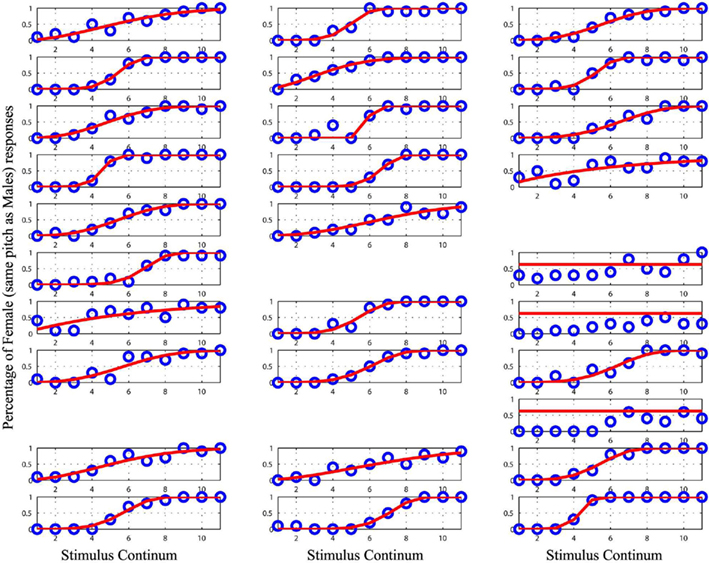
Figure 4. Plot of the raw data (blue circles) and the cumulative Weibull function (red lines) for each subject in the male/female condition with equalized pitch. Empty spaces mark missing data for subject 15, 17, 25, and 26. Data from the subject 18, 21, and 27 were removed from the analyses as they could not be modeled.
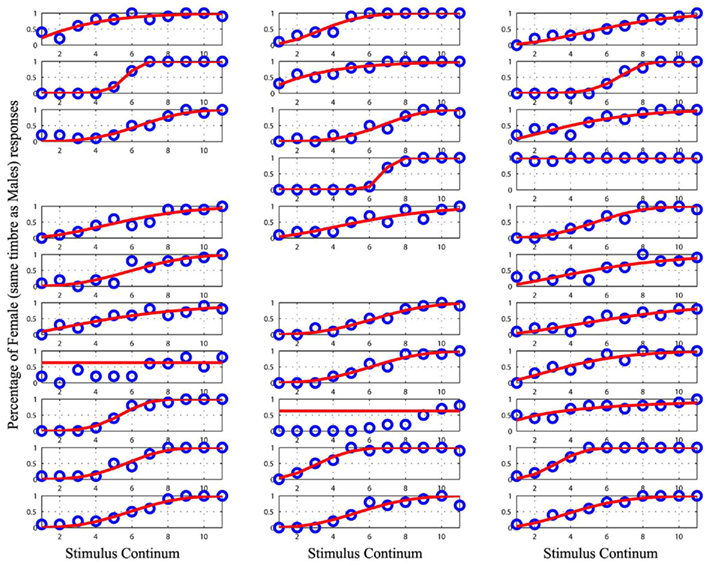
Figure 5. Plot of the raw data (blue circles) and the cumulative Weibull function (red lines) for each subject in the male/female condition with equalized timbre. Empty spaces mark missing data for subject 10 and 17. Data from the subject 1, 12, 22, 26, and 27 were removed from the analyses as they could not be modeled.
Analyses of the PSE between original voice stimuli and musical instruments showed no difference between conditions. However there was a significant difference between male and female participants across conditions (Table 1; Figure 7B): male participant’s mean PSE (PSE = 5.99) was closer to the physical average (point of physical equality = 6) than female participant’s mean PSE, which was shifted toward male/bass clarinet stimuli (PSE = 5.4 – see Table 2 for details).
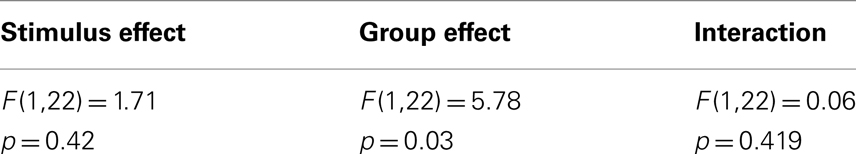
Table 1. Results of the MANOVA on the PSE with the stimulus type (musical instruments/voices) as the repeated measure and the participants’ gender (male/female) as the independent measure.

Table 2. Mean PSE and SD for the bass clarinet and original voices stimuli split by participant’s gender.

Table 3. Results of the MANOVA on the PSE with the stimulus type (the original, pitch equalized, and timbre equalized male/female voices) as the repeated measure and the participants’ gender (male/female) as the independent measure.

Table 4. Mean PSE and SD for the original, pitch equalized, and timbre equalized male/female voice stimuli split by participant’s gender.
Percentages of female/oboe responses were next compared for the whole response curves averaging data across subjects (with the same subjects as above excluded – Figure 7A). Sigmoid shaped mean responses were obtained and subjected to ANOVAs using a logit link function (Figure 6). The comparison of the male/female vs. bass clarinet/oboe revealed, as expected, a significant difference in performance along the continua [t(35) = 59.88, p < 0.0001], but also significant differences between conditions [stimulus type t(35) = 1.62, p = 0.0013] and a significant interaction condition by continuum [t(35) = 3.38, p < 0.0001]. Post hoc bootstrap percentiles t-tests showed that the percentages of oboe vs. female differed for morphs 7 [−15% (−23.3 −5.4)] and 8 [−7.9% (−14.5 −1.6)] only (Figures 7D,E). In addition to the difference between conditions, a main effect of participant gender [t(35) = −3.47, p = 0.03] and an interaction participant gender by continuum [t(35) = 0.68, p = 0.016] were observed. Pair-wise post hoc tests show that female participants had a higher rating than male participants for morphs 1 [100% male/bass clarinet; +2.08% (0.11 4.05)], 7 [60% female/oboe; +12.5% (1.85 23.14)], and 8 [70% female/oboe; +8.75% (2.03 15.46); Figure 7F].
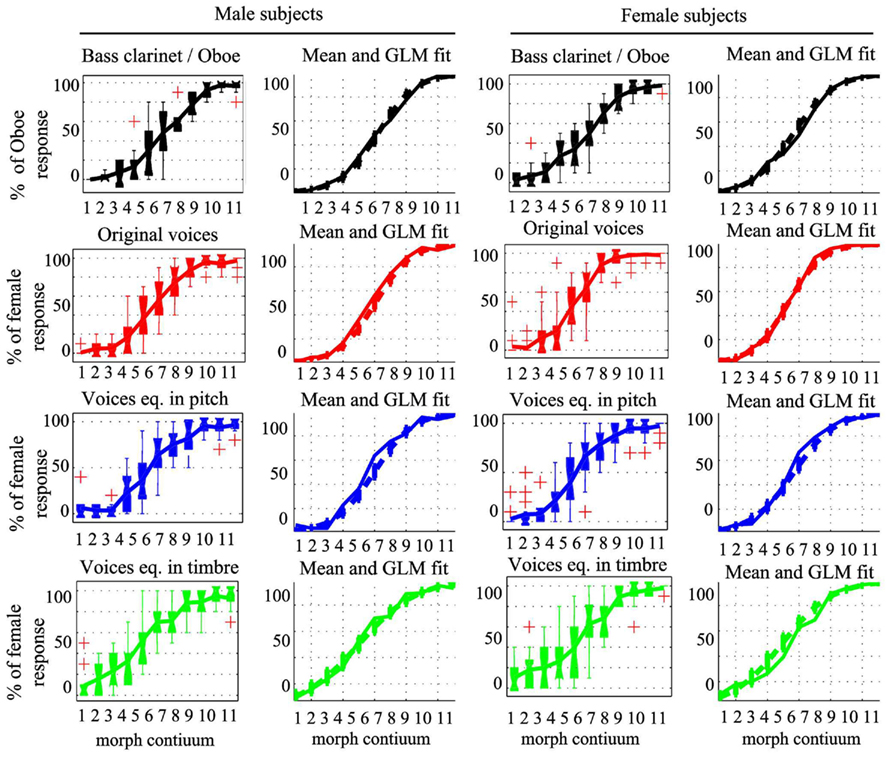
Figure 6. Plot of the observed averaged responses and data fit from the general linear model. Box plots show the median and interquartile range with whiskers extending to the most extreme points. Crosses denote outliers (above 1.5* the 75th percentiles or 1.5*below the 25th percentile). Mean responses in the bass clarinet/oboe (black), original male/female voices (red), male/female voices equalized in pitch (blue), and male/female voices equalized in timber (green) conditions are plotted in solid lines along with the modeled data (dashed lines) and their SE obtained using the GLM with a logit link function.
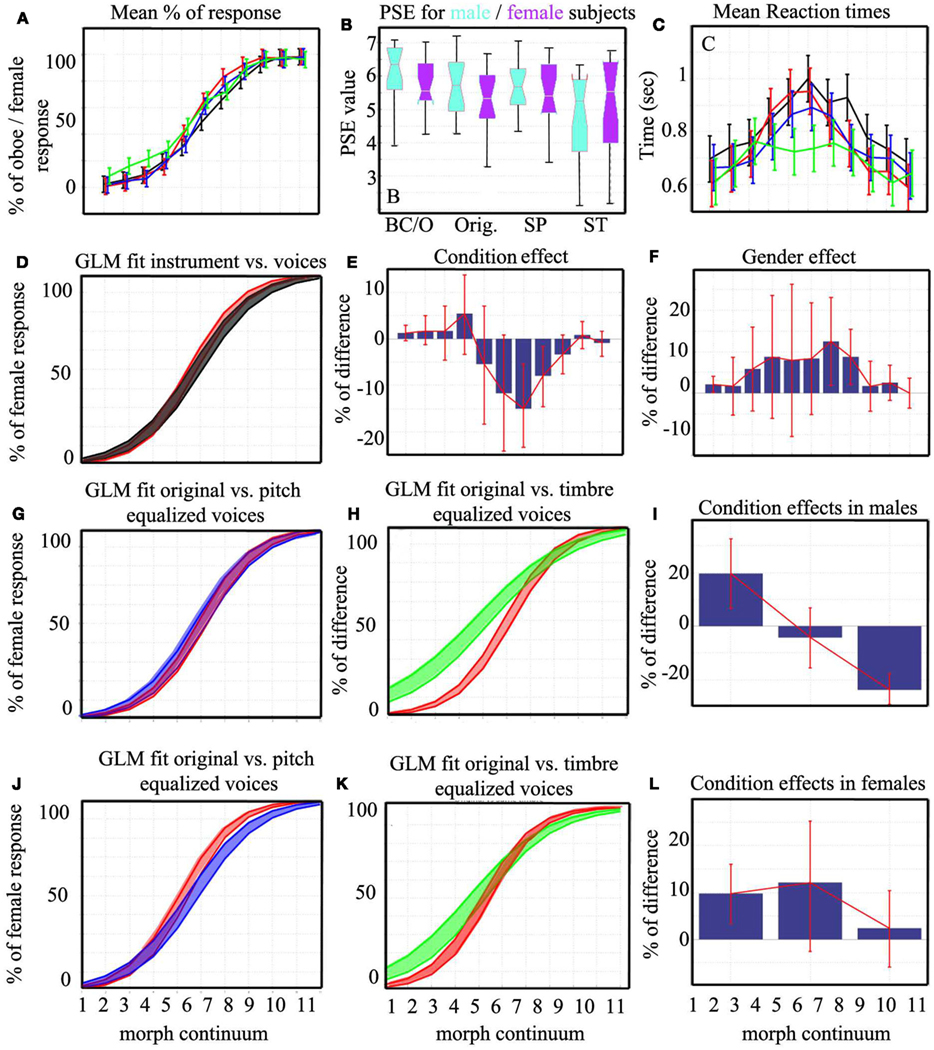
Figure 7. Mean responses and differences between conditions and participants. Displayed at the top are the mean percentages of responses (A), the mean PSE split per participant’s gender and conditions (BC/O, bass clarinet/oboe; Orig., original voices; SP, voices equalized in pitch; ST, voices equalized in timbre) (B), and the mean RTs (C). On the second row is illustrated the logit models for BC/O vs. Orig. voices continua (D) and the differences (BC/O–Orig.) computed at each step (E). The gender difference (female–male) observed over both conditions (BC/O, Orig.) is displayed in (F). The last two rows show the logit models for Orig., SP, and ST voices continua observed in male (G,H) and female (J,K) participants. The corresponding average differences between conditions (Orig.–SP, Orig.–ST, SP–ST) are shown in (I,L). The color code follows Figure 6: bass clarinet/oboe in black, original voices in blue, voices equalized in pitch in red, and voices equalized in timbre in green. The box plot for PSE shows the median and interquartile range with whiskers extending to the most extreme points. Bars represent 95% confidence intervals within subjects for mean responses and mean RTs and across bootstrap differences for pair-wise tests.
Analysis of the corresponding RTs showed a main effect of the continuum [F(1,32) = 6.7, p = 0], no differences between conditions [F(1,21) = 2.03, p = 0.28], and an interaction continuum by condition [F(1,21) = 1.21, p = 0.03] such as RTs differed between conditions but for the first morph only (Figure 7C). There was no effect of participant’s gender on RTs.
Analysis of the PSE among the three voice conditions (original, same pitch, same timbre) showed no effect (Tables 3 and 4). However, analysis of the whole response curves showed a main effect of the continuum [t(54) = 59.75, p < 0.0001] and significant interactions between continuum and conditions (Figure 7A). Overall, original voices led to higher female rating than voices equalized in pitch [+14.6% (4.63 23.54)] but did not differ from voices equalized in timbre [+3.95% (−8.45 14.9)]. Similarly, voices equalized in timber had higher female rating than voices equalized in pitch [+10.68% (6.13 15.5)]. This overall effect varied considerably along the continua, such that timber equalized stimuli were in fact most different with a flatter response curve: higher rating for stimuli 1, 2, 3, 4, and lower for 9, 10, 11. A significant effect of participant’s gender [t(54) = −1.14, p = 0.25] and significant interactions with conditions and continua were also observed. Post hoc tests showed that male participants (Figures 7G–I) followed the main interaction: original voices led to higher female rating than voices equalized in pitch [+19.54% (6.63 32.54)]; original voices did not differ from voices equalized in timbre [−4.18% (−15.5 6.8)]; voices equalized in timber had higher female rating than voices equalized in pitch [+23.72% (17.6 29.18)]. However, for female participants (Figures 7J–L), original voices had a higher female rating for voices equalized in pitch [+9.72% (2.45 15.81)] only [original voices vs. voices equalized in timbre + 12.09% (−1.72 25.9); voices equalized in timber vs. voices equalized in pitch −2.36% (−11.09 6.09)]. As illustrated on Figures 7G,H,J,K these effects observed on the averages are explained by the “flat” response observed for timbre equalized voices.
Analysis of the corresponding RTs showed a main effect of the continuum [F(1,10) = 6.4, p = 0], no main differences between conditions [F(2,22) = 1.003, p = 0.6] but an interaction continuum by conditions [F(2,22) = 3.06, p = 0]. RTs for original voices differed from voices equalized in pitch for the fifth morph only [+97 ms (8.5 182)], whereas they differed from voices equalized in timbre for morphs 4 [+129 ms (23 247)], 5 [+213 ms (123 304)], and 6 [+208 ms (122 296)]. RTs for voices equalized in timbre were also faster than voices equalized in pitch for morphs 5 [+116 ms (23 215)] and 6 [+132 ms (28 229)]. There was no effect of participant’s gender on RTs.
Analysis of d′ values (perceptual distance between successive pairs) showed no differences among conditions [F(1,22) = 1.69, p = 0.35], a significant difference between pairs along the continuum [F(9,14) = 19.62, p = 0], and a significant interaction [F(9,14) = 3.08, p = 0]. However, post hoc tests did not reveal any significant pair-wise differences between conditions or between adjacent pairs.
Analysis of the response bias (tendency to say “oboe or female” for two successive pairs) showed no differences among conditions [F(1,22) = 2.12, p = 0.28], a significant difference between pairs along the continuum [F(9,14) = 124, p = 0], and a significant interaction [F(9,14) = 2.12, p = 0]. Post hoc tests showed that there was a stronger tendency to answer “female” than “oboe” for stimuli located just above the middle of the continuum (pairs 6/7 and 7/8). Independently, a main gender effect was observed [F(1,23) = 9.25, p = 0.02], such that female participants were more biased toward the “oboe/female” response than male participants (+0.16 vs. −0.03).
The analysis of d′ values across voices conditions revealed a main condition effect [F(2,20) = 6.3, p = 0], a significant effect of the continuum [F(9,13) = 24.5, p = 0], and a significant interaction [F(4,18) = 3.9, p = 0]. Subjects had overall similar perceptual thresholds for original (mean d′ = 0.3176) and pitch equalized (mean d′ = 0.3084) stimuli but larger threshold than timbre equalized (mean d′ = 0.2853) stimuli (Figure 8D). The profile of perceptual distances along the continuum was, however, similar for the three types of stimuli with an increase of the thresholds toward the middle (pairs 4/5 and 5/6 being significantly different from the other). A significant three-way interaction with the participant gender was observed [F(1,21) = 10.006, p = 0] and was driven by differences between various pairs along the continuum but without clear pattern between male/female participants.
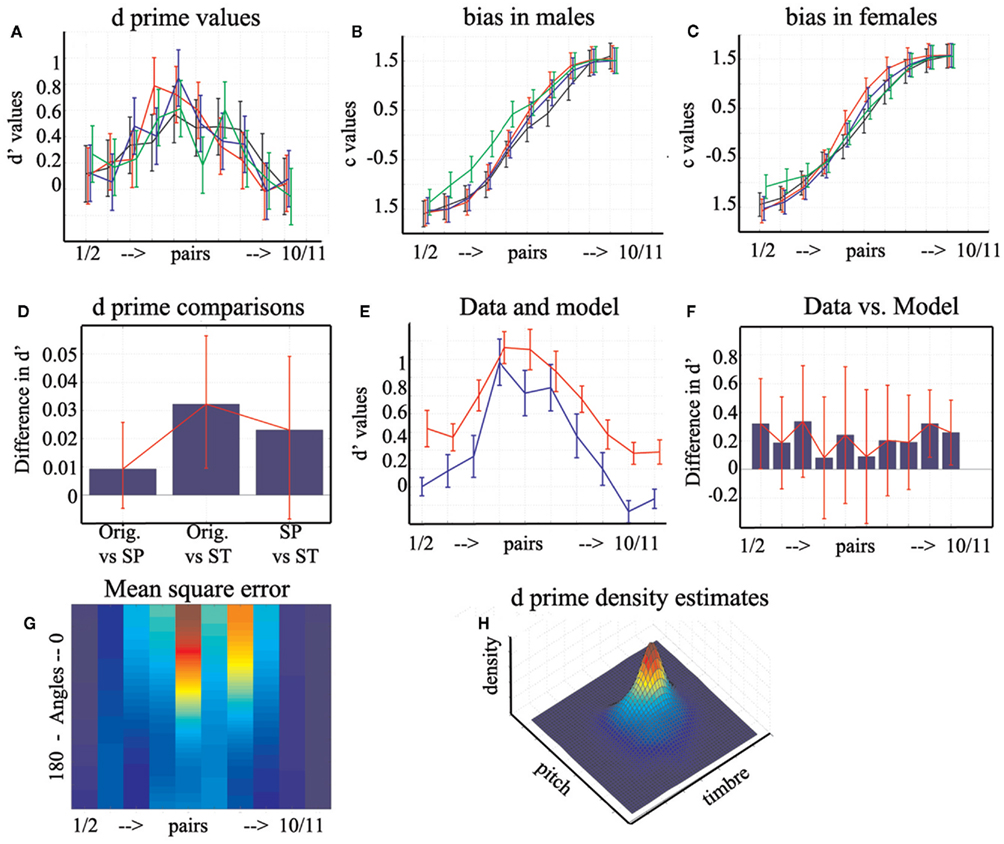
Figure 8. Perceptual distances d′, perceptual bias, and model. Displayed at the top are the original d′ (A) and bias values split by participants gender (B,C) with 95% within subjects CI. Color coding follows Figure 6. Displayed in (D) is the pair-wise comparisons and 95% CI between d ′ values for each condition. In (E), the original d ′ (blue) and modeled (red) values are displayed with their SE. The pair-wise comparisons and 95% CI between the data and model are displayed in (F). Presented at the bottom is the mean square error for each pair across all angles (G) from 0.21 in dark blue to 1.66 in red, along with the 3D representation of the joint kernel density estimates (H). Note that because the axes are at 90° between pitch and timbre, the distribution is not spherical nor at the center of the space. Instead the distribution is elongated mainly in the timbre direction, i.e., high d ′ values observed for ambiguous stimuli are biased toward using more timbre information.
Analysis of the response bias showed no condition effect [F(2,20) = 1.95, p = 0.24], an effect of the continuum [F(9,13) = 307, p = 0], and a significant interaction [F(4,18) = 1.36, p = 0]. A significant three-way interaction with the participant gender was also observed [F(1,21) = 5.86, p = 0.006]. Post hoc tests showed that in male participants original voices did not differ from pitch equalized voices whereas there was a difference for female participants for pairs 7/8 and 8/9. By contrasts, original voices differed from timbre equalized voices for pairs 1, 2, 2/3 for both male and female participants and for pairs 3/4, 4/5 in males, and 7/8 and 8/9 in females (Figures 8B,C).
The model predicts that observed d′ values for original voices are the sum of the d′ values for pitch equalized voice, timbre equalized voices, and their interaction (Figure 8A). After running the model for each possible angle, the best angles (the ones minimizing the MSE – Figure 8G) were selected. The modeled data were then compared with the observed one (Figures 8E,F): pair-wise comparisons for each step show that the model was not different from the data for pairs 2/3, 3/4, 4/5, 5/6, 6/7, 7/8, and 8/9.
To generalize those results, data were resampled 1000 times and the median angles that minimized the MSE were obtained (Table 5). The Friedman ANOVA revealed significant difference among angles [χ(9,8991) = 2582, p = 0]. The two most extreme pairs of male stimuli (1/2 and 2/3) were modeled using high value angles of 139° and 166° demonstrating an anti-correlation between pitch and timbre. These values were significantly different from all other pairs of stimuli (non-overlap of confidence intervals). Pairs 3/4, 4/5, 5/6, 6/7, 7/8, and 8/9 showed small angles between 5° and 47° (correlation pitch, timbre) with identical angles for pairs 3/4 and 7/8 vs. 4/5 and 6/7. Finally, for the pair 9/10 and 10/11, only values of 180° (perfect anti-correlation) and 0° (perfect correlation) modeled the data well, and those angles differed significantly from all others.
All voices and musical instruments elicited sigmoid shape responses typical of categorization tasks. As expected, all middle range stimuli were perceived as ambiguous as indexed by their lower percentage of categorization and slower RTs.
No significance differences were observed in the PSE of the three voice conditions but response curves differed markedly for voices equalized in timbre (i.e., only pitch information was available). Previous studies suggested that voice gender categorization does not depend on pitch perception since there is a large overlap between male and female fundamental phonation frequencies. Here, along with other authors (Coleman, 1976; Klatt and Klatt, 1990; Mullennix et al., 1995; Whiteside, 1998; Hanson and Chuang, 1999; Lavner et al., 2000) we demonstrated that, indeed, voice gender categorization can be performed using timbre information only. Pitch equalized stimuli had an overall percentage of responses lower than the original voices (−14.6%), but the response curves and perceptual distances were similar (−0.009) to those observed with original voices, suggesting that voice gender perception (rather than performance) can operate on timbre information alone. The opposite relationship was observed for pitch information: timbre equalized stimuli showed a flatter response especially for male stimuli but the overall rating did not differ from original voices (+3.95%). By contrast the perceived distances between pairs were significantly lower (−0.3) suggesting that pitch information alone can be used to perform gender categorization tasks, leading to a similar overall performance but with an impaired ability to discriminate voice. The absence of difference between original voice and musical instruments also suggests that this distinction pitch/timbre is general although formal testing is needed to confirm this hypothesis.
The predominant use of timbre information in voice gender categorization was also observed when modeling perceptual thresholds of original voices by a mixture of pitch and timbre. Although the model was not perfect (suggesting other measures are needed to fully characterize subjects performances), it was enough to account for most of the observed data. Of course, the model applies to the data at hand: a single set of averaged male/female voices. It is possible that there was something specific to those voices although averaging should have removed any “personal” features. This model simply described the response to original stimuli as a vector in a 2D space. The bases of this space were the responses observed for pitch equalized and timbre equalized stimuli. If the perception of the voice gender was an independent mixture of pitch and timbre (original = pitch + timbre), the angle between the two bases had to be 90°, i.e., the interaction term in the model equals 0. Since the angle between two vectors also reflects their correlations [r = cos(θ)], angles of 0° (perfect correlation) or 180° (perfect anti-correlation) means that only 1D (pitch or timbre) was used. By contrast, angles below 90° means that both pitch and timbre interact positively, whilst angles above 90° (anti-correlations) means an inhibition between pitch and timbre. Since the MSE for extreme stimuli were almost identical for all angles (Figure 8G) and that pitch equalized stimuli show similar d′ than the original one, we can infer that subjects inhibited the pitch over the timbre information to categorize the most male stimuli (best angles 139°, 166°), and relied only on pitch or timbre information for the most female stimuli (best angles 180° and 0°). Note that for this last result with female stimuli it is not obvious how acoustic information is used since (i) we observed a reversal between pairs 9/10 and 10/11, and (ii) the model performed the worst for those stimuli. In addition, non-linearities observed for females voices when pitch information is present suggest that pitch can interfere (and thus needs to be inhibited) with timbre. One possibility is that differences of pitch in our stimuli were too small for extreme stimuli since we used a linear morph among stimuli but auditory perception follows a log scale (Stevens et al., 1937). Despite this lack of fit of extreme values, it appears possible that for male and female stimuli, voice gender categorization relies primarily on timbre. More importantly, the model shows that voice gender categorization relies on the interaction timbre by pitch; most distinguishable pairs rely heavily on timbre (high density d′ shifted toward high timbre and low pitch values – Figure 8H), and ambiguous stimuli rely on both timbre and pitch (angles between 7° and 47°).
We hypothesized that differences between pairs of stimuli should be enhanced for voices compared to musical instrument with similar pitch and energy, but a non-vocal timbre, since voice perception has been proposed to rely on specific gender representation (Schweinberger et al., 2008) and on dedicated cognitive abilities (Belin et al., 2004). The current results did not support this hypothesis as both response curves and d′ values were similar for both voices and match musical instruments.
We also hypothesized that pitch is not required to perform gender categorization but it is likely to be used at least for ambiguous stimuli. These predictions were confirmed. Altogether, these results show that although pitch is not a useful acoustic feature to predict gender, and gender categorization can be performed using timbre alone (Titze, 1994; Rendall et al., 2005), pitch can be used to perform categorize gender and is used in combination with timbre when categorization is difficult.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Special thanks to Guylaine Belizaire and Jean Pierre Chartrand who collected the data. Cyril R. Pernet is partly funded by the SINAPSE collaboration – http://www.sinapse.ac.uk, a pooling initiative funded by the Scottish Funding Council and the Chief Scientist Office of the Scottish Executive.
Belin, P., Fecteau, S., and Bédard, C. (2004). Thinking the voice: neural correlates of voice perception. Trends Cogn. Sci. 8, 129–135.
Childers, G., and Wu, K. (1991). Gender recognition from speech. Part II: fine analysis. J. Acoust. Soc. Am. 90, 1841–1856.
Coleman, R. O. (1976). A comparison of the contributions of two voice quality characteristics to the perception of maleness and femaleness in the voice. J. Speech Hear. Res. 19, 168–180.
Hanson, H. M., and Chuang, E. S. (1999). Glottal characteristics of male speakers: acoustic correlates and comparison with female data. J. Acoust. Soc. Am. 106, 1064–1077.
Hillenbrand, J., Getty, L. A., Clark, M. J., and Wheeler, K. (1995). Acoustic characteristics of American English vowels. J. Acoust. Soc. Am. 97, 3099–3111.
Kawahara, H. (2003). “Exemplar-based voice quality analysis and control using a high quality auditory morphing procedure based on straight,” in VOQUAL’03, Geneva.
Kawahara, H. (2006). Straight, exploitation of the other aspect of vocoder: perceptually isomorphic decomposition of speech sounds. Acoust. Sci. Technol. 27, 349–353.
Klatt, D. H., and Klatt, L. C. (1990). Analysis, synthesis, and perception of voice quality variations among female and male talkers. J. Acoust. Soc. Am. 87, 820–857.
Kreiman, J. (1997). “Listening to voices: theory and practice in voice perception research”, in Talker Variability in Speech Processing, eds K. Johnson, and J. W. Mullennix (San Francisco: Morgan Kaufmann Publishers), 85–108.
Lavner, Y., Gath, I., and Rosenhouse, J. (2000). The effects of acoustic modifications on the identification of familiar voices speaking isolated vowels. Speech Commun. 30, 9–26.
Macmillan, N. A., and Creelman, C. D. (2005). Detection Theory: A User’s Guide. Mahwah, NJ: Lawrence Erlbaum Associates.
Mullennix, J. W., Johnson, K. A., Topcu-Durgun, M., and Farnsworth, L. M. (1995). The perceptual representation of voice gender. J. Acoust. Soc. Am. 98, 3080–3095.
Rendall, D., Kollias, S., Ney, C., and Lloyd, P. (2005). Pitch (f0) and formant profiles of human vowels and vowel-like baboon grunts: the role of vocalizer body size and voice acoustic allometry. J. Acoust. Soc. Am. 117, 944–955.
Schweinberger, S. R., Casper, C., Hauthal, N., Kaufmann, J. M., Kawahara, H., Kloth, N., Robertson, D. M. C., Simpson, A. P., and Zaske, R. (2008). Auditory adaptation in voice perception. Curr. Biol. 18, 684–688.
Stevens, S. S., Volkman, J., and Newman, E. (1937). A scale for the measurement of the psychological magnitude pitch. J. Acoust. Soc. Am. 8, 185–190.
Whiteside, S. P. (1998). Identification of a speaker’s sex: a study of vowels. Percept. Mot. Skills 86, 579–584.
Wilcox, R. R. (2005). Introduction to Robust Estimation and Hypothesis Testing, 2nd Edn, San Diego, CA: Academic Press.
Keywords: audition, categorical perception, voice, mixture model
Citation: Pernet CR and Belin P (2012) The role of pitch and timbre in voice gender categorization. Front. Psychology 3:23. doi: 10.3389/fpsyg.2012.00023
Received: 27 May 2011; Accepted: 18 January 2012;
Published online: 03 February 2012.
Edited by:
David J. Freedman, University of Chicago, USAReviewed by:
Ricardo Gil-da-Costa, Salk Institute, USACopyright: © 2012 Pernet and Belin. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Cyril R. Pernet, Division of Clinical Neurosciences, Brain Research Imaging Centre, University of Edinburgh, Western General Hospital, Crewe Road, Edinburgh EH4 2XU, UK. e-mail:Y3lyaWwucGVybmV0QGVkLmFjLnVr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.