- 1 Centre de Recherche Cerveau et Cognition, Université Paul Sabatier, Université de Toulouse, Toulouse, France
- 2 Faculté de Médecine de Purpan, CNRS, UMR 5549, Toulouse, France
- 3 Division of Biology, California Institute of Technology, Pasadena, CA, USA
It is becoming increasingly apparent that brain oscillations in various frequency bands play important roles in perceptual and attentional processes. Understandably, most of the associated experimental evidence comes from human or animal electrophysiological studies, allowing direct access to the oscillatory activities. However, such periodicities in perception and attention should, in theory, also be observable using the proper psychophysical tools. Here, we review a number of psychophysical techniques that have been used by us and other authors, in successful and sometimes unsuccessful attempts, to reveal the rhythmic nature of perceptual and attentional processes. We argue that the two existing and largely distinct debates about discrete vs. continuous perception and parallel vs. sequential attention should in fact be regarded as two facets of the same question: how do brain rhythms shape the psychological operations of perception and attention?
Introduction
Neurons convey information by means of electrical signals. Due to intrinsic properties of neuronal networks (e.g., conduction delays, balance between excitation and inhibition, membrane time constants), these electrical pulses give rise to large-scale periodic fluctuations of the background electric potential, which constitute the brain “rhythms” and oscillations (Buzsaki, 2006). Some oscillations – like the “alpha” rhythm at 8–13 Hz can be seen with the naked eye on an electro-encephalographic trace (Berger, 1929), while others require sophisticated analysis methods or recordings with a higher signal-to-noise ratio (using intra-cerebral probes in animals and, more rarely, in humans). There are many theories implicating brain oscillations in the performance of particular cognitive functions such as perception (Eckhorn et al., 1988; Gray et al., 1989; Engel et al., 1991; Singer and Gray, 1995; von der Malsburg, 1995), attention (Niebur et al., 1993; Fell et al., 2003; Womelsdorf and Fries, 2007), consciousness (Koch and Braun, 1996; Gold, 1999; Engel and Singer, 2001), and memory (Lisman and Idiart, 1995; Klimesch, 1999; Kahana et al., 2001). There are also flurries of experimental studies supporting (and sometimes, invalidating) these theories based on electrophysiological measurements of brain activity (Revonsuo et al., 1997; Tallon-Baudry et al., 1997, 1998; Fries et al., 2001; Jensen et al., 2002; Gail et al., 2004; Ray and Maunsell, 2010). It is somewhat less ordinary, on the other hand, to investigate the consequences of brain oscillations using psychophysical techniques. Yet one major prediction of the above-mentioned theories is directly amenable to psychophysical experimentation: indeed, an oscillatory implementation at the neuronal level should imply that the relevant cognitive function fluctuates periodically, and such fluctuations should be measurable with standard (or slightly more sophisticated) experimental psychology techniques.
The purpose of this article is to review some of the psychophysical techniques that have been applied recently to the study of brain oscillations. In so doing, we will touch upon two classical debates in perception research. First, scientists have long theorized that oscillations could divide the continuous sequence of inputs feeding into our perceptual systems into a series of discrete cycles or “snapshots” (Pitts and McCulloch, 1947; Stroud, 1956; Harter, 1967; Allport, 1968; Sanford, 1971), but this idea is far from mainstream nowadays; we refer to this debate as “discrete vs. continuous perception” (VanRullen and Koch, 2003). Second, there is another long-standing debate known as “parallel vs. sequential attention”: does attention concentrate its resources simultaneously or sequentially when there are multiple targets to focus on? Though this discussion is generally disconnected from the topic of brain oscillations, we will argue that it is in fact germane to the previous question. The sequential attention idea – which has traditionally been the dominant one – originated with the assumption that high-level vision cannot process more than one object at a time, and must therefore shift periodically between the stimuli (Eriksen and Spencer, 1969; Treisman, 1969; Kahneman, 1973), just like our gaze must shift around because our fovea cannot fixate on multiple objects simultaneously. Interestingly, sequential attention theories require a (possibly irregular) cyclic process for disengaging attention at the current target location and engaging it anew. It is easy to see – although little noticed in the literature – that discrete perception is merely an extension of this idea, obtained by assuming that the “periodic engine” keeps running, even when there is only one stimulus to process. This connection between the two theories will be a recurring thread in the present narrative.
Of course, the primary source of evidence about these topics is (and should remain) based on neurophysiological recordings, which provide direct measurements of the neuronal oscillations. For example, we have recently reviewed our past EEG work on the perceptual correlates of ongoing oscillations, with a focus on linking these oscillations to the notion of discrete perception (VanRullen et al., 2011). Another example is a recent study in macaque monkeys revealing that oscillatory neuronal activity in the frontal eye field (FEF, a region involved in attention and saccade programming) reflects the successive cycles of a clearly sequential attentional exploration process during visual search (Buschman and Miller, 2009). In this review we focus on purely psychophysical methods, not because they are better than direct neurophysiological measurements, but because they also inform us about psychological and perceptual consequences of the postulated periodicities. However, due to the inherent temporal limitations of most psychophysical methods, it should be kept in mind that in practice this approach is probably restricted to the lower end of the frequency spectrum, i.e., oscillations in the delta (0–4 Hz), theta (4–8 Hz), alpha (8–14 Hz), and possibly beta (14–30 Hz) bands. Higher-frequency oscillations (e.g., gamma: 30–80 Hz) may still play a role in sensory processing, but they are generally less amenable to direct psychophysical observation.
There exist many psychophysical paradigms designed to test the temporal limits of sensory systems but that do not directly implicate periodic perception or attention, because their results can also be explained by temporal “smoothing” or integration, in the context of a strictly continuous model of perception (Di Lollo and Wilson, 1978). These paradigms are nonetheless useful to the discrete argument because they constrain the range of plausible periodicities: for example, temporal numerosity judgments or simultaneity judgments indicate that the temporal limit for individuating visual events is only around 10 events per second (White et al., 1953; Lichtenstein, 1961; White, 1963; Holcombe, 2009), suggesting a potential oscillatory correlate in the alpha band (Harter, 1967). We will not develop these results further here, focusing instead on paradigms that unequivocally indicate periodic sampling of perception or attention. Similarly, although some psychophysical studies have demonstrated that perception and attention can be entrained to a low-frequency rhythmic structure in the stimulus sequence (Large and Jones, 1999; Mathewson et al., 2010), we will only concentrate here on studies implicating intrinsic perceptual and attentional rhythms (i.e., rhythms that are not present in the stimulus). We will see that progress can be made on the two debates of discrete vs. continuous perception and sequential vs. parallel attention by addressing them together rather than separately.
Rhythmic Sampling of a Single Stimulus: Discrete vs. Continuous Perception
Suppose that a new stimulus suddenly appears in your visual field, say a red light at the traffic intersection. For such a transient onset, a sequence of visual processing mechanisms from your retina to your high-level visual cortex will automatically come into play, allowing you after a more or less fixed latency to “perceive” this stimulus, i.e., experience it as part of the world in front of you. Hopefully you should then stop at the intersection. What happens next? For as long as the stimulus remains in the visual field, you will continue to experience it. But how do you know it is still there? You might argue that if it were gone, the same process as previously would now signal the transient offset (together with the onset of the green light), and you would then recognize that the red light is gone. But in-between those two moments, you did experience the red light as present – did you only fill in the mental contents of this intervening period after the green light appeared? This sounds unlikely, at least if your traffic lights last as long as they do around here. Maybe the different stages of your visual system were constantly processing their (unchanged) inputs and feeding their (unchanged) outputs to the next stage, just in case the stimulus might happen to change right then – a costly but plausible strategy. An intermediate alternative would consist in sampling the external world periodically to verify, and potentially update, its contents; the period could be chosen to minimize metabolic effort, while maximizing the chances of detecting any changes within an ecologically useful delay (e.g., to avoid honking from impatient drivers behind you when you take too long to notice the green light). These last two strategies are respectively known as continuous and discrete perception.
The specific logic of the above example may have urged you to favor discrete perception, but the scientific community traditionally sides with the continuous idea. It has not always been so, however. In particular, the first observations of EEG oscillations in the early twentieth century (Berger, 1929), together with the simultaneous popularization of the cinema, prompted many post-war scientists to propose that the role of brain oscillations could be to chunk sensory information into unitary events or “snapshots,” similar to what happens in the movies (Pitts and McCulloch, 1947; Stroud, 1956; Harter, 1967). Much experimental research ensued, which we have already reviewed elsewhere (VanRullen and Koch, 2003). The question was never fully decided, however, and the community’s interest eventually faded. The experimental efforts that we describe in this section all result from an attempt to follow up on this past work and revive the scientific appeal of the discrete perception theory.
Periodicities in Reaction Time Distributions
Some authors have reasoned that if the visual system samples the external world discretely, the time it would take an observer to react after the light turns green would depend on the precise moment at which this event occurred, relative to the ongoing samples: if the stimulus is not detected within one given sample then the response will be delayed at least until the next sampling period. This relation may be visible in histograms of reaction time (RT). Indeed, multiple peaks separated by a more or less constant period are often apparent in RT histograms: these multimodal distributions have been reported with a period of approximately 100 ms for verbal choice responses (Venables, 1960), 10–40 ms for auditory and visual discrimination responses (Dehaene, 1993), 10–15 ms for saccadic responses (Latour, 1967), 30 ms for smooth pursuit eye movement initiation responses (Poppel and Logothetis, 1986). It must be emphasized, however, that an oscillation can only be found in a histogram of post-stimulus RTs if each stimulus either evokes a novel oscillation, or resets an existing one. Otherwise (and assuming that the experiment is properly designed, i.e., with unpredictable stimulus onsets), the moment of periodic sampling will always occur at a random time with respect to the stimulus onset; thus, the peaks of response probability corresponding to the recurring sampling moments will average out, when the histogram is computed over many trials. In other words, even though these periodicities in RT distributions are intriguing, they do not unambiguously demonstrate that perception samples the world periodically – for example, it could just be that each stimulus onset triggers an oscillation in the motor system that will subsequently constrain the response generation process. In the following sections, we present other psychophysical methods that can reveal perceptual periodicities within ongoing brain activity, i.e., without assuming a post-stimulus phase reset.
Double-Detection Functions
As illustrated in the previous section, there is an inherent difficulty in studying the perceptual consequences of ongoing oscillations: even if the pre-stimulus oscillatory phase modulates the sensory processing of the stimulus, this pre-stimulus phase will be different on successive repetitions of the experimental trial, and the average performance over many trials will show no signs of the modulation. Obviously, this problem can be overcome if the phase on each trial can be precisely estimated, for example using EEG recordings (VanRullen et al., 2011). With purely psychophysical methods, however, the problem is a real challenge.
An elegant way to get around this challenge has been proposed by Latour (1967). With this method, he showed preliminary evidence that visual detection thresholds could fluctuate along with ongoing oscillations in the gamma range (30–80 Hz). The idea is to present two stimuli on each trial, with a variable delay between them, and measure the observer’s performance for detecting (or discriminating, recognizing, etc.) both stimuli: even if each stimulus’s absolute relation to an ongoing oscillatory phase cannot be estimated, the probability of double-detection should oscillate as a function of the inter-stimulus delay (Figure 1). In plain English, the logic is that when the inter-stimulus delay is a multiple of the oscillatory period, the observer will be very likely to detect both stimuli (if they both fall at the optimal phase of the oscillation) or to miss both stimuli altogether (if they both fall at the opposite phase); on the other hand, if the delay is chosen in-between two multiples of the oscillatory period, then the observer will be very likely to detect only one of the two stimuli (if the first stimulus occurs at the optimal phase, the other will fall at the opposite, and vice-versa).
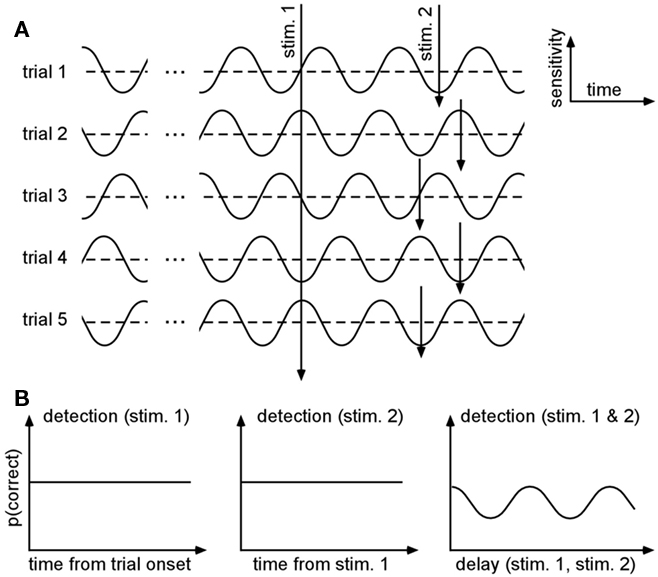
Figure 1. Double-detection functions can reveal periodicities even when the phase varies across trials. (A) Protocol. Let us assume that the probability of detecting a stimulus (i.e., the system’s sensitivity) fluctuates periodically along with the phase of an ongoing oscillatory process. By definition, this process bears no relation with the timing of each trial, and thus the phase will differ on each trial. On successive trials, not one but two stimuli are presented, with a variable delay between them. (B) Expected results. Because the phase of the oscillatory process at the moment of stimulus presentation is fully unpredictable, the average probability of detecting each stimulus as a function of time (using an absolute reference, such as the trial onset) will be constant (left). The probability of detecting the second stimulus will also be independent of the time elapsed since the first one (middle). However, the probability of detecting both stimuli (albeit smaller) will oscillate as a function of the delay between them, and the period of this oscillation will be equal to the period of the original ongoing oscillatory process (adapted from Latour, 1967).
More formally, let us assume that the probability of measuring our psychological variable ψ (e.g., target detection, discrimination, recognition, etc.) depends periodically (with period 2π/ω) on the time of presentation of the stimulation s; to a first approximation this can be noted:
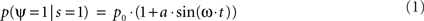
where p0 is the average expected measurement probability, and a is the amplitude of the periodic modulation. Since the time t of stimulation (with respect to the ongoing oscillation) may change for different repetitions of the measurement, only p0 can be measured with classical trial averaging methods (i.e., the “sine” term will average out to a mean value of zero). However, if two identical stimulations are presented, separated by an interval δt, the conditional probability of measuring our psychological variable twice can be shown to be (there is no room here, unfortunately, for the corresponding mathematical demonstration):
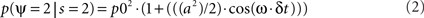
The resulting probability only depends on the interval δt (chosen by the experimenter), and thus does not require knowledge of the exact oscillatory phase on every trial. This means that, using double stimulations and double-detection functions, one can derive psychophysically the rate ω of the periodic process, and its modulation amplitude a (Figure 1).
In practice, unfortunately, this method is not as easy to apply as it sounds. One important caveat was already mentioned by Latour: the inter-stimulus delay must be chosen to be long enough to avoid direct interactions between the two stimuli (e.g., masking, apparent motion, etc.). This is because the mathematical derivation of Eq. 2 assumes independence between the detection probabilities for the two stimuli. To ensure that this condition is satisfied, the stimuli should be separated by a few 100 ms (corresponding to the integration period for masking or apparent motion); on the other hand, this implies that several oscillatory cycles will occur between the two stimuli, and many external factors (e.g., phase slip, reset) can thus interfere and decrease the measured oscillation. This in turn suggests that the method may be more appropriate for revealing low-frequency oscillations than high-frequency ones (e.g., gamma). Another important limitation is that the magnitude of the measured oscillation in the double-detection function (2) is squared, compared to the magnitude of the original perceptual oscillation. Although this is not a problem if the perceptual oscillation is strong (i.e., the square of a number close to 1 is also close to 1), it can become troublesome when the original perceptual oscillation is already subtle (e.g., for a 20% modulation of the visual threshold, one can only expect a 4% modulation in the double-detection function). Altogether, these limitations may explain why Latour’s results have, so far, not been replicated or extended.
Temporal Aliasing: The Wagon Wheel Illusion
Engineers know that any signal sampled by a discrete or periodic system is subject to potential “aliasing” artifacts (Figure 2): when the sampling resolution is lower than a critical limit (the “Nyquist rate”) the signal can be interpreted erroneously. This is true, for instance, when a signal is sampled in the temporal domain (Figure 2A). When this signal is a periodic visual pattern in motion, aliasing produces a phenomenon called the “wagon wheel illusion” (Figure 2B): the pattern appears to move in the wrong direction. This is often observed in movies or on television, due to the discrete sampling of video cameras (generally around 24 frames per second). Interestingly, a similar perceptual effect has also been reported under continuous conditions of illumination, e.g., daylight (Schouten, 1967; Purves et al., 1996; VanRullen et al., 2005b). In this case, however, because no artificial device is imposing a periodic sampling of the stimulus, the logical conclusion is that the illusion must be caused by aliasing within the visual system itself. Thus, this “continuous version of the wagon wheel illusion” (or “c-WWI”) has been interpreted as evidence that the visual system samples motion information periodically (Purves et al., 1996; Andrews et al., 2005; Simpson et al., 2005; VanRullen et al., 2005b).

Figure 2. Temporal aliasing. (A) Concept. Sampling a temporal signal using too low a sampling rate leads to systematic errors about the signal, known as “aliasing errors.” Here, the original signal is periodic, but its frequency is too high compared with the system’s sampling rate (i.e., it is above the system’s “Nyquist” frequency, defined as half of its sampling rate). As a result, the successive samples skip ahead by almost one full period of the original oscillation: instead of normally going through the angular phases of zero, π/2, π, 3π/2, and back to zero, the successive samples describe the opposite pattern, i.e., zero, 3π/2, π, π/2, and so on. The aliasing is particularly clear in the complex domain (right), where the representations of the original and estimated signals describe circles in opposite directions. (B) The wagon wheel illusion. When the original signal is a periodically moving stimulus, temporal aliasing transpires as a reversal of the perceived direction. This wagon wheel illusion is typically observed in movies due to the discrete sampling of video cameras. The continuous version of this wagon wheel illusion (c-WWI) differs in that it occurs when directly observing the moving pattern in continuous illumination; in this case, it has been proposed that reversed motion indicates a form of discrete sampling occurring in the visual system itself.
There are many arguments in favor of this “discrete” interpretation of the c-WWI. First, the illusion occurs in a very specific range of stimulus temporal frequencies, compatible with a discrete sampling rate of approximately 13 Hz (Purves et al., 1996; Simpson et al., 2005; VanRullen et al., 2005b). As expected according to the discrete sampling idea, this critical frequency remains unchanged when manipulating the spatial frequency of the stimulus (Simpson et al., 2005; VanRullen et al., 2005b) or the type of motion employed, i.e., rotation vs. translation motion, or first-order vs. second-order motion (VanRullen et al., 2005b). EEG correlates of the perceived illusion confirm these psychophysical findings and point to an oscillation in the same frequency range around 13 Hz (VanRullen et al., 2006; Piantoni et al., 2010). Altogether, these data suggest that (at least part of) the motion perception system proceeds by sampling its inputs periodically, at a rate of 13 samples per second.
There are, of course, alternative accounts of the phenomenon. First, it is noteworthy that the illusion is not instantaneous, and does not last indefinitely, but it is instead a bistable phenomenon, which comes and goes with stochastic dynamics; such a process implies the existence of a competition between neural mechanisms supporting the veridical and the erroneous motion directions (Blake and Logothetis, 2002). Within this context, the debate centers around the source of the erroneous signals: some authors have argued that they arise not from periodic sampling and aliasing, but from spurious activation in low-level motion detectors (Kline et al., 2004; Holcombe et al., 2005) or from motion adaptation processes that would momentarily prevail over the steady input (Holcombe and Seizova-Cajic, 2008; Kline and Eagleman, 2008). We find these accounts unsatisfactory, because they do not seem compatible with the following experimental observations: (i) the illusion is always maximal around the same temporal frequency, whereas the temporal frequency tuning of low-level motion detectors differs widely between first and second-order motion (Hutchinson and Ledgeway, 2006); (ii) not only the magnitude of the illusion, but also its spatial extent and its optimal temporal frequency – which we take as a reflection of the system’s periodic sampling rate – are all affected by attentional manipulations (VanRullen et al., 2005b; VanRullen, 2006; Macdonald et al., under review); in contrast, the amount of motion adaptation could be assumed to vary with attentional load (Chaudhuri, 1990; Rezec et al., 2004), but probably not the frequency tuning of low-level motion detectors; (iii) motion adaptation itself can be dissociated from the wagon wheel illusion using appropriate stimulus manipulations; for example, varying stimulus contrast or eccentricity can make the motion aftereffects (both static and dynamic versions) decrease while the c-WWI magnitude increases, and vice-versa (VanRullen, 2007); (iv) finally, the brain regions responsible for the c-WWI effect, repeatedly identified in the right parietal lobe (VanRullen et al., 2006, 2008; Reddy et al., 2011), point to a higher-level cause than the mere adaptation of low-level motion detectors.
Disentangling the neural mechanisms of the continuous wagon wheel illusion could be (and actually, is) the topic of an entirely separate review (VanRullen et al., 2010). To summarize, our current view is that the reversed motion signals most likely originate as a form of aliasing due to periodic temporal sampling by attention-based motion perception systems, at a rate of ∼13 Hz; the bistability of the illusion is due to the simultaneous encoding of the veridical motion direction by other (low-level, or “first-order”) motion perception systems. The debate, however, is as yet far from settled. At any rate, this phenomenon illustrates the potential value of temporal aliasing as a paradigm to probe the discrete nature of sensory perception.
Other Forms of Temporal Aliasing
The sampling frequency evidenced with the c-WWI paradigm may be specific to attention-based motion perception mechanisms. It is only natural to try and extend the temporal aliasing methodology to perception of other types of motion, to perception of visual features other than motion or to perception in sensory modalities other than vision. If evidence for temporal aliasing could be found in these cases, the corresponding sampling frequencies may then be compared to one another and further inform our understanding of discrete perception. Is there a single rhythm, a central (attentional) clock that samples all sensory inputs? Or is information from any single channel of sensory information read out periodically at its own rate, independently from other channels? While the first proposition reflects the understanding that most have of the theory of discrete perception (Kline and Eagleman, 2008), the latter may be a much more faithful description of reality; additionally, the sampling rate for a given channel may vary depending on task demands and attentional state, further blurring intrinsic periodicities.
The simple generic paradigm which we advocate to probe the brain for temporal aliasing is as follows. Human observers are presented with a periodic time-varying input which physically evolves in an unambiguously defined direction; they are asked to make a two-alternative forced choice judgment on the direction of evolution of this input, whose frequency is systematically varied by the experimenter across trials. A consistent report of the wrong direction at a given input frequency may be taken as a behavioral correlate of temporal aliasing, and the frequencies at which this occurs inform the experimenter about the underlying sampling frequency of the brain for this input.
Two main hurdles may be encountered in applying this paradigm. The first one lies in what should be considered a “consistent” report of the wrong direction. Clearly, for an engineered sampling system, one can find input frequencies at which the system will always output the wrong direction. For a human observer, however, several factors could be expected to lower the tendency to report the wrong direction, even at frequencies that are subject to aliasing: measurement noise, the potential variability of the hypothetical sampling frequency over the duration of the experiment, and most importantly, the potential presence of alternate sources of information (as in the c-WWI example, where competition occurs between low-level and attention-based motion systems). In the end, even if aliasing occurs, it may not manifest as a clear and reliable percept of the erroneous direction, but rather as a subtle increase of the probability of reporting the wrong direction at certain frequencies. Recently, we proposed a method to evaluate the presence of aliasing in psychometric functions, based on model fitting (Dubois and VanRullen, 2009). (A write-up of this method and associated findings can be accessed at http://www.cerco.ups-tlse.fr/∼rufin/assc09/). Results of a 2-AFC motion discrimination experiment were well explained by considering two motion sensing systems, one that functions continuously and one that takes periodic samples of position to infer motion. These two systems each give rise to predictable psychometric functions with few parameters, whose respective contributions to performance can be inferred by model fitting. Evidence for a significant contribution of a discrete process sampling at 13 Hz was found – thus confirming our previous conclusions from the c-WWI phenomenon. Furthermore, the discrete process contributed more strongly to the perceptual outcome when motion was presented inter-ocularly, than binocularly; this is compatible with our postulate that discrete sampling in the c-WWI is a high-level effect, since inter-ocular motion perception depends on higher-level motion perception systems (Lu and Sperling, 2001).
The second pitfall is that the temporal resolution for discriminating the direction of the time-varying input under consideration should be at least as good as the hypothesized sampling frequency. If the psychometric function is already at chance at the frequency where aliasing is expected to take place, this aliasing will simply not be observed – whether the perceptual process relies on periodic sampling or not. Our lab learned this the hard way: many of the features that we experimented with so far, besides luminance and contrast-defined motion, can only be discriminated at low-temporal frequencies – they belong to Holcombe’s “seeing slow” category (Holcombe, 2009). For example, we hypothesized that motion stimuli designed to be invisible to the first-order motion perception system, such as stereo-defined motion (Tseng et al., 2006), would yield maximal aliasing as there is no other motion perception system offering competing information. Unfortunately, these stimuli do not yield a clear percept at temporal frequencies beyond 3–4 Hz, meaning that any aliasing occurring at higher frequencies would have escaped our notice. The “motion standstill” phenomenon reported by Lu and colleagues (Lu et al., 1999; Tseng et al. 2006) with similar stimuli at frequencies around 5 Hz remains a potential manifestation of temporal aliasing, although we have not satisfactorily replicated it in our lab yet. We also hypothesized that binding of spatially distinct feature conjunctions, such as color and motion, could rely on sequential attentional sampling of the two features (Moutoussis and Zeki, 1997), and should thus be subject to aliasing. Again, we were disappointed to find that performance was at chance level at presentation rates higher than 3–4 Hz (Holcombe, 2009), precluding further analysis. We also attempted to adapt the wagon wheel phenomenon to the auditory modality. Here, perception of sound source motion (e.g., a sound rotating around the listener) also appeared limited to about 3 Hz (Feron et al., 2010). We then reasoned that frequency, rather than spatial position, was the primary feature for auditory perception, and designed periodic stimuli that moved in particular directions in the frequency domain – so-called Shepard or Risset sequences (Shepard, 1964). Again, we found that the direction of these periodic frequency sweeps could not be identified when the temporal frequency of presentation was increased beyond 3–4 Hz.
In sum, although temporal aliasing is, in principle, a choice paradigm to probe the rhythms of perception, our attempts so far at applying this technique to other perceptual domains than motion (the c-WWI) have been foiled by the strict temporal limits of the corresponding sensory systems. What we can safely conclude is that, if discrete sampling exists in any of these other perceptual domains, it will be at a sampling rate above 3–4 Hz. We have not exhausted all possible stimuli and encourage others to conduct their own experiments. There are two faces to the challenge: finding stimuli that the brain “sees fast” enough, and using an appropriate model to infer the contribution of periodic sampling to the psychometric performance (in case other sources of information and sizeable variability across trials should blur the influence of discrete processes).
Rhythmic Sampling of Multiple Stimuli: Sequential vs. Parallel Attention
Let us return to our previous hypothetical situation. Now you have passed the traffic lights and driven home, and you turned on the TV to find out today’s lottery numbers. There are a handful of channels that can provide this information at this hour, so you go to “multi-channel” mode to monitor them simultaneously. The lottery results are not on, so you will wait until any channel shows them. How will you know which one? You try to process all channels at once, but their contents collide and confuse you. What if one of them shows the numbers but you notice it too late? By focusing on a single channel you would be sure not to miss the first numbers, but then what if you picked the wrong channel? In such a situation, it is likely that you will switch your attention rapidly between the different candidate channels until you see one that provides the required information. Your brain often faces the same problem when multiple objects are present in the visual field and their properties must be identified, monitored or compared.
A Long-Standing Debate
Visual search
Whether your brain simultaneously and continuously shares its attentional resources (i.e., in “parallel”) between candidate target objects, or switches rapidly and sequentially between them, has been the subject of intense debate in the literature. We refer to this debate as “parallel vs. sequential attention.” Originally, attention was assumed to be a unitary, indivisible resource, and consequently the sequential model was favored, often implicitly (Eriksen and Spencer, 1969; Treisman, 1969; Kahneman, 1973). The first two decades of studies using the visual search paradigm were heavily biased toward this assumption (Treisman and Gelade, 1980; Wolfe, 1998): when a target had to be identified among a varying number of distractors and the observer’s RT was found to increase steadily with the number of items, it was assumed that the additional time needed for each item reflected the duration of engaging, sampling and disengaging attention (hence the term “serial search slope”). It was only in the 1990s that this assumption was seriously challenged by proponents of an alternate model, according to which attention is always distributed in parallel among items, and the increase in RT with increasing item number simply reflects the increasing task difficulty or decreasing “signal-to-noise ratio” (Palmer, 1995; Carrasco and Yeshurun, 1998; Eckstein, 1998; McElree and Carrasco, 1999; Eckstein et al., 2000). Both models are still contemplated today – and indeed, they are extremely difficult to distinguish experimentally (Townsend, 1990).
Multi-object tracking
The same difficulty also plagues paradigms other than visual search. Multi-object tracking, for instance, corresponds to a situation in which several target objects are constantly and randomly moving around the visual field, often embedded among similarly moving distractors (Pylyshyn and Storm, 1988). Sometimes, the objects are moving in feature space (i.e., changing their color or their orientation) rather than in physical space (Blaser et al., 2000). The common finding that up to four – or sometimes more (Cavanagh and Alvarez, 2005) objects can be efficiently tracked at the same time has been taken as evidence that attention must be divided in parallel among the targets (Pylyshyn and Storm, 1988). However, in the limit where attention would be assumed to move at lightning speed, it is obvious that this simultaneous tracking capacity could be explained equally well by sequential shifts of a single attention spotlight, than by divided or parallel attention. Indeed, at least some of the existing data have been found compatible with a sequential process (Howard and Holcombe, 2008; Oksama and Hyona, 2008). Since there is no general agreement concerning the actual speed of attention (Duncan et al., 1994; Moore et al., 1996; Hogendoorn et al., 2007), the question remains open.
Simultaneous/sequential paradigm
Other paradigms have been designed with the explicit aim of teasing apart the parallel and serial attention models. In the simultaneous/sequential paradigm, the capacity of attention to process multiple items simultaneously is assessed by presenting the relevant information for a limited time in each display cycle. In one condition (simultaneous) this information is delivered at once for all items; in the other condition (sequential) each item’s information is revealed independently, at different times. In both conditions the critical information is thus shown for the same total amount of time, such that a parallel model of attentional allocation would predict comparable performance; however, a serial attentional model would suffer more in the simultaneous condition, because attention would necessarily miss the relevant information in one stimulus while it is sampling the other(s), and vice-versa (Eriksen and Spencer, 1969; Shiffrin and Gardner, 1972). The paradigm was recently applied to the problem of multiple-object tracking (Howe et al., 2010), and the data were deemed incompatible with serial attention sampling. A major source of confounds in this paradigm, however, is that, depending on stimulus arrangement parameters, certain factors (e.g., grouping, crowding) can improve or decrease performance in the simultaneous condition independently of attention; similarly, other factors (e.g., apparent motion, masking) can improve or decrease performance in the sequential condition. It is unclear in the end how to tease apart the effects of attention from the potentially combined effects of all these extraneous factors.
Split spotlight studies
To finish, there is yet another class of experiments that were intended to address a distinct albeit related question: when attention is divided among multiple objects, does the focus simply expand its size to include all of the targets, or does it split into several individual spotlights? To test this, these paradigms generally measure an improvement of performance due to attention at two separate locations concurrently; the critical test is then whether a similar improvement can also be observed at an intervening spatial location: if yes, the spotlight may have been simply enlarged, if not it may have been broken down into independent spotlights. Psychophysical studies tend to support the multiple spotlights account (Bichot et al., 1999; Awh and Pashler, 2000). The same idea has also been applied to physiological measurements of the spotlight, demonstrating that EEG or fMRI brain activations can be enhanced by attention at two concurrent locations, without any enhancement at intervening locations (Muller et al., 2003; McMains and Somers, 2004). Now, how do these results on the spatial deployment of attention pertain to our original question about the temporal dynamics of attention? Inherent in the logic of this paradigm is the assumption that attentional resources are divided constantly over time; multiple spotlights are implicitly assumed to operate simultaneously, rather than as a single, rapidly shifting focus. To support this assumption, authors often use limited presentation times (so attention does not have time to shift between targets), and speculate on the speed of attention. As mentioned before, since this speed is largely unknown, a lot of the data remain open to interpretation. In fact, our recent results in a very similar paradigm (in which we varied the delay between stimulus onset and the subsequent measurement of attentional deployment) showed that multiple simultaneous spotlights can in fact be observed, but are short-lived; when several target locations need to be monitored for extended periods of time, the attentional system quickly settles into a single-spotlight mode (Dubois et al., 2009). In another related study we found that attention could not simultaneously access information from two locations, but instead relied on rapid sequential allocation (Hogendoorn et al., 2010).
The conclusion from studies that have used this kind of paradigm is also fairly representative of the current status of the entire “sequential vs. parallel attention” debate, which we have briefly reviewed here. As summarized in a recent (and more thorough) review by Jans et al. (2010), most of the so-called demonstrations of multiple parallel attention spotlights rely on strong – and often unsubstantiated – assumptions about the temporal dynamics of attention. In sum, parallel attention has by no means won the prize.
Temporal Aliasing Returns
Could aliasing (see Temporal Aliasing: the Wagon Wheel Illusion and Other Forms of Temporal Aliasing) provide a way of resolving the “sequential vs. parallel attention” debate? If attention focuses on each target sequentially rather than continuously, the target information will be sampled more or less periodically, and should thus be subject to aliasing artifacts; furthermore, the rate of sampling for each target should be inversely related to the number of targets to sample (i.e., the “set size”). On the other hand, parallel attention models have no reason to predict aliasing; and, even if aliasing were to occur, no reason to predict a change of aliasing frequency as a function of set size. We recently tested this idea using a variant of the continuous wagon wheel illusion phenomenon (Macdonald et al., under review). On each 40 s trial, we showed one, two, three or four wheels rotating in the same direction; the frequency of rotation was varied between trials. From time to time, a subset of the wheels briefly reversed their direction, and the subjects’ task was to count and report how many of these reversal events had occurred in each trial. We reasoned that any aliasing would be manifested as an overestimation of the number of reversals. As expected from our experiments with the c-WWI, we found significant aliasing in a specific range of rotation frequencies. Most importantly, the frequency of maximum aliasing significantly decreased as set size was increased, as predicted by the “sequential attention” idea. Although the magnitude of this decrease was lower than expected (the sampling frequency was approximately divided by 2, from ∼13 Hz down to ∼7 Hz, while the set size was multiplied by 4), this finding poses a very serious challenge to the “parallel attention” theory.
The Blinking Spotlight of Attention
The crucial difficulty in distinguishing parallel and sequential accounts of attention is a theoretical one: any “set size effect” that can be explained by a division of attentional resources in time can, in principle, be explained equally well using a spatial division of the same resources (Townsend, 1990; Jans et al., 2010). There is a form of equivalence between the temporal and spatial domains, a sort of Heisenberg uncertainty principle, that precludes most attempts at jointly determining the spatial and temporal distributions of attention. In a recent experiment, however, we tried to break down this equivalence by measuring set size effects following a temporal manipulation of the stimuli – namely, after varying their effective duration on each trial (VanRullen et al., 2007). Thus we could tell, for example, how well three stimuli were processed when they were presented for 300 ms, and we could compare this to the performance obtained for one stimulus presented 100, or 300 ms (or any other combination of set size and duration). The interest of this procedure was that different models of attentional division (e.g., sequential and parallel models) would make different predictions about how the psychometric function for processing one stimulus as a function of its duration should translate into corresponding psychometric functions for larger set sizes. To simplify, the space–time equivalence was broken, because performance for sequentially sampling two (or three, or four) stimuli each for a fixed period could be predicted exactly, by knowing the corresponding performance for a single stimulus that lasted for a duration equivalent to the sampling period; a simple parallel model, of course, could be designed to explain the change in performance from one to two (or three, or four) stimuli, but if the model was wrong it would then do a poor job at explaining performance obtained at other set sizes.
We compared three distinct models of attention allocation, each with a single free parameter. In the “parallel” model, all stimuli were processed simultaneously, and only the efficiency of this processing varied as a function of attentional load (i.e., set size); the cost in efficiency was manipulated by the model’s free parameter. The second model, coined “sample-when-divided,” corresponded to the classic idea of a switching spotlight: when more than one stimulus was present, the otherwise constant attentional resource was forced to sequentially sample the stimulus locations; the model’s free parameter was its sampling period, which affected its ability to process multiple stimuli. Finally, we decided to consider a third model, termed “sample-always,” similar to the previous one except for the fact that it still collected and integrated successive attentional samples even when a single stimulus was present (see Figure 3 for an illustration); this model’s behavior was also governed by its sampling period. Our strategy was, then, to compare the three models’ ability to emulate the actual psychometric functions of human observers.
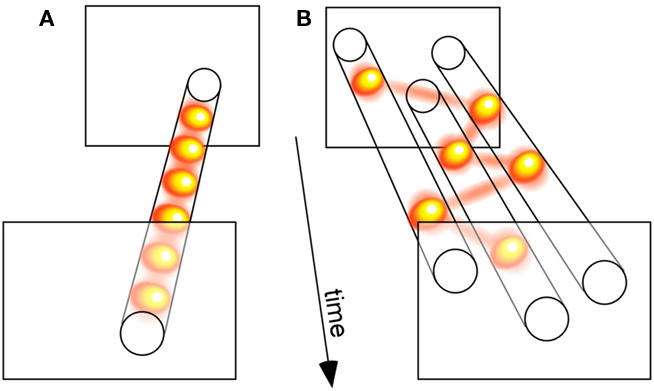
Figure 3. Relating discrete perception with sequential attention. (A) A sensory process that samples a single visual input periodically illustrates the concept of discrete perception. (B) A sensory process that serially samples three simultaneously presented visual stimuli demonstrates the notion of a sequential attention spotlight. Since many of our findings implicate attention in the periodic sampling processes displayed in (A), we propose that both types of periodic psychological operations (A,B) actually reflect a common oscillatory neuronal process. According to this view, the spotlight of attention is intrinsically rhythmic, which gives it both the ability to rapidly scan multiple objects, and to discretely sample a single source. (The yellow balls linked by red lines illustrate successive attentional samples.)
Compatible with existing findings (Palmer, 1995), we revealed that the parallel model could outperform the classic version of the sequential model – the “sample-when-divided” one, which considers that the attentional spotlight shifts around sequentially, but only when attention must be divided. However, the truly optimal model to explain human psychometric functions was the other variant of the sequential idea, a model in which attention always samples information periodically, regardless of set size. The rate of sampling was found to be ∼7 Hz. When attention is divided, successive samples naturally focus on different stimuli, but when it is concentrated on a single target, the samples continue to occur repeatedly every ∼150 ms, simply accumulating evidence for this one stimulus. In other words, our findings supported a “blinking spotlight” of attention (VanRullen et al., 2007) over the sequentially “switching spotlight” (and over the multiple “parallel spotlights”).
Conclusion
The notion of a blinking spotlight illustrates a fundamental point: that discrete sampling and sequential attention could be two facets of a single process (Figure 3). Proponents of the discrete sampling theory should ask themselves: what happens when there are more than one relevant stimuli in the visual field? Can they all be processed in a single “snapshot”? Advocates of sequential attention should ponder about the behavior of attention when it has only one target to monitor: is it useful – or even possible – for attention to pause its exploratory dynamics?
The simple theory that we propose is that periodic “covert” attentional sampling may have evolved from “overt” exploratory behavior (i.e., eye movements), as a means to quickly and effortlessly scan internal representations of the environment (VanRullen et al., 2005a; Uchida et al., 2006). Just as eye movements continue to occur even when there is only one object in the scene – lest the object quickly fade from awareness (Ditchburn and Ginsborg, 1952; Coppola and Purves, 1996; Martinez-Conde et al., 2006) – it is sensible to posit that attentional sampling takes place regardless of the number of objects to sample. Perception can then be said to be “discrete” or “periodic,” insofar as a very significant portion of its inputs (those depending on attentional mechanisms) are delivered periodically. For example, the ∼13 Hz discrete sampling responsible for the continuous wagon wheel illusion was found to be driven by attention (VanRullen et al., 2005b; VanRullen, 2006; Macdonald et al., under review). The frequency of this sampling progressively decreased to ∼7 Hz when two, three, and finally four “wagon wheel” stimuli had to be simultaneously monitored (Macdonald et al., under review). Interestingly, this ∼7 Hz periodicity was also the one indicated by our model of the “blinking spotlight” of attention (VanRullen et al., 2007). Altogether, our data raise the intriguing suggestion that attention creates discrete samples of the visual world with a periodicity of approximately one tenth of a second.
To conclude, we argue that it is constructive to unite the two separate psychophysical debates about discrete vs. continuous perception (see Rhythmic Sampling of a Single Stimulus: Discrete vs. Continuous Perception) and sequential vs. parallel attention (see Rhythmic Sampling of Multiple Stimuli: Sequential vs. Parallel Attention). Discrete perception and sequential attention may represent perceptual and psychological manifestations of a single class of periodic neuronal mechanisms. Therefore, psychophysical progress in solving those debates could, ultimately, contribute to uncovering the role of low-frequency brain rhythms in perception and attention.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was funded by a EURYI Award and an ANR grant 06JCJC-0154 to RV.
References
Allport, D. A. (1968). Phenomenal simutaneity and the perceptual moment hypothesis. Br. J. Psychol. 59, 395–406.
Andrews, T., Purves, D., Simpson, W. A., and VanRullen, R. (2005). The wheel keeps turning: reply to Holcombe et al. Trends Cogn. Sci. (Regul. Ed.) 9, 561.
Awh, E., and Pashler, H. (2000). Evidence for split attentional foci. J. Exp. Psychol. Hum. Percept. Perform. 26, 834–846.
Berger, H. (1929). Über das Elektroenkephalogramm des Menschen. Arch. Psychiatr. Nervenkr. 87, 527–570.
Bichot, N. P., Cave, K. R., and Pashler, H. (1999). Visual selection mediated by location: feature-based selection of noncontiguous locations. Percept. Psychophys. 61, 403–423.
Blaser, E., Pylyshyn, Z. W., and Holcombe, A. O. (2000). Tracking an object through feature space. Nature 408, 196–199.
Buschman, T. J., and Miller, E. K. (2009). Serial, covert shifts of attention during visual search are reflected by the frontal eye fields and correlated with population oscillations. Neuron 63, 386–396.
Carrasco, M., and Yeshurun, Y. (1998). The contribution of covert attention to the set-size and eccentricity effects in visual search. J. Exp. Psychol. Hum. Percept. Perform. 24, 673–692.
Cavanagh, P., and Alvarez, G. A. (2005). Tracking multiple targets with multifocal attention. Trends Cogn. Sci. (Regul. Ed.) 9, 349–354.
Chaudhuri, A. (1990). Modulation of the motion aftereffect by selective attention. Nature 344, 60–62.
Coppola, D., and Purves, D. (1996). The extraordinarily rapid disappearance of entopic images. Proc. Natl. Acad. Sci. U.S.A. 93, 8001–8004.
Di Lollo, V., and Wilson, A. E. (1978). Iconic persistence and perceptual moment as determinants of temporal integration in vision. Vision Res. 18, 1607–1610.
Ditchburn, R. W., and Ginsborg, B. L. (1952). Vision with a stabilized retinal image. Nature 170, 36–37.
Dubois, J., Hamker, F. H., and VanRullen, R. (2009). Attentional selection of noncontiguous locations: the spotlight is only transiently “split.” J. Vis. 9, 1–11.
Dubois, J., and VanRullen, R. (2009). Evaluating the contribution of discrete perceptual mechanisms to psychometric performance. Paper presented at the Association for the Scientific Study of Consciousness, Berlin.
Duncan, J., Ward, R., and Shapiro, K. (1994). Direct measurement of attentional dwell time in human vision. Nature 369, 313–315.
Eckhorn, R., Bauer, R., Jordan, W., Brosch, M., Kruse, W., Munk, M., and Reitboeck, H. J. (1988). Coherent oscillations: a mechanism of feature linking in the visual cortex? Multiple electrode and correlation analyses in the cat. Biol. Cybern. 60, 121–130.
Eckstein, M. (1998). The lower visual search efficiency for conjunctions is due to noise and not serial attentional processing. Psychol. Sci. 9, 111–118.
Eckstein, M., Thomas, J. P., Palmer, J., and Shimozaki, S. S. (2000). A signal detection model predicts the effects of set size on visual search accuracy for feature, conjunction, triple conjunction, and disjunction displays. Percept. Psychophys. 62, 425–451.
Engel, A. K., Kreiter, A. K., Konig, P., and Singer, W. (1991). Synchronization of oscillatory neuronal responses between striate and extrastriate visual cortical areas of the cat. Proc. Natl. Acad. Sci. U.S.A. 88, 6048–6052.
Engel, A. K., and Singer, W. (2001). Temporal binding and the neural correlates of sensory awareness. Trends Cogn. Sci. (Regul. Ed.) 5, 16–25.
Eriksen, C. W., and Spencer, T. (1969). Rate of information processing in visual perception: some results and methodological considerations. J. Exp. Psychol. 79, 1–16.
Fell, J., Fernandez, G., Klaver, P., Elger, C. E., and Fries, P. (2003). Is synchronized neuronal gamma activity relevant for selective attention? Brain Res. Brain Res. Rev. 42, 265–272.
Feron, F. X., Frissen, I., Boissinot, J., and Guastavino, C. (2010). Upper limits of auditory rotational motion perception. J. Acoust. Soc. Am. 128, 3703–3714.
Fries, P., Reynolds, J. H., Rorie, A. E., and Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563.
Gail, A., Brinksmeyer, H. J., and Eckhorn, R. (2004). Perception-related modulations of local field potential power and coherence in primary visual cortex of awake monkey during binocular rivalry. Cereb. Cortex 14, 300–313.
Gold, I. (1999). Does 40-Hz oscillation play a role in visual consciousness? Conscious Cogn. 8, 186–195.
Gray, C. M., Konig, P., Engel, A. K., and Singer, W. (1989). Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 338, 334–337.
Harter, M. R. (1967). Excitability cycles and cortical scanning: a review of two hypotheses of central intermittency in perception. Psychol. Bull. 68, 47–58.
Hogendoorn, H., Carlson, T. A., VanRullen, R., and Verstraten, F. A. (2010). Timing divided attention. Atten. Percept. Psychophys. 72, 2059–2068.
Hogendoorn, H., Carlson, T. A., and Verstraten, F. A. (2007). The time course of attentive tracking. J. Vis. 7, 1–10.
Holcombe, A. O. (2009). Seeing slow and seeing fast: two limits on perception. Trends Cogn. Sci. (Regul. Ed.) 13, 216–221.
Holcombe, A. O., Clifford, C. W., Eagleman, D. M., and Pakarian, P. (2005). Illusory motion reversal in tune with motion detectors. Trends Cogn. Sci. (Regul. Ed.) 9, 559–560.
Holcombe, A. O., and Seizova-Cajic, T. (2008). Illusory motion reversals from unambiguous motion with visual, proprioceptive, and tactile stimuli. Vision Res. 48, 1743–1757.
Howard, C. J., and Holcombe, A. O. (2008). Tracking the changing features of multiple objects: progressively poorer perceptual precision and progressively greater perceptual lag. Vision Res. 48, 1164–1180.
Howe, P. D., Cohen, M. A., Pinto, Y., and Horowitz, T. S. (2010). Distinguishing between parallel and serial accounts of multiple object tracking. J. Vis. 10, 11.
Hutchinson, C. V., and Ledgeway, T. (2006). Sensitivity to spatial and temporal modulations of first-order and second-order motion. Vision Res. 46, 324–335.
Jans, B., Peters, J. C., and De Weerd, P. (2010). Visual spatial attention to multiple locations at once: the jury is still out. Psychol. Rev. 117, 637–684.
Jensen, O., Gelfand, J., Kounios, J., and Lisman, J. E. (2002). Oscillations in the alpha band (9-12 Hz) increase with memory load during retention in a short-term memory task. Cereb. Cortex 12, 877–882.
Kahana, M. J., Seelig, D., and Madsen, J. R. (2001). Theta returns. Curr. Opin. Neurobiol. 11, 739–744.
Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Res. Brain Res. Rev. 29, 169–195.
Kline, K., and Eagleman, D. M. (2008). Evidence against the temporal subsampling account of illusory motion reversal. J. Vis. 8, 11–15.
Kline, K., Holcombe, A. O., and Eagleman, D. M. (2004). Illusory motion reversal is caused by rivalry, not by perceptual snapshots of the visual field. Vision Res. 44, 2653–2658.
Koch, C., and Braun, J. (1996). Towards the neuronal correlate of visual awareness. Curr. Opin. Neurobiol. 6, 158–164.
Large, E. W., and Jones, M. R. (1999). The dynamics of attending: how people track time-varying events. Psychol. Rev. 106, 119–159.
Latour, P. L. (1967). Evidence of internal clocks in the human operator. Acta Psychol. (Amst) 27, 341–348.
Lichtenstein, M. (1961). Phenomenal simultaneity with irregular timing of components of the visual stimulus. Percept. Mot. Skills 12, 47–60.
Lisman, J. E., and Idiart, M. A. (1995). Storage of 7 ± 2 short-term memories in oscillatory subcycles. Science 267, 1512–1515.
Lu, Z. L., Lesmes, L. A., and Sperling, G. (1999). Perceptual motion standstill in rapidly moving chromatic displays. Proc. Natl. Acad. Sci. U.S.A. 96, 15374–15379.
Lu, Z. L., and Sperling, G. (2001). Three-systems theory of human visual motion perception: review and update. J. Opt. Soc. Am. A. Opt. Image Sci. Vis. 18, 2331–2370.
Martinez-Conde, S., Macknik, S. L., Troncoso, X. G., and Dyar, T. A. (2006). Microsaccades counteract visual fading during fixation. Neuron 49, 297–305.
Mathewson, K. E., Fabiani, M., Gratton, G., Beck, D. M., and Lleras, A. (2010). Rescuing stimuli from invisibility: inducing a momentary release from visual masking with pre-target entrainment. Cognition 115, 186–191.
McElree, B., and Carrasco, M. (1999). The temporal dynamics of visual search: evidence for parallel processing in feature and conjunction searches. J. Exp. Psychol. Hum. Percept. Perform. 25, 1517–1539.
McMains, S. A., and Somers, D. C. (2004). Multiple spotlights of attentional selection in human visual cortex. Neuron 42, 677–686.
Moore, C. M., Egeth, H., Berglan, L. R., and Luck, S. J. (1996). Are attentional dwell times inconsistent with serial visual search? Psychon. Bull. Rev. 3, 360–365.
Moutoussis, K., and Zeki, S. (1997). A direct demonstration of perceptual asynchrony in vision. Proc. R. Soc. Lond. B Biol. Sci. 264, 393–399.
Muller, M. M., Malinowski, P., Gruber, T., and Hillyard, S. A. (2003). Sustained division of the attentional spotlight. Nature 424, 309–312.
Niebur, E., Koch, C., and Rosin, C. (1993). An oscillation-based model for the neuronal basis of attention. Vision Res. 33, 2789–2802.
Oksama, L., and Hyona, J. (2008). Dynamic binding of identity and location information: a serial model of multiple identity tracking. Cogn. Psychol. 56, 237–283.
Palmer, J. (1995). Attention in visual search: distinguishing four causes of a set-size effect. Curr. Dir. Psychol. Sci. 4, 118–123.
Piantoni, G., Kline, K. A., and Eagleman, D. M. (2010). Beta oscillations correlate with the probability of perceiving rivalrous visual stimuli. J. Vis. 10, 18.
Pitts, W., and McCulloch, W. S. (1947). How we know universals: the perception of auditory and visual forms. Bull. Math. Biophys. 9, 127–147.
Poppel, E., and Logothetis, N. (1986). Neuronal oscillations in the human brain. Discontinuous initiations of pursuit eye movements indicate a 30-Hz temporal framework for visual information processing. Naturwissenschaften 73, 267–268.
Purves, D., Paydarfar, J. A., and Andrews, T. J. (1996). The wagon wheel illusion in movies and reality. Proc. Natl. Acad. Sci. U.S.A. 93, 3693–3697.
Pylyshyn, Z. W., and Storm, R. W. (1988). Tracking multiple independent targets: evidence for a parallel tracking mechanism. Spat. Vis. 3, 179–197.
Ray, S., and Maunsell, J. H. (2010). Differences in gamma frequencies across visual cortex restrict their possible use in computation. Neuron 67, 885–896.
Reddy, L., Remy, F., Vayssiere, N., and VanRullen, R. (2011). Neural correlates of the continuous wagon wheel illusion: a functional MRI study. Hum. Brain Mapp. 32, 163–170.
Revonsuo, A., Wilenius-Emet, M., Kuusela, J., and Lehto, M. (1997). The neural generation of a unified illusion in human vision. Neuroreport 8, 3867–3870.
Rezec, A., Krekelberg, B., and Dobkins, K. R. (2004). Attention enhances adaptability: evidence from motion adaptation experiments. Vision Res. 44, 3035–3044.
Sanford, J. A. (1971). “A periodic basis for perception and action,” in Biological Rhythms and Human Performance, ed. W. Colquhuon (New York: Academic Press), 179–209.
Schouten, J. F. (1967). “Subjective stroboscopy and a model of visual movement detectors,” in Models for the Perception of Speech and Visual Form I. ed. Wathen-Dunn (Cambridge, MA: MIT Press), 44–45.
Shepard, R. N. (1964). Circularity in judgments of relative pitch. J. Acoust. Soc. Am. 36, 2346–2353.
Shiffrin, R. M., and Gardner, G. T. (1972). Visual processing capacity and attentional control. J. Exp. Psychol. 93, 72–82.
Simpson, W. A., Shahani, U., and Manahilov, V. (2005). Illusory percepts of moving patterns due to discrete temporal sampling. Neurosci. Lett. 375, 23–27.
Singer, W., and Gray, C. M. (1995). Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 18, 555–586.
Stroud, J. M. (1956). “The fine structure of psychological time,” in Information Theory in Psychology, ed. H. Quastler (Chicago, IL: Free Press), 174–205.
Tallon-Baudry, C., Bertrand, O., Delpuech, C., and Permier, J. (1997). Oscillatory gamma-band (30-70 Hz) activity induced by a visual search task in humans. J. Neurosci. 17, 722–734.
Tallon-Baudry, C., Bertrand, O., Peronnet, F., and Pernier, J. (1998). Induced gamma-band activity during the delay of a visual short-term memory task in humans. J. Neurosci. 18, 4244–4254.
Townsend, J. (1990). Serial vs. parallel processing: sometimes they look like tweedledum and tweedledee but they can (and should) be distinguished. Psychol. Sci. 1, 46–54.
Treisman, A., and Gelade, G. (1980). A feature-integration theory of attention. Cogn. Psychol. 12, 97–136.
Tseng, C. H., Gobell, J. L., Lu, Z. L., and Sperling, G. (2006). When motion appears stopped: stereo motion standstill. Proc. Natl. Acad. Sci. U.S.A. 103, 14953–14958.
Uchida, N., Kepecs, A., and Mainen, Z. F. (2006). Seeing at a glance, smelling in a whiff: rapid forms of perceptual decision making. Nat. Rev. Neurosci. 7, 485–491.
VanRullen, R. (2006). The continuous wagon wheel illusion is object-based. Vision Res. 46, 4091–4095.
VanRullen, R. (2007). The continuous wagon wheel illusion depends on, but is not identical to neuronal adaptation. Vision Res. 47, 2143–2149.
VanRullen, R., Busch, N. A., Drewes, J., and Dubois, J. (2011). Ongoing EEG phase as a trial-by-trial predictor of perceptual and attentional variability. Front. Psychology 2:60. doi: 10.3389/fpsyg.2011.00060
VanRullen, R., Carlson, T., and Cavanagh, P. (2007). The blinking spotlight of attention. Proc. Natl. Acad. Sci. U.S.A. 104, 19204–19209.
VanRullen, R., Guyonneau, R., and Thorpe, S. J. (2005a). Spike times make sense. Trends Neurosci. 28, 1–4.
VanRullen, R., Reddy, L., and Koch, C. (2005b). Attention-driven discrete sampling of motion perception. Proc. Natl. Acad. Sci. U.S.A. 102, 5291–5296.
VanRullen, R., and Koch, C. (2003). Is perception discrete or continuous? Trends Cogn. Sci. 7, 207–213.
VanRullen, R., Pascual-Leone, A., and Battelli, L. (2008). The continuous wagon wheel illusion and the ‘when’ pathway of the right parietal lobe: a repetitive transcranial magnetic stimulation study. PLoS ONE 3, e2911. doi: 10.1371/journal.pone.0002911
VanRullen, R., Reddy, L., and Koch, C. (2006). The continuous wagon wheel illusion is associated with changes in electroencephalogram power at approximately 13 Hz. J. Neurosci. 26, 502–507.
VanRullen, R., Reddy, L., and Koch, C. (2010). “A motion illusion revealing the temporally discrete nature of awareness,” in Space and Time in Perception and Action, ed. R. Nijhawan (Cambridge: Cambridge University Press), 521–535.
von der Malsburg, C. (1995). Binding in models of perception and brain function. Curr. Opin. Neurobiol. 5, 520–526.
White, C. (1963). Temporal numerosity and the psychological unit of duration. Psychol. Monogr. 77, 1–37.
White, C. T., Cheatham, P. G., and Armington, J. C. (1953). Temporal numerosity: II. Evidence for central factors influencing perceived number. J. Exp. Psychol. 46, 283–287.
Wolfe, J. M. (1998). “Visual Search” in Attention ed. H. Pashler (London: University College London Press), 13–73.
Keywords: oscillation, perception, attention, psychophysics, discrete perception, sequential attention
Citation: VanRullen R and Dubois J (2011) The psychophysics of brain rhythms. Front. Psychology 2:203. doi: 10.3389/fpsyg.2011.00203
Received: 07 March 2011; Accepted: 09 August 2011;
Published online: 27 August 2011.
Edited by:
Gregor Thut, University of Glasgow, UKReviewed by:
Hinze Hogendoorn, Utrecht University, NetherlandsAyelet Nina Landau, Ernst Strüngmann Institute in Cooperation with Max Planck Society, Germany
Copyright: © VanRullen and Dubois. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Rufin VanRullen, Centre de Recherche Cerveau et Cognition, Pavillon Baudot, Hopital Purpan, Place du Dr. Baylac, 31052 Toulouse, France. e-mail: rufin.vanrullen@cerco.ups-tlse.fr

