
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol. , 05 April 2023
Sec. Computational Physiology and Medicine
Volume 14 - 2023 | https://doi.org/10.3389/fphys.2023.1162436
This article is part of the Research Topic New Experimental and Numerical Insights on Cardiovascular Biomechanics through In-vivo and Ex-vivo Methods View all 9 articles
In this work an Artificial Neural Network (ANN) was developed to help in the diagnosis of plaque vulnerability by predicting the Young modulus of the core (Ecore) and the plaque (Eplaque) of atherosclerotic coronary arteries. A representative in silico database was constructed to train the ANN using Finite Element simulations covering the ranges of mechanical properties present in the bibliography. A statistical analysis to pre-process the data and determine the most influential variables was performed to select the inputs of the ANN. The ANN was based on Multilayer Perceptron architecture and trained using the developed database, resulting in a Mean Squared Error (MSE) in the loss function under 10–7, enabling accurate predictions on the test dataset for Ecore and Eplaque. Finally, the ANN was applied to estimate the mechanical properties of 10,000 realistic plaques, resulting in relative errors lower than 3%.
Cardiovascular diseases (CVDs) are the leading cause of death in the world. An estimated 17.9 million people died from CVDs in 2019, representing 32% of all global deaths. Atherosclerosis is one of the most common CVDs, causing more than 50% of the sudden deaths (Wilkins et al., 2017; Roth et al., 2020; World Health Organization, 2021). This pathology may start at a premature age (Napoli et al., 1997; Napoli et al., 1999; Pederiva et al., 2021), but, over time, it can result in acute events such as strokes and heart attacks. One of the main causes that trigger atherosclerosis is endothelial damage. From a mechanical point of view, a decrease in Wall Shear Stress (WSS) will eventually reshape the endothelial cells into a more circular shape causing an increase in their permeability (Malek et al., 1999; Esper et al., 2006).
An atherosclerotic coronary artery is usually divided into the following parts (Figure 1): a necrotic lipid-rich core or fatty tissue; a fibrotic tissue, which is the result of a thickening of the tunica intima due to a migration of synthetic smooth muscle cells from the tunica media; the fibrous cap, which is the thin layer of fibrotic tissue separating the lipid-rich core from the lumen; the tunica media and the tunica adventitia (Falk et al., 1995; Lee and Libby, 1997; Virmani et al., 2000; Akyildiz et al., 2018). The major risk of a plaque is when there is an evident risk that the fibrous cap ruptures, releasing the necrotic content into the lumen, and causing a thrombus that may result in a myocardial infarction (Finn et al., 2010; Stefanadis et al., 2017).
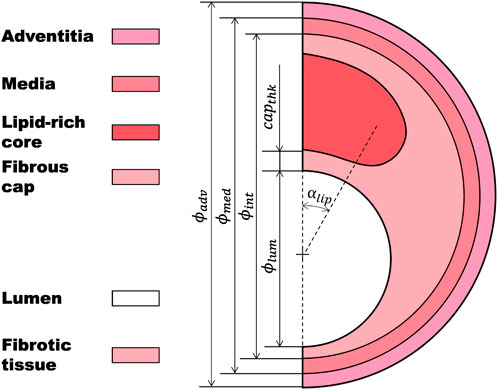
FIGURE 1. Idealized atherosclerotic coronary artery including lipid-rich core, fibrotic tissue, fibrous cap, tunica media, and tunica adventitia.
The mechanical characterization of atherosclerotic arteries has been shown to be valuable for diagnosing vulnerable plaques. Additive manufacturing can leverage this mechanical characterization to create replicas that can be useful in surgical simulation (Henriques et al., 2023). In addition, other approaches, such as the one proposed by Gold et al. (2019), highlight the importance of mechanical characterization of each layer of the artery in developing predictive models of vascular pathophysiology.
In order to make a diagnosis of this pathology, the gold standard technique is intravascular ultrasound echography (IVUS) (Moore et al., 1998; Nair et al., 2002; Nasu et al., 2006; Gogas et al., 2011; Li et al., 2014). Using this procedure in combination with endovascular elastography (EVE), it is possible to estimate artery wall strains and, therefore, predict those areas more prone to rupture (Maurice et al., 2004; Maurice et al., 2005; 2007). In addition, several techniques exist to detect vulnerable plaques (VPs) by predicting their morphology and the type of tissue conforming the plaque, such as the intraluminal ultrasonic palpation imaging technique (Gómez et al., 2019), which combines the radio-frequency technique with Finite Element Analysis (FEA); virtual histology, based on the spectral analysis of retro-dispersed radio-frequency ultrasounds (Moore et al., 1998; Kovarnik et al., 2011; Layland et al., 2011; De Graaf et al., 2013); or near-infrared spectroscopy (NIRS), that quantifies the lipid content in the atheroma plaque (Erlinge et al., 2021). However, an approach performed with adult mini-pigs prone to atherosclerosis showed that necrotic core sizes determined by virtual and real histology were different, thus questioning the capacity of virtual histology to detect prone plaques (Thim, 2010). Moreover, none of these techniques have the capacity to quantify the mechanical properties of the arterial wall, which is essential to estimate stress distribution (Akyildiz et al., 2011; Wang et al., 2019). One promising approach is the iMOD elastography (Le Floc’h et al., 2010), which developed several computational algorithms to rebuild elasticity strain maps inside the wall based on the prediction of the stress maps using IVUS-derived techniques. Since 2009, some remarkable improvements have been developed, such as two powerful stability plaque bio-markers of the coronary artery based on radial strains and its gradient, which allow Young’s modulus to be obtained under linear isotropic elasticity, plane strain, and incompressibility hypothesis (Le Floc’h et al., 2009; Tacheau et al., 2016; Gómez et al., 2019). However, all these methods share a common issue: the waiting time between acquiring the image and obtaining the results from the computational model is prolonged due to the need to optimize the problem specific to the patient.
Recently, a new promising study used a combination of magnetic resonance imaging (MRI), FEA, and a Bayesian optimization process for material property assessment under physiological loading conditions (Torun et al., 2022). This study demonstrated the feasibility of estimating material properties through an optimization algorithm. However, its applicability is limited by the small number of specimens tested and the fact that the specimens were ex-vivo.
In Wang et al. (2023), the mechanical properties were predicted in-vivo starting from IVUS images, where a close link between plaque morphological characteristics and mechanical properties was reported, but the statistical approach of this work was performed with little data (n = 32).
On the contrary, Deep Learning (DL) frameworks have been trained using large databases to predict the mechanical properties of living tissue. For instance, Ma et al. (2022) used DL to predict the elastic modulus of 3D-printed lattice structures. Another noteworthy study employed a 5-layer fully connected neural network to extract tissue optical properties (Hokr and Bixler, 2021).
Therefore, the aim of this project is to propose an approach that may help in the diagnosis of VPs by estimating the in-vivo patient-specific mechanical properties (Ecore and Eplaque) of the plaque constituents. For this reason, we developed a large in silico database and explored the utility of Artificial Neural Networks (ANNs) in elastic properties prediction of the atheroma plaque components. Similar machine learning techniques have been previously used to predict the maximum principal stress as one of the most common mechanical predictors for plaque vulnerability (Cilla et al., 2012). However their approach was based on the geometry, but artery mechanical properties were not considered.
Figure 2 shows the workflow used to develop a computational framework for the estimation of Ecore and Eplaque of a patient-specific atheroma plaque. Based on the information taken from the IVUS images previously published (Le Floc’h et al., 2009) and the anatomy of the atherosclerotic coronary artery, we performed the Finite Element Method (FEM) on 540 different 2D idealized geometries. As seen in other works (Nong et al., 2022; Shen et al., 2022; Le Floc’h et al., 2009; Finet et al., 2004), 2D models are commonly used when artery geometries are obtained from the segmentation of IVUS images. One of the key advantages of using 2D models for studying the mechanical properties of atherosclerotic coronary arteries is that the IVUS images provide 2D cross-sectional information of the coronary artery geometry. Furthermore, 2D models are favored over 3D models as they offer a more streamlined and efficient analysis process, requiring fewer computational resources and yielding quicker results. Subsequently, a statistical analysis was carried out on the outputs of the FEA (strains), in order to select the most influential variables on Ecore and Eplaque as the inputs of the ANN. We then trained and tested the ANN by minimizing a loss function (MSE), and computed the relative error in the prediction of the mechanical properties of the training and testing datasets. Finally, we applied the ANN to estimate the mechanical properties of 10,000 plaque geometries and computed the relative error.
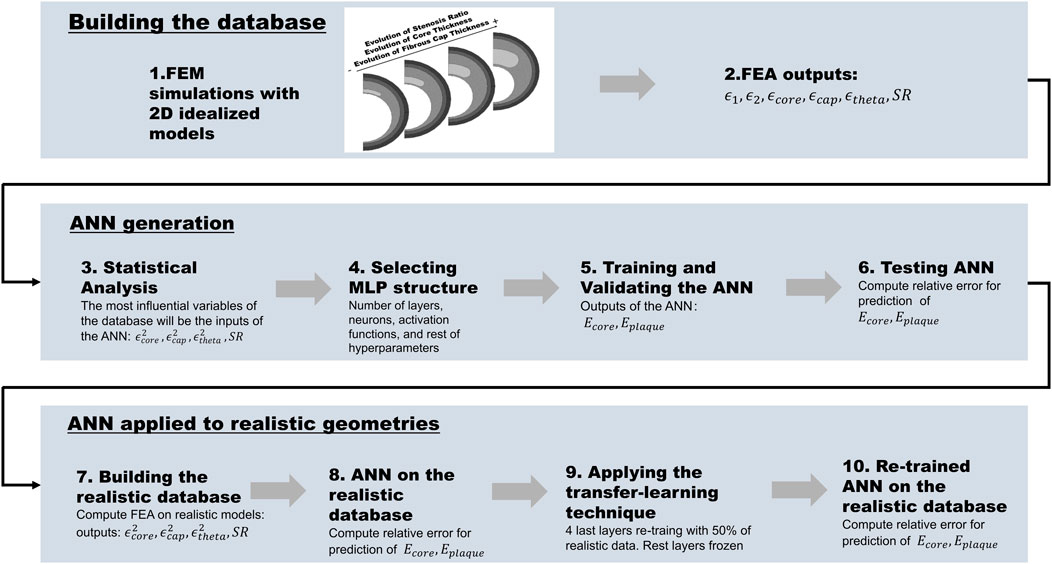
FIGURE 2. The workflow is divided into building the database, generating the ANN, and applying it to realistic geometries: 1) Building the idealized database and performing the FEA simulations; 2) Selecting the outputs of the FEA (ϵ1, ϵ2, ϵcore, ϵplaque, ϵtheta, and SR); 3) Statistical analysis of the FEA output variables and selection of the inputs of the ANN (
The idealized 2D geometry of the atherosclerotic coronary artery was divided into four main parts: a lipid-rich core; a thickened tunica intima, which is considered as a fibrotic tissue (where the fibrous cap is the most critical area); the tunica media; and the tunica adventitia (Figure 1). The main geometrical characteristics of the base geometry were: the diameter of the lumen (ϕlum = 3.6 mm), the diameter of the intima layer (ϕint = 5.596 mm), the diameter of the media layer (ϕmed = 6.05 mm), the diameter of the adventitia layer (ϕadv = 6.5 mm), the thickness of the fibrous cap (capthk = 65 μm), the angle of the lipid-rich core (αlipid = 60o), and the stenosis ratio (SR = 70%) (Equation 1).
where Aplaque and Alumen are the area of the plaque and the lumen respectively.
In order to build a solid database, 540 distinct idealized geometries were generated by varying the following parameters (Table 1): nine variations of stenosis ratio (SR = 40%–80%) (Finn et al., 2010), ten variations of the thickness of the fibrous cap (capthk = 65 μm − 300 μm) (Loree et al., 1992) and six variations of the thickness of the lipid-rich core (corethk = 300 μm − 800 μm) (Virmani et al., 2000).
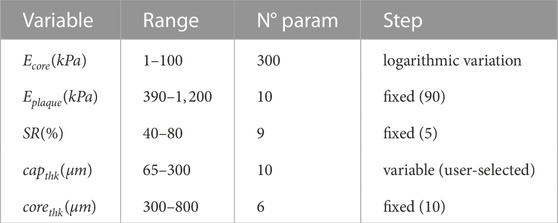
TABLE 1. Proposed ranges for each variable of the model composing the database. Mechanical properties (Ecore and Eplaque) in kPa. Geometrical variables (SR, capthk and corethk) in % and μm respectively.
Due to the high variability found in experimental studies on the coronary artery, setting the mechanical properties of each area in the model was a challenging task. Therefore, in this study, we established the range of Young’s modulus for the lipid-rich core (Ecore = 1–100 kPa) and the fibrotic tissue (Eplaque = 390–1,200 kPa) after conducting a thorough analysis of the mechanical properties reported by different authors (Akyildiz et al., 2018; Baldewsing et al., 2004; Cheng et al., 1993; Finet et al., 2004; Le Floc’h et al., 2009; Peña et al., 2021; Gómez et al., 2019). We proposed the ranges of material properties with the aim of covering all possible variability (Table 1). In addition, given the greater variability found in the Ecore range, we performed 300 variations with a variable step that followed a logarithmic function, in order to obtain a higher density of data in the lower part of the range. On the other hand, only 10 variations of Eplaque were accomplished with a fixed step of 90 kPa, as the variability found in this tissue was lower.
As our objective was to predict the Young’s modulus for both the lipid-rich core and fibrotic tissue, which were assumed to be isotropic, we selected the widely-used and simple neo-Hookean hyperelastic material model. This model is known to provide a good approximation of the true material behavior when working with low strains. Its energy function for incompressible materials in 3D is described in Equation 2:
where I1 is the first invariant of the right Cauchy-Green deformation tensor and C10 is a material parameter representing the slope of the stress-strain curve that can be written as a function of Young’s modulus (E) (Equation 3).
On the contrary, we did not predict the mechanical properties of the media and adventitia layers because of the limitations of the IVUS imaging technique in accurately identifying them. As a result, the material model selected for these layers was the GOH model (Gasser et al., 2006), and their mechanical properties were selected from the literature (Latorre et al., 2022) (Table 2).
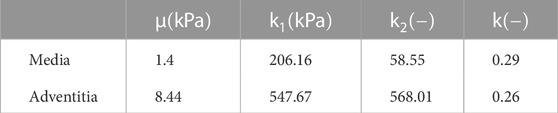
TABLE 2. Material parameters used in the FEA for the media and adventitia layers where the GOH strain energy was considered.
All models were subject to the same boundary conditions, loading, and mesh size. In order to avoid rigid solid displacements and rotations, the model was constrained in y direction in a peripheral point. Due to symmetry, only half of the model was considered. A load of 18.66 kPa was applied, representing the high blood pressure (140 mmHg) of a hypertensive patient (Banegas, 2005). However, since IVUS images catch the geometrical information in an increment of 5 mmHg (Maurice et al., 2004), results were obtained in the last increment of 5 mmHg (135–140 mmHg). The database was generated with a full factorial approach where all the possible combinations were considered, resulting in a total of 1,782,000 cases.
From each model, several potential input variables for the ANN were obtained such as the maximum (ϵ1) and minimum (ϵ2) principal strains, the variation of the thickness of the core (ϵcore) and the fibrous cap (ϵcap), the lumen diameter variation (ϵtheta) (Equation 5), and the SR (%). A statistical analysis was then performed to identify the most relevant variables, their significance, and multicollinearity.
where
It is widely known that Artificial Intelligence (AI) relies its predictive capacity on statistics (Gardner and Dorling, 1998). Therefore, both descriptive and inferential statistical analyses were carried out. The descriptive statistical analysis allows to detect if there is any pattern or trend followed by the candidate variables against the response variables. Complementary, the inferential statistical analysis helps in identifying those variables that most influence the response. The objective of analyzing the statistics from these two points of view is to have a better criterion to select the inputs of the ANN. For this purpose, we performed a regression analysis of each candidate variable against each response variable separately. After that, a multivariate regression analysis was executed to detect which were the most influential variables when predicting the two response variables (Ecore, Eplaque) simultaneously. The inferential analysis was accomplished using the step-wise method with a significance of p < 0.05. Additionally, in order to keep the model as simple as possible, we paid special attention to the multicollinearity of the variables, using the most common method: VIF (Variable Inflation Factor). If two variables were significant but the multicollinearity factor was high, we repeated the analysis without one of the variables (Siotani et al., 1985).
AI is believed to be capable of giving quick responses to patient-specific clinical problems. Since our start point is the geometrical data available from the IVUS, we used a multi-layer perceptron (MLP) (Gardner and Dorling, 1998) based on supervised learning (Kotsiantis et al., 2007) to develop our Artificial Neural Network (ANN). An MLP has to extract a relation solely from the presented examples, which together are assumed to implicitly contain the necessary information for this relation (Park and Lek, 2016). The structure of an ANN consists of a collection of neurons grouped in layers, connected through weights, and activated by activation functions (Agatonovic-Kustrin and Beresford, 2000).
To develop the ANN the open-source software library for machine learning PyTorch (version 1.13.1) was used.
The learning algorithm of the ANN starts with the division of the database into training data (80%), internal validation (10%), and testing data (10%). Next, in order to avoid one variable could predominate over the others (SR takes values of 40%–80% while strains take values of 0.5%) the data was normalized using a z-score scaler (Equation 6):
where x is the sample, μ is the mean and σ is the standard deviation.
Then, a forward propagation step followed by a backward propagation step is conducted (LeCun et al., 1988). In the forward propagation step, the information of each neuron (xi) passes to each neuron of the following layers (hidden layers) according to a weight (wi) previously assigned. The information passes through an activation function (ψ) providing the non-linearity to the network, and then, it is transferred to the following layer. Each neuron receives the sum of information from all the connected neurons activated in the previous layer. This process is summed up in Equation 7:
where y is the output signal, ψ is the activation function and wbias is the bias.
When the flow of information arrives at the last layer, it generates the outputs of the ANN, which in this study are Ecore and Eplaque. The weights and biases are randomly assigned in the first iteration and will be adjusted in the following iterations in order to minimize a loss function, which for the current study is the Mean Squared Error (MSE) (Equation 8).
where
After that, the backward propagation starts. This process relies on assigning a level of responsibility for the error to each neuron. Those neurons with a major influence in the error will have to change their weights more than those whose error’s responsibility is lower. This iterative process is the training step.
Once the training step finishes, the validation step begins. In this step, the ANN checks its capacity for predicting new values of the response variables out of the training dataset. The loss function values obtained in training and validation steps are compared in order to analyze how different they are and if the ANN suffers overfitting (Dietterich, 1995). In case they are similar and low enough, we could say the ANN has good prediction quality. In addition, in order to better quantify the error in the predictions, we computed and compared the relative error in the prediction of Ecore and Eplaque for both training and testing datasets (Equation 9).
Once the ANN was trained and tested, we applied it to 10,000 realistic geometries generated from the four real IVUS images previously published in Le Floc’h et al. (2009). The realistic in silico database was obtained by creating 20 different geometries varying the fibrous cap thickness from 65 μm to 300 μm, and assigning 500 different material combinations. According to this, 50 variations of Ecore in a range of 1 kPa–100 kPa and 10 variations of Eplaque in a range of 390 kPa–1,200 kPa were conducted (see Figure 3).

FIGURE 3. Construction of realistic database using 20 cases with varied fibrous cap thickness, based on a real geometry (65μm–300 μm).
When analyzing the predictions of the mechanical properties for the realistic geometries, the ANN predictions were not accurate (see Section 3.2). Therefore, the ANN was improved by fine-tuning the parameters using the transfer-learning technique (Tan et al., 2018; Yu et al., 2022).
Other studies have used this technique in a hybrid model based on a convolutional neural network (CNN) and a long short-term memory recurrent neural network (LSTM RNN) to classify benign and malignant breast cancer subtypes (Ikemoto et al., 2023).
Transfer learning is a machine learning technique that involves the transfer of knowledge learned in one task to improve the performance of another related task. This technique can be used to improve the prediction of the realistic dataset by leveraging the knowledge learned from a more extensive idealized dataset, improving the model’s ability to generalize to new data.
The initial layers of an MLP are responsible for identifying and extracting the fundamental and more generalized features within a dataset, whilst the later layers are supposed to learn the most specific patterns within the dataset. This is where the transfer-learning technique, known as fine-tuning, comes into play. The majority of the ANN’s weights are preserved, but the weights of the later layers are updated by re-training them with the new realistic dataset. Specifically, the last four layers of our proposed ANN were fine-tuned using the 50% of our realistic dataset, while the remaining layers were kept frozen. The other 50% of the realistic dataset was reserved for testing the ANN.
Hereby, we report the results of the statistical analysis (Figure 4). In order to avoid repetitions, we show only the results of the variables ϵ1 and ϵ2 vs Ecore and Eplaque, since all presented a similar behavior and the conclusions drawn from them were the same. Besides, to preserve image legibility, a representative sample of the data population is reported in each plot.
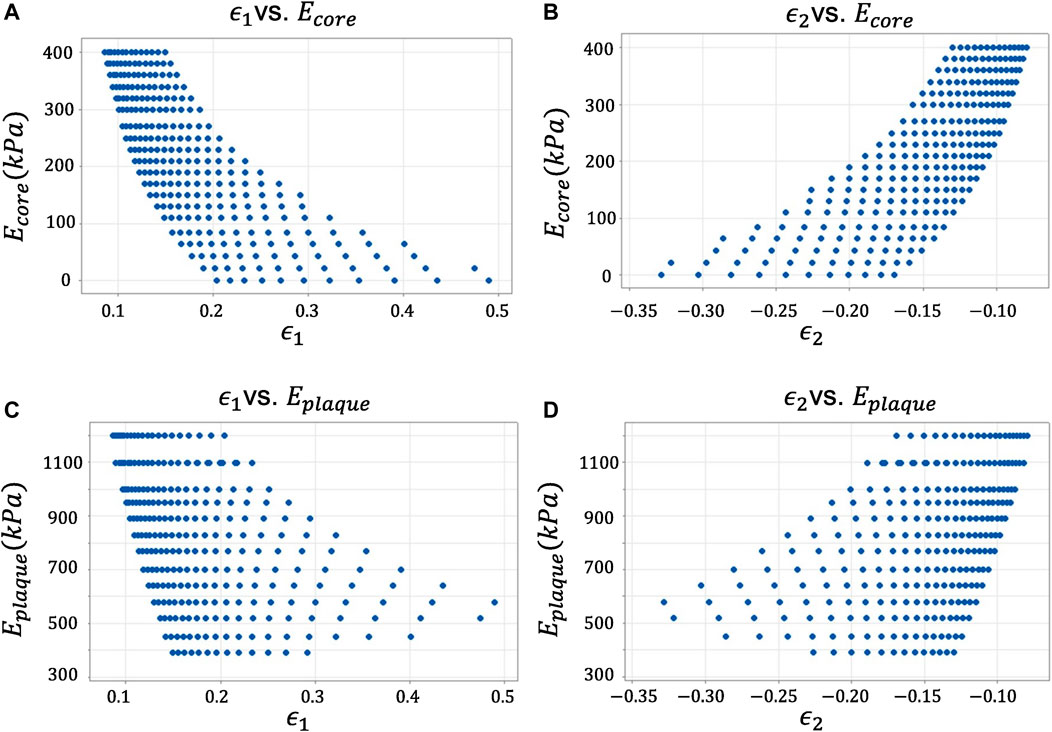
FIGURE 4. Descriptive statistical analysis of the candidate variables against the response variables. (A) Maximum Principal Strain ϵ1 vs. Young’s modulus of the lipid core Ecore. (B) Minimum Principal Strain ϵ2 vs. Young’s modulus of the lipid core Ecore. (C) Maximum Principal Strain ϵ1 vs. Young’s modulus of the lipid core Eplaque. (D) Minimum Principal Strain ϵ2 vs. Young’s modulus of the lipid core Eplaque.
As mentioned in Section 2.2, the inferential statistical analysis for the study of the most influential variables in the response was divided into: a single-output regression analysis for the prediction of Ecore and Eplaque separately; and, a multivariate regression analysis for the prediction of Ecore and Eplaque simultaneously. The single-output regression analysis started considering the nine candidate variables (ϵ1, ϵ2, ϵcore, ϵcap, ϵtheta,
According to these results, the inputs of the ANN were:
In this study, a 14-layer ANN was employed, with rectified linear unit (ReLU) activation function applied to each hidden layer (Equation 10). The Adam optimization algorithm (Kingma and Ba, 2014) was used for training the model, and the training process was conducted over 7,000 epochs. The learning rate was dynamically adjusted along the training process, starting from 1e-3 and decreasing sequentially one order of magnitude at epochs 500, 1,000, 1,500, 2000, 3,500, and 5,000. As can be seen in Figure 5, the loss function (MSE) of this ANN achieves values under 10–7.
To evaluate the performance of the ANN, the relative error in the prediction of Ecore and Eplaque was computed in three different cases.
• First case: Original ANN tested with the idealized dataset
• Second case: Original ANN tested with the realistic dataset
• Third case: Transfer-learned ANN tested with the realistic dataset
The results of the first case showed a low relative error
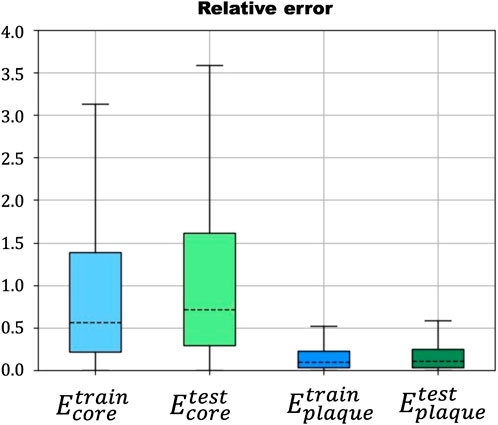
FIGURE 6. Relative error in the prediction of Ecore (blue) and Eplaque (green) in the training and testing steps of the ANN.

FIGURE 7. Relative error in the prediction of Ecore (blue) and Eplaque (green) using the transfer-learned ANN with the realistic database.
In this study, we investigated the potential of artificial neural networks (ANN) for accurately estimating the mechanical properties of the atherosclerotic coronary artery. We employed a methodology that involved analyzing the statistics of the candidate variables prior to developing the ANN, which allowed us to establish a more informed criterion for selecting the inputs for the model. It is important to note that while these statistics provided useful guidance, they were not considered definitive. Given the scarcity of real-world data, our database was initially constructed using idealized geometries. To assess the ANN’s ability to generalize to more realistic scenarios, we applied it to a sample of 10,000 realistic geometries, providing a thorough evaluation of its performance.
The inferential statistical analysis was an interactive process (data not shown) where all the candidate variables were first included. In a preliminary model, almost all the candidate variables and their interactions were included as significant by the step-wise method. The model showed problems of multicollinearity, so, due to the non-linear behavior previously observed, all the linear strains were removed. Now, the step-wise method selected the SR (%),
The same methodology was followed for the analysis of the candidate variables over Eplaque. The analysis with all the candidate variables and their interactions with each other and themselves considered the following variables as significant: ϵ1, ϵtheta, SR (%),
Based on the statistical analysis, it was determined that the most influential input parameters for the prediction of Ecore and Eplaque were
The proposed ANN trained with the large and idealized database presented low relative errors in the prediction of Ecore and Eplaque both during the training and the testing step. However, when applied to a realistic dataset, the ANN struggled to accurately predict the mechanical properties. To improve its performance, a fine-tuning process was applied, utilizing 50% of the realistic dataset to update the weights of the last four layers of the ANN. The result was a significant improvement in accuracy, as evidenced by a relative error lower than 3% when predicting the remaining 50% of the realistic dataset. Our results align with recent studies in the field (Torun et al., 2022), further confirming the effectiveness of using ANNs for predicting mechanical properties in the atherosclerotic coronary artery.
Other studies have also accomplished a mechanical characterization of the plaque constituents. Specifically, Akyildiz et al. (2011) studied the effects of the intima stiffness and the plaque morphology on the stress of the fibrous cap using idealized geometries based on histology images of human coronary arteries; O’Reilly et al. (2020) carried out an investigation of morphological and mechanical properties of iliofemoral and carotid atherosclerotic plaque constituents starting from μCT images; Maher et al. (2009) characterized the mechanical behavior by performing tensile and compressive tests on fresh human carotid plaques removed from endarterectomy; Davis et al. (2016) studied the fracture behavior of human atherosclerotic fibrous cap using a miniature single edge notched tensile test; and, Teng et al. (2009) determined the uniaxial tensile strength of the adventitia and media of human carotid artery throughout an experimental study.
However, our novel perspective is based on the estimation of the material properties throughout a large and representative database that takes into account different lipid-rich core sizes, fibrous cap thicknesses, and stenosis ratio values.
This project is an initial step in the development of neural networks for the prediction of mechanical properties of atherosclerotic coronary arteries. There are some limitations associated. 1) The geometry used for training the ANN is an idealized geometry that only includes one lipid-rich core, which may not fully capture the complex and variable nature of real-world arterial morphology. 2) The database has been generated completely in silico, starting from the before mentioned idealized geometries. However, it does not exist a database of real images with mechanical properties. Therefore, we tried to overcome this limitation by applying a wide variety of mechanical properties as they can be found in the published literature. In our opinion, a possible solution for this limitation could be to develop an image-driven database. This would allow the neural network to learn directly from real cases. 3) The use of a neo-Hookean material model may be a limitation as it may not accurately capture the non-linear behavior of the plaque constituents. However, the assumption of linear material behavior is a good approximation for low ΔP, and in this work ΔP was assumed as 5 mmHg. 4) The study only characterized the mechanical behavior of the fibrous cap and the lipid-rich core, and did not take into account the contribution of other plaque constituents such as calcified regions.
The estimation of the mechanical properties may provide rich information to identify plaque vulnerability, such as whether an atherosclerotic coronary artery suffers from a reduced collagen synthesis, local overexpression of collagenase, or smooth muscle cell apoptosis (Libby, 2001; Akyildiz et al., 2011; Davis et al., 2016; Wang et al., 2019; O’Reilly et al., 2020). This information can also be used to evaluate the impact of different drugs in treating atherosclerosis.
As future steps, we suggest the use of 3D geometries, more complex material models for the lipid-rich core and the fibrotic tissue and if possible, a large database of images to build a neural network with different suitable architectures such as convolutional neural networks (LeCun and Bengio, 1995; Lawrence et al., 1997; Gu et al., 2018).
The proposed ANN model was able to accurately predict the mechanical properties of the atherosclerotic coronary artery using input parameters of
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Conceiving and designing the study: MM and EP Development of the in silico database and the Artificial Neural Network: RC, MM, and EP. Writing, reviewing and editing: RC., MM, and EP.
Support was obtained from the Spanish Ministry of Science and Technology through research project PID 2019-107517RB-I00 and financial support to RC from the funding through grant PRE 2020-095671.
The authors thank the research support from the CIBER initiative. CIBER actions are financed by the Instituto de Salud Carlos III with assistance from the European Regional Development Fund. We extend our gratitude to Carlos Bermejo and Beatriz Moya, members of the Applied Mechanics and Bioengineering group (AMB), for their assistance in this project.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Agatonovic-Kustrin, S., and Beresford, R. (2000). Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Analysis 22, 717–727. doi:10.1016/S0731-7085(99)00272-1
Akyildiz, A. C., Speelman, L., van Brummelen, H., Gutiérrez, M. A., Virmani, R., van der Lugt, A., et al. (2011). Effects of intima stiffness and plaque morphology on peak cap stress. Biomed. Eng. Online 10, 13–25. doi:10.1186/1475-925X-10-25
Akyildiz, A. C., Speelman, L., Velzen, B. V., Stevens, R. R., Van Der Steen, A. F., Huberts, W., et al. (2018). Intima heterogeneity in stress assessment of atherosclerotic plaques. Interface Focus 8, 20170008. doi:10.1098/rsfs.2017.0008
Baldewsing, R. A., De Korte, C. L., Schaar, J. A., Mastik, F., and Van der Steen, A. F. (2004). Finite element modeling and intravascular ultrasound elastography of vulnerable plaques: Parameter variation. Ultrasonics 42, 723–729. doi:10.1016/j.ultras.2003.11.017
Banegas, J. B. (2005). Epidemiología de la hipertensión arterial en España. Situación actual y perspectivas. Hipertensión 22, 353–362. doi:10.1016/S0212-8241(05)71587-5
Cheng, G. C., Loree, H. M., Kamm, R. D., Fishbein, M. C., and Lee, R. T. (1993). Distribution of circumferential stress in ruptured and stable atherosclerotic lesions: A structural analysis with histopathological correlation. Circulation 87, 1179–1187. doi:10.1161/01.CIR.87.4.1179
Cilla, M., Martinez, J., Pena, E., and Martínez, M. Á. (2012). Machine learning techniques as a helpful tool toward determination of plaque vulnerability. IEEE Trans. Biomed. Eng. 59, 1155–1161. doi:10.1109/TBME.2012.2185495
Davis, L. A., Stewart, S. E., Carsten, C. G., Snyder, B. A., Sutton, M. A., and Lessner, S. M. (2016). Characterization of fracture behavior of human atherosclerotic fibrous caps using a miniature single edge notched tensile test. Acta Biomater. 43, 101–111. doi:10.1016/j.actbio.2016.07.027
De Graaf, M. A., Broersen, A., Kitslaar, P. H., Roos, C. J., Dijkstra, J., Lelieveldt, B. P., et al. (2013). Automatic quantification and characterization of coronary atherosclerosis with computed tomography coronary angiography: Cross-correlation with intravascular ultrasound virtual histology. Int. J. Cardiovasc. Imaging 29, 1177–1190. doi:10.1007/s10554-013-0194-x
Dietterich, T. (1995). Overfitting and undercomputing in machine learning. ACM Comput. Surv. (CSUR) 27, 326–327. doi:10.1145/212094.212114
Erlinge, D., Maehara, A., Ben-Yehuda, O., Bøtker, H. E., Maeng, M., Kjøller-Hansen, L., et al. (2021). Identification of vulnerable plaques and patients by intracoronary near-infrared spectroscopy and ultrasound (prospect II): A prospective natural history study. Lancet 397, 985–995. doi:10.1016/S0140-6736(21)00249-X
Esper, R. J., Nordaby, R. A., Vilariño, J. O., Paragano, A., Cacharrón, J. L., and Machado, R. A. (2006). Endothelial dysfunction: A comprehensive appraisal. Cardiovasc. Diabetol. 5, 4–18. doi:10.1186/1475-2840-5-4
Falk, E., Shah, P. K., and Fuster, V. (1995). Coronary plaque disruption. Circulation 92, 657–671. doi:10.1161/01.cir.92.3.657
Finet, G., Ohayon, J., and Rioufol, G. (2004). Biomechanical interaction between cap thickness, lipid core composition and blood pressure in vulnerable coronary plaque: Impact on stability or instability. Coron. Artery Dis. 15, 13–20. doi:10.1097/00019501-200402000-00003
Finn, A. V., Nakano, M., Narula, J., Kolodgie, F. D., and Virmani, R. (2010). Concept of vulnerable/unstable plaque. Arteriosclerosis, Thrombosis, Vasc. Biol. 30, 1282–1292. doi:10.1161/ATVBAHA.108.179739
Gardner, M. W., and Dorling, S. (1998). Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 32, 2627–2636. doi:10.1016/S1352-2310(97)00447-0
Gasser, T. C., Ogden, R. W., and Holzapfel, G. A. (2006). Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35. doi:10.1098/rsif.2005.0073
Gogas, B. D., Farooq, V., Serruys, P. W., and Garcìa-Garcìa, H. M. (2011). Assessment of coronary atherosclerosis by IVUS and IVUS-based imaging modalities: Progression and regression studies, tissue composition and beyond. Int. J. Cardiovasc. Imaging 27, 225–237. doi:10.1007/s10554-010-9791-0
Gold, K., Gaharwar, A. K., and Jain, A. (2019). Emerging trends in multiscale modeling of vascular pathophysiology: Organ-on-a-chip and 3d printing. Biomaterials 196, 2–17. doi:10.1016/j.biomaterials.2018.07.029
Gómez, A., Tacheau, A., Finet, G., Lagache, M., Martiel, J.-L., Le Floc’h, S., et al. (2019). Intraluminal ultrasonic palpation imaging technique revisited for anisotropic characterization of healthy and atherosclerotic coronary arteries: A feasibility study. Ultrasound Med. Biol. 45, 35–49. doi:10.1016/j.ultrasmedbio.2018.08.020
Gu, J., Wang, Z., Kuen, J., Ma, L., Shahroudy, A., Shuai, B., et al. (2018). Recent advances in convolutional neural networks. Pattern Recognit. 77, 354–377. doi:10.1016/j.patcog.2017.10.013
Henriques, J., Amaro, A. M., and Piedade, A. P. (2023). Understanding atherosclerosis pathophysiology: Can additive manufacturing be helpful? Polymers 15, 480. doi:10.3390/polym15030480
Hokr, B. H., and Bixler, J. N. (2021). Machine learning estimation of tissue optical properties. Sci. Rep. 11, 6561–6567. doi:10.1038/s41598-021-85994-w
Ikemoto, D., Taniguchi, T., Hirota, K., Nishikawa, K., Okubo, K., and Abe, T. (2023). Application of neural network-based image analysis to detect sister chromatid cohesion defects. Sci. Rep. 13, 2133. doi:10.1038/s41598-023-28742-6
Kingma, D. P., and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. doi:10.48550/arXiv.1412.6980
Kotsiantis, S. B., Zaharakis, I., and Pintelas, P. (2007). Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 160, 3–24.
Kovarnik, T., Mintz, G. S., Skalicka, H., Kral, A., Horak, J., Skulec, R., et al. (2011). Virtual histology evaluation of atherosclerosis regression during atorvastatin and ezetimibe administration–heaven study. Circulation J. 76, 176–183. doi:10.1253/circj.cj-11-0730
Latorre, Á. T., Martínez, M. A., Cilla, M., Ohayon, J., and Peña, E. (2022). Atherosclerotic plaque segmentation based on strain gradients: A theoretical framework. Mathematics 10, 4020. doi:10.3390/math10214020
Lawrence, S., Giles, C. L., Tsoi, A. C., and Back, A. D. (1997). Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 8, 98–113. doi:10.1109/72.554195
Layland, J., Wilson, A., Lim, I., and Whitbourn, R. (2011). Virtual histology: A window to the heart of atherosclerosis. Heart, Lung Circulation 20, 615–621. doi:10.1016/j.hlc.2010.12.002
Le Floc’h, S., Cloutier, G., Finet, G., Tracqui, P., Pettigrew, R. I., and Ohayon, J. (2010). On the potential of a new IVUS elasticity modulus imaging approach for detecting vulnerable atherosclerotic coronary plaques: In vitro vessel phantom study. Phys. Med. Biol. 55, 5701–5721. doi:10.1088/0031-9155/55/19/006
Le Floc’h, S., Ohayon, J., Tracqui, P., Finet, G., Gharib, A. M., Maurice, R. L., et al. (2009). Vulnerable atherosclerotic plaque elasticity reconstruction based on a segmentation-driven optimization procedure using strain measurements: Theoretical framework. IEEE Trans. Med. Imaging 28, 1126–1137. doi:10.1109/TMI.2009.2012852
LeCun, Y., and Bengio, Y. (1995). “Convolutional networks for images, speech, and time series,” in The handbook of brain theory and neural networks. Cambridge, MA United States: The MIT Press, 3361, 1995.
LeCun, Y., Touresky, D., Hinton, G., and Sejnowski, T. (1988). “A theoretical framework for back-propagation,” in Proceedings of the 1988 connectionist models summer school. Pittsburg, PA: Morgan Kaufmann, 1, 21–28.
Lee, R. T., and Libby, P. (1997). The unstable atheroma. Arteriosclerosis, Thrombosis, Vasc. Biol. 17, 1859–1867. doi:10.1161/01.ATV.17.10.1859
Li, J., Li, X., Mohar, D., Raney, A., Jing, J., Zhang, J., et al. (2014). Integrated IVUS-OCT for real-time imaging of coronary atherosclerosis. JACC Cardiovasc. Imaging 7, 101–103. doi:10.1016/j.jcmg.2013.07.012
Libby, P. (2001). Current concepts of the pathogenesis of the acute coronary syndromes. Circulation 104, 365–372. doi:10.1161/01.cir.104.3.365
Loree, H. M., Kamm, R. D., Stringfellow, R. G., and Lee, R. T. (1992). Effects of fibrous cap thickness on peak circumferential stress in model atherosclerotic vessels. Circulation Res. 71, 850–858. doi:10.1161/01.res.71.4.850
Ma, S., Tang, Q., Liu, Y., and Feng, Q. (2022). Prediction of mechanical properties of three-dimensional printed lattice structures through machine learning. J. Comput. Inf. Sci. Eng. 22, 031008. doi:10.1115/1.4053077
Maher, E., Creane, A., Sultan, S., Hynes, N., Lally, C., and Kelly, D. J. (2009). Tensile and compressive properties of fresh human carotid atherosclerotic plaques. J. Biomechanics 42, 2760–2767. doi:10.1016/j.jbiomech.2009.07.032
Malek, A. M., Alper, S. L., and Izumo, S. (1999). Hemodynamic shear stress and its role in atherosclerosis. Jama 282, 2035–2042. doi:10.1001/jama.282.21.2035
Maurice, R. L., Brusseau, É., Finet, G., and Cloutier, G. (2005). On the potential of the Lagrangian speckle model estimator to characterize atherosclerotic plaques in endovascular elastography: In vitro experiments using an excised human carotid artery. Ultrasound Med. Biol. 31, 85–91. doi:10.1016/j.ultrasmedbio.2004.07.009
Maurice, R. L., Fromageau, J., Brusseau, É., Finet, G., Rioufol, G., and Cloutier, G. (2007). On the potential of the Lagrangian estimator for endovascular ultrasound elastography: In vivo human coronary artery study. Ultrasound Med. Biol. 33, 1199–1205. doi:10.1016/j.ultrasmedbio.2007.01.018
Maurice, R. L., Ohayon, J., Finet, G., and Cloutier, G. (2004). Adapting the Lagrangian speckle model estimator for endovascular elastography: Theory and validation with simulated radio-frequency data. J. Acoust. Soc. Am. 116, 1276–1286. doi:10.1121/1.1771615
Moore, M., Spencer, T., Salter, D., Kearney, P., Shaw, T., Starkey, I., et al. (1998). Characterisation of coronary atherosclerotic morphology by spectral analysis of radiofrequency signal: In vitro intravascular ultrasound study with histological and radiological validation. Heart 79, 459–467. doi:10.1136/hrt.79.5.459
Nair, A., Kuban, B. D., Tuzcu, E. M., Schoenhagen, P., Nissen, S. E., and Vince, D. G. (2002). Coronary plaque classification with intravascular ultrasound radiofrequency data analysis. Circulation 106, 2200–2206. doi:10.1161/01.cir.0000035654.18341.5e
Napoli, C., D’Armiento, F. P., Mancini, F. P., Postiglione, A., Witztum, J. L., Palumbo, G., et al. (1997). Fatty streak formation occurs in human fetal aortas and is greatly enhanced by maternal hypercholesterolemia. Intimal accumulation of low density lipoprotein and its oxidation precede monocyte recruitment into early atherosclerotic lesions. J. Clin. Investigation 100, 2680–2690. doi:10.1172/JCI119813
Napoli, C., Glass, C. K., Witztum, J. L., Deutsch, R., D’Armiento, F. P., and Palinski, W. (1999). Influence of maternal hypercholesterolaemia during pregnancy on progression of early atherosclerotic lesions in childhood: Fate of early lesions in children (felic) study. Lancet 354, 1234–1241. doi:10.1016/S0140-6736(99)02131-5
Nasu, K., Tsuchikane, E., Katoh, O., Vince, D. G., Virmani, R., Surmely, J.-F., et al. (2006). Accuracy of in vivo coronary plaque morphology assessment: A validation study of in vivo virtual histology compared with in vitro histopathology. J. Am. Coll. Cardiol. 47, 2405–2412. doi:10.1016/j.jacc.2006.02.044
Nong, J.-c., You, W., Xu, T., Meng, P.-n., Xu, Y., Wu, X.-q., et al. (2022). Dynamic natural morphologies and component changes in nonculprit subclinical atherosclerosis in patients with acute coronary syndrome at 1-year follow-up and clinical significance at 3-year follow-up. Atherosclerosis 356, 1–8. doi:10.1016/j.atherosclerosis.2022.07.013
O’Reilly, B. L., Hynes, N., Sultan, S., McHugh, P. E., and McGarry, J. P. (2020). An experimental and computational investigation of the material behaviour of discrete homogenous iliofemoral and carotid atherosclerotic plaque constituents. J. Biomechanics 106, 109801. doi:10.1016/j.jbiomech.2020.109801
Park, Y. S., and Lek, S. (2016). Artificial neural networks: Multilayer perceptron for ecological modeling, 28. Amsterdam, Netherlands: Elsevier. doi:10.1016/B978-0-444-63623-2.00007-4
Pederiva, C., Capra, M. E., Viggiano, C., Rovelli, V., Banderali, G., and Biasucci, G. (2021). Early prevention of atherosclerosis: Detection and management of hypercholesterolaemia in children and adolescents. Life 11, 345. doi:10.3390/life11040345
Peña, E., Cilla, M., Latorre, Álvaro T., Martínez, M. A., Gómez, A., Pettigrew, R. I., et al. (2021). “Chapter 16 - emergent biomechanical factors predicting vulnerable coronary atherosclerotic plaque rupture,” in Biomechanics of coronary atherosclerotic plaque. Editors J. Ohayon, G. Finet, and R. I. Pettigrew (Cambridge, Massachusetts, United States: Academic Press), 361–380. vol. 4 of Biomechanics of Living Organs. doi:10.1016/B978-0-12-817195-0.00016-0
Roth, G. A., Mensah, G. A., Johnson, C. O., Addolorato, G., Ammirati, E., Baddour, L. M., et al. (2020). Global burden of cardiovascular diseases and risk factors, 1990–2019: Update from the gbd 2019 study. J. Am. Coll. Cardiol. 76, 2982–3021. doi:10.1016/j.jacc.2020.11.010
Shen, R., Tong, X., Li, D., Ning, Z., Han, H., Han, Y., et al. (2022). Slice-based and time-specific hemodynamic measurements discriminate carotid artery vulnerable atherosclerotic plaques. Comput. Methods Programs Biomed. 225, 107050. doi:10.1016/j.cmpb.2022.107050
Siotani, T., Fujikoshi, Y., and Hayakawa, T. (1985). Modern multivariate statistical analysis, a graduate course and handbook. United States: American Sciences Press.
Stefanadis, C., Antoniou, C.-K., Tsiachris, D., and Pietri, P. (2017). Coronary atherosclerotic vulnerable plaque: Current perspectives. J. Am. Heart Assoc. 6, e005543. doi:10.1161/JAHA.117.005543
Tacheau, A., Le Floc’h, S., Finet, G., Doyley, M. M., Pettigrew, R. I., Cloutier, G., et al. (2016). The imaging modulography technique revisited for high-definition intravascular ultrasound: Theoretical framework. Ultrasound Med. Biol. 42, 727–741. doi:10.1016/j.ultrasmedbio.2015.11.015
Tan, C., Sun, F., Kong, T., Zhang, W., Yang, C., and Liu, C. (2018). “A survey on deep transfer learning,” in Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, October 4-7, 2018 (Berlin, Germany: Springer), 270–279. Proceedings, Part III 27. doi:10.48550/arXiv.1808.01974
Teng, Z., Tang, D., Zheng, J., Woodard, P. K., and Hoffman, A. H. (2009). An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. J. Biomechanics 42, 2535–2539. doi:10.1016/j.jbiomech.2009.07.009
Thim, T. (2010). Human-like atherosclerosis in minipigs: A new model for detection and treatment of vulnerable plaques. Dan. Med. Bull. 57, 41611.
Torun, S. G., Torun, H. M., Hansen, H. H., de Korte, C. L., van der Steen, A. F., Gijsen, F. J., et al. (2022). Multicomponent material property characterization of atherosclerotic human carotid arteries through a bayesian optimization based inverse finite element approach. J. Mech. Behav. Biomed. Mater. 126, 104996. doi:10.1016/j.jmbbm.2021.104996
Virmani, R., Kolodgie, F. D., Burke, A. P., Farb, A., and Schwartz, S. M. (2000). Lessons from sudden coronary death: A comprehensive morphological classification scheme for atherosclerotic lesions. Arteriosclerosis, Thrombosis, Vasc. Biol. 20, 1262–1275. doi:10.1161/01.atv.20.5.1262
Wang, L., Maehara, A., Zhang, X., Lv, R., Qu, Y., Guo, X., et al. (2023). Quantification of patient-specific coronary material properties and their correlations with plaque morphological characteristics: An in vivo ivus study. Int. J. Cardiol. 371, 21–27. doi:10.1016/j.ijcard.2022.09.051
Wang, S., Tokgoz, A., Huang, Y., Zhang, Y., Feng, J., Sastry, P., et al. (2019). Bayesian inference-based estimation of normal aortic, aneurysmal and atherosclerotic tissue mechanical properties: From material testing, modeling and histology. IEEE Trans. Biomed. Eng. 66, 2269–2278. doi:10.1109/TBME.2018.2886681
Wilkins, E., Wilson, L., Wickramasinghe, K., Bhatnagar, P., Leal, J., Luengo-Fernandez, R., et al. (2017). European cardiovascular disease statistics 2017. Brussels, Belgium: European Heart Network. doi:10.1093/eurheartj/ehx628
World Health Organization (2021). Cardiovascular diseases (CVDs). Available at: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (Accessed july 26, 2022).
Keywords: cardiovascular diseases, atheroma plaque, in silico modeling, deep learning, artificial neural network
Citation: Caballero R, Martínez MÁ and Peña E (2023) Coronary artery properties in atherosclerosis: A deep learning predictive model. Front. Physiol. 14:1162436. doi: 10.3389/fphys.2023.1162436
Received: 09 February 2023; Accepted: 21 March 2023;
Published: 05 April 2023.
Edited by:
Dalin Tang, Worcester Polytechnic Institute, United StatesReviewed by:
Xiaoya Guo, Nanjing University of Posts and Telecommunications, ChinaCopyright © 2023 Caballero, Martínez and Peña. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Estefanía Peña, ZmFueUB1bml6YXIuZXM=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.