Efficient (k, n) threshold semi-quantum secret sharing protocol

Most (k, n) threshold quantum secret sharing protocols are fully quantum. The message receivers must be equipped with complex quantum devices so as to prepare various quantum resources and perform complex quantum operations, which may affect the practice of these protocols. On the other hand, the qubit efficiency of most (k, n) threshold quantum secret sharing protocols is not more than 1/2. To simplify the (k, n) threshold quantum secret sharing protocol and improve its practice and qubit efficiency, a new (k, n) threshold secret sharing protocol with semi-quantum properties is proposed. In this protocol, the dealer prepares decoy particles and sends them to the receivers. The receivers insert particles carrying secret information along with Z-basis decoy particles into the received particle sequence to generate mixed-particle sequences, which are returned to the dealer. The dealer measures the received particle sequences to check for eavesdropping and establishes shared secret keys with the receivers. With the shared secret keys, the dealer distributes the secret pieces among the receivers using Shamir’s secret sharing scheme. Multiple secret messages can be recovered by k or more receivers. The qubit efficiency of our protocol is k/n. For an (n, n) threshold protocol, the qubit efficiency would be 100%. The proposed scheme is based on single particles without using any entangled system. Therefore, its quantum resources are relatively easy to prepare. Receivers must only prepare simple Z-basis qubits. Its semi-quantum properties enhance practice implementation. The proposed protocol has robust security against various types of attacks, including eavesdropping, internal, and collusion attacks. Furthermore, it can resist the unitary attack, which is seldom analyzed in other protocols.

1 Introduction

Quantum secret sharing is a critical research area in quantum cryptography. A quantum secret sharing protocol allows the secret holder to divide a secret into multiple shares and distribute them among receivers. Only through collaborative computation can the participants reconstruct the original secret.

Typically, the security of the quantum secret sharing protocol [1] (QSSP) hinges on fundamental principles of quantum mechanics. For instance, the non-orthogonality of quantum states used in these protocols ensures that an attacker cannot accurately measure transmitted particles without introducing detectable disturbances. Consequently, the attacker cannot obtain useful information about the secret pieces from the measurement results. Moreover, an attacker’s invalid operation on the transmitted particles can be detected using eavesdropping check technologies. Therefore, the quantum secret sharing protocol has better merits in protecting the shared secret against quantum attackers.

Since Hillery [1] proposed the concept of QSSP, numerous QSSPs have been proposed [2–33]. Early works primarily focused on two-party secret sharing [2–14, 33]. The protocol in [15] was a (k, n) threshold one, allowing k of n participants to reconstruct the secret by cooperative operations, where n ≥ k > n/2. In [16], subsequent advancements eliminated the need for a third party to achieve the threshold property, enhancing protocol to be more flexible. The QSSPs in [17–19] support multi-receiver secret sharing and analyze various attack vectors to ensure robust security. However, most of these methods are static QSSPs. In these protocols, the identities of participants were predefined. Most of them did not consider adding or removing the participants. To make QSSPs more flexible, some novel dynamic QSSPs(DQSSPs) were proposed [20–32]. Li [20] proposed the (k, n) threshold DQSSP based on the d-dimensional Greenberg–Horn–Zehlinger (GHZ) state. In their protocol, participants could be dynamically added and removed. Furthermore, any k receivers could recover the holder’s secret. The DQSSP in [21] realized secret distribution by one-time sharing of messages and qubits. Additionally, in [21], the receivers only applied X-basis measurements, which could improve the practicality of the protocol. In [22], not only could the receivers dynamically leave or join the protocol, but the active partners from different hierarchical levels could also reconstruct the same secret. Li [23] proposed the DQSSP based on the Chinese Remainder Theorem and GHZ states. In their protocol, the participants were dynamically updated without alerting them of the shared secret, which could greatly improve the computational efficiency of the protocol. In [24], a (k, n) threshold DQSSP with weights was proposed. This scheme can realize the update of the partners with the help of a third party without changing the secret pieces. Moreover, the scheme enables participants with different authorities to share the same secret. You [25] presented DQSSP based on a single particle. In their scheme, when a new partner joined the protocol, verifying the secret pieces was unnecessary. This makes their scheme more practical and efficient. In [26], based on linear-feedback shift register (LFSR) sequences and Pauli operators, a novel (k, n) threshold DQSSP was proposed. In this protocol, Bell states were used as quantum resources. The distributor determined the secret, and the update of the participants could be realized without the cooperation of other participants. Tian [27] realized multi-participant to multi-participant secret sharing, which had enhanced security against various eavesdropping attacks. Some other DQSSPs have also been proposed to realize certain special properties or improve the communication efficiency of protocols [28–32]. Gong [34] devised a one-way quantum private comparison protocol that facilitates one-way transmission between third party (TP) and classical participants in quantum communication. Zhou [35] proposed an innovative protocol that can make size comparisons by exploiting more manageable two-dimensional Bell states and significantly enhanced its feasibility with current quantum technologies.

The analysis above shows that most of the QSSPs were full quantum protocols, in which all users were assumed to be able to apply various unitary operations and generate complex quantum resources. To make the QSSP more practicable, Boyer [36] showed how to simplify the quantum operations of users in a quantum protocol. They introduced the “classical participant” in the quantum protocol so that communicators could achieve communication goals without performing complex quantum operations. In particular, in the semi-quantum protocol, a classical participant must only apply a simple measurement with Z-basis, prepare Z-basis qubits, and rearrange and reflect the particles. Without complex quantum operations and quantum technologies, the semi-quantum protocol is more practical than the full quantum protocol. The semi-QSSP in [37] is based on the idea of quantum key distribution technologies and GHZ-like states. Using Bell states as quantum resources, Gao [38] proposed a novel semi-QSSP in which the receivers only reordered the qubits. The semi-QSSPs in [33, 39, 40] used single particles as quantum resources, which could further improve the practice of semi-QSSP. Zhou [41] simplified the private comparison protocol by using the semi-quantum technology. In the semi-quantum private comparison protocol of [41], the size relation between two classical participants’ secrets could be compared with each other in a one-time execution without disclosing the secrets. Wang [42, 43] proposed two kinds of semi-quantum private comparison protocols so that the consumption of quantum devices could be reduced and the qubit efficiency could also be improved. Zhou [44] proposed a novel measurement-free mediated semi-quantum key distribution protocol based on single-particle states to simplify the third party’s role to solely generating qubits in X-basis and conducting Bell measurements. Gong [45] proposed a new semi-quantum private comparison protocol that enables two classical users to securely compare the equality of their private information with the aid of a semi-honest third party, which does not need to measure and prepare any quantum state. Other semi-QSSPs have also been proposed as well so as to improve the security and efficiency of protocols [46–49].

Although various QSSPs have been proposed, only a few (k, n) threshold QSSPs with semi-quantum properties have been proposed. A (k, n) threshold QSSP with semi-quantum properties should satisfy the following requirements. First, it should be secure against quantum adversary attacks. Second, it should have the (k, n) threshold property such that any k or more participants in the receivers can efficiently recover the secret. Third, it should possess semi-quantum properties. Recently, Zhou [50] presented a (t, n)-threshold semi-QSSP that could efficiently achieve the secret sharing goal. Unfortunately, according to our security analysis, it lacks security against unitary attacks. (In the Supplementary Appendix, we show the unitary attack on the protocol in [50]. For more details, please refer to the Supplementary Appendix.)

In this paper, a new (k, n) threshold QSSP with semi-quantum properties is proposed. Compared with the similar schemes, the contributions of this work are as follows.

(1) The proposed protocol overcomes the security drawback of the threshold protocol in [50], and it can resist various attacks, including the unitary attack.

(2) Most of the existing (k, n) threshold QSSPs are full quantum ones, in which the receivers must perform various complex quantum operations, while the proposed one is a semi-quantum (k, n) threshold protocol. In the proposed protocol, all the receivers are classical participants, and they only need to perform a simple operation, such as preparing qubits |0⟩ and |1⟩.

(3) Most of the existing (k, n) threshold QSSPs are based on multi-entangled particles, while the proposed protocol is based on the simple single qubits such as |0⟩, |1⟩, |+⟩ and |−⟩, which are relatively easier to prepare.

(4) Most of the existing (k, n) threshold QSSPs can only recover one secret message at one time, and their qubit efficiency is not more than 1/2. In the proposed protocol, the receivers can recover k secret messages at one time. Therefore, its qubit efficiency is k/n. Then, the qubit of its (n, n) threshold version can be 100%.

The remainder of this paper is organized as follows. In the next section, we propose a (k, n) threshold QSSPs with semi-quantum properties. The security analysis is presented in Section 3. In Section 4, comparisons are presented. In Section 5, the quantum circuit simulation of the protocol is presented. Finally, conclusions are presented in the last section.

2 Methods

Let Trent be the secret distributor who is a quantum party. He distributes his secret messages a₀, a₁, … , a_k-1∈Z_p among n classical receivers Tom₁, Tom₂, … , Tom_n, where p is a prime number, and 1 < n < p. The protocol’s goal is that Trent securely distributes all his secret messages among the n receivers such that k or more of their partners may securely reconstruct all the secret messages at one time, even if the attacker performs eavesdropping attacks and unitary attacks on the quantum channels. Assume that the bit length of all the data a₀, a₁, … , a_k-1, p is l.

The protocol includes two phases: distributing multi-secret messages and recovering multi-secret messages.

2.1 The phase of distributing multi-secret messages

In this phase, Trent and all Tom_i perform the following steps.

D-Step 1. Trent sets his polynomial

$f\left(x\right)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1}\left(\mathrm{mod}p\right),(1)$

where a₀, a₁, …, a_k-1 are the secret messages to be split. Then, he calculates f(i) for each i = 1, 2, …, n. Let b_i denote the binary repression of f(i), whose bit length is l as well.

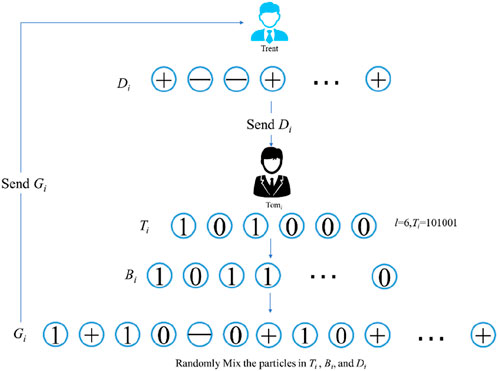
D-Step 2. Trent generates the decoy particle sequence D_i, in which the state of each particle is randomly chosen from the set {|+⟩, |−⟩}. Then, he sends D_i to Tom_i. This step is performed for i = 1, 2, …, n.

D-Step 3. Tom_i randomly creates a binary string t_i, whose bit length is l. Then, he encodes t_i into the particle sequence T_i with state |t_i⟩ according to the following rules: If the bit is 0, it is encoded as the particle with state |0⟩; If the bit is 1, it is encoded as the particle with state |1⟩. For example, if l = 6 and t_i = 101001, the state of the particle sequence T_i is |t_i⟩ = |101001⟩. On the other hand, he randomly creates the decoy particle sequence B_i, in which the state of each particle is randomly chosen from the set {|0⟩, |1⟩}. When Tom_i obtains D_i from Trent, he mixes the particles in T_i, B_i, and D_i and rearranges them with delay lines, forming a new sequence G_i. Then, Tom_i sends G_i to Trent. This step is performed for i = 1, 2, …, n.

D-Step 4. This is the eavesdropping step. When Trent gets G_i, Tom_i publishes the original position of each particle of B_i, D_i, and T_i mixed in G_i. Trent measures sequence D_i in the X-basis and compares the state of D_i with its initial state. If the error rate of the measurement results is more than the predefined threshold, the protocol is aborted. Trent also measures the sequence B_i in the Z-basis and declares the measurement results. Tom_i compares the published measurement results with the original states of the particles in B_i. If the error rate of the comparison is greater than the predefined threshold, the protocol is aborted. This step is performed for i = 1, 2, …, n.

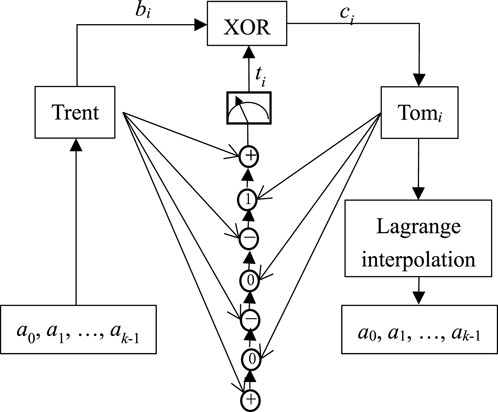
D-Step 5. Trent measures each particle in T_i in the Z-basis and obtains the measurement result t_i. Then, he calculates c_i = b_i⊕t_i and announces the result c_i. According to the announced c_i, each Tom_i can obtain b_i by calculating b_i = c_i⊕t_i. This step is performed for i = 1, 2, …, n.

In Figure 1, taking l = 6 as an example, the preparation and processing procedures of the quantum states in the protocol are presented in detail.

Figure 1

Figure 1. Preparation and processing processes of quantum states.

2.2 The phase of recovering the multi-secret messages

In the proposed protocol, if the attacker does not disturb the quantum channels, each Tom_i can obtain f(i) from the binary b_i. Therefore, by the Lagrange interpolation [51], any k receivers ${\text{Tom}}_{i_1}$, ${\text{Tom}}_{i_2}$,…, ${\text{Tom}}_{i_k}$ can corporately recover the first secret message:

$a_0=f\left(0\right)=\sum _{r=1}^{k}f\left(i_r\right){\displaystyle \prod _{\begin{array}{l}t=1\\ r\ne t\end{array}}^k}\frac{-i_t}{i_r-i_t}\left(\mathrm{mod}p\right).(2)$

According to Equation 1, it follows that

$f_1\left(x\right)=\left(f\left(x\right)-a_0\right)x^{-1}=a_1+a_{2}x+\cdots +a_{k-1}{x}^{k-2}\left(\mathrm{mod}p\right).(3)$

Therefore, with the help of a₀, each ${\text{Tom}}_{i_j}$ (j = 1, 2, … , k) can get f₁ (i_j) by calculating

$f_1\left(i_j\right)=\left(f\left(i_j\right)-a_0\right){i_j}^{-1}\mathrm{mod}p.(4)$

Using Equations 2–4, the cooperators can recover the second secret message.

$a_1=f_1\left(0\right)=\sum _{r=1}^{k-1}{f}_1\left(i_r\right){\displaystyle \prod _{\begin{array}{l}t=1\\ r\ne t\end{array}}^{k-1}}\frac{-i_t}{i_r-i_t}\mathrm{mod}p.(5)$

By the similar idea of Equations 2–5, the cooperators can gradually reduce the degree of the polynomial f_i(x) and get f_i+1(x) (i = 1, 2, …, k-2) and recover the other secret messages a₂, a₃, …, a_k-1.

Figure 2 shows the diagram of the proposed (k, n) threshold QSSP with semi-quantum properties.

Figure 2

Figure 2. Diagram of the (k, n) threshold QSSP with semi-quantum properties.

3 Security analysis

Usually, an attacker tries to eavesdrop on quantum channels to obtain some useful information. The attacker may also attempt to disturb the quantum channel by performing a unitary operation to break the protocol without being detected. In this section, first, the eavesdropping and Trojan horse attacks are analyzed. Then, the internal attack and collusion attack are analyzed. Finally, the unitary attack on the quantum channel is analyzed.

3.1 Eavesdropping attacks

There are three types of eavesdropping attacks.

The first type is known as a measuring attack. During this attack, the attacker intercepts the sender’s quantum sequence and measures it to obtain information about the transmitted secret piece. Subsequently, the attacker resends the measured quantum sequence to the receiver. In our protocol, the attacker may intercept the sequence D_i and measure it. However, the attacker gains no information because D_i carries no message about the secret piece. The attacker tries to intercept the sequence G_i and measure it. However, G_i includes decoy sequences D_i and B_i. The attacker does not know which measurement basis to use to measure each decoy particle in G_i. Assume the original decoy state is |+⟩. If the attacker uses the correct basis to make a measurement, his action cannot be detected. If he measures |+⟩ with Z-basis, the decoy state will collapse into |0⟩ or |1⟩. In this case, Trent can detect that the decoy state has been disturbed by the attacker with a probability of 1/2. Similarly, assume the original decoy state is |0⟩. If the attacker uses the correct basis to make a measurement, his action cannot be detected. However, if he measures |0⟩ with X-basis, the decoy state is changed into |+⟩ or |−⟩. In this case, Tom_i can find that the decoy state is disturbed by the attacker with probability 1/2. Therefore, the attacker’s measuring attack can be found out with probability

$p=1-{\left(\frac{1}{2}+\frac{1}{2}\times \frac{1}{2}\right)}^{\alpha }=1-{\left(\frac{3}{4}\right)}^{\alpha }\to 1\left(\alpha \to \infty \right),(6)$

where α is the number of the decoy particles in G_i.

The second attack is a faking attack. During this attack, the attacker intercepts the sender’s quantum sequence. Then, he fakes a new quantum sequence and sends it to the receivers so that he can break the protocol without being detected. For our protocol, the attacker may intercept the sequence G_i, fake a new $G_i^{\prime }$, and send it to Trent. However, the attacker does know the correct state of each decoy particle in mixed sequence G_i. For example, suppose the correct decoy state should be |0⟩. If the attacker happens to fake the decoy state |0⟩, he can luckily pass the eavesdropping check. If his faked state is |1⟩, the attacker’s forgery will be discovered. If his faked state is |+⟩ or |−⟩, his disturbance can be found with probability 1/2. Therefore, the attacker’s faking attack can be found out with probability

$p=1-{\left(\frac{1}{4}\times 1+\frac{1}{4}\times 0+\frac{1}{4}\times \frac{1}{2}\times 2\right)}^{\alpha }=1-\frac{1}{2^{\alpha }}\to 1\left(\alpha \to \infty \right),(7)$

where α is the number of the decoy states used in G_i. Therefore, as elucidated by Equations 6, 7, it is infeasible for the attacker to steal useful information buy the measuring attack and faking attack without being caught during the eavesdropping inspection.

The third attack is an entanglement attack. In this attack, the attacker makes the transmitted quantum particle entangle with his own auxiliary particle by applying some unitary operation on them so that he can obtain some information on the secret by measuring the auxiliary particle. For our protocol, when some particle x with state |x⟩ is sent from Tom_i to Trent, the attacker makes x entangle with his own auxiliary particle y with state |y⟩ by applying some unitary operation V on them. Suppose

$\left\{\begin{array}{l}V{\left|0\rangle \right.〉}_x\left|y\rangle \right.〉=v_{00}{\left|0\rangle \right.〉}_x\left|y_{00}\right.〉\rangle +v_{01}{\left|1\rangle \right.〉}_x\left|y_{01}\right.〉\rangle \\ V{\left|1\rangle \right.〉}_x\left|y\rangle \right.〉=v_{10}{\left|0\rangle \right.〉}_x\left|y_{10}\right.〉\rangle +v_{11}{\left|1\rangle \right.〉}_x\left|y_{11}\right.〉\rangle \end{array}\right.,(8)$

where the index “x” denotes the transmitted particle x. Note the entanglement attack should not change the state of the decoy |0⟩ or |1⟩, or it could be detected by the partners during the eavesdropping inspection. Therefore, Equation 8 folllows.

$\left\{\begin{array}{l}V{\left|0\rangle \right.〉}_x\left|y\rangle \right.〉={\left|0\rangle \right.〉}_{x〉}\left|y_{00}\right.〉\rangle \\ V{\left|1\rangle \right.〉}_{x〉}\left|y\rangle \right.〉={\left|1\rangle \right.〉}_x\left|y_{11}\right.〉\rangle \end{array}\right..(9)$

Equation 9 follows.

$\left\{\begin{array}{l}V{\left|+\rangle \right.〉}_x\left|y\rangle \right.〉=\frac{1}{2}{\left|+\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle +\left|y_{11}\right.〉\rangle \right)+\frac{1}{2}{\left|-\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle -\left|y_{11}\right.〉\rangle \right)\\ V{\left|-\rangle \right.〉}_x\left|y\rangle \right.〉=\frac{1}{2}{\left|+\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle -\left|y_{11}\right.〉\rangle \right)+\frac{1}{2}{\left|-\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle +\left|y_{11}\right.〉\rangle \right)\end{array}\right..(10)$

However, the entanglement attack should not change the state of the decoy state |+⟩ or |−⟩, or it could be detected by Trent during the eavesdropping inspection. Therefore, Equation 10 follows.

$\left\{\begin{array}{l}V{\left|+\rangle \right.〉}_x\left|y\rangle \right.〉=\frac{1}{2}{\left|+\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle +\left|y_{11}\right.〉\rangle \right)\\ V{\left|-\rangle \right.〉}_x\left|y\rangle \right.〉=\frac{1}{2}{\left|-\rangle \right.〉}_x\left(\left|y_{00}\right.〉\rangle +\left|y_{11}\right.〉\rangle \right)\end{array}\right.,(11)$

which means

$\left|y_{00}\right.〉\rangle =\left|y_{11}\right.〉\rangle .(12)$

Therefore, from Equations 9–12, it can be inferred

$\left\{\begin{array}{l}V{\left|0\rangle \right.〉}_x\left|y\rangle \right.〉={\left|0\rangle \right.〉}_x\left|y_{00}\right.〉\rangle \\ V{\left|1\rangle \right.〉}_x\left|y\rangle \right.〉={\left|1\rangle \right.〉}_x\left|y_{00}\right.〉\rangle \\ V{\left|+\rangle \right.〉}_x\left|y\rangle \right.〉={\left|+\rangle \right.〉}_x\left|y_{00}\right.〉\rangle \\ V{\left|-\rangle \right.〉}_x\left|y\rangle \right.〉={\left|-\rangle \right.〉}_x\left|y_{00}\right.〉\rangle \end{array}\right..(13)$

Equation 13 means that the attacker has no advantage in guessing which state is transmitted from Tom_i to Trent by measuring his own auxiliary particle y. Therefore, it is infeasible for the attacker to steal useful information by the entanglement attack without being caught during the eavesdropping inspection.

3.2 Trojan horse attack

A secure quantum protocol should be resilient against a Trojan horse attack. In this attack, the attacker attaches some invisible photons to the transmitted particles and inserts some delay photons into the quantum channel between Trent and Tom_i so as to steal some information about the order of the transmitted particles and the secret key. For this kind of attack, participants can deploy a wavelength filter and a photon number splitter on the quantum channel to detect the Trojan horse attack [52–54].

3.3 Internal attack

An internal partner may be an attacker. Suppose Tom_i is the internal attacker. He tries to eavesdrop on the channel between Trent and Tom_j (i ≠ j) to obtain some information about the piece b_j. However, according to the analysis in Section 3.1, Tom_i’s eavesdropping efforts will be detected due to the use of decoy particles for eavesdropping inspection in our protocol.

3.4 Collusion attack

In this kind of attack, t (t < k) malicious receivers, such as Tom₁, Tom₂, …, and Tom_t, may collude and try to recover Trent’s secret without the cooperation of the other receivers. However, according to the threshold property of Shamir’s secret sharing technology, only k or more secret pieces can recover all the secret messages. Therefore, the colluded attackers must eavesdrop on the quantum channels between Trent and the other participants so as to obtain some other secret pieces. However, according to the security analysis in Sections 3.1–3.2, their eavesdropping will be detected due to the use of decoy particles for eavesdropping inspection in our protocol. Therefore, the proposed protocol can resist the collusion attack as well.

3.5 Unitary attack

For the unitary attack, the attacker may try to apply some unitary attack (such as a NOT gate discussed in the Supplementary Appendix) to the quantum channel to disrupt the protocol without being detected by the participants during the eavesdropping check phase.

This kind of attack can usually be applied to the semi-quantum protocol. In particular, when a sender with full quantum ability sends a quantum sequence mixed with decoy particles selected from the set {|0⟩, |1⟩, |+⟩, |−⟩} to a classical participant, the attacker may perform some unitary operations on the quantum sequence so that the information transmitted by the quantum sequence is changed. Because the classical receiver has no ability to measure the decoy particles selected from the set {|0⟩, |1⟩, |+⟩, |−⟩}, he (she) cannot efficiently check eavesdropping. Then, when the classical receiver measures some qubits of the received quantum sequence with a Z-basis, he (she) may get some wrong information from the measurements. When the classical receiver returns the quantum sequence to the sender, the attacker may perform the inverse of the unitary operations on the returned quantum sequence so that the states of the decoy particles are changed into their initial states. Then, after receiving the returned quantum sequence, the quantum sender may check the eavesdropping by measuring the decoy particles mixed in the quantum sequence. However, he (she) can detect nothing because the states of the decoy particles are unchanged. Note that the classical receiver has received incorrect information from the quantum sender. Therefore, compared with the other attacks, this kind of attack may break the communication goal of the semi-quantum protocol, while the attacker may escape from eavesdropping detection. Therefore, it is very important to analyze the security of the semi-quantum protocol against the unitary attack.

In our protocol, without being detected by Trent and Tom_i, the attacker attempts to perform some unitary operation U on the quantum particles sent from Trent (Tom_i) to Tom_i (Trent). Note that in the transmitted particles, some decoy particles are used to detect eavesdropping. When the decoy particles are transmitted from Trent to Tom_i, if the attacker performs some unitary operations U on them, it follows that

$\left\{\begin{array}{l}\left|+\rangle \right.〉\to \left|{\delta }_{+}\right.〉\rangle =U\left|+\rangle \right.〉\\ \left|-\rangle \right.〉\to \left|{\delta }_{-}\right.〉\rangle =U\left|-\rangle \right.〉\end{array}\right..(14)$

However, to escape the eavesdropping check, the attacker must perform the same unitary operations U on the particles of G_i so that $\left|{\delta }_{+}\right.〉\rangle$ ($\left|{\delta }_{-}\right.〉\rangle$) is changed into the original state |+⟩ (|−⟩), when G_i is sent from Tom_i to Trent. Thus, Equation 14 follows:

$\left\{\begin{array}{l}\left|{\delta }_{+}\right.〉\rangle \to U\left|{\delta }_{+}\right.〉\rangle =\left|+\rangle \right.〉\\ \left|{\delta }_{-}\right.〉\rangle \to U\left|{\delta }_{-}\right.〉\rangle =\left|-\rangle \right.〉\\ \left|0\rangle \right.〉\to U\left|0\rangle \right.〉=\left|{\delta }_0\right.〉\rangle \\ \left|1\rangle \right.〉\to U\left|1\rangle \right.〉=\left|{\delta }_1\right.〉\rangle \end{array}\right..(15)$

To check for eavesdropping, Trent will measure the received decoy states ($\left|{\delta }_0\right.〉\rangle$ and $\left|{\delta }_1\right.〉\rangle$) of B_i with Z-basis and announce the measurement results. Then, Tom_i compares the announced results with the original states of the decoy particles prepared by himself. If U is not the identity operation, Equation 15 follows $0<\left|〈\langle 0\left|{\delta }_0\right.〉\rangle \right|<1$ and $0<\left|〈\langle 1\left|{\delta }_1\right.〉\rangle \right|<1$. Therefore, Tom_i can find the attacker’s disturbance with probability

$p=1-{\left|〈\langle 0\left|{\delta }_0\right.〉\rangle \right|}^{2{\alpha }_0}\cdot {\left|〈\langle 1\left|{\delta }_1\right.〉\rangle \right|}^{2{\alpha }_1}\to 1\left({\alpha }_0,{\alpha }_1\to \infty \right),(16)$

where α₀ (α₁) denotes the number of the decoy states |0⟩(|1⟩) in the decoy sequence B_i. Hence, Equation 16 means, it is infeasible for the attacker to disturb the quantum channel between Trent and Tom_i by performing the unitary operation without being detected. Therefore, the attacker’s unitary attack will fail.

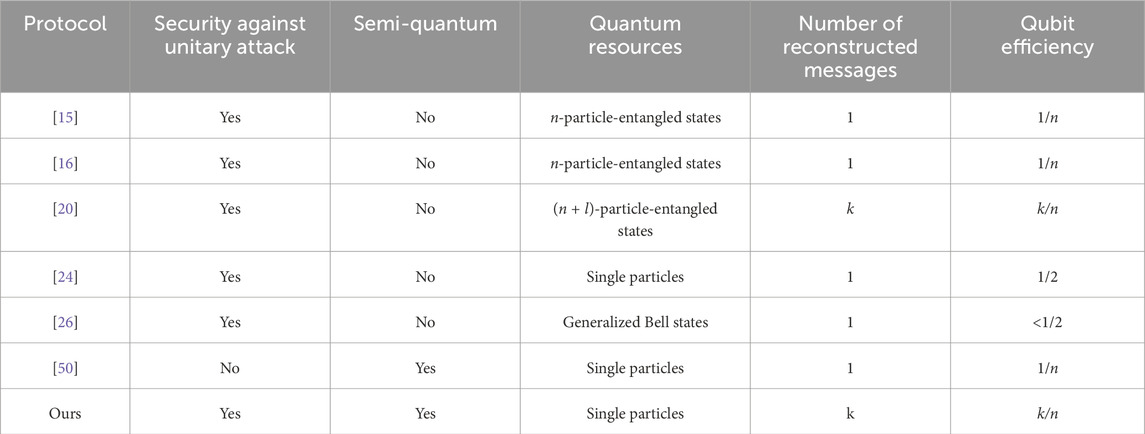
4 Comparisons of similar threshold protocols

This section provides a comparative analysis of similar threshold protocols.

First, the proposed protocol offers robust security against various types of attacks, including eavesdropping, Trojan horse attacks, internal attacks, and collusion attacks. Notably, it can also resist unitary attacks, which are seldom analyzed in most quantum secret sharing protocols (QSSPs).

Second, most existing threshold protocols require receivers to perform complex quantum operations. In contrast, the proposed protocol is semi-quantum, where all receivers are classical parties that must only perform simple operations, such as preparing qubits in the Z-basis.

Third, many similar protocols [15, 16] rely on multi-entangled particles as quantum resources, which are more challenging to prepare. The proposed protocol uses single particles as the quantum resources, making its quantum resources relatively easier to prepare.

Fourth, most of the (k, n) protocols require that only when k or more receivers cooperate can they reconstruct the distributor’s secret. The threshold property in [24] differs from others by using weight rather than the number of participants as the threshold. Specifically, in [24], the secret can only be recovered if the sum of the active partners’ weights exceeds a given threshold.

Fifth, most similar threshold protocols can only recover one secret message at a time, with qubit efficiency inversely proportional to the number of participants. In contrast, the proposed protocol allows receivers to recover multiple secret messages simultaneously. According to the definition of qubit efficiency provided in [48], the qubit efficiency is defined as γ = λ₁/λ₂ (the decoy states used for eavesdropping checks are not counted), where λ₁ and λ₂ are the length of shared secret messages and the number of the transmitted qubits, respectively. In our protocol, the shared secret messages are a₀, a₁, …, and a_k-1. Therefore, λ₁ = kl. On the other hand, nl qubits are used to transmit the secret messages (the decoy states used for eavesdropping checks are not counted). Hence, λ₂ = nl. Then, the qubit efficiency of the proposed protocol should be $\gamma =\frac{kl}{nl}=\frac{k}{n}$. If k > 0.8n, the qubit efficiency of the protocol can be more than 80%. If it is a (n, n) threshold protocol, its qubit efficiency can be 100%.

The protocols in [15, 16, 24, 50] are static threshold protocols, while the protocols in [20, 26] are dynamic ones, in which the participants could be dynamically added and removed.

In Table 1, comparisons of the similar protocols are presented.

Table 1

Table 1. Comparisons of the similar threshold protocols.

5 Quantum circuit simulation of the proposed protocol

A quantum circuit is an important research topic in the field of quantum communication. The quantum circuit can be used to simulate the physical realization of quantum protocols, in which all the unitary evolutions may be accomplished by universal quantum logic gates [55].

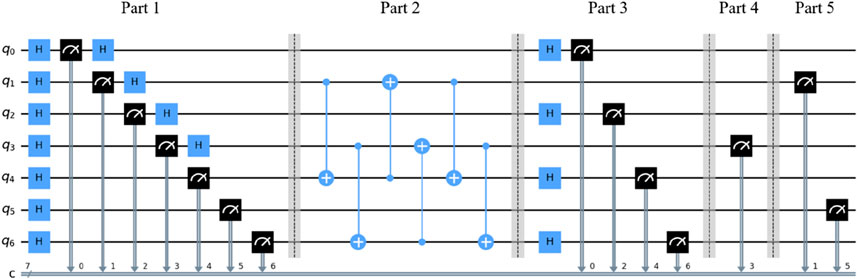
In the proposed protocol, Trent performs the same steps with each Tom_i. Therefore, in Figure 3, the quantum circuit simulation of the steps performed by Trent and Tom_i is shown. The quantum circuit is simulated by using the IBM Qiskit software. The quantum circuit simulation includes five parts.

Figure 3

Figure 3. Quantum circuit simulation of the steps performed by Trent and Tom_i.

Let l = 2. In Figure 3, the quantum circuit in Part 1 is the simulation of the quantum state preparation. Initially, Trent prepares the decoy particles q₀, q₁, q₂, and q₃ with the same initial state |0⟩. By performing the Hadamard gate and measurement with Z-basis on q₀, q₁, q₂, and q₃ in an orderly fashion, Trent can randomly generate four decoy states selected from the set {|+⟩, |−⟩}, and these four decoy states form the decoy quantum sequence D_i. Tom_i prepares the particles q₄ and q₅, whose initial states are the |0⟩. The particles q₄ and q₅ form the quantum sequence T_i, which carries the binary message t_i. By performing the Hadamard gate and measurement with Z-basis operations on q₄ and q₅, the binary message t_i carried by the quantum sequence T_i can be randomized. On the other hand, Tom_i prepares the decoy particle q₆ with an initial state |0⟩. By performing the Hadamard gate and measurement with Z-basis on q₆, the state of q₆ is randomly changed into |0⟩ or |1⟩. The particle q₆ forms the quantum sequence B_i.

When Tom_i obtains D_i from Trent, he mixes the particles in T_i, B_i, and D_i and rearranges them with delay lines, forming a new sequence G_i. The quantum circuit in Part 2 is the simulation of mixing the particles in T_i, B_i, and D_i and rearranging them with a delay line. Six CNOT gates are performed on the particles q₁, q₄, q₃, and q₆ so that the quantum sequence G_i can be rearranged. At last, G_i is sent to Trent.

Trent can know the locations of D_i, T_i, and B_i in G_i after Tom_i publishes the original position of each particle. Therefore, Trent will measure the decoy particles in D_i (B_i) with X-basis (Z-basis), and he can get the binary string t_i by measuring the particles in T_i with Z-basis. In Part 3 of the quantum circuit, it is necessary to perform the Hadamard gate and measurement with Z-basis on the decoy particles in D_i in an orderly fashion so that measuring the decoy particles in D_i with X-basis can be simulated. If the measurement result is 0 (1), the state of the decoy particle should be |+⟩ (|−⟩). The quantum circuit in Part 4 is the simulation of measuring the decoy particles in B_i with Z-basis. If the measured result is 0 (1), the state of the decoy particle should be |0⟩ (|1⟩). The partners can compute the error rate from the measurement results. If the error rate is over the given threshold, the protocol will abort. The quantum circuit in Part 5 is the simulation of measuring the decoy particles in T_i with Z-basis. The measurement result on T_i is recorded as t_i. Finally, Trent will publish the result c_i = b_i⊕t_i.

The quantum circuit simulation result is shown in Figure 4, in which the horizontal axis denotes all the possible measurement results. Because the states of all the particles are randomly created, there are 2⁷ = 128 possible measurement results. The vertical axis represents the frequency of occurrence of each measurement result.

Figure 4

Figure 4. Quantum circuit simulation results.

6 Conclusion

Seldom do QSSPs possess both semi-quantum and threshold properties. In this paper, a (k, n) threshold QSSP with semi-quantum properties is proposed. In the proposed protocol, the secret distributor divides k secret messages into shares and distributes them among n receivers. Both the dealer and the receivers prepare decoy particles to enable eavesdropping detection. The proposed protocol offers several advantages. (1) Its quantum resources are simple single particles, which are easy to prepare. (2) It is a semi-quantum protocol in which all the receivers are classical participants that only prepare simple qubits with Z-basis. (3) It has the (k, n) threshold property. (4) It can recover multiple secret messages simultaneously, achieving a qubit efficiency of k/n. If it is a (n, n) threshold protocol, its qubit efficiency can be 100%. (5) It is secure against various eavesdropping, Trojan horse, internal, and collusion attacks. Furthermore, it can resist the unitary attack, which is not analyzed in most QSSPs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JC: writing–original draft. JX: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project was supported by the Excellent Innovative Research Team of Universities in Anhui Province (2023AH010056), Anhui Province University Collaborative Innovation Project (GXXT-2023-050), and Research on Key Technologies for Intelligent Decision Making in Copper Processing Production Lines Driven by Manufacturing Big Data. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1542675/full#supplementary-material

References

1. Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Lett A (1999) 59(3):1829–34. doi:10.1103/physreva.59.1829

CrossRef Full Text | Google Scholar

2. Guo GP, Guo GC. Quantum secret sharing without entanglement. Phys Lett A (2003) 310(4):247–51. doi:10.1016/s0375-9601(03)00074-4

CrossRef Full Text | Google Scholar

3. Qin SJ, Gao F, Wen QY, Zhu FC. Cryptanalysis of the Hillery-Bužek-Berthiaume quantum secret-sharing protocol. Phys Rev A (2007) 76(6):062324. doi:10.1103/physreva.76.062324

CrossRef Full Text | Google Scholar

4. Lin J, Yang CW, Tsai CW, Hwang T. Intercept-resend attacks on semi-quantum secret sharing and the improvements. Int J Theor Phys (2013) 52:156–62. doi:10.1007/s10773-012-1314-4

CrossRef Full Text | Google Scholar

5. Xie C, Li L, Qiu D. A novel semi-quantum secret sharing scheme of specific bits. Int J Theor Phys (2015) 54:3819–24. doi:10.1007/s10773-015-2622-2

CrossRef Full Text | Google Scholar

6. Yin A, Fu F. Eavesdropping on semi-quantum secret sharing scheme of specific bits. Int J Theor Phys (2016) 55:4027–35. doi:10.1007/s10773-016-3031-x

CrossRef Full Text | Google Scholar

7. Gao X, Zhang S, Chang Y. Cryptanalysis and improvement of the semi-quantum secret sharing protocol. Int J Theor Phys (2017) 56:2512–20. doi:10.1007/s10773-017-3404-9

CrossRef Full Text | Google Scholar

8. Gao G, Wang Y, Wang D. Cryptanalysis of a semi-quantum secret sharing scheme based on Bell states. Mod Phys Lett B (2018) 32(09):1850117. doi:10.1142/s0217984918501178

CrossRef Full Text | Google Scholar

9. Li Z, Li Q, Liu C, Peng Y, Chan WH, Li L. Limited resource semiquantum secret sharing. Quan Inf Process (2018) 17:285–11. doi:10.1007/s11128-018-2058-8

CrossRef Full Text | Google Scholar

10. Xiang Y, Liu J, Bai MQ, Yang X, Mo ZW. Limited resource semi-quantum secret sharing based on multi-level systems. Int J Theor Phys (2019) 58:2883–92. doi:10.1007/s10773-019-04171-y

CrossRef Full Text | Google Scholar

11. Tsai CW, Chang YC, Lai YH, Yang CW. Cryptanalysis of limited resource semi-quantum secret sharing. Quan Inf Process (2020) 19:224–8. doi:10.1007/s11128-020-02690-w

CrossRef Full Text | Google Scholar

12. Zhou MK. Improvement of the semi-quantum secret sharing protocol of specific bits. Int J Theor Phys (2020) 59(6):1772–6. doi:10.1007/s10773-020-04443-y

CrossRef Full Text | Google Scholar

13. Gan ZG. Improvement of Gao et al.’s semi-quantum secret sharing protocol. Int J Theor Phys (2020) 59:930–5. doi:10.1007/s10773-019-04378-z

CrossRef Full Text | Google Scholar

14. Li L, Qiu D, Mateus P. Quantum secret sharing with classical Bobs. J Phys A. (2013) 46(4):045304. doi:10.1088/1751-8113/46/4/045304

CrossRef Full Text | Google Scholar

15. Cleve R, Gottesman D, Lo HK. How to share a quantum secret. Phys Rev Lett (1999) 83(3):648–51. doi:10.1103/physrevlett.83.648

CrossRef Full Text | Google Scholar

16. Li Q, Long DY, Chan WH, Qiu DW. Sharing a quantum secret without a trusted party. Quan Inf Process (2011) 10:97–106. doi:10.1007/s11128-010-0180-3

CrossRef Full Text | Google Scholar

17. Zhou P, Li XH, Liang YJ, Deng FG, Zhou HY. Multiparty quantum secret sharing with pure entangled states and sample photons. Physica A Stat Mech its Appl (2007) 381:164–9. doi:10.1016/j.physa.2007.04.018

CrossRef Full Text | Google Scholar

18. Zhang ZJ, Gao G, Wang X, Han LF, Shi SH. Multiparty quantum secret sharing based on the improved Boström–Felbinger protocol. Opt Commun (2007) 269:418–22. doi:10.1016/j.optcom.2006.08.021

CrossRef Full Text | Google Scholar

19. Lin S, Wen QY, Gao F, Zhu FC. Improving the security of multiparty quantum secret sharing based on the improved Boström–Felbinger protocol. Opt Commun (2008) 281(17):4553–4. doi:10.1016/j.optcom.2008.05.026

CrossRef Full Text | Google Scholar

20. Li F, Hu H, Zhu S, Yan J, Ding J. A verifiable (k, n)-threshold dynamic quantum secret sharing schemen. Quan Inf Process (2022) 21:259. doi:10.1007/s11128-022-03617-3

CrossRef Full Text | Google Scholar

21. Li F, Chen T, Zhu S. An efficient and secure dynamic quantum direct two-secrets sharing scheme. Mod Phys Lett B (2023) 37(34):2350180. doi:10.1142/s0217984923501804

CrossRef Full Text | Google Scholar

22. Li F, Chen T, Zhu H, Zhu S, Pang B. Dynamic hierarchical quantum secret sharing with general access structure. Quan Inf Process (2023) 22(8):320. doi:10.1007/s11128-023-04076-0

CrossRef Full Text | Google Scholar

23. Li L, Han Z, Li Z, Guan F, Zhang L. Authenticable dynamic quantum multi-secret sharing based on the Chinese remainder theorem. Quan Inf Process (2024) 23(2):46. doi:10.1007/s11128-023-04236-2

CrossRef Full Text | Google Scholar

24. Li F, Luo M, Zhu H, Zhu S, Pang B. A (w, t,n)-weighted threshold dynamic quantum secret sharing scheme with cheating identification. Physica A-Statistical Mechanic Its Appl (2023) 612:128494. doi:10.1016/j.physa.2023.128494

CrossRef Full Text | Google Scholar

25. You Z, Wang Y, Dou Z, Li J, Chen X, Li L. Dynamic quantum secret sharing between multiparty and multiparty based on single photons. Physica A-Statistical Mechanic Its Appl (2023) 624:128893. doi:10.1016/j.physa.2023.128893

CrossRef Full Text | Google Scholar

26. Li F, Chen T, Zhu H. Dynamic (t, n) threshold quantum secret sharing based on d-dimensional Bell state. Physica A-Statistical Mechanic Its Appl (2022) 606:128122. doi:10.1016/j.physa.2022.128122

CrossRef Full Text | Google Scholar

27. Tian Y, Wang JL, Bian GQ, Chang J, Li J. Dynamic multi-party to multi-party quantum secret sharing based on bell states. Adv Quan Tech (2024) 7. doi:10.1002/qute.202400116

CrossRef Full Text | Google Scholar

28. Lai H, Pieprzyk J, Pan L. Dynamic and compressed quantum many-body state secret sharing based on site-independent matrix product states. Quan Inf Process (2022) 21(3):83. doi:10.1007/s11128-022-03420-0

CrossRef Full Text | Google Scholar

29. Lai H, Pieprzyk J, Pan L. Dynamic hierarchical quantum secret sharing based on the multiscale entanglement renormalization ansatz. Phys Rev A (2022) 106(5):052403. doi:10.1103/physreva.106.052403

CrossRef Full Text | Google Scholar

30. Lin J, Chen CC, Huang CY. Efficient dynamic quantum secret sharing in pre-measurement and post-measurement phases. Physica A-Statistical Mechanic Its Appl (2024) 638:129615. doi:10.1016/j.physa.2024.129615

CrossRef Full Text | Google Scholar

31. Dong YM, Luo Y, Fu YY. A novel verifiable weighted threshold quantum secret sharing scheme. Physica Scripta (2023) 98(6):065105. doi:10.1088/1402-4896/accf4c

CrossRef Full Text | Google Scholar

32. Chang W, Li ZZ, You FC, Pan XB. Dynamic quantum fully homomorphic encryption scheme based on universal quantum circuit. J Inf Security Appl (2023) 75:103510. doi:10.1016/j.jisa.2023.103510

CrossRef Full Text | Google Scholar

33. Ye CQ, Ye TY, He D, Gan ZG. Multiparty semi-quantum secret sharing with d-level single-particle states. Int J Theor Phys (2019) 58:3797–814. doi:10.1007/s10773-019-04248-8

CrossRef Full Text | Google Scholar

34. Gong LH, Ye ZJ, Liu C, Zhou S. One-way semi-quantum private comparison protocol without pre-shared keys based on unitary operations. Laser Phys Lett (2024) 21(3):035207. doi:10.1088/1612-202x/ad21ec

CrossRef Full Text | Google Scholar

35. Zhou NR, Chen ZY, Liu YY, Gong LH. Multi-party semi-quantum private comparison protocol of size relation with d-level GHZ states. Adv Quan Tech (2024). doi:10.1002/qute.202400530

CrossRef Full Text | Google Scholar

36. Boyer M, Kenigsberg D, Mor T. Quantum key distribution with classical bob. Phys Rev Lett (2007) 99(14):140501–14050. doi:10.1103/physrevlett.99.140501

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yu KF, Gu J, Hwang T, Gope P. Multi-party semi-quantum key distribution-convertible multi-party semi-quantum secret sharing. Quan Inf Process (2017) 16:194–14. doi:10.1007/s11128-017-1631-x

CrossRef Full Text | Google Scholar

38. Gao G, Wang Y, Wang D. Multiparty semiquantum secret sharing based on rearranging orders of qubits. Mod Phys Lett B (2016) 30(10):1650130. doi:10.1142/s021798491650130x

CrossRef Full Text | Google Scholar

39. Deng FG, Zhou HY, Long GL. Bidirectional quantum secret sharing and secret splitting with polarized single photons. Phys Lett A (2005) 337(4-6):329–34. doi:10.1016/j.physleta.2005.02.001

CrossRef Full Text | Google Scholar

40. Ye CQ, Ye TY. Circular semi-quantum secret sharing using single particles. Commun Theor Phys (2018) 70(6):661. doi:10.1088/0253-6102/70/6/661

CrossRef Full Text | Google Scholar

41. Zhou NR, Xu QD, Du NS, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional Bell states. Quan Inf Process (2021) 20:124. doi:10.1007/s11128-021-03056-6

CrossRef Full Text | Google Scholar

42. Wang B, Liu SQ, Gong LH. Semi-quantum private comparison protocol of size relation with d-dimensional GHZ states. Chin Phys B (2022) 31:010302. doi:10.1088/1674-1056/ac1413

CrossRef Full Text | Google Scholar

43. Wang B, Gong LH, Liu SQ. Multi-party semi-quantum private comparison protocol of size relation based on two-dimensional Bell states. Chin Phys B (2024) (33):110303. doi:10.1088/1674-1056/ac1413

CrossRef Full Text | Google Scholar

44. Zhou S, Xie QM, Zhou NR. Measurement-free mediated semi-quantum key distribution protocol based on single-particle states. Laser Phys Lett (2024) 21(6):065207. doi:10.1088/1612-202x/ad3f96

CrossRef Full Text | Google Scholar

45. Gong LH, Li ML, Cao H, Wang B. Novel semi-quantum private comparison protocol with Bell states. Laser Phys Lett (2024) 21(5):055209. doi:10.1088/1612-202x/ad3a54

CrossRef Full Text | Google Scholar

46. Tian Y, Li J, Chen XB, Ye CQ, Li HJ. An efficient semi-quantum secret sharing protocol of specific bits. Quan Inf Process (2021) 20(6):217. doi:10.1007/s11128-021-03157-2

CrossRef Full Text | Google Scholar

47. He F, Xin XJ, Li C, Li F. Security analysis of the semi-quantum secret-sharing protocol of specific bits and its improvement. Quan Inf Process (2024) 23(2):51. doi:10.1007/s11128-023-04255-z

CrossRef Full Text | Google Scholar

48. Xing D, Wang YF, Dou Z, Li J, Chen XB, Li LX. Efficient semi-quantum secret sharing protocol using single particles. Chin Phys B (2023) 32(7):070308. doi:10.1088/1674-1056/ace159

CrossRef Full Text | Google Scholar

49. Gao G. Cryptanalysis of efficient semi-quantum secret sharing protocol using single particles. Chin Phys B (2024) 33:040301. doi:10.1088/1674-1056/ad2bee

CrossRef Full Text | Google Scholar

50. Zhou Z, Wang Y, Dou Z, Li J, Chen X, Li L. A (t, n) threshold protocol of semi-quantum secret sharing based on single particlesn. Front Phys (2023) 11:1225059. doi:10.3389/fphy.2023.1225059

CrossRef Full Text | Google Scholar

51. Shamir A. How to share a secret. Commun ACM (1979) 22(11):612–3. doi:10.1145/359168.359176

CrossRef Full Text | Google Scholar

52. Cai QY. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys Lett A (2006) 351(1-2):23–5. doi:10.1016/j.physleta.2005.10.050

CrossRef Full Text | Google Scholar

53. Deng FG, Li XH, Zhou HY, Zhang ZJ. Improving the security of multiparty quantum secret sharing against Trojan horse attack. Phys Rev A (2005) 72(4):044302. doi:10.1103/physreva.72.044302

CrossRef Full Text | Google Scholar

54. Gisin N, Ribordy GG, Tittel W, Zbinden H. Quantum cryptography. Rev Mod Phys (2002) 74(1):145–95. doi:10.1103/revmodphys.74.145

CrossRef Full Text | Google Scholar

55. Barenco A, Bennett CH, Cleve R, DiVincenzo DP, Margolus N, Shor P, et al. Elementary gates for quantum computation. Phys Rev A (1995) 52(5):3457–67. doi:10.1103/physreva.52.3457

PubMed Abstract | CrossRef Full Text | Google Scholar