A mini-review on ancient mathematics’ modern applications with an emphasis on the old Babylonian mathematics for MEMS systems

This paper offers a concise overview regarding ancient Chinese mathematics, centering on the Ying Buzu Shu, He Chengtian inequality, and the frequency formulation stemming from them. Moreover, it delves into the Max-min approach and Chunhui He’s iterative algorithm. What’s more, the spotlight is cast on ancient Chinese mathematics, which bears certain similarities to the ancient Babylonian mathematical tradition. Subsequently, the old Babylonian algorithm for computing square roots is adapted to tackle the hurdle of nonlinear differential equations. To showcase the potential of this approach, a set of Micro-Electro-Mechanical systems (MEMS) problems are utilized to exemplify the effectiveness of the modified old Babylonian algorithm in attaining high-precision analytical solutions, accompanied by an exploration of its prospective applications.

1 Introduction

Every student knows Newton’s iteration method from a textbook, but few may be aware of an ancient Chinese algorithm called Ying Buzu Shu, which has some advantages over Newton’s method and is also widely used in numerical simulations. Ying Buzu Shu is a sophisticated method for approximating solutions to a variety of mathematical problems. It involves the initialization of two estimates and the subsequent refinement of the solution through a series of calculations. Since Ying Buzu Shu is insensitive to initial estimates, but predicts a fast rate of convergence, it has great practical implications for many real-world challenges in various fields of engineering, such as industrial engineering, civil engineering, electrical engineering, and mechanical engineering. The applications of Ying Buzu Shu in modern sciences to nonlinear differential equations can be found in references [1–3].

A modern mathematical perspective on ancient mathematics can offer a fresh insight into the applications of mathematics to practical problems. The application of ancient Chinese mathematics to modern engineering problems was first initiated in 2006 by Chinese mathematician Dr. He [4]. Subsequently, many highly regarded analytical techniques have been developed. Notable among these are methods of approximating solutions to differential equations. In addition, methods for studying the frequency-amplitude relationship of oscillators have been developed. The simplicity and effectiveness of the formulation have contributed to its widespread use for quickly and reliably gaining insight into the periodic characteristics of nonlinear vibration systems. Professor He further developed the ancient Chinese mathematical algorithm into a modern numerical method called He’s frequency formula [5, 6]. It was proposed as a means of solving nonlinear oscillators and has since been regarded as the simplest method of doing so. The Chinese mathematician Chun-Hui He provided a rigorous mathematical analysis and then proposed a modification that was subsequently named the Chun-Hui He iteration algorithm [7, 8]. The Max-min approach [9, 10], as a major extension, has been the subject of considerable research and is widely used in engineering.

Another topic of considerable interest in the field of ancient Chinese mathematics is He Chengtian inequality, which was used for astronomical problems such as calculating the lunar cycle. It has been proved that Ying Buzu Shu and He Chengtian inequality are equivalent under some special cases, that means He Chengtian inequality can be derived from the method of Ying Buzu Shu [11]. Although both methods are originally proposed to solve nonlinear algebraic equations, they can also be extended to solve various nonlinear differential equations [4, 12].

2 Old Babylonian mathematics

Closely related to the He Chengtian inequality is the old Babylonian algorithm, which can even be seen as a special case of the He Chengtian inequality in a sense.

The old Babylonian mathematics, a brilliant mathematical treasure of ancient civilization, not only made outstanding achievements in algebra, geometry, astronomy and other fields, but also made unique contributions to numerical computation [13, 14]. The algorithm used by the old Babylonians to solve square roots was not only practical at the time, but also had a profound impact on the later development of mathematics [15–17]. It inspired later mathematicians to develop more efficient and accurate numerical solution methods, such as Newton’s iteration method. In addition, the ideas of the old Babylonian algorithm are widely used in fields such as computer science, engineering and physics, and have become one of the foundations of numerical computation.

The algorithm used by the old Babylonians to solve square roots is known as the predecessor of the old Babylonian algorithm or the Newton-Raphson algorithm [18]. The principle of the old Babylonian algorithm is based on the property of square roots, which means that the square root of a number is approximately equal to the value obtained by adding it to another approximation and dividing by 2. As the number of iterations increases, this approximation becomes closer to the true square root value. Modern mathematics has proven the correctness of this algorithm and extended it to more general numerical solution methods.

With its simplicity, efficiency and practicality, the old Babylonian algorithm has become a shining pearl of ancient mathematics. Through in-depth research on this algorithm, we can not only understand the development process and achievements of ancient mathematics, but also draw wisdom from it, providing reference and inspiration for the development of modern mathematics and scientific technology. Recently, Professor He studied the application of the old Babylonian algorithm in modern technology and proposed for the first time that the old Babylonian algorithm can solve equations, including differential equations [18].

Differential equations are an important branch of mathematics. By establishing the relationship between variables and their rates of change, differential equation models can be used to predict and analyze the behavior of systems, such as the vibrations of physical systems, economic market fluctuations, population growth, etc. Differential equations have wide applications in fields such as physics, engineering, biology, chemistry, economics and demography, and can be used to describe numerous dynamic processes in nature and engineering. As a bridge between mathematics and practical applications, differential equations provide us with an important tool for quantifying and predicting how systems evolve over time. Among them, MEMS differential equations refer to the differential equations in mathematical models related to Micro-Electro-Mechanical systems (MEMS). These equations are commonly used to describe the dynamic properties and behavior of MEMS devices. MEMS systems are a revolutionary high-tech industry, highly valued by governments and experts around the world. They have wide applications in biotechnology, aerospace and military fields. The pull-in phenomenon is an important characteristic in MEMS systems, especially in electrostatically driven micro actuators. It refers to the suction phenomenon that occurs when two polar plates reach a critical position under the drive of electrostatic force. The pull-in phenomenon in MEMS systems is a complex and important research area, and obtaining accurate pull-in point data is crucial for both theoretical research and practical applications [19–22]. Studying the differential equations of MEMS is of great importance for promoting the development of micro-nano electronics technology, optimizing the performance of MEMS systems and providing theoretical support.

In this article, we attempt for the first time to apply the old Babylon algorithm to a class of MEMS differential equations and search for high-precision frequency and approximate solutions, in order to apply it to the study of more differential equations that cannot provide analytical solutions.

3 The old Babylonian algorithm

Friberg analyzed the effectiveness of the old Babylonian approximation method for finding square roots in quadratic equations [23]. Ilic et al. gave a note on the old square root algorithm and related variants [24]. Below, we will provide a detailed introduction to this method.

Consider the following algebraic equation

${\mathit{x}}^{\mathbf{2}}=\mathit{a}\left(\mathit{a}>\mathbf{0}\right)(1)$

To find the square root of a, the iterative formula of Equation 1 is

${\mathit{x}}_{\mathit{n}}=\frac{\mathbf{1}}{\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}+\frac{\mathbf{1}}{\mathbf{2}}\frac{\mathit{a}}{{\mathit{x}}_{\mathit{n}-\mathbf{1}}}(2)$

An initial guess $x_0$ is chosen, an approximation $x_n$ is calculated by Equation 2

$x_0\frac{a}{x_0}$

$x_1=\frac{1}{2}{x}_0+\frac{1}{2}\frac{a}{x_0}\frac{a}{x_1}$

$x_2=\frac{1}{2}{x}_1+\frac{1}{2}\frac{a}{x_1}\frac{a}{x_2}$

$x_3=\frac{1}{2}{x}_2+\frac{1}{2}\frac{a}{x_2}\frac{a}{x_3}$

$x_4=\frac{1}{2}{x}_3+\frac{1}{2}\frac{a}{x_3}\frac{a}{x_4}$

$x_5=\frac{1}{2}{x}_4+\frac{1}{2}\frac{a}{x_4}\frac{a}{x_5}$

$\dots \dots$

$x_n=\frac{1}{2}{x}_{n-1}+\frac{1}{2}\frac{a}{x_{n-1}}\frac{a}{x_n}$

$\dots \dots$

This results in a closed interval set $\left[\frac{a}{x_n},x_n\right]$ (or $\left[x_n,\frac{a}{x_n}\right]$). As the number of iterations increases, the length of the interval set becomes shorter. Continuing in sequence will yield the exact value of the square root. Table 1 displays the iterative process of solving $\sqrt{3}$ in old Babylonian mathematics. Taking the calculation of $\sqrt{3}$ as an example, here $\sqrt{3}=1.7320508075\cdots \cdots$. After the fourth iteration, the interval [$1.7320508100$, $1.7320508051$] appeared. This interval already contains a high-precision approximate solution of $\sqrt{3}$, which can be accurate to the seventh decimal place, that is, millions of decimal places.

Table 1

Table 1. Four iterations to seek the value of $\sqrt{3}$.

4 The modified old Babylonian algorithm

Recently, He studied the application of old Babylonian mathematics in finding high-precision approximate solutions for differential equations [18]. Now we are studying a more general extension of this method.

4.1 Ordinary differential equation

The third part elaborates on the iterative method for the square root of a real number a. It is easy to find that in the iterative formula for finding $\sqrt{a}$, the sum of the coefficients of $x_{n-1}$ and $\frac{a}{x_{n-1}}$ is 1, so it is advisable to introduce parameter $\alpha$ (a positive integer) to make the recursive formula more generalized. The formula is as follows

${\mathit{x}}_{\mathit{n}}=\frac{\mathit{\alpha }}{\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}+\frac{\left(2-\mathit{\alpha }\right)}{\mathbf{2}}\frac{\mathit{a}}{{\mathit{x}}_{\mathit{n}-\mathbf{1}}}\left(\mathbf{0}<\mathit{\alpha }<\mathbf{2}\right)(3)$

When $\alpha =1$, Equation 3 becomes Equation 2.

For a general equation as follows

${\mathit{x}}^{\mathit{m}}-\mathit{a}=\mathbf{0}(4)$

The modified old Babylonian algorithm of Equation 4 is

${\mathit{x}}_{\mathit{n}}=\frac{\mathit{\alpha }}{\mathit{m}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}+\frac{\left(\mathit{m}-\mathit{\alpha }\right)}{\mathit{m}}\frac{\mathit{a}}{{\mathit{x}}_{\mathit{n}-\mathbf{1}}}\left(\mathit{m}-\mathbf{2}<\mathit{\alpha }<\mathit{m}\right)(5)$

This method can not only solve algebraic equations but also differential equations. Let’s take a second-order differential equation as an example

${\mathit{x}}^{″}+\mathit{f}\left(\mathit{x}\right)=\mathbf{0}(6)$

Construct an iteration algorithm based on Equation 5 as follows:

${\mathit{x}}_{\mathit{n}}=\frac{\mathit{\alpha }}{\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}+\frac{\left(2-\mathit{\alpha }\right)}{\mathbf{2}}\frac{{\mathit{x}}_{\mathit{n}-\mathbf{1}}^{″}+\mathit{f}\left({\mathit{x}}_{\mathit{n}-\mathbf{1}}\right)+{\left({\mathit{x}}_{\mathit{n}-\mathbf{1}}\right)}^{\mathbf{2}}}{{\mathit{x}}_{\mathit{n}-\mathbf{1}}}\left(\mathbf{0}<\mathit{\alpha }<\mathbf{2}\right)(7)$

Firstly, select trial solution $x_0$ that meets the initial conditions. For Equation 6, we often choose

${\mathit{x}}_{\mathbf{0}}=\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}+\mathit{\phi }\right)(8)$

Here, A and $\phi$ are two constants determined by the initial conditions, and $w$ is the undetermined parameter. The method for finding $w$ is given by the following Equation 9 [18]

${\mathit{x}}_{\mathbf{1}}\left(\overline{\mathit{t}}\right)=\frac{\mathit{\alpha }}{\mathbf{2}}{\mathit{x}}_{\mathbf{0}}\left(\overline{\mathit{t}}\right)+\frac{\left(2-\mathit{\alpha }\right)}{\mathbf{2}}\frac{{\mathit{x}}_{\mathbf{0}}^{″}\left(\overline{\mathit{t}}\right)+\mathit{f}\left({\mathit{x}}_{\mathbf{0}}\left(\overline{\mathit{t}}\right)\right)+{\left({\mathit{x}}_{\mathbf{0}}\left(\overline{\mathit{t}}\right)\right)}^{\mathbf{2}}}{{\mathit{x}}_{\mathbf{0}}\left(\overline{\mathit{t}}\right)}(9)$

where $\overline{t}$ is a location point.

4.2 MEMS systems

With the advancement of science and technology, the MEMS system has become a widespread technology due to its miniature size, minimal power consumption, high integration, and sophisticated intelligence. However, a major challenge in the application of these devices is the pull-in phenomenon, which can lead to device malfunction.

A thorough study of the pull-in phenomenon in electrostatic actuation devices is of paramount importance to ensure the optimal performance and reliability of these devices. Pull-in instability has become a topic of great interest in both industry and academia, and numerous studies have been conducted on the dynamic pull-in of MEMS models. Tian and her colleagues proposed a fractal MEMS system and demonstrated that the pull-in instability can be transformed into a stable state [25]. He established a variational principle that can be used for both analytical and numerical analysis of the MEMS system [26, 27].

As a practical application, we consider the following nonlinear equation arising in MEMS systems

${\mathit{y}}^{″}+\mathit{y}+\frac{\mathit{\theta }}{\mathit{y}-\mathbf{1}}=\mathbf{0},\mathit{y}\left(\mathbf{0}\right)=\mathbf{0},{\mathit{y}}^{\prime }\left(\mathbf{0}\right)=\mathbf{0},\mathit{\theta }>\mathbf{0}(10)$

Here y is the dimensionless distance, $\theta$ represents a voltage-related parameter.

The system displays periodic or unsteady behavior. When θ does not exceed a critical value, the phase space trajectory closes on itself and the system moves periodically, and when θ exceeds the critical value, it becomes the pull-in instability. The critical value is $\theta =0.203632188$. The pull-in behavior is an inherent property of the MEMS oscillator, which occurs when the voltage is larger than its threshold value. It plays an important role in electrostatic drive sensors because of their efficient and reliable operation [28–30].

The transcendental equation describing the pull-in phenomenon is

${\left(\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}\mathit{\theta }}}{\mathbf{2}}\right)}^{\mathbf{2}}+\mathbf{2}\mathit{\theta }\mathbf{ln}\left|\mathbf{1}-\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}\mathit{\theta }}}{\mathbf{2}}\right|=\mathbf{0}(11)$

where $\theta$ is a positive root of Equation 11.

We need to solve this nonlinear equation to discuss the effect of the MEMS oscillator parameter on the pull-in voltage. For this purpose, we use the improved old Babylonian algorithm and we have

$\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}{\mathit{\theta }}_{\mathit{n}}}}{\mathbf{2}}=\frac{\mathbf{1}}{\mathbf{2}}\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}{\mathit{\theta }}_{\mathit{n}-\mathbf{1}}}}{\mathbf{2}}+\frac{\mathbf{1}}{\mathbf{2}}\frac{-\mathbf{2}{\mathit{\theta }}_{\mathit{n}-\mathbf{1}}\mathbf{ln}\left|\mathbf{1}-\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}{\mathit{\theta }}_{\mathit{n}-\mathbf{1}}}}{\mathbf{2}}\right|}{\frac{\mathbf{1}+\sqrt{\mathbf{1}-\mathbf{4}{\mathit{\theta }}_{\mathit{n}-\mathbf{1}}}}{\mathbf{2}}}(12)$

The process is initiated with a value of ${\theta }_0=0.2$, and the initial iteration produces ${\theta }_1=0.202812891$ based on Equation 12. The relative error for the first iteration result is 0.4023%.

Subsequently, the improved old Babylonian algorithm will be employed to ascertain approximate solutions to differential equations. However, it is important to acknowledge that this method is not applicable to differential equations with zero initial conditions. So, the first objective is to introduce a transformation to overcome the drawbacks.

Assuming $x=A-y$ and substituting it into Equation 10, we obtain

${\mathit{x}}^{″}+\mathit{x}-\mathit{A}+\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}+\mathit{x}}=\mathbf{0},\mathit{x}\left(\mathbf{0}\right)=\mathit{A},{\mathit{x}}^{\prime }\left(\mathbf{0}\right)=\mathbf{0}(13)$

The nonlinear term $\frac{\theta }{1-A+x}$ could be expanded in the form

$\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}+\mathit{x}}=\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}}\left(\mathbf{1}+\frac{\mathit{x}}{\mathit{A}-\mathbf{1}}+\frac{{\mathit{x}}^{\mathbf{2}}}{{\left(\mathit{A}-\mathbf{1}\right)}^{\mathbf{2}}}+\cdots \right)(14)$

Substituting Equation 14 into Equation 13 yields

${\mathit{x}}^{″}+\mathit{x}+\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}}\left(\frac{\mathit{x}}{\mathit{A}-\mathbf{1}}+\frac{{\mathit{x}}^{\mathbf{2}}}{{\left(\mathit{A}-\mathbf{1}\right)}^{\mathbf{2}}}+\cdots \right)-\mathit{A}+\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}}=\mathbf{0}(15)$

This equation $-A+\frac{\theta }{1-A}=0$ needs to be assumed to eliminate the constant term, and it gets $\theta =A\left(1-A\right)$ in Equation 15.

He’s frequency formula ${\omega }_{He}$ of Equation 13 is approximated as follows [31–34]

${\mathit{\omega }}_{\mathit{H}\mathit{e}}={\left.\sqrt{\frac{\mathit{d}\left(\mathit{x}-\mathit{A}+\frac{\mathit{\theta }}{\mathbf{1}-\mathit{A}+\mathit{x}}\right)}{\mathit{d}\mathit{x}}}\right|}_{\mathit{x}=\frac{\mathit{A}}{\mathbf{2}},\mathit{\theta }=\mathit{A}\left(\mathbf{1}-\mathit{A}\right)}=\sqrt{\frac{\mathbf{5}{\mathit{A}}^{\mathbf{2}}-\mathbf{8}\mathit{A}+\mathbf{4}}{{\left(\mathit{A}-\mathbf{2}\right)}^{\mathbf{2}}}}(16)$

The frequency formula has been utilized to gain rapid and reliable insights into the frequency-amplitude relationship of nonlinear vibration systems. The location point is a topic that has been the subject of considerable debate, with a lot of modifications having been proposed. Lyu and colleagues put forward an alternative location point [35], while He and others recommended the use of multiple location points, followed by the calculation of an average value [36]. Shen suggested the employment of Lagrange interpolation for the location points [37], while Mohammadian introduced a novel approach for determining the location point [38].

According Equation 8 and Equation 16, the approximate solution of Equation 10 is

$\mathit{y}=\mathit{A}-\mathit{A}\mathit{cos}\left(\sqrt{\frac{\mathbf{5}{\mathit{A}}^{\mathbf{2}}-\mathbf{8}\mathit{A}+\mathbf{4}}{{\left(\mathit{A}-\mathbf{2}\right)}^{\mathbf{2}}}}\mathit{t}\right)(17)$

Rewrite Equation 13

${\mathit{x}}^{\mathbf{2}}=\left(\mathit{A}-\mathbf{1}-\mathit{x}\right){\mathit{x}}^{″}+\left(\mathbf{2}\mathit{A}-\mathbf{1}\right)\mathit{x},\mathit{x}\left(\mathbf{0}\right)=\mathit{A},{\mathit{x}}^{\prime }\left(\mathbf{0}\right)=\mathbf{0}(18)$

For Equation 7, the iteration algorithm of Equation 18 can be set as

${\mathit{x}}_{\mathit{n}}=\frac{\mathit{\alpha }}{\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}+\frac{\left(2-\mathit{\alpha }\right)}{\mathbf{2}}\frac{\left(\mathit{A}-\mathbf{1}-{\mathit{x}}_{\mathit{n}-\mathbf{1}}\right){\mathit{x}}_{\mathit{n}-\mathbf{1}}^{″}+\left(\mathbf{2}\mathit{A}-\mathbf{1}\right){\mathit{x}}_{\mathit{n}-\mathbf{1}}}{{\mathit{x}}_{\mathit{n}-\mathbf{1}}}(19)$

We can assume the trial solution is

${\mathit{x}}_{\mathbf{0}}=\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}\right)(20)$

Here, $\alpha$ will also be taken as 1. Substituting Equation 20 into Equation 19 yields

$\begin{array}{ll}\hfill {\mathit{x}}_{\mathbf{1}}& =\frac{\mathbf{1}}{\mathbf{2}}\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}\right)\hfill \\ \hfill & +\frac{1}{\mathbf{2}}\frac{\left(\mathit{A}-\mathbf{1}-\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}\right)\right)\left(-\mathit{A}{\mathit{w}}^{\mathbf{2}}\right)\mathit{cos}\left(\mathit{w}\mathit{t}\right)+\left(\mathbf{2}\mathit{A}-\mathbf{1}\right)\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}\right)}{\mathit{A}\mathit{cos}\left(\mathit{w}\mathit{t}\right)}\hfill \end{array}$

$=\frac{\mathit{A}+\mathit{A}{\mathit{w}}^{\mathbf{2}}}{\mathbf{2}}\mathit{cos}\left(\mathit{w}\mathit{t}\right)+\mathbf{2}\mathit{A}-\mathbf{1}-\mathit{A}{\mathit{w}}^{\mathbf{2}}+{\mathit{w}}^{\mathbf{2}}(21)$

By the initial condition, Equation 21 becomes

${\mathit{x}}_{\mathbf{1}}\left(\mathbf{0}\right)=\frac{\mathit{A}+\mathit{A}{\mathit{w}}^{\mathbf{2}}}{\mathbf{2}}+\mathbf{2}\mathit{A}-\mathbf{1}-\mathit{A}{\mathit{w}}^{\mathbf{2}}+{\mathit{w}}^{\mathbf{2}}=\mathit{A}(22)$

Based on Equation 22, the frequency $w$ has the following form

$\mathit{w}=\sqrt{\frac{\mathbf{1}-\mathbf{1.5}\mathit{A}}{\mathbf{1}-\mathbf{0.5}\mathit{A}}}(23)$

So, based on Equation 23, the approximate solution of Equation 10 is

$\mathit{y}=\mathit{A}-\mathit{A}\mathit{cos}\left(\sqrt{\frac{\mathbf{1}-\mathbf{1.5}\mathit{A}}{\mathbf{1}-\mathbf{0.5}\mathit{A}}}\mathit{t}\right)(24)$

We compare the numerical solution with the analytical solution according to Equation 17 and Equation 24 in Figure 1 for different values of $\theta$. We can find that the approximation is better and the error is smaller. The example shows that He’s frequency formula method and the modified old Babylonian algorithm are all useful tools for nonlinear systems. But as the value of $\theta$ increases, the error between the approximate solution and the exact solution becomes larger and larger.

Figure 1

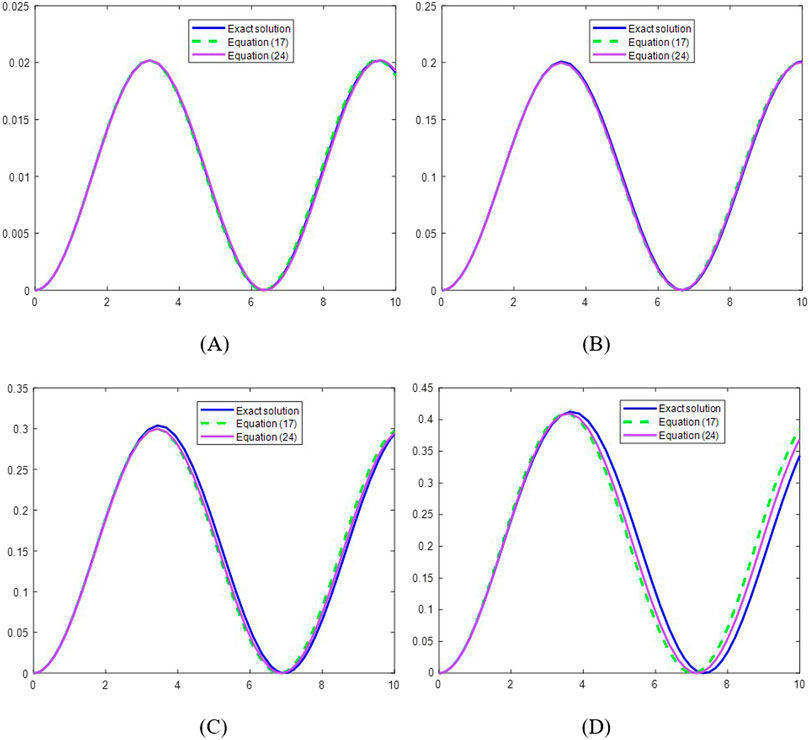
Figure 1. Comparison of the approximate solutions of Equation 17 and Equation 24 with the exact ones for (A) $\theta =0.0475$, A = 0.05; (B) $\theta =0.09$, A = 0.1; (C) $\theta =0.1275$, A = 0.15; and (D) $\theta =0.16$, A = 0.2.

In order to increase the accuracy of the approximation, it is usually advisable to search for a trial solution in the following way

${\mathit{x}}_{\mathbf{0}}=\mathit{\mu }\mathit{cos}\left(\mathit{w}\mathit{t}\right)+\left(\mathit{A}-\mathit{\mu }\right)\mathit{cos}\left(\mathbf{3}\mathit{w}\mathit{t}\right)(25)$

where $\mu$ is an unknown constant that satisfying the following form according to Equation 13: $x_0\left(0\right)=A$, $x_0^{\prime }\left(0\right)=0$, $x_0^{″}\left(0\right)=A^2-A$.

Using the above formula, it is easy to obtain

$\mathit{\mu }=\mathit{A}\left(\frac{\mathit{A}-\mathbf{1}}{\mathbf{8}{\mathit{w}}^{\mathbf{2}}}+\frac{\mathbf{9}}{\mathbf{8}}\right)(26)$

By Equation 19 and Equation 25, it yields

$\begin{array}{ll}\hfill {\mathit{x}}_{\mathbf{1}}\left(\mathit{t}\right)& =\frac{\mathbf{1}}{\mathbf{2}}\left(\mathit{\mu }\mathit{cos}\left(\mathit{w}\mathit{t}\right)+\left(\mathit{A}-\mathit{\mu }\right)\mathit{cos}\left(\mathbf{3}\mathit{w}\mathit{t}\right)\right)\hfill \\ \hfill & +\frac{1}{\mathbf{2}}\left[\frac{\left(\mathit{A}-\mathbf{1}-\mathit{\mu }\mathit{cos}\left(\mathit{w}\mathit{t}\right)-\left(\mathit{A}-\mathit{\mu }\right)\mathbf{cos}\left(\mathbf{3}\mathit{w}\mathit{t}\right)\right)\left(-\mathit{\mu }{\mathit{w}}^{\mathbf{2}}\mathit{cos}\left(\mathit{w}\mathit{t}\right)-\mathbf{9}{\mathit{w}}^{\mathbf{2}}\left(\mathit{A}-\mathit{\mu }\right)\mathit{cos}\left(\mathbf{3}\mathit{w}\mathit{t}\right)\right)}{\mathit{\mu }\mathit{cos}\left(\mathit{w}\mathit{t}\right)+\left(\mathit{A}-\mathit{\mu }\right)\mathit{cos}\left(\mathbf{3}\mathit{w}\mathit{t}\right)}\right.\hfill \\ \hfill & \left.+\left(\mathbf{2}\mathit{A}-\mathbf{1}\right)\right]\hfill \end{array}(27)$

The location point [18] is chosen as

$\mathit{w}\mathit{t}=\frac{\mathit{\pi }}{\mathbf{6}}(28)$

This means

${\mathit{x}}_{\mathbf{1}}\left(\mathit{t}\right)=\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }(29)$

By Equations 27–29, we have

${\mathit{w}}^{\mathbf{2}}=\frac{\mathbf{2}\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}{\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}(30)$

Substituting Equation 26 into Equation 30 yields

$\left[\left(\mathbf{8}-\frac{\mathbf{9}\sqrt{\mathbf{3}}}{\mathbf{2}}\right)\mathit{A}-\mathbf{8}\right]{\mathit{w}}^{\mathbf{4}}-\left[\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}{\mathit{A}}^{\mathbf{2}}+\left(\mathbf{16}-\mathbf{5}\sqrt{\mathbf{3}}\right)\mathit{A}-\mathbf{8}\right]{\mathit{w}}^{\mathbf{2}}+\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{A}\left(\mathit{A}-\mathbf{1}\right)=\mathbf{0}(31)$

Equation 31 is a fourth-order equation about frequency $w$, which can also be seen as a quadratic equation of $w^2$. For different values of A, solving this equation can obtain the frequency values.

Then a higher precision approximate solution of Equation 10 is

$\mathit{y}=\mathit{A}-\mathit{\mu }\mathit{cos}\left(\sqrt{\frac{\mathbf{2}\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}{\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}}\mathit{t}\right)-\left(\mathit{A}-\mathit{\mu }\right)\mathit{cos}\left(\mathbf{3}\sqrt{\frac{\mathbf{2}\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}{\mathit{A}-\mathbf{1}-\frac{\sqrt{\mathbf{3}}}{\mathbf{2}}\mathit{\mu }}}\mathit{t}\right)(32)$

Figure 2 shows that the images of the approximate solution (32) and the exact solution of Equation 10 almost overlap. By selecting slightly more complex trial solutions, errors can be reduced and the accuracy of the approximate solutions can be improved. This demonstrates that if the initial point is selected with care, a superior result can be obtained. Similarly, in the homotopy perturbation method [32–34], where a suitable starting point facilitates the attainment of dependable outcomes in a timely manner, it is of paramount importance to have the appropriate initial condition in this equation. This also indicates that the modified old Babylonian algorithm is a very effective method for obtaining highly accurate approximate solutions to differential equations.

Figure 2

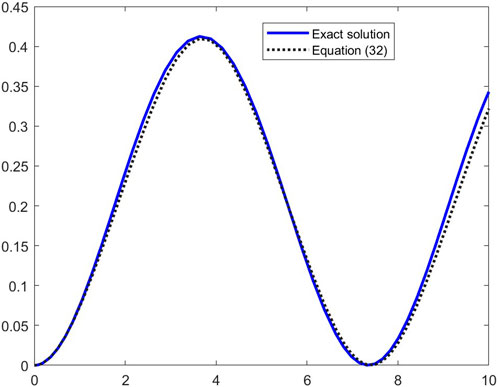
Figure 2. Comparison of the approximate solutions of Equation 32 with the exact ones for $\theta =0.16$, and A = 0.2.

5 Summary and conclusion

This article provides an overview on ancient mathematics’ modern application with a focus on the old Babylonian mathematics. It is an amazingly effective way to solve more complex problems. The algorithm is then successfully extended vertically to solve general algebraic equations and horizontally extended to solve differential equations. However, further research is needed to evaluate its convergence and reliability in solving nonlinear systems. The modified old Babylonian algorithm is applied to solve a class of MEMS systems. Comparisons demonstrate the effectiveness and correctness of the modified algorithm. The iterative process illustrates that this traditional old Babylonian methodology provides a novel and highly effective approach for addressing contemporary issues with remarkable ease, offering a promising solution to a wide range of modern challenges. Although old Babylonian mathematics originated in ancient times, its core ideas and certain techniques still play a significant role in modern society and demonstrate potential application prospects. With the continuous development of science and technology, we believe that more applications and innovations of old Babylonian mathematics will be discovered and realized.

Author contributions

J-YN: Supervision, Writing–original draft. G-QF: Investigation, Software, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. He JH. Ancient Chinese algorithm: the Ying Buzu Shu (method of surplus and deficiency) vs Newton iteration method. Appl Math Mech English Edition (2002) 23(12):1407–12. doi:10.1007/BF02438379

CrossRef Full Text | Google Scholar

2. He CH. An introduction to an ancient Chinese algorithm and its modification. Int J Numer Methods Heat and Fluid Flow (2016) 26:2486–91. doi:10.1108/HFF-09-2015-0377

CrossRef Full Text | Google Scholar

3. He JH, Kou SJM, Sedighi H. An ancient Chinese algorithm for two-point boundary problems and its application to the Michaelis-Menten kinetics. Math Model Control (2021) 1(4):172–6. doi:10.3934/mmc.2021016

CrossRef Full Text | Google Scholar

4. He JH. Some asymptotic methods for strongly nonlinear equations. Int J Mod Phys B (2006) 20:1141–99. doi:10.1142/s0217979206033796

CrossRef Full Text | Google Scholar

5. He JH. The simpler, the better: analytical methods for nonlinear oscillators and fractional oscillators. J Low Frequency Noise Vibration Active Control (2019) 38(3-4):1252–60. doi:10.1177/1461348419844145

CrossRef Full Text | Google Scholar

6. He JH. The simplest approach to nonlinear oscillators. Results Phys (2019) 15:102546. doi:10.1016/j.rinp.2019.102546

CrossRef Full Text | Google Scholar

7. Khan WA. Numerical simulation of Chun-Hui He's iteration method with applications in engineering. Int J Numer Methods Heat and Fluid Flow (2022) 32(3):944–55. doi:10.1108/hff-04-2021-0245

CrossRef Full Text | Google Scholar

8. Khan WA, Arif M, Mohammed M, Farooq U, Farooq FB, Elbashir MK, et al. Numerical and theoretical investigation to estimate Darcy friction factor in water network problem based on modified Chun-Hui He's algorithm and applications. Math Probl Eng (2022) 2022:1–11. doi:10.1155/2022/8116282

CrossRef Full Text | Google Scholar

9. Durmaz S, Demirbag SA, Kaya MO. Approximate solutions for nonlinear oscillation of a mass attached to a stretched elastic wire. Comput Math Appl (2011) 61:578–85. doi:10.1016/j.camwa.2010.12.003

CrossRef Full Text | Google Scholar

10. Bayat M, Bayat M, Kia M, Ahmadi HR, Pakar I. Nonlinear frequency analysis of beams resting on elastic foundation using max-min approach. Geomech Eng (2018) 16:355–61. doi:10.12989/gae.2018.16.4.355

CrossRef Full Text | Google Scholar

11. Liu YQ, He JH. On relationship between two ancient Chinese algorithms and their application to flash evaporation. Results Phys (2017) 7:320–2. doi:10.1016/j.rinp.2016.12.047

CrossRef Full Text | Google Scholar

12. He JH. An elementary introduction to recently developed asymptotic methods and nanomechanics in textile engineering. Int J Mod Phys (2008) 22:3487–578. doi:10.1142/s0217979208048668

CrossRef Full Text | Google Scholar

13. Liu P. The traditional academy of mathematics at the fenglong mountain of China. Math Intell (2021) 43:45–9. doi:10.1007/s00283-021-10080-y

CrossRef Full Text | Google Scholar

14. Saito K. Re-examination of the different origins of the arithmetical books of Euclid’s Elements. Hist Math (2019) 47:39–53. doi:10.1016/j.hm.2019.03.002

CrossRef Full Text | Google Scholar

15. Kline M Mathematical Thought from ancient to modern times, 6. New York, NY, USA: Oxford University Press (1972).

Google Scholar

16. Eves H. An Introduction to the history of mathematics. 5th ed., 7. New York, NY, USA: CBS College Publishing (1983).

Google Scholar

17. Eves H. Great moments in mathematics. New York, NY, USA: The Mathematical Association of America (1983).

Google Scholar

18. He JH. An old Babylonian algorithm and its modern applications. Symmetry (2024) 16:1467. doi:10.3390/sym16111467

CrossRef Full Text | Google Scholar

19. He CH. A simple analytical approach to a nonlinear equation arising in porous catalyst. Int J Numer Methods Heat Fluid Flow (2017) 27:861–6. doi:10.1108/hff-03-2016-0129

CrossRef Full Text | Google Scholar

20. Feng GQ, Zhang L, Tang W. Fractal pull-in motion of electrostatic MEMS resonators by the variational iteration method. Fractals (2023) 31. doi:10.1142/S0218348X23501220

CrossRef Full Text | Google Scholar

21. He JH. Periodic solution of a micro-electromechanical system. Facta Univ Ser Mech Eng (2024) 22:187–98. doi:10.22190/fume240603034h

CrossRef Full Text | Google Scholar

22. Yang Q. A mathematical control for the pseudo-pull-in stability arising in a micro-electromechanical system. J Low Freq Noise Vib Act Control (2023) 42:927–34. doi:10.1177/14613484221133603

CrossRef Full Text | Google Scholar

23. Friberg J. Geometric division problems, quadratic equations, and recursive geometric algorithms in Mesopotamian mathematics. Arch Hist Exact Sci (2014) 68:1–34. doi:10.1007/s00407-013-0122-4

CrossRef Full Text | Google Scholar

24. Ilic S, Petkovic MS, Herceg D. A note on Babylonian square root algorithm and related variants. Novi Sad J Math (1996) 26:155–62.

Google Scholar

25. Tian D, He CH, He JH. Fractal pull-in stability theory for microelectromechanical systems. Front Phys (2021) 9. doi:10.3389/fphy.2021.606011

CrossRef Full Text | Google Scholar

26. He CH. A variational principle for a fractal nano/microelectromechanical (N/MEMS) system. Int J Numer Methods Heat Fluid Flow (2022) 33:351–9. doi:10.1108/HFF-03-2022-0191

CrossRef Full Text | Google Scholar

27. He JH, Qie N, He CH, Gepreel K. Fast identification of the pull-in voltage of a nano/micro-electromechanical system. J Low Frequency Noise, Vibration Active Control (2022) 41(2):566–71. doi:10.1177/14613484211068252

CrossRef Full Text | Google Scholar

28. He JH, He CH, Qian MY, Alsolami AA. Piezoelectric Biosensor based on ultrasensitive MEMS system. Sens Actuators A Phys (2024) 376:115664. doi:10.1016/j.sna.2024.115664

CrossRef Full Text | Google Scholar

29. Zhang YN, Tian D, Pang J. A fast estimation of the frequency property of the microelectromechanical system oscillator. J Low Freq Noise Vib Act Control (2022) 41:160–6. doi:10.1177/14613484211051837

CrossRef Full Text | Google Scholar

30. Lv G. Dynamic behaviors for the graphene nano/microelectromechanical system in a fractal space. J Low Freq Noise Vib Act Control (2023) 42:1107–16. doi:10.1177/14613484231162657

CrossRef Full Text | Google Scholar

31. Faghidian SA, Tounsi A. Dynamic characteristics of mixture uniffed gradient elastic nanobeams. Facta Univ Ser Mech Eng (2022) 20:539–52. doi:10.22190/fume220703035f

CrossRef Full Text | Google Scholar

32. He JH, El-Dib YO. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int J Mod Phys B (2021) 35(24):2150244. doi:10.1142/S0217979221502441

CrossRef Full Text | Google Scholar

33. He JH, El-Dib YO. The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer Methods Partial Differential Equations (2020) 37:1800–8. doi:10.1002/num.22609

CrossRef Full Text | Google Scholar

34. He JH, El-Dib YO. Homotopy perturbation method with three expansions. J Math Chem (2021) 59:1139–50. doi:10.1007/s10910-021-01237-3

CrossRef Full Text | Google Scholar

35. Lyu GJ, He JH, He CH, Sedighi HM Straightforward method for nonlinear oscillators. J Donghua Univ (English Edition) (2023) 40(1):105–9. doi:10.19884/j.1672-5220.202112008

CrossRef Full Text | Google Scholar

36. He JH, Kou SJ, He CH, Zhang ZW, Gepreel KA. Fractal oscillation and its frequency-amplitude property. Fractals (2021) 29(4):2150105. doi:10.1142/s0218348x2150105x

CrossRef Full Text | Google Scholar

37. Shen Y. The Lagrange interpolation for He’s frequency formulation. J Low Frequency Noise Vibration Active Control (2021) 40(3):1387–91. doi:10.1177/1461348420972824

CrossRef Full Text | Google Scholar

38. Mohammadian M. Application of He’s new frequency-amplitude formulation for the nonlinear oscillators by introducing a new trend for determining the location points. Chin J Phys (2024) 89:1024–40. doi:10.1016/j.cjph.2024.03.047

CrossRef Full Text | Google Scholar