Dynamics analysis of epidemic spreading with individual heterogeneous infection thresholds

In the real world, individuals may become infected with an epidemic after multiple exposures to the corresponding virus. This occurs because each individual possesses certain physical defenses and immune capabilities at the time of exposure to the virus. Repeated exposure to the virus can lead to a decline in immune competence, consequently resulting in epidemic infection. The susceptibility of individuals to an epidemic is heterogeneous. We model this characteristic as the individual heterogeneous infection threshold. Then, we propose an individual logarithmic-like infection threshold function on a single-layer complex network to reflect the heterogeneity of individual susceptibility on infecting the virus and the associated epidemic. Next, we introduce a partition theory based on the edge and logarithmic-like infection threshold function to qualitatively analyze the mechanisms of virus infection and epidemic spreading. Finally, simulation results on Erdő–Rényi (ER) and scale-free (SF) networks indicate that increasing both the epidemic infection initial threshold and outbreak threshold, as well as decreasing the virus and epidemic infection probability, can all effectively suppress epidemic spreading and epidemic infection outbreak. With an increase in the epidemic infection outbreak threshold, the increasing pattern of the final epidemic infection scale transitions from a second-order continuous phase transition to a first-order discontinuous phase transition. Additionally, degree distribution heterogeneity also significantly impacts the outbreak and spread of diseases. These findings provide valuable guidance for the formulation of immunization strategies.

1 Introduction

As early as 1760, Bernoulli proposes the first model for the spread of smallpox, marking the birth of transmission dynamics [1]. In 2001, Pastor-Satorras and Vespignani were the first to utilize complex networks to describe transmission pathways and explore the impact of network topology on epidemic spread, subsequently investigating its implications on transmission dynamics [2]. This work garners widespread attention from scholars domestically and internationally, signaling the emergence of complex network transmission dynamics. Virus infection and epidemic spreading is one of the primary research subjects within this field. In most real-world networks, common phenomena such as the spread of computer viruses and epidemics are interpreted through the lens of epidemic dynamics on complex networks [3–5]. The epidemic and infectious disease spreading not only affects public health but also leads to significant economic losses.

The study of epidemic spreading on complex networks primarily focuses on “simple” propagation, where the probability of epidemic infection remains constant across two consecutive contacts. Scholars have proposed several classic compartmental models tailored to different types of diseases, including the susceptible–infectious (SI) model, the susceptible–infectious–recovered (SIR) model, and the susceptible–infectious–susceptible (SIS) model [6]. [7] offered new perspectives for establishing a precise theoretical framework for spreading dynamics on complex networks by integrating the most commonly utilized theoretical methods which include mean-field [8], heterogeneous mean-field, quench mean-field [9], dynamical message-passing, link percolation, and pairwise approximation.

In the era of big data, we have more opportunities to access relevant data on human behavioral activities, including social activity data [10]. This authentic big data allow for a greater possibility of uncovering the true mechanisms behind epidemic and disease transmission [11]. Through the analysis of real-world data, researchers have discovered that human behavioral activities significantly influence epidemic and disease transmission [12]. Some scholars focus on accurately identifying the epidemic outbreak thresholds as these thresholds are crucial in many real-world scenarios. When the number of exposures an individual has to the virus reaches a certain threshold, the individual may become infected with the epidemic. The epidemic threshold represents the critical condition under which a system is in an active outbreak state [13]. A substantial amount of theoretical research has been conducted to predict the outbreak thresholds of SIR models [14–17].

In theoretical terms, accurately determining the epidemic infection outbreak thresholds can identify the critical conditions for the emergence of global large-scale epidemics [18]. It also significantly impacts the study of critical phenomena, including the determination of critical exponents [19]. In practical applications, epidemic infection outbreak thresholds can characterize the effectiveness of immunization strategies [20] and assist in identifying the optimal initial transmission source [21].

[22] utilized numerical computations based on the SIR epidemic model to relatively accurately predict the spread of COVID-19 and other pandemics. [23] employed time-varying networks to simulate the disease transmission process and proposed the most effective measures for controlling epidemic spread. [24] investigated the impact of vaccination on the dynamics of epidemic models, introducing a novel fractional-order discrete-time SIR epidemic model aimed at illustrating and quantifying the complex dynamics of the system. [25] considered the influence of individual and mass media information dissemination on epidemic spread, exploring the dynamic interactions between information transmission and susceptible-exposed-infectious-recovered (SEIR)-based epidemic spread. Additionally, unlike traditional information transmission, most current studies on epidemic spreading focus on “simple” propagation, i.e., a fixed infection threshold, overlooking the threshold heterogeneity [26–28].

From the factors discussed above, it is recognized that epidemic infection outbreak thresholds are critical in epidemic spreading, influencing not only the scale of outbreaks and their critical conditions but also providing effective guidance for the formulation of immunization strategies. Traditional studies on viral infection and epidemic transmission often assume that the probability of epidemic infection from two consecutive exposures is constant, suggesting that epidemic transmission lacks memory. Although this simplification facilitates the analysis of epidemic spread, it does not accurately reflect reality. In fact, human activities lead to a certain degree of memory and cumulative effects in the viruses and epidemic infections. As individuals are repeatedly exposed to the virus, the likelihood of epidemic infection outbreak increases.

Individuals possess certain physical defenses and immune capabilities. During initial exposure to the virus, factors such as the distance between individuals, the distribution of medical resources like masks, and variations in immune response may prevent the onset of disease. However, with an increasing number of viral exposures, individual immunity diminishes, significantly raising the probability of disease infection. Moreover, repeated epidemic infections can reduce sensitivity to the virus, leading to a diminishing marginal effect on the likelihood of developing the disease. Therefore, the individual susceptibility to infection epidemic is heterogeneous. Based on this understanding, we propose an individual heterogeneous infection threshold function, a logarithmic-like function, to explore the impact of individual characteristics on sensitivity to the virus and disease.

Based on the aforementioned motivations, we introduce a generalized SIR model on complex networks and propose an individual heterogeneous infection threshold function, a logarithmic-like function, to reflect the heterogeneity of individual susceptibility on infecting the virus and the associated disease. Furthermore, a partition theory based on the edge and individual heterogeneous infection threshold is proposed to theoretically analyze the dynamic processes of epidemic spreading. Finally, computer simulation results are presented to validate the findings of disease transmission, which align with the theoretical analysis. This study aims to leverage complex networks, computer simulations, and theoretical analyses to reveal the mechanisms and patterns of epidemic and disease transmission, thereby providing necessary theoretical support for early warning and control of epidemics and public sentiment. The rest of this paper is organized as follows: in Section 2, we build an epidemic spreading model with the individual heterogeneous infection threshold on complex networks. Section 3 exhibits an edge partition theory. In Section 4, the experimental results are discussed. Finally, Section 5 describes the conclusion.

2 Epidemic spreading model with individual heterogeneity

To investigate the impact of heterogeneity in individual susceptibility to infection epidemic on epidemic spreading mechanisms, we first construct two types of single-layer artificial complex network models, called the Erdő–Rényi (ER) networks [29] and the scale-free (SF) networks [30], for spreading dynamics. Each network has $N$ nodes which represent individuals and degree distribution $P(k)$. The edges depict the interactions between individuals. We then apply a generalized SIR model, where each node can exist in one of three potential states: the susceptible state (S-state), where individuals are at risk of disease infection; the infected state (I-state), where individuals have contracted the disease and can spread the corresponding virus to their S-state neighbors; and the recovered state (R-state), where individuals have recovered from the infection and are no longer able to transition to any other state for a certain period of time.

Let the probability of one S-state node successfully being infected by the virus after coming into contact with its I-state neighbor node be $\lambda$. We introduce the concept of accumulated received infections (ARIs) to describe the infection accumulative total number of one S-state node by the virus from its I-state neighbors. Let $n$ be the ARIs successfully received by the S-state node. Initially, $n_i=0$ for the S-state node $i$, i.e., the virus has not yet spread within the population. At each time step, each I-state node transmits the virus to its S-state neighbors with a transmission probability of $\lambda$ through the corresponding edge. If an S-state neighbor, denoted as node $i$, successfully receives the virus from an I-state node, the APIs of node $i$ increases by 1, that is, $n_i\to n_i+1$.

To investigate the impact of individual susceptibility heterogeneity to viruses and epidemic infection, an individual logarithmic-like infection threshold function, as shown in Figure 1, is proposed:

$y\left(x,a,b\right)=\left\{\begin{array}{cc}0,\hfill & 0\le x\le a,\hfill \\ \frac{\text{ln}\left(x+1\right)-\text{ln}\left(a+1\right)}{\text{ln}\left(b+1\right)-\text{ln}\left(a+1\right)},\hfill & a<x<b,\hfill \\ 1,\hfill & x\ge b,\hfill \end{array}\right.(1)$

where $a$ represents the virus and epidemic infection initial threshold, while $b$ denotes the epidemic infection outbreak threshold. The difference $\delta =b-a$ indicates the interval between the disease infection threshold outbreak and the initial threshold.

Figure 1

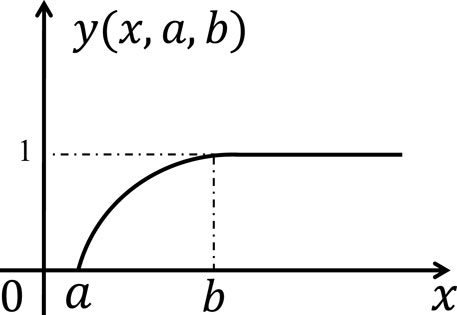
Figure 1. Illustration of the individual heterogeneous infection threshold model. The symbol $x$ represents APIs of an S-state node, $a$ represents the virus and epidemic infection initial threshold, and $b$ denotes the epidemic infection outbreak threshold.

Specifically, $a$ indicates that the S-state node is infected with a certain number of viruses from its I-state neighbors, indicating the likelihood of converting to an I-state, i.e., the disease breaks out with a certain probability. $\delta$ denotes the interval length of the disease spreading probability for the S-state node. $b$ indicates that the S-state node has received a sufficient quantity of viral infections from its I-state neighbors to make disease infection outbreak probability 1, that is, the probability that the S-state node infects epidemic and converts to I-state reaches 1. In other words, when the APIs of an S-state node are equal to or greater than $b$, the node will inevitably experience an epidemic infection outbreak and transition to the I-state.

The human body possesses immune capabilities and physical defenses. As individuals are exposed to the virus more frequently, the probability of epidemic infection outbreak increases. However, due to the increasing of APIs, individuals’ sensitivity to the virus decreases, leading to a diminishing marginal effect of epidemic infection. Therefore, the logarithmic-like infection threshold function for individual heterogeneous infection is relevant and meaningful.

Next, we summarize the process of virus and epidemic spreading within complex networks. Initially, a proportion ${\rho }_0$ of nodes is randomly selected to be infected with the epidemic, while the remaining nodes are in the S-state. S-state nodes may come into contact with I-state nodes and have a probability of $\lambda$ to contract the virus. As APIs of S-state nodes increase, the probability of an epidemic infection outbreak is $y(x,a,b)$. For I-state nodes, recovery occurs with a probability of $\gamma$ due to factors such as physical isolation, medical treatment, and immune enhancement, after which they are not susceptible to reinfection for a certain period. Ultimately, the epidemic spreading ceases when there are no longer any infections or diseases present in the network. The proportion of individuals in the R-state at this point characterizes the final scale of the epidemic transmission process.

3 The analysis of partition theory based on edge and individual heterogeneity

To better investigate the epidemic spreading process, we develop a partition theory incorporating edge and the epidemic infection outbreak thresholds to analyze the effect of the individual heterogeneity on epidemic spreading. In this approach, we assume that nodes with identical degrees are statistically equivalent. The variables $S(t)$, $I(t)$, and $R(t)$ are employed to derive the evolution of epidemic spreading and depict the proportions of nodes in the $S$, $I$, and $R$ states at time $t$, respectively. When $t\to \infty$, $R(\infty )$ is the final proportion of individuals in the complex network who have ever been infected by epidemic. Therefore, we can express the relationship as

$S\left(t\right)+I\left(t\right)+R\left(t\right)=1.(2)$

Let $\theta (t)$ be the probability that an S-state node has not been infected by the virus through a randomly chosen edge by time $t$. The probability that the S-state node $i$ of degree $k$ has $q$ APIs from its I-state neighbors up to time $t$ is

$\varphi \left(k_i,q,t\right)={\text{C}}_{k_i}^q\theta {\left(t\right)}^{k_i-q}{\left[1-\theta \left(t\right)\right]}^q.(3)$

By time $t$, the S-state node $i$ has been infected $q$-times virus from its I-state neighbors. The node $i$ does not experience an disease infection outbreak and remains in the S-state with the probability ${\prod }_{m=0}^q[1-y(m,a,b)]$.

According to the logarithmic threshold function for epidemic spreading, the probability that an S-state node $i$ has been infected by the virus $q$ times without experiencing a disease infection outbreak by time $t$ is

$\begin{array}{cc}\hfill s\left(k_i,q,t\right)& ={\displaystyle \sum _{q=0}^{\infty }}\varphi \left(k_i,q,t\right)\prod _{m=0}^q\left[1-y\left(m,a,b\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{q=0}^a}\varphi \left(k_i,q,t\right)+{\displaystyle \sum _{q=a+1}^{b-1}}\varphi \left(k_i,q,t\right)\prod _{m=a+1}^q\left(1-\frac{\text{ln}\left(m+1\right)-\text{ln}\left(a+1\right)}{\text{ln}\left(b+1\right)-\text{ln}\left(a+1\right)}\right)\hfill \\ \hfill & ={\displaystyle \sum _{q=0}^a}\varphi \left(k_i,q,t\right)+{\displaystyle \sum _{q=a}^{b-1}}\varphi \left(k_i,q,t\right)\prod _{m=a+1}^q\frac{\text{ln}\left(b+1\right)-\text{ln}\left(m+1\right)}{\text{ln}\left(b+1\right)-\text{ln}\left(a+1\right)}.\hfill \end{array}(4)$

The probability that the APIs of a randomly selected S-state nodes by time $t$ are less than the corresponding epidemic infection outbreak threshold is

$s\left(k,t\right)={\displaystyle \sum _{k_i}}P\left(k_i\right)s\left(k_i,q,t\right).(5)$

Therefore, at time $t$, a randomly selected individual is in S-state, i.e., the proportion of S-state nodes in the network is

$S\left(t\right)=\left(1-{\rho }_0\right)s\left(k,t\right).(6)$

Our goal is to solve for the three terms in Equation 2, specifically to derive the values of $S(t)$, $I(t)$, and $R(t)$. As indicated from Equations 3–6, it is necessary to calculate $\theta (t)$ in order to obtain the expression for $S(t)$. Consider the neighbor node $j$ of the I-state node $i$. The node $j$ can only be in one of three states: S-state, I-state, or R-state. Let ${\psi }_S(t)$, ${\psi }_I(t)$ and ${\psi }_R(t)$ represent the probabilities of node $j$ being in the S-state, I-state, and R-state, respectively. Additionally, $\theta (t)$ can be expressed as

$\theta \left(t\right)={\psi }_S\left(t\right)+{\psi }_I\left(t\right)+{\psi }_R\left(t\right).(7)$

Since node $i$ is in the S-state, its neighbor $j$ can only likely to be infected by the virus from the $k_j-1$ neighbors except node $i$. Therefore, the probability of node $j$ being infected by the virus $u$ times at time $t$ is denoted as

$\varphi \left(k_j-1,u,t\right)={\text{C}}_{k_j-1}^u\theta {\left(t\right)}^{k_j-1-u}{\left[1-\theta \left(t\right)\right]}^u.(8)$

According to the logarithmic threshold function for disease spreading, the probability that an S-state node $j$ has been infected by the virus $u$ times without experiencing a disease infection outbreak by time $t$ is

$\begin{array}{cc}\hfill \phi \left(k_j,t\right)& ={\displaystyle \sum _{u=0}^{\infty }}\varphi \left(k_j-1,u,t\right)\prod _{m=0}^u\left[1-y\left(u,a,b\right)\right]\hfill \\ \hfill & ={\displaystyle \sum _{u=0}^a}\varphi \left(k_i-1,u,t\right)+{\displaystyle \sum _{u=a+1}^{b-1}}\varphi \left(k_i-1,u,t\right)\prod _{m=a+1}^u\left(1-y\left(u,a,b\right)\right)\hfill \\ \hfill & ={\displaystyle \sum _{u=0}^a}\varphi \left(k_i-1,u,t\right)+{\displaystyle \sum _{u=a+1}^{b-1}}\varphi \left(k_i-1,u,t\right)\prod _{m=a+1}^u\frac{\text{ln}\left(b+1\right)-\text{ln}\left(m+1\right)}{\text{ln}\left(b+1\right)-\text{ln}\left(a+1\right)}.\hfill \end{array}(9)$

Let $⟨k⟩$ be the average degree of the network, the probability that node $i$ connects to node $j$ with degree $k_j$ is $k_{j}P(k_j)/⟨k⟩$. Therefore, the probability that the node $i$ connects to the S-state node $j$ with degree $k_j$ is

${\psi }_S\left(t\right)=\left(1-{\rho }_0\right)\frac{{\sum }_{k_j}{k}_{j}P\left(k_j\right)\phi \left(k_j,t\right)}{⟨k⟩}.(10)$

Due to variations in the distance between individuals, differences in individual immunity, and the protective measures taken by individuals, after the S-state node $i$ comes into contact with the I-state node $j$, the node $i$ has a probability of $\lambda$ to become infected by the virus. Thus, the variation in $\theta (t)$ can be expressed as

$\frac{d\theta \left(t\right)}{dt}=-\lambda {\psi }_I\left(t\right).(11)$

The I-state node has a probability of $\lambda$ to infect its neighbors and a probability of $\gamma$ to alter to the R-state. Therefore, the variation in ${\psi }_R(t)$ can be expressed as

$\frac{d{\psi }_R\left(t\right)}{dt}=\gamma \left(1-\lambda \right){\psi }_I\left(t\right).(12)$

Combining Equations 11, 12 and the initial conditions $\theta (0)=1$ and ${\psi }_R(0)=0$, we can obtain the evolution of ${\psi }_R(t)$:

${\psi }_R\left(t\right)=\gamma \left[1-\theta \left(t\right)\right]\left(\frac{1}{\lambda }-1\right).(13)$

Substituting Equation 10 and Equation 13 into Equation 7, we obtain

$\begin{array}{c}{\psi }_A\left(t\right)=\theta \left(t\right)-{\psi }_S\left(t\right)-{\psi }_R\left(t\right)=\theta \left(t\right)-\left(1-{\rho }_0\right)\frac{{\sum }_{k_j}{k}_{j}P\left(k_j\right)\phi \left(k_j,t\right)}{⟨k⟩}\hfill \\ \hfill & -\gamma \left[1-\theta \left(t\right)\right]\left(\frac{1}{\lambda }-1\right).\hfill \end{array}(14)$

Substituting Equation 14 into Equation 11, the evolution of $\theta (t)$ can be rewritten as

$\begin{array}{cc}\hfill \frac{d\theta \left(t\right)}{dt}& =-\lambda \left\{\theta \left(t\right)-\left(1-{\rho }_0\right)\frac{\sum _{k_j}{k}_{j}P\left(k_j\right)\phi \left(k_j,t\right)}{⟨k⟩}-\gamma \left[1-\theta \left(t\right)\right]\left(\frac{1}{\lambda }-1\right)\right\}\hfill \\ \hfill & =\left(1-{\rho }_0\right)\lambda \frac{\sum _{k_j}{k}_j{P}_X\left(k_j\right)\phi \left(k_j,t\right)}{⟨k⟩}+\gamma \left(1-\lambda \right)-\left[\lambda +\left(1-\lambda \right)\gamma \right]\theta \left(t\right).\hfill \end{array}(15)$

Throughout the network, we have the density variation of each state

$\frac{dA\left(t\right)}{dt}=-\frac{dS\left(t\right)}{dt}-\gamma A\left(t\right)(16)$

and

$\frac{dR\left(t\right)}{dt}=\gamma A\left(t\right).(17)$

Equations 2–6; Equations 15–17 provide a comprehensive description of the transmission dynamics of viruses and diseases. By combining and iterating these equations, the density of each state at arbitrary time step, i.e., the values of $S(t)$, $A(t)$, and $R(t)$, can be calculated.

As $t\to \infty$, there are no I-state nodes, leaving only S-state nodes and R-state nodes in the network. $R(\infty )$ is the epidemic infection outbreak scale. Let $\frac{d\theta (t)}{dt}{|}_{t=\infty }\to 0$. The viruses and disease propagation of the network reaches a steady state. We obtain

$\theta \left(\infty \right)=\frac{\left(1-{\rho }_0\right)\lambda \sum _{k_j}{k}_{j}P\left(k_j\right)\phi \left(k_j,\infty \right)+⟨k⟩\gamma \left(1-\lambda \right)}{⟨k⟩\gamma +\left(1-\gamma \right)\lambda ⟨k⟩}.(18)$

In epidemic spreading, the maximum value of the steady-state fixed point of Equation 18 is of paramount importance and is denoted by the critical probability point ${\theta }_c(\infty )$. By determining when the critical probability point appears, the crucial conditions under which an epidemic infection outbreak occurs can be derived by

$g\left[\theta \left(\infty \right),{\rho }_0,q,\gamma ,\lambda \right]=\frac{\left(1-{\rho }_0\right)\lambda \sum _{k}kP\left(k\right)\phi \left(k,\infty \right)}{⟨k⟩\gamma +\left(1-\gamma \right)\lambda ⟨k⟩}+\frac{\gamma \left(1-\lambda \right)}{\gamma +\left(1-\gamma \right)\lambda }-\theta \left(\infty \right)(19)$

and

$\frac{dg}{d\theta \left(\infty \right)}{|}_{{\theta }_c\left(\infty \right)}=0.(20)$

From Equation 20, the critical infection probability can be calculated as

${\lambda }_c=\frac{\gamma }{\epsilon +\gamma -1},(21)$

where

$\epsilon =\left(1-{\rho }_0\right)\frac{\sum _{k}kP\left(k\right)\phi \left(k_j,\infty \right){|}_{{\theta }_c\left(\infty \right)}}{⟨k⟩}.(22)$

Combining Equation 8 and Equation 9, we derive the expression of $\frac{d\phi (k_j,\infty )}{d\theta (\infty )}$. Numerically solving Equation 18, Equation 21, and $\frac{d\phi (k_j,\infty )}{d\theta (\infty )}$, we can obtain the critical value of the virus infection probability $\lambda$.

4 Results and discussions

Our paper focus on numerical experiments and theoretical analyses conducted on artificial ER networks and SF networks. The network size is $N=10^4$, with an average network degree of $⟨k⟩$ = 10. For I-state nodes, measures such as physical isolation, physical defense, medication, and immune enhancement are implemented, so let the recovery probability be $\gamma =1.0$. In ER networks, the degree distribution of nodes follows the Poisson distribution, i.e., $P(k)=e^{-⟨k⟩}\frac{{⟨k⟩}^k}{k!}$. In SF networks, the heterogeneity of node degree distribution is negatively correlated with the degree exponent $v$, with the heterogeneity decreasing as the degree exponent $v$ increases. The degree distribution of nodes follows the power-law distribution $P(k)=\xi k^{-v}$, where $\xi =1/{\sum }_k{k}^{-v}$. The minimum and maximum degree are $k_{\mathit{min}}=4$ and $k_{\mathit{max}}\sim 100$, respectively. Our simulation results are the average value by running the simulation 1,000 times.

We use the relative variance $\mathcal{V}$ [31, 32] to illustrate the critical infection probability and critical conditions. The relative variance is

$\mathcal{V}=N\frac{⟨R{\left(\infty \right)}^2⟩-{⟨R\left(\infty \right)⟩}^2}{⟨R\left(\infty \right)⟩},(23)$

where $⟨\cdots ⟩$ represents the ensemble average. The peak values of the relative variance represent the critical point of global epidemic spreading.

4.1 The epidemic spreading on the ER network

Figure 2A indicates that when $a=1$, an increase in $\delta$ slows down the spread of the virus and the epidemic infection outbreak. The outbreak scale exhibits a first-order discontinuous phase transition. Figure 2B reveals that for the same $\delta$, when $a=0$, the epidemic outbreak scale corresponds to a second-order continuous phase transition. As $a$ increases from 0 to 1, there is a significant suppression of virus transmission and epidemic infection outbreak, with the final epidemic infection outbreak scale transitioning from a second-order continuous phase transition to a first-order discontinuous phase transition. Similarly, an increase in $\delta$ also mitigates the outbreak of the epidemic. Overall, increasing $a$ and $\delta$, as well as decreasing $\lambda$, can all effectively suppress the epidemic outbreak. Furthermore, Figures 2C, D display the relative variances of the theoretical analyses and the critical infection probabilities corresponding to (a) and (b), respectively. At the critical point, a phase transition occurs, leading to a global disease infection state. Our theoretical predictions (lines) align well with the simulation results (symbols).

Figure 2

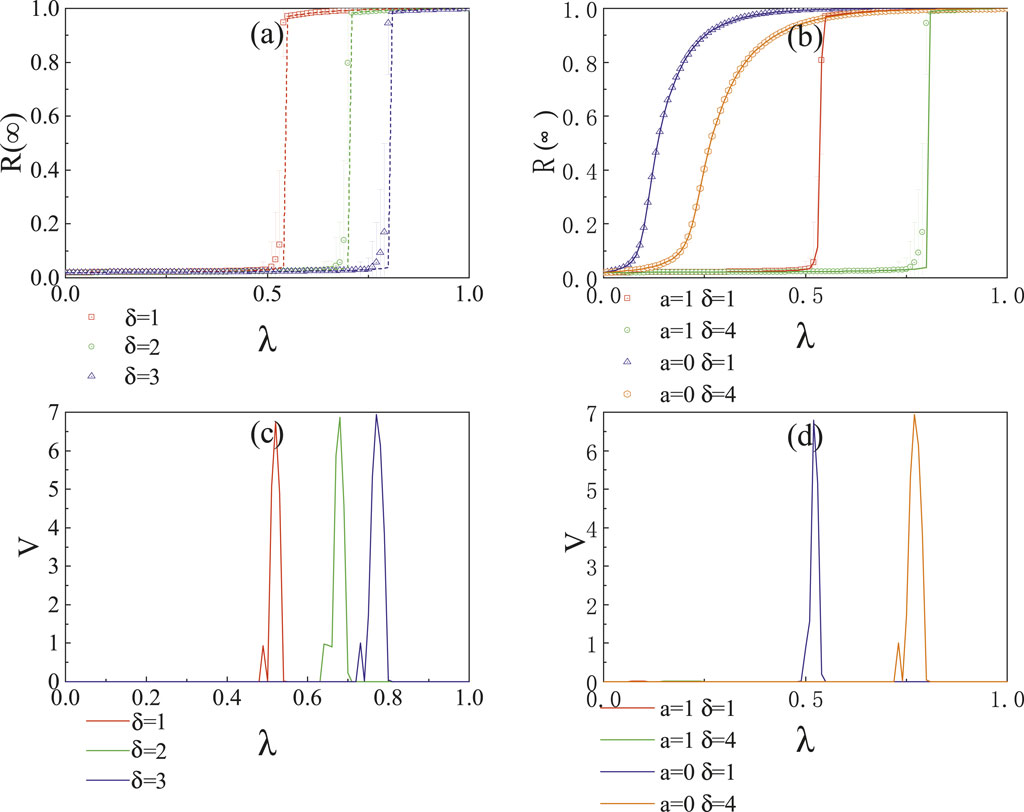
Figure 2. In the ER network, the impact of the infection probability $\lambda$ on the final size $R(\infty )$ of the viral and epidemic outbreak with different $a$ and $\delta$. (A) illustrates the effect of $\delta$ on $R(\infty )$ when $a=1$. (B) Combined effects of $a$ and $\delta$ on $R(\infty )$. The number of seeds is set to 200. Symbols represent the simulation results, while the curves depict the theoretical results.

Figure 3A shows the influence of the infection probability $\lambda$ on the final epidemic outbreak size $R(\infty )$ when $a=0$. As $\lambda$ increases, the virus and disease spread more rapidly through the network, ultimately leading to a global epidemic infection outbreak. An increase in the epidemic infection outbreak threshold parameter $b$ suppresses the occurrence of the disease. When $b$ is small, the epidemic infection outbreak size exhibits second-order continuous phase transition. As $b$ increases, the epidemic infection outbreak size transitions from a second-order continuous phase transition to a first-order discontinuous phase transition. Figure 3B illustrates the effect of $b$ on the final epidemic infection outbreak size $R(\infty )$ when $a=0$. With increasing $b$, the epidemic outbreak threshold becomes significantly higher, greatly reducing the likelihood of an epidemic outbreak. When $\lambda$ is small, even a small $b$ can effectively suppress the outbreak. However, when $\lambda$ is large, variations in $b$ become less effective in preventing the outbreak. Therefore, a combined approach of reducing $\lambda$ and increasing $b$ is necessary to effectively suppress the epidemic. Additionally, our theoretical predictions (lines) align well with the simulation results (symbols).

Figure 3

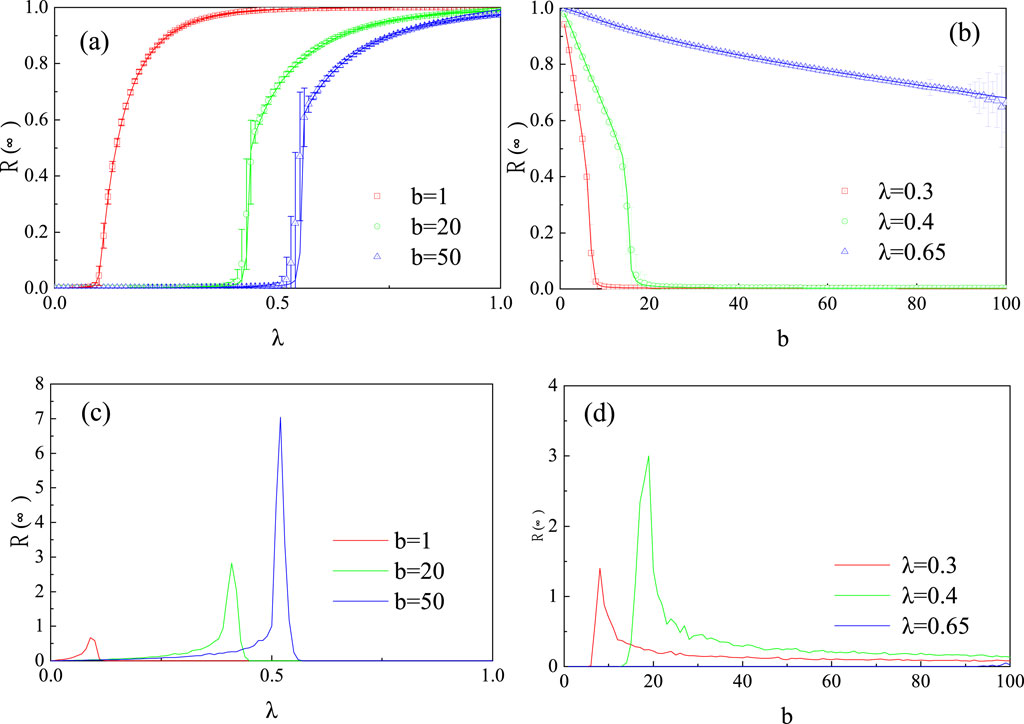
Figure 3. In the ER network, (A) illustrates the influence of the infection probability $\lambda$ on the final epidemic outbreak size $R(\infty )$ when $a=0$. (B) depicts the effect of the epidemic outbreak threshold parameter $b$ on $R(\infty )$ under the same condition of $a=0$. ${\rho }_0=0.0001$. Symbols represent simulation results, while curves denote theoretical predictions.

Figure 4 illustrates the joint effects of the infection probability $\lambda$ and the epidemic infection outbreak threshold parameter $b$ on the final scale of the epidemic outbreak $R(\infty )$. As shown in the figure, with an increase in $\lambda$, individuals become more susceptible to infection, leading to a gradual rise in the number of infected individuals, ultimately resulting in a global individual infection. Conversely, as $b$ increases, the epidemic infection threshold probability decreases, resulting in a reduction in the number of individuals infected. Additionally, as $b$ increases, a crossover phenomenon emerges in the trend of the graphical representation. The parameter space $(b,\lambda )$ can be divided into two regions. In Region I, as $\lambda$ increases, the increasing pattern of $R(\infty )$ exhibits characteristics of a second-order continuous phase transition. In Region II, as $\lambda$ increases, the pattern of increase in $R(\infty )$ displays traits of a first-order discontinuous phase transition.

Figure 4

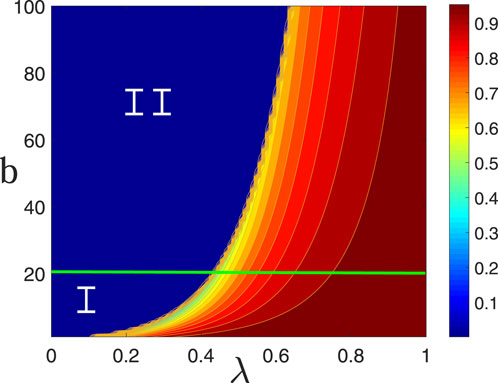
Figure 4. Joint effects of the infection probability $\lambda$ and the epidemic outbreak threshold parameter $b$ on the final outbreak size $R(\infty )$ in an ER network, with other parameters $a=0$ and ${\rho }_0=0.0001$.

4.2 The epidemic spreading on the SF network

Figure 5 illustrates the effect of the epidemic infection probability $\lambda$ on the final epidemic infection size $R(\infty )$ in scale-free networks characterized by heterogeneous degree distributions. The vertical subplots utilize the same degree distribution exponent, with the subplots in the first and second columns corresponding to $v=2.1$ and $v=4$, respectively. The initial seed density is set to ${\rho }_0=0.0001$. $a=0$. When $b$ is small, $R(\infty )$ gradually increases to global infection as $\lambda$ increases, exhibiting a second-order continuous phase transition in the growth pattern of the final epidemic infection size. However, larger values of $b$ suppress epidemic spreading. On one hand, epidemic spreading only occurs when $\lambda$ is sufficiently high. On the other hand, higher values of $b$ inhibit epidemic global epidemic infection and spreading. Furthermore, when $b$ is large, the growth pattern of the final epidemic size displays a weak first-order discontinuous phase transition. Additionally, increasing the heterogeneity of the degree distribution (i.e., by using smaller values of the degree distribution exponent) facilitates disease infection.

Figure 5

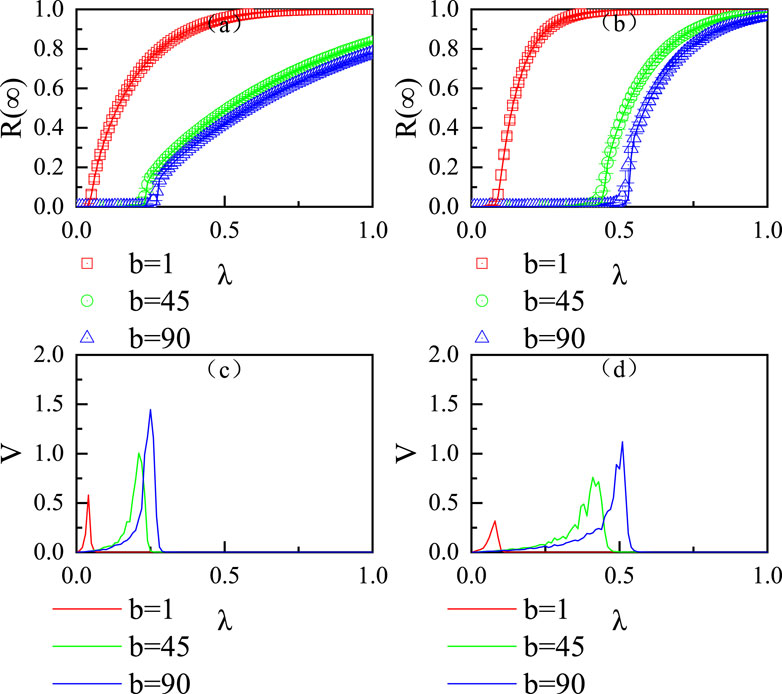
Figure 5. Influence of the virus infection probability $\lambda$ on the final epidemic infection size $R(\infty )$ in SF networks with different degree distributions $v$. Specifically, (A) $v=2.0$ and (B) $v=4.0$, with ${\rho }_0=0.0001$ and $a=0$.

Figure 6A, B explores the variation in the final epidemic infection size $R(\infty )$ in the epidemic spreading parameter space $(\lambda ,b)$ with $v=2.0$ and $v=4.0$, respectively. The initial seed fraction is set to ${\rho }_0=0.0001$. As the epidemic infection outbreak threshold parameter $b$ increases, the growth pattern of $R(\infty )$ exhibits a crossover phase transition. The epidemic spreading parameter space $(\lambda ,b)$ is divided into three regions. In Region I, the epidemic spreads globally and the growth pattern of $R(\infty )$ displays second-order continuous phase transition characteristics. In Region II, the growth pattern of $R(\infty )$ remains a second-order continuous phase transition; however, the epidemic spreads locally due to the suppression by $b$ on epidemic spreading. In Region III, the epidemic spreads locally and the growth pattern of $R(\infty )$ changes to a first-order discontinuous phase transition. Comparing (a) and (b), when $v$ is smaller, epidemic spreading begins with lower values of the virus infection probability $\lambda$ and the epidemic outbreak threshold parameter $b$, but it is challenging for the epidemic to achieve global spread. However, when $v$ is larger, the epidemic spreads within the population only when $\lambda$ and $b$ exceed certain thresholds. However, under the same parameters, the weak degree distribution heterogeneity facilitates the occurrence of global epidemic spreading.

Figure 6

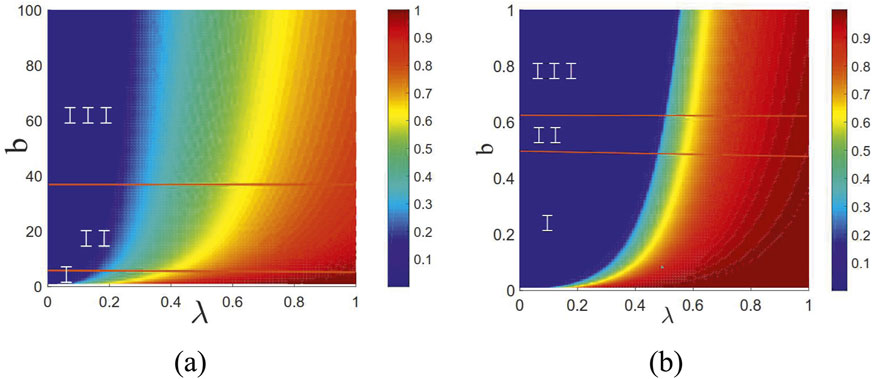
Figure 6. Joint effects of the virus infection probability $\lambda$ and the epidemic outbreak threshold parameter $b$ on the final epidemic size $R(\infty )$ in SF networks. Both scenarios of global epidemic infection outbreaks and localized epidemic infection outbreaks, as well as continuous and discontinuous phase transitions, are observed in (A) $(v=2.0)$ and (B) $(v=4.0)$. The other parameters are set to $a=0$ and ${\rho }_0=0.0001$.

5 Conclusion

This paper considers the heterogeneity of individual susceptibility to infection epidemic and employs transmission dynamics to investigate the epidemic spreading process on single-layer complex networks. First, we propose a logarithmic-like threshold model and thoroughly examine its validity under the heterogeneity of individual infection epidemic susceptibility. Subsequently, we enhance the edge partition theory based on the individual logarithmic-like threshold function to analyze the epidemic spreading dynamic process. Through theoretical analysis and numerical simulations on ER and SF networks, we identify the factors influencing the scale of disease outbreaks and propose several strategies for mitigating epidemic spread.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FL: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author would like to thank the reviewers for their insightful comments on the manuscript as their remarks led to an improvement of the work.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bernoulli D. Essai d’une nouvelle analyse de la mortalit́e causée par la petite vérole et des avantages de l’inoculation pour la prévenir. Histoire de l’Acad., Roy Sci.(Paris) avec Mém (1760) 1–45. Available at: https://inria.hal.science/hal-04100467v1

Google Scholar

2. Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett (2001) 86:3200–3. doi:10.1103/physrevlett.86.3200

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/revmodphys.87.925

CrossRef Full Text | Google Scholar

4. Li Z, Zhu P, Zhao D, Deng Z, Wang Z. Suppression of epidemic spreading process on multiplex networks via active immunization. Chaos: An Interdiscip J Nonlinear Sci (2019) 29:073111. doi:10.1063/1.5093047

CrossRef Full Text | Google Scholar

5. Yan G, Chen G, Eidenbenz S, Li N. Malware propagation in online social networks: nature, dynamics, and defense implications. In: Proceedings of the 6th acm symposium on information, computer and communications security (2011). p. 196–206.

CrossRef Full Text | Google Scholar

6. Keeling MJ, Rohani P. Modeling infectious diseases in humans and animals. Princeton, NJ: Princeton university press (2011).

Google Scholar

7. Wang W, Tang M, Stanley HE, Braunstein LA. Unification of theoretical approaches for epidemic spreading on complex networks. Rep Prog Phys (2017) 80:036603. doi:10.1088/1361-6633/aa5398

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Li W, Xue X, Pan L, Lin T, Wang W. Competing spreading dynamics in simplicial complex. Appl Mathematics Comput (2022) 412:126595. doi:10.1016/j.amc.2021.126595

CrossRef Full Text | Google Scholar

9. Feng L, Zhao Q, Zhou C. Epidemic spreading in heterogeneous networks with recurrent mobility patterns. Phys Rev E (2020) 102:022306. doi:10.1103/physreve.102.022306

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chun H, Kwak H, Eom YH, Ahn YY, Moon S, Jeong H. Comparison of online social relations in volume vs interaction: a case study of cyworld. In: Proceedings of the 8th ACM SIGCOMM conference on Internet measurement (2008). p. 57–70.

CrossRef Full Text | Google Scholar

11. Zhang N, Yang Q, Zhu X. The impact of social resource allocation on epidemic transmission in complex networks. Appl Mathematics Comput (2022) 433:127405. doi:10.1016/j.amc.2022.127405

CrossRef Full Text | Google Scholar

12. Gonzalez MC, Hidalgo CA, Barabasi AL. Understanding individual human mobility patterns. nature (2008) 453:779–82. doi:10.1038/nature06958

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Moreno Y, Pastor-Satorras R, Vespignani A. Epidemic outbreaks in complex heterogeneous networks. The Eur Phys J B-Condensed Matter Complex Syst (2002) 26:521–9. doi:10.1140/epjb/e20020122

CrossRef Full Text | Google Scholar

14. Zhu X, Wang Y, Zhang N, Yang H, Wang W. Influence of heterogeneity of infection thresholds on epidemic spreading with neighbor resource supporting. Chaos: An Interdiscip J Nonlinear Sci (2022) 32:083124. doi:10.1063/5.0098328

CrossRef Full Text | Google Scholar

15. Basnarkov L, Tomovski I, Sandev T, Kocarev L. Non-markovian sir epidemic spreading model of covid-19. Chaos, Solitons and Fractals (2022) 160:112286. doi:10.1016/j.chaos.2022.112286

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kabir KA, Kuga K, Tanimoto J. Analysis of sir epidemic model with information spreading of awareness. Chaos, Solitons and Fractals (2019) 119:118–25. doi:10.1016/j.chaos.2018.12.017

CrossRef Full Text | Google Scholar

17. Yavuz M, Özdemir N. Analysis of an epidemic spreading model with exponential decay law. Math Sci Appl E-Notes (2020) 8:142–54. doi:10.36753/mathenot.691638

CrossRef Full Text | Google Scholar

18. Dorogovtsev SN, Goltsev AV, Mendes JF. Critical phenomena in complex networks. Rev Mod Phys (2008) 80:1275–335. doi:10.1103/revmodphys.80.1275

CrossRef Full Text | Google Scholar

19. Mata AS, Boguñá M, Castellano C, Pastor-Satorras R. Lifespan method as a tool to study criticality in absorbing-state phase transitions. Phys Rev E (2015) 91:052117. doi:10.1103/physreve.91.052117

CrossRef Full Text | Google Scholar

20. Cohen R, Havlin S, Ben-Avraham D. Efficient immunization strategies for computer networks and populations. Phys Rev Lett (2003) 91:247901. doi:10.1103/physrevlett.91.247901

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kitsak M, Gallos LK, Havlin S, Liljeros F, Muchnik L, Stanley HE, et al. Identification of influential spreaders in complex networks. Nat Phys (2010) 6:888–93. doi:10.1038/nphys1746

CrossRef Full Text | Google Scholar

22. Marinov TT, Marinova RS. Dynamics of covid-19 using inverse problem for coefficient identification in sir epidemic models. Chaos, Solitons and Fractals (2020) 5:100041. doi:10.1016/j.csfx.2020.100041

CrossRef Full Text | Google Scholar

23. Rizi AK, Faqeeh A, Badie-Modiri A, Kivelä M. Epidemic spreading and digital contact tracing: effects of heterogeneous mixing and quarantine failures. Phys Rev E (2022) 105:044313. doi:10.1103/physreve.105.044313

PubMed Abstract | CrossRef Full Text | Google Scholar

24. He ZY, Abbes A, Jahanshahi H, Alotaibi ND, Wang Y. Fractional-order discrete-time sir epidemic model with vaccination: chaos and complexity. Mathematics (2022) 10:165. doi:10.3390/math10020165

CrossRef Full Text | Google Scholar

25. Ma W, Zhang P, Zhao X, Xue L. The coupled dynamics of information dissemination and seir-based epidemic spreading in multiplex networks. Physica A: Stat Mech its Appl (2022) 588:126558. doi:10.1016/j.physa.2021.126558

CrossRef Full Text | Google Scholar

26. Li Z, Xiong F, Wang X, Chen H, Xiong X. Topological influence-aware recommendation on social networks. Complexity (2019) 2019:6325654. doi:10.1155/2019/6325654

CrossRef Full Text | Google Scholar

27. Hu Y, Xiong F, Pan S, Xiong X, Wang L, Chen H. Bayesian personalized ranking based on multiple-layer neighborhoods. Inf Sci (2021) 542:156–76. doi:10.1016/j.ins.2020.06.067

CrossRef Full Text | Google Scholar

28. Yang Q, Zhu X, Tian Y, Wang G, Zhang Y, Chen L. The influence of heterogeneity of adoption thresholds on limited information spreading. Appl Mathematics Comput (2021) 411:126448. doi:10.1016/j.amc.2021.126448

CrossRef Full Text | Google Scholar

29. Erdos P, Rényi A, et al. On the evolution of random graphs. Publ Math Inst Hung Acad Sci (1960) 5:17–60. Available at: https://api.semanticscholar.org/CorpusID:18045682

Google Scholar

30. Catanzaro M, Boguná M, Pastor-Satorras R. Generation of uncorrelated random scale-free networks. Phys Rev E (2005) 71:027103. doi:10.1103/physreve.71.027103

CrossRef Full Text | Google Scholar

31. Shu P, Wei W, Ming T, Do Y. Numerical identification of epidemic thresholds for susceptible-infected-recovered model on finite-size networks. Chaos (2015) 25:063104. doi:10.1063/1.4922153

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Chen X, Wang W, Cai S, Eugene SH, Braunstein LA. Optimal resource diffusion for suppressing disease spreading in multiplex networks. J Stat Mech Theor Exp (2018) 5:053501. doi:10.1088/1742-5468/aabfcc

CrossRef Full Text | Google Scholar