- 1MOE Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, School of Physics, Xi’an Jiaotong University, Xi’an, Shaanxi, China
- 2Texas Materials Institute, The University of Texas at Austin, Austin, TX, United States
Spin-glass thin films exhibit many features different from the bulk. The freezing temperatures of spin-glass films are suppressed for reduced thickness and follow the Kenning relation. The dynamics are altered near the vacuum interface. These phenomena are closely related to the lower critical dimension of spin glasses, the spin-glass correlation length, and the dimensional crossover from
1 Introduction
Spin glasses [1] with random spin orientations yet strong correlations have motivated theoretical developments [2] to understand their emergent complexities and continue to spur new findings in complex systems [3]. After more than half a century of intensive efforts to uncover the physics of spin-glass dynamics, controversies remain. A consensus regarding the density of ground states and the stability of the spin-glass phase [4, 5] in an external field is still lacking.
Finite-size effects of spin glasses, first reported by the pioneering work of Kenning, Slaughter, and Cowen [6], offer a new route to uncover some of their mysteries. A surge of research interest in spin-glass thin films focuses on the dimensional crossover from
2 The freezing temperature and dimensional crossover: experiments
The freezing temperature
The time dependence of
The technical difficulty of extracting
as proposed in the real-space droplet (domain) model, where
Because
Equation 3 is difficult to test experimentally, as an accurate estimation of
An alternative interpretation of the freezing temperature was given in [12]:
where
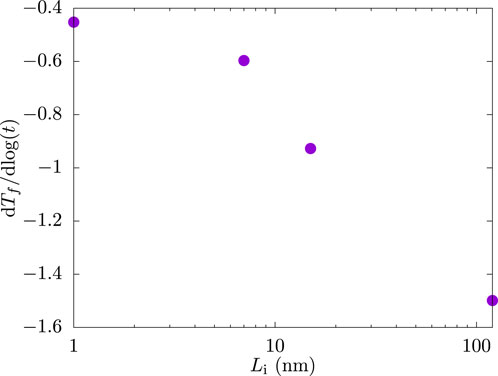
Figure 1 exhibits data for
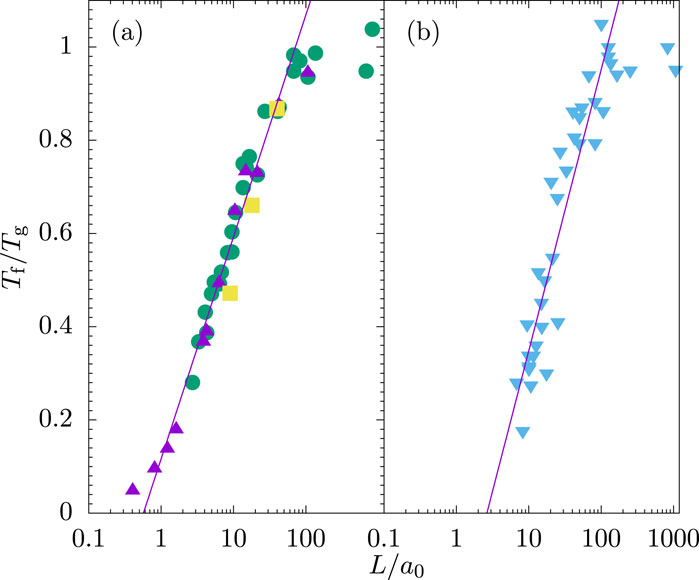
Figure 1.
Because the lower critical dimension
Additional support for the dimensional crossover of spin-glass thin films was obtained through polarized neutron reflectometry (PNR) [19, 20]. An asymmetry parameter
was measured for AuFe thin films, where
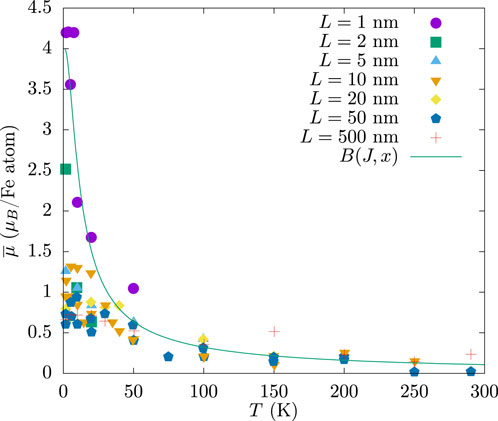
Figure 2. Averaged magnetic moment per Fe atom for AuFe films of different thickness
Below 50 K,
These measurements were performed in a very high magnetic field of 6 T. In large fields, the measured moment should correspond to a quasi-equilibrium spin-glass phase. Therefore, at large observation times and for ultra-thin film, Equation 4 implies a
According to calculations based on an Ising model, an A-T line [21] exists for the
3 Correlation length growth and dimensional crossover: simulations
It has been shown through Monte Carlo (MC) simulations and finite-size scaling [23–27] that the correlation length
Of particular interest is the aging dynamics of
where
where
which leads to a logarithmic scaling. The spatial correlation is calculated through Equation 10,
and the correlation length at
The growth of
However, Equation 12 naturally leads to the scaling form of Equation 8 when assuming
A twelve-time-decade MC simulation of the Ising EA model was carried out by Fernandez et al. [13]. They clarified growth dynamics for
where
The first MC simulation for dimensional crossover in a thin film geometry, comparable to experiments, was carried out by Victor Martin-Mayor and his coworkers [14]. The protocol used in this simulation closely resembled that of experiments: The sample was quenched to a working temperature, and the complete growth process (from nonequilibrium to equilibrium) of the correlation length was monitored. The correlation length is related to the autocorrelation function of Equation 14,
where
The estimator for the correlation length is given by Equation 15
Again, they found a power-law growth of the correlation length
Four time regimes were identified, with different
Further analysis leads to a scaling function,
where
The mapping given by Equation 17 is remarkable in that an effective temperature can allow for treating the
4 Interfacial effects on spin freezing
Much of our understanding of dimensional crossover in thin films arises from multilayers of spin-glass films separated by non-magnetic metallic or insulating layers. It is natural to ask whether the interface between the spin-glass layers and the decoupling layers leads to artificial or unwanted effects. For example, as illustrated in Figure 1, the
The first systematic study to address the effects of the decoupling layers was conducted by Granberg et al. [9]. They varied the thickness of Cu layers,
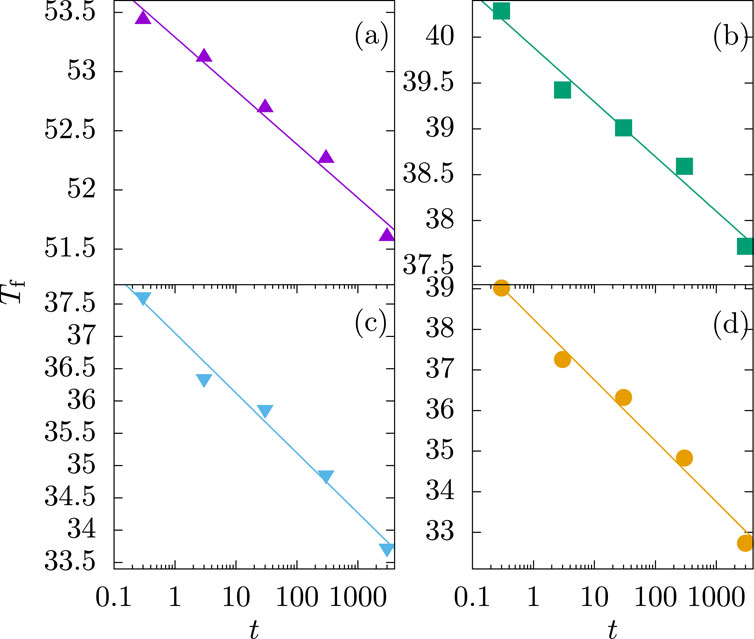
Figure 3. The freezing temperature decreases logarithmically with observation time
An explanation for the behaviors exhibited in Figures 3, 4 was given in [12]. For a given observation time, the inequality of Equation 18,
holds for
A direct probe of the surface dynamics has been carried out by depth-dependent muon-spin-relaxation (
where
The muons are assumed to take random interstitial sites in the sample and do not diffuse in the lattice. For a CuMn (1 at%) sample, the atomic dipolar field (
Taking into account the static random local fields and their fluctuation, a stochastic theory of muon-spin-relaxation for
where
where the brackets represent thermal averages, and the bar indicates spatial averages. Each spin
Therefore, the order parameter
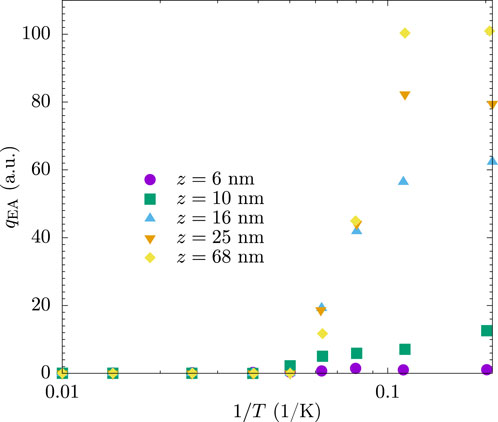
Figure 5. Self-overlap parameter,
Recent
5 Conclusion
We have examined the evidence for dimensional crossover from
Although much has been understood concerning the dynamics of thin film spin-glasses, in our opinion, a few questions remain to be addressed:
(1) In the low-temperature regime of the spin-glass phase, the dynamics become too slow to be probed by magnetometry and simulations. The validity of the Kenning relation remains to be tested with novel experimental protocols or data analyses.
(2) Both the vacuum and Si interfaces alter the spin-freezing process. It remains unknown how the interface affects the spin correlations. A theoretical treatment of the interfacial effects would not only contribute to a deeper understanding of spin-glass physics but also would benefit devices utilizing junctions between spin-glasses and other magnetic ordering materials [43, 44].
Author contributions
QZ: writing–original draft and writing–review and editing. RO: writing–original draft and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. QZ was supported by China Postdoc Fund Grant No. 2022M722548, Shaanxi NSF Grant No. 2023-JC-QN-0018, and Central University Basis Research Fund Grant No. xzy012023044. RO was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Division of Materials Science and Engineering, under Award No. DE-SC0013599.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Cannella V, Mydosh JA. Magnetic ordering in gold-iron alloys. Phys Rev B (1972) 6:4220–37. doi:10.1103/PhysRevB.6.4220
2. Mézard M, Parisi G, Virasoro MA. Spin glass theory and beyond: an introduction to the replica method and its applications, 9. World Scientific Publishing Company (1987).
3. Charbonneau P, Marinari E, Parisi G, Ricci-tersenghi F, Sicuro G, Zamponi F, et al. Spin glass theory and far beyond: replica symmetry breaking after 40 years. World Scientific (2023). doi:10.1142/13341
4. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Nature of the spin-glass phase. Phys Rev Lett (1984) 52:1156–9. doi:10.1103/PhysRevLett.52.1156
5. Fisher DS, Huse DA. Ordered phase of short-range ising spin-glasses. Phys Rev Lett (1986) 56:1601–4. doi:10.1103/PhysRevLett.56.1601
6. Kenning GG, Slaughter JM, Cowen JA. Finite-size effects in a cumn spin-glass. Phys Rev Lett (1987) 59:2596–9. doi:10.1103/PhysRevLett.59.2596
7. Sandlund L, Granberg P, Lundgren L, Nordblad P, Svedlindh P, Cowen JA, et al. Dynamics of cu-mn spin-glass films. Phys Rev B (1989) 40:869–72. doi:10.1103/PhysRevB.40.869
8. Granberg P, Nordblad P, Svedlindh P, Lundgren L, Stubi R, Kenning G, et al. Dimensionality crossover in cumn spin-glass films. J Appl Phys (1990) 67:5252–4. doi:10.1063/1.344627
9. Granberg P, Mattsson J, Nordblad P, Lundgren L, Stubi R, Bass J, et al. Dynamics of coupled two-dimensional cu(mn) spin-glass films. Phys Rev B (1991) 44:4410–4. doi:10.1103/PhysRevB.44.4410
10. Wood G. The spin glass correlation length and the crossover from three to two dimensions. J magnetism Magn Mater (2010) 322:1775–8. doi:10.1016/j.jmmm.2009.12.028
11. Guchhait S, Orbach R. Direct dynamical evidence for the spin glass lower critical dimension 2 ≤ dl ≤ 3. Phys Rev Lett (2014) 112:126401. doi:10.1103/PhysRevLett.112.126401
12. Zhai Q, Harrison DC, Tennant D, Dahlberg ED, Kenning GG, Orbach RL. Glassy dynamics in cumn thin-film multilayers. Phys Rev B (2017) 95:054304. doi:10.1103/PhysRevB.95.054304
13. Fernandez LA, Marinari E, Martin-Mayor V, Parisi G, Ruiz-Lorenzo JJ. An experiment-oriented analysis of 2d spin-glass dynamics: a twelve time-decades scaling study. J Phys A: Math Theor (2019) 52:224002. doi:10.1088/1751-8121/ab1364
14. Fernandez LA, Marinari E, Martin-Mayor V, Paga I, Ruiz-Lorenzo JJ. Dimensional crossover in the aging dynamics of spin glasses in a film geometry. Phys Rev B (2019) 100:184412. doi:10.1103/PhysRevB.100.184412
15. Fisher DS, Huse DA. Static and dynamic behavior of spin-glass films. Phys Rev B (1987) 36:8937–40. doi:10.1103/PhysRevB.36.8937
16. Kenning GG, Bass J, Pratt WP, Leslie-Pelecky D, Hoines L, Leach W, et al. Finite-size effects in cu-mn spin glasses. Phys Rev B (1990) 42:2393–415. doi:10.1103/PhysRevB.42.2393
17. Hoines L, Stubi R, Loloee R, Cowen JA, Bass J. How thin a spin glass is still a spin glass? Phys Rev Lett (1991) 66:1224–7. doi:10.1103/PhysRevLett.66.1224
18. Boettcher S. Stiffness of the edwards-anderson model in all dimensions. Phys Rev Lett (2005) 95:197205. doi:10.1103/PhysRevLett.95.197205
19. Saoudi M, Fritzsche H, Nieuwenhuys GJ, Hesselberth MBS. Size effect in the spin glass magnetization of thin aufe films as studied by polarized neutron reflectometry. Phys Rev Lett (2008) 100:057204. doi:10.1103/PhysRevLett.100.057204
20. Fritzsche H, van der Knaap JM, Hesselberth MBS, Nieuwenhuys GJ. Loss of spin glass behavior in ultrathin aufe films. Phys Rev B (2010) 81:132402. doi:10.1103/PhysRevB.81.132402
21. de Almeida J, Thouless D. Stability of the sherrington-kirkpatrick solution of a spin glass model. J Phys A: Math Gen (1978) 11:983–90. doi:10.1088/0305-4470/11/5/028
22. Young AP, Katzgraber HG. Absence of an almeida-thouless line in three-dimensional spin glasses. Phys Rev Lett (2004) 93:207203. doi:10.1103/PhysRevLett.93.207203
23. Palassini M, Caracciolo S. Universal finite-size scaling functions in the 3d ising spin glass. Phys Rev Lett (1999) 82:5128–31. doi:10.1103/PhysRevLett.82.5128
24. Ballesteros HG, Cruz A, Fernández LA, Martín-Mayor V, Pech J, Ruiz-Lorenzo JJ, et al. Critical behavior of the three-dimensional ising spin glass. Phys Rev B (2000) 62:14237–45. doi:10.1103/PhysRevB.62.14237
25. Katzgraber HG, Körner M, Young AP. Universality in three-dimensional ising spin glasses: a Monte Carlo study. Phys Rev B (2006) 73:224432. doi:10.1103/PhysRevB.73.224432
26. Hasenbusch M, Pelissetto A, Vicari E. Critical behavior of three-dimensional ising spin glass models. Phys Rev B (2008) 78:214205. doi:10.1103/PhysRevB.78.214205
27. Baity-Jesi M, Baños RA, Cruz A, Fernandez LA, Gil-Narvion JM, Gordillo-Guerrero A, et al. Critical parameters of the three-dimensional ising spin glass. Phys Rev B (2013) 88:224416. doi:10.1103/PhysRevB.88.224416
28. Fernandez LA, Martin-Mayor V, Perez-Gaviro S, Tarancon A, Young AP. Phase transition in the three dimensional heisenberg spin glass: finite-size scaling analysis. Phys Rev B (2009) 80:024422. doi:10.1103/PhysRevB.80.024422
29. Baity-Jesi M, Fernández LA, Martín-Mayor V, Sanz JM. Phase transition in three-dimensional heisenberg spin glasses with strong random anisotropies through a multi-gpu parallelization. Phys Rev B (2014) 89:014202. doi:10.1103/PhysRevB.89.014202
30. Morgenstern I, Binder K. Magnetic correlations in two-dimensional spin-glasses. Phys Rev B (1980) 22:288–303. doi:10.1103/PhysRevB.22.288
31. Kawamura H, Yonehara H. Ordering of the heisenberg spin glass in two dimensions. J Phys A: Math Gen (2003) 36:10867–80. doi:10.1088/0305-4470/36/43/013
32. Rieger H, Steckemetz B, Schreckenberg M. Aging and domain growth in the two-dimensional ising spin glass model. Europhysics Lett (1994) 27:485–90. doi:10.1209/0295-5075/27/6/013
33. Rieger H, Schehr G, Paul R. Growing length scales during aging in 2d disordered systems. Prog Theor Phys Suppl (2005) 157:111–9. doi:10.1143/ptps.157.111
34. Joh Y, Orbach R, Wood G, Hammann J, Vincent E. Extraction of the spin glass correlation length. Phys Rev Lett (1999) 82:438–41. doi:10.1103/physrevlett.82.438
35. Kasuya T. s–d and s–f interaction and rare earth metals. Magnetism, 2. Academic Press New York (1966). 215–94.
36. Morenzoni E, Luetkens H, Prokscha T, Suter A, Vongtragool S, Galli F, et al. Depth-dependent spin dynamics of canonical spin-glass films: a low-energy muon-spin-rotation study. Phys Rev Lett (2008) 100:147205. doi:10.1103/PhysRevLett.100.147205
37. Uemura YJ, Yamazaki T, Hayano RS, Nakai R, Huang CY. Zero-field spin relaxation of µ+ as a probe of the spin dynamics of AuFe and CuMn spin-glasses. Phys Rev Lett (1980) 45:583–7. doi:10.1103/PhysRevLett.45.583
38. Heffner R, Leon M, Schillaci M, MacLaughlin D, Dodds S. Muon spin relaxation studies of the spin glass agmn. J Appl Phys (1982) 53:2174–8. doi:10.1063/1.330771
39. Uemura YJ, Yamazaki T, Harshman DR, Senba M, Ansaldo EJ. Muon-spin relaxation in aufe and cumn spin glasses. Phys Rev B (1985) 31:546–63. doi:10.1103/PhysRevB.31.546
40. Edwards SF, Anderson PW. Theory of spin glasses. J Phys F: Metal Phys (1975) 5:965–74. doi:10.1088/0305-4608/5/5/017
41. Harrison DC, Dahlberg ED, Orbach RL. Effect of anisotropy on 1/f noise measurements of cumn spin glasses. Phys Rev B (2019) 100:064411. doi:10.1103/PhysRevB.100.064411
42. Harrison DC, Dahlberg ED, Orbach RL. Extraction of the spin-glass free-energy landscape from 1/f noise measurements. Phys Rev B (2022) 105:014413. doi:10.1103/PhysRevB.105.014413
43. Ali M, Adie P, Marrows CH, Greig D, Hickey BJ, Stamps RL. Exchange bias using a spin glass. Nat Mater (2007) 6:70–5. doi:10.1038/nmat1809
Keywords: spin glasses, dimensional crossover, freezing temperature, correlation length, interfacial effects
Citation: Zhai Q and Orbach RL (2024) Toward understanding the dimensional crossover of canonical spin-glass thin films. Front. Phys. 12:1488275. doi: 10.3389/fphy.2024.1488275
Received: 29 August 2024; Accepted: 07 October 2024;
Published: 05 November 2024.
Edited by:
Ralph Chamberlin, Arizona State University, United StatesReviewed by:
Aakansha, Banasthali University, IndiaCopyright © 2024 Zhai and Orbach. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Raymond L. Orbach, b3JiYWNoQHV0ZXhhcy5lZHU=
 Qiang Zhai
Qiang Zhai Raymond L. Orbach
Raymond L. Orbach