- 1Lawrence Livermore National Laboratory, Livermore, CA, United States
- 2Department of Physics, Washington University in St. Louis, St. Louis, MO, United States
An overview of neutron skin predictions obtained using an empirical nonlocal dispersive optical model (DOM) is presented. The DOM links both scattering and bound-state experimental data through a subtracted dispersion relation which allows for fully consistent, data-informed predictions for nuclei where such data exist. Large skins were predicted for both 48Ca (
1 Introduction
A fundamental question in nuclear physics is how the constituent neutrons and protons are distributed in the nucleus. In particular, for a nucleus which has a substantial excess of neutrons over protons, are the extra neutrons distributed evenly over the nuclear volume or are these excess neutrons localized in the periphery of the nucleus forming a neutron skin? A quantitative measure is provided by the neutron-skin thickness,
The nuclear symmetry energy, which characterizes the variation of the binding energy as a function of neutron–proton asymmetry, opposes the creation of nuclear matter with excesses of either type of nucleon. The extent of the neutron skin is determined by the relative strengths of the symmetry energy between the central near-saturation and peripheral less-dense regions. Therefore,
Given the rich physics packed in this observable, a large number of studies (both experimental and theoretical) have been devoted to determining neutron skins [8, 9]. Whereas
There currently exists no theory that predicts a thick skin in 208Pb and a thin skin in 48Ca. All theoretical studies of these nuclei based on a mean-field approach predict a strong, positive correlation between the neutron skins of 208Pb and 48Ca; however, it has been argued that the large error bars for PREX-2 may not provide a stringent constraint on the isovector part of energy density functionals [16]. Separate ab initio approaches exist for both nuclei. In Ref. [17], a neutron skin for 48Ca that is consistent with the CREX experiment was predicted, whereas the results of Refs. [18, 19] exhibit mild tension with the PREX-2 results. Furthermore, studies of the relation between neutron skins and the nuclear equation of state (EOS) conclude that these skins are tightly correlated with the slope of the symmetry energy,
In this article, we review an alternative theoretical method to predict
The underlying Green’s function ingredients of the single-particle propagator are presented in Section 2.1, whereas the DOM framework is introduced in Section 2.2. The DOM description of relevant experimental data for 48Ca and 208Pb is presented in Section 2.3. A discussion of the neutron skin results for these nuclei is given in Section 3. Conclusions and some outlook are presented in Section 4.
2 Theory
This section is organized to provide brief introductions into the underlying theory of the DOM.
2.1 Single-particle propagator
The single-particle propagator describes the probability amplitude for adding (removing) a particle in state
with
where
where the
where the
This expression assumes that the dominant contribution involves the two-nucleon interaction [28, 29] and the
To visualize the spectral function of Equation 3, it is useful to sum (or integrate) over the basis variables,
where
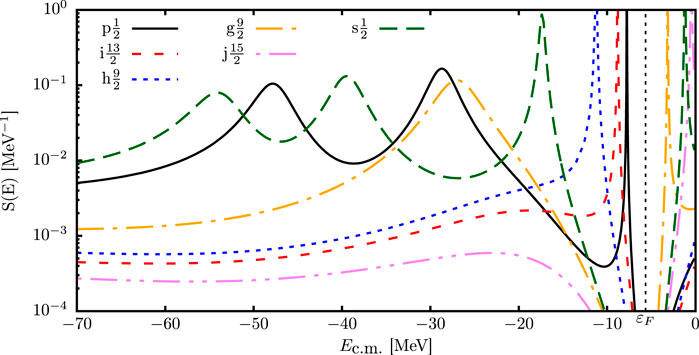
Figure 1. Neutron spectral functions of a representative set of
When solutions to Equation 6 are found near the Fermi energy where there is naturally no imaginary part of the self-energy, the normalization of the quasihole is well defined as the spectroscopic factor,
where
2.2 Dispersive optical model
The Dyson equation, Equation 2, simplifies the complicated task of calculating
where
2.2.1 Functional form of DOM self-energy
We employ a nonlocal representation of the self-energy following Ref. [22] where
where the Coulomb potential,
where
and
Nonlocality is introduced in a similar way for
where
As mentioned previously, it was customary in the past to replace nonlocal potentials by local, energy-dependent potentials [21, 24, 34, 43]. The introduction of an energy dependence alters the dispersive correction from Equation (9) and distorts the normalization, leading to incorrect spectral functions and related quantities [38]. Thus, a nonlocal implementation permits the self-energy to accurately reproduce important observables such as charge density, particle number, and ground-state binding energy.
2.3 DOM fits of 208Pb and 48Ca
To use the DOM self-energy for predictions, the parameters of the self-energy are constrained through weighted
When constraining the 48Ca self-energy, the isoscalar part is largely determined by the nearby
Proton reaction cross sections together with the DOM result are displayed in panel (a) of Figure 2. The neutron total cross section is shown in panel (b) of Figure 2. Both aggregate cross sections play an important role in determining volume integrals of the imaginary part of the self-energy, thereby providing strong constraints on the depletion of IPM orbits. The elastic differential cross sections of proton and neutrons up to 200 MeV are shown in panel (a) of Figure 3. Panel (b) contains the analyzing powers for neutrons and protons which strongly constrain the spin-orbit components of the self-energy.
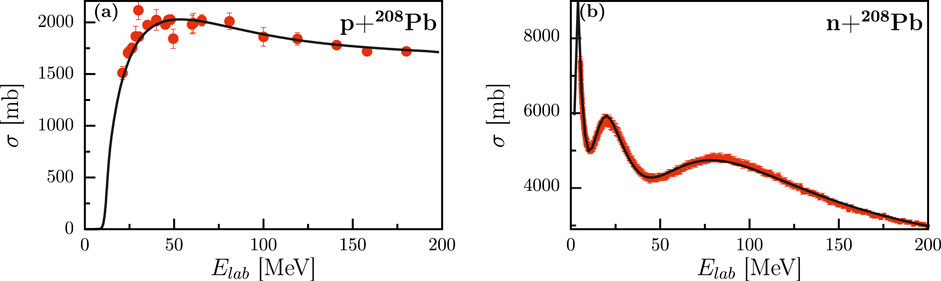
Figure 2. (A) Proton reaction cross section in 208Pb. The solid line is generated from the DOM self-energy, whereas the filled circles are from the experiment. (B) Neutron total cross section in 208Pb. The solid line is generated from the DOM self-energy for 208Pb, whereas the filled circles are from the experiment (see Ref. [37] for the experimental data. Figure adapted from Ref. [30]).
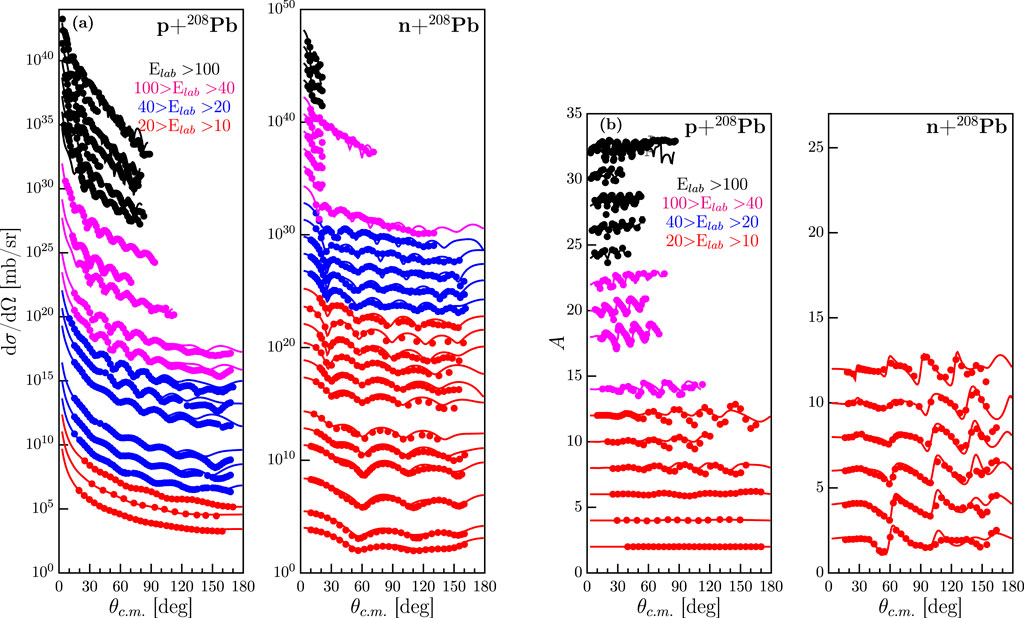
Figure 3. (A) Calculated and experimental proton and neutron elastic-scattering angular distributions of the differential cross section
The charge density of 208Pb is shown in panel (a) of Figure 4. The experimental band is extracted from elastic electron scattering differential cross sections [49]. This dataset is well reproduced after using the DOM charge density from Figure 4 as the ingredient in a relativistic elastic electron scattering code [52]. The corresponding elastic electron scattering cross section is shown in panel (b) of Figure 4 and compared to experiment with all available data transformed to electron energy of 502 MeV in the center-of-mass frame [51].
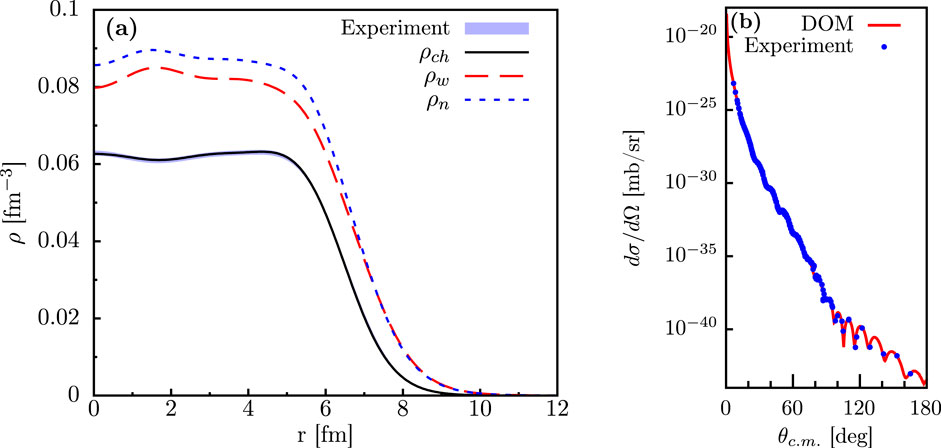
Figure 4. (A) Experimental and fitted 208Pb charge density. The solid black line is calculated using Equation 4 and folding with the proton charge distribution, whereas the experimental band represents the 1% error associated with the extracted charge density from elastic electron scattering experiments using the sum of Gaussians parametrization [49, 50]. Also shown is the deduced weak charge distribution,
In Figure 5, single-particle levels calculated using Equation 6 are compared to the experimental values for protons and neutrons in panels (a) and (b), respectively. The middle column consists of levels calculated using the full DOM and the right column contains the experimental levels. The first column of the figures represents a calculation using only the static part of the self-energy, corresponding to the Hartree–Fock (mean-field) contribution. It is clear from these level diagrams that the mean-field overestimates the particle-hole gap (see also Ref. [53]). The inclusion of the dynamic part of the self-energy is necessary to reduce this gap and properly describe the energy levels [21]. Furthermore, the effect of including the dynamic part of the self-energy on the proton levels is stronger than the effect on the neutron levels. This suggests that protons deviate more from the IPM than neutrons in 208Pb.
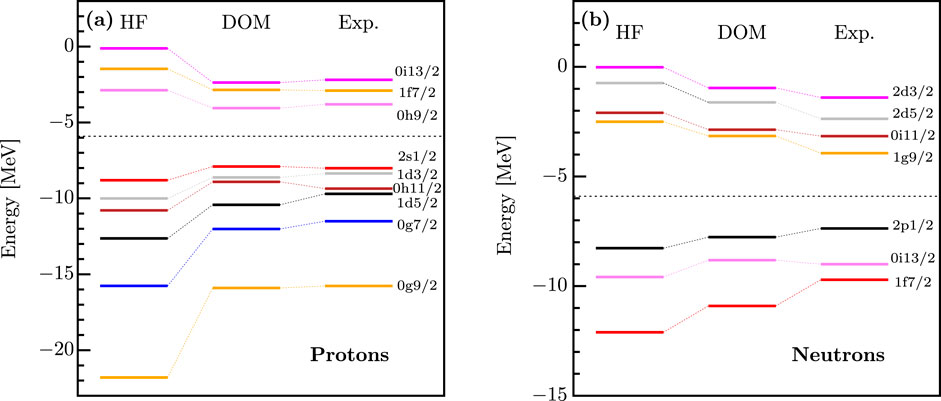
Figure 5. (A) Proton and (B) neutron energy levels in 208Pb. The energies on the left are calculated using only the static part of the DOM self-energy, corresponding to a Hartree–Fock calculation. The middle energies are those calculated using the full DOM self-energy. The energies on the right correspond to the experimental values. The change from the left energies to the middle energies is the result of including the dynamic part of the self-energy. Figure adapted from Ref. [30].
The number of neutrons and protons in the DOM fit of 208Pb, calculated by integrating Equation 4 using shells up to
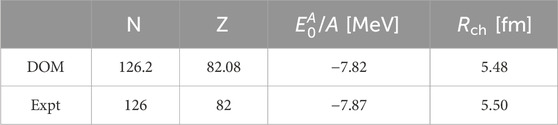
Table 1. Comparison of the calculated DOM particle numbers and binding energy of 208Pb and the corresponding experimental values. The experimental binding energy was taken from Ref. [54]. The experimental charge radius is from Ref. [49].
The reproduction of all available experimental data indicates that we have realistic self-energies of 208Pb and similarly for 48Ca [25, 32] capable of describing both bound-state and scattering processes. With these self-energies, we can therefore make predictions of observables such as the neutron skin. Additionally, a parallel DOM analysis of these and other nuclei was conducted using Markov Chain Monte Carlo (MCMC) to optimize the potential parameters employing the same experimental data and a very similar functional form but with a reduced number of parameters. All observables from this MCMC fit fell within one standard deviation of those presented above [55, 56].
2.4 DOM predictions
Spectroscopic factors come directly from the self-energy through Equation 8, making the DOM ideal for predicting
The valence spectroscopic factors in 208Pb are consistent with the observations of Ref. [58] and the interpretation of Ref. [59]. The past extraction of spectroscopic factors using the
Correlations can also be studied through the momentum distribution,
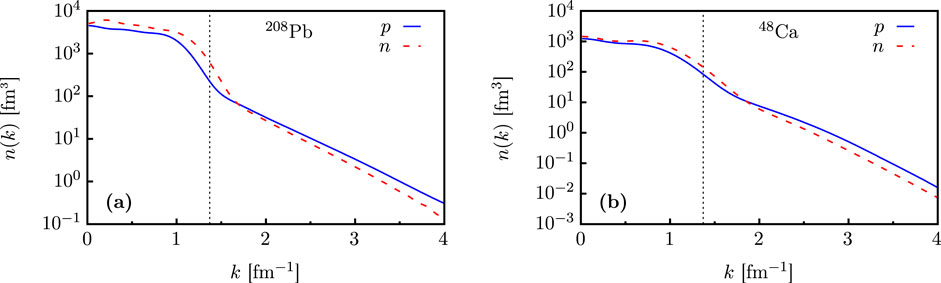
Figure 6. Comparison of calculated DOM momentum distributions of protons (solid blue line) and neutrons (dashed red line). The vertical dotted line marks the location of
In the DOM, this high-momentum content is determined by how much strength exists in the hole spectral function at large, negative energies. The hole spectral function is constrained in the fit by the particle number, binding energy, and charge density. Whereas the particle number and charge density can only constrain the total strength of the hole spectral function, the binding energy constrains how the strength of the spectral function is distributed in energy. This arises from the energy-weighted integral in Equation 5, which will push strength of the spectral function to more negative energies in order to achieve more binding. This, in turn, alters the momentum distribution, thus partially constraining the high-momentum content. It should be noted that the DOM does not exhibit the characteristic energy dependence of high-momentum strength distributions [71] as reported in Ref. [22]. Such a dependence is more difficult to be implemented as it requires abandoning the factorization of spatial and energy dependence of the DOM self-energy (see Equation 14).
3 Neutron skin
As demonstrated in the previous section, our constrained self-energies for 48Ca and 208Pb utilize both scattering and bound-state data for a robust picture of nuclei. These fits resulted in thick skins in both 48Ca,
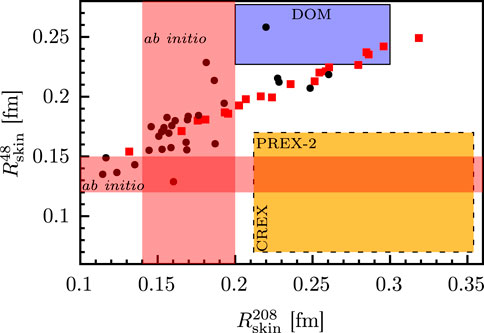
Figure 7. Dashed rectangle represents the CREX and PREX-2 analysis [73, 74]. The shaded rectangle labeled DOM represents the DOM results for 208Pb and 48Ca [25, 30]. Smaller squares and circles refer to relativistic and non-relativistic mean-field calculations, respectively, cited in Ref. [72]. The ab initio predictions from Ref. [17] for 48Ca and Refs. [18, 19] for 208Pb are represented by horizontal and vertical bands labeled ab initio, respectively. All uncertainties are reported at the
At the time of our calculations, CREX had not been reported and only the first PREX experiment with large uncertainty had been reported, meaning that there was not an easy metric to gauge the accuracy of our predictions. Therefore, we took advantage of the unique characteristic of the DOM to explore which measurements, in either the bound or scattering domains, provide signatures of the neutron skin. To accomplish this, additional 48Ca fits were performed in which selected values of
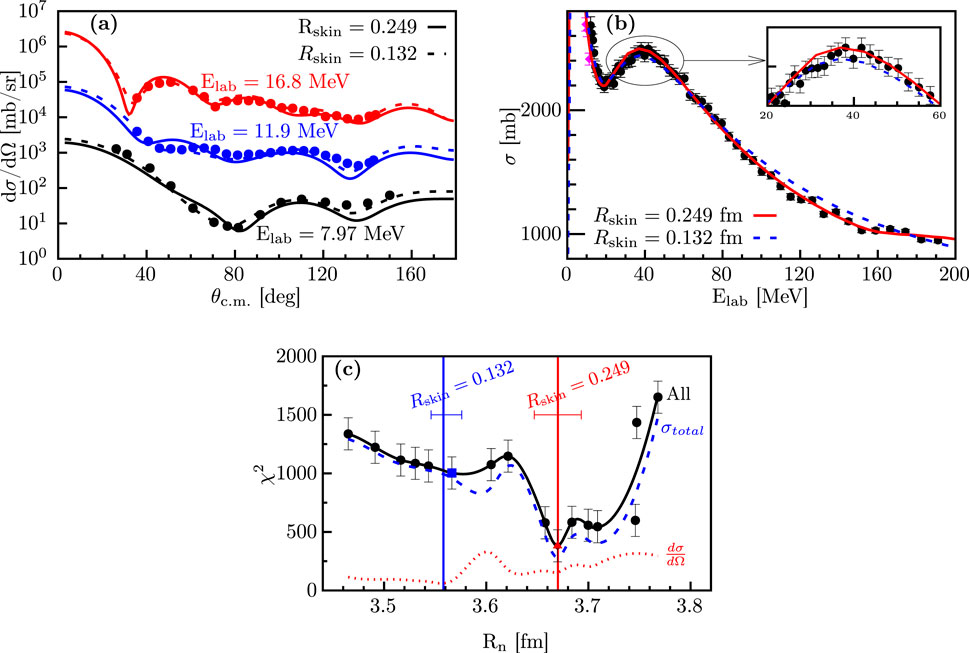
Figure 8. (A) Comparison of experimental
The location of the ab initio coupled-cluster result [17] is also indicated at
The total cross section exhibits larger sensitivity and the experimental data cover a large range of neutron energies (6–200 MeV). Two datasets are available (circles and diamonds in Figure 8B) but are inconsistent by
It appeared that the total cross section provided a strong constraint on the neutron skin (as an example of a scattering observable that can affect bound-state observables through the dispersion relation). Faced with the thin skin reported by CREX, it appears that we did not attribute enough uncertainty in the total cross-sectional data to allow a wider range of skin values. This concept will be explored in future DOM investigations of
Provided with a sufficiently complete set of data, which is the case for protons in 48Ca, the DOM framework allows for accurate predictions (see Sec. 2.4). The thin skin of CREX demonstrates that, unlike protons, there are not sufficient experimental data for neutrons in 48Ca to accurately predict the neutron skin. The number of proton elastic-scattering datasets at different energies shown for 208Pb in Figure 3 is representative of
To accommodate the thin skin extracted by CREX, one would expect the distribution of neutrons to favor a configuration with more neutrons in the interior of 48Ca. This concentration of neutrons near the origin implies an increase in the fraction of high-momentum neutrons, thanks to the Heisenberg uncertainty principle. This could lead to a larger percentage of high-momentum neutrons than protons, which would be a departure from the current DOM picture (see Figure 6) as well as from the evidence suggested by the CLAS experiments on other asymmetric nuclei. It could turn out that the size of 48Ca is inadequate to apply bulk nuclear properties to. We observed this in Ref. [28], where we consider the interiors of 48Ca and 208Pb as representing saturated nuclear matter. We found that the smaller size of 48Ca than that of 208Pb is harder to connect with saturated nuclear matter.
The neutron and proton point distributions in 208Pb and 48Ca, weighted by
where
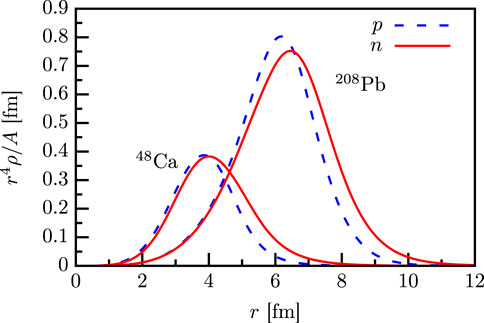
Figure 9. Neutron (red solid line) and proton (blue dashed line) point distributions in 208Pb and 48Ca weighted by
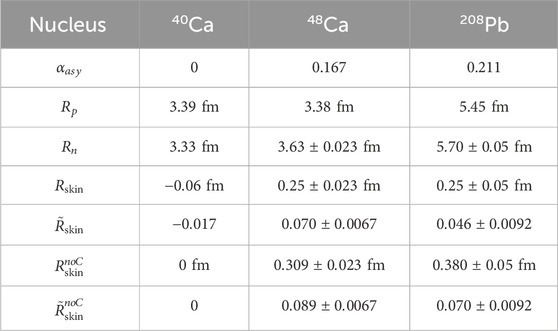
Table 2. DOM predicted neutron skins for 40Ca,48Ca, and208Pb. Also shown are the neutron skins normalized by
If one is to scale by the size of the nucleus, then the extension of the proton distribution due to Coulomb repulsion (which scales with the number of protons) should also be considered. As 208Pb has four times as many protons as 48Ca, the effect of Coulomb repulsion on the neutron skin of 208Pb could be up to four times more than its effect on the 48Ca neutron skin, which can reasonably be taken from the predicted skin of
4 Conclusion
We have reviewed a nonlocal dispersive optical-model analysis of 48Ca and 208Pb in which we fit elastic-scattering angular distributions, absorption and total cross sections, single-particle energies, charge densities, ground-state binding energies, and particle numbers. When sufficient data are available to constrain our self-energies, the DOM is capable of accurate predictions. With our well-constrained self-energies, we report non-negligible high-momentum content in both 48Ca and 208Pb, which is consistent with the experimental observations at JLAB [64, 65, 69]. Spectroscopic factors are automatically generated and reproduce 48Ca
To reproduce the reduced neutron RMS radius reported by CREX, we expect that the neutron distribution in 48Ca would shrink such that more neutrons concentrate in the interior of 48Ca. This redistribution would translate to increased high-momentum neutrons which could invert the hierarchy of the current DOM fit in which there is a higher percentage of high-momentum protons than neutrons (see Figure 6), counter to the evidence suggested by the CLAS experiments on other asymmetric nuclei [65, 69]. Currently, this is speculation, but we are exploring new DOM fits using CREX as an additional constraint so we can reach a better understanding. We must also consider the possibility that the size of 48Ca is inadequate for extracting/applying bulk nuclear properties. The shell-closure of the
The DOM analysis provides an alternative approach to the multitude of mean-field calculations that provide a large variety of results for the neutron skins of 48Ca and 208Pb [72] while also contrasting with the ab initio result of Ref. [17] for 48Ca and Refs. [18, 19] for 208Pb. The experiments employing parity-violating elastic electron scattering on these nuclei [14, 15] therefore remain the most unambiguous approach to determine the neutron skin. A systematic study of more nuclei with similar asymmetry,
Author contributions
MA: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. WD: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing–original draft, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 and was supported by the LLNL-LDRD Program under Project No. 24-LW-062. This work was also supported by the U.S. National Science Foundation under grants PHY-1912643 and PHY-2207756.
Acknowledgments
The authors acknowledge the important early contributions to this research from Bob Charity, Hossein Mahzoon, Cole Pruitt, and Lee Sobotka.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Typel S, Brown BA. Neutron radii and the neutron equation of state in relativistic models. Phys Rev C (2001) 64:027302. doi:10.1103/PhysRevC.64.027302
3. Steiner A, Prakash M, Lattimer J, Ellis P. Isospin asymmetry in nuclei and neutron stars. Phys Rep (2005) 411:325–75. doi:10.1016/j.physrep.2005.02.004
4. Roca-Maza X, Centelles M, Viñas X, Warda M. Neutron skin of 208Pb, nuclear symmetry energy, and the parity radius experiment. Phys Rev Lett (2011) 106:252501. doi:10.1103/PhysRevLett.106.252501
5. Horowitz CJ, Piekarewicz J. Neutron star structure and the neutron radius of 208pb. Phys Rev Lett (2001) 86:5647–50. doi:10.1103/PhysRevLett.86.5647
6. Steiner AW, Lattimer JM, Brown EF. The equation of state from observed masses and radii of neutron stars. The Astrophysical J (2010) 722:33–54. doi:10.1088/0004-637x/722/1/33
7. Li BA, Chen LW, Ko CM. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys Rep (2008) 464:113–281. doi:10.1016/j.physrep.2008.04.005
8. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C (2012) 86:015803. doi:10.1103/PhysRevC.86.015803
9. Mammei JM, Horowitz CJ, Piekarewicz J, Reed BT, Sfienti C. Neutron skins: weak elastic scattering and neutron stars. Annu Rev Nucl Part Sci (2024) 74:321–42. doi:10.1146/annurev-nucl-102122-024207
10. Angeli I, Marinova K. Table of experimental nuclear ground state charge radii: an update. At Data Nucl Data Tables (2013) 99:69–95. doi:10.1016/j.adt.2011.12.006
11. Garcia Ruiz RF, Bissell ML, Blaum K, Ekstrom A, Frommgen N, Hagen G, et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat Phys. (2016) 594–8. doi:10.1038/nphys3645
12. Horowitz CJ. Parity violating elastic electron scattering and coulomb distortions. Phys Rev C (1998) 57:3430–6. doi:10.1103/PhysRevC.57.3430
13. Abrahamyan S, Ahmed Z, Albataineh H, Aniol K, Armstrong DS, Armstrong W, et al. Measurement of the neutron radius of 208Pb through parity violation in electron scattering. Phys Rev Lett (2012) 108:112502. doi:10.1103/PhysRevLett.108.112502
14. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong D, Averett T, et al. Accurate determination of the neutron skin thickness of 208Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502
15. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong D, Averett T, et al. Precision determination of the neutral weak form factor of 48Ca. Phys Rev Lett (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501
16. Reinhard PG, Roca-Maza X, Nazarewicz W. Combined theoretical analysis of the parity-violating asymmetry for 48Ca and 208Pb. Phys Rev Lett (2022) 129:232501. doi:10.1103/PhysRevLett.129.232501
17. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the 48ca nucleus. Nat Phys (2016) 12:186–90. doi:10.1038/nphys3529
18. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Ab initio predictions link the neutron skin of 208pb to nuclear forces. Nat Phys (2022) 18:1196–200. doi:10.1038/s41567-022-01715-8
19. Hu B, Jiang W, Miyagi T, Sun Z, Ekström A, Forssén C, et al. Author correction: ab initio predictions link the neutron skin of 208pb to nuclear forces. Nat Phys (2024) 20:169. doi:10.1038/s41567-023-02324-9
20. Reed BT, Fattoyev FJ, Horowitz CJ, Piekarewicz J. Density dependence of the symmetry energy in the post–prex-crex era. Phys Rev C (2024) 109:035803. doi:10.1103/PhysRevC.109.035803
21. Mahaux C, Sartor R. Single-particle motion in nuclei. Boston, MA: Springer US (1991). p. 1–223. doi:10.1007/978-1-4613-9910-0_1
22. Mahzoon MH, Charity RJ, Dickhoff WH, Dussan H, Waldecker SJ. Forging the link between nuclear reactions and nuclear structure. Phys Rev Lett (2014) 112:162503. doi:10.1103/PhysRevLett.112.162503
23. Dickhoff WH, Charity RJ, Mahzoon MH. Novel applications of the dispersive optical model. J Phys G: Nucl Part Phys (2017) 44:033001. doi:10.1088/1361-6471/44/3/033001
25. Mahzoon MH, Atkinson MC, Charity RJ, Dickhoff WH. Neutron skin thickness of Ca48 from a nonlocal dispersive optical-model analysis. Phys Rev Lett (2017) 119:222503. doi:10.1103/PhysRevLett.119.222503
26. Descouvemont P, Baye D. The r -matrix theory. Rep Prog Phys (2010) 73:036301. doi:10.1088/0034-4885/73/3/036301
27. Atkinson MC. Developing nucleon self-energies to generate the ingredients for the description of nuclear reactions. Springer (2020).
28. Atkinson MC, Dickhoff WH, Piarulli M, Rios A, Wiringa RB. Reexamining the relation between the binding energy of finite nuclei and the equation of state of infinite nuclear matter. Phys Rev C (2020) 102:044333. doi:10.1103/PhysRevC.102.044333
29. Atkinson MC, Dickhoff WH, Piarulli M, Rios A, Wiringa RB. Reply to “comment on ‘reexamining the relation between the binding energy of finite nuclei and the equation of state of infinite nuclear matter’ ”. Phys Rev C (2021) 104:059802. doi:10.1103/PhysRevC.104.059802
30. Atkinson MC, Mahzoon MH, Keim MA, Bordelon BA, Pruitt CD, Charity RJ, et al. Dispersive optical model analysis of 208Pb generating a neutron-skin prediction beyond the mean field. Phys Rev C (2020) 101:044303. doi:10.1103/PhysRevC.101.044303
31. Atkinson MC, Blok HP, Lapikás L, Charity RJ, Dickhoff WH. Validity of the distorted-wave impulse-approximation description of Ca40(e,e′p)K39 data using only ingredients from a nonlocal dispersive optical model. Phys Rev C (2018) 98:044627. doi:10.1103/PhysRevC.98.044627
32. Atkinson MC, Dickhoff WH. Investigating the link between proton reaction cross sections and the quenching of proton spectroscopic factors in 48ca. Phys Lett B (2019) 798:135027. doi:10.1016/j.physletb.2019.135027
33. Bell JS, Squires EJ. A formal optical model. Phys Rev Lett (1959) 3:96–7. doi:10.1103/PhysRevLett.3.96
34. Perey F, Buck B. A non-local potential model for the scattering of neutrons by nuclei. Nucl Phys (1962) 32:353–80. doi:10.1016/0029-5582(62)90345-0
35. Charity RJ, Sobotka LG, Dickhoff WH. Asymmetry dependence of proton correlations. Phys Rev Lett (2006) 97:162503. doi:10.1103/PhysRevLett.97.162503
36. Charity RJ, Mueller JM, Sobotka LG, Dickhoff WH. Dispersive-optical-model analysis of the asymmetry dependence of correlations in ca isotopes. Phys Rev C (2007) 76:044314. doi:10.1103/PhysRevC.76.044314
37. Mueller JM, Charity RJ, Shane R, Sobotka LG, Waldecker SJ, Dickhoff WH, et al. Asymmetry dependence of nucleon correlations in spherical nuclei extracted from a dispersive-optical-model analysis. Phys Rev C (2011) 83:064605. doi:10.1103/PhysRevC.83.064605
38. Dickhoff WH, Van Neck D, Waldecker SJ, Charity RJ, Sobotka LG. Nonlocal extension of the dispersive optical model to describe data below the fermi energy. Phys Rev C (2010) 82:054306. doi:10.1103/PhysRevC.82.054306
39. Waldecker SJ, Barbieri C, Dickhoff WH. Microscopic self-energy calculations and dispersive optical-model potentials. Phys Rev C (2011) 84:034616. doi:10.1103/PhysRevC.84.034616
40. Dussan H, Waldecker SJ, Dickhoff WH, Müther H, Polls A. Microscopic self-energy of 40ca from the charge-dependent bonn potential. Phys Rev C (2011) 84:044319. doi:10.1103/PhysRevC.84.044319
41. Brida I, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of spectroscopic overlaps inA⩽7nuclei. Phys Rev C (2011) 84:024319. doi:10.1103/physrevc.84.024319
42. Lane AM. Isobaric spin dependence of the optical potential and quasi-elastic (p, n) reactions. Nucl Phys 35 (1962) 676. doi:10.1016/0029-5582(62)90153-0
43. Fiedeldey H. The equivalent local potential and the perey effect. Nucl Phys (1966) 77:149–56. doi:10.1016/0029-5582(66)90682-1
44. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in fortran 90. Cambridge University Press (1996).
45. Khoa DT, Than HS, Cuong DC. Folding model study of the isobaric analog excitation: isovector density dependence, lane potential, and nuclear symmetry energy. Phys Rev C (2007) 76:014603. doi:10.1103/PhysRevC.76.014603
46. Loc BM, Khoa DT, Zegers RGT. Charge-exchange scattering to the isobaric analog state at medium energies as a probe of the neutron skin. Phys Rev C (2014) 89:024317. doi:10.1103/PhysRevC.89.024317
47. Danielewicz P, Singh P, Lee J. Symmetry energy III: isovector skins. Nucl Phys A (2017) 958:147–86. doi:10.1016/j.nuclphysa.2016.11.008
48. Koning A, Delaroche J. Local and global nucleon optical models from 1 kev to 200 mev. Nucl Phys A (2003) 713:231–310. doi:10.1016/S0375-9474(02)01321-0
49. de Vries H, de Jager CW, de Vries C. Nuclear charge-density-distribution parameters from elastic electron scattering. Nucl Data Tables (1987) 36:495–536. doi:10.1016/0092-640x(87)90013-1
50. Sick I, Bellicard JB, Cavedon JM, Frois B, Huet M, Leconte P, et al. Charge density of 40Ca. Phys Lett B (1979) 88:245–8. doi:10.1016/0370-2693(79)90458-1
51. Frois B, Bellicard JB, Cavedon JM, Huet M, Leconte P, Ludeau P, et al. High-momentum-transfer electron scattering from 208Pb. Phys Rev Lett (1977) 38:152–5. doi:10.1103/PhysRevLett.38.152
52. Salvat F, Jablonski A, Powell CJ. Elsepa - Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Computer Phys Commun (2005) 165:157–90. doi:10.1016/j.cpc.2004.09.006
53. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys (2003) 75:121–80. doi:10.1103/RevModPhys.75.121
54. Wang M, Huang W, Kondev F, Audi G, Naimi S. The ame 2020 atomic mass evaluation (ii). tables, graphs and references. Chin Phys C (2021) 45:030003. doi:10.1088/1674-1137/abddaf
55. Pruitt CD, Charity RJ, Sobotka LG, Atkinson MC, Dickhoff WH. Systematic matter and binding-energy distributions from a dispersive optical model analysis. Phys Rev Lett (2020) 125:102501. doi:10.1103/PhysRevLett.125.102501
56. Pruitt CD, Charity RJ, Sobotka LG, Elson JM, Hoff DEM, Brown KW, et al. Isotopically resolved neutron total cross sections at intermediate energies. Phys Rev C (2020) 102:034601. doi:10.1103/PhysRevC.102.034601
57. Anderson BD, Bevington PR, Cverna FH, McNaughton MW, Willard HB, Barrett RJ, et al. Proton total reaction cross section measurements for 40,44,48Ca at 700 mev. Phys Rev C (1979) 19:905–12. doi:10.1103/PhysRevC.19.905
58. Lichtenstadt J, Heisenberg J, Papanicolas CN, Sargent CP, Courtemanche AN, McCarthy JS. High-spin states of Jπ = 12−, 14− in 208Pb studied by (e,e ′). Phys Rev C (1979) 20:497–503. doi:10.1103/PhysRevC.20.497
59. Pandharipande VR, Papanicolas CN, Wambach J. Occupation probabilities of shell-model orbits in the lead region. Phys Rev Lett (1984) 53:1133–6. doi:10.1103/PhysRevLett.53.1133
60. Sick I, de Witt Huberts PKA. Comm Nucl Part Phys (1991) 20:177. Available online at: https://inspirehep.net/literature/1406038
61. Quint ENM, van den Brand JFJ, den Herder JWA, Jans E, Keizer PHM, Lapikás L, et al. Relative 3s spectroscopic strength in 206Pb and 208Pb studied with the (e, e ′ p) knockout reaction. Phys Rev Lett (1986) 57:186–9. doi:10.1103/PhysRevLett.57.186
62. Quint ENM, Barnett BM, van den Berg AM, van den Brand JFJ, Clement H, Ent R, et al. Evidence for partial occupancy of the 3s1/2 proton orbit in 208Pb. Phys Rev Lett (1987) 58:1088–91. doi:10.1103/PhysRevLett.58.1088
64. Hen O, Miller GA, Piasetzky E, Weinstein LB. Nucleon-nucleon correlations, short-lived excitations, and the quarks within. Rev Mod Phys (2017) 89:045002. doi:10.1103/RevModPhys.89.045002
65. Egiyan KS, Dashyan NB, Sargsian MM, Strikman MI, Weinstein LB, Adams G, et al. Measurement of two- and three-nucleon short-range correlation probabilities in nuclei. Phys Rev Lett (2006) 96:082501. doi:10.1103/PhysRevLett.96.082501
66. Frick T, Müther H, Rios A, Polls A, Ramos A. Correlations in hot asymmetric nuclear matter. Phys Rev C (2005) 71:014313. doi:10.1103/PhysRevC.71.014313
67. Rios A, Polls A, Dickhoff WH. Depletion of the nuclear fermi sea. Phys Rev C (2009) 79:064308. doi:10.1103/PhysRevC.79.064308
68. Rios A, Polls A, Dickhoff WH. Density and isospin-asymmetry dependence of high-momentum components. Phys Rev C (2014) 89:044303. doi:10.1103/PhysRevC.89.044303
69. Duer M, Hen O, Piasetzky E, Hakobyan H, Weinstein LB, Braverman M, et al. Probing high-momentum protons and neutrons in neutron-rich nuclei. Nature (2018) 560:617–21. doi:10.1038/s41586-018-0400-z
70. Wiringa RB, Schiavilla R, Pieper SC, Carlson J. Nucleon and nucleon-pair momentum distributions in a ≤ 12 nuclei. Phys Rev C (2014) 89:024305. doi:10.1103/PhysRevC.89.024305
71. Rohe D, Armstrong CS, Asaturyan R, Baker OK, Bueltmann S, Carasco C, et al. Correlated strength in the nuclear spectral function. Phys Rev Lett (2004) 93:182501. doi:10.1103/PhysRevLett.93.182501
72. Horowitz CJ, Kumar KS, Michaels R. Electroweak measurements of neutron densities in CREX and PREX at JLab, USA. Eur Phys A (2014) 50:48. doi:10.1140/epja/i2014-14048-3
73. Adhikari D, Albataineh H, Androic D, Aniol KA, Armstrong DS, Averett T, et al. Precision determination of the neutral weak form factor of 48Ca. Phys Rev Lett (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501
74. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong DS, Averett T, et al. Accurate determination of the neutron skin thickness of 208Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502
75. Hicks SF, Hicks SE, Shen GR, McEllistrem MT. Collective doorway configurations in 49Ca through neutron scattering on 48Ca. Phys Rev C (1990) 41:2560–70. doi:10.1103/PhysRevC.41.2560
76. Harvey JA, Johnson CH, Carlton RF, Castel B. Single-particle 2d5/2 strength in the 48ca+n reaction. Phys Rev C (1985) 32:1114–7. doi:10.1103/PhysRevC.32.1114
77. Shane R, Charity R, Elson J, Sobotka L, Devlin M, Fotiades N, et al. Total neutron cross-sections for rare isotopes using a digital-signal-processing technique: case study 48ca. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2010) 614:468–74. doi:10.1016/j.nima.2010.01.005
Keywords: neutron skin, structure, reactions, optical potential, Green’s function
Citation: Atkinson MC and Dickhoff WH (2024) Neutron skins: A perspective from dispersive optical models. Front. Phys. 12:1487314. doi: 10.3389/fphy.2024.1487314
Received: 27 August 2024; Accepted: 30 September 2024;
Published: 28 October 2024.
Edited by:
Oscar Moreno, Complutense University of Madrid, SpainReviewed by:
Francesco Giovanni Celiberto, University of Alcalá, SpainShuichiro EBATA, Saitama University, Japan
Copyright © 2024 Atkinson and Dickhoff. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: M. C. Atkinson, bWFja2VuemllLmMuYXRraW5zb25AZ21haWwuY29t
 M. C. Atkinson
M. C. Atkinson W. H. Dickhoff2
W. H. Dickhoff2